2015-2016学年北师大版必修二 平行关系的性质学案word版
高中数学学案北师大版必修2 平行关系的性质 教案

教学设计5.2平行关系的性质导入新课思路1.(情境导入)三角板的一条边所在直线与桌面平行,这个三角板所在的平面与桌面平行吗?三角板的两条边所在直线分别与桌面平行,情况又如何呢?下面我们讨论平面与平面平行的性质问题.思路2.(直接导入)前面学习了平行关系的判定,本节我们学习平行关系的性质,教师点出课题.推进新课新知探究提出问题①回忆空间两条直线的位置关系.②若一条直线与一个平面平行,探究这条直线与平面内直线的位置关系.③用三种语言描述直线与平面平行的性质定理.④试证明直线与平面平行的性质定理.⑤应用线面平行的性质定理的关键是什么?⑥总结应用线面平行性质定理的要诀.活动:问题①引导学生回忆两条直线的位置关系.问题②借助模型锻炼学生的空间想象能力.问题③引导学生进行语言转换.问题④引导学生用排除法.问题⑤引导学生找出应用的难点.问题⑥鼓励学生总结,教师归纳.讨论结果:①空间两条直线的位置关系:相交、平行、异面.②若一条直线与一个平面平行,这条直线与平面内直线的位置关系不可能是相交(可用反证法证明),所以,该直线与平面内直线的位置关系还有两种,即平行或异面.怎样在平面内作一条直线与该直线平行呢(排除异面的情况)?经过这条直线的平面和这个平面相交,那么这条直线和交线平行.③直线与平面平行的性质定理用文字语言表示为:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.这个定理用符号语言可表示为:⎭⎪⎬⎪⎫a ∥αa ⊂ββ∩α=b ⇒a ∥b . 这个定理用图形语言可表示为:如图1.图1④已知a ∥α,a ⊂β,α∩β=b .求证:a ∥b.⑤应用线面平行的性质定理的关键是:过这条直线作一个平面.⑥应用线面平行性质定理的要诀:“见到线面平行,先过这条直线作一个平面找交线.” 提出问题①利用空间模型探究:如果两个平面平行,那么一个平面内的直线与另一个平面内的直线具有什么位置关系?②回忆线面平行的性质定理,结合模型探究线面平行的性质定理. ③用三种语言描述平面与平面平行的性质定理. ④应用面面平行的性质定理的难点在哪里? ⑤应用面面平行的性质定理口诀是什么?讨论结果:①如图2,借助长方体模型,我们看到,B ′D ′所在的平面A ′C ′与平面AC 平行,所以B ′D ′与平面AC 没有公共点.也就是说,B ′D ′与平面AC 内的所有直线没有公共点.因此,直线B ′D ′与平面AC 内的所有直线要么是异面直线,要么是平行直线.图2②直线与平面平行的性质定理用文字语言表示为:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.因为,直线B ′D ′与平面AC 内的所有直线要么是异面直线,要么是平行直线,只要过B ′D ′作平面BDD ′B ′与平面AC 相交于直线BD ,那么直线B ′D ′与直线BD 平行.如图3.图3③两个平面平行的性质定理用文字语言表示为:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.两个平面平行的性质定理用符号语言表示为:⎭⎪⎬⎪⎫α∥βα∩γ=a β∩γ=b ⇒a ∥b . 两个平面平行的性质定理用图形语言表示为:如图4.图4④应用面面平行的性质定理的难点是:过某些点或直线作一个平面.⑤应用面面平行性质定理的口诀:“见到面面平行,先过某些直线作两个平面的交线.”应用示例思路1例1 如图5,A ,B ,C ,D 在同一平面内,AB ∥平面α,AC ∥BD ,且AC ,BD 与α分别交于点C ,D ,求证:AC =BD.图5证明:连接CD .因为A ,B ,C ,D 在同一平面内,AB ∥平面α, 所以AB ∥CD .又因为AC ∥BD ,所以四边形ABCD 是平行四边形. 因此AC =BD .点评:已知线面平行时,常用到线面平行的性质定理. 变式训练已知AB ,CD 为异面线段,E ,F 分别为AC ,BD 中点,过E ,F 作平面α∥AB .求证:CD ∥α.证明:如图6,连接AD 交α于G ,连接GF ,图6∵AB ∥α,面ADB ∩α=GF ⇒AB ∥GF . 又∵F 为BD 中点, ∴G 为AD 中点.又∵AC ,AD 相交,确定的平面ACD ∩α=EG ,E 为AC 中点,G 为AD 中点,∴EG ∥CD .⎭⎪⎬⎪⎫EG ⊂αCD ⊄αEG ∥CD ⇒CD ∥α. 例2 如图7,平面α,β,γ两两平行,且直线l 与α,β,γ分别相交于点A ,B ,C ,直线m 与α,β,γ分别相交于点D ,E ,F ,AB =6,BC =2,EF =3.求DE 的长.图7解:连接DC .设DC 与β相交于点G ,则平面ACD 与α,β分别相交于直线AD ,BG ,平面DCF 与β,γ分别相交于直线GE ,CF .因为α,β,γ两两平行, 所以BG ∥AD ,GE ∥CF .因此AB BC =DG GC ,DG GC =DE EF .所以AB BC =DE EF .又因为AB =6,BC =2,EF =3,所以DE =9.点评:本题利用面面平行得到线线平行,从而得到线段成比例. 变式训练如图8,平面α∥平面β,平面γ与α交于直线a ,γ与β交于直线b ,直线c 在β内,且c ∥b .图8(1)判断c与α的位置关系,并说明理由;(2)判断c与a的位置关系,并说明理由.答案:(1)c∥α;(2)c∥a.(理由略.)思路2例1 求证:如果两个相交平面分别经过两条平行直线中的一条,那么它们的交线和这两条直线平行.图9解:已知:如图9,a∥b,a⊂α,b⊂β,α∩β=c.求证:c∥a∥b.证明:变式训练求证:一条直线与两个相交平面都平行,则这条直线与这两个相交平面的交线平行.图10解:已知:如图10,a∥α,a∥β,α∩β=b.求证:a∥b.证明:如图10,过a作平面γ,δ,使得γ∩α=c,δ∩β=d,那么有点评:本题证明过程,实际上就是不断交替使用线面平行的判定定理、性质定理及公理4的过程.这是证明线线平行的一种典型的思路.例2 已知:a ,b 是异面直线,a ⊂平面α,b ⊂平面β,a ∥β,b ∥α. 求证:α∥β.证明:如图11,在b 上任取点P ,显然P ∉a .于是a 和点P 确定平面γ,且γ与β有公共点P.图11设γ∩β=a ′,∵a ∥β.∴a ′∥a .∴a ′∥α.这样β内相交直线a ′和b 都平行于α,∴α∥β.知能训练1.如果两个平面分别平行于第三个平面,那么这两个平面互相平行.图12解:已知:α∥β,γ∥β,求证:α∥γ.证明:如图12,作两个相交平面分别与α,β,γ交于a ,c ,e 和b ,d ,f ,⎭⎬⎫α∥β⇒⎩⎪⎨⎪⎧ a ∥cb ∥d β∥γ⇒⎩⎪⎨⎪⎧ c ∥ed ∥f⇒⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ∥e ⇒a ∥γb ∥f ⇒b ∥γ⇒α∥γ. 点评:欲将面面平行转化为线线平行,先要作平面. 2.如图13,EFGH 的四个顶点分别在空间四边形ABCD 的边AB ,BC ,CD ,DA 上,求证:BD ∥面EFGH ,AC ∥面EFGH .证明:∵四边形EFGH 是平行四边形⎭⎪⎬⎪⎫⇒EH ∥FGFG ⊂面BDC EH ⊄面BDC ⇒⎭⎪⎬⎪⎫EH ∥面BDCEH ⊂面ABD 面ABD ∩面BDC =BD图13⎭⎪⎬⎪⎫⇒EH ∥BDEH ⊂面EFGH BD ⊄面EFGH ⇒BD ∥面EFGH . 同理,可证AC ∥面EFGH .拓展提升如图14,两条异面直线AB ,CD 与三个平行平面α,β,γ分别相交于A ,E ,B 及C ,F ,D ,又AD ,BC 与平面的交点为H ,G .求证:四边形EHFG 为平行四边形.图14证明:⎭⎪⎬⎪⎫平面ABC ∩α=AC 平面ABC ∩β=EG α∥β⇒AC ∥EG .同理,AC ∥HF .⎭⎪⎬⎪⎫AC ∥EG AC ∥HF ⇒EG ∥HF .同理,EH ∥FG .故四边形EHFG 是平行四边形.课堂小结1.线线平行、线面平行、面面平行的相互转化是解决立体几何中平行关系的关键. 2.学会作辅助线,特别是利用平行关系的性质作辅助线.作业习题1—5 B 组第2,3题.设计感想本节教学设计注重培养学生直觉感知和应用能力,在实际教学中,可选择使用例题和练习题.备课资料备用习题1.如图15,P 是△ABC 所在平面外的一点,A ′,B ′,C ′分别是△PBC ,△PCA ,△P AB 的重心.图15(1)求证:平面ABC ∥平面A ′B ′C ′; (2)求△A ′B ′C ′与△ABC 的面积之比.证明:(1)连接P A ′,PB ′,PC ′并延长交BC ,AC ,AB 于D ,E ,F ,连接DE ,EF ,DF .∵A ′,C ′分别是△PBC ,△P AB 的重心, ∴P A ′=23PD ,PC ′=23PF .∴A ′C ′∥DF .∵A ′C ′⊄平面ABC ,DF ⊂平面ABC , ∴A ′C ′∥平面ABC .同理,A ′B ′∥平面ABC .又A ′C ′∩A ′B ′=A ′,A ′C ′、A ′B ′⊂平面A ′B ′C ′,∴平面ABC ∥平面A ′B ′C ′.(2)由(1)知A ′C ′23DF ,又DF 12AC ,∴A ′C ′13AC . 同理,A ′B ′13AB ,B ′C ′13BC .∴△A ′B ′C ′∽△ABC . ∴S △A ′B ′C ′∶S △ABC =1∶9.2.已知:如图16,α∥β,AB ∥CD ,A ∈α,C ∈α,B ∈β,D ∈β.图16求证:AB=CD.证明:∵AB∥CD,∴过AB,CD的平面γ与平面α和β分别交于AC和BD.∵α∥β,∴BD∥AC.∴四边形ABCD是平行四边形.∴AB=CD.3.如图17,已知平面α∥平面β,A,C∈α,B,D∈β,E,F分别为AB,CD的中点.求证:EF∥α,EF∥β.图1图18证明:当AB,CD共面时,平面ABCD∩α=AC,平面ABCD∩β=BD.∵α∥β,∴AC∥BD.∵E,F分别为AB,CD的中点,∴EF∥AC.∵ACα,EFα,∴EF∥α.同理,EF∥β.当AB,CD异面时,如图18,∵E CD,∴可在平面ECD内过点E作C′D′∥CD,与α,β分别交于C′,D′.平面AC′BD′∩α=AC′,平面AC′BD′∩β=BD′,∵α∥β,∴AC′∥BD′.∵E是AB中点,∴E也是C′D′的中点.平面CC′D′D∩α=CC′,平面CC′D′D∩β=DD′,∵α∥β,∴CC′∥DD′.∵E,F分别为C′D′,CD的中点,∴EF∥CC′,EF∥DD′.∵CC′α,EFα,∴EF∥α.同理,EF∥β.(设计者:释翠香)。
1.5.1平行关系的判定学案(北师大版必修2)

§5 平行关系5.1 平行关系的判定自主学习1.通过直观感知、操作确认,归纳出直线与平面平行的判定定理、平面与平面平行的判定定理.2.在理解、掌握两个判定定理的基础上,灵活运用解决一些实际问题.1.直线与平面平行的判定定理若__________一条直线与____________的一条直线平行,则该直线与此平面平行.符号:__________________________________________________________________.2.平面与平面平行的判定定理如果一个平面内的________________都平行于另一个平面,那么这两个平面平行.符号:___________________________________________________________________.对点讲练直线与平面平行的判定例1如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱BC、C1D1的中点.求证:EF∥平面BDD1B1.变式训练1如图所示,P是▱ABCD所在平面外一点,E、F分别在P A、BD上,且PE∶EA=BF∶FD.求证:EF∥平面PBC.平面与平面平行的判定例2已知E、F、E1、F1分别是三棱柱A1B1C1—ABC棱AB、AC、A1B1、A1C1的中点.求证:平面A1EF∥平面E1BCF1.点评 要证平面平行,依据判定定理只需要找出一个平面内的两条相交直线分别平行于另一个平面即可.另外在证明线线、线面以及面面平行时,常进行如下转化:线线平行――→线面平行的判定线面平行――→面面平行的判定面面平行.变式训练2 如图所示,B 为△ACD 所在平面外一点,M 、N 、G 分别为△ABC 、△ABD 、△BCD 的重心.(1)求证:平面MNG ∥平面ACD ;(2)求S △MNG ∶S △ADC .线面平行、面面平行的综合应用例3 如图所示,在正方体ABCD —A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,问:当点Q 在什么位置时,平面D 1BQ ∥平面P AO?点评 解答开放性问题,要结合题目本身的特点与相应的定理,大胆地猜想,然后证明. 变式训练3 如图所示,已知点S 是正三角形ABC 所在平面外的一点,且SA =SB =SC ,SG 为△SAB 上的高,D 、E 、F 分别是AC 、BC 、SC 的中点,试判断SG 与平面DEF 的位置关系,并给予证明.2.平行关系的判定基本思路:线线平行⇒线面平行⇒面面平行.面面平行,归根到底是找线面平行,但一定是找两条相交的直线.课时作业一、选择题1.若三条直线a,b,c满足a∥b∥c,且a⊂α,b⊂β,c⊂β,则两个平面α、β的位置关系是()A.平行B.相交C.平行或相交D.不能确定2.已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是() A.平面ABC必平行于αB.平面ABC必与α相交C.平面ABC必不垂直于αD.存在△ABC的一条中位线平行于α或在α内3.正方体EFGH—E1F1G1H1中,下列四对截面中,彼此平行的一对截面是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G4.经过平面α外两点,作与平面α平行的平面,则这样的平面可以作()A.1个或2个B.0个或1个C.1个D.0个5.点E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点,则空间四边形的六条棱中与平面EFGH平行的条数是()A.0 B.1 C.2 D.3二、填空题6.经过直线外一点有________个平面与已知直线平行;经过直线外一点有________条直线与已知直线平行.7.下面的命题在“________”处缺少一个条件,补上这个条件,使其构成真命题(m,n 为直线,α,β为平面),则此条件应为________________.8.如图所示,在正方体ABCD—A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足__________________时,有MN∥平面B1BDD1.三、解答题9.如图所示,ABCD与ABEF均为平行四边形,且不在同一平面内,M为对角线AC 上的一点,N为对角线FB上的一点,AM∶FN=AC∶BF.求证:MN∥平面BCE.10.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC和SC的中点.求证:平面EFG∥平面BDD1B1.§5 平行关系5.1 平行关系的判定答案自学导引1.平面外 此平面内 a ⊆α,b α,且a ∥b ⇒a ∥α2.两条相交直线 a β,b β,a ∩b =P ,a ∥α,b ∥α⇒β∥α对点讲练例1 证明 取D 1B 1的中点O ,连接OF ,OB .∵OF 綊12B 1C 1,BE 綊12B 1C 1,∴OF 綊BE .∴四边形OFEB 是平行四边形,∴EF ∥BO .∵EF ⊆平面BDD 1B 1,BO 平面BDD 1B 1,∴EF ∥平面BDD 1B 1.变式训练1 证明 连接AF 延长交BC 于G ,连接PG .在▱ABCD 中,易证△BFG ∽△DF A .∴GF F A =BF FD =PE EA, ∴EF ∥PG .而EF ⊆平面PBC ,PG 平面PBC ,∴EF ∥平面PBC .例2 证明∵EF 是△ABC 的中位线,∴EF ∥BC .∵EF ⊆平面E 1BCF 1,BC 平面E 1BCF 1,∴EF ∥平面E 1BCF 1.∵A 1E 1綊EB ,∴四边形EBE 1A 1是平行四边形,∴A 1E ∥E 1B .∵A 1E ⊆平面E 1BCF 1,E 1B 平面E 1BCF 1,∴A 1E ∥平面E 1BCF 1.又∵A 1E ∩EF =E ,∴平面A 1EF ∥平面E 1BCF 1.变式训练2 (1)证明 连接BM 、BN 、BG 并延长交AC 、AD 、CD 分别于P 、F 、H .∵M 、N 、G 分别为△ABC 、△ABD 、△BCD 的重心,则有BM MP =BN NF =BG GH=2. 连接PF 、FH 、PH ,有MN ∥PF .又PF 平面ACD ,MN ⊆平面ACD ,∴MN ∥平面ACD .同理MG ∥平面ACD ,MG ∩MN =M ,∴平面MNG ∥平面ACD .(2)解 由(1)可知MG PH =BG BH =23, ∴MG =23PH .又PH =12AD ,∴MG =13AD . 同理NG =13AC ,MN =13CD . ∴△MNG ∽△DCA ,其相似比为1∶3,∴S △MNG ∶S △ACD =1∶9.例3 解 当Q 为CC 1的中点时,平面D 1BQ ∥平面P AO .∵Q 为CC 1的中点,P 为DD 1的中点,∴QB ∥P A .∵P 、O 分别为DD 1、DB 的中点,∴D 1B ∥PO .∴D 1B ∥面P AO ,QB ∥面P AO ,又D 1B ∩QB =B ,∴平面D 1BQ ∥平面P AO .变式训练3 解 SG ∥平面DEF .证明如下:连接GC 交DE 于点H ,连接FH .∵DE 是△ABC 的中位线,∴DE ∥AB .在△ACG 中,D 是AC 的中点,且DH ∥AG ,∴H 为CG 的中点.∴FH 是△SCG 的中位线,∴FH ∥SG .又SG ⊆平面DEF ,FH 平面DEF ,∴SG∥平面DEF.课时作业1.C2.D[A,B,C在平面α的异侧时,A错;而A,B,C在平面α同侧时,B错;A,B,C在平面α的异侧时,平面ABC有可能垂直于平面α,C错.]3.A4.B[两点的连线可能与平面相交,此时为0个;两点的连线也可能与平面平行,此时可作一个平面.]5.C[由线面平行的判定定理知:BD∥平面EFGH,AC∥平面EFGH.]6.无数17.m,n相交8.M∈线段FH解析∵HN∥BD,HF∥DD1,HN∩HF=H,BD∩DD1=D,∴平面NHF∥平面B1BDD1,故线段FH上任意点M与N连接,有MN∥平面B1BDD1.9.证明如图所示,过M作MM1∥AB,交BC于M1,过N作NN1∥AB,交BE于N1,则MM1∥NN1,又AM∶FN=AC∶BF,∴AMAC=FNBF,∴MM1AB=NN1EF.又∵AB=EF,∴MM1=NN1.连接M1N1,则四边形MNN1M1是平行四边形.∴MN∥M1N1,又M1N1⊂平面BCE.∴MN∥平面BCE.10.证明如图所示,连接SB,SD,∵F、G分别是DC、SC的中点,∴FG∥SD.又∵SD平面BDD1B1,FG 平面BDD1B1,∴直线FG∥平面BDD1B1.同理可证EG∥平面BDD1B1,又∵直线EG平面EFG,直线FG平面EFG,直线EG∩直线FG=G,∴平面EFG∥平面BDD1B1.。
北师大版高一数学必修2第一章第5节平行关系的判定教案

【课题】§5.1 平行关系的判定第一课时直线与平面平行的判定【教学目标】1.掌握直线和平面平行的判定定理,并会运用2.培养发展空间想象能力,推理论证能力,运用图形语言进行交流的能力,几何直观能力3.通过典型例子的分析和自主探索活动,理解数学概念,体会数学思想方法.【教学重点】直线和平面平行的判定定理【教学难点】判定定理的运用【教学思路】通过教师提问式的引导方法引导学生得到直线与平面平行的判定定理,结合学生的自主讨论、自主探索活动写出定理的文字、图形以及符号语言培养空间想象能力.然后利用典型例题加强学生的推理论证能力【教学内容】直线和平面平行的判定定理以及三种语言表述【教学方法】启发引导式教学法、讲议练相结合教学法【教学手段】以传统教学手段为主,多媒体教学以及实物模型教学手段为辅【教学设计理念】1.通过播放幻灯片,激发学生学习的兴趣,体现直观教学的灵便性2.实物举例让学生觉得直线和平面平行的情况在生活中随处可见3.在设计例题与练习时,增加了除长方体、正方体以外的不规则图形以扩大学生视野【教学过程】一、复习回顾:〔师〕直线和平面有哪几种位置关系?〔生〕直线在平面内;直线与平面相交;直线与平面平行〔师〕回答的很好,那么能否分别用文字、图形和符号语言描述这几种位置关系(在学生回答时,教师同时在多媒体课件或用幻灯片1投影出直线和平面的位置关系)直线与平面的位置关系:文字语言:直线a在平面α内;直线a与平面α相交;直线a与平面α平行图形语言:符号语言:a⊆αa⋂α=A a∥α〔师〕如何判定一条直线和一个平面平行?﹙教师一边提问一边演示长方体模型,组织学生讨论﹚如图所示:直线BC 与平面A ‘B ‘C ‘D ‘的关系如何?直线AC 与平面A ‘B ‘C ‘D ‘呢?〔生〕B C ∥ A ‘B ‘C ‘D ‘ A C ∥A ‘B ‘C ‘D ‘二、 讲授新课﹙生叙述,教师板书﹚1、定理5.1:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行〔师〕请同学们讨论并写出这个定理的三种表示方法﹙生回答时,教师同时演示幻灯片2﹚ 图形语言: 符号语言:a b a a ααα⊄⎫⎪⊆⇒⎬⎪⎭∥∥b 〔师〕判定一条直线和一个平面平行需要几个条件?能不能缺少一个或几个?〔生〕需要三个条件,缺一不可〔师〕那么如果缺少一个会得到什么结论?并画出图形﹙组织学生讨论﹚〔生甲〕若缺少a α⊄,则结论为a a αα⊆∥或〔生乙〕若缺少b α⊆,则结论为a a αα⋂∥或〔生丙〕若缺少a b ∥,则结论为a a αα⋂∥或(即时训练)幻灯片3: 1.已知直线l 、a 、b 及平面α,下列命题正确的个数是﹙ ﹚(1),l a a l αα⇒∥∥∥(2),l a l l ααα⊆⊆⇒∥∥b,a ,b ∥ (3)l 平行与平面α内无数条直线⇒l α∥A .0B .1C .2D .32.l α⊆直线∥直线m,m ,则直线l 与平面α的位置关系是﹙ ﹚A .相交B .平行C .在平面α内D .平行或在平面α内三、例题讲解﹙幻灯片4﹚〔师〕请同学们自行分析此题〔生〕E 、F 分别为AB 、AD 的中点可知EF BD ∥,而BD BCD ⊆平面,根据判定定理可得EF BCD ∥平面〔师〕若此题改为“空间四边形ABCD 中,AE AF EB FD =则EF 与平面BCD 的位置关系如何?”幻灯片4 例1:空间四边形 ABCD 中,E 、F 分别为AB 、AD 的中点,判断EF 与平面BCD 的位置关系例 2.如图, 空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,试证明EFGH是平行四边形﹙师生共同讨论证明﹚〔师〕﹙分析﹚根据平面几何知识怎么证明一个四边形是平行四边形?〔生〕证明一组对边平行且相等;两组对边分别平行;两条对角线互相平分;两组对边分别相等;两组对角分别相等即可〔师〕那这几种方法在这里都可使用吗?〔生甲〕都可使用〔师〕请同学们讨论甲同学的回答是否正确?〔生乙〕甲同学的回答不正确,前三种在立体几何中可以使用,而后两者无法证明是平行四边形〔师〕乙同学回答完全正确,在立几中这个四边形首先是在同一平面内,其次再证明是平行的(生证明,师板书)证明:连接AC、BD∵E、F、G、H分别是AB、BC、CD、DA的中点∴11112222EF AC GH AC EF AC GH AC ==∥,∥且, ∴EF GH EF GH =∥且∴EFGH 是平行四边形〔师〕在证明线面平行的问题中,最关键的是在平面内找到与平面外的直线平行的直线四、课堂练习课本P31、T1、2、3、4(1)五、课堂小结〔师〕请同学们自行总结这节课的主要内容〔生甲〕直线与平面平行的判定定理〔生乙〕判定直线和平面平行需要三个条件,缺一不可〔师〕证明直线与平面平行的关键是什么?〔生丙〕 关键是在这个平面内找到一直线与已知直线平行即可六、课后作业课本P34 ,B 组T1、T3七、板书设计。
1.5.1平行关系的判定 学案(高中数学必修2北师版)

§5平行关系5.1平行关系的判定教室的门通过门轴可以自由的开关,在开关的过程中,门上竖直的一边与门轴所在边什么关系?与门轴所在墙面又是什么关系?【提示】门上竖直的一边与门轴所在边平行,与墙面也平行.三角板的一边所在直线与桌面平行,这个三角板所在平面与桌面平行吗?三角板的两条边所在直线分别与桌面平行,情况又如何呢?【提示】三角板的一条边所在直线与桌面平行时,三角板所在平面与桌面可能平行,也可能相交.三角板的两条边所在直线分别与桌面平行时,三角板所在平面与桌面平行.如图1-5-1,四边形ABCD ,ADEF 都是正方形,M ∈BD ,N ∈AE ,且BM =AN .图1-5-1求证:MN ∥平面CED .【思路探究】 要证明MN ∥平面CED ,需在平面CED 中找一条直线平行于MN ,进而转化为线线平行的证明.【自主解答】 如图,连接AM 并延长交CD 于点G ,连接GE ,因为AB ∥CD ,所以AM MG =BMMD .所以AM MG +AM =BMMD +BM ,即AM AG =BM BD. 又因为BD =AE 且AN =BM , 所以AM AG =ANAE.所以MN ∥GE .又GE 平面CED ,MN 平面CED ,所以MN ∥平面CED .1.本题也可通过过M、N分别作AD的平行线构造平行四边形来寻找平行线证明.2.线面平行的判定方法(1)利用定义证线面无公共点.(2)利用线面平行的判定定理,将线线平行转化为线面平行.本例条件不变,求证:BF∥平面CDE.【证明】∵四边形ABCD,ADEF都是正方形,∴BC綊AD綊EF,∴BC綊EF.∴四边形BCEF是平行四边形,∴BF∥CE.∵BF平面CDE,CE 平面CDE,∴BF∥平面CDE.已知四棱锥P—ABCD中,底面ABCD为平行四边形.点M、N、Q 分别在P A、BD、PD上,且PM∶MA=BN∶ND=PQ∶QD.图1-5-2求证:平面MNQ∥平面PBC.【思路探究】(1)你认为证明线面平行、面面平行关键是什么?(2)题中所给成比例线段有什么用?(3)能否找到两条相交直线都和平面PBC平行?【自主解答】∵PM∶MA=BN∶ND=PQ∶QD,∴MQ∥AD,NQ∥BP.∵BP 平面PBC,NQ平面PBC,∴NQ∥平面PBC.又底面ABCD为平行四边形,∴BC∥AD,∴MQ∥BC.∵BC 平面PBC,MQ平面PBC,∴MQ∥平面PBC.又MQ∩NQ=Q,根据平面与平面平行的判定定理,得平面MNQ∥平面PBC.1.利用比例线段推出平行关系是解答本题的关键.2.面面平行的判定方法(1)利用定义,证面面无公共点.(2)利用面面平行的判定定理转化为证明线面平行,即证明一个平面内的两条相交直线平行于另一个平面.图1-5-3如图1-5-3在正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、B1C1、C1D1的中点.求证:平面MNP∥平面A1BD.【证明】如图所示,连接B1D1,∵P、N分别是D1C1、B1C1的中点,∴PN∥B1D1.又B1D1∥BD,∴PN∥BD,又PN平面A1BD,BD 平面A1BD,∴PN∥平面A1BD,同理可得MN∥平面A1BD,又∵MN∩PN=N,∴平面PMN∥平面A1BD.心,P是DD1的中点,设Q是CC1上的点,图1-5-4问:当点Q在什么位置时,平面D1BQ∥平面P AO?【思路探究】(1)由条件“P是DD1中点”,你猜想Q应在CC1的什么位置?(2)PO与BD1平行吗?。
5.2平行关系的性质导学案

5.2平行关系的性质自主备课 学习目标1. 掌握直线与平面平行的性质定理及其应用;2.掌握两个平面平行的性质定理及其应用。
学习重点:两个性质定理学习难点:性质定理的证明;性质定理的正确运用。
自主学习阅读课本,回答以下问题1、如果一条直线与一个平面平行,那么这条直线是否与这个平面内所有直线平行吗?2、分别位于两个平行平面内的直线有什么位置关系?3、两个平面互相平行,其中一个平面内的直线与另一个平面有什么位置关系?4、若一个平面与两个平行平面同时相交,则交线有什么位置关系?41-65,,,////,,,.A B C D AB AC BD AC BD C D AC BDαα=例题如图在同一平面内,面, 且与面分别交于点求证: A BC Dα12..//..//b a b b A B b C b D b b αααααααα≠≠≠⊂⊂⊂课本练习、如果直线a//平面,直线,那么与一定平行吗?为什么?、如果直线a//直线b,且a//平面,那么与的位置关系是()相交 或5-l ,,,,623A B C D E F AB BC EF αβγαβγαβγ===例题 如图168,平面,,两两平行,且直线与,, 分别交于点。
直线m 与,,分别交于, ,,,求DE 的长αβγ1,2ααααααααα课本练习题、已知两条直线m,n 及平面,判定下面四个命题是否正确:(1)若m//,n//,则m//n(2)若m//,m//n 则n// (3)若m//,则m 平行于内的所有直线(4)若m 平行于内无数条直线,则m//、如果一条直线与两个平行平面中的一个平行,那么这条 直线与另一个平面的位置关系是()A.平行B.相交C.在平面内D.平行或在平面内3、如果3个平面把空间分成4个部分,那么这3个平面有怎样 的位置关系?分成6部分呢?G F D E CB A l m自学检测1、已知直线L∥平面α,直线m在平面α内,则直线L和m的位置关系是()A.相交B.平行C.平行或异面D.异面⊂α,点B∈β,则在β内过点B 2、若平面α∥平面β,直线a≠的所有直线中()A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线3、如果一条直线和一个平面平行,则这条直线()A 只和这个平面内一条直线平行;B 只和这个平面内两条相交直线不相交;C 和这个平面内的任意直线都平行;D 和这个平面内的任意直线都不相交。
2015-2016学年高中数学必修二北师大版 1.5.1平行关系的判定 教案

5.1平行关系的判定一、教材的地位与作用平行关系的判定是在线与线、线与面、面与面的知识结构中起着承上启下的作用,也是今后学习共面向量的基础。
在此之前,学生已学习了空间两直线的位置关系,这为过渡到本节的学习起着铺垫作用。
本节的主要内容有直线和平面的三种位置关系和直线与平面平行的判定两部分。
平行关系是全章的主要内容之一,而直线与平面平行的判定是平行关系的初步。
因此,在立体几何中,占据重要的地位。
二、教学目标1.知识与技能: (1)理解并掌握线面平行、面面平行的判定定理及其应用;(2)能将数学三种语言(自然语言、图形语言、符号语言)相互转化2. 过程与方法:借助已有知识,通过观察模型,抽象概况出线面平行、面面平行的定义,类比线面平探索面面平行的判定定理,培养学生的划归思想、空间想象力和抽象概括能力3.情感态度与价值观:在学习过程中,使学生获得积极的情感,培养数学学习的兴趣三、教学重难点教学重点:线面平行和平面与平面平行的定义和判定定理教学难点:线面平行和平面与平面平行的判定定理的推导和应用四、教法学法:采用直观类比法、探究发现法、观察实验法等教学方法,教师通过创设问题探究,引导学生通过直观感知,操作确认逐步发现知识的形成过程,使教学活动真正建立在学生自主活动和探究的基础上,着力培养学生的抽象概括能力和空间想象能力.五、教学过程(一)温故知新:复习回顾1. 空间直线与平面的位置关系有_3_种:||a a A a ααα⊂⎧⎪=⎨⎪⎩2. 空间平面与平面的位置关系有_2_种: ||B C αβαβ⎧⎨=⎩一、直线与平面平行的判定1.问题提出: 如何判定一条直线和一个平面平行?//,,a b b a αα⊂⊄⇒ //.a α2.抽象概括:直线与平面平行的判定定理如果平面外一条直线和这个平面内的一条直线平行, 那么这条直线和这个平面平行. ||||a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭3.应 用:例1.求证:空间四边形相邻两边的中点的连线,平行于经过另外两边的平面. 已知:空间四边形ABCD 中,E 、F 分别是AB 、AD 的中点. 求证:EF //平面BCD .证明:连结BD ,////,平面,平面平面A E E B E F B D E F B C D B D B C DA F F D E FBC D=⎫⇒⊄⊂⎬=⎭⇒例2. 如图所示, 空间四边形ABCD中, E, F, G, H分别是AB, BC, CD, AD的中点. 试指出图中满足线面平行位置关系的所有情况.二、平面与平面平行的判定1.问题提出:如何判定一个平面和另一个平面平行?1.空间线面有哪些位置关系呢?2.学习过几种判断直线与平面平行的方法(1)定义法;(2)直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.设计意图:回顾探究与线面平行的转化思想方法,自然语言的描述、图形语言画法和符号语言的表述,为类比学习面面平行做铺垫2.探究发现,得出定理观察:长方体和三棱柱两个教具模型1.上表面两直线,B C C D与底面的关系,符号语言如何表述?2上表面和下表面是否有交点?抽象概况出面面平行的定义:①αβφ=,②记作:||αβ③ 图形如何画?设计意图:由线面平行定义直观映射出面面平行的定义,从直观过渡到抽象推理.探究活动1:①将长方体和三棱柱平移和旋转,上下地面是否还平行? ②将长方体底面的边11A D 和三棱柱底面顶点1B 抬起是否上表面平行桌面?探究活动2: 1、平面α内有一条直线与平面β平行, 则平面α,β平行吗?2、平面α内有两条直线与平面β平行,平面α,β平行吗?3、平面α内有无数条直线与平面β平行,平面α,β平行吗? 设计意图: 由知识回顾到问题提出很自然。
北师大版必修二1.5《平行关系》word学案

1.5平行关系学案【教学目标】掌握空间元素的平行关系的判定与性质的有关知识, 并能运用这些知识解决与平行有关的问题。
【教学重点】 空间线线、线面、面面平行关系的转化。
【教学难点】线面平行的各种判定方法。
【教学过程】 一. 课前预习1. ( 05北京)在正四面体 P — ABC 中, D, E , F 分别是AB BC CA 的中点,下面四个结论中不成立的是()。
A . BC 〃平面PDFB . DF 丄平面PA EC .平面PDF 丄平面 ABCD .平面 PAE 丄平面 ABC2. (05湖北)如图,在三棱柱 ABC - ABC 中,点 E 、F 、H 、K 分别为AC\ CB \ A B 、BC 的中点,ABC 的重心•从K 、 HG B •中取一点作为P ,使得该棱柱恰有2条棱与平面PEF 平行, 则P 为()。
A. K B . H C . G D . B 3.(05广东)给出下列关于互不相同的直线ml 、n 和平面a 、m 二x,l - = A,点A ; m,则l 与m 不共面;② 若m l 是异面直线,l//ot,m//c (,且n 丄I, n 丄m,则n 丄a ③ 若 1〃 : ,m 〃 一: // 一则l//m ; ④若 I 二:s m 二 x ,1 ' m =点A,l // :,m// :,则:// :.其中为假命题的是()。
A .①B .②C .③D .④4. ( 05辽宁)已知 m n 是两条不重合的直线, a 、3、丫是三个两两不重合的平面,给出下列四个命题:①若m_〉,m_ [,则:// ■-;②若一:」二】」⑦则〉// ■-; ③若 m : , n :, m// n,则-// 1; m 二用,m// 1, n 二.,n // :,则:// 1其中真命题是(A'K B' C'嘗 HEFaV ,11 f r J占 B3的四个命题:①若④若m n 是异面直线,A.①和②5. 如图所示,在正四棱柱 棱CG 、GD 、DD 、DC 的中点,N 是BC 中点,点M 在四边形EFGH 及其内部运动,则 M 只须满足 ___________________ 时,就有MN//平面BBDD (请填出你认为正确的一个条件即可,不B .①和③ C.③和④ ABCD-AB i CD 中,E 、F 、G H 分别是D.①和④1必考虑所有可能情况)。
高中数学第一章立体几何初步5.1平行关系的判定学案北师大版必修2

高中数学第一章立体几何初步5.1平行关系的判定学案北师大版必修2[学习目标] 1.理解直线与平面平行、平面与平面平行判定定理的含义. 2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用. 3.能运用直线与平面平行的判定定理、平面与平面平行的判定定理证明一些空间线面关系的简单问题.【主干自填】1.直线与平面位置关系的表示文字语言符号语言直线a与平面α平行a∥α直线a与平面α相交a∩α=A直线a在平面α内aα23.平面与平面平行的判定定理【即时小测】1.思考下列问题(1)一条直线与一个平面的位置关系有哪几种?提示:有三种位置关系如下图:直线a在平面α内(记作aα),直线a与平面α相交(记作a∩α=A),直线a与平面α平行(记作a∥α).(2)如下图,平面α外的直线a平行于平面α内的直线b.这两条直线共面吗?直线a 与平面α相交吗?提示:两条直线共面,直线a与平面α不相交.(3)因为两条相交直线确定唯一一个平面,这启示我们尝试用两条相交直线来讨论平面的平行问题.当三角板的两条边或课本的两条相交边所在直线分别与桌面平行时,情况又如何呢?提示:当三角板的两条边或课本的两条相交边所在直线分别与桌面平行时,这个三角板或课本所在平面与桌面平行.符号表示:aβ,bβ,a∩b=P,a∥α,b∥α⇒α∥β.图形表示如图.2.若A是直线m外一点,过A且与m平行的平面( )A.存在无数个B.不存在C.存在但只有一个D.只存在两个提示:A3.圆柱的两个底面的位置关系是( )A.相交B.平行C.平行或异面D.相交或异面提示:B4.若a,b是异面直线,过b且与a平行的平面( )A.不存在B.存在但只有一个C.存在无数个D.只存在两个提示:B 如右图所示,a、b是异面直线,在b上任取一点P,过P作a′∥a,∴a′与b确定平面α.由于两条相交直线仅确定一个平面,故α是唯一的.例1 如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:(1)EH∥平面BCD;(2)BD∥平面EFGH.[证明] (1)∵E、H为AB,AD的中点,∴EH∥BD.∵EH⊆/平面BCD,BD平面BCD,∴EH∥平面BCD.(2)∵BD∥EH,BD⊆/平面EFGH,EH平面EFGH,∴BD∥平面EFGH.类题通法1利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.2证线线平行的方法常用三角形中位线定理、平行四边形性质、平行线分线段成比例定理、平行公理等.[变式训练1]如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.证明连接AC交BD于O点连接OM.∵M为SC的中点,O为AC的中点,∴OM∥SA.∵OM平面MDB,SA⊆/平面MDB,∴SA∥平面MDB.例2 如图,在长方体ABCD-A′B′C′D′中,求证:平面C′DB∥平面AB′D′.[证明] ∵AB綊CD綊D′C′,∴四边形ABC′D′是平行四边形,∴BC′∥AD′.又∵BC′⊆/平面AB′D′,AD′平面AB′D′,∴BC′∥平面AB′D′.同理C′D∥平面AB′D′,∵BC′∩C′D=C′,∴平面C′DB∥平面AB′D′.类题通法1要证明两平面平行,只需在其中一个平面内找到两条相交直线平行于另一个平面.2判定两个平面平行与判定线面平行一样,应遵循先找后作的原则,即先在一个面内找到两条与另一个平面平行的相交直线,若找不到再作辅助线.[变式训练2]如图,已知三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,求证:平面DEF∥平面ABC.证明在△PAB中,因为D,E分别是PA,PB的中点,所以DE∥AB,又知DE⊆/平面ABC,因此DE∥平面ABC,同理EF∥平面ABC.又因为DE∩EF=E,所以平面DEF∥平面ABC.例3 如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC、SC 的中点,求证:(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.[证明] (1)如图,连接SB,∵E、G分别是BC、SC的中点,∴EG∥SB.又∵SB平面BDD1B1,EG⊆/平面BDD1B1,∴直线EG∥平面BDD1B1.(2)连接SD ,∵F 、G 分别是DC 、SC 的中点,∴FG ∥SD . 又∵SD 平面BDD 1B 1,FG ⊆/ 平面BDD 1B 1, ∴FG ∥平面BDD 1B 1.∵EG 平面EFG ,FG 平面EFG ,EG ∩FG =G , ∴平面EFG ∥平面BDD 1B 1. 类题通法要证明面面平行,由面面平行的判定定理知需在某一平面内寻找两条相交且与另一平面平行的直线.要证明线面平行,又需根据线面平行的判定定理,在平面内找与已知直线平行的直线,即:线线平行――→线面平行的判定线面平行――→面面平行的判定面面平行[变式训练3] 如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 分别是CB ,CD ,CC 1的中点,求证:平面AB 1D 1∥平面EFG .证明 如图,连接BD .∵E 、F 分别为BC 、CD 的中点, ∴EF ∥BD .又BD ∥B 1D 1,∴EF ∥B 1D 1. 又∵EF ⊆/ 平面AB 1D 1,B 1D 1平面AB 1D 1, ∴EF ∥平面AB 1D 1, 同理可得EG ∥平面AB 1D 1,又∵EF ∩EG =E ,EF 、EG 平面EFG , ∴平面EFG ∥平面AB 1D 1.易错点⊳不能全面考虑空间问题[典例] 设P是异面直线a,b外的一点,则过点P与a,b都平行的平面( )A.有且只有一个B.恰有两个C.没有或只有一个D.有无数个[错解] 如图所示,过点P作a1∥a,b1∥b.∵a1∩b1=P,∴过a1,b1有且只有一个平面.故选A.[错因分析] 错解对空间概念理解不透彻,对P点位置没有作全面的分析,只考虑了一般情况,而忽略了特殊情形.事实上,当直线a(或b)与点P确定的平面恰与直线b(或a)平行时,与a,b都平行的平面就不存在了.[正解] C课堂小结1.判定直线与平面平行的方法(1)定义法:直线与平面没有公共点则线面平行;(2)判定定理:(线线平行⇒线面平行),2.用定理证明线面平行时,在寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成.3.证明面面平行的方法(1)面面平行的定义;(2)面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行;(3)两个平面同时平行于第三个平面,那么这两个平面平行.1.过直线l外两点,作与l平行的平面,则这样的平面( )A.不可能作出B.只能作出一个C.能作出无数个D.上述三种情况都存在答案 D解析设直线外两点为A、B,若直线AB∥l,则过A、B可作无数个平面与l平行;若直线AB与l异面,则只能作一个平面与l平行;若直线AB与l相交,则过A、B没有平面与l平行.2.若直线l不平行于平面α,且l⊆/α,则( )A.α内的所有直线与l异面B.α内不存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交答案 B解析直线l不平行于平面α,且l⊆/α,所以l与α相交.故选B.3.能保证直线a与平面α平行的条件是( )A.bα,a∥bB.bα,c∥α,a∥b,a∥cC.bα,A、B∈a,C、D∈b,且AC=BDD.a⊆/α,bα,a∥b答案 D解析A错误,若bα,a∥b,则a∥α或aα;B错误,若bα,c∥α,a∥b,a∥c,则a∥α或aα;C错误,若满足此条件,则a∥α或aα或a与α相交;根据线面平行的判定定理可知D正确.4.在正方体EFGH-E1F1G1H1中,下列四对截面彼此平行的一对是( )A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G答案 A解析如图,∵EG∥E1G1,EG⊆/平面E1FG1,E1G1平面E1FG1,∴EG∥平面E1FG1,又G1F∥H1E,同理可证H1E∥平面E1FG1,又H1E∩EG=E,∴平面E1FG1∥平面EGH1.。
1.5.2平行关系的性质 学案(高中数学必修2北师版)
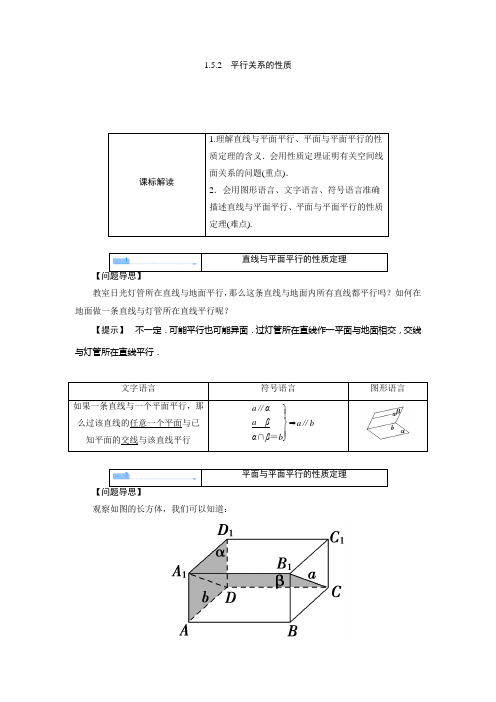
1.5.2平行关系的性质教室日光灯管所在直线与地面平行,那么这条直线与地面内所有直线都平行吗?如何在地面做一条直线与灯管所在直线平行呢?【提示】不一定.可能平行也可能异面.过灯管所在直线作一平面与地面相交,交线与灯管所在直线平行.观察如图的长方体,我们可以知道:直线a ∥平面α,平面ADD 1A 1∥平面BCC 1B 1. 思考直线a 与直线b 的关系? 【提示】 平行.如图1-5-12所示,四边形ABCD 是平行四边形,点P 是平面ABCD外一点,M 是PC 的中点,在DM 上取一点G ,过G 和AP 作平面交平面BDM 于GH ,求证:AP ∥GH .图1-5-12【思路探究】 (1)猜想一下,AP 与平面BDM 平行吗? (2)如何证明你的猜想?由“M 是PC 的中点”你能想什么? (3)由AP ∥平面BDM 如何证明AP ∥GH?【自主解答】 如图所示,连接AC ,交BD 于O ,连接MO .∵四边形ABCD 是平行四边形, ∴O 为AC 中点, 又∵M 为PC 中点, ∴AP ∥OM . 又∵AP平面BDM ,OM 平面BDM ,∴AP ∥平面BDM , 又∵AP 平面APGH ,且平面APGH ∩平面BDM =GH , ∴AP ∥GH .1.直线与平面平行的性质定理作为线线平行的依据,可以用来证明线线平行. 2.运用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与这个平面相交的交线,然后确定线线平行,证题过程应认真领悟线线平行与线面平行的相互转化关系.简记为“过直线,作平面,得交线,得平行”.如图1-5-13所示,已知异面直线AB ,CD 都平行于平面α,且AB ,CD 在α的两侧,若AC ,BD 与α分别交于M ,N 两点,求证:AM MC =BN ND.图1-5-13【证明】 如图所示,连接AD 交平面α于Q ,连接MQ 、NQ .MQ 、NQ 分别是平面ACD 、平面ABD 与α的交线.∵CD ∥α,AB ∥α,∴CD ∥MQ ,AB ∥NQ . 于是AM MC =AQ DQ ,DQ AQ =DN NB ,∴AM MC =BN ND .已知:平面α∥平面β∥平面γ,两条异面直线l 、m 分别与平面α、β、γ相交于点A 、B 、C 和点D 、E 、F .求证:AB BC =DEEF. 【思路探究】 (1)证明线段成比例问题,常用什么方法? (2)如何寻求线线平行?【自主解答】 如图,连接DC , 设DC 与平面β相交于点G ,则平面ACD 与平面α、β分别相交于直线AD 、BG .平面DCF 与平面β、γ分别相交于直线GE 、CF . 因为α∥β,β∥γ,所以BG ∥AD ,GE ∥CF . 于是在△ADC 内有AB BC =DGGC ,在△DCF 内有DG GC =DEEF .∴AB BC =DE EF.1.本题关键是利用面面平行的性质得出线线平行.2.应用两个平面平行的性质一是可以证明直线与直线平行,二是可以解决线面平行的问题.注意使用性质定理证明线线平行时,一定是第三个平面与两个平行平面相交,其交线互相平行.图1-5-14如图1-5-14所示,设AB ,CD 为夹在两个平行平面α,β之间的线段,且直线AB ,CD 为异面直线,M ,P 分别为AB ,CD 的中点.求证:直线MP ∥平面β.图1-5-14【证明】过点A作AE∥CD交平面β于E,连接DE,BE,∵AE∥CD,∴AE、CD确定一个平面,设为γ,则α∩γ=AC,β∩γ=DE.由于α∥β,∴AC∥DE(面面平行的性质定理)取AE中点N,连接NP,MN,∵M、P分别为AB、CD的中点,∴NP∥DE,MN∥BE.又NPβ,DE β,MNβ,BE β,∴NP∥β,MN∥β.又NP∩MN=N,∴平面MNP∥β.∵MP 平面MNP,∴MP∥β.如图1-5-15,直线CD、AB分别平行于平面EFGH,E、F、G、H 分别在AC、AD、BD、BC上,且CD=a,AB=b,CD⊥AB.。
高中数学 第一章 立体几何初步 1.5 平行关系 1.5.2 平行关系的性质学案 北师大版必修2

5.2 平行关系的性质1.理解直线与平面平行、平面与平面平行的性质定理的含义,会用性质定理证明空间线面关系的问题.(重点)2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的性质定理.(难点)3.综合应用平行关系的判定和性质定理进行线线平行、线面平行、面面平行的相互转化.(重点、难点)[基础·初探]教材整理1 直线与平面平行的性质定理阅读教材P 32“练习”以下至P 33“例4”以上部分,完成下列问题.aα∩如图1519所示,在空间四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 上的点,EH ∥FG ,则EH 与BD 的位置关系是( )图1519A.平行B.相交C.异面D.不确定 【解析】 ∵EH ∥FG ,EH ⊆/平面BCD ,FG 平面BCD ,∴EH ∥平面BCD ,∵EH平面ABD ,平面ABD ∩平面BCD =BD ,∴EH ∥BD . 【答案】 A教材整理2 面面平行的性质定理阅读教材P 33“练习1”以下至P 34“练习2”以上部分,完成下列问题.六棱柱的两底面为α和β,且A ∈α,B ∈α,C ∈β,D ∈β,且AD ∥BC ,则AB 与CD的位置关系为__________.【解析】 ∵AD ∥BC ,∴A ,B ,C ,D 共面,设为γ,由题意知,α∩γ=AB ,β∩γ=CD ,又α∥β, ∴AB ∥CD . 【答案】 平行[小组合作型]如图11111B 1,D 1C 1上的点,且EH ∥A 1D 1,过EH 的平面与棱BB 1,CC 1相交,交点分别为F ,G ,求证:FG ∥平面ADD 1A 1.【导学号:39292030】图1520【精彩点拨】 从图形上看,若我们能设法证明FG ∥A 1D 1即可证明FG ∥平面ADD 1A 1. 【自主解答】 因为EH ∥A 1D 1,A 1D 1∥B 1C 1,EH ⊆/平面BCC 1B 1,B 1C 1平面BCC 1B 1,所以EH ∥平面BCC 1B 1.又平面FGHE ∩平面BCC 1B 1=FG , 所以EH ∥FG ,即FG ∥A 1D 1.又FG⊆/平面ADD1A1,A1D1平面ADD1A1,所以FG∥平面ADD1A1.1.直线与平面平行的性质定理,可以用来证明线线平行.2.运用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与这个平面的交线,然后确定线线平行.证题过程应认真领悟线线平行与线面平行的相互转化关系.简记为“过直线,作平面,得交线,得平行”.[再练一题]1.如图1521所示,已知AB∥平面α,AC∥BD,且AC,BD与α分别相交于点C,D.图1521(1)求证:AC=BD;(2)满足什么条件时,四边形ABDC为正方形?【解】(1)证明:如图所示,连接CD,∵AC∥BD,∴AC与BD确定一个平面β,又∵AB∥α,ABβ,α∩β=CD,∴AB∥CD,∴四边形ABDC是平行四边形,∴AC=BD.(2)由(1)知ABDC为平行四边形,所以当AB=AC且AB⊥AC时,四边形ABDC为正方形.如图1522,已知α∥β,点P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.图1522(1)求证:AC∥BD;(2)已知PA =4 cm ,AB =5 cm ,PC =3 cm ,求PD 的长.【精彩点拨】 由PB 与PD 相交于点P ,可知PB ,PD 确定一个平面,结合α∥β,可使用面面平行的性质定理推出线线平行关系,这样就转化为平面问题.【自主解答】 (1)证明:∵PB ∩PD =P , ∴直线PB 和PD 确定一个平面γ, 则α∩γ=AC ,β∩γ=BD . 又α∥β,∴AC ∥BD . (2)由(1),得AC ∥BD ,∴PA AB =PCCD,∴45=3CD ,∴CD =154(cm), ∴PD =PC +CD =274(cm).1.利用面面平行的性质定理证明线线平行的基本步骤:(1)先找两个平面,使这两个平面分别经过这两条直线中的一条; (2)判定这两个平面平行;(3)再找一个平面,使这两条直线都在这个平面上; (4)由定理得出结论.2.面面平行的性质定理的本质:化面面平行为线线平行是面面平行性质定理的本质,而转化的关键是作辅助平面,通过作辅助平面得到交线,就可把面面平行转化为线线平行.[再练一题]2.已知α∥β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于点S ,且SA =8,SB =9,CD =34,求当S 在α,β之间时SC 的长.【解】 如图所示.∵AB 与CD 相交于S ,∴AB ,CD 可确定平面γ,且α∩γ=AC ,β∩γ=BD . ∵α∥β,∴AC ∥BD ,∴SA SB =SC SD ,∴SA SA +SB =SC CD ,即SC 34=817,解得SC =16.[探究共研型]探究1 如图1523所示,已知P是▱ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l,直线l与直线BC平行吗?请说明理由.图1523【提示】法一:平行.因为BC∥AD,BC⊆/平面PAD,AD平面PAD,所以BC∥平面PAD.又因为BC平面PBC,平面PBC∩平面PAD=l,所以BC∥l.法二:连接CM,并延长交AD于Q,连接PQ,由AD∥BC,且AM=BM,得QM=CM又PN=CN,则MN是△CPQ的中位线,所以MN∥PQ,又MN⊆/平面PAD,PQ平面PAD,则MN∥平面PAD.探究2 上述问题中条件不变,试判断MN与平面PAD是否平行,并证明你的结论.【提示】平行.取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.可知四边形AMNE为平行四边形,所以MN∥AE,MN⊆/平面PAD,AE平面PAD,所以MN∥平面PAD.如图1524所示,四边形ABCD是平行四边形,点P是平面ABCD外一点,M 是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:GH∥平面PAD.图1524【精彩点拨】连接AC交BD于O,连接MO→MO是△PAC的中位线→PA∥MO→PA∥平面BMD→PA∥GH→GH∥平面PAD【自主解答】如图所示,连接AC交BD于点O,连接MO.∵ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴PA∥MO,而AP⊆/平面BDM,OM平面BDM,∴PA∥平面BMD,又∵PA平面PAHG,平面PAHG∩平面BMD=GH,∴PA∥GH.又PA平面PAD,GH⊆/平面PAD,∴GH∥平面PAD.1.本题综合考查了线面平行的判定和性质,体现了线线平行、线面平行之间的相互转化.2.空间平行关系的转化图:[再练一题]3.如图1525,三棱锥ABCD被一平面所截,截面为平行四边形EFGH,求证:CD∥平面EFGH.图1525【证明】由于四边形EFGH是平行四边形,∴EF∥GH.∵EF⊆/平面BCD,GH平面BCD,∴EF∥平面BCD.又∵EF平面ACD,平面ACD∩平面BCD=CD,∴EF∥CD.又∵EF 平面EFGH ,CD ⊆/平面EFGH ,∴CD ∥平面EFGH .1.已知a ,b 表示直线,α,β,γ表示平面,下列推理正确的是( ) A.α∩β=a ,bα⇒a ∥bB.α∩β=a ,a ∥b ⇒b ∥α且b ∥βC.a ∥β,b ∥β,aα,bα⇒α∥βD.α∥β,α∩γ=a ,β∩γ=b ⇒a ∥b 【解析】 由面面平行的性质定理知D 正确. 【答案】 D2.若平面α∥平面β,直线a α,点B ∈β,则在β内过点B 的所有直线中( )A.不一定存在与a 平行的直线B.只有两条与a 平行C.存在无数多条直线与a 平行D.存在唯一一条直线与a 平行【解析】 设点B 与直线a 确定一平面为γ,γ∩β=b , ∴a ∥b . 【答案】 D3.已知直线a ∥平面α,平面α∥平面β,则a 与β的位置关系为________. 【解析】 若aβ,则显然满足题目条件.若a ⊆/β,过直线a 作平面γ,γ∩α=b ,γ∩β=c ,于是由直线a ∥平面α得a ∥b ,由α∥β得b ∥c ,所以a ∥c ,又a ⊆/β,cβ,所以a ∥β.【答案】 aβ或a ∥β4.过两平行平面α,β外的点P 的两条直线AB 与CD ,它们分别交α于A ,C 两点,交β于B ,D 两点,若PA =6,AC =9,PB =8,则BD 的长为________.【解析】 两条直线AB 与CD 相交于P 点,所以可以确定一个平面,此平面与两平行平面α,β的交线AC ∥BD ,所以PA PB =ACBD,又PA =6,AC =9,PB =8,故BD =12.【答案】 125.如图1526,直四棱柱ABCD A 1B 1C 1D 1的底面是梯形,AB ∥CD ,AD ⊥DC ,CD =2,DD 1=AB =1,P ,Q 分别是CC 1,C 1D 1的中点.求证:AC ∥平面BPQ .【导学号:39292031】图1526【证明】连接CD1,AD1,∵P,Q分别是CC1,C1D1的中点,CD1⊆/平面BPQ,∴PQ∥CD∴CD1∥平面BPQ.又D1Q=AB=1,D1Q∥AB,∴四边形ABQD1是平行四边形,∴AD1∥BQ,又∵AD1⊆/平面BPQ,∴AD1∥平面BPQ.又AD1∩CD1=D1,∴平面ACD1∥平面BPQ.∵AC平面ACD1,∴AC∥平面BPQ.。
高中数学:平行关系的判定学案北师大版必修2

平行关系的判定(学案)一、学习目标1.理解并掌握线面平行与两个平面平行的定义.2.掌握线面平行与两个平面平行的判定定理的证明.3.会画平行或相交平面的空间图形,并用字母或符号表示,进一步培养学生的空间想象能力.二、学习重点、难点1.学习重点:掌握线面平行与两个平面平行的判定定理.2.学习难点:掌握平行的判定定理的证明及其应用.学习过程:一、课前准备:阅读课本P 2 8 – 3 1自主学习1.直线和平面的位置关系有、、2.两个平面的位置关系有、3.直线与面平行的判定4.平面与面平行的判定自主测评1.下列条件中,能得出直线a与平面α平行的条件是()//,//,//.,//,,//.,,,,,,..c a a b cDb a b b a bCA aB aC bD b AC BDA B abbαααααα∈∈∈∈=且2.判断下列命题的正误.(1).如果一个平面内的所有直线都和另一个平面平行,那么这两个平面平行.(2). 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(3).垂直于同一直线的两直线平行.(4).分别在两个平行平面内的两条直线都平行(5).如果一个平面内的无数条直线平行于另一个平面,那么这两个平面平行.(6).如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行.(7).如果一条直线平行于平面内的无数条直线,则此直线行平该平面.//aA aB aC aD aβββββ3.如果直线平面,那么()平面内不存在与垂直的直线()平面内有且只有一条直线与垂直()平面内有且只有一条直线与平行()平面内有无数条直线与不平行二、新课导学探究一:如何两个判定直线与平面平行三、巩固应用例 1.已知:空间四边形ABCD 中,E 、F 分别是AB 、AD 的中点.判断EF 与平面BCD 的位置关系.变式练习: 如图空间四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC满足线面平行位置关系的所有情况.探究二:如何两个判定平面平行例2 已知:在正方体1111D C B A ABCD -中;求证:平面11AB D //平面1C四、能力拓展1.如图所示,在正方体ABCD -A 1B 1C 1D 1中,下列四条直线中与平面AB 1C 平行的是( ) A .. DD 1 B . A 1D 1 C. C 1D 1 D . A 1D 2.平面α 与平面β平行的条件可以是 () A. 平面 α内有无数条直线都与平面β平行B.直线//,//,a a a αβ且直线不在α内,也不在平面β内C. 直线,,//,//b a b a βαβα直线且D. 平面 α内的任意直线都与平面β平行3.如图,长方体ABCD -A 1B 1C 1D 1中,P ,Q ,R 分别为BC ,CD ,CC 1的中点 (1)判断直线B 1D 1与平面PQR 的位置关系 (2)判断平面AB 1D 1与平面PQR 的位置关系 (3)判断平面D D 1B 1B 与平面PQR 的位置关系4.已知如图,四棱锥P-ABCD ,四边形ABCD 为平行四边形,O 为AC 的中点,E 为PB 的中点,求证:EO // 面P AD五、总结提升1.直线和平面相互平行证明方法有哪些2.证明两平面平行的方法:(1)利用定义证明 (2)判定定理 (3)垂直于同一直线的两个平面平行.用符号表示是:a ⊥α,a ⊥β则α∥β. (4)平行于同一个平面的两个平面平行.//,////αβαγβγ⇒。
高中数学 第一章 立体几何初步 5.2 平行关系的性质学案 北师大版必修2-北师大版高一必修2数学学

5.2 平行关系的性质[学习目标] 1.理解直线与平面平行、平面与平面平行的性质定理,并能用文字、符号和图形语言描述定理. 2.会用线面平行、面面平行的性质定理证明相关问题. 3.理解“平行”与“平行”之间的转化.【主干自填】1.直线与平面平行的性质2.平面与平面平行的性质【即时小测】1.思考下列问题(1)分别在两个平行平面的直线有什么位置关系?提示:平行或异面,因为两平面平行无公共点,所以两直线无公共点,即平行或异面.(2)两个平面互相平行,其中一个平面内的直线与另一个平面有什么位置关系?提示:平行.因为两平面平行所以两平面无公共点,所以其中一个平面内的直线与另一个平面无公共点,所以直线与平面平行.(3)若一个平面与两个平行平面同时相交,则交线有什么位置关系?提示:平行.因为交线在同一平面内且无公共点所以两直线平行. 2.已知直线l ∥平面α,直线m α,则直线l 和m 的位置关系是( ) A .相交 B .平行 C .异面 D .平行或异面 提示:D3.如下图所示,直线a ∥平面α,A ∉α,并且a 和A 位于平面α两侧,点B ,C ∈a ,AB 、AC 分别交平面α于点E 、F ,若BC =4,CF =5,AF =3,则EF =________.提示:32 由于点A 不在直线a 上,则A 、B 、C 确定一个平面β,∴α∩β=EF .∵a ∥平面α,∴EF ∥a .∴EF BC =AFAC. ∴EF =AF ×BC AC =3×45+3=32.例1 ABCD 是平行四边形,点P 是平面ABCD 外一点,M 是PC 的中点,在DM 上取一点G ,过G 和AP 作平面交平面BDM 于GH .求证:AP ∥GH .[证明] 连接AC 交BD 于O ,连接MO .∵ABCD是平行四边形,∴O是AC的中点.又M是PC的中点,∴AP∥OM.根据直线和平面平行的判定定理,则有PA∥平面BMD.∵平面PAHG∩平面BMD=GH,根据直线和平面平行的性质定理,∴PA∥GH.[变式训练1]已知:a∥b,aα,bβ,α∩β=l,求证:a∥b∥l. 证明如图所示,∵a∥b,bβ,∴a∥β,又aα,α∩β=l,∴a∥l,又a∥b,∴a∥b∥l.例2 已知α∥β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于点S ,且SA =8,SB =9,CD =34,求当S 在α,β之间时SC 的长.[解] 如图所示.∵AB 与CD 相交于S ,∴AB ,CD 可确定平面γ,且α∩γ=AC ,β∩γ=BD . ∵α∥β,∴AC ∥BD ,∴SA SB =SCSD, ∴SA SA +SB =SC CD ,即SC 34=817,解得SC =16.类题通法由面面平行得到线线平行,进而由成比例线段得解,体现了立体几何与平面几何间的转化关系.另外,面面平行还有许多性质,如要证明线面平行,可先证面面平行,再由性质证得.[变式训练2] 如图,平面α∥β,线段AB 分别交α,β于M ,N ,线段AD 分别交α,β于C ,D ,线段BF 分别交α,β于F ,E .若AM =9,MN =11,NB =15,S △FMC =78.求△END的面积.解 ∵平面α∥β,又平面AND ∩平面α=MC ,平面AND ∩平面β=ND , ∴MC ∥ND ,同理EN ∥FM . 又AM =9,MN =11,NB =15,∴MCND=AMAN=920,FMEN=BMBN=2615,又∠FMC=∠END,∴S△FMCS △END=12FM·MC·sin∠FMC12EN·ND·sin∠END=920×2615=78100,∵S △FMC=78,∴△END的面积S△END=100.例3 如图所示,已知P是▱ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.(1)求证:l∥BC;(2)MN与平面PAD是否平行?试证明你的结论.[解]解法一:(1)证明:因为BC∥AD,BC⊆/平面PAD,AD平面PAD,所以BC∥平面PAD.又因为BC平面PBC,平面PBC∩平面PAD=l,所以BC∥l.(2)平行.取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.可知四边形AMNE为平行四边形.所以MN∥AE,MN⊆/平面APD,AE平面APD,解法二:(1)证明:由AD∥BC,AD⊆/平面PBC,BC平面PBC,所以AD∥平面PBC.又因为AD平面PAD,平面PBC∩平面PAD=l,所以l∥AD∥BC.(2)设Q是CD的中点,连接NQ,MQ,则MQ∥AD.又MQ⊆/平面PAD,AD平面PAD,所以MQ∥平面PAD.同理,由NQ∥PD,可得NQ∥平面PAD,而MQ∩NQ=Q,所以平面MNQ∥平面PAD.又MN平面MNQ,所以MN∥平面PAD.类题通法在空间平行的判断与证明时要注意线线、线面、面面平行关系的转化过程:[变式训练3]在长方体ABCD-A1B1C1D1中,点M是BC的中点,点N是AA1的中点.求证:MN∥平面A1CD.证明设点P为AD的中点,连接MP,NP.∵点M是BC的中点,∴MP∥CD.∵CD平面A1CD,MP⊆/平面A1CD,∵点N是AA1的中点,∴NP∥A1D.∵A1D平面A1CD,NP⊆/平面A1CD,∴NP∥平面A1CD.∵MP∩NP=P,MP平面MNP,NP平面MNP,∴平面MNP∥平面A1CD.∵MN平面MNP,∴MN∥平面A1CD.易错点⊳线面之间平行关系转化不当致错[典例] 如右图所示,平面α∥平面β,AC与BD为异面直线,且ACα,BDβ,M,N分别为AB,CD的中点,求证:MN∥平面β.[错解] 错解一:∵α∥β,ACα,∴AC∥β.又BDβ,∴AC∥BD.∵M,N分别为AB,CD的中点,∴MN∥BD.∵MN⊆/β,BDβ,∴MN∥平面β.错解二:连接BC,取BC的中点P,连接MP,NP,如下图所示.在△ABC中,M,P分别是AB,BC的中点,∴MP∥AC.∵MP⊆/平面α,ACα,∴MP∥平面α.同理,PN∥平面β.∵α∥β,∴MP∥平面β.又PN∩MP=P,∴平面MPN∥平面β,而MN平面MPN,∴MN∥平面β.[错因分析] 错解一中,由AC∥平面β得不到AC与平面β内的所有直线平行.因此,由AC∥平面β,BD平面β得不到AC∥BD.这是对线面平行的性质定理理解不透彻所致.而且若AC∥BD,则A,B,C,D四点共面,与已知条件中AC,BD异面矛盾.错解二中,“∵α∥β,MP∥平面α,∴MP∥平面β”这一步是没有依据的,尽管当MP⊆/β时结论成立,但仍需要证明.[正解]∵AB∩AC=A,∴AB,AC确定一个平面,设该平面为γ,则γ∩α=AC.∵B∈AB,ABγ,B∈β,∴B是γ与β的公共点,于是可设β∩γ=BE,如图所示.连接CE,DE,取CE的中点P,连接MP,PN.∵α∥β,α∩γ=AC,β∩γ=BE,∴AC∥BE.又M,P分别为AB,CE的中点,∴MP∥BE.∵BEβ,MP⊆/β,∴MP∥β.在△CED中,P,N分别为CE,CD的中点,∴PN∥DE.又PN⊆/β,DEβ,∴PN∥β.又MP∩PN=P,∴平面MNP∥平面β.∵MN平面MNP,∴MN∥平面β.课堂小结1.三种平行关系可以任意转化,其相互转化关系如图所示:2.证明线与线、线与面的平行关系的一般规律是:“由已知想性质,由求证得判定”,是分析和解决问题的一般思维方法,而作辅助线和辅助面往往是沟通已知和未知的有效手段.1.如果相异点A、B和相异点C、D分别在异面直线a,b上,那么正确的结论是( ) A.直线AC与BD可能相交B.直线AD与BC可能相交C.AC与BD,AD与BC都是异面直线D.AC与BD,AD与BC不一定都是异面直线答案 C解析本题适合用反证法:假设AC与BD共面,不妨设该平面为α,则A∈α,B∈α,C∈α,D∈α.因为相异点A、B和相异点C、D分别是在异面直线a,b上,所以aα,bα,这与已知a,b是异面直线矛盾,所以假设不成立,即得AC与BD是异面直线;同理可证AD 与BC也是异面直线.2.直线a∥平面α,α内有n条直线交于一点,那么这n条直线中与直线a平行的( ) A.至少有一条B.至多有一条C.有且只有一条D.没有答案 B解析因为n条直线交于一点,所以这n条直线肯定不平行,因此至多有一条直线与a 平行.3.已知直线l∥平面α,P∈α,那么过点P且平行于l的直线( )A.只有一条,不在平面α内B.只有一条,在平面α内C.有两条,不一定都在平面α内D.有无数条,不一定都在平面α内答案 B解析如图所示,∵l∥平面α,P∈α,∴直线l与点P确定一个平面β,α∩β=m,∴P∈m,∴l∥m且m是唯一的.4.过两平行平面α,β外的点P的两条直线AB与CD,它们分别交α于A,C两点,交β于B,D两点,若PA=6,AC=9,PB=8,则BD的长为________.答案12解析两条直线AB与CD相交于P点,所以可以确定一个平面,此平面与两平行平面α,β的交线AC∥BD,所以PAPB=ACBD,又PA=6,AC=9,PB=8,故BD=12.。
北师大版数学高一(北师大)必修2学案 1.5平行关系

5.1平行关系的判定(一)【课时目标】1.理解直线与平面平行的判定定理的含义.2.会用图形语言、文字语言、符号语言准确描述直线与平面平行的判定定理,并知道其地位和作用.3.能运用直线与平面平行的判定定理证明一些空间线面关系的简单问题.1.直线与平面平行的定义:直线与平面无公共点.2.直线与平面平行的判定定理:__________一条直线与______________的一条直线平行,则该直线与此平面平行.用符号表示为________________________.一、选择题1.以下说法(其中a,b表示直线,α表示平面)①若a∥b,bα,则a∥α;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,bα,则a∥b.其中正确说法的个数是()A.0个B.1个C.2个D.3个2.已知a,b是两条相交直线,a∥α,则b与α的位置关系是()A.b∥α B.b与α相交C.bα D.b∥α或b与α相交3.如果平面α外有两点A、B,它们到平面α的距离都是a,则直线AB和平面α的位置关系一定是()A.平行B.相交C.平行或相交D.ABα4.在空间四边形ABCD中,E、F分别是AB和BC上的点,若AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是()A.平行B.相交C.在内D.不能确定5.过直线l外两点,作与l平行的平面,则这样的平面()A.不存在B.只能作出一个C.能作出无数个D.以上都有可能6.过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有()A.4条B.6条C.8条D.12条二、填空题7.经过直线外一点有________个平面与已知直线平行.8.如图,在长方体ABCD-A1B1C1D1的面中:(1)与直线AB平行的平面是______________;(2)与直线AA1平行的平面是______________;(3)与直线AD平行的平面是______________.9.在正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与过点A,E,C的平面的位置关系是_______________________________________________________________.三、解答题10.如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱BC、C1D1的中点.求证:EF∥平面BDD1B1.11.如图所示,P是▱ABCD所在平面外一点,E、F分别在PA、BD上,且PE∶EA=BF∶FD.求证:EF∥平面PBC.能力提升12.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥面MNP的图形的序号是________.(写出所有符合要求的图形序号)13.正方形ABCD与正方形ABEF所在平面相交于AB,在AE,BD上各有一点P,Q,且AP=DQ.求证PQ∥平面BCE.(用两种方法证明)直线与平面平行的判定方法(1)利用定义:证明直线a与平面α没有公共点.这一点直接证明是很困难的,往往借助于反证法来证明.(2)利用直线和平面平行的判定定理:a⊆α,a∥b,bα,则a∥α.使用定理时,一定要说明“不在平面内的一条直线和平面内的一条直线平行”,若不注明和平面内的直线平行,证明过程就不完整.因此要证明a∥平面α,则必须在平面α内找一条直线b,使得a∥b,从而达到证明的目的.证明线线平行时常利用三角形中位线、平行线分线段成比例定理等.5.1平行关系的判定(一)答案知识梳理2.平面外此平面内a⊆α,bα,且a∥b⇒a∥α作业设计1.A[①aα也可能成立;②a,b还有可能相交或异面;③aα也可能成立;④a,b 还有可能异面.]2.D3.C4.A5.D6.D[如图所示,与BD平行的有4条,与BB1平行的有4条,四边形GHFE的对角线与面BB1D1D平行,同等位置有4条,总共12条,故选D.]7.无数8.(1)平面A1C1和平面DC1(2)平面BC1和平面DC1(3)平面B1C和平面A1C19.平行解析设BD的中点为F,则EF∥BD1.10.证明 取D 1B 1的中点O ,连接OF ,OB .∵OF 綊12B 1C 1,BE 綊12B 1C 1,∴OF 綊BE .∴四边形OFEB 是平行四边形,∴EF ∥BO .∵EF ⊆平面BDD 1B 1,BO 平面BDD 1B 1,∴EF ∥平面BDD 1B 1.11.证明 连接AF 延长交BC 于G ,连接PG .在▱ABCD 中, 易证△BFG ∽△DFA .∴GF FA =BF FD =PE EA, ∴EF ∥PG .而EF ⊆平面PBC ,PG 平面PBC ,∴EF ∥平面PBC .12.①③13.证明 方法一 如图(1)所示,作PM ∥AB 交BE 于M ,作QN ∥AB 交BC 于N ,连接MN .∵正方形ABCD 和正方形ABEF 有公共边AB ,∴AE =BD .又∵AP =DQ ,∴PE =QB .又∵PM ∥AB ∥QN ,∴PM AB =PE AE ,QN DC =BQ BD.∴PM ∥QN .∴四边形PQNM 是平行四边形.∴PQ ∥MN .又MN 平面BCE ,PQ ⊆平面BCE , ∴PQ ∥平面BCE .方法二 如图(2)所示,连接AQ 并延长交BC(或其延长线)于K ,连接EK .∵KB ∥AD ,∴DQ BQ =AQ QK. ∵AP =DQ ,AE =BD , ∴BQ =PE .∴DQ BQ =AP PE .∴AQ QK =AP PE.∴PQ ∥EK . 又PQ ⊆面BCE ,EK 面BCE ,∴PQ ∥面BCE .5.1 平行关系的判定(二)【课时目标】 1.理解平面与平面平行的判定定理的含义.2.能运用平面与平面平行的判定定理,证明一些空间面面平行的简单问题.1.平面α与平面β平行是指两平面______公共点.若α∥β,直线a α,则a 与β的位置关系为________.2.定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.一、选择题1.经过平面α外的两个点作该平面的平行平面,可以作出( )A .0个B .1个C .0个或1个D .1个或2个2.α和β是两个不重合的平面,在下列条件中,可判定α∥β的是()A.α内有无数条直线平行于βB.α内不共线三点到β的距离相等C.l、m是平面α内的直线,且l∥α,m∥βD.l、m是异面直线且l∥α,m∥α,l∥β,m∥β3.给出下列结论,正确的有()①平行于同一条直线的两个平面平行;②平行于同一平面的两个平面平行;③过平面外两点,不能作一个平面与已知平面平行;④若a,b为异面直线,则过a与b平行的平面只有一个.A.1个B.2个C.3个D.4个4.若不在同一直线上的三点A、B、C到平面α的距离相等,且A α,则()A.α∥平面ABCB.△ABC中至少有一边平行于αC.△ABC中至多有两边平行于αD.△ABC中只可能有一边与α相交5.两个平面平行的条件是()A.一个平面内一条直线平行于另一个平面B.一个平面内两条直线平行于另一个平面C.一个平面内的任意一条直线平行于另一个平面D.两个平面都平行于同一条直线6.正方体EFGH—E1F1G1H1中,下列四对截面中,彼此平行的一对截面是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G二、填空题7.已知直线a、b,平面α、β,且a∥b,a∥α,α∥β,则直线b与平面β的位置关系为________.8.有下列几个命题:①平面α内有无数个点到平面β的距离相等,则α∥β;②α∩γ=a,α∩β=b,且a∥b(α,β,γ分别表示平面,a,b表示直线),则γ∥β;③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边,则α∥β;④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行,则α∥β.其中正确的有________(填序号).9.如图所示,在正方体ABCD—A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________时,有MN∥平面B1BDD1.三、解答题10.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC和SC的中点.求证:平面EFG∥平面BDD1B1.11.如图所示,B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD,△BCD 的重心.(1)求证平面MNG∥平面ACD;(2)求S△MNG∶S△ADC.能力提升12.三棱柱ABC-A1B1C1,D是BC上一点,且A1B∥平面AC1D,D1是B1C1的中点.求证:平面A1BD1∥平面AC1D.13.如图所示,在正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?判定或证明面面平行的方法(1)面面平行的定义;(2)面面平行的判定定理:如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行;(3)两个平面同时平行于第三个平面,那么这两个平面平行.5.1平行关系的判定(二) 答案知识梳理1.无a∥β作业设计1.C2.D3.B4.B5.C6.A7.b∥β或bβ8.③解析①不正确,当两平面相交时,在一个平面两侧分别有无数点满足条件;②不正确,当平面β与γ相交时也可满足条件;③正确,满足平面平行的判定定理;④不正确,当两平面相交时,也可满足条件.9.M∈线段FH解析∵HN∥BD,HF∥DD1,HN∩HF=H,BD∩DD1=D,∴平面NHF∥平面B1BDD1,故线段FH上任意点M与N连接,有MN∥平面B1BDD1.10.证明如图所示,连接SB,SD,∵F、G分别是DC、SC的中点,∴FG∥SD.又∵SD平面BDD1B1,FG 平面BDD1B1,∴直线FG∥平面BDD1B1.同理可证EG∥平面BDD1B1,又∵EG平面EFG,FG平面EFG,EG∩FG=G,∴平面EFG∥平面BDD1B1.11.(1)证明(1)连接BM,BN,BG并延长分别交AC,AD,CD于P,F,H.∵M,N,G分别为△ABC,△ABD,△BCD的重心,则有BM MP =BN NF =BG GH=2,且P ,H ,F 分别为AC ,CD ,AD 的中点. 连接PF ,FH ,PH ,有MN ∥PF . 又PF 平面ACD ,MN 平面ACD , ∴MN ∥平面ACD .同理MG ∥平面ACD ,MG∩MN =M , ∴平面MNG ∥平面ACD . (2)解 由(1)可知MG PH =BG BH =23,∴MG =23PH .又PH =12AD ,∴MG =13AD .同理NG =13AC ,MN =13CD .∴△MNG ∽△ACD ,其相似比为1∶3. ∴S △MNG ∶S △ACD =1∶9. 12.证明 连接A 1C 交AC 1于点E , ∵四边形A 1ACC 1是平行四边形, ∴E 是A 1C 的中点,连接ED , ∵A 1B ∥平面AC 1D , ED 平面AC 1D , ∴A 1B 与ED 没有交点,又∵ED 平面A 1BC ,A 1B 平面A 1BC , ∴ED ∥A 1B .∵E 是A 1C 的中点,∴D 是BC 的中点. 又∵D 1是B 1C 1的中点, ∴BD 1∥C 1D ,A 1D 1∥AD ,∴BD 1∥平面AC 1D ,A 1D 1∥平面AC 1D .又A1D1∩BD1=D1,∴平面A1BD1∥平面AC1D.13.解当Q为CC1的中点时,平面D1BQ∥平面PAO.∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.∵P、O为DD1、DB的中点,∴D1B∥PO.∴D1B∥平面PAO,QB∥平面PAO,又PO∩PA=P,D1B∩QB=B,∴平面D1BQ∥平面PAO.5.2平行关系的性质(一)【课时目标】1.能应用文字语言、符号语言、图形语言准确地描述直线与平面平行的性质定理.2.能运用直线与平面平行的性质定理,证明一些空间线面平行关系的简单问题.直线与平面平行的性质定理:如果一条直线与一个平面平行,那么________________________________________________________.(1)符号语言描述:________________.(2)性质定理的作用:可以作为直线和直线平行的判定方法,也提供了一种作平行线的方法.一、选择题1.a,b是两条异面直线,P是空间一点,过P作平面与a,b都平行,这样的平面() A.只有一个B.至多有两个C.不一定有D.有无数个2.两条直线都和一个平面平行,则这两条直线的位置关系是()A.平行B.相交C.异面D.以上均可能3.如图,在四面体ABCD中,若截面PQMN是正方形,则在下列命题中,错误的为()A.AC⊥BDB.AC∥截面PQMNC.AC=BDD.异面直线PM与BD所成的角为45°4.如图所示,长方体ABCD-A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF 的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是()A.平行B.相交C.异面D.平行和异面5.直线a∥平面α,α内有n条直线交于一点,则这n条直线中与直线a平行的直线() A.至少有一条B.至多有一条C.有且只有一条D.没有6.如图所示,平面α∩β=l1,α∩γ=l2,β∩γ=l3,l1∥l2,下列说法正确的是()A.l1平行于l3,且l2平行于l3B.l1平行于l3,且l2不平行于l3C.l1不平行于l3,且l2不平行于l3D.l1不平行于l3,但l2平行于l3二、填空题7.设m、n是平面α外的两条直线,给出三个论断:①m∥n;②m∥α;③n∥α.以其中的两个为条件,余下的一个为结论,构造三个命题,写出你认为正确的一个命题:______________.(用序号表示)8.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=a3,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.9.已知(如图)A、B、C、D四点不共面,且AB∥平面α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG的形状是______________.三、解答题10.ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.11.如图所示,三棱锥A—BCD被一平面所截,截面为平行四边形EFGH.求证:CD∥平面EFGH.能力提升12.如图所示,在空间四边形ABCD中,E、F、G、H分别是四边上的点,它们共面,并且AC∥平面EFGH,BD∥平面EFGH,AC=m,BD=n,当四边形EFGH是菱形时,AE∶EB=________.13.如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.(1)求证:BC∥l;(2)MN与平面PAD是否平行?试证明你的结论.直线与平面平行判定定理和直线与平面平行性质定理经常交替使用,也就是通过线线平行推出线面平行,再通过线面平行推出新的线线平行,复杂的题目还可继续推下去.可有如下示意图:线线平行――→在平面内作或找一直线线面平行――→经过直线作或找平面与平面相交的交线线线平行.5.2 平行关系的性质(一) 答案知识梳理过该直线的任意一个平面与已知平面的交线与该直线平行 (1)⎭⎪⎬⎪⎫a ∥αa ββ∩α=b ⇒a ∥b作业设计 1.C 2.D3.C [∵截面PQMN 为正方形, ∴PQ ∥MN ,PQ ∥面DAC .又∵面ABC∩面ADC =AC ,PQ 面ABC , ∴PQ ∥AC ,同理可证QM ∥BD . 故有选项A 、B 、D 正确,C 错误.] 4.A [∵E 、F 分别是AA 1、BB 1的中点, ∴EF ∥AB .又AB ⊆平面EFGH ,EF 平面EFGH , ∴AB ∥平面EFGH .又AB 平面ABCD ,平面ABCD∩平面EFGH =GH , ∴AB ∥GH .]5.B [设这n 条直线的交点为P ,则点P 不在直线a 上,那么直线a 和点P 确定一个平面β,则点P 既在平面α内又在平面β内,则平面α与平面β相交,设交线为直线b ,则直线b 过点P .又直线a ∥平面α,则a ∥b .很明显这样作出的直线b 有且只有一条,那么直线b 可能在这n 条直线中,也可能不在,即这n 条直线中与直线a 平行的直线至多有一条.]6.A [∵l 1∥l 2,l 2γ,l 1⊆γ, ∴l 1∥γ. 又l 1β,β∩γ=l 3,∴l 1∥l 3 ∴l 1∥l 3∥l 2.]7.①②⇒③(或①③⇒②)解析 设过m 的平面β与α交于l . ∵m ∥α,∴m ∥l ,∵m ∥n ,∴n ∥l , ∵n ⊆α,l α,∴n ∥α. 8.223a解析 ∵MN ∥平面AC ,平面PMN∩平面AC =PQ , ∴MN ∥PQ ,易知DP =DQ =2a3,故PQ =PD 2+DQ 2=2DP =22a3.9.平行四边形解析 平面ADC∩α=EF ,且CD ∥α, 得EF ∥CD ;同理可证GH ∥CD ,EG ∥AB ,FH ∥AB . ∴GH ∥EF ,EG ∥FH . ∴四边形EFGH 是平行四边形.10.解 如图所示,连接AC 交BD 于O ,连接MO , ∵ABCD 是平行四边形,∴O 是AC 中点,又M 是PC 的中点, ∴AP ∥OM .根据直线和平面平行的判定定理,则有PA ∥平面BMD .∵平面PAHG∩平面BMD =GH , 根据直线和平面平行的性质定理, ∴PA ∥GH .11.证明 ∵四边形EFGH 为平行四边形, ∴EF ∥GH .又GH 平面BCD ,EF ⊆平面BCD . ∴EF ∥平面BCD .而平面ACD∩平面BCD =CD ,EF 平面ACD , ∴EF ∥CD .而EF 平面EFGH ,CD ⊆平面EFGH , ∴CD ∥平面EFGH . 12.m ∶n解析 ∵AC ∥平面EFGH , ∴EF ∥AC ,GH ∥AC ,∴EF =HG =m·BE BA ,同理EH =FG =n·AEAB .∵EFGH 是菱形,∴m·BE BA =n·AEAB ,∴AE ∶EB =m ∶n .13.(1)证明 因为BC ∥AD ,AD 平面PAD , BC ⊆平面PAD ,所以BC ∥平面PAD . 又平面PAD∩平面PBC =l ,BC 平面PBC , 所以BC ∥l .(2)解 MN ∥平面PAD . 证明如下:如图所示,取DC 的中点Q . 连接MQ 、NQ . 因为N 为PC 中点, 所以NQ ∥PD .因为PD 平面PAD ,NQ ⊆平面PAD ,所以NQ ∥平面PAD .同理MQ ∥平面PAD . 又NQ 平面MNQ ,MQ 平面MNQ , NQ∩MQ =Q ,所以平面MNQ ∥平面PAD . 所以MN ∥平面PAD .5.2 平行关系的性质(二)【课时目标】 1.会用图形语言、文字语言、符号语言准确地描述平面与平面平行的性质定理.2.能运用平面与平面平行的性质定理,证明一些空间面面平行关系的简单命题.平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,________________________.(1)符号表示为:⎭⎪⎬⎪⎫α∥βα∩γ=a β∩γ=b ⇒a ∥b . (2)性质定理的作用:利用性质定理可证线线平行,也可用来作空间中的平行线. (3)面面平行的其他性质:①两平面平行,其中一个平面内的任一直线平行于另一个平面,即⎭⎪⎬⎪⎫α∥βaα⇒______,可用来证明线面平行;②夹在两个平行平面间的平行线段相等; ③平行于同一平面的两个平面平行.一、选择题1.下列说法正确的是( )A .如果两个平面有三个公共点,那么它们重合B .过两条异面直线中的一条可以作无数个平面与另一条直线平行C .在两个平行平面中,一个平面内的任何直线都与另一个平面平行D .如果两个平面平行,那么分别在两个平面中的两条直线平行 2.设平面α∥平面β,直线aα,点B ∈β,则在β内过点B 的所有直线中( )A .不一定存在与a 平行的直线B .只有两条与a 平行的直线C .存在无数条与a 平行的直线D .存在惟一一条与a 平行的直线3.如图所示,P 是三角形ABC 所在平面外一点,平面α∥平面ABC ,α分别交线段PA 、PB 、PC 于A′、B′、C′,若PA′∶AA′=2∶3,则S △A′B′C′∶S △ABC 等于( )A .2∶25B .4∶25C .2∶5D .4∶54.α,β,γ为三个不重合的平面,a ,b ,c 为三条不同的直线,则有下列命题,不正确的是( )① ⎭⎪⎬⎪⎫a ∥c b ∥c ⇒a ∥b; ② ⎭⎪⎬⎪⎫a ∥γb ∥γ⇒a ∥b ; ③ ⎭⎪⎬⎪⎫α∥c β∥c ⇒α∥β; ④ ⎭⎪⎬⎪⎫α∥γβ∥γ⇒α∥β; ⑤ ⎭⎪⎬⎪⎫α∥c a ∥c ⇒α∥a; ⑥⎭⎪⎬⎪⎫α∥γa ∥γ⇒a ∥α. A .④⑥ B .②③⑥C .②③⑤⑥D .②③5.设α∥β,A ∈α,B ∈β,C 是AB 的中点,当A 、B 分别在平面α、β内运动时,那么所有的动点C( )A .不共面B .当且仅当A 、B 分别在两条直线上移动时才共面C .当且仅当A 、B 分别在两条给定的异面直线上移动时才共面D .不论A 、B 如何移动,都共面6.已知平面α∥平面β,P 是α,β外一点,过点P 的直线m 与α,β分别交于点A ,C ,过点P 的直线n 与α,β分别交于点B ,D ,且PA =6,AC =9,PD =8,则BD 的长为( )A .16B .24或245C .14D .20二、填空题7.分别在两个平行平面的两个三角形,(1)若对应顶点的连线共点,那么这两个三角形具有______关系;(2)若对应顶点的连线互相平行,那么这两个三角形具有________关系.8.过正方体ABCD -A 1B 1C 1D 1的三个顶点A 1、C 1、B 的平面与底面ABCD 所在平面的交线为l ,则l 与A 1C 1的位置关系是________.9.已知平面α∥β∥γ,两条直线l 、m 分别与平面α、β、γ相交于点A 、B 、C 与D 、E 、F .已知AB =6,DE DF =25,则AC =________.三、解答题10.如图所示,已知正方体ABCD -A 1B 1C 1D 1中,面对角线AB 1,BC 1上分别有两点E 、F ,且B 1E =C 1F .求证:EF ∥平面ABCD .11.如图,在三棱柱ABC -A 1B 1C 1中,M 是A 1C 1的中点,平面AB 1M ∥平面BC 1N ,AC∩平面BC 1N =N .求证:N 为AC 的中点.能力提升12.如图所示,在底面是平行四边形的四棱锥P-ABCD中,点E在PD上,且PE∶ED=2∶1,在棱PC上是否存在一点F,使BF∥平面AEC?并证明你的结论.13.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,能否确定截面的形状?如果能,求出截面的面积.1.在空间平行的判断与证明时要注意线线、线面、面面平行关系的转化过程:2.强调两个问题(1)一条直线平行于一个平面,就平行于这个平面内的一切直线,这种说法是不对的,但可以认为这条直线与平面内的无数条直线平行.(2)两个平面平行,其中一个平面内的直线必定平行于另一平面,但这两个平面内的直线不一定相互平行,也有可能异面.5.2平行关系的性质(二) 答案知识梳理那么它们的交线平行(3)①a∥β作业设计1.C[由两平面平行的定义知:一平面内的任何直线与另一平面均无交点,所以选C.]2.D [直线a 与B 可确定一个平面γ,∵B ∈β∩γ,∴β与γ有一条公共直线b .由线面平行的性质定理知b ∥a ,所以存在性成立.因为过点B 有且只有一条直线与已知直线a 平行,所以b 惟一.]3.B [面α∥面ABC ,面PAB 与它们的交线分别为A′B′,AB ,∴AB ∥A′B′,同理B′C′∥BC ,易得△ABC ∽△A′B′C′,S △A′B′C′∶S △ABC =(A′B′AB )2=(PA′PA )2=425.] 4.C [由公理4及平行平面的传递性知①④正确.举反例知②③⑤⑥不正确.②中a ,b 可以相交,还可以异面;③中α,β可以相交;⑤中a 可以在α内;⑥中a 可以在α内.]5.D [如图所示,A′、B′分别是A 、B 两点在α、β上运动后的两点,此时AB 中点变成A′B′中点C′,连接A′B ,取A′B 中点E .连接CE 、C′E 、AA′、BB′、CC′.则CE ∥AA′,∴CE ∥α.C′E ∥BB′,∴C′E ∥β.又∵α∥β,∴C′E ∥α.∵C′E∩CE =E .∴平面CC′E ∥平面α.∴CC′∥α.所以不论A 、B 如何移动,所有的动点C 都在过C 点且与α、β平行的平面上.]6.B [当P 点在平面α和平面β之间时,由三角形相似可求得BD =24,当平面α和平面β在点P 同侧时可求得BD =245.] 7.(1)相似 (2)全等8.平行解析 由面面平行的性质可知第三平面与两平行平面的交线是平行的.9.15解析 由题可知DE DF =AB AC ⇒AC =DF DE ·AB =52×6=15. 10.证明 方法一 过E 、F 分别作AB 、BC 的垂线,EM 、FN 分别交AB 、BC 于M 、N,连接MN.∵BB1⊥平面ABCD,∴BB1⊥AB,BB1⊥BC,∴EM∥BB1,FN∥BB1,∴EM∥FN,∵AB1=BC1,B1E=C1F,∴AE=BF,又∠B1AB=∠C1BC=45°,∴Rt△AME≌Rt△BNF,∴EM=FN.∴四边形MNFE是平行四边形,∴EF∥MN.又MN平面ABCD,EF 平面ABCD,∴EF∥平面ABCD.方法二过E作EG∥AB交BB1于G,连接GF,∴B1EB1A=B1GB1B,B1E=C1F,B1A=C1B,∴C1FC1B=B1GB1B,∴FG∥B1C1∥BC.又∵EG∩FG=G,AB∩BC=B,∴平面EFG∥平面ABCD.又EF平面EFG,∴EF∥平面ABCD.11.证明∵平面AB1M∥平面BC1N,平面ACC1A1∩平面AB1M=AM,平面BC1N∩平面ACC1A1=C1N,∴C1N∥AM,又AC∥A1C1,∴四边形ANC1M为平行四边形,∴AN 綊C 1M =12A 1C 1=12AC , ∴N 为AC 的中点.12.解当F 是棱PC 的中点时,BF ∥平面AEC .证明如下: 取PE 的中点M ,连接FM ,则FM ∥CE , ①由EM =12PE =ED ,知E 是MD 的中点, 设BD∩AC =O ,则O 为BD 的中点,连接OE , 则BM ∥OE , ② 由①②可知,平面BFM ∥平面AEC ,又BF 平面BFM ,∴BF ∥平面AEC .13.解 能.取AB ,C 1D 1的中点M ,N ,连接A 1M ,MC ,CN ,NA 1,∵A 1N ∥PC 1且A 1N =PC 1,PC 1∥MC ,PC 1=MC ,∴四边形A 1MCN 是平行四边形,又∵A 1N ∥PC 1,A 1M ∥BP ,A 1N∩A 1M =A 1,C 1P∩PB =P ,∴平面A 1MCN ∥平面PBC 1,因此,过点A 1与截面PBC 1平行的截面是平行四边形. 连接MN ,作A 1H ⊥MN 于点H ,∵A 1M =A 1N =5,MN =22,∴A 1H =3.∴S △A 1MN =12×22×3=6.故S▱A1MCN=2S△A1MN=26.。
北师大版数学高一必修二1.5.1《平行关系的判定》导学案1

1.5.1平行关系的判定 导学案【学习目标】 掌握线面平行的判定定理及应用【重点难点】 线面平行的判定定理【学法指导】归纳推理【知识链接】平面内能证明两条直线平行的方法有哪些?【学习过程】一、直线与平面平行的判定定理:符号表示为 ⎫⎪⎬⎪⎭⇒ l ∥α 图形表示为看课本29页例1填空⎫⎪⎬⎪⎭⇒EF ∥α例2空间四边形ABCD 中,,,,E F G H 分别是AB ,BC ,CD ,DA 的中点,求证:BD∥平面EFGH例2 图 例3 图例3.如图所示,P 是平行ABCD 所在平面外一点,E ,F 分别是PA ,BD 的中点,求证:EF ∥平面PBC练习:1,2,3【回顾小结】本节课学习了线面平行的判定定理及应用【课堂检测】1下列叙述正确的个数是( )① 如果,a b 是两条直线a ∥b ,,那麽a 平行经过b 的任何一个平面 ② 如果直线a 平面PDA Bα,那麽a 与α内的任何直线平行 ③如果,a b 满足a ∥α,b ∥α,则直线a ∥bA 0 1 C 2 D 32可以得到一条直线与一个平面平行的条件是A 直线和平面内两条直线平行线不相交B 直线和平面内两条相交直线不相交C 直线和平面内无数条相交直线不相交D 直线 和平面内任何直线不相交3.在长方体中1111ABCD A B C D -中(1)与直线AB 平行的平面是(2)与直线1AA 平行的平面是(3)与直线1AB 平行的平面是4 在正方体中 求证:A C ∥平面11A BC【作业布置】学案61页例1变试训练及例2【自我反思】。
高中数学新北师大版精品学案《平行关系的性质》

平行关系的性质【学习目标】1.会用图形语言、文字语言、符号语言准确地描述平面与平面平行的性质定理。
2.能运用平面与平面平行的性质定理,证明一些空间面面平行关系的简单命题。
【学习重难点】学习重点理解平行关系的性质定理。
学习难点平行关系性质定理的应用。
【学习过程】一、知识梳理平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,________________________。
(1)符号表示为:错误!⇒a∥B.(2)性质定理的作用:利用性质定理可证线线平行,也可用来作空间中的平行线。
(3)面面平行的其他性质:①两平面平行,其中一个平面内的任一直线平行于另一个平面,即错误!⇒______,可用来证明线面平行;②夹在两个平行平面间的平行线段相等;③平行于同一平面的两个平面平行。
【达标检测】一、选择题1.下列说法正确的是()A.如果两个平面有三个公共点,那么它们重合B.过两条异面直线中的一条可以作无数个平面与另一条直线平行C.在两个平行平面中,一个平面内的任何直线都与另一个平面平行D.如果两个平面平行,那么分别在两个平面中的两条直线平行2.设平面α∥平面β,直线aα,点B∈β,则在β内过点B的所有直线中()A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在惟一一条与a平行的直线3.如图所示,与α,β分别交于点A,C,过点分别与平面α、β、γ相交于点A、B、C与D.E、F。
已知AB=6,错误!=错误!,则AC=________。
三、解答题10如图所示,已知正方体ABCD-A1B1C1D1中,面对角线AB1,BC1上分别有两点E、F,且B1E=C1F。
求证:EF∥平面ABCD.11.如图,在三棱柱ABC-A1B1C1中,M是A1C1的中点,平面AB1M∥平面BC1N,AC∩平面BC1N=N。
求证:N为AC的中点。
【学习拓展】12.如图所示,在底面是平行四边形的四棱锥、FN分别交AB.BC于M、N,连接MN。
北师大版数学高一(北师大)必修2学案 1.5直线、平面平行的判定与性质

1.5《直线、平面平行的判定与性质》导学案【学习目标】(1)理解并掌握直线与平面平行的判定定理;理解并掌握两平面平行的判定定理。
(2)进一步培养学生观察、发现的能力和空间想象能力; (3)掌握直线与平面平行的性质定理及其应用; (4)掌握两个平面平行的性质定理及其应用。
【导入新课】观察身边的实物,如教材第55页观察题:封面所在直线与桌面所在平面具有什么样的位置关系?如何去确定这种关系呢?这就是我们本节课所要学习的内容。
新授课阶段1. 直线与平面平行的判定定理:简记为:线线平行,则线面平行。
符号表示: a αb β => a ∥α a ∥ b例1 如图,已知点P 是平行四边形ABCD 所在平面外的一点,E ,F 分别是PA ,BD 上的点且PE EA BF FD ∶∶,求证:EF //平面PBC .αa αabP EA CBDF证明:例2 如图,长方体1111ABCD A B C D 中,11E F 是平面11A C 上的线段,求证:11E F //平面AC .证明:2.两个平面平行的判定定理:ABCD1A1D 1B1C 1F1E符号表示: a β b β a∩b = P β∥α a ∥α b ∥α指出:判断两平面平行的方法有三种: (1)用定义; (2)判定定理;(3)垂直于同一条直线的两个平面平行。
例3 如图,在正方体1111ABCD A B C D 中,求证:平面1A BD //平面11CD B . 证明:3. 直线与平面平行的性质定理。
1D1A1C1BABDC定理:。
符号表示:a∥αa β a∥bα∩β= b作用:利用该定理可解决直线间的平行问题。
4. 两个平面平行的性质定理定理:。
符号表示:α∥βα∩γ= a a∥bβ∩γ= b指出:可以由平面与平面平行得出直线与直线平行例4 如图,线段AB,CD所在直线是异面直线,E,F,G,H分别是线段AC,CB,BD,DA的中点.(1)求证:EFGH共面且AB∥面EFGH,CD∥面EFGH;(2)设P,Q分别是AB和CD上任意一点,求证:PQ被平面EFGH平分.AE HCFBGD M PQ N证明:课堂小结1、面面平行的定义;2、面面平行的判定定理和性质定理;3、面面平行判定定理的应用:要证面面平行,只要证线面平行,而要证线面平行,只要证线线平行。
北师大版高中必修25.1平行关系的判断课程设计 (2)

北师大版高中必修25.1平行关系的判断课程设计1. 课程目标本课程旨在通过对平行关系的掌握,使学生掌握平行关系的定义、性质和判定方法,进一步提高他们的数学素养和解决实际问题的能力。
2. 教学内容本课程主要包括以下内容:1.平行线的定义和性质2.平行线的判定方法3.平行四边形的性质3. 教学流程3.1 教学准备1.教师应提前准备好课件和讲义,并测试好电脑和投影仪等教学设备。
2.教师应准备好学生所需的教材和教具。
3.2 知识点讲解3.2.1 平行线的定义和性质平行线是指不相交的两条直线,在同一平面内留下的两个对应的内角或外角相等的直线。
平行线的性质:•平行线与同一直线上的点所成的相邻角互补;•平行线分别与一条横穿它们的第三条直线所成的对应角相等;•平行线分别与一条穿过它们的截线所成的内角互补。
3.2.2 平行线的判定方法平行线的判定方法有以下三种:•利用相邻角或对应角相等来判定;•利用平行四边形的对角线相等来判定;•利用相交线上的内角互补来判定。
3.2.3 平行四边形的性质平行四边形是指四边形中对边平行的四边形。
平行四边形的性质:•对边平行;•对角线相交于他们的中点;•相邻角互补;•对角线等长;•对角线平分另一对角。
3.3 实例演练教师通过展示实例进行讲解,并邀请学生举手回答问题。
3.4 作业布置教师布置作业,要求学生在家完成相关练习。
4. 教学评估教师可以采用小组讨论、课堂测试等方式对学生进行教学评估。
5. 结束语本课程主要讲解了平行关系的定义、性质和判定方法,以及平行四边形的性质。
希望同学们能够认真学习,提高自己的数学素养和解决问题的能力。
