第四章+空间轴对称问题的有限元
有限单元法 第4章 空间轴对称问题的有限元分析

am ui bm u j cm um
am wi bm w j cm wm
其中:
1 A 1 rj 2 1 rm 1 ri zi zj zm
有限单元法
ai rj zm zmrj a j rm zi zi rm
有限单元法
4.1 概述
在工程中有许多结构,如活塞、厚壁容器等,他们的几 何形状、约束情况及所受的荷载都对称于空间的某一根轴, 因此在物体中通过该轴的任何平面都是对称面,所有应力、 应变和位移也对称于该轴,这类问题称为空间轴对称问题。 研究轴对称问题时通常采用圆柱坐标系 (r, z, ) ,以 z 轴为 对称轴。
6.1.1 基本假设 分析薄板弯曲的挠度问题时,和材料力学中分析直梁的 弯曲问题时相似(薄板的中面相当于直梁的轴线,薄板的弹 性曲面相当于直梁的挠曲线),也采用一些由实践经验得到
的基本假设,使问题大大简化,但同时又能在一定程度上反
映实际情况。这些基本假设是: (1)薄板的法线变形后没有伸缩。
(2)变形前的中面法线在变形后仍是弹性曲面的法线。
z (rm , zm) m wm um wj uj
wi ui
j ( r j, z j)
i ( r i, z i) O
r
参照平面问题的三角形单元位移函数,轴对称问题的三结点 三角形单元位移函数取为,
u a1 a2 r a3 z w a4 a5 r a6 z
有限单元法
教学要求:本章要求学生重点掌握运用三角形单元进行 薄板的有限元分析,包括位移模式、单元分析、整体分析、 等效结点荷载计算等。同时要熟悉矩形单元的运用,了解八 结点四边形等参单元的分析过程。
第4章 轴对称问题和空间问题有限元法

(1 )(1 2) 1 1
1
0
0
0
0
1 2 2(1 )
7
轴对称单元的特点(与平面三角形单元的区别)
轴对称单元为圆环体,单元与单元间为节圆相连接;
节点力与节点载荷是施加于节圆上的均布力;
单元边界是一回转面;
应变分量 中出现了 ur r ,即应变不是常量;
且应变矩阵在r→0时,存在奇异点,需特殊处
由于几何矩阵中的元素不是常量,单元刚度矩阵需要通过积分得到,
为简化计算可以用三角形单元形心位置的坐标 rc , zc代替 B 矩阵中的变
量 。r, z
rc
1 3
(ri
rj
rm )
zc
1 3
(
zi
zj
zm )
实践证明采用近似积分也能达到一定的精度,具体对于三角形环单元
用形心处坐标代替应变矩阵中的坐标变量。
uj wj
N
q
um
wm
单元应变:
将单元位移函数代入几何方程得:
u r
1 2A (biuiBiblioteka bju jbmum )
u r
1 2A
(
fi
ui
f
ju j
f mum )
11
其中,
fs
as r
bs
cs zs r
(s i, j, m)
w z
1 2A
(ci
wi
cjwj
cmwm )
u z
1 2A (ciui
Fe
Fir
Fiz
=
2A
15
9rc2
0
2ri2
rjrm
(3) 分布面力移置
有限元 第四章轴对称问题

其中子矩阵
K k
st
s 1,2,, n; t 1,2, , n
返回
e 1
st
(4-29)
第三节
等效结点载荷计算
与平面问题类似,当结构外载荷不作用在结点上时,也 需要将这些作用在环形单元上的集中力、表面力和体积力分 别等效移置到结点上。移置的原则也是要求这些外力和等效 结点载荷在任意虚位移上所作的虚功相等,即
z
d
c
m j
i i
m j
a b
r
图4-1 轴对称结构
相邻的单元由圆环形 的铰链相连接。单元的棱 边都是圆,故称为结圆。 每个结圆与rz平面的交点称 为结点。 如图4-2中的 i, j, m点。
z rj j
rm
m
v
u ri i
这样,各单元在子午面rz平 面上形成三角形网格,就如 同平面问题中在xy平面上的 网格一样。采用位移法有限 元分析,其基本未知量为结 点位移。单元的结点位移列 阵如下:
T * e
Re * rdrdzd
T
(4-17)
上式等号左边为单元结点力所作的虚功,与平面问题不同的是 这里所说的结点力是指作用在整个结圆上的力,等式右边是指 整个三角形环状单元中应力的虚功。 将(4-14)式和(4-16)式代入(4-17)式,则得
R
单元的各应力分量可通过将式(5-12)代入轴对称问题 的物理方程得到
r e Z D D B S i rZ
Sj
S m
e
(4-14)
式中:[S]是三角形截面环形单元的应力矩阵。它的子矩阵为
第4章 空间问题有限元分析-轴对称

Re N T f p
FL e 2 r0 N T 62 f p 21
圆环 2 r0 Ni f pr Ni f pz N j f pr
N j f pz
Nm f pr
T
Nm f pz
r0 -- 集中力作用点的径向坐标。
2019/10/18
第4章 空间问题有限元分析 空间轴对称问题
曹国华
2019/10/18
空间有限元分析-轴对称
1
主要内容
§ 4.1位移模式 § 4.2几何方程 § 4.3单元刚度 § 4.4等效载荷
2019/10/18
空间有限元分析-轴对称
3
1、研究对象
当弹性体的几何形状,约束情况,以及所受的外力都 轴对称于某一轴,则这种弹性体的应力分析问题称为轴对 称应力分析问题,在工程中如 活塞,压力容器等 。
空间有限元分析-轴对称
12
几何方程与物理方程
PA线应变
0,(略去高阶小量).
PB线应变
εφ
PB PB PB
(u
φ
uφ φ
d φ)
u
ρdφ
1 uφ ; ρ φ
PA转角
α
DA
uφ ρ
d
ρ
uφ
,
PA d ρ ρ
2019/10/18
空间有限元分析-轴对称
空间有限元分析-轴对称
28
等效载荷
r Niri N j rj Nmrm
2、体积力移置
FFGee 2 [N] f rdrdz
若体积力为重,则单位体积 的力为
f
=-0
轴对称问题的有限元分析

第1节基本知识本节的有限元对象为轴对称问题,目的是学习将3D问题转化为2D问题分析的轴对称方法,涉及如何选取轴对称单元、建模规律、载荷的施加方法和后处理技术。
一、轴对称问题的定义轴对称问题是指受力体的几何形状、约束状态,以及其它外在因素都对称于某一根轴(过该轴的任一平面都是对称面)。
轴对称受力体的所有应力、应变和位移均对称于这根轴。
二、用ANSYS解决2D轴对称问题的规定用ANSYS解决2D轴对称问题时,轴对称模型必须在总体坐标系XOY平面的第一象限中创建,并且Y轴为轴旋转的对称轴。
求解时,施加自由约束、压力载荷、温度载荷和Y方向的加速度可以像其它非轴对称模型一样进行施加,但集中载荷有特殊的含义,它表示的是力或力矩在360°范围内的合力,即输入的是整个圆周上的总的载荷大小。
同理,在求解完毕后进行后处理时,轴对称模型输出的反作用力结果也是整个圆周上的合力输出,即力和力矩按总载荷大小输出。
在ANSYS中,X方向是径向,Z方向是环向,受力体承载后的环向位移为零,环向应力和应变不为零。
常用的2D轴对称单元类型和用途见表11-1。
表11-1 2D轴对称常用结构单元列表的高阶单的高阶单在利用ANSYS进行有限元分析时,将这些单元定义为新的单元后,设置单元配置项KEYOPT(3)为Axisymmetric(Shell51和Shell61单元本身就是轴对称单元,不用设置该项),单元将被指定按轴对称模型进行计算。
后处理时,可观察径向和环向应力,它对应的是SX与SZ应力分量,并且在直角坐标系下观察即可。
可以通过轴对称扩展设置将截面结果扩展成任意扇型区域大小的模型,以便更加真实地观察总体模型的各项结果。
轴对称问题有限元分析实例 2D节2第p=1000 N/mF2y611xO61211-1 圆柱筒壳示意图图——圆柱筒的静力分析一、案例1问题,直0.1 m1000 N/m的压力作用,其厚度为如图11-1所示,圆柱筒材质为A3钢,受,并且圆柱筒壳的下部轴线方向固定,其它方向自由,试计算其变形、mm,高度为16 径12径向应力和轴向应力。
轴对称问题的有限元分析

第1节基本知识本节的有限元对象为轴对称问题,目的是学习将3D问题转化为2D问题分析的轴对称方法,涉及如何选取轴对称单元、建模规律、戦荷的施加方法和后处理技术。
一、轴对称问题的定义轴对称问题是指受力体的几何形状、约束状态,以及其它外在因素都对称于某•根轴(过该轴的任•平而都是对称而)。
轴对称受力体的所有应力、应变和位移均对称于这根轴。
二、用ANSYS解决2D轴对称问题的规定用ANSYS解决2D轴对称问题时,轴对称模型必须在总体坐标系XOY平面的第•象限中创建,并且Y 轴为轴旋转的对称轴。
求解时,施加自由约束、压力载荷、温度载荷和Y方向的加速度可以像其它非轴对称模型•样进行施加,但集中戦荷有特殊的含义,它农示的是力或力矩在360。
范圉内的合力,即输入的是整个圆周上的总的载荷人小。
同理,在求解完毕后进行后处理时,轴对称模型输出的反作用力结果也是整个圆周上的合力输出,即力和力矩按总载荷大小输出。
在ANSYS中,X方向是径向,Z方向是环向,受力体承载后的环向位移为零,环向应力和应变不为零。
常用的2D轴对称单元类型和用途见衣U-U表11-1 2D轴对称當用结构单元列表的岛阶单的阶恥在利用ANSYS进行有限元分析时,将这些单元定义为新的单元后,设置单元配置项KEYOPT (3) 为Axis\Tnmetric (ShellSl和She 1161单元本身就是轴对称单元,不用设置该项),单元将彼指定按轴对称模型进行计算。
后处理时,可观察径向和环向应力,它对应的是SX与SZ应力分量,并且在直角坐标系下观察即可。
可以通过轴对称扩展设置将藏而结果扩展成任意扇型区域大小的模型,以便更加真实地观察总体模型的各项结果。
轴对称问题有限元分析实例2D节2第2y611xO612n-i閲柱简壳示总图图——圆柱筒的静力分析•、案例1问题,宜O.lmlOOON/m的压力作用,其厚度为如图11-1所示,圆柱筒材质为A3钢,受,并且圆柱筒壳的下部轴线方向固定,其它方向自由,试计算其变形、mm.高度为16径12径向应力和轴向应力。
4 弹性力学轴对称问题的有限元法

4. 彈性力學軸對稱問題的有限元法本章包括以下內容:4.1用虛功方程建立有限元方程 4.2三結點單元位移函數 4.3三結點單元剛度矩陣 4.4載荷移置4.5軸對稱分析舉例4.1用虛功方程建立有限元方程物體的幾何形狀、約束情況及所受的外力都對稱於空間的某一根軸,因此在物體中通過該軸的任何平面都是對稱面,所有應力、應變和位移也對稱於該軸,這類問題稱為軸對稱問題。
研究軸對稱問題時通常採用圓柱坐標系(r ,θ,z ),以z 軸為對稱軸。
圖4.1受均布內壓作用的長圓筒如圖4.1所示的受均布內壓作用的長圓筒,通過Z 軸的一個縱截面就是對稱面。
由於對稱性,軸對問題共有4個應力分量:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zrz r τσσσσθ}{ (4-1)其中r σ表示沿半徑方向的正應力,稱為徑向應力;θσ表示沿θ方向的正應力,稱為環向應力或切向應力;z σ表示沿z 方向的正應力,稱為軸向應力;zr τ表示在圓柱面上沿z 方向作用的剪應力。
同樣,軸對稱問題共有4個應變分量:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=zrz r γεεεεθ}{ (4-2)其中r ε表示沿半徑方向的正應變,稱為徑向正應變;θε表示沿θ方向的正應變,稱為環向正應變或切向正應變;z ε表示沿z 方向的正應變,稱為軸向正應變;zrγ表示沿r 和z方向的剪應變。
在軸對稱問題中,彈性體內任意一點上,不存在切向位移,只存在徑向位移u 和軸向位移w ,兩個位移分量表示為,⎭⎬⎫⎩⎨⎧=w u f }{(4-3)在討論彈性力學平面問題的有限元法時,我們先由將彈性體劃分為有限個單元的組合體,由虛功方程得到單元剛度矩陣,集成後得到整體剛度矩陣。
在這裏,我們用虛功方程直接得到軸對稱問題的有限元列式。
由虛功方程可得,外力虛功等於內力虛功或虛應變能, ds p f dxdydz F f dxdydz TsTT}{}{}{}{}{}{***⎰⎰⎰⎰⎰⎰⎰⎰+=σε(4-4)其中{F}為體力,{p}為面力。
空间与轴对称问题有限元分析课件

02
CATALOGUE
有限元分析基础
有限元分析的基本概念
有限元分析是一种数值分析方法,通过将复杂 的物理系统离散化为有限个简单元(或称为元 素)的组合,以求解复杂系统的物理行为。
它基于变分原理和加权余量法,通过数学模型 将实际工程问题转化为数学问题,从而得到近 似的数值解。
有限元分析广泛应用于工程领域,如结构分析 、流体动力学、电磁场等。
求解线性方程组
通过求解线性方程组得到每个节 点的位移和应力等物理量。
有限元分析的常用软件
ANSYS
功能强大的有限元分析软件,适用于各种工 程领域。
COMSOL Multiphysics
多物理场有限元分析软件,适用于模拟复杂 的多物理场耦合问题。
ABAQUS
专业的有限元分析软件,广泛应用于结构分 析、流体动力学等领域。
空间与轴对称问题有限元分析的优缺点
01
数值误差
有限元分析依赖于离散化的网格 ,存在数值误差,可能影响结果 的精度。
建模难度
02
03
计算资源需求
对于复杂问题的建模,需要较高 的专业知识和技巧,建模难度较 大。
对于大规模问题,有限元分析需 要大量的计算资源,如内存和计 算时间。
未来发展方向与挑战
优化算法
建筑领域
建筑设计中的对称和均衡问题需要考虑空间对称 性,以提高建筑的美观性和稳定性。
机械工程领域
机械零件的形状和结构需要考虑轴对称性,以确 保零件的稳定性和可靠性。
空间与轴对称问题的解析方法
解析法
通过数学公式和定理推导出问题的解 ,适用于简单的问题和特定条件下的 求解。
有限元法
将问题分解为有限个小的单元,通过 求解每个单元的近似解来逼近原问题 的解,适用于复杂的问题和不规则区 域的处理。
弹性力学空间轴对称问题有限元法

7.1 弹性力学空间轴对称问题的描述
一、柱坐标系
由于轴对称性质,采用柱坐标系( r、θ、z ) 分析轴对称问题
w r
u z
• 尽管点的位移发生在平面内,但是,对于垂直于 平面的线元素却存在着伸缩的可能,因此,轴对 称问题的环向应变不为零。
2)几何方程
• 对于周向应变,尽管不存在周向位移,但由于A点 发生径向位移后,它与轴的距离变为,从而导致 产生周向的变形,如图所示,则产生周向应变为
(r u)d rd rd
Ke
B
eT
e
DB
dv
Ve
Fbe NeTf dv
Ve
Fqe NeT f dS Se
Fe 0
BeT0 dv
Ve
Fe 0
BeTD0 dv
Ve
Ke 2
BeT
e
DB
rdrdz
e
Fbe 2 NeTf rdrdz e
Fqe 2 NeT f rds Se
Fe 0
2
BeT0 rdrdz
u r
u
r
z
r u r w
rz
z
w
u
r z
7.1 弹性力学空间轴对称问题的描述 三、基本方程
(2)应力应变关系 —物理方程
1
1 1
0
r
σ
z rz
E 1 1 1
2
1 1
1
1
1
1
有限单元法 第4章 空间轴对称问题有限元分析
+
# % ! 5 & +
习 !! 题
# " 如图 ! " ) 所示两个轴对称三角形单元 $ 其形状 ) 大小 ) 方位均相 同 $ 但位置 不同 ( 设材料弹性模量为 1$ 泊松比为&$/ 坐标!) " # ($ 试分别计算两单元的刚度矩阵 # " 取平 均值 ) ) % ( " ,
! ’ -! !
&
’
& " / / / ) $ * , / $ ) ! # 0 *$+% / $ /* ! !
! "# "$! 等效结点荷载的计算 %集中力 # 集中力的处理很简单 $ 一般直接把集中力作用点取为结点 $ 不需要作特殊处理 $ 就可 以直接把集中力加入到结点荷载列阵中去 ( %体积力 & 设单元内单位体积上作用的体积力为 ’ ’ $ 则移置到单元各结点的等效结点力为
"$# #’ #$ $ # # #+ % )! *! , / / # % / / # 0 & # / $ ) ! " *&+# /$ & ( / /
.
" # ! # # & " # ! # # )
" # ! # # !
/ , / $ & 由于在 0 是坐标 & 的函数 & ! " $ / ! 分量在单元中不为常量 & 其他三 个应变 分量 在单元
图! "!! 习题 # 图
$ 所示的是受轴向压缩的圆柱体 " 直径5$ ) " 如图! " (# 1 # / 3 6" 长度6 $ # & 3 6" 两端面 受均布载荷" & 如图 ! $ 所示$ % + / 7 8 1作用 % 现取轴对称面的 # ! 均匀划分单元 # " (# 2 "$ # $写出离散体的位移约束条件 % # # $求单元 " ’ # ’ $ ’ % 的等效结点荷载 % & $写出结点 #’&’)’!’(’+ 的荷载矩阵 % # )
2014-计算力学-4-轴对称问题有限元

Nj 0
0 Nj
Nm 0
e
N m I
0 i j Nm m
(4-11)
N
其中:[I]为二阶单位矩阵
1 0 I 0 1
因此,形函数矩阵的表达式为
Ni N 0 0 Ni Nj 0 0 Nj Nm 0 0 Nm
bi A1 f i 2 A3 A1 bi f i Si A b f 1 i i A2 ci A1ci ci A1ci A2 bi
i, j, m
单元分析
其中
u A1 1 u , 1 2u A2 21 u
rr
于是
1 ri r j rm 3 1 z z zi z j z m 3
fi fi ai cz bi i r r
i, j, m
有限元网格确定后,各单元的就是定值。这样就可以把轴对称问题的各 单元看成是常应变矩阵,所求得的应变是形心处的应变值。当轴对称结 构的单元划分比较小时,这种近似所引起的误差是很小的。特别当结构 上各单元的形心离 Z 轴 较远时,产生的误差就更小了。
u N i ui N j u j N m um w N i wi N j w j N m wm
(4-5)
单元分析
其中形函数
Ni
a
i
bi r ci z
2
i,
j, m
(4-6) (4-7)
而
1 1 rj 2 1 rm
1 ri
zi zj zm
ai
rj rm
zj zm
空间与轴对称问题有限元分析

划分网格
将连续的求解域离散化为有限个简单 元,形成网格。
建立刚度矩阵和载荷向量
根据每个简单元的特性,建立刚度矩 阵和载荷向量,以描述简单元之间的 力和力矩关系。
求解线性方程组
通过求解线性方程组,得到每个节点 的位移和应力分布。
有限元分析的优势与局限性
优势
有限元方法具有较高的灵活性和通用性,可以处理复杂的几何形状和边界条件, 适用于各种物理问题的求解。此外,有限元方法可以通过并行计算等技术提高 计算效率。
05
空间与轴对称问题有限元分析 的未来发展
新型有限元方法的研究与应用
混合有限元方法
结合不同类型有限元的优点,以更好地适应复 杂问题的需求。
自适应有限元方法
根据问题求解的实际情况,自动调整有限元的 尺寸和形状,以提高求解精度和效率。
非标准有限元方法
针对特定问题开发非标准的有限元,以获得更好的求解效果。
复杂空间与轴对称问题的挑战与解决方案
高维空间问题
01
随着问题维度的增加,有限元的构造和求解变得更加复杂,需
要发展更高效的算法和软件。
不规则区域问题
02
有限元的构造和处理在不规则区域上更具挑战性,需要研究新
的方法和技巧。
多物理场耦合问题
03
多物理场耦合的空间与轴对称问题需要发展能够同时处理多个
物理场的有限元方法。
误差估计
对称性有助于更准确地估计误差。
空间对称性问题的有限元模型建立
01
02
03
定义对称轴
明确对称轴的位置,以便 在建立模型时考虑对称性。
选取合适的有限元
根据对称性选择合适的有 限元类型,如四边形、六 面体等。
建立对称约束
轴对称问题的有限元分析

第1节基本知识本节的有限元对象为轴对称问题,目的是学习将3D问题转化为2D问题分析的轴对称方法,涉及如何选取轴对称单元、建模规律、载荷的施加方法和后处理技术。
一、轴对称问题的定义轴对称问题是指受力体的几何形状、约束状态,以及其它外在因素都对称于某一根轴(过该轴的任一平面都是对称面)。
轴对称受力体的所有应力、应变和位移均对称于这根轴。
二、用ANSYS解决2D轴对称问题的规定用ANSYS解决2D轴对称问题时,轴对称模型必须在总体坐标系XOY平面的第一象限中创建,并且Y轴为轴旋转的对称轴。
求解时,施加自由约束、压力载荷、温度载荷和Y方向的加速度可以像其它非轴对称模型一样进行施加,但集中载荷有特殊的含义,它表示的是力或力矩在360°范围内的合力,即输入的是整个圆周上的总的载荷大小。
同理,在求解完毕后进行后处理时,轴对称模型输出的反作用力结果也是整个圆周上的合力输出,即力和力矩按总载荷大小输出。
在ANSYS中,X方向是径向,Z方向是环向,受力体承载后的环向位移为零,环向应力和应变不为零。
常用的2D轴对称单元类型和用途见表11-1。
在利用ANSYS进行有限元分析时,将这些单元定义为新的单元后,设置单元配置项KEYOPT(3)为Axisymmetric(Shell51和Shell61单元本身就是轴对称单元,不用设置该项),单元将被指定按轴对称模型进行计算。
后处理时,可观察径向和环向应力,它对应的是SX与SZ应力分量,并且在直角坐标系下观察即可。
可以通过轴对称扩展设置将截面结果扩展成任意扇型区域大小的模型,以便更加真实地观察总体模型的各项结果。
第2节 2D轴对称问题有限元分析实例图11-1 圆柱筒壳示意图 一、案例1——圆柱筒的静力分析问题 如图11-1所示,圆柱筒材质为A3钢,受1000 N/m 的压力作用,其厚度为0.1 m ,直径12 m ,高度为16 m ,并且圆柱筒壳的下部轴线方向固定,其它方向自由,试计算其变形、径向应力和轴向应力。
有限元第6讲
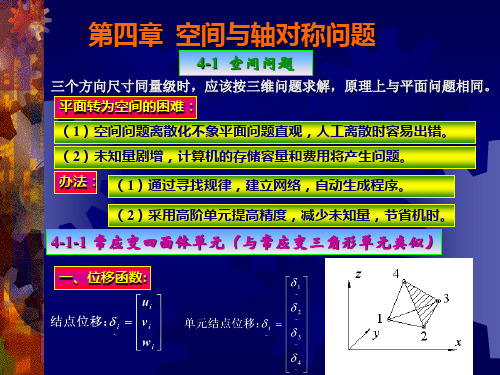
4-1-1 常应变四面体单元(与常应变三角形单元类似)
一、位移函数:
N i 为形函数,性质与平面问题相同。
由于 是线性的,故使各单元 边界上位移连续 — 协调元
~
二、应变矩阵,应力矩阵
几何方程:
三、单元刚度矩阵,单元等效结点荷载矩阵。
四、形成四面体的对角线划分法 首先将空间域化分为若干个六面体,然后再将每个六面体划分成四面 体的组合。 两种方法 1.将六面体划成5和四面体 2.先将六面体划成2个五面体,再将每个五面体划成3个四面体。
一. 位移函数
单元位移场:
二、应变场、应力场 由弹性力学知,柱 坐标几何方程为:
将位移函数代入:
应力场:由物理方程有:
弹性矩阵:
应力矩阵的子矩阵:
显然方程:除 rZ 为常数,其他均不为常 数。
三、单元刚度矩阵 积分应在整个圆环上积分
简化方法:用单元处的 形心直接代替B 总的坐标变量。
~
四、等效结点荷载
1.将六面体划成5个四面体 用“三对”对角线将六面体分割成5个四面体 两种形式:A5型和B5型
A5型
B5型
2.将六面体划分为 6个四面体
六面体划分成六个四面体
2367划分结果
3456划分结果
取A6还是B6决定于6个四面体角点编号于六面体角点编号的关系, 其规律为: 设D[1:8]为六面体交点的整体编码
单元刚度方程为
4-2 轴对称问题
轴对称问题:物体的几何形状,约束条件,作用的荷载都对称于某 一固定轴。如烟囱在重力作用下,位移、应变、应力也对称于轴线。 * 此类问题属空间问题,但利用轴对称特点,可将其简化为平面问题 求解
离散化:取环单元,单元之间结点形成环状的铰链。
有限元 空间问题
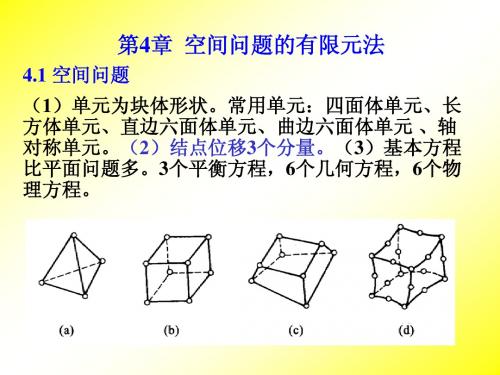
{ } [B]{ }e [Bi Bj Bm Bn ]{ }e
{ f } [ N ]{ }e
bi 0 1 0 [ Bi ] 6V ci 0 常量 d i
0 ci 0 bi di 0
0 0 di (i, j , m, n) 0 ci bi
1
A2
1 2 E (1 ) A3 2(1 ) (1 )(1 2 )
4、单元刚度矩阵 [k ] v[ B] [ D][ B]dV
T
[k ] [ B] [ D][B]V
T
分块矩阵的形式
[k ]1212
kii k ji kmi kni
kij k jj kmj knj
kim k jm kmm knm
kin k jn kmn knn
式中子矩阵[krs]为3×3的矩阵 :
[k rs ] [ Br ]T [ D][Bs ]V A1br c s A2 cr bs A1br d s A2 d r d s br bs A2 (cr c s d r d s ) A3 A1cr bs A2 br c s cr c s A2 (d r d s br bs ) A1cr d s A2 d r c s 36V A1d r bs A2 br d s A1d r c s A2 cr d s d r d s A2 (br bs cr c s ) (r , s i, j, m, n)
Ni 子矩阵: N i ] 0 [ 0 0 Ni 0 0 0 N i I (i , j , m, n ) Ni
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
e
( r , s = i, j , m )
由于在轴对称问题的矩阵 [ B ] 中出现坐标 r , z , 所以上式的积分运算比平面问题要复杂得多。 现在仍 取单元形心的坐标 r ≈ r =
1 1 ri + rj + rm ) , z ≈ = z ( ( zi + z j + zm ) 来替代矩阵 [ B ] 中的坐标 r , z , 3 3
γ rθ = γ θz =0
空间轴对称问题的平衡微分方程为
∂σ r ∂τ zr σ r − σ θ 0 + + + Fr = ∂r r ∂z ∂σ z + ∂τ zr + τ zr + F = 0 z ∂z ∂r r
空间轴对称问题的几何方程
∂u ∂r εr u ε θ r = ε z ∂w τ rz ∂z ∂u ∂w + ∂z ∂r
T
{ p} rdrdz
式中右边第一项是环形单元上的集中力 {G} 移置到结点的等效结点力,第二项是环形单元边界上表 面力 {q} 的等效结点力,第三项是环形单元体积力 { p} 的等效结点力。 采用平面问题中相同的符号: 集中力的等效结点力
{F }
表面力的等效结点力
e
= 2π rc [ N ] {G}
1 ( ri + rj + rm ) 3 1 z≈= z ( zi + z j + zm ) 3 r≈r =
所以有
fi ≈ fi =
ai cz + bi + i r r
( i = i, j , m )
这样就可以把各个单元近似地当作常应变单元,求得单元形心处应变和应力的近似值。
202
§4.2
单元刚度矩阵
e T 1 2 ne
T
{Rn }
T
T
{Ri }
T
= [ Rir
Riz ]
和平面问题一样,等效结点力也是由作用在环形单元上的集中力、表面力和体积力分别移置到 结点上而得到的。移置的原则也是根据这些力和等效结点力在任意虚位移上所作的虚功相等,即
{δ } {R}
eT
e
=
({u } ) 2π r {G} + ∫ {u}
201
的径向坐标 r 有关. 单元的应力分量为
= {σ }
= S ]{δ } [ D ][ B ]{δ } [ = [ Si ]
e e
S j
[ S m ] {δ }
e
( λ + 2G ) bi + λ fi 1 ( λ + 2G ) fi + λbi [ Si ] = 2∆ λ ( bi + fi ) Gci
T T
{Q}
体积力的等效结点力
e
= 2π ∫ [ N ] {q} rdsT源自{P}于是:e
= 2π ∫∫ [ N ]
e e
{ p} rdrdz
e e
{R} = {F } + {Q} + {P}
整体结构的等效载荷列阵可写成:
{R} = ∑ ({F } + {Q} + {P}
e e ne
e
) = {F} + {Q} + {P}
ui w i uj wj um wm
fi =
则应变可写成
ai z + bi + ci r r
e
( i = i, j , m )
Bj
= {ε }
其中
B ]{δ } [= [ Bi ]
[ Bm ] {δ }
e
(4.1.3)
带入几何方程得到单元体内的应变:
0 0 u ∂ w ∂z ∂ ∂r
bi 1 fi = 2∆ 0 ci
其中
0 0 ci bi
bj fj 0 cj
0 0 cj bj
bm fm 0 cm
0 0 cm bm
T ne Se
{R} = ∑ {R}
ne
e
于是有整体结构的有限元方程
[ K ]{δ } = {R}
和平面问题一样,整体刚度矩阵[K]是对称的带状稀疏阵,在消除刚度位移后,它是正定的。
204
§4.3 等效结点力计算载荷列阵
现在来讨论等效结点力的计算。上节中的载荷列阵
= {R}
其中
= R R {R} ∑ { } { }
则
{u} =
u e = [ N ]{δ } = N j [ N i ] w
∂ ∂r εr 1 ε r θ = {ε } = ε z 0 τ rz ∂ ∂z
[ N m ] {δ }
单元内一点的位移可写为 (4.1.2)
ui w i 0 0 0 N N N u r z , ) uj i j m r ( = {u} = = w ( r, z ) 0 Ni 0 N j 0 N m w j um wm N i ui + N j u j + N mum N i wi + N j w j + N m wm
作为一次近似,得到一个近似的单元刚度矩阵
[ krs= ]
e
2π r∆ [ Br ] [ D ][ Bs ]
T
203
=
π r ( λ + 2G ) br bs + f r f s + λ br f s + f r bs + Gcr cs 2∆
r s s s r
(
) ( λ c ( b + f ) + Gc b
e e [ k ] {δ } = {R} e
e
我们仍然假设单元的虚位移为
{u} = [ N ]{δ }
2π
e
注意到
∫ dθ = 2π ,则得
0
2π ∫∫ [ B ] [ D ][ B ] rdrdz {δ } = { R}
T e Se
e
则单元刚度矩阵
[k ]
它可以写成
e
= 2π ∫∫ [ B ] [ D ][ B ] rdrdz
图 4.1 轴对称问题的有限元离散(环形单元) 离散轴对称体时,采用的单元是一些圆环。这些圆环单元与 rz 平面正交的截面可以有不同的形 状,例如 3 结点三角形、6 结点三角形或其它形式。图 4.1 所示为 3 结点三角形环状单元。
图 4.2 三节点轴对称单元(环形单元) 在轴对称问题中(图 4.1),通常采用的单元是截面为三角形的圆环状单元,它是由rz面的三角 形环绕对称轴z回转一周而得到的。 在相邻单元之间通过圆环形的铰链互相连接。 单元的棱边都是圆, 称为节圆;节圆与 rz平面的交点就是节点。这样,各单元将在rz平面上形成三角形网络,就像平面问 题中各三角形单元在xy平面上形成的网络一样。但是,在轴对称问题中,单元体积是圆环的体积, 单元是圆环状的,所有的结点载荷都应理解为作用在单元结点所在的圆周上,也就是说,节点力和节 点荷载都施加在圆环形的铰上,这些方面显然与平面问题不同。
都加以扩大到整个结构的自由度 的维数,然后叠加得到:
T e 2π ∑ ∫∫ [ B ] [ D ][ B ] rdrdz {δ } = ∑ { R} ne S e ne
整体刚度矩阵
= [K ]
载荷列阵:
= [k ] ∑
e ne
2π ∑ ∫∫ [ B ] [ D ][ B ] rdrdz
eT c c
eT
{q} rdθ ds + ∫∫ {u} { p} rdθ drdz
eT
式中 rc 为集中载荷 {G} 作用点的径向坐标。考虑到
2π
∫ dθ = 2π ,则上式可以化成
0
{R}
e
= 2π rc [ N ] {G} + 2π ∫ [ N ] {q} rds + 2π ∫∫ [ N ]
T T
矩阵形式表达
198
σ r σ θ {σ } = σ z τ rθ
{σ } = [ D ]{ε }
0 (1 − 2µ ) 2 0 0
µ µ 1 − µ µ µ 1− µ E µ [ D] = µ 1− µ (1 + µ )(1 − 2µ ) 0 0 0
第四章 轴对称问题的有限元
工程问题中经常会遇到一些实际结构,它们的几何形状、约束条件以及作用的载荷都对称于某 一固定轴,我们把它称为对称轴,则在载荷作用下产生的位移、应变和应力也对称于此轴。这种问 题称为轴对称问题。 在轴对称问题中,通常采用圆柱坐标 ( r,θ ,z ) 。以对称轴作为 z 轴,所有应力、应变和位移都与 θ 方向无关,只是 r 和 z 的函数,任一点的位移只有两个方向的分量,即沿 r 方向向的径向位移 u 和 沿 z 方向的轴向位移 w 。由于轴对称, θ 方向的位移 v 等于零。因此轴对称问题是二维问题。 基本方程 环向位移 uθ = 0
( λ + 2G ) ci Gbi
λ ci λ ci
显然,只有应力分量 τ rz 在单元中为常量外,其余三个正应力在单元中都不是常量。在实用上,为了 简化计算和消除对称轴上由于 r=0 所引起的麻烦,常把各个单元中的 r 和 z 近似地当作常量,并且 分别等于各单元形心的坐标,即
式中 N i ,N j ,N m 是插值函数. 其中
