半边图模型之聚合归约演算
知识表示

第二章知识表示方法教学内容:本章讨论知识表示的各种方法,是人工智能课程三大内容(知识表示、知识推理、知识应用)之一,也是学习人工智能其他内容的基础。
教学重点:谓词逻辑法、语义网络法、状态空间法、问题归约法。
教学难点:语义网络法、状态描述与状态空间图示。
教学方法:课堂教学为主,同时结合《离散数学》等已学的内容实时提问、收集学生学习情况,充分利用网络课程中的多媒体素材来表示抽象概念。
教学要求:重点掌握用状态空间法、问题归约法、谓词演算法、语义网络法来描述问题;解决问题;掌握几种主要方法之间的差别;并对其它几种表示方法有一般了解。
2.1 概述∙主要内容:∙知识原则∙知识表示的作用∙知识表示的功能∙知识表示的性能∙基本的知识表示方式1 知识原则里南(D.B.Lenat)和费根鲍姆(E.A.Feigenbaum),IJCAI-10一个系统展示高级的智能理解和行为,主要是因为拥有应用领域特有的知识:概念、事实、表示、方法、模型、隐喻和启发式。
∙特有——意指应用领域中有效地求解问题主要靠该领域特有的知识。
∙足够的约束来自特别知识——通用知识作用微弱,不能提供足够的约束。
∙系统拥有的知识和其性能(问题求解能力和效率)的关系,参见图3.1。
∙知识门槛:(1)使能门槛W——指知识量超过该门槛时,系统就拥有了为执行任务所需的最低限度知识。
(2)胜任门槛C——到达C点时成为某应用领域中求解问题的专家,胜任只有专家才能解决的问题求解任务。
(3)全能门槛E——.到了这个门槛,由于知识量的空前增加(丰富),使系统能解决该应用领域内的几乎所有问题,成为全能专家。
∙知识门槛的分析:∙知识量差异——达到C级,只需50~1000条规则;再加等量的规则,就可达E级。
∙智能体知识是逐步积累的,涉及到获取新知识、修正和学习。
∙系统的能力主要由知识库中包含的领域特有的知识来决定——作为启发式知识(经验性关联知识)指导问题求解。
∙许多其它的人工智能研究也开始转向基于知识的观点。
离散数学-第11章

图 论
主讲:熊焕亮
图论简介
• 图论(graph theory)是研究节点和边组成的图 形的数学理论和方法,为离散数学的一个重要分 支。图论的基本元素是节点和边(也称线、弧、 枝),用节点表示所研究的对象,用边表示研究 对象之间的某种特定关系。因此,图论可用节点 和边组成的图形及其有关的理论和方法来描述、 分析和解决各种实际问题,已广泛地应用于物理、 化学、运筹学、计算机科学、电子学、信息论、 控制论、网络理论、管理科学、社会科学等几乎 所有学科领域的有关问题。图论与组合数学、线 性规划、群论、矩阵论、概率论、数值分析等数 学分支有密切的关系。
均为偶数,所以 d (v)为偶数,但因中顶点度数为奇数,
vV1
vV1
d (v ) d (v )
vV2
所以 | V1 |必为偶数。
14
11.1.2 简单图、多重图和同构图
V {v1 , v2 ,., vn } 设 G V , E 为一个阶无向图, 称 d (v1 ), d (v2 )d (vn ),为 G 的度数列。对于顶点标定的无向图,它的度数列是唯一的。反之, 对于给定的非负整数列d (d1 , d 2 ,d n ),若存在以 V (v1 , v2 ,, vn ) 为顶点 集的n阶无向图G,使得 d (vi ) d i ,则称d是可图化的。特别地,若所得 的图是简单图,则称d是可简单图化的。 例11.1.2 (1)(3,5,1,4),(1,2,3,4,5)能成为图的度 数列吗?为什么? (2)已知图G 中有15条边,2个度数为4的结点,4个度数为3的结点, 其余结点度数均小于等于2,问G 中至少有多少个结点?为什么? 解 (1)由于给定的两个度数列中奇度顶点个数均为奇数,由上述 推论可知,他们都不能成为图的度数列。 (2)图中边数为15,由握手定理可知,G 中所有结点度数和为30。 除去2个度数为4的结点和4个度数为3的结点,还剩下10度。其余结 点度数小于等于2,假设均为2,则至少要5个结点,所以总共至少要1 1个结点。
第二章 知识表示方法

第二章知识表示方法教学内容智能系统问题求解所采用的几种主要的知识表示方法(状态空间法.问题归约法.谓词逻辑法.语义网络法)以及基于不同表示法的问题求解方法。
教学重点1. 状态空间表示法中问题的状态描述.改变状态的操作和问题目标状态的搜索;2. 问题规约的一般步骤.规约的与或图表示;3. 谓词逻辑的语法和语义.量词的辖域.谓词公式的置换与合一;4. 语义网络的构成.语义基元的选择.语义网络的推理等。
教学难点状态描述与状态空间图示.问题归约机制.置换与合一。
教学方法课堂教学为主,同时结合《离散数学》等已学的内容实时提问.收集学生学习情况,充分利用网络课程中的多媒体素材来表示抽象概念。
教学要求1. 重点掌握用状态空间法.问题归约法.谓词逻辑法.语义网络法来描述问题.解决问题;2. 掌握这些表示方法之间的差别;并对其它表示方法有一般了解2.1 状态空间法教学内容本节讨论基于解答空间的问题表示和求解方法,即状态空间法,它以状态和操作符为基础来表示和求解问题。
教学重点问题的状态描述,操作符。
教学难点选择一个好的状态描述与状态空间表示方案。
教学方法以课堂教学为主;充分利用网络课程中的多媒体素材来阐述抽象概念。
教学要求重点掌握对某个问题的状态空间描述,学会组织状态空间图.用搜索图来求解问题。
2.1.1 问题状态描述1.基本概念状态(state)它是为描述某类不同事物间的差别而引入的一组最少变量q0,q1,…,qn的有序集合,其矢量形式如下:Q=[q0,q1,…,qn]' (2.1)式中每个元素qi(i=0,1,…,n)为集合的分量,称为状态变量。
给定每个分量的一组值就得到一个具体的状态,如Qk=[q0k,q1k,…,qnk]' (2.2)操作符(operator)称使问题从一种状态变化到另一种状态的手段为操作符或算符。
状态空间(state space)它是表示一个问题全部可能状态及其关系的图,它包含所有可能的问题初始状态集合S、操作符集合F以及目标状态集合G。
lambda演算

//3 = λf. λx.f (f (f x))
= λf. λx.(( λf. λx.f (f (f x))))f )(f (f x))
//将f 和(f (f x))应用于f 和x上
= λf. λx.(f (f (f (f (f x)))))
//正好等于5的邱奇数定义
邱奇-图灵论题(又称邱奇-图灵猜想,邱奇论题,邱奇猜想,图灵论题) 是一个关于可计算性理论的假设。该假设论述了关于函数特性的,可有效 计算的函数值(用更现代的表述来说–在算法上可计算的)。简单来说,邱 奇-图灵论题认为“任何在算法上可计算的问题同样可由图灵机计算”。 20世纪上半叶,对可计算性进行公式化表示的尝试有:
龙国星海 (山海螄)
λ 演算
March 23, 2016 9 / 17
λ演算
λ演算的定义 归约
在 λ 演算中有许多方式都可以定义自然数,但最常见的还是邱奇数
Church数 邱奇编码是把数据和运算符嵌入到λ演算内的一种方式,它是使用λ符 号的自然数的表示法。这种方法得名于阿隆佐·邱奇,他首先以这种方 法把数据编码到λ演算中。
0 ≡ λf. λx.x 1 ≡ λf. λx.f x 2 ≡ λf. λx.f (f x) 3 ≡ λf. λx.f (f (f x)) n ≡ λf. λx.f nx
在λ演算中,计算系统用数f 作为参数并以f 的n次幂为返回值的 函数
龙国星海 (山海螄)
λ 演算
March 23, 2016 11 / 17
λ演算
λ演算的定义 归约
PLUS 3 2 = λm. λn. λf. λx.((mf )((nf )x))3 2
//将3和2应用于m,n这两个自由变量
数学专业术语

一阶理论
相容性
可定义性
斯科伦壳
初等等价的
初等子模型
进退构造
原子理论
万有模型
稳定性
递归结构
非标准分析
直觉主义逻辑
抽象化
数词可表示性
相对相容性
元逻辑
可判定性
集合论
策梅洛-弗兰克尔集合论
确定性
选择函数
广义连续统假设
对称多项式
结式
一元一次方程
一般方程
三项方程
待定系数法
有理根
虚根
二重根
线性代数
矩阵的元
单位矩阵
矩阵的对角线
矩阵的秩
矩阵的迹
初等矩阵
分块对角矩阵
转置伴随矩阵
梯矩阵
酉矩阵
埃尔米特矩阵
正半定矩阵
实矩阵
极式分解
相似矩阵
顶点
邻顶点
重图
图同构
顶点子图
通道
圈秩
全不连通图
顶点次数
补图
团
完全二部图
无圈图
回路
拟图
边连通度
哈密顿圈
递归边图
彼得松图
边覆盖
独立顶点集
临界边
平面嵌入
对偶地图
最大亏格
舍弃运算
四色问题
色剖分
邻接矩阵
顶点传递图
齐次图
标号图
树
顶点的权
出次数
出树
弱连通的
超图
平凡序的
保序映射
半边图模型与多层次认知系统

半边图模型与多层次认知系统孟朝晖河海大学计算机及信息工程学院南京(210024)E-mail(mengzhaohui@)摘要:提出一个动态可增殖的多层次自组织认知系统,每个层次具有形式上一致的知识表示方法,各层的自组关联、自组聚合、归约和样本表达四个知识处理模型是实现系统自组织层次增殖的核心模型.指出,若要实现层次可自组织增殖的系统,其关键是要设计一个合理的聚合归约演算系统.提出一个适用于各个层次的基于可结合半边的自组图知识表示法,先给出自组图形式化的静态定义和动态定义,然后给出三种演算模型,半边图构造演算,聚合演算和归约演算.在此基础上,提出一个多层次自组织认知系统的框架模型.关键词:多层次认知系统, 构造演算, 聚合演算, 归约演算, 半边自组图1. 多层次自组织认知系统概述人们对事物的认识总是遵循从简单到复杂、从低层次到高层次的认知规律,所以,认知的层次性是认知过程的重要特性;同时,认知系统的自组织性也是认知过程的另一个重要特性,首先认知的层次是自组织产生的,即认知的层次是逐渐地、根据被认知事物复杂性的增长而自组织增加的;其次,自组织还体现在各个层次的内部信息处理中,即每个层次内的主要认知过程就是对认知样本的自组织识别与表达.多层次自组织认知系统是为模拟认知过程的层次性和自组织性而设计的系统,系统的每个层次包含知识表示和知识处理两个主要部分,不同层次的知识表示的内容不同,但知识表示的抽象形式是一致的,这样,不同层次的知识处理方法就可以是一致的.层次之间的知识表示遵循从简单到复杂的顺序递阶关系,最底层为最简单、最细粒度、最具体的知识表示,随着层次的提升,知识表示的内容逐级组合、粒度逐渐增大、抽象度不断提高,这样,就模拟了认知过程的层次性.为了实现上述知识表示的层次性,每层的知识处理主要由以下几个算法组成: 知识处理模型1(自组关联模型:依据基元模式的结合性从训练样本中学习组合模式).已知:(1)一个基元模式集合:其中的每个基元模式是从实际问题中抽象出的基本概念或基本模式;(2)一个基本关系集合:其中的每个基本关系表示两个基元模式之间可能的结合性;(3)一个训练样本:仅用基元模式表达的样本,其中不包含基本关系;这个训练样本从上一个层次获得,本层若是第一层,则训练样本直接来源于系统的输入样本;求解过程:在用基元模式表达的训练样本中,用基元模式之间可能的结合性自组织建立基本关系;输出:从训练样本提取出的组合模式,组合模式用基元模式和基本关系表达.- 1 -上述自组关联模型的提出受到了超分子自组装机制[1]的启发,其中的核心思想是基元模式之间存在有内禀的可结合性,基本关系建立在这种结合性的基础之上;复杂组合模式可以通过基元模式的可结合性自组织获得,表现形式为在基元模式之间自组织建立起基本关系.这一知识处理模型可以作为数据挖掘中的多维关联分析[2]的理论模型.知识处理模型2(自组聚合模型:复杂组合模式分解为聚合模式).已知:(1)一个由基元模式和基本关系构成的大的复杂的组合模式;(2)一些针对基元模式和基本关系的不同的聚合准则;求解过程:将大的复杂的组合模式,按不同的聚合准则自组织聚合为若干小的相对简单一些的子组合模式,称为聚合模式;输出:聚合模式集合,满足如下两个条件:(1)各个聚合模式是按互不相同的聚合准则获得的;(2)各个聚合模式之间可以相交,相交的部分表达了各个聚合模式之间的关系.上述知识处理模型类似于聚类分析算法,例如DBSCAN[3]和CHAMELEON[4],但在聚类准则和聚类结果上,自组聚合模型与已有的聚类分析算法有很大不同,首先,已有的一些聚类算法的聚类准则均是单一的,如DBSCAN中的聚类准则是一个依据距离计算出的统一的密度度量准则,CHAMELEON中的聚类准则是根据距离计算出的相似度准则,而自组聚合模型的聚合准则可以是性质和表现均不相同的特异性准则;其次,已有的一些聚类算法虽然不强调各个聚类后的子类之间一定不相交,但在算法的实现上均是按照聚类的各个子类不交这一准则来做的,即基元要素不能同时属于两个以上的子类,这也是在统一的距离准则或相似度准则的制约下的自然做法,而自组聚合模型的各个聚合模式之间可以相交,而相交的这一部分所表达的各个子模式之间的关系及其抽象表示恰恰是多层次归约算法的核心内容.- 2 -知识处理模型3(归约模型:从聚合模式中归约出下一层的基元模式和基本关系). 已知:一个聚合模式集合;求解过程:(1)将聚合模式对应为下一层的基元模式;(2)从聚合模式之间的关系中抽象出下一层的基本关系;输出:下一层的基元模式集合和基本关系集合.知识处理模型4(样本表达模型:将本层次的样本用下一层的基元模式表示).已知:用本层基元模式和基本关系表示的训练样本;求解过程:(1)将训练样本用本层的聚合模式表示;(2)将聚合模式表示的样本对应为用下一层基元模式表示的样本;输出:仅用下一层基元模式表示的训练样本,其中不包含下一层的基本关系.归约模型提供的算法保证了每个层次具有统一的知识表示形式,即每个层次均有属于本层的基元模式和基本关系,而高层次的基元模式和基本关系是从低层次逐级归约而来的.有了各层形式上一致的知识表示方法,再加上样本表达模型对样本的逐层表达,上述四个知识处理模型也就成为了各层通用的模型了.多层次是复杂系统的重要特征,但将自组织性引入多层次系统尚未有很完整的研究,有关自组织性的研究一般均是针对一个局部的、单层的系统,比较典型的如Kohonen 自组织特征映射(SOM)模型[5];多层次自组织认知系统的自组织性不但针对每个层次的具体的知识处理模型,而且整个系统也通过层次之间的知识表示归约而实现了多层次的自组织增殖.为了实现层次可自组织增殖的系统,其关键是要设计一个合理的、用于知识表示和知识处理的形式化演算系统,合理性指的是适合于多层次的知识表达与归约.演算系统首先要给出知识表示的形式化模型,然后在此基础上描述知识处理的具体算法.在随后的论述中,给出了一个基于可结合半边的自组图演算系统,包含三个主要演算模型,为自组图构造演算、自组图聚合演算和自组图归约演算,分别对应于自组关联模型、自组聚合模型和归约模型.最后,本篇论文以自组图演算系统为理论基础,进一步研究多层次自组织认知系统的实现方法.2. 半边自组图半边自组图(Half Edge Self-Organization Graph)是知识表示的形式化模型,以下也可简称为图或半边图或自组图.图由顶点和边组成,顶点是知识表示中的基本概念、基本模式等知识单元的抽象表达,即顶点表示基元模式;顶点有若干属性,不同顶点的属性可以互相识别与结合,这样,顶点之间就实现了关联,在自组图中用边表示顶点之间的关联,即边表示基本关- 3 -系.用图的顶点表示实体,用边表示关系,是知识表示的常用方法,例如,基于图的语义网知识表示法已成为人工智能研究中的基本方法[6].这种方法将顶点和边均作为不可分割的原子概念,多层次自组织认知系统若采用这种知识表示方法,在多层次认知的过程中就会产生出过多的特异性顶点和边,而由于这些顶点和边的原子性,除非人为地提出一些附加性的归约准则,否则很难将它们进行合理的归约.而如果每个层次均需人工附加针对各层的归约准则,那么层次的自组织性也就无法实现了.针对上述问题,本文提出一个比顶点和边更基本的图元素,称为可结合半边,简称半边,在自组图中,顶点的属性表示为半边,不同顶点的半边依据可结合性而结合起来称为边,边就表示了顶点之间的关联.或者说,顶点由若干个半边组成,边由分别属于两个顶点的可结合半边组成.有了半边,顶点和边就不再是不可分的原子了,而顶点和边的多层次自组织归约难题也就可以通过设计一些针对半边的更有普遍意义的归约原则而得到解决.2.1半边、顶点和边定义2.1(半边).半边是组成顶点的基本元素,一个半边属于某个顶点且分为不同的半边类型,半边与其它的半边可以相结合,每个半边还有一个数值性度量值,称为半边权值,一般取大于0的实数.一个半边可以表示为如下形式的赋名异构表,half_edge(self_name,vertex_name,type,weight,mate_status,mate_half_edge_name,mate_edge)其中的元素称为半边的属性,各属性标识的含义如下:half_edge 为半边的赋名,也是对整个异构表这个数据结构的标识;half_edge.self_name 为半边名标识符本身;half_edge.vertex_name 为该半边所属顶点的名字,即宿主顶点的名字;half_edge.type 为该半边所属的半边类型的类型名;half_edge.weight 为该半边的权值;half_edge.mate_status 为该半边是否与其它半边结合的状态标识;half_edge.mate_half_edge_name 为与该半边结合的另一个半边的名(如果有结合的情况下);half_edge.mate_edge 为该半边与另一个半边组成的边的标识.定义2.2(顶点).顶点是组成图的基本元素,顶点本身由有序的若干个半边组成.具有i 个半边的顶点,称为i度顶点,表示为如下赋名广义表(即可嵌套表):vertex(self_name,degree,half_edge_list(half_edge1,...,half_edgei))其中vertex 为顶点的整体标识;vertex.self_name 为顶点名;vertex.degree 为顶点度,表示该顶点包含有几个半边,vertex.degree = i;vertex.half_edge_list(half_edge1,...,half_edgei) 为半边链表;- 4 -half_edge1,...,half_edgei 为顶点的i个半边;顶点的半边可以表示为vertex.half_edge1,也可以表示为half_edge1∈vertex,而vertex称为这些半边的宿主顶点.由所有的顶点组成的集合称为顶点全集,表示如下:ALL_VERTEX_SET =ALL_VERTEX_SET(1)∪ALL_VERTEX_SET(2)∪ ...∪ALL_VERTEX_SET(k)其中ALL_VERTEX_SET(i) ={ vertex(i) | vertex(i) 为i度顶点 },在不需要标明顶点所含半边的个数时,可以简记为vertex∈ALL_VERTEX_SET.不同的顶点包含了不同的半边,顶点之间的关联是由其所属的半边之间的结合而实现的,但半边之间的结合要依赖于半边的类型属性,即需要定义哪些半边之间可以结合,哪些半边之间不可以结合.定义2.3(半边类型).半边可以分为不同的类型,用不同的名称表示,如HALF_EDGE_TYPE1, HALF_EDGE_TYPE2等等.半边类型集合表示为HALF_EDGE_TYPE_SET={HALF_EDGE_TYPE1,HALF_EDGE_TYPE2,...,HALF_EDGE_TYPEn}其中的元素为不同的半边类型.定义2.4(半边结合类型).称有序半边类型对(HALF_EDGE_TYPEi,HALF_EDGE_TYPEj)为半边结合类型,表示什么类型的两个半边可以结合在一起,所有的半边结合类型所成的集合称为半边结合类型集合HALF_EDGE_MATE_TYPE_SET = { (HALF_EDGE_TYPEi,HALF_EDGE_TYPEj) |HALF_EDGE_TYPEi∈HALF_EDGE_TYPE_SET,HALF_EDGE_TYPEj∈HALF_EDGE_TYPE_SET }. 不属于集合HALF_EDGE_MATE_TYPE_SET的半边类型对所对应的两个半边不能结合在一起.进一步,若有(HALF_EDGE_TYPEi,HALF_EDGE_TYPEi) ∈HALF_EDGE_MATE_TYPE_SET,则称(HALF_EDGE_TYPEi,HALF_EDGE_TYPEi)为自反结合类型.定义2.5(边).若两个顶点的两个半边的类型对是半边结合类型,则这两个半边就可以相结合,若两个半边已结合在一起,则两个半边合起来称为一个边.设有两个顶点vertex1∈ALL_VERTEX_SET,vertex2∈ALL_VERTEX_SET,又有两个半边half_edge1与half_edge2,分别属于两个顶点,half_edge1∈vertex1,half_edge2∈vertex2,且满足(half_edge1.type,half_edge2.type )∈HALF_EDGE_MATE_TYPE_SET则称半边half_edge1 与half_edge2可结合;称赋名广义表edge =(self_name,weight,type,vertex_couple(vertex1,vertex2),half_edge_couple(half_edge1,half_edge2))为边,其中- 5 -edge 为边的整体标识;edge.self_name 为边名;edge.weight 为边的权值;edge.type 为边的类型,edge.type =(half_edge1.type,half_edge2.type);进一步,称 EDGE_TYPE_SET = HALF_EDGE_MATE_TYPE_SET 为边类型集合;edge.vertex_couple(vertex1,vertex2) 为边edge的关联顶点对,称顶点vertex1与vertex2通过边edge实现关联,称顶点vertex1与vertex2为边edge的关联顶点;edge.half_edge_couple(half_edge1,half_edge2)为组成边edge的半边对.定义2.6(边的权值).每个边可以依据其两个组成半边的权值由边权计算函数计算出一个数值作为边的权值.为此,先定义边权计算函数.称二元函数EdgeWeightFunction(x,y)为边权计算函数(可取min/max/average等),满足如下条件:(1)非负性:EdgeWeightFunction(x,y) >= 0,∀x,y >= 0 ;(2)单调性:∀ 固定x,EdgeWeightFunction(x,y)为y的单调函数;∀ 固定y,EdgeWeightFunction(x,y)为x的单调函数;若边edge.half_edge_couple = (half_edge1,half_edge2),则edge.weight = EdgeWeightFunction(half_edge1.weight,half_edge2.weight)为边edge的权值.已定义的三个主要概念及它们之间的基本关系如下:(1)半边是一个有各种属性的基元概念,这些属性还可以根据不同问题的需要而添加和修改;半边不独立存在于图中,一个半边一定依附于某个顶点;(2)顶点的主要组份为若干个半边,顶点是图演算中能够独立存在与运算的基本要素;(3)边由两个可结合的半边组成,但由于半边必须附属于顶点,所以,边不能独立于顶点而存在于图中,或可以认为边是由顶点导出的.定义2.7(自由半边).仅属于其宿主顶点,尚未与其它半边相结合的半边,记为free_half_edge.定义2.8(已结合半边).不仅属于其宿主顶点,而且已与其它半边相结合的半边,这样的半边也属于一个边,记为mated_half_edge.定义2.9(自由顶点).若一个顶点所属的各半边均为自由半边,则称该顶点为自由顶点,记为free_vertex.2.2自组图的静态定义定义2.10(自组图).自组图由顶点和边组成,表示为一个三元组GRAPH =(VERTEX_NAME_SET,VERTEX_SET,EDGE_SET)其中VERTEX_NAME_SET 为图的顶点名字集,表示图中包含了哪些顶点,其中的元素来自每个顶点广义表中的vertex.self_name表项;VERTEX_SET 为图的顶点集,是表示图中顶点现状的集合,即由若干顶点广义表为元素- 6 -组成的集合,包含了每个顶点的全部信息,描述了每个顶点所属的各个半边的属性取值情况;EDGE_SET 为图的边集,是由边广义表组成的集合.由前述半边、顶点和边的基本关系可得,一个图中的顶点集与边集必须满足图的顶点与边协调原则(Vertex Matching Edge Principle of Graph):准则1(图的顶点与边协调原则).设一个图GRAPH =(VERTEX_NAME_SET,VERTEX_SET,EDGE_SET),若GRAPH满足以下两个充要条件,则称该图满足顶点与边协调原则:(1)顶点准则:对任意的边edge =(self_name,weight,type,vertex_couple(vertex1,vertex2),half_edge_couple(half_edge1,half_edge2))其中half_edge1、half_edge2为组成边的两个半边,vertex1、vertex2分别为half_edge1、half_edge2的宿主顶点;若edge∈EDGE_SET,则当且仅当有vertex1、vertex2∈VERTEX_SET ;(2)边准则:设顶点vertex∈VERTEX_SET,对vertex中的任何一个半边,设为vertex.half_edge;若vertex.half_edge.mate_status = ture,则当且仅当有vertex.half_edge.mate_edge∈EDGE_SET.定理2.1.图的顶点与边协调原则之顶点准则与边准则是等价的.(证明略)顶点与边协调原则实际上是半边、顶点、边这三个概念之间的关系在图的定义中的体现. 由图的顶点与边协调原则,可以得到图的两种表示法:顶点表示法和边表示法.顶点表示法:设一个图GRAPH =(VERTEX_NAME_SET,VERTEX_SET,EDGE_SET)满足顶点与边协调原则,又因为顶点所属的各个半边有描述结合性的三个属性(mate_status、mate_half_edge_name、mate_edge),则图的每个边的信息已在顶点集VERTEX_SET中每个顶点所属半边的属性中反映了,该图就可以表示为GRAPH =(VERTEX_NAME_SET,VERTEX_SET)称为图的顶点表示式,即边集EDGE_SET可以由顶点集VERTEX_SET导出.进一步,VERTEX_NAME_SET与VERTEX_SET事实上是一一对应关系,所以,在许多情况下,顶点名字集VERTEX_NAME_SET也可以省略,即GRAPH =(VERTEX_SET) 或GRAPH =(VERTEX_SET,EDGE_SET)注意,(VERTEX_SET)不等同于VERTEX_SET.边表示法:设一个图GRAPH=(VERTEX_NAME_SET,VERTEX_SET,EDGE_SET)满足顶点与边协调原则,则图的每个顶点所属的半边的结合属性已反映在边的信息中了,该图就可以表示为GRAPH =(VERTEX_NAME_SET,EDGE_SET)称为图的边表示式,即顶点集VERTEX_SET也可以由边集EDGE_SET导出.这时,顶点名字集VERTEX_NAME_SET就不可以省略了.注意,因为从半边、顶点和边的本质关系看,边毕竟是建立在顶点基础之上,所以,边表示法会失去顶点及其半边的描述非结合性的其它属性.- 7 -事实上,半边是构成图的最基本要素,构成图的两个要素,顶点和边均由半边组成,但半边不直接属于图,半边直接属于其宿主顶点,自由半边仅属于其宿主顶点,已连接半边不仅属于其宿主顶点,还属于相应的边.2.3自组图的交运算和并运算定义2.11(图的交运算).设有两个图GRAPH1=(VERTEX_NAME_SET1,VERTEX_SET1,EDGE_SET1),GRAPH2=(VERTEX_NAME_SET2,VERTEX_SET2,EDGE_SET2),则GRAPH1、GRAPH2的交仍为一个图,表示为INTERSECT_GRAPH = GRAPH1∩GRAPH2=(INTERSECT_VERTEX_NAME_SET,INTERSECT_VERTEX_SET,INTERSECT_EDGE_SET)其中INTERSECT_VERTEX_NAME_SET =VERTEX_NAME_SET1∩VERTEX_NAME_SET2INTERSECT_EDGE_SET = EDGE_SET1∩EDGE_SET2INTERSECT_VERTEX_SET’ = VERTEX_SET1∩VERTEX_SET2将INTERSECT_VERTEX_SET’按图的顶点与边协调原则之边准则做出修改,得到新的INTERSECT_VERTEX_SET.即上述INTERSECT_VERTEX_SET’中各个顶点所属的半边的属性要按INTERSECT_EDGE_SET的现状做修改.解释:如果顶点交集中的顶点所属的已结合半边所关联的边不在边交集中,则将该半边改为自由半边;或保留边交集中的各个边所关联的半边的已结合属性,其它的半边均改为自由半边.定义2.12(图的并运算).设有两个图GRAPH1=(VERTEX_NAME_SET1,VERTEX_SET1,EDGE_SET1),GRAPH2=(VERTEX_NAME_SET2,VERTEX_SET2,EDGE_SET2),则GRAPH1、GRAPH2的并仍为一个图,表示为UNION_GRAPH = GRAPH1∪GRAPH2=(UNION_VERTEX_NAME_SET,UNION_VERTEX_SET,UNION_EDGE_SET)其中UNION_VERTEX_NAME_SET = VERTEX_NAME_SET1∪VERTEX_NAME_SET2 UNION_EDGE_SET = EDGE_SET1∪EDGE_SET2UNION_VERTEX_SET’ = VERTEX_SET1∪VERTEX_SET2将UNION_VERTEX_SET’按图的顶点与边协调原则之边准则做出修改,得到新的UNION_VERTEX_SET.即上述UNION_VERTEX_SET’中各个顶点所属的半边的属性要按UNION_EDGE_SET的现状做修改.解释:两个图按顶点名字集与边集的并运算合并后,有些顶点的半边的属性要按顶点与边协调原则之边准则从自由的改为已结合的.- 8 -3. 自组图的构造前述图的定义是一种静态的定义,即客观上图已经存在了,静态定义的目的是将客观存在的确定的图描述清楚.但是,按前面的定义,图不是演算系统中的最基本要素,图是一种由半边、顶点以及边构成的组合体,实际问题中的静态概念可以用图的静态定义表达,而实际问题中的动态过程则需要图的构造过程来模拟.下面给出一种图的构造方法:在已知若干个顶点的情况下,通过顶点所属的半边之间的结合性逐步建立边而动态导出一个图.即图不是人为确定的,也不是客观上预先存在的,而是由自由顶点集合导出的.3.1在图中加边和减边定义3.1(加边操作).全称为在图中导出一条边,设一个图GRAPH=(VERTEX_NAME_SET,VERTEX_SET,EDGE_SET),有两个顶点vertex1∈VERTEX_SET,vertex2∈VERTEX_SET,又有两个自由半边half_edge1与half_edge2,分别属于两个顶点,half_edge1 ∈vertex1,half_edge2∈vertex2,满足(1) half_edge1.mate_status = false,half_edge2.mate_status = false;(2)(half_edge1.type,half_edge2.type)∈HALF_EDGE_MATE_TYPE_SET则可在图GRAPH =(VERTEX_NAME_SET,VERTEX_SET,EDGE_SET)中添加一条新的边new_edge:new_edge =(self_name,weight,type,vertex_couple(vertex1,vertex2),half_edge_couple(half_edge1,half_edge2))称为在图中导出一条边,或称对图GRAPH执行一次加边操作,或简称加边,其中 new_edge.self_name= NameFunction( ),其中的NameFunction( )为一个名字生成函数;new_edge.weight = EdgeWeightFunction(half_edge1.weight,half_edge2.weight);new_edge.type =(half_edge1.type,half_edge2.type)∈EDGE_TYPE_SET;加边操作可以记为EdgeOperate(GRAPH,ADD,new_edge,i)上述EdgeOperate(GRAPH,ADD,new_edge,i)完成以下具体操作:(1)将新边new_edge添加进GRAPH的边集EDGE_SET中;(2)按如下方法修改两个半边的相应属性:half_edge1.mate_status = turehalf_edge2.mate_status = turehalf_edge1.mate_half_edge_name = half_edge2half_edge2.mate_half_edge_name = half_edge1half_edge1.mate_edge = new_edgehalf_edge2.mate_edge = new_edge(3)将上述半边属性的修改结果保存进GRAPH的顶点集VERTEX_SET中;加边操作EdgeOperate(GRAPH,ADD,new_edge,i)中GRAPH为执行加边操作的主- 9 -体,new_edge为导出边的名字,ADD为操作属性标记,i为操作本身的编号.定义3.2(减边操作).全称为在图中注销一条边,设一个图GRAPH =(VERTEX_NAME_SET,VERTEX_SET,EDGE_SET),边集中有一条边old_edge∈EDGE_SET,old_edge =(self_name,weight,type,vertex_couple(vertex1,vertex2),half_edge_couple(half_edge1,half_edge2))其中的两个半边half_edge1 与half_edge2 分别属于两个顶点,half_edge1∈vertex1,half_edge2∈vertex2则可以将此边从图GRAPH中注销,称为在图中注销一条边,或称对图GRAPH执行一次减边操作,或简称减边,减边操作可以记为EdgeOperate(GRAPH,DELETE,old_edge,i)减边操作EdgeOperate(GRAPH,DELETE,old_edge,i)完成以下具体操作:(1)将旧边new_edge从GRAPH的边集EDGE_SET中除去;(2)按如下方法修改两个半边的相应属性:half_edge1.mate_status = falsehalf_edge2.mate_status = falsehalf_edge1.mate_half_edge_name = nullhalf_edge2.mate_half_edge_name = nullhalf_edge1.mate_edge = nullhalf_edge2.mate_edge = null(3)将上述半边属性的修改结果保存进GRAPH的顶点集VERTEX_SET中.3.2由自由顶点集导出自组图定义3.3(种子顶点集).称一个由若干个自由顶点组成的集合SEED_VERTEX_SET = { free_vertex | free_vertex 为自由顶点 }⊆ALL_VERTEX_SET为种子顶点集,其中的每个free_vertex均为自由顶点,即每个顶点的每个半边均未与其它半边结合.定义 3.4(种子顶点集的导出图).设有种子顶点集SEED_VERTEX_SET,其导出图递推定义如下:(1)若图GRAPH =(SEED_VERTEX_NAME_SET,VERTEX_SET,EDGE_SET),其中SEED_VERTEX_NAME_SET为种子顶点集SEED_VERTEX_SET一一对应的名字集,若GRAPH中的EDGE_SET为空集,而VERTEX_SET = SEED_VERTEX_SET即该图只含有种子顶点集而不含有边,则该图称为种子顶点集的平凡导出图,也称为导出图,并改名为DEDUCE_GRAPH,也可记为(SEED_VERTEX_SET)⇒DEDUCE_GRAPH, 或- 10 -GRAPH⇒DEDUCE_GRAPH;(2)若图GRAPH=(SEED_VERTEX_NAME_SET,VERTEX_SET,EDGE_SET)为导出图,则对图GRAPH执行一次加边操作(要符合加边条件)后形成的新图亦为导出图;(3)若图GRAPH=(SEED_VERTEX_NAME_SET,VERTEX_SET,EDGE_SET)为导出图,则对图GRAPH执行一次减边操作(要有边可减)后形成的新图亦为导出图;(4)经过有限次(2)或(3)步骤所得到的图为导出图.定义3.5(边操作序列).设有种子顶点集SEED_VERTEX_SET及其导出图 DEDUCE_GRAPH = (SEED_VERTEX_NAME_SET,VERTEX_SET,EDGE_SET) 由导出图的定义可知,导出图是由种子顶点集为初始条件,由一个加边操作和减边操作组成的边操作序列所确定的图,称这个序列为导出图的边操作序列.边操作序列可以表示为一个列表,记为EDGE_OPERATE_LIST = (EdgeOperate(1),...,EdgeOperate(n))其中的边操作省略了边名字与操作属性.若需描述导出图构造过程及当前状态,一个导出图可以表示为如下形式:DEDUCE_GRAPH =(SEED_VERTEX_SET,EDGE_OPERATE_LIST,VERTEX_SET,EDGE_SET)其中SEED_VERTEX_SET为导出图的种子顶点集,这个集不改变;EDGE_OPERATE_LIST 为边操作序,表示当前的导出图做过哪些边的加减操作;VERTEX_SET为当前顶点集,表示当前导出图的各个顶点及半边的具体状态;EDGE_SET为导出图的边集,表示当前导出图含有的边.定义 3.6(边操作序列结果等价).若有从一个种子顶点集导出的两个图,GRAPH1和GRAPH2,GRAPH1 =(SEED_VERTEX_SET,EDGE_OPERATE_LIST1,VERTEX_SET1,EDGE_SET1 ) GRAPH2 =(SEED_VERTEX_SET,EDGE_OPERATE_LIST2,VERTEX_SET2,EDGE_SET2 ) 称这两个导出图为同源导出图;若GRAPH1 = GRAPH2,即VERTEX_SET1 = VERTEX_SET2 且 EDGE_SET1 = EDGE_SET2则称两个边操作序列结果等价,记为EDGE_OPERATE_LIST1≅EDGE_OPERATE_LIST2.3.3图构造算法前面的论述已指出,顶点可以对应于实际问题中的一些基本概念和基本模式,则边就是这些基本概念和基本模式之间的关系,而图则可以表示更加复杂的一些组合概念与组合关系.对许多实际问题而言,基本概念和基本模式容易获得与识别,最通用的方法就是各种基元匹配法[7];但更复杂的组合性的概念与模式就不易分辨、不易表达且不易识别,尤其难以做到操作过程的自组织和自适应,往往需要人为设计一些具有针对性的复杂算法.图构造算法就是为解决上述问题而提出的一种通用算法,其原理是,已知一些顶点(对应于实际问题中的一些基本模式),由顶点所属半边的结合性逐渐自组构造连接顶点的边(对应于基本模式的关联性),进而就构造出了已知顶点集的导出图(对应于实际问题中的一些更加复杂的组合模式),这样获得的图就称为自组图.图构造算法对应于第一个知识处理模型---- 11 -自组关联模型.算法1(图构造算法).GRAPH GENERATE ALGORITHM,也称为自由顶点关联算法VERTEX CONNECTION ALGORITHM.输入数据:有n个自由顶点的种子顶点集SEED_VERTEX_SET = { free_vertex(1),...,free_vertex(n) },第i个种子顶点有mi个自由半边free_vertex(i)={ free_half_edge(i,1),...,free_half_edge(i,mi) }参考数据库:(1)半边类型集合 HALF_EDGE_TYPE_SET(2)半边结合类型集合 HALF_EDGE_MATE_TYPE_SET输出:导出图GRAPH =(SEED_VERTEX_SET,EDGE_OPERATE_LIST,VERTEX_SET,EDGE_SET)过程:步骤1:将种子顶点集 SEED_VERTEX_SET 拷贝给导出图的当前顶点集 VERTEX_SET ;步骤2:将当前顶点集 VERTEX_SET中的顶点做一次随机排序,得到一个新的顶点序列;步骤3:按新得到的顶点次序将各个顶点两两组合,方法为第一个与第二个组合,第三个与第四个组合,依次类推;若顶点个数n为偶数,则得到n/2个顶点组合对,若n为奇数,则最后一个顶点放弃组合,而得到(n-1)/2个顶点对; 步骤4:对步骤3得到的每对顶点对做如下操作(n/2对或(n-1)/2对):设当前顶点对为 vertex_couple(vertex1,vertex2)IF (两个顶点各有一个半边可以结合),设为half_edge1 与 half_edge2THENDO 将half_edge1与half_edge2可能结合成的新边记为new_edge =(self_name,weight,type,vertex_couple(vertex1,vertex2),half_edge_couple(half_edge1,half_edge2))IF (两个可结合半边均为自由半边) THENDO 做一次加边操作EdgeOperate(GRAPH,ADD,new_edge,i)DO将本次加边操作加入EDGE_OPERATE_LIST中ELSE (两个可结合半边不是均为自由半边)IF (两个可结合半边一个为自由半边,另一个已结合) THENDO记自由半边为half_edge1,DO记已结合半边为half_edge2,并记其边为旧边old_edge =(self_name,weight,type,vertex_couple(vertex2,another_vertex),half_edge_couple(half_edge2,another_half_edge))DO将half_edge1与half_edge2可能结合成的新边记为new_edge =(self_name,weight,type,vertex_couple(vertex1,vertex2),half_edge_couple(half_edge1,half_edge2))IF (new_edge.weight > old_edge.weight) THENDO先做一次减边操作EdgeOperate(GRAPH,DELETE,old_edge,i)DO将本次减边操作加入EDGE_OPERATE_LIST中DO再做一次加边操作EdgeOperate(GRAPH,ADD,new_edge,i+1)DO将本次加边操作加入EDGE_OPERATE_LIST中END IF (new_edge.weight > old_edge.weight)END IF (两个可结合半边一个为自由半边,另一个已结合)END IF (两个可结合半边均为自由半边)END IF (两个顶点各有一个半边可以结合)步骤5:若步骤4中不再有可结合的半边对,或达到计算次数要求,则结束;否则,转步骤2.4. 聚合归约演算协调准则动态可增殖的多层次自组织认知系统的每个层次具有形式上一致的知识表示方法,各层的自组关联、自组聚合、归约和样本表达四个知识处理模型是实现系统自组织层次增殖的核- 12 -。
计算理论与算法

将问题分解为若干个子 问题,通过求解子问题 的最优解来得到原问题 的最优解的思想,适用 于具有重叠子问题和最 优子结构性质的问题。
03
复杂度理论
时间复杂度与空间复杂度
1 2
时间复杂度
评估算法执行时间随输入规模增长的速度,常用 大O表示法(如O(n), O(n^2), O(log n)等)来 描述。
广度优先搜索(BFS)
从某个顶点出发,逐层访问图中所有顶点,直到达到指定顶点或无 法再访问为止。
图的遍历应用
用于解决图的连通性问题、寻找图中的路径、生成拓扑排序等问题。
最小生成树与最短路径算法
01
最小生成树(MST)
对于连通的无向图,一个包含图中所有顶点的连通子图,且所有边的权
值之和最小。常用算法有Prim算法和Kruskal算法。
时间复杂度
动态规划和分治策略的时间复杂度通常取决于问题的规模 和子问题的数量。在某些情况下,动态规划可能比分治策 略更高效,因为它避免了重复计算子问题。
06
计算几何与算法
计算几何基本概念与性质
点、线、面的表示与性质
计算几何中的基本元素包括点、线、面等,它们在计算机中的表 示方式及其性质是研究计算几何的基础。
01
几何搜索
02
最近点对问题
03
应用场景
几何搜索是指在几何数据集中查找满 足特定条件的几何对象,如查找最近 的点、线、面等。常见的几何搜索算 法有KD树、四叉树、R树等。
最近点对问题是指在给定的点集中找 到距离最近的两个点。该问题可以通 过分治算法在O(nlogn)的时间复杂度 内解决。
几何搜索和最近点对问题在计算机图 形学、计算机视觉、机器人学等领域 有着广泛的应用,如三维模型检索、 图像特征匹配、机器人避障等。
【人工智能】《人工智能》课程习题

【⼈⼯智能】《⼈⼯智能》课程习题《⼈⼯智能》课程习题第⼀章绪论1-1. 什么是⼈⼯智能?试从学科和能⼒两⽅⾯加以说明。
1-2. 在⼈⼯智能的发展过程中,有哪些思想和思潮起了重要作⽤?1-3. 为什么能够⽤机器(计算机)模仿⼈的智能?1-4. 现在⼈⼯智能有哪些学派?它们的认知观是什么?1-5. 你认为应从哪些层次对认知⾏为进⾏研究?1-6. ⼈⼯智能的主要研究和应⽤领域是什么?其中,哪些是新的研究热点?第⼆章知识表⽰⽅法2-1状态空间法、问题归约法、谓词逻辑法和语义⽹络法的要点是什么?它们有何本质上的联系及异同点?2-2设有3个传教⼠和3个野⼈来到河边,打算乘⼀只船从右岸渡到左岸去。
该船的负载能⼒为两⼈。
在任何时候,如果野⼈⼈数超过传教⼠⼈数,那么野⼈就会把传教⼠吃掉。
他们怎样才能⽤这条船安全地把所有⼈都渡过河去?再定义描述过河⽅案的谓词:L-R(x, x1, y, y1,S):x1个修道⼠和y1个野⼈渡船从河的左岸到河的右岸条件:Safety(L,x-x1,y-y1,S’)∧Safety(R,3-x+x1,3-y+y1,S’)∧Boat(L,S)动作:Safety(L,x-x1,y-y1,S’)∧Safety(R,3-x+x1,3-y+y1,S’)∧Boat(R,S’)R-L (x, x1, y, y1,S):x2个修道⼠和y2个野⼈渡船从河的左岸到河的右岸条件:Safety(R,3-x-x2,3-y-y2,S’)∧Safety(L,x+x2,y+y2,S’)∧Boat(R,S)动作:Safety(R,3-x-x2,3-y-y2,S’)∧Safety(L,x+x2,y+y2,S’)∧Boat(L,S’)(2) 过河⽅案Safety(L,3,3,S0)∧Safety(R,0,0,S0)∧Boat(L,S0)L-R(3, 1, 3, 1,S0) L-R(3, 0, 3, 2,S0)Safety(L,2,2,S1)∧Safety(R,1,1,S1)∧Boat(R,S1)Safety(L,3,1,S1’)∧Safety(R,0,2,S1’)∧Boat(R,S1’)R-L (2, 1, 2, 0,S1) R-L (3,0, 1, 1,S1’)Safety(L,3,2,S2)∧Safety(R,0,1,S2)∧Boat(L,S2)L-R(3, 0, 2, 2,S2)Safety(L,3,0,S3)∧Safety(R,0,3,S3)∧Boat(R,S3)R-L (3, 0, 0, 1,S3)Safety(L,3,1,S4)∧Safety(R,0,2,S1)∧Boat(L,S4)L-R(3, 2, 1, 0,S4)Safety(L,1,1,S5)∧Safety(R,2,2,S5)∧Boat(R,S5)R-L (1, 1, 1, 1,S5)Safety(L,2,2,S6)∧Safety(R,1,1,S6)∧Boat(L,S6)L-R(2, 2, 2, 0,S6)Safety(L,0,2,S7)∧Safety(R,3,1,S7)∧Boat(R,S7)R-L (0, 0, 2, 1,S7)Safety(L,0,3,S8)∧Safety(R,3,0,S8)∧Boat(L,S8)L-R(0, 0, 3, 2,S8)Safety(L,0,1,S9)∧Safety(R,3,2,S9)∧Boat(R,S9)R-L (0, 1, 1, 0,S9)Safety(L,1,1,S10)∧Safety(R,2,2,S10)∧Boat(L,S10)2-3利⽤图2.3,⽤状态空间法规划⼀个最短的旅⾏路程:此旅程从城市A开始,访问其他城市不多于⼀次,并返回A。
【计算机科学】_推导_期刊发文热词逐年推荐_20140724

2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
科研热词 随机波束成形 软件架构 记录分辨率 蛰伏进程 蓝牙 空间逻辑 移动界程演算 架构描述语言 数据吞吐量 数据传输 损失函数 头指消解 动态软件架构 关联聚类 信道反馈 优化参数 三维重建分辨率 三维全景图像技术 π 演算 msk mimo
53 54 55 56 57 58 59 60 61 62 63 64
倒立摆 信道互质 伪逆矩阵 优先约束 代谢算子 人工代谢算法 三维信息提取 z变换 tsp问题 smo算法 pca模型 cpu/fpga
1 1 1 1 1 1 1 1 1 1 1 1
2011年 科研热词 旁路攻击 中国剩余定理 rsa密码算法 故障分析 马尔可夫定位 错误检验 连通性 贝叶斯滤波 蒙特卡罗定位 等度规映射 瑞利衰落 流形 正交等度规映射 机器人定位 无线多跳网络 无线信道 故障模型 差分故障分析 导频辅助 对数阴影衰落 子空间 信道估计 人脸识别 mimo-ofdm log-gabor 推荐指数 3 3 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
科研热词 推荐指数 高维形象几何与仿生信息学 1 量化门限 1 软件质量 1 路由模型 1 跨层设计 1 行为一致性 1 蓝牙 1 自适应调制编码 1 自动要求重传 1 聚类中心 1 网构软件 1 系统行为 1 粗糙集 1 短期预报 1 直觉模糊集合 1 直觉模糊三角模 1 消息通信 1 正交频分复用 1 模糊c均值聚类 1 模块化神经网络 1 构件演化 1 构件 1 有限反馈 1 最小一乘方法 1 数据传输吞吐量 1 抽象质量类型 1 性能分析 1 彩色图像增强 1 广播 1 委员会机器 1 多输入多输出 1 多标准问题 1 剩余蕴涵 1 偏好信息 1 信噪比 1 优势关系 1 不可微函数 1 p2p 1 netshot 1
谓词演算与消解(归结)原理-图文

3.3.3 合一的一个例子
在此基础上又调用: unify (((father bill) (mother bill)), ((father bill) Y )) 导致调用: (1) unify((father bill),(father bill)) unify (father, father) unify (bill, bill) unify (( ), ( )) 所有的调用都成功,返回空代入集 { }。 (2) unify ((mother bill), Y)
与谓词相关的一个正整数称为元数或“参数数目”, 具有相同的名但元数不同的谓词是不同的。
真值true和false也是原子命题。
任何原子命题都能够用逻辑操作符将其变成谓词演 算的命题。用的联结词也和命题演算一样: ∨,∧, ~, => 和=。
当一个变元在一个命题中作为参数出现时,它代表 的是域中不特定的对象。谓词演算包括两个符号, 量词(全称量词)和彐(存在量词), 用于限定 包含变元的命题的含义。
3.2.2 谓词演算的语义
谓词演算表达式的真值 设有表达式E和在非空论域D上对E的一个解释I,E的
真值按以下规律决定: 1)一个常元的值是根据I指派给它的D的一个元素。 2)一个变元的值是根据I指派给它的D的一个元素集合
。 3)一个函词的值是根据由I指派给它的参数值计算得
到的D的元素。 4)真值符号true的值是T,false的值是F。 5)原子命题的值或者为T,或者为F,取决于解释I。 6)如果一个命题的值为F,则其否定式为T,否则为F
▪
~ (P∧Q) = (~P∨~Q)
▪分配律:P∨(Q∧R) = (P∨Q)∧(P∨R)
▪ 分配律:P∧(Q∨R)=(P∧Q)∨(P∧R)
计算理论6章 Lambda演算模型

类型系统 (表示类型上下文)
x: T ├ x: T
├ x: T1,├ y:T2
, y:T2 ├ x:T1
├ x: T1, ├ E: T2 ├ x:T. E : T1 T2
├ E1: T1 T2, ├ E2:T1 ├ E1E2: T2
2 纯Lambda演算实例
逻辑运算
布尔值 T = a.b.a F = a.b.b
布尔运算 and = x.y. x y F or = x. y. x T y not = x. x F T
2 纯Lambda演算实例
and T T = T T F = (ab. a) T F =T
or T F = T T F = (ab. a) T F =T
扩展-表达式 扩展-变换规则 扩展数据类型
3 纯Lambda演算的扩展
扩展-表达式 E ::= true | false | n | f | x | E1 E2 | x.E | (E) | (E0 E1, E2 ) | let x= E0 in E
3 纯Lambda演算的扩展
带类型Lambda演算
y
1 纯Lambda演算理论
定义6. 最左归约
依据归约基中符号出现的顺序进行的归约称 为最左归约。也称标准归约。
Church-Rosser定理
Lambda表达式若有范式则一定唯一,并且按 最左归约一定能求到该范式。
2 纯Lambda演算实例
实例
整数运算 逻辑运算 关系运算
2 纯Lambda演算实例
MINUS m n = m-n n <m 0 否则
2 纯Lambda演算实例
【计算机科学】_形式化语言_期刊发文热词逐年推荐_20140724
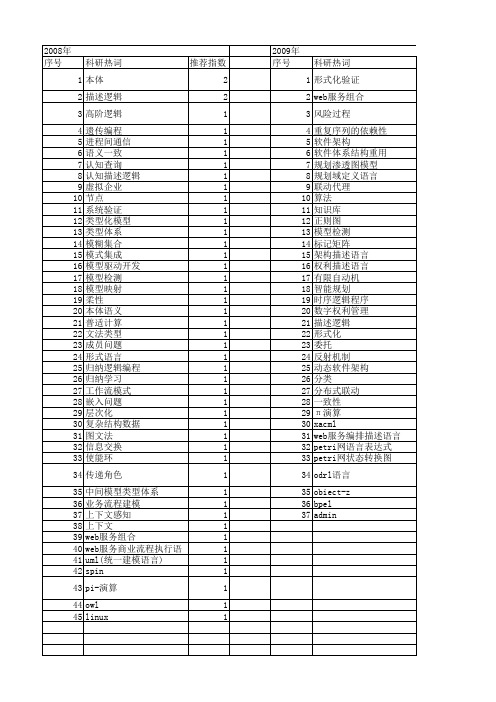
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
科研热词 推荐指数 本体 2 描述逻辑 2 高阶逻辑 1 遗传编程 1 进程间通信 1 语义一致 1 认知查询 1 认知描述逻辑 1集合 1 模式集成 1 模型驱动开发 1 模型检测 1 模型映射 1 柔性 1 本体语义 1 普适计算 1 文法类型 1 成员问题 1 形式语言 1 归纳逻辑编程 1 归纳学习 1 工作流模式 1 嵌入问题 1 层次化 1 复杂结构数据 1 图文法 1 信息交换 1 使能环 1 传递角色 1 中间模型类型体系 1 业务流程建模 1 上下文感知 1 上下文 1 web服务组合 1 web服务商业流程执行语言 1 uml(统一建模语言) 1 spin 1 pi-演算 1 owl 1 linux 1
科研热词 推荐指数 形式化 2 飞行控制软件 1 面向方面软件体系结构描述语言 1 面向方面软件体系结构 1 需求建模 1 集合运算 1 集合特征码 1 重复模式 1 运行支撑平台体系结构 1 语言知识特征 1 语法分析 1 网络本体语言 1 网络中心化仿真 1 统计特征 1 统计框架 1 统一建模语言 1 组合定义 1 组件组合 1 线性化 1 算法 1 模型驱动工程 1 模型检测 1 模型抽取 1 模型 1 查询 1 本体 1 时间自动机 1 时态数据 1 无人机系统 1 方面编织 1 新词检测 1 数据库 1 推导 1 形式语言 1 形式语义 1 形式化验证 1 形式化语义 1 形式化方法 1 归约 1 巴科斯范式 1 定理证明 1 完整性约束 1 安全本体 1 安全性 1 子图替换 1 子图匹配 1 基于模型的测试 1 图文法 1 列车自动防护 1 切点指示器 1 信息安全 1 作战管理语言 1
半边图模型之构造演算

半边图模型之构造演算
孟朝 晖 ( 海 大学计 算机 及信 息工程 学 院 , 河 南京 202 ) 104
E— i : n z a h i h u e u c mal me g h o u @.h .d .n
摘 要
提 出一 个 动 态 可 增 殖 的 多层 次 自组 织 认 知 系统 , 个层 次 具 有 形 式 上 一 致 的知 识 表 示 方 法 , 层 的 自组 关联 、 每 各
e c a e , e f s d l i s l o g n z g c n e t n mo e , e s c n s s l— ra i n g r g t n mo e , e h r a h ly r t rt mo e s e - r a i n o n c i d l t e o d i e og n z g a g e a i d l t tid h i f i o h f i o h i e u t n mo e n h a t i s mp e r p e e tt n s d ci d l a d t e l s a l e r s n a i mo e. h s o r mo es r h o e l o t ms or t e d - r o s o d 1 e e fu d l T ae t e c r ag r h f y i h n mia rw r c g i o y tm t i rr h c l s l o g n z t nT i p p r p i t o t t e in a r a o a l g e a a c l go e o n t n s s i e wi h e ac ia ef r a iai . s a e on s u , d sg e s n be a g g - h - o h o r t n a d rd c in c c l s mo e s t e c t a tp or te r c g i o y t m a a r w i ir r hc e - r i n e u t a u u d l i r il se f e o n t n s se t tc l g o w t h e a c i a s l o - o o l h i c h i h l h l f
λ演算的概念-概念解析以及定义

λ演算的概念-概述说明以及解释1.引言1.1 概述λ演算是一种重要的计算机科学理论,它是由数学家阿兰·图灵和斯蒂芬·科尔克霍夫在上世纪30年代提出的。
λ演算是一种用来研究函数定义、函数应用和递归的形式系统,它在计算理论、编程语言设计、人工智能等领域都有广泛的应用。
本文将介绍λ演算的起源、基本概念和应用领域,并探讨λ演算在计算机科学中的重要性。
通过对λ演算的深入理解,我们将能更好地应用它来解决实际问题,同时也能够对计算机科学理论有更深刻的认识。
1.2 文章结构文章结构部分的内容:本文主要分为三个部分:引言、正文和结论。
引言部分主要包括概述、文章结构和目的。
在概述中简要介绍了λ演算的概念和重要性,引出了本文的主题。
文章结构部分则给出了整篇文章的大纲和目录,让读者对文章的整体结构有一个清晰的了解。
目的部分则说明了本文撰写的目的和意义,为读者阐明了本文的重要性和价值。
正文部分分为λ演算的起源、λ演算的基本概念和λ演算的应用领域三个部分。
在λ演算的起源部分,将介绍λ演算的历史渊源和发展背景;在λ演算的基本概念部分,将详细介绍λ演算的基本概念,包括λ演算的语法和语义规则等内容;在λ演算的应用领域部分,将探讨λ演算在计算机科学和其他领域中的应用和意义。
结论部分包括对λ演算的展望、λ演算在计算机科学中的重要性和总结三个部分。
在对λ演算的展望部分,将展望λ演算在未来的发展方向和应用前景;在λ演算在计算机科学中的重要性部分,将总结λ演算在计算机科学中的重要地位和作用;在总结部分,将对本文的主要内容进行总结和概括。
通过以上结构,本文将全面系统地介绍λ演算的概念和相关内容,为读者提供一个清晰的了解和认识。
1.3 目的本文的目的是通过对λ演算的介绍,让读者了解λ演算的起源、基本概念以及在计算机科学领域的应用。
通过阐述对λ演算的展望和在计算机科学中的重要性,希望能够引发读者对λ演算的兴趣,并深入了解其在计算机科学领域的重要作用。
ELNF归约演算

ELNF归约演算
阳富民;吴永英
【期刊名称】《华中理工大学学报》
【年(卷),期】1994(022)012
【摘要】ELNF演算是在LNF演算的基础上扩充而成的函数/逻辑归约演算系统,扩充的主要工作包括逻辑变量、谓词名的引进。
提出并描述了逻辑函子SOLUTION和PROVE及其归约规则。
讨论了ELNF演算的基本概念。
为表征HORN子句提供了一种有效方式。
【总页数】4页(P27-30)
【作者】阳富民;吴永英
【作者单位】不详;不详
【正文语种】中文
【中图分类】TP301.6
【相关文献】
1.半边图模型之聚合归约演算 [J], 孟朝晖
2.函数/逻辑归约演算系统ELNF [J], 卢炎生;阳富民
3.泛函程序设计语言实现中的图归约演算 [J], 杨祥金
4.ELNF演算的解释技术 [J], 金海;李智勇
5.模态谓词演算的判定问题(Ⅰ)——关于Kripke归约 [J], 高恆珊
因版权原因,仅展示原文概要,查看原文内容请购买。
制造单元设计中心半边图与拆分重组算法

制造单元设计中心半边图与拆分重组算法
孟朝晖
【期刊名称】《计算机工程》
【年(卷),期】2005(031)023
【摘要】提出了半边自组图理论,半边附属于顶点,一对半边可结合为边.用半边图来描述复杂组合优化问题的可能解,在此基础上设计了针对图的拆分重组算法,用此算法求解了一个典型的复杂组合优化问题,制造单元设计问题.示例表明,半边图语言能够准确地表达可能解中的复杂结构和各种约束,20台机器50种零件分组实验证明,7次迭代计算即可达到优化目标.
【总页数】3页(P151-153)
【作者】孟朝晖
【作者单位】河海大学计算机及信息工程学院,南京,210024
【正文语种】中文
【中图分类】TP18
【相关文献】
1.基于EDA算法的敏捷制造单元重组方法 [J], 任义丰;曾进
2.基于遗传算法的制造单元重组技术研究 [J], 付宜利;石旭东;何霆;马玉林
3.半边图与挤出吸入算法及制造单元设计 [J], 孟朝晖
4.机器可选制造单元设计的半边图划分模型 [J], 孟朝晖
5.机器可选制造单元设计的半边图挤出吸入算法 [J], 孟朝晖
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半边图模型之聚合归约演算
孟 朝 晖
( 河海 大学 计算机及 信 息工 程 学院 , 南京 2 0 2 ) 104
E- i: n z a h i h u e u c mal me g h o u @.h . .n d
摘
要 : 出了 实现 自组 织 多层 次 归约 的一 个 指 导 原 则 , 自组 聚合 与 归约 的 协调 准 则 , 核心 思 想是 , 于 多 聚合 准 则 提 即 其 基
Ab t a t A g n r l y g i e p n i l f r e u t n a r c : e e a i u d r cp e o rd c i wi h e a c i a s l — r a iai n s p o o e . h t s t e t i o t h ir r h c l e f o g nz t i o r p s d T a i h c o d n t n rtr n f r e f o g n zn a g e ae p o e s a d rd c p o e s h c r t i k n i ,h v ro s o r i ai c e o o s l - r a ii g g r g t r c s n e u e r c s . e o e h n i g s t e a u o i i T i a g e ai n s b es b s d p n t e s l o g n zn g r g t n c lu u i ie sf d a g e ai n c tr n c ud h v g g t u s t a e u o h e f r a iig a g e ai ac l s w t d v ri e g r g t r e o o l a e r o - o h i o i i t e n es c a t.h s i t re t a t a e h fu d t n o te e u t n a c l s h i t re t p r T e e n e c p rs r t e o n ai f r h r d c i c lu u wh c f l we t e g r g t n s s o o ih ol d h a g e a i o o c c lsT e a s l o g n zn g e a in c lu u d l f r s l o g nz t n g a h s v nT e e ac l mo e s n l a u u . n, ef r a ii g a g g t a c l s mo e ef r a iai r p i h - r o o - o e . h s c u i l d li i k e ig i te o r i ai n rtr n o s l — r a iig g rg t r c s a d e u e r c s . h a g e ae u e p n w t h c o n t c e o f r ef o g n zn a g e ae h d o i i p o e s n rd c p o e sT e g rg t s b g a h a e t e u c me f t e s l- r a ii g a g e ai n ac l sT e r p s r h o to o h ef o g nzn g r g t c lu u . h mu u r lt n a n t e u g a h c u d o t a ea i s mo g h s b r p s o l l o d d c r m h s b e u e fo t e u me e f t e u g a h . e ts o h s b r p s h T mo t mp ra t ac l s s i o t n c l uu mo e . . e r d c in ac ls d l et e u t c lu u mo e i i h o dl s gv n I h s mo e ,h g r g t s b g a h e u e o t e e u t n v r x o e o n ,h u t f t e s b g a h i e . ti d l t e a g e ae u p rd c s t h r d c i e e n n o e t e s b mee o h u r p n r o t r d c s t h e u t n h l e g n n o e as a d t e mu u l r lt n b t e h w u g a h e u e o t e e u e o t e r d c i af d e o e o n o, n h ta e ai ewe n t e t o s b r p s r d c s t h o l o r d ci n e g . e eo e, oma u i e u t n w t i r r h c ls l o g n z t n c me o r aie e u t d eT r fr a f r l n t rd ci i h e a c i a ef r a iai o s t e l . o h y o h - o z Ke r s y wo d :h e a c i a e f og nz t n a g e ai n c lu u ;e u t n c c l s h l d e s l o g nz t n g a h ir r h c l s l r a iai ; g rg t ac l s rd ci a u u ; a f e g ; ef r a iai r p - o o o l - o
的 自组 聚合 演 算 中 的 各 个 聚合 子 集 是 可 以 相 交 的 , 交 的部 分是 下一 步 归 约 演算 的基 础 。 出 了符 合 上述 协 调 准 则 的 自 相 给
组 图 聚合 归约 演 算模 型 , 合 子 图是 聚合 演 算 的结 果 , 归约 演 算 中 , 合 子 图对 应 为 归约 顶 点 , 图 的子 边 界 对应 为 归 聚 在 聚 子
Ag r g t n a d Re u t n Ca c l s o l g a h g e a i n d ci lu u f Ha f Ed e Gr p o o
M ENG a - u Zh o h i
( o p tr& Ifr t n E g er g C l g , o a U ies y N ni 1 0 4 C ia C m ue noma o n 0 2 ,hn ) i n n l t n
约 半 边 . 由子 图相 交部 分 抽 象 出的子 图 边界 之 间的 关 系则 对 应 为 归约 边 , 而 构 成 了形 式上 完整 统 一 的 自组 织 多层 次 而 从
归约。
关键 词 : 多层 次 自组 织 ; 合 演 算 ; 约 演 算 ; 边 ; 聚 归 半 自组 图
文章 编 号 : 0 2 8 3 ( 0 6 3 - 0 1 0 文 献标 识 码 : 中 图分 类 号 : P 0 10 — 3 12 0 ) 10 7 — 6 A T3 1
