2010年黑龙江省高职院校对口招收中职毕业生统一考试数学模拟试卷14

合集下载

中职毕业生对口专业升高职院校招生统一考试

黑龙江省中职毕业生对口专业升高职院校招生统一考试英语试卷第一部分选择题（共60 分）一、单项选择题（本大题共40 小题，每小题 1 分，共40 分）1. My grandpa went to see his doctor for _____ about his heart trouble yesterday.A. adviceB. advicesC. an adviceD. the advices2. There ____ a teacher 'ro s om and many classroom in this new building.A. isB. areC. wasD. were3. ____ like to eat fried chicken but ______ like to eat fish.A. the American, the JapaneseB. the Americans, the JapanesesC. the Americans, the JapaneseD. the American, the Japaneses4. ___ Monday morning, I missed the bus and was late for class.A. InB. OnC. AtD. Of5. I won't believe you ____ I have seen it with my own eyes.A. beforeB. afterC. whenD. until6. They went to the village on foot ____ by bus.A. insteadB. instead ofC. take placeD. take place of7. My mother asked me if I ___ well ___ my classmate.A. get on withB. got on; withC. go on; withD. went on; with8. The film ____ him ___ what he had seen in London.9. I will never give up ____ English and I shall go on to study it hard.A. remind; ofB. reminded; ofC. reminded; offD. remind; offA. learnB. learningC. learnedD. to learn10. An interesting sports meet _____ next month.A. will holdB. are heldC. will be holding11. He had no way to find a hotel __ .D. will be heldA. to liveB. to live inC. living12. If ___ tomorrow, we' lsl tay at home.A .it will rain B. it rains C. it 'to s rain D. to be livingD. it will raining13. ---- " Your shoes are very beautiful. They must be expansive" No. They ____ only me 20 dollars. "A. spentB. tookC. paidD. cost14. Johnny, you ___ play with the knife; you ___ hurt yourself.A. won't,can 'tB. can ',s t houldn 'tC. shouldn ',m t ust D . mustn 'm t ay15. ___ is your English teacher?A . Who B. whom C. which D. what35. 1 don 'k t now here the day after tomorrow16. John was made ___ the truck for a \week as a punishment.A. to washB. washingC. washD. to be washing17. Too much time is one of the reasons to get you __ .A. into troubleB. to troubleC. in the troubleD. to the trouble18. A close friend is the person to ____ you are willing to lend a helping hand.A. whoB. whomC. thatD. himhe can know where we are.19. I will leave a noteA. in order toB. in orderC. so thatD. so as to me since I didn 'c t lean the blackboard at the beginning of the class. A. get angry withB. got angry withC. got angry about 21. Weather ____ , we are going to have picnic next week. B. permits C. permitted is necessary _____ us to protect the grass B. it; for C. it; of 20. Our monitorD. got angry at A. permit22. I thinkA. that; for23. MikeA. doD. permitting D. that; of tell me the matter, but I didn 'ta t ke it seriously at that time. B. does C. did 24. We were all very tired, but _ A. any B. someD. was doing of us stopped to have a rest. C. none D. neither 25. The roomA. whichwindow is still bright is our English teacher 'of s fice. C. whose B. its D. that 26. He will come backthis month. A. in the end of B. at the end of C. at end of D. at the end27. There are several huge trees ____ the temple. A. in the front of B. on the front of C. in front of D. on front of28. I 'li d ke share this bedroom other two students. A. for B. in C. with D. to29. The Mid-Autumn Festival is A. on the fiveteenth of the lunar August. B. in the fifteenth C. on the fifteenth D. in fifteenth30. Red lanterns A. are hanging up to celebrate the National Day every year. B. are hung up C. hung up D. are hanged up31. It is he is the best teacher in my school. A. known that B. known as C. know D. knowing32. Bob said would do what he could you with your study. A. help B. helped33. Excuse me, sir, could you tell me C. helpingD. to help A. where the nearest bank is B. where is the nearest bankC. where the nearest bank wasD. the nearest bank is where34. Written English is the same in both British and America A. more and less B. more or littleC. more or lessD. much or littleA. when does he comeB. why will he comeC. if he does comeD. how he will come36. The medicine has _____ the growth of children.A. a good affect inB. a good affect onC. an good effect onD. a good effect on37. We should ____ the trees.A. prevent them to cuttingB. prevent them from cuttingC. prevent them cuttingD. prevent them cut38. Some people ____ pay more trouble the air-conditioned-bus _____ take the ordinary public bus because it is too slow crowded.A. would; thatB. would rather; thanC. had rather; thanD. rather; than39. The only language ____ is easy to learn is the mother tongueA. whichB. thatC. /D. it40. If it should rain, the crops ___ saved.A. will beB. would beC. areD. were二．阅读理解（本大题共10 小题，每小题 2 分，共20 分）在每小题列出的四个备选项中只有无分。

职高对口高考模拟数学试卷

#### 一、填空题（每空2分，共20分）1. 若函数 \( f(x) = ax^2 + bx + c \) 在 \( x = 1 \) 处取得极值，则 \( a + b + c = \) ________。

2. 在等差数列 \(\{a_n\}\) 中，若 \( a_1 = 3 \)，公差 \( d = 2 \)，则\( a_5 = \) ________。

3. 已知圆的方程为 \( x^2 + y^2 - 4x - 6y + 9 = 0 \)，则该圆的半径为________。

4. 若 \( \cos \alpha = \frac{1}{3} \)，则 \( \sin \alpha \) 的值为________。

5. 函数 \( y = \frac{1}{x} \) 的图像关于 ________ 对称。

6. 若 \( \sqrt{a^2 + b^2} = 5 \)，\( a = 3 \)，则 \( b \) 的值为________。

7. 三个数的和为 12，其中两个数分别为 3 和 5，则第三个数为 ________。

8. 若 \( \triangle ABC \) 中，\( a = 5 \)，\( b = 6 \)，\( c = 7 \)，则\( \cos A \) 的值为 ________。

9. 下列不等式中，正确的是 ________（选项：A. \( 2x > 4 \)；B. \( 3x \leq 9 \)；C. \( x^2 \geq 4 \)；D. \( \frac{1}{x} < 1 \)）10. 已知 \( \log_2 8 = 3 \)，则 \( \log_2 32 = \) ________。

#### 二、选择题（每题3分，共30分）1. 函数 \( y = x^3 - 3x \) 的图像在 \( x = 0 \) 处的切线斜率为：A. 0；B. -3；C. 3；D. 不存在。

2013黑龙江职中对口升学数学模拟考试试题一（含答案）

版权所有-中职教学资源网电话：************ Email:**************2013黑龙江职中对口升学数学模拟考试试题一（含答案）一、选择题（本题共有12小题，每小题5分, 共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.考察下列每组对象, 能组成一个集合的是（）① 一中高一年级聪明的学生 ②直角坐标系中横、纵坐标相等的点 ③ 不小于3的正整数 ④3的近似值A. ①②B. ③④C. ②③D. ①③2. 图中阴影部分表示的集合是( )A 、（C U A ）∩B B 、A ∩（C U B ） C 、C U (A ∩B) D 、C U (A ∪B)3. 设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（）A ．{}01，B ．{}101-，，C ．{}012，， D ．{}1012-，，， 4. 已知)(x f 是一次函数，且满足,172)1(3+=+x x f 则=)(x f （） A.532+x B. 132+x C. 32-x D. 52+x 5.李明放学回家的路上，开始和同学边走边讨论问题，走的比较慢；然后他们索性停下来将问题彻底解决；最后他快速地回到了家。

下列图象中与这一过程吻合得最好的是（）6. 函数2211()31x x f x x x x ⎧-⎪=⎨-->⎪⎩，，，，≤则1(3)f f ⎛⎫⎪⎝⎭的值为（） A ．1516 B ．2716- C ．89D ．18 7. 如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上是减函数，那么实数a 的取值范围是（）A 、3a -≤B 、3a -≥C 、a ≤5D 、a ≥5时间时间时间时间A ．C ．D ．B ．版权所有-中职教学资源网电话：************ Email:**************8.已知函数2221()x x f x x ++=的值域为C ，则（）A ．0C ∈B ．1C -∈ C ．2C ∈D ．1C ∈ 9. 若)1(-x f 的定义域为[1，2]，则)2(+x f 的定义域为（）A ．[0，1]B ．[2，3]C ．[－2，－1]D ．无法确定10.如果偶函数)(x f 在区间[3,7] 上是增函数且最大值为5，那么)(x f 在区间[]3,7-- 上是（）A ．增函数且最小值是5-B ．增函数且最大值是5C ．减函数且最大值是5D ．减函数且最小值是5-11. 已知()12g x x =- , ()221(0)x f g x x x +=≠⎡⎤⎣⎦, 则12f⎛⎫⎪⎝⎭等于（） A ．1 B ．3 C ．15 D ．1712. 定义域为R 的函数()f x 满足条件:①12121212[()()]()0,(0,0,)f x f x x x x x x x -->>>≠； ②()()0f x f x +-= ()x R ∈； ③(3)0f -=. 则不等式()0x f x ⋅<的解集是（）A ．{}|303x x x -<<>或B ．{}|303x x x <-≤<或 C ．{}|33x x x <->或 D ．{}|3003x x x -<<<<或二、填空题（本题共有4小题, 每小题5分, 共20分）13. 已知集合A ＝{－2，3，4m －4}，集合B ＝{3，2m }．若B ⊆A ，则实数m ＝．14. 已知{}12{1,2,34}P ⊆⊆，，，则这样的集合P 有个. 15. 已知()y f x =是定义在R 上的奇函数，当0x >时, 2()1f x x x =++, 则当0x <时,版权所有-中职教学资源网电话：************ Email:**************()f x = ___________ .16. 设βα,是方程02222=-+-m mx x ()R m ∈的两个实根, 则22βα+的最小值为 __________.三、解答题（本题共4小题, 共40分, 解答应写出文字说明、证明过程或演算步骤） 17. （本题满分10分）已知全集{},10U x x N x =∈<，{}2,,A x x k k N x U ==∈∈，{}2320B x x x =-+=.（1）用列举法表示集合,,U A B ；（2）求A B ，A B ，U C A 。

黑龙江高职对口招生考试数学模拟试题一(含答案)

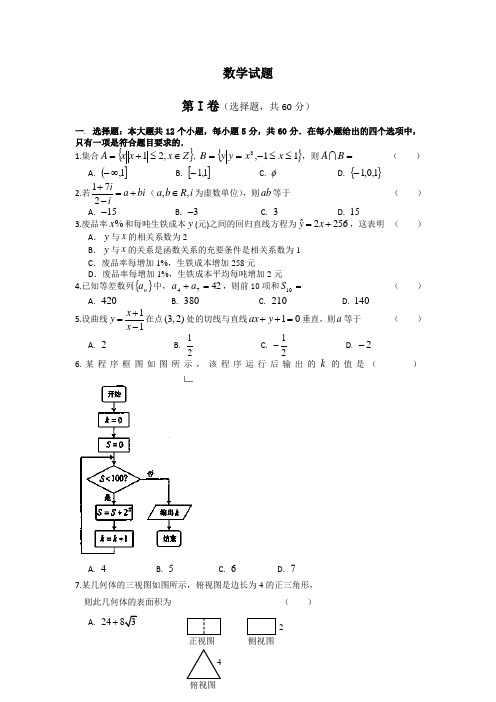
数学试题第I 卷（选择题，共60分）一. 选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.集合{}Z x x x A ∈≤+=,21,{}11,3≤≤-==x x y y B ，则=B A （） A. (]1,∞-B. []1,1-C. φD. {}1,0,1-2.若172ia bi i+=+-（,,a b R i ∈为虚数单位），则ab 等于（） A. 15- B. 3- C. 3 D. 153.废品率%x 和每吨生铁成本y (元)之间的回归直线方程为ˆ2256y x =+，这表明（）A ．y 与x 的相关系数为2B ．y 与x 的关系是函数关系的充要条件是相关系数为1C ．废品率每增加1%，生铁成本增加258元D ．废品率每增加1%，生铁成本平均每吨增加2元4.已知等差数列{}n a 中，4274=+a a ，则前10项和=10S （） A. 420 B. 380C. 210D. 1405.设曲线11x y x +=-在点(3,2)处的切线与直线10ax y ++=垂直，则a 等于（） A. 2 B. 12 C. 12- D. 2-6.某程序框图如图所示，该程序运行后输出的k 的值是（）A. 4B. 5C. 6D. 7 7.某几何体的三视图如图所示，俯视图是边长为4的正三角形，则此几何体的表面积为（） A. 2483+ 4正视图侧视图俯视图2B.C. 12+D. 24+8.已知函数()2xf x =的反函数()g x 满足()()4g a g b +=，则11a b+的最小值为（） A. 1 B. 13 C. 12 D. 149.定义运算：12142334a a a a a a a a =-，将函数cos2()sin2xf x x =的图像向左平移m （0m >）个单位，所得图像对应的函数为偶函数，则m 的最小值是（）A. 3πB. 32πC. 34πD. 37π10.已知函数2()f x x bx c =++，其中04,04b c ≤≤≤≤，记事件A 为 “函数()f x 满足条件：(2)12(1)1f f ≤⎧⎨-≤⎩”，则事件A 发生的概率为（）A. 49B. 13C. 12D. 1911.已知12,F F 分别为双曲线22221x y a b-=（a ＞0,b ＞0）的左、右焦点，P 为双曲线左支上的任意一点，若221||||PF PF 的最小值为8a ，则双曲线离心率e 的取值范围是（）A. (1,)+∞B. (0,3]C. (1,3]D. (1,2] 12.定义域为R 的偶函数()f x ，对x R ∀∈，有(2)()(1)f x f x f +=+，且当[2,3]x ∈ 时，2()21218f x x x =-+-，若函数()log (1)a y f x x =-+在()0,+∞上至少有三个零点，则a 的取值范围是（）A.B.C.D. 第Ⅱ卷（非选择题，共90分）本卷包括必考题和选考题两部分.第（13）题～第（21）题为必考题，每个试题考生都必须做答.第（22）题～（24）题为选考题，考生根据要求做答.二. 填空题：本大题共4小题，每小题5分，共20分.13.已知圆C 与直线04=--y x 及0=-y x 都相切，且圆心在直线0=+y x 上，则圆C 的方程为 .14.某高中在校学生2000人，高一年级与高二年级人数相同并且都比高三年级多1人，为了响应市教育局“阳光体育”号召，该校开展了跑步和跳绳两项比赛，要求每人都参加而其中::2:3:5a b c =，全校参与跳绳的人数占总人数的5，为了了解学生对本次活动的满意度，采用分层抽样从中抽取一个200人的样本进行调查，则高二年级中参与跑步的同学应抽取人. 15.已知向量13(,),,22a OA ab OB a b =-=-=+，若OAB ∆是等边三角形，则OAB ∆的面积为 .16.数列{}n a 满足11a =，且对任意的正整数,m n 都有m n m n a a a mn +=++，则12201220131111a a a a ++++= .三. 解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分12分）已知向量()sin m x x =，()sin ,cos n x x =，设函数()n m x f ⋅=. （Ⅰ）求函数()f x 的解析式，并求()f x 在区间⎥⎦⎤⎢⎣⎡-6,4ππ上的最小值；（Ⅱ）在ABC ∆中，c b a ,,分别是角C B A ,,的对边，A 为锐角，若()()32f A f A +-=， 7b c +=，ABC ∆的面积为32，求a .18.（本小题满分12分）甲、乙两个盒子中各有3个球，其中甲盒中有2个黑球1个白球，乙盒中有1个黑球2个白球，所有球之间只有颜色区别.（Ⅰ）若从甲、乙两个盒子中各取一个球，求取出的2个球颜色相同的概率；（Ⅱ）将这两个盒子中的球混合在一起，从中任取2个，求取出的2个球中至少有一个黑球的概率. 19.（本小题满分12分）四棱锥S ABCD -中，底面ABCD 为平行四边形，侧面SBC ⊥底面ABCD ，E 为SD 的中点，已知452ABC AB BC ∠===，，SB SC == （Ⅰ）求证：SA BC ⊥；（Ⅱ）在BC 上求一点F ，使//EC 平面SAF ；（Ⅲ）求三棱锥D EAC -的体积.20.（本小题满分12分）已知椭圆C 的焦点在x 轴上，离心率2e =，且经过点(2,1)A -. （Ⅰ）求椭圆C 的标准方程；（Ⅱ）斜率为1-的直线l 与椭圆C 相交于,P Q 两点，求证：直线AP 与AQ 的倾斜角互补.21.（本小题满分12分）已知函数()ln f x x a x =-，1(), (R).ag x a x+=-∈（Ⅰ）若1a =，求函数()f x 的极值；（Ⅱ）设函数()()()h x f x g x =-，求函数()h x 的单调区间；（Ⅲ）若在区间[]1,e （e 2.718=）上存在一点0x ，使得0()f x <0()g x 成立，求a 的取值范围.AB C D S E答案一、选择题：（本大题共12小题，每小题5分，共60分）题号123456789 10 11 12 答案 D B D C D A A C CBCA二、填空题：（本大题共4小题，每小题5分，共20 分） 13. ()()21122=++-y x 14. 36 15.33 16.10072013 三、解答题：（本大题共6小题，共70分。

数学_2010年黑龙江省某校高考数学一模试卷(文科)(含答案)

2010年黑龙江省某校高考数学一模试卷（文科）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的．1. 已知复数z=a+i(a∈R)在复平面内对应的点在二象限，且|z⋅(1+i)|>2，则实数a 的取值范围是（）A a>1或a<−1B a<−1C a>√2+1或a<1−√2D a>12. 已知S n是等差数列{a n}的前n项和，若S3=6，a5=8，则S12−S9的值是（）A 24B 42C 60D 783. 用二分法求函数f(x)=lgx+x−3的一个零点，根据参考数据，可得函数f(x)的一个零点的近似解（精确到0.1）为（）（参考数据：lg2.5≈0.398，lg2.75≈0.439，lg2.5625≈0.409）A 2.4B 2.5C 2.6D 2.564. 已知点P(x, y)满足约束条件{y≤xx+y≥2y≥3x−6，则z=x−2y的最大值是（）A −3B −2C −1D 25. 如下程序框图的功能是：给出以下十个数：5，9，80，43，95，73，28，17，60，36，把大于60的数找出来，则框图中的①②应分别填入的是（）A x>60∘，i=i+1B x<60∘，i=i+1C x>60∘，i=i−1D x<60∘，i= i−16. 已知双曲线x2a2−y2b2=1(a>0，b>0)的焦点到渐近线的距离为2√3，且双曲线右支上一点P到右焦点的距离的最小值为2，则双曲线的离心率为( )A √3B 3C 2D 127. 设a∈{−1,1,12，3}，则使函数y=x a的定义域是R，且为奇函数的所有a的值是（）A 1，3 B −1，1 C −1，3 D −1，1，38. 已知函数f(x)=cos(x+ϕ)(0<ϕ<π)的导函数f′(x)的图象如图所示，则ϕ=()A π6 B 2π3C π3D 5π69. 设l，m，n表示三条不同的直线，α，β，γ表示三个不同的平面，给出下列四个命题：①若l ⊥α，m ⊥l ，m ⊥β，则α⊥β；②若m ⊂β，n 是l 在β内的射影，m ⊥n ，则m ⊥l ；③若m 是平面α的一条斜线，A ∉α，l 为过A 的一条动直线，则可能有l ⊥m ，l ⊥α； ④若α⊥β，α⊥γ，则α // β 其中真命题的个数为（） A 1 B 2 C 3 D 410. 在直角梯形ABCD 中，AB // CD ，∠BAD =90∘，且AB =AD =12CD =1，M 是AB 的中点，且BN →=2ND →，则CM →⋅AN →的值为（）A 54 B −54 C 76 D −7611. 利用计算机在区间(0, 1)上产生两个随机数a 和b ，则方程bx =2a −x 有实根的概率为（）A 13 B 12 C 23 D 112. 设函数f(x)={x −[x],x ≤0f(x −1),x >0，其中[x]表示不超过x 的最大整数，如[−1.2]=−2，[1.2]=1，[1]=1，若f(x)=kx +k(k >0)有三个不同的根，则实数k 的取值范围是（）A (14，13] B (0,14] C [14，13] D [14，13)二、填空题：本大题共4小题，每小题5分，共20分．将答案填在机读卡上相应的位置． 13. 抛物线y 2=2px(p >0)的焦点为F ，准线l 与x 轴交于点M ，若N 为l 上一点，当△MNF 为等腰三角形，NF =2√2时，则p =________．14. 如图一个几何体的正视图和俯视图如图所示，其中俯视图为边长为2√3的正三角形，且圆与三角形内切，则侧视图的面积为________15. 已知数列{a n }满足a n 2=a n−1a n+1(n ∈N ∗, n ≥2)，若1a 4+1a 5+1a 6=1，a 4a 6=4，则a 4+a 5+a 6=________．16. 已知圆C 1：(x −2cosθ)2+(y −2sinθ)2＝1与圆C 2:x 2+y 2＝1，在下列说法中： ①对于任意的θ，圆C 1与圆C 2始终相切；②对于任意的θ，圆C 1与圆C 2始终有四条公切线；③当θ=π6时，圆C 1被直线l:√3x −y −1=0截得的弦长为√3； ④P ，Q 分别为圆C 1与圆C 2上的动点，则|PQ|的最大值为4．其中正确命题的序号为________．三、解答题：本大题共8小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤．17. “神州”号飞船返回舱顺利到达地球后，为了及时将航天员救出，地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心（记为B ，C ，D ）．当返回舱距地面1万米的P 点时（假定以后垂直下落，并在A 点着陆），C 救援中心测得飞船位于其南偏东60∘方向，仰角为60∘，B 救援中心测得飞船位于其南偏西30∘方向，仰角为30∘．D 救援中心测得着陆点A 位于其正东方向．（1）求B ，C 两救援中心间的距离；（2）D 救援中心与着陆点A 间的距离．18. 班主任为了对本班学生的考试成绩进行分析，决定从全班25位女同学，15位男同学中随机抽取一个容量为8的样本进行分析．（1）如果按性别比例分层抽样，则样本中男、女生各有多少人；（2）随机抽取8位同学，数学分数依次为：60，65，70，75，80，85，90，95；物理成绩依次为：72，77，80，84，88，90，93，95，①若规定80分（含80分）以上为良好，90分（含90分）以上为优秀，在良好的条件下，求两科均为优秀的概率；②若这8位同学的数学、物理分数事实上对应下表：根据上表数据可知，变量y 与x 之间具有较强的线性相关关系，求出y 与x 的线性回归方程（系数精确到0.01）．（参考公式：y ̂=bx +a ，其中b =∑n ∑(ni=1x i −x ¯)2，a =y ¯−bx ¯；参考数据：x ¯=77.5，y ¯=84.875，∑(8i=1x i −x ¯)2≈1050，∑(8i=1x i −x ¯)(y i −y ¯)≈688，√1050≈32.4，√457≈21.4，√550≈23.5）19. 在四棱锥P −ABCD 中，底面ABCD 是一直角梯形，∠BAD =90∘，AD // BC ，AB =AD =a ，BC =2a ，PD ⊥底面ABCD ，PD =3a ．（1）求三棱锥B −PAC 的体积；（2）在PD 上是否存在一点F ，使得PB // 平面ACF ，若存在，求出PFFD 的值；若不存在，试说明理由；20. 已知椭圆x 2a2+y 2b 2=1(a >b >0)的离心率为√22，且短轴长为2．（1）求椭圆的方程；（2）若与两坐标轴都不垂直的直线l 与椭圆交于A ，B 两点，O 为坐标原点，且OA →⋅OB →=23，S △AOB =23，求直线l 的方程．21. 已知f(x)=lnx ，g(x)=x +ax(a ∈R)．（1）求f(x)−g(x)的单调区间；（2）若x ≥1时，f(x)≤g(x)恒成立，求实数a 的取值范围． 22. 选修4−1：几何证明选讲如图，已知C 点在⊙O 直径的延长线上，CA 切⊙O 于A 点，DC 是∠ACB 的平分线，交AE 于F 点，交AB 于D 点．（1）求∠ADF 的度数；（2）若AB ＝AC ，求AC:BC ．23. 已知曲线C 1的参数方程为{x =2sinθy =cosθ（θ为参数），曲线C 2的参数方程为{x =2ty =t +1（t 为参数）．（1）若将曲线C 1与C 2上各点的横坐标都缩短为原来的一半，分别得到曲线C 1′和C 2′，求出曲线C 1′和C 2′的普通方程；（2）以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系，求过极点且与C 2′垂直的直线的极坐标方程．24. 设函数f(x)=|2x −1|+|2x −3|，x ∈R ．（1）解不等式f(x)≤5；（2）若g(x)=1f(x)+m 的定义域为R ，求实数m 的取值范围．2010年黑龙江省某校高考数学一模试卷（文科）答案1. B2. C3. C4. D5. A6. C7. A8. B9. B 10. D 11. A 12. D 13. 2 14. 6+π 15. 416. ①③④ 17. 解：（1）由题意知PA ⊥AC ，PA ⊥AB ，则△PAC ，△PAB 均为直角三角形在Rt △PAC 中，PA =1，∠PCA =60∘，解得AC =√33在Rt △PAB 中，PA =1，∠PBA =30∘，解得AB =√3 又∠CAB =90∘，BC =√AC 2+BC 2=√303万米（2）sin∠ACD =sin∠ACB =√10，cos∠ACD =√10，又∠CAD =30∘，所以sin∠ADC =sin(30∘+∠ACD)=√3−12√10在△ADC 中，由正弦定理，AC sin∠ADC=ADsin∠ACDAD =AC⋅sin∠ACD sin∠ADC=9+√313万米18. 解：（1）从全班25位女同学，15位男同学中随机抽取一个容量为8的样本进行分析抽取男生数2540×8=5人，1540×8=3（2）①规定80分（含80分）以上为良好，90分（含90分）以上为优秀，这是一个条件概率，在良好的条件下，两科均为优秀，一个学生两科都良好的概率是48×68=38 两科都优秀的概率是28×38=332在良好的条件下，两科均为优秀的概率为33238=14②x ¯=60+65+70+75+80+85+90+958=77.5y ¯=72+77+80+84+88+90+93+958=84.8b ≈0.655，a ≈34.11则线性回归方程为：y =0.655x +34.11 19. 解：（1）∵ PD ⊥底面ABCD∴ PD 是三棱锥B −PAC 的高， ∴ v =13×PD ×S △ABC =13×3a ×12a ×2a =a 3 （2）存在点F 使PB // 平面ACF ，PFDF =2连接BD 交AC 于E ，连接EF ，AD // BC ，AD =a ，BC =2a ，所以AD BC=DE EB=DF PF=12，所以PB // EF又EF ⊆平面ACF ，PB 不在平面ACF 内，所以PB // 平面ACF 20. 解：（1）短轴长2b =2，b =1，e =c a=√22又a 2=b 2+c 2，所以a =√2，c =1，所以椭圆的方程为x 22+y 2=1（2）设直线l 的方程为y =kx +m(k ≠0)，A(x 1, y 1)，B(x 2, y 2){y =kx +mx 2+2y 2=2，消去y 得，(1+2k 2)x 2+4mkx +2m 2−2=0{x 1+x 2=−4mk 1+2k 2⋅，OA →⋅OB →=x 1x 2+y 1y 2=23即3m 2−2k 2−21+2k 2=23即9m 2=10k 2+8S △AOB =12|m||x 1−x 2|=12√m 2[(x 1+x 2)2−4x 1x 2]=12√8m 2(1+2k 2−m 2)(1+2k 2)2=23即9m 2(1+2k 2−m 2)=(1+2k 2)2 {9m 2(1+2k 2−m 2)=(1+2k 2)29m 2=10k 2+8，解得k 2=1，m 2=2，所以y =±x ±√221. 解：（1）F(x)=f(x)−g(x)=lnx −x −ax(x >0)，F ′(x)=1x−1+a x 2=−x 2+x+ax 2当△=1+4a ≤0，即a ≤−14时，F′(x)≤0，∴ F(x)在(0, +∞)上单调递减当△>0，即a >−14时，F ′(x)=0，x 1=−√1+4a+12，x 2=√1+4a+12， ①−14<a ≤0时，x 1≤0，x 2>0，单调增区间为(0, x 2)，单调减区间为(x 2, +∞) ②a >0时，x 1>0，x 2>0，单调增区间为(x 1, x 2)，，单调减区间为(0, x 1)，(x 2, +∞) 综上：①a ≤−14时，F(x)在(0, +∞)上单调递减②−14<a ≤0时，x 1≤0，x 2>0，单调增区间为(0, x 2)，单调减区间为(x 2, +∞)③a >0时，x 1>0，x 2>0，单调增区间为(x 1, x 2)，单调减区间为(0, x 1)，(x 2, +∞) （2）lnx ≤x +ax 恒成立，等价于a ≥[xlnx −x 2]max k(x)=xlnx −x 2，k′(x)=1+lnx −2x ，[k ′(x)]′=1x −2<0k′(x)在[1, +∞)上单调递减， k′(x)≤k′(1)=−1<0， k(x)在[1, +∞)上单调递减，∴ k(x)的最大值为k(1)=−1，所以a ≥−122. 因为AC 为⊙O 的切线，所以∠B ＝∠EAC 因为DC 是∠ACB 的平分线，所以∠ACD ＝∠DCB所以∠B +∠DCB ＝∠EAC +∠ACD ，即∠ADF ＝∠AFD ，又因为BE 为⊙O 的直径，所以∠DAE ＝90∘．所以∠ADF =12(180−∠DAE)=45．因为∠B ＝∠EAC ，所以∠ACB ＝∠ACB ，所以△ACE ∽△BCA ，所以AC BC =AEAB ，在△ABC 中，又因为AB ＝AC ，所以∠B ＝∠ACB ＝30∘，Rt △ABE 中，AC BC=AE AB=tanB =tan30=√3323. 解：（1）C 1′:{x =sinθy =cosθ（θ为参数），C 2′:{x =ty =t +1（t 为参数）C 1′的普通方程：x 2+y 2=1，C 2′的普通方程：y =x +1（2）在直角坐标系中过极点即为过原点与曲线C 2′垂直的直线方程：即为y =−x 在极坐标系中，直线化为tanθ=1，方程为θ=π4或θ=3π424. 解：(1){x <124−4x ≤5或{12≤x ≤322≤5或{x >324x −4≤5不等式的解集为x ∈[−14，94]（2）若g(x)=1f(x)+m的定义域为R ，则f(x)+m ≠0恒成立，即f(x)+m =0在R 上无解又f(x)=|2x −1|+|2x −3|≥|2x −1−2x +3|=2，f(x)的最小值为2，所以m >−2．。

高职高考数学14年级试卷【含答案】

高职高考数学14年级试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 若函数f(x) = x² 4x + 3，则f(2)的值为：A. 0B. 1C. -1D. 22. 下列函数中，奇函数是：A. f(x) = x³B. f(x) = x²C. f(x) = |x|D. f(x) = x² + 13. 若直线y = 2x + 3与x轴的交点为A，与y轴的交点为B，则线段AB的长度为：A. 3B. 4C. 5D. 64. 已知等差数列{an}的前n项和为Sn = 2n² + 3n，则a1的值为：A. 2B. 3C. 4D. 55. 若复数z满足|z 1| = |z + 1|，则z在复平面内对应点的轨迹为：A. 直线B. 圆C. 椭圆D. 双曲线二、判断题（每题1分，共5分）1. 若a, b是实数，则(a + b)² = a² + b². ( )2. 任何实系数多项式都有实数根. ( )3. 若函数f(x)在区间(a, b)内单调递增，则f'(x) ≥ 0. ( )4. 若函数f(x)在点x = a处连续，则f(x)在点x = a处可导. ( )5. 若直线y = kx + b与x轴的夹角为θ，则tanθ = k. ( )三、填空题（每题1分，共5分）1. 若函数f(x) = 2x³ 3x² + 4x 5，则f'(x) = ______.2. 若等差数列{an}的前n项和为Sn = 3n² + 2n，则a3 = ______.3. 若复数z = 3 + 4i，则|z| = ______.4. 若直线y = 2x + 3与圆(x 1)² + (y + 2)² = 16相交，则交点坐标为 ______.5. 若函数f(x) = x² + 2x + 1，则f(x)的最小值为 ______.四、简答题（每题2分，共10分）1. 简述导数的定义及其几何意义。

职高对口高考数学模拟试题精编版

职高对口高考数学模拟试题精编版MQS system office room 【MQS16H-TTMS2A-MQSS8Q8-MQSH16898】临河一职对口高考模拟试题命题人：王春江一、选择题（本大题共10个小题，满分50分，每小题5分） 1若M N 是两个集合，则下列关系中成立的是 A ．∅MB ．M N M ⊆⋂)(C ．N N M ⊆⋃)(D ．N )(N M U 2若a>b ，R c ∈，则下列命题中成立的是 A ．bc ac >B ．1>ba C ．22bc ac ≥D ．ba 11< 3下列等式中，成立的是A ．)2cos()2sin(x x -=-ππB ．x x sin )2sin(-=+πC ．x x sin )2sin(=+πD ．x x cos )cos(=+π4“a=0”是“ab=0”的A ．充分但不必要条件B ．必要但不充分条件C ．充要条件D ．既不充分也不必要条件5对于实数0λ≠，非零向量a →及零向量0→，下列各式正确的是（）A 00=•→a B →→=0a C a a →→-＝0D a a →→-＝0→6下列通项公式表示的数列为等差数列的是A ．1+=n na n B ．12-=n a n C ．n n n a )1(5-+=D ．13-=n a n7直角边之和为12的直角三角形面积的最大值等于A ．16B ．18C ．20D ．不能确定8若f(x)是周期为4的奇函数，且f （－5）=1，则A ．f(5)=1B ．f(－3)=1C ．f(1)=－1D ．f(1)=19若021log >a ，则下列各式不成立的是 A ．31log 21log a a <B ．3a a <C ．)1(log )1(log a aa a a a ->+D ．)1(log )1(log a aa a a a -<+ 10已知 m 、 n 、 l 为三条不同的直线, α、 β为两个不同的平面，则下列命题中正确的是 // , , //m n m n αβαβ⊂⊂⇒B ． , //l l βαβα⊥⊥⇒C ． , //m m n n αα⊥⊥⇒D ．// , ,l n l n αβαβ⊥⊂⇒⊥第II 卷（非选择题，共100分）二、填空题（本大题共5小题，每小题5分，共25分，请把答案填在题中的横线上）11点（－2，1）到直线3x －4y －2=0的距离等于_________12在],[ππ-内，函数)3sin(π-=x y 为增函数的区间是__________13若)2,0(,54sin παα∈=，则cos2α等于__________14函数11)(+-=x x x f 的定义域是__________15不等式21<-x 的解集是.三、解答题（满分75分，解答应写出文字说明和演算步骤）16（9分）求25lg 50lg 2lg )2(lg 2+⋅+的值17（10分已知5,4==→→b a ，→a 与→b的夹角为60→→-b a 。

黑龙江中职毕业生对口升学高职院校招生模拟考试数学试卷（中职工作）

黑龙江中职毕业生对口升学高职院校招生模拟考试数学试卷（中职工作）黑龙江中职毕业生对口升学高职院校招生模拟考试数学试卷一、单项选择题（共40分）（）1.与角35π终边相同的角是: A.32π B.3π C.-32π D.-3π （）2.x 220y +=是xy=0的（）条件A. 充分不必要B.必要不充分C.充要D.既不充分也不必要（）3.设集合M={x|x ≤10}， a=3，下列关系中正确的是：A.a ?MB.a ∈MC.{a}∈MD.{a}?M（）4.斜线与平面所成角的范围是：A.20π，B.[]π，0 C.()π，0 D.02π?? ???，（）5.直线053=+-y x 的倾斜角为：A ．6πB ．3πC ．23πD ．56π （）6.直线L:4x+3y-12=0与两坐村轴围成三角形的面积是：A.24B.12C.6D.18（）7.设向量a =(2,-1), b =(x,3)且a ⊥b 则x=（） A. 21 B.3 C.23 D.-2（）8.已知2(2,1),(3,2),3A B AM AB --=，则点M 的坐标是：A. )21,21(-- B ．)1,34(-- C ．)0,31( D ．)51,0(-（）9.若4,6m n ==，m 与n 的夹角是 135，则n m ?等于：A ．12 B ．212 C ．212- D ．12-（）10.已知向量(3,1),(1,2),a b =-=-则b a 23--的坐标是：A ．)1,7(B ．)1,7(--C ．)1,7(-D ．)1,7(-（）11.设5，1+x ，55成等比数列，则x 为 :A ．4或－4B ．－4或6C ．4或－6D ．4或6（）12.如果a ，b ，c 成等比数列，那么函数c bx ax x f ++=2)(的图象与x 轴交点的个数是：A ．0个B ．恰有一个C ．两个D ．不能确定（）13若直线3610x y ++=与063=++m y x 平行，则m 的值不为：A 4B ．2C ． 1D ． 0（）14.斜率为－21，在y 轴上的截距为5的直线方程是 :A ． x －2y = 10B ． x + 2y = 10C ． x －2y + 10 = 0D ． x + 2y + 10 = 0（）15.已知2=a , 3=b , 且3,π=b a , 则向量b a ,的内积是： A ．33 B ．3 C ．32 D ．23（）16.若sinAcosA>0,则角A 在第几象限？A ．二B ．四C ．一或三D ．二或四（）17.若直线0=++m y x （m 为常数）经过圆25)3()1(22=-++y x 的圆心，则m 的值为：A ．-2B ．2C ．-1D ．1（）18.下列函数为同一函数的是：A. )(x f =x ，)(x g =2xB. )(x f =x,)(x g =33xC. )(x f =2n+1，)(x g = 2n (n ∈N +)D. )(x f =112-+x x , )(x g =11-x。

2010年高职数学高考试题 (1)

装订线2013年对口升学模拟试题（2）1、关于下列关系中正确的的是（） A 、{}00∈ B 、φ=0 C 、φ⊂0 D 、{}φ⊂02、“x,y 中至少有一个小于0”是“x+y<0”的（）条件（） A 、充分条件 B 、必要条件 C 、充要条件 D 、既不充分也不必要条件3、0)3(x ≥+x 的解集（） A 、{}30≤≤x x B 、{}30-≤≥x x x 或 C 、{}03≤≤-x x D 、{}03≤≥x x x 或4、下列函数中为奇函数的是（）A 、x y 3log =B 、xy ⎪⎭⎫⎝⎛=21 C 、x y sin 2= D 、 23x y =5、241xy -=的定义域（）A 、{}22≤≤-x xB 、{}22-≤≥x x x 或C 、{}2±≥x xD 、{}22<<-x x6、如果二次函数 ,2)(2-+-=mx x x f ()3-，在∞-上是增函数，()∞+-，在3上是减函数，则m= ( )A 、-3B 、3C 、-6D 、 67、函数,63)(2x x x f +-=的顶点坐标为（）A 、（0，0）B 、（-3，6）C 、（1，-1）D 、（1，3）8、1cos -=m α,m 的取值范围 ( ) A 、20<<m B 、 2≤m C 、0≥m D 、20≤≤m9、ααα,0tan sin <⋅在第（）象限（）A 、第一、第二象限B 、第二、第三象限C 、第三、第四象限D 、第一、第四象限 10、α终边上一点()=αin s 3-1，则，（） A 、21 B 、23- C 、3- D 、33- 11、.已知=-+=zx xx •x cos 2sin cos sin 2,3tan 则（）A 、6B 、7C 、8D 、 912、 537537-+与的等比中项为（） A 、2 B 、-2 C 、4± D 、2±13、.已知等差数列{}n a ，64=a ，=7S 则（） A 、24 B 、42 C 、21 D 、少条件无法确定 14、.如果A(-3,2)与B(a,5)之间的距离为5，则a 的值是（） A 、1 B 、7 C 、-7 D 、1或-715、设点A(6,4)、点B(2,9)、点C(1.3)则AC AB ⋅= ( ) A 、25 B 、(20,-5) C 、15 D 、 (-20,5){}{}{}、空间中，两条直线能确定一个平面29、=∈=x x os sin ),2,23(,53c ππα30、一年级一班有男生35人，女生14人，选派一人参加学校的学生代表会议，共有种选派法。

黑龙江职业学院单招数学模拟试题(附答案)

黑龙江职业学院单招数学模拟试题(附答案)一、选择题（本大题共小题，每小题分，共分，在每小题给出的四个选项中，只有一项是符合题目要求的,答案涂在答题卡上）．设为全集，、是的两个子集，且P M P P M C U ⋂=⋂则,)(等于（）．．．．○、若函数()的定义域是［－］,则(－)的定义域为（）.［,25］ .［－］ .［－］ .［－］.若三点O 、A 、B 不共线,则“存在唯一一对实数1λ、2λ,使12OP OA OB λλ=+”是“P 点在直线AB 上”的（）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件．在等差数列{}n a 中，若4681012120a a a a a ++++=，则91113a a -的值为（）．．．．．已知椭圆2214x y n +=与双曲线2218x y m-=有相同的准线，则动点(,)P n m 的轨迹为（）．椭圆的一部分．双曲线的一部分．抛物线的一部分．直线的一部分 . 函数()()()()0cos sin >+⋅+=ωϕωϕωx x x f 以为最小正周期，且能在时取得最大值，则φ的一个值是（）、π43- 、π45- 、π47、2π . .给出下列四个命题：①有两个面平行，其余各面都是平行四边形的几何体是棱柱； ②有两侧面与底面垂直的棱柱是直棱柱；③过斜棱柱的侧棱作棱柱的截面，所得图形不可能是矩形；④所有侧面都是全等的矩形的四棱柱一定是正四棱柱。

其中正确的命题的个数为（）个、、、、．满足不等式()()*1221223log log N n n x x n ∈-≥-⋅+-的正整数x 的个数记为n a ，数列{}n a 的前n 项和记为n S ，则n S = （）．12-+n n ．12-n ．12+n ．12--n n、如图所示是年北京奥运会的会徽，其中的“中国印”由四个色块构成，可以用线段在不穿越其他色块的条件下将其中任意两个色块连接起来(如同架桥)，如果用三条线段将这四个色块连接起来，不同的连接方法共有( )种种种种.如图所示,面积为的平面凸四边形的第i 条边的边长记为(1,2,3,4),i a i =此四边形内任一点到第i 条边的距离记为(1,2,3,4)i h i =，若4312412,()1234i i a a a a Sk ih k ======∑则.类比以上性质，体积为三棱锥的第i 个面的面积记为(1,2,3,4)i S i =，此三棱锥内任一点到第i 个面的距离记为(1,2,3,4)i H i =，若431241,()1234i i S S S S K iH ======∑则（）. 4V K . 3VK .2V K . V K二、填空题．已知正方体1111ABCD A B C D -,E 为11A B 的中点，则异面直线DE 与1B C 所成角的余弦是 .. .已知满足条件20y x x y y ⎧≤⎪+≤⎨⎪≥⎩，则的取值范围. 如图，半径为的半球内有一内接正六棱锥P ABCDEF -，则此正六棱锥的侧面积是．．设命题p ：⎪⎩⎪⎨⎧≥+-≤-->-+06208201243y x y x y x （R y x ∈,），命题q ：222r y x ≤+（0,,,>∈r R r y x ），若命题q 是命题p ⌝的充分非必要条件，则r 的取值范围是 ..已知双曲线22221(0,0)x y a b a b-=>>，若它的一条准线与抛物线24y x =的准线重合.设双曲线与抛物线的一个交点为P ,抛物线的焦点为F ，则||PF = .．非空集合关于运算⊕满足：（）对任意的,M b ∈，都有M b a ∈⊕；（）存在M e ∈，使得对一切M a ∈，都有a a e e a =⊕=⊕，则称关于运算⊕为“理想集”．现给出下列集合与运算：①＝{非负整数}，⊕为整数的加法；②＝{偶数}，⊕为整数的乘法；③＝{二次三项式}，⊕为多项式的加法；④＝{平面向量}，⊕为平面向量的加法；其中关于运算⊕为“理想集”的是．（只需填出相应的序号）三、解答题．（本小题满分分）已知向量a ＝（cos ,sin θθ）, b ＝（cos 2,sin 2θθ），c ＝（－，）, d ＝（，）．（）求证：a ⊥（b c ） )(πθk ≠其中;（）设()f θ=a ·（b －d ）,且(0,)θπ∈,求()f θ的值域． .(本小题满分分)已知直线1y kx =+与双曲线2231x y -=有、两个不同的交点. （）如果以为直径的圆恰好过原点，试求的值；（）是否存在，使得两个不同的交点、关于直线2y x =对称？试述理由..（本大题满分分）如图，在五面体中，四边形为矩形，对角线的交点为，△和△为等边三角形，棱∥ 为的中点， ①求证：⊥平面； ②求二面角－－的大小； ③求点到平面的距离。

黑龙江省高职院校对口招收中职毕业生统一考试数学模拟试卷

20XX 年黑龙江省高职院校对口招收中职毕业生统一考试数学模拟试卷3（本试卷满分150分，考试时间150分钟）1、下列不等式组中解集为空集的是（）（A ）⎩⎨⎧≥≥05x x （B ）⎩⎨⎧><-109)4(3x x （C ）⎩⎨⎧>->-02503x x （D ）⎩⎨⎧<+>-0201x x 2、集合A 含有12个元素，集合B 含有8个元素，集合B A 含有5个元素，则集合B A 中含有（）（A ）15个元素（B ）20个元素（C ）17个元素（D ）13个元素3、两三角形两角对应相等是两个三角形全等的（）（A ）充分必要条件（B ）充分非必要条件（C ）必要非充分条件（D ）既非充分也非必要条件4、已知一次函数2)(+=kx x f 满足89)]([+=x x f f ，则k 的值为（）（A ）-3 （B ）5 （C ）-5 （D ）35、下列函数（1）121)4(,1)3.(211)2(,3322+==++=++=x y x y x x y x x y 中定义域为R 的数函数个数为（）（A ）1个（B ）2个（C ）3个（D ）4个6、设函数)6,(,48a x x x y ∈+=为偶函数，则a 的取值情况是（）（A ）0=a （B ）6-<a （C ）6->a （D ）6-=a7、设),3,2,1(21312111)( =+++++++=n n n n n n f ，则=-+)()1(n f n f （）（A ）121+n （B ）221+n （C ）221121+-+n n （D ）221121+++n n 8、设3,3>>q p ，则pq 与q p +的大小关系是（）（A ）q p pq +> （B ）q p pq +<（C ）q p pq += （D ）不确定9、若直线l 经过原点和点（-2，2），则l 日报倾斜角是（）（A ）43π （B ）47π （C ）2π （D ）4π 10、设圆的方程为04322=+++y x y x ，则该圆的圆心坐标为（）（A ）)2,23( （B ）)2,23(- （C ）)2,23(- （D ）)2,23(-- 二、填空题：（将答案填在题中横线上，每小题5分，共计50分）11、已知集合}0132{},056{22=+-==+-=x x x B x x x A ，则=B A .12、不等式652+-x x ≤0的解集是 .13、设实数233)1(,)2(ππ-=-=b a ，则=+b a .14、设8)(35-++=bx ax x x f ，且10)2(=-f ，则=)2(f .15、设实数}{n a 是首项为27、公差为整数的等差数列，并且前7项为正，从第8项开始为负，则此数列的公差=d .16、=-)8sin 8(cos 8cos 8sin 422ππππ.17、若543,5432211=+=+y x y x ，且21x x ≠，则过点),(),,(2211y x B y x A 的直线方程为 .18、将4名医生和6名护士分配到两个社区为居民检查身体，每个社区分配2名医生和3名护士，则不同的分配方法共有种.19、设55443322105)2(x a x a x a x a x a a x +++++=-，则=++531a a a .20、=-++++)532(log )532(log 2424三、解答题：（应写出文字说明，演算步骤，每题10分，共计50分。

职中对口数学试卷高考模拟

一、选择题（本大题共10小题，每小题4分，共40分）1. 下列各数中，绝对值最小的是（）A. -3B. -2C. 0D. 12. 若m，n是方程x^2 - (m+n)x + mn = 0的两根，则m+n的值是（）A. 0B. 1C. 2D. m+n3. 下列函数中，是奇函数的是（）A. y = x^2B. y = |x|C. y = x^3D. y = x^44. 在直角坐标系中，点P(2,3)关于x轴的对称点是（）A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,3)5. 若等差数列{an}的首项为2，公差为3，则第10项a10的值是（）A. 29B. 28C. 27D. 266. 下列各式中，正确的是（）A. a^2 = b^2，则a = bB. a^2 = b^2，则a = ±bC. a^2 = b^2，则a = ±b，b = ±aD. a^2 = b^2，则a = b，b = a7. 若等比数列{an}的首项为1，公比为2，则第n项an的值是（）A. 2nB. 2n-1C. 2^nD. 2^(n-1)8. 在△ABC中，若∠A=60°，∠B=45°，则∠C的度数是（）A. 75°B. 120°C. 45°D. 60°9. 下列函数中，是反比例函数的是（）A. y = 2xB. y = x^2C. y = 1/xD. y = x^310. 若sinα = 1/2，则cosα的值是（）A. √3/2B. -√3/2C. 1/2D. -1/2二、填空题（本大题共5小题，每小题5分，共25分）11. 已知函数y = -x^2 + 4x - 3，则该函数的对称轴是________。

12. 若等差数列{an}的首项为a1，公差为d，则第n项an = ________。

13. 在直角坐标系中，点P(-2,1)关于原点的对称点是________。

对口高职高考数学模拟试卷

2024对口高职高考数学模拟试卷随着社会的发展和科技的进步，教育也在不断地发展和变革。

其中，高职教育越来越受到人们的关注。

在高职教育中，对口高职高考数学模拟试卷是一个重要的组成部分。

本文将对2024年的对口高职高考数学模拟试卷进行介绍和分析。

一、试卷整体结构2024年的对口高职高考数学模拟试卷整体结构相对稳定，由选择题、填空题和解答题三个部分组成。

选择题注重对基础知识的考查，填空题侧重对计算和推理能力的考查，解答题则注重对应用能力的考查。

整个试卷难度适中，题目数量和分值分配合理。

二、选择题选择题是对学生基础知识的考查，包括数学概念、公式、计算等。

2024年的对口高职高考数学模拟试卷中，选择题的数量为10道，每道题目有5个选项。

题目涉及的内容主要包括数与式、方程与不等式、函数与数列、平面几何、立体几何等。

这些题目注重对基础知识点的考查，要求学生能够准确理解和应用相关概念和公式。

三、填空题填空题注重对计算和推理能力的考查，要求学生能够准确计算和推导。

2024年的对口高职高考数学模拟试卷中，填空题的数量为6道，每道题目有1个或2个空需要填写。

题目涉及的内容主要包括概率与统计、排列与组合、解析几何等。

这些题目注重对计算和推理能力的考查，要求学生能够准确计算和推导。

四、解答题解答题注重对应用能力的考查，要求学生能够运用所学的数学知识解决实际问题。

2024年的对口高职高考数学模拟试卷中，解答题的数量为4道，每道题目涉及的内容不同。

题目涉及的内容主要包括微积分、线性代数、离散数学等。

这些题目注重对应用能力的考查，要求学生能够准确理解和应用相关概念和公式，并能够将实际问题转化为数学问题，运用所学的数学知识进行求解。

五、总结通过对2024年的对口高职高考数学模拟试卷的分析，我们可以发现该试卷注重对基础知识和应用能力的考查。

在复习过程中，学生应该注重对基础知识的掌握和应用能力的提高。

学生应该多做模拟试题，熟悉考试形式和题型特点，提高解题速度和准确率。

2010年黑龙江省高职学院招收中职毕业生统一考试数控加工技术模拟试卷

2010年黑龙江省高职学院招收中职毕业生统一考试数控加工技术模拟试卷(数控技术类专业) (本试卷满200分，考试时间150 分钟)一、单项选择题（在每小题的四个备选答案中选出一个正确的答案，并将其号码填在题后的括号内。

11、12 两小题每题2分，其它每小题3分，共40分)1、构成正交平面参考系中没有( )A、基面B、法平面C、正交平面D、切削平面2、不适合用高性能高速钢制造的刀具加工的工件材料是( )A、高温合金B、钛合金C、不锈钢D、硬质合金3、使切削变形减少的方法是( )A、增大前角和背吃刀量B、增大前角和主偏角C、增大前角和后角D、增大前角和副偏角4、不限制工件自由度的定位元件是( )A、固起支承B、可调支承C、自位支承D、辅助支承5、能限制工件四个自由度的定位元件是( )A、定位销B、圆柱心轴C、圆锥心轴D、支承板6、切削液的四个作用中不包括( )A、冷却作用B、润滑作用C、除锈作用D、防冻作用7、车削加工指令G96S150中S150是( )A、主轴最高转速为150r/minB、切削速度为150m/minC、主轴转速为恒线速度150m/minD、进给量为150mm/min8、工序图上标注本工序被加工表面加工后的尺寸、形状、位置的基准是( )A、设计基准B、工序基准C、定位基准D、测量基准9、形状精度获得的方法中不包括( )A、轨迹法B、成形法C、展成法D、试切法10、加工误差中属于原理误差的是( )A、成形运动产生的误差B、调整误差C、定位误差D、测量误差11、数控钻削固定循环指令的基本动作有( )A、4个B、5个C、6个D、7个12、撤消固定循环指令是( )A、G40B、G49C、G80D、G9213、不属于电火花加工的缺点是( )A、主要用于加工金属导电材料B、加丁速度慢C、适合加工难切削材料D、有电极损耗14、引起误差复映的原因是( )A、切削力的变化B、传动力的变化C、重力的变化D、惯性力的变化二、填空题(每空1分，共40分)15、刀具材料经济性指取材、，可最大限度地降低生产成本。

2010年高职单招数学试卷

2010年高职单招数学试卷一、单项选择题（在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干后的括号内.本大题12小题,每小题3分,共36分.）1、设全集I={小于8的自然数}, , ,则 =（）A、 B、 C、 D、2、角的终边经过点P(-1,2),则( )A、sin =B、cos =C、tan =D、cot =-23、下列函数的图像关于轴对称的是( )A、 B、 C、 D、4、函数的最小正周期为( )A、4π2B、4πC、2πD、π5、的定义域是（）A、 B、C、 D、6、已知直线l⊥直线a, 直线l⊥平面 ,则a与关系是（）A．直线a与平面平行 B．直线a与平面垂直C．直线a在平面内 D．直线a与平面平行或直线a在平面内7、2名老师和4名学生站一排照相,其中2名老师恰好站中间的概率为（）A、 B、 C、 D、8、等差数列中，，则（）A、126B、63C、36D、189、已知A(-1,3),B(-3,-1),则线段AB的垂直平分线方程为（）A、 B、C、 D、10、中,D是BC的中点, 则 =（）A、 B、 C、 D、11、若满足，则下列各式正确的是（）A、 B、C、 D、12、若椭圆与双曲线有公共的焦点，且经过点（0，4），则椭圆的标准方程是（）A、 B、C、 D、二、填空题（把答案写在横线上，本大题8小题，每小题3分，共24分.）1、计算 ___________2、不等式的解集为3、已知向量 =(3,0), =(-5,5)，则的夹角为4、设、是方程的两根，则 ___5、已知函数的反函数图像经过点(1,-2),则 ______6、二项式展开式的常数项是_________7、棱长为2的正方体中, 到直线AC的距离是______8、若双曲线上的点P到一个焦点的距离为6，则点P到另一个焦点的距离为________三、解答题（本大题6个小题，共40分.解答应写出推理、演算步骤.）1、（本题6分）设集合，，且，求实数的取值范围.2、（本题6分）证明:3、（本题6分）二次函数的图象顶点是（6，－12），且它的图象与x轴的一个交点是（8，0），求:①二次函数的解析式；②二次函数的图象与x轴的两个交点之间的距离。

(完整版)职高数学试卷及答案

试卷说明:本卷满分100分，考试时间90分钟。

一、选择题。

（共10小题，每题3分） 1、设{}a M =，则下列写法正确的是（）A ．M a = B.M a ∈ C. M a ⊆ D.M a ∉ 2、下列语句为命题的是（）A 、等腰三角形B 、x ≥0C 、对顶角相等D 、0是自然数吗？ 3、 a>b 是a ≥b 成立的（）A 、充分而不必要条件B 、必要而不充分条件C 、充分必要条件D 、既不充分也不必要条件 4、不等式732>-x 的解集为（）。

A ．2<x B. 2>x C . 5<x D. 5>x 5、不等式组⎩⎨⎧<->+0302x x 的解集为( ).A ．()3,2- B. ()2,3- C. φ D. R 6、下列各点中，在函数13-=x y 的图像上的点是（）。

A ．（3,4） B. （1，2） C.(0,1) D.(5,6) 7、点P （-2，1）关于x 轴的对称点坐标是（）。

A ．（-2，1） B.（2，1） C.(2，-1) D.(-2，-1) 8、下列函数中是奇函数的是（）。

A ．3+=x y B.12+=x y C.3x y = D.13+=x y 9、将54a 写成根式的形式可以表示为（）。

A ．4a B.5a C.45a D.54a10、下列函数中，在()+∞∞-,内是减函数的是（）。

A ．x y 2= B. x y 3= C.xy ⎪⎭⎫ ⎝⎛=21 D. xy 10=二、填空题（共10小题，每题3分）11、用列举法表示小于5 的自然数组成的集合：。

12、用描述法表示不等式062<-x 的解集。

13、已知集合{}4,3,21，=A ，集合{},7,5,3,1=B ，则=B A ，=B A 。

14、已知全集{}6,5,4,3,2,1=U ，集合{}5,2,1=A ，则=A C U 。

2010年黑龙江省职高对口升学C语言编程基础模拟试卷一及答案

2010年黑龙江省中职升高职C语言编程基础模拟试卷一说明：本试卷共五大题，试卷满分100分，考试时间120分钟。

一．填空题（每题2分，共20分）1.一个C程序有且仅有一个________________函数。

2.表达式10/3的结果是_______________。

3.以下程序的输出结果是_______________。

void main(){double a=365.7189;int b=12,c;c=(int)a+b;printf("c=%d\n",c);}｝4.以下程序的执行结果是______________。

void main(){char c='A'+10;printf("c=%c\n",c);}5.要表示一个整数num在10到20之间（包括10和20）的C语言的表达式应是____________。

6.执行下面的C程序段后，输出结果是_______________。

void main(){int a=5;while(a--);printf("%d",a);}7.执行下面的C程序段后，输出结果是_______________。

void main(){int a[]={1,2,3,4},i,j,s=0;j=1;for(i=3;i>=0;i--) {s=s+a[i]*j;j=j*10;}printf("s=%d\n",s);}8.执行下面的C程序段后，输出结果是_______________。

int run(int a,int b){return (a+b);}void main(){int x=2,y=5,z=8,r;r=run(run(x,y),z);printf("%d\n",r);}9.执行下面的C程序段后，输出结果是_______________。

int fac(int n){static int f=1;f=f*n;return (f);}main(){int i,a;for(i=1;i<=5;i++)a=fac(i);printf("%d\n",a);}10.若有定义：int a[]={1,3,5,7,9,10},*p=a,则*(p+2)的值是________ 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2010年黑龙江省高职院校对口招收中职毕业生统一考试数学模拟试卷14（本试卷满分150分，时间150分钟）一、选择题(5分×12=60分)1．设集合P={1，2，3，4}，Q={R x x x ∈≤,2}，则P ∩Q 等于（） A ．{1，2} B ． {3，4} C ． {1} D ． {-2，-1，0，1，2}2．函数y=2cos 2x+1(x ∈R )的最小正周期为（）A ．2πB ．πC ．π2D ．π43．从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有（） A ．140种 B ．120种 C ．35种 D ．34种4．一平面截一球得到直径是6cm 的圆面，球心到这个平面的距离是4cm ，则该球的体积是（） A ．33π100cm B ． 33π208cmC ．33π500cmD ．33π3416cm 5．若双曲线18222=-by x 的一条准线与抛物线x y 82=的准线重合，则双曲线的离心率为（）A ．2B ．22C ． 4D ．246．某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，结果用右侧的条形图表示. 根据条形图可得这50名学生这一天平均每人的课外阅读时间为（）A ．0.6小时B ．0.9小时C ．1.0小时D ．1.5小时7．4)2(x x +的展开式中x 3的系数是（）A ．6B ．12C ．24D ．48时间(小时)8．若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(-1，0)和(0，1)，则（）A ．a =2,b=2B ．a = 2 ,b=2C ．a =2,b=1D ．a = 2 ,b= 29．将一颗质地均匀的骰子（它是一种各面上分别标有点数1，2，3，4，5，6的正方体玩具）先后抛掷3次，至少出现一次6点向上的概率是（）A ．5216B ．25216C ．31216D ．9121610．函数13)(3+-=x x x f 在闭区间[-3，0]上的最大值、最小值分别是（）A ．1，-1B ．1，-17C ．3，-17D ．9，-1911．设k>1，f(x)=k(x-1)(x ∈R ) . 在平面直角坐标系xOy 中，函数y=f(x)的图象与x 轴交于A 点，它的反函数y=f -1(x)的图象与y 轴交于B 点，并且这两个函数的图象交于P 点. 已知四边形OAPB 的面积是3，则k 等于（）A ．3B ．32C ．43D ．6512．设函数)(1)(R x xxx f ∈+-=，区间M=[a ，b](a<b)，集合N={M x x f y y ∈=),(}，则使M=N 成立的实数对(a ，b)有（）A ．0个B ．1个C ．2个D ．无数多个第II 卷（非选择题共90分）二、填空题(4分×4=16分)13．二次函数y=ax 2+bx+c(x ∈R )的部分对应值如下表：则不等式ax 2+bx+c>0的解集是_______________________.14．以点(1，2)为圆心，与直线4x+3y-35=0相切的圆的方程是________________.15．设数列{a n }的前n 项和为S n ，S n =2)13(1-n a (对于所有n ≥1)，且a 4=54，则a 1的数值是_______________________.16．平面向量a ，b 中，已知a =(4，-3)，b =1，且a ·b =5，则向量b =__________. 三、解答题(12分×5+14分=74分) 17．已知0<α<2π，tan 2α+cot 2α=25，求sin(3πα-)的值.18．在棱长为4的正方体ABCD-A 1B 1C 1D 1中，O 是正方形A 1B 1C 1D 1的中心，点P 在棱CC 1上，且CC 1=4CP. (Ⅰ)求直线AP 与平面BCC 1B 1所成的角的大小（结果用反三角函数值表示）； (Ⅱ)设O 点在平面D 1AP 上的射影是H ，求证：D 1H ⊥AP ；(Ⅲ)求点P 到平面ABD 1的距离.19．制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目. 根据预测，甲、乙项目可能的最大盈利率分别为100﹪和50﹪，可能的最大亏损率分别为30﹪和10﹪. 投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？20．设无穷等差数列{a n }的前n 项和为S n .(Ⅰ)若首项=1a 32 ，公差1=d ，求满足2)(2k k S S =的正整数k ；(Ⅱ)求所有的无穷等差数列{a n }，使得对于一切正整数k 都有2)(2k k S S =成立.· B 1P A C D A 1C 1D 1 B O H·21．已知椭圆的中心在原点，离心率为12 ，一个焦点是F （-m,0）(m 是大于0的常数).(Ⅰ)求椭圆的方程；(Ⅱ)设Q 是椭圆上的一点，且过点F 、Q 的直线l 与y 轴交于点M. =，求直线l 的斜率.22．已知函数))((R x x f ∈满足下列条件：对任意的实数x 1，x 2都有 )]()()[()(λ2121221x f x f x x x x --≤-和2121)()(x x x f x f -≤-，其中λ是大于0的常数. 设实数a 0，a ，b 满足 0)(0=a f 和)(λa f a b -= (Ⅰ)证明1λ≤，并且不存在00a b ≠，使得0)(0=b f ； (Ⅱ)证明20220))(λ1()(a a a b --≤-； (Ⅲ)证明222)]()[λ1()]([a f b f -≤.2010年黑龙江省高职院校对口招收中职毕业生统一考试数学模拟试卷14参考答案一、选择题：每小题5分，满分60分.1．A 2．B 3．D 4．C 5．A 6．B 7．C 8．A 9．D 10．C 11．B 12．A二、填空题：每小题4分，满分16分. 13．),3()2,(+∞--∞ 14．25)2()1(22=-+-y x 15．2 16．)53,54(-三、解答题17．本小题满分12分.解：由已知54sin ,25sin 22cot2tan===+αααα得..53sin 1cos ,202=-=∴<<ααπα从而 3sincos 3cossin )3sin(παπαπα⋅-⋅=-)334(10123532154-=⨯-⨯=. 18．本小题满分12分. 解法一：（I ）连结BP.∵AB ⊥平面BCC 1B 1， ∴AP 与平面BCC 1B 1所成的角就是∠APB, ∵CC 1=4CP,CC 1=4，∴CP=I.在Rt △PBC 中，∠PCB 为直角，BC=4，CP=1，故BP=17.在Rt △APB 中，∠ABP 为直角，tan ∠APB=,17174=BP AB∴∠APB=.17174arctan19．本小题满分12分.解：设投资人分别用x 万元、y 万元投资甲、乙两个项目.由题意知⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+.0,0,8.11.03.0,10y x y x y x目标函数z =x +0.5y.上述不等式组表示的平面区域如图所示，阴影部分（含边界）即可行域. 作直线05.0:0=+y x l ，并作平行于直线0l 的一组直线,,5.0R z z y x ∈=+与直线05.0=+y x 的距离最大，这里M 点是直线10=+y x和8.11.03.0=+y x 的交点.解方程组⎩⎨⎧=+=+,8.11.03.0,10y x y x 得x =4，y=6此时765.041=⨯+⨯=z （万元）.07> ∴当x =4，y=6时z 取得最大值.答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大. 20．本小题满分12分. 解：（I ）当1,231==d a 时， n n n n n d n n na S n +=-+=-+=21212)1(232)1( 由22242)21(21,)(2k k k k S S k k +=+=得，即 0)141(3=-k k 又4,0=≠k k 所以.（II ）设数列{a n }的公差为d ，则在2)(2n n S S =中分别取k=1,2,得⎪⎩⎪⎨⎧⨯+=⨯+=⎪⎩⎪⎨⎧==211211224211)2122(2344,,)()(d a d a a a S S S S 即由（1）得 .1011==a a 或当,60)2(,01===d d a 或得代入时若21)(,0,0,0,0k k n n S S S a d a =====从而则成立若知由则216,324)(,18),1(6,6,02331===-===n n S S S n a d a ,)(239S s ≠故所得数列不符合题意. 当20,)2(64)2(,121==+=+=d d d d a 或解得得代入时若;)(,,1,0,1212成立从而则k k n n S S n S a d a =====若成立从而则221)(,)12(31,12,2,1n n n S S n n S n a d a ==-+++=-=== .综上，共有3个满足条件的无穷等差数列： ①{a n } : a n =0，即0，0，0，…； ②{a n } : a n =1，即1，1，1，…；（1）（2）21．本小题满分12分.解：（I ）设所求椭圆方程是).0(12222>>=+b a by a x由已知，得 ,21,==a c m c 所以m b m a 3,2==.故所求的椭圆方程是1342222=+my m x （II ）设Q （Q Q y x ,），直线),0(),(:km M m x k y l 则点+=当),,0(),0,(,2km M m F -=由于由定比分点坐标公式，得,62.139494,)3,32(.31210,32212022222±==+-=++=-=+-=k mm k m m kmm Q km km y m m x Q Q 解得所以在椭圆上又点km kmy m m x Q Q -=-=-=--⨯-+=-=21,221)()2(0,2当.于是.0,134422222==+k mm k m m 解得故直线l 的斜率是0，62±. 22．本小题满分14分. 证明：（I ）任取则由,,,2121x x R x x ≠⊂ )]()()[()(2121221x f x f x x x x --≤-λ 和|||)()(|2121x x x f x f -≤- ②可知 22121212121221|||)()(|||)]()()[()(x x x f x f x x x f x f x x x x -≤-⋅-≤--≤-λ，从而 1≤λ. 假设有则由使得,0)(,000=≠b f a b ①式知.0)]()()[()(00000200矛盾=--≤-<b f a f b a b a λ∴不存在.0)(,000=≠b f a b 使得（II ）由)(a f a b λ-= ③可知 220202020)]([)()(2)()]([)(a f a f a a a a a f a a a b λλλ+---=--=- ④ 由和0)(0=a f ①式，得20000)()]()()[()()(a a a f a f a a a f a a -≥--=-λ ⑤由0)(0=a f 和②式知，20202)()]()([)]([a a a f a f a f -≤-= ⑥由⑤、⑥代入④式，得 2022022020)()(2)()(a a a a a a a b -+---≤-λλ202))(1(a a --=λ（III ）由③式可知22)]()()([)]([a f a f b f b f +-=22)]([)]()()[(2)]()([a f a f b f a f a f b f +-+-=22)]([)]()([2)(a f a f b f ab a b +--⋅--≤λ（用②式）222)]([)]()()[(2)]([a f a f b f a b a f +---=λλ2222)]([)(2)([a f a b a f +-⋅⋅-≤λλλ （用①式）2222222)]()[1()]([)]([2)]([a f a f a f a f λλλ-=+-=。