各种迭代法编程

c语言迭代法自洽计算简单举例

c语言迭代法自洽计算简单举例迭代法是一种常用的数值计算方法，特别适用于需要反复迭代求解的问题。

在C语言中，我们可以通过循环来实现迭代计算。

下面我将列举10个简单的例子，来说明如何使用C语言迭代法进行自洽计算。

1. 求解平方根：假设我们需要计算一个数的平方根，可以使用迭代法来逼近平方根的值。

我们可以从一个初始值开始，通过不断迭代计算来逼近平方根的真实值。

2. 求解方程的根：对于一元方程 f(x) = 0，我们可以使用迭代法来求解方程的根。

通过不断迭代计算，我们可以逼近方程的根的值。

3. 计算圆周率：圆周率是一个无理数，它的值可以使用迭代法进行计算。

通过不断迭代计算，我们可以逼近圆周率的真实值。

4. 计算斐波那契数列：斐波那契数列是一个经典的数列，可以使用迭代法来计算。

通过不断迭代计算，我们可以得到斐波那契数列的前n个数。

5. 计算阶乘：阶乘是一个常见的数学运算，可以使用迭代法来计算。

通过不断迭代计算，我们可以得到给定数的阶乘值。

6. 求解最大公约数：最大公约数是两个数的公共因子中最大的一个，可以使用迭代法来求解。

通过不断迭代计算，我们可以得到两个数的最大公约数。

7. 求解矩阵乘法：矩阵乘法是一种常见的数学运算，可以使用迭代法来计算。

通过不断迭代计算，我们可以得到两个矩阵的乘积。

8. 求解线性方程组：线性方程组是一组线性方程的集合，可以使用迭代法来求解。

通过不断迭代计算，我们可以得到线性方程组的解。

9. 进行排序算法：排序算法是一种常见的算法，可以使用迭代法来实现。

通过不断迭代计算，我们可以将一组数据按照一定的规则进行排序。

10. 进行图像处理：图像处理是一种常见的应用领域，可以使用迭代法来实现。

通过不断迭代计算，我们可以对图像进行增强、滤波等操作。

以上是我列举的10个使用C语言迭代法进行自洽计算的简单例子。

通过这些例子，我们可以看到迭代法在数值计算中的广泛应用。

希望这些例子能够帮助你更好地理解和应用迭代法。

几种迭代计算方法

几种迭代计算方法迭代计算方法是一种重要的计算技术，它是基于不断逼近的原理，通过多次迭代运算来逼近所要求解的问题的计算结果。

下面将介绍几种常见的迭代计算方法。

1.不动点迭代不动点迭代是指通过选择一个合适的迭代函数来不断逼近一个不动点的过程。

不动点指的是在迭代函数中，当迭代到其中一步时，迭代函数的值等于该迭代的值，即f(x)=x。

常见的不动点迭代有牛顿迭代法和迭代法求解方程。

牛顿迭代法通过选择一个初始值x0，利用迭代函数f(x)=x-f(x)/f'(x)来逼近方程f(x)=0的根。

每次迭代中，通过计算迭代函数的值来更新x的值，直至满足一定的精度要求。

迭代法求解方程是通过将方程f(x) = 0转化为x = g(x)的形式，并选择一个合适的g(x)来进行不断迭代求解的方法。

通过选择不同的g(x)，可以得到不同的迭代方法，如简单迭代法、Jacobi迭代法、Gauss-Seidel迭代法等。

2.逐次平方根法逐次平方根法是一种通过不断迭代计算来求解线性方程组的方法。

该方法通过对原始的线性方程组进行变换，将其转化为对角线元素全为1的上三角矩阵，并将方程组的解表示为逐次迭代的形式。

在每次迭代中，通过求解一个线性方程组来更新解的值，直至满足一定的精度要求。

逐次平方根法是一种迭代计算方法，其主要适用于对称正定矩阵，能够有效地求解大规模线性方程组。

3.迭代加权法迭代加权法是一种通过引入权重来加快迭代收敛速度的方法。

该方法在每次迭代更新解的时候，通过对解的不同分量引入不同的权重来控制更新的幅度。

通过合理选择权重，可以加快迭代收敛速度，提高求解效率。

迭代加权法是一种通用的迭代计算方法，在多个领域中有不同的应用，如求解矩阵特征值问题、求解最优化问题等。

以上介绍的是常见的几种迭代计算方法，它们在不同的问题中有着广泛的应用。

这些方法通过迭代运算不断逼近所要求解的问题的计算结果，具有较好的收敛性和计算效率，是一种重要的计算技术。

C语言求解一元二次方程的解源码(迭代法,二分法,牛顿迭代法)

#include <stdio.h>#include <stdlib.h>#include <math.h>#define maxint 32767.0#define minint -32768.0#define accuracy 0.0000001//精确度，值越小计算结果越精确float a,b,c;//系数float dt;//b^2-4acfloat x1=0.0,x2=0.0;//方程的解void read();void setDt();int assertX();void binarySolution();void interation();void newtonInteration();double f(double x);double f1(double x);double absolute(double x);void accurate();int main(void){int end=1;while(end!=0)//继续运算{accurate();printf("按任意键继续（输入0退出）：\n");scanf("%d",&end);}}//读取a,b,cvoid read(){printf("请输入方程ax^2+bx+c=0的系数a,b,c：\n");printf("请输入二次项系数a：");while(0==scanf("%f",&a)||a==0){while('\n' != getchar()){}printf("输入无效！请重新输入二次项系数a：");}printf("请输入一次项系数b：");while(0==scanf("%f",&b)){while('\n' != getchar()){}printf("输入无效！请重新输入一次项系数b：");}printf("请输入常数项c：");while(0==scanf("%f",&c)){while('\n' != getchar()){}printf("输入无效！请重新输入常数项c：");}}//计算dtvoid setDt(){dt=b*b-4*a*c;}//判断是否有解int assertX(){if(dt>=0) return 1;return 0;}//循环计算控制void accurate(){read();setDt();int method=0;printf("请选择求解方法：\n\t1.二分法\n\t2.迭代法\n\t3.牛顿迭代法\n请选择：");while((0==scanf("%d",&method))||(method!=1&&method!=2&&method!=3)){while('\n' != getchar()){}printf("输入无效！请重新选择：");}if(!assertX()){printf("该方程无解！\n");}else{switch(method){case 1:binarySolution();break;case 2:interation();break;case 3:newtonInteration();break;}printf("方程%fx^2+%fx+%f=0的解为：x1=%.10f x2=%.10f\n",a,b,c,x1,x2); }}//二分法void binarySolution(){double min=minint,temp=(-1.0*b)/(2*a),max=maxint,middle=0.0;//求解X1while((max-temp)>=accuracy){middle=(max+temp)/2;if(a>0)//开口向上{if(f(middle)>0)max=middle;elsetemp=middle;}else//开口向下{if(f(middle)>0)temp=middle;elsemax=middle;}}x2=temp;//求解X2temp=(-1.0*b)/(2*a);while((temp-min)>=accuracy){middle=(min+temp)/2;if(a>0)//开口向上{if(f(middle)>0)min=middle;elsetemp=middle;}else//开口向下{if(f(middle)>0)temp=middle;elsemin=middle;}}x1=temp;}//迭代法void interation(){//求解X1，在曲线对称轴处选择初始点double index=(-1.0*b)/(2*a),temp;if(b!=0)//b不等于0时进行迭代{temp=index;index=-1.0*(a*temp*temp+c)/b;while((absolute(index-temp))>accuracy) {temp=index;index=-1.0*(a*temp*temp+c)/b;}x1=index;x2=(-1.0*b)/a-x1;}else//b=0时ax^2+c=0直接求解{x1=sqrt(-1.0*c/a);x2=-x1;}}//牛顿迭代法void newtonInteration(){//求解X1，在曲线对称轴右侧选取初始点double index=(-1.0*b)/(2*a)+10,temp; temp=index;index=temp-f(temp)/f1(temp);while((absolute(index-temp))>accuracy) {temp=index;index=temp-f(temp)/f1(temp);}x1=index;//求解X2，在曲线对称轴左侧选取初始点index=(-1.0*b)/(2*a)-10,temp;temp=index;index=temp-f(temp)/f1(temp);;while((absolute(index-temp))>accuracy) {temp=index;index=temp-f(temp)/f1(temp);}x2=index;}//函数f(x)double f(double x){return a*x*x+b*x+c;}//函数f(x)的一次导函数double f1(double x){return 2.0*a*x+b;}//求解绝对值double absolute(double x) {if(x<=0) return (-1.0*x); return x*1.0;}。

数值分析迭代法 C++程序

课题三解线性方程组的迭代法实验目标：分别采用Jacobi迭代法，Gauss-Seidel迭代法和SOR迭代法求解线性方程组。

Jocabi迭代法：#include<iostream>#include<math.h>using namespace std;int i,j,k; //计数器int M = 2000;int Array(double ***Arr, int n){double **p;int i;p=(double **)malloc(n*sizeof(double *));if(!p)return 0;for(i=0;i<n;i++){p[i]=(double *)malloc(n*sizeof(double));if(!p[i])return 0;}*Arr=p;return 1;}void main(){double eps ;cout<<"默认最多迭代次数为2000次"<<endl<<"迭代精度为：";cin>>eps;double **matrix;int n;cout<<"矩阵大小为：";cin>>n;double *X;X= new double[n];double *Y;Y= new double[n];double *G;G= new double[n];for(i=0;i<n;i++){Y[i]=0;}if(!Array(&matrix,n))cout<<"内存分配失败！";elsecout<<"请输入矩阵:"<<endl;for( i=0;i<n;i++){for( j=0;j<n;j++){cin>>matrix[i][j];}}cout<<"请输入右端项："<<endl;double *B;B = new double[n];for(i=0;i<n;i++){cin>>B[i];}for (i = 0 ;i< n;i++){if (fabs(matrix[i][i]) < eps){cout <<"打印失败"<<endl;return;}double T = matrix[i][i];for ( j = 0 ; j< n;j++){matrix[i][j] = -matrix[i][j]/T;}matrix[i][i] = 0;G[i] = B[i]/T;}int counter = 0;while (counter < M){for (i = 0;i < n; i++){double temp = 0;for (j = 0;j<n; j++){temp = temp + matrix[i][j]*Y[j];}X[i] = G[i] + temp;}double temp = 0;for (i = 0 ;i< n ; i++){temp = temp + fabs(X[i] - Y[i]);}if (temp <= eps)break;else{for( i = 0; i < n ;i++){Y[i] = X[i];}}counter++;}cout << "迭代次数为："<<counter<<"次。

python迭代法求解方程

Python 迭代法求解方程本文介绍了使用 Python 编写迭代法求解方程的程序，并举例说明了如何使用迭代法求解一元二次方程、指数方程和三角方程。

下面是本店铺为大家精心编写的5篇《Python 迭代法求解方程》，供大家借鉴与参考，希望对大家有所帮助。

《Python 迭代法求解方程》篇1引言迭代法是一种常用的数值计算方法，用于求解各种方程。

在Python 中，可以使用迭代法来求解各种方程，例如一元二次方程、指数方程和三角方程等。

本文将介绍如何使用 Python 编写迭代法求解方程的程序，并举例说明如何使用迭代法求解不同类型的方程。

一、一元二次方程一元二次方程的一般形式为:$$x^2+bx+c=0$$其中，$a,b,c$为常数，$x$为未知数。

使用迭代法求解一元二次方程的步骤如下:1. 选择一个初始值$x_0$。

2. 计算下一次的值$x_{n+1}$。

$$x_{n+1}=frac{x_n^2+bx_n+c}{x_n+b}$$3. 重复步骤 2，直到$x_n$满足精度要求。

下面是一个使用 Python 求解一元二次方程的程序:```pythondef quadratic(a, b, c, x0, tolerance):x = x0while abs(x - x0) > tolerance:x0 = xx = (x**2 + b*x + c) / (x + b)return x```其中，$a, b, c, x0$为输入参数，$tolerance$为精度要求。

二、指数方程指数方程的一般形式为:$$a^x=b$$其中，$a,b$为常数，$x$为未知数。

使用迭代法求解指数方程的步骤如下:1. 选择一个初始值$x_0$。

2. 计算下一次的值$x_{n+1}$。

$$x_{n+1}=frac{1}{2}(x_n+frac{b}{a^{x_n}})$$3. 重复步骤 2，直到$x_n$满足精度要求。

```pythondef exponent(a, b, x0, tolerance):x = x0while abs(x - x0) > tolerance:x0 = xx = 0.5 * (x + b / a**x)return x```其中，$a, b, x0$为输入参数，$tolerance$为精度要求。

sqrt方法(一)

sqrt方法(一)sqrt相关方法简介在数学和编程中，sqrt用于计算一个数的平方根。

计算平方根的方法有多种，本文将介绍几种常用的方法。

方法一：牛顿迭代法1.初始化一个猜测值x作为平方根的近似值。

2.使用迭代公式x = (x + n / x) / 2来更新猜测值x，其中n是待求平方根的数字。

3.重复步骤2，直到x的平方接近于n。

方法二：二分查找法1.初始化左边界left为0，右边界right为n。

2.当左边界小于等于右边界时，执行以下步骤：–计算中间值mid，mid = (left + right) / 2。

–如果mid的平方接近于n，则返回mid作为平方根。

–如果mid的平方大于n，则将右边界更新为mid-1。

–如果mid的平方小于n，则将左边界更新为mid+1。

3.返回left作为平方根。

方法三：使用数学库函数1.在许多编程语言中，都提供了sqrt函数来计算平方根。

只需要调用该函数，并传入待求平方根的数字作为参数，即可得到结果。

方法四：二进制近似法1.将n转换为二进制表示。

2.初始化一个近似值x为1。

3.对每一位的二进制数字进行迭代处理：–x的平方不断逼近n。

–如果该位为1，则将x更新为x = (x + n / x) / 2，否则保持不变。

4.重复步骤3，直到迭代收敛。

5.返回x作为平方根。

方法五：插值法1.将平方根的求解问题转化为多项式的求解问题。

2.构造一个具有稀疏系数的多项式。

3.使用插值法来求解多项式的根，即可得到平方根。

结论根据不同的场景和需求，选择合适的方法来计算平方根。

牛顿迭代法和二分查找法是比较常用的方法，而使用数学库函数则是最简单快速的方式。

二进制近似法和插值法则是更为复杂的求解方式，适用于特定的问题。

在实际应用中，可以根据具体情况进行选择。

方法一：牛顿迭代法1.初始化一个猜测值x作为平方根的近似值。

2.使用迭代公式x = (x + n / x) / 2来更新猜测值x，其中n是待求平方根的数字。

matlab迭代法解方程

matlab迭代法解方程在MATLAB中，可以使用迭代法求解方程。

迭代法的一般步骤如下：1. 选择一个初始猜测值。

2. 根据某种迭代公式，计算下一个近似解。

3. 根据设定的停止准则，判断迭代是否结束。

常见的停止准则可以是近似解的相对误差小于某个给定的值，或者迭代次数达到了预设的最大次数。

4. 如果迭代未结束，将计算得到的近似解作为新的猜测值，回到步骤2；否则，停止迭代，并输出最终的近似解。

下面是一个使用迭代法求解方程的示例代码：```matlabfunction x = iterativeMethod(equation, x0, epsilon, maxIter)syms x;f = equation;df = diff(f, x);x_prev = x0;for i = 1:maxIterx_new = x_prev - subs(f, x, x_prev) / subs(df, x, x_prev);if abs(x_new - x_prev) < epsilonx = x_new;return;endx_prev = x_new;enderror('Maximum iteration reached. No solution found.');end```使用该函数时，需要传入四个参数：`equation`是方程的符号表达式，`x0`是初始猜测值，`epsilon`是停止迭代的相对误差阈值，`maxIter`是最大迭代次数。

例如，要求方程sin(x) - x^2 = 0的解，可以使用以下代码：```matlabequation = sin(x) - x^2;x0 = 1;epsilon = 1e-6;maxIter = 100;x = iterativeMethod(equation, x0, epsilon, maxIter);disp(x);```该代码会输出方程sin(x) - x^2 = 0的近似解。

python迭代法

Python迭代法1. 简介迭代法（Iterative Method）是一种通过反复迭代计算来逼近最终结果的方法。

在计算机科学与数学领域，迭代法被广泛应用于解决各种问题，特别是在数值计算、优化和模拟等方面。

Python作为一种高级编程语言，提供了丰富的迭代工具和库，使得迭代法在Python程序中得以方便地应用和实现。

本文将介绍迭代法的概念、原理以及在Python中的具体实现。

2. 迭代法概念与原理2.1 迭代法的定义迭代法是一种通过逐步逼近的方法，将问题分解成多个较简单或者相似的子问题，并通过反复迭代计算来逐渐逼近最终解决方案的方法。

2.2 迭代法的基本原理迭代法的基本原理是通过不断重复执行某个操作，直到满足停止条件。

在每一次迭代中，根据当前的状态和问题的特点，通过某种转换或者计算方法，得出下一次迭代的状态，如此依次迭代下去，直到达到停止条件。

2.3 迭代法的应用场景迭代法适用于很多问题的求解，特别是对于那些难以通过解析方法求解的问题，迭代法往往是一种有效的选择。

例如，求解非线性方程的根、求解线性方程组、最优化问题等都可以使用迭代法来逼近解决。

3. 迭代法在Python中的实现3.1 内置迭代器Python提供了一些内置的迭代器（Iterator），使得使用迭代法来处理数据和执行操作变得简单和高效。

其中，常用的内置迭代器包括： - range()迭代器：生成一个指定范围的整数序列。

- enumerate()迭代器：同时返回索引和元素。

- zip()迭代器：将多个迭代器的元素组合在一起。

3.2 自定义迭代器除了使用内置迭代器，Python还允许用户自定义迭代器来实现更加灵活和复杂的迭代算法。

自定义迭代器需要实现__iter__()和__next__()两个特殊方法。

其中__iter__()方法返回迭代器对象本身，__next__()方法返回下一个迭代的值。

3.3 使用迭代器处理数据在Python中，迭代器常常用于处理大量的数据集合，例如列表、元组、字典等。

三坐标六点迭代法编程步骤

三坐标六点迭代法编程步骤
三坐标六点迭代法是一种用于解决三维空间中点的坐标的迭代
方法。

下面是编程步骤：
1. 定义初始点坐标，首先，你需要定义初始的六个点的坐标，
这些点可以是在三维空间中的任意位置。

2. 计算新的坐标，根据三坐标六点迭代法的原理，你需要编写
计算新坐标的函数。

这个函数通常会使用一定的数学公式和迭代方
法来更新每个点的坐标。

3. 迭代更新，在主程序中使用循环结构，对每个点进行迭代更新，直到满足停止条件为止。

停止条件可以是达到一定的迭代次数，或者当点的坐标变化小于某个阈值时停止迭代。

4. 输出结果，最后，将迭代更新后的点坐标输出或者进行其他
处理。

这些点的坐标可能会用于绘图、计算距离或者其他应用。

需要注意的是，在编程实现这个方法时，你需要考虑到数值稳
定性、收敛性以及计算效率等方面的问题。

另外，对于特定的应用
场景，可能需要对迭代方法进行一定的调整和优化。

总的来说，编写三坐标六点迭代法的程序需要深入理解这个方法的原理，并结合具体的编程语言来实现上述步骤。

希望这些步骤能够帮助你更好地理解和实现这个迭代方法。

简单迭代法的代码实现

for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>A[i][j];
}
}
cout<<endl;
cout<<"请输入方程组的值向量："<<endl;
for(int k=0;k<n;k++){
cin>>B[k];
}
cout<<endl;
cout<<"您输入的方程组为："<<endl;
double a=x;
double b=f(a);
int k=0; //记录循环的次数
while(((a-b)>d) || ((a-b)<-1*d)){
cout<<a<<endl;
a=b;
b=f(a);
k++;
if(k>100){
cout<<"迭代失败！（可能是函数不收敛）"<<endl;
return ;
double a=x;
double b=f(a);
int k=0;//记录循环的次数
while(((a-b)>d) || ((a-b)<-1*d)){
cout<<a<<endl;
a=b;
b=f(a);
k++;
if(k>100){
cout<<"迭代失败！（可能是函数不收敛）"<<endl;

C语言复习---迭代法，牛顿迭代法，二分法求根

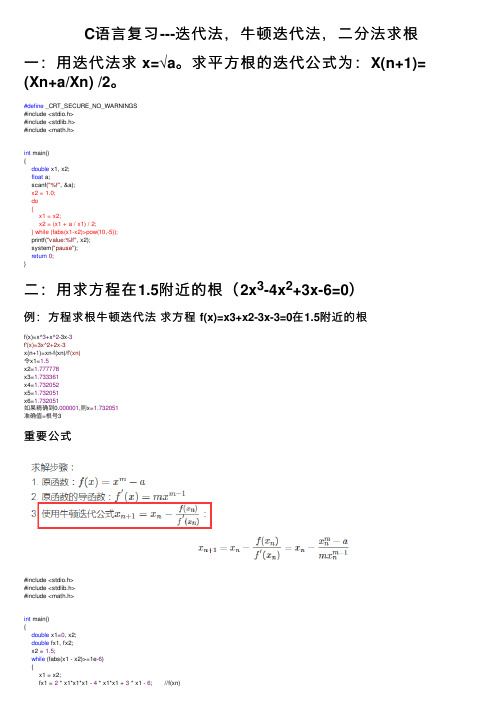
C语⾔复习---迭代法，⽜顿迭代法，⼆分法求根⼀：⽤迭代法求 x=√a。

求平⽅根的迭代公式为：X(n+1)= (Xn+a/Xn) /2。

#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1, x2;float a;scanf("%f", &a);x2 = 1.0;do{x1 = x2;x2 = (x1 + a / x1) / 2;} while (fabs(x1-x2)>pow(10,-5));printf("value:%lf", x2);system("pause");return0;}⼆：⽤求⽅程在1.5附近的根（2x3-4x2+3x-6=0）例：⽅程求根⽜顿迭代法求⽅程 f(x)=x3+x2-3x-3=0在1.5附近的根f(x)=x^3+x^2-3x-3f'(x)=3x^2+2x-3x(n+1)=xn-f(xn)/f'(xn)令x1=1.5x2=1.777778x3=1.733361x4=1.732052x5=1.732051x6=1.732051如果精确到0.000001,则x=1.732051准确值=根号3重要公式#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1=0, x2;double fx1, fx2;x2 = 1.5;while (fabs(x1 - x2)>=1e-6){x1 = x2;fx1 = 2 * x1*x1*x1 - 4 * x1*x1 + 3 * x1 - 6; //f(xn)fx2 = 6 * x1*x1 - 8 * x1 + 3; //f(xn)'x2 = x1 - fx1 / fx2;}printf("value:%lf", x2);system("pause");return0;}三：⼆分法求⽅程的根给定精确度ξ,⽤⼆分法求函数f(x)零点近似值的步骤如下:1确定区间[a,b],验证f(a)·f(b)<0（这是前提，选取的区间必须满⾜这个条件）,给定精确度ξ. 2求区间(a,b)的中点c.3计算f(c).(1) 若f(c)=0,则c就是函数的零点;(2) 若f(a)·f(c)<0,则令b=c;(3) 若f(c)·f(b)<0,则令a=c.(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.#include <stdio.h>#include <stdlib.h>#include <math.h>double fx(double x){return2 * x*x*x - 4 * x*x + 3 * x - 6;}int main(){double x1 , x2;double fx1, fx2;double e = 1e-6;do{printf("enter (x1,x2):\n");scanf("%lf", &x1);scanf("%lf", &x2);if (x1>x2){double temp = x1;x1 = x2;x2 = temp;}fx1 = fx(x1);fx2 = fx(x2);} while (fx1*fx2>0);if (fabs(fx1) < e)printf("solution1:%lf\n", x1);else if (fabs(fx2) < e)printf("solution2:%lf\n", x2);else{while (fabs(x1 - x2) >= e){double mid = (x1 + x2) / 2;if (fx(mid)*fx2 < 0)x1 = mid;elsex2 = mid;}printf("solution3:%lf", x2);}system("pause");return0;}。

matlab的迭代法编程

在MATLAB 中，迭代法是一种通过重复执行一系列步骤来解决问题的方法。

以下是一个使用迭代法求解方程根的示例：
matlab
function=iterative_Method(,,,)
=;
while abs(f())>
=-f()/df();
endend
function=df()
=-1;end
=@()^2-2;
=1;
=2;
=1e-6;
=iterative_Method(,,,);disp(['方程 x^2 - 2 = 0 的根为 ',
num2str()]);
在上述代码中，iterative_Method函数接受一个函数f、区
间[a,b]和精度eps作为输入。

它通过迭代更新x的值，直到abs(f(x))小于eps为止。

在每次迭代中，它使用导数df(x)来更新x的值。

df函数返回导数-1，因为对于方程x^2 - 2 = 0，其导数为2x，在区
间[a,b]内恒为-1。

最后，我们定义了函数f和区间[a,b]，并调用iterative_Method函数求解方程的根。

结果将显示在命令窗口中。

运行上述代码，输出结果为：
plaintext
1.41421
这表示方程x^2 - 2 = 0的根约为1.41421，与方程的实际根√2非常接近。

你可以根据需要调整精度eps的值来获得更精确的结果。

python n阶乘的迭代方法

python n阶乘的迭代方法
Python有很多不同的方法可以计算n的阶乘，其中一种是迭代方法。

迭代方法是通过循环来计算阶乘的，它的实现非常简单，只需要一个变量来保存结果并在每次循环中更新。

下面是一个Python的迭代方法来计算n的阶乘的示例代码：
```python
def factorial(n):
result = 1
for i in range(1, n+1):
result *= i
return result
```
在这个代码中，我们首先定义了一个名为`factorial`的函数，该函数接收一个整数n作为参数。

我们使用一个变量`result`来保存计算的结果，并将其初始化为1。

然后，我们使用一个for循环来遍历从1到n的所有整数（包括n），并将它们乘以`result`。

每次迭代，我们都会将`result`与当前的整数相乘，并将结果保存回`result`中。

当循环结束时，`result`将包含n的阶乘。

最后，我们返回`result`作为函数的结果。

我们可以使用这个函数来计算任意整数的阶乘，例如：
```python
print(factorial(5)) # 输出120
print(factorial(10)) # 输出3628800
```
这个迭代方法是计算n的阶乘最简单的方法之一，它非常容易理解和实现。

但是，当n很大时，它的时间复杂度将会非常高，导致运行时间非常长。

在这种情况下，我们可能需要使用一些更高效的算法来计算阶乘。

迭代法前序遍历

迭代法前序遍历
具体的实现步骤如下：
1.初始化一个栈，并将根节点入栈。

2.重复执行以下步骤，直到栈为空：
弹出栈顶元素，将该节点的值加入结果列表。

若该节点存在右子节点，则将右子节点入栈。

若该节点存在左子节点，则将左子节点入栈。

下面是一个示例的代码实现：
python
defpreOrderTraversal(root): ifnotroot:
return[]
stack=[]
result=[]
stack.append(root)
whilestack:
node=stack.pop()
result.append(node.val)
ifnode.right:
stack.append(node.right)
ifnode.left:
stack.append(node.left)
returnresult
这个算法的时间复杂度是O(n)，其中n是二叉树的节点数。

算法的空间复杂度是O(h)，其中h是二叉树的高度，h最坏情况下可以达到O(n)。

迭代法的程序

#include<iostream>#include<math.h>#include<iomanip>using namespace std;#define kk 50 //定义最大方程元数int n,i,c,j,ll,hh,gg,mm;double A[kk][kk],x[kk][kk],b[kk],y[kk],a[kk],z[kk],m,nn,d,e=1,w,fff ;void main(){cout<<"********************************************************************* *"<<endl;cout<<" ***本程序可以用雅可比迭代法,塞德尔迭代法,逐次超松弛法求解线性方程组***"<<endl;cout<<"********************************************************************* *"<<endl;//*********************************数据的输入********************************/*bb:*/cout<<"输入的方程元数"<<endl;cin>>n;cout<<"请输入方程系数矩阵:"<<endl;for(i=0;i<n;i++)for(j=0;j<n;j++)cin>>A[i][j];cout<<"请输入右边向量:"<<endl;for(i=0;i<n;i++)cin>>b[i];cout<<"输入你想要的迭代精度(建议1e-5以上)！"<<endl;cin>>fff;cout<<"输入最大迭代次数（建议300次以上）！"<<endl;cin>>mm;////*******************************判断是否对角占优*************************// for(i=0;i<n;i++)// {// for(j=0;j<n;j++)// {// nn=0;// if(i==j)// {// d=fabs(A[i][i]);// }// else// nn=nn+fabs(A[i][j]);// }// if(nn>d)// {// cout<<"该方程不对角占优，迭代不收敛"<<endl; // cout<<"是否继续？是（0），否（1）"<<endl; // cin>>hh;// if(hh!=1)// goto bb;// else exit(1);// }// }//********************************计算出迭代矩阵*************************for(i=0;i<n;i++){b[i]=b[i]/A[i][i];for(j=0;j<n;j++){if(i==j){x[i][i]=0;}else{x[i][j]=-A[i][j]/A[i][i];}}}//*******************************输出迭代矩阵*****************************cout<<"计算出迭代矩阵为："<<endl;for(i=0;i<n;i++){for(j=0;j<n;j++)cout<<x[i][j]<<" ";cout<<b[i]<<" ";cout<<endl;}//****************************迭代方法的选择*****************************cout<<"请你选择迭代方法！"<<endl;cout<<endl;cout<<endl;cout<<"选用雅可比迭代法，请输入（1）！"<<endl; cout<<endl;cout<<endl;cout<<"选用塞德尔迭代法，请输入（2）！"<<endl; cout<<endl;cout<<endl;cout<<"选用逐次超松弛法，请输入（3）！"<<endl; cout<<endl;cout<<endl;cin>>ll;//*****************************赋迭代初值***********************************cout<<"输入迭代初值"<<endl;for(i=0;i<n;i++)cin>>y[i];int f=1;switch(ll){case 1:goto cc;break;case 2:goto aa;break;case 3:goto dd;}//***************************雅可比迭代法************************************cc:cout<<" ";for(i=1;i<n+1;i++)cout<<"X["<<i<<"]"<<" ";cout<<"精度";cout<<endl;cout<<"迭代初值为： ";cout<<setiosflags(ios::fixed);for(i=0;i<n;i++)cout<<y[i]<<" ";cout<<endl;while(e>fff){for(i=0;i<n;i++)z[i]=y[i];for(i=0;i<n;i++){nn=0;for(j=0;j<n;j++){if(i!=j)nn=nn+x[i][j]*z[j];y[i]=nn+b[i];}e=fabs(z[0]-y[0]);if(fabs(z[i]-y[i])>e)e=fabs(z[i]-y[i]);if(i==0){cout<<setiosflags(ios::fixed);cout<<"第"<<setw(3)<<setprecision(3)<<f++<<"次迭代"<<" "; }cout<<setiosflags(ios::fixed);cout<<setw(8)<<setprecision(8)<<y[i]<<" ";}cout<<e;cout<<endl;if(f>mm){cout<<"迭代次数大于"<<mm<<"次"<<endl;cout<<"认为方程发散，迭代不收敛"<<endl;exit(1);}}cout<<endl;cout<<endl;cout<<"方程迭代了"<<f-1<<"次,达到你所要求的精度"<<fff<<endl; cout<<"最后结果为："<<endl;cout<<endl;for(i=0;i<n;i++){cout<<"X"<<"["<<i+1<<"]"<<"="<<y[i];cout<<endl;}exit(1);//***********************************塞德尔迭代法********************************aa:cout<<" ";for(i=1;i<n+1;i++)cout<<"X["<<i<<"]"<<" ";cout<<"精度";cout<<endl;cout<<"迭代初值为： ";cout<<setiosflags(ios::fixed);for(i=0;i<n;i++)cout<<y[i]<<" ";cout<<endl;while(e>fff){for(i=0;i<n;i++){z[i]=y[i];nn=0;for(j=0;j<n;j++){nn=nn+x[i][j]*y[j];y[i]=nn+b[i];}e=fabs(z[0]-y[0]);if(fabs(z[i]-y[i])>e)e=fabs(z[i]-y[i]);if(i==0){cout<<setiosflags(ios::fixed);cout<<"第"<<setw(3)<<setprecision(3)<<f++<<"次迭代"<<" "; }cout<<setiosflags(ios::fixed);cout<<setw(8)<<setprecision(8)<<y[i]<<" ";}cout<<e;cout<<endl;if(f>mm){cout<<"迭代次数大于"<<mm<<"次"<<endl;cout<<"认为方程发散，迭代不收敛"<<endl;exit(1);}}cout<<endl;cout<<endl;cout<<"方程迭代了"<<f-1<<"次,达到你所要求的精度"<<fff<<endl; cout<<"最后结果为："<<endl;cout<<endl;for(i=0;i<n;i++){cout<<"X"<<"["<<i+1<<"]"<<"="<<y[i];cout<<endl;}exit(1);//***********************************逐次超松弛法********************************dd: cout<<"输入加速因子W(0<W<2)："<<endl; cin>>w;/*if((w>2)||(w<0)){cout<<"输入错误！加速因子W(0<W<2)："<<endl; cout<<"请重新输入："<<endl;cin>>w;}if(w>=2){cout<<"输入错误！加速因子W(0<W<2)："<<endl; cout<<"请重新输入："<<endl;cin>>w;}if(w<=0){cout<<"输入错误！加速因子W(0<W<2)："<<endl; cout<<"请重新输入："<<endl;cin>>w;}cout<<" ";for(i=1;i<n+1;i++)cout<<"X["<<i<<"]"<<" ";cout<<"精度";cout<<endl;cout<<"迭代初值为： ";cout<<setiosflags(ios::fixed);for(i=0;i<n;i++)cout<<y[i]<<" ";cout<<endl;while(e>fff){for(i=0;i<n;i++){z[i]=y[i];nn=0;for(j=0;j<n;j++){nn=nn+x[i][j]*y[j];y[i]=(1-w)*z[i]+w*(nn+b[i]);}e=fabs(z[0]-y[0]);if(fabs(z[i]-y[i])>e)e=fabs(z[i]-y[i]);if(i==0){cout<<setiosflags(ios::fixed);cout<<"第"<<setw(3)<<setprecision(3)<<f++<<"次迭代"<<" "; }cout<<setiosflags(ios::fixed);cout<<setw(8)<<setprecision(8)<<y[i]<<" ";}cout<<e;cout<<endl;if(f>mm){cout<<"迭代次数大于"<<mm<<"次"<<endl;cout<<"认为方程发散，迭代不收敛"<<endl;exit(1);}}cout<<endl;cout<<endl;cout<<"方程迭代了"<<f-1<<"次,达到你所要求的精度"<<fff<<endl; cout<<"最后结果为："<<endl;cout<<endl;for(i=0;i<n;i++){cout<<"X"<<"["<<i+1<<"]"<<"="<<y[i];cout<<endl;}exit(1);}//**************************************程序结束****************************************。

matlab迭代法代码

matlab迭代法代码1、%用不动点迭代法求方程 x-e^x+4=0的正根与负根，误差限是10^-6% disp('不动点迭代法');n0=100;p0=-5;for i=1:n0p=exp(p0)-4;if abs(p-p0)<=10^(-6)if p<0disp('|p-p0|=')disp(abs(p-p0))disp('不动点迭代法求得方程的负根为:')disp(p);break;elsedisp('不动点迭代法无法求出方程的负根.')endelsep0=p;endendif i==n0disp(n0)disp('次不动点迭代后无法求出方程的负根')endp1=1.7;for i=1:n0pp=exp(p1)-4;if abs(pp-p1)<=10^(-6)if pp>0disp('|p-p1|=')disp(abs(pp-p1))disp('用不动点迭代法求得方程的正根为')disp(pp);elsedisp('用不动点迭代法无法求出方程的正根');endbreak;elsep1=pp;endendif i==n0disp(n0)disp('次不动点迭代后无法求出方程的正根') end2、%用牛顿法求方程 x-e^x+4=0的正根与负根，误差限是10^-6 disp('牛顿法')n0=80;p0=1;for i=1:n0p=p0-(p0-exp(p0)+4)/(1-exp(p0));if abs(p-p0)<=10^(-6)disp('|p-p0|=')disp(abs(p-p0))disp('用牛顿法求得方程的正根为')disp(p);break;elsep0=p;endendif i==n0disp(n0)disp('次牛顿迭代后无法求出方程的解') end p1=-3;for i=1:n0p=p1-(p1-exp(p1)+4)/(1-exp(p1));if abs(p-p1)<=10^(-6)disp('|p-p1|=')disp(abs(p-p1))disp('用牛顿法求得方程的负根为')disp(p);break;elsep1=p;endendif i==n0disp(n0)disp('次牛顿迭代后无法求出方程的解') end。

雅可比迭代法：function x=jacobi(a,b,p,delta,n)%a为n维非奇异矩阵；b为n维值向量%p为初值；delta为误差界；n为给定的迭代最高次数N=length（b）;for k=1:nfor j=1：Nx(j)=(b(j)-a(j,[1:j-1,j+1:N])*p([1:j-1,j+1:N]))/a(j,j);enderr=abs(norm(x’-p));p=x’;if(err<delta)break;endendp %显示迭代过程x=x’；k,err高斯塞德尔法迭代：function x=saidel(a,b,p,delta,n)%a为n维非奇异矩阵；b为n维值向量%p为初值；delta为误差界；n为给定的迭代最高次数N=length（b）;for k=1:nfor j=1：Nif j==1x(1)=(b(1)-a(1,2:N)*p(2:N))/a(1,1);else if j=Nx(N)=(b(N)-a(N,1:N-1)*(x(1:N-1))’)/a(N,N);elsex(j)=(b(j)-a(j,(1:j-1)*x(1:j-1）-a(j,j+1:N)*p(j+1:N))/a(j,j);endenderr=abs(norm(x’-p));p=x’;if(err<delta)break;endendx=x’；k,err不动点迭代法：function [x,k,err,p]=ddf(f,x0,tol,n)%ddl.m为用迭代法求非线性方程的解%f为给定的迭代函数；x0为给定的初始值%tol为给定的误差界；n为所允许的最大迭代次数%k为迭代次数；x为不动点的近似值；err为误差p(1)=x0;for k=2:np(k)=feval(f,p(k-1));k,err=abs(p(k)-p(k-1))x=p(k);if(err<tol)break;endif k==ndisp('迭代超过最大次数！')endendx=p'牛顿法：function [x,k,err,y]=Newtun(f,df,x0,tol,n)%Newtun.m为用迭代法求非线性方程的解%f为给定的非线性方程；df为f的微分方程；x0为给定的初始值%tol为给定的误差界；n为所允许的最大迭代次数%k为迭代次数；x为不动点的近似值；err为误差%x为牛顿迭代法得到得近似解y(1)=x0;for k=1:nx=x0-feval(f,x0)/feval(df,x0);err=abs(x-x0);x0=x;if(err<tol)|(y==0);break;endend必要编辑M文件qfun.m,代码如下：function y=qfun(x);y=x^3-3*x-1;弦截法：function [x,err,k,y]=xjf(f,x0,x1,tol,n)%xjf.m为用弦截法迭代法求非线性方程的解%f为给定的非线性方程；x0,x1为给定的初始值%tol为给定的误差界；n为所允许的最大迭代次数%k为迭代次数；x为牛顿迭代法的近似值；err为x1-x0的绝对值y(1)=x0;for k=1:nx=x1-feval('li6_5fun',x1)*(x1-x0)/(feval('li6_5fun',x1)-feval('li6_5fun',x0));err=abs(x-x1);x0=x1;x1=x;if(err<tol)|(y==0);break;endend必要编辑M文件li6_5.m,代码如下：function y=li6_5(x);y=x^3-3*x-1;复化梯形公式matlab:function t=tixing(f,a,b,n)h=(b-a)/n;sum=0;for k=0:n-1x=a+k*h;sum=sum+feval(f,x);endt=h/2*(feval(f,a)+feval(f,b)+2*sum);运行程序结果：>> format long>> tixing(inline('x./(x.^2+4)'),0,1,8)ans =0.111402354529548复化辛普森公式matlab:function y=xinpusen(f,a,b,n)h=(b-a)/n;sn=h/6*(feval(f,a)+feval(f,b));s=0;for i=0:n-1s=s+4*feval(f,a+h/2+i*h)+2*feval(f,a+i*h);endy=sn+h*s/6;运行结果：>> xinpusen(inline('x./(x.^2+4)'),0,1,8)ans =0.111571813252631改进欧拉法:function y=gjEuler(f,x0,y0,xn,N)%gjEuler.m函数为改进的欧拉法求微分方程的解%f为一阶常微分方程的一般表达式的右端函数%x0,y0为初始条件%xn为取值范围的一个端点%N为区间的个数%y为求解微分方程组的解x=zeros(1,N+1);y=zeros(1,N+1);x(1)=x0;y(1)=y0;h=(xn-x0)/N;for n=1:Nx(n+1)=x(n)+h;z0=y(n)+h*feval(f,x(n),y(n));y(n+1)=y(n)+h/2*(feval(f,x(n),y(n))+feval(f,x(n+1),z0));endT=[x',y']梯形法：function y=TXF(f,x0,y0,xn,N)%TXF.m函数为改进的梯形法求微分方程的解%f为一阶常微分方程的一般表达式的右端函数%x0,y0为初始条件%xn为取值范围的一个端点%N为区间的个数%y为求解微分方程组的解x=zeros(1,N+1);y=zeros(1,N+1);x(1)=x0;y(1)=y0;h=(xn-x0)/N;for n=1:Nx(n+1)=x(n)+h;y(n+1)=y(n)+h/2*(feval(f,x(n),y(n))+feval(f,x(n+1),y(n+1)));endT=[x',y']function y=LG4(f,x0,y0,xn,N)%LG4.m函数为四阶龙格库塔法求微分方程的解%f为一阶微分方程%x0,y0为左右端点%xn为给定的初始值%N为给定的迭代步长%y为求解微分方程组的解x=zeros(1,N+1);y=zeros(1,N+1);h=(y0-x0)/N;T=x0:h:y0;y(1)=xn;for n=1:Nk1=h*feval(f,T(n),y(n));k2=h*feval(f,T(n)+h/2,y(n)+k1/2);k3=h*feval(f,T(n)+h/2,y(n)+k2/2);k4=h*feval(f,T(n)+h,y(n)+k3);y(n+1)=y(n)+(k1+2*k2+2*k3+k4)/6;endR=[T',y']直接三角分解：function dxl=dxllu(a,b)format rat[n n] =size(a);RA=rank(a);if RA~=ndisp('请注意：因为A的n阶行列式hl等于零，所以A不能进行LU分解.A的秩RA如下:')RAhl=det(a)returnendif RA==nfor p=1:nh(p)=det(a(1:p, 1:p));endhl=h(1:n);for i=1:nif h(i)==0disp('请注意：因为A的r阶主子式等于零，所以A不能进行LU分解.A的秩RA 和各阶顺序主子式值hl依次如下：')hlRAreturnendenddisp('请注意：因为A的各阶主子式都不等于零，所以A能进行LU分解.A的秩RA和各阶顺序主子式值hl依次如下：')u(1,1:n)=a(1,1:n);l(2:n,1)=a(2:n,1)/u(1,1);for i=1:nl(i,i)=1;endfor k=2:nfor j=k:ns=0;for m=1:(k-1)s=s+l(k,m)*u(m,j);endu(k,j)=a(k,j)-s;endfor i=(k+1):ns=0;for m=1:(k-1)s=s+l(i,m)*u(m,k);endl(i,k)=(a(i,k)-s)/u(k,k);endendy(1)=b(1);for i=2:np=0;for k=1:i-1p=p+l(i,k)*y(k);endy(i)=b(i)-p;endx(n)=y(n)/u(n,n);for i=(n-1):(-1):1q=0;for k=i+1:nq=q+u(i,k)*x(k);endx(i)=(y(i)-q)/u(i,i);enddisp('各阶主子式:')hldisp('系数矩阵的秩:')RAdisp('单位下三角:') ldisp('上三角:')udisp('结果Y为:') ydisp('结果x为:') xend。

循环编程实战--迭代法专题

循环编程实战—迭代法专题※班级学号姓名※迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程，跟迭代法相对应的是直接法(或者称为一次解法)，即一次性解决问题。

迭代算法是用计算机解决问题的一种基本方法，它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令(或一定步骤)进行重复执行，在每次执行这组指令(或这些步骤)时，都从变量的原值推出它的一个新值，迭代法又分为精确迭代和近似迭代。

例1已知：A1=1, A2=1/(1+A1), A3=1/(1+A2), A4=1/(1+A3), ……, 求A50。

例2已知Fibonacci数列：1，1，2，3，5，8，……，它可由下面公式表述：F(1)=1，F(2)=1，F(n)=F(n-1)+F(n-2)。

试求F(45)值以及F(1) + F(2) + …… + f(45)的和。

例3 1/2 + 2/3 + 3/5 + 5/8 + ……的前30项的和。

解法1：分子和分母看成不同的数列tn2 = 1: tn1 = 2: bn2 = 2: bn1 = 3s = 1/2 + 2/3For i = 3 To 30tn = tn2 + tn1: bn = bn2 + bn1s = s + tn / bntn2 = tn1: bn2 = bn1: tn1 = tn: bn1 = bnNext i解法2：从第三项开始，分母是分子+前一项的分子。

tn2 = 1: tn1 = 2s = 1/2 + 2/3For i = 3 To 30tn = tn2 + tn1s = s + tn / (tn + tn1)tn2 = tn1: tn1 = tnNext i实战1.已知f(n) = f(n-1) + 2*f(n-2) – 5*f(n-3), f(0)=1, f(1)=2, f(2)=3,求f(0) + f(1) + …… + f(30)的总和sum以及f(0)到f(30)中最大值max。

牛顿迭代法c++代码

牛顿迭代法c 代码牛顿迭代法是求方程根的一种解法。

一、求一个数a的平方根，可以用迭代法无限逼近。

迭代法公式如下X2 = (x1+a/x1)/2• 1• 2• 3 S1，要先预估一个值x1，通常取x1=a/2;S2，带入迭代公式，得到x2；S3，计算x1 和 x2 的差的绝对值是否符合精确度；若符合则x2便是结果，若不符合进入S4；S4，x1 = x2，然后重复S2、S3，直到符合精确度。

以下是使用牛顿迭代法求解方程的C代码示例：c#include<stdio.h>#include<math.h>double f(double x) {return x*x - 2; // 要求解的方程，此处为 x^2 - 2}double df(double x) {return2*x; // 函数的导数，此处为 2x}double newton(double x0, double eps) {double x = x0;while (fabs(f(x)) > eps) {x = x - f(x) / df(x);}return x;}int main() {double x0 = 1.0; // 初始值double eps = 0.0001; // 精度要求double result = newton(x0, eps);printf("The solution of x^2 - 2 = 0 is %f\n", result);return0;}在这个例子中，我们要求解方程x2−2=0。

我们首先定义了两个函数 f 和df，分别表示方程和其导数。

然后我们定义了一个newton 函数，它接受一个初始值x0 和一个精度要求eps，并使用牛顿迭代法来求解方程。

最后，我们在main 函数中调用newton 函数来计算方程的解，并将结果打印出来。

不动点迭代法c语言

不动点迭代法c语言不动点迭代法是一种求解非线性方程的数值方法。

在这个过程中，通过迭代公式不断逼近方程的不动点（即方程的根）。

以下是一个使用C语言实现不动点迭代法的示例代码：```c#include <stdio.h>#include <math.h>// 定义迭代函数double iterate(double x){return (x - (x * x * x - 1) / (3 * x * x - 1));}// 计算不动点迭代法的迭代次数int iterations(double x0, double tol, double max_iter){int n = 0;double x = x0;double x_prev;do{x_prev = x;x = iterate(x);n++;} while (fabs(x - x_prev) > tol && n < max_iter);return n;}int main(){double x0, tol, max_iter;printf("请输入初始值x0、收敛容差tol和最大迭代次数max_iter：");scanf("%lf %lf %lf", &x0, &tol, &max_iter);int n = iterations(x0, tol, max_iter);printf("迭代次数：%d\n", n);printf("不动点近似值：%lf\n", x0);return 0;}```这个示例代码中，我们首先定义了迭代函数`iterate()`，它用于计算方程的迭代值。

然后，我们实现了`iterations()`函数，该函数计算不动点迭代法的迭代次数。

在`main()`函数中，我们获取用户输入的初始值、收敛容差和最大迭代次数，并调用`iterations()`函数求解不动点。