信号检测与估计理论(9)第九章 矩方法

第9章 矩估计方法
北京理工大学信息与电子学院 王菊
参数估计
若x1， … ， xn是样本的一个观测值。若统计量 g(X1， … ， Xn)可作为θ的一个估计，则
θˆ = g ( x1 ,
, x n )称为 θ 的估计值 ,
由于g(x1， … ， xn) 是实数域上的一个点， 现用它来估计θ， 故称这种估计为点估计。 矩估计法是一种点估计的经典方法。
2
( 2πσ )
1 2 2 1
的随机变量组成，其中 0 < ε < 1 为未知参数。
σ
2 1
,σ
2 2
已知。 混合参数
例2：高斯混合PDF
观测到的样本 x[n], n = 0,1,..., N − 1 是从高斯混合 PDF中得到的IID样本。
⎡ 1 x2[n] ⎤ ⎡ 1 x2[n] ⎤ ε p( x[n]; ε ) = exp ⎢− ( 2 )⎥ + exp ⎢− ( 2 )⎥ 1 1 2 2 ⎣ 2 σ1 ⎦ ( 2πσ 2 ) 2 ⎣ 2 σ2 ⎦ ( 2πσ1 ) 2 1− ε
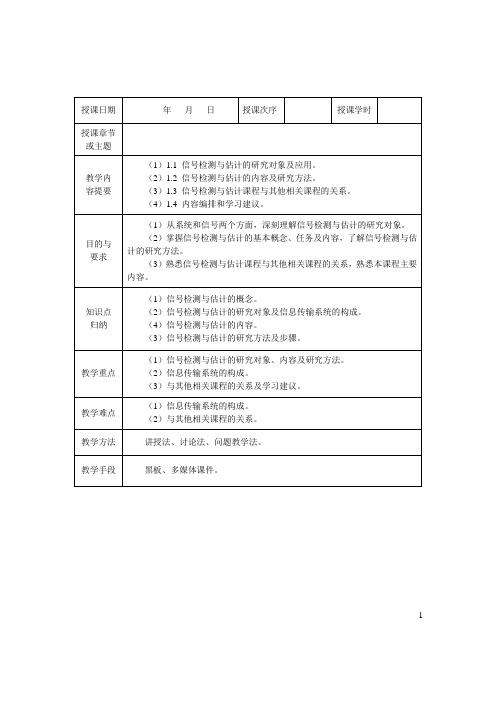
⎧ λ exp(−λ x[n]) p ( x[n]; λ ) = ⎨ ⎩0
估计参量 λ ，其中 λ > 0 。
x[n] > 0 x[n] < 0
例3：指数PDF
一阶矩为
μ
1
= E ( x[n ]) =
∫
∞ 0
x [ n ]λ e x p ( − λ x [ n ] )d x [ n ] = 1
(令 ξ = λ x[n ]), μ
1
λ
∫
∞ 0
ξ e x p ( − ξ )d ξ =
1
λ
λ＝ λˆ ＝
1
μ
1 N
1
1
∑
N −1
x[n ]
n = 0
矢量参数的矩方法
对p个未知参数，需要p阶理论矩方程 μ1 = h1 (θ1 , θ 2 ,...,θ p )
μ 2 = h2 (θ1 , θ 2 ,..., θ p ) μ p = hp (θ1 , θ 2 ,..., θ p )
上述方程将未知参数 ε 与二阶矩联系起来。
例2：高斯混合PDF
如果用估计量
1 N
1 N
∑
N −1 n=0
x 2 [ n ] 来代替 E ( x 2 [ n ]) ，则有
∑
N −1 n=0
2 x 2 [ n ] = (1 − ε )σ 12 + εσ 2
解出 ε ，得到矩方法的估计量为
εˆ =
1 N
矩估计法
1 n l 因为样本矩 Al = ∑ X i 依概率收敛于相应的 n i =1 总体矩 μl ( l = 1, 2, , k ),
用样本矩来估计总体矩,用样本矩的连 续函数来估计总体矩的连续函数,这种估计 法称为矩估计法.
例
X ~ N ( μ ,σ 2 ), μ , σ 2 未知, 即得 μ ,σ 2 的矩估计量 1 n 2 σ = ∑ ( X i − X )2 . ˆ μ = X, ˆ 一般地, n i =1 1 n 用样本均值 X = ∑ X i 作为总体 X的均值的矩估计 , n i =1 1 n 2 用样本二阶中心矩 B2 = ∑ ( X i − X ) 作为总体 n i =1
2 1 2 2
例4：高斯混合PDF
有三个未知参数，需要三个矩方程。
μ 2 = E ( x [n]) = (1 − ε )σ + εσ
2 2 1 4 4 1 6 6 1
2 2 4 2 6 2
μ 4 = E ( x [n]) = 3(1 − ε )σ + 3εσ
μ6 = E ( x [ n]) = 15(1 − ε )σ + 15εσ
, θ k 的函数 , 即
μl = E ( X ) = ∫ x l f ( x;θ1 ,θ 2 , ,θ k )dx
l −∞
+∞
(X为连续型)
或 μl = E ( X l ) =
x∈RX
x l p( x;θ1 ,θ 2 , ∑
,θ k ), (X为离散型)
, l = 1,2 , ,k
其中 R X 是 x 可能取值的范围
例4：高斯混合PDF
方程组是非线性的，然而通过令
2 u = σ12 + σ 2 2 v = σ12σ 2
可得
u6 − 5u4u2 u= 2 5u4 −15u2
σ σ
2 1 2 2
u4 v = u2u − 3
u +
2 1
进一步可得
=
u 2 − 4v 2
= v /σ
u 2 − σ 12 ε = σ 22 − σ 12
X的方差的矩估计 .
矩估计法的具体步骤
k 假定第k阶矩 μk = E( x [n]) 与未知参数的关系为
μ k = h (θ )
假定
h − 1 (θ ) 存在，求解 θ
为
θ = h −1 ( μ k )
然后将它的估计量代替理论上（总体）的矩，
μ
k
1 = N
∑
N −1
x k [n ]
n=0
得到矩方法的估计量 θ = h −1 ( 1 ˆ N
矩
1. 设X是随机变量，若 E ( X k ) k = 1, 2, 存在， 称它为X的k 阶(原点)矩，简称k 阶矩。 2. 样本 k 阶矩
1 n Ak = ∑ X ik , k = 1 , 2 , n i =1
;
矩
若 X1 , X 2 , , X n 为来自 X 的样本，
假设总体 X 的前 k 阶矩存在,且均为 θ 1 , θ 2 ,
用矩阵形式表示为
μ = h(θ)
θ = h -1 (μ)
假定 h − 1 存在，求解 θ 为
1 然后将它的估计量代替理论上的矩，即 μ k = N
∑
N −1x k [n] Nhomakorabean=0得到矩方法的估计量
ˆ ˆ θ = h -1 (μ)
例4：高斯混合PDF
设噪声过程由IID的零均值、PDF为
p ( w[ n]) = 1− ε
x k [ n]) ∑
n=0
N −1
矩估计法关键点：
用样本矩作为总体同阶矩的估计，即
1 n 若 α k = E ( X k ), 则 α k = ∑ X ik . n i =1 若 β k = E ⎡ X − E ( X )⎤ ⎣ ⎦
{
k
}
1 n ,则βk = ∑ ( X i − X n i =1
例2：高斯混合PDF
这时，常用的MVU方法不能使用；使用MLE方 法则需解决一个非线性函数取最大值的问题，可 以通过网格搜索方法来实现。 但是如使用矩方法则可以提供一个非常简单的 估计量！
例2：高斯混合PDF
⎡ ⎤ 2 2 ∞ ⎡ 1 w [n] ⎤ ⎡ 1 w [n] ⎤ ⎥ ε ⎢ 1− ε 2 2 exp ⎢− ( 2 )⎥ + exp ⎢− ( 2 )⎥ ⎥dx[n] E( x [n]) = ∫ x [n] ⎢ 1 1 −∞ ⎣ 2 σ1 ⎦ ( 2πσ 2 ) 2 ⎣ 2 σ 2 ⎦⎥ ⎢ ( 2πσ12 ) 2 2 ⎣ ⎦ 2 = (1 − ε )σ12 + εσ 2
∑
N −1
x
2 2
2
[ n ] −σ
2 1
n = 0
2 1
σ
− σ
此估计量是无偏的。
例2：高斯混合PDF
εˆ
的方差可以求得为
1 1 var(εˆ ) = var( 2 2 2 (σ 2 − σ 1 ) N
∑x
n=0
N −1
2
[ n ])
1 2 var( x [ n ]) = 2 2 2 N (σ 2 − σ 1 ) 1 [ E ( x 4 [ n ]) − E 2 ( x 2 [ n ])] = 2 N (σ 2 − σ 12 ) 2
估计量的统计评价
矩方法中，无法预先知道估计量性能的好 坏。 可以利用近似的均值和近似方差进行评 价。（利用统计的线性化方法得到）
)
k
例1
设总体 X 在[a , b]上服从均匀分布 , 其中 a , b 未知, ( X 1 , X 2 , b 的估计量 . , X n ) 是来自总体 X的样本 , 求a ,
求解:
a+b 1 E( X ) = D( X ) = ( b − a ) 2 12 2
⎧a = E ( X ) − 3D( X ) ≡ μ − 3σ 2 ⎪ ∴⎨ 2 ⎪b = E ( X ) + 3D( X ) ≡ μ + 3σ ⎩
( 2πσ )
1 2 2 1
⎡ 1 w2 [ n] ⎤ ⎡ 1 w2 [ n] ⎤ ε exp ⎢ − ( 2 ) ⎥ + exp ⎢ − ( 2 ) ⎥ 1 ⎣ 2 σ 1 ⎦ ( 2πσ 2 ) 2 ⎣ 2 σ2 ⎦
2
的随机变量组成，其中未知参数为混合 参数 0 < ε < 1 以及 σ , σ 。
求解:
由:
μ=X
∧
1 n σ = ∑ ( X i − X )2 n i =1
∧ 2
⎧∧ ⎪a = X − ⎪ ∴ ⎨ ∧ ⎪b = X + ⎪ ⎩
3 n 3 n
∑ ∑
n
n
(X (X
i=1
i
− X )2 − X )2
i=1
i
例2：高斯混合PDF
设噪声过程由IID的零均值、PDF为
p( w[n]) = 1− ε ⎡ 1 w2 [ n ] ⎤ ⎡ 1 w2 [ n ] ⎤ ε exp ⎢ − ( 2 ) ⎥ + exp ⎢ − ( 2 ) ⎥ 1 ⎣ 2 σ 1 ⎦ ( 2πσ 2 ) 2 ⎣ 2 σ2 ⎦