2014-2015上高二文数期末质检评分标准(B卷)
黑龙江省哈三中2014-2015学年度高二上学期期末考试语文试卷扫描版含答案

2014年黑龙江省学业水平考试语文答案1. B(偷换概念,“承担着对本家族成员的社会保障功能”的是“家族组织”)2. A(理解不当,“社会主义核心价值观是现阶段全国人民价值观的最大公约数”,“两者互为补充,各有侧重”错误)3. B(递进反了)4. C (第:宅第,家)5. A(今天命已定,谁复敢有异心,陛下何为出此言耶?)6. D (威武郡王是石守信死后追封的,活着的时候并没有得到这个封号)7.(1)(6分)人生(短暂),如同白驹过隙(或译为:光阴易逝),不如多积攒些金子,多买些田产和房子来留给子孙。
让歌童唱歌,让舞女跳舞来终了余生。
(市:买;1分。
遗:馈赠,赠予,1分。
歌:让……唱歌;1分。
舞:让……跳舞;1分。
句意2分)(2)(4分)陛下想到这些,(真是)所说的使死去的活了过来,使骨头上长出了肉。
(生:使……活;1分。
肉:使……长肉;1分。
句意2分)8.前四句表达了作者的离愁别绪。
(2分)一、二句写离别的时间、地点,“秋”“夜”体现出悲凉的意味,为全曲定下情感基调。
(2分)三、四句用永无中止的江潮、重叠连绵的山峦等表现作者汹涌澎湃却无法排遣的离愁别绪。
(2分)9.①寓情于景,哀景抒哀情。
(1分)通过写寒雁的到来、芙蓉花的凋谢、秋雨的清冷和油灯的昏黄,表现了作者悲凉的情怀。
(2分)②渲染烘托。
(1分)用“冷雨”“青灯”烘托出秋夜书斋的凄清冷寂。
(1分)(答其他手法言之成理亦可得分)【译文】钱塘江边,吴山脚下,正值清秋之夜。
离愁随江奔涌去,别恨似吴山重重叠叠。
北雁南来,荷花凋谢。
清冷的秋雨,灯盏的青光,更增添了书斋的凄凉、寂寞,怕离别却又这么早就离别。
今晚且图一醉,既然明朝终将离去,还是忍耐一些。
【鉴赏】“浙江秋,吴山夜”,清秋的美景被作者剪裁入曲,别有一番滋味。
“愁随潮去,恨与山叠”,愁,如钱塘之潮,恨,似吴山之峰,重重叠叠。
潮去,极具汹涌之感;山叠,极写沉重之感。
这一动一静,便状出了心头汹涌澎湃却无法排遣的愁恨,极为警策。
潮州市2014-2015学年上学期期末考试高二语文试卷扫瞄版分解

潮州市2014~2015学年度第一学期期末高二级教学质量检测语文参考答案及评分标准一、1.C(A yǎn shūzhì/shí B gēng/gèn wùyǒu C líu/mìu niè/shèruì/nèD pípiāo xiān/qiàn)(3分)2.A(乏善可陈:表示一件事物没有什么优点可以提出来称道,用此成语,表示不太满意,而这里指的是数量的缺少。
相得益彰:互相配合和补充更能显出长处,发挥作用。
任重道远:担子重,路途远,比喻肩负需经历长期奋斗的重任。
耕耘:比喻辛勤地从事研究,创作等工作。
)(3分)3.B( A“获得了观众的一致喜爱是毋庸置疑的”结构混乱;C“选出”和“行为”搭配不当,“列车”做“行为”的定语不当,最后一句无明确主语;D介词“自……以来”误用导致主语缺失) (3分)4. C(解析:本题主要考查语言表达连贯的能力。
答题时要善于根据所给句子的语体特点来组合句子。
此题所给的写景的描述性文字,既有时间上的先后顺序,写景上又有空间的层次感,依照先时间顺序,再空间顺序及句间关系就可选出答案C)(3分)二、5.A(披:拨开,用手分开。
)6. C (以:连词,同“而”;“且”不能与下句形成对应。
“坐”“眺”之间应是因果关系,所以应选择“因”。
“心”与“万化”不能用“则”。
)7. D8. B(第一段,概括描写平日一般游览情况,为具体描写西山宴游作对比。
不是“对比”,而是“陪衬”)9.(1)①我认为凡是这个州有奇特形状的山,都被我游览过了。
(“以为”1分,“定语后置”1分,“有”:被拥有1分,大意1分)②(游过西山)之后才知我以前不曾真正游赏过,真正的游赏是从这里开始的。
(“向”,“始”各1分;大意1分)(2)①观景方面,作者领略了西山的“高下之势”,“萦青缭白,外与天际,四望如一”的高峻特立,欣赏到了难得一见的美景。
—度第二学期期末考试高二语文参考答案及评分标准

2014—2015学年度第二学期期末考试高二语文试题参考答案及评分标准一、(9分)1.A(A项中“进而在摹仿中提高诗歌创作水平”错误,文中强调“我们今天学习唐诗,当然就更不是要去摹仿唐诗)2.B(B项说法夸大其词。
“唐代以后的诗歌都只知摹仿,陈陈相因,了无生气”与事实不符。
文中所说的“只知摹仿,陈陈相因,了无生气”指的是朱彝尊对明诗的批评,并不能代表唐代以后的所有诗歌)3.C(C项中唐诗“明白易懂、一览无余”的理解错误,文中“明白易懂自然更不等于一览无余,一览无余又怎能百读不厌呢?”“唐诗中有一些人人传诵的名篇,其间的诗歌语言就不一定都那么明白易懂”等文字说明唐诗尽管在语言艺术上达到了深入浅出的高度,但并不“明白易懂、一览无余”)二、(36分)(一)(19分)4.A 逾:超过,越过。
(3分)5.C (3分)6.B “始终赞同皇帝看法”不准确。
应是“为皇帝提出中肯的意见”。
(3分)7.(10分)(1)(5分)皇帝责问翟銮,翟銮就叩头谢罪说:“陛下圣明,我要顺从还来不及,(哪里)有什么建议呢。
”(译出大意给2分;“诘”“谢”“不暇”“何……之有”,每译对一处给1分。
)(2)(5分)事毕之后,翟銮归来时的行装装了千辆车,用这些财物赠送权贵,得以再次执掌政事,他的声誉立刻就衰落了。
(译出大意给2分;“竣”“遗”“柄政”三处,每译对一处给1分。
)(二)(11分)8.①动静结合,“雁飞”是动景,“白雪”是静景,动静结合,写出了边地特有的大雪铺地、雁群南飞的景象,含蓄地传达出痛苦无奈之情。
②视听结合,“雁飞”“白草”“雪”“黄榆”是目中所见,“笳”声是耳中所闻,调动视觉听觉,渲染了悲凉的氛围,给人身临其境之感。
③色彩点染(或色彩渲染),“白”“黄”的色彩点染,写出了边地景色的苍凉凄清。
注:任选其中两点即可,对一点得3 分,共6 分。
9.“空”,徒然、白白地,写出因为边城苦寒,五月还未见花开,因而妻子给自己寄来的春衣,白白空放在那里穿不着。
河南省郑州市2014-2015学年高二数学上学期期末试卷 文(含解析)

河南省郑州市2014-2015学年高二上学期期末数学试卷(文科)一、选择题(共12小题,每小题5分,满分60分)1.(5分)抛物线x2=2y的焦点坐标是()A.B.C.(1,0)D.(0,1)2.(5分)设a,b∈R,则a>b是(a﹣b)b2>0的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.(5分)不等式x2+2014x﹣2015>0的解集为()A.{x|﹣2015<x<1} B.{x|x>1或x<﹣2015}C.{x|﹣1<x<2015} D.{x|x<﹣1或x>2015}4.(5分)等差数列{a n}的前n项和为S n,且S3=6,a3=0,则公差d等于()A.﹣1 B.1 C.2 D.﹣25.(5分)如图所示,为了测量某障碍物两侧A,B间的距离,给定下列四组数据,不能确定A,B间距离的是()A.α,a,b B.α,β,a C.a,b,γD.α,β,b6.(5分)下列关于星星的图案构成一个数列,该数列的一个通项公式是()A.a n=n2﹣n+1 B.a n=C.a n=D.a n=7.(5分)设变量x,y满足约束条件:,则目标函数z=2x+3y的最小值为()A.6 B.7 C.8 D.238.(5分)已知a>0,b>0,且2是2a与b的等差中项,则的最小值为()A.B.C.2 D.49.(5分)已知点(2,1)和(﹣1,3)在直线3x﹣2y+a=0的两侧,则a的取值范围是()A.﹣4<a<9 B.﹣9<a<4 C.a<﹣4或a>9 D.a<﹣9或a>410.(5分)已知各项为正的等比数列{a n}中,a4与a14的等比中项为,则2a7+a11的最小值为()A.16 B.8 C.D.411.(5分)已知f(x)=x2+2xf′(1),则f′(0)等于()A.0 B.﹣2 C.﹣4 D.212.(5分)已知方程=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是()A.sinα=﹣αcosβB.sinα=αcosβC.cosα=βsinβD.sinβ=βsinα二、填空题(共4小题,每小题5分,满分20分)13.(5分)命题“∃x<0,有x2>0”的否定是.14.(5分)若2、a、b、c、9成等差数列,则c﹣a=.15.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,若sinA=sinC,B=30°,b=2,则边c=.16.(5分)现有甲、乙两人相约到登封爬嵩山,若甲上山的速度为v1,下山的速度为v2(v1≠v2),乙上山和下山的速度都是(甲、乙两人中途不停歇且下山时按原路返回),则甲、乙两人上下山所用的时间t1、t2的大小关系为.三、解答题(共6小题,满分70分)17.(10分)设等差数列{a n}满足a3=5,a10=﹣9.(Ⅰ)求{a n}的通项公式;(Ⅱ)求{a n}的前n项和S n的最大值.18.(12分)命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立.命题q:抛物线y2=4ax 的焦点在(1,0)的左侧,若p或q为真命题,p且q为假命题,求实数a的取值范围.19.(12分)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且b=2csinB(1)求角C的大小;(2)若c2=(a﹣b)2+6,求△ABC的面积.20.(12分)汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.某市的一条道路在一个限速为40km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相撞了.事后现场勘查测得甲车刹车距离刚好12m,乙车刹车距离略超过10m.又知甲、乙两种车型的刹车距离 S(m)与车速x(km/h)之间分别有如下关系:S甲=0.1x+0.01x2,S乙=0.05x+0.005x2.问:甲、乙两车有无超速现象?21.(12分)已知函数f(x)=e x﹣2x(e为自然对数的底数)(1)求函数f(x)的单调区间(2)若存在使不等式f(x)<mx成立,求实数m的取值范围.22.(12分)已知圆C:x2+y2=3的半径等于椭圆E:+=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x﹣的距离为﹣,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).(Ⅰ)求椭圆E的方程;(Ⅱ)求证:|AF|﹣|BF|=|BM|﹣|AM|.河南省郑州市2014-2015学年高二上学期期末数学试卷(文科)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)抛物线x2=2y的焦点坐标是()A.B.C.(1,0)D.(0,1)考点:抛物线的简单性质.专题:计算题.分析:根据抛物线的定义可得,x2=2py(p>0)的焦点坐标(0,)可直接求解解答:解:根据抛物线的定义可得,x2=2y的焦点坐标(0,)故选B.点评:本题主要考查了抛物线的简单的性质,属于基础试题.2.(5分)设a,b∈R,则a>b是(a﹣b)b2>0的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:规律型.分析:结合不等式的性质,利用充分条件和必要条件的定义进行判断.解答:解:当a>b,b=0时,不等式(a﹣b)b2>0不成立.若(a﹣b)b2>0,则b≠0,且a﹣b>0,∴a>b成立.即a>b是(a﹣b)b2>0的必要不充分条件.故选:B.点评:本题主要考查充分条件和必要条件的判断,利用不等式的性质是解决本题的关键,比较基础.3.(5分)不等式x2+2014x﹣2015>0的解集为()A.{x|﹣2015<x<1} B.{x|x>1或x<﹣2015}C.{x|﹣1<x<2015} D.{x|x<﹣1或x>2015}考点:一元二次不等式的解法.专题:不等式的解法及应用.分析:把不等式化为(x+2015)(x﹣1)>0,求出解集即可.解答:解:不等式x2+2014x﹣2015>0可化为(x+2015)(x﹣1)>0,解得x<﹣2015或x>1;∴不等式的解集为{x|x>1或x<﹣2015}.故选:B.点评:本题考查了一元二次不等式的解法与应用问题,是基础题目.4.(5分)等差数列{a n}的前n项和为S n,且S3=6,a3=0,则公差d等于()A.﹣1 B.1 C.2 D.﹣2考点:等差数列的前n项和.专题:等差数列与等比数列.分析:由题意结合等差数列的性质和求和公式可得a2的值,进而可得公差d.解答:解:∵等差数列{a n}的前n项和为S n,且S3=6,a3=0,∴S3=a1+a2+a3=3a2=6,∴a2=2,∴公差d=a3﹣a2=0﹣2=﹣2故选:D点评:本题考查等差数列的求和公式和通项公式,属基础题.5.(5分)如图所示,为了测量某障碍物两侧A,B间的距离,给定下列四组数据,不能确定A,B间距离的是()A.α,a,b B.α,β,a C.a,b,γD.α,β,b考点:解三角形的实际应用.专题:应用题;解三角形.分析:给定α,a,b,由正弦定理,β不唯一确定,故不能确定A,B间距离.解答:解:给定α,a,b,由正弦定理,β不唯一确定,故不能确定A,B间距离.故选:A.点评:本题考查解三角形的实际应用,考查学生的计算能力,比较基础.6.(5分)下列关于星星的图案构成一个数列,该数列的一个通项公式是()A.a n=n2﹣n+1 B.a n=C.a n=D.a n=考点:数列递推式.专题:规律型.分析:由图中所给的星星个数:1,1+2,1+2+3,…,1+2+3+…+n;得出数列第n项,即通项公式.解答:解析:从图中可观察星星的构成规律,n=1时,有1个;n=2时,有3个;n=3时,有6个;n=4时,有10个;∴a n=1+2+3+4+…+n=.答案:C点评:这是一个简单的自然数求和公式,由观察得出猜想,一般不需要证明.考查学生的观察猜想能力.7.(5分)设变量x,y满足约束条件:,则目标函数z=2x+3y的最小值为()A.6 B.7 C.8 D.23考点:简单线性规划的应用.专题:不等式的解法及应用.分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件.画出满足约束条件的可行域,再用角点法,求出目标函数的最小值.解答:解:画出不等式.表示的可行域,如图,让目标函数表示直线在可行域上平移,知在点B自目标函数取到最小值,解方程组得(2,1),所以z min=4+3=7,故选B.点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.8.(5分)已知a>0,b>0,且2是2a与b的等差中项,则的最小值为()A.B.C.2 D.4考点:基本不等式;等差数列.专题:不等式的解法及应用.分析:利用等差中项及基本不等式的性质即可求出答案.解答:解:∵2是2a与b的等差中项,∴2a+b=4,又∵a>0,b>0,∴=,当且仅当2a=b=2,即a=1,b=2时取等号,∴.故选B.点评:充分理解基本不等式及其变形是解题的关键.9.(5分)已知点(2,1)和(﹣1,3)在直线3x﹣2y+a=0的两侧,则a的取值范围是()A.﹣4<a<9 B.﹣9<a<4 C.a<﹣4或a>9 D.a<﹣9或a>4考点:直线的斜率.专题:直线与圆.分析:由点(2,1)和(﹣1,3)在直线3x﹣2y+a=0的两侧,把两点的坐标代入3x﹣2y+a 所得的值异号,由此列不等式求得a的范围.解答:解:∵点(2,1)和(﹣1,3)在直线3x﹣2y+a=0的两侧,∴(3×2﹣2×1+a)(﹣1×3﹣2×3+a)<0,即(a+4)(a﹣9)<0.解得﹣4<a<9.故选:A.点评:本题考查了简单的线性规划,考查了二元一次不等式所表示的平面区域,是基础题.10.(5分)已知各项为正的等比数列{a n}中,a4与a14的等比中项为,则2a7+a11的最小值为()A.16 B.8 C.D.4考点:等比数列的通项公式.专题:计算题;等差数列与等比数列.分析:由各项为正的等比数列{a n}中,a4与a14的等比中项为,知a4•a14=(2)2=8,故a7•a11=8,利用均值不等式能够求出2a7+a11的最小值.解答:解:∵各项为正的等比数列{a n}中,a4与a14的等比中项为,∴a4•a14=(2)2=8,∴a7•a11=8,∵a7>0,a11>0,∴2a 7+a11≥2=2=8.故选B.点评:本题考查等比数列的通项公式的应用,是中档题.解题时要认真审题,仔细解答.11.(5分)已知f(x)=x2+2xf′(1),则f′(0)等于()A.0 B.﹣2 C.﹣4 D.2考点:导数的运算.专题:导数的概念及应用.分析:把给出的函数求导得其导函数,在导函数解析式中取x=1可求2f′(1)的值.解答:解:由f(x)=x2+2xf′(1),得:f′(x)=2x+2f′(1),取x=1得:f′(1)=2×1+2f′(1),所以,f′(1)=﹣2.所以f′(x)=2x﹣4故f′(0)=2f′(1)=﹣4,故选:C.点评:本题考查了导数运算,解答此题的关键是理解原函数解析式中的f′(1),在这里f′(1)只是一个常数,此题是基础题.12.(5分)已知方程=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是()A.sinα=﹣αcosβB.sinα=αcosβC.cosα=βsinβD.sinβ=βsinα考点:根的存在性及根的个数判断.专题:计算题;作图题;函数的性质及应用;导数的综合应用.分析:由题意,方程=k可化为|sinx|=kx,作函数y=|sinx|与y=kx的图象,从而可求得y′|x=β=﹣cosβ,即k=﹣cosβ,从而可得=﹣cosβ,化简即可.解答:解:在(0,+∞)上,方程=k可化为|sinx|=kx,作函数y=|sinx|与y=kx的图象如下,在x=β时,==k,又∵在x=β处直线与y=|sinx|相切,∴y′|x=β=﹣cosβ,故k=﹣cosβ,则=﹣cosβ,即sinα=﹣αcosβ;故选A.点评:本题考查了导数的几何意义的应用及方程的根与函数图象的关系应用,同时考查了数形结合的思想应用,属于中档题.二、填空题(共4小题,每小题5分,满分20分)13.(5分)命题“∃x<0,有x2>0”的否定是∀x<0,有x2≤0.考点:命题的否定.分析:对特称命题的否定是一个全称命题,对一个全称命题的否定是全称命题,即:对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”;对命题“∀x∈A,P(X)”的否定是:“∃x∈A,¬P(X)”,由此不难得到对命题“∃x<0,有x2>0”的否定.解答:解:∵对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”∴对命题“∃x<0,有x2>0”的否定是“∀x<0,有x2≤0”故答案为:∀x<0,有x2≤0点评:对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”;对命题“∀x∈A,P(X)”的否定是:“∃x∈A,¬P(X)”,即对特称命题的否定是一个全称命题,对一个全称命题的否定是全称命题14.(5分)若2、a、b、c、9成等差数列,则c﹣a=.考点:等差数列的性质.专题:等差数列与等比数列.分析:由等差数列的性质可得2b=2+9,解之可得b值,再由等差中项可得a,c的值,作差即可得答案.解答:解:由等差数列的性质可得2b=2+9,解得b=,又可得2a=2+b=2+=,解之可得a=,同理可得2c=9+=,解得c=,故c﹣a=﹣==故答案为:点评:本题考查等差数列的性质和通项公式,属基础题.15.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,若sinA=sinC,B=30°,b=2,则边c=2.考点:正弦定理;余弦定理.专题:解三角形.分析:在△ABC中,由正弦定理求得a=c,结合余弦定理,即可求出c的值解答:解:∵在△ABC中,sinA=sinC∴a= c又∵B=30°,由余弦定理,可得:cosB=cos30°===解得c=2故答案为:2.点评:本题考查的知识点是正弦定理和余弦定理,熟练掌握定理是解题的关键,属于中档题.16.(5分)现有甲、乙两人相约到登封爬嵩山,若甲上山的速度为v1,下山的速度为v2(v1≠v2),乙上山和下山的速度都是(甲、乙两人中途不停歇且下山时按原路返回),则甲、乙两人上下山所用的时间t1、t2的大小关系为t1>t2.考点:有理数指数幂的化简求值.专题:计算题;函数的性质及应用.分析:由题意,甲用的时间t1=+=S;乙用的时间t2=2×=;从而作差比较大小即可.解答:解:由题意知,甲用的时间t1=+=S•;乙用的时间t2=2×=;∴t1﹣t2=S﹣=S(﹣)=S>0;故t1>t2;故答案为:t1>t2.点评:本题考查了有理指数幂的化简求值,属于基础题.三、解答题(共6小题,满分70分)17.(10分)设等差数列{a n}满足a3=5,a10=﹣9.(Ⅰ)求{a n}的通项公式;(Ⅱ)求{a n}的前n项和S n的最大值.考点:等差数列的前n项和;等差数列的通项公式.专题:计算题;等差数列与等比数列.分析:(Ⅰ)运用等差数列的通项公式,列出方程,解得首项和公差,即可得到通项公式;(Ⅱ)运用前n项和的公式,配方,结合二次函数的最值,即可得到.解答:解:(Ⅰ)由a n=a1+(n﹣1)d,及a3=5,a10=﹣9得,,解得,数列{a n}的通项公式为a n=11﹣2n.(Ⅱ)由(1)知.因为.所以n=5时,S n取得最大值25.点评:本题考查等差数列的通项公式和前n项和公式的运用,考查解方程组和二次函数的最值的求法,属于基础题.18.(12分)命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立.命题q:抛物线y2=4ax 的焦点在(1,0)的左侧,若p或q为真命题,p且q为假命题,求实数a的取值范围.考点:复合命题的真假.专题:计算题;简易逻辑.分析:先分别求出p,q为真时实数a的取值范围,再由p或q为真,p且q为假,可知p 和q一真一假,从而解得.解答:解:设g(x)=x2+2ax+4,由于关于x的不等式x2+2ax+4>0对一切x∈R恒成立,故△=4a2﹣16<0,∴﹣2<a<2.又∵抛物线y2=4ax的焦点在(1,0)的左侧,∴a<1.a≠0.又由于p或q为真,p且q为假,可知p和q一真一假.(1)若p真q假,则∴1≤a<2;或a=0.(2)若p假q真,则∴a≤﹣2.综上可知,所求实数a的取值范围为1≤a<2,或a≤﹣2.或a=0.点评:本题考查了复合命题的真假性的应用,属于基础题.19.(12分)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且b=2csinB(1)求角C的大小;(2)若c2=(a﹣b)2+6,求△ABC的面积.考点:余弦定理;正弦定理.专题:解三角形.分析:(1)已知等式利用正弦定理化简,根据sinB不为0求出sinC的值,由C为锐角求出C的度数即可;(2)利用余弦定理列出关系式,把cosC的值代入并利用完全平方公式变形,结合已知等式求出ab的值,再由sinC的值,利用三角形面积公式求出三角形ABC面积即可.解答:解:(1)由正弦定理==,及b=2csinB,得:sinB=2sinCsinB,∵sinB≠0,∴sinC=,∵C为锐角,∴C=60°;(2)由余弦定理得:c2=a2+b2﹣2abcosC=a2+b2﹣ab=(a﹣b)2+ab,∵c2=(a﹣b)2+6,∴ab=6,则S△ABC=absinC=.点评:此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.20.(12分)汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.某市的一条道路在一个限速为40km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相撞了.事后现场勘查测得甲车刹车距离刚好12m,乙车刹车距离略超过10m.又知甲、乙两种车型的刹车距离 S(m)与车速x(km/h)之间分别有如下关系:S甲=0.1x+0.01x2,S乙=0.05x+0.005x2.问:甲、乙两车有无超速现象?考点:函数模型的选择与应用.专题:函数的性质及应用.分析:由题意列出不等式组,分别求解两种车型的事发前的车速,判断它们是不是超速行驶,即可得到结论.解答:解:由题意知,对于甲车,有0.1x+0.01x2=12.即x2+10x﹣1200=0,…(2分)解得x=30或x=﹣40(x=﹣40不符合实际意义,舍去).…(4分)这表明甲车的车速为30km/h.甲车车速不会超过限速40km/h.…(6分)对于乙车,有0.05x+0.005x2>10,即x2+10x﹣2000>0,…(8分)解得x>40或x<﹣50(x<﹣50不符合实际意义,舍去).…(10分)这表明乙车的车速超过40km/h,超过规定限速.…(12分)点评:本题的考点是函数模型的选择与应用,考查不等式模型的构建,考查利用数学知识解决实际问题.解题的关键是利用函数关系式构建不等式.21.(12分)已知函数f(x)=e x﹣2x(e为自然对数的底数)(1)求函数f(x)的单调区间(2)若存在使不等式f(x)<mx成立,求实数m的取值范围.考点:利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(Ⅰ)先求出函数的导数,令f′(x)=0,解得x=ln2,从而求出函数的单调区间;(Ⅱ)问题转化为求的最小值.令,通过求导得到函数g(x)的最小值,从而求出m的范围.解答:解:(Ⅰ)f′(x)=e x﹣2,令f′(x)=0,即e x﹣2=0,解得x=ln2,x∈(﹣∞,ln2)时,f′(x)<0,x∈(ln2,+∞)时,f′(x)>0,∴f(x)的单调递减区间为(﹣∞,ln2),单调递增区间为(ln2,+∞).(Ⅱ)由题意知使f(x)<mx成立,即使成立;所以的最小值.令,,所以g(x)在上单调递减,在上单调递增,则g(x)min=g(1)=e﹣2,所以m∈(e﹣2,+∞).点评:本题考查了函数的单调性,函数的最值问题,考查了导数的应用,考查转化思想,是一道中档题.22.(12分)已知圆C:x2+y2=3的半径等于椭圆E:+=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x﹣的距离为﹣,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).(Ⅰ)求椭圆E的方程;(Ⅱ)求证:|AF|﹣|BF|=|BM|﹣|AM|.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(Ⅰ)设点F(c,0)(c>0),由已知条件得,圆C的半径等于椭圆E的短半轴长,由此能求出椭圆方程.(Ⅱ)由圆心O到直线l的距离为,得,由已知条件推导出|AF|+|AM|=2,|BF|+|BM|=2,由此能证明|AF|﹣|BF|=|BM|﹣|AM|.解答:(Ⅰ)解:设点F(c,0)(c>0),则F到直线l的距离为,即,…(2分)因为F在圆C内,所以,故c=1;…(4分)因为圆C的半径等于椭圆E的短半轴长,所以b2=3,椭圆方程为.…(6分)(Ⅱ)证明:因为圆心O到直线l的距离为,所以直线l与圆C相切,M是切点,故△AOM为直角三角形,所以,又,得,…(7分),又,得,…(9分)所以|AF|+|AM|=2,同理可得|BF|+|BM|=2,…(11分)所以|AF|+|AM|=|BF|+|BM|,即|AF|﹣|BF|=|BM|﹣|AM|.…(12分)点评:本题考查椭圆方程的求法,考查两组线段差相等的证明,解题时要认真审题,注意点到直线的距离公式的合理运用.。
___2014-2015学年高二上学期期末考试 数学文 Word版含答案

___2014-2015学年高二上学期期末考试数学文 Word版含答案合肥一六八中学高二年级2014-2015学年第一学期期末考试数学试卷(文科)满分150分,时间120分钟一、选择题1.椭圆$\frac{x^2}{169}+\frac{y^2}{x^2}=1$的焦距为()。
A。
10 B。
5 C。
7 D。
272.已知A,B,C,D是空间四点,命题p:A,B,C,D四点不共面,命题q:直线AB和CD不相交,则p是q的()。
A。
充分不必要条件B。
必要不充分条件C。
充要条件D。
既不充分也不必要条件3.平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为()。
A。
3 B。
4 C。
5 D。
64.直线$y=kx+1$与曲线$y=x+ax+b$相切于点A(1,3),则$2a+b$的值为()。
A。
2 B。
-1 C。
1 D。
-25.已知命题p:$\exists x\in R,x-ax+1\leq 0$为假命题,则a 的取值范围为()。
A。
(-2,2) B。
[-2,2] C。
(-∞,-2)∪(2,+∞) D。
(-∞,-2)∪[2,+∞)6.在同一坐标系中,方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$与$ax+by^2=0(a>b>0)$的曲线大致是()。
7.在正方体ABCD-A1B1C1D1中,E、F分别是线段A1B1,B1C1上不与端点重合的动点,若A1E=B1F,有下面四个结论:①EF⊥AA1;②EF//AC;③EF与AC异面;④EF//平面ABCD。
其中一定正确的有()。
A。
①② B。
②③ C。
②④ D。
①④8.如图,空间四边形ABCD中,M、N分别是BC、DA 上的点,且A。
αβ D。
不确定9.某几何体的三视图如右图所示,则该几何体的体积不可能是()。
A。
1 B。
1.5 C。
2 D。
310.已知两点M(-1,1)和N(1,-3),若直线上存在点P,使PM+PN=4,则称该直线为“T型直线”。
河南省郑州市2014-2015学年高二上学期期末数学试卷(文科)参考答案与试题解析

河南省郑州市2014-2015学年高二上学期期末数学试卷(文科)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)抛物线x2=2y的焦点坐标是()A.B.C.(1,0)D.(0,1)考点:抛物线的简单性质.专题:计算题.分析:根据抛物线的定义可得,x2=2py(p>0)的焦点坐标(0,)可直接求解解答:解:根据抛物线的定义可得,x2=2y的焦点坐标(0,)故选B.点评:本题主要考查了抛物线的简单的性质,属于基础试题.2.(5分)设a,b∈R,则a>b是(a﹣b)b2>0的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:规律型.分析:结合不等式的性质,利用充分条件和必要条件的定义进行判断.解答:解:当a>b,b=0时,不等式(a﹣b)b2>0不成立.若(a﹣b)b2>0,则b≠0,且a﹣b>0,∴a>b成立.即a>b是(a﹣b)b2>0的必要不充分条件.故选:B.点评:本题主要考查充分条件和必要条件的判断,利用不等式的性质是解决本题的关键,比较基础.3.(5分)不等式x2+2014x﹣2015>0的解集为()A.{x|﹣2015<x<1} B.{x|x>1或x<﹣2015}C.{x|﹣1<x<2015} D.{x|x<﹣1或x>2015}考点:一元二次不等式的解法.专题:不等式的解法及应用.分析:把不等式化为(x+2015)(x﹣1)>0,求出解集即可.解答:解:不等式x2+2014x﹣2015>0可化为(x+2015)(x﹣1)>0,解得x<﹣2015或x>1;∴不等式的解集为{x|x>1或x<﹣2015}.故选:B.点评:本题考查了一元二次不等式的解法与应用问题,是基础题目.4.(5分)等差数列{a n}的前n项和为S n,且S3=6,a3=0,则公差d等于()A.﹣1 B.1 C.2 D.﹣2考点:等差数列的前n项和.专题:等差数列与等比数列.分析:由题意结合等差数列的性质和求和公式可得a2的值,进而可得公差d.解答:解:∵等差数列{a n}的前n项和为S n,且S3=6,a3=0,∴S3=a1+a2+a3=3a2=6,∴a2=2,∴公差d=a3﹣a2=0﹣2=﹣2故选:D点评:本题考查等差数列的求和公式和通项公式,属基础题.5.(5分)如图所示,为了测量某障碍物两侧A,B间的距离,给定下列四组数据,不能确定A,B间距离的是()A.α,a,b B.α,β,a C.a,b,γD.α,β,b考点:解三角形的实际应用.专题:应用题;解三角形.分析:给定α,a,b,由正弦定理,β不唯一确定,故不能确定A,B间距离.解答:解:给定α,a,b,由正弦定理,β不唯一确定,故不能确定A,B间距离.故选:A.点评:本题考查解三角形的实际应用,考查学生的计算能力,比较基础.6.(5分)下列关于星星的图案构成一个数列,该数列的一个通项公式是()A.a n=n2﹣n+1 B.a n=C.a n=D.a n=考点:数列递推式.专题:规律型.分析:由图中所给的星星个数:1,1+2,1+2+3,…,1+2+3+…+n;得出数列第n项,即通项公式.解答:解析:从图中可观察星星的构成规律,n=1时,有1个;n=2时,有3个;n=3时,有6个;n=4时,有10个;∴a n=1+2+3+4+…+n=.答案:C点评:这是一个简单的自然数求和公式,由观察得出猜想,一般不需要证明.考查学生的观察猜想能力.7.(5分)设变量x,y满足约束条件:,则目标函数z=2x+3y的最小值为()A.6 B.7 C.8 D.23考点:简单线性规划的应用.专题:不等式的解法及应用.分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件.画出满足约束条件的可行域,再用角点法,求出目标函数的最小值.解答:解:画出不等式.表示的可行域,如图,让目标函数表示直线在可行域上平移,知在点B自目标函数取到最小值,解方程组得(2,1),所以z min=4+3=7,故选B.点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.8.(5分)已知a>0,b>0,且2是2a与b的等差中项,则的最小值为()A.B.C.2 D.4考点:基本不等式;等差数列.专题:不等式的解法及应用.分析:利用等差中项及基本不等式的性质即可求出答案.解答:解:∵2是2a与b的等差中项,∴2a+b=4,又∵a>0,b>0,∴=,当且仅当2a=b=2,即a=1,b=2时取等号,∴.故选B.点评:充分理解基本不等式及其变形是解题的关键.9.(5分)已知点(2,1)和(﹣1,3)在直线3x﹣2y+a=0的两侧,则a的取值范围是()A.﹣4<a<9 B.﹣9<a<4 C.a<﹣4或a>9 D.a<﹣9或a>4考点:直线的斜率.专题:直线与圆.分析:由点(2,1)和(﹣1,3)在直线3x﹣2y+a=0的两侧,把两点的坐标代入3x﹣2y+a 所得的值异号,由此列不等式求得a的范围.解答:解:∵点(2,1)和(﹣1,3)在直线3x﹣2y+a=0的两侧,∴(3×2﹣2×1+a)(﹣1×3﹣2×3+a)<0,即(a+4)(a﹣9)<0.解得﹣4<a<9.故选:A.点评:本题考查了简单的线性规划,考查了二元一次不等式所表示的平面区域,是基础题.10.(5分)已知各项为正的等比数列{a n}中,a4与a14的等比中项为,则2a7+a11的最小值为()A.16 B.8 C.D.4考点:等比数列的通项公式.专题:计算题;等差数列与等比数列.分析:由各项为正的等比数列{a n}中,a4与a14的等比中项为,知a4•a14=(2)2=8,故a7•a11=8,利用均值不等式能够求出2a7+a11的最小值.解答:解:∵各项为正的等比数列{a n}中,a4与a14的等比中项为,∴a4•a14=(2)2=8,∴a7•a11=8,∵a7>0,a11>0,∴2a 7+a11≥2=2=8.故选B.点评:本题考查等比数列的通项公式的应用,是中档题.解题时要认真审题,仔细解答.11.(5分)已知f(x)=x2+2xf′(1),则f′(0)等于()A.0 B.﹣2 C.﹣4 D.2考点:导数的运算.专题:导数的概念及应用.分析:把给出的函数求导得其导函数,在导函数解析式中取x=1可求2f′(1)的值.解答:解:由f(x)=x2+2xf′(1),得:f′(x)=2x+2f′(1),取x=1得:f′(1)=2×1+2f′(1),所以,f′(1)=﹣2.所以f′(x)=2x﹣4故f′(0)=2f′(1)=﹣4,故选:C.点评:本题考查了导数运算,解答此题的关键是理解原函数解析式中的f′(1),在这里f′(1)只是一个常数,此题是基础题.12.(5分)已知方程=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是()A.sinα=﹣αcosβB.sinα=αcosβC.cosα=βsinβD.sinβ=βsinα考点:根的存在性及根的个数判断.专题:计算题;作图题;函数的性质及应用;导数的综合应用.分析:由题意,方程=k可化为|sinx|=kx,作函数y=|sinx|与y=kx的图象,从而可求得y′|x=β=﹣cosβ,即k=﹣cosβ,从而可得=﹣cosβ,化简即可.解答:解:在(0,+∞)上,方程=k可化为|sinx|=kx,作函数y=|sinx|与y=kx的图象如下,在x=β时,==k,又∵在x=β处直线与y=|sinx|相切,∴y′|x=β=﹣cosβ,故k=﹣cosβ,则=﹣cosβ,即sinα=﹣αcosβ;故选A.点评:本题考查了导数的几何意义的应用及方程的根与函数图象的关系应用,同时考查了数形结合的思想应用,属于中档题.二、填空题(共4小题,每小题5分,满分20分)13.(5分)命题“∃x<0,有x2>0”的否定是∀x<0,有x2≤0.考点:命题的否定.分析:对特称命题的否定是一个全称命题,对一个全称命题的否定是全称命题,即:对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”;对命题“∀x∈A,P(X)”的否定是:“∃x∈A,¬P(X)”,由此不难得到对命题“∃x<0,有x2>0”的否定.解答:解:∵对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”∴对命题“∃x<0,有x2>0”的否定是“∀x<0,有x2≤0”故答案为:∀x<0,有x2≤0点评:对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”;对命题“∀x∈A,P(X)”的否定是:“∃x∈A,¬P(X)”,即对特称命题的否定是一个全称命题,对一个全称命题的否定是全称命题14.(5分)若2、a、b、c、9成等差数列,则c﹣a=.考点:等差数列的性质.专题:等差数列与等比数列.分析:由等差数列的性质可得2b=2+9,解之可得b值,再由等差中项可得a,c的值,作差即可得答案.解答:解:由等差数列的性质可得2b=2+9,解得b=,又可得2a=2+b=2+=,解之可得a=,同理可得2c=9+=,解得c=,故c﹣a=﹣==故答案为:点评:本题考查等差数列的性质和通项公式,属基础题.15.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,若sinA=sinC,B=30°,b=2,则边c=2.考点:正弦定理;余弦定理.专题:解三角形.分析:在△ABC中,由正弦定理求得a=c,结合余弦定理,即可求出c的值解答:解:∵在△ABC中,sinA=sinC∴a= c又∵B=30°,由余弦定理,可得:cosB=cos30°===解得c=2故答案为:2.点评:本题考查的知识点是正弦定理和余弦定理,熟练掌握定理是解题的关键,属于中档题.16.(5分)现有甲、乙两人相约到登封爬嵩山,若甲上山的速度为v1,下山的速度为v2(v1≠v2),乙上山和下山的速度都是(甲、乙两人中途不停歇且下山时按原路返回),则甲、乙两人上下山所用的时间t1、t2的大小关系为t1>t2.考点:有理数指数幂的化简求值.专题:计算题;函数的性质及应用.分析:由题意,甲用的时间t1=+=S;乙用的时间t2=2×=;从而作差比较大小即可.解答:解:由题意知,甲用的时间t1=+=S•;乙用的时间t2=2×=;∴t1﹣t2=S﹣=S(﹣)=S>0;故t1>t2;故答案为:t1>t2.点评:本题考查了有理指数幂的化简求值,属于基础题.三、解答题(共6小题,满分70分)17.(10分)设等差数列{a n}满足a3=5,a10=﹣9.(Ⅰ)求{a n}的通项公式;(Ⅱ)求{a n}的前n项和S n的最大值.考点:等差数列的前n项和;等差数列的通项公式.专题:计算题;等差数列与等比数列.分析:(Ⅰ)运用等差数列的通项公式,列出方程,解得首项和公差,即可得到通项公式;(Ⅱ)运用前n项和的公式,配方,结合二次函数的最值,即可得到.解答:解:(Ⅰ)由a n=a1+(n﹣1)d,及a3=5,a10=﹣9得,,解得,数列{a n}的通项公式为a n=11﹣2n.(Ⅱ)由(1)知.因为.所以n=5时,S n取得最大值25.点评:本题考查等差数列的通项公式和前n项和公式的运用,考查解方程组和二次函数的最值的求法,属于基础题.18.(12分)命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立.命题q:抛物线y2=4ax 的焦点在(1,0)的左侧,若p或q为真命题,p且q为假命题,求实数a的取值范围.考点:复合命题的真假.专题:计算题;简易逻辑.分析:先分别求出p,q为真时实数a的取值范围,再由p或q为真,p且q为假,可知p 和q一真一假,从而解得.解答:解:设g(x)=x2+2ax+4,由于关于x的不等式x2+2ax+4>0对一切x∈R恒成立,故△=4a2﹣16<0,∴﹣2<a<2.又∵抛物线y2=4ax的焦点在(1,0)的左侧,∴a<1.a≠0.又由于p或q为真,p且q为假,可知p和q一真一假.(1)若p真q假,则∴1≤a<2;或a=0.(2)若p假q真,则∴a≤﹣2.综上可知,所求实数a的取值范围为1≤a<2,或a≤﹣2.或a=0.点评:本题考查了复合命题的真假性的应用,属于基础题.19.(12分)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且b=2csinB(1)求角C的大小;(2)若c2=(a﹣b)2+6,求△ABC的面积.考点:余弦定理;正弦定理.专题:解三角形.分析:(1)已知等式利用正弦定理化简,根据sinB不为0求出sinC的值,由C为锐角求出C的度数即可;(2)利用余弦定理列出关系式,把cosC的值代入并利用完全平方公式变形,结合已知等式求出ab的值,再由sinC的值,利用三角形面积公式求出三角形ABC面积即可.解答:解:(1)由正弦定理==,及b=2csinB,得:sinB=2sinCsinB,∵sinB≠0,∴sinC=,∵C为锐角,∴C=60°;(2)由余弦定理得:c2=a2+b2﹣2abcosC=a2+b2﹣ab=(a﹣b)2+ab,∵c2=(a﹣b)2+6,∴ab=6,则S△ABC=absinC=.点评:此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.20.(12分)汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.某市的一条道路在一个限速为40km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相撞了.事后现场勘查测得甲车刹车距离刚好12m,乙车刹车距离略超过10m.又知甲、乙两种车型的刹车距离 S(m)与车速x(km/h)之间分别有如下关系:S甲=0.1x+0.01x2,S乙=0.05x+0.005x2.问:甲、乙两车有无超速现象?考点:函数模型的选择与应用.专题:函数的性质及应用.分析:由题意列出不等式组,分别求解两种车型的事发前的车速,判断它们是不是超速行驶,即可得到结论.解答:解:由题意知,对于甲车,有0.1x+0.01x2=12.即x2+10x﹣1200=0,…(2分)解得x=30或x=﹣40(x=﹣40不符合实际意义,舍去).…(4分)这表明甲车的车速为30km/h.甲车车速不会超过限速40km/h.…(6分)对于乙车,有0.05x+0.005x2>10,即x2+10x﹣2000>0,…(8分)解得x>40或x<﹣50(x<﹣50不符合实际意义,舍去).…(10分)这表明乙车的车速超过40km/h,超过规定限速.…(12分)点评:本题的考点是函数模型的选择与应用,考查不等式模型的构建,考查利用数学知识解决实际问题.解题的关键是利用函数关系式构建不等式.21.(12分)已知函数f(x)=e x﹣2x(e为自然对数的底数)(1)求函数f(x)的单调区间(2)若存在使不等式f(x)<mx成立,求实数m的取值范围.考点:利用导数研究函数的单调性;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(Ⅰ)先求出函数的导数,令f′(x)=0,解得x=ln2,从而求出函数的单调区间;(Ⅱ)问题转化为求的最小值.令,通过求导得到函数g(x)的最小值,从而求出m的范围.解答:解:(Ⅰ)f′(x)=e x﹣2,令f′(x)=0,即e x﹣2=0,解得x=ln2,x∈(﹣∞,ln2)时,f′(x)<0,x∈(ln2,+∞)时,f′(x)>0,∴f(x)的单调递减区间为(﹣∞,ln2),单调递增区间为(ln2,+∞).(Ⅱ)由题意知使f(x)<mx成立,即使成立;所以的最小值.令,,所以g(x)在上单调递减,在上单调递增,则g(x)min=g(1)=e﹣2,所以m∈(e﹣2,+∞).点评:本题考查了函数的单调性,函数的最值问题,考查了导数的应用,考查转化思想,是一道中档题.22.(12分)已知圆C:x2+y2=3的半径等于椭圆E:+=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x﹣的距离为﹣,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).(Ⅰ)求椭圆E的方程;(Ⅱ)求证:|AF|﹣|BF|=|BM|﹣|AM|.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(Ⅰ)设点F(c,0)(c>0),由已知条件得,圆C的半径等于椭圆E的短半轴长,由此能求出椭圆方程.(Ⅱ)由圆心O到直线l的距离为,得,由已知条件推导出|AF|+|AM|=2,|BF|+|BM|=2,由此能证明|AF|﹣|BF|=|BM|﹣|AM|.解答:(Ⅰ)解:设点F(c,0)(c>0),则F到直线l的距离为,即,…(2分)因为F在圆C内,所以,故c=1;…(4分)因为圆C的半径等于椭圆E的短半轴长,所以b2=3,椭圆方程为.…(6分)(Ⅱ)证明:因为圆心O到直线l的距离为,所以直线l与圆C相切,M是切点,故△AOM为直角三角形,所以,又,得,…(7分),又,得,…(9分)所以|AF|+|AM|=2,同理可得|BF|+|BM|=2,…(11分)所以|AF|+|AM|=|BF|+|BM|,即|AF|﹣|BF|=|BM|﹣|AM|.…(12分)点评:本题考查椭圆方程的求法,考查两组线段差相等的证明,解题时要认真审题,注意点到直线的距离公式的合理运用.。
广东省深圳市翠园中学2014至2015学年上学期高二文科数学期末试卷及评分标准
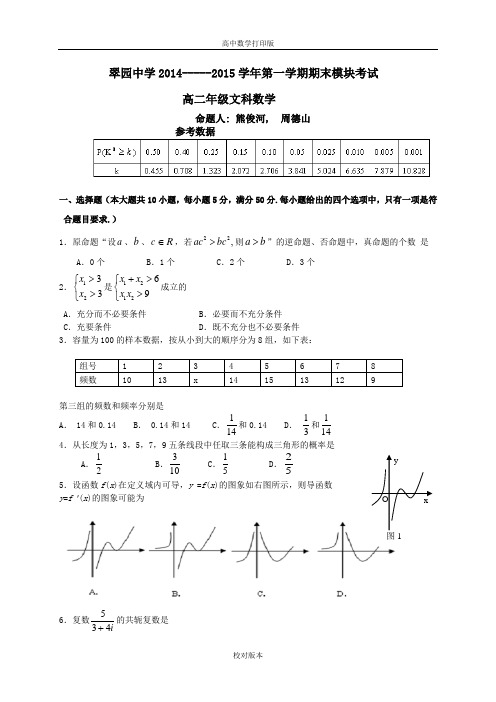
翠园中学2014-----2015学年第一学期期末模块考试高二年级文科数学命题人: 熊俊河, 周德山参考数据一、选择题(本大题共10小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项是符合题目要求.)1.原命题“设a、b、c R∈,若22,ac bc>则a b>”的逆命题、否命题中,真命题的个数是A.0个B.1个C.2个D.3个2.1233xx>⎧⎨>⎩是121269x xx x+>⎧⎨>⎩成立的A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件3.容量为100的样本数据,按从小到大的顺序分为8组,如下表:组号 1 2 3 4 5 6 7 8频数10 13 x 14 15 13 12 9第三组的频数和频率分别是A. 14和0.14 B. 0.14和14 C.114和0.14 D.13和1144.从长度为1,3,5,7,9五条线段中任取三条能构成三角形的概率是A.12B.310C.15D.255.设函数f(x)在定义域内可导,y =f(x)的图象如右图所示,则导函数y=f'(x)的图象可能为6.复数534+i的共轭复数是xyOA .34-iB .3545+i C .34+i D .3545-i7.已知回归直线的斜率的估计值是 1.23,样本点的中心为(4,5),则回归直线的方程是 A. y=1.23x +4 B. y=1.23x+5 C. y=1.23x+0.08 D. y=0.08x+1.238.工人月工资(元)依劳动生产率(千元)变化的回归直线方程为ˆ6090yx =+,下列判断正确的是A.劳动生产率为1000元时,工资为50元B.劳动生产率提高1000元时,工资提高150元C.劳动生产率提高1000元时,工资提高90元D.劳动生产率为1000元时,工资为90元9.利用独立性检验来考虑两个分类变量X 和Y 是否有关系时,通过查阅临界值表来确定断言“X 和Y 有关系”的可信度。
—学年度第一学期期末考试高二政治参考答案及评分标准

2014—2015学年度第一学期期末考试参考答案及评分标准高二政治一、选择题(每小题2分,共24小题48分)二、非选择题(共3小题52分)25.(12分)①文化对经济、政治具有反作用,给予经济政治以重大影响。
(2分)设立孔子学院,有利于我国扩大对外开放,促进我国经济发展,展现我国国际形象。
(2分)②当今世界,文化越来越成为民族凝聚力和创造力的重要源泉,越来越成为经济社会发展的重要支撑,越来越成为综合国力竞争的重要因素。
(2分)设立孔子学院,传播中国文化,有利于提高我国的综合国力。
(2分)③设立孔子学院,可以推动中华文化向世界的传播,促进世界文化的繁荣发展,提高国家的文化软实力,增强中华文化的国际影响力。
(4分)26.(14分)答案一:赞同。
(2分)理由:①传统文化具有鲜明的民族性和历史继承性。
保持汉语言的纯洁性有利于延续中华传统文化,树立文化自觉与自信,增强中华文化的认同感。
(4分)②文化继承是文化发展的必要前提,汉语言的发展必须植根于传统文化。
(4分)③语言是文化传播的媒介。
外来语的过度使用会破坏了汉语言文字的严整和和谐,影响了汉语表意功能的发挥,不利于中华文化的传播。
(4分)答案二:反对。
(2分)理由:①文化需要交流。
不同民族文化之间的交流、借鉴与融合是人类文明发展的重要动力。
(3分)面向世界,博采众长,积极吸收借鉴其他民族语言的合理成分,有利于汉语言的丰富和发展,更好地融入世界。
(3分)②中华文化具有包容性。
(3分)顺应时代变化,坚持与时俱进,吸收外来语言,是具有高度文化自信的体现,不会损害中华文化的独立和尊严。
(3分)27.(26分)(1)(18分)①文化作为一种精神力量,能够对社会发展产生深刻的影响。
(3分)培育和践行社会主义核心价值观有利于引领社会思潮,凝聚社会共识。
(3分)②文化与经济、政治相互影响、相互交融。
(3分)培育和践行社会主义核心价值观能够为我国经济、政治建设提供正确的方向保证、不竭的精神动力,建设富强民主文明和谐的社会主义现代化国家。
广东省惠州市2014-2015学年高二上学期期末考试数学文_Word版及答案

惠州市2014-2015学年第一学期期末考试高二文科数学试题说明:1.全卷满分150分,时间120 分钟;2.答卷前,考生务必将自己的姓名、县区、学校、班级、试室、座位号,填写在答题卷上;3.考试结束后,考生将答题卷交回。
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项.1.从集合1234{}5,,,,中随机抽取一个数为a ,则3a >的概率是( )A .45B .35C .25D .152.已知命题p :若x y ==p 的否命题是( )A=x y =B .若x y ≠≠C .若x y =≠D≠x y ≠3.下列函数求导正确的是( )A .()2x x '= B .211x x '⎛⎫=- ⎪⎝⎭C.'=D .()1ln 33'=4.在如图所示的茎叶图中,乙组数据的中位数是( )A .84B .85C .86D .87 5.若:,sin 1,p x R x ∀∈≤则( )A .:,sin 1p x R x ⌝∃∈>B .:,sin 1p x R x ⌝∀∈>C .:,sin 1p x R x ⌝∃∈≥D . :,sin 1p x R x ⌝∀∈≥ 6.十进制数15化为二进制数为( )A . 1011B .1001 (2)C .1111(2)D .11117.函数)(x f 的定义域为),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在),(b a 内有极小值点( )A .1个B .2个C .3个D . 4个 8. 双曲线221169x y-=的渐近线方程为( ) A .43y x =±B .34y x =±C .35y x =±D .45y x =± 8 4 4 6 4 7m 9 310 7 9乙(第4题图)(第7题图)9. 如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( ) A .4π B .5π C .6π D .7π10. 以双曲线221124y x -=的顶点为焦点,长半轴长为4的椭圆方程为( )A .2216452x y += B .2211612x y += C .221164x y += D .221416x y += 二、填空题:本大题共4小题,每小题5分,满分20分,请将答案填在答题卡相应位置. 11. 交警部门随机测量了高架桥南下口某一时间段经过的2000辆汽车的时速,时速的频率分布直方图如下图所示,则时速超过70 km/h 的汽车数量为 辆.12.曲线3y x =在点P(1,1)处的切线方程是 .13.执行如图所示的程序框图,输出的结果是_______.14.设圆锥曲线C 的两个焦点分别为F 1,F 2,若曲线C 上存在点P 满足1122::PF F F PF =6:5:4,则曲线C 的离心率等于 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 15.(本题满分14分)某网站体育版块足球栏目组发起了“射手的上一场进球与本场进球有无关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:有关系 无关系 不知道 人数500600900(1)在所有参与调查的人中,用分层抽样的方法抽取样本,已知从持“有关系”态度的(第11题图) x=1,y=1,z =210?z ≤开始结束否是z =x +y 输出z y = z x = y(第13题图)(第9题图)人中抽取了5人,求总样本容量。
2014-2015东城区第一学期期末数学文科和评分标准

东城区2014-2015学年第一学期期末教学统一检测高三数学 (文科)学校_____________班级_______________姓名______________考号___________本试卷共5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合{}12A x x =∈-≤≤Z ,集合{}420,,=B ,则AB =(A ){}02, (B ){}420,, (C ){}4,2,0,1- (D ){}4,2,1,0,1-(2)下列函数中,既是奇函数,又在区间(0+)∞,上为增函数的是 (A )x y ln = (B )3y x = (C )3x y = (D )x y sin = (3)设x ∈R ,则“1x >”是“21x >”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 (4)当3n =时,执行如图所示的程序框图,输出的S 值为(A )6 (B )8 (C )14(D )30(5)已知3cos 4α=,(,0)2απ∈-,则sin 2α的值为(A )38 (B )38- (C (D )(6)如图所示,为了测量某湖泊两侧A ,B 间的距离,某同学首先选定了与A ,B 不共线的一点C ,然后给出了四种测量方案:(△ABC 的角A ,B ,C 所对的边分别记为a ,b ,c ) ①测量A ,C ,b ②测量a ,b ,C ③测量A ,B ,a ④测量a ,b ,B 则一定能确定A ,B 间距离的所有方案的序号为(A )①②③ (B )②③④(C )①③④ (D )①②③④(7)已知向量(1,3)=a ,(,23)m m =-b ,平面上任意向量c 都可以唯一地表示为+λμ=c a b (,)λμ∈R ,则实数m 的取值范围是(A )(,0)(0,)-∞+∞ (B )(,3)-∞ (C )(,3)(3,)-∞--+∞ (D )[3,3)-(8)已知两点(1,0)M -,(1,0)N ,若直线(2)y k x =-上至少存在三个点P ,使得△MNP 是直角三角形,则实数k 的取值范围是 (A )11[,0)(0,]33- (B )3[,0)(0,]33- (C )11[,]33-(D )[5,5]- 第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
—学年度第一学期期末高二语文试卷参考答案及评分标准(B卷).doc

宁德市2013-2014学年度第一学期期末高二质量检测语文试题参考答案(B卷)1.(2分)D (A.蜃ch4n应为shen,溢hE应为kQ ; B.濯di应为zhuo,鲜xidn应为xi an; C.蜕dui应为tui,濒pin 应为bln)2.(2分)B (A. “地”应为“的”;C. “触”应为“蹴";D. “缅”应为“湎”)3.(2分)C (“始作俑者”原指开始用陶俑殉葬的人。
后用来比喻某种坏事或恶劣风气的肇始人)4.(2分)D (前面说“是否”,后面只说一种情况,属“搭配不当”,应在“有效调整”前面加“能否”)5.(2分)B (岑参、高适应为王维、孟浩然)6.(2分)A (适:往)7.(2分)B (B.这样。
A.①兼词,之于/②各,众;C.①连词,表承接/②连词,表假设或转折;D.①代词,这/②助词,取消句了独立性)8.(2分)B (B项和例句均为宾语前置。
A.省略句;C.状语后置;D.判断句)9.(3分)D (发:打开粮仓,赈济百姓)10.(3分)D (①比;②在;③用,拿;④按)11.(3分)C.(要统一天下,还得注重教化,发展学校教育,让老百姓憧得“孝悌之义”)12.(1)(3分)只不过他们没有跑到一百步罢了,但这也是逃跑呀。
(“直”、“走”各1 分,句子通顺1分)(2)(3分)大王不归罪于年成,这样,天下的老百姓就到你这里了。
(“罪”、“岁”各1分,句子通顺1分)13.(1)海上生明月;(2)千金散尽还复来;(3)小弦切切如私语;(4)人人尽说江南好;(5)也无风雨也无晴;(6)八千里路云和月;(7)茕茕孑立;(8)俯察品类之盛(每句1分。
错字、漏字和添字均不得分)14.(1)描绘了画眉鸟在林间花丛中自由飞翔,尽情歌唱的图景。
(2分)(2)对比。
(1分)通过笼中鸟和林中鸟的对比(1分),表达了诗人对自由的赞美之情和对束缚个性、窒息性灵的憎恶之意(2分)o(如果学生答出象征、托物言志、拟人等手法,只要言之成理,亦可的情给分)15.C. E.解析:C.查理有钱后违约,|门|到法国后和侯爵女儿私定终身,抛弃欧也妮。
广东省东莞市2014-2015学年高二上学期期末考试数学(文)试题(B卷) 扫描版含答案

东莞市2014-2015学年度第一学期高二文科数学期末考试试卷(B卷)2014—2015学年度第一学期期末教学质量检查高二文科数学(B 卷)参考答案及评分标准一、选择题二、填空题11. {}34x x -<< 12. 9 13.3- 141三、解答题 15.解:(1) 不等式20x mx n ++≤的解集为[1,4]A =1,4∴是方程20x mx n ++=的两个根,……………2分由韦达定理得14m +=-,14n ⨯= ……………4分∴实数,m n 的值分别为5,4- ……………………6分(2) q 是p 的充分条件, ∴q p ⇒,即B 是A 的子集, ……………………8分即 {114a a -≥≤, …………………11分解得24a ≤≤.所以实数a 的取值范围为|{a 24a ≤≤}.…………12分16.解:由()1f A =得2cos 12A =, 即1cos 22A = ∵A 是ABC ∆的内角, ∴23A π= ∴23A π=……………3分 由正弦定理:BAC A BC sin sin = ……………………6分又∵BC=7,sin 14B =得7sin 5sin BC B AC A ⋅=== ……………8分 又∵A AC AB AC AB BC cos 2222⋅⋅-+=, 即222175222AB AB =++⋅⨯⨯ ,解得3=AB ……………12分 17.解:(1)由已知{}n a 为等差数列,设其公差为d ,首项为1a ,则………1分11234a d a d +=⎧⎨+=⎩. ……………3分 解之得111a d =⎧⎨=⎩∴1(1)1n a n n =+-⨯=……………5分 各项为正数的等比数列{}nb 中,公比设为q (0q >).由11b =,1237b b b ++=得217q q ++=解之得2q =或3q =-(舍去)……………7分(2)由(1)知n a n =,12n n b -=∴12n n n n a n c b -==……………8分 ∴0121123...2222n n n S -=++++...............① ...............9分 1231123 (22222)n n n S =++++...............② ...............10分 ①-②得:012111111 (222222)n n n n S -=++++- ……………11分 11[1()]21212n n n ⨯-=--222n n +=-……………………………………13分 ∴n S 1242n n -+=-即为所求.18.解:设每天生产甲种产品x 吨,乙种产品y 依题意可得线性约束条件5346355000x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩……………4分目标函数为 1012z x y =+, ……………5分作出线性约束条件所表示的平面区域如图所示……………8分将1012z x y =+变形为5612z y x =-+ 当直线5612z y x =-+在纵轴上的截距12z 达到最大值时,……………9分 即直线5612z y x =-+经过点M 时,z 也达到最大值. ……………10分 由53463550x y x y +=⎧⎨+=⎩得M 点的坐标为(5,7) ……………12分 所以当7,5==y x 时,max 510712134z =⨯+⨯= ……………13分因此,该厂每天生产甲种产品5吨,乙种产品7吨,才能使该厂日产值最大,最大的产值是134万元. ……………14分19.解:(1)依题意知曲线C 是抛物线,设其为22(0)x py p =>,由定义可得12p =,解得2p =,………2分∴抛物线C 的方程为24x y =.……………3分(2)设点00(,)P x y ,点P 到直线2y x =-的距离为d ,则有2004x y =,由点到直线距离公式得d===………………7分 ∴当02x =,01y =即(2,1)P 时,点P 到直线2y x =-的距离最短,最短距离为.……………………8分 (3)由题意,联立y x m =+和24x y =消去y 并整理得2440x x m --=,………………10分直线l 与曲线C 有交点∴2(4)160m ∆=-+≥…………12分解之得1m ≥-即为所求. …………14分20.解:(1)由题知221()ln 22e f e e a e =-+=,解得0a =……………2分(2)由题可知函数()f x 的定义域为(0,)+∞,……………3分 又22'2221()()()x e x e x e x f x x e e x e x-+-=-== …………5分 由2()()0e x e x e x +->得0x e <<;2()()0e x e x e x+-<得x e >;…………7分 故函数()f x 单调增区间为(0,)e ,单调减区间为(,)e +∞……………8分 (3)因为22()ln 2x f x x e=-,由(1)知函数()f x 的单调减区间为(,)e +∞,故()f x 在2[,]e e 上单调递减,………………9分 ∴2max 211()()ln 1222e f x f e e e ==-=-=; 4222min 2()()ln 222e ef x f e e e ==-=-;………………10分 ∴max min ()()f x f x -=2213(2)222e e ---= max min ()()f x f x ∴-2332e -=<………① …………11分 依题意任取212,[,]x x e e ∈,欲证明12()()3f x f x -<,只需要证明max min ()()f x f x -3<,…………13分由①可知此式成立,所以原命题得证. …………14分。
—学年度第一学期期末考试高二语文参考答案及评分标准

2014—2015学年度第一学期期末考试高二语文试题参考答案及评分标准一、(9分)1. B 偷换概念,好的文学批评才如灯光,才能起到那个作用。
(3分)2. C 因果倒置,将诗歌批评庸俗化的表现当成原因。
(3分)3. D 以偏概全,只是某些诗歌批评家犯了“以偏概全,搞门派之争,以自己的喜好为唯一或主要标准”的错误。
(3分)二、(36分)(一)(19分)4.C(尊:尊封)(3分)5.A(③表现其雍容礼让④表现其治军严谨)(3分)6.B(司马穰苴未逆君命杀庄贾)(3分)7.(10分)(1)齐景公召见田穰苴,与他谈论军事,心里很高兴,(于是)任命田穰苴为将军,(让他)领兵去抗击燕、晋的军队。
(“说”、“以为”、“将”、“扞”各1分,句意1分)(2)将领接受命令的那一天,就要忘掉自己的家;面向军队宣布纪律的时候,就必须连自己的双亲也忘掉;(到了)擂响战鼓的危急时刻,就要把自身的安危也忘掉。
(“受命”1分,“约束”1分,“援枹鼓之急”1分,句意1分,句式整齐1分)(二)(11分)8.(5分)上片:实写了石头城天地无物、惟有青山如壁的空旷寂寥之景;(2分)虚写了昔日战争连年的激烈残酷、豪杰消逝的苍凉悲壮之景。
(2分)虚实结合使意境更深远,情感更深沉。
(1分)9.(6分)①对世事(历史)变迁/昔盛今衰的悲哀。
(1分)曾经的繁华六朝,现已成空荡的江山;曾经的行宫内院,早已是芳草萋萋。
世事(历史)沧桑/盛衰无常,让人倍加感伤。
(1分)②对自然永恒、物是人非/人生短暂的无奈。
(1分)曾经的江山明月离宫依旧存在,而曾经的豪杰宫人却已随时光流逝而“消磨”,一片空冷孤寂,让人顿觉自然永恒、人生短暂。
(1分 ) ③对战争残酷的心痛。
(1分)战火纷飞,摧毁了往日的繁华,只剩下生灵涂炭,白骨遍野,让人心痛。
(1分)④对青春易逝的感伤。
(1分)多少美丽如花的歌舞粉黛,对镜施粉理鬓,却又青丝变白发,消磨了青春美丽,这应该是诗人对自已也是对世人青春易逝的感伤。
河北省邯郸市2014-2015学年高二上学期期末考试文科数学试题Word版含答案

高二:文科 一、选择题1.在等比数列{}n a 中,22a = ,48a =,则6a =A. 64B. 32C. 28D. 14 2.已知命题p 为真命题,命题q 为假命题,则A .()p q ∧⌝为真B . p q ∧为真C .()p q ⌝∨为真 D. ()p q ⌝∧为真3.在ABC ∆中,15a =,10b =,sin A =,则sin B =4.下列双曲线中,渐近线方程是32y x =±的是 A.22132x y -= B. 22149x y -= C. 22132y x -= D. 22149y x -= 5.已知命题p :23x <<,q :2540x x -+<,则p 是q 的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 6.已知ABC ∆的三条边长分别为8,10,15,则该三角形为A.钝角三角形B.直角三角形C.锐角三角形D.不能确定7.已知曲线23ln 2x y x =-的一条切线的斜率为2-,则该切线的方程为 A. 323ln 32y x =--- B. 322y x =-+ C. 2123ln 32y x =-+- D. 522y x =-+ 8.已知变量x ,y ,满足约束条件32122y x y x y ≤⎧⎪+≥⎨⎪-≤⎩,则3z x y =+的最大值为A. 3B. 12C.212 D. 10 9.已知正数a ,b 满足21a b +=,则23a b+的最小值为A. 8B. 8+8+2010.已知抛物线212y x =的焦点与椭圆2212y x m +=的一个焦点重合,则m = A.74 B. 12764 C. 94 D. 1296411.若非零实数a ,b ,c 成等差数列,则函数214y ax bx c =++的图像与x 轴交点的个数是A. 0B. 1C. 2D. 1或212.过点(1,1)M -作斜率为12的直线与椭圆C :22221(0)x y a b a b+=>>相交于,A B 两点,若M 是线段AB 的中点,则椭圆C 的离心率为A.12 B. 2 C. 2 D. 3二.填空题13.命题“R x ∈∃0,使00sin lg x x =”的否定是 .用电量y 与月份x 之间有较好的线性相关关系,其线性回归方程为ˆ0.7yx a =-+,则a = .15.下图是函数()y f x =的导函数的图像,给出下面四个判断:①()f x 在区间[2,1]--上是增函数; ②1x =-是()f x 的极小值点;③()f x 在区间[1,2]-上是增函数,在区间[2,4]上是减函数; ④1x =是()f x 的极大值点.其中,判断正确的有__________.(写出所有正确的编号)16.已知函数2()f x x bx =+的图象在点(1,(1))A f 处的切线l 与直线320x y +-=垂直,若三.解答题17.已知数列{}n a 是等差数列,n S 是其前n 项和,12a =,312S =.(1)求数列{}n a 的通项公式;(2)设4n n n b a =+,求数列{}n b 的前n 项和n T .18.在ABC ∆中,三个内角A ,B ,C 的对边分别是a ,b ,c ,且2cos cosA c aB b-=. (1)求角B ;(2)若a c +=ABC S ∆=b 的值.19.已知抛物线C :()022>=p px y 的焦点为F 并且经过点(1,2)A -. (1)求抛物线C 的方程;(2)过F 作倾斜角为45的直线l ,交抛物线C 于,M N 两点, O 为坐标原点,求OMN ∆的面积.20.某大学为了准备2014年秋季的迎新晚会,招募了14名男志愿者和16名女志愿者,调查发现,男女志愿者中分别有8名和12名喜欢参与节目表演,其余人不喜欢参与节目表演. 22⨯(2)能否在犯错误的概率不超过的前提下认为性别与喜欢参与节目表演有关.参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++;参考数据:21.已知函数32()29128f x x x x a =-++. (1)若2a =,求()f x 的极大值和极小值;(2)若对任意的[0,4]x ∈,2()4f x a <恒成立,求a 的取值范围.22.已知椭圆22221(0)x y a b a b+=>>,12F F 、分别为其左右焦点,点B 为椭圆与y 轴的一个交点,12BF F ∆的周长为6+(1)求椭圆的方程;(2)若点A 为椭圆的左顶点,斜率为k 的直线l 过点(1,0)E ,且与椭圆交于C ,D 两点,AC k ,AD k 分别为直线AC ,AD 的斜率,对任意的k ,探索AC AD k k ⋅是否为定值。
河北唐山市1415学年度上学期高二期末——数学(文)数学(文)

唐山市2014~2015学年度高二年级第一学期期末考试文科数学参考答案及评分标准一、选择题:A 卷:AACDB BCCBDCD B 卷:BDCDB ACACDBD 二、填空题:(13)y =-116(14)23 (15)30︒ (16)2三、解答题:(17)解:若命题p 为真,则有∆=m 2-6<0,解得-6<m <6. 若命题q 为真,则有⎩⎨⎧m -1>0,m -3<0,解得1<m <3. …6分因为“p ∧q ”为真命题,所以p ,q 均为真命题,故有⎩⎨⎧-6<m <6,1<m <3,解得1<m <6. 故所求实数m 的取值范围是1<m <6. …10分(18)解:(Ⅰ)设圆C 的方程为x 2+y 2+Dx +Ey +F =0.因为O ,A ,B 三点都在圆C 上,所以它们的坐标都是圆C 方程的解, 故⎩⎪⎨⎪⎧F =0,50-D -7E +F =0,80+8D -4E +F =0,解此方程组,得D =-6,E =8,F =0. 故所求圆C 的方程为x 2+y 2-6x +8y =0. …6分 (Ⅱ)直线AB 的方程为x -3y -20=0,故设直线l 的方程为3x +y +m =0. 由题意,圆心C (3,-4)到直线AB 与直线l 的距离相等, 故有|3-3×(-4)-20|12+(-3)2=|3×3+(-4)+m |32+12, 解得m =0或m =-10.所以直线l 的方程为3x +y =0或3x +y -10=0. …12分(19)解:连结BD ,设BD ∩AC =O ,易知O 为DB 的中点.又E 为PD 的中点,所以在△PDB 中,OE 为其一条中位线,所以PB ∥OE .又OE ⊂平面EAC ,PB ⊂/平面EAC ,故PB ∥平面EAC .…6分(Ⅱ)因为FD = 1 3PD , 所以点F 到平面ACD (也是平面ABCD )的距离与点P 到平面ABCD 的距离比为1∶3,又易知△ACD 的面积等于四边形ABCD 面积的一半,所以三棱锥F -ADC 与四棱锥P -ABCD 的体积比为1∶6.…12分(20)解:(Ⅰ)抛物线y 2=2px (p >0)的准线方程为x =- p 2, 由抛物线的定义可知:|MF |=1-(- p 2)=2,解得p =2, 因此,抛物线C 的方程为y 2=4x . …5分 (Ⅱ)设正三角形OAB 的顶点A ,B 在抛物线上,且A (x 1,y 1),B (x 2,y 2),则y 21=4x 1,y 22=4x 2.∵|OA |=|OB |,∴x 21+y 21=x 22+y 22,即x 21-x 22+4x 1-4x 2=0⇒(x 1-x 2)(x 1+x 2+4)=0.∵x 1>0,x 2>0,∴x 1=x 2,即|y 1|=|y 2|,即线段AB 关于x 轴对称.…8分因为x 轴垂直于AB ,且∠AOx =30︒,不妨取y 1>0,所以y 1x 1=tan 30︒=33. 因为x 1=y 214,所以y 1=43, 故正三角形的边长|AB |=2y 1=83. …12分(21)解: (Ⅰ)因为BC =2,CC 1=BB 1=2,∠BCC 1= π4, 在△BCC 1中,由余弦定理,可求得C 1B =2,所以C 1B 2+BC 2=CC 21,C 1B ⊥BC .又AB ⊥侧面BCC 1B 1,故AB ⊥BC 1,又CB ∩AB =B ,所以C 1B ⊥平面ABC . …6分(Ⅱ)易知BB 1∥平面ACC 1,又点E 在BB 1上,所以点E 到平面ACC 1的距离等于点B 到平面ACC 1的距离.在Rt △ABC 中,AB =2,BC =2,所以AC =6.同理可求得AC 1=6.设点B 到平面ACC 1的距离为d ,在四面体C 1-ABC 中,V B -ACC 1=V A -BCC 1,即 1 3S △ACC 1×d = 1 3S △BCC 1×AB , 所以 1 3× 1 2×2×5×d = 1 3× 1 2×2×2×2,解得d =25 5. 即点E 到平面ACC 1的距离为25 5. …12分(22)解:(Ⅰ)由题意,有e 2=1-b 2a 2= 23,所以得a 2=3b 2,即椭圆C 的方程为x 23b 2+y 2b 2=1. 因为点P 在C 上,将点P (3 2,3 2)的坐标代入,得b 2=1,进而a 2=3, 所以椭圆C 的方程为x 23+y 2=1. …5分(Ⅱ)当直线l 的斜率不存在时,不妨设l 的方程为x =1,代入x 23+y 2=1, 得M (1,63),N (1,-63),|MN |=263≠3,不合题意. …7分 当直线l 的斜率存在时,设l 的方程为y =kx +m , 由题意,有|m |1+k 2=1,即m 2=k 2+1. 将y =kx +m 代入x 23+y 2=1,得(1+3k 2)x 2+6kmx +3m 2-3=0, 设M (x 1,y 1),N (x 2,y 2),则x 1+x 2=-6km 1+3k 2,x 1x 2=3m 2-31+3k 2,所以 |MN |=(1+k 2)(x 2-x 1)2 =(1+k 2)[(x 2+x 1)2-4x 1x 2] =1+k 2×23(3k 2+1-m 2)1+3k 2 =26|k |1+k 21+3k2=3,整理,得k 4-2k 2+1=0,解得k 2=1,k =±1. 综上,可知直线l 的斜率为±1. …12分。
—学年度第一学期期末考试高二数学(文理)参考答案及评分标准

2014—2015学年度第一学期期末考试高二数学(文、理)参考答案及评分标准一、选择题: (文科) (1)—(12) DDBCBCBACA BA (理科) (1)—(12) DDBCA CBACD BA二、填空题:(13)5 (14) 7 (15) 4 (16)①③④三、解答题:(17)(本小题满分10分)解:若P 为真。
则0 ≤<4 ---------------------------(2分)若q 为真,则≤ ---------------------------------(4分)因为“p ∨q ”为真,“p ∧q ”为假,所以p 与q 是“一真一假”,P 真q 假时<<4 -------------------------------(6分)P 假q 真时<0 --------------------------------------(8分)综上的范围为:<0或<<4 -----------------------(10分)(18)(本小题满分12分)解:(Ⅰ)由正弦定理得,,所以, -------------(2分) 又,所以⎪⎩⎪⎨⎧==41,1c a 或⎪⎩⎪⎨⎧==.1,41c a -----------------(6分) (Ⅱ)由余弦定理,B ac ac c a B ac c a b cos 22)(cos 22222--+=-+=,------------(7分) 即)cos 1(212222B b b p b +-=, 所以. -------------------(9分)由是锐角,得,所以. 由题意知,所以⎪⎪⎭⎫ ⎝⎛∈2,26p . -----------------------------(12分)(19)(本题满分12分)解:(20)(本题满分12分)(文科) 解:(Ⅰ)当时,)0(ln )(2>+-=x x x x x f , xx x x x x f )1)(12(121)('-+=+-= 由得 (舍)或当时, ,当时, ,所以,当时,取极大值,无极小值 ----------------(6分) (Ⅱ))0()1)(12()('>-+=x xax ax x f , 当时,在区间上,所以的增区间是;当时,由得或.当时,在区间上,在区间上,所以的增区间是,减区间是;当时,在区间上,在区间上,所以的增区间是,减区间是 ------------------(12分)(理科)解 (Ⅰ)6cos 3n AP AP n n AP ⋅<>==,以为坐标原点,直线,,分别为轴,轴,轴,如图建立空间直角坐标系, 则,,∴,.∵平面∴为平面的法向量,,设平面的一个法向量为,由,且,得 令,则,,所以所以,即所求二面角的余弦值为-----------------------(6分)(21)(本题满分12分)021033a b b c +=⎧⎪⎨+=⎪⎩,,(22)解:(Ⅰ)因为122PF PF a +==,所以 又,所以,所以222211b a c =-=-=所以椭圆的标准方程为 -------------------------------(6分) (Ⅱ)已知设直线的方程为,2221212k k k k+=++,即,所以斜率的取值为.----------------------------(12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁德市2014—2015学年度第一学期高二期末质量检测
数学(文科B 卷)参考答案及评分标准
说明:
1、本解答指出了每题要考察的主要知识和能力,给出一种或几种解法供参考。
如果考生的解法与给出的解法不同,可根据试题的主要考察内容比照评分标准确定相应的评分细则。
2、对解答题,当考生的解答在某一步出现错误,但整体解决方案可行且后续步骤没有出现推理或计算错误,则错误部分依细则扣分,并根据对后续步骤影响的程度决定后继部分的给分,但不得超过后续部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
3、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
4、解答题只给整数分数,选择题和填空题不给中间分。
一、选择题(本大题共12小题,每小题5分,共60分)
1.B 2.C 3.B 4.A 5.B 6.B 7.C 8.A 9.C 10.D 11.D 12.A 二、填空题(本大题共4小题,每小题4分,共16分)
13.若1≠x ,则0232
≠+-x x 14.
34 15.33
16.()()1,01,-⋃+∞ 三、解答题(本大题共6小题,共74分)
17.(满分12分)本题主要考查简易逻辑、不等式的解法、圆锥曲线等基本知识,考查运
算求解能力.
解:(Ⅰ)若()(2)0t a t a --<,又0a >,所以 2a t a <<,
当1a =时, 12t << ……………………… 3分 ∵p 为假命题 ∴实数t 的取值范围是1t ≤或2t ≥ ………………………… 6分
(Ⅱ)由
22
126
x y t +=-表示双曲线,得6t <,即q 为真时实数t 的取值范围是6t <…8分 若p 是q 的充分条件,即p q ⇒,
设A={|2}t a t a <<,B={|6}t t <,则A B ⊆, ……………………10分 则026a <≤,所以实数a 的取值范围是03a <≤. …………………………12分
18.(满分12分)本题主要考查解三角形、正余弦定理等基础知识。
考查运算求解能力、
推理论证能力以及化归的思想.
解:(Ⅰ)∵2
2
2
0a c b ac +-+=由余弦定理得2221
cosB=
22
a c
b a
c +-=-……………3分 ∵0<B π<,∴2
B 3
π=
…………………………5分
(Ⅱ)∵A C sin 2sin =,由正弦定理得c 2a = ………………7分 由余弦定理2
2
2
1(14)42.2.()2
a a a a =+-- …………………………10分
解得2
2a = ∴2a =
………………………12分
19.(满分12分)本题主要考查数列的基本知识,考查运算求解能力及化归思想.
解(Ⅰ)设等差数列的首项为1a 公差为d ,由题意4853
a a =-⎧⎨=⎩
可得 11
35
73a d a d +=-⎧⎨
+=⎩ -----------------------2分
解得,111
2a d =-⎧⎨
=⎩
-----------------------4分
∴213n a n =- ……………………………………6分
(Ⅱ)由数列{}n a 的通项公式可知,
当6n ≤时,0n a <,当7n ≥时,0n a >, --------------------9分 所以当6n =时,n s 取得最小值为6
36s =-。
-----------------12分
20.(满分12分)本题主要考查函数、导数等基本知识,考查运算求解能力及化归思想、
函数方程思想,培养应用意识. 解:(I )因为5x =时,2y =,所以
122
a
+= ∴2a = …………………………3分 (II )由(I )可知,该商品每日的销售量22
(6)3
y x x =
+--所以商场每日销售该商品所获得的利润222()(3)(6)2(3)(6)3f x x x x x x ⎡⎤
=-+-=+--⎢
⎥-⎣⎦
其中36x <<………6分 从而,/
()3(4)(6)f x x x =--, …………………………8分 于是当x 变化时,/
(),()f x f x 的变化情况如下表:
x (3,4) 4 (4,6) /()f x + 0 - ()f x
单调递增
极大值6
单调递减
由上表可得,4x =是函数()f x 在区间(3,6)内的极大值点,也是最大值点;所以,当4x =千克时,函数()f x 取得最大值,且最大值等于6万元. ………11分 答:当销售价格为4万元/千克时,商场每日销售该商品所获得的利润最大. ……12分 21.(满分12分)本题主要考查直线与圆锥曲线等基础知识,考查运算求解能力、推理论证能力,考查数形结合、化归的思想.
解:(Ⅰ) 解:设1C :)0(12222>>=+b a b
y a x ,∵点(2,0)、(2,22)在椭圆上
代入方程得2
22
4
12112a a b ⎧=⎪⎪⎨⎪+=⎪⎩ …………………………………………2分
解得⎩⎨⎧==1
4
22b a , …………………………………………3分
∴1C 的方程为:2
214
x y += …………………………………………4分 设抛物线2C :px y 22
=)0(≠p ,(4,4)在抛物线上 …………5分
解得2p =, ∴2C :2
4y x =. ……………………………6分
(Ⅱ)设两交点坐标为),(),,(2211y x N y x M ,则联立得2
24x my y x
=+⎧⎨
=⎩ ……7分
消去x 得2
480y my --= ……………………………8分 ∵2
16320m ∆=+>,12.8y y =- ……………………………9分 又2114y x =,2224y x = 可得12.4x x = ……………………………11分
∴12124OM ON x x y y ⋅=+=- ……………………………12分
22.(满分14分)本题主要考查函数与导数等基础知识,考查运算求解能力、推理论证能力,
考查函数与方程思想、化归与转化思想等.
解:(Ⅰ)已知()e x f x x =,得(0)0f = ……………………………………1分
求导得()()1e x f x x '=+ ………………………………………2分 所以()01f '=, ………………………………………3分 所以切线方程为y x = ………………………………………4分 (Ⅱ)令()()1e 0x f x x '=+=,则1x =-.………………………………………5分
当x 变化时,()(),f x f x '的变化情况如下表:
x (),1-∞-
1-
()1,-+∞
()f x ' -
+
()f x
递减
极小值
递增
………………………………………7分
所以()f x 在区间(),1-∞-内是减函数,在区间()1,-+∞内是增函数 ………8分 函数()f x 在1x =-处取得极小值()1f -,且()1
1e
f -=-
,无极大值. ………9分 (Ⅲ)由题意可构造函数()(1)x
e g x x x =>, …………………………11分 求导得2(1)
()x e x g x x -'= ………………………………………12分
因为1,x >()0g x '> 所以()g x 在+∞(1,)为增函数
所以当1a b >>,()()g a g b >, ………………………………13分
得a b
e e a b
>即.22e e a b b a a b >∴22()()b f a a f b > ………………………14分。
