天津市红桥区2014届下学期高三年级第一次模拟考试数学试卷(文科 有答案)
9-红桥区高三年级模拟考试(一)

红桥区高三年级模拟考试(一) (考试时间:2014年4月3日)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试用时120分钟。
第Ⅰ卷(选择题 共40分)一、选择题:(本大题共8/J~N_。
每小题5分,共40分.在每小题所给出的四个选项中。
只有一项是符合题目要求的)1.复数1ii 1i-++等于( ) A .i - B .1 C .1- D .02.设 cos 12θ⎛⎫= ⎪⎝⎭,a 与 2(c 1o )s θ=-,b 垂直,则cos2θ的值等于( ) A. B .12- C .0 D .1-3.设m 、n 是两条不同的直线,α、β是两个不同的平面,则( )A .若m ∥ n α,∥α,则m ∥nB. 若m ∥ m α,∥β,则α∥βC .若m ∥ n m α⊥,,则n α⊥D .若m ∥ ααβ⊥,,则m β⊥ 4.一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于()俯视图A.B. C.D.5.·函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间20 ⎡π⎤⎢⎥⎣⎦,上的最小值是( )A. 1-BC. D. 06.已知333log 0.1log 2.7log 4.11 2 22b ac ⎛⎫== =⎪⎝⎭,,,则( ) A .a b c >>B .b a c >>C .a c b >>D .c a b >>7.设0r >,那么直线cos sin x y r θθ+=(θ是常数)与圆cos sin x r y r ϕϕ=⎧⎨=⎩(ϕ是参数)的位置关系是( )A .相交B .相切C .相离D .视r 的大小而定8.·在区间[11] -,上随机取一个数 cos2x r π,等的值介于0到12之间的概率为( )A.12B .2πC.13D.23第Ⅱ卷(非选择题 共110分)二、填空题:(本大题共6小题,每小题5分,共30分,将答案填在题中横线上)9.设集合2{|||4} {|430}B x x A x x x =<=-+>,,则集合 {|}x A x x A B ∉∈= ,且 . 10.设抛物线24y x =上一点P 到直线2x =-的距离为5,则点P 到该抛物线焦点的距离是 .11.二项式6⎛ ⎝展开式中含2x 项的系数是 .12.已知正项等比数列{}n a 满足7652a a a =+,若存在两项 m n a a ,,使14a ,则14m n+的最小值为 . 13.如图,AB 是圆O 的直径,CD AB ⊥于D ,且 2 A D B D E =,为AD 的中点,连接CE 并延长交圆O 于F.若CD =,则EF = .B14.·定义某种运算S a b =⊗,运算原理如图所示,则式子1512tan ln lg10043e -π⎛⎫⎛⎫⊗+⊗ ⎪ ⎪⎝⎭⎝⎭的值为.三、解答题:(本大题共6小题。
天津红桥区高三第一次模拟考试数学(文)试题(扫描)

高三数学(文)本试卷分第I 卷(选择题)和第n 卷(非选择题)两都幼 共1帥分.考试用时no 分钟,第[卷I 至2孤第ij 卷3至6页.答卷前.考生务必将自己的蛭名.准考号填写在答題卡上.井在规定位■粘贴考试用 条晤码.答iffi 时.务必将菩案涂写在答JB 卡上,答在试卷上的无效.考试结束后,将本试 卡一并交回.祝各竝韦生考试颇利! 參考公式『•如果事件X. R 互斥.那么 •公式・"7*茸中$衰乘柱体底面积.占衰示柱体的高.+• «***^式『・耳中需袁示柱体雇術枳,方衰示注体的髙. •球休表血积公式・S = 4nR\其中R 表示球体的丰径-*4•球体体积公式,V^-nR\梵申R 莪示球体的半左.3 *注童事项」r 每小JH 选出答案后.用钮笔把答趣責上对应题目的答褰标号涂JUL 如需改动.用 It皮擦干净后・再选獄其他答案标号.2・本卷共8 Bi 共㈱分.J 、在毎小艇给出的四个选项中.只有一项是符合HSK5R 的.(»> i 是虚敷单fib R«^=1 ~2ix^2y^2,(2)设变量工j 潤足酌東罢件V" F 鼻$则目标函9Hz = -x-y 的量大值为 '|/事"2,(3)已知命题p : Sx€ R t x 2+2dur + a + 2^0.若命题卩是假命题•则实数。
的取值范国是(A) (-2J) (B) [-1,2] (C) (-1,2} (D) (0, 2]高三敷学(文科〉第1页(共®頁)(A)(A) 0(B) V CC)"(4)已to a = iog OT 0^ * = 2M t C = log 20.9,t 则(S 》执行如图的程序框图.输入x=-2.那么输出的各个数的和等于(A) 0CB) 1 (0 2<D> 3(6)以抛物线y 2= 20x 的焦点为圆心.且与双曲线= i 的渐近线相切的圆的方程为 9 16+/ *16(B) (x + 5):+/=4 (C) (x-10)'+/ =64 (D) (x-5)!+r = 4(?)若»«t y = 5in(2x + ^) + ^cos(2^ + 为奇确数.且在[0芒]上是减函数,则卩的一个 4值是 (A)壬(B) —(C) —(D)—3333<8)吕知/⑴是定文在[-“]上的奇函数*满足r ⑴… 且当/底卜1,小 *界o,'-*•■ . 1 >有V若/V) W m :-2^1+1 (M 0),对所有的"[-1J ] t a€ [-IJ ]恒成立*4j + n实数册的取值范围是.:(A) (-2,2)(B) (-2,0)ME (0,2)(C) (Y .-2]或(D) (-2,-1)或(匕2)高三敷学(文科)<.m2页(共玉S )--■<H1tt■ I(A) a<6<c(B) a<c<b<C) c<6<a(D) c<a<bJJ B第II卷注意事项r用黑色靂水的钢笔或签字笔将答案写在答题卡上*» * » ■二*填空本大題共B个小题,毎小甄5分,共加分*■沙)某班同学利用国庆节进行社会实践.对[25,55]岁的人群1»机抽取獰人班行了一决生活习tfIJft否符合低碳观念的调査「若生活习惯符合低碳观念的称为理低碳族匕若则称为*•非低碳娱3褂到如下藐计浪,但由于不小心表中字母衰示的部分失.現知遭檢M査的人申低碳集占65%.则40岁及其以上人群中.低碳族占该部分人数的频率为请将弄余再在苓亀卓上.分组|组内人数频率低碳族的人数第一组[25,30)2001 0.2no '第二组[30.35)30003196第三组[3530)110a100第四组[40,45)2507 b~ c ~ _第五组[45.50)X30I第六组{50,55)y J24(10)若西数/(x)-/;丈〔则不等式Ax) > -2的解集为it出沁崔菱亦x - 2x - x 1(11 > 已知/二{l,2,3}B = (r €/?” 一朋+ ! = 0卫€ 川}・则AC\B - B时口的值是(12)如图所禾,圆。
数学_2014年天津市五区县高考数学一模试卷(文科)(含答案)

2014年天津市五区县高考数学一模试卷(文科)一、选择题(共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.)1. 已知全集U=R,集合A=﹛x|x−2>0﹜,B=﹛x|x|≤1﹜.则(∁U A)∪B=()A {x|−1≤x≤1}B {x|−1≤x≤1或x>2}C {x|−1≤x≤2}D {x|x≤2}2. 设双曲线x z−y z=1的两条渐近线与直线x=3围成的平面区域D内(包括边界)的任一点为(x, y),则目标函数z=x+4y的最大值为()A 15B 12C 9D 03. 阅读如图的程序框图,运行相应的程序,则输出S的值为()A 2013×1006B 2013×1007C 2015×1007D 2015×10084. “a>1”是“函数y=x2−2ax+a有两个零点”的()A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件5. 点P(2, −1)为圆(x−1)2+y2=25的弦AB的中点,则直线AB的方程为()A x+y−1=0B 2x+y−3=0C x−y−3=0D 2x−y−5=06. 当x∈[−π2, π2]时,函数f(x)=sinx+√3cosx的最大值与最小值分别是()A 1,−1B 1,−12C 2,−2D 2,−17. 已知x=log32,y=log95,z=0.5−0.2,则()A x<y<zB z<x<yC z<y<xD y<z<x8. 定义一种新运算:a⊗b={b,a≥ba,a<b,已知函数f(x)=(1+2x)⊗3log2(x+1),若方程f(x)−k=0恰有两个不相等的实根,则实数k的取值范围为()A (−∞, 3)B (1, 3)C (−∞, −3)∪(1, 3)D (−∞, −3)∪(0, 3)二、填空题:本大题共6小题,每小题5分,共30分.9. i是虚数单位,5i3−4i=________.10. 如图是某几何体的三视图,则该几何体的体积等于________.11. 若抛物线y2=2px的焦点与双曲线x2−y2=2的右焦点重合,则p的值为________.12. 在△ABC中,已知AB=2,BC=3,∠ABC=60∘,AH⊥BC于H,M为AH的中点,若AM →=λAB →+μBC →,则λ+μ=________.13. 如图,已知圆中两条弦AB 与CD 相交于点F ,且DF =CF =√2,E 是AB延长线上一点,AF:BF:BE =4:2:1,若CE 与圆相切,则线段CE 的长为________.14. 若满足ab =a +b +3的任意正数a ,b 均有|x −6|≤ab ,则实数x 的取值范围是________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15. 某学校甲、乙两个班参加体育达标测试,统计测试成绩达标人数情况得到如下所示的列联表,已知在全部学生中随机抽取1人为不达标的概率为110.(1)请完成列联表;(2)若用分层抽样的方法在所有测试不达标的学生中随机抽取6人,问其中从甲、乙两个班分别抽取多少人?(3)从(2)中的6人中随机抽取2人,求抽到的两人恰好都来自甲班的概率. 16. △ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知a =2√3,cosA =−12,b =2. (1)求c 的值;(2)设f(x)=cos2x +2sin 2(x +B),求函数f(x)的单调递增区间.17. 如图,在三棱柱ABC −A 1B 1C 1中,B 1B ⊥平面A 1B 1C 1,AC =CB =CC 1=2,∠ACB =90∘,D ,E 分别是A 1B 1,CC 1的中点. (1)求证:C 1D // 平面A 1BE ;(2)求证:平面A 1BE ⊥平面AA 1B 1B ;(3)求直线BC 1与平面A 1BE 所成角的正弦值.18. 在等差数列{an}和正项等比数列{bn}中,a 1=b 1=1,b 2⋅b 4=16,{a n }的前8项和S 8=92.(1)求{a n }和{b n }的通项公式; (2)令T n =a 1bn+1+a 2bn+2+...+an b 2n⋅n ∈N ∗,求T n .19. 已知椭圆C:x 2a 2+y 2b 2=1(a >b >0),D(1, 0),过椭圆C 的焦点F(√2, 0)且垂直于1x 轴的直线与椭圆交于A ,B 两点,OA →⋅OB →=53. (1)求椭圆C 的方程;(2)过点D 的直线与椭圆C 交于M ,N 两点,若MD →=2DN →,求直线MN 的方程; (3)设直线y =kx +2交椭圆于P ,Q 两点,若DP →⋅DQ →=0,求k 的值.20. 已知函数f(x)=x 3−3x 的图象和函数g(x)=2x 2+x +m 的图象在y 轴右侧有两个不同的交点,设两个交点分别为A(x 1, y 1),B(x 2, y 2). (1)求实数m 的取值范围;(2)设直线AB 的斜率为k ,求证:x 1x 2<2(x 1+x 2−2)<k .2014年天津市五区县高考数学一模试卷(文科)答案1. D2. A3. B4. A5. C6. D7. A8. C9. −45+35i 10. 54π 11. 4 12. 2313. √72 14. [−3, 15]15. 解:(1)在全部学生中随机抽取1人为不达标的概率为110,总人数为120,故不达标的人数为12,达标的人数为108,乙班不达标为4人,甲班达标的人数为54,故有(2)由表可知:用分层抽样的方法从甲班抽取的人数为812×6=4人,…从乙班抽取的人数为412×6=2人…(3)设从甲班抽取的人为a,b,c,d,从乙班抽取的人为1,2;“抽到的两个人恰好都来自甲班”为事件A.…所得基本事件共有15种,即:ab,ac,ad,a1,a2,bc,bd,b1,b2,cd,c1,c2,d1,d2,12…其中事件A包含基本事件ab,ac,ad,bc,bd,cd,共6种,…由古典概型可得P(A)=615=25…16. 解:(1)在△ABC中,由a=2√3,cosA=−12,b=2,∴ cosA=b2+c2−a22bc =4+c2−124c=−12,解得:c=2或c=−4(舍去),则c的值为2;(2)∵ cosA=−12,A为三角形的内角,∴ A=2π3,∵ b=c=2,∴ B=C=π6,∴ f(x)=cos2x+2sin2(x+π6)=cos2x+1−cos(2x+π3)=cos2x−12cos2x+√32sin2x+1=12cos2x+√32sin2x+1=sin(2x+π6)+1,即f(x)=sin(2x+π6)+1,令2kπ−π2≤2x+π6≤2kπ+π2(k∈Z),得到kπ−π3≤x≤kπ+π6(k∈Z),则f(x)的单调递增区间为[kπ−π3, kπ+π6](k∈Z).17. (1)证明:取AB的中点F,连接DF交A1B于点M,可知M为DF中点,连接EM,易知四边形C1DME为平行四边形,所以C1D // EM.又C1D⊄平面A1BE,EM⊂平面A1BE,所以C1D // 平面A1BE.(2)证明:因为A1C1=C1B1,且D是A1B1的中点,所以C1D⊥A1B1.因为BB1⊥平面A1B1C1,所以BB1⊥C1D.所以C1D⊥平面AA1B1B.又C1D // EM,所以EM⊥平面AA1B1B.又EM⊂平面A1BE,所以平面A1BE⊥平面AA1B1B.(3)解:如图建立空间直角坐标系C −xyz ,则B(0, 2, 0),C 1(0, 0, 2),E(0, 0, 1),A 1(2, 0, 2), 所以BC 1→=(0, −2, 2),EA 1→=(2, 0, 1),EB →=(0, 2, −1). 设平面A 1BE 的法向量为n →=(x, y, z),则{2x +z =0,2y −z =0,令x =1,则n →=(1, −1, −2), 所以cos <BC 1→,n →>=BC 1→⋅n→|BC 1→||n →|=−√36, 所以直线BC 1与平面A 1BE 所成角的正弦值为√36.18. 解:(1)设{an}解得的公差为d ,{bn}的公比为q ,q >0依题意 S 8=8+8×72×d =92,b 2⋅b 4=b 32=q 4=16解得d =3,q =2.∴ a n =1+(n −1)×3=3n −2, b n =1×2n−1=2n−1 (2)T n =12n +42n+1+72n+2+⋯+3n−222n−1①12T n=12n+1+42n+2+72n+3+⋯+3n−522n−1+3n−222n②①-②得12T n =12n +3(12n+1+12n+2+12n+3+⋯+122n−1)−3n−222n=12n +3×12n+1(1−12n−1)1−12−3n −222n =42n −3n +422n ∴ T n =82n −6n+822n19. 解:(1)由已知得A(√2, b 2a ),B(√2, −b 2a ), ∴ OA →⋅OB →=2−b 4a 2=53,得b 4a 2=13,又a 2=b 2+2,∴ a 2=3,b 2=1, ∴ 椭圆C 的方程为x 23+y 2=1.(2)若直线MN 的斜率为0,则MD →≠2DN →, 若直线MN 的斜率不为0,设MN:x =ty +1, 代入x 23+y 2=1,得(t 2+3)y 2+2ty −2=0, 由MD →=2DN →,得y 1=−2y 2, y 1+y 2=−y 2=−2t t 2+3,y 1y 2=−2y 22=−2t 2+3,整理,得−2(2tt 2+3)2=−2t 2+3,解得t =±1, 直线MN 的方程:x =±y +1,即y =x −1或y =−x +1. (3)将y =kx +2代入x 23+y 2=1,得(3k 2+1)x 2+12kx +9=0,(∗)记P(x 3, y 3),Q(x 4, y 4),则x 3+x 4=−12k 3k 2+1,①,x 3x 4=93k 2+1,②,PD →⋅QD →=(x 3−1, y 3)⋅(x 4−1, y 4)=(x 3−1)(x 4−1)+y 3y 4=0, 又y 3=kx 3+2,y 4=kx 4+2,∴ (k 2+1)x 3x 4+(2k −1)(x 3+x 4)+5=0,③ 将①②代入③,得: k =−76,此时(∗)中,△>0.∴ k =−76.20. (1)解:f(x)=x 3−3x ,g(x)=2x 2+x +m , 令ℎ(x)=f(x)−g(x)=x 3−2x 2−4x −m , 则ℎ′(x)=3x 2−4x −4.由ℎ′(x)=0,得:x =−23,x =2.当x ∈(0, 2)时,ℎ′(x)<0,ℎ(x)为增函数; 当x ∈(2, +∞)时,ℎ′(x)>0,ℎ(x)为减函数. 又ℎ(0)=−m ,ℎ(2)=−8−m .且f(x)与g(x)的图象的两个交点都在y 轴右侧, ∴ {−m >0−m −8<0,解得:−8<m <0;(2)证明:由(1)知,0<x 1<2,x 2>2.∴ (x 1−2)(x 2−2)<0,即x 1x 2−2(x 1+x 2)+4<0, x 1x 2<2(x 1+x 2−2).∵ y 1=2x 12+x 1+m ,y 2=2x 22+x 2+m .∴ y1−y2=(x1−x2)(2x1+2x2+1).∴ k=y1−y2x1−x2=2(x1+x2+12).∵ 2(x1+x2+12)>2(x1+x2−2),∴ x1x2<2(x1+x2−2)<k.。
天津市红桥区高三下学期数学一模试卷附解析
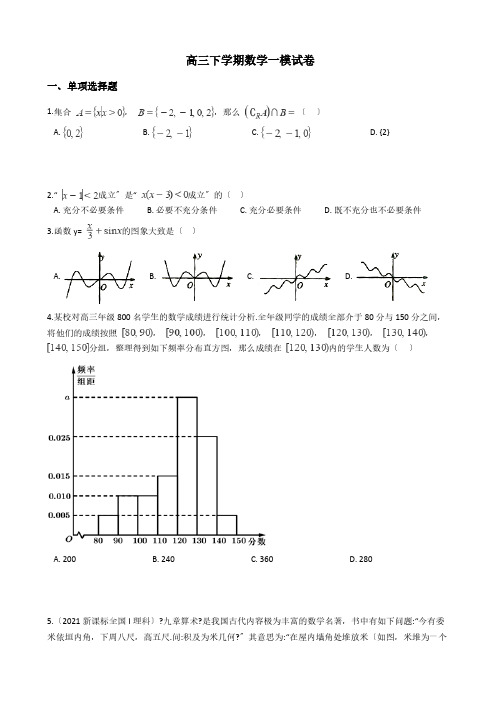
高三下学期数学一模试卷一、单项选择题1.集合,,那么〔〕A. B. C. D. {2}2.“ 成立〞是“ 成立〞的〔〕A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件3.函数y= 的图象大致是〔〕A. B. C. D.4.某校对高三年级800名学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间,将他们的成绩按照,,,,,,分组,整理得到如下频率分布直方图,那么成绩在内的学生人数为〔〕A. 200B. 240C. 360D. 2805.〔2021新课标全国I理科〕?九章算术?是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?〞其意思为:“在屋内墙角处堆放米〔如图,米堆为一个圆锥的四分之一〕,米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?〞1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有〔〕A. 14斛B. 22斛C. 36斛D. 66斛6.函数在区间内单调递增,且,假设,,,那么、、的大小关系为〔〕A. B. C. D.7.抛物线上一点到其焦点的距离为,双曲线的左顶点为,假设双曲线的一条渐近线与直线平行,那么实数的值是〔〕A. B. C. D.8.函数,,给出以下四个命题:①函数的最小正周期为;②函数的最大值为1;③函数在上单调递增;④将函数的图象向左平移个单位长度,得到的函数解析式为.其中正确命题的个数是〔〕A. 1 B. 2 C. 3 D. 49.函数,,假设关于x的方程恰有三个不相等的实数解,那么m的取值范围是〔〕A. B.C. D.二、填空题10.i是虚数单位,那么复数________.11.的展开式中,项的系数为________.12.直线与圆心为的圆相交于两点,且为等边三角形,那么实数________.A,B两队参加建党100周年知识竞赛,每队3人,每人答复一个问题,答对者为本队赢1分,答错得0分;A队中每人答对的概率均为,B队中3人答对的概率分别为,,,且各答题人答题正确与否互不影响,假设事件M表示“A队得2分〞,事件N表示“B队得1分〞,那么________.14. ,,且,那么最小值为________.15.在等腰梯形中, ,动点和分别在线段和上,且, 那么的最小值为________.三、解答题16. 的内角A,B,C的对边分别为a,b,c,满足〔1〕求角B的大小;〔2〕假设,求的值;〔3〕假设,,求边a的值.17.如下列图,直角梯形中,,,,四边形EDCF为矩形,,平面平面.〔1〕求证:平面;〔2〕求平面与平面所成锐二面角的余弦值.18.如图,椭圆经过点,且离心率为.(I)求椭圆的方程;(II)经过点,且斜率为的直线与椭圆交于不同两点〔均异于点〕,问:直线与的斜率之和是否为定值?假设是,求出此定值;假设否,说明理由.19.数列的前n项和满足:,.〔1〕求数列的前3项,,;〔2〕求证:数列是等比数列:〔3〕求数列的前n项和.20.函数,.〔1〕假设,求曲线在点处的切线方程;〔2〕当时,求函数的单调区间和极值;〔3〕假设对于任意,都有成立,求实数m的取值范围.答案解析局部一、单项选择题1.【解析】【解答】据题意,所以。
2014年普通高等学校招生全国统一考试数学文试题(天津卷, 解析版)

x2014年普通高等学校招生全国统一考试(某某卷)数学(文史类)解析本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的某某、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2本卷共8小题,每小题5分,共40分。
参考公式:•如果事件A ,B 互斥,那么•圆锥的体积公式13V Sh =. ()()()P A B P A P B =+其中S 表示圆锥的底面面积,•圆柱的体积公式V Sh =.h 表示圆锥的高. 其中S 表示棱柱的底面面积,h 表示棱柱的高.一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)i 是虚数单位,复数734i i( )(A )1i (B )1i (C )17312525i (D )172577i 解:73472525134343425i i i i i i i i,选(2)设变量x ,y 满足约束条件0,20,12,y x y y x +-⎧≥--≤≥⎪⎨⎪⎩则目标函数2z x y =+的最小值为( )(A )2 (B )3 (C )4 (D )5 解:作出可行域,如图结合图象可知,当目标函数通过点1,1时,z 取得最小值3,选B. (3)已知命题p :0x,总有11xx e ,则p 为( )(A )00x ,使得011x x e (B )00x ,使得011x x e(C )0x ,总有11x x e (D )0x,总有11xx e解:依题意知p 为:00x ,使得0011x x e ,选B.(4)设2log a,12log b,2c,则( )(A )a b c (B )b a c (C )ac b (D )c b a解:因为1a,0b ,01c,所以acb ,选C.(5)设n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和.若124,,S S S 成等比数列,则1a ( )(A )2 (B )-2 (C )12 (D )12- 解:依题意得2214S S S ,所以21112146a a a ,解得112a ,选D. (6)已知双曲线22221x y a b 0,0a b 的一条渐近线平行于直线l :210yx,双曲线的一个焦点在直线l 上,则双曲线的方程为( )(A )221520x y (B )221205x y (C )2233125100x y (D )2233110025x y解:依题意得22225ba cc a b ,所以25a,220b ,选A.(7)如图,ABC 是圆的内接三角形,BAC 的平分线交圆于点D ,交BC 于点E ,过点B 的圆的切线与AD 的延长线交于点F .在上述条件下,给出下列四个结论:①BD 平分CBF ;②2FB FD FA ;③AE CE BE DE ;④AF BDAB BF .FED CBA 则所有正确结论的序号是( )(A )①② (B )③④ (C )①②③ (D )①②④ 解:由弦切角定理得FBD EAC BAE ,又BFD AFB ,所以BFD ∽AFB ,所以BF BDAFAB, 即AF BD AB BF ,排除A 、C. 又FBDEACDBC ,排除B ,选D.(8)已知函数3sin cos f x x x0,x R ,在曲线y f x 与直线1y 的交点中,若相邻交点距离的最小值为3,则f x 的最小正周期为( )(A )2(B )23(C ) (D )2 解:因为2sin6f x x,所以1f x得1sin 62x, 所以266xk或5266xk ,k Z .因为相邻交点距离的最小值为3,所以233,2,T,选C.第Ⅱ卷注意事项: 1.答卷前将密封线内的项目填写清楚。
2014年天津市高考数学试卷(文科)答案与解析

2014年天津市高考数学试卷(文科)参考答案与试题解析一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2014•天津)i是虚数单位,复数=()+i +i 解:复数==2.(5分)(2014•天津)设变量x,y满足约束条件,则目标函数z=x+2y的最小值为()e≤e≤e≤4.(5分)(2014•天津)设a=log2π,b=logπ,c=π,则()logn1n124成等比数列,得:即,解得:6.(5分)(2014•天津)已知双曲线﹣=1(a>0,b>0)的一条渐近线平行于直线l:y=2x+10,双曲线的﹣=1 B﹣=1﹣=1 D﹣=1先求出焦点坐标,利用双曲线﹣=1=2∵双曲线﹣=2∴双曲线的方程为﹣的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分∠CBF;②FB2=FD•FA;③AE•CE=BE•DE;④AF•BD=AB•BF.由由若相邻交点距离的最小值为,则f(x)的最小正周期为()x+的交点中,相邻交点距离的最小值为,)的周期的=x+的交点中,若相邻交点距离的最小值为,正好等于)的周期的=正好等于倍,是解题的关键,9.(5分)(2014•天津)某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方向,从该校四个年级的本科生中抽取一个容量为300的样本进行调查,已知该校一年级、二年级、三年级、四年级的本解:根据分层抽样的定义和方法,一年级本科生人数所占的比例为=,×10.(5分)(2014•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.4+ππ故答案为:.复合而成,再分别讨论内层函数和外层函数的单调性,根据方法二:原函数是由复合而成,DC=λDF,若•=1,则λ的值为2.=,,=++=,=++=,||=|••=1∴()+)•××)整理得14.(5分)(2014•天津)已知函数f(x)=,若函数y=f(x)﹣a|x|恰有4个零点,则实(Ⅰ)用表中字母列举出所有可能的结果;.16.(13分)(2014•天津)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a﹣c=b,sinB=sinC,(Ⅰ)求cosA的值;(Ⅱ)求cos(2A﹣)的值.sinB=b=bcosA==;cosA=sinA==﹣sin2A=2sinAcosA=,﹣=cos2Acos=×+×=.E,F分别是棱AD,PC的中点.(Ⅰ)证明EF∥平面PAB;(Ⅱ)若二面角P﹣AD﹣B为60°,(i)证明平面PBC⊥平面ABCD;BA=BD=PA=PD=PB=BA=BD=,﹣,,),=,﹣,),),的法向量为,∴,令=,,﹣),=,),===所成角的正弦值为18.(13分)(2014•天津)设椭圆+=1(a>b>0)的左、右焦点分别为F1、F2,右顶点为A,上顶点为B,已知|AB|=|F1F2|.(Ⅰ)求椭圆的离心率;(Ⅱ)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过点F2的直线l与该圆相切于点解:(Ⅰ)依题意可知==.∴椭圆方程为=1点坐标(•或,坐标为(﹣,c cr=|OB|===+8=c∴椭圆的方程为+19.(14分)(2014•天津)已知函数f(x)=x2﹣ax3(a>0),x∈R.(Ⅰ)求f(x)的单调区间和极值;))时,(B={.)(,单调递增区间为)))时,(B={|x><)<时,有([A={x|x=x1+x2q+…+x n q n﹣1,x i∈M,i=1,2,…n}.(Ⅰ)当q=2,n=3时,用列举法表示集合A;(Ⅱ)设s,t∈A,s=a1+a2q+…+a n q n﹣1,t=b1+b2q+…+b n q n﹣1,其中a i,b i∈M,i=1,2,…,n.证明:若a n<b n,A={x|+≤A={x|,11。
【2014红桥一模】天津市红桥区2014届高三第一次模拟考试 数学(文) 扫描版含答案

高三数学(文)答案(2014、04)一、选择题:本大题共8小题,每小题5分,满分40分. 题号1 2 3 4 5 6 7 8 答案 D B C C A B D C二、填空题:本大题共6小题,每小题5分,满分30分.9.{}4314<<<<-x x x 或 10.3 11.4 12.3 13.23 14.13三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.15.(本小题满分13分)(Ⅰ)因为sinC=2sinA 21sin sin ==∴C A c a .............................................2 522==∴BC AB . (4)(Ⅱ)bc a c b A 2cos 222-+==552……………………………7 55cos 1sin 2=-=∴A A …………………..8 所以54cos sin 22sin ==A A A 531c o s 22c o s 2=-=A A ..…10 sin 24A π⎛⎫- ⎪⎝⎭=4sin 2cos 4cos 2sin ππA A -102= (13)16.(本小题满分13分)(Ⅰ) ① 树形图:……………………………………2 ②所以爸爸抽出的牌的牌面数字比4大的概率是32 (4)(Ⅱ)不公平,理由如下: (5)…………………………………………….9 爸爸抽出的牌的牌面数字比亮亮的大有5种情况,其余均为小于等于亮亮的牌面数字 所以爸爸胜的概率只有125,显然对爸爸来说是不公平的.................................11 只需把黑5改成3即可 (13)17.(本小题满分13分)(Ⅰ)在等边三角形ABC 中,AD AE = A D A E D B E C ∴= (1)在折叠后的三棱锥A BCF -中 也成立,//DE BC ∴ .........................................2 DE ⊄ 平面BCF , BC ⊂平面BCF ,//DE ∴平面BCF ...................................4 (Ⅱ)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥,12BF CF == (5)在三棱锥A BCF -中,22BC =,222BC BF CF CF BF ∴=+∴⊥ …………7 BF CF F CF ABF ⋂=∴⊥ 平面 ………………………………………………9 (Ⅲ)由(Ⅰ)可知//GE CF ,结合(Ⅱ)可得GE DFG ⊥平面.11111131332323323324F DEG E DFG V V DG FG GF --⎛⎫∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎪ ⎪⎝⎭ (13)18.(本小题满分13分)…………………………………..13(Ⅰ)当1a =时, (1)所以2()6126(2)242466f x x x f ''=-+∴=-+=…………………………4 ()y f x =在(2,(2))f 处的切线方程是:46(2)680y x x y -=-⇒--=…..6 (Ⅱ)22()66(1)66[(1)]6(1)()f x x a x a x a x a x x a '=-++=-++=-- (8)①当1a >时,时,()y f x =递增,(1,)x a ∈时,()y f x =递减 所以当 [0,2||]x a ∈时,且2||2a >,时,()y f x =递增,(1,)x a ∈时,()y f x =递减 (10)所以最小值是32223()23(1)63f a a a a a a a =-++=- ②当1a <-时,且2||2a >,在[0,2||]x a ∈时,(0,1)x ∈时,()y f x =递减,[1,2||]x a ∈时,()y f x =递增,所以最小值是(1)31f a =- 综上所述:当1a >时,函数()y f x =最小值是233a a -;当1a <-时,函数()y f x =最小值是31a - (13)19.(本小题满分14分) 解:(Ⅰ)由题意可知,b=1, 又因为23==a c e ,且a 2=b 2+c 2,解得a=2 所以椭圆的方程为1422=+y x ………………………………………………4 (Ⅱ)由题意可得:A (﹣2,0),B (2,0).设P (x 0,y 0),由题意可得:﹣2<x 0<2,所以直线AP 的方程为)2(200++=x x y y …………………………………6 令,则)222(200++=x y y , 即2)222(00++=x y DE (8)同理:直线BP 的方程为)2(200--=x x y y , 令,则)222(200--=x y y , 即2)222(00--=x y DF ………………………………………………………10 所以=202020204444x y x y -=-……………………………………………………..12 而,即4y 02=4﹣x 02,代入上式,所以|DE|.|DF|=1,所以|DE|.|DF|为定值1. (14)20.(本小题满分14分) (Ⅰ)在11()22n n n S a -=--+中,令n=1,可得1112n S a a =--+=,即112a =..............1 当2n ≥时,21111111()2()22n n n n n n n n n S a a S S a a ------=--+∴=-=-++,, (4) (5)112,1,n 21n n n n n n b a b b b --=∴=+≥-= n 即当时,b (6)又1121,b a ==∴数列}{n b 是首项和公差均为1的等差数列.............................................7 于是1(1)12,2n n n n n n b n n a a =+-⋅==∴=.........................................................................9 (II)由(I )得11(1)()2n n n n c a n n +==+,所以 (10)由①-②得11111[1()]133421(1)()122212332n n n n n n n n T -++-+=+-+=--+∴=- 023>+n n 所以3<n T (14)。
天津市红桥区2014届高三第一次模拟数学(理)试题

天津市红桥区2014届高三第一次模拟考试数学(理)试题本试卷分为第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结束后,将本试卷和答题卡一并交回。
第I卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A,B互斥,那么P(AB)=P(A)+P(B)如果事件A,B相互独立,那么P(AB)=P(A)P(B).棱柱的体积公式V=Sh.其中S表示棱柱的底面面积 h表示棱柱的高圆锥的体积公式V=Sh.其中S表示圆锥的底面面积h表示圆锥的高一、选择题:在每小题给出的四个选项中只有一项是符合题目要求的。
1.复数等于A. -i B.1 C. -l D.02.设与垂直,则的值等于A. B. C.0 D.-l3.设m、n是两条不同的直线,、是两个不同的平面,则A.若m//,n//,则m//n B.若m//,m//,则//C.若m//n,m,则n D.若m//,,则m4.一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于A.4B.3C.2D.5.函数在区间上的最小值是A.-l B. C. D.06.已知,,则A. a>b>c B.b>a>c C.a>c>b D.c>a>b7.设r>0,那么直线(是常数)与圆(是参数)的位置关系是A.相交 B.相切 C.相离 D.视r的大小而定8.在区间上随机取一个数x,的值介于0到之间的概率为A. B. C. D.第II卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上.2.本卷共12小题,共110分.二.填空题:本大题共6小题,每小题5分,共30分。
6-2014红桥区高三年级模拟考试(一)

6 2014红桥区高三年级模拟考试(一)(考试时间:2014年4月3日)理科综合分为物理、化学、生物三部分,共300分,考试用时150分钟。
物理试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共100分。
祝各位考生考试顺利! 以下数据可供解题时参考:相对原子质量:H 1C 12N 14O 16Na 23Cl 35.5------第Ⅰ卷(选择题 共36分)本卷共6题,每小题6分,共36分。
每小题给出的四个选项中,只有一个选项是最符合题目要求的。
1.下列有关说法正确的是( )A .苯酚沾到皮肤上,应立即用浓NaOH 溶液洗涤B .为了防止蛋白质盐析,疫苗等生物制剂应冷冻保藏C .亚硝酸钠是一种食品防腐剂,使用时其用量可以不加限制D .回收废弃塑料制成燃油替代汽、柴油,可减轻环境污染和节约化石能源 2.下列说法正确的是( )A .所有的复分解反应都是非氧化还原反应B .能与酸反应的氧化物,一定是碱性氧化物C .同一元素不可能既表现金属性,又表现非金属性D .以共价键形成的单质中只存在非极性键,以共价键形成的化合物中只存在极性键 3.下列解释事实的化学方程式或离子方程式不正确的是( ) A .钢铁发生吸氧腐蚀:()2222Fe O 2H O 2Fe OH ++=B .2SO 使紫色石蕊溶液变红色:2223SO H O 2H SO +-+=+C .利用NaOH 溶液除去金属铝表面的氧化膜:2322Al O 2OH 2AlO H O --+=+D .84消毒液和洁厕灵混合使用会产生有毒气体:22Cl ClO 2H Cl H O --+++=↑+ 4.下列说法正确的是( )A .图①铜锌原电池工作时,盐桥中的K +移向4ZnSO 溶液B .图②装置反应一段时间,将湿润的KI 淀粉试纸靠近碳电极管口,试纸变蓝C .图③是用海水制取蒸馏水的装置D .图④装置可用于乙醇提取碘水中的碘5.常温下,某氨水的pH a =,某盐酸的pH b =,已知a b 14+=,将上述氨水与盐酸等体积混合后,所得溶液中各种离子浓度的关系正确的是( )A .()()()()4NH ClH OH +-+->>>c c c c B .()()()()4444NH NH NH NH ++++>>>c c c cC .()()()()4Cl NH HOH -++->>>c c c c D .()()()()4NH HCl OH ++--+=+c c c c 已知:()()()252533325O O O||||||C H O C OC H g CH O C OCH g 2CH O C OC H g --+---- 是碳酸甲乙酯的工业生产原理。
数学_2014年天津市某校高考数学模拟试卷(10)(文科)(含答案)

2014年天津市某校高考数学模拟试卷(10)(文科)一.选择题1. 已知集合A ={x ∈R||x|≤2},B ={x ∈R|x ≤1},则A ∩B =( ) A (−∞, 2] B [1, 2] C [−2, 2] D [−2, 1]2. 设变量x ,y 满足约束条件{3x +y −6≥0x −y −2≤0y −3≤0 ,则目标函数z =y −2x 的最小值为( )A −7B −4C 1D 23. 阅读如图所示的程序框图,运行相应的程序,则输出n 的值为( )A 7B 6C 5D 44. 设a ,b ∈R ,则“(a −b)a 2<0”是“a <b”的( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分也不必要条件 5. 已知过点P(2, 2)的直线与圆(x −1)2+y 2=5相切,且与直线ax −y +1=0垂直,则a =( )A −12 B 1 C 2 D 126. 函数f(x)=sin(2x −π4)在区间[0, π2]上的最小值是( ) A −1 B −√22 C √22D 0 7. 已知函数f(x)是定义在R 上的偶函数,且在区间[0, +∞)单调递增.若实数a 满足f(log 2a)+f(log 12a)≤2f(1),则a 的取值范围是( )A [1, 2]B (0,12] C [12,2] D (0, 2]8. 设函数f(x)=e x +x −2,g(x)=lnx +x 2−3.若实数a ,b 满足f(a)=0,g(b)=0,则( )A g(a)<0<f(b)B f(b)<0<g(a)C 0<g(a)<f(b)D f(b)<g(a)<0二.填空题9. i 是虚数单位.复数(3+i)(1−2i)=________.10. 已知一个正方体的所有顶点都在一个球面上.若球的体积为9π2,则正方体的棱长为________.11. 已知抛物线y 2=8x 的准线过双曲线x 2a 2−y 2b 2=1(a >0,b >0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________x 2−y 23=1 .12. 在平行四边形ABCD 中,AD =1,∠BAD =60∘,E 为CD 的中点.若AC →⋅BE →=1,则AB 的长为________.13. 如图,在圆内接梯形ABCD 中,AB // DC ,过点A 作圆的切线与CB 的延长线交于点E .若AB =AD =5,BE =4,则弦BD 的长为________. 14. 设a +b =2,b >0,则12|a|+|a|b的最小值为________.三.解答题15. 某小组共有A 、B 、C 、D 、E 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如表所示:(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率 (2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5, 23.9)中的概率.16. 在锐角△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2asinB =√3b . (1)求角A 的大小;(2)若a =6,b +c =8,求△ABC 的面积.17. 如图所示,四棱锥P −ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60∘,E 是CD 的中点,PA ⊥底面ABCD ,PA =2. (1)证明:平面PBE ⊥平面PAB ;(2)求平面PAD 和平面PBE 所成二面角(锐角)的大小.18. 已知动点M(x, y)到直线l:x =4的距离是它到点N(1, 0)的距离的2倍. (1)求动点M 的轨迹C 的方程;(2)过点P(0, 3)的直线m 与轨迹C 交于A ,B 两点.若A 是PB 的中点,求直线m 的斜率.19. 等比数列{a n }的各项均为正数,且2a 1+3a 2=1,a 32=9a 2a 6.(1)求数列{a n}的通项公式;(2)设b n=log3a1+log3a2+⋯+log3a n,求数列{1b n}的前n项和T n.20. 设a∈[−2, 0],已知函数f(x)={x3−(a+5)x,x≤0x3−a+32x2+ax,x>0(Ⅰ)证明f(x)在区间(−1, 1)内单调递减,在区间(1, +∞)内单调递增;(Ⅱ)设曲线y=f(x)在点P i(x i, f(x i))(i=1, 2, 3)处的切线相互平行,且x1x2x3≠0,证明x1+x2+x3>−13.2014年天津市某校高考数学模拟试卷(10)(文科)答案1. D2. A3. D4. A5. C6. B7. C8. A9. 5−5i10. √311. x2−y23=112. 1213. 15214. 3415. (1)从身高低于1.80的同学中任选2人,其一切可能的结果组成的基本事件有:(A, B),(A, C),(A, D),(B, C),(B, D),(C, D)共6个.由于每个同学被选到的机会均等,因此这些基本事件的出现是等可能的.选到的2人身高都在1.78以下的事件有:(A, B),(A, C),(B, C)共3个.因此选到的2人身高都在1.78以下的概率为P=36=12;(2)从该小组同学中任选2人,其一切可能的结果组成的基本事件有:(A, B),(A, C),(A, D),(A, E),(B, C),(B, D),(B, E),(C, D),(C, E),(D, E)共10个.由于每个同学被选到的机会均等,因此这些基本事件的出现是等可能的.选到的2人的身高都在1.70以上且体重指标都在[18.5, 23.9)中的事件有:(C, D)(C, E),(D, E)共3个.因此选到的2人的身高都在1.70以上且体重指标都在[18.5, 23.9)中的概率P=310.16. 解:(1)由2asinB=√3b,利用正弦定理得:2sinAsinB=√3sinB,∵ sinB≠0,∴ sinA=√32,又A为锐角,则A=π3;(2)由余弦定理得:a2=b2+c2−2bc⋅cosA,即36=b2+c2−bc=(b+c)2−3bc=64−3bc,∴ bc=283,又sinA=√32,则S△ABC=12bcsinA=7√33.17. 解:解法一(1)如图所示,连接BD,由ABCD是菱形且∠BCD=60∘知,△BCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB // CD,所以BE⊥AB.又因为PA⊥平面ABCD,BE⊂平面ABCD,所以PA⊥BE.而PA∩AB=A,因此BE⊥平面PAB.又BE⊂平面PBE,所以平面PBE⊥平面PAB.(2)延长AD、BE相交于点F,连接PF.过点A作AH⊥PB于H,由(1)知平面PBE⊥平面PAB,所以AH⊥平面PBE.在Rt△ABF中,因为∠BAF=60∘,所以,AF=2AB=2=AP.在等腰Rt△PAF中,取PF的中点G,连接AG.则AG⊥PF.连接HG,由三垂线定理的逆定理得,PF⊥HG.所以∠AGH是平面PAD和平面PBE所成二面角的平面角(锐角).在等腰Rt△PAF中,2010=2在Rt△PAB中,AH=AP⋅ABPB =AP⋅AB√AP2+AB2=2√5=2√55.所以,在Rt△AHG中,sin∠AGH=AHAG =2√55√2=√105.故平面PAD和平面PBE所成二面角(锐角)的大小是arcsin√105.解法二:如图所示,以A为原点,建立空间直角坐标系.则相关各点的坐标分别是A(0, 0, 0),B(1, 0, 0),C(32,√32,0),D(12,√32,0),P(0, 0, 2),E(1,√32,0). (1)因为BE ¯=(0,√32,0), 平面PAB 的一个法向量是n 0¯=(0,1,0), 所以BE ¯和n 0¯共线.从而BE ⊥平面PAB . 又因为BE ⊂平面PBE ,故平面PBE ⊥平面PAB .(2)易知PB →=(1,0,−2),BE →=(0,√32,0),PA→=(0,0,−2),AD →=(12,√32,0) 设n →_=(x 1,y 1,z 1)是平面PBE 的一个法向量,则由{n 1→⋅BE →=0˙得{x 1+0×y 1−2z 1=00×x 1+√32y 2+0×z 2=0.所以y 1=0,x 1=2z 1.故可取n 1→=(2, 0, 1). 设n 2→=(x 2,y 2,z 2)是平面PAD 的一个法向量,则由{n 2→⋅AD →=0˙得{0×x 2+0×y 2−2z 2=012x 2+√32y 2+0×z 2=0所以z 2=0,x 2=−√3y 2.故可取n 2→=(√3,−1,0). 于是,cos <n 1→,n 2→>=|n 1→|⋅|n 2→|˙=2√3√5×2=√155. 故平面PAD 和平面PBE 所成二面角(锐角)的大小是arccos√155. 18. 解:(1)点M(x, y)到直线x =4的距离是它到点N(1, 0)的距离的2倍,则|x −4|=2√(x −1)2+y 2,即(x −4)2=4[(x −1)2+y 2], 整理得x 24+y 23=1.所以,动点M 的轨迹是椭圆,方程为x 24+y 23=1;(2)P(0, 3),设A(x 1, y 1),B(x 2, y 2),由A 是PB 的中点,得2x 1=0+x 2,2y 1=3+y 2. 椭圆的上下顶点坐标分别是(0,√3)和(0,−√3),经检验直线m 不经过这两点,即直线m 的斜率k 存在.设直线m 的方程为:y =kx +3. 联立{y =kx +3x 24+y 23=1,整理得:(3+4k 2)x 2+24kx +24=0. x 1+x 2=−24k3+4k 2,x 1x 2=243+4k 2. 因为2x 1=x 2. 则x1x 2+x 2x 1=12+2,得(x 1+x 2)2−2x 1x 2x 1x 2=52,所以(−24k 3+4k 2)2−2⋅243+4k 2243+4k 2=52.即(−24k)2(3+4k 2)⋅24=92,解得k =±32. 所以,直线m 的斜率k =±32. 19. 解:(1)设数列{a n }的公比为q ,由a 32=9a 2a 6得a 32=9a 42, 所以q 2=19.由条件可知各项均为正数,故q =13. 由2a 1+3a 2=1得2a 1+3a 1q =1, 所以a 1=13.故数列{a n }的通项式为a n =13n .(2)b n =log 3a 1+log 3a 2+...+log 3a n =−(1+2+...+n)=−n(n+1)2,故1b n=−2n(n+1)=−2(1n −1n+1),则T n =1b 1+1b 2+...+1b n=−2[(1−12)+(12−13)+...+(1n −1n +1)]=−2nn+1,所以数列{1b n}的前n 项和T n 为−2nn+1.20. (1)令f 1(x)=x 3−(a +5)x(x ≤0),f 2(x)=x 3−a+32x 2+ax(x >0).①f 1′(x)=3x 2−(a +5),由于a ∈[−2, 0],从而当−1<x <0时,f 1′(x)=3x 2−(a +5)<3−a −5≤0,所以函数f 1(x)在区间(−1, 0)内单调递减,②f 2′(x)=3x 2−(a +3)x +a =(3x −a)(x −1),由于a ∈[−2, 0],所以0<x <1时,f 2′(x)<0;当x >1时,f 2′(x)>0,即函数f 2(x)在区间(0, 1)内单调递减,在区间(1, +∞)上单调递增. 综合①②及f 1(0)=f 2(0),可知:f(x)在区间(−1, 1)内单调递减,在区间(1, +∞)内单调递增;(2)证明:由(Ⅰ)可知:f′(x)在区间(−∞, 0)内单调递减,在区间(0,a+36)内单调递减,在区间(a+36,+∞)内单调递增.因为曲线y =f(x)在点P i (x i , f(x i ))(i =1, 2, 3)处的切线相互平行,从而x 1,x 2,x 3互不相等,且f ′(x 1)=f ′(x 2)=f ′(x 3).不妨x 1<0<x 2<x 3,由3x 12−(a +5)=3x 22−(a +3)x 2+a =3x 32−(a +3)x 3+a .可得3x 22−3x 32−(a +3)(x 2−x 3)=0,解得x 2+x 3=a+33,从而0<x 2<a+36<x 3.设g(x)=3x 2−(a +3)x +a ,则g(a+36)<g(x 2)<g(0)=a .由3x 12−(a +5)=g(x 2)<a ,解得−√2a+53<x 1<0,所以x 1+x 2+x 3>−√2a+53+a+33,设t =√2a+53,则a =3t 2−52,∵ a ∈[−2, 0],∴ t ∈[√33,√153], 故x 1+x 2+x 3>−t +3t 2+16=12(t −1)2−13≥−13,故x 1+x 2+x 3>−13.。
天津市红桥区届高三下学期第一次模拟考试数学(文)答案

高三数学(文)(2016、03)一、选择题:每小题5分,共40分二、填空题:每小题5分,共30分.三、解答题:共6小题,共80分. (15)(本小题满分13分)在锐角ABC △中,内角A B C ,,所对的边分别为a b c ,,,且满足2sin b A . (Ⅰ)求角B 的大小;(Ⅱ)若5a c +=,且a c >,b =,求cos(2)A B +. 解:(Ⅰ)因为3a -2b sin A =0,所以3sin A -2sin B sin A =0.--------------------------------------2分 因为sin A ≠0,所以sin B =32. 又B 为锐角,则B =π3.---------------------------------------------5分(Ⅱ)由(Ⅰ)可知,B =π3,因为b =7,根据余弦定理得7=a 2+c 2-2ac cos π3,--------------------7分整理得(a +c )2-3ac =7. 由已知a +c =5,则ac =6.又a >c ,可得a =3,c =2.---------------------------------------9分于是cos A =b 2+c 2-a 22bc =7+4-947=714,故sin A 13cos214A =-,sin 2A =所以11cos(2)cos2cos sin 2sin 14A B A B A B +=-=---------------------------13分 (16)(本小题满分13分)要将两种大小不同的较大块儿钢板,裁成,,A B C 三种规格的小钢板,每张较大块儿钢板可同时裁成的三种规格小钢板的块数如下表:第一种钢板面积为21m ,第二种钢板面积为22m ,今分别需要A 规格小钢板15块,B 规格小钢板27块,C 规格小钢板13块.(Ⅰ)设需裁第一种钢板x 张,第二种钢板y 张,用x y ,列出符合题意的数学关系式,并在给出的平面直角坐标系中画出相应的平面区域;(Ⅱ)在满足需求的条件下,问各裁这两种钢板多少张,所用钢板面积最小? 解:(Ⅰ)由已知,x ,y 满足的数学关系式为2153271300x y x y xy x y +≥⎧⎪+≥⎪⎪+≥⎨⎪≥⎪≥⎪⎩,,,,.--------------------4分 该二元一次不等式组所表示的平面区域为图中的阴影部分.----------------------8分(Ⅱ)设所用钢板的面积为2m z ,则目标函数为2z x y =+.------------------9分把2z x y =+变形为1122y x z =-+,这是斜率为12-,在y 轴上的截距为12z ,随z 变化的一族平行直线.当12z 取最小值时,z 的值最小.又因为x ,y 满足约束条件,所以由图可知,当直线2z x y =+经过可行域上的点M 时,截距12z 最小,即z 最小.-------------------10分解方程组32713x y x y +=⎧⎨+=⎩,,得点M 的坐标为(67),.所以min 62720z =+⨯=.-------------------------------------------------------------------------12分答:在满足需求的条件下,裁第一种钢板6张,第二种钢板7张,所用钢板的面积最小.13分(17)(本小题满分13分)设{}n a 是等差数列,{}n b 是各项都为正数的等比数列(N n *∈),且11a =,13b =,已知2330a b +=,3214a b +=.(Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)设(1)n n n c a b =+⋅,12n n T c c c =+++L ,(N n *∈),求证:3(1)2n n n T a b =+. 解:(Ⅰ)设等差数列{}n a 公差为d ,等比数列{}n b 公比为q依题意:2232921502313d q q q d q ⎧+=⇒--=⎨+=⎩-------------------------2分 解得:3q =,2d =-----------------------------------------------4分所以21n a n =-,3nn b =.------------------------------------------6分(Ⅱ)(1)23n n n n c a b n =+⋅=⋅,211223432(1)323n n n n T c c c n n -=+++=⋅+⋅++-⋅+⋅L L ①231323432(1)323n n n T n n +=⋅+⋅++-⋅+⋅L ②②得:23122(3333)23n n n T n +-=++++-⋅L ,-------------------------------------8分113(13)2133()31322n n n n n T n ++--=⋅-=⋅+-------------------------------------------------------9分 因为1333213(1)(21)3()322222n n n n n a b n +-+=-+=+ 所以3(1)2n n n T a b =+.---------------------------------------------------------------------------------13分 (18)(本小题满分13分)如图,在三棱锥P ABC -中,点D ,E ,F 分别为棱PC ,AC ,AB 的中点.已知PA ⊥平面ABC ,AB BC ⊥,且AB BC =.(Ⅰ)求证:平面BED ⊥平面PAC ; (Ⅱ)求二面角F DE B --的大小;(Ⅲ)若6PA =,5DF =,求PC 与平面PAB 所成角的正切值. 解:(Ⅰ)证明:因为PA ⊥平面ABC ,所以PA BE ⊥又AB BC =,E 为AC 中点,故AC BE ⊥又AC PA A =I ,所以BE ⊥平面PAC ,BE ⊂平面BED ,所以平面BED ⊥平面PAC .-----------------------------------------4分(Ⅱ)由已知得:DE ⊥平面ABC ,所以FEB ∠为二面角F DE B --的平面角, 因为E ,F 分别为棱AC ,AB 的中点,AB BC ⊥,故90EFB ∠=o,EF FB =,所以,二面角F DE B --的大小为45o.--------------------------------------8分(Ⅲ)因为PA ⊥平面ABC ,所以PA BC ⊥, 又AB BC ⊥所以BC ⊥平面PAB .所以BPC ∠为PC 与平面PAB 所成角,由6PA =,5DF =,得4EF =,8BC AB ==,10PB =,84tan 105BC BPC PB ∠===, 所以,PC 与平面PAB 所成角的正切值为45.--------------------------------------13分 (19)(本小题满分14分)已知椭圆C :22221x y a b +=(0a b >>)的离心率e =,左顶点A 与右焦点F的距离2AF =(Ⅰ)求椭圆C 的方程;(Ⅱ)过右焦点F 作斜率为k 的直线l 与椭圆C 交于,M N 两点,(2,1)P 为定点,当 △MNP 的面积最大时,求l 的方程. 解:(Ⅰ)由e =得:c a --------------------------------------1分由2AF =2a c +=,②----------------------------------------3分由①②得:a =2c =,1b =,---------------------------------------5分椭圆C 的方程为2215x y +=.--------------------------------------------6分(Ⅱ)过右焦点(2,0)F 斜率为k 的直线l :(2)y k x =-,--------------------7分 联立方程组:2215(2)x y y k x ⎧+=⎪⎨⎪=-⎩消元得:2222(15)202050k x k x k +-+-=---------------------------8分 设交点1122(,),(,)M x y N x y则21222015k x x k +=+,212220515k x x k -=+------------------------------------------9分MN==---------------------------------------------------10分点(2,1)P 到直线l的距离d =,所以△MNP的面积S ==1t =≥,则5S t t==- 记4()5g t t t=-,单调递增,min ()(1)1g t g ==,所以S, 此时,0k =,l 的方程:0y =.---------------------------------------------14分 (20)(本小题满分14分)设函数()()2ln f x ax x a R =--?. (Ⅰ)若()()(),f x e f e 在点处的切线斜率为1e,求a 的值; (Ⅱ)当0a >时,求()f x 的单调区间;(Ⅲ)若()xg x ax e =-,求证:在0x >时,()()f x g x >.解:(Ⅰ)若()()(),f x e f e 在点处的切线斜率为1e ,11()k f e a e e ¢==-=,得2a e=.----------------------------------------------3分(Ⅱ)由11'()(0)ax f x a x x x-=-=> 当0a >时,令'()0f x =解得:1x a=-------------------------5分 当x 变化时,'(),()f x f x 随x 变化情况如下表:由表可知:()f x 在1(0,)a 上是单调减函数,在(,)a+∞上是单调增函数所以,当0a >时,()f x 的单调减区间为1(0,)a ,单调增区间为1(,)a+∞------8分(Ⅲ)当0x >时,要证()0xf x ax e -+>,即证ln 20xe x -->令()ln 2(0)xh x e x x =-->,只需证()0h x >1'()x h x e x=-Q由指数函数及幂函数的性质知:1'()x h x e x=-在(0,)+∞上是增函数 又121'(1)10,'()302h e h e =->=-<∴1'(1)'()02h h g <'()h x 在1(,1)2内存在唯一的零点,也即'()h x 在(0,)+?上有唯一零点----------10分设'()h x 的零点为t ,则1'()0,t h t e t =-=即11(1),2t e t t =<< 由'()h x 的单调性知:当),0(t x ∈时,'()'()0h x h t <=,()h x 为减函数 当(,)x t ??时,'()'()0h x h t >=,()h x 为增函数,所以当0x >时,11()()ln 2ln 212220t t h x h t e t t et t?--=--=+-?=又11,2t <<,等号不成立∴()0h x >-------------------------------14分。
【2014红桥一模】天津市红桥区2014届高三第一次模拟考试 数学(理)答案

高三数学(理)答案(2014、04)一、选择题:本大题共8小题,每小题5分,满分40分. 题号 1 2 3 4 5 6 7 8 答案DBCDCDBC二、填空题:本大题共6小题,每小题5分,满分30分. 9.{}31≤≤x x 10.4 11.-192 12.2313.332 14.13三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分13分) (Ⅰ)因为sinC=2sinA 21sin sin ==∴C A c a .............................................2 522==∴BC AB . (4)(Ⅱ)bca cb A 2cos 222-+==552 (7)55cos 1sin 2=-=∴A A ……8 所以54cos sin 22sin ==A A A 531c o s 22c o s 2=-=A A …10 sin 24A π⎛⎫-⎪⎝⎭=4sin2cos 4cos2sin ππA A -102=…………13 16.(本小题满分13分)设“A 级第一次考试合格”为事件1A ,“A 级补考合格”为事件A 2;“B 级第一次考试合格”为事件1B ,“B 级补考合格”为事件2B .(Ⅰ)不需要补考就获得合格证书的事件为A 1·B 1,注意到A 1与B 1相互独立,则答:该考生不需要补考就获得合格证书的概率为13………………………4 (Ⅱ)由已知得,ξ=2,3,4,注意到各事件之间的独立性与互斥性,可得)()()2(1111B A P B A P P ⋅+⋅==ξ2111114.3233399=⨯+⨯=+= (6))()()()3(221211211B A A P B B A P B B A P P ⋅⋅+⋅⋅+⋅⋅==ξ (8))()()4(21212121B B A A P B B A A P P ⋅⋅⋅+⋅⋅⋅==ξ12111211111,3322332218189=⨯⨯⨯+⨯⨯⨯=+=………………….10 故4418234.9993E ξ=⨯+⨯+⨯=答:该考生参加考试次数的期望为83 (13)17.(本小题满分13分)(Ⅰ)作SO BC ⊥,垂足为O ,连结AO ,由侧面SBC ⊥底面ABCD , 得SO ⊥平面ABCD ...........2 因为SA SB =,所以AO BO = (3)又45ABC =∠,AOB △为等腰直角三角形,AO OB ⊥……………4 如图,以O 为坐标原点,OA 为x 轴正向,建立直角坐标系O xyz -.(200)A ,,,(020)B ,,,(020)C -,,,(001)S ,,,)0,22,2(-D ………6 (201)SA =- ,,,(0220)CB =,,,0=⋅CB SA ,所以SA BC ⊥ (8)(Ⅱ)设),,(z y x n =为平面SAB 的法向量则⎪⎩⎪⎨⎧=⋅=⋅00AS n AB n 得 ⎪⎩⎪⎨⎧=+-=+-02022z x y x 所以 ⎩⎨⎧==x z yx 2 令x=1 )2,1,1(=n (10)1122,cos =⋅=><SDn SD n SD n ………………………………12 SD 与平面SAB 所成的角与SD 与n 所成的角互余.所以,直线SD 与平面SAB 所成的角正弦值为1122……………………………13 18.(本小题满分13分)函数2()ln(1)f x x b x =++的定义域为()1,-+∞ (2)222'()211b x x bf x x x x ++=+=++ (4)令2()22g x x x b =++,则()g x 在1,2⎛⎫-+∞ ⎪⎝⎭上递增,在11,2⎛⎫-- ⎪⎝⎭上递减,min 11()()22g x g b =-=-+.当12b >时,min 1()02g x b =-+>,2()220g x x x b =++>在()1,-+∞上恒成立.'()0,f x ∴>即当12b >时,函数()f x 在定义域()1,-+∞上单调递增……………………………6 (II )分以下几种情形讨论:(1)由(I )知当12b >时函数()f x 无极值点.(2)当12b =时,212()2'()1x f x x +=+,11,2x ⎛⎫∴∈-- ⎪⎝⎭时,'()0,f x > 1,2x ⎛⎫∈-+∞ ⎪⎝⎭时,'()0,f x >12b ∴=时,函数()f x 在()1,-+∞上无极值点 (8)(3)当12b <时,解'()0f x =得两个不同解11122b x ---=,21122b x -+-=.当0b <时,111212b x ---=<-,211212bx -+-=>-,()()121,,1,,x x ∴∉-+∞∈-+∞此时()f x 在()1,-+∞上有唯一的极小值点21122bx -+-= (10)当102b <<时,()12,1,,x x ∈-+∞ '()f x 在()()121,,,x x -+∞都大于0 ,'()f x 在12(,)x x 上小于0 ,此时()f x 有一个极大值点11122b x ---=和一个极小值点21122bx -+-=综上可知,0b <时,()f x 在()1,-+∞上有唯一的极小值点21122bx -+-=;102b <<时,()f x 有一个极大值点11122b x ---=和一个极小值点21122b x -+-=12b ≥时,函数()f x 在()1,-+∞上无极值点.………………………………………13 19.(本小题满分14分) (Ⅰ)由题意可知,b=1, 又因为23==a c e ,且a 2=b 2+c 2,解得a=2 所以椭圆的方程为1422=+y x ………………………………………………4 (Ⅱ)由题意可得:A (﹣2,0),B (2,0). 设P (x 0,y 0),由题意可得:﹣2<x 0<2,所以直线AP 的方程为)2(200++=x x y y …………………………………6 令,则)222(200++=x y y ,即2)222(00++=x y DE (8)同理:直线BP 的方程为)2(200--=x x y y ,令,则)222(200--=x y y , 即2)222(00--=x y DF (10)所以=22020204444x y x y -=-……………………………………………………..12 而,即4y 02=4﹣x 02,代入上式,所以|DE|·|DF|=1,所以|DE|·|DF|为定值1.…………………………………………14 20.(本小题满分14分) (Ⅰ)在11()22n n n S a -=--+中,令n=1,可得1112n S a a =--+=,即112a =..............1 当2n ≥时,21111111()2()22n n n n n n n n n S a a S S a a ------=--+∴=-=-++,,..................2 11n 1112a (),212n n n n n a a a ----∴=+=+n 即2.112,1,n 21nn n n n n b a b b b --=∴=+≥-= n 即当时,b又1121,b a ==∴数列}{n b 是首项和公差均为1的等差数列................................................4 于是1(1)12,2nn n n nnb n n a a =+-⋅==∴=.........................................................................6 (II)由(I )得11(1)()2n n n n c a n n +==+,所以由①-②得 (9)535(3)(221)3212212(21)n n n nn n n n n T n n n ++---=--=+++……………………………………11 于是确定521n n T n +与的大小关系等价于比较221nn +与的大小......猜想:当322 1.nn n ≥>+时,证明如下: 证法1:(1)当n=3时,由猜想显然成立. (2)假设k n =时猜想成立.即122+>k k则1n k =+时,1)1(2)12(1)1(224)12(22221++>-+++=+=+>⋅=+k k k k k k k所以当1n k =+时猜想也成立综合(1)(2)可知 ,对一切3n ≥的正整数,都有22 1.nn >+ 证法2:当3n ≥时综上所述,当1,2n =时521n n T n <+,当3n ≥时521n nT n >+ (14)。
2014年高考天津文科数学试题及答案(精校版)

2014年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2本卷共8小题,每小题5分,共40分。
参考公式:•如果事件A ,B 互斥,那么•圆锥的体积公式13V Sh =.()()()P AB P A P B =+ 其中S 表示圆锥的底面面积,•圆柱的体积公式V Sh =. h 表示圆锥的高. 其中S 表示棱柱的底面面积, h 表示棱柱的高.一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1. i 是虚数单位,复数=++ii437( ) A. i -1 B. i +-1 C.i 25312517+ D. i 725717+- 2. 设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥≤--≥-+.1,02,02y y x y x 则目标函数y x z 2+=的最小值为( )A. 2B. 3C. 4D. 53. 已知命题为则总有p e x x p x ⌝>+>∀,1)1(,0:( )A. 00≤∃x ,使得1)1(00≤+x e xB. 00>∃x ,使得1)1(00≤+x e xC. 0>∀x ,总有 1)1(≤+x e xD. 0≤∀x ,总有1)1(≤+x e x 4. 设,,log ,log 2212-===πππc b a 则( )A. c b a >>B. c a b >>C. b c a >>D. a b c >>5. 设{}n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和,若,,,421S S S 成等比 数列,则1a =( )A. 2B. -2C.21 D . 21 6. 已知双曲线)0,0(12222>>=-b a by a x 的一条渐近线平行于直线,102:+=x y l 双曲线的一个焦点在直线l 上,则双曲线的方程为( )A.120522=-y x B. 152022=-y x C. 1100325322=-y x D. 1253100322=-y x 7. 如图,ABC ∆是圆的内接三角行,BAC ∠的平分线交圆于点D ,交BC 于E ,过点B的圆的切线与AD 的延长线交于点F ,在上述条件下,给出下列四个结论:① BD 平分CBF ∠;②FA FD FB ⋅=2;③DE BE CE AE ⋅=⋅;④BF AB BD AF ⋅=⋅.则所有正确结论的序号是( )A. ①②B. ③④C.①②③ D. ①②④8. 已知函数()cos (0),.f x x x x R ωωω=+>∈在曲线()y f x =与直线1y =的交点中,若相邻交点距离的最小值为3π,则()f x 的最小正周期为( ) A.2πB. 23πC. πD. 2π二.填空题:本大题共6小题,每小题5分,共30分.9. 某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取 _________名学生. 10. 一个几何体的三视图如图所示(单位:m ),则该几何体的体积为 3m .11. 阅读右边的框图,运行相应的程序,输出S 的值为________. 12. 函数()3lg f x x =的单调递减区间是________.13. 已知菱形ABCD 的边长为2,120BAD ∠=︒,点E ,F 分别在边BC 、DC 上,俯视图侧视图正视图PFECBA3BC BE =,DC DF λ=.若1=⋅AF AE ,则λ的值为________.14. 已知函数()⎪⎩⎪⎨⎧>-≤++=0,220,452x x x x x x f 若函数x a x f y -=)(恰有4个零点,则实数a的取值范围为_______三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤 15.(本小题满分13分)某校夏令营有3名男同学C B A ,,和3名女同学Z Y X ,,,其年级情况如下表:现从这6 (1) 用表中字母列举出所有可能的结果(2) 设M 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M 发生的概率.16.(本小题满分13分)在ABC ∆中,内角C B A ,,所对的边分别为c b a ,,,已知b c a 66=-,C B sin 6sin =(1) 求A cos 的值;(2) 求)62cos(π-A 的值.17.(本小题满分13分)如图,四棱锥ABCD P -的底面ABCD 是平行四边形,2==BD BA ,AD=2,5==PD PA , E ,F 分别是棱AD ,PC 的中点.(1) 证明: //EF 平面PAB ; (2) 若二面角P-AD-B 为60,① 证明:平面PBC ⊥平面ABCD② 求直线EF 与平面PBC 所成角的正弦值.18.(本小题满分13分)设椭圆22221x y b +=(0a b >>)的左、右焦点为12,F F ,右顶点为A ,上顶点为B .已知12AB F =.(1)求椭圆的离心率;(2)设P 为椭圆上异于其顶点的一点,以线段PB 为直径的圆经过点1F ,经过点2F的直线l 与该圆相切于点M ,2MF =,求椭圆的方程.19.(本小题满分14分) 已知函数232()(0),3f x x ax a x R =->∈ (1) 求()f x 的单调区间和极值;(2) 若对于任意的1(2,)x ∈+∞,都存在2(1,)x ∈+∞,使得12()()1f x f x ⋅=,求a 的取值范围20(本小题满分14分)已知q 和n 均为给定的大于1的自然数,设集合{}12,1,0-=q M ,集合{}n i M x q x q x x x x A i n n ,2,1,,121=∈++==-,(1) 当3,2==n q 时,用列举法表示集合A ;(2) 设,,,,121121--++=+++=∈n n n n q b q b b t q a q a a s A t s 其中,,2,1,,n i M b a i i =∈证明:若,n n b a <则t s <.2014年天津高考数学(文科)试卷参考答案一、选择题A B B C D A D C 1. 解:()()()()73472525134343425i i i i i i i i +-+-===-++-,选A . 2. 解:作出可行域,如图,结合图象可知,当目标函数通过点()1,1时,z 取得最小值3,选B . 3. 解:依题意知p ⌝为:00>∃x ,使得1)1(00≤+x ex ,选B .4. 解:因为1a >,0b <,01c <<,所以a c b >>,选 C .5. 解:依题意得2214S S S =,所以()()21112146a a a -=-,解得112a =-,选D . 6. 解:依题意得⎪⎩⎪⎨⎧+===22252b a c c a b ,所以25a =,220b =,选A .7. 解: 由弦切角定理得EAC BAE FBD ∠=∠=∠,又A F B B F D ∠=∠,所以BFD ∆∽AFB ∆,所以BF BDAF AB=,即BF AB BD AF ⋅=⋅,故④正确,排除A 、C . 又DBC EAC FBD ∠=∠=∠,故①正确,排除B ,选D .8. 解:因为)6sin(2)(πω+=x x f ,所以()1f x =得21)6sin(=+πωx ,所以626πππω+=+k x 或6526πππω+=+k x ,Z k ∈.因为相邻交点距离的最小值为3π,所以332πωπ=,2w =,π=T ,选C . 二、填空题9. 60 10.320π11.-4 12. )0,(-∞ 13. 2 14. )2,1( 9. 解: 应从一年级抽取6065544300=+++⨯名. 10.解: 该几何体的体积为32041223122πππ=⨯⨯+⨯⨯=V 3m . 11. 解:3n =时,8S =-;2n =时,4S =-,所以输出的S 的值为-4. 12. 解:由复合函数的单调性知,)(x f 的单调递减区间是)0,(-∞.13. 解:因为120BAD ∠=︒,菱形的边长为2,所以2-=⋅. 因为1)1()31(=+⋅+=⋅AB AD AD AB AF AE λ,所以1323442=-++-λλ,解得2=λ. [解2] 建立如图所示的坐标系,则A (-1,0),B (0,-3),C (1,0),D (0,3).设E (x 1,y 1),F (x 2,y 2),由BC →=3BE →,得(1,3)=3(x 1,y 1+3),可得E ⎝⎛⎭⎫13,-233;由DC →=λDF →,得(1,-3)=λ(x 2,y 2-3),可得F ⎝ ⎛⎭⎪⎫1λ,3-3λ. ∵AE ·AF =⎝⎛⎭⎫43,-233·⎝ ⎛⎭⎪⎫1λ+1,3-3=103λ-23=1,∴λ=2.14.解: 在同一坐标系内分别作出y =f (x )与y =a |x |的图像,如图所示,当y =a |x |与y =f (x )的图像相切时,联立⎩⎪⎨⎪⎧-ax =-x 2-5x -4,a >0,整理得x 2+(5-a )x +4=0,则Δ=(5-a )2-414=0,解得a =1或a =9(舍去),∴当y =a |x |与y =f (x )的图像有四个交点时,有1<a <2.三、解答题15.解:(1)从6名同学中随机选出2人参加知识竞赛的所有可能结果为{A ,B },{A ,C },{A ,X },{A ,Y },{A ,Z },{B ,C },{B ,X },{B ,Y },{B ,Z },{C ,X },{C ,Y },{C ,Z },{X ,Y },{X ,Z },{Y ,Z },共15种.(2) 选出的2人来自不同年级且恰有1名男同学和1名女同学的所有可能结果为{A ,Y },{A ,Z },{B ,X },{B ,Z },{C ,X },{C ,Y },共6种.因此,事件M 发生的概率P (M )=615=25.16.解:(1)在△ABC 中,由b sin B =c sin C ,及sin B =6sin C ,可得b =6c .又由a -c =66b ,有a =2c .所以cos A =b 2+c 2-a 22bc =6c 2+c 2-4c 226c 2=64.(2) 在△ABC 中,由cos A =64,可得sin A =104.于是cos 2A =2cos 2A -1=-14,sin2A =2sin A ·cos A =154. 所以cos ⎝⎛⎭⎫2A -π6=cos 2A ·cos π6+sin 2A ·sin π6=15-38.17.解:(1)证明:如图所示,取PB 中点M ,连接MF ,AM .因为F 为PC 中点,所以MF ∥BC ,且MF =12BC .由已知有BC ∥AD ,BC =AD ,又由于E 为AD 中点,因而MF ∥AE 且MF =AE ,故四边形AMFE 为平行四边形,所以EF ∥AM .又AM ⊂平面P AB ,而EF ⊄平面P AB ,所以EF ∥平面P AB .(2) (i) 证明:连接PE ,BE .因为P A =PD ,BA =BD ,而E 为AD 中点,所以PE ⊥AD ,BE ⊥AD ,所以∠PEB 为二面角P - AD -B 的平面角.在△P AD 中,由P A =PD =5,AD =2,可解得PE =2.在△ABD 中,由BA =BD =2,AD =2,可解得BE =1.在△PEB 中,PE =2,BE =1,∠PEB =60˚,由余弦定理,可解得PB =3,从而∠PBE =90˚,即BE ⊥PB .又BC ∥AD ,BE ⊥AD ,从而BE ⊥BC ,因此BE ⊥平面PBC .又BE ⊂平面ABCD ,所以平面PBC ⊥平面ABCD .(ii) 连接BF ,由(i)知,BE ⊥平面PBC ,所以∠EFB 为直线EF 与平面PBC 所成的角.由PB =3及已知,得∠ABP 为直角,而MB =12PB =32,可得AM =112,故EF =112.又BE =1,故在直角三角形EBF 中,sin ∠EFB =BE EF =21111.所以直线EF 与平面PBC 所成角的正弦值为21111.18.解:(1)设椭圆右焦点F 2的坐标为(c ,0).由|AB |=32|F 1F 2|,可得a 2+b 2=3c 2.又b 2=a 2-c 2,则c 2a 2=12,所以椭圆的离心率e =22.(2) 由(1)知a 2=2c 2,b 2=c 2,故椭圆方程为x 22c 2+y 2c 2=1.设P (x 0,y 0).由F 1(-c ,0),B (0,c ),有F 1P →=(x 0+c ,y 0),F 1B →=(c ,c ).由已知,有F 1P →·F 1B →=0,即(x 0+c )c +y 0c =0. 又c ≠0,故有x 0+y 0+c =0.①因为点P 在椭圆上,所以x 202c 2+y 20c2=1.②由①和②可得3x 20+4cx 0=0.而点P 不是椭圆的顶点,故x 0=-43c ,代入①得y 0=c 3,即点P 的坐标为⎝⎛⎭⎫-4c 3,c 3.设圆的圆心为T (x 1,y 1),则x 1=-43c +02=-23c ,y 1=c 3+c 2=23c ,进而圆的半径r =(x 1-0)2+(y 1-c )2=53c .由已知,有|TF 2|2=|MF 2|2+r 2.又|MF 2|=22,故有⎝⎛⎭⎫c +23c 2+⎝⎛⎭⎫0-23c 2=8+59c 2,解得c 2=3,所以所求椭圆的方程为x 26+y 23=1.19.解:(1)由已知,有f ′(x )=2x -2ax 2(a >0).令f ′(x )=0,解得x =0或x =1a.当x 递减 递增 递减所以,f (x )的单调递增区间是⎝⎭⎫0,1a ;单调递减区间是(-∞,0),⎝⎛⎭1a ,+∞. 当x =0时,f (x )有极小值,且极小值f (0)=0;当x =1a时,f (x )有极大值,且极大值f ⎝⎛⎭⎫1a =13a 2. (2)由f (0)=f ⎝⎛⎭⎫32a =0及(1)知,当x ∈⎝⎛⎭⎫0,32a 时,f (x )>0;当x ∈⎝⎛⎭⎫32a ,+∞时,f (x )<0. 设集合A ={f (x )|x ∈(2,+∞)},集合B =⎩⎨⎧⎭⎬⎫1f (x )x ∈(1,+∞),f (x )≠0,则“对于任意的x 1∈(2,+∞),都存在x 2∈(1,+∞),使得f (x 1)·f (x 2)=1”等价于A ⊆B ,显然0∉B .下面分三种情况讨论:(i)当32a >2,即0<a <34时,由f ⎝⎛⎭⎫32a =0可知,0∈A ,而0∉B ,所以A 不是B 的子集. (ii)当1≤32a ≤2,即34≤a ≤32时,有f (2)≤0,且此时f (x )在(2,+∞)上单调递减,故A=(-∞,f (2)),因而A ⊆(-∞,0).由f (1)≥0,有f (x )在(1,+∞)上的取值范围包含(-∞,0),则(-∞,0)⊆B ,所以A ⊆B .(iii)当32a <1,即a >32时,有f (1)<0,且此时f (x )在(1,+∞)上单调递减,故B =⎝⎛⎭⎫1f (1),0,A =(-∞,f (2)),所以A 不是B 的子集. 综上,a 的取值范围是⎣⎡⎦⎤34,32.20.解:(1)当q =2,n =3时,M ={0,1},A ={x |x =x 1+x 2·2+x 3·22,x i ∈M ,i =1,2,3},可得A ={0,1,2,3,4,5,6,7}.(2) 证明:由s ,t ∈A ,s =a 1+a 2q +…+a n q n -1,t =b 1+b 2q +…+b n q n -1,a i ,b i ∈M ,i =1,2,…,n 及a n <b n ,可得s-t=(a1-b1)+(a2-b2)q+…+(a n-1-b n-1)q n-2+(a n-b n)q n-1≤(q-1)+(q-1)q+…+(q-1)q n-2-q n-1=(q-1)(1-q n-1)1-q-q n-1=-1<0,所以s<t.。
2014年天津市区县重点校第一次模拟考试数学试卷及答案WORD版

2014年天津市十二区县重点学校高三毕业班联考(一)数 学(理)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟. 祝各位考生考试顺利!第Ⅰ卷 选择题 (共40分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+∙柱体的体积公式Sh V=. 其中S 表示柱体的底面积,h 表示柱体的高.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 集合N M x N x y y M x则},44|{)},1lg(|{2<=+==等于 ( ) A .[)+∞,0B .[)1,0C .()+∞,1D .(]1,02. 已知y ,x 满足线性约束条件⎪⎩⎪⎨⎧≤≥+-≥-305x y x y x ,则y x z 42+=的最小值是( )A.-6B.5C.38D.-10 3. 二项式612⎪⎪⎭⎫⎝⎛+x x 展开式中的常数项是( ) A .15B .60C .120D .2404. 对于实数a 和b ,定义运算b a *,运算原理如右图所示,则式子2221e ln *-⎪⎭⎫ ⎝⎛的值为( )A .8B .10C .12D .23 5. 在ABC ∆中,A C AC BC sin 2sin ,3,5===,则⎪⎭⎫ ⎝⎛π-4A tan 的值为( )A .31B .43C .31-D .36. 线段AB 是圆10221=+y x C :的一条直径,离心率为5的双曲线2C 以,A B 为焦点.若P是圆1C 与双曲线2C 的一个公共点,则PB PA +的值为( )A. 152C.7. 已知实数n ,m ,若100=+≥≥n m ,n ,m 且,则1222+++n n m m 的最小值为( ) A.41B. 154 C.81D.31 8. 函数[]11,0,2()1(2),(2,)2x x f x f x x ⎧--∈⎪=⎨-∈+∞⎪⎩,则下列说法中正确命题的个数是( )①函数()ln(1)y f x x =-+有3个零点;②若0x >时,函数()k f x x ≤恒成立,则实数k 的取值范围是3,2⎡⎫+∞⎪⎢⎣⎭; ③函数()f x 的极大值中一定存在最小值;④()()()N k ,k x f x f k∈+⋅=22,对于一切[)0,x ∈+∞恒成立.A .1B .2C .3D .4第Ⅱ卷 非选择题 (共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卷中相应的横线上. 9.设i 是虚数单位,复数ii21+= . 10. 某几何体的三视图如图所示,其俯视图是中心角为60︒的扇形,则该几何体的体积为 .11. 直线()为参数m m y mx ⎩⎨⎧=λ+=1被抛物线()为参数t t x ty ⎪⎩⎪⎨⎧==241所截得的弦长为4,则=λ . 12.在ABC ∆中,060=∠A ,A ∠的平分线交BC 于D ,若3=AB ,且)R (∈μμ+=31,则13. 如图所示,已知PA 与⊙O 相切,为切点,过点的割线交圆于C B 、两点,弦AP CD //,BC AD 、相交于点E ,F 为CE 上一点,且EDF P ∠=∠,若2:3:=BE CE , 2,3==EF DE ,则PA =___________.三、解答题:本大题6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)已知函数()2132++=x cos x cos x sin x f .(Ⅰ)求()x f 的最小正周期,并求出当[,]62x ππ∈时,函数)(x f 的值域; (Ⅱ)当[,]62x ππ∈时,若8()5=f x , 求()12f x π-的值. 16.(本小题满分13分)由于雾霾日趋严重,政府号召市民乘公交出行.但公交车的数量太多会造成资源的浪费,太少又难以满足乘客需求.为此,某市公交公司在某站台的60名候车乘客中进行随机抽样,共抽取(Ⅰ)估计这60名乘客中候车时间少于分钟的人数;(Ⅱ)现从这10人中随机取3人,求至少有一人来自第二组的概率; (Ⅲ)现从这10人中随机抽取3人进行问卷调查,设这3个人共来自X 个组,求X 的分布列及数学期望.17.(本小题满分13分)如图,多面体ABCDEF 中,,,BA BC BE 两两垂直,且EF AB ∥,BE CD ∥,2AB BE ==,1BC CD EF ===.(Ⅰ)若点G 在线段AB 上,且3BG GA =,求证:ADF 平面∥CG ;(Ⅱ)求直线DE 与平面ADF 所成的角的正弦值; (Ⅲ)求锐二面角A DF B --的余弦值. 18.(本小题满分13分)设()xx f +=121,若()()[]()(),f f a ,x f f x f n n n n n 201011+-==+其中*N n ∈.(Ⅰ)求1a ;(Ⅱ)求证:{}n a 为等比数列,并求其通项公式;(Ⅲ)若.n n nn Q ,na a a a T n n n 9363642322223212+++=+++= 其中*N n ∈,试比较n2T 与n Q 的大小,并说明理由.19.(本小题满分14分)已知椭圆12222=+by a x :C (0>>b a )的离心率为22,椭圆的四个顶点所围成菱形的面积为28. (Ⅰ)求椭圆的方程;(Ⅱ)四边形BCD A 的顶点在椭圆C 上,且对角线BD AC ,均过坐标原点O ,若21-=⋅BD AC k k .(i) 求⋅的范围;(ii) 求四边形BCD A 的面积.20.(本小题满分14分)已知函数2()(0)f x x ax a =-≠,()ln g x x =,()f x 图象与x 轴交于点M (M 异于原点),()x f 在M 处的切线为1l ,()1-x g 图象与x 轴交于点N 且在该点处的切线为2l ,并且1l 与2l 平行. (Ⅰ)求(2)f 的值;(Ⅱ)已知实数R t ∈,求函数[][()+],1,y f xg x t x e =∈的最小值;(Ⅲ)令()()'()F x g x g x =+,给定1212,(1,),x x x x ∈+∞<,对于两个大于1的正数βα,,存在实数m 满足:21)1(x m mx -+=α,21)1(mx x m +-=β,并且使得不等式12|()()||()()|F F F x F x αβ-<-恒成立,求实数m 的取值范围.2014年天津市十二区县重点学校高三毕业班联考(一)数学理科参考答案9.i 5152+;10.π2 ; 11.0; 12 13.4315; 14.()+∞,1 三、解答题15.解:(1)1cos 21()22212cos 212sin(2)16+=++=++=++x f x x x x x ππ=π=22T ………4分由26ππ≤≤x ,得67622πππ≤+≤x ………5分 1)62sin(21≤+≤-∴πx ………6分26ππ≤≤∴x 时,函数)(x f 的值域为1,22⎡⎤⎢⎥⎣⎦………7分(2)83()sin(2)1,sin(2)6565=++=+=f x x x ππ则67622,26πππππ≤+≤≤≤x x 得; 所以4cos(2),65x π+=- ………9分1212+=⎪⎭⎫ ⎝⎛π-x sin x f………10分...........2分 ...........3分 ...........8分=1662+⎪⎭⎫⎝⎛π-π+x sin………11分=571033+………13分16.解:(Ⅰ)候车时间少于10分钟的人数为 3610510160=⎪⎭⎫⎝⎛+⨯人; ………3分 (Ⅱ)设“至少有一人来自第二组为事件A ”()1211131035=-=C C A P…………7分(Ⅲ)X 的可能值为1,2,3()1201113103335=+==C C C X P ()1207122310152313252325=++⨯+==C C C C C )C C (X P ()120382331013151513=++⨯==C C C C C X P …………10分 所以X 的分布列为…………11分 408912026712038371211==⨯+⨯+=EX…………13分17.解:(Ⅰ)分别取,AB AF 的中点,M H ,连结,,MF GH DH ,则有,AG GM MF BE = . ∵AH HF =∴ 12GH MF ……………………………………………1分 又∵1,2CD BE BE MF∴CD GH∴四边形CDHG 是平行四边形∴CG DH ……………………………………………………2分又∵,CG ADF DH ADF ⊄⊂平面平面∴CG 平面ADF ……………………………………………4分(Ⅱ)如图,以B 为原点,分别以,,BC BE BA 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系O xyz -.则(0,0,2),(1,0,0),(1,1,0),(0,2,0),(0,2,1)A C D E F(1,1,0),(1,1,2),(0,2,1)DE DA FA =-=--=-……………………………………6分设平面ADF 的一个法向量(,,)n x y z =,则有2020n DA x y z n FA y z ⎧⋅=--+=⎪⎨⋅=-+=⎪⎩,化简,得32x y z y =⎧⎨=⎩ 令1y =,得(3,1,2)n =……………8分设直线DE 与平面ADF 所成的角为θ,则有sin 7n DE n DEθ⋅==⋅ . ………………………9分 所以直线DE 与平面ADF 所成的角的正弦值为77. (Ⅲ)由已知平面A DF 的法向量1n (3,1,2),BF (0,2,1)==设平面BDF 的一个法向量2n (x,y,z ),BD (1,1,0)==22n BF 02y z 0x y 0n BD 0⎧=+=⎧⎪∴∴⎨⎨+==⎩⎪⎩ z 2y,x y ∴=-=-令y 1,=-则2n (1,1,2)=-……………………………………………………11分设锐二面角B DF A --的平面角为θ则121212n ncos|cos n,n||||n||n|θ=<>===12分所以锐二面角B DF A--的余弦值为7………………………13分18.解:(Ⅰ).)(f)(fa,)(f412121111=+-==…2分(Ⅱ))(f)](f[f)(fnnn01211+==+.a)(f)(f)(f)(f)(f)(fannnnnnnn21212124121111-=+-⋅-=+-=+-=+++...3分∴}a{n是首项为41,公比为21-的等比数列.…4分∴}a{n的通项公式是.*Nn.)21(41a1nn∈-⋅=-…5分(Ⅲ),naa)n(aaaTnnn212321221232+-++++=-.naa)n(aaTnnn2232212221--+++=- …6分两式相减得.naaaaaTnnn22321223+++++=∴122221412112114123--⋅⋅++--=nnn)(n])([T1222142116161--⋅+--=nn)(n)(…7分∴).n(Tnn22213191+-=…8分,)n()n(nQn212914++=]21)1n2(1[91n3291n3)1n2(91n3QTn22n22nn2-++=⋅+-+⋅+=-.)1n2(2)1n2(291n32n22n2++-⋅+=…9分.*N n ∈ ∴只要比较n 22与212)n (+大小. 当n =1时,.05)1n 2(22n 2<-=+-即.Q T 12< …10分 当n =2时,.07)1n 2(22n 2<-=+-即.Q T 24<…11分当,3n 时≥.)1n 2()n n 1(]2)1n (n n 1[)C C C (])11[(22222n n 1n 0n 2n n 2+=++≥-++>+++=+< n n 2Q T >∴故n =1或2时,3n ,Q T n n 2≥<时,n n 2Q T >.(结论不写不扣分) …13分19.解:(I )由已知,22228222122a b c ,b a ,a c =+=⋅⋅= …………2分 于是8222===a ,b ,c …………3分所以椭圆的方程为14822=+y x …………4分 (II )当直线AB 的斜率不存在时,2OA OB ⋅=,所以⋅的最大值为2. ……5分当直线AB 的斜率存在时,设直线AB 的方程为m kx y +=,设),(),,(2211y x B y x A 联立⎩⎨⎧=++=8222y x m kx y ,得0824)21(222=-+++m kmx x k …………6分()2222244(12)(28)8840km k m k m ∆=-+-=-+>()…………7分⎪⎩⎪⎨⎧+-=+-=+22212212182214k m x x k km x x ∵21-=⋅=⋅BD AC oB oA k k k k 212121-=∴x x y y 2222212121421822121k m k m x x y y +--=+-⋅⋅-=-=∴…………8分2212122121)())((m x x km x x k m kx m kx y y +++=++==222222142182m k km km k m k ++-++-222812m k k -=+22222218214kk m k m +-=+--∴2228)4(k m m -=--∴ 2242k m ∴+= …………9分 2121y y x x +=⋅2222222222844424421212121212m m m k k k k k k---+-=-===-+++++……10分 2242OA OB ∴-=-≤⋅<因此,[]22,OB OA -∈⋅…………11分另解:设直线AB 方程:kx y =,CD 方程:x ky 21-= 分别求出B 、A 的坐标 (2)分情况讨论, k >0时,分析B 、A 所在的象限,求范围 …………占3分 同理0<k 时 …………占1分 结论 …………占1分 (ii)设原点到直线AB 的距离为d ,则22442)4(16642||218242142||4)(2||1||||121||212222222222212212122=+-=--=+--⎪⎭⎫ ⎝⎛+-=-+=+⋅-⋅+=⋅=∆m k mm m k m k m k km m x x x x m k m x x k d AB S AOB 13分284==∴∆AOB ABCD S S 四边形.…………14分20. 解: ()y f x =图象与x 轴异于原点的交点(,0)M a ,'()2f x x a =-(1)ln(1)y g x x =-=-图象与x 轴的交点(2,0)N ,1'(1)1g x x -=- 由题意可得12l l k k =,即1a =, …………………2分 ∴2(),f x x x =-,2(2)222f =-= ………………3分 (2)2[()+][ln +](ln +)y f xg x t x x t x x t ==-=22(ln )(21)(ln )x x t x x t t +-+-………4分令ln u x x =,在 []1,x e ∈时,'ln 10u x =+>,∴ln u x x =在[]1,e 单调递增,0,u e ≤≤ …………5分22(21)y u t u t t =+-+-图象的对称轴122tu -=,抛物线开口向上 ①当1202t u -=≤即12t ≥时,2min 0|u y y t t ===- ……………6分 ②当122t u e -=≥即122e t -≤时,22min |(21)u e y y e t e t t ===+-+- …………7分 ③当1202t e -<<即12122e t -<<时,22min 12212121|()(21)224tu t t y y t t t -=--==+-+-=- ……………8分 1(3)()()'()ln F x g x g x x x =+=+,22111'()0x F x x x x-=-=≥1x ≥得所以()F x 在区间(1,)+∞上单调递增 ……………………………………9分∴1x ≥当时,F F x ≥>()(1)0①当(0,1)m ∈时,有12111(1)(1)mx m x mx m x x α=+->+-=,12222(1)(1)mx m x mx m x x α=+-<+-=,得12(,)x x α∈,同理12(,)x x β∈, …………………10分∴ 由)(x f 的单调性知 0<1()()F x F α<、2()()F F x β<从而有12|()()||()()|F F F x F x αβ-<-,符合题设. ………………11分 ②当0m ≤时,12222(1)(1)mx m x mx m x x α=+-≥+-=,12111(1)(1)m x mx m x mx x β=-+≤-+=,由)(x f 的单调性知 0<12()()()()F F x F x F βα≤<≤,∴12|()()||()()|F F F x F x αβ-≥-,与题设不符 ………………12分③当1m ≥时,同理可得12,x x αβ≤≥,得12|()()||()()|F F F x F x αβ-≥-,与题设不符. ……………………13分 ∴综合①、②、③得(0,1)m ∈ …………………14分。
天津市天津一中2014届高三上学期零月考 文科数学 含答案--含答案

天津一中2013-2014-1高三年级零月考数学试卷(文科)一、选择题:(本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设i 为虚数单位,则ii+-15等于( ) A .i 32-- B .i 32+- C .i 32- D .i 32+2.若变量y x ,满足约束条件⎪⎩⎪⎨⎧≤+≥-≥5231y x x y x ,则y x z +=2的最大值为( )A .1B .2C .3D .4 3.阅读右面的程序框图,则输出的S =( ) A. 14 B.20 C.30 D.554.设π3log =a ,3log 2=b ,2log 3=c ,则( )A .c b a >>B .b c a >>C .c a b >>D .a c b >>5.已知集合}{1log 2≤=x x M ,}{022≤-=x x x N ,则“M a ∈”是“N a ∈”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 6.在平行四边形ABCD 中,a AB = ,b AD =,NC AN 3=,M 为BC 的中点,则MN =( ) A .b a 4141+-B .b a 2121+-C .b a 21+D .b a 4343+-7.要得到一个奇函数,只需将函数()x x x f 2cos 32sin -=的图象( )A .向右平移6π个单位 B .向左平移6π个单位 C .向右平移4π个单位 D .向左平移3π个单位8.若函数()x f 满足()()111+=+x f x f ,当[]1,0∈x 时,()x x f =,若在区间(]1,1-上,()()m mx x f x g --=有两个零点,则实数m 的取值范围是( )A .⎪⎭⎫⎢⎣⎡21,0B .⎪⎭⎫⎢⎣⎡+∞,21C .⎪⎭⎫⎢⎣⎡31,0D .⎥⎦⎤ ⎝⎛21,0第II 卷二、填空题:(本大题共6小题,每小题5分,共30分。
红桥区高三数学第一次模拟考试试题.doc

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答题时,务必将答案涂写在答题卡上,答在试卷上的无效。
祝各位考生考试顺利! 参考公式:柱体的体积公式 Sh V =柱体,其中S 表示柱体的底面积,h 表示柱体的高.锥体的体积公式 Sh V 31=锥体 ,其中S 表示锥体的底面积,h 表示锥体的高.球的体积公式 334R V π=球 ,其中R 表示球的半径.第Ⅰ卷 注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共9题,每小题5分,共45分。
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知全集{}1,2,3,4,5U =, 集合{}3,4,5M =, {}1,2,5N =, 则集合{}1,2可以表示为(A) M N I (B) N M C U I )( (C) )(N C M U I (D) )()(N C M C U U I (2)下列函数中,既是奇函数又在区间()0,+∞上单调递减的是(A) 12+-=x y (B) 1y x=(C) 2xy -= (D) ln y x = (3)方程2log 2=+x x 的解所在的区间为(A) ()0.5,1 (B) ()1,1.5 (C) ()1.5,2 (D) ()2,2.5(4)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为(A) π (B)4π(C) 2π (D) 43π(5)已知函数()ϕω+=x y sin 的两条相邻的对称轴的间距为π2,现将()ϕω+=x y sin 的图像向左平移π8个单位后得到一个偶函数,则ϕ的一个可能取值为 (A)3π4 (B) π4(C) 0 (D) π4-(6)在ABC △中,“π3A >”是“1cos 2A <”的 (A) 充分不必要条件 (B) 必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件(7)已知一个口袋中装有3个红球和2个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则中奖,否则不中奖,设三次摸球中(每次摸球后放回)中奖的次数为ξ,则ξ的期望为(A)59 (B) 518(C) 56 (D) 524(8)已知双曲线221y x m-=与抛物线28y x =的一个交点为P ,F 为抛物线的焦点,若5PF =,则双曲线的渐近线方程为(A) 20x y ±= (B) 20x y ±=0y ±=(D) 0x ±=(9)如图所示,在菱形ABCD 中,1=AB ,60DAB ∠=o,E 为CD 的中点,则AB AE ⋅u u u r u u u r的值是(A) 1 (B) 1-(C) 2 (D) 2-二、填空题:本大题共6个小题,每小题5分,共30分. (10)若i 是虚数单位,则21i=+______. (11)函数xe x xf ⋅=2)(单调减区间是______.(12)过原点且倾斜角为60o的直线被圆2240x y y +-=所截得的弦长为______. (13)6)12(xx -的二项展开式中的常数项为______.(用数字作答) (14)若441x y+=,则x y +的取值范围是______.(15)设()f x 与()g x 是定义在同一区间[]a b ,上的两个函数,若函数()()()h x f x g x =-在[]a b ,上有两个不同的零点,则称()f x 与()g x 在[]a b ,上是“关联函数”.若31()3f x x m =+与21()22g x x x =+在[03],上是“关联函数”,则实数m 的取值范围是______.三、解答题:本大题共5个小题,共75分.解答写出文字说明、证明过程或演算步骤. (16)(本小题满分15分)设ABC ∆的内角A ,B ,C 所对边的长分别是a ,b ,c ,且3b =,4=c ,B C 2=. (Ⅰ)求B cos 的值;BCDEA(Ⅱ)求)42sin(π-B 的值.(17)(本小题满分15分)如图,在四棱锥ABCD P -中,AD PD 2=,CD PD ⊥,AD PD ⊥,底面ABCD 为正方形,N M ,分别为PD AD ,的中点.(Ⅰ)证明:PA //平面MNC ;(Ⅱ)求直线PB 与平面MNC 所成角的正弦值; (Ⅲ)求二面角D NC M --的余弦值.CD MP(18)(本小题满分51分)已知椭圆)0(12222>>=+b a b y a x 的离心率22=e ,且右焦点到直线02=+-y x 的距离为22.(Ⅰ)求椭圆的方程;(Ⅱ)四边形ABCD 的顶点在椭圆上,且对角线BD AC ,过原点O ,若22ab k k BD AC -=⋅,证明:四边形ABCD 的面积为定值.(19)(本小题满分51分)已知数列{}n a 是等差数列,其前n 项和为n S ,数列{}n b 是公比大于0的等比数列,且2211=-=a b ,123-=+b a ,7233=+b S .(Ⅰ)求数列{}n a 和{}n b 的通项公式;(Ⅱ)令⎪⎩⎪⎨⎧-=为偶数,为奇数n b a n c nn n 2,2,求数列的{}n c 前项n 和n T .(20)(本小题满分51分)已知函数x a x x x f ln 2)(2++=.(Ⅰ)若函数)(x f 在区间(]10,为单调函数,求实数a 的取值范围; (Ⅱ)当1≥m 时,不等式3)(2)12(-≥-m f m f 恒成立,求实数a 的取值范围.高三数学 参考答案一、选择题 每题5分二、填空题 每题5分10. i -1 11. ()0,2-或[](][)0,2,0,2,0,2--- 12. 13. 160- 14. (],1-∞- 15. 31023⎡⎫⎪⎢⎣⎭, 三、解答题16.(本小题满分15分) 解:(Ⅰ)因为B C 2=,所以B C 2sin sin =,..........1分B BC cos sin 2sin =,..................3分 B b c cos 2=,................................5分且3b =,4=c ,所以32cos =B . ..........................7分因为954cos sin 22sin ==B B B ..................................9分 91sin cos 2cos 22-=-=B B B .......................................11分故4sin2cos 4cos2sin )42sin(πππB B B -=-...............13分182104+=。
天津市红桥区2014届高三第一次模拟考试文科数学试卷(带解析)

天津市红桥区2014届高三第一次模拟考试文科数学试卷(带解析)1.复数11ii i-++等于 A .-i B .1 C .-l D .0 【答案】D. 【解析】试题分析:因为21(1)201(1)(1)2i i i i ii i ii i i ---+=+=+=-+=++-,或因为1(1)(1)01(1)1i i i i i i i i i i i i i i ---+=+=+=-+=++-,所以选D.复数运算中注意分母实数化时不要出错.考点:复数运算2.设1(,cos )2a θ=与(1,2cos )b θ=-垂直,则cos 2θ的值等于A .2-B .12-C .0D .-l【答案】B【解析】试题分析:由题意得:211(,cos )(1,2cos )2cos 0,22a b θθθ⋅=⋅-=-+=所以111cos 2,cos 2.22θθ+==-因此选B.考点:向量数量积,二倍角公式3.设m 、n 是两条不同的直线,α、β是两个不同的平面,则 A .若m//α,n//α,则m//n B .若m//α,m//β,则α//β C .若m//n ,m α⊥,则n α⊥ D .若m//α,α⊥β,则m ⊥β【答案】C【解析】试题分析:因为两直线与同一平面平行,两直线位置关系不定,所以选项A 错误.当直线平行于两相交平面的交线时,该直线与两平面皆平行,所以选项B 错误.同样理由可得:选项D 错误.当 m α⊥,则m α⊥内任一直线l ,因为m//n ,所以n α⊥内任一直线l ,即n α⊥,因此选项C 正确. 考点:线面关系判定4.函数()sin 24f x x π⎛⎫=-⎪⎝⎭在区间[0,]2π上的最小值是A .-l B.2 C.2- D .0 【答案】C 【解析】试题分析:因为[0,]2x π∈,所以32[,],444x πππ⎛⎫-∈- ⎪⎝⎭因此()s i n 2[,14f x x π⎛⎫=-∈ ⎪⎝⎭即函数最小值是. 考点:三角函数最值5.函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是A .2,3π-B .2,6π-C .4,6π-D .4,3π【答案】A 【解析】试题分析:由题意得:1152,, 2.212122T T Tπππππω=-====又522,(),2,(),1223k k Z k k Z πππϕπϕπ⨯+=+∈=-+∈而22ππϕ-<<,所以.3πϕ=- 考点:求三角函数解析式6.设双曲线221mx ny +=的一个焦点与抛物线218y x =的焦点相同,离心率为2,则此双曲线的方程为A .2213y x -= B .2213x y -= C .2211612y x -= D .2211612x y -= 【答案】B【解析】试题分析:因为抛物线218y x=的焦点为(0,2),双曲线离心率为2,所以22112,1,1,3,c a a b n m =====-=-因此2211,, 1.33x n m y ==--=考点:抛物线及双曲线性质7.已知3log 4.12a =,3log 2.72b =,3log 0.112c ⎛⎫= ⎪⎝⎭则A .a>b>cB .b>a>cC .a>c>bD .c>a>b 【答案】D 【解析】 试题分析:因为33lo g10log4.1l>>,所以33333log 10log 4.1log 2.7log 10log 0.11222,2(),2>>=因此c>a>b.比较指对数大小,首先将底数化为一样.考点:指对数比较大小8.在区间[1,1]-上随机取一个数x ,cos 2x π的值介于0到12之间的概率为 A .12 B .2πC .13D .23 【答案】C 【解析】试题分析:本题是求几何概型概率,测度为长度.由1cos[0,]22xπ∈得:[,][,],22332xπππππ∈--即22[1,][,1],33x ∈--所以所求概率为1213.23⨯= 考点:几何概型概率9.设集合A={|||4x x <},B={2|430x x x -+>},则A B =【答案】{}4314<<<<-x x x 或 【解析】试题分析:因为(4,4),A =-(3,)(,1)B =+∞-∞,所以(4,1)(3,4).A B =-考点:集合的运算10.一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积= .【解析】试题分析:由题意得几何体为:底面为上底为1,下底为2,高为2的直角梯形,顶点在地面上射影为直角梯形高的中点,即锥的高为的四棱锥,因此体积为11(12)232V =+⨯=考点:三视图11.设抛物线y 2=4x 上一点P 到直线x =-2的距离为5,则点P 到该抛物线焦点的距离是 【答案】4 【解析】试题分析:由抛物线的定义知:点P 到抛物线焦点的距离等于点P 到准线x=-1的距离,所以点P 到该抛物线焦点的距离是5-1=4. 考点:抛物线的定义12.如图,AB 是半圆O 直径,∠BAC=30o。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津市红桥区2014届下学期高三年级第一次模拟考试数学试卷(文科)本试卷分为第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结束后,将本试卷和答题卡一并交回。
第I 卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:如果事件A ,B 互斥,那么P (AB)=P (A)+P (B)如果事件A ,B 相互独立,那么P (AB)=P (A)P (B).棱柱的体积公式V =Sh .其中S 表示棱柱的底面面积h 表示棱柱的高,圆锥的体积公式V=13Sh 其中S 表示圆锥的底面面积h 表示圆锥的高 一、选择题:在每小题给出的四个选项中只有一项是符合题目要求的。
1.复数11ii-++i 等于 A . -i B .1 C . -l D .02.设1(,cos )2a θ=与(1,2cos )b θ=-垂直,则cos 2θ的值等于A .2-B .12-C .0D .-l3.设m 、n 是两条不同的直线,α、β是两个不同的平面,则 A .若m//α,n//α,则m//n B .若m//α,m//β,则α//β C .若m//n ,m α⊥,则n α⊥ D .若m//α,α⊥β,则m ⊥β4.函数()sin 24f x x π⎛⎫=-⎪⎝⎭在区间[0,]2π上的最小值是A .-lB .2 C .2- D .0 5.函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是 A .2,3π-B .2,6π-C .4,6π-D .4,3π6.设双曲线221mx ny +=的一个焦点与抛物线218y x =的焦点相同,离心率为2,则此双曲线的方程为A .2213y x -= B .2213x y -= C .2211612y x -= D .2211612x y -= 7.已知3log 4.12a =,3log 2.72b =,3log 0.112c ⎛⎫= ⎪⎝⎭则A .a>b>cB .b>a>cC .a>c>bD .c>a>b 8.在区间[1,1]-上随机取一个数x ,cos2x π的值介于0到12之间的概率为 A .12 B .2πC .13D .23 第II 卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上. 2.本卷共l2小题。
共110分.二.填空题:本大题共6小愿.每小题5分.共30分.9.9.设集合A={|||4x x <},B={2|430x x x -+>},则AB = 。
10.一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积= . 11.设抛物线y 2=4x 上一点P 到直线x =-2的距离为5,则点P 到该抛物线焦点的距离是 。
12.如图,AB 是半圆O 直径,∠BAC=30o。
BC 为半圆的切线,且O 到AC 的距离OD= .13.已知正项等比数列{a n }满足a 7=a 6+2a 5,若存在两项a m ,a n 14a =,则14m n+的最小值为 .14.定义某种运算S a b =⊗,运算原理如右图所示,则式子151(2tan )ln lg10043e π-⎛⎫⊗+⊗ ⎪⎝⎭的值为 。
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤。
15.(本小题满分l3分)在∆ABC 中,AC=3,sinC=2sinA . (I)求AB 的值; (Ⅱ)求sin 24A π⎛⎫-⎪⎝⎭的值. 16.(本小题满分l3分)爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回. (I)若爸爸恰好抽到了黑桃4.①请把右面这种情况的树形图绘制完整; ②求亮亮抽出的牌的牌面数字比4大的概率.(II)爸爸、亮亮约定,若爸爸抽到的牌的牌面数字比亮亮的大,则爸爸胜;反之,则亮亮赢,你认为这个游戏是否公平?如果公平,请说明理由,如果不公平,更换一张扑克牌使游戏公平.17.(本小题满分13分)如图①,已知∆ABC 是边长为l 的等边三角形,D ,E 分别是AB ,AC 边上的点,AD=AE ,F 是BC 的中点,AF 与DE 交于点G ,将∆ABF 沿AF 折起,得到如图②所示的三棱锥A-BCF ,其中. (I)证明:DE//平面BCF ; (II)证明:CF ⊥平面ABF ; (III)当AD=23时,求三棱锥F-DEG 的体积F DEG V -18.(本小题满分13分)己知a ∈R,函数32()23(1)6f x x a x ax =-++ (I)若a =1,求曲线()y f x =在点(2,f (2))处的切线方程; (II)若|a |>1,求()f x 在闭区间[0,|2a |]上的最小值. 19.(本小题满分14分)已知椭圆C :22221x y a b +=(a>b>0),过点(0,1)(I)求椭圆C 的方程;(II)A ,B 为椭圆C 的左右顶点,直线l :x x 轴交于点D ,点P 是椭圆C 上异于A ,B 的动点,直线AP ,BP 分别交直线l 于E ,F 两点.证明:当点P 在椭圆C 上运动时,|DE||DF|恒为定值.20.(本小题满分14分)已知数列{n a }的前n 项和11()22n n n S a +=--+ (n 为正整数)。
(I)令2n n n b a =,求证数列{n b }是等差数列,并求数列{n a }的通项公式; (Ⅱ)令1n n n c a n+=,12...n n T c c c =+++,求n T 并证明:n T <3.高三数学(文)答案(2014、04)一、选择题:本大题共8小题,每小题5分,满分40分.二、填空题:本大题共6小题,每小题5分,满分30分.9.{}4314<<<<-x x x 或 10.4 12.3 13.23 14.13 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分13分) (Ⅰ)因为sinC=2sinA 21sin sin ==∴C A c a .............................................2 522==∴BC AB . (4)(Ⅱ)bc a c b A 2cos 222-+==552 (7)55cos 1sin 2=-=∴A A …………………..8 所以54cos sin 22sin ==A A A 531cos 22cos 2=-=A A ..…10 sin 24A π⎛⎫-⎪⎝⎭=4sin 2cos 4cos 2sin ππA A -102= …………13 16.(本小题满分13分) (Ⅰ) ① 树形图:……………………………………2 ②所以爸爸抽出的牌的牌面数字比4大的概率是32...................................4 (Ⅱ)不公平,理由如下: (5)…………………………………………….9 爸爸抽出的牌的牌面数字比亮亮的大有5种情况,其余均为小于等于亮亮的牌面数字 所以爸爸胜的概率只有125,显然对爸爸来说是不公平的.................................11 只需把黑5改成3即可 (13)17.(本小题满分13分)(Ⅰ)在等边三角形ABC 中,AD AE =AD AEDB EC ∴= (1)在折叠后的三棱锥A BCF -中 也成立,//DE BC ∴ (2)DE ⊄平面BCF , BC ⊂平面BCF ,//DE ∴平面BCF (4)(Ⅱ)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥,12BF CF ==…………5在三棱锥A BCF -中,2BC =,222BC BF CF CF BF ∴=+∴⊥ (7)BF CF F CF ABF ⋂=∴⊥平面 (9)(Ⅲ)由(Ⅰ)可知//GE CF ,结合(Ⅱ)可得GE DFG ⊥平面.11111113232333F DEG E DFG V V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅= ⎝⎭ (13)18.(本小题满分13分)…………………………………..13 (Ⅰ)当1a=时, (1)所以2()6126(2)242466f x x x f ''=-+∴=-+= (4)()y f x =在(2,(2))f 处的切线方程是:46(2)680y x x y -=-⇒--= (6)(Ⅱ)22()66(1)66[(1)]6(1)()f x x a x a x a x a x x a '=-++=-++=-- (8)①当1a>时,时,()y f x =递增,(1,)x a ∈时,()y f x =递减所以当 [0,2||]x a ∈时,且2||2a >,时,()y f x =递增,(1,)x a ∈时,()y f x =递减 (10)所以最小值是32223()23(1)63f a a a a a a a =-++=-②当1a <-时,且2||2a >,在[0,2||]x a ∈时,(0,1)x ∈时,()y f x =递减,[1,2||]x a ∈时,()y f x =递增,所以最小值是(1)31f a =-综上所述:当1a>时,函数()y f x =最小值是233a a -;当1a <-时,函数()y f x =最小值是31a - (13)19.(本小题满分14分)解:(Ⅰ)由题意可知,b=1, 又因为23==a c e ,且a 2=b 2+c 2,解得a=2 所以椭圆的方程为1422=+y x ………………………………………………4 (Ⅱ)由题意可得:A (﹣2,0),B (2,0). 设P (x 0,y 0),由题意可得:﹣2<x 0<2, 所以直线AP 的方程为)2(200++=x x y y …………………………………6 令,则)222(200++=x y y , 即2)222(00++=x y DE (8)同理:直线BP 的方程为)2(200--=x x y y , 令,则)222(200--=x y y , 即2)222(00--=x y DF (10)所以=22020204444x y x y -=-……………………………………………………..12 而,即4y 02=4﹣x 02,代入上式,所以|DE|·|DF|=1,所以|DE|·|DF|为定值1.…………………………………………14 20.(本小题满分14分) (Ⅰ)在11()22n n n S a -=--+中,令n=1,可得1112n S a a =--+=,即112a =..............1 当2n ≥时,21111111()2()22n n n n n n n n n S a a S S a a ------=--+∴=-=-++,,........................................................ (4) (5)112,1,n 21n n n n n n b a b b b --=∴=+≥-=n 即当时,b (6)又1121,b a ==∴数列}{nb 是首项和公差均为1的等差数列 (7)于是1(1)12,2n n n n nnb n n a a =+-⋅==∴= (9)(II)由(I )得11(1)()2n n n n c a n n +==+,所以 (10)11 由①-②得11111[1()]133421(1)()122212332n n n n nn n n T -++-+=+-+=--+∴=- 023>+n n所以3<n T (14)。
