定积分及其简单的应用
例谈定积分的应用

例谈定积分的应用
定积分是利用积分技术来搭建企业系统的一种服务方式,通过定积分,企业可以解决营销,客户追踪,价格管理,订单跟踪等问题,让企业
既有资源利用效率,又能惠及消费者。
一、定积分的应用
1、促销活动:利用定积分可以创建各种丰富多彩的促销活动,满减、
团购、买赠、金币锁定等,激励消费者购买和积累积分。
2、客户管理:定积分能够建立细致复杂的客户档案,包括客户经理内容,购买次数,消费金额,积分余额等,更好地进行客户管理。
3、价格管理:通过定积分,可以根据不同客户的特征,设置特定的价格,比如会员价,大客户价等,更好地提高定价精确度和竞争力。
4、订单追踪:定积分的订单追踪系统可以记录客户的订单信息,有利
于企业更好地追溯客户信息以及及时为客户提供优质服务。
二、定积分的优势
1、可靠性:定积分系统可以提供可靠性能,降低前端和后端系统出现
的异常和故障,防止客户和企业受到损害。
2、安全性:定积分的安全性也得到有效保障,内部数据交换完全采用
加密技术,保证信息不受外部干涉。
3、兼容性:定积分具有可行性和兼容性,它可以按照各种不同环境定
制与企业系统相协调的服务,能够提供企业最适合的解决方案。
4、易用性:定积分使用界面简洁明了,业务流程简单可靠,容易上手,操作简单易懂,为客户提供更贴心的服务。
三、总结
定积分的引入为企业的经营活动带来了更多的便利,有效提高了企业
的经营效率,也让消费者能够从消费上受到更多的好处。
由此可见,
定积分不仅是企业的一种低成本的服务方式,也是一个更加有效的、
更加充分的消费积分服务体系,为企业和消费者都更好地搭建企业系统。
定积分的应用

定积分的应用定积分是微积分的重要概念之一,它在许多实际问题的求解中起着重要作用。
本文将介绍一些定积分的应用,并探讨它们在不同领域中的具体应用情况。
1. 几何学中的应用在几何学中,我们经常需要计算曲线与坐标轴之间的面积。
通过使用定积分,可以轻松解决这个问题。
以求解曲线 y = f(x) 与 x 轴之间的面积为例,我们可以将其划分为无穷多个宽度非常小的矩形,然后将这些矩形的面积相加,最终得到曲线与 x 轴之间的面积。
这个过程可以通过定积分来表示,即∫[a,b] f(x) dx,其中 a 和 b 分别是曲线的起始点和终止点。
2. 物理学中的应用在物理学中,定积分广泛应用于求解各种与物理量有关的问题。
例如,在动力学中,我们可以通过计算物体的位移和速度的定积分来求解物体的加速度。
同样地,在力学中,定积分可以用于计算物体所受的力的功。
这些应用都需要将物理量表示成关于时间的函数,并使用定积分来求解相关问题。
3. 经济学中的应用经济学也是定积分的应用领域之一。
在经济学中,我们经常需要计算一段时间内的总收益或总成本。
通过将这段时间划分为无数个非常小的时间段,然后计算每个时间段内的收益或成本,最后再将这些值相加,我们可以用定积分来表示这段时间内的总收益或总成本。
这种方法在经济学中有着广泛的应用,例如计算企业的总利润等。
4. 概率统计学中的应用在概率统计学中,定积分可以用于求解概率密度函数下的某个区间的概率。
在概率密度函数中,曲线下的面积表示了该事件发生的概率。
通过将概率密度函数在某个区间上的定积分,我们可以得到该区间内事件发生的概率。
这种方法在概率论和数理统计中具有重要的应用,例如计算正态分布下的概率,或者计算随机变量的期望值等。
综上所述,定积分在几何学、物理学、经济学和概率统计学等各个领域都有着重要的应用。
无论是计算面积、求解物理量、计算总收益还是计算概率,定积分都提供了一种有效的数学工具。
通过理解和掌握定积分的应用,我们可以更好地解决实际问题,并深入研究各个领域中的相关理论。
定积分求平面图形面积在实际生活中的应用

定积分求平面图形面积在实际生活中的应用把复杂的积分问题求解出来就可以计算出平面图形的面积,在实际生活中也可以看到它的很多应用。
其中有一类是涉及设计的,比如建筑设计中的空间分配、土地开发等;另一类是分析的,比如海洋表面的波浪分析等。
1、建筑设计建筑设计中,定积分可以用来求解空间分配问题。
比如,在房屋设计中,它可以用来确定楼层、楼梯、墙壁、门窗等占用了多少面积。
此外,它还可以用来求解不规则房间布局时,室外墙体和室内墙体的面积分配。
同样,在土地开发中也可以看到定积分的应用,如计算出道路两端的封闭区域面积,以及计算建筑的总面积。
定积分也可以帮助规划者精确计算出规划区域的面积,从而更好地管理规划区域的开发。
2、海洋表面的波浪分析定积分也可以用来求解海洋表面的波浪。
水波的主要性质是在洋流中运动,它的变化符合泊松方程,这是一个带积分的方程,可以用定积分来求解。
这种波浪分析可以更好地解释海洋表面的复杂性,进而指导航管理者和建筑者采取更安全有效的导航措施。
此外,在海岸线上,可以使用定积分来计算海岸线内各子区域的面积,以及海岸线及其各个部分的面积,为海洋管理者提供有形的参考数据。
3、农业此外,定积分在农业中也有非常广泛的应用。
比如,在种植作物时,可以使用定积分来计算出作物地的面积,以及需要灌溉地区的面积;在研究农田开发时,可以利用定积分来计算出耕作面积。
通过计算出具体的面积数据,可以更好地规划农田的分布和种植规模,从而节约农业资源,提高农作物的产量。
总结定积分是一种有用的数学技术,可以把复杂的数学问题转化成计算机可计算的简单形式,在计算平面图形面积上表现出很强的优势。
它在实际生活中有很多应用,比如建筑设计、土地开发、海洋洋面波浪分析,以及农业规划等。
定积分在物理上的应用举例
浅谈定积分的意义
纯粹几何图形而言,定积分的意义是由曲线、x轴,区间起点的垂直线x=a、
区间终点的垂直线x=b,所围成的面积。
也可以广义而言,定积分的几何意义就是“抽象的面积”。例如:如果横 轴是体积,纵轴是压强,“抽象面积”的意义是热力学系统对外做功; 如果横轴是时间,纵轴是电流,“抽象面积”的意义是电源对外放出的电 量、、、、、、 定积分是一种重要的数学思想,如今定积分思想广泛应用于物理、医学、 经济学、化工等领域,具有极大的应用价值。
上述公式计算,而是应用定积分思想,采用元素法来计算。
例.有一长度为L,密度为ρ的均匀细棒,在其中垂线上距棒a单位处有一质量为m
的质点M,计算该棒对质点M的引力。
解:建立坐标系
取y为积分变量,y∈[这一区间对应
y+dy],
的棒上小段可近似看成质点,
质量为ρdy,小段与质点的距 离为
定积分在物理上的应用举例
目录
1.用定积分求解平均功率问题 2.用定积分求解引力问题
一、平均功率问题
二、引力问题
质量分别为M、m的质点,相距r,两者间引力: 大小:
F K
Mm
方向:沿两质点的连线
r
2
如果要计算一根细棒对一个质点的引力,那么,由于细棒上各点与该
点的距离是变化的,且各点对该点的引力方向也是变化的,故不能用
THANK YOU
r
a
2
y
2
细杆对质点的引力:
dF k mρdy
a
2
y
2
水平方向的分力:
dFx dF cos( π - ) -dF cos a amρdy
a
定积分的应用

定积分的应用在我们的生活中,有很多场景都需要用到定积分。
而在数学上,定积分也起到了重要的作用。
定积分可以计算曲线下的面积,如求函数 $f(x)$ 在区间 $[a,b]$ 上的面积。
接下来,我们将介绍一些常见的定积分的应用。
一、曲线下的面积假设我们有一个区间 $[a,b]$,以及一个函数 $f(x)$。
我们可以使用定积分来计算这个函数在该区间上的曲线下的面积。
这个面积可以用下面的式子来计算:$$ S=\int_{a}^{b}f(x)dx $$ 其中,$\int$ 表示定积分。
如果我们以 $f(x)\geq 0$ 的形式进行了定义,那么定积分就可以计算出曲线下的正面积。
例如,如果我们要计算函数 $f(x)=x^2$ 在区间 $[0,1]$ 上的曲线下的面积,我们可以通过下面的定积分来计算:$$ S=\int_{0}^{1}x^2dx $$利用积分的定义,可以将该式子化简为:$$ S=\lim_{n\rightarrow\infty}\sum_{i=1}^{n}f(x_i)\Deltax=\lim_{n\rightarrow\infty}\sum_{i=1}^{n}x_i^2\Delta x $$ 其中,$\Delta x=\frac{1}{n}$ 且 $x_i=i\Delta x$。
如果我们取 $n=100$,你会发现:$$ S=0.010050167\cdots $$ 这时,我们就可以知道函数 $f(x)=x^2$ 在区间 $[0,1]$ 上的曲线下的面积为约为 $0.010050167$。
二、体积类似于计算曲线下的面积,定积分也可以用于计算体积。
我们可以使用定积分来计算旋转曲面的体积,例如旋转曲面、扫描曲面等。
例如,假设我们需要计算曲线 $y=x^2$ 从 $x=0$ 到 $x=1$ 周围在 $y$ 轴旋转一周所形成的立体的体积,我们可以使用下面的公式计算出体积:$$ V=\int_{0}^{1}\pi y^2dx $$替换掉 $y=x^2$ 的值,我们得到:$$ V=\int_{0}^{1}\pi x^4dx $$ 计算该定积分的结果为:$$ V=\frac{\pi}{5} $$ 所以,曲线$y=x^2$ 从 $x=0$ 到 $x=1$ 周围所形成的立体的体积为$\frac{\pi}{5}$。
定积分的计算与应用

定积分的计算与应用定积分是微积分的重要概念之一,用于计算曲线下的面积、质量、体积等问题。
本文将介绍定积分的计算方法和应用场景。
一、定积分的计算方法定积分的计算基于微积分中的积分运算,可以通过以下方法进行计算:1. 几何解释法:定积分可以视为曲线下的面积,因此可以利用几何图形的面积公式进行计算。
将曲线下的区域分割成无数个小矩形,并求取它们的面积之和,即可得到定积分的近似值。
通过增加小矩形的个数,可以不断提高计算精度。
2. 集合解释法:定积分可以被视为一组数的和,其中这组数是将函数值与对应的间隔长度相乘而得到的。
通过将曲线下的区域分割成若干个小区间,并计算每个小区间内的函数值与对应的间隔长度的乘积,再将这些乘积进行加和,即可得到定积分的近似值。
3. 牛顿-莱布尼茨公式:对于可微函数,可以使用牛顿-莱布尼茨公式进行定积分的计算。
该公式表达了函数的原函数(即不定积分)与定积分之间的关系。
通过求取函数的原函数,并在积分的上下限处进行代入计算,即可得到定积分的准确值。
二、定积分的应用场景定积分在物理学、经济学、工程学等领域都有广泛的应用。
以下将介绍一些常见的应用场景:1. 面积计算:最简单的应用是计算平面图形的面积。
通过确定曲线的方程以及积分的上下限,可以计算出曲线所围成区域的面积。
2. 质量计算:如果将曲线下的区域视为物体的密度分布,则可以利用定积分计算物体的质量。
通过将物体分割成无数个小区域,并计算每个小区域内的密度值与对应的区域面积的乘积,再将这些乘积进行加和,即可得到物体的总质量。
3. 体积计算:类似质量计算,定积分可以被用于计算三维物体的体积。
通过将物体分割成无数个小体积,并计算每个小体积的大小,再将这些体积进行加和,即可得到物体的总体积。
4. 概率计算:在概率论中,定积分可以用于计算随机变量的概率密度函数下的概率。
通过计算概率密度函数在某个区间上的定积分,可以得到该区间内事件发生的概率。
5. 积累量计算:定积分还可以用于计算积累量,例如距离、速度、加速度等。
定积分的基本性质及应用

定积分的基本性质及应用定积分是微积分的重要概念之一,它在数学和各个学科中都有广泛的应用。
本文将重点介绍定积分的基本性质和在实际问题中的应用,并且通过具体的例子来加深理解。
定义:定积分是对一个函数在闭区间上的加权平均值进行求和的过程。
在数学中,一个函数f(x)在[a, b]上的定积分表示为:∫(a to b) f(x) dx其中,∫代表求和的过程,a和b是积分的上下限,f(x)是被积函数。
基本性质:1. 线性性质:定积分具有线性性质,即对于任意两个函数f(x)和g(x),以及任意的实数k,有以下等式成立:∫(a to b) (f(x) + g(x)) dx = ∫(a to b) f(x) dx + ∫(a to b) g(x) dx∫(a to b) k*f(x) dx = k * ∫(a to b) f(x) dx2. 区间可加性:如果一个函数在闭区间[a, b]上有定义,且在其中一个点c上可导,则该函数在[a, b]上的定积分等于该函数在子区间[a, c]和[c, b]上的定积分之和:∫(a to b) f(x) dx = ∫(a to c) f(x) dx + ∫(c to b) f(x) dx3. 积分中值定理:如果一个函数f(x)在闭区间[a, b]上连续,且在该区间内不恒为0,那么至少存在一个点c,使得:∫(a to b) f(x) dx = f(c) * (b - a)4. 边界性质:对于定积分∫(a to b) f(x) dx,当a等于b时,定积分的值为0。
若a小于b,则定积分的值为正数或负数,具体取决于函数f(x)在[a, b]上的正负性。
5. 非负性质:如果一个函数f(x)在闭区间[a, b]上连续且非负,那么定积分的值也是非负的。
应用:定积分在实际问题中有着广泛的应用,下面将介绍两个具体的应用。
1. 几何应用:定积分可以用于计算曲线与坐标轴之间的面积。
如果一个函数在闭区间[a, b]上非负,那么该函数与x轴围成的曲边梯形的面积可以通过定积分来计算:面积= ∫(a to b) f(x) dx同样的,若函数f(x)在闭区间[a, b]上非正,那么面积可以表示为定积分的绝对值。
定积分的若干应用

定积分的若干应用定积分是微积分中的重要概念之一,它可以用来计算曲线下面的面积、求解物理学中的质心、计算概率密度函数等。
下面将分别介绍定积分在这些应用中的具体应用。
一、计算曲线下面的面积定积分最基本的应用就是计算曲线下面的面积。
具体来说,如果我们要计算函数$f(x)$在区间$[a,b]$上的曲线下面的面积,可以使用下面的公式:$$\int_a^b f(x)dx$$其中,$\int$表示积分符号,$a$和$b$分别是积分区间的下限和上限,$f(x)$是被积函数。
这个公式的意义是将区间$[a,b]$分成无数个小区间,然后计算每个小区间内$f(x)$的面积,最后将所有小区间的面积相加得到整个区间$[a,b]$下面的面积。
二、求解物理学中的质心在物理学中,我们经常需要求解物体的质心。
如果物体是由一些离散的质点组成的,那么可以使用下面的公式求解质心:$$\bar{x}=\frac{\sum_{i=1}^n m_ix_i}{\sum_{i=1}^n m_i}$$其中,$\bar{x}$表示质心的位置,$m_i$表示第$i$个质点的质量,$x_i$表示第$i$个质点的位置。
但是,如果物体是由一些连续的质点组成的,那么就需要使用定积分来求解质心。
具体来说,如果物体的密度分布函数为$\rho(x)$,那么可以使用下面的公式求解质心:$$\bar{x}=\frac{\int_a^b x\rho(x)dx}{\int_a^b \rho(x)dx}$$其中,$a$和$b$分别是物体的起始点和终止点。
这个公式的意义是将物体分成无数个小区间,然后计算每个小区间内的质心位置和质量,最后将所有小区间的质心位置和质量相加得到整个物体的质心位置。
三、计算概率密度函数在概率论中,我们经常需要计算概率密度函数。
如果一个随机变量$X$的概率密度函数为$f(x)$,那么可以使用下面的公式计算$X$在区间$[a,b]$内的概率:$$P(a\leq X\leq b)=\int_a^b f(x)dx$$其中,$P(a\leq X\leq b)$表示$X$在区间$[a,b]$内的概率。
定积分的应用优秀案例名称

定积分的应用优秀案例名称定积分是微积分学中的一个重要概念,其应用范围广泛,涉及到数学、物理、工程学等多个学科领域。
下面将围绕定积分的应用优秀案例,通过分步骤阐述,从实际问题入手,深入探讨定积分的应用。
一、汽车行驶里程问题汽车行驶里程问题是定积分的一个典型应用案例。
假设一个汽车匀速行驶,行驶速度为v,行驶时间为t,我们想知道汽车行驶的总里程。
首先,我们需要通过公式来表示汽车的行驶里程。
行驶里程=速度*时间,即s=v*t。
由此得到定积分公式为:∫sdt=∫vtdt因为汽车是匀速行驶,速度v为常数,因此可将上公式化简为:∫sdt=vt+C其中C是常数项,表示汽车的起始点。
因此,我们只需知道汽车的起始点和行驶时间,就可根据上述公式计算出汽车的行驶里程。
二、物理问题定积分在物理学中也有重要的应用。
例如,假设一个物体受到力F,进行相应的位移d,则所做的功为:W=∫Fds其中,F为力的大小,ds为位移的微小距离元素。
通过定积分,可以计算出物体所做的总功。
例如,假设一个物体受到的力F=2x+10 N,在位移为x的时候对它进行功的计算,其功为:W=∫Fdx=∫(2x+10)dx解上式的不定积分:W=∫(2x+10)dx=x^2+10x+C其中,C为常数项,表示物体的起始点。
通过此公式,我们可以计算出物体受到力F在位移为x时所做的功。
三、金融问题除了数学和物理领域外,定积分在金融领域也有涉及。
例如,假设一家公司每年的营业额为f(x),其中x为年份。
我们想要计算该公司在某一时期内的总营业额。
由于营业额是一种累积变量,我们可以使用定积分来计算总营业额。
假设该公司在t1到t2年间营业额为f(x),则总营业额为:∫t1到t2 f(x)dx通过定积分公式,我们可以计算出该公司在t1到t2年间的总营业额。
综上所述,定积分的应用范围十分广泛,涉及到多个领域,例如,数学、物理、金融等等。
通过具体的实例,我们可以更好地理解定积分的应用,并进一步掌握定积分的求解方法。
定积分的计算及应用

定积分的计算及应用一、定积分的概念设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点,把区间[a,b]分成n个小区间,当区间的长度趋于零时,和S总趋于确定的极限I,这时我们称这个极限I为函数在区间[a,b]上的定积分,记作∫baf(x)dx,即∫baf(x)dx=I=limλ→0∑ni=1f(ξi)·Δxi.二、定积分的意义(一)几何意义设y=f(x)≥0且在[a,b]上连续,若f(x)为曲线,则∫baf(x)dx表示[a,b]上曲边梯形的面积.(二)物理意义设y=f(x)≥0且在[a,b]上连续,若f(x)为速度,则∫baf(x)dx表示[a,b]上变速运动的路程.三、定积分概念的应用及推广1.可以把积分区间[a,b]推广到无限区间上,如[a,+∞)等,或者,函数推广到无界函数,也就是广义积分.2.可以把积分区间[a,b]推广到一个平面区域,被积函数为二元函数,那么积分就是二重积分;同样当被积函数成为三元函数、积分区域变成空间区域时就是三重积分.(一)积分的计算方法定义法:定积分的定义法计算是运用极限的思想,简单地说就是分割求和取极限.任意分割任意取值所计算出的i值如果全部相同的话,则定积分存在.第一步:分割.将区间[a,b]分成n个小区间,一般情况下采取等分的形式.h=b-an,那么分割点的坐标为(a,0),(a+h,0),(a+2h,0),…,(a+(n-1)h,0),(b,0),ξk在[xk-1,xk]任意選取,但是我们在做题过程中会选取特殊的ξk,即左端点,右端点或者中点.经过分割将曲边梯形分成n个小曲边梯形.我们近似的看作是n个小长方形.第二步:求和.计算n个小长方形的面积之和,也就是∑nk=1f(ξk)h.第三步:取极限I=limh→0∑nk=1f(ξk)h=hlimh→0∑nk=1f(ξk),h→0即n→∞,也就是说分的越细,那么小曲边梯形就越接近小长方形,当n趋于无穷之时,小曲边梯形也就是小长方形,那么小长方形的面积和即为曲边梯形的面积,也就是定积分的积分值.(二)牛顿-莱布尼茨公式牛顿-莱布尼茨公式很好地把定积分与不定积分联系在一起.利用此公式,可以根据不定积分的计算计算出定积分.这个公式要求函数在区间内必须连续.求连续函数的定积分只需求出的一个原函数,再按照公式计算即可.定理若函数f(x)在区间[a,b]连续,且F(x)是f(x)的原函数,则∫baf(x)dx=F(b)-F(a).例1 用牛顿-莱布尼茨公式计算定积分∫10xdx.解原式=12x210=12.总结:我们知道,不定积分与定积分是互不相关的,独立的.但是在连续的条件下,微积分基本定理把这两个互不相关的概念联系起来,这是数学分析的卓越成果,有着重大的意义.同样的一道题目,用牛顿-莱布尼茨公式明显比定义法简单.四、定积分的换元积分法应用牛顿-莱布尼茨公式求定积分,首先求被积函数的原函数,其次再按公式计算.一般情况下,把这两步截然分开是比较麻烦的,换元积分法解决了这一问题.例2 求定积分∫21lnxdx.解∫21lnxdx=xlnx“21-∫21xdlnx=2ln2-0-x|21=2ln2-1.:因为u(x),v(x)在[a,b]有连续导函数,并且u(x)易求微分,v(x)容易被计算出来时用分部积分法比较简单.五、定积分在数学中的应用(一)概率问题例3 在区间[-1,1]上任取两数a,b,求方程有两个正根的概率.解由题意,样本空间Ω={(a,b)|-1≤a≤1,-1≤b≤1}表示边长为2的正方形区域,面积SΩ=4.要使方程两根均正,需Δ=4a2-4b≥0,x1+x2=2a0,x1x2=b0,即a2≥b,a0,b0.记方程有两正根为事件A,它对应的区域是由抛物线b=a2,直线a=1和a=0围成的,于是SA=∫10a2da=13.所以P(A)=SASΩ=112.:用定积分求概率问题更多是把问题分为样本空间区域求其覆盖面积,并且找到所求事件的空间区域求其面积,从而求出题目所要求的概率问题,运用了最基本的方法来运用到较复杂问题上.。
定积分的几个简单应用

定积分的几个简单应用(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--定积分的几个简单应用一、定积分在经济生活中的应用在经济管理中,由边际函数求总函数,一般采用不定积分来解决,或者求一个变上限的定积分;如果求总函数在某个范围的改变量,则采用定积分来解决.例1 某商场某品牌衬衫的需求函数是q p 15.065-=,如果价格定在每件50元,试计算消费者剩余.解 由p 50=,q p 15.065-=,得10000=q ,于是dq q )5015.065(100000--⎰10000023)1.015(q q -=50000=,所求消费者剩余为50000元.例2 已知某产品总产量的变化率为t t Q 1240)(+='(件/天),求从第5天到第10天产品的总产量.解 所求的总产量为⎰⎰+='=105105)1240()(dt t dt t Q Q 1052)640(t t +=650=(件).二、用定积分求极限例1 求极限 ∑=∞→n k n n k 123lim .解 nn n n n n n n k n k 12111123+++=∑= )21(1n n n n n +++=.上式是函数[]1,0)(在x x f =的特殊积分和.它是把[]1,0分成n 等分,i ξ取⎥⎦⎤⎢⎣⎡-n i n i ,1的右端点构成的积分和.因为函数[]1,0)(在x x f =可积,由定积分定义,有∑=∞→n k n n k 123lim ⎥⎦⎤⎢⎣⎡+++=∞→)21(1lim n n n n n n 3210==⎰dx x . 例2 求极限 2213lim k n n k n k n -∑=∞→. 解 212213)(11n k nk n k n n k n k n k -⋅=-∑∑==. 上式是函数[]1,01)(2在x x x f -=的特殊积分和.它是把区间[]1,0分成n 等分,i ξ取⎥⎦⎤⎢⎣⎡-n i n i ,1的右端点构成的积分和.因为函数21)(x x x f -=在[]1,0可积,由定积分定义,有2213lim k n n k n k n -∑=∞→31)1(31110232102=⎥⎦⎤⎢⎣⎡--=-=⎰x dx x x . 三、用定积分证明不等式 定积分在不等式的证明中有着重要的应用.在不等式的证明中,可根据函数的特点,利用定积分的性质来证明.例1 设)(x f 是闭区间[]b a ,上的连续函数,且单调增加,求证:⎰⎰+≥b a b a dx x f b a dx x xf )(2)(. 证明 作辅助函数 dt t f x a dt t tf x xa x a ⎰⎰+-=)(2)()(ϕ, 显然0)(=a ϕ,且)(2)(21)()(x f x a dt t f x xf x x a ⎰+--='ϕ )(2))((21)(2x f a a x f x f x ---=ξ [])()(2ξf x f a x --=,其中[]x a ,∈ξ.因为)(x f 在[]b a ,上单调增加,所以0)(≥'x ϕ,从而)(x ϕ在闭区间[]b a ,上单调增加,所以0)()(=≥a x ϕϕ,取b x =得⎰⎰+≥b a ba dx x fb a dx x xf )(2)(. 定积分在许多领域中有着重要应用,它是解决一些几何学问题、物理学问题和经济学问题的重要工具.这一章主要介绍了定积分在不同学科中的应用问题.。
35定积分及其简单应用(理)
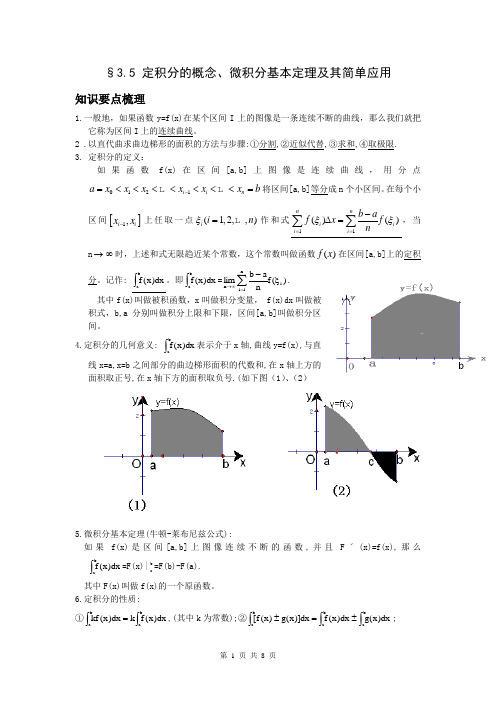
§3.5 定积分的概念、微积分基本定理及其简单应用知识要点梳理1.一般地,如果函数y=f(x)在某个区间I 上的图像是一条连续不断的曲线,那么我们就把它称为区间I 上的连续曲线。
2 .以直代曲求曲边梯形的面积的方法与步骤:①分割,②近似代替,③求和,④取极限. 3. 定积分的定义:如果函数f(x)在区间[a,b]上图像是连续曲线,用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[a,b]等分成n 个小区间。
在每个小区间[]1,i i x x -上任取一点(1,2,,)i i n ξ=作和式11()()nni i i i b af x f nξξ==-∆=∑∑,当n →∞时,上述和式无限趋近某个常数,这个常数叫做函数()f x 在区间[a,b]上的定积分。
记作: ⎰ba dx )x (f 。
即⎰ba dx )x (f =)(f n ab lim i n1i n ξ-∑=∞→.其中f(x)叫做被积函数,x 叫做积分变量, f(x)dx 叫做被积式,b,a 分别叫做积分上限和下限,区间[a,b]叫做积分区间。
4.定积分的几何意义: ⎰badx )x (f 表示介于x 轴,曲线y=f(x),与直线x=a,x=b 之间部分的曲边梯形面积的代数和,在x 轴上方的面积取正号,在x 轴下方的面积取负号.(如下图(1)、(2)5.微积分基本定理(牛顿-莱布尼兹公式):如果f(x)是区间[a,b]上图像连续不断的函数,并且F ˊ(x)=f(x),那么⎰ba dx )x (f =F(x)|b a=F(b)-F(a).其中F(x)叫做f(x)的一个原函数。
6.定积分的性质:①⎰⎰=babadx )x (f k dx )x (kf ,(其中k 为常数);②⎰⎰⎰±=±bababadx )x (g dx )x (f dx )]x (g )x (f [;③⎰⎰⎰+=bcc ab adx )x (f dx )x (f dx )x (f (其中a<b<c)。
定积分的应用公式总结

定积分的应用公式总结定积分是微积分中的重要概念,具有广泛的应用范围。
在实际问题中,定积分可以用于求解曲线下的面积、求解容积、质量、中心矩等问题。
接下来,我们将总结定积分的应用公式,包括面积、体积、质量、中心矩等几个重要应用。
1. 曲线下的面积定积分最常见的应用是求解曲线下的面积。
对于一个函数f(x),在区间[a, b]上,曲线y=f(x)与x轴所围成的面积可以通过定积分来计算。
公式为:S = ∫(a到b)f(x)dx其中S表示曲线下的面积,∫表示定积分,f(x)是函数曲线在x轴上的对应值。
2. 旋转体的体积定积分还可以用于计算旋转体的体积。
考虑一个曲线y=f(x),在[a, b]区间上绕x轴旋转一周,所形成的旋转体体积可以通过定积分来计算。
公式为:V = π∫(a到b)f(x)^2dx其中V表示旋转体的体积,π表示圆周率。
3. 弧长定积分可以用于计算曲线的弧长。
设有曲线y=f(x),在区间[a,b]上的弧长可以通过定积分来计算。
公式为:L = ∫(a到b)√(1+(f'(x))^2)dx其中L表示曲线的弧长,f'(x)表示f(x)的导数。
4. 质量和质心对于一条位于直角坐标系中的线密度分布曲线,其质量可以通过定积分来计算。
设密度函数为ρ(x),曲线上的质量可以表示为:m = ∫(a到b)ρ(x)dx其中m表示曲线上的质量,ρ(x)表示密度函数。
同时,还可以通过定积分来计算曲线的质心。
曲线的质心可以通过以下公式来计算:x_c = (1/m)∫(a到b)xρ(x)dxy_c = (1/m)∫(a到b)yρ(x)dx其中x_c和y_c表示曲线的质心的坐标。
以上的公式总结了定积分的一些重要应用,包括面积、体积、弧长、质量和质心等。
在实际问题中,我们可以根据具体的问题情况,选择适当的公式来计算所需的结果。
这些公式可以帮助我们更好地理解和应用定积分的概念,解决实际问题。
定积分的物理应用

定积分的物理应用在物理学中,定积分是一种重要的数学工具,广泛应用于各个领域。
定积分可以用于求解某一物理量在给定范围内的总量、平均值、功率等问题,为理解和解决物理问题提供了强大的数学支持。
本文将探讨定积分在物理学中的几个典型应用。
一、质点运动中的位移和路径长度在物理学中,研究质点在空间中的运动是一项基础工作。
定积分可以用来计算质点在一段时间内的位移和质点沿着某一曲线运动的路径长度。
假设质点在一维坐标轴上运动,位移是计算质点所在位置与初始位置之间的距离差。
可以用定积分来描述质点在一段时间内的位移,其计算公式为:\[ s = \int_{t_1}^{t_2} v(t) dt \]其中,v(t)表示质点运动的速度函数,t1和t2表示计算位移的时间段。
路径长度是描述质点沿着某一曲线运动的总距离。
即使质点速度在不同位置的大小和方向都不同,也可以通过定积分来计算路径长度。
计算公式如下:\[ L = \int_{t_1}^{t_2} \sqrt{[dx(t)]^2 + [dy(t)]^2 + [dz(t)]^2} \]其中,x(t)、y(t)、z(t)分别表示质点在x轴、y轴和z轴上的位置函数。
二、力学中的功和能量在力学中,定积分可以用来计算力学系统中的功和能量。
功是描述力对物体做功的量,可以通过定积分来计算。
在一维情况下,力对物体做功的公式为:\[ W = \int_{x_1}^{x_2} F(x) dx \]其中,F(x)表示作用在物体上的力,x1和x2表示计算功的位置范围。
能量是物理系统的重要性质,也可以通过定积分来计算。
例如,在弹簧振子系统中,弹性势能可以用以下定积分表示:\[ E = \frac{1}{2} \int_{x_1}^{x_2} kx^2 dx \]其中,k表示弹簧的弹性系数,x1和x2表示弹簧伸缩的位置范围。
三、流体力学中的流量和质量在流体力学中,定积分可以用来计算流体在一定时间内通过某一截面的流量和质量。
定积分的简单应用李用
b
a
f
x
g
xd. x
注:
两曲线围成的平面图形的面积的计算 例 1. 计算由两条抛物线 y2 x和 y x2围成图形的面积.
解:作出y2=x,y=x2的图象如图所示:
解方程组
y y
x x2
x
y
00或xy
1 1
y
y y2 xx B
即两曲线的交点为(0,0),(1,1)
S = S曲边梯形OABC - S曲边梯形OABD
返回
(2)∵v(t)=t2-4t+3=(t-1)(t-3),
∴在区间[0,1]及[3,4]上的v(t)≥0,
在区间[1,3]上,v(t)≤0.
∴在t=4 s时的路程为
1
3
4
s=0(t2-4t+3)dt-1(t2-4t+3)dt+3(t2-4t+3)dt
=(13t3-2t2+3t)|10-(13t3-2t2+3t)|31+(13t3-2t2+3t)|43=4(m).
图1.7 3
s 30 60 30 1350
2
二、变力沿直线所作的功
1、恒力作功
由物理学知道,如果物体在作直线运动的过
程中有一个不变的力F 作用在这物体上,且这力
的方向与物体的运动方向一致,那么,在物体移
动了距离 s时,力 F 对物体所作的功为W F s .
2、变力所做的功
问题:物体在变力F(x)的作用下做直线运动,并
例 2 计算由曲线 y 2x ,直线 y x 4以及 x 轴所
围成的图形的面积.
y 2x
解: 两曲线的交点
y
2x
(0, 0), (8, 4).
y x 4
直线与x轴交点为(4,0)
定积分经济学应用

定积分经济学应用
定积分是微积分的一个重要分支,它在经济学中有广泛的应用。
下面将从不同的角度来阐述定积分在经济学中的应用。
一、利润和成本的计算
在商业经济学中,利润和成本是企业最为关注的指标。
通过定积分,可以精确地计算企业的利润和成本。
例如,利润可以用销售额减去成本来计算,而成本中的各项费用可以通过定积分来计算。
这样,企业就可以更加准确地了解自己的利润和成本情况,从而做出更好的经营决策。
二、消费者剩余的测算
在市场经济中,商品的价格由供需关系决定。
为了衡量市场价格的合理性,经济学家引入了消费者剩余这一概念。
消费者剩余是指消费者愿意为某种商品支付的最高价格与实际支付的价格之差。
通过定积分的计算,可以精确地测算消费者剩余的大小,进而了解市场经济的运行情况,为政策制定和市场规划提供参考。
三、市场需求的计算
市场需求是指所有购买该商品的消费者的数量总和。
定积分常常用于计算市场需求,这能够帮助企业预测未来市场的走势以及生产规模。
除此之外,市场需求的计算还可以帮助政府了解市场需求量的大小,从而决定政策的制定方向。
四、投资决策的分析
在投资决策中,经济学家需要对不同投资方案的收益率进行计算。
通过定积分,可以计算出不同时期内各种投资方案的收益率,并选择其中最优的投资方案。
这样,企业就可以获得更大的收益。
总而言之,定积分在经济学中有着广泛的应用。
其中,利润和成本的计算、消费者剩余的测算、市场需求的计算以及投资决策的分析都是常见的应用。
这些应用帮助企业和政府更好地了解市场经济的运行情况,从而做出更加合理的决策。
定积分的应用

定积分的应用在微积分中,定积分是一种重要的概念和工具。
它不仅可以用于求解曲线下的面积,还可以应用于多个领域,包括物理、经济学和工程学等。
本文将介绍定积分的应用,并通过实际问题进行说明。
一、曲线下的面积定积分最基本的应用之一是求解曲线下的面积。
假设有一个函数f(x),我们想要计算其在区间[a, b]上的曲线下的面积。
我们可以将[a, b]的区间划分为若干小区间,然后在每个小区间上取一个点,通过计算这些小区间的面积之和来逼近整个曲线下的面积。
随着小区间数目的增加,逼近的精度也会提高,最终可以得到非常准确的结果。
二、物理学中的应用定积分在物理学中有广泛的应用。
例如,在力学中,我们可以利用定积分来计算物体的质量、速度和加速度等。
通过将物体运动过程中的力和加速度关系用函数表示,然后对这个函数在一定时间内的积分,就可以得到物体在该时间内的位移。
同样地,通过对速度函数在一段时间内的定积分,可以计算出物体在该时间内的位移。
三、经济学中的应用定积分在经济学中也有重要的应用。
一种常见的应用是计算曲线下的总收益或总成本。
假设有一个企业的收益函数为R(x),我们可以通过对该函数在某个时间段内的定积分,得到该时间段内企业的总收益。
同样地,如果有一个成本函数C(x),我们可以通过对该函数在某个时间段内的定积分,得到该时间段内企业的总成本。
这种方法可以帮助经济学家更好地了解企业的经营状况并作出相应的决策。
四、工程学中的应用定积分也在工程学中有广泛的应用。
例如,在建筑工程中,我们可以利用定积分来计算建筑物的体积。
假设有一个建筑物的截面曲线为f(x),我们可以通过对该曲线在一定范围内的定积分,得到该范围内建筑物的体积。
同样地,在水力学中,我们可以利用定积分来计算河流的流量,以便更好地了解水流情况并采取相应的措施。
综上所述,定积分是一种重要的工具,可以应用于求解曲线下的面积、物理学、经济学和工程学等多个领域。
通过对函数在一定范围内的定积分,我们可以得到与实际问题相关的重要信息,从而更好地理解和解决问题。
定积分的应用(13

定积分的应用(13定积分是高中数学中十分重要的概念之一,其应用范围很广。
在这篇文章中,我们将会介绍一些定积分的应用。
1. 计算曲线下的面积对于一个平面上的曲线,我们可以通过计算它与 $x$ 轴之间的定积分来计算它所占的面积。
如果我们已知一个函数 $f(x)$,并且想要计算它的图像和 $x$ 轴之间的面积,可以使用下面的公式:$$\int_{a}^{b}f(x)dx$$其中,$a$ 和 $b$ 是积分的上下限。
这个公式是一个重要的几何概念,可以用于计算圆的面积、三角形的面积等。
2. 计算速度和位移可以使用定积分来计算物体的速度和位移。
当物体的速度是一个连续函数时,我们可以用定积分来计算它的位移。
例如,一个物体的速度曲线可以表示为 $v(t)$,则物体的位移可以通过下面的公式计算:这个公式表示的是从时间 $a$ 到时间 $b$ 的总位移。
如果我们知道物体的位移曲线,并且想要计算它的速度,可以通过求导来得到速度曲线。
3. 动量和力的计算在物理学中,动量是一个十分重要的概念。
如果我们知道一个系统中各个物体的质量和速度,可以使用下面的公式计算它的总动量:$$p = \sum_{i=1}^{n}m_iv_i$$其中,$m_i$ 表示物体 $i$ 的质量,$v_i$ 表示它的速度。
如果我们需要计算某个时间段内系统的总动量,可以使用在这个时间段内速度的平均值。
其中,$F_i$ 表示物体 $i$ 受到的力。
4. 发现未知函数的性质定积分可以帮助我们发现一个未知函数的性质。
例如,我们可以通过计算一个函数在所有可能的 $x$ 值上的定积分,来探究函数的奇偶性、增减性等。
同时,如果我们已知一个函数的一些性质(如连续性、单调性等),可以使用定积分来证明这些性质。
总的来说,定积分在科学和工程领域中有着广泛的应用。
无论是求解面积、计算速度和位移、计算动量和力、还是探究未知函数的性质,所有这些应用都用到了定积分的概念。
定积分是数学中一个极为重要的工具,掌握定积分的应用是我们进行科学研究和实践工作的必备技能。
定积分的物理应用

定积分的物理应用定积分是微积分中的重要概念,它在物理学中有着广泛的应用。
本文将探讨定积分在物理学中的几个主要应用领域。
一、质点运动的位移与速度质点在一定时间内的位移可以通过定积分来计算。
假设质点在时间区间[a, b]内的速度函数为v(t),则质点在该时间区间内的位移可以用定积分表示为:S = ∫[a,b] v(t) dt其中,S表示质点的位移量。
这个定积分表示了质点在从a时刻到b时刻的速度变化的累积效果,即位移量。
二、质点运动的加速度与速度速度的变化率称为加速度。
根据牛顿第二定律,质点的加速度可以表示为质点所受的力对质点质量的比值。
因此,如果我们知道质点在某个时间区间内的加速度函数a(t),那么质点在该时间区间内的速度变化可以用定积分表示为:Δv = ∫[a,b] a(t) dt其中,Δv表示速度的变化量。
这个定积分表示了质点在从a时刻到b时刻的加速度变化的累积效果,即速度的变化量。
三、质点受力的功与能量在物理学中,功可以理解为力对质点产生的能量转移。
假设一个质点在沿着一个直线运动,并受到一个作用力F(x)的作用。
则质点在从点a到点b的位移过程中所受到的力的功可以用定积分表示:W = ∫[a,b] F(x) dx其中,W表示受力的功。
这个定积分表示了力F(x)对质点在从点a 到点b的位移过程中所作的功。
四、连续介质的质量与密度在连续介质力学中,定积分也有着重要的应用。
考虑一个线密度为ρ(x)的连续介质,它在区间[a, b]中的质量可以用以下定积分表示:m = ∫[a,b] ρ(x) dx其中,m表示连续介质的质量。
这个定积分表示了在区间[a, b]中,密度函数ρ(x)所围成的面积,即连续介质的质量。
五、物体的质心与力矩物体的质心是物体质量均匀分布时的平衡点。
对于一个质量为m(x)的物体,可以用定积分来求解其质心位置:x_c = ∫[a,b] x * m(x) dx / ∫[a,b] m(x) dx其中,x_c表示物体的质心位置。
定积分计算及其应用

定积分计算及其应用
一、定积分计算
1、图像法:通过图像来计算定积分,一般会将被定积函数的图像在
其中一区间内分割成许多小矩形,每一小矩形的面积就是定积分的值,然
后通过将多个小矩形的面积加和=求出定积分。
2、定积分计算公式:定积分是由定积分计算公式来计算的,定积分
公式结构为:∫a b f(x) dx,它代表的是从a到b的定积分,f(x)是定
积函数,dx是微元。
二、定积分应用
定积分的应用范围广泛,主要有三个方面:
1、地理学:定积分在地理学中有着广泛的应用,可以用定积分计算
地理曲线下面积、地球表面圆锥曲线的一定高度投影的面积等等。
2、力学、物理学:定积分在力学、物理学等学科中有着重要的应用,可以用定积分来计算绳、杆、轴旋转运动的角动量,以及各种复杂力场的
重力矩等等。
3、经济学:在经济学中,定积分可以用来求解复杂的经济关系,如
决定消费者及生产者福利的函数关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定积分及其简单的应用
自主梳理
1.微积分基本定理
一般地,如果f (x )是区间[a ,b ]上的连续函数,并且F ′(x )=f (x ),那么ʃb a f (x )d x =F (b )-F (a ),这个结论叫做__________________,为了方便,我们常把F (b )-F (a )记成
__________________,即ʃb a f (x )d x =F (x )|b
a =F (
b )-F (a ).
2.定积分ʃb a f (x )d x 的几何意义:如果在区间[a ,b ]上函数f (x )连续且恒有f (x )≥0,那么函数f (x )在区间[a ,b ]上的定积分的几何意义是直线________________________所围成的曲边梯形的________.
3.定积分在几何中的应用
(1)当x ∈[a ,b ]且f (x )>0时,由直线x =a ,x =b (a ≠b ),y =0和曲线y =f (x )围成的曲边梯形的面积S =__________________.
(2)当x ∈[a ,b ]且f (x )<0时,由直线x =a ,x =b (a ≠b ),y =0和曲线y =f (x )围成的曲边梯形的面积S =__________________.
(3)当x ∈[a ,b ]且f (x )>g (x )>0时,由直线x =a ,x =b (a ≠b )和曲线y =f (x ),y =g (x )围成的平面图形的面积S =______________________.
(4)若f (x )是偶函数,则ʃa -a f (x )d x =2ʃa 0f (x )d x ;若f (x )是奇函数,则ʃa
-a f (x )d x =0.
4.定积分在物理中的应用 (1)匀变速运动的路程公式
做变速直线运动的物体所经过的路程s ,等于其速度函数v =v (t )[v (t )≥0]在时间区间[a ,b 上的定积分,即________________________.
(2)变力做功公式
一物体在变力F (x )(单位:N)的作用下做直线运动,如果物体沿着与F 相同的方向从x =a 移动到x =b (a <b )(单位:m),则力F 所做的功W =__________________________.
探究点一 利用公式求定积分的值 例1 计算下列定积分: (1)21
11()e
x dx x x
++⎰
; (2)2
0sin 2cos )x x dx π
-⎰(;
(3)ʃπ0(2sin x -3e x +2)d x ; (4)ʃ20|x 2-1|d x . (5)ʃ2π
0|sin x |d x ;
巩固训练
1. ʃ421x d x 等于 ( ) A .-2ln 2
B .2ln 2
C .-ln 2
D .ln 2
2.计算定积分ʃ503x d x 的值为 ( ) A.752
B .75 C.25
2
D .25
探究点二 求曲线围成的面积
例2 计算由抛物线y =1
2x 2和y =3-
(x -1)2所围成的平面图形的面积S .
巩固训练
3. 计算曲线y =x 2-2x +3与直线y =x +3所围图形的面积.
4.如右图所示,阴影部分的面积是 ( )
A .2 3
B .2- 3 C.32
3
D.353
例3:
.
巩固训练
5.ʃ204-x 2d x =__________ ʃ2-24-x 2
d x =______________
=⎰
定积分课后练习(A )
(满分: 70分)
一、选择题(每小题5分,共25分)
1.下列值等于1的积分是 ( )
A .ʃ1
0x d x
B .ʃ10(x +1)d x
C .ʃ101
2
d x
D .ʃ1
01d x
2.设函数f (x )=⎩
⎪⎨⎪⎧
x 2
+1,0≤x ≤1,
3-x ,1<x ≤2,则ʃ20f (x )d x 等于 ( )
A.1
3 B.17
6
C .6
D .17 3.已知f (x )为偶函数且ʃ60f (x )d x =8,则ʃ6
-6f (x )d x 等于 ( )
A .0
B .4
C .8
D .16
4. y =sin x ,y =cos x 与直线x =0,x =π
2所围成的平面区域的面积为
( )
A .ʃπ20(sin x -cos x )d x
B .2ʃπ
40(sin x -cos x )d x
C .ʃπ20(cos x -sin x )d x
D .2ʃπ
40(cos x -sin x )d x
5.函数f (x )=ʃx 0t (t -4)d t 在[-1,5]上 ( ) A .有最大值0,无最小值 B .有最大值0,最小值-323
C .有最小值-32
3
,无最大值 D .既无最大值也无最小值
6.ʃ10(2x k
+1)d x =2,则k =________.
7.(10分)计算以下定积分:
(1)ʃ21⎝⎛⎭
⎫2x 2-1x d x ; (4)ʃ21|3-2x |d x .
8.设y =f (x )是二次函数,方程f (x )=0有两个相等的实根,且f ′(x )=2x -2. (1)求y =f (x )的表达式;
(2)求y =f (x )的图象与两坐标轴所围成图形的面积.
9.求曲线y =e x -1与直线x =-ln 2,y =e -1所围成的平面图形的面积.
10:在区间[—1,1]上任取两数a 、b ,求二次方程02
=++b ax x 的两根都是正数的
概。
