2020年上期明德初中联盟四校初三4月份限时训练 答案
2020年明德中学七年级上学期第一次限时训练语文试卷及答案

2020年明德中学七年级上学期第一次限时训练语文试卷时量:120分钟满分120分一、积累运用(共28分)1.下列选项中字形和加点字的注音完全正确..的一项是()(2分)A.匿.笑(nì)憔悴.(cuì)酝酿.(liàng)人声顶沸B.贮.蓄(zhù)决.(jué)别攲.斜(jī)咄咄逼人C.吝啬.(sè)粗犷.(guǎng)黄晕.(yùn)波光粼粼D.应和.(hè)云宵.(xiāo)静谧.(mì)翻来复去2.下列词语使用,不恰当的一项是()(2分)A.你看,迎面走来的那一群俏姑娘,个个都打扮得花枝招展的。
B.他成绩一向优秀,这次考试又得了满分,真是喜出望外。
C.中岛熏先生于8月底莅临香港,分别出席了安利直销商大会和安利领导人聚会。
D.小李当了演员,小白当了作家,他们都各得其所。
3.下列语句中没有语病....的一项是()(2分)A在这故事中,使我懂得了做人的艰难。
B.通过检查,大家讨论、发现、解决了社会实践活动中的一些问题。
C.调查显示,我国近90%的青少年认为“诚实守信”、“助人为乐”是优秀的传统美德。
D.一个人能否成为真正的读者,关键在于他青少年时期养成良好的读书习惯。
4.下列句子排列最恰当...的一项是()(2分)①面对身边诸多纠结,多一点智慧和勇气,保持一份平和的心态,可助我们削弱对“纠结”的纠缠。
②随着现代生活节奏的加快,生活压力的增大,“纠结”的事越来越多。
③如今,随着信息技术的快速发展,“纠结”一词事先在网络上爆红,不但使用率颇高,而且使用更加广泛灵活。
④纠结的本意就是“相互缠绕”,常作动词用。
语出唐代诗人李白的《古意》一诗:“枝枝相纠结,叶叶竞飘扬。
”A.③②④①B.③④①②C.②①④③D.②④③①5.下列选项中表述错误..的一项是()(2分)A.古时候,用“令尊”“尊君”尊称对方的父亲,用“家严”“家君”谦称自己的父亲。
2020年上学期初三4月入学作业检测卷答案

2020年上学期初三4月入学作业检测卷答案1-5 DBCAD 6-10 CDBAC 11-12 BC13.2x > 14. 23(1)a b - 15.23 16. 3 17. 4 18. 7419.解:原式=22212⨯+-+=1 20.解:由①得3x ≥- 2分由②得1x < 4分∴ 31x -≤< 5分画数轴 6分21. 解:(1)12÷30%=40人,40×20%=8人,补全条形统计图如图所示: 2分(2)10,40,144; 5分(3)设除小明以外的三个人记作A 、B 、C ,从中任意选取2人,所有可能出现的情况如下:共有12中可能出现的情况,其中小明被选中的有6种,所以小明被选中参加区知识竞赛的概率为=. 8分(2,3,3给分)22. (1)证明:∵四边形ABCD 是矩形,∴BD =AC ,DO =BO ,AO =CO ,∴OD =OC ,∵CE ∥BD ,DE ∥AC ,∴四边形CODE 是平行四边形,∴四边形CODE 是菱形;(2)解:∴矩形ABCD 的面积=2菱形OCED 的面积,∴矩形ABCD 的面积=2菱形OCED 的面积=2×18=36∵∠ABC =60°,∴设AB k = ,则BC =2= ,∴6k =∴BC =23. 解:(1)设A 品牌每个的进价为x 元,根据题意的 7200500020.7x x=⨯+ 解得x =1.8经检验x =1.8是原方程的解 x +0.7=2.5(元)答:A 种品牌每个的进价为1.8元,B 种品牌每个的进价为2.5元.(2)设购进B 品牌的口罩m 个,根据题意的0.3(8000﹣m )+0.5m ≥3000解得m ≥3000∵m 为整数∴m 的最小值为3000.答:最少购进B 品牌的口罩3000个24. 解:(1)如图1,连结AC ,∵AD 为⊙C 的直径,∴∠ABD =∠AOE =90°,∵∠AEB =∠ADB ,∠OAE +∠AEB =∠BAD +∠ADB =90°,∴∠OAE =∠BAD .(2)∵∠BOA =90°,A (6,0),B (- ,0)∴OB =,OA =6,∴AB =12∴9BD ==∵∠OAE =∠BAD ,∴tan OAE BAD ∠∠=tan ∴BD OE AB AO= ∴92OE = (3)∵BD ⊥AB ,∴当OD 最小时,OD ⊥BD ,此时,OD =OB sin ∠OBD =92=求得点D 的坐标为92⎛⎫- ⎪⎝⎭ . 又∵点C 为AD 的中点∴点C 的坐标为34⎛⎫ ⎪⎝⎭. 25.解:(1) y =2x +2(2)∵抛物线C :2+1(0)y ax bx a =+≠过点E (1)a ,∴1b =-令2x +2=ax 2﹣x +1,则ax 2﹣3x ﹣1=0,若直线y =2x +2与抛物线y =ax 2﹣x +1(a ≠0)有两个不同的交点,则△=(﹣3)2﹣4a ×(﹣1)>0,解得,a >﹣,∵抛物线y =ax 2﹣x +1(a ≠0)与线段AB 有两个不同的交点,点A (﹣,1)和B (1,4),∴当﹣<a <0时, 解得,﹣2;当a >0时,, 解得,a ≥4;由上可得,﹣2或a ≥4,(3)平移后直线解析式为2y x =联立221y x y ax bx =⎧⎨=++⎩ 得2(2)10ax b x +-+= ∴ 121x x a ⋅=,122b x x a -+= ∵ 12-2x x =∴()212-4x x =∴()()222244211b a a a -=+=+- ∵121x x a⋅= 0a > 12x < ∴122x -<< 且10x ≠∴244x -<< ∴1218x x a ⋅=< ∴18a > ∴()29216b -> ∴114b > 或54b < 26. 解:(1) y =21322x x -- (2)01 当ABC PCF ∠=∠时∵090ABC OCB ∠+= ∴090PCF OCB ∠+= 直线CB 解析式为1322y x =- ∴直线PC 解析式为322y x =--23221322y x y x x ⎧=--⎪⎪⎨⎪=--⎪⎩解得120,x 2x ==- ∴5(2,)2P -02当ABC PCF ∠=∠时 设直线PC 与x 轴交于点M , ∴tan tan ABC PCF ∠=∠ ∴3(,0)4M∴直线PC 解析式为322y x =-23221322y x y x x ⎧=-⎪⎪⎨⎪=--⎪⎩解得340,x 6x == ∴21(6,)2P ∴5(2,)2P -或21(6,)2P(3)设P A 的解析式y =k 1x +k 1, ∴11223y k x k y ax ax a =+⎧⎨=--⎩∴ax 2﹣(2a +k 1)x -3a -k 1=0, ∴13p k x a =+PB 的解析式y =k 2x ﹣3k 2, ∴222323y k x k y ax ax a =-⎧⎨=--⎩ ∴ax 2﹣(2a +k 2)x -3a +3k 2=0 ∴21p k x a =-+ ∴1231p k k x a a=+=-+ ∴214k k a -= 又∵EC =k 1+3 a ,DE =k 1+3k 2, ∴=14 .。
2020-2021年明德教育集团九年级第一学期期末考试【附答案】

题的概率是
.
15.使二次根式 2 x 有意义的 x 的取值范围是
.
16.已知圆锥的底面圆半径为 3,母线长为 5,则该圆锥的侧面积是
.
17.著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规,如图所示,有
两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端 A、B 能在滑槽内自由滑动,将
4
22.如图,在矩形 ABCD 中,E、F 分别是边 AB、CD 上的点,AE=CF,连接 EF、BF,EF 与对角线 AC 交于 点 O,且 BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF; (2)若 AC=6 ,求 AB 的长.
23.“炎陵黄桃”是生态营养安全的绿色食品,为国家地理标志商标保护产品,享有“炎陵黄桃,桃醉天下”的 美誉,同时也是国家精准扶贫项目,炎陵县黄桃种植基地计划种植 A、B 两种黄桃共 30 亩,已知 A、B 两 种黄桃的年产量分别为 2 000 千克/亩、2 500 千克/亩,收购单价分别是 8 元/千克、7 元/千克.
(1)本次抽取调查的学生共有 人,估计该校 1000 名学生中“非常了解”的有 人; (2)请补全条形统计图; (3)“不了解”的 4 人中有 3 名男生 A1,A2,A3,1 名女生 B,为了提高学生对禁毒知识的了解,对这 4 人 进行了培训,然后随机抽取 2 人对禁毒知识的掌握情况进行检测,请用画树状图或列表的方法,求恰好抽 到 2 名男生的概率.
交直线 AB 于点 F , M 为线段 FA 上的一个动点,求 DM 5 MF 的最小值.
5
6
26.如图 1,在平面直角坐标系 th 中,抛物线 :h t 1
与 轴相交于 , 两点,顶点为 D,
湖南四大名校内部资料答案-2019-2020-1明德九上期中考试

2019-2020明德教育集团初中联盟初三第一学期期中考试数学参考答案一、选择题二、填空题13.11214.10315.2- 16.2x ≥且3x ≠17.224cm π18.2三、解答题∴1121k b ⎧=⎪⎨⎪=-⎩ ∴1112y x =- (2)2x <-或04x <<22.【解析】(1)设温馨提示牌单价为x 元,垃圾箱单价为y 元,由题意得:325503x y y x+=⎧⎨=⎩ ∴50150x y =⎧⎨=⎩答:温馨提示牌单价为50元,垃圾箱单价为150元 (2)设购买温馨提示牌a 个,则()100481501005010000a a a -≥⎧⎪⎨-+≤⎪⎩解得5052a ≤≤方案一:温馨提示牌50个,垃圾箱50个 方案二:温馨提示牌51个,垃圾箱49个 方案三:温馨提示牌52个,垃圾箱48个 当52a =时,费用最少,最少为9800元24.【解析】(1)∵»»BE BE =∴EDB EAB ∠=∠ 又AB 为O e 的直径 ∴90AEB ∠=o ∴90EAB EBA ∠+∠=o∴90EBA EBC ∠+∠=o,即90ABC ∠=o∴BC 为O e 的切线(2)∵»»AD AD = ∴DEA DBA ∠=∠ 又BD 平分ABE ∠∴DBA DBE ∠=∠ ∴DEA DBE ∠=∠ 又D D ∠=∠ ∴DEF DBE ∆∆∽ ∴DE DBDF DE=∴2DE DF DB -=⋅ (3)连DO ∵OB OD = ∴ODB OBD ∠=∠ 又DBO EBD ∠=∠ ∴ODB DBE ∠=∠ ∴//DO BE∴PD PODE OB =∴221PD =∴4PD =25.【解析】(1)3412S =⨯=(2)①C 坐标为()2,3时,直线:1AC y x =+ ②C 坐标为()2,3-时,直线:1AC y x =--(3)若O e 上存在N ,使MN 的“衍生矩形”为正方形 则直线MN 斜率为1±∴当1k =-时,极限位置是直线与O e 相切 如图1l ,2l直线1l 与O e 相切于点1N12ON =,190ON M ∠=o∴1l 与y 轴交于()10,2P -,()11,3M m ∴()1320m --=- ∴15m =-。
2019届九年级4月期中联考化学试题(附答案)

明德教育集团初中联盟期中考试初三年级化学试卷18-19学年第二学期(可能要用到的相对原子质量:H-1,C-12,O-16,Ca-40,Cl-35.5)一、选择题(本大题共15小题,每小题3分,共45分。
每小题只有一个选项符合题意)1.日常生活中的下列变化,属于物理变化的是( )A.干冰升华B.铁锅生锈C.燃放鞭炮D.食物腐败2、下列有关物质用途的说法错误的是()A.氧气能用作燃料B.氮气可用来制造硝酸和氮肥C.稀有气体可用于填充霓虹灯D.红磷可用于运动会上的发令枪3.如图表示初中化学常见实验操作,其中正确的是()A.过滤B.检查装置的气密性C.读出液体的体积D.液体的取用4. 铁元素、铁原子的部分信息如图所示。
下列说法正确的是()A.y=18B.人体缺铁会导致甲状腺肿大C.铁原子在化学反应中易失去电子D.铁原子的相对原子质量为55.85g5.水是生命之源,下列有关水的说法错误的是()A.农药、化肥的不合理使用会造成水体污染B.长期饮用蒸馏水不利于人体的健康C.生活中可用煮沸的方法降低水的硬度D.过滤可以除去水中的可溶性杂质6.如图是一个化学反应的微观示意图。
从该示意图中获取的信息错误的是()A.反应前后分子种类发生改变B.反应前后,原子的种类、数目不变C.参加反应的两种分子的个数比是1:2 D.该反应属于化合反应7.下列有关碳和碳的氧化物的说法,错误..的是()A.仅由碳元素组成的物质不一定是单质B.金刚石和石墨的物理性质不相似是因为碳原子的排列方式不同C.二氧化碳能使紫色石蕊溶液变红,说明二氧化碳具有酸性D.一氧化碳能与血液中的血红蛋白结合导致中毒8. 下列有关生产、环保、资源问题的叙述错误的是()A.pH<5.6的雨水称为酸雨B.只要温度达到着火点时,燃料就一定能燃烧C.使用乙醇汽油能减少污染,节约石油资源D.煤、石油、天然气都是化石燃料,是不可再生能源9.下列有关金属材料的说法正确的是()A.硫酸铜溶液不宜用铁桶来盛放B.黄铜、焊锡都属于金属单质C.铜的化学性质不活泼,在潮湿的空气中不会被腐蚀D.生铁的含碳量低于钢10.下列有关溶液的说法,不正确的是()A.蔗糖溶液是均一的、稳定的混合物B.洗涤剂能洗掉油污是因为洗涤剂对油污有乳化作用C.溶液组成中一定含有水D.降温能使接近饱和的硝酸钾溶液达到饱和11. 下列实际应用中,利用中和反应原理的是( )①用稀氨水涂抹在蚊子叮咬处(分泌出蚁酸)止痒;②用碳酸氢钠治疗胃酸过多;③用熟石灰改良酸性土壤。
2020-2021学年长沙明德教育集团九年级期中考试物理试卷及答案

2020-2021学年长沙明德教育集团九年级期中考试物理试卷一、选择题1.下列几种估测中符合实际情况的是()A.一节新干电池电压2VB.对人体的安全电压不高于36VC.家用电冰箱正常工作时电流约5AD.普通教室一盏日光灯正常工作电流是2A2.关于热现象,下列说法正确的是()A.沿海地区昼夜温差小,是因为水的比热容小B.火箭一般用液态氢做燃料,是因为液态氢的热值小C.发生热传递时,热量总是从内能大的物体传递给内能小的物体D.六月栀子花飘香,说明分子在永不停息地做无规则运动3.关于图片中物理过程的描述,下列分析中正确的是()A.甲图中圆筒内的空气被压缩时温度降低B.乙图中塞子跳起时,瓶内气体的温度升高C.丙图中试管内的水蒸气对活塞做功D.丁图为内燃机的压缩冲程4.如图所示,把一根中间戳有小孔(没戳穿)的轻质饮料吸管放在转动轴上,吸管能在水平面内自由转动,用餐巾纸摩擦吸管使其带电。
用丝绸摩擦过的玻璃棒靠近吸管的一端,两者相互吸引。
下列说法中正确的是()A.玻璃棒带负电B.吸管带正电C.吸管与玻璃棒带异种电荷D.餐巾纸与吸管带同种电荷5.塑料外壳的手电筒的构造如图所示,手电筒内装了两节新干电池,关于手电筒的电路,下列说法正确的是()A.金属弹簧不属于电路的一部分B.灯泡发光时是通路C.灯泡发光时,电能转化为化学能D.电路中电流是由正电荷定向移动形成的6.小明家所在的小区安装了自动售水机.售水机既可以通过刷卡闭合“感应开关”,接通供水电机取水,也可以通过投币闭合“投币开关”,接通供水电机取水;光线较暗时“光控开关”自动闭合,接通灯泡提供照明.以下简化电路符合要求的是()A. B. C. D.7.在如图所示的电路中,电源电压恒定,闭合开关S后,将滑动变阻器的滑片P向右移动,下列说法中正确的是()A.电流表A1的示数变大B.电压表V的示数变大C.电压表V与电流表A2的示数之比变大D.电流表A2与A1的示数之差变大8.下列关于电阻的说法正确的是()A.当导体两端的电压增大为原来的2倍时,导体的电阻R也增大为原来的2倍B.当通过导体的电流增大为原来的2倍时,导体的电阻R减小为原来的1 2C.导体的电阻是导体本身的一种性质,与导体中电流和导体两端电压无关D.通过导体的电流若为零,该导体的电阻也为零9.某智能百叶窗的叶片上贴有太阳能板,在光照时发电,给电动机供电以调节百叶窗的开合.该过程中发生的能量转换是()A.电能→机械能→光能B.光能→机械能→电能C.光能→电能→机械能D.机械能→电能→光能10.在如下图所示的电路中,闭合开关时,灯泡L1比L2亮,L1和L2的电阻分别为R1和R2,则下列说法一定成立的是()A.I1=I2B.I1>I2C.U1<U2D.R1<R211.某一温度下,连接在电路中的两段导体A和B中的电流与其两端电压的关系如图所示.由图中信息可知()A.B导体的电阻为5ΩB.A导体的电阻大于B导体的电阻C.AB串联的电路中电流为0.3A时,串联电路两端的电压为4.5VD.AB并联在2V的电路中,干路中电流为0.5A12.如图所示,当滑动变阻器R1的滑片P从最右端滑动到最左端的过程中,电压表示数变化范围是6V~0V,电流表示数变化范围是0.2A~0.4A,下列说法中正确的是()A.电源电压12VB.滑动变阻器R1最大阻值15ΩC.R2的阻值为20ΩD.滑片P移动到中点时,电压表示数3V二、填空题13.为了应对新型冠状病毒肺炎,我们会将消毒液喷洒在室外楼道、走廊里,过一会室内也闻到消毒液的气味,这是______现象;在家中通过蒸煮加热给餐具高温消毒,这是采用______方式增加餐具内能。
2020-2021深圳明德外语实验学校初三数学上期中试卷带答案
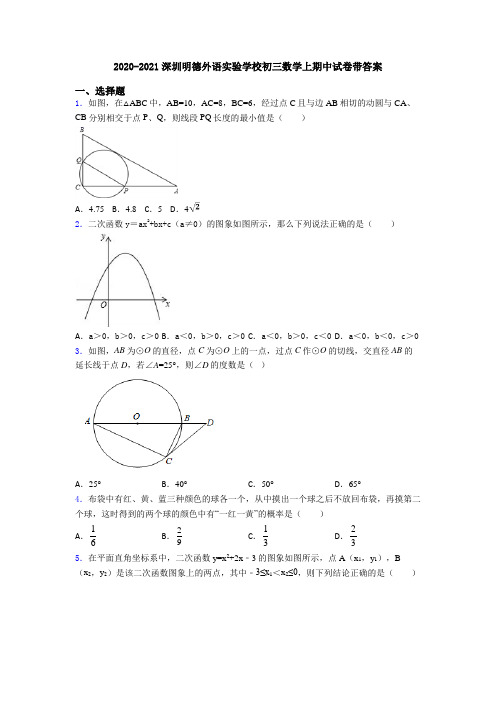
2020-2021深圳明德外语实验学校初三数学上期中试卷带答案一、选择题1.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是()A.4.75 B.4.8 C.5 D.42.二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么下列说法正确的是()A.a>0,b>0,c>0 B.a<0,b>0,c>0 C.a<0,b>0,c<0D.a<0,b<0,c>0 3.如图,AB为⊙O的直径,点C为⊙O上的一点,过点C作⊙O的切线,交直径AB的延长线于点D,若∠A=25°,则∠D的度数是()A.25°B.40°C.50°D.65°4.布袋中有红、黄、蓝三种颜色的球各一个,从中摸出一个球之后不放回布袋,再摸第二个球,这时得到的两个球的颜色中有“一红一黄”的概率是()A.16B.29C.13D.235.在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是()A .y 1<y 2B .y 1>y 2C .y 的最小值是﹣3D .y 的最小值是﹣46.如图,某小区计划在一块长为32m ,宽为20m 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪.若草坪的面积为570m 2,道路的宽为xm ,则可列方程为( )A .32×20﹣2x 2=570 B .32×20﹣3x 2=570 C .(32﹣x )(20﹣2x )=570D .(32﹣2x )(20﹣x )=570 7.若2245a a x -+-=,则不论取何值,一定有( )A .5x >B .5x <-C .3x ≥-D .3x ≤- 8.某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y (间)与定价x (元/间)之间满足y =14x ﹣42(x ≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )A .252元/间B .256元/间C .258元/间D .260元/间9.如图,Rt AOB 中,AB OB ⊥,且AB OB 3==,设直线x t =截此三角形所得阴影部分的面积为S ,则S 与t 之间的函数关系的图象为下列选项中的( )A .B .C .D .10.用1、2、3三个数字组成一个三位数,则组成的数是偶数的概率是( ) A .13 B .14 C .15 D .1611.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m ,另一边减少了2m ,剩余空地的面积为18m 2,求原正方形空地的边长.设原正方形的空地的边长为xm ,则可列方程为( )A .(x+1)(x+2)=18B .x 2﹣3x+16=0C .(x ﹣1)(x ﹣2)=18 D .x 2+3x+16=0 12.有两个一元二次方程2:0M ax bx c ++=,2:0N cx bx a ++=,其中,0ac ≠,a c ≠,下列四个结论中错误的是( )A .如果方程M 有两个不相等的实数根,那么方程N 也有两个不相等的实数B .如果4是方程M 的一个根,那么14是方程N 的另一个根 C .如果方程M 有两根符号相同,那么方程N 的两符号也相同 D .如果方程M 和方程N 有一个相同的根,那么这个根必是1x =二、填空题13.已知方程x 2﹣3x+k=0有两个相等的实数根,则k=_____.14.已知一元二次方程x 2+kx -3=0有一个根为1,则k 的值为__________.15.如图,AB 为⊙O 的直径,点C 、D 在⊙O 上,若∠D =20°,则∠CBA 的度数是__.16.请你写出一个二次函数,其图象满足条件:①开口向下;②与y 轴的交点坐标为(0,3).此二次函数的解析式可以是______________17.若圆锥的底面周长为4π,母线长为6,则圆锥的侧面积等于________.(结果保留π)18.将一元二次方程x 2﹣6x +5=0化成(x ﹣a )2=b 的形式,则ab =__.19.用半径为12cm ,圆心角为90°的扇形纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为_______cm .20.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列4个结论:①abc >0;②b <a +c ;③4a +2b +c >0;④b 2﹣4ac >0;其中正确的结论有_____.(填序号)三、解答题21.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.()1求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;()2求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?()3如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本⨯每天的销售量) 22.2021年我省开始实施“ 3+1+2”高考新方案,其中语文、数学、外语三门为统考科目(必考),物理和历史两个科目中任选 1门,另外在思想政治、地理、化学、生物四门科目中任选 2门,共计6门科目,总分750 分,假设小丽在选择科目时不考虑主观性.(1)小丽选到物理的概率为;(2)请用“画树状图”或“列表”的方法分析小丽在思想政治、地理、化学、生物四门科目中任选 2门选到化学、生物的概率.23.(1)解方程:x2﹣2x﹣8=0;(2)解不等式组3(2)1112x xx--<⎧⎪⎨-<⎪⎩24.在2017年“KFC”篮球赛进校园活动中,某校甲、乙两队进行决赛,比赛规则规定:两队之间进行3局比赛,3局比赛必须全部打完,只要赢满2局的队为获胜队,假如甲、乙两队之间每局比赛输赢的机会相同,且乙队已经赢得了第1局比赛,那么甲队获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)25.鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.(1)求出y与x的函数关系式,并写出自变量x的取值范围.(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】设QP的中点为F,圆F与AB的切点为D,连接FD,连接CF,CD,则有FD⊥AB;由勾股定理的逆定理知,△ABC是直角三角形,FC+FD=PQ,由三角形的三边关系知,FC+FD>CD;只有当点F在CD上时,FC+FD=PQ有最小值,最小值为CD的长,即当点F在直角三角形ABC的斜边AB的高CD上时,PQ=CD有最小值,由直角三角形的面积公式知,此时CD=BC•AC÷AB=4.8.【详解】如图,设QP的中点为F,圆F与AB的切点为D,连接FD、CF、CD,则FD⊥AB.∵AB=10,AC=8,BC=6,∴∠ACB=90°,FC+FD=PQ,∴FC+FD>CD,∵当点F在直角三角形ABC的斜边AB的高CD上时,PQ=CD有最小值,∴CD=BC•AC÷AB=4.8.故选B.【点睛】本题利用了切线的性质,勾股定理的逆定理,三角形的三边关系,直角三角形的面积公式求解.2.B解析:B【解析】【分析】利用抛物线开口方向确定a的符号,利用对称轴方程可确定b的符号,利用抛物线与y轴的交点位置可确定c的符号.【详解】∵抛物线开口向下,∴a<0,∵抛物线的对称轴在y轴的右侧,∴x =﹣2b a>0, ∴b >0, ∵抛物线与y 轴的交点在x 轴上方,∴c >0,故选:B .【点睛】本题考查了二次函数图象与系数的关系:对于二次函数y =ax 2+bx +c (a ≠0),二次项系数a 决定抛物线的开口方向和大小:当a >0时,抛物线向上开口;当a <0时,抛物线向下开口;一次项系数b 和二次项系数a 共同决定对称轴的位置:当a 与b 同号时(即ab >0),对称轴在y 轴左; 当a 与b 异号时(即ab <0),对称轴在y 轴右;常数项c 决定抛物线与y 轴交点位置:抛物线与y 轴交于(0,c );抛物线与x 轴交点个数由△决定:△=b 2﹣4ac >0时,抛物线与x 轴有2个交点;△=b 2﹣4ac =0时,抛物线与x 轴有1个交点;△=b 2﹣4ac <0时,抛物线与x 轴没有交点. 3.B解析:B【解析】连接OC ,∵CD 是切线,∴∠OCD=90°,∵OA=OC ,∴∠ACO=∠BAC=25°,∴∠COD=∠ACO+∠BAC=50°,∴∠D=90°-∠COD=40°,故选B.4.C解析:C【解析】解:画树状图如下:一共有6种情况,“一红一黄”的情况有2种,∴P (一红一黄)=26=13.故选C . 5.D解析:D【解析】试题分析:抛物线y=x2+2x﹣3与x轴的两交点横坐标分别是﹣3、1;抛物线的顶点坐标是(﹣1,﹣4),对称轴为x=﹣1.选项A,无法确定点A、B离对称轴x=﹣1的远近,无法判断y1与y2的大小,该选项错误;选项B,无法确定点A、B离对称轴x=﹣1的远近,无法判断y1与y2的大小,该选项错误;选项C,y的最小值是﹣4,该选项错误;选项D,y 的最小值是﹣4,该选项正确.故答案选D.考点:二次函数图象上点的坐标特征;二次函数的最值.6.D解析:D【解析】【分析】六块矩形空地正好能拼成一个矩形,设道路的宽为xm,根据草坪的面积是570m2,即可列出方程.【详解】解:设道路的宽为xm,根据题意得:(32-2x)(20-x)=570,故选D.【点睛】本题考查的知识点是由实际问题抽象出一元二次方程,解题关键是利用平移把不规则的图形变为规则图形,进而即可列出方程.7.D解析:D【解析】【分析】由﹣2a2+4a﹣5=﹣2(a﹣1)2﹣3可得:x≤﹣3.【详解】∵x=﹣2a2+4a﹣5=﹣2(a﹣1)2﹣3≤﹣3,∴不论a取何值,x≤﹣3.故选D.【点睛】本题考查了配方法的应用,熟练运用配方法解答本题的关键.8.B解析:B【解析】【分析】根据:总利润=每个房间的利润×入住房间的数量-每日的运营成本,列出函数关系式,配方成顶点式后依据二次函数性质可得最值情况.【详解】设每天的利润为W元,根据题意,得:W=(x-28)(80-y)-5000()128804245000x x ⎛⎫=--- ⎪⎝⎡⎤-⎢⎥⎣⎦⎭ 2112984164x x =-+- ()2125882254x =--+, ∵当x=258时,12584222.54y =⨯-=,不是整数, ∴x=258舍去,∴当x=256或x=260时,函数取得最大值,最大值为8224元,又∵想让客人得到实惠,∴x=260(舍去)∴宾馆应将房间定价确定为256元时,才能获得最大利润,最大利润为8224元. 故选:B .【点睛】本题考查二次函数的实际应用,利用数学知识解决实际问题,解题的关键是建立函数模型,利用配方法求最值.9.D解析:D【解析】【分析】Rt △AOB 中,AB ⊥OB ,且AB=OB=3,所以很容易求得∠AOB=∠A=45°;再由平行线的性质得出∠OCD=∠A ,即∠AOD=∠OCD=45°,进而证明OD=CD=t ;最后根据三角形的面积公式,解答出S 与t 之间的函数关系式,由函数解析式来选择图象.【详解】解:∵Rt △AOB 中,AB ⊥OB ,且AB=OB=3,∴∠AOB=∠A=45°,∵CD ⊥OB ,∴CD ∥AB ,∴∠OCD=∠A ,∴∠AOD=∠OCD=45°,∴OD=CD=t ,∴S △OCD =12×OD×CD=12t 2(0≤t≤3),即S=12t 2(0≤t≤3). 故S 与t 之间的函数关系的图象应为定义域为[0,3],开口向上的二次函数图象; 故选D .【点睛】本题主要考查的是二次函数解析式的求法及二次函数的图象特征,解答本题的关键是根据三角形的面积公式,解答出S 与t 之间的函数关系式,由函数解析式来选择图象.10.A解析:A【解析】【分析】【详解】解:用1,2,3三个数字组成一个三位数的所有组合是:123,132,213,231,312,321,是偶数只有2个, 所以组成的三位数是偶数的概率是13; 故选A . 11.C解析:C【解析】【分析】【详解】试题分析:可设原正方形的边长为xm ,则剩余的空地长为(x ﹣1)m ,宽为(x ﹣2)m .根据长方形的面积公式列方程可得()()-1-2x x =18.故选C .考点:由实际问题抽象出一元二次方程.12.D解析:D【解析】【分析】分别根据判别式的意义、方程根的意义、根与系数的关系进行分析判断即可.【详解】解:A 、∵方程M 有两个不相等的实数根,∴△=b 2−4ac >0,∵方程N 的△=b 2−4ac >0,∴方程N 也有两个不相等的实数根,故不符合题意;B 、把x =4代入ax 2+bx +c =0得:16a +4b +c =0, ∴110164c b a ++=, ∴即14是方程N 的一个根,故不符合题意; C 、∵方程M 有两根符号相同, ∴两根之积c a >0,∴a c>0,即方程N 的两根之积>0, ∴方程N 的两根符号也相同,故本选项不符合题意;D 、如果方程M 和方程N 有一个相同的根,那么这个根也可以是x =-1,故本选项符合题意;故选:D .【点睛】本题考查了根的判别式、根与系数的关系以及一元二次方程的解,逐一分析四个选项的正误是解题的关键.二、填空题13.【解析】∵x2﹣3x+k=0有两个相等的实数根∴△=∴9﹣4k=0∴k=故答案为 解析:94【解析】 ∵x 2﹣3x +k=0有两个相等的实数根,∴△=2(3)410k --⨯⨯=,∴9﹣4k=0,∴k=94. 故答案为94. 14.2【解析】【分析】把x=1代入已知方程列出关于k 的新方程通过解新方程来求k 的值【详解】∵方程x2+kx−3=0的一个根为1∴把x=1代入得12+k×1−3=0解得k =2故答案是:2【点睛】本题考查了解析:2【解析】【分析】把x=1代入已知方程,列出关于k 的新方程,通过解新方程来求k 的值.【详解】∵方程x 2+kx−3=0的一个根为1,∴把x=1代入,得12+k×1−3=0,解得,k=2.故答案是:2.【点睛】本题考查了一元二次方程的知识点,解题的关键是熟练的掌握一元二次方程解的应用. 15.70°【解析】【分析】根据圆周角定理可得:∠ACB=90°∠A=∠D =20°根据三角形内角和定理可求解【详解】因为AB 为⊙O 的直径所以∠ACB=90°因为∠D =20°所以∠A=∠D =20°所以∠CB解析:70°【解析】【分析】根据圆周角定理可得:∠ACB=90°,∠A=∠D =20°,根据三角形内角和定理可求解.【详解】因为AB 为⊙O 的直径,所以∠ACB=90°因为∠D =20°所以∠A=∠D =20°所以∠CBA=90°-20°=70°故答案为:70°【点睛】考核知识点:圆周角定理.熟记圆周角定理是关键.16.【解析】【分析】根据二次函数图像和性质得a0c=3即可设出解析式【详解】解:根据题意可知a0c=3故二次函数解析式可以是【点睛】本题考查了二次函数的性质属于简单题熟悉概念是解题关键解析:223,y x =-+【解析】【分析】根据二次函数图像和性质得a <0,c=3,即可设出解析式.【详解】解:根据题意可知a <0,c=3,故二次函数解析式可以是2y 2x 3,=-+【点睛】本题考查了二次函数的性质,属于简单题,熟悉概念是解题关键. 17.【解析】【分析】底面周长即为侧面展开图扇形的弧长然后根据圆锥的侧面积列式进行计算即可得解【详解】解:圆锥的侧面积故答案为:【点睛】本题考查了圆锥的计算熟练掌握圆锥的侧面积公式是解题的关键解析:12π【解析】【分析】 底面周长即为侧面展开图扇形的弧长,然后根据圆锥的侧面积12lr =列式进行计算即可得解.【详解】解:圆锥的侧面积11641222==⨯⨯=lr ππ. 故答案为:12π.【点睛】 本题考查了圆锥的计算,熟练掌握圆锥的侧面积公式是解题的关键.18.12【解析】x2−6x+5=0x2−6x=−5x2−6x+9=−5+9(x −3)2=4所以a=3b=4ab=12故答案为:12解析:12【解析】x 2−6x+5=0,x 2−6x=−5,x 2−6x+9=−5+9,(x−3)2=4,所以a=3,b=4,ab=12,故答案为:12.19.【解析】【分析】根据扇形的弧长等于圆锥的底面周长利用扇形的弧长公式即可求得圆锥的底面周长然后根据圆的周长公式即可求解【详解】解:圆锥的底面周长是:=6π设圆锥底面圆的半径是r 则2πr=6π则r=3故解析:【解析】【分析】根据扇形的弧长等于圆锥的底面周长,利用扇形的弧长公式即可求得圆锥的底面周长,然后根据圆的周长公式即可求解.【详解】 解:圆锥的底面周长是:9012180π⨯=6π,设圆锥底面圆的半径是r ,则2πr=6π,则r=3. 故答案为:3.【点睛】本题考查圆锥的计算. 20.③④【解析】【分析】【详解】由抛物线的开口向下可得a <0;由与y 轴的交点为在y 轴的正半轴上可得c >0;因对称轴为x==1得2a=-b 可得ab 异号即b >0即可得abc <0所以①错误;观察图象根据抛物线解析:③④【解析】【分析】【详解】由抛物线的开口向下,可得a <0;由与y 轴的交点为在y 轴的正半轴上,可得c >0;因对称轴为x=2b a-=1,得2a=-b ,可得a 、b 异号,即b >0,即可得abc <0,所以①错误;观察图象,根据抛物线与x 轴的交点可得,当x=-1时,y <0,所以a-b+c <0,即b >a+c ,所以②错误;观察图象,抛物线与x 轴的一个交点的横坐标在-1和0之间,根据对称轴为x=2b a -=1可得抛物线与x 轴的一个交点的横坐标在2和3之间,由此可得当x=2时,函数值是4a+2b+c >0,所以③正确;由抛物线与x 轴有两个交点,可得b 2-4ac >0,所以④正确.综上,正确的结论有③④.【点睛】本题考查了二次函数y=ax 2+bx+c (a≠0)的图象与系数的关系:①二次项系数a 决定抛物线的开口方向和大小:当a >0时,抛物线向上开口;当a <0时,抛物线向下开口;a 还可以决定开口大小,a 越大开口就越小.②一次项系数b 和二次项系数a 共同决定对称轴的位置:当a 与b 同号时(即ab >0),对称轴在y 轴左; 当a 与b 异号时(即ab <0),对称轴在y 轴右.(简称:左同右异) ③常数项c 决定抛物线与y 轴交点, 抛物线与y 轴交于(0,c ).④抛物线与x 轴交点个数:△=b 2-4ac >0时,抛物线与x 轴有2个交点;△=b 2-4ac=0时,抛物线与x 轴有1个交点;△=b 2-4ac <0时,抛物线与x 轴没有交点.三、解答题21.()()21y 5x 800x 2750050x 100=-+-≤≤;()2当x 80=时,y 4500=最大值;()3 销售单价应该控制在82元至90元之间.【解析】【分析】(1)根据每天销售利润=每件利润×每天销售量,可得出函数关系式;(2)将(1)的关系式整理为顶点式,根据二次函数的顶点,可得到答案;(3)先求出利润为4000元时的售价,再结合二次函数的增减性可得出答案.【详解】解:由题意得:()()y x 50505100x ⎡⎤=-+-⎣⎦()()x 505x 550=--+25x 800x 27500=-+-()2y 5x 800x 2750050x 100∴=-+-≤≤;()22y 5x 800x 27500=-+-25(x 80)4500=--+a 50=-<,∴抛物线开口向下.50x 100≤≤,对称轴是直线x 80=,∴当x 80=时,y 4500=最大值;()3当y 4000=时,25(x 80)45004000--+=,解得1x 70=,2x 90=.∴当70x 90≤≤时,每天的销售利润不低于4000元.由每天的总成本不超过7000元,得()505x 5507000-+≤,解得x 82≥.82x 90∴≤≤,50x 100≤≤,∴销售单价应该控制在82元至90元之间.【点睛】本题考查二次函数的应用,熟练掌握二次函数的图像与性质是解题的关键.22.(1)12;(2)16 【解析】【分析】(1)由题意可知小丽只有两种可选择:物理或历史,即可求解; (2)从所有等可能结果中找到同时包含生物和化学的结果数,再根据概率公式计算可得. 【详解】(1)因为小丽只有两种可选择:物理或历史,所以小丽选到物理的概率为12(2)设思想政治为 A , 地理为 B , 化学为 C , 生物为 D ,画出树状图如下:共有 12 种等可能情况, 选中化学、生物的有2 种,∴P (选中化学、生物)=212=16. 【点睛】本题考查列表法与树状图法,解答本题的关键是明确题意,写出所有的可能性,求出相应的概率.23.(1)x=﹣2或x=4;(2)52<x <3 【解析】【分析】(1)用因式分解法求解;(2)分别求不等式,再确定公共解集.【详解】解:(1)∵(x+2)(x﹣4)=0,∴x+2=0或x﹣4=0,解得:x=﹣2或x=4;(2)解不等式x﹣3(x﹣2)<1,得:x>52,解不等式12x-<1,得:x<3,∴不等式组的解集为52<x<3.【点睛】考核知识点:解一元二次方程方程,解不等式组.掌握解不等式组和一元二次方程的基本方法是关键.24.1 4【解析】【分析】根据甲队第1局胜画出第2局和第3局的树状图,然后根据概率公式列式计算即可得解.【详解】根据题意画出树状图如下:一共有4种情况,确保两局胜的有1种,所以,P=14.考点:列表法与树状图法.25.(1)y=-2x+200(30≤x≤60)(2)w=-2(x-65)2 +2000);(3)当销售单价为60元时,该公司日获利最大,为1950元【解析】【分析】(1)设出一次函数解析式,把相应数值代入即可.(2)根据利润计算公式列式即可;(3)进行配方求值即可.【详解】(1)设y=kx+b,根据题意得806010050k bk b=+⎧⎨=+⎩解得:k2b200=-⎧⎨=⎩∴y=-2x+200(30≤x≤60)(2)W=(x-30)(-2x+200)-450=-2x2+260x-6450=-2(x-65)2 +2000)(3)W =-2(x-65)2 +2000∵30≤x≤60∴x=60时,w有最大值为1950元∴当销售单价为60元时,该公司日获利最大,为1950元考点:二次函数的应用.。
2019-2020学年湖南长沙明德集团初中联盟四校九年级下学期4月限时训练物理试题

2019-2020学年湖南长沙明德集团初中联盟四校九年级下学期4月限时训练物理试题1.如图是著名钢琴家郎朗音乐会演出时的情景,下列有关说法正确的是()A.演奏高音时,钢琴发出悦耳的超声波十分好听B.手指按压不同的琴键是为了改变声音的响度C.钢琴声清脆、明亮,易与其他乐器区分,因为它们的音色不同D.禁止听众喧哗是从传播过程中减弱噪声2.如图是丰子恺的一幅漫画,画中配诗“临水种桃知有意,一株当作两株看”其中包含的光学原理与下列现象光学原理相同的是()A.小孔成像B.海市蜃楼C.雨后彩虹D.猴子捞月3.如图所示,在旧社会每逢干旱人们便把希望寄托在“半仙”身上,来实现所谓的“呼风唤雨”,如今我们已经可以用“人工降雨”来把它变成现实了,在空中喷洒干冰是人工增雨的一种方法,关于人工降雨,下列说法错误的是 ( )A.干冰升华吸热,使周围空气温度骤降B.空气中的小水珠变成小冰粒是凝固过程C.空气中的水蒸气变成小冰粒是凝华过程D.“人工降雨”中降落下来的雨水是干冰熔化成的4.下列关于物理科学家们的说法中,正确的是()A.安培发现了电流的磁效应B.牛顿最早提出“物体的运动不需要力来维持”C.法拉第发现了电磁感应现象D.奥斯特记述了地理的两极和地磁场的两极并不重合5.图是有关家庭用电中的几个实例,下列对图中的实例描述正确的是()A.甲中测电笔的使用方法是错误的B.乙中用湿手接触台灯的做法是正确的C.丙中电路的接法是正确的D.丁中有关家庭用电中电路的连接是错误的6.保密室有两把不同的钥匙,分别由两个人保管.只有当两把钥匙都插入匙孔(相当于闭合开关)电动门才会打开,单独使用某一把钥匙不能使门打开.图中符合要求的电路是()A.B.C.D.7.如图,是加油站里常见的“静电释放器”司机或工人提油枪加油前,必须用手触摸金属球清除身体上的静电.下列说法中正确的是A.人体带的电荷是人体与衣服摩擦过程中创造出来的.B.“除电”时,人体、金属球、大地连通C.若人体带有负电“除电”时,电流方向是从金属球流向大地D.“静电”消除后,人体的正负荷载全部消失8.如图,全球最大的太阳能飞机“阳光动力2号”曾飞经我国,它的能源全部来自太阳能,白天它爬升到9km高空充分吸收阳光并转化为电能,部分储存在锂电池内。
2019-2020-1明德九上第三次月考-答案

当 x 0 时, y 36a 4
a 1 9
y 1 x 3 x 12 1 x2 x 4
9
9
2 存在
tan OCA OA 3 , tan OAD 3 , OD OA tan OAD 9
OC 4
4
4
点
A,
D
坐标分别为
A
3,
0
,
D
0,
9 4
直线 AD 解析式为 y 3 x 9 44
当 a 3时,原式= 4 3 3 9
21.【解析】 1 8 , 0.35 2 84.5 89.5 3 图略, 8 2
12 3
15. 4
33 2
18.
8
22.【解析】
证: 1 依题 AFE D 900
AFB EFC 1800 AFE 900 又 RtABF中,BAF AFB 900
PQ : BQ MF : BF 1: 5
BQ 5PQ 5
xB
5, yB
M 5
点
A
坐标为
A
5,
m 5
直线 AM 解析式为 y=- m x 6 m 55
点
C,
D
坐标分别为
C
6,
0
,
D
0,
6 5
m
SOCD
1 2
6
6 5
m
18 5
m
20
m 50 9
26,【解】 1 依题
设 y a x 3 x 12a 0
当 SOA1G
SOM1H
S矩形OGNH
S四边形OA1NM1
0.9 时, 1 n 1 n 1 1 5 2 5 2nn
0.9
n4 9n2 25 0
四中2020年4月月考数学试题

出这个等量关系, 并加以证明.
2 如图 2, 点 P 在? #%(外, 那么R、S之间的数量关系是否改变? 若改变, 请直接写出
它们的数量关系; 若不变, 请说明理由.
P
A D
A
P
B
图1
C
B
C
图2
第 7 页 /共 8 页
28. 对于平面直角坐标系 xOy 上的点 P 和⊙C, 定义如下: 若⊙C 上存在两个点 A, B,
(1) 对于点 M 在 BC 上的不同位置, 画图、测量, 得到了线段 BM, DF, DM 的长度的
几组值, 如下表:
位置 位置 位置 位置 位置 位置 位置 位置 位置
1
2
3
4
5
BM/cm 0.00 0.53 1.00 1.69 2.17
DF/cm 0.00 1.00 1.74 2.49 2.69
A. 70°
B. 90°
C. 110°
D. 120°
7. 定点投篮是同学们喜爱的体育项目之一, 某位同学投出篮球的飞行路线可以看作是
抛物线的一部分, 篮球飞行的竖直高度 + 单位: m 与水平距离 - 单位: m 近似满足
函数关系 + - -
. 0 . 下表记录了该同学将篮球投出后的 x 与 y 的三
ห้องสมุดไป่ตู้13. 两个小组同时从甲地出发, 匀速步行到乙地, 甲乙两地相距 7500 米. 第一组的步行
速度是第二组的1.2倍, 并且比第二组早 15 分钟到达乙地. 设第二组的步行速度为
x 千米/小时, 根据题意可列方程
.
第 2 页 /共 8 页
14. 我们知道:四边形具有不稳定性.如图,在平面直角
深圳明德外语实验学校2020-2021年上册期中初三化学试题(含答案)

深圳明德外语实验学校2020-2021年上册期中化学试题(含答案)一、选择题(培优题较难)1.根据如图所示的四种微粒结构示意图,判断下列说法中正确的是( )A.它们都带有电荷B.它们表示同一种元素C.它们核外电子排布相同D.它们都具有相对稳定结构2.下列有关燃烧和灭火说法正确的是A.油锅着火后向锅中放入菜叶目的是降低油的着火点B.家用煤加工成蜂窝煤是力了增大煤与氧气的接触面积C.高层建筑物起火立即乘电梯撤离D.不慎碰倒了酒精灯,酒精在桌面燃烧,用水来灭火3.河水净化的主要步骤如下图所示。
有关说法错误的是A.步骤Ⅰ可出去难溶性杂质B.X试剂可以是活性炭C.步骤Ⅲ可杀菌.消毒D.净化后的水是纯净物4.下列关于空气的说法中,不正确的是( )A.工业上采用分离液态空气法获得氧气B.二氧化硫是空气污染物之一C.空气中氧气质量占空气质量的21% D.空气中的氧气来源于绿色植物的光合作用5.如图,将充满CO2的试管倒扣在滴有紫色石蕊的蒸馏水中,一段时间后,下列实验现象描述正确的是①试管内液面上升②试管内溶液变红③试管内液面不上升④试管内溶液变蓝⑤试管内溶液不变色A.①②B.①④C.②③D.③⑤6.化学实验操作应严谨规范,下列操作符合要求的是A.看B.听C.闻D.吹7.正确记录实验数据是一项实验基本技能,某同学记录的实验数据错误的是A.用托盘天平称取2.9gNaCl固体B.用10mL量筒量取8.3mL蒸馏水C.在10mL试管中倒入约3mL蒸馏水进行加热D.用温度计测得水温为25.15C8.对立统一是物质运动的普遍规律,下列①一④描述的是两种物质的性质或变化,其中属于物质的物理性质或物理变化的是①氧气的氧化性和一氧化碳的还原性②水的汽化和氦气的液化③氯化钠的溶解和硝酸钾结晶④盐酸的酸性和氢氧化钠的碱性A.②③B.②④C.①④D.①③9.下列古代文明或工艺一定包含化学变化的是A.在甲骨上刻文字B.指南针指引航海C.用泥土烧制陶瓷D.用石块修筑长城10.在一密闭容器中放入X、Y、Z、Q四种物质,在一定条件下发生化学反应,一段时间后,测得有关数据如下表,则关于此反应的认识正确的是()物质X Y Z Q反应前质量/g202137反应后质量/g15321未知A.物质Y一定是单质B.反应后物质Q的质量为12gC.反应过程中X、Q的质量比为9:4D.物质Z一定的该反应的催化剂11.下列有关二氧化碳的检验、制备和用途能达到目的的是( )A.干冰用于人工降雨B.二氧化碳气体通入紫色石蕊试液中,溶液变为蓝色C.用块状石灰石和稀硫酸迅速制备大量二氧化碳D.将燃着的木条伸入集气瓶,火焰立即熄灭,证明瓶内原有气体就是二氧化碳12.如图是五种粒子的结构示意图,下列说法错误的是()A.图中粒子共能表示四种元素B.图中表示阴离子的是c、eC.图中b粒子的化学符号为Mg2+D.图中d粒子在化学反应中易失去电子13.“”和“”表示两种不同元素的原子,下列可能表示氧化物的是A.B.C.D.14.关于下列五种粒子结构示意图的说法中正确的是( )A.①④属于不同种元素B.②⑤属于金属元素C.④⑤均具有稳定结构D.①③两种粒子可以形成化合物MgCl215.根据下图的有关信息判断,下列说法正确的是()A.镁离子(Mg2+)核内有12个质子B.镁的相对原子质量为24.31gC.在化学反应中,氯原子容易失去1个电子D.镁离子(Mg2+)与氯离子(Cl-)的最外层电子数不相等16.如图是用燃磷法测定“空气中氧气含量”的实验,下列说法正确的是A.装置中的红磷可以用铁丝来代替B.待红磷熄灭并冷却后,打开弹簧夹,再观察现象C.红磷在空气中燃烧产生大量的白雾D.实验测定氧气的质量约占空气总质量的1/517.实验室用如图所示装置制取氧气,下列实验操作正确的是A.加热前,将集气瓶注满水,用玻璃片盖着倒立在盛水的水槽中B.先将导管口移入集气瓶,再开始加热C.收集O2后,将集气瓶移出水槽,然后盖上玻璃片D.停止加热时,先熄灭酒精灯,再移出导气管18.化学实验是化学学习的重要方法。
2020年上期明德初中联盟四校初三4月份限时训练 数学

2020年上期明德初中联盟四校初三4月份限时训练数学试卷时量:120分钟满分:120分一、选择题(本大题共12个小题,每小题3分,共36分)1.-3的绝对值是()A .3B .-3C .13-D .132.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列美术字是轴对称图形的是()A .诚B .信C .友D .善3.随着科技的发展,中国经济正由“中国制造”向“中国创造”转型,除华为外,中国的另一个科技巨头已经崛起,这个科技巨头是全球无人机市场唯一的“垄断者”——大疆,在无人机领域,大疆已有4600多项专利申请,是无人机领域当之无愧的“领头羊”,将4600用科学记数法表示为()A .4.6×103B .46×102C .4.6×102D .0.46×1044.下列等式成立的是()A .B .23246)a b a b =(C .(2a 2+a )÷a =2aD .5x 2y -2x 2y =35.为配合全科大阅读活动,学校团委对全校学生阅读兴趣调查的数据进行整理.欲反映学生感兴趣的各类图书所占百分比,最适合的统计图是()A .条形统计图B .频数直方图C .折线统计图D .扇形统计图6.如图,足球图片正中的黑色正五边形的内角和是()A .180°B .360°C .540°D .720°7.某班40名同学一周参加体育锻炼时间统计如下表所示:那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是()A .17,8.5B .17,9C .8,9D .8,8.58.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是()A .84B .336C .510D .1326第6题第8题9.已知m ,n 是方程x 2+2x -1=0的两个实数根,则m 2-2n +2015的值是()A .2021B .2020C .2019D .201810.如图,正比例函数y =kx 与反比例函数y =x4的图象相交于A 、C 两点,过点A 作x 轴的垂线交x 轴于点B ,连接BC ,则△ABC 的面积等于()A .8B .6C .4D .211.如图,在△ABC 中,AC =2,BC =4,D 为BC 边上的一点,且∠CAD =∠B .若△ADC 的面积为a ,则△ABD 的面积为()A .2aB .52aC .3aD .72a 12.二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的自变量x 与函数值y 的部分对应值如下表,且当12x =-时,与其对应的函数值y >0,有下列结论:(1)abc >0;(2)-2和3是关于x 的方程ax 2+bx +c =t 的两个根;(3)0<m +n <203,其中,正确结论的个数是()x…-2-1012…y =a x 2+b x +c …t m -2-2n …A .3B .2C .1D .0二、填空题(本大题共6小题,每小题3分,共18分)13.因式分解:2a 2-8=.14.若扇形的圆心角为90°,半径为6,则该扇形的弧长为.15.毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗.小红将这五位名人简介分别写在五张完全相同的知识卡片上.小哲从中随机抽取一张,卡片上介绍的人物是三国以后的人物的概率是.16.中国象棋是中华名族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点(4,﹣2),则“兵”位于点.第10题第11题17.如图,某海防哨所O 发现在它的西北方向,距离哨所400米的A 处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B 处,则此时这艘船与哨所的距离OB 为______米.18.七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为的正方形ABCD 可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH 内拼成如图2所示的“拼搏兔”造型(其中点Q 、R 分别与图2中的点E 、G 重合,点P 在边EH 上),则“拼搏兔”所在正方形EFGH 的边长是_____.三、解答题(本大题共8小题,共66分)19.(6分)计算:01202011)2sin 30()(1)3---︒++-.20.(6分)先化简,再求值:2361369x x x x -⎛⎫÷- ⎪+++⎝⎭,其中x 3-.21.(8分)随着我国经济的不断增强,人们生活水平不断提高,对健康的追求也越来越重视,但如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此长沙市某中学九年级(1)班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:(1)这个班级有多少名同学?并补全条形统计图;(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?饮品名称白开水瓶装矿泉水碳酸饮料非碳酸饮料平均价格(元/瓶)0234(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为A,B其余三位记为C,D,E)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.22.(8分)如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H 在菱形ABCD的对角线BD上.(1)求证:BG=DE;(2)若E为AD中点,FH=2,求菱形ABCD的周长.23.(9分)2020年新冠肺炎疫情影响全球,各国感染人数持续攀升,医用口罩供不应求,很多企业纷纷加入生产口罩的大军中来,长沙某企业临时增加甲、乙两个厂房生产口罩,甲厂房每天生产的数量是乙厂房每天生产数量的1.5倍,两厂房各加工6000箱口罩,甲厂房比乙厂房少用5天.(1)求甲、乙两厂房每天各生产多少箱口罩;(2)已知甲、乙两厂房生产这种口罩每天的生产费分别是1500元和1200元,现有30000箱口罩的生产任务,甲厂房单独生产一段时间后另有安排,剩余任务由乙厂房单独完成.如果总生产费不超过78000元,那么甲厂房至少生产了多少天?24.(9分)如图,在等腰三角形ABC 中,AB =AC ,以AC 为直径的⊙O 分别交AB 、BC 于点M 、N ,过点C 作⊙O 的切线交AB 的延长线于点P .(1)求证:∠CAB =2∠BCP ;(2)若⊙O 的直径为5,s i n ∠BCP =55,求△A B C 内切圆的半径;(3)在(2)的条件下,求△ACP 的周长.25.(10分)面对新冠疫情,中国举全国之力采取了很多强有力的措施,将疫情及时控制,其中对感染者和接触者进行隔离治疗和观察有效地控制住病毒的传播,数学中为对两个图形进行隔离,在平面直角坐标系中,对“隔离直线”给出如下定义:点P(x1,y1)是图形G1上的任意一点,点Q(x2,y2)是图形G2上的任意一点,若存在直线l:y=kx+b(k≠0)满足y1≤k x1+b且y2≥kx2+b,则称直线l:y=kx+b(k≠0)是图形G1与G2的“隔离直线”.例如:如图1,直线l:y=﹣x﹣4是函数6yx=(x<0)的图象与正方形OABC的一条“隔离直线”.(1)在直线y1=﹣3x,y2=4x﹣1,y3=﹣2x+3中,是图1函数6yx=(x<0)的图象与正方形OABC的“隔离直线”的为;(2)如图2,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标1),△EDF与⊙O的“隔离直线”有且只有一条,求出此“隔离直线”的表达式;(3)正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点M(1,t)是此正方形的中心.若存在直线y=2x+b是函数y=x2﹣2x﹣3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,求t的取值范围.26.(10分)已知抛物线2y ax bx c =++(a 、b 、c 为常数,且a ≠0).(1)已知抛物线的对称轴为x =3,若抛物线与x 轴的两个交点的横坐标比为1:2,求这两个交点的坐标;(2)已知抛物线的顶点为C ,抛物线与x 轴交点分别为A 、B ,若△ABC 为等边三角形,求证:2412b ac -=;(3)已知当x >﹣1时,y 随x 的增大而增大,且抛物线与直线1y ax c a =-+相切于点D ,若OD ≥c 的取值范围.。
丹徒区第四中学明德教育集团初中联盟九年级物理上学期期末考试试题

湖南省长沙市明德教育集团初中联盟2020-2021学年九年级物理上学期期末考试试题时量:60分钟满分:100分一、选择题(本大题共12个小题,每小题3分,共36分,每小题只有一个正确答案)1.关于温度、内能和热量的说法错误的是()A. 0 ℃的冰也具有内能B. 物体放出热量,温度不一定降低C. 同一物体的温度升高,内能变大D. 内能大的物体所含的热量多2.下列说法错误的是()A.热机的做功冲程是把机械能转化为内能 B.汽车发动机用循环水冷却,是因为水的比热容大C.不管热量、质量和温度如何变化,物质的比热容不变D.吸气冲程、压缩冲程、排气冲程都是依靠飞轮的惯性来完成的3.如图所示,取两个相同的不带电的验电器A和B,用丝绸摩擦过的玻璃棒与验电器A的球接触后,再用带有绝缘手柄的金属棒把A和B连接起来。
下列说法正确的是()A.用丝绸摩擦过的玻璃棒带负电B.用金属棒把A和B连接起来后,正电荷沿金属棒从A移动到BC.用金属棒把A和B连接起来后,瞬间电流方向是从金属棒的左端到右端D.验电器金属箔片张开,说明金属箔片带了异种电荷4.下列关于电阻的说法错误的是()A.导体的电阻都随温度的升高而增大B.当导体中的电流为零时,导体的电阻不为零C.架设输电线用铝线而不用铁线,是因为长度相同、横截面积相同的铝线比铁线电阻小D.一段导体无论是否有电流通过,它的电阻总是存在的5..常用智能手机是通过指纹开关S1或密码开关S2来解锁的,若其中任一方式解锁失败后,锁定开关S3均会断开而暂停手机解锁功能,S3将在一段时间后自动闭合而恢复解锁功能。
若用灯泡L发光模拟手机解锁成功,则符合要求的模拟电路是 ( )6. POS刷卡机的广泛应用给人们的生活带来了便利.POS机的刷卡位置有一个绕有线圈的小铁环制成的检测头(如图所示).在使用时,将带有磁条的信用卡在POS机指定位置刷一下,检测头的线圈中就会产生变化的电流,POS机便可读出磁条上的信息.下图中能反映POS刷卡机读出信息原理的是()A. B. C. D.7.在如图甲所示电路中,当闭合开关后,两个电压表指针偏转均如图乙所示,则电阻R1和R2两端的电压分别为()A.2.3V、9.2V B.11.5V、2.3V C.2.3V、11.5V D.9.2V、2.3V(第7题图)(第8题图)8..如图为居民家中某房间的电路,闭合开关S1、S2,电灯L与电热壶均正常工作,在三孔插座上接入电饭煲后,电热壶突然停止工作,灯L仍正常发光,拔出电饭煲的插头,用测电笔分别测试三孔插座的左右两孔,氖管均不发光,此时电路故障可能是()A.9.如下图所示,电源电压不变,闭合开关S后,当滑动变阻器的滑片P向左移动时,下列判断正确的()A.三电表的示数都变大 B.A1、A2示数变小,V的示数不变C.三电表的示数都变小 D.A1表的示数变小,A2、V表示数不变10.能源、信息和材料是现代社会发展的三大支柱,下列说法正确的是()A.太阳能、石油、风能都属于可再生能源 B.我国已建成的核电站是利用核聚变来发电的C.条形码扫描器中的光敏二极管使用的材料是超导材料D.火电厂提供的电能是二次能源11.标有“6V 3W”的小灯泡,通过它的电流与电压的关系如图所示.若把它与一只阻值为8Ω的电阻并联接在电压为4V的电路中,则整个电路消耗的功率为()A.3W B.3.3WC.3.6W D.5W(第9题图)(第11题图)(第12题图)12.在如图甲所示的电路中,电源电压不变,闭合开关S,将变阻器R的滑片P从一端滑至另一端,得到两个电压表V1及V2的示数随电流表A示数的图线如图乙所示。
最新2019-2020年度湘教版九年级数学上学期第四次月考综合测试及答案解析-精编试题

湘教版最新九年级数学上学期第四次月考数学试卷一、选择题(共12小题,每小题3分,满分36分)1.(3分)下列四个数中,是负数的是()A.|﹣1| B.(﹣2)2C.(﹣1)2015D.2.(3分)如图是一个正方体被截去一角后得到的几何体,它的俯视图是()A.B.C.D.3.(3分)已知点P(﹣a,a﹣1)在平面直角坐标系的第二象限,则a的取值范围在数轴上可表示为()A. B.C. D.4.(3分)已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是()A.20或16 B.20C.16 D.以上答案均不对5.(3分)下列计算正确的是()A.a2•a3=a6B.(a+b)(a﹣2b)=a2﹣2b2C.(ab3)2=a2b6D. 5a﹣2a=36.(3分)小朱要到距家1500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱速度是x米/分,则根据题意所列方程正确的是()A.B.C.D.7.(3分)已知关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,则m的取值范围是()A.m<﹣1 B.m>1 C.m<1且m≠0 D.m>﹣1且m≠08.(3分)如图,点A、B、O是正方形网格上的三个格点,⊙O的半径是OA,点P是优弧上的一点,则tan∠APB的值是()A . 1B .C .D .9.(3分)如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,若△ABC 的面积为,则△ADE 的面积S △ADE 为()A . 6B .9 C .12 D . 1810.(3分)如图,矩形ABCD 的两条对角线相交于点O ,∠AOB=60°,AB=2,则矩形的对角线AC 的长是()A . 2B .4 C .2D . 411.(3分)设二次函数y=x 2+bx+c ,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c 的取值范围是() A . c=3B . c≥3C . 1≤c≤3D .c ≤312.(3分)如图,正方形ABCD 中,AB=8cm ,对角线AC ,BD 相交于点O ,点E ,F 分别从B ,C 两点同时出发,以1cm/s 的速度沿BC ,CD 运动,到点C ,D 时停止运动,设运动时间为t (s ),△OEF 的面积为s (cm 2),则s (cm 2)与t (s )的函数关系可用图象表示为()A.B.C.D.二.填空题(每小题3分,共18分)13.(3分)钓鱼岛列岛是我国固有领土,共由8个岛屿组成,其中最大的岛是钓鱼岛,面积约为4.3平方公里,最小的岛是飞濑屿,面积约为0.0008平方公里.请用科学记数法表示飞濑屿的面积约为平方公里.14.(3分)将抛物线y=x2﹣2向右平移一个单位后,得到一条新抛物线,则新的抛物线的顶点坐标是.15.(3分)若圆锥的母线长为5cm,底面半径为3cm,则它的侧面展开图的面积为cm2(结果保留π)16.(3分)函数的自变量取值范围是.17.(3分)如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=2,OH=1,则∠APB的度数是.18.(3分)如图,已知动点A在函数的图象上,AB⊥x轴于点B,AC⊥y 轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于.三、解答题(共66分)19.(6分)计算:(﹣π)0﹣.20.(6分)先化简,再求值:,其中.21.(8分)2014年,长沙市被教育部列为“减负”工作改革试点地区.学生的学业负担过重会严重影响学生对待学习的态度.为此该市教育部门对部分学校的2014-2015学年八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共调查了名学生;(2)将图①补充完整;(3)求出图②中C级所占的圆心角的度数;(4)根据抽样调查结果,在我市2014-2015学年八年级学生中任意抽一名学生,该学生学习态度达标的概率为多少?(达标包括A级和B级)22.(8分)如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.(1)求证:四边形ADCE是矩形;(2)若△ABC是边长为4的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.23.(9分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元?(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.24.(9分)如图,在△AB C中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.(1)求证:OD∥AC;(2)当AB=10,cos∠ABC=时,求AF及BE的长.25.(10分)对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.(1)分别判断函数y=(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;(3)将函数y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足≤t≤1?26.(10分)如图,在平面直角坐标系中,直线y=x+1与抛物线y=ax2+bx﹣3交于A、B 两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A、B点重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.(1)求a、b及sin∠ACP的值;(2)设点P的横坐标为m;①用含有m的代数式表示线段PD的长,并求出线段PD长的最大值;②连接PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积之比为9:10?若存在,直接写出m的值;若不存在,说明理由.参考答案与试题解析一、选择题(共12小题,每小题3分,满分36分)1.(3分)下列四个数中,是负数的是()A.|﹣1| B.(﹣2)2C.(﹣1)2015D.考点:实数.专题:计算题.分析:原式各项计算得到结果,即可做出判断.解答:解:A、|﹣1|=1,不合题意;B、(﹣2)2=4,不合题意;C、(﹣1)2015=﹣1,符合题意;D、=|﹣2|=2,不合题意,故选C点评:此题考查了实数,熟练掌握运算法则是解本题的关键.2.(3分)如图是一个正方体被截去一角后得到的几何体,它的俯视图是()A.B.C.D.考点:简单组合体的三视图;截一个几何体.分析:根据俯视图是从上面看到的图形判定则可.解答:解:从上面看,是正方形右边有一条斜线,故选:A.点评:本题考查了三视图的知识,根据俯视图是从物体的上面看得到的视图得出是解题关键.3.(3分)已知点P(﹣a,a﹣1)在平面直角坐标系的第二象限,则a的取值范围在数轴上可表示为()A. B.C. D.考点:在数轴上表示不等式的解集;点的坐标.专题:计算题.分析:由P为第二象限点求出a的范围,表示在数轴上即可.解答:解:∵点P(﹣a,a﹣1)在平面直角坐标系的第二象限,∴,解得:a>1,表示在数轴上,如图所示:,故选A.点评:此题考查了在数轴上表示不等式的解集,以及点的坐标,熟练掌握运算法则是解本题的关键.4.(3分)已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是()A.20或16 B.20C.16 D.以上答案均不对考点:等腰三角形的性质;非负数的性质:绝对值;非负数的性质:算术平方根;三角形三边关系.专题:分类讨论.分析:根据非负数的意义列出关于x、y的方程并求出x、y的值,再根据x是腰长和底边长两种情况讨论求解.解答:解:根据题意得,解得,(1)若4是腰长,则三角形的三边长为:4、4、8,不能组成三角形;(2)若4是底边长,则三角形的三边长为:4、8、8,能组成三角形,周长为4+8+8=20.故选B.点评:本题考查了等腰三角形的性质、非负数的性质及三角形三边关系;解题主要利用了非负数的性质,分情况讨论求解时要注意利用三角形的三边关系对三边能否组成三角形做出判断.根据题意列出方程是正确解答本题的关键.5.(3分)下列计算正确的是()A.a2•a3=a6B.(a+b)(a﹣2b)=a2﹣2b2C.(ab3)2=a2b6D. 5a﹣2a=3考点:多项式乘多项式;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.分析:根据同底数幂的乘法法则:底数不变,指数相加;多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn;积的乘方:等于把积的每一个因式分别乘方再把所得的幂相乘;合并同类项:只把系数相加,字母部分完全不变,一个个计算筛选,即可得到答案.解答:解:A、a2•a3=a 2+3=a5,故此选项错误;B、(a+b)(a﹣2b)=a•a﹣a•2b+b•a﹣b•2b=a2﹣2ab+ab﹣2b2=a2﹣ab﹣2b2.故此选项错误;C、(ab3)2=a2•(b3)2=a2b6,故此选项正确;D、5a﹣2a=(5﹣2)a=3a,故此选项错误.故选C.点评:本题主要考查多项式乘以多项式,同底数幂的乘法,积的乘方,合并同类项的法则,注意正确把握每一种运算的法则,不要混淆.6.(3分)小朱要到距家1500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱速度是x米/分,则根据题意所列方程正确的是()A.B.C.D.考点:由实际问题抽象出分式方程.分析:首先表示出爸爸和小朱的速度,再根据题意可得等量关系:小朱走1440米的时间=爸爸走1440米的时间+10分钟,根据等量关系,表示出爸爸和小朱的时间,根据时间关系列出方程即可.解答:解:设小朱速度是x米/分,则爸爸的速度是(x+100)米/分,由题意得:=+10,即:=+10,故选:B.点评:此题主要考查了由实际问题抽象出分式方程,关键是分析题意,表示出爸爸和小朱的时间各走1440米所用时间,再由时间关系找出相等关系,列出方程.7.(3分)已知关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,则m的取值范围是()A.m<﹣1 B.m>1 C.m<1且m≠0 D.m>﹣1且m≠0考点:根的判别式;一元二次方程的定义.分析:由关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,根据一元二次方程的定义和根的判别式的意义可得m≠0且△>0,即22﹣4•m•(﹣1)>0,两个不等式的公共解即为m的取值范围.解答:解:∵关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,∴m≠0且△>0,即22﹣4•m•(﹣1)>0,解得m>﹣1,∴m的取值范围为m>﹣1且m≠0.∴当m>﹣1且m≠0时,关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根.故选D.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△<0,方程有两个相等的实数根;当△=0,方程没有实数根;也考查了一元二次方程的定义.8.(3分)如图,点A、B、O是正方形网格上的三个格点,⊙O的半径是OA,点P是优弧上的一点,则tan∠APB的值是()A. 1 B. C. D.考点:圆周角定理;锐角三角函数的定义.专题:压轴题;网格型.分析:由题意可得:∠AOB=90°,然后由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠APB的度数,又由特殊角的三角函数值,求得答案.解答:解:由题意得:∠AOB=90°,∴∠APB=∠AOB=45°,∴tan∠APB=tan45°=1.故选A.点评:此题考查了圆周角定理与特殊角的三角函数值问题.此题难度不大,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用.9.(3分)如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为,则△ADE的面积S△ADE为()A. 6 B.9 C.12 D.18考点:相似三角形的判定与性质.分析:直接利用三角形中位线定理得出DE BC,即可得出△ADE∽△ABC,再利用相似三角形的性质求出答案.解答:解:∵D、E分别是AB、AC的中点,∴DE BC,∴△ADE∽△ABC,∴==,∴=,∵△ABC的面积为,∴△ADE的面积S△ADE=9cm2.故选:B.点评:此题主要考查了相似三角形的判定与性质,得出△ADE∽△ABC是解题关键.10.(3分)如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是()A. 2 B. 4 C.2 D. 4考点:矩形的性质;等边三角形的判定与性质.专题:计算题.分析:本题的关键是利用等边三角形和矩形对角线的性质求长度.解答:解:因为在矩形ABCD中,所以AO=AC=BD=BO,又因为∠AOB=60°,所以△AOB是等边三角形,所以AO=AB=2,所以AC=2AO=4.故选B.点评:本题难度中等,考查矩形的性质.11.(3分)设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是()A.c=3 B.c≥3C.1≤c≤3 D.c≤3考点:二次函数的性质.分析:因为当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,所以函数图象过(1,0)点,即1+b+c=0①,由题意可知当x=3时,y=9+3b+c≤0②,所以①②联立即可求出c 的取值范围.解答:解:∵当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,∴函数图象过(1,0)点,即1+b+c=0①,∵当1≤x≤3时,总有y≤0,∴当x=3时,y=9+3b+c≤0②,①②联立解得:c≥3,故选B.点评:本题考查了二次函数的增减性,解题的关键是由给出的条件得到抛物线过(1,0),再代入函数的解析式得到一次项系数和常数项的关系.12.(3分)如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为()A.B.C.D.考点:动点问题的函数图象.专题:压轴题.分析:由点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,得到BE=CF=t,则CE=8﹣t,再根据正方形的性质得OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE=S△OCF,这样S四边形OECF=S△OBC=16,于是S=S四边形OECF﹣S△CEF=16﹣(8﹣t)•t,然后配方得到S=(t﹣4)2+8(0≤t≤8),最后利用解析式和二次函数的性质对各选项进行判断.解答:解:根据题意BE=CF=t,CE=8﹣t,∵四边形ABCD为正方形,∴OB=OC,∠OBC=∠OCD=45°,∵在△OBE和△OCF中,∴△OBE≌△OCF(SAS),∴S△OBE=S△OCF,∴S四边形OECF=S△OBC=×82=16,∴S=S四边形OECF﹣S△CEF=16﹣(8﹣t)•t=t2﹣4t+16=(t﹣4)2+8(0≤t≤8),∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8.故选:B.点评:本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.二.填空题(每小题3分,共18分)13.(3分)钓鱼岛列岛是我国固有领土,共由8个岛屿组成,其中最大的岛是钓鱼岛,面积约为4.3平方公里,最小的岛是飞濑屿,面积约为0.0008平方公里.请用科学记数法表示飞濑屿的面积约为8×10﹣4平方公里.考点:科学记数法—表示较小的数.分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解答:解:0.0008=8×10﹣4.故答案为:8×10﹣4.点评:本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.14.(3分)将抛物线y=x2﹣2向右平移一个单位后,得到一条新抛物线,则新的抛物线的顶点坐标是(1,﹣2).考点:二次函数图象与几何变换.专题:常规题型.分析:先得到原抛物线的顶点坐标,让横坐标加1,纵坐标不变即为新抛物线的顶点坐标.解答:解:∵抛物线y=x2﹣2的顶点坐标为(0,﹣2),向右平移1个单位得到新抛物线的解析式,∴所得抛物线的顶点坐标是(1,﹣2).故答案为:(1,﹣2).点评:本题考查二次函数图象与几何变换的知识,讨论两个二次函数的图象的平移问题,只需看顶点坐标的平移即可.15.(3分)若圆锥的母线长为5cm,底面半径为3cm,则它的侧面展开图的面积为15πcm2(结果保留π)考点:圆锥的计算.专题:计算题.分析:先计算出圆锥底面圆的周长2π×3,再根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长,然后根据扇形的面积公式计算即可.解答:解:圆锥的侧面展开图的面积=×2π×3×5=15π(cm2).故答案为15π.点评:本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.也考查了扇形的面积公式.16.(3分)函数的自变量取值范围是x>﹣1.考点:函数自变量的取值范围.专题:计算题.分析:根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.解答:解:根据题意得:x+1>0,解得:x>﹣1.故答案为:x>﹣1.点评:本题考查了函数自变量的取值范围.函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.17.(3分)如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=2,OH=1,则∠APB的度数是60°.考点:垂径定理;圆周角定理;特殊角的三角函数值.专题:探究型.分析:连接OA,OB,先根据锐角三角函数的定义求出∠AOH的度数,故可得出∠AOB 的度数,再根据圆周角定理即可得出结论.解答:解:连接OA,OB,∵OH⊥AB,AB=2,∴AH=AB=,∵OH=1,∴tan∠AOH===.∴∠AOH=60°,∴∠AOB=2∠AOH=120°,∴∠APB=∠AOB=×120°=60°.故答案为:60°.点评:本题考查的是垂径定理及圆周角定理,根据题意作出辅助线,构造出圆心角是解答此题的关键.18.(3分)如图,已知动点A在函数的图象上,AB⊥x轴于点B,AC⊥y 轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于.考点:反比例函数综合题.专题:压轴题.分析:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t,),则AD=AB=DG=,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=t2+×,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=,再由△EFQ∽△DAE,求出QE=,△ADE∽△GPD,求出DP=:,然后根据QE:DP=4:9,即可得出t2=.解答:解:解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t,),则AD=AB=DG=,AE=AC=EF=t.在直角△ADE中,由勾股定理,得DE====.∵△EFQ∽△DAE,∴QE:DE=EF:AD,∴QE=,∵△ADE∽△GPD,∴DE:PD=AE:DG,∴DP=.又∵QE:DP=4:9,∴:=4:9,解得t2=.∴图中阴影部分的面积=AC2+AB2=t2+×=+3=;解法二:∵QE:DP=4:9,∴EF:PG=4:9,设EF=4t,则PG=9t,∴A(4t,),由AC=AE AD=AB,∴AE=4t,AD=,DG=,GP=9t,∵△ADE∽△GPD,∴AE:DG=AD:GP,4t:=:9t,即t2=,图中阴影部分的面积=4t×4t+××=.故答案为:.点评:本题考查了反比例函数的性质,勾股定理,相似三角形的判定与性质,三角形的面积等知识,综合性较强,有一定难度.根据QE:DP=4:9,得出t2的值是解题的关键.三、解答题(共66分)19.(6分)计算:(﹣π)0﹣.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:本题涉及零指数幂、开方、特殊角的三角函数值、负整数指数幂四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:解:原式=1﹣×+2﹣3=1﹣3+2﹣3=﹣3.点评:本题考查实数的综合运算能力,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.20.(6分)先化简,再求值:,其中.考点:分式的化简求值.分析:先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.解答:解:原式=÷=•=,当x=﹣时,原式=﹣6.点评:本题考查的是分式的化简求值及实数的运算,熟知分式混合运算的法则是解答此题的关键.21.(8分)2014年,长沙市被教育部列为“减负”工作改革试点地区.学生的学业负担过重会严重影响学生对待学习的态度.为此该市教育部门对部分学校的2014-2015学年八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共调查了200名学生;(2)将图①补充完整;(3)求出图②中C级所占的圆心角的度数;(4)根据抽样调查结果,在我市2014-2015学年八年级学生中任意抽一名学生,该学生学习态度达标的概率为多少?(达标包括A级和B级)考点:条形统计图;扇形统计图;概率公式.分析:(1)利用A级的人数是50,所占的百分比是25%,即可求得总人数;(2)利用总数200乘以对应的百分比即可;(3)利用360°乘以对应的百分比;(4)达标的概率就是所长的比例.解答:解:(1)调查的总人数是:50÷25%=200(人);(2)C级的人数是:200×(1﹣25%﹣60%)=30(人).;(3)C级所占的圆心角的度数是:360×(1﹣25%﹣60%)=54°;(4)在我市2014-2015学年八年级学生中任意抽一名学生,该学生学习态度达标的概率是:0.85.点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.22.(8分)如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.(1)求证:四边形ADCE是矩形;(2)若△ABC是边长为4的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.考点:矩形的判定与性质;等边三角形的性质.分析:(1)根据平行四边形判定得出平行四边形,再根据矩形判定推出即可;(2)分别求出AE、OH、CE、CF的长,再求出三角形AEC和三角形COF的面积,即可求出答案.解答:(1)证明:∵CE∥AD且CE=AD,∴四边形ADCE是平行四边形,∵在△ABC中,AB=AC,AD平分∠BAC,∴AD⊥BC(等腰三角形三线合一性质),∴∠ADC=90°,∴四边形ADCE是矩形;(2)解:∵△ABC是等边三角形,边长为4,∴AC=4,∠DAC=30°,∴∠ACE=30°,AE=2,CE=2,∵四边形ADCE为矩形,∴OC=OA=2,∵CF=CO,∴CF=2,过O作OH⊥CE于H,∴OH=OC=1,∴S 四边形AOFE=S△AEC﹣S△COF=×2×2﹣×2×1=2﹣1.点评:本题考查了矩形的性质和判定,等边三角形的性质,含30度角的直角三角形性质,勾股定理等知识点的应用,题目是一道综合性比较强的题目,难度适中.23.(9分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元?(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.考点:一元一次不等式组的应用;二元一次方程组的应用.专题:方案型.分析:(1)先设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元列出方程组,求出x,y的值即可;(2)先设需购进电脑a台,则购进电子白板(30﹣a)台,根据需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元列出不等式组,求出a的取值范围,再根据a只能取整数,得出购买方案,再根据每台电脑的价格和每台电子白板的价格,算出总费用,再进行比较,即可得出最省钱的方案.解答:解:(1)设每台电脑x万元,每台电子白板y万元,根据题意得:,解得:,答:每台电脑0.5万元,每台电子白板1.5万元;(2)设需购进电脑a台,则购进电子白板(30﹣a)台,根据题意得:,解得:15≤a≤17,∵a只能取整数,∴a=15,16,17,∴有三种购买方案,方案1:需购进电脑15台,则购进电子白板15台,方案2:需购进电脑16台,则购进电子白板14台,方案3:需购进电脑17台,则购进电子白板13台,方案1:15×0.5+1.5×15=30(万元),方案2:16×0.5+1.5×14=29(万元),方案3:17×0.5+1.5×13=28(万元),∵28<29<30,∴选择方案3最省钱,即购买电脑17台,电子白板13台最省钱.点评:本题考查了二元一次方程组和一元一次不等式组的应用,解题的关键是读懂题意,找出之间的数量关系,列出二元一次方程组和一元一次不等式组,注意a只能取整数.24.(9分)如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.(1)求证:OD∥AC;(2)当AB=10,cos∠ABC=时,求AF及BE的长.考点:切线的性质;相似三角形的判定与性质.分析:(1)若要证明OD∥AC,则可转化为证明∠C=∠ODB即可;(2)连接AD,首先利用已知条件可求出BD的长,再证明△ADC∽△AFD,利用相似三角形的性质:对应边的比值相等即可求出AF及BE的长.解答:解:(1)∵AB=AC,∴∠ABC=∠C,∵OB=OD,∴∠OBD=∠ODB,∴∠C=∠ODB,∴OD∥AC,(2)连接AD,∵AB为直径,∴AD⊥BD,∴∠ADC=90°,∵AB=10,cos∠ABC=,∴BD=AB•cos∠ABC=2,∴AD=4,∵DF是圆的切线,∴OD⊥DF,∴∠ODF=90°,∵AC∥OD,∴∠AFD=90°,∵∠ADC=∠AFD,∠DAF=∠CAD,∴△ADC∽△AFD,∴,∴,∴AF=8,∵OD∥AF,∴,∴,∴BE=.点评:本题考查了圆的切线性质,及解直角三角形的知识和相似三角形的判定和性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.25.(10分)对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.(1)分别判断函数y=(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;(3)将函数y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足≤t≤1?考点:二次函数综合题.专题:代数综合题;压轴题.分析:(1)根据有界函数的定义和函数的边界值的定义进行答题;(2)根据函数的增减性、边界值确定a=﹣1;然后由“函数的最大值也是2”来求b的取值范围;(3)需要分类讨论:m<1和m≥1两种情况.由函数解析式得到该函数图象过点(﹣1,1)、(0,0),根据平移的性质得到这两点平移后的坐标分别是(﹣1,1﹣m)、(0,﹣m);最后由函数边界值的定义列出不等式≤1﹣m≤1或﹣1≤﹣m≤﹣,易求m取值范围:0≤m≤或≤m≤1.解答:解:(1)根据有界函数的定义知,函数y=(x>0)不是有界函数.y=x+1(﹣4≤x≤2)是有界函数.边界值为:2+1=3;。
湖南省长沙市2020年九年级中考数学4月份模拟考试卷(含答案)

湖南省长沙市2020年中考数学4月份模拟考试卷一.选择题(每小题3分,满分36分)1.的倒数是()A.﹣B.C.2020 D.﹣20202.科学家发现一种病毒的直径为0.0043微米,则用科学记数法表示0.0043为()A.4.3×10﹣3B.4.3×10﹣2C.0.43×10﹣2D.4.3×1033.如图图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.4.估计的值在()A.4和5之间B.5和6之间C.6和7之间D.7和8之间5.如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为()A.7 B.8 C.9 D.106.下列说法正确的是()A.“清明时节雨纷纷”是必然事件B.为了解某灯管的使用寿命,可以采用普查的方式进行C.两组身高数据的方差分别是S甲2=0.01,S乙2=0.02,那么乙组的身高比较整齐D.一组数据3,5,4,5,6,7的众数、中位数和平均数都是57.如图,一个公共房门前的台阶高BC=1.3米,台阶拆除后,换成供轮椅行走的斜坡∠BAC =10°,则下列关系式或说法正确的是()A.斜坡AB的坡度是10°B.斜坡AB的坡度是tan10°C.AC=1.3tan10°D.AB=1.3sin10°8.如图,是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断()A.甲正确,乙错误B.甲错误,乙正确C.甲、乙均正确D.甲、乙均错误9.如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为()A.B.12πC.2πD.24π10.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺.设木长为x尺,绳子长为y 尺,则下列符合题意的方程组是()A.B.C.D.11.关于x的不等式组恰好只有4个整数解,则a的取值范围为()A.﹣2≤a<﹣1 B.﹣2<a≤﹣1 C.﹣3≤a<﹣2 D.﹣3<a≤﹣2 12.如图,以▱ABCD的四条边为边,分别向外作正方形,连结EF,GH,IJ,KL.如果▱ABCD 的面积为8,则图中阴影部分四个三角形的面积和为()A.8 B.12 C.16 D.20二.填空题(满分18分,每小题3分)13.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣2,4),B(1,1),则关于x的方程ax2﹣bx﹣c=0的解为.14.函数中自变量x的取值范围是.15.方程的解是.16.如图,在4×3的矩形方框内有一个不规则的区域A(图中阴影部分所示),小明同学用随机的办法求区域A的面积.若每次在矩形内随机产生10000个点,并记录落在区域A 内的点的个数,经过多次试验,计算出落在区域A内点的个数的平均值为6700个,则区域A的面积约为.17.如图,在矩形ABCD中,AB:BC=3:4,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为.18.如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴与点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.三.解答题19.(6分)计算:|﹣3|﹣(﹣π)0+()﹣1+(﹣1)2019﹣.20.(6分)化简求值:,其中x=.21.(8分)今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:(1)本次抽样调查的养殖户的总户数是;把图2条形统计图补充完整.(2)若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?(3)某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.22.(8分)如图,在▱ABCD中,点E是BC上的一点,连接DE,在DE上取一点F使得∠AFE =∠ADC.若DE=AD,求证:DF=CE.23.(9分)人们常常在室内摆放一些绿色植物,这样做不仅增加了温馨舒适度,还有助于提高室内空气的质量.前年某小区为更好地提高住户的居住感受,为已入住的住户购置A、B两个品种的绿色植物共900盆.其中,A品种每盆20元,B品种每盆30元(1)已知该小区前年购置这900盆绿色植物共花费23000元,请分别求出已购置的A、B 品种的数量;(2)今年该小区决定再次为已入住的住户购置绿色植物C、D两个新品种.已知C品种今年每盆的价格比A品种前年的价格优惠a%,D品种今年每盆的价格比B品种前年的价格优惠a%.由于小区入住率的提高,今年需要购置C品种的数量比A品种前年购置的数量增加了a%,购置D品种的数量比B品种前年购置的数量增加了a%,于是今年的总花费比前年增加了a%.求a的值.24.(9分)如图,AB是⊙O的直径,AC⊥AB,BC交⊙O于点D,点E在劣弧BD上,DE的延长线交AB的延长线于点F,连接AE交BD于点G.(1)求证:∠AED=∠CAD;(2)若点E是劣弧BD的中点,求证:ED2=EG•EA;(3)在(2)的条件下,若BO=BF,DE=2,求EF的长.25.(10分)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=(n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=.(1)求该反比例函数和一次函数的解析式.(2)点E是x轴上一点,且△AOE是等腰三角形,求E点的坐标.26.(10分)已知:抛物线y=x2+x+m交x轴于A,B两点,交y轴于点C,其中点B在点A的右侧,且AB=7.(1)如图1,求抛物线的解析式;(2)如图2,点D在第一象限内抛物线上,连接CD,AD,AD交y轴于点E.设点D的横坐标为d,△CDE的面积为S,求S与d之间的函数关系式(不要求写出自变量d的取值范围);(3)如图3,在(2)的条件下,过点D作DH⊥CE于点H,点P在DH上,连接CP,若∠OCP=2∠DAB,且HE:CP=3:5,求点D的坐标及相应S的值.参考答案一.选择1.解:的倒数是2020,故选:C.2.解:用科学记数法表示0.0043为4.3×10﹣3.故选:A.3.解:A、不是轴对称图形,是中心对称图形,不合题意;B、不是轴对称图形,是中心对称图形,不合题意;C、是轴对称图形,也是中心对称图形,符合题意;D、不是轴对称图形,也不是中心对称图形,不合题意.故选:C.4.解:∵49<51<64,∴7<<8,∴在7到8之间,故选:D.5.解:连结AD,如图,∵AB为直径,∴∠ADB=90°,∴∠1+∠ADE=90°,∠2+∠C=90°,∵DE为切线,∴ED=EA,∴∠ADE=∠2,∴∠1=∠C,∴ED=EC,∴CE=AE,∵EF∥AB,∴EF为△ABC的中位线,∴BF=CF,而BO=AO,∴OF为△ABC的中位线,∴OF∥AE,∴AE=OF=7.5,∴AC=2AE=15,在Rt△ACD中,BC===25,∵∠DCA=∠ACB,∴△CDA∽△CAB,∴=,即=,∴CD=9.故选:C.6.解:A,B,C选项中,可能发生也可能不发生,是随机事件,不符合题意,是必然事件的是:一组数据3,5,4,5,6,7的众数、中位数和平均数都是5,符合题意,故选:D.7.解:斜坡AB的坡度i=,不是坡角,因此A选项不符合题意;斜坡AB的坡度i==tan10°,因此选项B符合题意;∵tan10°=,∴AC==,因此选项C不符合题意;∵sin10°=,∴AB==,因此选项D不符合题意,故选:B.8.解:甲的作法正确;∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠ACB,∵EF是AC的垂直平分线,∴AO=CO,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴AE=CF,又∵AE∥CF,∴四边形AECF是平行四边形,∵EF⊥AC,∴四边形AECF是菱形;乙的作法正确;∵AD∥BC,∴∠1=∠2,∠6=∠7,∵BF平分∠ABC,AE平分∠BAD,∴∠2=∠3,∠5=∠6,∴∠1=∠3,∠5=∠7,∴AB=AF,AB=BE,∴AF=BE∵AF∥BE,且AF=BE,∴四边形ABEF是平行四边形,∵AB=AF,∴平行四边形ABEF是菱形;故选:C.9.解:由三视图可判断该几何体是圆锥,底面直径为4,母线长为6,故这个几何体的侧面积为:×4π×6=12π.故选:B.10.解:由题意可得,,故选:B.11.解:不等式组整理得:,解得:a+1<x<,由解集中恰好只有4个整数解,得到整数解为0,1,2,3,∴﹣1≤a+1<0,解得:﹣2≤a<﹣1,故选:A.12.解:过D作DN⊥AB于N,过E作EM⊥FA交FA延长线于M,连接AC,BD,∵四边形ABGF和四边形ADLE是正方形,∴AE=AD,AF=AB,∠FAB=∠EAD=90°,∴∠EAF+∠BAD=360°﹣90°﹣90°=180°,∵∠EAF+∠EAM=180°,∴∠EAM=∠DAN,∴sin∠EAM=,sin∠DAN=,∵AE=AD,∴EM =DN ,∵S △AEF =AF ×EM ,S △ADB =AB ×DN ,∴S △AEF =S △ABD ,同理S △BHG =S △ABC ,S △CIJ =S △CBD ,S △DLK =S △DAC ,∴阴影部分的面积S =S △AEF +S △BGH +S △CIJ +S △DLK =2S 平行四边形ABCD =2×8=16.故选:C .二.填空13.解:∵抛物线y =ax 2与直线y =bx +c 的两个交点坐标分别为A (﹣2,4),B (1,1), ∴方程组的解为,,即关于x 的方程ax 2﹣bx ﹣c =0的解为x 1=﹣2,x 2=1.故答案为x 1=﹣2,x 2=1.14.解:由题意得:x ﹣1≠0且1+2x ≥0,∴x ≥﹣且x ≠1,故答案为:x ≥﹣且x ≠1.15.解:方程的两边同乘(x ﹣4),得2﹣(x ﹣1)=0,解得x =3.检验:把x =3代入(x ﹣4)=﹣1≠0.∴原方程的解为:x =3.16.解:由题意,∵在矩形内随机产生10000个点,落在区域A 内点的个数平均值为6700个,∴概率P ==0.67,∵4×3的矩形面积为12,∴区域A的面积的估计值为0.67×12=8.04故答案为:8.04;17.解:∵AB:BC=3:4,设AB=3x,BC=4x,∵四边形ABCD是矩形,∴CD=AB=3x,AD=BC=4x,分两种情况:①如图所示,当∠DFE=90°时,△DEF为直角三角形,∵∠CDF+∠CFD=∠EFN+∠CFD=90°,∴∠CDF=∠EFN,由折叠可得,EF=EB,BN=FN,∴∠EFN=∠EBN,∴∠CDF=∠CBD,又∵∠DCF=∠BCD=90°,∴△DCF∽△BCD,∴=,即=,∴CF=x,∴FN=NB==,∴CN=CF+NF=x+x=x,∴BN=∴CN:BN=x:x=25:7.②如图所示,当∠EDF=90°时,△DEF为直角三角形,∵∠CDF +∠CDB =∠CDF +∠CBD =90°, ∴∠CDF =∠CBD ,又∵∠DCF =∠BCD =90°,∴△DCF ∽△BCD ,∴=,即=, ∴CF =x ,∴NF =BN ==x ,∴CN =NF ﹣CF =x ﹣x =x ,∴CN :BN =7:25,综上所述,CN :BN 的值为或,故答案为:或. 18.解:连DC ,如图,∵AE =3EC ,△ADE 的面积为3,∴△CDE 的面积为1,∴△ADC 的面积为4,设A 点坐标为(a ,b ),则AB =a ,OC =2AB =2a ,而点D 为OB 的中点,∴BD =OD =b ,∵S 梯形OBAC =S △ABD +S △ADC +S △ODC ,∴(a +2a )×b =a ×b +4+×2a ×b ,∴ab =,把A(a,b)代入双曲线y=,∴k=ab=.故答案为:.三.解答19.解:原式=3﹣1+4﹣1﹣3=2.20.解:原式=•==﹣x(x+1)=﹣x2﹣x当x=时,原式=﹣2﹣.21.解:(1)21÷35%=60户,60﹣9﹣21﹣9=21户,故答案为:60,补全条形统计图如图所示:(2)1500×=750户,答:若该地区建档的养殖户有1500户中非常严重与严重的养殖户一共有750户;(3)用表格表示所有可能出现的情况如下:共有20种不同的情况,其中选中e的有8种,∴P(选中e)==,22.证明:∵四边形ABCD是平行四边形,∴∠B=∠ADC,AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC,∵∠AFD+∠AFE=180°,∠AFE=∠ADC,∴∠AFD=∠C,在△AFD和△DEC中,,∴△AFD≌△DCE(AAS),∴DF=CE.23.解:(1)设前年已购置的A、B品种的数量分别为x盆和y盆,由题意得:解得:答:前年已购置的A品种400盆,B品种500盆.(2)由题意得:20(1﹣a%)×400(1+a%)+30(1﹣a%)×500(1+a%)=23000(1+a%)设a%=t则20(1﹣t)×400(1+)+30(1﹣t)×500(1+t)=23000(1+t)化简得:﹣10t2+3t=0∴t(﹣10t+3)=0∴t1=0(舍),t2=∴a%=∴a=30答:a的值为30.24.(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∵AC⊥AB,∴∠CAB=90°,∴∠ABD=∠CAD,∵=,∴∠AED=∠ABD,∴∠AED=∠CAD;(2)证明:∵点E是劣弧BD的中点,∴=,∴∠EDB=∠DAE,∵∠DEG=∠AED,∴△EDG∽△EAD,∴,∴ED2=EG•EA;(3)解:连接OE,∵点E是劣弧BD的中点,∴∠DAE=∠EAB,∵OA=OE,∴∠OAE=∠AEO,∴∠AEO=∠DAE,∴OE∥AD,∴,∵BO=BF=OA,DE=2,∴,∴EF=4.25.解:(1)∵AD⊥x轴,∴∠ADO=90°,在Rt△ADO中,AD=3,tan∠AOD=,∴OD=2,∴A(﹣2,3),∵点A在反比例函数y=的图象上,∴n=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣,∵点B(m,﹣1)在反比例函数y=﹣的图象上,∴﹣m=﹣6,∴m=6,∴B(6,﹣1),将点A(﹣2,3),B(6,﹣1)代入直线y=kx+b中,得,∴,∴一次函数的解析式为y=﹣x+2;(2)设E(m,0),由(1)知,A(﹣2,3),∴OA2=13,OE2=m2,AE2=(m+2)2+9,∵△AOE是等腰三角形,∴①当OA=OE时,∴13=m2,∴m=±,∴E(﹣,0)或(,0),②当OA=AE时,13=(m+2)2+9,∴m=0(舍)或m=﹣4,∴E(﹣4,0),③当OE=AE时,m2=(m+2)2+9,∴m=﹣,∴E(﹣,0),∴满足条件的点E的坐标为(,0)或(﹣,0)或(﹣4,0)或(﹣,0).26.(1)由y=x2+x+m,令y=0,则(x+2)(x﹣m)=0,∴AO=2,BO=m,∴A(﹣2,0),B(m,0),∵AB=7,∴m﹣(﹣2)=7,m=5,∴y=;(2)过点D作DK⊥x轴于点K,设∠DAB=α,则D(d,﹣),∴=.∴EO=AO•tanα=5﹣d,CE=5﹣(5﹣d)=d,∴;(3)过点E作CE的垂线,过C作∠OCP的平分线交DE于点J,交CE的垂线于点F,过点F作ED的平行线交HD于点N.∴∠ECF=∠HDE=α,HE=3k,CP=5k,CE=HD=d,∵CE=HD,∠CEF=∠CHD=90°,∴△CEF≌△DHE(ASA),∵EF∥DN,NF∥DE,∴四边形EDNF为平行四边形,∴EF=HE=DN=3k,CF=DE=FN,∴△CFN为等腰直角三角形,∴∠PCN=∠FNC=45°,∴∠PCN=∠PNC=45°﹣α,∴PC=PN=5k,∴PD=2k,∴CH=d﹣3k,PH=d﹣2k,∴(d﹣3k)2+(d﹣2k)2=(5k)2,∴(d﹣6k)(d+k)=0,∴d=6k,∴在Rt△DHE中,tan,由(2)知,∴.∴d=4,知识像烛光,能照亮一个人,也能照亮无数的人。
2019-2020-2明德集团初三下4月份限时训练

2019-2020-2明德集团初三下4月份限时训练英语试卷分四个部分,共8页,75小题,时量120分钟,满分120分。
I.听力技能(两部分,共20小题,计20分)第一节对话理解根据所听到的对话,从题中所给的A、B、C三个选项中选出最佳答案回答问题。
听每段对话前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
(共15小题,计15分)听下面五段对话,每听完一段对话后,回答1个小题。
1. What was the coat made of?A. Silk.B. Cotton.C. Wood.2. How often does Jane dance?A. Once a week.B. Twice a week.C. Three times a week.3. What are the two speakers talking about?A. School rules.B. School uniforms.C. Their favorite clothes.4. How may the woman go to the restaurant?A. On foot.B. By bus.C. By subway.5. What can the man do first if he wants to be a doctor?A. Learn medicine.B. Go to college.C. Study hard.第二节听下面6段对话或独白。
每段对话或独白后有2-3个小题,从题中所给的A、B、C三个选项中选出最佳选项回答问题。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
(共15小题,计15分)听第六段对话,回答第6、7小题。
6. Who is afraid of the dark?A. Mary.B. Cathy.C. Linda.7. Why is Cathy afraid of high places?A. Because she is afraid to close her eyes.B. Because she thinks she may fall down.C. Because she hates to climb mountains.听第七段对话,回答第8、9小题。
明德中学初中英语九年级全册Unit 4阶段测试(培优提高)

一、选择题1.-My father __________ to his workplace by bus, but now he __________there by bike.-Really? You have an environmentally-friendly father.A.used to go, is used to go B.used to going, is used to goC.is used to go, is used to going D.used to go, is used to going D解析:D【详解】句意:-----我父亲以前乘公共汽车去他的工作场所,但现在他习惯了骑自行车去那里。
------真的吗?你有一个爱环保的父亲。
考查固定短语。
1. used to do sth.:过去常常做某事,曾经做某事;2. be used to doing sth.:习惯于做某事;3. be used to do sth.:被用来做某事;结合句意可知填used to go, is used to going;选D。
2.- Could I borrow two books ______?- Sorry. You can borrow only one.A.at a time B.at the time C.for a time D.from time to time A 解析:A【详解】句意:——我可以一次借两本书吗?——对不起。
你只能借一本。
本题考查介词短语。
at a time一次,at the time在那时,for a time暂时,一段时间;from time to time不时,有时。
结合句意,此处表示一次借两本书,故选A。
3.There are a number of reporters________ the famous singer, and the ________ with him are covered live on TV.A.interviewing, interviewing B.interviews , interviews C.interviewing, interviews D.interviews, interviewing C解析:C【解析】句意:有很多记者在采访那个著名的歌手,对他的采访在电视现场报道。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即c 2
当t
1 2
时, OD2min
(c
3)2 2
1 4
8
解得: c 3 31 或c 3 31
2
2
∴ c 3 31 2
综上所述: c 5 或 c 3 31 2
第一次
第二次 A
B
C
D
E
A
(A,B) (A,C) (A,D) (A,E)
B (B,A)
(B,C) (B,D) (B,E)
C (C,A) (C,B)
(C,D) (C,E)
D (D,A) (D,B) (D,C)
(D,E)
E (E,A) (E,B) (E,C) (E,D)
共有
20
种等可能的结果,其中,抽到两位班长的结果有
∵⊙O 的半径为 2,∴点 D 在⊙O 上. 过点 D 作 DH⊥OD 交 y 轴于点 H,
∴直线 DH 是⊙O 的切线,也是△EDF 与⊙O 的“隔离直线”.
在 Rt△ODH 中,OH=
=4,
∴点 H 的坐标是(0,4),∴直线 DH 的表达式为 y=﹣ x+4, 即所求“隔离直线”的表达式为 y=﹣ x+4. (3)如图, 由题意 F(4,5),当直线 y=2x+b 经过点 F 时,5=8+b, ∴b=﹣3, ∴直线 y=2x﹣3,即图中直线 EF, ∵正方形 A1B1C1D1 的中心 M(1,t), 易知正方形 A1B1C1D1 的边长为 2, 当 x=2 时,y=1, ∴C1(2,1),直线 EF 是函数 y=x2﹣2x﹣3(0≤x≤4)的图象与正方形 A1B1C1D1 的“隔离 直线”,此时 t=2, 当直线 y=2x+b 与 y=x2﹣2x﹣3 只有一个交点时,
23.解:(1)设乙厂房每天生产 x 箱口罩,则甲厂房每天生产 1.5x 箱口罩,由题意得: 6000 6000 5
x 1.5x 解得 x 400 1.5x 600 经检验, x 400 是分式方程的解且符合实际意义. 答:甲每天生产 600 箱口罩,乙每天生产 400 箱口罩. (2)设甲生产了 x 天,乙生产了 y 天,则由题意得
(2)△A B C 内切圆的半径为: 5 5 2
(3)△APC 的周长是 AC+PC+AP=20; 25.解:(1)根据的“隔离直线”的定义可知:y1=﹣3x.
(2)连接 OD,过点 D 作 DG⊥x 轴于点 G,如图.
在 Rt△DGO 中,OD=
=2,
sin∠1= = ,∴∠1=30°,∠2=60°,
2
种,∴P(抽到两位班长)=
2 20
=
1 10
.答:
恰好抽到 2 名班长的概率为 1 . 10
22.解:(1)在矩形 EFGH 中,EH=FG,EH∥FG, ∴∠GFH=∠EHF 又∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,∴∠BFG=∠DHE, 在菱形 ABCD 中,AD∥BC,∠GBF=∠EDH, ∴△BGF≌△DEH(AAS),BG=DE; (2) 连接 EG, 在菱形 ABCD 中,AD∥BC,AD=BC, ∵E 为 AD 中点,AE=ED,BG=DE,∴AE=BG, ∴四边形 ABGE 是平行四边形, ∴AB=EG,在矩形 EFGH 中,EG=FH=2,AB=2, ∴菱形周长为 8.
x1 x1
: x2 1: x2 6
2
解得:
x1 x2
2 4
∴这两个交点坐标为(2,0),(4,0)
(2)由题意得: C( b , 4ac b2 ) , AB b2 4ac
2a 4a
a
∵△ABC 为等边三角形
∴ 4ac b2 3 b2 4ac
4a
2a
∴ b2 4ac 12 或 b2 4ac 0 (舍)
3
2
20.解:原式=
x3
x 32
x3= x3
x3
x 32
x x
3 3
=
1 x3
,
当 x= 2 3 时,原式= 1 1 2 . 2 33 2 2
21.解:(1)15÷30%=50(人),50-10-15-5=20(人)
(2)(0×10+2×15+3×20+4×5)÷50=2.2(元).答:该班同学每天用于饮品的人均花费是 2.2 元; (3)从 5 名班委干部中随机抽取 2 名班委干部的所有结果如下表:
∴ b2 4ac 12
a 0
(3)由题意得:
b 2a
1
∴ b 2a 0
y
ax 2
bx
c
联立
y
ax
1 a
c
得: ax2 (b a)x 1 0 a
(b a)2 4 0
∴b-a=2 或 b-a=-2(舍) ∴ a 2 2a 0 ∴ 0 a 2
∴
x1
x2
1 a
∴ D( 1 , 1 1 c) aa
消去 y 得到 x2﹣4x﹣3﹣b=0,
由△=0,可得 16﹣4(﹣3﹣b)=0,解得 b=﹣7,此时易知 M(1,﹣8),t=﹣8, 根据图象可知,当 t≥2 或 t≤﹣8 时,直线 y=2x+b 是函数 y=x2﹣2x﹣3(0≤x≤4)的图象 与正方形 A1B1C1D1 的“隔离直线”.
26.解:(1)设这两个交点的横坐标为 x1,x2
600x 400 y 30000 ① 1500x 1200 y78000 ②
解得 x 40 , 答:甲至少生产了 40 天.
24.解:(1)连接 AN, ∵AC 是⊙O 的直径,∴AN⊥BC,∴∠CAN+∠ACN=90° 又∵AB=AC ∴∠CAN=∠BAN,即∠CAB=2∠CAN ∵CP 与⊙O 相切 ∴∠BCP +∠ACN=90° ∴∠CAN=∠BCP, ∴∠CAB=2∠BCP,
∴ OD2
1 a2
(1
1 a
c)2
2 a2
(1 c)
2 a
(c
1)2
令 t 1 则 t 1 OD2 2t 2 2(1 c)t (c 1)2
a
2
1 若 c 1 1 即c 2 22
当t
ห้องสมุดไป่ตู้
c
2
1
时,
OD
2 min
(c 1)2 2
8
解得: c 5或c 3
∴c 5 2 若 c 1 1
2020 年上期明德初中联盟四校初三 4 月份限时训练
数学参考答案
一、选择题(本题共 12 个小题,每小题 3 分,共 36 分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D A B D C D C B C C B
二、填空题(本题共 6 个小题,每小题 3 分,共 18 分)
13.2(a+2)(a-2)
14. 3
3
15.
5
16. (-1,1)
17、 400 2
18. 4 5
三、解答题(本题共 8 个小题,第 19、20 小题每小题 6 分,第 21、22 小题每小题 8 分,
第 23、24 小题每小题 9 分,第 25、26 小题每小题 10 分,共 66 分.)
19.解: ( 2 1)0 2sin 30 (1)1 (1)2020 1 2 1 3 1 4 .
