二重循环解题思路
双循环知识点总结

双循环知识点总结一、for循环1. for循环的语法结构for循环的基本语法结构如下:for (初始化表达式; 循环条件; 循环迭代) {// 循环体}其中,初始化表达式用于初始化循环变量;循环条件用于判断是否继续执行循环;循环迭代用于更新循环变量的值;循环体是需要重复执行的代码段。
2. for循环的使用方法for循环通常用于已知循环次数的情况,例如遍历数组、列表或执行固定次数的操作。
在循环体内,可以使用循环变量来控制循环的执行流程。
3. for循环的注意事项在使用for循环时,需要注意循环变量的初始值和条件表达式的判断条件,避免出现死循环或循环次数不符合预期的情况。
此外,循环体内的代码也需要谨慎编写,避免因为逻辑错误导致程序出现异常。
4. for循环的实例应用for循环在实际编程中应用广泛,例如遍历数组进行元素访问、执行固定次数的循环操作等。
下面是一个使用for循环求1-100的和的示例代码:int sum = 0;for (int i = 1; i <= 100; i++) {sum += i;}System.out.println("1-100的和为:" + sum);二、while循环1. while循环的语法结构while循环的基本语法结构如下:while (循环条件) {// 循环体}其中,循环条件用于判断是否继续执行循环;循环体是需要重复执行的代码段。
2. while循环的使用方法while循环通常用于循环次数不明确的情况,例如根据条件判断是否继续执行循环。
在循环体内,通常需要更新循环条件的值,以避免出现死循环。
3. while循环的注意事项在使用while循环时,需要注意循环条件的初始值和更新方式,避免出现循环次数不可知的情况。
此外,循环体内的代码也需要谨慎编写,避免因为逻辑错误导致程序出现异常。
4. while循环的实例应用while循环同样在实际编程中得到广泛应用,例如根据条件判断是否继续执行循环、读取文件中的内容等。
百钱买百鸡实验报告

一、题目描述我国古代数学家张丘建在《算经》一书中曾提出过著名的“百钱买百鸡”问题,该问题叙述如下:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?翻译过来,意思是公鸡一个五块钱,母鸡一个三块钱,小鸡三个一块钱,现在要用一百块钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?二、解题思路对n=100的情况,因为有三个变量,则有三重循环和二重循环两种算法1、算法一:三重循环(1)变量变化范围的确定:由于公鸡5钱一只,则100钱最多可购买100/5=20只公鸡,此即为第一个变量的变化上限;由于母鸡3钱一只,则100钱最多可购买100/3≈33只母鸡,此即为第二个变量的变化上限;由于小鸡三只一钱,而所有鸡的总数不得超过100只,则100即为第三个变量的变化上限;(2)条件的控制:由百钱买百鸡可知,鸡的数量为100只,买鸡所用的钱数为100钱,即控制条件为a+b+c=100且a*5+b*3+c/3=100;2、二重循环:(1)变量变化范围的确定:由于整题共有3个变量,所以当前两个变量确定后,第三个变量自然被确定下来,故可采用二重循环解题。
前两个变量的确定同三重循环,第三个变量则用c=n-a-b来确定;(2)条件的控制:由百钱买百鸡可知,鸡的数量为100只,买鸡所用的钱数为100钱,即控制条件为a+b+c=100且a*5+b*3+c/3=100;由于需要讨论算法的时间性能,在程序中加入时间函数计算程序运行所需的时间进行比较。
用控制变量的方法,对两种算法中的n进行同样的变化处理,来讨论两种算法的时间性能,e.g.分别令n=100,n=200,n=500,n=1000,n=2000,n=5000三、自我评估、反思由于较长时间未使用C语言编程,所以在使用语法上略显生疏了些,通过这次作业的实践过程,对C语言的编程语法规则熟悉了许多,虽然在运行过程中出现了一些错误,但也都能够较快地解决,第一次的数据结构实验作业总体完成的还算比较顺利。
Python基础—05-总结:双重循环,数据类型

Python基础—05-总结:双重循环,数据类型总结双重循环冒泡排序lt = [1, 5, 7, 3, 2, 4]# 计算元素的个数n = len(lt)# 外层循环控制圈数for i in range(n-1):for j in range(n-1-i):# 不合适,交换数据# 此处是升序排序,若想降序需要将 > 改为 <if lt[j] > lt[j+1]:# 其他语⾔# temp = lt[j]# lt[j] = lt[j+1]# lt[j+1] = temp# python特有lt[j], lt[j+1] = lt[j+1], lt[j]print(lt)选择排序(练习)思想:取出第⼀个元素,依次与后⾯的元素进⾏⽐较,不合适交换位置,直⾄⽐较结束,⼀轮可以确定开头⼀个每轮确定⼀个元素,依次向后,n个元素需要n-1轮⽐较⽰例:lt = [3, 5, 2, 1, 8, 4]第⼀轮:1 5 3 2 8 4第⼆轮:1 2 5 3 8 4第三轮:1 2 3 5 8 4提⽰:仍然使⽤双重循环进⾏解决,外层循环控制循环多少轮,内⼼循环控制元素⽐较数据类型集合添加:add删除:remove,元素存在就删除,不存在就爆粗discard,元素存在就删除,不存在也不保存pop,随机弹出⼀个元素,返回后删除元素清空:clear并集:union交集:intersection:不改变原集合intersection_update:使⽤交集更新原集合差集:difference:不会改变原集合difference_update:使⽤差集更新原集合判断:isdisjoint:是否没有交集issubset:是否是另⼀集合的⼦集issuperset:是否是另⼀集合的超集(⽗集)字典获取:d[key]:根据键获取值,不存在时或报错d.get(key, '默认值'):不存在时默认返回None,也可以指定默认值更新:d[key] = value 键存在就更新,不存在就添加d.update(d2) 将字典d2中的键值对依次添加到d中,已经存在的键会覆盖删除:del d[key]d.pop(key) 返回删除的值清空:clear所有键:keys 返回可迭代对象所有值:values 返回可迭代对象字符串join:拼接split:切割,从左边rsplit:从右边切割splitlines:按照换⾏符切割⾃⾏测试:find:查找第⼀次出现指定字符串的位置,没有时返回-1 rfind:从右边开始查,返回第⼀次出现的位置upper:全⼤写lower:全⼩写swapcase:⼤⼩写转换capitalize:⾸字符⼤写title:每个单词⾸字母⼤写count:统计某个字符串出现的次数startswith:是否以指定字符串开头endswith:是否以指定字符串结尾istitle:是否每个单词⾸字母⼤写islower:是否是全⼩写isupper:是否是全⼤写isdecimal:是否是数字isalpha:是否是字母isalnum:是否是数字或字母。
repeat双循环算法伪代码写法

repeat双循环算法伪代码写法
双循环算法,也称嵌套循环算法,通常用于处理需要对数据集
合进行多次迭代和比较的情况。
以下是一个常见的双循环算法的伪
代码示例:
for i from 0 to n-1 do.
for j from 0 to n-1 do.
// 在这里执行循环体内的操作。
end for.
end for.
在这段伪代码中,我们使用两个嵌套的循环结构。
外部的循环
从0到n-1进行迭代,而内部的循环也从0到n-1进行迭代。
这样
就实现了对数据集合的双重遍历,可以在循环体内执行所需的操作。
这种双循环算法常用于对数组、矩阵或者其他多维数据结构进
行处理,比如查找最大最小值、排序、矩阵运算等。
在实际编程中,可以根据具体的需求对双循环算法进行修改和优化,以提高效率和
减少资源消耗。
需要注意的是,双循环算法可能会导致较高的时间复杂度,特
别是当数据集合较大时。
因此,在实际应用中,需要仔细评估算法
的性能,并考虑是否有更优的算法可以替代双循环算法。
c语言中的二重循环
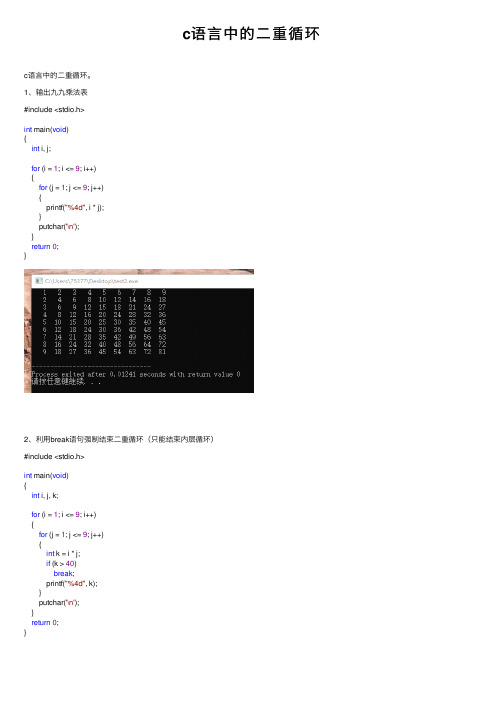
c语⾔中的⼆重循环c语⾔中的⼆重循环。
1、输出九九乘法表#include <stdio.h>int main(void){int i, j;for (i = 1; i <= 9; i++){for (j = 1; j <= 9; j++){printf("%4d", i * j);}putchar('\n');}return0;}2、利⽤break语句强制结束⼆重循环(只能结束内层循环)#include <stdio.h>int main(void){int i, j, k;for (i = 1; i <= 9; i++){for (j = 1; j <= 9; j++){int k = i * j;if (k > 40)break;printf("%4d", k);}putchar('\n');}return0;}3、输出指定长宽的矩形#include <stdio.h>int main(void){int i, j;int height, width;puts("please input the height and width.");printf("height = "); scanf("%d", &height);printf("width = "); scanf("%d", &width);for (i = 1; i <= height; i++){for (j = 1; j <= width; j++){putchar('*');}putchar('\n');}return0;}4、输出直⾓在左下⾓的等腰直⾓三⾓形#include <stdio.h>int main(void){int i, j, len;puts("please input the side length of the triangle."); printf("side length = "); scanf("%d", &len);for (i = 1; i <= len; i++){for (j = 1; j <= i; j++){putchar('*');}putchar('\n');}return0;}5、输出直⾓在右下⾓的等腰直⾓三⾓形#include <stdio.h>int main(void){int i, j, len;puts("please input the side length of the triangle."); printf("side length = "); scanf("%d", &len);for (i = 1; i <= len; i++){for (j = 1; j <= (len - i); j++){putchar('');}for (j = 1; j <= i; j++){putchar('*');}putchar('\n');}return0;}。
二重循环结构进阶if,java

插入算法
1、数组中的英文歌曲按照名称升序排列。 增加一首新歌,并保持歌曲名称升序排列
通过比较找到插入位置 将该位置后的元素后移一个位置 将新歌插入到该位置
插入算法
String[ ] musics = new String[]{"Island","Ocean","Pretty","Sun"}; 字符串比较 ) :不忽略大小写 String[ ] newMusics = new compareTo( String[musics.length+1];// 新歌曲数组 compareToIgnoreCase( ):忽略大小写 String music = ""; //保存用户输入的歌曲名称 …… for(int i = 0; i < musics.length; i++){ if(musics[i].compareToIgnoreCase(music) > 0){ index = i; break; 找到新元素的插入位置 } } for(int i = newMusics.length-1; i > index; i--){ newMusics[i] = newMusics[i-1]; 元素后移 } newMusics[index] = music; 新元素放在index的位置 …… 演示示例 1:插入算法
二重循环中continue和break对比
for(…){ for(…) { …… continue; …… } ……
继 续 本 层 下 一 轮 循 环
for(…){ for(…) { …… break; …… } ……
跳 出 本 层 循 环
}
二重循环的解析

⼆重循环的解析1.什么是⼆重循环:⼀个循环体内⼜包含另⼀个完整的循环结构语法:while(循环条件1) {//循环操作1while(循环条件2) {//循环操作2}}do {//循环操作1do {//循环操作2}while(循环条件1);}while(循环条件2);for(循环条件1) {//循环操作1for(循环条件2) {//循环操作2}}while(循环条件1) {//循环操作1for(循环条件2) {//循环操作2}}※各种循环可以相互嵌套2.⼆重循环执⾏顺序:外层循环执⾏1次内层循环执⾏1周案例:若有3个班级各4名学员参赛,如何计算每个班级参赛学员的平均分?public class Demo02 {public static void main(String[] args) {Scanner input=new Scanner(System.in);//⼆重循环/**** 外层循环执⾏⼀次,内层循环执⾏1周**/for (int i = 1; i <=3; i++) {System.out.println("*************************************");System.out.println("请输⼊第"+i+"个班级4位学员的成绩:");int [] scores=new int[4]; //学员成绩数组double sum=0.0; //计算总和for (int j = 0; j <scores.length; j++) {System.out.println("请输⼊第"+(j+1)+"位学员的成绩:");scores[j]=input.nextInt();sum=sum+scores[j];}System.out.println("第"+i+"个班级的平均分为:"+sum/scores.length);}}}案例:打印矩形public class Demo03 {public static void main(String[] args) {//外层循环控制⾏数for (int i = 1; i <=5; i++) {//内层循环控制个数for (int j = 1; j <=5; j++) {System.out.print("*");}System.out.println();}}}3.在⼆重循环中使⽤ continue:使⽤continue代表结束当前循环,继续下⼀次循环案例:若有3个班级各4名学员参赛,计算每个班级参赛学员平均分,统计成绩⼤于85分学员数public class Demo04 {public static void main(String[] args) {Scanner input=new Scanner(System.in);//⼆重循环/**** 外层循环执⾏⼀次,内层循环执⾏1周**/int count=0; //存储⼤于85分的⼈数for (int i = 1; i <=3; i++) {System.out.println("*************************************");System.out.println("请输⼊第"+i+"个班级4位学员的成绩:");int [] scores=new int[4]; //学员成绩数组double sum=0.0; //计算总和for (int j = 0; j <scores.length; j++) {System.out.println("请输⼊第"+(j+1)+"位学员的成绩:");scores[j]=input.nextInt();sum=sum+scores[j];if(scores[j]<85){//结束本次循环,进⼊下⼀次循环continue;}count++;}System.out.println("第"+i+"个班级的平均分为:"+sum/scores.length);}System.out.println("分数⼤于85的⼈数:"+count);}}4.在⼆重循环中使⽤ break:使⽤break代表结束(跳出)当前循环案例:有5家⾐服专卖店,每家最多购买3件。
第九章二重循环

第九章⼆重循环⼀、回顾3种循环结构1、whilel 语法条件表达式的初始值;while(条件表达式){循环操作;更改条件表达式的语句;}l 特点:先判断,再执⾏,有可能⼀次循环都没有l 适⽤的场合:循环次数未知l 表现形式n 第⼀种:循环的次数确定u 条件表达式,判断整型的变量在某个范围u while(i<=5){ //不需要接收⽤户输⼊}n 第⼆种:循环次数不限,⽤户输⼊某个值结束循环u 条件表达式,根据⽤户输⼊的值进⾏判断u while(⽤户输⼊的值和某个值做⽐较){如输⼊0或(yes/no)结束循环u }2、do…whilel 语法条件表达式的初始值;do{循环操作;更改条件表达式的语句;}while(条件表达式);l 特点:先执⾏,再判断,⾄少循环1次l 适⽤场合,同while循环l 表现形式,同while循环3、forl 语法for(初始值;条件表达式;迭代部分){//循环操作}l 特点:同while循环,都先判断,再执⾏,有可能1次循环都不执⾏l 适⽤场合:循环次数固定⼆、循环中常见的2个语句break——终⽌循环(循环未完毕时,提前结束循环)continue——结束本次循环,进⼊下⼀次循环三、回顾数组1、声明数组数据类型【】数组名;【】也可以放到数组名后⾯2、为数组分配空间(长度)⽅式1:【长度】来分配空间,元素只有默认值数据类型[]数组名=new 数据类型[长度];int类型的数组,元素的默认值为0String类型的数组,默认值为null⽅式2:根据值的个数,确定已分配的空间数据类型[] 数组名={值列表};int[]nums={1,2,3};⽅式3:根据值的个数,确定已分配的空间数据类型[] 数组名=new 数据类型[]{值列表};int [] nums= new int[]{1,2,3};3、遍历数组,⼀般情况都采⽤for循环取值或动态赋值for(int 变量=初始值; 条件表达式; 变量变更){根据下标取值,下标>=0且下标<数组名.length }四、⼆重循环1、循环中,嵌套另外⼀个循环,将内层的循环,看成外层循环的⼀个循环操作2、常见的⼆重循环形式1:外层while或do…while内层为for循环形式2:外层、内层都是for循环形式3:外层为for循环,内层为while或do…while3、⼆重循环的执⾏顺序1、⾸先执⾏1次外层循环;2、进⼊外层循环后,必须要将内层循环全部循环完毕,才继续进⾏外层的第2….N次循环。
C语言5(5.6双重循环)

main() { int i,k;
long s, t; printf("\nInput n:"); scanf("%d",&n); s=0; for(k=1;k<=n;k++) { t=1;
for(i=1;i<=k;i++) t=t*i;
s=s+t; } printf("\ns=%ld",s); } Input n: 3↙
}
运行后,输出: 123
第十三页,编辑于星期五:十点 十八分。
例4:
main()
{
int i, j;
for( i=0; i<3; i++)
printf(" %d", i );
printf("\n" ) ;
for( i=1; i<=4; i++)
printf("%d", i ) ;
}
运行后,
输出:
012
{ int i,k;
Input n:5↙
long s, t; printf("\nInput n:");
1!+2!+…+5!=153
scanf("%d",&n);
s=0;
for(k=1;k<=n;k++)
{ t=1;
for(i=1;i<=k;i++)
t=t*i; /* 求t! */
s=s+t;
} /* 求s=1!+2!+…+n!*/
表达式2 非零 循环体语句
双重循环嵌套执行原理

双重循环嵌套执⾏原理双重循环嵌套执⾏原理执⾏原理循环嵌套是外循环⾥套个内循环,外循环执⾏⼀次,内循环全部执⾏完,直到外循环执⾏完毕,整个循环结束。
案例解析下⾯将分别⽤while循环和for循环进⾏案例解析,来更好地理解双重循环嵌套。
while循环var j = 0;while (j < 3) {//外层循环var str = "<ul>";var i = 0;// 每⼀次进⼊这⾥,就会执⾏下⾯10次循环while (i < 10) {//内层循环str += "<li>" + i + "</li>";i++;}str += "</ul>";document.write(str);j++;}该代码运⾏效果如下:如效果所⽰,在外部循环执⾏了第⼀步之后,优先执⾏内部的循环。
for循环var sum = 0;for (var num = 2; num < 100; num++) {//外层内部循环for (var i = 2; i <=num; i++) {//内层循环if(i<num){if (num % i === 0)break;//当num与i整除时,跳出循环回到第⼀个内部循环} else sum += num;}}console.log(sum);该代码运⾏效果如下:如代码所⽰,每⼀个 for 的执⾏过程相同,第⼆个内部循环中i变量与第⼀个内部循环有关。
需要注意的是:外层循环的变量,不要在内层循环重复定义。
总结1. 外循环执⾏⼀次,内循环全部执⾏完,直到外循环执⾏完毕。
2. 外层循环的变量,不要在内层循环重复定义。
3. 内层循环的变量常常与外层循环变量有关。
双重循环排序与冒泡排序算法

双重循环排序与冒泡排序算法双重循环排序双重循环排序算法是⼀种⾮常简单的排序算法,这种算法很容易让⼈理解,也很实⽤,但是排序的效率很低。
基本思路是⽤第⼀个数与后⾯的所有数进⾏⽐较,然后把最⼩的数放到第⼀个位置,然后⽤第⼆个数与后⾯的所有数进⾏⽐较,然后把第⼆个最⼩的数放到第⼆个位置,然后⽤第三个数....最后⽤倒数第⼆个数进⾏⽐较,这样最终形成从⼩到⼤的排列顺序。
C语⾔源代码:1 #include<stdio.h>23int main()4 {5int i, j, t;6int a[10] = {2, 5, 8, 1, 3, 4, 7, 9, 0, 6}; // 共10个数据7// 双重for循环排序8for(i=0; i<9; i++) // 从第1个到第9个9 {10for(j=i+1; j<10; j++) // 将a[i]和后⾯的所有数进⾏⽐较11 {12if(a[i]>a[j]) // 如果a[i]⼤于后⾯的数则进⾏交换13 {14 t=a[i];15 a[i]=a[j];16 a[j]=t;17 }18 }19 }20 printf("排序后:\n");21for(i=0; i<10; i++)22 {23 printf("%d ", a[i]);24 }25return0;26 }冒泡排序算法:基本思路:假设有10个数,则需要进⾏10-1趟(即9趟)⽐较,每趟从第⼀个数开始与后⾯相邻的⼀个数⽐较,如果前⾯的数⽐后⾯相邻的数⼤则相互交换,经过⼀趟⽐较之后,最⼤的那个数被放在最后⾯。
然后进⾏下⼀趟⽐较,⼜从第⼀个数开始⽐较,但不包括前⾯⼀趟已经找出来的那个最⼤的数,因此下⼀趟要⽐前⼀趟⽐较的次数少⼀次。
可见这种算法每进⾏⼀趟后会把本趟最⼤的数“升到”末尾,如⽓泡⼀样逐步升出⽔⾯,故称为“冒泡法”或“起泡法”。
C语⾔源代码:1 #include<stdio.h>23int main()4 {5int i, j, t;6int a[10] = {2, 5, 8, 1, 3, 4, 7, 9, 0, 6}; // 共10个数据7// 冒泡排序8for(i=0; i<9; i++) // 总共需要⽐较9趟9 {10for(j=0; j<9-i; j++) // 只需⽐较前⾯的数,最后的是最⼤数,第⼀趟i为0时⽐较9次,第⼆趟⽐较8次,第三趟⽐较7次....11 {12if(a[j]>a[j+1]) // 如果a[j]⼤于后⾯相邻的⼀个数则进⾏交换13 {14 t=a[j];15 a[j]=a[j+1];16 a[j+1]=t;17 }18 }19 }20 printf("排序后:\n");21for(i=0; i<10; i++)22 {23 printf("%d ", a[i]);24 }25return0;26 }。
0125双重for循环:语法、执行思路、打印m行n列、打印倒三角形、正三角、九九乘法表、f。。。

0125双重for循环:语法、执⾏思路、打印m⾏n列、打印倒三⾓形、正三⾓、九九乘法表、f。
1.2.1 双重 for 循环概述循环嵌套是指在⼀个循环语句中再定义⼀个循环语句的语法结构,例如在for循环语句中,可以再嵌套⼀个for 循环,这样的 for 循环语句我们称之为双重for循环。
1.2.2 双重 for 循环语法for (外循环的初始; 外循环的条件; 外循环的操作表达式) {for (内循环的初始; 内循环的条件; 内循环的操作表达式) {需执⾏的代码;}}内层循环可以看做外层循环的循环体语句内层循环执⾏的顺序也要遵循 for 循环的执⾏顺序外层循环执⾏⼀次,内层循环要执⾏全部次数demo:打印五⾏五列星星核⼼逻辑:1、内层循环负责⼀⾏打印五个星星2、外层循环负责打印五⾏var star = '';for (var j = 1; j <= 3; j++) {for (var i = 1; i <= 3; i++) {star += '☆'}// 每次满 5个星星就加⼀次换⾏star += '\n'}console.log(star);demo;打印n⾏n列的星星var rows = prompt('请您输⼊⾏数:');var cols = prompt('请您输⼊列数:');var str = '';for (var i = 1; i <= rows; i++) {for (var j = 1; j <= cols; j++) {str = str + '★';}str += '\n';}console.log(str);demo:打印倒三⾓形、正三⾓案例var str = '';for (var i = 1; i <= 10; i++) { // 外层循环控制⾏数for (var j = i; j <= 10; j++) { // ⾥层循环打印的个数不⼀样 j = istr = str + '★';}str += '\n';}console.log(str);// 我的正三⾓写法for (var i = 1; i <= 9; i++) {var s = '';for (var j = 1; j <= i; j++) {s += '★';}console.log(s);}// 我的倒三⾓写法,i--var s = '';// 注意,这⾥是 i >= 1,不是i <= 10。
《用二重循环打印图形》教学设计

《用二重循环打印图形》教学设计一、教材分析本文选自高中信息技术选修《算法与程序设计》第二章。
二重循环建立在一重循环的基础之上,虽然内容不多,但用它来实现图形打印,内外循环就被赋予了特殊的含义,即控制行数和每行的字符数。
由于图形的多样性,需要灵活设置内外循环的变化范围。
为了让学生掌握各种图形的打印方法,学会总结图形规律,理解用二重循环打印图形的原理是非常重要的。
二、教学目标知识与技能:掌握二重循环语句For…Next的基本格式,并能运用它打印图形;理解Tab函数的含义并能进行运用;学会用数学函数思想归纳变量与定量之间的关系表达式。
过程与方法:通过打印各种“*”图形,熟练运用二重循环,提高分析问题、解决问题的能力。
情感、态度与价值观:通过图形打印,增强对程序设计的兴趣。
三、教学重点、难点重点:根据“*”图形的排列情况,运用数学函数思想总结其规律,灵活运用二重循环语句实现图形打印。
难点:根据“*”图形的排列情况,运用数学函数思想总结其规律。
四、学生分析学生已经学习了一重循环的基本格式,并且能够编写相应程序,具备了用二重循环解决问题的能力,加上以图形打印为载体,更能激发他们的学习兴趣。
五、教学环境网络机房、VB6.0程序、投影仪。
六、教学过程1.创设问题情境,引入新课师:有这样一条VB语句(print“*”;),大家思考一下它的执行结果是什么?学生在VB窗体打印一个*。
师:这里的“;”有什么作用?生:后面打印的内容紧跟此*显示,不换行。
师:如果将这条语句(print“*”;)作为如下循环语句(代码略)的循环体,运行结果是什么?学生在VB窗体打印4个连续的*。
师:如果将这里的循环语句,再作为如下循环语句(代码略)的循环体,这样写行不行呢?会产生运行结果吗?生:行,结果是在VB窗体打印出16个连续的*。
师:大家可以看到这里出现了比较特殊的情况,即循环语句套循环语句的情况,这就是“二重循环”。
2.总结二重循环语句格式师:根据此例,可以总结出二重循环语句的基本格式为:For 循环变量= 初值To 终值For 循环变量= 初值To 终值循环体Next 循环变量Next 循环变量师:刚才这个例子,执行结果是打印16个连续的*,如果要将16个*分成4行,该如何修改代码呢?大家还记得前面讲过的实现换行的语句吗?生:用print。
(m,n)型二重(r,r)-循环线性系统求解的快速傅里叶算法

收稿日期:2002-06-11作者简介:王正华(1963-),男,副教授(m ,n )型二重(R ,r )-循环线性系统求解的快速傅里叶算法王正华, 何承源(成都师范高等专科学校数学系,四川彭州611930) 摘要:利用快速傅里叶变换(FFT )技术,给出了计算系数矩阵为非奇异的(m ,n )型二重(R ,r )-循环矩阵的线性方程的求解、非奇异(m ,n )型二重(R ,r )-循环矩阵求逆的快速算法,证明了它们的计算复杂性均为o (mn log 2mn ).关键词:(m ,n )型二重(R ,r )-循环矩阵;线性系统;快速求解;唯一解;逆矩阵中图分类号:O151.21 文献标识码:A 文章编号:1001-8395(2003)02-0143-050 引言循环矩阵及循环线性系统的求解在实际中有着广泛的应用,如在线性预测、误差控制码、自回归滤波器设计、计算机时序分析、自回归时序模型滤波以及石油勘探等许多大型计算中经常遇到,因而引起人们的广泛重视[1~6].近年来人们又研究了一类更广泛的R -循环分块矩阵[7].本文利用快速傅里叶变换(FFT )技术,给出了计算系数矩阵为非奇异的(m ,n )型二重(R ,r )-循环矩阵的线性方程组的求解、非奇异(m ,n )型二重(R ,r )-循环矩阵求逆的快速算法,证明了它们的计算复杂性均为o (mn log 2mn ).该方法无需先计算逆矩阵,再计算逆矩阵乘以常数列.1 预备知识定义1 具有如下形式的n 阶矩阵A =a 0a 1…a n -2a n -1ra n -1a 0…a n -3a n -2ra 1ra 2…ra n -1a 0称为r -循环矩阵,记作A CirC r (a 0,a 1,…,a n -1).定义2[7] 设A 0,A 1,…,A m -1,R 均为n 阶矩阵,且R 非奇异,R 与A j (j =0,m -1)可换,而且具有下列形式的mn 阶矩阵A =A 0A 1…A m -2A m -1RA m -1A 0…A m -3A m -2RA 1RA 2…RA m -1A 0称为R -循环分块矩阵,记作A ■≡CirC R (A 0,A 1,…,A m -1).特别地,R =r I n 时称为r -循环分块矩阵,R =I n (I n )时称为循环分块矩阵(斜循环分块矩阵).定义3 若A =CirC R (A 0,A 1,…,A m -1),而A j =CirC r (a (j )0,a (j )1,…,a (j )n -1),j =0,m -1,R =CirC r (r 0,r 1,…,r n -1),则称A 为mn 阶(m ,n )型二重(R ,r )-循环矩阵.引理1 r -循环矩阵A =CirC r (a 0,a 1,…,a n -1)的必要充分条件是存在矩阵D =diag (1,λ,…,λn -1),酉矩阵F *n ,使得A =DF *ndiag (∑n -1j =0a j λj,∑n -1j =0a j (ωn λ)j,…,∑n -1j =0a j (ωn -1n λ)j )F n D -1,其中ωn =cos 2πn +isin 2πn,i 2=-1,λ=n r (r ≠0)(下同).引理2[8] 设{x j }m -1j =0为n 阶矩阵序列,Z 是n 2003年3月 第26卷 第2期四川师范大学学报(自然科学版)Journal of Sichuan Normal University (Natural Science )Mar .,2003 Vol .26,No .2 阶非奇异矩阵,且Z 与X j (j =0,m -1)可换,作下列矩阵变换r t =∑m -1j =0X j (ωtm Z )j, t =0,m -1,(1)则其逆变换为X j =1m∑m -1t =0Y t(ωt mZ )-j, j =0,m -1.(2) 引理3 R -循环分块矩阵A =CirC R (A 0,A 1,…,A m -1)的必要充分条件是存在矩阵H =diag (I n ,K ,…,K m -1),酉分块矩阵F *mn,使得A =HF *mndiag (M 0,M 1,…,M m -1)F mn H-1,其中H =diag (I n ,K ,…,Km -1),M t =∑m -1j =0A j (ωtm K )j(t =0,m -1),K =mR ,ωm =cos 2πm +isin 2πm,i 2=-1. 证明 由文[7]以及直接验证知结论正确.引理4 设mn 阶矩阵A 、B 均是(m ,n )型二重(R ,r )-循环矩阵,则AB 也是(m ,n )型二重(R ,r )-循环矩阵.证明 因为A 、B 均是mn 阶(m ,n )型二重(R ,r )-循环矩阵,所以可设A =CirC R (A 0,A 1,…,A m -1),B =CirC R (B 0,B 1,…,B m -1).其中A j 、B j (j =0,m -1)、R 均是n 阶r -循环矩阵.于是由引理3,有A =HF *mn diag (M 0,M 1,…,M m -1)F mn H -1,B =HF *mn diag (N 0,N 1,…,N m -1)F mn H-1,其中M t =∑m -1j =0A j (ωtmK )j、N t =∑m -1j =0B j (ωt mK )j.又由引理3,知AB =HF *mndiag (M 0N 0,M 1N 1,…,M m -1N m -1)F mn H -1是mn 阶R -循环分块矩阵,并设AB =C =CirC R (C 0,C 1,…,C m -1),所以由引理3,有∑m -1j =0C j(ωtm K )j=M tN t, t =0,m -1,(3)由于A j 、B j 、K j(j =0,m -1)均为n 阶r -循环矩阵,根据r -循环矩阵关于矩阵相乘运算、线性运算的封闭性知M t N t 为r -循环矩阵.于是由引理2和(3)式,得C j =1m∑m -1t =0M tN t(ωtmK )-j,j =0,m -1.由于M t N t (t =0,m -1)、K 均为n 阶r -循环矩阵,根据r -循环矩阵关于求逆运算、相乘运算、线性运算的封闭性知C j (j =0,m -1)是r -循环矩阵.故AB 是mn 阶(m ,n )型二重(R ,r )-循环矩阵.引理5[8] 设A 是非奇异mn 阶(m ,n )型二重(R ,r )-循环矩阵,则A-1也是mn 阶(m ,n )型二重(R ,r )-循环矩阵.2 主要结论定理1 若设非奇异矩阵A =CirC R (A 0,A 1,…,A m -1),其中A j =CirC r (a (j )0,a (j )1,…,a (j )n -1),R =CirC r (r 0,r 1,…,r n -1),且设X =(x (m -1)n -1,…,x (m -1),…,x (0)n -1,…,x (0)0)′,b =(b (m -1)n -1,…,b (m -1),…,b (0)n -1,…,b (0)0)′.又令r (x )=∑n -1t =0r t λt x t,f j (x )=∑n -1t =0a (j )tλt x t , f j (x )=∑n -1t =0b(j )tλt x t,g k (x )=∑m -1j =0f j (ωkn )λj k x j, g k (x )=∑m -1j =0f j (ωk n )λj k x j,h k (x )=1m∑m -1p =0g -1k (ωpm ) g k (ωpm )x p,d j (x )=1n∑n -1k =01λj kh k (ω-j m )x k,k =0,n -1, j =0,m -1,则线性方程组AX =b 的唯一解X =(X ′m -1,…,X ′1,X ′0)′,X j =(λ-(n -1)d j (ω-(n -1)n),…,λ-1d j (ω-1n ),d j (1))′,j =0,m -1.144 四川师范大学学报(自然科学版)26卷其中λk =mr (ωkn )(下同),k =0,n -1.证明 因为X =(x (m -1)n -1,…,x (m -1)0,x (m -2)n -1,…,x (m -2)0,…,x (0)n -1,…,x (0)0)′,b =(b (m -1)n -1,…,b (m -1),b (m -2)n -1,…,b (m -2)0,…,b (0)n -1,…,b (0)0)′,所以令X j =CirC r (x (j )0,x (j )1,…,x (j )n -1),B j =CirC r (b (j )0,b(j )1,…,b(j )n -1)(j =0,m -1),从而令X =CirC R (X 0,X 1,…,X m -1),B =CirC R (B 0,B 1,…,B m -1),于是根据分块矩阵相乘的意义和mn 阶(m ,n )型的二重(R ,r )-循环矩阵的特点得线性方程组AX =b 的一个必要充分条件是A X =B .(4)因为A 、 X 和B 均是mn 阶(m ,n )型二重(R ,r )-循环矩阵,所以A X =HF *mn diag (M 0D 0,M 1D 1,…,M m -1D m -1)F mn H-1,(5)B =HF *mn diag (N 0,N 1,…,N m -1)F m -1H -1,(6)其中M p =∑m -1j =0A j(ωpmk )j,D p =∑m -1j =0X j(ωp mk )j,N p =∑m -1j =0B j (ωpm k )j,p =0,m -1.于是由(4)~(6)式,得M p (∑m -1j =0X j (ωpmk )j)=N p .(7)由于矩阵A 非奇异,所以M p 非奇异,从而由(7)式有M -1pN p =∑m -1j =0X j (ωp m k )j, p =0,m -1,由引理2,有X j =1m∑m -1p =0M-1pN p (ωp m k )-j,j =0,m -1.(8)易知1m∑m -1p =0M -1p N p (ωpm k )-j的第k +1个特征值为λ-jkh k (ω-jm ),而r -循环矩阵X j 的第k +1个特征值为∑n -1t =0x(j )t(ωknλ)t.由于M-1p、N p 、K-j、X j 均是r -循环矩阵,所以由(8)式,得λ-jj h k (ω-jm)=∑n -1t =0x (j )t (ωkn λ)t,k =0,n -1.由傅里叶变换之逆变换,得x(j )t=λ-t1n∑n -1k =0λ-j khk(ω-j m )(ω-t n )k =λ-t d j (ω-tn ),t =0,n -1.故线性方程组AX =b 的唯一解X =(X ′m -1,…,X ′1,X ′0)′,X j =(λ-(n -1)d j (ω-(n -1)n),…,λ-1d j (ω-1n ),d j (1))′,j =0,m -1. 推论1 设非奇异矩阵A =CirC R (A 0,A 1,…,A m -1),其中A j =CirC r (a (j )0,a (j )1,…,a (j )n -1),R =CirC r (r 0,r 1,…,r n -1).令r (x )=∑n -1t =0r tλt x t,f j (x )=∑n -1t =0a (j )t λt x t, j =0,m -1,g k (x )=∑m -1j =0f j (ωkn )λj k x j, k =0,n -1,h k (x )=1m ∑m -1p =0g -1k (ωp m )x p, k =0,n -1,d j (x )=1n ∑n -1k =0λ-jk h k (ω-jm )x k,j =0,m -1.则A-1=CirC R (C 0,C 1,…,C m -1),C j =CirC r (d j (1),λ-1d j (ω-1n ),…,λ-(n -1)d j (ω-(n -1)n)),j =0,m -1. 证明 因为非奇异矩阵A 是mn 阶(m ,n )型二重(R ,r )-循环矩阵,所以它的一个必要充分条件是AX =b有唯一解,其中b =(0,…,0,1)′mn ×1.于是由引理5与和定理1知推论的结论成立.3 快速算法及其复杂性分析设线性方程组AX =b ,其中A =CirC R (A 0,A 1,…,A m -1),145第2期王正华等:(m ,n )型二重(R ,r )-循环线性系统求解的快速傅里叶算法R =CirC r (r 0,r 1,…,r n -1),A j =CirC r (a (j )0,a (j )1,…,a (j )n -1),j =0,m -1,X =(x (m -1)n -1,…,x (m -1)0,…,x (0)n -1,…,x (0)0)′,b =(b (m -1)n -1,b (m -1),…,b (0)n -1,…,b (0)0)′. Step 1 由r (x )=∑n -1t =0r t λt x t,计算r (ωkn),k =0,n -1.再计算λk =mr (ωkn ),k =0,n -1,λjk (j =0,m -1).Step 2 由f j (x )=∑n -1t =0a(j )tλt x t, f j (x )=∑n -1t =0b (j )t λtx t,计算f j (ωkn ), f j (ωkn ),j =0,m -1,k =0,n -1.Step 3 由g k (x )=∑m -1j =0f j(ωk n )λj kx j , g k (x )=∑m -1j =0f j(ωkn)λj kx j ,计算g k (ωp m), g k (ωp m),k=0,n -1,p =0,n -1.Step 4 计算g -1k (ωpm )、g -1k (ωpm ) g k (ωpm ),k =0,n -1,p =0,m -1,并由h k (x )=1m∑m -1p =0g-1k(ωpm ) g k (ωpm )x p,计算h k (ω-jm ),k=0,n -1,j =0,m -1.Step 5 由d j (x )=1n∑n -1k =0λ-jk h k (ω-jm)x k,计算d j (ω-t n),j =0,m -1,t =0,n -1.Step 6 计算x (j )t=λ-td j (ω-tn ),j =0,m -1,j =0,m -1,t =0,n -1.现在来估计用上述算法求系数矩阵为mn 阶(m ,n )型二重(R ,r )-循环矩阵的线性方程组的唯一解所需的运算量.Step 1相当于计算1个n 点DFT ,附加2n +m -5个乘法运算和n 个开方运算.Step 2相当于计算2m 个n 点DFT ,附加2(m +1)(n -1)-2个乘法运算.Step 3相当于计算2n 个m 点DFT ,附加2n (2m -3)个乘法运算.Step 4相当于计算n 个m 点IDFT ,附加mn除法和mn 个乘法运算.Step 5相当于计算m 个n 点IDFT .Step 6计算需(m +1)(n -1)个乘、除法运算对于m 、n 点DFT 和IDFT ,借助于快速傅里叶变换(FFT )来计算,立即可得.定理2 求解系数矩阵为非奇异的mn 阶(m ,n )型二重(R ,r )-循环矩阵的线性方程组的计算复杂性为o (mn log 2mn ).推论2 求mn 阶(m ,n )型二重(R ,r )-循环矩阵逆阵的计算复杂性为o (mn log 2mn ).4 应用举例例 求线性方程组AX =b ,的唯一解.这里A =CirC R (A 0,A 1),R =CirC 4(2,12),A 0=CirC 4(1,2),A 1=CirC 4(-1,2),b =(1,2,1,2)′.解 (1)λ2=2,ωn =-1,由r (ω0n )r (ωn )=111ωnr 0λr 1,计算得r (1)=3,r (-1)=1,从而λ0=3,λ1=1.(2)由f j (ω0n )f j (ωn )=111ωn a (j )0λa(j )1,f j (ω0n) f j (ωn )=111ωnb(j )0λb (j )1,j =0,1,计算得f 0(1)f 0(-1)=5-3,f 1(1)f 1(-1)=3-5;f 0(1)f 0(-1)=40,f 1(1) f 1(-1)=40. (3)由g k (ω0n )g k (ωn )=111ωnf 0(ωkn )λk f 1(ωkn ),g k (ω0n ) g k (ωn )=111ωnf 0(ωkn )λk f 1(ωkn ),k =0,1,146 四川师范大学学报(自然科学版)26卷 (4)g -10(1)g -10(-1)=15+3315-33,g -11(1)g -11(-1)=-1812,g -10(1) g 0(1)=8-43,g -10(-1) g 0(-1)=8+43,g -11(1) g 1(1)=g -11(-1) g 1(-1)=0,由h k (ω0n )h k (ω-1n )=12111ω-1ng -1k (1) g k (1)g -1k(-1) g k (-1),k =0,1,计算得h 0(1)=8,h 0(-1)=-43,h 1(1)=h 1(-1)=0. (5)由d j (ω0n )d j (ω-1n )=12111ω-1nλ-j 0h 0(ω-jn )λ-j1h 1(ω-jn ),(j =0,1),计算得d 0(1)d 0(-1)=44, d 1(1)d 1(-1)=-2-2. (6)由x j )t=λ-t d j (ωtn )(j =0,1;t =0,1),计算得x (1)1=-1,x (1)0=-2,x (0)1=2,x (0)=4,所以线性方程组AX =b 的唯一解X =(-1,-2,2,4)′.参考文献[1]Blahut R E .Fast Algorithm for Digital Signal Processing [M ].M ass :Addison -Wesley Reading ,1984.[2]Smith R L .Moore -penrose inverses of block circulant and block k -circulant matrices [J ].Linear Algebra Appl ,1977,16:237~245.[3]Linzer E ,Vetterli M .Structure and arithmetic complexity of products and inverses of Toeplitz matrices [J ].Linear Algebra Appl ,1991,145:159~175.[4]B ini D ,Parallel solution of certain Toeplitz linear s ystems [J ].SIAMJ Comput ,1984,13(2):268~276.[5]游兆永,李磊.关于三角形Toeplitz 系统的复杂性[J ].计算数学,1987,9(3):262~265.[6]沈光星.(n 1,n 2)型二重(r 1,r 2)-循环矩阵及有关算法的计算复杂性[J ].高等学校计算数学学报,1998,20(4):336~344.[7]Claeyss en J C R .Diagonalization and spectral d ecomposltion of factor block circulant matrices [J ].Linear Algebra Appl ,1988,99:41~61.[8]何承源.R -循环分块矩阵求逆的快速傅里叶算法[J ].数值计算与计算机应用,2000,28(1):21.The Fast Fourier Transform Algorithm for the Solution of theLevel -2(R ,r )-Ciculant Linear Systems of Type (m ,n )WANG Zheng -hua , HE Cheng -yuan(De partment of Mat hematic s ,C hengdu Teacher 's College ,Pe ngzhou 611930,Sichuan )A bstract :B y using the fast Fourier transform (FFT ),a fast algorithm for the solution of level -2(R ,r )-circulant linear syst mes of type (m ,n )is given .It is proved that when the level -2(R ,r )-circulant matrix of type (m ,n )is nonsingular ,the complexity of the computation is o (mn log 2mn ).Key words :Level -2(R ,r )-circulant matrices of type (m ,n );Linear systems ;Fast s olution ;Solitary solution ;Inverse matrices 2000MSC :65F10;65T99;65Y20(编辑 李德华)147第2期王正华等:(m ,n )型二重(R ,r )-循环线性系统求解的快速傅里叶算法。
python双for循环原理

python双for循环原理Python中的双重循环是一种常见的循环结构,它可以用来遍历嵌套的数据结构或执行复杂的操作。
双重循环由外部循环和内部循环组成,外部循环控制内部循环的执行次数,并在每次内部循环执行完毕后更新外部循环条件。
本文将详细介绍Python双重循环的原理以及常见的应用场景。
在Python中,双重循环的基本语法结构如下:```for outer_item in outer_iterable:for inner_item in inner_iterable:# 执行内部循环的操作```在这个例子中,`outer_iterable`和`inner_iterable`分别是外部循环和内部循环的遍历对象,可以是列表、元组、字符串或任何可迭代对象。
`outer_item`和`inner_item`分别代表外部循环和内部循环中当前迭代的元素。
双重循环的执行过程如下:1. 外部循环首次执行,取出外部循环的第一个元素为`outer_item`。
2. 内部循环开始执行,取出内部循环的第一个元素为`inner_item`。
3. 执行内部循环的操作,可访问`outer_item`和`inner_item`进行计算和处理。
4. 内部循环执行完毕后,取出内部循环的下一个元素,重复步骤3。
直到内部循环遍历完所有元素为止。
5. 外部循环更新条件,取出下一个元素为`outer_item`,重复步骤2-4。
直到外部循环遍历完所有元素为止。
双重循环的应用场景非常广泛,以下是几个常见的例子:1. 矩阵遍历:对于二维列表或矩阵,可以使用双重循环逐个访问每个元素。
例如,计算一个矩阵的转置矩阵可以使用双重循环,外部循环遍历行,内部循环遍历列,然后交换元素位置。
2. 数据组合与筛选:双重循环可以用于生成两个数据集的所有组合,比如对两个列表进行笛卡尔积运算。
此外,使用双重循环可以进行数据筛选,比如在一个学生列表中筛选出成绩优秀的学生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二重循环习题的思路蓝桥软件学院-艳群本文通过一道习题,讲解做二重循环习题的思路:题目:使用二重循环打印如下图形:分析:首先要明确我们需要打印的种类有:字符串”*”,字符串””(空格)。
比如第一行,先打印了4个空格””,然后打印了一个”*”。
我们分析一下每行的具体打印情况:第0行:先打印4个空格,然后打印1个”*”第1行:先打印3个空格,然后打印3个”*”第2行:先打印2个空格,然后打印5个”*”第3行:先打印1个空格,然后打印7个”*”第4行:先打印0个空格,然后打印9个”*”通过上面分析,我们不难发现,”第0行”, ”第1行”… ”第4行”这些行数在重复,所以我们可以用外层循环控制行数(即打印第几行)。
在每行的内部,”打印n个空格”又是一个重复的过程,所以可以用内层循环来控制打印空格的个数。
同理,在每行的内部,”打印n个*”也是一个重复的过程,所以可以用内层循环来控制打印”*”的个数。
即:用外层循环控制打印的行数,用两个内层循环分别控制打印空格的个数和打印”*”的个数。
还要注意,在把每行的空格和”*”打印完后,还需要换行。
即可得伪代码:public static void main(String[] args) {int rows = 5;for (int i = 0; i < 行数; i++) {for (int j = 0; j < 空格的个数; j++) {System.out.print(" ");}for (int j = 0; j < "*"的个数; j++) {System.out.print("*");}System.out.println();//每行的空格和”*”打印完后,需要换行}}我们在用i表示行数(第几行),用j表示打印空格的个数,用k表示打印”*”的个数,可得下表:分析外层循环和内层循环的数学关系,可得:i+j=4 即j=4-i=(rows-1)-i,即空格的个数等于:(当前行数-1)-ik=2*i+1 ,即”*”的个数等于:2*当前行数+1现在,用计算后的关系式将伪代码中的汉字替换,即可实现等腰三角形的打印:public static void main(String[] args) throws Exception { int rows = 5;for (int i = 0; i < rows; i++) {for (int j = 0; j < rows - i - 1; j++) {System.out.print(" ");}for (int j = 0; j < 2 * i + 1; j++) {System.out.print("*");}System.out.println();//每行的空格和”*”打印完后,需要换行}}运行结果:思考:现将题目变为:打印倒等腰三角形,如图:该如何实现呢?分析:对比“正等腰三角形”和“倒等腰三角形”,如下不难发现,“倒等腰三角形”的第0行,就是“正等腰三角形”的最后一行;“倒等腰三角形”的第1行,就是“正等腰三角形”的倒数第二一行;…;“倒等腰三角形”的最后一行,就是“正等腰三角形”的第一行。
即:把“正等腰三角形”的行数逆序输出,就变成了“倒等腰三角形”。
控制“正等腰三角形”行数的是外层循环for(int i = 0; i < rows; i++),将它逆序输出,即改为for (int i = rows-1; i>=0; i--),就实现了“倒等腰三角形”的打印,如下:public static void main(String[] args) throws Exception { int rows = 5;// for (int i = 0; i < rows; i++)正等腰三角形for (int i = rows - 1; i >= 0; i--) {// 将“正等腰三角形”等行数逆序输出for (int j = 0; j < rows - i - 1; j++) {System.out.print(" ");}for (int j = 0; j < 2 * i + 1; j++) {System.out.print("*");}System.out.println();// 每行的空格和”*”打印完后,需要换行}}运行结果:思考:现将题目变为:打印菱形,如图:该如何实现呢?分析:将菱形上下拆开、一分为二,即可分为“正等腰三角形”和“到等腰三角形”,如图:因此,只需要先打印“正等腰三角形”,然后再打印“到等腰三角形”即可。
需要注意,菱形的中间那一行,既是“正等腰三角形”的最后一行,同时也是“倒等腰三角形”的第一行。
因此,在打印“正等腰三角形”时,不需要打印最后一行,如下:public static void main(String[] args) throws Exception { int rows = 5;// 正等腰三角形//for (int i = 0; i < rows; i++) {for (int i = 0; i < rows-1; i++) {//将for的第二个参数从row变为row-1,即无需打印"正等腰三角形"的最后一行for (int j = 0; j < rows - i - 1; j++) {System.out.print(" ");}for (int j = 0; j < 2 * i + 1; j++) {System.out.print("*");}System.out.println();// 每行的空格和”*”打印完后,需要换行}// 倒等腰三角形for (int i = rows - 1; i >= 0; i--) {// 将“正等腰三角形”等行数逆序输出for (int j = 0; j < rows - i - 1; j++) {System.out.print(" ");}for (int j = 0; j < 2 * i + 1; j++) {System.out.print("*");}System.out.println();// 每行的空格和”*”打印完后,需要换行}}运行结果:思考:现将题目变为:打印空心菱形,如图:该如何实现呢?分析:实心菱形与空心菱形的区别是:空心菱形就是实心菱形的边界,如下图:,即在打印“实心菱形”的“*”时,只需要把每一行“*”的开头第一个“*”和结尾最后一个“*”打印出来,每行中间部分的“*”用空格替代即可。
即对System.out.print("*");进行判断,伪代码如下:if (开头第一个“*”或结尾最后一个“*”) {System.out.print("*");} else {//即中间部分打印空格System.out.print(" ");}完整代码如下:public static void main(String[] args) throws Exception { int rows = 5;// 正等腰三角形for (int i = 0; i < rows; i++) {for (int j = 0; j < rows - i - 1; j++) {System.out.print(" ");}for (int j = 0; j < 2 * i + 1; j++) {if (j == 0 || j == 2 * i) {//开头第一个“*” 或结尾最后一个“*”System.out.print("*");} else {//即中间部分打印空格System.out.print(" ");}}System.out.println();// 每行的空格和”*”打印完后,需要换行}// 倒等腰三角形// for (int i = rows - 1; i >= 0; i--) {for (int i = rows - 2; i >= 0; i--) {// “倒等腰三角形”的第0行(即rows-1)不用打,直接从第1行(rows-2)开始打印for (int j = 0; j < rows - i - 1; j++) {System.out.print(" ");}for (int j = 0; j < 2 * i + 1; j++) {if (j == 0 || j == 2 * i) {//开头第一个“*” 或结尾最后一个“*”System.out.print("*");} else {//即中间部分打印空格System.out.print(" ");}}System.out.println();// 每行的空格和”*”打印完后,需要换行}}运行结果:本文由蓝桥软件学院()原创,转载请注明出处。
