高一数学基础知识专题训练1
高一上《1-4章》数学基础知识填空题

数学基础知识训练题1(集合部分)1.集合{0,1,2}的子集有,真子集有 .2.已知A={不大于3的自然数},U={0,1,2,3,4,5},则C U A= .3.已知A={a,b,c,d,e,f },B={b,d,e,g },则A∩B= ,A∪B = .4.集合M∩N=M是M N的条件,M∪N=是M=N=的条件5.满足关系{1,2}ÍMÍ{1,2,3,4,5}的集合M的个数是 .6.已知集合A={x|x≤2}, B={x|x<a},满足A ÊB,则a的取值范围是 .7.命题:“一个实数x,使得2x+3<0”的非命题是 .8.若p真q假,则p∧q为命题;p∨q为命题; (p∨q)为命题;p→q为命题;p→q为命题.9.A={( x , y )| x+y=1},B={( x , y )| x-y=-1}则A∩B.10.设U=Z,A={2m-1| m∈Z} 则C U A=11.空集表示的集合,记为,它是任意非空集合的.12. x2=4是x=-2或x=2的________________条件;13. ab=0是a=0或b=0的__________________条件;14. 已知M={ x│x≤19},a=32,则a与M的关系是 .15.已知A={ x│-5≤x<1},B={ x│-3<x<4},则A∩B= .16.设全集U=N,A={ n│n∈N且n≥3},则C U A=.数学基础知识训练题 2(不等式)1. 方程x 2-2x -1=0的解集为 .2. 不等式-3x ≤6的解集为 .3. 不等式5+x£3≥312-4x £«18的解集为 . 4. 不等式组x 2£x 3£¾£ 1 ¡¢Ù2(x £3)£3(x £2)£¼0¡¡ ¢Ú的解集为 .5. 不等式x 2-2x -3>0的解集为 .6. 不等式-x2-3x +4≥0的解集为 .7. 不等式|2x +3|≤7的解集为 .8. 不等式|x -3|>2的解集为 .11. 不等式x 2+2x +1≥0的解集为 .12. 不等式x2+2x +3>0的解集为 .13.不等式x 2-3x +5<0的解集为 .14.不等式3x £«1x £3>0的解集为 .15.求不等式3£2x x £4≥1的解集为 .16.二次不等式ax 2+bx +1>0的解集是(-1,13)则a = ,b = . (均值定理) 1.若x >0, 则4x -2+ 的最小值是 .2.函数f (x )=1+4x 2+21x 的最小值是 .3.y =2-3x -4x(x >0)的最大值是 . 4.y =x +1x £3-2(x >3)最小值是 .数学基础知识训练题3(函数的定义域、值域)1. 函数y=£x2£«2x£«3的定义域是 ,值域是 .2. f(x)=1的定义域是,值域是 .3. 函数y=(x£2)0lgx的定义域是 .4. 函数y=log0. 5(1£x)的定义域是 .5. 函数y=-3sin(2x+φ)-5的值域是 .6. 函数y=3cos2x-4sin2x的值域是 .7. 函数y=sin x-sin2x+cos x的值域是 .8. 函数y=cos2x-2sin x cos x-sin2x的值域是 .9. 函数y=x2-3x-5的值域是 .10.函数y=3-x-1x(x>0)的值域是 .数学基础知识训练题 4 (函数的奇偶性、单调性)1. 函数y=x3的奇偶性是;在R上的单调性是 .2. 函数y=-ax-3+bx5(其中a、b不同时为0)的奇偶性是 .3. 函数y=2x2的奇偶性是;若x∈(-1,1],则该函数的奇偶性是 .4. 函数y=-x4+1的奇偶性是 .5. 函数y=0的奇偶性是 .6. 函数y=cos x的奇偶性是;y=cos x+1的奇偶性是 .7. 函数y=sin x的奇偶性是;y=sin x+cos x的奇偶性是 .8. 函数y=x cos x的奇偶性是;y=x sin x的奇偶性是 .9. 函数y=sin x cos x的奇偶性是;y=(sin x-2)2的奇偶性是10.函数y=cos(3x+11p2)的奇偶性是;函数y=sin(2x-2001p2)的奇偶性是 .11.若函数y=mx2+(1+m)x-3是偶函数,则该函数在[0, +∞)上的单调性是 .12.若函数y=f(x)是R上的奇函数,且在[0, +∞)上是增函数,则此函数在(-∞,0]上的单调性是;f(-1),f(2),f(π)的大小关系是;f(0)= .13. 若函数y=f(x)是R上的偶函数,且在[0, +∞)上是增函数,则此函数在(-∞,0]上的单调性是;f(-1),f(2),f(π)的大小关系是 .14.已知y=f(x)是R上的奇函数,f(3)=5,则f(-3)= .15.已知y=f(x)是R上的奇函数,f(-3)=5,则f(3)= .16.已知y=f(x)是R上的偶函数,f(3)=5,则f(-3)= .17.已知y=f(x)是R上的偶函数,f(-7)=-2,则f(7)= .数学基础知识训练题5(函数的对称性)1.奇函数的图像关于对称;2.偶函数的图像关于对称;3.互为反函数的两个函数的图像关于对称。
人教版高一数学(必修1)基础知识试题选及答案

人教版高一数学(必修1)基础知识试题选及答案高一数学(必修1)基础知识试题选及答案一、选择题1. 下列数列中,等差数列是:A. 1, 3, 6, 10, 15B. 1, 2, 4, 7, 11C. 1, 4, 9, 16, 25D. 1, 3, 9, 27, 81答案:A2. 设等差数列的首项为a, 公差为d, 则该等差数列的第n项为:A. anB. a + (n-1)dC. a + ndD. a + (n+1)d答案:B3. 设等差数列的前n项和为Sn,则Sn的通项公式为:A. Sn = n(a + l)/2B. Sn = n(a + 2l)/2C. Sn = (a + l)n/2D. Sn = (a + 2l)n/2答案:A4. 已知等差数列的前n项和为Sn,公差为d,则该等差数列的第n 项可以表示为:A. Sn - Sn-1B. Sn - Sn+1C. Sn - Sn-dD. Sn - Sn+d答案:B5. 下列数列中,等比数列是:A. 2, 5, 8, 11, 14B. 4, 8, 16, 32, 64C. 1, 3, 6, 10, 15D. 1, 1, 2, 3, 5答案:B6. 设等比数列的首项为a, 公比为q, 则该等比数列的第n项为:A. a^nB. a + (n-1)qC. aq^nD. aq^(n-1)答案:C7. 设等比数列的前n项和为Sn,则该等比数列的第n项可以表示为:A. Sn - Sn-1B. Sn - Sn+1C. Sn/q - Sn/qdD. Snq - Snqd答案:A8. 如果在等比数列的前n项和中,n趋于无穷大,且公比小于1,则该等比数列的前n项和趋于:A. 1B. 0C. ∞D. 不存在答案:B二、解答题1. 将下列数列排列成由小到大的顺序:8, 5, 2, 9, 6答案:2, 5, 6, 8, 92. 求下列数列的前n项和:1, 3, 5, 7, ...答案:Sn = n^23. 求解下列方程:2x - 5 = 7答案:x = 64. 用配方法求解下列二次方程:x^2 - 5x + 6 = 0答案:x = 2, 35. 确定下列函数的定义域:f(x) = √(x + 4)答案:x ≥ -46. 求解下列不等式:2x - 5 > 7答案:x > 67. 已知点A(2, 1)和B(-3, 4),求线段AB的斜率。
人教版高一数学(必修1)基础知识试题选及答案

必修1高一数学基础知识试题选说明:本试卷分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷60分,第Ⅱ卷60分,共120分,答题时间90分钟.第Ⅰ卷(选择题,共60分)一、选择题:(每小题5分,共60分,请将所选答案填在括号内)1.已知集合M ⊂≠{4,7,8},且M 中至多有一个偶数,则这样的集合共有()(A)3个(B)4个(C)5个(D)6个2.已知S={x|x=2n,n ∈Z},T={x|x=4k ±1,k ∈Z},则()(A)S ⊂≠3P Q 等()}2y ≤4(A)16-5.已知(f 6.函数y 7.函数8.若函数(A)a 9(A)(B)(C)12(D)12 10.已知函数f(x)14x a -=+的图象恒过定点p ,则点p 的坐标是()(A )(1,5)(B )(1,4)(C )(0,4)(D )(4,0)11.函数y =的定义域是 ( ) (A )[1,+∞](B)(23,)+∞(C)[23,1](D)(23,1]12.设a,b,c 都是正数,且346a b c ==,则下列正确的是 ()(A)111c a b =+(B)221C a b =+(C)122C a b =+(D)212c a b =+第Ⅱ卷(非选择题,共60分)二、填空题:(每小题4分,共16分,答案填在横线上)13.已知(x,y )在映射f 下的象是(x-y,x+y),则(3,5)在f 下的象是,原象是。
14.已知函数f(x)的定义域为[0,1],则f(2x )的定义域为。
15.若log a 23<1,则a 的取值范围是161221718.19.20.(1(213.(17.略19.解:()f x 在R 2(4f x x --223x ++=由2(2x x ++∴解集为{|1}x x <-.20.(1)1a =-或3a =-(2)当A B A = 时,B A ⊆,从而B 可能是:{}{}{},1,2,1,2∅.分别求解,得3a ≤-;。
高一数学基础知识专题训练

高一数学基础知识专题训练高一基础知识专题训练011.设集合{}{}1,2,3,4,2,==|-2≤≤∈P Q x x x R ,则P Q 等于 ( )A 、{1,2}B 、{3,4}C 、{1}D 、{-2,-1,0,1,2} 2.已知全集}6,5,4,3,2,1{=U ,集合}5,2,1{=A ,U {4,5,6}C B =,则集合=B A ( )A .}2,1{B .}5{C .}3,2,1{D .}6,4,3{ 3. 已知集合}12|{+==x y x A ,}1|{2++==x x y y B ,则B A 等于 ( )A .)}3,1(),1,0{( C.),0(+∞ D.),43[+∞4.设{}{}(,)46,(,)38A x y y x B x y y x ==-+==-,则A B =( ) {}{}{}{}.(2,1).(2,2).(3,1).(4,2).A B C D ----5. 已知集合M 满足{}{}3,2,12,1= M , 则集合M 的个数是( ) A. 1 B. 2 C. 3 D. 46. {()}2137x x x -<-,则 A Z 的元素的个数 .7. 满足},,,{}{d c b a M a ⊂⊆的集合M 有 个8、集合}02)6(|{2=+-+=x a ax x A 是单元素集合,则实数 9. 集合{3,2},{,},{2},a A B a b A B A B ====若则.10. 已知集合 {|lg(1)}x y x =-,集合e R x e y y N x }(,|{∈==为自然对数的底数),则N M =11..已知集合N M M a a x x N M 则集合},,2|{},2,1,0{∈===等于 12. 设全集为U ,用集合A 、B 、C 的交、并、补集符号表图中的阴影部分。
(1) (2)高一基础知识专题训练02⎧≥-)10(,2x x2. 下列函数中,在区间()0,1上是增函数的是( )A .x y = B .x y -=3 C . D .42+-=x y3.若偶函数)(x f 在(]1,-∞-上是增函数,则下列关系式中成立的是( )A .B .C .D .4.已知3()4f x ax bx =+-其中,a b 为常数,若(2)2f -=,则(2)f 的值等于( )A .2-B .4-C .6-D .10-5.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程. 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )6.下列函数中,在其定义域内既是奇函数又是减函数的是 ( )(A )R x x y ∈-=,3 (B ) R x x y ∈=,sin (C ) R x x y ∈=, (D ) 7.若函数x x x f 2)12(2-=+,则)3(f = . 8.函数的定义域 。
专题1第一章集合与函数的概念知识点与基础巩固题(原卷版)高一数学复习巩固练习(人教A版)
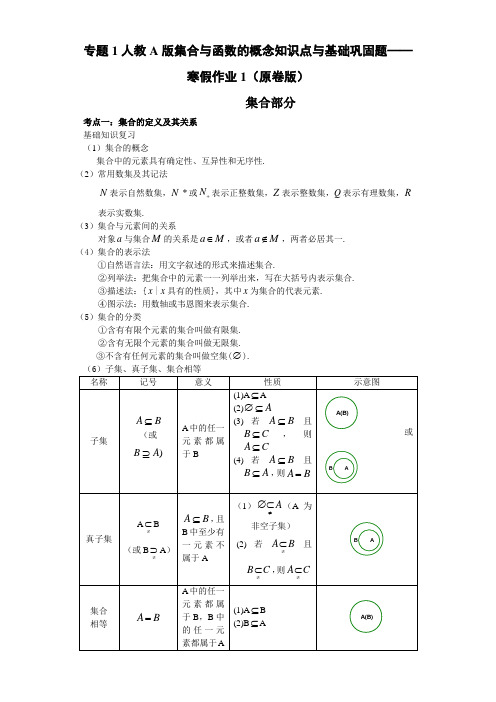
专题1人教A 版集合与函数的概念知识点与基础巩固题——寒假作业1(原卷版)集合部分考点一:集合的定义及其关系 基础知识复习 (1)集合的概念集合中的元素具有确定性、互异性和无序性. (2)常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R表示实数集.(3)集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集. ③不含有任何元素的集合叫做空集(∅).(7)已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它有21n -个非空子集,它有22n -非空真子集.考点二:集合的基本运算 基础知识复习1.交集的定义:一般地,由所有属于A 且属于B 的元素所组成的集合,叫做A,B 的交集.记作A ∩B(读作”A 交B ”),即A ∩B={x|x ∈A ,且x ∈B}.2、并集的定义:一般地,由所有属于集合A 或属于集合B 的元素所组成的集合,叫做A,B 的并集。
记作:A ∪B(读作”A 并B ”),即A ∪B={x|x ∈A ,或x ∈B}.3、交集与并集的性质:A ∩A = A ,A ∩φ= φ, A ∩B = B ∩A ,A ∪A = A ,A ∪φ= A , A ∪B = B ∪A.4、全集与补集(1)全集:如果集合S 含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集。
通常用U 来表示。
(2)补集:设S 是一个集合,A 是S 的一个子集(即A ⊆S ),由S 中 所有不属于A 的元素组成的集合,叫做S 中子集A 的补集(或余集)。
高一数学必修1函数的单调性和奇偶性专题训练(题型全)

专题 抽象函数的单调性和奇偶性一、选择题1.设()f x 是定义在(),-∞+∞上的单调递减函数,且()f x 为奇函数.若()11f =-,则不等式()121f x -≤-≤的解集为A . []1,1-B . []0,4C . []2,2-D . []1,32.若函数()f x 的定义域为()32,1a a -+,且函数()1f x -为奇函数,则实数a 的值为( ) A . 2 B . 4 C . 6 D . 83.已知()f x 是偶函数,它在[)0,+∞上是减函数,若()()lg 1f x f > ,则x 的取值范围是( )学=科网A . 1,110⎛⎫⎪⎝⎭ B . 1,1010⎛⎫⎪⎝⎭ C . ()10,1,10⎛⎫⋃+∞ ⎪⎝⎭D . ()()0,110,⋃+∞ 4.已知函数()y f x =是R 上的偶函数,且在[)0+∞,上单调递增,则下列各式成立的是( ) A . ()()()201f f f ->> B . ()()()102f f f >>- C . ()()()210f f f ->> D . ()()()120f f f >-> 5.已知偶函数在区间上单调递减,则满足的的取值范围是( )A .B .C .D .6. ()(),f x g x 是定义在R 上的函数, ()()()h x f x g x =+若()(),f x g x 均为奇函数则下列说法不正确的是( )A . 一定是奇函数B . 不可能是偶函数C . 可以是偶函数D . 不可能是非奇非偶函数7.若偶函数()f x 在(],0-∞上单调递减, ()()3224log 3,log 5,2a f b f c f ⎛⎫=== ⎪⎝⎭,则满足( )A . a b c <<B . b a c <<C . c a b <<D . c b a <<8.已知函数()f x 为定义在[]2,1b b -上的偶函数,且在[]0,1b -上单调递增,则()()1f x f ≤的解集为( )A . []1,2B . []3,5C . []1,1-D . 13,22⎡⎤⎢⎥⎣⎦9.【河北省定州市2016-2017学年期末】已知函数()f x 是定义在R 上的偶函数,在(],0-∞上有单调性,且()()21f f -<,则下列不等式成立的是 ( )A . ()()()123f f f -<<B . ()()()234f f f <<-C . ()()1202f f f ⎛⎫-<< ⎪⎝⎭D . ()()()531f f f <-<-二、填空题10.已知函数()f x 是定义在R 上的奇函数, 在区间(),0-∞上单调递减,且()10f =. 若实数a满足()515log log f a f a ⎛⎫≥ ⎪⎝⎭, 则实数a 的取值范围是____________.11.已知函数f (x )是定义在区间[0,+∞)上的函数,且在该区间上单调递增,则满足的x 的取值范围是______________. 12.已知定义在上的函数满足,且,若,则实数的取值范围为______.学*科网13.定义在区间[]2,2-上的偶函数()g x ,当0x ≥时()g x 单调递减,若()()1g m g m -<,则实数m 的取值范围是____________.14.定义在R 上的偶函数()f x 在(),0-∞上是减函数且()10f =,则不等式12log 0f x ⎛⎫> ⎪⎝⎭的解集为__________.15.已知()f x 是定义在R 上的偶函数,在[)0,+∞上单调增,且()21f =,则满足()11f x ->的x 的取值范围是_______________.16.已知定义在R 上的函数()f x 满足()()f x f x -=,且对于任意1x , [)20,x ∈+∞, 12x x ≠,均有()()21120f x f x x x ->-.若1132f ⎛⎫-= ⎪⎝⎭, 182log 1f x ⎛⎫< ⎪⎝⎭,则x 的取值范围为__________.三、解答题17.已知函数()y f x =是定义在()0,+∞上的增函数,对于任意的0,0x y >>,都有()()()f xy f x f y =+,且满足()21f =. (1)求()()14f f 、的值;(2)求满足()()32f x f x +->的x 的取值范围.18.定义在R 上的函数()y f x =对任意的,x y R ∈,满足条件: ()()()1f x y f x f y +=+-,且当0x >时, ()1f x >. (1)求()0f 的值;(2)证明:函数()f x 是R 上的单调增函数; (3)解关于t 的不等式()221f t t -<.19.定义在R 上的函数()y f x =对任意的,x y R ∈,满足条件: ()()()1f x y f x f y +=+-,且当0x >时, ()1f x >. (1)求()0f 的值;(2)证明:函数()f x 是R 上的单调增函数; (3)解关于t 的不等式()221f t t -<.20.若()f x 是定义在()0,+∞上的增函数,且对一切x , 0y >,满足()()x f f x f y y ⎛⎫=- ⎪⎝⎭.(1)求()1f 的值;(2)若()61f =,解不等式()1323f x f ⎛⎫+-< ⎪⎝⎭.21.已知()f x 是定义在[]1,1-上的奇函数,且()11f =,若m , []1,1n ∈-, 0m n +≠时,有()()0f m f n m n+>+.(1)证明()f x 在[]1,1-上是增函数;(2)解不等式1121f x f x ⎛⎫⎛⎫+< ⎪ ⎪-⎝⎭⎝⎭; (3)若()221f x t at ≤-+对任意[]1,1x ∈-, []1,1a ∈-恒成立,求实数t 的取值范围. 22.函数()f x 的定义域为{|0}D x x =≠,且满足对任意12,x x D ∈,有()()1212f x x f x x ⋅=+)(. (1)求()1f 的值;(2)判断()f x 的奇偶性并证明你的结论;(3)如果()41f =, ()12f x -<,且()f x 在()0,+∞上是增函数,求x 的取值范围. 23.设函数()y f x =是定义在R 上的函数,并且满足下面三个条件:①对任意正数,x y ,都有()()()f xy f x f y =+;②当1x >时, ()0f x <;③()31f =-.(1)求()1f , 19f ⎛⎫⎪⎝⎭的值;(2)证明()f x 在()0,+∞上是减函数;(3)如果不等式()()22f x f x +-<成立,求x 的取值范围.24.已知函数()f x 满足:对任意,x y R ∈,都有()()()()()2f x y f x f y f x f y +=--+成立,且0x >时, ()2f x >,(1)求()0f 的值,并证明:当0x <时, ()12f x <<. (2)判断()f x 的单调性并加以证明.学-科网(3)若函数()()g x f x k =- 在(),0-∞上递减,求实数k 的取值范围. 25.已知函数的定义域为,若对于任意的实数,都有,且时,有.(1)判断并证明函数的奇偶性; (2)判断并证明函数的单调性;(3)设,若对所有,恒成立,求实数的取值范围.26.设()f x 是定义在R 上的奇函数,且对任意a b R ∈、,当0a b +≠时,都有()()0f a f b a b +>+.(1)若a b >,试比较()f a 与()f b 的大小关系;(2)若()()923290x x x f f k -+->对任意[)0,x ∈+∞恒成立,求实数k 的取值范围.专题7 抽象函数的单调性和奇偶性一、选择题1.【湖北省荆门市2016-2017学年期末】设()f x 是定义在(),-∞+∞上的单调递减函数,且()f x 为奇函数.若()11f =-,则不等式()121f x -≤-≤的解集为A . []1,1-B . []0,4C . []2,2-D . []1,3 【答案】D【解析】由题意可得()11,f -=,不等式()121f x -≤-≤可化为()()()121f f x f ≤-≤-,又因为()f x 是定义在(),-∞+∞上的单调递减函数,所以121,x ≥-≥-即13x ≤≤,选D .2.【山东省烟台市2016-2017学年期末】若函数()f x 的定义域为()32,1a a -+,且函数()1f x -为奇函数,则实数a 的值为( ) A . 2 B . 4 C . 6 D . 8 【答案】C3.【内蒙古赤峰市2016-2017学年期末】已知()f x 是偶函数,它在[)0,+∞上是减函数,若()()lg 1f x f > ,则x 的取值范围是( ) A . 1,110⎛⎫⎪⎝⎭ B . 1,1010⎛⎫⎪⎝⎭ C . ()10,1,10⎛⎫⋃+∞ ⎪⎝⎭D . ()()0,110,⋃+∞ 【答案】B【解析】试题分析:偶函数()f x 在[)0,+∞上是减函数,则在(],0-∞上为增函数,由()()lg 1f x f >可知,得,故选项B 正确.考点:偶函数的单调性及其运用.【易错点睛】解答本题时考生容易错误的理解为:偶函数在整个定义域上的单调性是一致的,而列出不等式,解得,没有正确的选项可选.偶函数的图象关于y 轴对称,则其在原点两侧对称区间的单调性也是不同的,即一侧为单调增函数,则对称的另一侧为单调减函数.只有清楚了函数的单调性,才能正确的列出不等式,进而求出正确的解.4.【海南省东方中学2016-2017学年期中】已知函数()y f x =是R 上的偶函数,且在[)0+∞,上单调递增,则下列各式成立的是( )A . ()()()201f f f ->>B . ()()()102f f f >>-C . ()()()210f f f ->>D . ()()()120f f f >-> 【答案】A5.【江西省玉山县第一中学2016-2017学年期中考】已知偶函数在区间上单调递减,则满足的的取值范围是( )A .B .C .D .【答案】B 【解析】,所以 的取值范围是,选B .点睛:利用函数单调性解函数不等式:首先根据函数的性质把不等式转化为的形式,然后根据函数的单调性去掉“”,转化为具体的不等式(组),此时要注意与的取值应在外层函数的定义域内6.【安徽省蚌埠市2015-2016学年期中】()(),f x g x 是定义在R 上的函数, ()()()h x f x g x =+若()(),f x g x 均为奇函数则下列说法不正确的是( )A . 一定是奇函数B . 不可能是偶函数C . 可以是偶函数D . 不可能是非奇非偶函数 【答案】B【解析】选项A 中,当()3f x x =-, ()3g x x =时,则()0h x =既是奇函数也是偶函数;选项B 中,两个奇函数的和不能成为偶函数,显然成立;则选项C 、D 均不正确,故选B .点睛:此题主要考查两个函数的和的奇偶性判断,属于中高档题型,也是常考知识点.函数的奇偶性的判断应从两个方面来进行,一是看函数的定义域是否关于原点对称(这是判断奇偶性的必要性),二是看()f x 与()f x -的关系,对于两个函数的和或差的奇偶性的判断,需要对特殊情况进行考虑,如解析中的两个函数等.7.【青海省西宁市2017届检测】若偶函数()f x 在(],0-∞上单调递减,()()3224log 3,log 5,2a f b f c f ⎛⎫=== ⎪⎝⎭,则满足( )A . a b c <<B . b a c <<C . c a b <<D . c b a << 【答案】B【解析】∵偶函数f (x )在(−∞,0]上单调递减, ∴f (x )在[0,+∞)上单调递增, ∵3224422log 3log 9log 5>>=>,∴()()3242log 5log 32f f f ⎛⎫<< ⎪⎝⎭,∴b <a <c . 本题选择B 选项.8.【江西省抚州市临川区第一中学2017届检测】已知函数()f x 为定义在[]2,1b b -上的偶函数,且在[]0,1b -上单调递增,则()()1f x f ≤的解集为( )A . []1,2B . []3,5C . []1,1- D . 13,22⎡⎤⎢⎥⎣⎦【答案】C【解析】由函数奇偶性的定义可知2101b b b +-=⇒=-,所以函数()f x 在[]0,2单调递增,则不等式可化为1{1102x x x ≤⇒-≤≤≤≤,应选答案C 。
高一知识点训练数学

高一知识点训练数学在高一学年,数学是一门非常重要的学科,它不仅是一种工具,还是一种逻辑思维的训练方法。
通过学习数学,我们可以培养自己的逻辑思维能力,提高解决问题的能力。
下面,我将通过对高一数学的知识点进行训练,来巩固我们的数学基础。
一、整式与分式1. 整式的定义整式是指只包含有限项的多项式,其中项是由常数和变量的积组成。
2. 整式的分类整式可分为单项式、多项式和常数。
3. 分式的定义分式是指由两个整式通过除法运算得到的式子。
4. 分式的性质- 分式的分母不能为0。
- 分式的分子和分母可以进行约分。
- 分式可以进行加、减、乘、除运算。
二、函数与方程1. 函数的定义函数是一种关系,它将一个自变量的值映射到一个因变量的值。
2. 函数的性质- 函数可以表示为映射图、列表、公式等形式。
- 函数的定义域和值域是它的重要属性。
- 函数的图像可以通过绘制函数的关系来表示。
3. 方程的定义方程是指在等式中含有未知数的代数式。
4. 方程的解与解集解是使方程成立的未知数的值。
解集是所有解的集合。
三、三角函数1. 三角函数的定义三角函数是描述角度与边长之间关系的函数。
2. 常用三角函数常用的三角函数包括正弦函数、余弦函数和正切函数等。
3. 三角函数的性质- 三角函数的定义域是所有实数。
- 三角函数是周期函数,其周期为2π。
四、数列与数列求和1. 数列的定义数列是按照一定规律排列的一组数。
2. 等差数列等差数列是指数列中相邻项之差为常数的数列。
3. 等差数列的性质- 等差数列可以通过公式an = a1 + (n-1)d来表示。
- 等差数列的前n项和可以通过公式Sn = (a1 + an) * n/2来计算。
五、平面解析几何1. 平面直角坐标系平面直角坐标系由两个相互垂直的数轴组成,分别称为x轴和y轴。
2. 点的坐标表示点在平面直角坐标系中的位置可以用坐标表示。
3. 直线的表示直线可以通过点斜式、一般式和截距式来表示。
4. 圆的表示圆可以通过圆心坐标和半径来表示。
高一数学必修1、4基础题及答案

必修1 第一章 集合基础测试一、选择题(共12小题,每题5分,四个选项中只有一个符合要求)1.下列选项中元素的全体可以组成集合的是 ( ) A.学校篮球水平较高的学生B.校园中长的高大的树木C.2007年所有的欧盟国家D.中国经济发达的城市2.方程组20{=+=-y x y x 的解构成的集合是( )A .)}1,1{(B .}1,1{C .(1,1)D .}1{3.已知集合A ={a ,b ,c },下列可以作为集合A 的子集的是 ( ) A. a B. {a ,c } C. {a ,e } D.{a ,b ,c ,d } 4.下列图形中,表示N M ⊆的是 ( )5.下列表述正确的是 ( ) A.}0{=∅ B. }0{⊆∅ C. }0{⊇∅ D. }0{∈∅ 6、设集合A ={x|x 参加自由泳的运动员},B ={x|x 参加蛙泳的运动员},对于“既参加自由泳又参加蛙泳的运动员”用集合运算表示为 ( ) A.A∩B B.A ⊇B C.A ∪B D.A ⊆B 7.集合A={x Z k k x ∈=,2} ,B={Z k k x x ∈+=,12} ,C={Z k k x x ∈+=,14} 又,,B b A a ∈∈则有 ( ) A.(a+b )∈ A B. (a+b) ∈B C.(a+b) ∈ C D. (a+b) ∈ A 、B 、C 任一个8.集合A ={1,2,x },集合B ={2,4,5},若B A ={1,2,3,4,5},则x =( ) A. 1 B. 3 C. 4 D. 5 9.满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是( )A. 8 B . 7 C. 6 D. 510.全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 , 6 },那么集合 { 2 ,7 ,8}是 ( )MNAMNBNMCMNDA. A BB. B AC. B C A C U UD. B C A C U U11.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤ ( )A .{}01,B .{}101-,,C .{}012,, D .{}1012-,,, 12. 如果集合A={x |ax 2+2x +1=0}中只有一个元素,则a 的值是 ( )A .0B .0 或1C .1D .不能确定二、填空题(共4小题,每题4分,把答案填在题中横线上)13.用描述法表示被3除余1的集合 . 14.用适当的符号填空:(1)∅ }01{2=-x x ; (2){1,2,3} N ; (3){1} }{2x x x =; (4)0 }2{2x x x =. 15.含有三个实数的集合既可表示成}1,,{aba ,又可表示成}0,,{2b a a +,则=+20042003b a .16.已知集合}33|{≤≤-=x x U ,}11|{<<-=x x M ,}20|{<<=x x N C U 那么集合=N ,=⋂)(N C M U ,=⋃N M .三、解答题(共4小题,共44分,解答应写出文字说明,证明过程或演算步骤)17. 已知集合}04{2=-=x x A ,集合}02{=-=ax x B ,若A B ⊆,求实数a 的取值集合.18. 已知集合}71{<<=x x A ,集合}521{+<<+=a x a x B ,若满足 }73{<<=x x B A ,求实数a 的值.19. 已知方程02=++b ax x .(1)若方程的解集只有一个元素,求实数a ,b 满足的关系式; (2)若方程的解集有两个元素分别为1,3,求实数a ,b 的值20. 已知集合}31{≤≤-=x x A ,},{2A x y x y B ∈==,},2{A x a x y y C ∈+==,若满足B C ⊆,求实数a 的取值范围.必修1 函数的性质一、选择题:1.在区间(0,+∞)上不是增函数的函数是( )A .y =2x +1B .y =3x 2+ 1C .y =x2D .y =2x 2+x +1 2.函数f (x )=4x 2-mx +5在区间[-2,+∞]上是增函数,在区间(-∞,-2)上是减函数,则f (1)等于 ( )A .-7B .1C .17D .253.函数f (x )在区间(-2,3)上是增函数,则y =f (x +5)的递增区间是 ( )A .(3,8)B .(-7,-2)C .(-2,3)D .(0,5) 4.函数f (x )=21++x ax 在区间(-2,+∞)上单调递增,则实数a 的取值范围是 ( ) A .(0,21) B .( 21,+∞) C .(-2,+∞) D .(-∞,-1)∪(1,+∞)5.函数f (x )在区间[a ,b ]上单调,且f (a )f (b )<0,则方程f (x )=0在区间[a ,b ]内 ( )A .至少有一实根B .至多有一实根C .没有实根D .必有唯一的实根6.若q px x x f ++=2)(满足0)2()1(==f f ,则)1(f 的值是 ( )A 5B 5-C 6D 6-7.若集合}|{},21|{a x x B x x A ≤=<<=,且Φ≠B A ,则实数a 的集合( )A }2|{<a aB }1|{≥a aC }1|{>a aD }21|{≤≤a a8.已知定义域为R 的函数f (x )在区间(-∞,5)上单调递减,对任意实数t ,都有f (5+t ) =f (5-t ),那么下列式子一定成立的是 ( ) A .f (-1)<f (9)<f (13) B .f (13)<f (9)<f (-1) C .f (9)<f (-1)<f (13) D .f (13)<f (-1)<f (9) 9.函数)2()(||)(x x x g x x f -==和的递增区间依次是 ( ) A .]1,(],0,(-∞-∞ B .),1[],0,(+∞-∞ C .]1,(),,0[-∞+∞ D ),1[),,0[+∞+∞10.若函数()()2212f x x a x =+-+在区间(]4,∞-上是减函数,则实数a 的取值范围 ( )A .a ≤3B .a ≥-3C .a ≤5D .a ≥311. 函数c x x y ++=42,则 ( )A )2()1(-<<f c fB )2()1(->>f c fC )2()1(->>f f cD )1()2(f f c <-<12.已知定义在R 上的偶函数()f x 满足(4)()f x f x +=-,且在区间[0,4]上是减函数则( )A .(10)(13)(15)f f f <<B .(13)(10)(15)f f f <<C .(15)(10)(13)f f f <<D .(15)(13)(10)f f f <<.二、填空题:13.函数y =(x -1)-2的减区间是___ _.14.函数f (x )=2x 2-mx +3,当x ∈[-2,+∞)时是增函数,当x ∈(-∞,-2]时是减函数,则f (1)= 。
必修1 高一数学基础知识学考复习卷

必修1 高一数学基础知识试题选一、选择题:(每小题5分,共60分,)1.已知集合M ⊂≠{4,7,8},且M 中至多有一个偶数,则这样的集合共有 ( )(A)3个 (B) 4个 (C) 5个 (D) 6个2.已知0.70.70.7log 0.8,log 0.9,log 1.1a b c ===,那么 ( )A .a b c <<B .a c b <<C .c b a <<D .c a b <<3.设集合{(,)|2},{(,)|1}A x y y x B x y y x ====+,则B A =( )A .{}1,2B .{}1,2x y ==C .(1,2)D .{}(1,2) 4.不等式042<-+ax ax 的解集为R ,则a 的取值范围是 ( ) (A)016<≤-a (B)16->a (C)016≤<-a (D)0<a 5. 已知()f x =5(6)(4)(6)x x f x x -≥⎧⎨+<⎩,则(3)f 的值为 ( ) (A)2 (B)5 (C)4 ( D)36.函数243,[0,3]y x x x =-+∈的值域为 ( )(A)[0,3] (B)[-1,0] (C)[-1,3] (D)[0,2]7.函数y=(2k+1)x+b 在(-∞,+∞)上是减函数,则 ( )8.若函数f(x)=2x +2(a-1)x+2在区间(,4]-∞内递减,那么实数a 的取值范围为( )(A)a≤-3 (B)a≥-3 (C)a≤5 (D)a≥39.函数2(232)xy a a a =-+是指数函数,则a 的取值范围是 ( )(A) 0,1a a >≠ (B) 1a = (C) 10.已知函数f(x)14x a -=+的图象恒过定点p ,则点p 的坐标是 ( )(A )( 1,5 ) (B )( 1, 4) (C )( 0,4) (D )( 4,0)11. ( )(A )[1,+∞] (B) (12.设全集=U {1,2,3,4,5,7},集合=A {1,3,5,7},集合=B {3,5},则( )(A )B A U = (B )B A C U U )(= (C ))(B C A U U = (D ))()(B C A C U U 二填空题13.满足条件{1,3}∪M ={1,3,5}的所有集合M 的个数是 .14.已知函数1()f x x x=-,若()f a b =,则()f a -= ; 15.若A={0,1,2,4,5,7,8},B={1,3,6,7,9},C={3,4,7,8},那么集合 (A ∩B )∪C=____________________.16. 已知=B A {}3, {9)()(<∈=x N x B C A C U U 且}3≠x ,(){}8,6,4=B A C U ,(){}5,1=B C A U ,则A = ,()=B A C U 。
高一数学基础训练题

高一数学基础训练题一、选择题:1.已知集合{}c b a A ,,=,集合{}1,0=B 。
映射)()()(:c f b f a f B A f =⋅→满足.那么这样的映射B A f →:有( )个. A 、0 B 、2 C 、3 D 、42.设的大小关系是、、,则,,c b a c b a 243.03.03log 4log -=== A.a <b <c B.a <c <b C.c <b <a D .b <a <c 3.指数函数y =f(x)的反函数的图象过点(2,-1),则此指数函数为A .x y )21(=B .x y 2=C .x y 3=D .x y 10=4.已知函数,,,且、、,00)(32213213>+>+∈--=x x x x R x x x x x x f 13x x +>0,则)()()(321x f x f x f ++的值A .一定大于零 B .一定小于零 C .等于零D .正负都有可能 5.若函数1log )(+=x x f a 在区间(-1,0)上有)(0)(x f x f ,则>的递增区间是A .(-∞,1)B .(1,+∞)C .(-∞,-1)D .(-1,+∞)6.已知b a b a 、,则2log 2log 0<<的关系是A .0<a <b <1B .0<b <a <1C .b >a >1D .a >b >17.若函数432--=x x y 的定义域为[0 , m],值域为]4,425[--,则m 的取值范围是( )A 、(0 , 4]B 、]4,23[C 、]3,23[D 、),23[+∞8.如果不等式x x m log 2-<0,在(0,21)内恒成立,那么实数m 的取值范围是( )A 、1161≠>m m 且 B 、1610<<m C 、410<<m D 、1161<≤m 9.已知函数f (x )是定义在R 上的奇函数,当x <0时,f (x )=(13)x ,那么f -1(-9)的值为A .2B .-2C .3D .-310.若x ≥0, y ≥0, 且x +2y =1, 则2x +3y 2的最小值为 ( )A. 2B. 43 C.32 D. 011.函数1log )(log 221212+-=x x y 的单调递增区间是( )(A)⎪⎪⎭⎫⎢⎣⎡+∞,284 (B)⎥⎦⎤ ⎝⎛41,0 (C)⎥⎦⎤ ⎝⎛22,0 (D) ⎥⎦⎤ ⎝⎛22,4112.若关于x 的方程043).4(9=+++x x a 有解,则实数a 的取值范围是( )A 、(-∞,-8)B 、(8,-∞-]C 、[),8+∞-D 、),(+∞-∞二、填空题:13.)2log (2)9(log )(91-==-f f x x f a ,则满足函数的值是__________________.14.使函数542+-=x x y 具有反函数的一个条件是____________________________.15.设函数)(x f y =的图象与x y 2=的图象关于直线0=-y x 对称,则函数)6(2x x f y -=的递增区间为 。
高一数学基础练习题

高一数学基础练习题一、选择题1.不等式|x -2|>0的解集是( ) A.{x|x ≠2}B.{x|x>2}C.RD.∅2.下列函数中是指数函数的是( ) A.12x y +=B.y =-2xC.y =(-2)xD.y =2x3.已知集合M ={x|x2+x +3=0},下列结论正确的是 ( ) A.集合M 中共有2个元素 B.集合M 中共有2个相同的元素 C.集合M 中共有1个元素 D.集合M 为空集4.若函数f (x )=(2a -1)x +b 是R 上的减函数,则a 的取值范围是 ( )A.{a|a>12}B.{a|a<12}C.{a|a≥12}D.{a|a ≤12}5.若二次函数的对称轴是直线x =1,且最大值为3,则此函数的一个解析式是 ( )A.y =(x -1)2-3B.y =(x +1)2+3C.y =(x +1)2-3D.y =-(x -1)2+3 6.下列等式成立的是 ( ) A.(-1)0=-1 B.(-1)-1=1C.3a -2=13a2D.(a 12-)2=1a7.若log264+log2x =5,则x 等于 ( )A.-2B.2C.-12D.128.已知f (2x )=x2-4x ,则f (2)等于 ( ) A.0 B.-1 C.-3 D.3 9.“a >b ”是“a -3>b -3”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件10.已知一次函数f (x )=kx +2的图象过点(2,0),则k 等于( ) A.0 B. 2 C.-2 D.±211.若tanα=-1,且角α为第二象限角,则sinα-cosα的值为( )A.-1B.0C.- 2D.212.已知单元素集合A ={x|x2-(a +2)x +1=0},则a 等于 ( ) A.0 B.-4 C.-4或1 D.-4或0 13.已知二次函数y=-2x2+6x -m 的值恒小于零,则( ) A.m=9B.92m =C.92m >D.92m <14.不等式x+6-x2≥0的解集是( ) A.[-6,1]B.[-2,3]C.[2,3]D.[-6,3]15.不等式x2+5x +25>0的解集是( ) A.RB.∅C.{x|x ≠-5}D.{x|x>-5}16.函数2(3)1y x =-+在区间(2,4)上是()A.递减函数B.递增函数C.先递减后递增D.先递增后递减17.函数223(50)y xx x =--+-≤≤的值域为( )A.(-∞,4]B.[3,12]C.[-12,4]D.[4,12]18.若关于x 的不等式kx2+kx -2>0的解集为空集,则实数k 的取值范围是 ( )A.[-8,0)B.[-8,0]C.(0,8]D.[0,8] 19.已知sinα=-513,且α为第四象限角,则α的正切值为 ( )A.125B.-125C.512D.-51220.已知sin α=22,α∈,22ππ⎛⎫- ⎪⎝⎭,则α=( ) A.4πB.34πC.-4πD.54π二、填空题21.已知cos α=12,α∈(0,π),则α= . 22.已知集合A ={x|x∈N ,126-x ∈N},用列举法表示集合A为 .23.已知函数f (x )=x2+mx -1,且f (-1)=-3,则f (x )在区间[2,3]上的最大值为 . 24.f (x11x ++(x +2)0的定义域为 .25.若函数f (x )=2x2+ax -1在区间(-∞,2]上是减函数,则实数a 的取值范围是 . 26.357log5log 7log 9••的值为.27.不等式211381x x -->的解集为 .28.设函数21,0()34,0ax x f x x x ->⎧=⎨+≤⎩若f (2)=3,则f (-2)= ,实数a 的值为 . 29.求值:22ln 203125e -++=.30.已知指数函数()xf x a =的图象经过点(-2,16),则log2a . 三、解答题(解答题应写出文字说明及演算步骤)31.设全集U ={7,3,a2-2a -3},A ={b ,7},∁UA ={5},求ab 的值. 32.已知一次函数f (x )=(m2-1)x +m2+3m +2在R 上是减函数,且f (1)=3,求m 的值.33.设α,β是方程lg2x -lgx2-2=0的两根,求log log αββα+的值. 34.已知角α的终边上一点P (x,y ),且x =-12,|OP|=13,求sin α,cos α,tan α的值.35.若不等式x2+ax +b >0的解集为(-∞,-2)∈(3,+∞),求不等式ax2-bx +7>0的解集.36.某汽车租赁公司拥有汽车100辆,当每辆车的租金为3000元时,可全部租出,当每辆车的租金增加50元时,未租出的车将会增加一辆,租出的车每月需养护费200元,未租出的车每月需养护费100元。
(完整版)高一数学必修一基础知识测试含答案

必修1 高一数学基础知识试题选说明:本试卷分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷60分,第Ⅱ卷60分,共120分,答题时间90分钟.第Ⅰ卷(选择题,共60分)一、选择题:(每小题5分,共60分,请将所选答案填在括号内)1.已知集合M ⊂≠{4,7,8},且M 中至多有一个偶数,则这样的集合共有 ( ) (A )3个 (B ) 4个 (C ) 5个 (D ) 6个2.已知S={x |x=2n ,n ∈Z}, T={x |x=4k ±1,k ∈Z},则 ( ) (A )S ⊂≠T (B ) T ⊂≠S (C )S ≠T (D)S=T3.已知集合P={}2|2,y y x x R =-+∈, Q={}|2,y y x x R =-+∈,那么P Q 等( )(A)(0,2),(1,1) (B ){(0,2 ),(1,1)} (C ){1,2} (D){}|2y y ≤4.不等式042<-+ax ax 的解集为R,则a 的取值范围是 ( ) (A)016<≤-a (B )16->a (C)016≤<-a (D)0<a5. 已知()f x =5(6)(4)(6)x x f x x -≥⎧⎨+<⎩,则(3)f 的值为 ( )(A)2 (B )5 (C)4 ( D )3 6。
函数243,[0,3]y x x x =-+∈的值域为 ( ) (A)[0,3] (B)[-1,0] (C )[-1,3] (D )[0,2] 7.函数y=(2k+1)x+b 在(—∞,+∞)上是减函数,则 ( )(A)k>12 (B )k 〈12 (C)k>12- (D).k 〈12-8.若函数f (x )=2x +2(a-1)x+2在区间(,4]-∞内递减,那么实数a 的取值范围为( )(A)a ≤—3 (B)a ≥-3 (C)a ≤5 (D )a ≥3 9.函数2(232)x y a a a =-+是指数函数,则a 的取值范围是 ( )(A ) 0,1a a >≠ (B) 1a = (C) 12a = ( D ) 121a a ==或10.已知函数f (x)14x a -=+的图象恒过定点p ,则点p 的坐标是 ( )(A )( 1,5 ) (B )( 1, 4) (C )( 0,4) (D )( 4,0)11。
专题1 集合中的含参问题-高一数学必修一专题复习训练含答案

专题1 集合中的含参问题-高一数学必修一专题复习训练含答案一、选择题 1.若集合,则实数的取值范围是 ( )A .B .C .D .【答案】D 【解析】2.已知集合{}0,5,10A =,集合{}22,1B a a =++,且{}5A B ⋂=,则满足条件的实数a 的个数有 ( )A . 0个B . 1 个C . 2 个D . 3 个【答案】B【解析】{}22,1B a a =++,且{}5A B ⋂=,则有25a +=或215a +=. 32a =,或-2. 当3a =时, {}5,10B =,此时{}510A B ⋂=,,不满足题意; 当2a =时, {}54B =,,满足题意;当2a =-时, {}0,5B =,此时{}50A B ⋂=,,不满足题意, 所以满足条件的实数a 只有1个. 故选B . 3.已知点)在平面直角坐标系的第二象限内,则的取值范围在数轴上可表示为(阴影部分)( )A .B .C .D .【答案】C 【解析】 因为在第二象限,所以, 所以,故选C.4.已知m ,,集合,集合,若,则A . 1B . 2C . 4D . 8 【答案】A 【解析】5.已知集合A ={x |x 2-2x -3≤0},B ={x |x <a },若A ⊆B ,则实数a 的取值范围是( )A . (-1,+∞)B . [-1,+∞)C . (3,+∞)D . [3,+∞)【答案】C【解析】[]13A =-,, (),B a =-∞;∵A B ⊆;∴3a >;∴a 的取值范围为3+∞(,),故选C . 点睛:研究一个集合,我们首先要看清楚它的研究对象,是实数还是点的坐标还是其它的一些元素,这是很关键的一步.第二步常常是解一元二次不等式,我们首先用十字相乘法分解因式,求得不等式的解集.在解分式不等式的过程中,要注意分母不能为零.解指数或对数不等式要注意底数对单调性的影响.元素与集合之间是属于和不属于的关系,集合与集合间有包含关系. 在求交集时注意区间端点的取舍,熟练画数轴来解交集、并集和补集的题目. 6.已知集合,,若,则实数的取值范围为( )A .B .C .D .【答案】C 【解析】7.已知集合A ={-1,0,a },B ={ x |0<x <1},若A ∩B ≠Ø,则实数a 的取值范围是A . {1}B . (0,1)C . (1,+∞)D . (-∞,0)【答案】B 【解析】1,0,B B -∉∉ 若A B φ⋂≠ ,则a B ∈ ,则01a << ,选B .8.已知集合2{|280}P x x x =--≤, {|}Q x x a =≥, ()C P Q ⋃=R R ,则a 的取值范围是A . ()2,∞-+B . ()4,∞+C . (],2∞--D . (],4∞-【答案】C【解析】因为{|24}P x x =-≤≤, {|}Q x x a =≥,则{|24}C P x x x =-R 或,又因为()C P Q ⋃=R R ,所以2a ≤- 本题选择C 选项. 9.集合,,若,则的取值范围是( )A .B .C .D .【答案】B 【解析】 根据题意,可得,,要使,则,故选B.二、填空题 10.已知集合,.若,则实数__________.【答案】0 【解析】11.设全集 ,,,则的值为____________.【答案】2或8 【解析】 由题意,可知,依据补集可得, 则有,即,解得或,即实数的值为或.12.集合{}{}1,|A x x B x x a ==<,若R A C B ⊆,则实数a 的取值范围_________ 【答案】1a ≤【解析】∵集合{}{}1,|,{|},1R R A x x B x x a C B x x a A C B a ==<∴=⊆∴,,厔∴实数a 的取值范围是 1.a ≤ 13.已知,若,则的取值范围是___________.【答案】【解析】14.已知集合,且有4个子集,则实数的取值范围是________.【答案】【解析】由题意得.所以.因为A∩B有4个子集,所以A∩B中有2个不同的元素,所以,所以,解得且.故实数a的取值范围是.故答案为.三、解答题15.已知,若,求实数的取值范围.【答案】【解析】①当时,即,有;②当,则,解得: ;综合①②,得的取值范围为.16.设全集,集合,集合,且,求的取值范围. 【答案】【解析】17.已知集合{}121A x a x a =-<<+, {}01B x x =<< (1)若12a =,求A B ⋂; (2)若A B ⋂=∅,求实数a 的取值范围. 【答案】(1){}01x x <<;(2)12a ≤-或2a ≥. 【解析】试题分析:(1)把a 的值代入A 求出解集,找出A 与B 的交集,求出A 与B 补集的并集即可; (2)根据A 与B 的交集为空集,确定出a 的范围即可. 试题解析: (1)当12a ={}12,012A x x B x x ⎧⎫=-<<=<<⎨⎬⎩⎭,∴A B ⋂= {}12012x x x x ⎧⎫-<<⋂<<⎨⎬⎩⎭{}01x x =<<(2)因为A B ⋂=∅,当A =∅时,则121a a ->+,即2a <- 当A ≠∅时,则11a -≥或210a +≤,解得: 12a ≤-或2a ≥. 综上: 12a ≤-或2a ≥. 18.设全集为R ,,,(1)求及(2)若集合,,求的取值范围. 【答案】(1);(2).【解析】19.已知的定义域为集合A,集合B=(1)求集合A;(2)若A B,求实数的取值范围.【答案】(1)(2)【解析】解:(1)由已知得即∴(2)∵∴解得∴20.已知集合A={x|x<-3或x≥2},B={x|x≤a-3}.(1)当a=2时,求(∁R A)∩B;(2)若A∩B=B,求实数a的取值范围.【答案】(1){}|31x x -≤≤-;(2)0a <.21.已知集合{}2|2940 A x x x =-+>,集合{}2|2, R B y y x x x C A ==-+∈,集合{}|12 1 C x m x m =+<≤-.(1)求集合B ;(2)若A C A ⋃=,求实数m 的取值范围. 【答案】(1)[]8,1-;(2)2m ≤或3m ≥.【解析】试题分析:(1)解出一元二次不等式得到集合A ,故而可求出R C A ,对一元二次函数通过配方法求出其在给定区间内的范围即可;(2)A C A ⋃=等价于C A ⊆,分为C =∅和C ≠∅两种情形,借助于数轴可得m 的取值范围.试题解析:(1)22940x x -+> , 12x ∴<或4x >,∴()1,4,2A ⎛⎫=-∞⋃+∞ ⎪⎝⎭, 1,42R A ⎡⎤=⎢⎥⎣⎦ð. 于是, ()221211,,42y x x x x ⎡⎤=-+=--+∈⎢⎥⎣⎦,解得[]8,1y ∈-, []8,1B ∴=-. (2)∵A C A ⋃=,∴C A ⊆. 若C =∅,则211m m -≤+,即2m ≤, 若C ≠∅,则2{1212m m >-<或2{14m m >+≥,解得3m ≥,综上,实数m 的取值范围是2m ≤或3m ≥.22.设集合()()222{|320},{|2150}A x x x B x x a x a =-+==+-+-=(1)若{}2A B ⋂=,求实数a 的值(2)若A B A ⋃=,求实数a 的取值范围 【答案】(1)5,1a a =-=.综上所述: 5,1a a =-=23.已知集合A ={x |x <-2或3<x ≤4},B ={x |x 2-2x -15≤0}. (1) 求A ∩B ;(2) 若C ={x |x ≥a },且B ∩C =B ,求实数a 的取值范围. 【答案】(1) A ∩B ={x |-3≤x <-2或3<x ≤4}.(2) a ≤-3.【解析】试题分析 :(1)对于集合的交并补运算,我们常画数轴来解决.(2)由B ∩C =B 得B C ⊆,也可以画数轴解决.试题解析:(1) B ={x |-3≤x ≤5},A ∩B ={x |-3≤x <-2或3<x ≤4}. (2) ∵ B ∩C =B ,∴ B ⊆C ,∴ a ≤-3. 24. 已知集合.(1)若,求实数的值; (2)若,求实数的取值范围.【答案】(1)2;(2).【解析】25.已知集合{}2|3 2 0A x R x x =∈-+=, {}|1 1 2B x Z x =∈-≤-≤, {}21,1,1C a a =++,其中a R ∈.(1)求A B ⋂, A B ⋃; (2)若A B A C ⋂=⋂,求C .【答案】(1) A ⋂ B ={1,2}, A ⋃ B ={0,1,2,3};(2) C ={0,1,2}.。
人教版高一数学上册基础训练试题(共3份)

第 1 页 共 5 页人教版高一数学上册基础训练题一选择题:1.把aa 1-化简为( ) a D a C a B aA ----....2.已知2222=+-x x,且1>x ,则=--22x x ( )A.2或-2B.-2C.6D.2 3.R b a ∈.,下列各式中总能成立的是( )2244222)(.)(b a b a B b a b a A +=+-=- b a b a D ba b a C -=--=-663344)(..4.若a a a 2114442-=+-则实数a 的取值范围是( )R D a C a B a A .21.21.21.≥=≤5.43)2(--x 有意义的x 的取值班范围是( ){}R D x x C B A .2.),2()2,.()2,2.(±≠+∞--∞- 6.下列4个命题中,真命题是( )12.+=x y A 和22x y =都是指数函数。
B.指数函数)1,0(≠>=a a a y x的最小值为0。
. C.对任意的R x ∈都有xx23>。
D.函数xa y =与)1,0()1(≠>=a a ay x的图象关于y 轴对称。
7.函数271312-=-x y 的定义域是( ) [)(]()2,.1,.,1.),2.(-∞--∞-+∞-+∞-D C B A8.若函数x y 2=的定义域是{}3,2,1,则其值域是( ){}{}{}[]8,2.8,4,2.8,2.3,1.D C B A9.若集合{}{}1,01),(,),(≠>+====a a a y y x Q k y y x P x,且Q P 只有一个子集,则有( )R k D k C k B k A ∈>≤<.1.1.1.10.函数)1,0(≠>=a a a y x 在区间[]1,0上的最大值与最小值之和为3,则=a ( )41.4.2.21.D c B A 11.有以下四个结论:)3(;0)lg(ln )2(;0)10lg(lg )1(==e 若x lg 10=,则10=x ;(4)若,ln x e =则2e x =。
高一数学必考知识点基础题库练习

高一数学必考知识点基础题库练习一、整式的定义和运算整式:只包含加法、减法和乘法运算,并且没有除法运算和无理式的代数式称为整式。
1. 计算以下整式的值:(1) 3x - 2y,当x = 4,y = 5时的值;(2) 2a^2b - 3ab^2 + 4a^2b,当a = 2,b = -3时的值。
二、二次根式二次根式:含有平方根的代数式称为二次根式。
1. 化简以下二次根式:(1) √(12);(2) √(18x^2y^4)。
三、整式的乘除法1. 计算以下整式的乘积:(1) (2x + 3)(x - 4);(2) (3a^2b - 5ab^2)(a - 2b)。
2. 计算以下整式的商:(1) (6x^3 - 9x^2 + 12x) ÷ 3x;(2) (9y^4 - 12y^3 + 15y^2) ÷ 3y^2。
四、一次函数一次函数:形如y = kx + b(k和b为常数,k ≠ 0)的函数称为一次函数。
1. 已知一次函数f(x) = 2x + 3,求:(1) f(-2)的值;(2) 使得f(x) = 0的x值;(3) 函数f(x)在x = 4处的函数值。
五、二次函数二次函数:形如f(x) = ax^2 + bx + c(a、b、c为常数,a ≠ 0)的函数称为二次函数。
1. 对于二次函数f(x) = 2x^2 - 5x + 3,求:(1) 函数f(x)的对称轴;(2) 函数f(x)的顶点;(3) 函数f(x)的零点或根。
2. 判断以下二次函数的开口方向,并指出其顶点所在的坐标:(1) y = -3x^2 + 4x - 1;(2) y = 2x^2 - 5x + 2。
六、立体几何1. 计算以下几何体的表面积:(1) 半径为5cm的球的表面积;(2) 边长为3cm的正方体的表面积;(3) 高为8cm,底边长为6cm的四棱锥的表面积。
2. 计算以下几何体的体积:(1) 半径为4cm的球的体积;(2) 边长为5cm的立方体的体积;(3) 高为10cm,底面积为20cm²的三棱柱的体积。
通用版高一数学集合基础知识题库

(每日一练)通用版高一数学集合基础知识题库单选题1、设集合A ={x|3x −1<m },若1∈A 且2∉A ,则实数m 的取值范围是( )A .2<m <5B .2≤m <5C .2<m ≤5D .2≤m ≤5答案:C解析:直接根据元素和集合之间的关系,列式求解即可.因为集合A ={x|3x −1<m},而1∈A 且2∉A ,∴3×1−1<m 且3×2−1≥m ,解得2<m ≤5.故选:C .小提示:本题主要考查元素与集合的关系,对描述法表示集合的理解,属于基础题.2、已知集合A ={(x,y )∣2x −y +1=0},B ={(x,y )∣x +ay =0},若A ∩B =∅,则实数a =()A .−12B .2C .−2D .12答案:A解析:根据集合的定义知{2x −y +1=0x +ay =0 无实数解.由此可得a 的值.因为A ∩B =∅,所以方程组{2x −y +1=0x +ay =0无实数解.所以12=a −1≠0,a =−12. 故选:A .3、已知集合M ={x |x =2k +1,k ∈Z },集合N ={y |y =4k +3,k ∈Z },则M ∪N =( )A .{x |x =6k +2,k ∈Z }B .{x |x =4k +2,k ∈Z }C .{x |x =2k +1,k ∈Z }D .∅答案:C解析:通过对集合N 的化简即可判定出集合关系,得到结果.因为集合M ={x|x =2k +1,k ∈Z},集合N ={y|y =4k +3,k ∈Z}={y|y =2(2k +1)+1,k ∈Z},因为x ∈N 时,x ∈M 成立,所以M ∪N ={x|x =2k +1,k ∈Z}.故选:C.解答题4、设全集是R ,集合A ={x |-x 2+2x <-3},B ={x |a <x <a +3}.(1)若a =1,求(∁R A )∩B ;(2)问题:已知_____,求实数a 的取值范围.从下面给出的三个条件中任选一个,补充在上面的问题中,并进行解答.①A ∩B =B ;②A ∪B =A ;③A ∩B =∅.答案:(1)(∁R A)∩B=(1,3];(2)答案见解析.解析:(1)把a=1代入后,结合集合的补集与交集运算即可求解;(2)根据所选条件,结合集合的交并运算与集合的包含关系的相互转化可求.(1)a=1时,A={x|-x2+2x<-3}={x|x>3或x<-1},B={x|a<x<a+3}={x|1<x<4},所以∁R A=[-1,3],(∁R A)∩B=(1,3];(2)若选①A∩B=B,则B⊆A,所以a+3≤-1或a≥3,所以a≤-4或a≥3,所以a的范围为{a|a≤-4或a≥3},若选②A∪B=A,则B⊆A,所以a+3≤-1或a≥3,所以a≤-4或a≥3,所以a的范围为{a|a≤-4或a≥3},若选③A∩B=∅,则{a≥−1a+3≤3,即-1≤a≤0,所以a的范围为[-1,0].5、已知集合A={x|2<x<4},B={x|a<x<3a}且B≠∅.(1)若x∈A是x∈B的充分条件,求a的取值范围;(2)若A ∩B =∅,求a 的取值范围.答案:(1)43≤a ≤2.(2)0<a ≤23或a ≥4. 解析:(1)根据条件可知,A ⊆B ,列不等式求参数a 的取值范围;(2)根据A ∩B =ϕ,且B ≠ϕ,可知a ≥4或{a >03a ≤2,求a 的取值范围. 解:(1)∵x ∈A 是x ∈B 的充分条件,∴A ⊆B .,∴{a ≤23a ≥4解得a 的取值范围为43≤a ≤2.(2)由B ={x |a <x <3a }且B ≠∅,∴a >0.若A ∩B =∅,∴a ≥4或{a >03a ≤2 ,所以a 的取值范围为0<a ≤23或a ≥4. 小提示:本题考查根据集合的关系求参数取值范围的问题,属于简单题型,一般涉及子集问题时,需考虑集合是空集或非空集两种情况,分析问题时还需借助数轴分析问题.。
高一数学专题
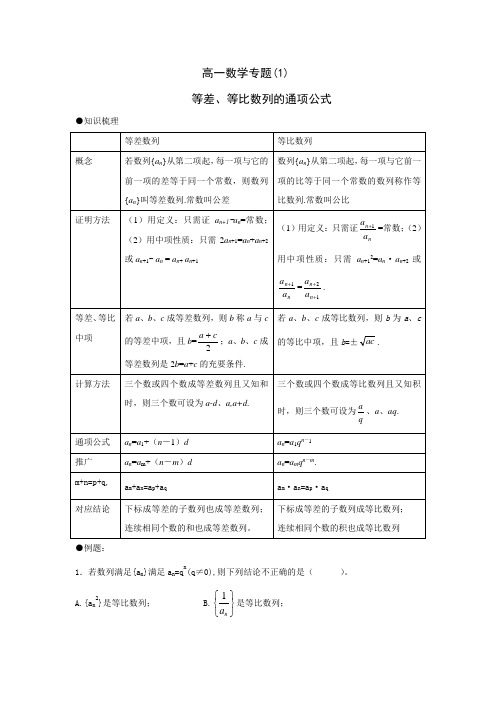
高一数学专题(1)等差、等比数列的通项公式●知识梳理●例题:1.若数列满足{a n }满足a n =q n(q ≠0),则下列结论不正确的是( )。
A.{a n 2}是等比数列; B.1n a ⎧⎫⎨⎬⎩⎭是等比数列;C .{lga n }是等差数列; D.{lg|a n |}是等差数列。
2.若三角形的三边成等比数列,则它的公比r 的取值范围为( )。
.0.A r B r C r <<<<> D.以上都不对。
3.“公差为0的等差数列是等比数列”;“公比为12的等比数列一定是递减数列”;“a,b,c 三数成等比数列的充要条件是b 2=ac ”;“a,b,c 三数成等差数列的充要条件是2b=a+c ”;以上四个命题中,正确的有( )。
A .1个; 个; 个; 个。
4.等比数列{a n }中各项为正数,公比q ≠1,则下列数列中为等比数列的是( )。
,2a 2,3a 3,…,na n ,…; B.312,,,,,n aa aae e e e+a 2,a 2+a 3,a 3+a 4,…,a n +a n+1,…; ,lga 2,…,lga n ,…5.在等比数列{a n }中,a 1+a 2+a 3=-3,a 1a 2a 3=8,则a n = .6.在△ABC 中,A 、B 、C 成等差数列,则tantan tan 2222A C A C+= ; 7.有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.8.某工厂三年的生产计划中,从第二年起每一年比上一年增长的产值都相同,三年的总产值为300万元,如果第一年、第二年、第三年分别比原计划产值多10万元、10万元、11万元,那么每一年比上一年的产值增长的百分数都相同,求原计划中每年的产值。
9.一个等差数列首项a 1=1,末项a n =100(n ≥3),若公差为自然数,那么项数n 的取值有 ( )。
