2020中考数学复习微专题：最值(“胡不归”问题)

合集下载

最值问题——胡不归

• ∵a,b是定值 ,所求问题即转化为求 b AD BD 的最值.
a

• 在图中构造出长度 b AD 的替换线段：在直线AC下方作一条射线AM,使得sin∠MAC=
a
DE⊥AM,则 DE =sin∠MAC= b
AD
a
b ,过点D作
a
• ∴DE= b AD，因为垂线段最短,即过点B做AM的垂线,与AC交点D1即为折往点
• 如图,A是出发点,B是目的地,直线AC是一条驿道,而驿道靠目的地一侧全是砂石,为了选择合适的路线,根据不同路面速度不同(驿道速度为a米/秒,砂士速度为b米/秒),小伙子需要在AC上选取一点D,再折往至B
• 他需要的时间是: t= AD BD
ab
• 式子变形得 : 1 b AD BD
ba
“化折为直”, 将三条线段和转化为PA+kPB型最值问题
步骤: ① 求角：sinα=m（注意有无特殊角） ② 找定点 ③ 画角：过定点作一个角,使其等于α (在另一固定点异侧同向） ④ 过动点做垂直，边长转化 ⑤ 垂线段最短
过关检测
学习要有三心，一信心，二决心，三恒心
19湖南长沙
最值问题求解
胡不归
胡不归模型的由来
从前有一个身在他乡的小伙子,得知老父亲病危的消息,便立即赶路回家.小伙子考虑到“两点之间线段最短”的数学知识,就选择走布满沙石的直线路径。当赶到家时,老人刚咽了气.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?”
这个故事引起了人们的思索：小伙子能否提前到家？由于在驿道行走比在砂砾地行走的速度快，有没有可能先在驿道上走一段再走砂砾地，虽然走的多了，反而用时更短呢？如果有，如何找到这个点呢？

胡不归问题解题方法和口诀

胡不归问题解题方法和口诀
胡不归问题是一种常见的计数问题，通常涉及到等差数列和等比数列的求和问题。

下面是胡不归问题的解题方法和口诀。

解题方法:
1. 对于等差数列的胡不归问题，可以通过求和公式求解。

设第 n 个数为 a_n，公差为 d，则前 n-1 个数的和为:
S(n-1) = n*(a_1 + a_2 + ... + a_n) = n*(a_1 + a_2 + ... + a_{n-1}) - n*a_n
当 n 趋近于无穷大时，S(n-1) 趋近于正无穷大，因此胡不归的时间点一定是在等差数列的最后一个数 a_n 取最大值或最小值的时候。

2. 对于等比数列的胡不归问题，可以通过乘法公式求解。

设第 n 个数为 a_n，公比为 q，则前 n-1 个数的和为:
S(n-1) = (a_1 + a_2 + ... + a_n)/n = a_1 + a_2 + ... + a_{n-1} + n*q^(n-1) - n*q^n
当 n 趋近于无穷大时，S(n-1) 趋近于正无穷大，因此胡不归的时间点一定是在等比数列的最后一个数 a_n 取最大值或最小值的时候。

口诀:
1. 胡不归问题，数列求解;等差数列求和，等比数列乘积;
2. 首项加末项，求和公式运用;数列趋近于正无穷大，胡不归时间确定;
3. 掌握等差数列和等比数列的特点，运用极限思想求解。

拓展:
胡不归问题不仅可以应用于计数问题，还可以应用于其他数学领域。

例如，在概率论中，胡不归问题可以应用于判断一个事件是否会发生;在组合数学中，胡不归问题可以应用于求解组合数的总和。

最值模型之胡不归(学生版)-中考数学专题解析

最值模型之胡不归“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。

1.当k值为1时，即可转化为“PA+PB”之和最短问题，就可用我们常见的“饮马问题”模型来处理，即可以转化为轴对称问题来处理(见专题08);2.当k取任意不为1的正数时，若再以常规的轴对称思想来解决问题，则无法进行，因此必须转换思路。

此类问题的处理通常以动点P所在图像的不同来分类，一般分为2类研究。

即点P在直线上运动和点P 在圆上运动。

(1)其中点P在直线上运动的类型称之为“胡不归”问题；(2)点P在圆周上运动的类型称之为“阿氏圆”问题(见专题11)。

胡不归：【模型建立】如图1：P是直线BC上的一动点，求PA+k·PB的最小值。

【作法】1.作∠CBE=α，使sinα=k,则PD=k·OP(图2)2.当AD最短，AD⊥BE时，则P为要求点。

(图3)AD长即为PA+k·PB的最小值.简记:胡不归,正弦作个角,作高求长即可.特别提醒：当k>1时，kAP+BP=k AP+1k BP按常规模型算即可1∠AOB=30°，OM=2，D为OB上动点，求MD+12OD的最小值．2(1)【问题探究】如图1，点E是等边△ABC高AD上的一定点，请在AB上找一点F，使EF=12AE，并说明理由；(2)【问题解决】如图2，在△ACD中，CO⊥AD，垂足为O，若AD=32，AC=2，OC=3，点P在OC上，求DP+12PC的最小值．(3)【问题拓展】如图3，△ABC中，AB=AC=10，tan∠A=2，BE⊥AC于点E，D是线段BE上的一个动点，求CD+ 55BD的最小值．1.实战训练1一．选择题(共8小题)1如图，在△ABC 中，P 为平面内的一点，连接AP 、PB 、PC ，若∠ACB =30°，AC =8，BC =10，则4PA +2PB +23PC 的最小值是()A.489B.36C.410+25+67D.1610-102如图，△ABC 为等边三角形，BD 平分∠ABC ，AB =2，点E 为BD 上动点，连接AE ，则AE +12BE 的最小值为()A.1B.2C.3D.23如图，在平面直角坐标系中，抛物线y =-49x 2+83x 与x 轴的正半轴交于点A ，B 点为抛物线的顶点，C 点为该抛物线对称轴上一点，则3BC +5AC 的最小值为()A.24B.25C.30D.364如图，在等边△ABC 中，AB =6，点E 为AC 中点，D 是BE 上的一个动点，则CD +12BD 的最小值是()A.3B.33C.6D.3+35如图，在菱形ABCD中，AB=AC=6，对角线AC、BD相交于点O，点M在线段AC上，且AM= 2，点P是线段BD上的一个动点，则MP+12PB的最小值是()A.2B.23C.4D.436如图，在Rt△ABC中，∠ACB=90°，∠A=30°，则AB=2BC．请在这一结论的基础上继续思考：若AC=2，点D是AB的中点，P为边CD上一动点，则AP+12CP的最小值为()A.1B.2C.3D.27如图，△ABC中，AB=AC=10，tan A=2，BE⊥AC于点E，D是线段BE上的一个动点，则CD +55BD的最小值是()A.25B.45C.53D.108如图，在菱形ABCD中，∠ABC=60°，E是边BC的中点，P是对角线BD上的一个动点，连接AE，AP，若AP+12BP的最小值恰好等于图中某条线段的长，则这条线段是()A.ABB.AEC.BDD.BE2二．填空题(共9小题)1如图，AC垂直平分线段BD，相交于点O，且OB=OC，∠BAD=120°．(1)∠ABC=．(2)E为BD边上的一个动点，BC=6，当AE+12BE最小时BE=2　．2如图，在△ABC中，∠A=90°，∠C=30°，AB=2，若D是BC边上的动点，则2AD+DC的最小值为．3如图，在平面直角坐标系中，直线y=-x+4的图象分别与y轴和x轴交于点A和点B．若定点P的坐标为(0，63)，点Q是y轴上任意一点，则12PQ+QB的最小值为3　．4如图，直线y=x-3分别交x轴、y轴于B、A两点，点C(0，1)在y轴上，点P在x轴上运动，则2PC+PB的最小值为．5如图，抛物线y=x2-2x-3与x轴交于A、B两点，过B的直线交抛物线于E，且tan∠EBA=4 3，有一只蚂蚁从A出发，先以1单位/s的速度爬到线段BE上的点D处，再以1.25单位/s的速度沿着DE爬到E点处觅食，则蚂蚁从A到E的最短时间是　649　s．6如图，在平面直角坐标系中，二次函数y=x2-2x+c的图象与x轴交于A、C两点，与y轴交于点B (0，-3)，若P是x轴上一动点，点D(0，1)在y轴上，连接PD，则C点的坐标是，2PD+PC的最小值是．7如图，四边形ABCD是菱形，AB=4，且∠BAD=30°，P为对角线AC(不含A点)上任意一点，则DP+12AP的最小值为．8如图，四边形ABCD中，AB=62，∠ABC=45°，E是BD上一点，若∠ABD=15°，则AE+12BE的最小值为．9如图，矩形OABC中，点A、C分别在x轴，y轴的正半轴上，且OA=3，AB=1，点P为线段OA上一动点，则12OP+PB最小值为．3三．解答题(共5小题)1如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过点A(-1，0)，B(0，-3)，C(2，0)，其对称轴与x轴交于点D．(1)求二次函数的表达式及其顶点坐标；(2)点M为抛物线的对称轴上的一个动点，若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，求点M的坐标；(3)若P为y轴上的一个动点，连接PD，求12PB+PD的最小值．2如图抛物线y=ax2+bx-4与x轴交于A(-1，0)，B(4，0)两点，与y轴交于点C．(1)求抛物线解析式．(2)连接BC，点P为BC下方上一动点，连接BP，CP．当△PBC的面积最大时，求点P的坐标和△PBC 面积的最大值．(3)点N为线段OC上一点，连接AN，求AN+12CN的最小值．3如图，在平面直角坐标系xOy中，已知抛物线y=x2+bx+c与x轴交于点A、B两点，其中A(1，0)，与y轴交于点C(0，3)．(1)求抛物线解析式；(2)如图1，过点B作x轴垂线，在该垂线上取点P，使得△PBC与△ABC相似，请求出点P坐标；(3)如图2，在线段OB上取一点M，连接CM，请求出CM+12BM的最小值．4(1)【问题探究】如图1，点E是等边△ABC高AD上的一定点，请在AB上找一点F，使EF=12AE，并说明理由；(2)【问题解决】如图2，在△ACD中，CO⊥AD，垂足为O，若AD=32，AC=2，OC=3，点P在OC上，求DP+12PC的最小值．(3)【问题拓展】如图3，△ABC中，AB=AC=10，tan∠A=2，BE⊥AC于点E，D是线段BE上的一个动点，求CD+ 55BD的最小值．。

2020年九年级数学中考复习专题：胡不归和阿氏圆问题教案设计(无答案)

2020年中考复习专题：“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如PA+PB最值，除此之外我们还可能会遇上形如“PA+kPB”这样的式子的最值，此类式子一般可以分为两类问题：(1)胡不归问题；(2)阿氏圆.本文简单介绍“胡不归”模型【故事介绍】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家，根据“两点之间线段最短”，虽然从他此刻位置A到家B之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭.邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归?胡不归?”(“胡”同“何”)而如果先沿着驿道AC先走一段，再走砂石地，会不会更早到家?【模型建立】如图，一动点P在直线MN外的运动速度为V1，在直线MN上运动的速度为V2，且V1＜V2，A、B为定点，点C在直线MN上，确定点C的位置使ACV2+BCV1的值最小【问题分析】AC V2+BCV1=1V1(BC+V1V2AC)，记k=V1V2，即求BC+kAC的最小值【问题解决】构造射线AD使得sin∠DAN＝k，CHAC=k，CH＝kAC.将问题转化为求BC+CH最小值，过B点作BH⊥AD交MN于点C，交AD于H点，此时BC+CH 取到最小值，即BC+kAC最小.【模型总结】在求形如“PA+kPB＂的式子的最值问题中，关键是构造与kPB相等的线段，将“PH+kPB”型问题转化为“PA+PC”型.而这里的PB必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB的等线段.【2019长沙中考】如图，△ABC中，AB＝AC＝10，tanA=2，BE⊥AC于点E，D是线段BEBD的最小值是上的一个动点，则CD+√55【2019南通中考】如图，平行四边形ABCD中，∠DAB=60°，AB＝6，BC=2，P为边CD上PD的最小值等于的一动点，则PB+√32【2014成都中考】如图，已知抛物线y＝k8(x+2)(x-4)(k为常数，且k>0)与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y＝−√33x+b与抛物线的另一交点为D.(1)若点D的横坐标为-5，求抛物线的函数表达式(2)在(1)的条件下，设F为线段BD上一点(不含端点)，连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F的坐标是多少时，点M在整个运动过程中用时最少?【2018重庆中考】抛物线y=−√66x2−2√33x+√6与x轴交于点A，B(点A在点B的左边)，与y轴交于点C.点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E;将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+12EC的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标。

2020年中考数学三轮复习专项冲刺：胡不归练习

胡不归最值练习1. 如图，在平面直角坐标系中，点()3,3A ，点P 为x 轴上的一个动点，当OP AP 21+最小时，点P 的坐标为___________.2. 如图，四边形ABCD 是菱形，AB=4，且∠ABC=60°，点M 为对角线BD （不含点B ）上的一动点，则BM AM 21+的最小值为___________.3. 如图，在平面直角坐标系中，二次函数y ＝ax 2+bx +c 的图象经过点A （﹣1，0），B （0，﹣），C（2，0），其对称轴与x 轴交于点D ．（1）求二次函数的表达式及其顶点坐标；（2）点M 为抛物线的对称轴上的一个动点，若平面内存在点N ，使得以A ，B ，M ，N 为顶点的四边形为菱形，求点M 的坐标；（3）若P 为y 轴上的一个动点，连接PD ，求PB +PD 的最小值．4. 【问题提出】如图∠，已知海岛A 到海岸公路BD 距离为AB 的长度，C 为公路BD 上的酒店，从海岛A 到酒店C ，先乘船到登陆点D ，船速为a ，再乘汽车，车速为船速的n 倍，点D 选在何处时，所用时间最短？【特例分析】若n ＝2，则时间t ＝+，当a 为定值时，问题转化为：在BC 上确定一点D ，使得+的值最小．如图∠，过点C做射线CM，使得∠BCM＝30°．（1）过点D作DE∠CM，垂足为E，试说明：DE＝；（2）请在图∠中画出所用时间最短的登陆点D′．【问题解决】（3）请你仿照“特例分析”中的相关步骤，解决图∠中的问题．（写出具体方案，如相关图形呈现、图形中角所满足的条件、作图的方法等）【综合运用】（4）如图∠，抛物线y＝﹣x2+x+3与x轴分别交于A，B两点，与y轴交于点C，E 为OB中点，设F为线段BC上一点（不含端点），连接EF．一动点P从E出发，沿线段EF以每秒1个单位的速度运动到F，再沿着线段FC以每秒个单位的速度运动到C后停止．若点P在整个运动过程中用时最少，请求出最少时间和此时点F的坐标．5. 如图，∠ABC是等边三角形．（1）如图1，AH∠BC于H，点P从A点出发，沿高线AH向下移动，以CP为边在CP的下方作等边三角形CPQ，连接BQ．求∠CBQ的度数；（2）如图2，若点D为∠ABC内任意一点，连接DA，DB，DC．证明：以DA，DB，DC为边一定能组成一个三角形；（3）在（1）的条件下，在P点的移动过程中，设x＝AP+2PC，点Q的运动路径长度为y，当x取最小值时，写出x，y的关系，并说明理由．6. 如图，已知抛物线y＝（x+2）（x﹣4）（k为常数，且k＞0）与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y＝﹣x+b与抛物线的另一交点为D．（1）若点D的横坐标为﹣5，求抛物线的函数表达式；（2）若在第一象限内的抛物线上有点P，使得以A，B，P为顶点的三角形与∠ABC相似，求k的值；（3）在（1）的条件下，设F为线段BD上一点（不含端点），连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F的坐标是多少时，点M在整个运动过程中用时最少？7. 已如二次函数y＝﹣x2+2x+3的图象和x轴交于点A、B（点A在点B的左侧），与y轴交于点C，（1）如图1，P是直线BC上方抛物线上一动点（不与B、C重合）过P作PQ∠x轴交直线BC于Q，求线段PQ的最大值；（2）如图2，点G为线段OC上一动点，求BG+CG的最小值及此时点G的坐标；（3）如图3，在（2）的条件下，M为直线BG上一动点，N为x轴上一动点，连接AM，MN，求AM+MN 的最小值．8. 如图，在Rt∠ABC 中，∠ACB ＝90°，∠B ＝30°，AB ＝4，点D 、F 分别是边AB ，BC 上的动点，连接CD ，过点A 作AE ∠CD 交BC 于点E ，垂足为G ，连接GF ，则GF +FB 的最小值是（）A ．B ．C ．D ．9.抛物线2y =-+x 轴交于点A ，B （点A 在点B 的左边），与y 轴交于点C ．点P 是直线AC 上方抛物线上一点，PF ∠x 轴于点F ，PF 与线段AC 交于点E ；将线段OB 沿x 轴左右平移，线段OB 的对应线段是O 1B 1，当12PE EC +的值最大时，求四边形PO 1B 1C 周长的最小值，并求出对应的点O 1的坐标．。

中考数学最值—胡不归问题(解析+例题)

中考数学最值——胡不归问题（点在直线上运动）（PA+k·PB型最值）【历史典故】从前，有一个小伙子在外地学徒，当他获悉在家的老父亲病危的消息后，便立即启程赶路。

由于思乡心切，他只考虑了两点之间线段最短的原理，所以选择了全是沙砾地带的直线路径A→B（如图所示），而忽视了走折线虽然路程多但速度快的实际情况，当他气喘吁吁地赶到家时，老人刚刚咽了气，小伙子失声痛哭。

邻居劝慰小伙子时告诉说，老人弥留之际不断念叨着“胡不归？胡不归？…”。

这个古老的传说，引起了人们的思索，小伙子能否提前到家？倘若可以，他应该选择一条怎样的路线呢？这就是风靡千百年的“胡不归问题”。

【知识储备】①三角形三边关系：两边之和大于第三边；两边之差小于第三边。

②两点之间线段最短。

③连接直线外一点和直线上各点的所有线段中，垂线段最短。

【模型分析】①条件：已知A、B为定点，P为射线AC上一动点。

②问题：P在何处时，BP+nm AP最短（nm＜1）。

③方法：第一步在AC的一侧，PB的异侧构造∠CAE=α，使得sinα=nm 第二步做BH⊥AE，交AC于P，点P就是所求位置，BH就是其最小值。

【模型分析】【问题提出】如图①，已知海岛A到海岸公路BD的距离为AB的长度，C为公路BD上的酒店，从海岛A到酒店C，先乘船到登陆点D，船速为a，再乘汽车，车速为船速的n倍，点D 选在何处时，所用时间最短?个运动过程中用时最少，请求出最少时间和此时点F的坐标。

【巩固训练】练习1：如图，四边形ABCD是菱形，AB=4，且∠ABC=60°，M为对角线BD（不含B点）上BM的最小值为_____。

任意一点，则AM＋12练习2：如图，等腰ΔABC中，AB=AC=3，BC=2，BC边上的高为A0，点D为射线A0上一点，一动点P从点A出发，沿AD-DC运动，动点P在AD上运动速度3个单位每秒，动点P在CD上运动的速度为1个单位每秒，则当 AD= 时，运动时间最短为秒。

中考数学常见几何模型最值模型-胡不归问题

专题10 最值模型---胡不归问题最值问题在中考数学常以压轴题的形式考查，可将胡不归问题看作将军饮马衍生，主要考查转化与化归等的数学思想。

在各类考试中都以高档题为主，中考说明中曾多处涉及。

本专题就最值模型中的胡不归问题进行梳理及对应试题分析，方便掌握。

在解决胡不归问题主要依据是：①两点之间，线段最短；②垂线段最短。

【模型背景】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据“两点之间线段最短”，虽然从他此刻位置A 到家B 之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？看到这里很多人都会有一个疑问，少年究竟能不能提前到家呢？假设可以提早到家，那么他该选择怎样的一条路线呢？这就是今天要讲的“胡不归”问题.【模型解读】一动点P 在直线MN 外的运动速度为V 1，在直线MN 上运动的速度为V 2，且V 1<V 2，A 、B 为定点，点C 在直线MN 上，确定点C 的位置使21AC BC V V 的值最小．（注意与阿氏圆模型的区分）V 1V 2V 1驿道砂石地AB C V 2V 1M N CBA1）121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭，记12V k V =，即求BC +kAC 的最小值. 2）构造射线AD 使得sin ∠DAN =k ，CH k AC=，CH =kAC ,将问题转化为求BC +CH 最小值. 3）过B 点作BH ⊥AD 交MN 于点C ，交AD 于H 点，此时BC +CH 取到最小值，即BC +kAC 最小．【解题关键】在求形如“P A +kPB ”的式子的最值问题中，关键是构造与kPB 相等的线段，将“P A +kPB ”型问题转化为“P A +PC ”型．（若k >1，则提取系数，转化为小于1的形式解决即可）。

几何最值之胡不归知识精讲-冲刺2020年中考几何专项复习

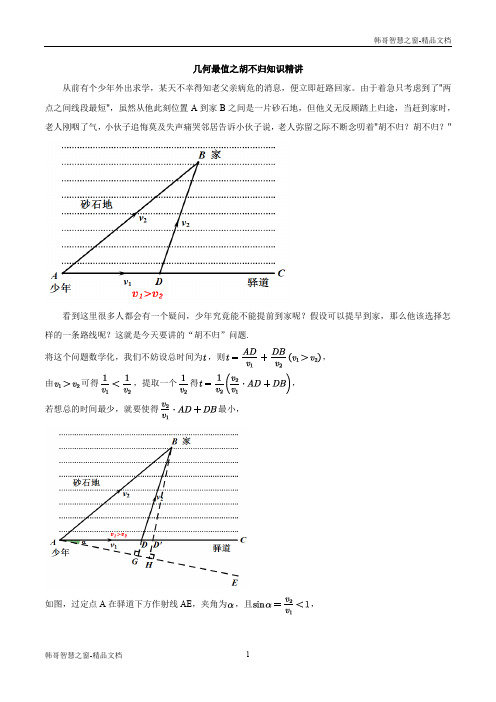
几何最值之胡不归知识精讲
从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家。

由于着急只考虑到了"两点之间线段最短"，虽然从他此刻位置A到家B之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭邻居告诉小伙子说，老人弥留之际不断念叨着"胡不归？胡不归？"
看到这里很多人都会有一个疑问，少年究竟能不能提前到家呢？假设可以提早到家，那么他该选择怎样的一条路线呢？这就是今天要讲的“胡不归”问题.
将这个问题数学化，我们不妨设总时间为，则，
由可得，提取一个得，
若想总的时间最少，就要使得最小，
如图，过定点A在驿道下方作射线AE，夹角为，且，
作DG⊥AE于点G，则，
将转化为DG＋DB，
再过点B作BH⊥AE于点H DG＋DB的最小值
为BH，
，
综上，所需时间的最小值为，
B路线回家，或许还能见到父亲的最后一面.
解决此类问题的一般方法：
第一步：将所求的线段和改写成的形式；
第二步：构造一个角，使得；
第三步：过目的地作所构造的角的一边的垂线，该垂线段的长度就是所求的最小值；
第四步：计算.
例1：如图，P为正方形ABCD对角线BD上一动点，若AB＝2，求AP＋BP＋CP的最小值.
【解析】连接AC，作∠DBE＝∠30º，交AC于点E，过点A作AF⊥BF，垂足为F，如图所示：。

中考数学最值—胡不归问题(解析+例题)

邻居劝慰小伙子时告诉说，老人弥留之际不断念叨着“胡不归？胡不归？…”。

这个古老的传说，引起了人们的思索，小伙子能否提前到家？倘若可以，他应该选择一条怎样的路线呢？这就是风靡千百年的“胡不归问题”。

【知识储备】①三角形三边关系：两边之和大于第三边；两边之差小于第三边。

②两点之间线段最短。

③连接直线外一点和直线上各点的所有线段中，垂线段最短。

【模型分析】①条件：已知A、B为定点，P为射线AC上一动点。

②问题：P在何处时，BP+nm AP最短（nm＜1）。

③方法：第一步在AC的一侧，PB的异侧构造∠CAE=α，使得sinα=nm 第二步做BH⊥AE，交AC于P，点P就是所求位置，BH就是其最小值。

【巩固训练】练习1：如图，四边形ABCD是菱形，AB=4，且∠ABC=60°，M为对角线BD（不含B点）上BM的最小值为_____。

2020年中考数学总复习最值系列：胡不归问题

2020年中考数学总复习最值系列：“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如P A +PB 最值，除此之外我们还可能会遇上形如“P A +kPB ”这样的式子的最值，此类式子一般可以分为两类问题：（1）胡不归问题；（2）阿氏圆．本文简单介绍“胡不归”模型．【故事介绍】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据“两点之间线段最短”，虽然从他此刻位置A 到家B 之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”（“胡”同“何”）而如果先沿着驿道AC 先走一段，再走砂石地，会不会更早些到家？2驿道【模型建立】如图，一动点P 在直线MN 外的运动速度为V 1，在直线MN 上运动的速度为V 2，且V 1<V 2，A 、B 为定点，点C 在直线MN 上，确定点C 的位置使21AC BCV V +的值最小．2M【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭，记12V k V =，即求BC +kAC 的最小值．【问题解决】构造射线AD使得sin∠DAN=k，CH/AC=k，CH=kAC．M将问题转化为求BC+CH最小值，过B点作BH⊥AD交MN于点C，交AD于H点，此时BC+CH取到最小值，即BC+kAC最小．M【模型总结】在求形如“P A+kPB”的式子的最值问题中，关键是构造与kPB相等的线段，将“P A+kPB”型问题转化为“P A+PC”型．而这里的PB必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB的等线段．。

胡不归问题归纳

中考数学压轴热点问题“胡不归模型近几年中考题中，常出现带系数的两线段和的最值问题，这类问题基本都要用到 “阿氏圆”和“胡不归”模型 .下面着重讲解“胡不归模型”的应用 .【背景】从前，有一个小伙子在外地当学徒，当他获悉在家乡的年老父亲病危的消息后，便立即启程日夜赶路。

由于思念心切，他选择了全是沙砾地带的直线路径 A--B(如图 1 所示： A 是出发地， B 是目的地， AC 是一条驿道，而驿道靠目的地的一侧全是沙砾地带)，当他气喘吁吁地赶到父亲眼前时，老人刚刚咽了气，小伙子不觉失声痛哭，邻舍劝慰小伙子时告诉说，老人在弥留之际还不断喃喃地叨念：胡不归胡不归这个古老的传说，引起了人们的思索，小伙子要提前到家是否有可能呢倘有可能，他应该选择条怎样的路线呢这就是风靡千年的 “胡不归问题” .由于在驿道和沙砾地的行走速度不一样，那么，小伙子有没有可能先在驿道上走一程后，再走沙砾地，虽然多走了路，但反而总用时更短呢如果存在这种可能，那么要在驿道上行走多远才最省时设在沙砾地行驶速度为 v 1 ，在驿道行驶速度为 v 2 ，显然 v 1 ＜ v 2 .不妨假设从 C 处进入砂砾地.设总共用时为 t,则BC AC 1 v t= + = (BC+ 1 AC). 因为v v v v 1 2 1 2v vv 1， v 2 是确定的，所以只要(BC+ v 1 AC)最小，用时就最少 . 问题就转化为求(BC+ v1 AC)的最2 2小值.v我们可以作出一条以 C 为端点的线段，使其等于 1 AC.并且与线段 CB 位于 AM 的两侧，v2然后，根据两点之间线段最短，不难找到最小值点 .怎么作呢由三角函数的定义，过 A 点， v在 AM 的另一侧以 A 为顶点，以 AM 为一边作∠MAN=∠α， sin α = 1 .然后，作 CE⊥AN，v2v v则 CE= 1 AC.最后，当点 B 、C 、E 在一条直线上时， BC+CE 最小，即(BC+ 1 AC)的值最小，v v2 2即用时最小 .1例1.如图，AC 是圆 O 的直径，AC=4，弧BA=120°，点 D 是弦 AB 上的一个动点，那么 OD+ BD2 的最小值为______.方法总结：“胡不归”问题中涉及到三个点。

中考数学几何复习---最值系列之胡不归问题

中考数学几何复习--最值系列之“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如P A +PB 最值，除此之外我们还可能会遇上形如“P A +kPB ”这样的式子的最值，此类式子一般可以分为两类问题：（1）胡不归问题；（2）阿氏圆．本文简单介绍“胡不归”模型．【故事介绍】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据“两点之间线段最短”，虽然从他此刻位置A 到家B 之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”（“胡”同“何”）而如果先沿着驿道AC 先走一段，再走砂石地，会不会更早些到家？2驿道【模型建立】如图，一动点P 在直线MN 外的运动速度为V 1，在直线MN 上运动的速度为V 2，且V 1<V 2，A 、B 为定点，点C 在直线MN 上，确定点C 的位置使21AC BCV V +的值最小．2M【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭，记12V k V =，即求BC +kAC 的最小值．【问题解决】构造射线AD使得sin∠DAN=k，CH/AC=k，CH=kAC．M将问题转化为求BC+CH最小值，过B点作BH⊥AD交MN于点C，交AD于H点，此时BC+CH取到最小值，即BC+kAC最小．M【模型总结】在求形如“P A+kPB”的式子的最值问题中，关键是构造与kPB相等的线段，将“P A+kPB”型问题转化为“P A+PC”型．而这里的PB必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB的等线段．【长沙中考】如图，△ABC 中，AB =AC =10，tan A =2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD 的最小值是_______．ABCDE【分析】本题关键在于处理”，考虑tan A =2，△ABE三边之比为1:2sin ∠，故作DH ⊥AB 交AB 于H点，则DH =． HEDCBAABCDEH问题转化为CD +DH 最小值，故C 、D 、H共线时值最小，此时CD DH CH BE +===．【小结】本题简单在于题目已经将BA 线作出来，只需分析角度的三角函数值，作出垂线DH ，即可解决问题，若稍作改变，将图形改造如下：EDCB则需自行构造α，如下图，这一步正是解决“胡不归”问题关键所在．αsin α5HEDC BAEDCB【南通中考】如图，平行四边形ABCD 中，∠DAB =60°，AB =6，BC =2，P 为边CD 上的一动点，则PB 的最小值等于________．ABCDP【分析】考虑如何构造”，已知∠A =60°，且sin60°，故延长AD ，作PH ⊥AD 延长线于H 点，即可得PH =，将问题转化为：求PB +PH 最小值． M HPDCBA当B 、P 、H 三点共线时，可得PB +PH 取到最小值，即BH 的长，解直角△ABH 即可得BH 长．ABCDPH M【成都中考】如图，已知抛物线()()248ky x x =+-（k 为常数，且k >0）与x 轴从左至右依次交于A ，B 两点，与y 轴交于点C ，经过点B的直线y b =+与抛物线的另一交点为D ．（1）若点D 的横坐标为-5，求抛物线的函数表达式；（2）在（1）的条件下，设F 为线段BD 上一点（不含端点），连接AF ，一动点M 从点A 出发，沿线段AF以每秒1个单位的速度运动到F ，再沿线段FD 以每秒2个单位的速度运动到D 后停止，当点F 的坐标是多少时，点M 在整个运动过程中用时最少？【分析】第一小问代点坐标，求解析式即可，此处我们直接写答案：A （y =+，D 点坐标为(-，故抛物线解析式为)()24y x x +-，化简为：2y =点M 运动的时间为12AF DF ⎛⎫+ ⎪⎝⎭，即求12AF DF ⎛⎫+ ⎪⎝⎭的最小值．接下来问题便是如何构造2DF，考虑BD 与x 轴夹角为30°，且DF 方向不变，故过点D 作DM ∥x 轴，过点F 作FH ⊥DM 交DM 于H 点，则任意位置均有FH =2DF．当A 、F 、H 共线时取到最小值，根据A 、D 两点坐标可得结果．【重庆中考】抛物线2y x =x 轴交于点A ，B （点A 在点B 的左边），与y 轴交于点C ．点P 是直线AC 上方抛物线上一点，PF ⊥x 轴于点F ，PF 与线段AC 交于点E ；将线段OB 沿x 轴左右平移，线段OB 的对应线段是O 1B 1，当12PE EC +的值最大时，求四边形PO 1B 1C 周长的最小值，并求出对应的点O 1的坐标．（为突出问题，删去了两个小问）【分析】根据抛物线解析式得A ()-、B )、C (，直线AC的解析式为：y =+知AC 与x 轴夹角为30°．根据题意考虑，P 在何处时，PE +2EC取到最大值．过点E 作EH ⊥y 轴交y 轴于H 点，则∠CEH =30°，故CH =2EC，问题转化为PE +CH 何时取到最小值．考虑到PE 于CH并无公共端点，故用代数法计算，设2,P m ⎛- ⎝，则E m ⎛+ ⎝，H ⎛ ⎝，2PE =-，CH =，22=PE CH m +=+sin ABE ∠=当P点坐标为(-时，取到最小值，故确定P 、C 、求四边形面积最小值，运用将军饮马模型解题即可．。

中考数学专题复习最值问题胡不归 (2)

中考数学专题复最值问题胡不归学校:___________姓名：___________班级：___________考号：___________评卷人得分一、单选题1．如图，在平面直角坐标系中，二次函数y＝x2﹣2x＋c的图象与x轴交于A、C两点，与y轴交于点B（0，﹣3），若P是x轴上一动点，点D（0，1）在y轴上，连接PD，则2PD＋PC的最小值是（）A．4B．2＋22C．22D．32223+2．如图，在ABC∆中，90A∠=︒，60B∠=︒，2AB=，若D是BC边上的动点，则2AD DC+的最小值（）A．236+B．6C．33+D．4评卷人得分二、填空题3．如图，正方形ABCD的边长为4，点E为边AD上一个动点，点F在边CD上，且线段EF＝4，点G为线段EF的中点，连接BG、CG，则BG+12CG的最小值为_____．4．如图，在平面直角坐标系中，直线l分别交x、y轴于B、C两点，点A、C的坐标分别为(3，0)、(0，﹣3)，且∠OCB＝60°，点P是直线l上一动点，连接AP，则32AP PC的最小值是______．5．如图，直线y＝x﹣3分别交x轴、y轴于B、A两点，点C（0，1）在y轴上，点P 在x轴上运动，则2PC＋PB的最小值为___．6．如图，矩形ABCD中AB＝3，BC=3，E为线段AB上一动点，连接CE，则12AE ＋CE的最小值为___．7．如图，∠ABC中，∠BAC＝75°，∠ACB＝60°，AC＝4，则∠ABC的面积为_；点D，点E，点F分别为BC，AB，AC上的动点，连接DE，EF，FD，则∠DEF的周长最小值为_．8．如图，在边长为4的正方形ABCD内有一动点P，且BP＝2．连接CP，将线段PC绕点P逆时针旋转90°得到线段PQ．连接CQ、DQ，则12DQ+CQ的最小值为___．9．如图，四边形ABCD是菱形，AB＝8，且∠ABC＝60°，M为对角线BD（不含B点）上任意一点，则AM+12BM的最小值为_____．10．如图，∠ABCD中，∠DAB＝30°，AB＝6，BC＝2，P为边CD上的一动点，则2PB+ PD的最小值等于______.11．如图，ABC中，10AB AC==，tan2A=，BE AC⊥于点E，D是线段BE上的一个动点，则55CD BD+的最小值是__________．12．如图，抛物线223y x x =--与x 轴交于A 、B 两点，过B 的直线交抛物线于E,，且tan ∠EBA=43，有一只蚂蚁从A 出发,先以1单位/s 的速度爬到线段BE 上的点D 处，再以1.25单位/s 的速度沿着DE 爬到E 点处觅食，则蚂蚁从A 到E 的最短时间是________s评卷人得分三、解答题 13．如果有一条直线经过三角形的某个顶点，将三角形分成两个三角形，其中一个三角形与原三角形相似，则称该直线为三角形的“自相似分割线”．如图1，在△ABC 中，AB =AC =1，∠BAC =108°，DE 垂直平分AB ，且交BC 于点D ，连接AD ．(1)证明直线AD 是△ABC 的自相似分割线；(2)如图2，点P 为直线DE 上一点，当点P 运动到什么位置时，P A +PC 的值最小？求此时P A +PC 的长度．(3)如图3，射线CF 平分∠ACB ，点Q 为射线CF 上一点，当514AQ CQ -+取最小值时，求∠QAC 的正弦值．14．如图1，已知正方形ABCD，AB＝4，以顶点B为直角顶点的等腰Rt∠BEF绕点B 旋转，BE＝BF＝10，连接AE，CF．(1)求证：∠ABE∠∠CBF．(2)如图2，连接DE，当DE＝BE时，求S△BCF的值．（S△BCF表示∠BCF的面积）(3)如图3，当Rt∠BEF旋转到正方形ABCD外部，且线段AE与线段CF存在交点G 时，若M是CD的中点，P是线段DG上的一个动点，当满足2MP+PG的值最小时，求MP的值．15．如图，在平面直角坐标系中，直线l1：y＝33x＋3和直线l2：y＝﹣3x＋b相交于y轴上的点B，且分别交x轴于点A和点C．（1）求∠ABC的面积；（2）点E坐标为（5，0），点F为直线l1上一个动点，点P为y轴上一个动点，求当EF＋CF最小时，点F的坐标，并求出此时PF＋22OP的最小值．16．如图，在平面直角坐标系中，直线l 13:33y x =+和直线l 2相交于y 轴上的点B ，分别交x 轴于A 、C 且∠OBC ＝30度．（1）求直线l 2的解析式；（2）点E 坐标为（5，0），点F 为直线l 1上一个动点，点P 为y 轴上一个动点，求当EF ＋CF 最小时，点F 的坐标，并求出此时22PF OP +的最小值．17．如图，矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上，点B 的坐标为(23,4)，一次函数33yx b 的图象与边OC 、AB 、x 轴分别交于点D 、E 、F ，30DFO ∠=，并且满足OD BE =，点M 是线段DF 上的一个动点．（1）求b 的值；（2）连接OM ，若ODM ∆的面积与四边形OAEM 的面积之比为1:3，求点M 的坐标；（3）求12OM MF +的最小值．18．如图，在平面直角坐标系中，二次函数y＝ax2＋bx＋c的图象经过点A（﹣1，0），B（0，3），C（2，0），其对称轴与x轴交于点D．（1）求二次函数的表达式及其顶点坐标；（2）点M为抛物线的对称轴上的一个动点，若平面内存在点N，使得以A，B，M，N 为顶点的四边形为菱形，求点M的坐标；（3）若P为y轴上的一个动点，连接PD，求12PB＋PD的最小值．19．∠AOB＝30°，OM＝2，D为OB上动点，求MD1+2OD的最小值．20．已知抛物线y＝ax2＋bx＋c与x轴交于A（﹣1，0），B（5，0）两点，C为抛物线的顶点，抛物线的对称轴交x轴于点D，连接BC，且tan∠CBD4=3，如图所示．（1）求抛物线的解析式；（2）设P是抛物线的对称轴上的一个动点．∠过点P作x轴的平行线交线段BC于点E，过点E作EF∠PE交抛物线于点F，连接FB、FC，求∠BCF的面积的最大值；∠连接PB，求35PC＋PB的最小值．21．在平面直角坐标系中，将二次函数()20y ax a=>的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x轴交于点A、B(点A在点B 的左侧)，1OA=，经过点A的一次函数()0y kx b k=+≠的图象与y轴正半轴交于点C，且与抛物线的另一个交点为D，ABD∆的面积为5．(1)求抛物线和一次函数的解析式；(2)抛物线上的动点E在一次函数的图象下方，求ACE∆面积的最大值，并求出此时点E的坐标；(3)若点P为x轴上任意一点，在(2)的结论下，求35PE PA+的最小值．22．已知抛物线2(0)y ax bx c a=++≠过点(1,0)A，(3,0)B两点，与y轴交于点C，=3OC．(1)求抛物线的解析式及顶点D的坐标；(2)过点A作AM BC⊥，垂足为M，求证：四边形ADBM为正方形；(3)点P为抛物线在直线BC下方图形上的一动点，当PBC∆面积最大时，求点P的坐标；(4)若点Q为线段OC上的一动点，问：12AQ QC+是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．23．如图，在平面在角坐标系中，抛物线y=x2-2x-3与x轴交于点A，B（点A在点B的左侧）交y轴于点C，点D为抛物线的顶点，对称轴与x轴交于点E．（1）连结BD，点M是线段BD上一动点（点M不与端点B，D重合），过点M作MN⊥BD交抛物线于点N（点N在对称轴的右侧），过点N作NH⊥x轴，垂足为H，交BD于点F，点P是线段OC上一动点，当MN取得最大值时，求HF+FP+13PC 的最小值；（2）在（1）中，当MN 取得最大值HF +FP +1/3PC 取得小值时，把点P 向上平移个22单位得到点Q ，连结AQ ，把∠AOQ 绕点O 瓶时针旋转一定的角度α（0°<α<360°），得到∠AOQ ，其中边AQ 交坐标轴于点C 在旋转过程中，是否存在一点G 使得''Q Q OG ∠=∠？若存在，请直接写出所有满足条件的点Q 的坐标；若不存在，请说明理由．24．已知抛物线2y x bx c =-+（b c ，为常数，0b >）经过点(1,0)A -，点(,0)M m 是x 轴正半轴上的动点．（∠）当2b =时，求抛物线的顶点坐标；（∠）点(,)D D b y 在抛物线上，当AM AD =，5m =时，求b 的值；（∠）点1(,)2Q Q b y +在抛物线上，当22AM QM +的最小值为3324时，求b 的值．25．如图，抛物线y=-x2+bx+c与直线AB交于A(-4，-4)，B(0，4)两点，直线AC：y=-1x-6交y轴与点C．点E是直线AB上的动点，过点E作EF∠x轴交AC于点F，2交抛物线于点G.（1）求抛物线y=-x2+bx+c的表达式；（2）连接GB、EO，当四边形GEOB是平行四边形时，求点G的坐标；（3）∠在y轴上存在一点H，连接EH、HF，当点E运动到什么位置时，以A、E、F、H为顶点的四边形是矩形？求出此时点E、H的坐标；∠在∠的前提下，以点E为圆心，EH长为半径作圆，点M为∠E上一动点，求12AM+CM的最小值.26．如图，已知抛物线()()248k y x x =+-（k 为常数，且0k >）与x 轴从左至右依次交于A ，B 两点，与ｙ轴交于点C ，经过点B 的直线33yx b 与抛物线的另一交点为D ．（1）若点D 的横坐标为-5，求抛物线的函数表达式；（2）若在第一象限的抛物线上有点P ，使得以A ，B ，P 为顶点的三角形与∠ABC 相似，求k 的值；（3）在（1）的条件下，设F 为线段BD 上一点（不含端点），连接AF ，一动点M 从点A 出发，沿线段AF 以每秒1个单位的速度运动到F ，再沿线段FD 以每秒2个单位的速度运动到D 后停止．当点F 的坐标是多少时，点M 在整个运动过程中用时最少．参考答案：1．A【解析】【分析】过点P作PJ∠BC于J，过点D作DH∠BC于H．根据()22222PD PC PD PC PD PJ⎛⎫+=+=+⎪⎪⎝⎭，求出DP PJ+的最小值即可解决问题．【详解】解：过点P作PJ∠BC于J，过点D作DH∠BC于H．∠二次函数y＝x2﹣2x+c的图象与y轴交于点B（0，﹣3），∠c＝﹣3，∠二次函数的解析式为y＝x2﹣2x﹣3，令y＝0，x2﹣2x﹣3＝0，解得x＝﹣1或3，∠A（﹣1，0），B（0，-3），∠OB＝OC＝3，∠∠BOC＝90°，∠∠OBC＝∠OCB＝45°，∠D（0，1），∠OD＝1，BD＝4，∠DH∠BC，∠∠DHB＝90°，设DH x=，则BH x=,∠222DH BH BD+=，∠2224x x+=，∠22x=，∠22DH ＝，∠PJ ∠CB ，∠90PJC ∠︒＝，∠22PJ PC ＝， ∠()22222PD PC PD PC PD PJ ⎛⎫+=+=+ ⎪ ⎪⎝⎭， ∠DP PJ DH +≥，∠22DP PJ +≥，∠DP +PJ 的最小值为22，∠2PD PC +的最小值为4．故选：A ．【点睛】本题考查了二次函数的相关性质，以及等腰直角三角形的判定和性质，垂线段最短等知识，解题的关键是学会用转化的思想思考问题．2．B【解析】【分析】作点A 关于BC 的对称点A'，连接AA', A'D,过D 作DE∠AC 于E ，易得2DE = CD ，AD= A'D ，从而得出AD+ DE = A'D+ DE ，当A'，D, E 在同一直线上时，AD + DE 的最小值等于A' E 的长是3，进而求出2AD 十CD 的最小值．【详解】如图所示，作点A 关于BC 的对称点A',连接AA', A'D,过D 作DE∠AC 于E∠∠BAC = 90o ，∠B = 60o ，AB= 2∠BH=1,AH=3,AA'=23，∠C= 30o∠DE =12CD,即2DE = CD∠A 与A'关于BC 对称∠AD= A'D∠AD+ DE = A'D+ DE∠当A'，D, E 在同一直线上时AD + DE的最小值等于A' E的长,在Rt∠AA' E中：A' E= sin60o×AA'=32×23= 3∠AD十DE的最小值为3∠2AD十CD的最小值为6故选B【点睛】本题主要考察了三角形的动点最值问题，做完辅助线后先求出AD + DE的最小值是解题关键．3．5【解析】【分析】因为DG＝12EF＝2，所以G在以D为圆心，2为半径圆上运动，取DI＝1，可证∠GDI∠∠CDG，从而得出GI＝12CG，然后根据三角形三边关系，得出BI是其最小值【详解】解：如图，在Rt∠DEF中，G是EF的中点，∠DG＝122EF ，∠点G 在以D 为圆心，2为半径的圆上运动，在CD 上截取DI ＝1，连接GI ，∠DI DG ＝DG CD＝12， ∠∠GDI ＝∠CDG ，∠∠GDI ∠∠CDG ，∠IG DI CG DG=＝12， ∠IG ＝12CG ， ∠BG +12CG ＝BG +IG ≥BI ， ∠当B 、G 、I 共线时，BG +12CG 最小＝BI ，在Rt∠BCI 中，CI ＝3，BC ＝4，∠BI ＝5，故答案是：5．【点睛】本题考查了相似三角形的性质与判定，圆的概念，求得点G 的运动轨迹是解题的关键．4．3332+##3332+ 【解析】【分析】作∠OCE =120°，过点P 作PG ∠CE 于点G ，利用含30度角的直角三角形的性质以及勾股定理求得PG =32PC ；当A 、P 、G 在同一直线时，AP +32PC = AP +PG = AG 的值最小，再利用含30度角的直角三角形的性质以及勾股定理即可求解．【详解】解：∠点A 、C 的坐标分别为(3，0)、(0，﹣3)，∠OA =3，OC =3，作∠OCE =120°，∠∠OCB =60°，则∠OCB =∠BCE =∠FCE =60°，过点P 作PG ∠CE 于点G ，如图：在Rt△PCG中，∠PCG=60°，则∠CPG=30°，∠CG=12PC，由勾股定理得PG=32PC，∠AP+32PC= AP+PG，当A、P、G在同一直线时，AP+PG= AG的值最小，延长AG交y轴于点F，∠∠FCG=60°，∠CGF=90°，∠∠CFG=30°，∠CF=2CG，GF=32CF，在Rt△OAF中，∠AOF=90°，∠OF A=30°，∠AF=2OA=6，OF=333OA=，∠CF=OF-OC=333-，∠GF=32(333-)=93322-，∠AG=AF-FG=93333362222-+=+，即AP+32PC的最小值为33322+．故答案为：3332+．【点睛】本题考查了坐标与图形，含30度角的直角三角形的性质以及勾股定理，作出合适的辅助线，得到当A、P、G在同一直线时，AP+32PC= AP+PG= AG的值最小是解题的关键．5．4【解析】【分析】【详解】思路引领：过P作PD∠AB于D，依据∠AOB是等腰直角三角形，可得∠BAO＝∠ABO＝45°＝∠BPD，进而得到∠BDP是等腰直角三角形，故PD22=PB，当C，P，D在同一直线上时，CD∠AB，PC+PD的最小值等于垂线段CD的长，求得CD的长，即可得出结论．答案详解：如图所示，过P作PD∠AB于D，∠直线y＝x﹣3分别交x轴、y轴于B、A两点，令x＝0，则y＝﹣3；令y＝0，则x＝3，∠A（0，﹣3），B（3，0），∠AO＝BO＝3，又∠∠AOB＝90°，∠∠AOB是等腰直角三角形，∠∠BAO＝∠ABO＝45°＝∠BPD，∠∠BDP是等腰直角三角形，∠PD22=PB，∠2PC+PB2=（PC22+PB）2=（PC+PD），当C，P，D在同一直线上，即CD∠AB时，PC+PD的值最小，最小值等于垂线段CD的长，此时，∠ACD是等腰直角三角形，又∠点C（0，1）在y轴上，∠AC ＝1+3＝4，∠CD 22=AC ＝22，即PC +PD 的最小值为22，∠2PC +PB 的最小值为222⨯=4，故答案为：4．6．3【解析】【分析】【详解】思路引领：在射线AB 的下方作∠MAB ＝30°，过点E 作ET ∠AM 于T ，过点C 作CH ∠AM 于H ．易证ET 12=AE ，推出12AE +EC ＝CE +ET ≥CH ，求出CH 即可解决问题．答案详解：∠四边形ABCD 是矩形，∠∠B ＝90°，∠tan∠CAB 33CB AB ==， ∠∠CAB ＝30°，∠AC ＝2BC ＝23，在射线AB 的下方作∠MAB ＝30°，过点E 作ET ∠AM 于T ，过点C 作CH ∠AM 于H ． ∠ET ∠AM ，∠EAT ＝30°，∠ET12=AE，∠∠CAH＝60°，∠CHA＝90°，AC＝23，∠CH＝AC•sin6°＝2332⨯=3，∠12AE+EC＝CE+ET≥CH，∠12AE+EC≥3，∠12AE+EC的最小值为3，故答案为3．7．6+23326+【解析】【分析】（1）过点A作AH∠BC于H，根据∠BAC＝75°，∠C＝60°，即可得到（2）过点B作BJ∠AC于J，作点F关于AB的对称点M，点F关于BC的对称点N，连接BM，BN，BJ，MN，MN交AB于E′，交BC于D′，此时∠FE′D′的周长＝MN的长，然后证明∠BMN是等腰直角三角形，BM的值最小时，MN的值最小，再根据垂线段最短可知，当BF与BJ重合时，BM的值最小，由此求解即可.【详解】解：∠如图，过点A作AH∠BC于H．∠∠AHB=∠AHC=90°，∠∠BAC＝75°，∠C＝60°，∠∠B＝180°﹣∠BAC﹣∠C＝45°，∠HAC=30°∠BH=AH，122HC AC==∠2223AH AC HC=-=∠AH＝BH＝23，∠BC＝BH+CH＝23+2，∠S△ABC＝12•BC•AH＝12•（23+2）3＝6+23．∠如图，过点B作BJ∠AC于J，作点F关于AB的对称点M，点F关于BC的对称点N，连接BM，BN，BJ，MN，MN交AB于E′，交BC于D′，此时∠FE′D′的周长＝MN的长．∠BF＝BM＝BM，∠ABM＝∠ABJ，∠CBJ＝∠CBN，∠∠MBN＝2∠ABC＝90°，∠∠BMN是等腰直角三角形，∠BM的值最小时，MN的值最小，根据垂线段最短可知，当BF与BJ重合时，BM的值最小，∠21243==334ABCSBJAC+=+△,∠MN的最小值为2BJ＝326+，∠∠DEF的周长的最小值为326+．故答案为：6+23，326+．【点睛】本题主要考查了勾股定理，含30度角的直角三角形的性质，等腰直角三角形的性质与判定，垂线段最短，解题的关键在于能够熟练掌握相关知识进行求解.8．5【解析】【分析】连接AC 、AQ ，先证明∠BCP ∠∠ACQ 得22AQ BP =即AQ ＝2，在AD 上取AE ＝1，证明∠QAE ∠∠DAQ 得EQ ＝12QD ，故12DQ +CQ ＝EQ +CQ ≥CE ，求出CE 即可．【详解】解：如图，连接AC 、AQ ，∠四边形ABCD 是正方形，PC 绕点P 逆时针旋转90°得到线段PQ ，∠∠ACB ＝∠PCQ ＝45°，∠∠BCP ＝∠ACQ ，cos∠ACB ＝22BC AC =，cos∠PCQ ＝22PC QC =， ∠∠ACB =∠PCO ，∠∠BCP ∠∠ACQ ，∠22AQ BP = ∠BP ＝2，∠AQ ＝2，∠Q 在以A 为圆心，AQ 为半径的圆上，在AD 上取AE ＝1，∠12AE AQ =，12AQ AD =，∠QAE ＝∠DAQ ， ∠∠QAE ∠∠DAQ ，∠12EQ QD =即EQ ＝12QD ， ∠12DQ +CQ ＝EQ +CQ ≥CE ，连接CE ，∠225CE DE CD =+=，∠12DQ +CQ 的最小值为5．故答案为：5．【点睛】本题主要考查了正方形的性质，旋转的性质，相似三角形的性质与判定，三角函数，解题的关键在于能够连接AC、AQ，证明两对相似三角形求解.9．43【解析】【分析】如图，过点A作AT∠BC于T，过点M作MH∠BC于H，根据菱形的性质和30°角的直角三角形的性质可得MH＝12BM，于是可得AM+12BM的最小值即为AT的长，再利用解直角三角形的知识求解即可．【详解】解：如图，过点A作AT∠BC于T，过点M作MH∠BC于H．∠四边形ABCD是菱形，∠ABC＝60°，∠∠DBC＝12∠ABC＝30°，∠MH∠BC，∠∠BHM＝90°，∠MH＝12BM，∠AM+12BM＝AM+MH，∠AT∠BC，∠∠ATB＝90°，∠AT＝AB•sin60°＝43，∠AM+MH≥AT，∠AM+MH≥43，∠AM+1BM≥43，2BM的最小值为43，∠AM+12故答案为：43．【点睛】本题考查了菱形的性质、30°角的直角三角形的性质、垂线段最短以及解直角三角形等知识，属于常考题型，熟练掌握上述知识、明确解答的方法是解题关键．10．6【解析】【分析】过点P作PE∠AD交AD的延长线于点E，根据四边形ABCD是平行四边形，得到PD，由此得到当PB+PE最小时2PB+ PD有最小值，此时P、B、E AB∠CD，推出PE=12三点在同一条直线上，利用∠DAB＝30°，∠AEP=90°，AB=6求出PB+PE的最小值=12 AB=3，得到2PB+ PD的最小值等于6.【详解】过点P作PE∠AD交AD的延长线于点E，∠四边形ABCD是平行四边形，∠AB∠CD，∠∠EDC=∠DAB＝30°，PD，∠PE=12PD）=2(PB+PE)，∠2PB+ PD=2（PB+12∠当PB+PE最小时2PB+ PD有最小值，此时P、B、E三点在同一条直线上，∠∠DAB＝30°，∠AEP=90°，AB=6，∠PB+PE的最小值=1AB=3，2∠2PB+ PD的最小值等于6，故答案为：6.【点睛】此题考查平行四边形的性质，直角三角形含30°角的问题，动点问题，将线段2PB+PD 转化为三点共线的形式是解题的关键.11．45【解析】【分析】过点D 作DH AB ⊥于H ，过点C 作CM AB ⊥于M ，首先通过勾股定理及tan 2A =求出AE,BE 的长度，然后根据等腰三角形两腰上的高相等得出CM BE =，然后通过锐角三角函数得出55DH BD =，进而可得出55CD BD CD DH +=+，最后利用CD DH CM +即可求值．【详解】解：如图，过点D 作DH AB ⊥于H ，过点C 作CM AB ⊥于M ．∠BE AC ⊥，∠90AEB =︒∠，∠tan 2BE A AE==，设AE a =，2BE a =，222AB AE BE =+∠221004a a =+，∠220a =，∠25a =或25-（舍弃），∠245BE a ==，∠AB AC =，BE AC ⊥，CM AB ⊥，∠45CM BE ==（等腰三角形两腰上的高相等）∠DBH ABE ∠=∠，BHD BEA ∠=∠，∠5sin 5DH AE DBH BD AB ∠===， ∠55DH BD =， ∠55CD BD CD DH +=+，∠CD DH CM +，∠5455CD BD +， ∠55CD BD +的最小值为45, 故答案为：45．【点睛】本题主要考查解直角三角形，等腰三角形的性质，勾股定理，垂线段最短等，学会添加辅助线并利用转化的思想是解题的关键．12．649【解析】【详解】过点E 作EF ∠AB ，过点A 作AH ∠EF 于点H ，交EF 于点D ，易知A （-1，0），B （3，0），又4tan 3EBA ∠=，则4:43BE l y x =-+，所以E （73-，649），因为EF ∠AB ，所以∠DEH =∠ABE ，所以4tan 3DEH ∠=，则4sin 5DH DEH DE ∠==，故1.25DE DH =. 蚂蚁从A 到H 所用的时间t =1 1.25AD DE +=1AD DH AD DH AH +=+=. 因为AH =649，所以t 的最小值是649.点晴：本题是一个求最小时间的胡不归问题，解题的关键是化12v DE v =DH ，一般的以目的地E 为角的顶点，以12sin v BEF v ∠=构造直角三角形，得到直角边EF ，再过A 作AH ∠EF 交BE 于点D ，则可解决问题. 13．(1)直线AD 是∠ABC 的自相似分割线；(2)当点P 运动到D 点时，P A +PC 的值最小，此时512PA PC ++=； (3)∠QAC 的正弦值为514+ 【解析】【分析】（1）根据定义证明∠DBA ∠∠ABC 即可得证；（2）根据垂直平分线的性质可得PA PC PB PC BC +=+≥，当点P 与D 重合时，PA PC PB PC BC +=+=,此时PA PC +最小，设BD x =，则1BC x =+ 根据DBA ABC ∽，列出方程，解方程求解即可求得BD ，进而即可求得BC 的长，即PA PC +最小值；（3）过点A 作AH BC ⊥于点H ，过点Q 作QG BC ⊥于点G ，连接AG ，设CF 与AD 交于点M ，根据已知条件求得514GQ CQ -=，进而转化为514AQ CQ AQ GQ -+=+，则当Q 点落在AG 上时，点G 与点H 重合，此时514AQ CQ -+的值最小，最小值为AH ，进而根据sin sin CH QAC HAC AC ∠=∠=求解即可． (1)∠∠ABC 中，AB =AC =1，∠BAC = 108°∠∠B =∠C =12（180°-∠BAC ）= 36° ∠DE 垂直平分AB∠AD = BD∠∠B =∠BAD = 36°∠∠C =∠BAD又∠∠B =∠B∠∠DBA ∠∠ABC∠直线AD 是∠ABC 的自相似分割线．(2)如图，连接PB ，AD ，DE 垂直平分AB ，PA PB ∴=PA PC PB PC BC ∴+=+≥ 当点P 与D 重合时，PA PC PB PC BC +=+=,此时PA PC +最小， 72ADC B BAD ∠=∠+∠=︒，72DAC BAC BAD ∠=∠-∠=︒ ADC DAC ∴∠=∠1CD CA ∴==设BD x =，则1BC x =+ DBA ABC ∽ BD AB AB BC∴= 111x x ∴=+ 210x x ∴+-=解得：152x -±=0x x ∴=152-+ 5112BC x +∴=+= ∴P A +PC =512+ ∴当点P 运动到D 点时，P A +PC 的值最小，此时512PA PC ++=； (3)如图，过点A作AH BC⊥于点H，过点Q作QG BC⊥于点G，连接AG，设CF与AD交于点M，AB AC=，15124CH BC+∴==由（2）知，1DC AC==CF平分ACB∠CM AD∴⊥15124DM AM AD-===sinGQMCDCQ∴∠=514DMCD-==514GQ CQ-∴=514AQ CQ AQ GQ AG-∴+=+≥AG AH≥Q∴点落在AG上时，点G与点H重合，即此时514AQ CQ-+的值最小，最小值为AHQAC HAC∴∠=∠,AB AC AH BC=⊥15124CH BC+∴==51sin sin4CHQAC HACAC+∴∠=∠==∴∠QAC的正弦值为514+【点睛】本题考查了相似三角形的性质与判定，求角的正弦，垂直平分线的性质，两点之间线段最短，垂线段最短，胡不归问题，转化线段是解题的关键．14．(1)见解析(2)2或6(3)1152- 【解析】【分析】（1）由“SAS ”可证∠ABE ∠∠CBF ；（2）由“SSS ”可证∠ADE ∠∠ABE ，可得∠DAE ＝∠BAE ＝45°，可证AH ＝EH ，由勾股定理可求BE 的长，即可求解；（3）先确定点P 的位置，过点B 作BQ ∠CF 于Q ，由勾股定理可求CE 的长，由平行线分线段成比例可求解．(1)证明：∠四边形ABCD 是正方形，∠AB ＝BC ，∠ABC ＝90°，∠∠EBF ＝90°＝∠ABC ，∠∠ABE ＝∠CBF ，又∠BE ＝BF ，AB ＝BC ，在∠ABE 和∠CBF 中， AB CB ABE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩，∠∠ABE ∠∠CBF （SAS ）；(2)解：如图2，过点E 作EH ∠AB 于H ，∠∠ABE∠∠CBF，∠S△ABE＝S△CBF，∠AD＝AB，AE＝AE，DE＝BE，∠∠ADE∠∠ABE（SSS），∠∠DAE＝∠BAE＝45°，∠EH∠AB，∠∠EAB＝∠AEH＝45°，∠AH＝EH，∠BE2＝BH2+EH2，∠10＝EH2+（4﹣EH）2，∠EH＝1或3，当EH＝1时∠S△ABE＝S△BCF＝12AB×EH＝12×4×1＝2，当EH＝3时∠S△ABE＝S△BCF＝12AB×EH＝12×4×3＝6，∠S△BCF的值是2或6；(3)解：如图3，过点P作PK∠AE于K，由（1）同理可得∠ABE∠∠CBF，∠∠EAB＝∠BCF，∠∠BAE+∠CAE+∠ACB＝90°，∠∠BCF+∠CAE+∠ACB＝90°，∠∠AGC＝90°，∠∠AGC＝∠ADC＝90°，∠点A，点G，点C，点D四点共圆，∠∠ACD＝∠AGD＝45°，∠PK∠AG，∠∠PGK＝∠GPK＝45°，∠PK＝GK＝22PG，∠MP+22PG＝MP+PK，∠当点M，点P，点K三点共线时，且点E，点G重合时，MP+22PG值最小，即2 MP+PG最小，如图4，过点B作BQ∠CF于Q，∠BE＝BF＝10，∠EBF＝90°，BQ∠EF，∠EF＝25，BQ＝EQ＝FQ＝5，∠CQ＝2216511BC BQ-=-=，∠CE＝CQ﹣EQ＝115-，∠MK∠AE，CE∠AE，∠MK∠CE，∠DM MPDC CE=，又∠M是CD的中点，∠DC＝2DM，∠MP＝12CE＝1152-．【点睛】本题主要考查勾股定理、全等三角形的性质与判定、正方形的性质及圆的基本性质，熟练掌握勾股定理、全等三角形的性质与判定、正方形的性质及圆的基本性质是解题的关键．15．（1）S△ABC=23；（2）点F坐标为（1，433）；PF＋22OP的最小值为26232+．【解析】【分析】（1）根据l1的解析式可得A、B坐标，把点B坐标代入y＝﹣3x＋b可求出b值，进而可得出点C坐标，即可求出AC、OB的长，利用三角形面积公式即可得答案；（2）如图，作点C关于直线l1的对称点C′，连接C′E，交l1于F，根据A、B、C坐标可得∠ABC是直角三角形，可得点C′在直线l2上，根据两点间距离公式可得出C′坐标，可得C′E为EF＋CF的最小值，利用待定系数法可得出直线C′E的解析式，联立直线C′E与l1解析式即可得出得F的坐标；作二、四象限对角线l3，过点F作FG∠l3于G，交y轴于P，可得∠GOP=45°，可得PG=22OP，可得FG为PF＋22OP的最小值，过点F作FQ∠x轴，交l3于Q，可得∠FGQ为等腰直角三角形，可得FG=22FQ，由l3的解析式为y=-x及点F的坐标可得点Q坐标，进而可得FQ的长，即可得FG的长，可得答案．【详解】（1）∠l1：y＝33x＋3，∠当x=0时，y=3，当y=0时，x=-3，∠A（-3，0），B（0，3），∠点B直线l2：y＝﹣3x＋b上，∠b=3，∠直线l2的解析式为y＝﹣3x＋3，∠当y=0时，x=1，∠C（1，0），∠AC=4，OB=3，∠S△ABC=12AC OB⋅=1432⨯⨯=23．（2）如图，作点C关于直线l1的对称点C′，连接C′E，交l1于F，∠A（-3，0），B（0，3），C（1，0），∠AB2=（-3）2+（3）2=12，BC2=12+（3）2=4，AC2=42=16，∠AC 2=AB 2+BC 2，∠∠ABC 是直角三角形，∠点C ′在直线l 2上，∠点C 与点C ′关于直线l 1的对称，∠CC ′=2BC =4，设点C ′（m ，﹣3m ＋3，）∠（m -1）2+（﹣3m ＋3）2=42，解得：m 1=-1，m 2=3，∠点C ′在第二象限，∠m =-1，∠﹣3m ＋3=23，∠FC=FC′，∠EF ＋CF =EF+FC′，∠当C ′、F 、E 三点共线时EF ＋CF 的值最小，设直线C ′E 的解析式为y =kx +b ，∠2350k b k b ⎧-+=⎪⎨+=⎪⎩，解得：33533k b ⎧=-⎪⎪⎨⎪=⎪⎩， ∠直线C ′E 的解析式为35333y x =-+，联立直线C ′E 与l 1解析式得35333333y x y x ⎧=-+⎪⎪⎨⎪=+⎪⎩，解得：1433x y =⎧⎪⎨=⎪⎩， ∠F （1，433）．如图，作二、四象限对角线l 3，过点F 作FG ∠l 3于G ，交y 轴于P ，过点F 作FQ ∠x 轴，交l 3于Q ，∠直线l3的解析式为y=-x，∠GOP=45°，∠∠GOP是等腰直角三角形，∠PG=22OP，∠G、P、F三点共线时，PF＋22OP的值最小，最小值为FG的长，∠∠GOP=45°，∠POE=90°，∠∠EOQ=45°，∠∠FQO=45°，∠∠FGQ是等腰直角三角形，∠FG=22FQ，∠F（1，433），直线l3的解析式为y=-x，∠Q（1，-1），∠FQ=433-（-1）=433+1，∠FG=22FQ=22×（433+1）=26232+，∠PF＋22OP的最小值为26232+．【点睛】本题考查一次函数的综合、轴对称的性质、等腰直角三角形的判定与性质，正确添加辅助线，熟练掌握待定系数法求一次函数解析式及轴对称的性质是解题关键．16．（1）33y x=-+；（2）F（1，433），PF+22OP的最小值为22623+；【解析】【分析】（1）求出B（0，3），再由OC=BO•tan30°=1，求出C（1，0），再由待定系数法求直线解析式即可；（2）先确定∠ABC=90°，则可知C点关于直线l2的对称点C'在l2上，过点C'作C'K∠y轴交K点，易证△C'KB∠∠COB（AAS），则C'的纵坐标为23，即可求C'（-1，23），连接C'E交l1于F，因为EF+CF=EF+C'F≥C'E，所以当C'、E、F三点共线时，EF+CF的值最小为C'E；当P、F、Q三点共线时，PF+22OP的值最小，过F作FG∠x轴交l3，于点G，易证△FQG为等腰直角三角形，然后求出最小值即可．【详解】解：（1）令x=0，则y=3，∠B（0，3），∠OB=3，∠∠OBC=30°，∠OC=BO•tan30°=3×313=，∠C（1，0），设直线l2的解析式为y=kx+b，则3bk b⎧=⎪⎨+=⎪⎩，∠33kb⎧=-⎪⎨=⎪⎩，∠直线l2的解析式为33y x=-+；（2）令y=0，则3303x+=，∠x=-3，∠A（-3，0），∠OA=3，∠tan∠ABO=333AOBO==，∠∠ABO=60°，∠∠ABC=90°，∠C点关于直线l1的对称点C'在l2上，如图1，过点C '作C 'K ∠y 轴交K 点，∠∠KBC '=∠CBO ，∠C 'KB =∠BOC ，BC =BC '，∠∠C 'KB ∠∠COB （AAS ），∠BK =BO =3，∠C '的纵坐标为23，∠3323x -+=，∠x =-1，∠C '（-1，23），连接C 'E 交l 1于F ，∠EF +CF =EF +C 'F ≥C 'E ，∠当C '、E 、F 三点共线时，EF +CF 的值最小为C 'E ，设直线C 'E 的解析式为y =kx +b ，∠E （5，0），C '（-1，23），则5023k b k b +=⎧⎪⎨-+=⎪⎩， ∠33533k b ⎧=-⎪⎪⎨⎪=⎪⎩， ∠35333y x =-+，∠35333333y x y x ⎧=-+⎪⎪⎨⎪=+⎪⎩，解得x =1，∠F （1，433），作第二、四象限的角平分线l 3，，过点F 作FQ ∠l 3，，交y 轴于点P ，交l 3，于点Q ，在Rt △PQO 中，∠POQ =45°，∠22OP PQ =， ∠PF +22OP =PF +PQ ≥FQ ，当P 、F 、Q 三点共线时，PF +22OP 的值最小，过F 作FG ∠x 轴交l 3，于点G ，∠∠FQG 为等腰直角三角形，∠FQ =22FG ， ∠l 3，的解析式为y =-x ，∠G （1，-1），∠FG =1+433， ∠FQ =22+263， ∠PF +22OP 的最小值为22+263．【点睛】本题考查一次函数的综合，熟练掌握一次函数的图象及性质，通过构造坐标象限的角平分线将22PF OP 转化为求FQ 的长是解（2）问的关键，数形结合，利用坐标平移的性质是解题关键．17．（1）3b =；（2）237(,)33M ；（3）92 【解析】【分析】（1）利用矩形的性质，用b 表示点E 的坐标，再利用待定系数法即可求解；（2）首先求出四边形OAED 的面积，再根据条件求出ODM △的面积，即可解决问题；（3）过点M 作MN x ⊥轴交于点N ，则12OM MF OM MN +=+，即可转化为求OM MN +的最小值，作点O 关于一次函数的对称点O '，过点O '作x 轴的垂线交x 轴于点N '，交一次函数于点M ，即OM MN +的最小值为O N ''，算出长度即可．【详解】（1）在33y x b 中，令0x =，则y b =， ∴点D 的坐标为(0,)b ，OD BE =，(23,4)B ，(23,4)E b ∴-，把(23,4)E b -代入33yx b 中得：34233b b -=-⨯+，解得：3b =；（2）由（1）得一次函数为333y x =-+，(0,3)D ，(23,1)E ， 3OD ∴=，1AE =，23=OA ，11=()(31)234322OADE S OD AE OA ∴+⋅=⨯+⨯=四边形， ODM ∆的面积与四边形OAEM 的面积之比为1:3， ODM 的面积与四边形OADE 的面积之比为1:4，134ODM OADE S S ∴==四边形，设点M 的横坐标为a ，则1332a ⨯=，解得：233a =，把233x =代入333y x =-+中得：73y =， 237(,)33M ∴；（3）如图所示，过点M 作MN x ⊥轴交于点N ， 30DFO ∠=，12MN MF ∴=， 12OM MF OM MN ∴+=+，作点O 关于一次函数的对称点O '，且OO’与直线DF 交于Q 点，过点O '作x 轴的垂线交x 轴于点N '，OM O M '∴=，12OM MF OM MN O M MN '∴+=+=+，当O '、M 、N 在同一直线时O M MN '+最小，即12OM MF OM MN O M MN '+=+=+的最小值为O N ''，30DFO ∠=︒，60ODF ∴∠=︒，30DOQ ∠=︒，903060O ON ''∠=︒-︒=︒，在Rt ODQ 中，333sin 60322OQ OD =⋅︒=⨯=， 233OO OQ ∴=='，在Rt ON O ''中．39sin 603322O N OO =︒='⨯=''， 12OM MF ∴+的最小值为92．【点睛】本题考查几何图形与函数的综合题，包括一次函数、矩形的性质、四边形的面积，解直角三角形以及胡不归问题，属于中考压轴题． 18．（1）y =32（x 12-）2938-，（12，938-）；（2）（12，72）或（12，72-）或（12，153+2-）或（12，1532--）或（12，36-）；（3）334【解析】【分析】【详解】思路引领：（1）将A 、B 、C 三点的坐标代入y ＝ax 2+bx +c ，利用待定系数法即可求出二次函数的表达式，进而得到其顶点坐标；（2）当以A ，B ，M ，N 为顶点的四边形为菱形时，分三种情况：∠以A 为圆心AB 为半径画弧与对称轴有两个交点，此时AM ＝AB ；∠以B 为圆心AB 为半径画弧与对称轴有两个交点，此时BM ＝AB ；∠线段AB 的垂直平分线与对称轴有一个交点，此时AM ＝BM ，分别列出方程，求解即可；（3）连接AB ，作DH ∠AB 于H ，交OB 于P ，此时12PB +PD 最小．最小值就是线段DH ，求出DH 即可．答案详解：（1）由题意03420a b c c a b c -+=⎧⎪=-⎨⎪++=⎩，解得 32323a b c ⎧=⎪⎪⎪⎪=-⎨⎪⎪=-⎪⎪⎩，∠抛物线解析式为y 32=x 232-x 3-， ∠y 32=x 232-x 332-=（x 12-）2938-，∠顶点坐标（12，938-）；（2）设点M 的坐标为（12，y ）．∠A （﹣1，0），B （0，3-）， ∠AB 2＝1+3＝4．∠以A 为圆心AB 为半径画弧与对称轴有两个交点，此时AM ＝AB ，则（12+1）2+y 2＝4，解得y ＝±72，即此时点M 的坐标为（12，72）或（12，72-）；∠以B 为圆心AB 为半径画弧与对称轴有两个交点，此时BM ＝AB ，则（12）2+（y 3+）2＝4，解得y 1532=-+或y 1532=--，即此时点M 的坐标为（12，1532-+）或（12，1532--）；∠线段AB 的垂直平分线与对称轴有一个交点，此时AM ＝BM ，则（12+1）2+y 2＝（12）2+（y 3+）2，解得y 36=-，即此时点M 的坐标为（12，36-）．综上所述，满足条件的点M 的坐标为（12，72）或（12，72-）或（12，1532-+）或（12，1532--）或（12，36-）；（3）如图，连接AB ，作DH ∠AB 于H ，交OB 于P ，此时12PB +PD 最小．理由：∠OA ＝1，OB 3=，∠tan∠ABO 33OA OB ==， ∠∠ABO ＝30°， ∠PH 12=PB ， ∠12PB +PD ＝PH +PD ＝DH ， ∠此时12PB +PD 最短（垂线段最短）．在Rt∠ADH 中，∠∠AHD ＝90°，AD 32=，∠HAD ＝60°， ∠sin60°DHAD=， ∠DH 334=， ∠12PB +PD 的最小值为334． 19．3 【解析】【分析】【详解】思路引领：(胡不归经典)作∠BON ＝∠AOB ＝30°，过点M 作MC ∠ON 于点C ，交OB 于点D ′，当MC ∠ON 时，（此时点D ′即为点D ）MD 12+OD ＝MD +CD 的值最小，最小值是CM的长，答案详解：如图，作∠BON ＝∠AOB ＝30°，过点M 作MC ∠ON 于点C ，交OB 于点D ′，∠CD ′12=OD ′ 所以当MC ∠ON 时，（此时点D ′即为点D ）MD 12+OD ＝MD +CD 的值最小，最小值是CM 的长，∠在Rt∠OCM 中，∠OMC ＝30°，OM ＝2 ∠OC ＝1， ∠CM 3=．答：MD 12+OD 的最小值为3．20．（1）241620999x x -++；（2）∠32；∠245【解析】【分析】【详解】思路引领：（1）设抛物线的解析式为：y ＝a （x +1）（x ﹣5），可得对称轴为直线x ＝2，由锐角三角函数可求点C 坐标，代入解析式可求解析式；（2）∠先求出直线BC 解析式，设P （2，t ），可得点E （534-t ，t ），点2315244F t t t ⎛⎫-- ⎪⎝⎭，，可求EF 的长，由三角形面积公式和二次函数性质可求解；∠根据图形的对称性可知∠ACD ＝∠BCD ，AC ＝BC ＝5，过点P 作PG ∠AC 于G ，可得PG35=PC ，可得35PC PB PG PB +=+，过点B 作BH ∠AC 于点H ，则PG +PB ≥BH ，即BH 是35PC +PB 的最小值，由三角形面积公式可求解．答案详解：（1）根据题意，可设抛物线的解析式为：y ＝a （x +1）（x ﹣5）， ∠抛物线的对称轴为直线x ＝2， ∠D （2，0），又∠43CDtan CBD DB∠==， ∠CD ＝BD •tan∠CBD ＝4，即C （2，4），代入抛物线的解析式，得4＝a （2+1）（2﹣5），解得 49a =-，∠二次函数的解析式为 ()()441599y x x =-+-=-x 2162099x ++；（2）∠设P （2，t ），其中0＜t ＜4，设直线BC 的解析式为 y ＝kx +b ，∠0542.k b k b =+⎧⎨=+⎩，，解得 4320.3k b ⎧=-⎪⎪⎨⎪=⎪⎩，即直线BC 的解析式为 42033y x =-+，令y ＝t ，得：354x t =-，∠点E （534-t ，t ），把354x t =- 代入()()4159y x x =-+-，得 24t y t ⎛⎫=- ⎪⎝⎭，即2315244F t t t ⎛⎫-- ⎪⎝⎭，， ∠221244t EF t t t t ⎛⎫=--=- ⎪⎝⎭，∠∠BCF 的面积12=⨯EF ×BD 32=（t 24t -）()223334(2)882t t t =--=--+，∠当t ＝2时，∠BCF 的面积最大，且最大值为32；∠如图，据图形的对称性可知∠ACD ＝∠BCD ，AC ＝BC ＝5，∠35AD sin ACD AC ∠==，过点P 作PG ∠AC 于G ，则在Rt∠PCG 中，35PG PC sin ACD PC =⋅∠=，∠35PC PB PG PB +=+，过点B 作BH ∠AC 于点H ，则PG +PB ≥BH ， ∠线段BH 的长就是35PC PB +的最小值，∠11641222ABCSAB CD =⨯⨯=⨯⨯=，又∠1522ABCSAC BH BH =⨯⨯=， ∠5122BH =，即245BH =， ∠35PC PB +的最小值为245．21．(1)21322y x x =--；1122y x =+；(2)ACE ∆的面积最大值是2516，此时E 点坐标为315,28⎛⎫- ⎪⎝⎭；(3)35PE PA +的最小值是3.【解析】【分析】(1)先写出平移后的抛物线解析式，再把点()1,0A -代入可求得a 的值，由ABD ∆的面积为5可求出点D 的纵坐标，代入抛物线解析式可求出横坐标，由A 、D 的坐标可利用待定系数法求出一次函数解析式； (2)作EMy 轴交AD 于M ，如图，利用三角形面积公式，由ACE AME CME S S S ∆∆∆=-构建关。

胡不归及经典例题与解析

胡不归及经典例题与解析
胡不归问题属于初中数学中的“PA+k·PB”型的最值问题，当遇到“PA+k·PB”型的最值问题时，再用“将军饮马”模型就无法解决，此时可分为两种类型进行解决。

第一种类型是当P在圆周上运动时，即称为“阿氏圆”问题；第二种类型是当P在直线上运动时，即称为“胡不归”问题。

以“胡不归”问题中的45°角模型为例，具体解析如下：
- 构造三角函数模型，过直线上的定点A向这条直线的另一侧作一个锐角α，使其正弦值等于要处理的系数，转化为垂线段最短解决问题。

- 特殊角模型，即45°角模型，作一个45°角使其正弦值等于线段的系数。

- 过动点作上一步的角的边的垂线，构造直角三角形。

- 根据两点之间线段最短，找到最小值的位置。

- 计算。

在“胡不归”问题中，涉及到三个点，其中有两个定点，一个动点，且动点是在直线上运动。

请注意，在具体的题目中，需要根据题目所给条件进行分析和计算。

2020年中考线段最值问题之胡不归问题

初中线段最值问题之---胡不归问题【引入】胡不归问题是一个非常古老的数学问题，曾经是历史上非常著名的“难题”。

近年来陆续成为各地中考模拟题的小热门考点，学生做起题来失分非常高或是无从下手，今天我们一块来探究下。

【实际背景】话说，从前有一小伙子外出务工，某天不幸得知老父亲病危的消息，便立即赶路回家．小伙子略懂数学常识，考虑到“两点之间线段最短”的知识，就走布满沙石的路直线路径，而忽视了走折线虽然路程多但速度快的实际情况，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”这个问题引起了人们的思索，小伙子能否节省路上时间提前到家？如果可以，他应该选择一条怎样的路线呢？这就是流传千百年的“胡不归问题。

【模型建立】将上述问题归结为如下图(1)数学模型即是：如图，A 是出发点，B 是目的地，直线AC 是一条驿道，而驿道靠目的地一侧全是砂土，人们走在不同的道路上的速度不同，设走在驿站AC 的速度是m 米/秒，走在砂石道路上的速度是n 米/秒；1、如果小伙子直接从A 到B ，则他需要的时间就是：nAB 秒； 2、如果小伙子先走一段路程的驿站，即先走到D 点，在沿着DB 回到家，则他需要的时间就是：(nBD m AD +)秒。

现在问题就是n BD m AD +的结果有没有可能比n AB 更小呢？【宏观分析】虽然沿着折线A -D -B 行走，路程变成长了，但是折线AD 的速度更快，所需要的时间更少；沿着AB 行走，虽然路程变短，但是速度变慢，所需要的时间更多，所以： n BD m AD +完全有可能比nAB 更小。

(图1)【理论分析】小伙子所需要的时间为：nBD m AD +，对它进行变形处理如下： )(1BD AD mn n n BD m AD +=+，由于n m ,均为题目给定的定值，所以求BD AD mn +的值即可。

由于B A ，均是动点，而D 是动点，故转变为两条折线段之和，故想办法将两条折线段AD mn 和BD 拉直时，其值最小，因此需要在图中构造出一条线段，使得其长度刚好为AD m n ，如下图（2）所示：（图2）在直线AC 的一侧作射线AM ，过D 点作AM 的垂线'DH ，由ADDH 'sin =α可知，线段AD DH ⋅=αsin '，令mn =αsin ， ∴此时BD AD mn +=BD DH BD AD +=+⋅'sin α，故由点到直线的距离垂线段最短可知：过B 点作AM 的垂线交AM 于点0H ，0BH 即为最小值。

中考数学复习之线段和差最值问题胡不归问题,附练习题含参考答案

中考数学复习线段和差最值系列之“胡不归”问题从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据“两点之间线段最短”，虽然从他此刻位置A 到家B 之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”（“胡”同“何”）而如果先沿着驿道AC 先走一段，再走砂石地，会不会更早些到家？数学家们于是建立起模型来解决这个问题.【模型建立】如图，一动点P 在直线MN 外的运动速度为V 1，在直线MN 上运动的速度为V 2，且V 1<V 2，A 、B 为定点，点C 在直线MN 上，确定点C 的位置使21AC BCV V +的值最小．【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭，记12V k V =，即求BC +kAC 的最小值．【问题解决】构造射线AD 使得sin ∠DAN =k ，CH /AC =k ，CH =kAC ．将问题转化为求BC +CH 最小值，过B 点作BH ⊥AD 交MN 于点C ，交AD 于H 点，此时BC +CH 取到最小值，即BC +kAC 最小．【模型总结】2驿道2MMM在求形如“P A +kPB ”的式子的最值问题中，关键是构造与kPB 相等的线段，将“P A +kPB ”型问题转化为“P A +PC ”型．而这里的PB 必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB 的等线段．例：如图，△ABC 中，AB =AC =10，tan A =2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD BD +的最小值是_______．【分析】本题关键在于处理”，考虑tan A =2，△ABE三边之比为1:2sin ∠，故作DH ⊥AB 交AB 于H点，则DH ．问题转化为CD +DH 最小值，故C 、D 、H共线时值最小，此时CD DH CH BE +===．【小结】本题简单在于题目已经将BA 线作出来，只需分析角度的三角函数值，作出垂线DH ，即可解决问题，若稍作改变，将图形改造如下：则需自行构造α，如下图，这一步正是解决“胡不归”问题关键所在．ABCDEHEDCB AABCDEHEDCBαsin αHEDC BAEDCB练习题1.如图，平行四边形ABCD 中，∠DAB =60°，AB =6，BC =2，P 为边CD 上的一动点，则PB 的最小值等于________．2.如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，则AB ＝2BC ．若AC ＝2，点D 是AB 的中点，P 为边CD 上一动点，则AP +12CP 的最小值为_______3.如图，在平面直角坐标系中，二次函数y ＝x 2+3x ﹣4的图象与x 轴交于A 、C 两点，与y 轴交于点B ，若P 是x 轴上一动点，点Q （0，2）在y 轴上，连接PQ ，则PQ+2PC 的最小值是_______4．如图，平面直角坐标系中，一次函数3y x =-+x 轴、y 轴于A 、B 两点，若C 是x 轴上的动点，则2BC +AC 的最小值__________ABCDP5.如图，在△ABC中，∠A＝90°，∠B＝60°，AB＝2，若D是BC边上一动点，则AD+1 2DC的最小值为________6.如图．在平面直角坐标系xOy中，点A坐标为（0，，点C坐标为（2，0），点B为线段OA上一个动点，则12AB+BC的最小值为_______7.如图，在△ABC中，∠A＝15°，AB＝10，P为AC边上的一个动点（不与A、C重合），连接BP，则2AP+PB的最小值是________8.如图，△ABC中，AB＝AC＝10，∠A＝45°，BD是△ABC的边AC上的高，点P是BD上动点，则2BP+CP的最小值是（）9.在△ABC中，∠ACB＝90°，P为AC上一动点，若BC＝4，AC＝6BP+AP的最小值为________.10．如图所示，菱形ABCO的边长为5，对角线OB的长为P为OB上一动点，则AP+的最小值为__________.11.如图，△ABC为等边三角形，BD平分∠ABC，△ABC点P为BD上动点，连接AP，则AP+12BP的最小值为．12.如图，在Rt△ABC中，∠C＝90°，∠BAC＝60°，BC＝20cm，E是∠BAC平分线AD 上一点．现有一动点P沿着折线A﹣E﹣C运动，在AE上的速度是每秒4cm，在EC上的速度是每秒2cm，则点P从点A到点C的运动过程至少需_________s．13.如图，直角三角形ABC中，∠A＝30°，BC＝1，BD是∠ABC的平分线，点P是线段BD上的动点，求CP+12BP的最小值．14.如图，在△ABC 中，∠C ＝90°，AC ＝2，BC ＝6．点D 是在边BC 上的动点，则23BD +AD 的最小值是．15.如图，矩形ABCD 中，点P 是AD 边上的动点，AB ＝2，BC ＝3，以PC 为边作如图所示的矩形PEFC ，且PE ：EF ＝2：3，则2PB +3CF 的最小值是．16.如图，已知抛物线()()248ky x x =+-（k 为常数，且k >0）与x 轴从左至右依次交于A ，B两点，与y 轴交于点C ，经过点B 的直线y b =+与抛物线的另一交点为D ．（1）若点D 的横坐标为-5，求抛物线的函数表达式；（2）在（1）的条件下，设F 为线段BD 上一点（不含端点），连接AF ，一动点M 从点A 出发，沿线段AF 以每秒1个单位的速度运动到F ，再沿线段FD 以每秒2个单位的速度运动到D 后停止，当点F 的坐标是多少时，点M 在整个运动过程中用时最少？17.抛物线2y=x轴交于点A，B（点A在点B的左边），与y轴交于点C．点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E；将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当12PE EC+的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标．（为突出问题，删去了两个小问）参考答案4.65.66.29.10 10.4 12.5 15.1016.(1)2y x x=(2)F(-2，) 17.O1(，0)。

中考专题- 胡不归专题(解析版)

专题03 胡不归专题在前面的最值问题中往往都是求某个线段最值或者形如P A +PB 最值，除此之外我们还可能会遇上形如“P A +kP ”这样的式子的最值，此类式子一般可以分为两类问题：（1）胡不归问题；（2）阿氏圆．【故事介绍】从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据“两点之间线段最短”，虽然从他此刻位置A 到家B 之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”（“胡”同“何”）而如果先沿着驿道AC 先走一段，再走砂石地，会不会更早些到家？【模型建立】如图，一动点P 在直线MN 外的运动速度为V 1，在直线MN 上运动的速度为V 2，且V 1<V 2，A 、B 为定点，点C 在直线MN 上，确定点C 的位置使21AC BCV V的值最小．V 1V 2V 1驿道砂石地ABCV 2V 1MNCBA【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭，记12V k V =，即求BC +kAC 的最小值．【问题解决】构造射线AD 使得sin ∠DAN =k ，即CHk AC=，CH =kAC ．将问题转化为求BC +CH 最小值，过B 点作BH ⊥AD 交MN 于点C ，交AD 于H 点，此时BC +CH 取到最小值，即BC +kAC 最小．M M【模型总结】在求形如“P A+kPB”的式子的最值问题中，关键是构造与kPB相等的线段，将“P A+kPB”型问题转化为“P A+PC”型．而这里的PB必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB的等线段．例题1. 如图，△ABC中，AB=AC=10，tan A=2，BE⊥AC于点E，D是线段BE上的一个动点，则CD 的最小值是_______．【分析】本题关键在于处理BD”，考虑tan A=2，△ABE三边之比为1:2sin∠，故作DH⊥AB交AB于H点，则DH=．问题转化为CD+DH最小值，故C、D、H共线时值最小，此时CD DH CH BE+===．【小结】本题简单在于题目已经将BA线作出来，只需分析角度的三角函数值，作出垂线DH，即可解决问题，若稍作改变，将图形改造如下：则需自行构造α，如下图，这一步正是解决“胡不归”问题关键所在．变式练习>>>1．如图，平行四边形ABCD中，∠DAB=60°，AB=6，BC=2，P为边CD上的一动点，则PB+的最小值等于________．【分析】考虑如何构造”，已知∠A=60°，且，故延长AD，作PH⊥AD延长线于H点，即可得PH，将问题转化为：求PB+PH最小值．当B、P、H三点共线时，可得PB+PH取到最小值，即BH的长，解直角△ABH即可得BH长．AB CDEHEDCBA AB CDEHαsinα5H EDCBAEDCBA BCD PMHPD CBA A BCD PHM例题2. 如图，AC是圆O的直径，AC＝4，弧BA＝120°，点D是弦AB上的一个动点，那么OD+BD的最小值为（）A．B．C．D．【解答】解：∵的度数为120°，∵∵C＝60°，∵AC是直径，∵∵ABC＝90°，∵∵A＝30°，作BK∵CA，DE∵BK于E，OM∵BK于M，连接OB．∵BK∵AC，∵∵DBE＝∵BAC＝30°，在Rt∵DBE中，DE＝BD，∵OD+BD＝OD+DE，根据垂线段最短可知，当点E与M重合时，OD+BD的值最小，最小值为OM，∵∵BAO＝∵ABO＝30°，∵∵OBM＝60°，在Rt∵OBM中，∵OB＝2，∵OBM＝60°，∵OM＝OB•sin60°＝，∵DB+OD的最小值为，故选：B．变式练习>>>2．如图，∵ABC中，∵BAC＝30°且AB＝AC，P是底边上的高AH上一点．若AP+BP+CP的最小值为2，则BC＝﹣．【解答】解：如图将∵ABP绕点A顺时针旋转60°得到∵AMG．连接PG，CM．∵AB＝AC，AH∵BC，∵∵BAP＝∵CAP，∵P A＝P A，∵∵BAP∵∵CAP（SAS），∵PC＝PB，∵MG＝PB，AG＝AP，∵GAP＝60°，∵∵GAP是等边三角形，∵P A＝PG，∵P A+PB+PC＝CP+PG+GM，∵当M，G，P，C共线时，P A+PB+PC的值最小，最小值为线段CM的长，∵AP+BP+CP的最小值为2，∵CM＝2，∵∵BAM＝60°，∵BAC＝30°，∵∵MAC＝90°，∵AM＝AC＝2，作BN∵AC于N．则BN＝AB＝1，AN＝，CN＝2﹣，∵BC＝＝＝﹣．故答案为﹣．例题3. 等边三角形ABC的边长为6，将其放置在如图所示的平面直角坐标系中，其中BC边在x轴上，BC边的高OA在Y轴上．一只电子虫从A出发，先沿y轴到达G点，再沿GC到达C点，已知电子虫在Y轴上运动的速度是在GC上运动速度的2倍，若电子虫走完全程的时间最短，则点G的坐标为（0，）．【解答】解：如图作GM∵AB于M，设电子虫在CG上的速度为v，电子虫走完全全程的时间t＝+＝（+CG），在Rt∵AMG中，GM＝AG，∵电子虫走完全全程的时间t＝（GM+CG），当C、G、M共线时，且CM∵AB时，GM+CG最短，此时CG＝AG＝2OG，易知OG＝•×6＝所以点G的坐标为（0，﹣）．故答案为：（0，﹣）．变式练习>>>3．如图，∵ABC在直角坐标系中，AB＝AC，A（0，2），C（1，0），D为射线AO上一点，一动点P 从A出发，运动路径为A→D→C，点P在AD上的运动速度是在CD上的3倍，要使整个运动时间最少，则点D的坐标应为（）A．（0，）B．（0，）C．（0，）D．（0，）解：假设P在AD的速度为3V，在CD的速度为1V，总时间t＝+＝（+CD），要使t最小，就要+CD最小，因为AB＝AC＝3，过点B作BH∵AC交AC于点H，交OA于D，易证∵ADH∵∵ACO，所以＝＝3，所以＝DH，因为∵ABC是等腰三角形，所以BD＝CD，所以要+CD最小，就是要DH+BD最小，就要B、D、H三点共线就行了．因为∵AOC∵∵BOD，所以＝，即＝，所以OD＝，所以点D的坐标应为（0，）．例题4. 直线y＝与抛物线y＝（x﹣3）2﹣4m+3交于A，B两点（其中点A在点B的左侧），与抛物线的对称轴交于点C，抛物线的顶点为D（点D在点C的下方），设点B的横坐标为t（1）求点C的坐标及线段CD的长（用含m的式子表示）；（2）直接用含t的式子表示m与t之间的关系式（不需写出t的取值范围）；（3）若CD＝CB．∵求点B的坐标；∵在抛物线的对称轴上找一点F，使BF+CF的值最小，则满足条件的点F的坐标是（3，）．【解答】解：（1）抛物线y＝（x﹣3）2﹣4m+3的对称轴为x＝3，令x＝3，则有y＝×3＝4，即点C的坐标为（3，4）．抛物线y＝（x﹣3）2﹣4m+3的顶点D的坐标为（3，﹣4m+3），∵点D在点C的下方，∵CD＝4﹣（﹣4m+3）＝4m+1．（2）∵点B在直线y＝上，且其横坐标为t，则点B的坐标为（t，t），将点B的坐标代入抛物线y＝（x﹣3）2﹣4m+3中，得：t＝（t﹣3）2﹣4m+3，整理，得：m＝﹣t+3．（3）∵依照题意画出图形，如图1所示．过点C作CE∵x轴，过点B作BE∵y轴交CE于点E．∵直线BC的解析式为y＝x，∵BE＝CE，由勾股定理得：BC＝＝CE．∵CD＝CB，∵有4m+1＝（t﹣3）＝（+﹣3），解得：m＝﹣4，或m＝1．当m＝﹣4时，+4×（﹣4）＝﹣＜0，不合适，∵m＝1，此时t＝+＝6，y＝×6＝8．故此时点B的坐标为（6，8）．∵作B点关于对称轴的对称点B′，过点F作FM∵BC于点M，连接B′M、BB交抛物线对称轴于点N，如图2所示．∵直线BC的解析式为y＝x，FM∵BC，∵tan∵FCM＝＝，∵sin∵FCM＝．∵B、B′关于对称轴对称，∵BF＝B′F，∵BF+CF＝B′F+FM．当点B′、F、M三点共线时B′F+FM最小．∵B点坐标为（6，8），抛物线对称轴为x＝3，∵B′点的坐标为（0，8）．又∵B′M∵BC，∵tan∵NB′F＝，∵NF＝B′N•tan∵NB′F＝，∵点F的坐标为（3，）．故答案为：（3，）．变式练习>>>4．如图1，在平面直角坐标系中将y＝2x+1向下平移3个单位长度得到直线l1，直线l1与x轴交于点C；直线l2：y＝x+2与x轴、y轴交于A、B两点，且与直线l1交于点D．（1）填空：点A的坐标为（﹣2，0），点B的坐标为（0，2）；（2）直线l1的表达式为y＝2x﹣2；（3）在直线l1上是否存在点E，使S∵AOE＝2S∵ABO？若存在，则求出点E的坐标；若不存在，请说明理由．（4）如图2，点P为线段AD上一点（不含端点），连接CP，一动点H从C出发，沿线段CP以每秒1个单位的速度运动到点P，再沿线段PD以每秒个单位的速度运动到点D后停止，求点H在整个运动过程中所用时间最少时点P的坐标．【解答】解：（1）直线l2：y＝x+2，令y＝0，则x＝﹣2，令y＝0，则x＝2，故答案为（﹣2，0）、（0，2）；（2）y＝2x+1向下平移3个单位长度得到直线l1，则直线l1的表达式为：y＝2x﹣2，故：答案为：y＝2x﹣2；（3）∵S∵AOE＝2S∵ABO，∵y E＝2OB＝4，将y E＝4代入l1的表达式得：4＝2x﹣2，解得：x＝3，则点E的坐标为（3，4）；（4）过点P、C分别作y轴的平行线，分别交过点D作x轴平行线于点H、H′，H′C交BD于点P′，直线l2：y＝x+2，则∵ABO＝45°＝∵HBD，PH＝PD，点H在整个运动过程中所用时间＝+＝PH+PC，当C、P、H在一条直线上时，PH+PC最小，即为CH′＝6，点P坐标（1，3），故：点H在整个运动过程中所用最少时间为6秒，此时点P的坐标（1，3）．例题5. 已知抛物线y＝a（x+3）（x﹣1）（a≠0），与x轴从左至右依次相交于A、B两点，与y轴相交于点C，经过点A的直线y＝﹣x+b与抛物线的另一个交点为D．（1）若点D的横坐标为2，求抛物线的函数解析式；（2）若在（1）的条件下，抛物线上存在点P，使得∵ACP是以AC为直角边的直角三角形，求点P的坐标；（3）在（1）的条件下，设点E是线段AD上的一点（不含端点），连接BE．一动点Q从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段ED以每秒个单位的速度运动到点D后停止，问当点E的坐标是多少时，点Q在整个运动过程中所用时间最少？【解答】解：（1）∵y＝a（x+3）（x﹣1），∵点A的坐标为（﹣3，0）、点B两的坐标为（1，0），∵直线y＝﹣x+b经过点A，∵b＝﹣3，∵y＝﹣x﹣3，当x＝2时，y＝﹣5，则点D的坐标为（2，﹣5），∵点D在抛物线上，∵a（2+3）（2﹣1）＝﹣5，解得，a＝﹣，则抛物线的解析式为y＝﹣（x+3）（x﹣1）＝﹣x2﹣2x+3；（2）∵A的坐标为（﹣3，0），C（0，3），∵直线AC的解析式为：y＝x+3，∵∵∵ACP是以AC为直角边的直角三角形，∵CP∵AC，∵设直线CP的解析式为：y＝﹣x+m，把C（0，3）代入得m＝3，∵直线CP的解析式为：y＝﹣x+3，解得，（不合题意，舍去），∵P（﹣，）；∵∵∵ACP是以AC为直角边的直角三角形，∵AP∵AC，∵设直线CP的解析式为：y＝﹣x+n，把A（﹣3，0）代入得n＝﹣，∵直线AP的解析式为：y＝﹣x﹣，解y＝得，，∵P（，﹣），综上所述：点P的坐标为（﹣，）或（，﹣）；（3）如图2中，作DM∵x轴交抛物线于M，作DN∵x轴于N，作EF∵DM于F，则tan∵DAN＝＝＝，∵∵DAN＝60°，∵∵EDF＝60°，∵DE＝＝EF，∵Q的运动时间t＝+＝BE+32DE=BE+EF，∵当BE和EF共线时，t最小，则BE∵DM，此时点E坐标（1，﹣4）．变式练习>>>5．如图，已知抛物线y＝﹣x2+bx+c交x轴于点A（2，0）、B（﹣8，0），交y轴于点C，过点A、B、C三点的∵M与y轴的另一个交点为D．（1）求此抛物线的表达式及圆心M的坐标；（2）设P为弧BC上任意一点（不与点B，C重合），连接AP交y轴于点N，请问：AP•AN是否为定值，若是，请求出这个值；若不是，请说明理由；（3）延长线段BD交抛物线于点E，设点F是线段BE上的任意一点（不含端点），连接AF．动点Q 从点A出发，沿线段AF以每秒1个单位的速度运动到点F，再沿线段FB以每秒个单位的速度运动到点B后停止，问当点F的坐标是多少时，点Q在整个运动过程中所用时间最少？【解答】解：（1）抛物线解析式为y＝﹣（x+8）（x﹣2），即y＝﹣x2﹣x+4；当x＝0时，y＝﹣x2﹣x+4＝4，则C（0，4）∵BC＝4，AC＝2，AB＝10，∵BC2+AC2＝AB2，∵∵ABC为直角三角形，且∵ACB＝90°，∵AB为直径，∵圆心M点的坐标为（﹣3，0）；（2）以AP•AN为定值．理由如下：如图1，∵AB为直径，∵∵APB＝90°，∵∵APB＝∵AON，∵NAO＝∵BAP，∵∵APB∵∵AON．∵AN：AB＝AO：AP，∵AN•AP＝AB•AO＝20，所以AP•AN为定值，定值是20；（3）∵AB∵CD，∵OD＝OC＝4，则D（0，﹣4），易得直线BD的解析式为y＝﹣x﹣4，过F点作FG∵x轴于G，如图2，∵FG∵OD，∵∵BFG∵∵BDO，∵＝，即＝＝＝，∵点Q沿线段FB以每秒个单位的速度运动到点B所用时间等于点Q以每秒1个单位的速度运动到G点的时间，∵当AF+FG的值最小时，点Q在整个运动过程中所用时间最少，作∵EBI＝∵ABE，BI交y轴于I，作FH∵BI于H，则FH＝FG，∵AF+FG＝AF+FH，当点A、F、H共线时，AF+FH的值最小，此时AH∵BI，如图2，作DK∵BI，垂足为K，∵BE平分∵ABI，∵DK＝DO＝4，设DI＝m，∵∵DIK＝∵BIO，∵∵IDK∵∵IBO，∵＝＝＝，∵BI＝2m，在Rt∵OBI中，82+（4+m）2＝（2m）2，解得m1＝4（舍去），m2＝，∵I（0，﹣），设直线BI的解析式为y＝kx+n，把B（﹣8，0），I（0，﹣）代入得，解得，∵直线BI的解析式为y＝﹣x﹣，∵AH∵BI，∵直线AH的解析式可设为y＝x+q，把A（2，0）代入得+q＝0，解得q＝﹣，∵直线AH的解析式为y＝x﹣，解方程组，解得，∵F（﹣2，﹣3），即当点F的坐标是（﹣2，﹣3）时，点Q在整个运动过程中所用时间最少．1. 如图，在平面直角坐标系中，点()3,3A ，点P 为x 轴上的一个动点，当OP AP 21+最小时，点P 的坐标为___________.[答案]：()0,2P2. 如图，四边形ABCD 是菱形，AB=4，且∠ABC=60°，点M 为对角线BD （不含点B ）上的一动点，则BM AM 21+的最小值为___________.[答案]：323. 如图，在平面直角坐标系中，二次函数y ＝ax 2+bx +c 的图象经过点A （﹣1，0），B （0，﹣），C（2，0），其对称轴与x 轴交于点D ．（1）求二次函数的表达式及其顶点坐标；（2）点M 为抛物线的对称轴上的一个动点，若平面内存在点N ，使得以A ，B ，M ，N 为顶点的四边形为菱形，求点M 的坐标；（3）若P 为y 轴上的一个动点，连接PD ，求PB +PD 的最小值．【解答】（1）由题意，解得，∵抛物线解析式为y＝x2﹣x﹣，∵y＝x2﹣x﹣＝（x﹣）2﹣，∵顶点坐标（，﹣）；（2）设点M的坐标为（，y）．∵A（﹣1，0），B（0，﹣），∵AB2＝1+3＝4．∵以A为圆心AB为半径画弧与对称轴有两个交点，此时AM＝AB，则（+1）2+y2＝4，解得y＝±，即此时点M的坐标为（，）或（，﹣）；∵以B为圆心AB为半径画弧与对称轴有两个交点，此时BM＝AB，则（）2+（y+）2＝4，解得y＝﹣+或y＝﹣﹣，即此时点M的坐标为（，﹣+）或（，﹣﹣）；∵线段AB的垂直平分线与对称轴有一个交点，此时AM＝BM，则（+1）2+y2＝（）2+（y+）2，解得y＝﹣，即此时点M的坐标为（，﹣）．综上所述，满足条件的点M的坐标为（，）或（，﹣）或（，﹣+）或（，﹣﹣）或（，﹣）；（3）如图，连接AB，作DH∵AB于H，交OB于P，此时PB+PD最小．理由：∵OA＝1，OB＝，∵tan∵ABO＝＝，∵∵ABO＝30°，∵PH＝PB，∵PB+PD＝PH+PD＝DH，∵此时PB+PD最短（垂线段最短）．在Rt∵ADH中，∵∵AHD＝90°，AD＝，∵HAD＝60°，∵sin60°＝，∵DH＝，∵PB+PD的最小值为．4. 【问题提出】如图∵，已知海岛A到海岸公路BD的距离为AB的长度，C为公路BD上的酒店，从海岛A到酒店C，先乘船到登陆点D，船速为a，再乘汽车，车速为船速的n倍，点D选在何处时，所用时间最短？【特例分析】若n＝2，则时间t＝+，当a为定值时，问题转化为：在BC上确定一点D，使得+的值最小．如图∵，过点C做射线CM，使得∵BCM＝30°．（1）过点D作DE∵CM，垂足为E，试说明：DE＝；（2）请在图∵中画出所用时间最短的登陆点D′．【问题解决】（3）请你仿照“特例分析”中的相关步骤，解决图∵中的问题．（写出具体方案，如相关图形呈现、图形中角所满足的条件、作图的方法等）【综合运用】（4）如图∵，抛物线y＝﹣x2+x+3与x轴分别交于A，B两点，与y轴交于点C，E为OB中点，设F为线段BC上一点（不含端点），连接EF．一动点P从E出发，沿线段EF以每秒1个单位的速度运动到F，再沿着线段FC以每秒个单位的速度运动到C后停止．若点P在整个运动过程中用时最少，请求出最少时间和此时点F的坐标．【解答】解：（1）如图∵，∵DE∵CM，∵∵DEC＝90°，在Rt∵BCM中，DE＝CD sin30°＝CD；（2）如图∵过点A作AE′∵CM交BC于点D′，则点D′即为所用时间最短的登陆点；（3）如图∵，过点C作射线CM，使得sin∵BCM＝，过点A作AE∵CM，垂足为E交BC于点D，则点D为为所用时间最短的登陆点；（4）由题意得：t＝＝EF+CF，过点C作CD∵x轴交抛物线于点D，过点F作GF∵CD交CD于点G，∵ACB＝∵DCB＝α，sin∵ABC＝＝，则EF＝CF，EF+CF＝EF+FH，故当E、F、H三点共线且与CD垂直时，t最小，将点B、C坐标代入一次函数表达式并解得：直线BC的表达式为：y＝﹣x+3，点E是OB中点，其坐标为：（3，0），当x＝3时，对于y＝﹣x+3，y＝，点F坐标为（3，），t＝＝EF+CF，当H、F、E三点共线时，EF+FH＝OC＝3，即：最小时间为3秒．5. 如图，∵ABC是等边三角形．（1）如图1，AH∵BC于H，点P从A点出发，沿高线AH向下移动，以CP为边在CP的下方作等边三角形CPQ，连接BQ．求∵CBQ的度数；（2）如图2，若点D为∵ABC内任意一点，连接DA，DB，DC．证明：以DA，DB，DC为边一定能组成一个三角形；（3）在（1）的条件下，在P点的移动过程中，设x＝AP+2PC，点Q的运动路径长度为y，当x取最小值时，写出x，y的关系，并说明理由．【解答】（1）解：如图1中∵∵ABC是等边三角形，AH∵BC，∵∵CAP＝∵BAC＝30°，CA＝CB，∵ACB＝60°，∵∵PCQ是等边三角形，∵CP＝CQ，∵PCQ＝∵ACB＝60°，∵∵ACP＝∵BCQ，∵∵ACP∵∵BCQ，∵∵CBQ＝∵CAP＝30°．（2）证明：如图2中，将∵ADC绕当A顺时针旋转60°得到∵ABQ，连接DQ．∵∵ACD∵∵ABQ，∵AQ＝AD，CD＝BQ，∵∵DAQ＝60°，∵∵ADQ是等边三角形，∵AD＝DQ，∵DA，DB，DC为边一定能组成一个三角形（图中∵BDQ）．（3）如图3中，作PE∵AB于E，CF∵AB于F交AH于G．∵PE＝P A，∵P A+2PC＝2（P A+PC）＝2（PE+PC），根据垂线段最短可知，当E与F重合，P与G重合时，P A+2PC的值最小，最小值为2CF．由（1）可知∵ACP∵∵BCQ，可得BQ＝P A，∵P A＝BQ＝AG＝CG＝y，FG＝y，∵x＝2（y+y），∵y＝x．6. 如图，已知抛物线y＝（x+2）（x﹣4）（k为常数，且k＞0）与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y＝﹣x+b与抛物线的另一交点为D．（1）若点D的横坐标为﹣5，求抛物线的函数表达式；（2）若在第一象限内的抛物线上有点P，使得以A，B，P为顶点的三角形与∵ABC相似，求k的值；（3）在（1）的条件下，设F为线段BD上一点（不含端点），连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F 的坐标是多少时，点M在整个运动过程中用时最少？【解答】解：（1）抛物线y＝（x+2）（x﹣4），令y＝0，解得x＝﹣2或x＝4，∵A（﹣2，0），B（4，0）．∵直线y＝﹣x+b经过点B（4，0），∵﹣×4+b＝0，解得b＝，∵直线BD解析式为：y＝﹣x+．当x＝﹣5时，y＝3，∵D（﹣5，3）．∵点D（﹣5，3）在抛物线y＝（x+2）（x﹣4）上，∵（﹣5+2）（﹣5﹣4）＝3，∵k＝．∵抛物线的函数表达式为：y＝（x+2）（x﹣4）．即y＝x2﹣x﹣．（2）由抛物线解析式，令x＝0，得y＝﹣k，∵C（0，﹣k），OC＝k．因为点P在第一象限内的抛物线上，所以∵ABP为钝角．因此若两个三角形相似，只可能是∵ABC∵∵APB或∵ABC∵∵P AB．∵若∵ABC∵∵APB，则有∵BAC＝∵P AB，如答图2﹣1所示．设P（x，y），过点P作PN∵x轴于点N，则ON＝x，PN＝y．tan∵BAC＝tan∵P AB，即：，∵y＝x+k．∵P（x，x+k），代入抛物线解析式y＝（x+2）（x﹣4），得（x+2）（x﹣4）＝x+k，整理得：x2﹣6x﹣16＝0，解得：x＝8或x＝﹣2（与点A重合，舍去），∵P（8，5k）．∵∵ABC∵∵APB，∵，即，解得：k＝．∵若∵ABC∵∵P AB，则有∵ABC＝∵P AB，如答图2﹣2所示．设P（x，y），过点P作PN∵x轴于点N，则ON＝x，PN＝y．tan∵ABC＝tan∵P AB，即：＝，∵y＝x+．∵P（x，x+），代入抛物线解析式y＝（x+2）（x﹣4），得（x+2）（x﹣4）＝x+，整理得：x2﹣4x﹣12＝0，解得：x＝6或x＝﹣2（与点A重合，舍去），∵P（6，2k）．∵∵ABC∵∵P AB，＝，∵＝，解得k＝±，∵k＞0，∵k＝，综上所述，k＝或k＝．（3）方法一：如答图3，由（1）知：D（﹣5，3），如答图2﹣2，过点D作DN∵x轴于点N，则DN＝3，ON＝5，BN＝4+5＝9，∵tan∵DBA＝＝＝，∵∵DBA＝30°．过点D作DK∵x轴，则∵KDF＝∵DBA＝30°．过点F作FG∵DK于点G，则FG＝DF．由题意，动点M运动的路径为折线AF+DF，运动时间：t＝AF+DF，∵t＝AF+FG，即运动的时间值等于折线AF+FG的长度值．由垂线段最短可知，折线AF+FG的长度的最小值为DK与x轴之间的垂线段．过点A作AH∵DK于点H，则t最小＝AH，AH与直线BD的交点，即为所求之F点．∵A点横坐标为﹣2，直线BD解析式为：y＝﹣x+，∵y＝﹣×（﹣2）+＝2，∵F（﹣2，2）．综上所述，当点F坐标为（﹣2，2）时，点M在整个运动过程中用时最少．方法二：作DK∵AB，AH∵DK，AH交直线BD于点F，∵∵DBA＝30°，∵∵BDH＝30°，∵FH＝DF×sin30°＝，∵当且仅当AH∵DK时，AF+FH最小，点M在整个运动中用时为：t＝，∵l BD：y＝﹣x+，∵F X＝A X＝﹣2，∵F（﹣2，）．7. 已如二次函数y＝﹣x2+2x+3的图象和x轴交于点A、B（点A在点B的左侧），与y轴交于点C，（1）如图1，P是直线BC上方抛物线上一动点（不与B、C重合）过P作PQ∵x轴交直线BC于Q，求线段PQ的最大值；（2）如图2，点G为线段OC上一动点，求BG+CG的最小值及此时点G的坐标；（3）如图3，在（2）的条件下，M为直线BG上一动点，N为x轴上一动点，连接AM，MN，求AM+MN的最小值．【解答】解：（1）令y＝0，即：﹣x2+2x+3＝0，解得：x＝3或﹣1，即点A、B的坐标分比为（﹣1，0）、（3，0），令x＝0，则y＝3，则点C的坐标为（0，3），直线BC过点C（0，3），则直线表达式为：y＝kx+3，将点B坐标代入上式得：0＝3k+3，解得：k＝﹣1，则直线BC的表达式为：y＝﹣x+3，设点P的坐标为（m，n），n＝﹣m2+2m+3，则点Q坐标为（3﹣n，n），则PQ＝m﹣（3﹣n）＝﹣m2+3m，∵a＝﹣1＜0，则PQ有最大值，当m＝﹣＝，PQ取得最大值为；（2）过直线CG作∵GCH＝α，使CH∵GH，当sinα＝时，HG＝GC，则BG+CG的最小值即为HG+GB的最小值，当B、H、G三点共线时，HG+GB最小，则∵GBO＝α，∵sinα＝，则cosα＝，tanα＝，OG＝OB•tanα＝3×＝，即点G（0，），CG＝3﹣＝，而BG＝，BG+CG的最小值为：；（3）作点A关于直线BG的对称点A′，过A′作A′N∵x轴，交BG于点M，交x轴于点N，则此时AM+MN取得最小值，即为A′N的长度，则：∵GBA＝∵AA′N＝∵OGB＝α，AA′＝2AB sin∵ABG＝2×4×sinα＝，A′N＝A′A cosα＝×＝，即：AM+MN的最小值为．8. 如图，在Rt∵ABC中，∵ACB＝90°，∵B＝30°，AB＝4，点D、F分别是边AB，BC上的动点，连接CD，过点A作AE∵CD交BC于点E，垂足为G，连接GF，则GF+FB的最小值是（）A．B．C．D．【解答】解：延长AC到点P，使CP＝AC，连接BP，过点F作FH∵BP于点H，取AC中点O，连接OG，过点O作OQ∵BP于点Q，∵∵ACB＝90°，∵ABC＝30°，AB＝4，∵AC＝CP＝2，BP＝AB＝4∵∵ABP是等边三角形，∵∵FBH＝30°∵Rt∵FHB 中，FH ＝FB∵当G 、F 、H 在同一直线上时，GF +FB ＝GF +FH ＝GH 取得最小值 ∵AE ∵CD 于点G ，∵∵AGC ＝90° ∵O 为AC 中点，∵OA ＝OC ＝OG ＝AC∵A 、C 、G 三点共圆，圆心为O ，即点G 在∵O 上运动 ∵当点G 运动到OQ 上时，GH 取得最小值 ∵Rt∵OPQ 中，∵P ＝60°，OP ＝3，sin∵P ＝ ∵OQ ＝OP ＝，∵GH 最小值为故选：C ．9. 抛物线2623663y x x =--+与x 轴交于点A ，B （点A 在点B 的左边），与y 轴交于点C ．点P 是直线AC 上方抛物线上一点，PF ⊥x 轴于点F ，PF 与线段AC 交于点E ；将线段OB 沿x 轴左右平移，线段OB的对应线段是O 1B 1，当12PE EC +的值最大时，求四边形PO 1B 1C 周长的最小值，并求出对应的点O 1的坐标．【分析】根据抛物线解析式得A ()32,0-、B ()2,0、C ()0,6，直线AC 的解析式为：363y x =+，可知AC 与x 轴夹角为30°．根据题意考虑，P 在何处时，PE +2EC取到最大值．过点E 作EH ⊥y 轴交y 轴于H 点，则∠CEH =30°，故CH =2EC，问题转化为PE +CH 何时取到最小值．考虑到PE 于CH 并无公共端点，故用代数法计算，设2623,663P m m m ⎛⎫--+ ⎪ ⎪⎝⎭，则3,63E m m ⎛⎫+ ⎪ ⎪⎝⎭，30,63H m ⎛⎫+ ⎪ ⎪⎝⎭，2636PE m m =--，E B 1O 1P A BCFyx O H O xyFC BA P O 1B 1EC 1O xyF CBAP O 1B 1ECH=，22=PE CH m+=+∵当PE+EC的值最大时，x＝﹣2，此时P（﹣2，），∵PC＝2，∵O1B1＝OB＝，∵要使四边形PO1B1C周长的最小，即PO1+B1C的值最小，如图2，将点P向右平移个单位长度得点P1（﹣，），连接P1B1，则PO1＝P1B1，再作点P1关于x轴的对称点P2（﹣，﹣），则P1B1＝P2B1，∵PO1+B1C＝P2B1+B1C，∵连接P2C与x轴的交点即为使PO1+B1C的值最小时的点B1，∵B1（﹣，0），将B1向左平移个单位长度即得点O1，此时PO1+B1C＝P2C＝＝，对应的点O1的坐标为（﹣，0），∵四边形PO1B1C周长的最小值为+3.。

2020中考专题9——最值问题之胡不归

2020中考专题9——最值问题之胡不归班级姓名.【模型解析】◆条件：A、B 为定点，P 为射线AC 上一个动点◆问题：点P 在何处，AP m n BP +（1<mn）最短。

◆方法：第一步.在AC 的一侧，PB 的异侧，构造∠CAE=α,使得mn=αsin ;第二步.作BH ⊥AE 于点E，交AC 于点P,此时点P 就是所求位置，BH 就是AP mnBP +的最小值.【例题分析】例1.【问题提出】如图①，已知海岛A 到海岸公路BD 的距离为AB ，C 为公路BD 上的酒店，从海岛A 到酒店C ，先乘船到登陆点D ，船速为a ，再乘汽车，车速为船速的n 倍，点D 选在何处时，所用时间最短？【特例分析】若n ＝2，则时间t ＝aCDa AD 2+，当a 为定值时，问题转化为：在BC 上确定一点D ，使得2CDAD +的值最小．如图②，过点C 做射线CM ，使得∠BCM ＝30°．（1）过点D 作DE ⊥CM ，垂足为E ，试说明：2CDDE =；（2）请在图②中画出所用时间最短的登陆点D ′，并说明理由．【问题解决】（3）请你仿照“特例分析”中的相关步骤，解决图①中的问题（写出具体方案，如相关图形呈现、图形中角所满足的条件、作图的方法等）．【模型运用】（4）如图③，海面上一标志A 到海岸BC 的距离AB ＝300m ，BC ＝300m ．救生员在C 点处发现标志A 处有人求救，立刻前去营救，若救生员在岸上跑的速度都是6m /s ，在海中游泳的速度都是2m /s ，求救生员从C 点出发到达A 处的最短时间．2.（2019•南通）如图，▱ABCD 中，∠DAB ＝60°，AB ＝6，BC ＝2，P 为边CD 上的一动点，则PB +23PD 的最小值等于．例2图例3图例3.（2019•长沙）如图，△ABC 中，AB ＝AC ＝10，tan A ＝2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD +55BD 的最小值是（）A ．2B ．4C ．5D ．10【巩固训练】1.(2018台州仙居县一模）如图1，菱形ABCD 中，∠ABC ＝60°,边长为3，P 是对角线BD 上的一个动点，则PC BP +21的最小值是（）A.3B.233 C.3 D.23433+图1图2图32.（2015无锡二模）如图2，菱形ABCD 的对角线AC 上有一动点P ，BC=6,∠ABC=150°,则求PA+PB+PD的最小值为.3.如图3,△ABC 在直角坐标系中,AB=AC,A(0,22),C(1,0),D 为射线AO 上一点,一动点P 从A 出发,运动路径为A →D →C,点P 在AD 上的运动速度是在CD 上的3倍,要使整个运动时间最少,则点D 的坐标应为()A.(0,22)B.(0,22) C.(0,32) D.(0,42)图4图55.（2015内江）如图5，在△ACE 中，CA=CE ，∠CAE=30°，⊙O 经过点C ，且圆的直径AB 在线段AE 上．设点D 是线段AC 上任意一点（不含端点），连接OD ，当AB=8时，则21CD+OD 的最小值．中，BC=2,∠B=30°，求c bx ++的图象经过点A(-1,0)、图78.（2015日照）如图8，抛物线y=21x 2+mx+n 与直线y=-21x+3交于A，B 两点，交x 轴与D，C 两点，连接AC，BC，已知A（0，3），C（3，0）．（1）求抛物线的解析式；（2）求tan∠BAC 的值；（3）设E 为线段AC 上一点（不含端点），连接DE，一动点M 从点D 出发，沿线段DE 以每秒一个单位速度运动到E 点，再沿线段EA 以每秒2个单位的速度运动到A 后停止，当点E 的坐标是多少时，点M 在整个运动中用时最少？图82020中考专题9——最值问题之胡不归答案例1.解：（1）如图①，∵DE ⊥CM ，∴∠DEC ＝90°，∴在Rt △BCM 中，DE ＝CD •sin30°，∴DE ＝．（2）如图①过点A 作AE ⊥CM 交CB 于点D '，则D '点即为所用时间最短的登陆点．理由如下：由第（1）问可知，D 'E '＝．AD '+最短，即为AD '+D 'E ′最短．由直线外一点与这条直线上点的所有连线段中，垂线段最短．可知此时D '点即为所求．（3）如图②，过点C 做射线CM ，使得sin ∠BCM ＝n1，过点A 作AE ⊥CM ，垂足为E ，交CB 于点D ，则D 即为所用时间最短的登陆点．（4）∵救生员在岸上跑的速度都是6m /s ，在海中游泳的速度都是2m /s ，∴此时sin ∠BCM ＝，可得sin ∠DAB ＝，∴在Rt △ADB 中，AB ＝300，AD ＝225，DB ＝75，CD ＝300﹣75．∴时间为+＝（50+100）s ．例2.解：如图，过点P 作PE ⊥AD ，交AD 的延长线于点E ，∵AB ∥CD ∴∠EDP ＝∠DAB ＝60°，∴sin ∠EDP ＝∴EP ＝PD∴PB+PD＝PB+PE∴当点B，点P，点E三点共线且BE⊥AD时，PB+PE有最小值，即最小值为BE，∵sin∠A＝＝∴BE＝3故答案为3例3.解：如图，作DH⊥AB于H，CM⊥AB于M．∵BE⊥AC，∴∠AEB＝90°，∵tan A＝＝2，设AE＝a，BE＝2a，则有：100＝a2+4a2，∴a2＝20，∴a＝2或﹣2（舍弃），∴BE＝2a＝4，∵AB＝AC，BE⊥AC，CM⊥AB，∴CM＝BE＝4（等腰三角形两腰上的高相等））∵∠DBH＝∠ABE，∠BHD＝∠BEA，∴sin∠DBH＝＝＝，∴DH＝BD，∴CD+BD＝CD+DH，∴CD+DH≥CM，∴CD+BD≥4，∴CD+BD的最小值为4．【巩固训练】答案1.解：如图作PM⊥AB于M，CH⊥AB于H．∵四边形ABCD 是菱形，∴∠PBM ＝∠ABC ＝30°，∴PM ＝PB ，∴PB +PC ＝PC +PM ，根据垂线段最短可知，CP +PM 的最小值为CH 的长，在Rt △CBH 中，CH ＝BC •sin60°＝，∴PB +PC 的最小值为，故选：B ．2.26 3.D4.964 5.32 6.327.【解答】解：（1）由题意解得，∴抛物线解析式为y ＝x 2﹣x ﹣，∵y ＝x 2﹣x ﹣＝（x ﹣）2﹣，∴顶点坐标（，﹣）．（2）如图1中，连接AB ，作DH ⊥AB 于H ，交OB 于P ，此时PB +PD 最小．理由：∵OA ＝1，OB ＝，∴tan ∠ABO ＝＝，∴∠ABO ＝30°，∴PH ＝PB ，∴PB +PD ＝PH +PD ＝DH ，∴此时PB +PD 最短（垂线段最短）．在Rt △ADH 中，∵∠AHD ＝90°，AD ＝，∠HAD ＝60°，∴sin60°＝，∴DH ＝，∴PB +PD 的最小值为．故答案为．8.解：（Ⅰ）把A （0，3），C （3，0）代入y ＝x 2+mx +n ，得，解得：．∴抛物线的解析式为y＝x2﹣x+3联立，解得：或，∴点B的坐标为（4，1）．如图1．∵C（3，0），B（4，1），A（0，3），∴AB2＝20，BC2＝2，AC2＝18，∴BC2+AC2＝AB2，∴△ABC是直角三角形，∴∠ACB＝90°，∴tan∠BAC＝＝＝；（2）如图,过A作射线AF∥x轴，过D作射线DF∥y轴，DF与AC交于点E．∵A（0，3），C（3，0），∴l AC：y＝﹣x+3．∵OA＝OC，∠AOC＝90°，∴∠ACO＝45°，∵AF∥OC，∴∠FAE＝45°．∴EF＝AE•sin45°＝．∴当且仅当AF⊥DF时，DE+EF取得最小值，点M在整个运动中用时最少为：t＝+＝DE+EF，∵抛物线的解析式为y＝x2﹣x+3，且C（3，0），∴可求得D点坐标为（2，0）则E点横坐标为2，将x＝2代入l AC：y＝﹣x+3．，得y＝1．所以E（2，1）．9.（1）证明：∵四边形ABCD是矩形．∴OD＝OB＝OC＝OA，∵△EDC和△ODC关于CD对称，∴DE＝DO，CE＝CO，∴DE＝EC＝CO＝OD，∴四边形CODE是菱形．（2）①设AE交CD于K．∵四边形CODE是菱形，∴DE∥AC，DE＝OC＝OA，∴＝＝∵AB＝CD＝6，∴DK＝2，CK＝4，在Rt△ADK中，AK＝＝＝3，∴sin∠DAE＝＝，②作PF⊥AD于F．易知PF＝AP•sin∠DAE＝AP，∵点Q的运动时间t＝+＝OP+AP＝OP+PF，∴当O、P、F共线时，OP+PF的值最小，此时OF是△ACD的中位线，∴OF＝CD＝3．AF＝AD＝，PF＝DK＝1，∴AP＝＝，∴当点Q沿上述路线运动到点A所需要的时间最短时，AP的长为cm，点Q走完全程所需的时间为3s．。

2020中考数学复习微专题：最值(“胡不归”问题)

最值问题——胡不归

胡不归问题解题方法和口诀

最值模型之胡不归(学生版)-中考数学专题解析

2020年九年级数学中考复习专题：胡不归和阿氏圆问题 教案设计(无答案)

2020年中考数学三轮复习专项冲刺：胡不归练习

中考数学最值—胡不归问题(解析+例题)

中考数学常见几何模型最值模型-胡不归问题

几何最值之胡不归知识精讲-冲刺2020年中考几何专项复习

中考数学最值—胡不归问题(解析+例题)

2020年中考数学总复习最值系列：胡不归问题

胡不归问题归纳

中考数学几何复习---最值系列之胡不归问题

中考数学专题复习最值问题胡不归 (2)

胡不归及经典例题与解析

2020年中考线段最值问题之胡不归问题

中考数学复习之线段和差最值问题胡不归问题,附练习题含参考答案

中考专题- 胡不归专题(解析版)

2020中考专题9——最值问题之胡不归

2020年九年级数学中考复习专题：胡不归和阿氏圆问题教案设计(无答案)