中考数学 第一编 教材知识梳理篇 第二章 方程(组)与不等式(组)第一节 一次方程与方程组及应用试题
中考数学复习第二章方程组与不等式组讲义

第二章 方程(组)与不等式(组)第一节 一次方程与一次方程组【考点1】一元一次方程定义:只含有 未知数,并且未知数的次数都是 。
(系数不为0)的整式方程。
形式:一般形式ax+b=0 ; 最简形式 ax=b (a ≠0) 解 :abx(a ≠0) 【提示】判断一个方程是否为一元一次方程,一定要先把方程化简以后再用定义进行判别。
解一元一次方程的一般步骤:去分母;去括号;移项(移项要变号);合并同类项;化系数为1【考点2】二元一次方程组 1.二元一次方程定义:含有 个未知数,并且含有未知数的项的次数都是 的整式方程。
一般形式: ax+by=c ,有无数组解。
2. 二元一次方程组的解法⑴代入消元法:多适用于方程组中有一个未知数的系数是 或 的情形。
⑵ :多适用于方程组的两个方程中相同未知数的系数 或互为 的情形。
【考点3】一次方程(组)的应用 1.列方程组解应用题的一般步骤:⑴审:即审清题意,分清题中的已知量、未知量; ⑵设:即设关键未知数;⑶列:即找出适当等量关系,列出方程(组); ⑷解:即解方程(组);⑸验:即检验所解答案是否正确或是否符合题意; ⑹答:即规范作答,注意单位名称。
2.列一元一次方程常见的应用题类型及关系式 ⑴ 利润率问题:利润=售价-进价 ;利润率=进价利润×100﹪ (先确定售价、进价、再计算利润率,其中打折、降价的词义应清楚)⑵ 利息问题:利息=本金×利率×期数 ;本息和=本金+利息 ;利息税=利息×税率 ; 贷款利息=贷款数额×利率×期数⑶ 工程问题:工作量=工作效率× (把全部工作量看作单位1,各部分工作量之和=1)⑷ 浓度问题:浓度=溶液质量溶质质量×100﹪⑸ 行程问题:路程=速度×时间 ① 追击问题(追击过程时间相等)② 相遇问题 (甲走的路程 乙走的路程=A 、B 两地间的路程)③ 航行问题:顺水(风)速度= +静水(风);逆水(风)速度=船速-【中考试题精编】1.练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好花去14元,如果设水性笔的单价为x 元,那么下列方程正确的是( )A. 5(x-2)+3x=14B. 5(x+2)+3x=14C. 5x+3(x+2)=14D. 5x+3(x-2)=142.某班在学校组织的某场篮球比赛中,小杨和小方一共投进篮球21个,小杨比小方多投进5个。
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

∴原方程组的解为y=1,将y=1 代入 2kx-3y<5 得 2×k×2-3<5,解得 k<2.
命题点 2:一次方程(组)的应用(近 3 年考查 15 次)
7.(数学文化)(2021·武汉第 7 题 3 分)我国古代数学名著《九章算术》
中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价
32 人.2 艘大船与 1 艘小船一次共可以满载游客 46 人.则 1 艘大船与 1
艘小船一次共可以满载游客的人数为
( B)
A.30
B.26
C.24
D.22
11.★(2022·武汉第 10 题 3 分)幻方是古老的数学问题,我国古代的《洛 书》中记载了最早的幻方——九宫格.将 9 个数填入幻方的空格中,要 求每一横行、 每一竖列以及两条对角线上的 3 个数之和相等,例如图① 就是一个幻方.图②是一个未完成的幻方,则 x 与 y 的和是 ( D ) A.9 B.10 C.11 D.12
14.(2020·仙桃第 12 题 3 分)篮球联赛中,每场比赛都要分出胜负,每 队胜 1 场得 2 分,负 1 场得 1 分.某队 14 场比赛得到 23 分,则该队胜 了__99__场.
15.(2020·黄冈第 19 题 6 分)为推广黄冈各县市名优农产品,市政府组 织创办了“黄冈地标馆”,一顾客在“黄冈地标馆”发现,如果购买 6 盒 羊角春牌绿茶和 4 盒九孔牌藕粉,共需 960 元,如果购买 1 盒羊角春牌 绿茶和 3 盒九孔牌藕粉共需 300 元,请问每盒羊角春牌绿茶和每盒九孔 牌藕粉分别需要多少元?
【分层分析】设购进创意文具袋 x 个,由题干信息①得购进笔记本为
((2x2+x+10)个,由题干信息②可列方程为 xx++(2(x2+x1+0)1=0)190.
中考数学总复习 第一篇 教材知识梳理篇 第2章 方程(组
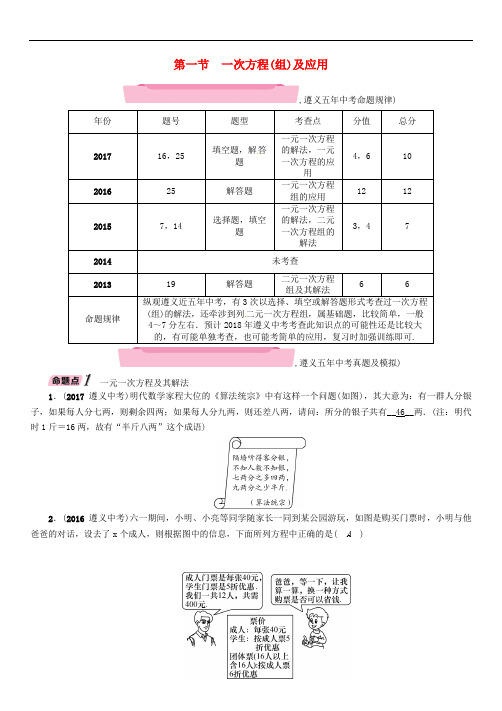
第一节 一次方程(组)及应用,遵义五年中考命题规律)填空题,解答的解法,还牵涉到列,遵义五年中考真题及模拟)一元一次方程及其解法1.(2017遵义中考)明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有__46__两.(注:明代时1斤=16两,故有“半斤八两”这个成语)2.(2016遵义中考)六一期间,小明、小亮等同学随家长一同到某公园游玩,如图是购买门票时,小明与他爸爸的对话,设去了x 个成人,则根据图中的信息,下面所列方程中正确的是( A )A .40x +20(12-x)=400B .40(12-x)+20x =400C .24(12-x)+20x =400D .24x +12(12-x)=4003.(2016遵义十一中一模)希望中学九年级(1)班共有学生49人,当该班少一名男生时,男生的人数恰好为女生人数的一半.设该班有男生x 人,则下列方程中,正确的是( A )A .2(x -1)+x =49B .2(x +1)+x =49C .x -1+2x =49D .x +1+2x =49二元一次方程组及其解法4.(2016遵义二中二模)小明在解关于x ,y 的二元一次方程组⎩⎪⎨⎪⎧x +y =△, 2x -3y =5时,解得⎩⎪⎨⎪⎧x =4,y =⊗,则△和⊗代表的数分别是( B )A .△=1,⊗=5B .△=5,⊗=1C .△=-1,⊗=3D .△=3,⊗=-15.(2013遵义中考)解方程组:⎩⎪⎨⎪⎧x -2y =4,① 2x +y -3=0.②解:由①得x =2y +4.将x =2y +4代入②,得2(2y +4)+y -3=0.解得y =-1.∴x=2y +4=2×(-1)+4=2.∴方程组的解是⎩⎪⎨⎪⎧x =2,y =-1.6.(2016遵义二中三模)某地为了打造风光带,将一段长为360 m 的河道整治任务交由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24 m ,乙工程队每天整治16 m .求甲、乙两个工程队分别整治了多长的河道.解:设甲工程队整治河道x m ,则乙工程队整治河道(360-x)m .由题意,得x 24+360-x16=20,解得x =120.当x =120时,360-x =240.答:甲工程队整治河道 120 m ,乙工程队整治河道240 m .7.(2017改编)已知关于x ,y 的二元一次方程ax +by =10(ab≠0)的两个解分别为⎩⎪⎨⎪⎧x =-1, y =2和⎩⎪⎨⎪⎧x =-2,y =-4,求1-a 2+4b 2的值.解:把⎩⎪⎨⎪⎧x =-1, y =2代入方程ax +by =10中,得-a +2b =10,把⎩⎪⎨⎪⎧x =-2,y =-4代入方程ax +by =10中,得-a -2b =5,∴(-a +2b)(-a -2b)=a 2-4b 2=50,∴1-a 2+4b 2=1-50=-49.一元一次方程组的应用8.(2017遵义中考)为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A ,B 两种不同款型,请回答下列问题:问题1:单价该公司早期在甲街区进行了试点投放,共投放A ,B 两型自行车各50辆,投放成本共计7 500元,其中B 型车的成本单价比A 型车高10元,A ,B 两型自行车的单价各是多少?问题2:投放方式该公司决定采取如下投放方式:甲街区每1 000人投放a 辆“小黄车”,乙街区每1 000人投放8a +240a 辆“小黄车”,按照这种投放方式,甲街区共投放1 500辆,乙街区共投放1 200辆,如果两个街区共有15万人,试求a 的值.解:问题1:设A 型车的成本单价为x 元,则B 型车的成本单价为(x +10)元.依题意,得 50x +50(x +10)=7 500, 解得x =70,∴x +10=80,答:A 、B 两型自行车的单价分别是70元和80元; 问题2:由题意可得1 500a ×1 000+1 2008a +24a×1 000=150 000,解得a =15.经检验,a =15是所列方程的解.故a 的值为15.9.(2016遵义中考)上网流量、语音通话是手机通信消费的两大主体.日前,某通信公司推出消费优惠新招——“定制套餐”.消费者可根据实际情况自由定制每月上网流量与语音通话时间,并按照二者的阶梯资费标准缴纳通信费.下表是流量与语音的阶梯定价标准.0.[小提示:阶梯定价收费计算方法,如600 min 语音通话费=0.15×500+0.12×(600-500)=87元] (1)甲定制了600 MB 的月流量,花费48元;乙定制了2 GB 的月流量,花费120.4元.求a ,b 的值;(注:1GB =1 024 MB )(2)甲的套餐费用为199元,其中含600 MB 的月流量;丙的套餐费用为244.2元,其中包含 1 GB 的月流量.二人均定制了超过1 000 min 的每月通话时间,并且丙的语音通话时间比甲多300 min ,求m 的值.解:(1)由题意,得⎩⎪⎨⎪⎧100a +(500-100)×0.07+(600-500)b =48,100a +(500-100)×0.07+(1 024×2-500)b =120.4, 解得⎩⎪⎨⎪⎧a =0.15, b =0.05;(2)设甲每月定制x(x >100)min 通话时间,则丙定制(x +300)min 通话时间,丙定制了1 GB 月流量套餐需花费100×0.15+(500-100)×0.07+(1 024-500)×0.05=69.2(元),由题意得⎩⎪⎨⎪⎧48+500×0.15+(1 000-500)×0.12+(x -1 000)m =199,69.2+500×0.15+(1 000-500)×0.12+(x +300-1 000)m =244.2. ∴m =0.08.,中考考点清单)方程、方程的解与解方程1.含有未知数的__等式__叫方程.2.使方程左右两边相等的__未知数__的值叫方程的解. 3.求方程__解__的过程叫解方程.等式的基本性质4.性质1:等式两边同时加上(或减去)同一个数或同一个式子,所得的结果仍__相等__.如果a =b ,那么a±c __=__b±c.性质2:等式两边同时乘以(或除以)同一个数(除数不为0),所得结果仍__相等__,如果a =b ,那么ac =bc(c≠0),a c =bc(c≠0).一次方程(组)5.概念与解法 (1)一元一次方程概念:含有__一个__未知数且未知数的次数是__1__,这样的方程叫做一元一次方程.解法:解一元一次方程的一般步骤:①去分母;②去括号;③移项;④合并同类项;⑤系数化为1. (2)二元一次方程概念:含有两个__未知数__,并且含有未知数的项的__次数__都是1的方程叫做二元一次方程. 解法:一般需找出满足方程的整数解即可. (3)二元一次方程组概念:两个__二元一次方程__所组成的一组方程,叫做二元一次方程组.解法:解二元一次方程组的基本思路是__消元__.基本解法有:__代入__消元法和__加减__消元法. (4)三元一次方程组概念:三个一次方程组成的含有三个未知数的一组方程叫三元一次方程组. 解法:解三元一次方程组的基本思想是:三元――→转化二元――→转化一元一次方程. 【温馨提示】(1)解一元一次方程去分母时,常数项不要漏乘,移项一定要变号;(2)二元一次方程组的解应写成⎩⎪⎨⎪⎧x =a ,y =b 的形式.列方程(组)解应用题的一般步骤6.(1)审:审清题意,分清题中的已知量、未知量;(2)设:设__未知数__,设其中某个量为未知数,并注意单位,对含有两个未知数的问题,需设两个未知数; (3)列:弄清题意,找出__相等关系__;根据__相等关系__,列方程(组); (4)解:解方程(组);(5)验:检验结果是否符合题意; (6)答:答题(包括单位).【方法点拨】一次方程(组)用到的思想方法:(1)消元思想:将二元一次方程组通过消元使其变成一元一次方程;(2)整体思想:在解方程时结合方程的结构特点,灵活采取整体思想,使整个过程简捷;(3)转化思想:解一元一次方程最终要转化成ax =b ;解二元一次方程组先转化成一元一次方程; (4)数形结合思想:利用图形的性质建立方程模型解决几何图形中的问题; (5)方程思想:利用其他知识构造方程解决问题.,中考重难点突破)一元一次方程及解法【例1】(1)(2017瑞安中考模拟)关于x 的方程2x -m3=1的解为2,则m 的值是( )A .2.5B .1C .-1D .3 (2)(河池中考)解方程:2x +13-5x -16=1.【解析】(1)把x =2代入方程,得4-m3=1,解得m =1.(2)按去分母→去括号→移项→合并同类项→系数化为1来解.【答案】(1)B ;(2)x =-3.1.(2017滨州中考)解方程:2-2x +13=1+x2.解:去分母,得12-2(2x +1)=3(1+x), 去括号,得12-4x -2=3+3x , 移项、合并同类项,得7x =7, 系数化为1,得x =1.二元一次方程组及解法【例2】(2017宝安中考)若方程mx +ny =6的两个解是⎩⎪⎨⎪⎧x =1, y =1和⎩⎪⎨⎪⎧x =2,y =-1,则m ,n 的值为( ) A .⎩⎪⎨⎪⎧m =4, n =2 B .⎩⎪⎨⎪⎧m =2, n =4 C .⎩⎪⎨⎪⎧m =-2, n =-4 D .⎩⎪⎨⎪⎧m =-4,n =-2 【解析】此题考查二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值. 【答案】A2.(2017天门中考)已知⎩⎪⎨⎪⎧x =2, y =1是二元一次方程组⎩⎪⎨⎪⎧mx +ny =8,nx -my =1的解,则2m -n 的算术平方根是( B )A .4B .2C . 2D .±23.(2017乐山中考)二元一次方程组x +y 2=2x -y3=x +2的解是__⎩⎪⎨⎪⎧x =-5, y =-1__.一次方程(组)的应用【例3】(2017宁阳中考)某服装店用6 000元购进A ,B 两种新式服装,按标价售出后可获得毛利润3 800元(毛利润=售价-进价),这两种服装的进价,标价如表所示.(1)求这两种服装各购进的件数;(2)如果A 种服装按标价的八折出售,B 种服装按标价的七折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?【解析】(1)设A 种服装购进x 件,B 种服装购进y 件,由总价=单价×数量,利润=售价-进价建立方程组求出其解即可;(2)分别求出打折后的价格,再根据少收入的利润=总利润-打折后A 种服装的利润-打折后B 种服装的利润,求出其解即可.【答案】解:(1)设A 种服装购进x 件,B 种服装购进y 件.由题意,得⎩⎪⎨⎪⎧60x +100y =6 000, (100-60)x +(160-100)y =3 800, 解得⎩⎪⎨⎪⎧x =50,y =30.答:A 种服装购进50件,B 种服装购进30件; (2)由题意,得3 800-50(100×0.8-60)-30(160×0.7-100) =3 800-1 000-360 =2 440(元).答:服装店比按标价售出少收入2 440元.4.(2017新泰中考模拟)某商场经销一种商品,由于进货时价格比原进价降低了 6.4%,使得利润率增加了8个百分点,那么经销这种商品原来的利润率是__17__%.(注:利润率=销售价-进价进价×100%)5.(安顺中考)某校住校生宿舍有大小两种寝室若干间,据统计该校高一年级男生740人,使用了55间大寝室和50间小寝室,正好住满;女生730人,使用了大寝室50间和小寝室55间,也正好住满,求该校的大小寝室每间各住多少人.解:设该校大寝室每间住x 人,小寝室每间住y 人.由题意,得⎩⎪⎨⎪⎧55x +50y =740, 50x +55y =730,解得⎩⎪⎨⎪⎧x =8,y =6.答:该校大寝室每间住8人,小寝室每间住6人.。
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
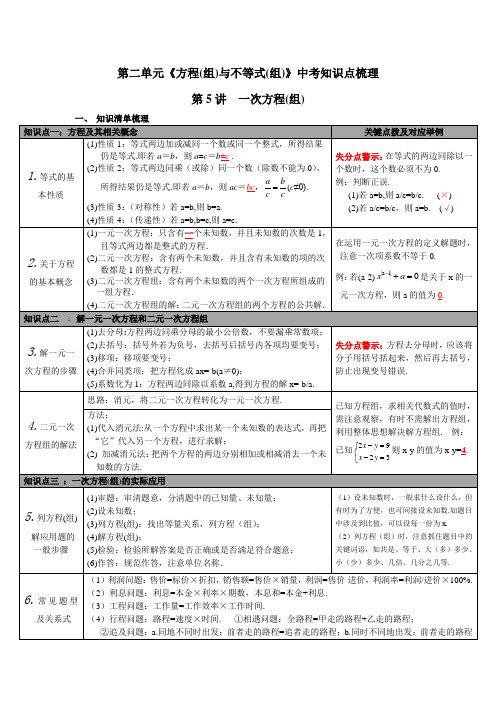
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
2025年湖南中考数学一轮复习考点研析 第二章 方程(组)与不等式(组)一元一次不等式(组)及其应用

(2)不等式②的解集为________;
(3)把不等式组的解集在如图的数轴上表示出来;
解:在数轴上表示不等式组的解集如解图.
1≤x<3
(4)不等式组的解集为____________;
1,2
(5)不等式组的整数解为________.
解图
解
答
变式2-1
是(
C
-+3<5,
(2023·娄底)不等式组ቊ
的单价为380元/个.若学校购买这两种灭火器的总价不超过21 000元,则最多
可购买这种型号的水基灭火器多少个?
解:设可购买这种型号的水基灭火器x个,则购买这种型
号的干粉灭火器(50-x)个.
根据题意,得540x+380(50-x)≤21 000,解得x≤12.5.
∵x为整数,∴x的最大值为12.
∴最多可购买这种型号的水基灭火器12个.
解
1.若a>b,则下列四个选项一定成立的是( A )
A.a+2>b+2
B.-3a>-3b
C. <
4
4
D.a-1<b-1
2.(2022·益阳)若x=2是下列四个选项中的某个不等式组的一个解,则这个不
等式组是( D )
<1,
A.ቊ
<-1
<1,
B.ቊ
> -1
> 1,
C.ቊ
<-1
> 1,
不等式的解集 不等式的解的全体称为不等式的解集
2.不等式的性质
性质
性质1
内容
应用
不等式两边都加上(或减去)同一个数(或式),不等号
b±c
的方向不变,即如果a>b,那么a±c>_______
中考数学 精讲篇 考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

5.(数学文化)《九章算术》是中国古代数学著作之一,书中有这样的一 个问题:五只雀、六只燕共重一斤,雀重燕轻,互换一只,恰好一样重.问: 每只雀、燕的质量各为多少?设一只雀的质量为 x 斤,一只燕的质量为 y
5x+6y=1, 斤,则可列方程组为__4x+y=5y+__x.
【考情分析】广西近 6 年主要考查解一元一次方程或二元一次方程组, 应用一元一次方程或二元一次方程组解决简单的实际问题,难度小,分 值 3-10 分,常在解答题中与不等式、一次函数的实际应用结合考查.
x=1, 则方程组的解为y=-1.
x-3y=-2, 5.(2020·玉林第 20 题 6 分)解方程组:2x+y=3.
x-3y=-2①, 解:2x+y=3②. ①+②×3 得 x+6x=-2+3×3, 解得 x=1, 将 x=1 代入②得 2+y=3, 解得 y=1.
x=1, 则方程组的解为y=1.
根据题意可列方程组为
y=3x-2, A.y=2x+9
y=3x-2, C.y=2x-9
y=3(x-2), B.y=2x+9
y=3(x-2), D.y=2x-9
( B)
7.(2021·桂林第 24 题 8 分)为了美化环境,建设生态桂林,某社区需 要进行绿化改造,现有甲、乙两个绿化工程队可供选择,已知甲队每天 能完成的绿化改造面积比乙队多 200 m2,甲队与乙队合作一天能完成 800 m2 的绿化改造面积. (1)甲、乙两工程队每天各能完成多少 m2的绿化改造面积? (2)该社区需要进行绿化改造的区域共有 12 000 m2,甲队每天的施工费 用为 600 元,乙队每天的施工费用为 400 元,比较以下三种方案: ①甲队单独完成;②乙队单独完成;③甲、乙两队全程合作完成. 哪一种方案的施工费用最少?
中考数学 考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

x+y=40, x+y=12, C.3x+4y=12 D.3x+4y=40
6.(2019·岳阳第 15 题 4 分)我国古代的数学名著《九章算术》中有下 列问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”其意思 为:今有一女子很会织布,每日加倍增长,5 日共织布 5 尺.问每日各织 多少布?根据此问题中的已知条件,可求得该女子第一天织布335115 尺.
8. (2019·娄底第 23 题 9 分)某商场用 14 500 元购进甲、乙两种矿泉水
共 500 箱,矿泉水的成本价与销售价如表所示:
类别
成本价(元/箱)
销售价(元/箱)
甲
25
35
乙
35
48
求:(1)购进甲、乙两种矿泉水各多少箱?
解:设购进甲矿泉水 x 箱,购进乙矿泉水 y 箱,依题意,得
x+y=500, 25x+35y=14 500,
2 次,2020 年考查 2 次)
2x-y=5, 1.(2021·郴州第 6 题 3 分)已知二元一次方程组x-2y=1,则 x-y 的
值为
( A)
A.2
B.6
C.-2
D.-6
2.(2021·株洲第 2 题 4 分)方程x2-1=2 的解是 A.x=2 B.x=3 C.x=5 D.x=6
( D)
3.(2019·湘潭第 6 题 4 分)若关于 x 的方程 3x-kx+2=0 的解为 2,则 k 的值为 44 .
m=8,m=5, m=2, ∴n=2,n=6,或n=10, ∴共有 3 种运输方案,
方案 1:安排 A 型车 8 辆,B 型车 2 辆, 所需费用:500×8+400×2=4 800(元); 方案 2:安排 A 型车 5 辆,B 型车 6 辆, 所需费用:500×5+400×6=4 900(元); 方案 3:安排 A 型车 2 辆,B 型车 10 辆, 所需费用:500×2+400×10=5 000(元). ∵4 800<4 900<5 000, ∴安排 A 型车 8 辆,B 型车 2 辆最省钱,最省钱的运输费用为 4 800 元.
中考数学 考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

13.(2021·毕节适应性考试)如图,点 A 在数轴上表示的数是-16.点 B 在数轴上表示的数是 8.若点 A 以 6 个单位长度/秒的速度向右匀速运动, 同时点 B 以 2 个单位长度/秒的速度向左匀速运动,问:当 AB=8 时,运 动时间为__2或4 __秒.
14.(2021·贺州)为了提倡节约用水,某市制定了两种收费方式:当每 户每月用水量不超过 12 m3时,按一级单价收费;当每户每月用水量超过 12 m3 时,超过部分按二级单价收费. 已知李阿姨家五月份用水量为 10 m3, 缴纳水费 32 元,七月份因孩子放假在家,用水量为 14 m3,缴纳水费 51.4 元. (1)问该市一级水费,二级水费的单价分别是多少? (2)某户某月缴纳水费为 64.4 元时,用水量为多少?
1 y=4 的一个解,则 a 的值为 2 .
7.(2020·南京)已知
x,y
x+3y=-1, 满足方程组2x+y=3, 则
x+y
的值为__11__.
8.(2020·牡丹江)某种商品每件的进价为 120 元,标价为 180 元.为了
拓展销路,商店准备打折销售.若使利润率为 20%,则商店应打__88__折.
解:(1)-1;5. (2)设铅笔的单价为 m 元,橡皮的单价为 n 元,日记本的单价为 p 元,依 题意,得 20m+3n+2p=32,① 39m+5n+3p=58,② 由 2×①-②可得 m+n+p=6, ∴5m+5n+5p=5×6=30. 答:购买 5 支铅笔、5 块橡皮、5 本日记本共需 30 元.
15.(2020·扬州)阅读感悟: 有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于 未知数的代数式的值,如以下问题: 已知实数 x,y 满足 3x-y=5①,2x+3y=7②,求 x-4y 和 7x+5y 的值. 本题常规思路是将①②两式联立组成方程组,解得 x,y 的值再代入欲求 值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方 程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式 的值,如由①-②可得 x-4y=-2,由①+②×2 可得 7x+5y=19.这样 的解题思想就是通常所说的“整体思想”.
河北省中考数学总复习 第一编 教材知识梳理篇 第2章

第二章方程(组)与不等式(组) 第一节一次方程(组)及应用及应用在河北五年中考真题及模拟)一次方程(组)的应用1.(2015河北中考)利用加减消元法解方程组⎩⎪⎨⎪⎧2x+5y=-10,①5x-3y=6,②下列做法正确的是( D) A.要消去y,可以将①×5+②×2B.要消去x,可以将①×3+②×(-5)C.要消去y,可以将①×5+②×3D.要消去x,可以将①×(-5)+②×22.(2017张家口中考模拟)小明在解关于x,y的二元一次方程组⎩⎪⎨⎪⎧x+y=△,2x-3y=5时,解得⎩⎪⎨⎪⎧x=4y=则△和代表的数分别是( B)A.△=1,=5 B.△=5,=1C.△=-1,=3 D.△=3,=-13.(2016石家庄二模)希望中学九年级(1)班共有学生49人,当该班少一名男生时,男生的人数恰好为女生人数的一半.设该班有男生x人,则下列方程中,正确的是( A)A.2(x-1)+x=49 B.2(x+1)+x=49C.x-1+2x=49 D.x+1+2x=494.(2017原创)已知⎩⎪⎨⎪⎧x=3,y=-2是关于⎩⎪⎨⎪⎧ax+by=3,bx+ay=-7的解,则(a+b)(a-b)的值为__-8__.5.(2016河北中考)已知n边形的内角和θ=(n-2)×180°.(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;(2)若n 边形变为(n +x)边形,发现内角和增加了360°,用列方程的方法确定x. 解:(1)甲对,乙不对.∵θ=360°,∴(n -2)×180°=360°.解得n =4.∵θ=630°,∴(n -2)×180°=630°,解得n =112.∵n 为整数,∴θ不能取630°;(2)依题意,得(n -2)×180°+360°=(n +x -2)×180°.解得x =2.,中考考点清单方程、方程的解与解方程1.含有未知数的__等式__叫方程.2.使方程左右两边相等的__未知数__的值叫方程的解. 3.求方程__解__的过程叫解方程.等式的基本性质4.一次方程(组)5.次方程【易错警示】(1)解一元一次方程去分母时常数项不要漏乘,移项一定要变号;(2)二元一次方程组的解应写成⎩⎪⎨⎪⎧x =a ,y =b的形式.列方程(组)解应用题的一般步骤6.; (1)消元思想:将二元一次方程组通过消元使其变成一元一次方程;(2)整体思想:在解方程时结合方程的结构特点,灵活采取整体思想,使整个过程简捷;(3)转化思想:解一元一次方程最终要转化成ax =b ;解二元一次方程组先转化成一元一次方程; (4)数形结合思想:利用图形的性质建立方程模型解决几何图形中的问题; (5)方程思想:利用其他知识构造方程解决问题.,中考重难点突破一元一次方程及解法【例1】(1)(2017成都中考)已知|a +2|=1,则a =________.(2)解方程:0.5x +20.03-x =0.3(0.5x +2)0.2-13112.【解析】(1)注意绝对值等于1的数有两个;(2)先根据分式的基本性质把各分母变成整数,再由等式的性质去分母,小心不要把两者混为一谈.【答案】(1)-1或-3;(2)解:原方程可化为:50x +2003-x =3(x +4)4-13112,解得x =-5.1.若代数式x +3值是2,则x =__-1__. 2.(滨州中考)解方程:2-2x +13=1+x2.解:去分母,得12-2(2x +1)=3(1+x), 去括号,得12-4x -2=3+3x , 移项,得-4x -3x =3+2-12, 合并同类项,得-7x =-7, 系数化为1,得x =1.二元一次方程组及解法【例2】已知关于x ,y 的二元一次方程组⎩⎪⎨⎪⎧2x +3y =m ,x +2y =-1的解互为相反数,则m =________.【解析】由解互为相反数可得x =-y ,而后把x =-y 代入方程组从而得到关于m ,y 的二元一次方程组,解之即可得m 的值.【答案】-13.(2017济南中考)如果13x a +2y 3与-3x 3y 2b -1是同类项,那么a ,b 的值分别是( A )A .⎩⎪⎨⎪⎧a =1,b =2B .⎩⎪⎨⎪⎧a =0,b =2C .⎩⎪⎨⎪⎧a =2,b =1D .⎩⎪⎨⎪⎧a =1,b =14.解方程组:⎩⎪⎨⎪⎧5x +10=10y , ①15x =20y +10. ②解:由①,得x -2y =-2.③由②,得3x -4y =2.④ ③×2-④,得x =6.把x =6代入③,得y =4,所以原方程组的解为⎩⎪⎨⎪⎧x =6,y =4.一元一次方程的应用【例3】(2017资阳中考)电器商城某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获纯利润500元,其利润率为20%,现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( A )A .562.5元B .875元C .550元D .750元【解析】本例涉及标价、打折后的新售价、进价、利润、利润率及它们之间的关系.进价为500÷20%=2 500(元).设标价为x 元,根据题意,得80%x -2 500=500,解得x =3 750.∴3 750×90%-2 500=875(元).【答案】B5.学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.求篮球和足球的单价.解:设一个篮球x 元,则一个足球(x -30)元. 由题意,得2x +3(x -30)=510. 解得x =120.x -30=90.答:一个篮球120元,一个足球90元.二元一次方程的应用【例4】(2017金华中考)某场音乐会贩卖的座位分成一楼与二楼两个区域.若一楼售出与未售出的座位数比为4∶3,二楼售出与未售出的座位数比为3∶2,且此场音乐会一、二楼未售出的座位数相等,则此场音乐会售出与未售出的座位数比为( A )A .2∶1B .7∶5C .17∶12D .24∶17【解析】设一楼售出的座位数为4x ,未售出的座位数为3x ,二楼售出的座位数为3y ,未售出的座位数为2y.由题意,得3x =2y ,则x =2y 3.那么4x +3y3x +2y =4×23y +3y2y +2y=17∶12.【答案】C6.(2017新疆中考)某班级为筹建运动会,准备用365元购买两种运动服,其中甲种运动服20元/套,乙种运动服35元/套,在钱都用尽的条件下,有多少种购买方案?解:设买甲种运动服x 套,乙种y 套. 由题意,得20x +35y =365,则x =73-7y 4,∵x ,y 必须为正整数, ∴73-7y 4>0,即0<y <737,∴当x =3时,x =13, 当y =7时,x =6. 答:有2种方案.二元一次方程组的应用【例5】(2017徐州中考)某景点的门票价格如下表:某校七年级50人且少于100人.如果两班都以班为单位单独购票,则一共支付 1 118元,如果两班联合起来作为一个团体购票,则只需花费816元.(1)两个班各有多少名学生?(2)团体购票与单独购票相比较,两个班各节约了多少钱?【解析】条件中只说(1)班学生人数少于50人,(2)班人数多于50人且少于100人.那么,两班共有人数是不到100人,还是比100人多,都不清楚,因此,需分类讨论是100多人,还是在50至100中.【答案】解:(1)设七年级(1)班有x 人、七年级(2)班有y 人.当50<x +y <100时,由题意,得 ⎩⎪⎨⎪⎧12x +10y =1 118,10(x +y )=816. ∴x +y =81.6,不是整数,不合题意. 当x +y >100时,由题意,得 ⎩⎪⎨⎪⎧12x +10y =1 118,8(x +y )=816.解得⎩⎪⎨⎪⎧x =49,y =53. 答:七年级(1)班有49人,七年级(2)班有53人;(2)七年级(1)班节约了(12-8)×49=196(元),七年级(2)班节约了(10-8)×53=106(元).7.(江西中考)小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦买了20支笔和2盒笔芯,用了56元;小丽买了2支笔和3盒笔芯,仅用了28元.求每支中性笔和每盒笔芯的价格.解:设每支中性笔x 元,每盒笔芯y 元. 根据题意,得 ⎩⎪⎨⎪⎧20x +2y =56,2x +3y =28,解得⎩⎪⎨⎪⎧x =2,y =8. 答:每支中性笔2元,每盒笔芯8元.8.(孝感中考)孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A ,B 两种树木共100棵进行校园绿化升级.经市场调查:购买A 种树木2棵,B 种树木5棵,共需600元;购买A 种树木3棵,B 种树木1棵,共需380元.(1)求A 种、B 种树木每棵各多少元;(2)因布局需要,购买A 种树木的数量不少于B 种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠.请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.解:(1)设A 种树木每棵x 元,B 种树木每棵y 元.根据题意,得⎩⎪⎨⎪⎧2x +5y =600,3x +y =380.解得⎩⎪⎨⎪⎧x =100y =80.答:A 种树木每棵100元,B 种树木每棵80元;(2)设购买A 种树木为a 棵,则购买B 种树木为(100-a)棵. 则a≥3(100-a),∴a≥75. 设实际付款总金额为w 元.则w =0.9[100a +80(100-a)]=18a +7 200, ∵18>0,w 随a 的增大而增大, ∴当a =75时,w 最小.即a =75,w 最小值=18×75+7 200=8 550(元).∴当购买A 种树木75棵,B 种树木25棵时,所需费用最少,最少费用为8 550元.。
中考方程(组)与不等式(组)知识点汇总

1、方程含有未知数的等式叫做方程。
2、方程的解能使方程两边相等的未知数的值叫做方程的解。
3、等式的性质(1)等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
(2)等式的两边都乘以(或除以)同一个数(除数不能是零),所得结果仍是等式。
4、一元一次方程只含有一个未知数,并且未知数的最高次数是1的整式方程叫做一元一次方程,其中方程)为未知数,(0a x 0≠=+b ax 叫做一元一次方程的标准形式,a 是未知数x 的系数,b 是常数项。
. 已知方程(m +1)x ︱m ︱+3=0是关于x 的一元一次方程,则m 的值是( )A 、1B 、1C 、-1D 、0或1.已知关于x 的方程432x m -=的解是x m =,则m 的值是________ .41x 5+-612-x =1-123x - 二元一次方程组1、二元一次方程含有两个未知数,并且未知项的最高次数是1的整式方程叫做二元一次方程,它的一般形式是(2、二元一次方程的解使二元一次方程左右两边的值相等的一对未知数的值,叫做二元一次方程的一个解。
3、二元一次方程组两个(或两个以上)二元一次方程合在一起,就组成了一个二元一次方程组。
4二元一次方程组的解使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
5、二元一次方正组的解法(1)代入法(2)加减法.若关于x ,y 的二元一次方程组⎩⎨⎧=-=+k y x ,k y x 95的解也是二元一次方程632=+y x 的解,则k 的值为A .43-B .43C . 34D .34- .若方程6=+ny mx 的两个解为 11x y =⎧⎨=⎩ 21x y =⎧⎨=-⎩,则m =__________. .在一本书上写着方程组21x py x y +=⎧⎨+=⎩ 的解是 0.5x y =⎧⎨=⎩口,其中y 的值被墨渍盖住了,不过,我们可解得出p =___________..32522(32)28x y xx y x+=+⎧⎨+=+⎩.⎪⎪⎩⎪⎪⎨⎧=+=+244263nmnm不等式的概念1、不等式用不等号表示不等关系的式子,叫做不等式。
最新届中考数学方程(组)与不等式(组)复习知识点总结及经典考题选编

中考数学方程(组)与不等式(组)复习知识点总结一、方程【知识梳理】1、知识结构方程分式方程的应用分式方程的解法分式方程的概念分式方程的关系根的判别式,根与系数一元二次方程的解法念一元二次方程的有关概一元二次方程二元一次方程组的应用二元一次方程组的解法二元一次方程组一元一次方程的应用一元一次方程的解法一元一次方程整式方程2、知识扫描(1)只含有一个未知数,并且未知数的次数是1的整式方程,叫做一元一次方程。
(2)含有2个未知数,并且所含未知数的项的次数都是1次,这样的方程叫二元一次方程.(3)含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.(4)二元一次方程组的解法有法和法.(5)只含有1 个未知数,并且未知数的最高次数是2且系数不为0的整式方程,叫做一元二次方程,其一般形式为)0(02a cbx ax。
(6)解一元二次方程的方法有:①直接开平方法;②配方法;③公式法;④因式分解法例:(1)042x(2)0342x x(3)4722x x (4)0232x x(7)一元二次方程的根的判别式:ac b42叫做一元二次方程的根的判别式。
对于一元二次方程)0(02a cbx ax当△>0时,有两个不相等的实数根;当△=0时,有两个相等的实数根;当△<0时,没有实数根;反之也成立。
(8)一元二次方程的根与系数的关系:如果)0(02acbx ax的两个根是21,x x 那么ab x x 21,ac x x 21(9)一元二次方程)0(02a cbx ax的求根公式:)04(2422ac baacb bx(10)分母中含有未知数的方程叫分式方程.(11)解分式方程的基本思想是将分式方程通过去分母转化为整式方程.◆解分式方程的步骤◆1、去分母,化分式方程为整式方程;◆2、解这个整式方程;◆3、验根。
注意:(1)解分式方程的基本思想是“转化”,即把分式方程化为我们熟悉的整式方程,转化的途径是“去分母”,即方程两边都乘以最简公分母.(2)因为解分式方程时可能产生增根,所以解分式方程必须检验,检验是解分式方程必要的步骤.二、不等式【知识梳理】1、知识结构解法性质概念不等式2、知识扫描(1) 只含有一个未知数,并且未知数的次数是1,系数不为 0 的不等式,叫做一元一次不等式。
中考数学总复习第一编教材知识梳理篇第二章方程(组)与不等式(组)第一节一次方程与方程组及应用(精练)

解得
24x + 18y= 750,
y= 15.
答:甲、乙两种票分别买了 20 张、 15 张.
19.情景:
试根据图 中的信息,解答下列问题: (1) 购买 6 根跳绳需 __150__元,购买 12 根跳绳需 __240__元; (2) 小红比小明多买 2 根,付款时小红反而比小明少 5 元,你认为有这种可能吗?若有,请求出小红购买跳绳 的根数;若没有,请说明理由. 解:有这种可能,小红购买跳绳 11 根.
x+ y=10,
__
__.
5 000x +3 000y =34 000
x 30-x 11. (1)( 2016 贺州中考 ) 解方程: 6- 4 = 5;
解: 2x- 3(30 -x) = 60, 2x- 90+ 3x= 60, 2x+ 3x= 150, x= 30;
(2)( 2015 重庆中考 ) 解二元一次方程组 x-2y= 1,① x+3y=6. ②
x- 2 1- 2x 4. ( 2015 荆州中考 ) 方程 2 = 3 去分母后是 ( B )
A. x-2= 1- 2x B. 3(x - 2) = 2(1 - 2x) C. 2(x - 2) = 3(1 - 2x) D. 2-x= 2x- 1
x+ 6y= 12,
5. ( 2016 宁夏中考 ) 已知 x, y 满足方程组
20. ( 2015 聊城中考 ) 某服装店用 6 000 元购进 A, B 两种新式服装,按标价售出后可获毛利润 润=售价-进价 ) ,这两种服装的进价、标价如下表所示:
3 800 元( 毛利
(1) 求这两种服装各购进的件数;
类型 价格 进价 ( 元 / 件 ) 标价 ( 元 / 件 )
A型 B型
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章方程(组)与不等式(组)第一节一次方程与方程组及应用年份题号考查点考查内容分值总分201622一元二次方程用一元一次方程确定多边形的边924(1)二元一次方程组用待定系数法确定一次函数解析式312201511二元一次方程组的解法考查二元一次方程组如何消元22201220(2)一元一次方程的应用与梯形结合,以行程问题为背景通过列一元一次方程求公路的长55201119二元一次方程的应用二元一次方程解的运用(与整式运算结合)4420108一元一次方程的应用以买书为背景,根据题意判断所列一元一次方程正确的是22200918一次方程(组)的应用以水桶中铁棒的长度为背景,通过列一元一次方程组或二元一次方程求水的深度33命题规律纵观河北八年中考,一次方程(组)及应用在中考中最多只考1题,分值2-5分,以填空、解答为,河北8年中考真题及模拟)一次方程(组)的应用(7次)1.(2015河北11题2分)利用加减消元法解方程组⎩⎪⎨⎪⎧2x +5y =-10 ①5x -3y =6 ②,下列做法正确的是( D )A .要消去y ,可以将①×5+②×2B .要消去x ,可以将①×3+②×(-5)C .要消去y ,可以将①×5+②×3D .要消去x ,可以将①×(-5)+②×22.(2010河北8题2分)小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张,设所用的1元纸币为x 张,根据题意,下面所列方程正确的是( A )A .x +5(12-x)=48B .x +5(x -12)=48C .x +12(x -5)=48D .5x +(12-x)=483.(2009河北18题3分)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的13,另一根露出水面的长度是它的15,两根铁棒长度之和为55 cm ,此时木桶中水的深度是__20__cm .4.(2016河北22题9分)已知n 边形的内角和θ=(n -2)×180°.(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;(2)若n 边形变为(n +x)边形,发现内角和增加了360°,用列方程的方法确定x. 解:(1)甲对,乙不对.∵θ=360°,∴(n -2)×180=360.解得n =4. ∵θ=630°,∴(n -2)×180=630,解得n =112.∵n 为整数,∴θ不能取630°;(2)依题意,得(n -2)×180+360=(n +x -2)×180.解得x =2.5.[2012河北20(2)题5分]如图,某市A ,B 两地之间有两条公路,一条是市区公路AB ,另一条是外环公路AD -DC -CB.这两条公路围成等腰梯形ABCD ,其中DC∥AB,AB ∶AD ∶DC =10∶5∶2.(1)求外环公路总长和市区公路长的比;(2)某人驾车从A 地出发,沿市区公路去B 地,平均速度是40 km /h .返回时沿外环公路行驶,平均速度是80km /h ,结果比去时少用了110h .求市区公路的长.解:(1)设AB =10x km ,则AD =5x km ,CD =2x km .∵四边形ABCD 是等腰梯形,∴BC =AD =5x km .∴AD +CD +CB =12x(km ).∴外环公路的总长和市区公路长的比为12x∶10x=6∶5;(2)由(1)可知,市区公路的长为10x km ,外环公路的总长为12x km ,由题意得10x 40=12x 80+110,解得x =1,∴10x =10.答:市区公路的长为10 km .6.(2016石家庄新华区模拟)若⎩⎪⎨⎪⎧x =1,y =2是关于x 、y 的二元一次方程ax -3y =1的解,则a 的值为( A )A .7B .2C .-1D .-57.(2016唐山路南区三模)小明在解关于x 、y 的二元一次方程组⎩⎪⎨⎪⎧x +y =△,2x -3y =5时,解得⎩⎪⎨⎪⎧x =4,y =⊗,则△和⊗代表的数分别是( B )A .△=1,⊗=5B .△=5,⊗=1C .△=-1,⊗=3D .△=3,⊗=-18.(2016石家庄二模)希望中学九年级1班共有学生49人,当该班少一名男生时,男生的人数恰好为女生人数的一半.设该班有男生x 人,则下列方程中,正确的是( A )A .2(x -1)+x =49B .2(x +1)+x =49C .x -1+2x =49D .x +1+2x =499.(2016原创)已知关于x ,y 的二元一次方程ax +by =10(ab≠0)的两个解分别为⎩⎪⎨⎪⎧x =-1,y =2和⎩⎪⎨⎪⎧x =-2,y =-4,求1-a 2+4b 2的值.解:将x =-1,y =2代入方程ax +by =10中得:-a +2b =10,将x =-2,y =-4同样代入方程得:-a -2b =5,∴(-a +2b)(-a -2b)=50,∴-a 2+4b 2=-50,∴1-a 2+4b 2=1-50=-49.,中考考点清单)方程、方程的解与解方程1.含有未知数的__等式__叫方程.2.使方程左右两边相等的__未知数__的值叫方程的解. 3.求方程__解__的过程叫解方程.等式的基本性质4.性质1等式两边同时加上(或减去)同一个数或同一个式子,所得的结果仍①__相等__.如果a=b,那么a±c②__=__b±c.续表性质2等式两边同时乘以(或除以)同一个数(除数不为0),所得结果仍③__相等__.如果a=b,那么ac=bc(c≠0),ac=bc(c≠0).一次方程(组)概念解法一元一次方程含有①__一个__未知数且未知数的次数是②__1__,这样的方程叫做一元一次方程.解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.二元一含有两个③__未知数__,并且含一般需找出满足方程的整数解⎩⎪⎨⎪⎧x =a ,y =b的形式.列方程(组)解应用题的一般步骤(1)消元思想:将二元一次方程组通过消元使其变成一元一次方程.(2)整体思想:在解方程时结合方程的结构特点,灵活采取整体思想,使整个过程简捷. (3)转化思想:解一元一次方程最终要转化成ax =b ;解二元一次方程组先转化成一元一次方程. (4)数形结合思想:利用图形的性质建立方程模型解决几何图形中的问题. (5)方程思想:利用其他知识构造方程解决问题.,中考重难点突破)一元一次方程及解法【例1】(1)(2015娄底中考)已知关于x 的方程2x +a -5=0的解是x =2,则a 的值为________; (2)解方程:0.5x +20.03-x =0.3(0.5x +2)0.2-13112.【学生解答】(1)1;(2)原方程可化为:50x +2003-x =3(x +4)4-13112,解得x =-5.【点拨】(1)把x =2代入即可;(2)先“化零为整”,再按去分母→去括号→移项→合并同类项→系数化为1来解.1.(2016厦门中考)方程x +5=12(x +3)的解是__x =-7__.2.(2016滨州中考)解方程2-2x +13=1+x2.解:去分母得:12-2(2x +1)=3(1+x),去括号得:12-4x -2=3+3x ,解得x =1.二元一次方程组及解法【例2】(2016无锡中考)解方程组:⎩⎪⎨⎪⎧2x -y =5,①x -1=12(2y -1).② 【学生解答】由②得2x -2y =1③. ①-③,得y =4. 把y =4代入①,得x =92.∴原方程组的解为⎩⎪⎨⎪⎧x =92,y =4.【点拨】解二元一次方程组的两种方法(代入法和加减法)用到的都是“消元”的思想,具体解题时两种方法可根据方程组中未知数系数的特点灵活运用.3.(2016杭州中考)设实数x ,y 满足方程组⎩⎪⎨⎪⎧13x -y =4,13x +y =2,则x +y =__8__.4.解方程组:⎩⎪⎨⎪⎧5x +10=10y , ①15x =20y +10. ②解:由①,得x -2y =-2. 由②,得3x -4y =2.①×2-②,得x =6.把x =6代入①得y =4,所以原方程组的解为⎩⎪⎨⎪⎧x =6,y =4.一次方程(组)的应用【例3】某公园的门票价格如下表:购票人数 1~50 51~100100以上票价(元/人)1085某校九年级甲、乙两个班共有100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人.如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共只要515元.问:甲、乙两班分别有多少人?【解析】由两班单独购票时甲班票价8元/人,乙班票价10元/人,两个班共付920元及购团体票时票价5元/人,共付款515元,可列方程组求解.【学生解答】设甲、乙两班分别有x 人和y 人,得⎩⎪⎨⎪⎧8x +10y =920,5x +5y =515.解得⎩⎪⎨⎪⎧x =55,y =48.答:甲班55人,乙班48人.【方法归纳】综合表格中的信息与文字叙述,理解题意是解决本题的关键.5.(2016江西中考)小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦买了20支笔和2盒笔芯,用了56元;小丽买了2支笔和3盒笔芯,仅用了28元.求每支中性笔和每盒笔芯的价格.解:设每支中性笔x 元,每盒笔芯y 元,根据题意得⎩⎪⎨⎪⎧20x +2y =56,2x +3y =28.解得⎩⎪⎨⎪⎧x =2,y =8. 答:每支中性笔2元,每盒笔芯8元.6.(2016资阳改编)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.求篮球和足球的单价.解:设一个篮球x 元,则一个足球(x -30)元,由题意得2x +3(x -30)=510.解得x =120. 答:一个篮球120元,一个足球90元.,中考备考方略)1.(2015重庆中考)已知关于x 的方程2x +m -8=0的解是x =3,则m 的值为( A )A .2B .3C .4D .52.(2016邯郸十一中模拟)若2a =3b ,则下列各式中不成立的是( D )A .4a =6bB .2a +5=3b +5C .a3=b2D .a =3b3.(2016株洲中考)在解方程x -13+x =3x +12时,方程两边同时乘以6,去分母后,正确的是( B )A .2x -1+6x =3(3x +1)B .2(x -1)+6x =3(3x +1)C .2(x -1)+x =3(3x +1)D .(x -1)+x =3(x +1)4.(2016广州中考)已知a ,b 满足方程组⎩⎪⎨⎪⎧a +5b =12,3a -b =4,则a +b 的值为( B )A .-4B .4C .-2D .25.(2016廊坊二模)已知⎩⎪⎨⎪⎧x =-1,y =2是二元一次方程组⎩⎪⎨⎪⎧3x +2y =m ,nx -y =1的解,则m -n 的值是( D )A .1B .2C .3D .46.(2016杭州中考)已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x 吨到乙煤场,则可列方程为( C )A .518=2(106+x)B .518-x =2×106C .518-x =2(106+x)D .518+x =2(106-x)7.(2016聊城中考)在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( D )日 一 二 三 四 五 六 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2627282930A .27B .51C .69D .8.(2016台湾中考)若二元一次联立方程式⎩⎪⎨⎪⎧2x +y =14,-3x +2y =21的解为x =a ,y =b ,则a +b 的值为( D )A .192 B .212C .7D .13 9.(2016温州中考)已知甲、乙两数的和是7,甲数是乙数的2倍.设甲数为x ,乙数为y ,根据题意,列方程组正确的是( A )A .⎩⎪⎨⎪⎧x +y =7,x =2yB .⎩⎪⎨⎪⎧x +y =7,y =2xC .⎩⎪⎨⎪⎧x +2y =7,x =2yD .⎩⎪⎨⎪⎧2x +y =7,y =2x 10.(2016临沂中考)为了绿化校园,30名学生共种78棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x 人,女生有y 人.根据题意,所列方程组正确的是( D )A .⎩⎪⎨⎪⎧x +y =78,3x +2y =30B .⎩⎪⎨⎪⎧x +y =78,2x +3y =30C .⎩⎪⎨⎪⎧x +y =30,2x +3y =78D .⎩⎪⎨⎪⎧x +y =30,3x +2y =7811.(2016深圳中考)某商品的标价为200元,8折销售仍赚40元,则商品进价为________元( B )A .140B .120C .160D .10012.(1)(2016永州中考)方程组⎩⎪⎨⎪⎧x +2y =2,2x +y =4的解是__⎩⎪⎨⎪⎧x =2,y =0__ ,;)(2)(2016温州中考)方程组⎩⎪⎨⎪⎧x +2y =5,3x -2y =7的解是__⎩⎪⎨⎪⎧x =3,y =1__ ,.)13.(2016扬州中考)以方程组⎩⎪⎨⎪⎧y =2x +2,y =-x +1的解为坐标的点(x ,y)在第__二__象限.14.(2016原创)已知⎩⎪⎨⎪⎧x =3,y =-2是方程组⎩⎪⎨⎪⎧ax +by =3,bx +ay =-7的解,则代数式(a +b)(a -b)的值为__-8__.15.(2016石家庄四十二中一模改编)若关于x ,y 的二元一次方程组⎩⎪⎨⎪⎧x +y =5k ,x -y =9k 的解也是二元一次方程2x+3y =6的解,求k 的值.解:解方程组⎩⎪⎨⎪⎧x +y =5k ,x -y =9k 得⎩⎪⎨⎪⎧x =7k ,y =-2k.代入2x +3y =6中得k =34.16.(2016福州中考)某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,那么甲、乙两种票各买了多少张?解:设甲种票买了x 张,则乙种票买了(35-x)张,由题意得24x +18(35-x)=750,解得x =20,∴35-x =15.答:甲种票买了20张,乙种票买了15张.17.(2016原创)按如图的运算程序,能使输出结果为3的x ,y 的值是( D )A .x =5,y =-2B .x =3,y =-3C .x =-4,y =2D .x =-3,y =-918.(2016原创)小亮解二元一次方程组⎩⎪⎨⎪⎧2x +y =●,3x -2y =19的解为⎩⎪⎨⎪⎧x =5,y =★,由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则●+★=__6__.19.(2016盐城中考)李师傅加工1个甲种零件和1个乙种零件的时间分别是固定的,现知道李师傅加工3个甲种零件和5个乙种零件共需55 min ;加工4个甲种零件和9个乙种零件共需85 min ,则李师傅加工2个甲种零件和4个乙种零件共需__40__min .20.(2016石家庄41中一模)定义一种新运算“⊕”:a ⊕b =a -2b ,比如:2⊕(-3)=2-2×(-3)=2+6=8.(1)求(-3)⊕2的值;(2)若(x -3)⊕(x+1)=1,求x 的值.解:(1)(-3)⊕2=(-3)-2×2=-3-4=-7; (2)∵(x-3)⊕(x+1)=1,∴(x -3)-2(x +1)=1.∴x=-6.21.(2016石家庄四十一中模拟)用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角不再利用).A 方法:剪6个侧面;B 方法:剪4个侧面和5个底面.现有19张硬纸板,裁剪时x 张用A 方法,其余用B 方法.(1)用x 的代数式分别表示裁剪出的侧面和底面个数; (2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?解:(1)裁剪出的侧面个数为6x +4(19-x)=(2x +76)个,裁剪出的底面个数为5(19-x)=(-5x +95)个; (2)由题意得2x +763=-5x +952,解得x =7.当x =7时,2x +763=30.答:能做30个盒子.22.(2016沧州八中模拟)P 表示n 边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P 与n 的关系式是:P =n (n -1)24·(n 2-an +b)(其中a ,b 是常数,n ≥4).(1)填空:通过画图可得:四边形时,P =__1__(填数字),五边形时,P =__5__(填数字);(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a ,b 的值.(注:本题的多边形均指凸多边形) 解:将上述值代入公式可得⎩⎪⎨⎪⎧4×(4-1)24·(16-4a +b )=1,①5×(5-1)24·(25-5a +b )=5.②化简得⎩⎪⎨⎪⎧4a -b =14,5a -b =19.解得⎩⎪⎨⎪⎧a =5,b =6.23.(2016连云港中考)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.(1)求该店有客房多少间?房客多少人?(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?解:(1)设该店有客房x 间,有房客y 人,根据题意得:⎩⎪⎨⎪⎧7x +7=y ,9(x -1)=y ,解得⎩⎪⎨⎪⎧x =8,y =63.答:该店有客房8间,房客63人;(2)若每间客房住4人,则63名客人至少需客房16间,需付费20×16=320钱;若一次性订客房18间,则需付费20×18×0.8=288钱<320钱;答:诗中“众客”再次一起入住,他们应选择一次性订房18间更合算.。
