气体的pVT关系
1.气体的pVT关系

1.4 真实气体状态方程
1.4.2 范德华方程
理想气体状态方程 pVm=RT 的实质为: (分子间无相互作用力时气体的压力)
×(1 mol 气体分子的自由活动空间)=RT
范德华方程的实际气体模型: 引入压力修正项和体积修正项
21
1.4 真实气体状态方程
1.4.2 范德华方程
∵分子间相互作用减弱了分子对器壁的碰撞, ∴ p= p理-p内
1.4.2 范德华方程
(1)范德华硬球模型和范德华方程
a ( p Vm2 )(Vm b) RT
n2a ( p V 2 )(V nb) nRT
1.4 真实气体状态方程
1.4.2 范德华方程
(2)范德华常数与临界参数的关系
根据(p Vm )Tc 0 和 (2 p Vm2 )Tc 0
p→0。
R
lim
p0
(
pVm )T T
8.3145 J mol -1 K-1
lim p0 ( pV ) nRT
1.2 理想气体混合物
1.2.1 混合物的组成(略)
(1)摩尔分数 xB (或yB ) nB / nA
A
(2)质量分数 wB mB / mA
A
(3)体积分数 B xBVm,B /( xAVm,A )
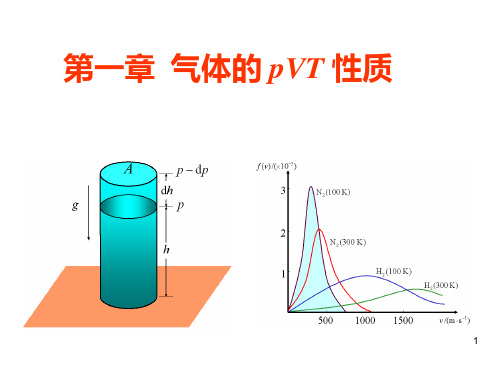
气体不同,TB不同。图1.1.2中300K时, CH4,N2,He分别属于上述三种情况。
1.4 真实气体状态方程
1.4.2 范德华方程
(1)范德华硬球模型和范德华方程 压力修正项(a/ Vm2)。p(真实)< p(理想)。
内压力 的大小与碰撞单位面积器壁上的分子数和 每个分子所受的向内的拉力有关,两者又都与Vm 成反比。 体积修正项(b)。 Vm(真实)>Vm(理想)。 范德华常数(a,b)。 气体不同,数值不一样。可 实测,也可由临界参数算得,与温度有关。
气体pvt公式

气体pvt公式气体PVT公式是描述气体行为的一种物理公式,它可以用来计算气体的压力、体积和温度之间的关系。
PVT代表了压力、体积和温度三个物理量,它们是描述气体状态的重要参数。
PVT公式是根据气体的状态方程推导而来的,常见的状态方程有理想气体状态方程、范德瓦尔斯状态方程等。
理想气体状态方程是最简单的状态方程,它假设气体是由大量完全弹性碰撞的质点组成,质点之间没有相互作用力,体积可以忽略不计。
根据理想气体状态方程,可以得到气体的PVT公式为P1V1/T1=P2V2/T2,其中P1、V1、T1分别表示气体的初始压力、体积和温度,P2、V2、T2表示气体的最终压力、体积和温度。
在实际应用中,气体的行为往往与理想气体状态方程存在一定的差异。
当气体的压力较高或温度较低时,分子之间的相互作用力就会显现出来,此时需要使用修正后的状态方程。
范德瓦尔斯状态方程是修正后的状态方程之一,它考虑了气体分子之间的吸引力和排斥力。
根据范德瓦尔斯状态方程,可以得到修正后的气体的PVT公式为(P+n^2a/V^2)(V-nb)=nRT,其中a和b分别是范德瓦尔斯常数,R是气体常数,n表示气体的摩尔数。
PVT公式的应用范围非常广泛。
例如在石油工程中,PVT公式可以用来描述油藏中的气体行为,从而帮助工程师判断油藏的性质和开发潜力。
在化学工程中,PVT公式可以用来计算气体的物理性质,如密度、粘度等,从而指导工程设计和操作。
在环境科学中,PVT 公式可以用来模拟大气中的气体运动和扩散过程,从而研究空气污染和气候变化等问题。
除了上述提到的理想气体状态方程和范德瓦尔斯状态方程,还有一些其他的状态方程和PVT公式可以用来描述气体行为。
例如,柯西状态方程适用于描述高温高压下的气体行为,它考虑了气体分子的非理想性和相互作用力的非线性性。
另外,对于特殊的气体,如湿气、混合气体等,还需要使用相应的状态方程和PVT公式进行描述和计算。
气体PVT公式是描述气体行为的重要工具,它可以用来计算气体的压力、体积和温度之间的关系。
物理化学主要公式

物理化学主要公式第一章 气体的pVT 关系1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1。
R =8.314510 J · mol -1 · K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2. 气体混合物 (1) 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量。
A m,*V 表示在一定T ,p 下纯气体A 的摩尔体积。
∑*AA m ,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2) 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3)V V p p n n y ///B B B B *=== 式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力。
*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
3. 道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体。
对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。
5. 德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa · m 6 · mol -2,b 的单位为m 3 · mol -1,a 和b 皆为只与气体的种类有关的常数,称为德华常数。
01气体的pVT关系

临界温度以上不再有液体存在,
p*=f (T) 曲线终止于临界温度; 临界温度 Tc 时的饱和蒸气压称为临界压力。
临界压力:(critical pressure ,pc)在临界温度下时
的饱和蒸气压。是在临界温度下使气体液化所需要 的最低压力。 临界摩尔体积:(critical molar volume,Vm,c)是在 临界温度和临界压力下物质的摩尔体积。 临界状态:物质处于临界温度、临界压力下的状态。
拐点C; S 型曲线两端有过饱和蒸气和 过热液体的含义。
图1.3.2 真实气体p-Vm等温线示意图
26
用范德华方程计算,在已知T , p,求Vm时,需解一元三次方程
T > Tc 时,Vm有 一个实根,两个虚根,虚根无意义; T = Tc时, 如 p = pc :Vm 有三个相等的实根; 如 p pc : 有一个实根,二个虚根,
对于任何气体混合物,分压为
pB yB p
对于理想气体混合物
p pB
B
pB nB RT / V
适用范围:理想气体混合物和低压下的真实气体混合物。
即理想混合气体的总压等于各组分单独存在于混合气体的T、 V 条件下所产生的压力总和 道尔顿分压定律
4.阿马加分体积定律(Amagat’s law of partial volume)
整理可得如下状态方程:
单位:p Pa TK
pV nRT 或 pVm RT 或 pV m M RT
V m3 n mol R J mol-1 K-1
2.理想气体(perfect gas)模型
吸引力 分子相距较远时,有范德华引力;
排斥力 分子相距较近时,电子云及核产生排斥作用。
物理化学主要公式

物理化学主要公式第一章 气体的pVT 关系1.理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1。
R =8.314510 J · mol -1 · K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2.气体混合物 (1) 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量。
A m,*V 表示在一定T ,p 下纯气体A 的摩尔体积。
∑*AA m ,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2) 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3)V V p p n n y ///B B B B *=== 式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力。
*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
3.道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体。
对于理想气体V RT n p /B B =4.阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。
5.范德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa · m 6 · mol -2,b 的单位为m 3 · mol -1,a 和b 皆为只与气体的种类有关的常数,称为范德华常数。
物理化学主要公式

物理化学主要公式第一章 气体的pVT 关系1.理想气体状态方程式或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa,m 3,K 及mol; m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1; R = J · mol -1 · K -1,称为摩尔气体常数;此式适用于理想气体,近似地适用于低压的真实气体; 2.气体混合物 (1) 组成摩尔分数 y B 或x B = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量;Am,*V表示在一定T ,p 下纯气体A 的摩尔体积;∑*AA m ,A V y 为在一定T ,p 下混合之前各纯组分体积的总和;(2) 摩尔质量式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量;上述各式适用于任意的气体混合物;3V V p p n n y ///B B B B *=== 式中p B 为气体B,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力;*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积; 3.道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体;对于理想气体 4.阿马加分体积定律 此式只适用于理想气体; 5.范德华方程式中a 的单位为Pa · m 6 · mol -2,b 的单位为m 3 · mol -1,a 和b 皆为只与气体的种类有关的常数,称为范德华常数;此式适用于最高压力为几个MPa 的中压范围内实际气体p ,V ,T ,n 的相互计算; 6.维里方程及 ......)1(3'2''m ++++=p D p C p B RT pV上式中的B,C,D,…..及B’,C’,D’….分别称为第二、第三、第四…维里系数,它们皆是与气体种类、温度有关的物理量;适用的最高压力为1MPa 至2MPa,高压下仍不能使用; 7.压缩因子的定义Z 的量纲为一;压缩因子图可用于查找在任意条件下实际气体的压缩因子;但计算结果常产生较大的误差,只适用于近似计算;第二章 热力学第一定律1. 热力学第一定律的数学表示式或 'amb δδδd δdU Q W Q p V W =+=-+规定系统吸热为正,放热为负;系统得功为正,对环境作功为负;式中 p amb 为环境的压力,W ’为非体积功;上式适用于封闭体系的一切过程; 2. 焓的定义式 3. 焓变1 )(pV U H ∆+∆=∆式中)(pV ∆为pV 乘积的增量,只有在恒压下)()(12V V p pV -=∆在数值上等于体积功; 2 2,m 1d p H nC T ∆=⎰此式适用于理想气体单纯pVT 变化的一切过程,或真实气体的恒压变温过程,或纯的液体、固体物质压力变化不大的变温过程; 4. 热力学能又称内能变此式适用于理想气体单纯pVT 变化的一切过程;5. 恒容热和恒压热6. 热容的定义式 1定压热容和定容热容2摩尔定压热容和摩尔定容热容pVU H +=2,m1d V U nC T ∆=⎰上式分别适用于无相变变化、无化学变化、非体积功为零的恒压和恒容过程; 3质量定压热容比定压热容式中m 和M 分别为物质的质量和摩尔质量; 4 ,m ,m p V C C R -= 此式只适用于理想气体;5摩尔定压热容与温度的关系 式中a , b , c 及d 对指定气体皆为常数; 6平均摩尔定压热容 7. 摩尔蒸发焓与温度的关系或 vap m vap ,m (/)p p H T C ∂∆∂=∆式中 vap ,m p C ∆ = ,m p C g —,m p C l,上式适用于恒压蒸发过程; 8. 体积功 1定义式或 V p W d amb ∑-=2 )()(1221T T nR V V p W --=--= 适用于理想气体恒压过程;3 )(21amb V V p W --= 适用于恒外压过程;4 )/ln()/ln(d 121221p p nRT V V nRT V p W V V =-=-=⎰ 适用于理想气体恒温可逆过程;5 ,m 21()V W U nC T T =∆=- 适用于,m V C 为常数的理想气体绝热过程;9. 理想气体可逆绝热过程方程上式中,,m ,m /p V C C γ=称为热容比以前称为绝热指数,适用于,m V C 为常数,理想气体可逆绝热过程p ,V ,T 的计算; 10. 反应进度上式是用于反应开始时的反应进度为零的情况,B,0B B n n n -=∆,B,0n 为反应前B 的物质的量;B ν为B 的反应计量系数,其量纲为一;ξ的量纲为mol; 11. 标准摩尔反应焓式中θf m (B,)H β∆及θc m (B,)H β∆分别为相态为β的物质B 的标准摩尔生成焓和标准摩尔燃烧焓;上式适用于ξ=1 mol,在标准状态下的反应;12. θm r H ∆与温度的关系式中 r ,m ,m B (B)p p C C ν∆=∑,适用于恒压反应;13. 节流膨胀系数的定义式T J -μ又称为焦耳-汤姆逊系数;3. 热力学第二定律 主要公式及使用条件1. 热机效率式中1Q 和2Q 分别为工质在循环过程中从高温热源T 1吸收的热量和向低温热源T 2放出的热;W 为在循环过程中热机中的工质对环境所作的功;此式适用于在任意两个不同温度的热源之间一切可逆循环过程; 2. 卡诺定理的重要结论任意可逆循环的热温商之和为零,不可逆循环的热温商之和必小于零; 3. 熵的定义 4. 克劳修斯不等式 5. 熵判据式中iso, sys 和amb 分别代表隔离系统、系统和环境;在隔离系统中,不可逆过程即自发过程;可逆,即系统内部及系统与环境之间皆处于平衡态;在隔离系统中,一切自动进行的过程,都是向熵增大的方向进行,这称之为熵增原理;此式只适用于隔离系统; 6. 环境的熵变7. 熵变计算的主要公式对于封闭系统,一切0=W δ的可逆过程的S ∆计算式,皆可由上式导出 1上式只适用于封闭系统、理想气体、,m V C 为常数,只有pVT 变化的一切过程 2 T 2112ln(/)ln(/)S nR V V nR p p ∆==此式使用于n 一定、理想气体、恒温过程或始末态温度相等的过程; 3 ,m 21ln(/)p S nC T T ∆=此式使用于n 一定、,m p C 为常数、任意物质的恒压过程或始末态压力相等的过程;8. 相变过程的熵变此式使用于物质的量n 一定,在α和β两相平衡时衡T ,p 下的可逆相变化; 9. 热力学第三定律或 0)0K ,(m =*完美晶体S 上式中符号*代表纯物质;上述两式只适用于完美晶体; 10. 标准摩反应熵上式中r ,m p C ∆=B ,m B(B)p C ν∑,适用于在标准状态下,反应进度为1 mol 时,任一化学反应在任一温度下,标准摩尔反应熵的计算; 11. 亥姆霍兹函数的定义12. r d δ'T A W = 此式只适用n 一定的恒温恒容可逆过程; 13. 亥姆霍兹函数判据只有在恒温恒容,且不做非体积功的条件下,才可用A ∆作为过程的判据; 14. 吉布斯函数的定义 15. ,r d δ'T P G W =此式适用恒温恒压的可逆过程; 16. 吉布斯函数判据只有在恒温恒压,且不做非体积功的条件下,才可用G ∆作为过程的判据; 17. 热力学基本方程式热力学基本方程适用于封闭的热力学平衡系统所进行的一切可逆过程;说的更详细些,它们不仅适用于一定量的单相纯物质,或组成恒定的多组分系统发生单纯p , V, T 变化的过程;也可适用于相平衡或化学平衡的系统,由一平衡状态变为另一平衡态的过程; 18. 克拉佩龙方程此方程适用于纯物质的α相和β相的两相平衡; 19. 克劳修斯-克拉佩龙方程此式适用于气-液或气-固两相平衡;气体可视为理想气体;(l)m *V 与(g)m *V 相比可忽略不计,在21T T -的温度范围内摩尔蒸发焓可视为常数;对于气-固平衡,上式vap m H ∆则应改为固体的摩尔升华焓;0)(lim m =*→完美晶体S T 0TH S /βαβα∆=∆20. ))(/Δ(/ln(m fus m fus )1212p p H ΔV T T -=式中fus 代表固态物质的熔化;m fus ΔV 和m fus H Δ为常数的固-液两相平衡才可用此式计算外压对熔点的T 的影响; 21. 麦克斯韦关系式 适用条件同热力学基本方程;第四章 多组分系统热力学 主要公式及其适用条件1. 偏摩尔量:定义: Cn p,T,n X X ⎪⎪⎭⎫⎝⎛∂∂=B B 1 其中X 为广延量,如V ﹑U ﹑S ......全微分式:d ⎛⎫∂∂⎛⎫=++ ⎪ ⎪∂∂⎝⎭⎝⎭∑B B B B Bd d d p,n T,n X X X T p X n T p 2 总和: ∑=BB B X n X 32. 吉布斯-杜亥姆方程在T ﹑p 一定条件下,0d BB B =∑X n , 或 0d BB B =∑X x ;此处,x B 指B 的摩尔分数,X B 指B 的偏摩尔量; 3. 偏摩尔量间的关系广延热力学量间原有的关系,在它们取了偏摩尔量后,依然存在; 例:H = U + PV H B = U B + PV B ; A = U - TS A B = U B - TS B ;G = H – TS G B = H B - TS B ;… 4. 化学势定义 Cn p,T,n G G μB B ⎪⎪⎭⎫⎝⎛∂∂==B 5. 单相多组分系统的热力学公式但按定义,只有 CBn p,T,n G ⎪⎪⎭⎫ ⎝⎛∂∂才是偏摩尔量,其余3个均不是偏摩尔量;6. 化学势判据在d T = 0 , d p = 0 δW ’= 0 的条件下,⎪⎭⎫⎝⎛≤α=<∑∑平衡自发,,00α0 )()d (αBB B n μ其中,∑α指有多相共存,)(αB μ指 α相内的B 物质;7. 纯理想气体B 在温度T ﹑压力p 时的化学势pg 表示理想气体, 表示纯态,(g)0μ为气体的标准化学势;真实气体标准态与理想气体标准态均规定为纯理想气体状态,其压力为标准压力 0p = 100 kPa;8. 理想气体混合物中任一组分B 的化学势 其中,总p y p B B =为B 的分压;9. 纯真实气体B 在压力为p 时的化学势其中,(g)*m V 为纯真实气体的摩尔体积;低压下,真实气体近似为理想气体,故积分项为零;10. 真实气体混合物中任一组分B 的化学势其中,V B g 为真实气体混合物中组分B 在该温度及总压B p 下的偏摩尔体积;低压下,真实气体混合物近似为理想气体混合物,故积分项为零; 11. 拉乌尔定律与亨利定律对非电解质溶液拉乌尔定律:A *A A x p p = 其中,*A p 为纯溶剂A 之饱和蒸气压,A p 为稀溶液中溶剂A 的饱和蒸气分压,x A 为稀溶液中A 的摩尔分数;亨利定律: B B B B B B B c k b k x k p c,b,x,===其中,B p 为稀溶液中挥发性溶质在气相中的平衡分压,B B B c,b ,x ,k k ,k 及为用不同单位表示浓度时,不同的亨利常数; 12. 理想液态混合物定义:其任一组分在全部组成范围内都符合拉乌尔定律的液态混合物; 其中,0≤x B ≤1 , B 为任一组分; 13. 理想液态混合物中任一组分B 的化学势其中,(l)*B μ为纯液体B 在温度T ﹑压力p 下的化学势;若纯液体B 在温度T ﹑压力0p 下标准化学势为(l)0B μ,则有:其中,m B (l)*,V 为纯液态B 在温度T 下的摩尔体积; 14. 理想液态混合物的混合性质① 0Δmix =V ; ② 0Δmix =H ; ③ B=-∑∑mix B BB BΔ()ln()S n Rxx ;④ S T G mix mix ΔΔ-=15. 理想稀溶液① 溶剂的化学势:当p 与0p 相差不大时,最后一项可忽略;② 溶质B 的化学势: 我们定义: 同理,有:注:1当p 与0p 相差不大时,最后一项积分均可忽略;2溶质B 的标准态为0p 下B 的浓度分别为...x ,c c ,b b 1B 0B 0B === , 时,B 仍然遵循亨利定律时的假想状态;此时,其化学势分别为)(0B,溶质b μ﹑)(0B ,溶质c μ﹑)(0B ,溶质x μ; 16. 分配定律在一定温度与压力下,当溶质B 在两种共存的不互溶的液体α﹑β间达到平衡时,若B 在α﹑β两相分子形式相同,且形成理想稀溶液,则B 在两相中浓度之比为一常数,即分配系数; 17. 稀溶液的依数性① 溶剂蒸气压下降:B *A AΔx p p = ② 凝固点降低:条件:溶质不与溶剂形成固态溶液,仅溶剂以纯固体析出 ③ 沸点升高:条件:溶质不挥发 ④ 渗透压: Π=B V n RT 18. 逸度与逸度因子气体B 的逸度~p B ,是在温度T ﹑总压力总p 下,满足关系式: 的物理量,它具有压力单位;其计算式为:逸度因子即逸度系数为气体B 的逸度与其分压力之比:理想气体逸度因子恒等于1 ; 19. 逸度因子的计算与普遍化逸度因子图用V m = ZRT / p 代V B ,Z 为压缩因子有:不同气体,在相同对比温度T r ﹑对比压力p r 下,有大致相同的压缩因子Z ,因而有大致相同的逸度因子ϕ; 20. 路易斯-兰德尔逸度规则混合气体中组分B 的逸度因子等于该组分B 在该混合气体温度及总压下单独存在时的逸度因子;适用条件:由几种纯真实气体在恒温恒压下形成混合物时,系统总体积不变;即体积有加和性;21. 活度与活度因子对真实液态混合物中溶剂:B B *B B *B B ln (l)ln (l)(l)f x RT μa RT μμ+=+= ,且有:1lim B1B =→f x ,其中a B 为组分B 的活度,f B 为组分B 的活度因子;若B 挥发,而在与溶液平衡的气相中B 的分压为B p ,则有BBB BB Bxp pxa f*==,且 *p p a B BB = 对温度T 压力p 下,真实溶液中溶质B 的化学势,有:其中,⎪⎭⎫⎝⎛=0B B B b b a γ/为B 的活度因子,且1Blim=∑→γ BB b 0 ;当p 与0p 相差不大时,B 0B Bln )(a RT μμ+=溶质(溶质),对于挥发性溶质,其在气相中分压为:BB b k γp b =,则,==BBB B Bbb p p a γk k b ;第五章 化学平衡 主要公式及其适用条件1. 化学反应亲和势的定义A 代表在恒温、恒压和'0W =的条件下反应的推动力,A >0反应能自动进行;A =0处于平衡态;A < 0反应不能自动进行; 2.摩尔反应吉布斯函数与反应进度的关系式中的()p ξ∂∂T,G 表示在T,p 及组成一定的条件下,反应系统的吉布斯函数随反应进度的变化率,称为摩尔反应吉布斯函数变; 3.化学反应的等温方程式中 νμ∆=∑θθr mB BG ,称为标准摩尔反应吉布斯函数变;()BB Bp J p pν=∏θ ,称为反应的压力商,其单位为1;此式适用理想气体或低压下真实气体,,在T ,p 及组成一定,反应进度为1 mol 时的吉布斯函数变的计算; 4.标准平衡常数的表达式式中eq B p 为参加化学反应任一组分B 的平衡分压力,γB 为B 的化学计量数;K θ量纲为一;若已知平衡时参加反应的任一种物质的量n B ,摩尔分数y B ,系统的总压力p ,也可采用下式计算θK :式中∑B n 为系统中气体的物质的量之和,∑B ν为参加反应的气态物质化学计量数的代数和;此式只适用于理想气体; 5.标准平衡常数的定义式或 θθr mexp()K G RT =-∆ 6. 化学反应的等压方程——范特霍夫方程微分式 θθ2r m d ln K T H RT =∆ 积分式 θθθ21r m 2121ln()()K K H T T RT T =∆- 不定积分式 θθr m ln K H RT C =-∆+对于理想气体反应,θr m r m H H ∆=∆,积分式或不定积分式只适用于r m H ∆为常数的理想气体恒压反应;若r m H ∆是T 的函数,应将其函数关系式代入微分式后再积分,即可得到θln K 与T 的函数关系式;()B θeq B Bθνp p K ∏=7.真实气体的化学平衡上式中eq B p,~eqBp,eqBϕ分别为气体B在化学反应达平衡时的分压力、逸度和逸度系数;θK则为用逸度表示的标准平衡常数,有些书上用θf K表示;上式中~eq eq eqB B Bp pϕ=⋅;第六章相平衡主要公式及其适用条件1.吉布斯相律式中F为系统的自由度数即独立变量数;P为系统中的相数;“2”表示平衡系统只受温度、压力两个因素影响;要强调的是,C称为组分数,其定义为C=S-R-R′,S为系统中含有的化学物质数,称物种数;R为独立的平衡化学反应数;'R为除任一相中∑=1Bx或1B=ω;同一种物质在各平衡相中的浓度受化学势相等限制以及R个独立化学反应的标准平衡常数θK对浓度限制之外,其他的浓度或分压的独立限制条件数;相律是表示平衡系统中相数、组分数及自由度数间的关系;供助这一关系可以解决:a计算一个多组分多平衡系统可以同时共存的最多相数,即F=0时,P值最大,系统的平衡相数达到最多;b计算一个多组分平衡系统自由度数最多为几,即是确定系统状态所需要的独立变量数;c分析一个多相平衡系统在特定条件下可能出现的状况;应用相律时必须注意的问题:a相律是根据热力学平衡条件推导而得的,故只能处理真实的热力学平衡系统;b相律表达式中的“2”是代表温度、压力两个影响因素,若除上述两因素外,还有磁场、电场或重力场对平衡系统有影响时,则增加一个影响因素,“2”的数值上相应要加上“1”;若相平衡时两相压力不等,则2+-=PCF式不能用,而需根据平衡系统中有多少个压力数值改写“2”这一项;c要正确应用相律必须正确判断平衡系统的组分数C和相数P;而C值正确与否又取决与R与R‘的正确判断;d自由度数F只能取0以上的正值;如果出现F<0,则说明系统处于非平衡态;2.杠杆规则杠杆规则在相平衡中是用来计算系统分成平衡两相或两部分时,两相或两部分的相对量,如图6-1所示,设在温度为T下,系统中共存的两相分别为α相与β相;BB B~eq eq eqB B BB BB()()()K p p p pνννϕ=∏⋅∏=∏θθθ图6-1 说明杠杆规则的示意图图中M ,α,β分别表示系统点与两相的相点;B M x ,B x α,B x β分别代表整个系统,α相和β相的组成以B 的摩尔分数表示;n ,αn 与βn 则分别为系统点,α相和β相的物质的量;由质量衡算可得 或上式称为杠杆规则,它表示α,β两相之物质的量的相对大小;如式中的组成由摩尔分数Bx α,B M x ,B x β换成质量分数B αω,B M ω,B βω时,则两相的量相应由物质的量αn 与βn 或αm 与βm ;由于杠杆规则是根据物料守恒而导出的,所以,无论两相平衡与否,皆可用杠杆规则进行计算;注意:若系统由两相构成,则两相组成一定分别处于系统总组成两侧;第七章 电 化 学 主要公式及其适用条件1.迁移数及电迁移率电解质溶液导电是依靠电解质溶液中正、负离子的定向运动而导电,即正、负离子分别承担导电的任务;但是,溶液中正、负离子导电的能力是不同的;为此,采用正负离子所迁移的电量占通过电解质溶液的总电量的分数来表示正负离子之导电能力,并称之为迁移数,用t + t - 表示;即正离子迁移数 负离子迁移数上述两式适用于温度及外电场一定而且只含有一种正离子和一种负离子的电解质溶液;式子表明,正负离子迁移电量与在同一电场下正、负离子运动速率+v 与 -v 有关;式中的u + 与u - 称为电迁移率,它表示在一定溶液中,当电势梯度为1V·m -1 时正、负离子的运动速率;若电解质溶液中含有两种以上正负离子时,则其中某一种离子B 的迁移数t B 计算式为2.电导、电导率与摩尔电导率衡量溶液中某一电解质的导电能力大小,可用电导G ,电导率κ与摩尔电导率m Λ来表述;电导G 与导体的横截面A s 及长度l 之间的关系为式中κ称为电导率,表示单位截面积,单位长度的导体之电导;对于电解质溶 液,电导率BB B B ()()MM x x n n x x βαβα-=-κ则表示相距单位长度,面积为单位面积的两个平行板电极间充满 电解质溶液时之电导,其单位为S · m -1;若溶液中含有B 种电解质时,则该溶液的电导率应为B 种电解质的电导率之和,即虽然定义电解质溶液电导率时规定了电极间距离、电极的面积和电解质溶液的体积,但因未规定相同体积电解质溶液中电解质的量,于是,因单位体积中电解质的物质的量不同,而导致电导率不同;为了反映在相同的物质的量条件下,电解质的导电能力,引进了摩尔电导率的概念;电解质溶液的摩尔电导率m Λ定义是该溶液的电导率κ与其摩尔浓度c 之比,即m Λ表示了在相距为单位长度的两平行电极之间放有物质的量为1 mol 电解质之溶液的电导;单位为S · m 2 · mol -1 ;使用m Λ时须注意:1物质的量之基本单元;因为某电解质B 的物质的量n B 正比于B 的基本单元的数目;例如,在25 0C 下,于相距为l m 的两平行电极中放人1mol BaSO 4基本单元时,溶液浓度为c ,其m ΛBaSO 4 ,= ×10-2 S · m 2 · mol -1 ;若基本单元取21BaS04,则上述溶液的浓度变为c ',且c '=2c ;于是,m Λ'21BaS04,= 21m ΛBaS04,=×10-2 S · m 2 · mol -1;2对弱电解质,是指包括解离与未解离部分在内总物质的量为1 mol 的弱电解质而言的;m Λ是衡量电解质导电能力应用最多的,但它数值的求取却要利用电导率κ,而κ的获得又常需依靠电导G 的测定; 3. 离子独立运动定律与单种离子导电行为摩尔电导率m Λ与电解质的浓度c 之间有如下关系: c A ΛΛ-=∞m m此式只适用于强电解质的稀溶液;式中A 与 ∞m Λ 在温度、溶液一定下均为常数;∞m Λ是c 0时的摩尔电导率,故称为无限稀释条件下电解质的摩尔电导率;∞m Λ是电解质的重要特性数据,因为无限稀释时离子间无静电作用,离子独立运动彼此互不影响,所以,在同一温度、溶剂下,不同电解质的∞m Λ数值不同是因组成电解质的正、负离子的本性不同;因此,进一步得出式中+ν与-ν分别为电解质-+ννA C 全部解离时的正、负离子的化学计量数,∞+, m Λ与∞-, m Λ则分别为溶液无限稀时正、负离子的摩尔电导率;此式适用溶剂、温度一定条件下,任一电解质在无限稀时的摩尔电导率的计算;而∞+, m Λ和∞-, m Λ可通过实验测出一种电解质在无限稀时的∞ m Λ与迁移数 ∞B t ,再由下式算出:利用一弱电解质的∞m Λ值及一同温同溶剂中某一浓度稀溶液的该弱电解质之 m Λ,则从下式可计算该弱电解质在该浓度下的解离度: 4.电解质离子的平均活度和平均活度系数强电解质-+ννA C 解离为++z C ν离子和--z A ν离子,它们的活度分别为a , a + ,a - ,三者间关系如下:-+-+⋅=ννa a a 因实验只能测得正、负离子的平均活度±a ,而±a 与a ,a +,a - 的关系为另外 ±±±⎛⎫= ⎪⎝⎭0b a γb式中:±b 称为平均质量摩尔浓度,其与正、负离子的质量摩尔浓度b +,b - 的关系为()νννb b b -+-+±⋅=; 式中±γ称离子平均活度系数,与正、负离子的活度系数+γ,-γ的关系为()νννγγγ-+-+±⋅= ;5. 离子强度与德拜—休克尔极限公式离子强度的定义式为 =∑2B B B12I b Z ;式中b B 与Z B 分别代表溶液中某离子B 的质量摩尔浓度与该离子的电荷数;单位为mol ﹒kg -1;I 值的大小反映了电解质溶液中离子的电荷所形成静电场强度之强弱;I 的定义式用于强电解质溶液;若溶液中有强、弱电解质时,则计算I 值时,需将弱电解质解离部分离子计算在内;德拜—休克尔公式:I z z A γ-+±-= lg上式是德拜—休克尔从理论上导出的计算 ±γ的式子,它只适用于强电解质极稀浓度的溶液;A 为常数,在25 0C 的水溶液中A = - kg ﹒mol -11/2 ;6. 可逆电池对环境作电功过程的m r m r m r ΔΔΔH ,S ,G ,oK 及Q r 的计算在恒T ,p ,可逆条件下,若系统经历一过程是与环境间有非体积功交换时, 则 G = W r当系统原电池进行1 mol 反应进度的电池反应时,与环境交换的电功W ’= - z FE ,于是 r G m = -zFE 式中z 为1mol 反应进度的电池反应所得失的电子之物质的量,单位为mol 电子/mol 反应,F 为1mol 电子所带的电量,单位为C · mol -1电子;如能得到恒压下原电池电动势随温度的变化率∂⎛⎫⎪∂⎝⎭pE T 亦称为电动势的温度系数,则恒压下反应进度为1mol 的电池反应之熵差 r S m 可由下式求得:r S m =∂∂⎛⎫⎛⎫-= ⎪ ⎪∂∂⎝⎭⎝⎭r m Δp pG E zF T T 再据恒温下,r G m = r H m –T r S m ,得r H m = -zFE + zFT ∂⎛⎫⎪∂⎝⎭p E T ;此式与r G m 一样,适用于恒T ,p 下反应进度为1mol 的电池反应;若电池反应是在温度为T 的标准状态下进行时,则 于是 =O O ln K zFE /RT此式用于一定温度下求所指定的原电池反应的标准平衡常数OK ;式中OE 称为标准电动势;7. 原电池电动势E 的求法计算原电池电动势的基本方程为能斯特方程;如电池反应aA a A +cC a C = dD a D +f F a F则能斯特方程为上式可以写成 =-∏BO B ln νRT E E a zF上式表明,若已知在一定温度下参加电池反应的各物质活度与电池反应的得失电子的物质的量,则E 就可求;反之,当知某一原电池的电动势,亦能求出参加电池反应某物质的活度或离子平均活度系数 ±γ;应用能斯特方程首要的是要正确写出电池反应式;在温度为T ,标准状态下且氢离子活度a H+为1时的氢电极定作原电池阳极并规定该氢电极标准电极电势为零,并将某电极作为阴极还原电极,与标准氢组成一原电池,此电池电动势称为还原电极的电极电势,根据能斯特方程可以写出该电极电势与电极上还原反应的还原态物质活度a 还原态及氧化态物质活度a 氧化态的关系利用上式亦能计算任一原电池电动势;其计算方法如下:对任意两电极所构成的原电池,首先利用上式计算出构成该原电池的两电极的还原电极电势,再按下式就能算出其电动势E : E = E 阴—E 阳式中E 阴与E 阳分别为所求原电池的阴极和阳极之电极电势;若构成原电池的两电极反应的各物质均处在标准状态时,则上式改写为:oo m r ΔzFE G -=(阴)O E 与(阳)O E 可从手册中查得; 8.极化电极电势与超电势当流过原电池回路电流不趋于零时,电极则产生极化;在某一电流密度下的实际电极电势E 与平衡电极电势E 平之差的绝对值称为超电势,它们间的关系为阳 = E 阳 E 阳,平 阴 = E 阴,平 E 阴上述两式对原电池及电解池均适用;第八章 量子力学基础概念与主要公式1.量子力学假设1 由N 个粒子组成的微观系统,其状态可由这N 个粒子的坐标或动量的函数来表示,Ψ被称为波函数; 为在体积元d τ中发现粒子的概率;波函数为平方可积的,归一化的,,彼此可相差因子;波函数是单值的、连续的;2与时间有关的Schrdinger 方程: 势能与时间无关时,系统的波函数:3系统所有可观测物理量由算符表示;量子力学中与力学量A 对应的算符的构造方法是:① 写出A 的经典表达式:A t ; q 1 ,q 2 , …; p 1, p 2, …;② 将时间t 与坐标q 1 ,q 2 , ….看作数乘算符,将动量p j 用算符代替,则A 的算符为:4测量原理:在一系统中对力学量A 进行测量,其结果为的本征值λn ;若系统所处态为的某一本征态ψn ,则对A测量的结果一定为λn;若系统所处态不是的本征态,则对A的测量将使系统跃迁到的某一本征态ψk,测量结果为该本征态对应的λk ,若系统的归一化的态Ψ可用的本征态展开:则测量结果为λk概率为|a k|2 ;一般说来,对处于态Ψ的系统进行测量,力学量A的平均值为:2.一维箱中粒子波函数;能级3. 一维谐振子哈密顿算符:能级:波函数:4. 拉普拉斯算符在球极座标中的表示5. 球谐函数6. 二体刚性转子若r及V r均为常数,二体问题即成为二体刚性转子问题;若μ = m1 m2/m1 +m2 则:其中为转动惯量;波函数即为球谐数Y J,mθ,φ;7. 类氢离子8. 多电子原子的哈密顿算符9. 多电子原子电子波函数计算的近似方法步骤1 忽略电子间库伦排斥项:步骤2处理电子间库伦排斥项方法①—中心力场近似。
第一章气体的pVT关系

世纪末,人们开始普遍地使用现行的理想气体状
态方程:
pV = nRT
2.理想气体模型(model)
(1)分子间力 -兰纳德-琼斯理论(Lennard-Jones theory)
E
Eattra
Erepul
A r6
B r12
E
0
r0 r
(2) 理想气体模型 ①分子之间无相互作用力,E = 0
pV=nRT
➢临界压力 pc ——临界温度下使气体液化所需要
的最低压力,即为临界压力
➢临界摩尔体积Vm,c ——临界温度和临界压力下气
体的摩尔体积,即为临界摩尔体积
➢临界参数——物质临界状态下的Tc、 pc 、Vm,c
统称为物质的临界参数,是物质的特性参数
➢临界点——物质具有Tc、 pc 、Vm,c临 界参数
的临界状态点,称为物质的临界点
p Vm
Tc
0
2 p Vm2
Tc
0
➢超临界流体SCF——
§1 .4 真实气体的状态方程
真
范德华方程 (Van der Waals equation)
实
气
维里方程 (Kammerlingh - Onnes
体
equation)
的 状
R-K 方程 (Redlich – Kwong equation)
p
a Vm2
0
2 p Vm2
Tc
0
p Vm
Tc
RTc (Vm b)2
2a Vm3
0
2 p Vm2
Tc
2RTc (Vm b)3
6a Vm4
0
V m,c 3b
8a Tc 27Rb
pc
第一章气体的pVT关系

mB wB mA
def A
1.2.2
其量纲为 1, wB = 1
(3)体积分数 B ,定义为混合前纯B的体积与各纯组分
体积总和之比
B
def
x V
A
* xBVm ,B * A m, A
1.2.3
(量纲为1) B = 1
2. 理想气体状态方程对理想气体混合物的应用
因理想气体分子间没有相互作用,分子本身又不占 体积,所以理想气体的 pVT 性质与气体的种类无关,因 而一种理想气体的部分分子被另一种理想气体分子置换, 形成的混合理想气体,其 pVT 性质并不改变,只是理想 气体状态方程中的 n 此时为总的物质的量。
以上三式结合 pV = nRT 单位:
理想气体状态方程
p Pa; V m3; T K; n mol ; R 摩尔气体常数 8.3145 10 J mol-1 K-1 理想气体状态方程也可表示为: pVm=RT pV = (m/M)RT 以此可相互计算 p, V, T, n, m, M, (= m/ V)。
第一章
低压气体定律:
气体的 pVT 关系
1. 理想气体状态方程
(1)波义尔定律:在物质的量和温度恒定的条件下, 气体的体积与压力成正比,即 pV = 常数 ( n ,T 一定) (2)盖.吕萨克定律:当物质的量和压力恒定时, 气体的体积与热力学温度成正比,即 V / T = 常数 (n , p 一定) (3)阿伏加德罗定律:在相同的温度,压力下,1mol 任何气体占有相同体积,即 V / n = 常数 (T, p 一定)
饱和蒸气压首先由物质的本性决定。对于同一种物质, 它是温度的函数,随温度升高而增大。
饱和蒸气压 = 外压时,液体沸腾,此时的的温度称为 沸点。饱和蒸气压 = 1个大气压时的沸点称为正常沸点。 在沸腾时,液体表面及内部分子同时汽化。
第1章气体的pVt关系

1.4.1 Van der Waals 方程 2 n ( p a 2 )(V nb) nRT V
b为1mol气体分子自身体积的影响。 分子间吸引力正比于(n/V)2 内压力 p′=a(n/V)2 pideal=preal+a(n/V)2 Van der Waals方 1 ( p a )( V b ) RT m 2 种的另一种形式 V
p1 p2 189 186 100% 1.61% p2 186 ’ 3 V 2.00dm3 p1 1.89103 kPa p’ 1 . 59 10 kPa 2
’ ’ 3 p1 p2 (1.89 1.59) 10 100% 18.9% ’ 3 p2 1.59 10
a (p )(Vm b) RT 2 TVm
22
1.5压缩因子与普遍化压缩因子图
1.5.1真实气体的pVm-p图及波义尔温度
pVm/[pVm] C B A pVm/[pVm]
TB
p/[p]
图1.5.1不同气体在同一温度
下的pVm-p等温线
p/[p]
图1.5.2同一种气体在不同温度 下的pVm-p等温线
第1章 气体的p-T-V关系
1.1理想气体状态方程
低压下气体的三个经验定律: 1)Boyle定律:
pV=常数 V/T=常数 V/n=常数
(n、T一定) (n、p一定) (T、p一定) pV= nRT
R—通用气体常数
2)Gay-Lussac定律: 3)Avogadro定律:
精确值:R=(8.314510±0.000070)J· mol-1· K-1
mB wB def mA
A
nB xB (或yB ) def nA
01气体的pVT关系

第二个容器中,组分2的压力 混合后,第三个容器中,混合组分的压力
n1 RT p1 V n2 RT p2 V ( n1 n2 ) RT p p1 p2 V
二.道尔顿分压定律
1、道尔顿分压定律
理想气体混合物的总压力等于各种气体单独存在,且具有 混合物温度和体积时的压力之和。
p pB
m ( H 2 ) n H 2 M ( H 2 ) (4.01 106 ) ( 2.016 10 3 )kg 8.08 103 kg
【例】某化工车间一反应器操作压力为 106.4kPa,温度为723K,每小时送入该反应器 的气体为4.00×104m3(STP),试计算每小时 实际通过反应器的气体体积(即体积流量)。
气体液化的必要条件: T<TC 气体液化的充分条件: p>p*
l2
C
673.2K
l3
g3 g2
496.3K 304.2K 293.2K
液体+气体
286.3K
Vm • 实际气体p - Vm等温线的一般规律
物质处于临界点时的特点:
物质气-液相间的差别消失,两相的摩尔体积相等 ,密度等物理性质相同,处于气液不分的混沌状 态。
盖-吕萨克(Gay J—Lussac J)定律 V / T C(n, p一定)
阿伏加德罗(Avogadro A)定律
V / n C(T , p一定)
气体p、V、T、n四个量中两个量不变时, 另外两个量的变化具有一定规律。
三. 理想气体(perfect gas)状态方程
整理以上三个定律,可得如下状态方程
§1.1 低压气体的P-V-T关系
一. 压力、体积和温度
第一章气体pVT关系

第一章 气体的pVT 关系§1.1 理想气体状态方程(1)状态方程状态方程:处于一定聚集态(气体、液体或固体)的物质都有一些可以直接测量的物理量,如p 、V 、T 等,这些物理量之间存在一定的函数关系,用来描述物质状态各物理量之间的函数关系的数学表达式称物质的状态方程(也称物态方程)。
气体的状态方程可写为:0f p V T n =(,,,)p - 压力V - 体积T - 热力学温度(绝对温度)n - 气体的物质的量(2)理想气体状态方程1、波义尔定律(Boyle )波义尔定律:在恒温条件下,一定量任何气体的体积与其压力成反比,即:1V p∝,或 .pV cont = 2、盖-吕萨克定律(Gay-Lussac )盖-吕萨克定律:在恒压条件下,一定量任何气体的体积均与其绝对温度成正比,即:T V ∝,或.V cont T = 3、阿伏加德罗定律(A. Avogadro ,1811)V / n =cont (T, p 一定)4、理想气体状态方程理想气体状态方程:pV nRT =或:m pV RT =,m V V n =(摩尔体积)R - 摩尔气体常数(或气体常数)。
R =8.314J.K -1.mol -1。
理想气体的特点:①分子自身无体积;②分子间无相互作用力。
精确实验证明,只有在压力趋近于零的极限情况下,各种气体才严格服从理想气体的状态方程。
理想气体状态方程的推导:已知气体的状态方程可写为:0n T V P f =),,,( 化为:),,(n T P f V =有: dn n V dT T V dP P V dV TP n P n T ,,,⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= 根据波义尔定律:.cont PV = 得:P V P C P V 2nT -=-=⎪⎭⎫ ⎝⎛∂∂, 根据盖-吕萨克定律:.cont T V =,即 'C TV = 有:T V 'C T V n,P ==⎪⎭⎫ ⎝⎛∂∂ 对于一定量气体(dn = 0),有:dT TV dP P V dV +-= 化为:TdT P dP V dV +-= 积分得:lnV +lnP =lnT +cont.,即 .cont T PV ⋅=若气体为 1 mol ,则常数写为R ,有 RT PV m =对于 n mol 气体,有 nRT PV =§1.2 理想气体混合物(1)道尔顿(Dalton )分压定律气体能以任意比例相互混合,而液体、固体一般不能。
第1章 气体的PVT关系

B
mB mB
B
* x BVm ,B B
B
B
1
③ 体积分数 B: (volume fraction) B
x
B
V
* m,B
B
B
1
2、道尔顿分压定律(1810年)
•理想气体混合物状态方程:
m pV ( nB ) RT RT M mix B
M mix yB M B
•波义尔温度(TB):
( pVm ) lim 0 p 0 p TB
① TB一般为气体临界温度 的2~2.5倍; ② TB下,气体在几百千帕 压力范围内较好符合理 想气体状态方程。
pVm
T TB
T TB T TB
p
•同一气体不同温度pVm-p图
2、范德华(van der waals)方程
理论联系实际
• 日常生活中使用的高压容器 • 秋天的露珠
pH 2O(空气中) 相对湿度 100% pH 2O
2、真实气体的p-Vm图及气体的液化
D
P
48 C
40 C
31.1C
压力表
CO2 ( g )
20 C
K
C
13 .1C
B
A
Vm
CO2的p-Vm恒温线
气体液化示意图
2、真实气体的p-Vm图及气体的液化
g´ 1
p 0 Vm Tc
2 p V 2 0 m Tc
l
g
Vm 真实气体 p –Vm 等温线示意图
超临界流体 (Super-critical Fluid)
•温度和压力略高于临界点的状态; •超临界流体兼具气液双重特性,高密度,扩散系 数大,具有很好的溶解性能; •超临界流体技术: ① 超临界萃取(extraction) ② 超临界流体干燥
气体的PVT关系专业知识

压力—临界压力(pc), pc(CO2)=7.38MPa 体积—临界摩尔体积(Vm,c),Vm,c(CO2)=94×10-6m3·mol-1
Tc , pc , Vm,c 统称临界参量。某些物质旳临界参量见表1.2。
表1.2 某些物质旳临界参量
物质
He H2 N2 O2 H2O CH4 C2H 4 C6H6 C2H5 OH
第一章 气体旳PVT关系 1.1 理想气体旳状态方程及微观模型
1.理想气体旳状态方程
PV=nRT
PVm=RT PV=mRT/M
R=8.3145J.K-1.mol-1
对于混合气体旳摩尔质量 Mmix=∑yBMB
例如
空气 y(O2)=0.21 y(N2)=0.79
则 M(空气)= y(O2) ×MO2+ y(N2) ×MN2=0.21×32+0.79×28
a=27R2Tc2/64pc, b=RTC/8Pc
3.维里方程
pVm
RT (1 B Vm
C Vm2
D Vm3
)
pVm RT (1 Bp Cp2 Dp3 )
4.其他主要方程举例
1.5 相应状态原理及普遍化压缩因子图
1.压缩因子
pV ZnRT或pVm ZRT
Z pV pVm nRT RT
以温度T1为例,曲线分为三段:
T1T2Tc T3
加压
{p} c
g(气体) 体积缩小 a(饱和气体)
l
定压
a(饱和气体)体积明显缩小 b(饱和液体)
b
a g
加压 b(饱和液体) 体积缩小(较小) l(液体)
{Vm,c} 图1-3 CO2 定温p-Vm,c 图
气体的pVT关系

nRT / p (
B
nB )RT / p
B
( nB RT ) p
B
VB*
分体积 VB* nB RT / p
2019/9/20
2019/9/20
小
结
对理想气体混合物中的任一组分B:
pBV nB RT pVB nB RT
2019/9/20
§1.3 气体的液化及临界参数
1.液体的饱和蒸气压
图及气体
2019/9/20
2019/9/20
2019/9/20
2019/9/20
2019/9/20
2019/9/20
2019/9/20
• 小结:
⑴ 温度一定时,只有一个平衡压力。
⑵ T 升高,水平段升高,对应压力增大。
⑶ T 升高,水平线右端点Vm(g), 左移;
左端点Vm(l),右移。即水平段变短。
2019/9/20
2019/9/20
2019/9/20
2019/9/20
• 理想气体混合物的总体积等于各个组分 以同混合物相同的温度和压力单独存在 时的分体积之和。
VO2
V VO2 VN2
VN2
2019/9/20
4. 阿马加定律
对于理想气体混合物,有 V VB*
B
V
2019/9/20
2019/9/20
Van der Waals 方程可 以
用于气相区和两相区。 这 是人类第一次将状态方程 应用于气液两相,因此这 是一 个伟大创举。
J. D.பைடு நூலகம்an der Waals 1837—1923
2019/9/20
van der Waals重大发现: 成功描述了气体的液化和临界现象; 将气体分子运动论成功推广到液体; 成功确立了“对应状态原理”。
热力学气体的 pVT关系

g1: 饱和蒸气摩尔体积Vm(g) l1: 饱和液体摩尔体积Vm(l) g1l1线上,气液共存。
C
l2 l1 g2 g1
T4 T3
T2 T1 g’2 g’1
Tc
若 n=n(g)+n(l)=1 mol 则 Vm n(g)Vm (g)+n(l)Vm (l)
Vm
图1.3.2 真实气体p-Vm等温线示意图
16
§1.3 真实气体的液化及临界参数 1. 液体的饱和蒸气压
理想气体不会变成液体(因分子间没有相互作用力) 实际气体:在某一定T 时,气-液可共存达到平衡 气-液平衡时: 气体称为饱和蒸气; 液体称为饱和液体; 饱和蒸气的压力称为饱和蒸气压。
图1.3.1 气-液平衡示意图
17
饱和蒸气压是温度函数,是物质的性质,与外压无关。
E吸引 –1/r 6 E排斥 1/r n 兰纳德-琼斯(Lennard-Jones)理论: n = 12
E总
A B E吸引+E排斥=- 6 12 r r
图1.1.1 兰纳德-琼斯势能 曲线示意图
7
物理化学-第一章气体的PVT关系-138

2020/9/7
气体的pVT关系
3
将三个经验定律综合起来,即得理想气体状态方程:
pV nRT
SI单位: Pa m3 mol K
(No.1)
R = NA·k = 8.3145 J·K-1·mol-1,称为摩尔气体常数 molar gas constant;n 为物质的量 amount-of-substance。
当饱和蒸气压与外压相等时,液体沸腾(液体内部分子和表 面分子同时气化),此时的温度即液体的沸点 boiling point
外压为标准大气压(101.325 kPa)时的沸点即正常沸点
2020/9/7
气体的pVT关系
14
沸点与外压和物质的本性有关:外压越大,沸点越高 (如水的沸点在高山顶上低于100℃,在高压锅内高于100℃); 挥发性强(蒸气压大)的物质,沸点较低。
2020/9/7
气体的pVT关系
19
超临界流体的应用:
从植物及其种子中萃取有用成分
用于食品、药物、保健品、化妆品、饮料和其他精细化学品的萃取
(1)从咖啡中萃取咖啡因(已大规模生产) (2)从啤酒花中萃取软性树脂类物质 (3)从种子中萃取食用油(已大规模生产)
无压榨损失和有机溶剂分离、残留问题
(4)从植物中萃取香精、调味品和药用产品
流体 fluid
结构最简单 结构最复杂
凝聚体 condensing
另有等离子态 plasma、超固态、中子态等。
状态方程 state equation:物质 p(pressure)、V (volume)、T(temperature)之间的关系方程。
第1章气体的PVT关系
n B RT nRT B V VB p p p B B n B RT VB p 即:理想气体混合物中物质B的分体积VB*,等 于纯气体B在混合物的温度及总压条件下所占有 的体积。
n
B
RT
阿马加定律表明理想气体混合物的体积具 有加和性,在相同温度、压力下,混合后的总 体积等于混合前各组分的体积之和。
北方冬季的湿度30%左右。液体水容易蒸发为水蒸 气,使人感觉气候干燥。
2. 临界参数
由表1.3.1可知:p*=f (T) T , p* Tc 临界温度:使气体能够液化所允许的最高温度 临界温度以上不再有液体存在,
当T=Tc 时,液相消失,加压不能再使气体液化。
p*=f (T) 曲线终止于临界温度;
在压力趋于0的极限条件下,各 种气体 的行为均服从pVm=RT的定 量关系。 R 是一个对各种气体都适用的常数
2000 1500 1000 0 20 40 60 80 100 120
p / MPa
§1.2 理想气体混合物
1. 混合物的组成
1) 摩尔分数 x 或 y xB (或 yB) 显然
def
nB / n B
饱和蒸气压=外压时的温度称为沸点
饱和蒸气压=1个标准大气压时的温度称为正常沸点
T一定时:
如 pB < pB*,B液体蒸发为气体至pB=pB*
pB > pB*,B气体凝结为液体至pB=pB*
(此规律不受其它气体存在的影响)
露珠现象? 夜晚温度降低,使大气中的p水蒸气 > p水*
空气中 pH 2O 100% 相对湿度的概念:相对湿度= pH 2O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 气体的pVT 关系§1.1 理想气体状态方程(1)状态方程状态方程:处于一定聚集态(气体、液体或固体)的物质都有一些可以直接测量的物理量,如p 、V 、T 等,这些物理量之间存在一定的函数关系,用来描述物质状态各物理量之间的函数关系的数学表达式称物质的状态方程(也称物态方程)。
气体的状态方程可写为:0f p V T n =(,,,)p - 压力V - 体积T - 热力学温度(绝对温度)n - 气体的物质的量(2)理想气体状态方程1、波义尔定律(Boyle )波义尔定律:在恒温条件下,一定量任何气体的体积与其压力成反比,即:1V p∝,或 .pV cont = 2、盖-吕萨克定律(Gay-Lussac )盖-吕萨克定律:在恒压条件下,一定量任何气体的体积均与其绝对温度成正比,即:T V ∝,或 .V cont T= 3、阿伏加德罗定律(A. Avogadro ,1811)V / n =cont (T, p 一定)4、理想气体状态方程理想气体状态方程:pV nRT =或:m pV RT =,m V V n= (摩尔体积)R - 摩尔气体常数(或气体常数)。
R =8.314J.K -1.mol -1。
理想气体的特点:①分子自身无体积;②分子间无相互作用力。
精确实验证明,只有在压力趋近于零的极限情况下,各种气体才严格服从理想气体的状态方程。
理想气体状态方程的推导:已知气体的状态方程可写为:0n T V P f =),,,( 化为:),,(n T P f V =有: dn n V dT T V dP P V dV TP n P n T ,,,⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= 根据波义尔定律:.cont PV = 得:P V P C P V 2nT -=-=⎪⎭⎫ ⎝⎛∂∂, 根据盖-吕萨克定律:.cont T V =,即 'C TV = 有:T V 'C T V n,P ==⎪⎭⎫ ⎝⎛∂∂ 对于一定量气体(dn = 0),有:dT TV dP P V dV +-= 化为:TdT P dP V dV +-= 积分得:lnV +lnP =lnT +cont.,即 .cont T PV ⋅=若气体为 1 mol ,则常数写为R ,有 RT PV m =对于 n mol 气体,有 nRT PV =§1.2 理想气体混合物(1)道尔顿(Dalton )分压定律气体能以任意比例相互混合,而液体、固体一般不能。
道尔顿分压定律:“混合气体的总压力为各气体单独占有混合气体的体积时所产生的压力之和”。
表示为: P = P 1 + P 2 + P 3 + … = ΣP i设各气体均为理想气体,则:V nRT n V RT V RT n V RT n V RT n P i 321=∑=+++= , i i i i y nn VnRT V RTn P P === 有 P i = y i P注意:只有低压混合气体才近似符合道尔顿分压定律。
(2)阿马格(Amgat )分体积定律阿马格分体积定律:“混合气体的总体积等于各气体在同温同压下单独存在时的体积(分体积)之和”。
表示为:V =ΣV i设各气体均为理想气体,则:i 212121V V V P RT n P RT n RT P )n n (P nRT V ∑=++=++=++== i i i y nn V V == , 有 V y V i i = 注意:只有低压混合气体才近似符合阿马格分体积定律。
§1.3 真实气体的液化和临界参数理论上,在一定条件下任何物质的气态 → 液态。
(1)气体的等温线在恒定温度下,测定不同压力p 时对应的体积V ,所得p ~V 曲线称等温线。
1、理想气体的等温线若气体是理想气体,则温度一定时有:PV = 常数,等温线是一条光滑的曲线。
2、实际气体的等温线对于实际气体,CO2的等温线具有代表性:CO2的等温线可分为三种类型:t c(31.04 ℃)—临界温度(气体可以液化的最高温度)① t > t c(实线)特征:①同一温度,压力越高,偏离理想气体行为越大。
②同一压力,温度越低,偏离理想气体行为越大。
③无论压力升高多少,气体不能被液化。
② t < t c(虚线)特征:①压力由小变大时,气体符合压缩时的一般规律。
②当压力升至第一折点时,气体开始液化。
这时P = 常数,V → 小,放热→ 多。
达到第二折点时,气体液化完毕。
③在第二折点处,压力升高,则水平曲线→ 垂直曲线,表明液体难以压缩。
③ t = t c(虚线)C点是气液共存之点,两者之间无界面、不可分,其物理性质如密度、折射率等均相同。
含C点的曲线(虚线)称饱和曲线。
(2)临界状态C点为临界点,对应的温度、压力和体积称为临界参数:t c —临界温度,气体可以液化的最高温度。
P c —临界压力,临界温度下气体可以液化的最低压力。
V c —临界体积。
临界参数通常由实验测得,应用时可查阅有关图、表。
临界点对应的状态称临界状态。
§1.4 真实气体状态方程实验发现,在低温、高压时,真实气体的行为与理想气体定律的偏差很大。
这是由于在低温、高压下,气体的密度增大,分子之间的距离缩小,分子之间的相互作用以及分子自身的体积就不能略去不计,不能把分子看作是自由运动的弹性质点,因此理想气体的分子运动模型需要予以修正。
1.实际气体的行为在压力较高或温度较低时,实际气体与理想气体的偏差较大。
今定义“压缩因子(Z )”(compressibility factor )以衡量偏差的大小。
nRT pV RT pV Z m ==理想气体的1,==Z RT pV m 。
对实际气体,若1>Z ,则RT pV m >,表明在同温、同压下,实际气体的体积要大于按理想气体方程计算的结果。
即实际气体的可压缩性比理想气体小。
当1<Z 时,情况则相反。
氮气的Z 一P 曲线也示于下图。
对于温度2T ,在相当的温度范围内,1≈Z ,随压力变化不大,并符合理想气体的状态方程,此时的温度称为Boyle 温度B T 。
在图形上表现为在此温度时,等温线的坡度等于零,即 00,=⎪⎪⎭⎫ ⎝⎛∂∂→p T m p pV2.Van der waals 方程式到目前为止,人们所提出的非理想气体的状态方程式至少有200种以上。
大体上可分为两类,一类是考虑了物质的结构(例如分子的大小,分子间的作用力等),在此基础上导出来的。
其特点是物理意义比较明确,也具有一定的普遍性。
但这些公式的一些参量仍常需要通过实验来确定,而且有一定的使用范围,因为经验证明,实际气体不可能在较大的温度和压力范围内都能用一个较简单的方程式来表示。
另一类是经验的或半经验的状态方程式,这一类状态方程式为数众多。
它一般只使用于特别的气体,并且只在指定的温度和压力范围内能给出较精确的结果。
在工业上常常使用后一类方程式.第一类中以Van der waals (范德华)方程式最为有名(以下简称为范氏方程),即 ()RT b V V a p m m =-⎪⎪⎭⎫ ⎝⎛+2它是1873年Van der waals 在前人研究的基础上提出来的。
范氏方程之所以特别受关注,并不是因为它比其它方程式更为准确,而是他在修正理想气体状态方程时,在体积和压力项上分别提出了两个具有物理意义的修正因子a 和b ,这两个因子揭示了真实气体与理想气体有差别的更根本原因。
此外,根据范氏方程所导出的对比状态方程式,在一定程度上可以说明气体和液体互相转变的某些现象。
在计算较高压力下热力学函数时,也常常要用到对比态的概念,这在工业计算中是很有用的。
推导:对于理想气体,假定:①分子间无相互作用力;②分子自身无体积。
对于实际气体,若用理想气体模型来处理,P 、V 项均要修正:(P 实 + 压力修正项)(V m 实 – 体积修正项)= RT(1)压力修正项*真实气体由于分子间存在引力(分子间还有一定距离,未表现出斥力),则真实气体分子施于器壁的压力要小于理想气体分子施于器壁的压力。
按理想气体模型处理,真实气体分子施于器壁的压力应为:P + P a P a — 内压力,由于分子间引力而产生因为 P ∝N 2,N ∝ρ N 、ρ— 分别为分子数目和密度所以 P ∝ρ2,有 2m V 1a P ∝, 即 2mV a a P = (2)体积修正项*在范德华方程中,(V m –b )为1 mol 真实气体分子可以自由活动的空间。
设气体分子为球型,半径为r ,则每个分子的体积为:3r 34π 。
A 和B 两个分子中心之间的距离: d = 2r 红线所围成的空间称为禁区,B 分子的中心是不能进入的。
禁区的空间为: 33r 348)r 2(34π⨯=π 任意一个分子的中心都不能进入其余(N m –1)个分子的禁区内(N m 为1 mol 真实气体分子的数目)。
则禁区的总体积为:3m r 34)1N (8π-⨯ 考虑两点因素:①由于N m »1,所以 N m –1≈N m 。
②某一个分子无论向什么方向运动,对于分子碰撞来说,都是将运动方向的一侧作为禁区。
因此,有效禁区应为:3m r 34N 821π⨯⨯⨯ 故有 mol 14r N 316b 3m ⨯=π=气体分子自身的体积。
范德华方程:RT )b V )(V a P (m 2m =-+或:nRT )nb V )(Van P (22=-+ a 、b — 与气体种类有关的特性常数,也称范德华常数。
(3)临界参数与范德华常数之间的关系*临界参数与范德华常数均涉及气体的P 、V 、T 行为,按照范德华方程绘制的CO 2的等温线与实验得到的CO 2的等温线大致相同,这说明范德华方程不仅可以近似描述实际气体的行为,而且还与气体的液化有某种联系。
这样可以由临界参数 → 范德华常数:范德华方程: RT )b V )(V a P (m 2m=-+ 用于临界状态: 2c c c c V a b V RT P --=对于临界点C 有: 0V P c T c c =⎪⎪⎭⎫ ⎝⎛∂∂,0V P cT 2c c 2=⎪⎪⎭⎫ ⎝⎛∂∂ 解方程可得: c 2c 2P T R 6427a ⋅=,cc P 8RT b = 3. 维里方程Virial: 拉丁文“力” 的意思Kammerling-Onnes 于二十世纪初提出的经验式式中:B ,C ,D 及B ',C ' ,D '分别为第二、第三……维里系数。
当 p → 0 时,V m → ∞,维里方程 ⇒ 理想气体状态方程。
维里方程后来用统计的方法得到了证明,成为具有一定理论意义的方程。
第二维里系数:反映了二分子间的相互作用对气体pVT 关系的影响; 第三维里系数:反映了三分子间的相互作用对气体pVT 关系的影响。
