八年级数学下册 知识点测试卷 一次函数与方程、不等式初级测试 新人教版word版
八年级数学下第19章一次函数知识点专题练习(含人教版答案)(可编辑修改word版)

八年级数学下第19 章一次函数知识点专题练习(含人教版答案) 一次函数知识点专题练习题(时间:90 分钟总分 120 分)一、相信你一定能填对!(每小题 3 分,共 30 分)知识点:求自变量的取值范围 1.下列函数中,自变量 x 的取值范围是x≥2的是() A.y= B.y= C.y= D.y= • 知识点:由一次函数的特点来求字母的取值5.若函数y=(2m+1)x2+(1-2m)x(m 为常数)是正比例函数,则m 的值为() A.m> B.m= C.m< D.m=- 11.已知自变量为x 的函数y=mx+2-m 是正比例函数,则m=,该函数的解析式为知识点:函数图像的意义2.下面哪个点在函数 y= x+1 的图象上() A.(2,1) B.(- 2,1) C.(2,0) D.(-2,0) 15.已知一次函数y=-x+a 与y=x+b 的图象相交于点(m,8),则a+b=. 18.已知一次函数y=-3x+1 的图象经过点(a,1)和点(-2,b),则a=,b=.17.已知直线y=x-3 与y=2x+2 的交点为(-5,-8),则方程组的解是.知识点:判断是否为一次函数或正比例函数 3.下列函数中,y 是x 的正比例函数的是() A.y=2x-1 B.y= C.y=2x2 D.y=-2x+1 知识点:k.、b 定位4.一次函数 y=-5x+3 的图象经过的象限是() A.一、二、三B.二、三、四 C.一、二、四 D.一、三、四 6.若一次函数y=(3-k)x-k 的图象经过第二、三、四象限,则 k 的取值范围是() A.k>3 B.0<k≤3 C.0≤k<3 D.0<k<3 知识点:确定一次函数的表达式 7.已知一次函数的图象与直线 y=-x+1 平行,且过点(8,2),那么此一次函数的解析式为() A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-1 10.一次函数y=kx+b 的图象经过点(2,- 1)和(0,3),那么这个一次函数的解析式为() A.y=-2x+3 B.y=-3x+2 C.y=3x-2 D.y= x-3 12.若点(1,3)在正比例函数y=kx 的图象上,则此函数的解析式为. 13.已知一次函数y=kx+b 的图象经过点A(1,3)和B(-1,-1),则此函数的解析式为.20.如图,一次函数 y=kx+b 的图象经过 A、B 两点,与 x 轴交于点C,则此一次函数的解析式为,△AOC的面积为.知识点:函数图象的理解 8.汽车开始行驶时,油箱内有油 40 升,如果每小时耗油 5 升,则油箱内余油量 y(升)与行驶时间 t(时)的函数关系用图象表示应为下图中的() 9.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程 y (千米)与行进时间 t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是()二、你能填得又快又对吗?(每小题3 分,共30 分)知识点:双直线的观察图象 14.若解方程x+2=3x-2 得x=2,则当x时直线y=x+ 2 上的点在直线y=3x-2 上相应点的上方.知识点:一次函数(或正比例函数)的增减性16.若一次函数y=kx+b 交于y 轴的负半轴,且y 的值随x 的增大而减少,则k 0,b 0.(填“>”、“<”或“=”)知识点:一次函数与坐标轴围成三角形的面积问题19.如果直线 y=-2x+k 与两坐标轴所围成的三角形面积是 9,则 k 的值为.三、认真解答,一定要细心哟!(共 60 分)知识点:确定一次函数的表达式 21.(14 分)根据下列条件,确定函数关系式:(1)y 与x 成正比,且当 x=9 时,y=16;(2)y=kx+b 的图象经过点(3,2)和点(-2,1).22.(12 分)一次函数 y=kx+b 的图象如图所示:(1)求出该一次函数的表达式;(2)当x=10 时,y 的值是多少?(3)当y=12 时, x 的值是多少?23.(12 分)一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4 元将剩余土豆售完,这时他手中的钱(含备用零钱)是 26 元,问他一共带了多少千克土豆? 24.(10 分)如图所示的折线 ABC 表示从甲地向乙地打长途电话所需的电话费 y(元)与通话时间 t(分钟)之间的函数关系的图象.(1)写出 y 与t 之间的函数关系式.(2)通话 2 分钟应付通话费多少元?通话 7 分钟呢?知识点:双函数经济型应用题的解决方案问题 25.(12 分)已知雅美服装厂现有 A 种布料 70 米,B 种布料 52 米,现计划用这两种布料生产 M、N 两种型号的时装共 80 套.已知做一套 M 型号的时装需用A 种布料 1. 1 米,B 种布料 0.4 米,可获利 50 元;做一套 N 型号的时装需用 A 种布料 0.6 米,B 种布料 0. 9 米,可获利 45 元.设生产 M 型号的时装套数为 x,用这批布料生产两种型号的时装所获得的总利润为 y 元.①求 y(元)与x(套)的函数关系式,并求出自变量的取值范围;②当 M 型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?答案 : 1.D 2.D 3.B 4.C 5.D 6.A 7.C 8.B 9.C 10.A 11.2;y=2x 12.y=3x 13.y=2x+1 14.<2 15.16 16.<;< 17.18.0;7 19.±6 20.y=x+2;4 21.①y= x;②y= x+ 22.y=x- 2;y=8;x=14 23.①5元;②0.5元;③45千克 24.①当0<t≤3 时,y=2.4;当t>3 时,y=t-0.6.②2.4元;6.4 元25.①y=50x+45(80-x)=5x+3600.∵两种型号的时装共用A 种布料[1.1x+0. 6(80-x)]米,共用 B 种布料[0.4x+0.9(80-x)]米,∴ 解之得40≤x≤44,而 x 为整数,∴x=40,41,42,43,44,∴y 与 x 的函数关系式是y=5x+3600(x=40,41,42,43,44);②∵y随x 的增大而增大,∴当 x=44 时,y 最大=3820,即生产 M 型号的时装 44 套时,该厂所获利润最大,最大利润是 3820 元.。
19.2.3 一次函数与方程、不等式 人教版数学八年级下册同步练习(含答案)

第十九章 一次函数19.2 一次函数19.2.3 一次函数与方程、不等式基础过关全练知识点1 一次函数与一元一次方程1.已知一次函数y=ax+b(a,b是常数且a≠0)中,x与y的部分对应值如下表:x-2-10123y6420-2-4则关于x的方程ax+b=0的解是( )A.x=-1B.x=0C.x=1D.x=22.【数形结合思想】同一平面直角坐标系中,一次函数y=k1x+b的图象与y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )A.x=0B.x=-1C.x=-2D.以上都不对知识点2 一次函数与一元一次不等式3.(2023甘肃武威期末)如图所示的是一次函数y=kx+b(k、b是常数,且k≠0)的图象,则不等式kx+b>0的解集是( )A.x<-2B.x>-2C.x>2D.x<24.【教材变式·P99T13】数形结合是解决数学问题常用的思想方法.如图,直线y=2x-1与直线y=kx+b(k≠0)相交于点P(2,3).根据图象可知,关于x的不等式2x-1>kx+b的解集是 ( )A.x<2B.x<3C.x>2D.x>35.如图,直线y=kx+b经过A(-1,-2),B(-3,0)和C(0,-3)三点,则不等式2x<kx+b<0的解集是 .知识点3 一次函数与二元一次方程(组)6.如图,直线l1、l2的交点坐标可以看作下列方程组 的解.( )A.y =x +1y =2x -1 B.y =x +1y =2x +1C.y =x -1y =2x -1 D.y =x -1y =2x +17.(2022陕西中考)在同一平面直角坐标系中,直线y=-x+4与y=2x+m 相交于点P(3,n),则关于x,y 的方程组x +y -4=0,2x -y +m =0的解为( )A.x =―1y =5 B.x =1y =3 C.x =3y =1 D.x =9y =―5能力提升全练8.(2023安徽无为期末,9,★☆☆)如图,观察图象可以得出不等式组3x +1>0,-0.5x +1>0的解集是( )A.x<13B.-13<x<0C.0<x<2D.-13<x<29.(2023福建泉州期末,7,★☆☆)一次函数y 1=kx+b(k≠0)和y 2=x+a 的图象如图,甲、乙两位同学给出下列结论:甲:方程kx+b=x+a 的解是x=3;乙:当x<3时,y 1<y 2.其中正确的结论是( )A.甲、乙都正确B.甲正确,乙错误C.乙正确,甲错误D.甲、乙都错误10.【一题多解】(2021福建中考,8,★★☆)如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式k(x-1)+b>0的解集是( )A.x>-2B.x>-1C.x>0D.x>111.(2022广西柳州中考,12,★★☆)如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=-x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )A.1B.2C.4D.612.(2023广东深圳中学月考,20,★★☆)如图,直线l:y=ax+b与直线m:y=-1x+2相交于点P(c,1).2(1)求c的值.(2)-y=―b,x+y=2的解.(3)直线n:y=bx+a能否经过点P?若能,求出a,b的值;若不能,请说明理由.素养探究全练13.【模型观念】规定:二元一次方程ax+by=c有无数组解,每组解记为P(x,y),称P(x,y)为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,回答下列问题:(1)已知A(-1,2),B(4,-3),C(-3,1),则是隐线y=-32x+3的亮点的是 ;(2)设P(0,-2),Q1,―t2x+hy=6的两个亮点,2+4 x-(t2+h+4)y=26中x,y的最小正整数解;(3)已知m,n是实数,且m+2|n|=7,若P(m,|n|)是隐线2x-3y=s的一个亮点,求隐线中s的最大值与最小值的和.答案全解全析基础过关全练1.C 根据题表可得,当x=1时,y=0,∴方程ax+b=0的解是x=1.故选C.2.B 由题图可得两直线的交点坐标是(-1,-2),所以关于x的方程k1x+b=k2x的解为x=-1,故选B.3.B 由图象得一次函数y=kx+b(k,b是常数,且k≠0)的图象经过点(-2,0),并且函数值y随x的增大而增大,所以不等式kx+b>0的解集是x>-2.故选B.4.C 根据图象可得,不等式2x-1>kx+b的解集为x>2,故选C.5.答案 -3<x<-1解析 如图,直线OA的解析式为y=2x,当x<-1时,2x<kx+b,当x>-3时,kx+b<0,所以不等式2x<kx+b<0的解集为-3<x<-1.6.A 由题图可知,直线l2过(2,3),(0,-1),所以直线l2的函数解析式为y=2x-1;直线l1过(2,3),(-1,0),所以直线l1的函数解析式为y=x+1.所以直线l1,l2的交点坐标可以看作二元一次方程组y=x+1,y=2x-1的解.故选A.7.C 将点P(3,n)代入y=-x+4,得n=-3+4=1,∴P(3,1),∴原方程组的解为x=3,y=1,故选C.能力提升全练8.D 根据图象可知3x+1>0的解集是x>-13,-0.5x+1>0的解集是x<2,∴不等式组的解集是-13<x<2.故选D.9.B ∵一次函数y1=kx+b(k≠0)与y2=x+a的图象的交点的横坐标为3,∴关于x的方程kx+b=x+a的解是x=3,故甲正确;当x<3时,y1>y2,故乙错误.故选B.10.C 解法一:把(-1,0)代入y=kx+b得-k+b=0,解得b=k,则k(x-1)+b>0可化为k(x-1)+k>0,因为k>0,所以x-1+1>0,所以x>0.故选C.解法二:将一次函数y=kx+b(k>0)的图象向右平移1个单位得到函数y=k(x-1)+b的图象,∵一次函数y=kx+b(k>0)的图象过点(-1,0),∴一次函数y=k(x-1)+b(k>0)的图象过点(0,0),由图象可知,当x>0时,k(x-1)+b>0,∴不等式k(x-1)+b>0的解集是x>0,故选C.11.B ∵点P(m,2)是△ABC内部(包括边上)的一点,∴点P在直线y=2上,如图所示,当P为直线y=2与直线y2的交点时,m取得最大值,当P为直线y=2与直线y1的交点时,m取得最小值,在y2=-x+3中,令y2=2,则x=1,在y 1=x+3中,令y 1=2,则x=-1,∴m 的最大值为1,最小值为-1,∴m 的最大值与最小值之差为1-(-1)=2.故选B.12.解析 (1)将点P(c,1)代入y=-12x+2,得1=-12c+2,解得c=2.(2)由(1)可知c=2,∴直线l 和直线m 的交点坐标为(2,1),即方程组-y =―b ,x +y =2的解为x =2,y =1.(3)直线n:y=bx+a 能经过点P.理由:将点(2,1)代入直线l:y=ax+b,得2a+b=1,将点(2,1)代入直线n:y=bx+a,得2b+a=1,联立2a +b =1,2b +a =1,解得a =13,b =13,∴当a=b=13时,直线n:y=bx+a 能经过点P.素养探究全练13.解析 (1)把三点的坐标代入隐线y=-32x+3,只有B 点满足,故答案为B(4,-3).(2)把P(0,-2),Q 1,―t 2x+hy=6,得-2ℎ=6,t 2-13h =6,∴ℎ=―3,t 2=5,把ℎ=―3,t 2=52+4x-(t 2+h+4)y=26,得5x-6y=26,∴x=26+6y 5=y+5+y +15,∵x 、y 都为正整数,∴最小正整数解为x =10,y =4.(3)把P(m ,|n|)代入隐线2x-3y=s 得s=2m -3|n|,∵m +2|n|=7,∴m =-2|n|+7,∴s=-4|n|+14-3|n|=14-7|n|,∵|n|≥0,m =-2|n|+7≥0,∴0≤|n|≤3.5,∴当|n|=0时,s=14-7|n|有最大值,最大值为14,当|n|=3.5时,s=14-7|n|有最小值,最小值为-10.5,∴s的最大值与最小值的和为14-10.5=3.5.。
人教版八年级数学下册19.2.3一次函数与方程、不等式同步测试(含答案)

19.2.3 一次函数与方程、不等式班级: 姓名:一、单选题1.如图,一次函数(0)y kx b k =+>的图象过点(0,2),则不等式20kx b +->的解集是( )A .0x >B .0x <C .2x <D .2x >2.如图,一次函数y =x+1与y =2x ﹣1图象的交点是(2,3),则方程组121x y x y -=-⎧⎨-=⎩的解为( )A .31x y =⎧⎨=-⎩B .23x y =⎧⎨=⎩C .31x y =⎧⎨=⎩ D .13x y =-⎧⎨=⎩3.一次函数1y kx b =+与2y x a =+的图象如图所示,则下列结论:①k <0;②a <0,b <0;③当x=3时,y 1=y 2;④不等式kx b x a +>+的解集是x <3,其中正确的结论个数是( )A .0B .1C .2D .34.已知方程()00kx b k +=≠的解是3x =,则函数()0y kx b k =+≠的图象可能是( )A.B.C.D.5.如图,直线y=ax+b与x轴交于点A(7,0),与直线y=kx交于点B(2,4),则不等式kx≤ax+b 的解集为()A.x≤2B.x≥2C.0<x≤2D.2≤x≤66.已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(12,12m),则不等式组mx﹣2<kx+1<mx的解集为()A.x>12B.12<x<32C.x<32D.0<x<327.如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-3,-5),则下列结论正确的是()A.x<-3时,y1<y2B.b<0 C.x<-3时,y1>y2D.a<08.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为()A .32x <B .32x >C .3x <D .3x >二、填空题9.如图,直线11y k x a =+与22y k x b =+的交点坐标为()1,2,当12k x a k x b +≤+时,则x 的取值范围是__________.10.一次函数y=kx+3的图象如图所示,则方程kx+3=0的解为__________.11.如图,函数y =-2x 和y =kx +b 的图像相交于点A(m ,4),则关于x 的不等式kx +b +2x >0的解集为_______12.如图,已知一次函数y mx n =-与24y x =-的图象交于x 轴上一点,则关于,x y 的二元一次方程组24mx y n x y -=⎧⎨-=⎩的解是__________.13.如图,已知函数y=x+b和y=ax+3的图象交点为P,则不等式x+b<ax+3的解集为_____.三、解答题14.在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.(1)如图,若x0=-1.①求点B的坐标及k的值;②求直线y=-2x+1、直线y=x+k与y轴所围成的△ABC的面积;(2)若-2<x0<-1,求整数k的值.15.如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为(,n)(1)则n= ,k= ,b=_______.(2)若函数y=kx+b 的函数值大于函数y=x+2的函数值,则x 的取值范围是_______. (3)求四边形AOCD 的面积.16.如图,正比例函数y=2x 的图象与一次函数y=kx+b 的图象交于点A(m,2),一次函数的图象经过点B(−2,−1).(1)求一次函数的解析式;(2)请直接写出不等式组−1<kx +b<2x 的解集.一、单选题1.如图,已知正比例函数y 1=ax 与一次函数y 2=12x+b 的图象交于点P .下面有四个结论:①a <0; ②b <0; ③当x >0时,y 1>0;④当x <﹣2时,y 1>y 2.其中正确的是( )A .①②B .②③C .①③D .①④2.一次函数y kx b =+的图象如图所示,则不等式0kx+b <的解集是( )A .2x >-B .2x <-C .3x <-D .3x >-3.如图,已知直线1y ax b =+与2y mx n =+相交于点A (2,1-),若12y y >,则x 的取值范围是( )A .2x <B .2x >C .1x <-D .1x >-4.如图,已知直线y mx =过点()2,4A --,过点A 的直线y nx b =+交x 轴于点()4,0B -,则关于的不等式组0nx b mx +≤<的解集为( )A .2x -≤B .42x -<≤-C .2x ≥-D .20x -≤<5.如图,直线y kx b =+经过()3,1A 和()6,0B 两点,则不等式1kx b +<的解集为( )A .3x <B .3x >C .6x <D .1x <6.已知直线2y x =与y x b =-+的交点的坐标为(1,a ),则方程组2y xy x b =⎧⎨=-+⎩的解是( )A .12x y =⎧⎨=⎩B .21x y =⎧⎨=⎩C .23x y =⎧⎨=⎩D .13x y =⎧⎨=⎩7.如图是一次函数y 1=kx+b 与y 2=x+a 的图象,则下列结论:①k <0;②a >0;③b >0:④方程kx+b=x+a 的解是x=3,错误的个数是( )A .1个B .2个C .3个D .4个8.观察下列图象,可以得出不等式组3100.510xx+⎧⎨-+⎩>>的解集是()A.x<13B.﹣13<x<0 C.0<x<2 D.﹣13<x<29.一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是()A.B.C.D.二、填空题10.已知关于x的一次函数11y k x=与22y k x b=+的图像如图所示,则关于x的不等式12k x k x b>+>的解集是_________.11.已知直线23y x b=--与两坐标轴围成的三角形面积为9,则b=__________.12.如图,观察两个一次函数在同一直角坐标系中的图象,当x__________时,12y y>.13.一次函数3y x b =-+和1y kx =+的图象如图所示,其交点为34P (,),则不等式、31k x b ≥(+)-的解集是__________.14.如图,函数y =2x 和y =ax+4的图象相交于点A (m ,3),则不等式2x≥ax+4的解集为_____.三、解答题15.已知:如图一次函数y 1=-x-2与y 2=x-4的图象相交于点A . (1)求点A 的坐标;(2)若一次函数y 1=-x-2与y 2=x-4的图象与x 轴分别相交于点B 、C ,求△ABC 的面积. (3)结合图象,直接写出y 1>y 2时x 的取值范围.16.如图,在平面直角坐标系xOy 中,一次函y=kx+b 的图象经过点A (-2,4),且与正比例函数23y x =-的图象交于点B (a ,2).(1)求a 的值及一次函数y=kx+b 的解析式;(2)若一次函数y=kx+b 的图象与x 轴交于点C ,且正比例函数y=-23x 的图象向下平移m (m >0)个单位长度后经过点C ,求m 的值; (3)直接写出关于x 的不等式0<23x -<kx+b 的解集. 17.已知一次函数112y x =+,在直角坐标系中画出一次函数的图象,利用图象求: (1)方程1102x += 的解; (2)不等式 1102x +≥的解集;(3)当01y ≤≤时,x 的取值范围.参考答案1-5.ABDCA 6-8.BAA 9.1x ≤ 10.x=-3 11.x >-2 12.20x y =⎧⎨=⎩13.x <114.(1)①B (-1,3),k=4;②32;(2)5、6 15.(1),−2,4;(2)x<;(3). 16.(1)一次函数的解析式为y=x+1;(2)x >11-5.DDBDB 6-9.AADA 10.23x << 11.±2 12.1>- 13.3x ≥ 14.x≥1.515.(1)(1,-3);(2)9;(3)y 1>y 2时x 的取值范围是x <1 16.(1)y=2x+8;(2)m=83;(3)-3<x <017.(1)x=-2;(2)x ≥-2;(3)-2≤x ≤0.。
新人教版八年级下《一次函数》测试题及答案

八年级(下)第十九章一次函数单元检测题班级____姓名_____得分_____一、选择题(本大题共12个小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是满足题目要求的,请把其代号填在答题栏中相应题号的下面)。
A.(0,2-)B.(32,0)C.(8,20)D.(12,12)2.变量x,y有如下关系:①x+y=10②y=x5-③y=|x-3④y2=8x.其中y是x的函数的是A.①②②③④B. ①②③C. ①②D. ①3.下列各曲线中不能表示y是x的函数是().A.B.C.D.4.已知一次函数2y x a=+与y x b=-+的图象都经过A(2-,0),且与y轴分别交于B、C两点,则△ABC的面积为().A.4 B.5 C.6 D.75.已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是A.k>5B.k<5C.k>-5D.k<-56.在平面直角坐标系xoy中,点M(a,1)在一次函数y=-x+3的图象上,则点N(2a-1,a)所在的象限是A.一象限B. 二象限C. 四象限D.不能确定7.如果通过平移直线3xy=得到53xy+=的图象,那么直线3xy=必须().A.向上平移5个单位B.向下平移5个单位C.向上平移53个单位D.向下平移53个单位8.经过一、二、四象限的函数是 A.y=7B.y=-2xC.y=7-2xD.y=-2x-79.已知正比例函数y=kx(k ≠0)的函数值y 随x 的增大而减小,则函数y=kx-k 的图象大致是10.若方程x-2=0的解也是直线y=(2k-1)x+10与x 轴的交点的横坐标,则k 的值为 A.2B.0C.-2D. ±211. 根据如图的程序,计算当输入3x =时,输出的结果y = .12.已知直线y 1=2x 与直线y 2= -2x+4相交于点A.有以下结论:①点A 的坐标为A(1,2);②当x=1时,两个函数值相等;③当x <1时,y 1<y 2④直线y 1=2x 与直线y 2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的是A. ①③④B. ②③C. ①②③④D. ①②③二、填空题(本大题共5个小题,每小题4分,共20分。
新人教版八年级下册一次函数测试题 含答案

一次函数测试题(60分钟)班级 姓名 学号 成绩一、填空题(每空3分,共30分)1.函数y =x 的取值范围是 .2.已知1(2)3n y m x -=-+是关于x 的一次函数,则m ,n .3.直线23y x =-与x 轴的交点坐标是__________,与y 轴的交点坐标是__________.4.当直线2y x b =+与直线1y kx =-平行时,k __________,b ___________.5.汽车行驶前,油箱中有油55升,已知每百千米汽车耗油10升,油箱中的余油量Q (升)与它行驶的距离s (百千米)之间的函数关系式为___ ________;为了保证行车安全,油箱中至少存油5升,则汽车最多可行驶____________千米.6.已知一次函数y kx b =-,请你补充一个条件 ,使y 随x 的增大而减小.二、选择题(每小题5分,共30分)7.下列各曲线中不能表示y 是x 的函数是( ).A .B .C .D .8.若点A (2,4)在函数2y kx =-的图象上,则下列各点在此函数图象上的是( ).A .(0,2-)B .(32,0)C .(8,20)D .(12,12) 9.已知一次函数2y x a =+与y x b =-+的图象都经过A (2-,0),且与y 轴分别交于B 、C 两点,则△ABC 的面积为 ( ).A . 4B . 5C . 6D . 710.如果通过平移直线3x y =得到53x y +=的图象,那么直线3x y =必须( ). A .向上平移5个单位 B .向下平移5个单位C .向上平移53个单位D .向下平移53个单位 11.如果点P (a ,b )关于x 轴的对称点'P 在第三象限,那么直线y ax b =+的图象不经过( ).A .第一象限B .第二象限C .第三象限D .第四象限12.根据如图的程序,计算当输入3x =时,输出的结果y = .A .2B .4C .6D .8三、解答题(第13题6分,第14题8分,第15题8分,共22分)13. 已知一次函数的图象过点(1,1-),(1-,2).(1)求这个函数的解析式;(2)求当2x =时的函数值.14.画出函数26y x =+的图象,利用图象:(1)求方程260x +=的解;(2)求不等式260x +>的解;(3)若13y -≤≤,求x 的取值范围.15.已知一次函数2y x b =+与两坐标轴围成的面积为4,求b 的值.四、应用题(第16题6分,第17题7分,共13分)16.为缓解用电紧张矛盾,某电力公司特别出台了新的用电收费标准:每月用电量x (度)与应付电费y (元)的关系如图所示.(1)根据图象,求出y 与x 的函数解析式.(2)请写出用电的收费标准.17.A 市和B 市分别有库存的某联合收割机12台和6台,现决定开往C 市10台和D 市8台,已知从A 市开往C 市、D 市的油料费分别为每台400元和800元,从B 市开往C 市和D 市的油料费分别为每台300元和500元.(1)设B 市运往C 市的联合收割机为x 台,求运费w 关于x 的函数关系式.(2)若总运费不超过9000元,问有几种调运方案?(3)求出总运费最低的调运方案,并求出最低运费.五、综合题(本题5分)18.如图,直线6y kx =+与x 轴、y 轴分别交于点E ,F .点E 的坐标为(8-,0),点A 的坐标为(6-,0). (1)求k 的值;(2)若点P (x ,y )是第二象限内的直线上的一个动点.当点P 运动过程中,试写出OPA ∆的面积S 与x 的函数关系式,并写出自变量x 的取值范围;(3)探究:当P 运动到什么位置时,OPA ∆的面积为278,并说明理由.参考答案1.2x ≥ 2.2m ≠;2n = 3.(32,0);(0,3-) 4.2k =;1b ≠- 5.5510Q s =-;500 6.0k <即可7.B 8.A 9.C 10.C 11.D 12.A 13.(1)3122y x =-+;(2)2x =时,52y =-. 14.图略(1)3x =-;(2)3x >-;(3)7322x -≤≤-. 15.4b =±. 16.(1)0.5 0500.920 50x x y x x ≤≤⎧=⎨->⎩(),();(2)用电量不足50度时,每度电费0.5元;用电量超过50度时,超过部分每度电费0.9元.17.(1)2008600w x =+(06x ≤≤);(2)有三种方案;(3)总运费最低的方案是,A C →10台,A D →2台,B C →0台,B D →6台,此时总运费为8600元.18.(1)34k =;(2)9184S x =+(80x -<<);(3)当P 点的坐标为(132-,98)时,OPA ∆的面积为278.。
八年级数学下册 19.2.3 一次函数与方程和不等式练习 (新版)新人教版
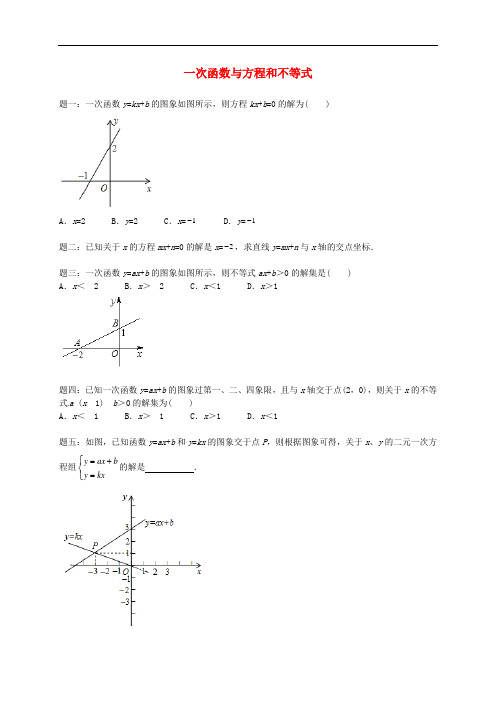
一次函数与方程和不等式题一:一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )A.x=2 B.y=2 C.x=1- D.y=1-题二:已知关于x的方程mx+n=0的解是x=2-,求直线y=mx+n与x轴的交点坐标.题三:一次函数y=ax+b的图象如图所示,则不等式ax+b>0的解集是( )A.x< 2 B.x> 2 C.x<1 D.x>1题四:已知一次函数y=ax+b的图象过第一、二、四象限,且与x轴交于点(2,0),则关于x的不等式a (x1)b>0的解集为( )A.x< 1 B.x> 1 C.x>1 D.x<1题五:如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组y ax by kx=+=⎧⎨⎩的解是.题六:如图,以两条直线l1,l2的交点坐标为解的方程组是( )A.121x yx y-=-=⎧⎨⎩B.121x yx y-=--=-⎧⎨⎩C.121x yx y-=--=⎧⎨⎩D.121x yx y-=-=-⎧⎨⎩题七:(1)已知关于x的方程mx+n=0的解是x=-2,那么,直线y=mx+n与x轴的交点坐标是.(2)如图,在平面直角坐标系中,直线AB:y=kx+b与直线OA:y=mx相交于点A(1,2),则关于x的不等式kx+b<mx的解是.(3)如图,直线l1和l2的交点坐标为( )A.(4,2) B.(2,-4) C.(-4,2) D.(3,1)题八:(1)已知方程2x+1=-x+4的解是x=1,那么,直线y=2x+1与直线y=-x+4的交点坐标是 __ __ .(2)在平面直角坐标系中,直线y=kx+1关于直线x=1对称的直线l刚好经过点(3,2),则不等式3x >kx+1的解集是__ __ .(3)如图,直线l1、l2交于点A,试求点A的坐标.题九:已知一次函数y1=kx+b和正比例函数y2=12-x的图象交于点A(2,m),又一次函数y1=kx+b的图象过点B(1,4).(1)求一次函数的解析式;(2)根据图象写出y1>y2的取值范围.题十:已知函数y1=kx+3,y2=4x-+b的图象相交于点(1,1)(1)求k、b的值,并在同一直角坐标系中画出两个函数的图象.(2)利用图象求出当x取何值时:①y1>y2;②y1>0且y2<0.题十一:如图,已知一次函数的图象经过点A(1,0)、B(0,2).(1)求一次函数的关系式;(2)设线段AB的垂直平分线交x轴于点C,求点C的坐标.题十二:如图,已知直线y=kx+b经过点A(1,4),B(0,2),与x轴交于点C,经过点D(1,0)的直线DE平行于OA,并与直线AB交于点E.(1)求直线AB的解析式;(2)求直线DE的解析式;(3)求△EDC的面积.题十三:每年的3月12日是我国植树节,某村计划在一山坡地上种A、B两种树,并购买这两种树2000棵,种植两种树苗的相关信息如表:项目/品种单价(元/棵) 成活率劳务费(元/棵)A 25 90% 5B 30 95% 7设购买A种树苗x棵,造这片林的总费用为y元,解答下列问题:(1)写出y(元)与x(棵)之间的函数关系式;(2)预计这批树苗种植后成活1860棵,则造这片林的总费用需多少元?题十四:随着人们节能环保意识的增强,绿色交通工具越来越受到人们的青睐,电动摩托成为人们首选的交通工具,某商场计划用不超过140000元购进A、B两种不同品牌的电动摩托40辆,预计这批电动摩托全部销售后可获得不少于29000元的利润,A、B两种品牌电动摩托的进价和售价如下表所示:品牌A品牌电动摩托B品牌电动摩托价格进价(元/辆) 4000 3000售价(元/辆) 5000 3500设该商场计划进A品牌电动摩托x辆,两种品牌电动摩托全部销售后可获利润y元.(1)写出y与x之间的函数关系式;(2)该商场购进A品牌电动摩托多少辆时?获利最大,最大利润是多少?题十五:在平面直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数为个.题十六:在平面直角坐标系中,点A、B的坐标分别为(2,0)、(2,4),点P在坐标轴上,△ABP是等腰三角形,符合条件的点P共有个.一次函数与方程和不等式课后练习参考答案题一:C.详解:∵一次函数y=kx+b的图象与x轴的交点为(1-,0),∴当kx+b=0时,x=1-.故选C.题二:(2-,0).详解:∵方程的解为x=2-,∴当x=2-时mx+n=0;又∵直线y=mx+n与x轴的交点的纵坐标是0,∴当y=0时,则有mx+n=0,∴x=2-时,y=0,∴直线y=mx+n与x轴的交点坐标是(2-,0).题三:B.详解:一次函数y=ax+b的图象经过点A(2,0),且函数值y随x的增大而增大,∴不等式ax+b>0的解集是x>2.故选B.题四:A.详解:∵一次函数y=ax+b的图象过第一、二、四象限,∴b>0,a<0,把(2,0)代入解析式y=ax+b得0=2a+b,解得2a=b-,ba=2-,∵a(x1)b>0,∴a(x1)>b,∵a<0,∴x1<ba,∴x<1,故选A.题五:31 xy=-=⎧⎨⎩详解:因为两函数图象交点坐标(3,1)为两函数解析式组成的方程组的解,因此方程组y ax by kx=+=⎧⎨⎩的解是31xy=-=⎧⎨⎩.题六:C.详解:直线l1经过(2,3)、(0,1),易知其函数解析式为y=2x1;直线l2经过(2,3)、(0,1),易知其函数解析式为y=x+1;因此以两条直线l1,l2的交点坐标为解的方程组是1 21x yx y-=--=⎧⎨⎩.故选C.题七:(1)(-2,0);(2)x>1;(3)A.详解:(1)∵方程的解为x=-2,∴当x=-2时mx+n=0;又∵直线y=mx+n与x轴的交点的纵坐标是0,∴当y=0时,则有mx+n=0,∴x=-2时,y=0.∴直线y=mx+n与x轴的交点坐标是(-2,0);(2)观察函数图象得到在点A的右边,直线y=kx+b都在直线y=mx的下方,即当x>1时,kx+b<mx,∴不等式kx+b<mx的解为x>1;(3)由图象可知l1过(0,2)和(2,0)两点.l2过原点和(2,1).根据待定系数法可得出l1的解析式为y=-x+2,l2的解析式为y=12-x ,两直线的交点满足方程组212y xy x=-+⎧⎪⎨=-⎪⎩,解得42xy=⎧⎨=-⎩,即交点的坐标是(4,2).故选A.题八:(1)(1,3);(2)x>14;(3)(53,53).详解:(1)∵x=1是方程2x+1=-x+4的解,∴y=2×1+1=3,∴交点坐标为(1,3);(2)∵点(3,2)关于直线x=1的对称点的坐标为(-1,2),∴点(-1,2)在直线y=kx+1上,∴-k+1=2,解得k=-1,∴直线y=kx+1的解析式为y=-x+1,∴不等式3x>kx+1,即3x>-x+1,解得x>14;(3)设l2的方程为y=kx+b,因为l2经过点(0,5)和(1,3),所以53bk b=⎧⎨=+⎩,解得25kb=-⎧⎨=⎩.即l2的方程为y=-2x+5,同理:l1的方程为y=x,两直线的交点满足方程组得25y xy x=-+⎧⎨=⎩,解得5353xy⎧=⎪⎪⎨⎪=⎪⎩,∴点A的坐标为(53,53).题九:(1)y1=x+3;(2)x>2.详解:(1)把点A(2,m)代入y2=12-x得m=12-×(2)=1,则A点坐标为(2,1),把A(2,1)、B(1,4)代入y1=kx+b得:214k bk b-+=⎧⎨+=⎩,解得13kb=⎧⎨=⎩,所以y1=x+3;(2)如图,当x>2时,y1>y2.题十:(1)k=2,b=-3;(2)①x>1,②x>34-.详解:(1)根据题意,得k+3=1,4-×(1)+b=1,解得k=2,b=-3,故两函数解析式为y1=2x+3,y2=4x-3.函数图象如下图:(2)由图可知,①当x>1时,y1>y2,②y2=0时,4x-3=0,解得x=34-,所以,当x>34-时,y1>0且y2<0.题十一:(1)y=2x+2;(2)(32,0).详解:(1)设一次函数的关系式为y=kx+b,依题意,得02k bk b⨯+=⎧⎨-+=⎩,解得22kb=⎧⎨=⎩,∴一次函数的关系式为y=2x+2;(2)设点C的坐标为(a,0),连接BC,则CA=a+1,CB2=OB2+OC2=a2+4,∵CA=CB∴CA2=CB2即(a+1)2=a2+4,∴a=32,即C(32,0).题十二:(1)y=2x+2;(2)y=4x-4;(3)8.详解:(1)∵直线y=kx+b经过点A(1,4),B(0,2),∴42k bb+=⎧⎨=⎩,解得22kb=⎧⎨=⎩,故直线AB的解析式为y=2x+2;(2)设AO的解析式为y=ax(a≠0),∵A(1,4),∴a=4,∴AO的解析式为y=4x,∵直线DE平行于OA,∴设直线DE的解析式为y=4x+n,∵D(1,0),∴4+n=0,解得n=-4,∴直线DE的解析式为y=4x-4;(3)∵直线y=2x+2与x轴交于C点,∴当y=0时,有2x+2=0,解得x=-1,∴C(-1,0),∵直线y=2x+2与直线y=4x-4交于点E,∴2244y xy x=+⎧⎨=-⎩,解得38xy=⎧⎨=⎩,∴点E的坐标为(3,8),∴S△ECD=12×2×8=8.题十三:(1)y=-7x+74000(0≤x≤2000);(2)68400元.详解:(1)购买A种树苗x棵,则购买B种树苗(2000-x)棵,则y=25x+30(2000-x)+5x+7(2000-x),即y=-7x+74000(0≤x≤2000);(2)根据题意得90%x+95%(2000-x)=1860,解得x=800,即y=-7×800+74000=68400(元),答:造这片林的总费用需68400元.题十四:(1)y=20000+500x(0≤x≤40);(2)30000.详解:(1)设该商场计划进A品牌电动摩托x辆,则进B品牌电动摩托(40x)辆,由题意可知每辆A品牌电动摩托的利润为1000元,每辆B品牌电动摩托的利润为500元,则y=1000x+500(40x)=20000+500x(0≤x≤40);(2)由题意可知40003000(40)1400002000050029000x xx+-≤⎧⎨+≥⎩,解得18≤x≤20;当x=20时,y=30000,∴该商场购进A品牌电动摩托20辆时,获利最大,最大利润是30000.题十五:4.详解:(1)若AO作为腰时,有两种情况,当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有1个,当O是顶角顶点时,P是以O为圆心,以OA为半径的圆与x轴的交点,有2个;(2)若OA是底边时,P是OA的中垂线与x轴的交点,有1个.以上4个交点没有重合的.故符合条件的点有4个.题十六:7.详解:∵点A、B的坐标分别为(2,0)、(2,4),∴AB⊥x轴,AB=4,①若AP=AB,以A为圆心,AB为半径画弧与坐标轴有4个交点,即满足△ABP是等腰三角形的P点有4个;②若BP=AB,以B为圆心,BA为半径画弧与坐标轴有2个交点(A点除外),即满足△ABP是等腰三角形的P点有2个;③若PA=PB,作AB的垂直平分线与坐标轴只有一个交点,即满足△ABP是等腰三角形的P点有1个;所以点P在坐标轴上,△ABP是等腰三角形,符合条件的点P共有 7个.。
(完整版)人教版八年级数学下学期一次函数测试题

轴上滑动 ( C 点在 y轴上, D 点在 x 轴上 ) ,且 CD AB ;当△ COD 和△ AOB 全等时,求 C、 D 两点
的坐标;
y
B
A
O
x
22、(9 分 ) 如图,直线 l1与 l2 相交于点 P , l1 的函数表达式 y 2 x 3 ,点 P 的横坐标为 -1 ,且 l2 交 y 轴于点 A(0, 1) ;求直线 l 2 的函数表达式 .
21、( 1)由题意,得 A(2, 0), B( 0, 4),即 AO=2 OB=4. …………………… 1 分 ①当线段 CD在第一象限时,点 C( 0, 4),D( 2, 0)或 C( 0, 2), D(4, 0).………………… 3 分 ②当线段 CD在第二象限时,点 C( 0, 4),D(- 2,0)或 C(0, 2),D(- 4,0).…………… 5 分 ③当线段 CD在第三象限时,点 C( 0,- 4), D(- 2, 0)或 C( 0,- 2), D(- 4, 0).……… 7 分 ④当线段 CD在第四象限时,点 C( 0,- 4), D( 2,0)或 C(0,- 2), D( 4,0) …………… 9 分
3 、直线 y kx 2 过点 (1, 2) ,则 k 的值是(
)
A、 4 B 、 -4 C 、 -8 D 、 8
4、打开某洗衣机开关,在洗涤衣服时(洗衣机内无水)
,洗衣机经历了进水、清洗、排水、脱水四个
连续过程,其中进水、清洗、排水时洗衣机中的水量
y (升)与时间 x (分钟)之间满足某种函数关系,
人教版八年级数学下学期一次函数测试题参考答案 一、选择题:(每题 3 分,共 12 分)
1— 4:A、 C、 B、 D;
惠州乐学!
八年级数学下册《一次函数与方程、不等式》练习题及答案(人教版)
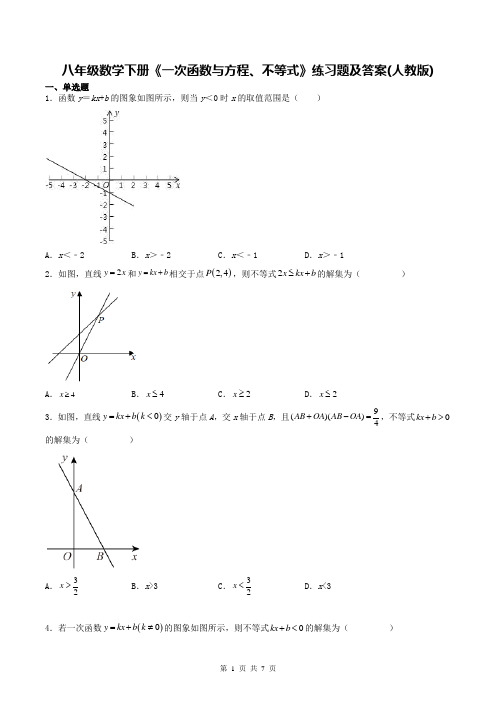
八年级数学下册《一次函数与方程、不等式》练习题及答案(人教版)A .x <﹣2B .x >﹣2C .x <﹣1D .x >﹣1A .4x ≥B .4x ≤C .2x ≥D .2x ≤33A .3x <B .3x >C .4x <D .>4x5.如图,已知一次函数y =ax +b 和y =kx 的图象相交于点P ,则根据图象可得二元一次方程组0ax y b kx y -+=⎧⎨-=⎩的解是( )A .24x y =⎧⎨=-⎩B .24x y =⎧⎨=⎩C .24x y =-⎧⎨=-⎩D .42x y =-⎧⎨=-⎩ 6.直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标系中的图象如图所示,则关于x 的不等式21+k x k x b >的解集为( )A .x >3B .x <3C .x >﹣1D .x <﹣17.数形结合是解决数学问题常用的的思想方法.如图,一次函数1y x b =+与一次函数24y kx =+的图象交于点()1,3P ,根据图象可知,关于x 的不等式4x b kx +>+的解集是( )A .3x >B .3x <C .1x >D .1x <8.已知一次函数y kx b =+的图象如图所示,当x <1时,y 的取值范围是( )A .-2<y <0B .-4<y <0C .y <-2D .y <-49.如图,直线y=-x+m 与y=nx+4n (n≠0)的交点的横坐标为-2.则下列结论:①m<0,n >0;②直线y=nx+4n 一定经过点(-4,0);③m 与n 满足m=2n-2;④当x >-2时,nx+4n >-x+m ,其中正确结论的个数是( )A .1个B .2个C .3个D .4个10.如图,直线y x m =-+与4y nx n =+的交点的横坐标为2-,则关于x 的不等式40nx n x m +>-+>的整数解可能是( )A .1-B .2-C .3-D .1二、填空题11.已知直线x+2y=5与直线x+y=3的交点坐标是(1,2),则方程组253x y x y +=⎧⎨+=⎩的解是_________. 12.一次函数1y mx n =+与2y x a =-+的图象如图所示,则mx n x a +<-+的解集为______.13.直线1l :y ax b =-与直线2l :y kx =-在同一平面直角坐标系中的图像如图所示,则关于x 的不等式ax b kx -+>的解集为____________.14.若方程x y c +=和x y p -=的公共解是21x y =⎧⎨=-⎩,则直线y c x =-与直线y x p =-的交点坐标是________. 15.对于一次函数y=-2x+1 ,当-2≤x≤3 时,函数值y 的取值范围是________________.三、解答题16.如图,直线1:l y kx b =+与直线2:4l y x =-+交于点(),2C m ,直线1l 经过点()4,6.(1)求直线1l 的函数表达式;(2)直接写出方程组4y kx b y x =+⎧⎨=-+⎩的解______; (3)若点()3,P n 在直线1l 的下方,直线2l 的上方,写出n 的取值范围______.17.已知函数y 4x 8=--.(1)当x 取哪些值时 y 0≥?(2)当x 取哪些值时 y 4≤?18.画出y =2x ﹣4的图象,确定x 取何值时(1)y >0;(2)y <﹣4.(1)求点A的坐标.参考答案1.B2.D3.C4.D5.D6.D7.C(1)当x>2时,y>0;。
人教版八年级数学下册一次函数与方程、不等式测试题

人教版八年级数学考试题测试题人教版初中数学第十九章 一次函数19.2.3 一次函数与方程、不等式一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.一次函数y =ax +b (a >0)与x 轴的交点坐标为(m ,0),则一元一次不等式ax +b ≤0的解集应为 A .x ≤m B .x ≤-m C .x ≥mD .x ≥-m2.如图,直线y =kx +b 交坐标轴于A (-3,0)、B (0,5)两点,则不等式-kx -b <0的解集为A .x >-3B .x <-3C .x >3D .x <33.如图,经过点(20)B -,的直线y kx b =+与直线42y x =+相交于点(12)A --,,则不等式42x +>kx b +的解集为A .2x <-B .1x >-C .1x <-D .2x >-4.如果直线y =3x +6与y =2x -4交点坐标为(a ,b ),则x ay b =⎧⎨=⎩是方程组__________的解.A .3624x y y x -=⎧⎨+=-⎩B .3624x y y x -=⎧⎨-=⎩C .3634x y x y -=⎧⎨-=⎩D .3624x y x y -=-⎧⎨-=⎩5.如图,直线y 1=k 1x +b 和直线y 2=k 2x +b 分别与x 轴交于A (-1,0)和B (3,0)两点,则不等式组120k x b k x b +>⎧⎨+>⎩的解集为A .13x -<<B .03x <<C .10x -<<D .3x >或1x <-二、填空题:请将答案填在题中横线上.6.如图,一次函数y =kx +b (k <0)的图象经过点A .当y <3时,x 的取值范围是__________.7.一次函数y =kx +b (k ≠0)中,x 与y 的部分对应值如下表:那么,一元一次方程kx +b =0在这里的解为__________.8.如图,直线y =kx +b 经过点A (-1,-2)和点B (-2,0),直线y =2x 过点A ,则不等式2x <kx +b <0的解集为__________.9.如图,一次函数y =kx +b 的图象与x 轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.其中说法正确的有__________(把你认为说法正确的序号都填上).10.已知关于x的一元一次不等式组232x bx b>+⎧⎨<-⎩有解,则直线y=-x+b不经过第__________象限.三、解答题:解答应写出文字说明、证明过程或演算步骤.11.如图,函数y=2x和y=-23x+4的图象相交于点A.(1)求点A的坐标;(2)根据图象,直接写出不等式2x≥-32x+4的解集.12.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=-3的解.13.如图,根据图中信息解答下列问题:(1)关于x的不等式ax+b>0的解集是__________;(2)关于x的不等式mx+n<1的解集是__________;(3)当x为何值时,y1≤y2?(4)当x<0时,比较y2与y1的大小关系.附赠材料:以学生为第一要务目标我们教育工作的最终目标只有一个:学生。
八年级数学下册 知识点汇聚测试卷 一次函数与方程、不等式初级测试(均2013最新中考试题,含详解) 新人教

八年级数学下册知识点汇聚测试卷一次函数与方程、不等式初级测试(均2013最新中考试题,含详解)新人教版一、选择题(每小题4分,共12分)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )A.x=2B.y=2C.x=-1D.y=-12.若关于x的方程4x-b=5的解为x=2,则直线y=4x-b一定经过( )A.(2,0)B.(0,3)C.(0,4)D.(2,5)3.(2013·荆州中考)体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是( )进球数0 1 2 3 4 5人数 1 5 x y 3 2A.y=x+9与y=x+B.y=-x+9与y=x+C.y=-x+9与y=-x+D.y=x+9与y=-x+二、填空题(每小题4分,共12分)4.已知关于x的方程ax-5=7的解为x=1,则一次函数y=ax-12的图象与x轴交点的坐标为.5.如图,已知直线y=ax-b,则关于x的方程ax-1=b的解x=.6.一次函数y1=kx+b与y2=x+a的图象如图,则方程kx+b=x+a的解是.三、解答题(共26分)7.(8分)(2013·绍兴中考)某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:(1)出租车的起步价是多少元?当x>3时,求y关于x的函数解析式.(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.8.(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=x的图象的交点为C(m,4).(1)求一次函数y=kx+b的解析式.(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,求点D的坐标.【拓展延伸】9.(10分)有一个一次函数的图象,小华和小云分别说出了它的两个特征.小华:图象与x轴交于点(6,0).小云:图象与x轴、y轴围成的三角形的面积是9.你知道这个一次函数的关系式吗?答案解析1.【解析】选C.∵一次函数y=kx+b的图象与x轴的交点为(-1,0),∴当kx+b=0时,x=-1.2.【解析】选D.由题意知对于函数y=4x-b,当x=2时,y=5.3.【解析】选C.根据进球总数为49个得:2x+3y=49-5-3×4-2×5=22,整理得:y=-x+,∵20人一组进行足球比赛,∴1+5+x+y+3+2=20,整理得:y=-x+9.4.【解析】关于x的方程ax-5=7(即ax-12=0)的解即为一次函数y=ax-12的图象与x轴交点的横坐标. 答案:(1,0)5.【解析】ax-1=b可变形为ax-b=1,即所求的x为函数值y=1时x对应的值,由图象知其对应x=4.答案:46.【解析】一次函数y1=kx+b与y2=x+a的图象的交点的横坐标是3,故方程的解是:x=3. 答案:x=37.【解析】(1)由图象得:出租车的起步价是8元;设当x>3时,y与x的函数解析式为y=kx+b,由函数图象,得解得:故y与x的函数解析式为y=2x+2.(2)当y=32时,32=2x+2,x=15.答:这位乘客乘车的里程是15k m.8.【解析】(1)∵点C(m,4)在直线y=x上,∴4=m,解得m=3.∵点A(-3,0)与C(3,4)在直线y=kx+b(k≠0)上,∴解得∴一次函数的解析式为y=x+2.(2)如图,过点D1作D1E⊥y轴于点E,过点D2作D2F⊥x轴于点F,∵点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,∴AB=BD1,AB=AD2,∵∠D1BE+∠ABO=90°,∠ABO+∠BAO=90°,∴∠BAO=∠D1BE.∵在△BED1和△AOB中,∴△BED1≌△AOB(AAS),∴BE=AO=3,D1E=BO=2,即可得出点D的一个坐标为(-2,5),同理可得出:△D2FA≌△AOB,∴FA=OB=2,D2F=AO=3,∴点D的另一个坐标为(-5,3),综上所述:点D的坐标为(-2,5)或(-5,3).9.【解析】设这个一次函数的关系式为y=kx+b,则该直线与y轴交于点(0,b),所以×6×︱b︱=9,所以b=±3.当b=3时,把x=6,y=0代入y=kx+3,得k=-;同理,当b=-3时,求得k=,因此这个一次函数的关系式为y=-x+3或y=x-3.。
最新人教版八年级下册数学一次函数与方程、不等式 同步测试

一次函数与方程、不等式同步测试一、选择题1.一次函数y=ax+b交x轴于点(-5,0),则关于x的方程ax+b =0的解是( )A. x=5B. x=-5C. x=0D. 无法求解2.若函数y=3x-6和y=-x+4有相等的函数值,则x的值为()A. B. C. 1 D. -x+2的图象上.则m的值为()3.若点(3,m)在函数y= 13A. 0B. 1C. 2D. 34.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A. B. C. D.5.直线向下平移4个单位后与x轴的交点坐标是()A. (0,1) B. (0,-1) C. (-1,0) D. (1,0)6.如图,已知函数和的图象交于点,则下列结论中错误的是()A. B. C. 当时, D.7.已知一次函数y=kx+b的图象如图所示,当x<0时,y的取值范围是( )A. y>0B. y<0C. y>-2D. -2≤y<08.如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P (1,m),则不等式组mx>kx+b>mx﹣2的解集是()A. 1<x<2B. 0<x<2C. 0<x<1D. 1<x9.观察下列图象,可以得出不等式组的解集是()A. x<B. ﹣<x<0C. 0<x<2D. ﹣<x<2二、填空题10.已知一次函数y=ax-b的图象经过一、二、三象限,且与x轴交于点(-2,0),则不等式ax>b的解集为_______11.如图直线与轴交于点,则时,的取值范围为__________.12.若一次函数的图象如图所示,点在函数图象上,则关于的不等式的解集是__________.13.如图,直线1y x b =+与21y kx =-相交于点11,2P ⎛⎫- ⎪⎝⎭,则关于x 的方程1x b kx +=-的解为.14.一次函数y kx b =+(k ,b 为常数,0k ≠)的图像如图所示,根据图像信息可求得关于x 的方程0kx b +=的解为__________.15.如图,直线y=﹣x+m 与y=nx+4n (n ≠0)的交点的横坐标为﹣2,则关于x 的不等式﹣x+m >nx+4n >0的整数解是__________.16.如图,一次函数与一次函数的图象交于点,则关于的不等式的解集是__________.三、解答题17.画出函数y=2x+6的图象,利用图象:①求方程2x+6=0的解;②求不等式2x+6>0的解;③若-1≤y≤3,求x的取值范围。
八年级数学下册 知识点汇聚测试卷 一次函数与方程、不等式深入测试(均最新中考试题,含详解) 新人教版
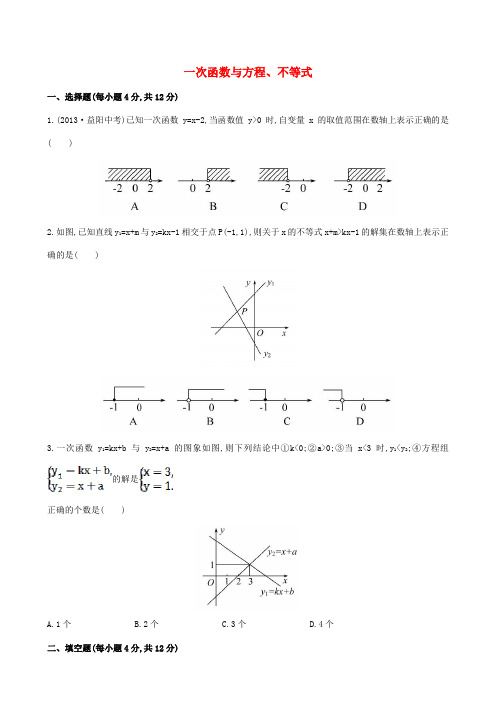
一次函数与方程、不等式一、选择题(每小题4分,共12分)1.(2013·益阳中考)已知一次函数y=x-2,当函数值y>0时,自变量x的取值范围在数轴上表示正确的是( )2.如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )3.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论中①k<0;②a>0;③当x<3时,y1<y2;④方程组的解是正确的个数是( )A.1个B.2个C.3个D.4个二、填空题(每小题4分,共12分)4.已知直线y=kx+4经过点(1,7),则方程y-kx=4的一个解为,k= .5.(2013·南通中考)如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为.6.函数y1=x+1与y2=ax+b的图象如图所示,这两个函数的交点在y轴上,那么y1,y2的值都大于零时x的取值范围是.三、解答题(共26分)7.(8分)如图,已知直线y=kx+b经过A(1,3),B(-1,-1)两点,求不等式kx+b>0的解集.8.(8分)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).(1)求b的值.(2)不解关于x,y的方程组请你直接写出它的解.(3)直线l3:y=nx+m是否也经过点P?请说明理由.【拓展延伸】9.(10分)作出函数y1=2x-4与y2=-2x+8的图象,并观察图象回答下列问题.(1)x取何值时,2x-4>0?(2)x取何值时,-2x+8>0?(3)x取何值时,2x-4>0与-2x+8>0同时成立?(4)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角形的面积吗?并写出过程.答案解析1.【解析】选B.当y>0时,即x-2>0,解得x>2.数轴上表示解集x>2,如B项图所示.2.【解析】选B.∵直线y1=x+m与y2=kx-1相交于点P(-1,1),∴根据图象可知:关于x的不等式x+m>kx-1的解集是x>-1,在数轴上表示为:.3.【解析】选B.∵y1=kx+b的函数值随x的增大而减小,∴k<0,故①正确;∵y2=x+a的图象与y轴交于负半轴,∴a<0,故②错误;当x<3时,相应的y1图象均高于y2的图象,∴y1>y2,故③错误;∵交点坐标为(3,1),∴方程组的解是故④正确.4.【解析】直线y=kx+4上任意一点的坐标都是二元一次方程y-kx=4的解,将代入,得7-k×1=4,解得k=3.答案: 35.【解析】原不等式可化为根据图象知道A点是两条已知直线的交点,当x=-1时,4x+2=kx+b,当x=-2时,kx+b=0,再结合图象的位置,易得出所求解集为-2<x<-1.答案:-2<x<-16.【解析】由图象可知,当x>-1时,y1>0;当x<2时,y2>0,所以当-1<x<2时,y1,y2的值都大于零.答案:-1<x<27.【解析】将点A,B的坐标代入y=kx+b,得:解得:所以函数解析式为y=2x+1,与x轴的交点为.观察图象可知不等式kx+b>0的解集是x>-.8.【解析】 (1)∵(1,b)在直线y=x+1上,∴当x=1时,b=1+1=2.(2)方程组的解是(3)直线y=nx+m也经过点P.理由如下:∵点P(1,2)在直线y=mx+n上,∴m+n=2,∴2=n×1+m,这说明直线y=nx+m也经过点P.9.【解析】图象如图:(1)当x>2时,2x-4>0.(2)当x<4时,-2x+8>0.(3)当2<x<4时,2x-4>0与-2x+8>0同时成立.(4)能.由2x-4=0,得x=2;由-2x+8=0,得x=4, 所以AB=4-2=2,由得交点C(3,2),所以△ABC中AB边上的高为2,所以S=×2×2=2.。
(word)新人教版八年级下《一次函数》测试题及答案,文档

2021—2021学年度第二学期八年级〔下〕第十九章一次函数单元检测题班级____姓名_____得分_____一、选择题〔本大题共12个小题,每题3分,共36分。
在每题给出的四个选项中,只有一项为哪一项满足题目要求的,请把其代号填在答题栏中相应题号的下面〕。
题号123456789101112答案1 .假设点A〔2,4〕在函数ykx2的图象上,那么以下各点在此函数图象上的是〔〕.A.〔0,2〕B.〔3,0〕C.〔8,20〕D.〔1,1〕2222 .变量x,y有如下关系:①x+y=10②y=5③y=|x-3④y2=8x.其中y是x的函数的是xA.①②②③④ B.①②③ C.①② D.①3 .以下各曲线中不能表示y是x的函数是〔〕.A.B.C.D.4.一次函数y 2x a与y x b的图象都经过A〔2,0〕,且与y轴分别交于B、C两点,那么△ABC的面积为〔〕.A.4B.5C.6D.7正比例函数y=(k+5)x,且y随x的增大而减小,那么k的取值范围是>5<5>-5<-56.在平面直角坐标系xoy中,点M(a,1)在一次函数y=-x+3的图象上,那么点N(2a-1,a)所在的象限是A.一象限B.二象限C.四象限D.不能确定7.如果通过平移直线y x x5yx〕.得到y的图象,那么直线必须〔333A.向上平移5个单位B.向下平移5个单位C.向上平移5个单位D.向下平移5个单位338.经过一、二、四象限的函数是A.y=7B.y=-2xC.y=7-2xD.y=-2x-79.正比例函数y=kx(k≠0)的函数值y随x的增大而减小,那么函数y=kx-k的图象大致是10.假设方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,那么D.±2k的值为11.根据如图的程序,计算当输入x 3时,输出的结果y.输y x5(x1)输入出x y x5(x≤1)y12.直线y1=2x与直线y2=-2x+4相交于点 A.有以下结论:①点A的坐标为A(1,2);②当x=1时,两个函数值相等;③当x<1时,y1<y2④直线y1=2x与直线y2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的选项是A.①③④B.②③C.①②③④D.①②③二、填空题〔本大题共5个小题,每题4分,共20分。
新人教版初中数学八年级下册一次函数与方程、不等式函数测试及答案解析-精品试卷

八年级下册第十九章19.2.3一次函数与方程、不等式第2课时(测)总分:100 时间:40分钟班级 姓名 总分一、选择题(每小题5分,共20分)1.若关于x 不等式组2020x k x ->⎧⎨-≤⎩有且只有四个整数解,且一次函数y=(k+3)x+k+5的图象不经过第三象限,则符合题意的整数k 有( )个.A .4B .3C .2D .1【答案】D .【解析】试题分析:解不等式组2020x k x ->⎧⎨-≤⎩得,2k <x ≤2,∵不等式组有且只有四个整数解,∴其整数解为:﹣1,0,1,2,∴﹣2≤2k <﹣1,即﹣4≤k <﹣2. ∵一次函数y=(k+3)x+k+5的图象不经过第三象限,∴30k 50k +<⎧⎨+⎩≥,解得﹣5≤k <﹣3,∴﹣4≤k <﹣3,∴k 的整数解只有﹣4.故选D .考点:一次函数与一元一次不等式. 2 .直线1l :y=1k x+b 与直线2l :y=2k x+c 在同一平面直角坐标系中的图形如图所示,则关于x 的不等式1k x+b <2k x+c 的解集为( )A.x >1B.x <1C.x >-2D.x <-2【答案】B【解析】试题分析:求1k x+b<2k x+c,实际上就是看两个函数图形中,2l在1l上面时的自变量的取值范围.考点:一次函数与一元一次不等式的关系3. 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是()A.x>﹣2 B.x>0 C.x>1 D.x<1【答案】C【解析】试题分析:当x>1时,x+b>kx+4,即不等式x+b>kx+4的解集为x>1.故选:C.考点:一次函数与一元一次不等式.4..如图,直线y1=x+b与y=kx﹣1相交于点P,点P的横坐标为﹣1,则2关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.【答案】A【解析】试题分析:根据函数图象可得:当x>-1时,x+b>kx-1.考点:函数与不等式.二、填空题(每小题5分,共20分)5.如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),则不等式4x+2<kx+b<0的解集为.【答案】﹣2<x<﹣1【解析】解:∵经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),∴直线y=kx+b与直线y=4x+2的交点A的坐标为(﹣1,﹣2),直线y=kx+b 与x轴的交点坐标为B(﹣2,0),又∵当x<﹣1时,4x+2<kx+b,当x>﹣2时,kx+b<0,∴不等式4x+2<kx+b<0的解集为﹣2<x<﹣1.故答案为:﹣2<x<﹣1.考点:本题考查了一次函数与一元一次不等式的关系.6. 直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(﹣1,0)和B(3,0)两点.则不等式组k1x+b>k2x+b>0的解集为.【答案】0<x<3 【解析】试题分析:当x=﹣1时,y1=k1x+b=0,则x>﹣1时,y1=k1x+b>0,当x=3时,y2=k2x+b=0,则x<3时,y2=k2x+b>0,因为x>0时,y1>y2,所以当0<x<3时,k1x+b>k2x+b>0,即不等式组k1x+b>k2x+b>0的解集为0<x<3.考点:一次函数与一元一次不等式7. 如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x +b >kx +6的解集是_____________.【答案】x >3.【解析】试题分析:由图象得到直线y =x +b 与直线y =kx +6的交点P (3,5),在点P (3,5)的右侧,直线y =x +b 落在直线y =kx +6的上方,该部分对应的x 的取值范围为x >3,即不等式x +b >kx +6的解集是x >3.考点:一次函数与一元一次不等式.8.如图,直线y 1=x+b 与y 2=kx ﹣1相交于点P ,点P 的横坐标为﹣1,则关于x 的不等式x+b >kx ﹣1的解集 .【答案】x >-1【解析】试题分析:根据题意可得即1y >2y ,也就是函数1y 在函数2y 的上方,根据图象可得当x>-1时,函数y在函数2y的上方.1考点:一次函数与一元一次不等式的关系.9. 如图,函数y=-2x和y=kx+b的图像相交于点A(m,3),则关于x的不等式kx+b+2x>0的解集是______________【答案】x>-3.2【解析】试题解析:∵函数y=-2x经过点A(m,3),∴-2m=3,,解得:m=-32则关于x的不等式kx+b+2x>0可以变形为kx+b>-2x,.由图象得:kx+b>-2x的解集为x>-32考点:一次函数与一元一次不等式.三、简答题(每题15分,共60分)10.暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人500元的两家旅行社。
新人教版八年级下《一次函数》测试题及答案

八年级(下)第十九章一次函数单元检测题班级____姓名_____得分_____一、选择题(本大题共12个小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是满足题目要求的,请把其代号填在答题栏中相应题号的下面)。
A.(0,2-)B.(32,0)C.(8,20)D.(12,12)2.变量x,y有如下关系:①x+y=10②y=x5-③y=|x-3④y2=8x.其中y是x的函数的是A.①②②③④B. ①②③C. ①②D. ①3.下列各曲线中不能表示y是x的函数是().A.B.C.D.4.已知一次函数2y x a=+与y x b=-+的图象都经过A(2-,0),且与y轴分别交于B、C两点,则△ABC的面积为().A.4 B.5 C.6 D.75.已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是A.k>5B.k<5C.k>-5D.k<-56.在平面直角坐标系xoy中,点M(a,1)在一次函数y=-x+3的图象上,则点N(2a-1,a)所在的象限是A.一象限B. 二象限C. 四象限D.不能确定7.如果通过平移直线3xy=得到53xy+=的图象,那么直线3xy=必须().A.向上平移5个单位B.向下平移5个单位C.向上平移53个单位D.向下平移53个单位8.经过一、二、四象限的函数是 A.y=7B.y=-2xC.y=7-2xD.y=-2x-79.已知正比例函数y=kx(k ≠0)的函数值y 随x 的增大而减小,则函数y=kx-k 的图象大致是10.若方程x-2=0的解也是直线y=(2k-1)x+10与x 轴的交点的横坐标,则k 的值为 A.2B.0C.-2D. ±211. 根据如图的程序,计算当输入3x =时,输出的结果y = .12.已知直线y 1=2x 与直线y 2= -2x+4相交于点A.有以下结论:①点A 的坐标为A(1,2);②当x=1时,两个函数值相等;③当x <1时,y 1<y 2④直线y 1=2x 与直线y 2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的是A. ①③④B. ②③C. ①②③④D. ①②③二、填空题(本大题共5个小题,每小题4分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数与方程、不等式
一、选择题(每小题4分,共12分)
1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()
A.x=2
B.y=2
C.x=-1
D.y=-1
2.若关于x的方程4x-b=5的解为x=2,则直线y=4x-b一定经过()
A.(2,0)
B.(0,3)
C.(0,4)
D.(2,5)
3.(2013·荆州中考)体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是
()
A.y=x+9与y=x+
B.y=-x+9与y=x+
C.y=-x+9与y=-x+
D.y=x+9与y=-x+
二、填空题(每小题4分,共12分)
4.已知关于x的方程ax-5=7的解为x=1,则一次函数y=ax-12的图象与x轴交点的坐标为.
5.如图,已知直线y=ax-b,则关于x的方程ax-1=b的解x=.
6.一次函数y1=kx+b与y2=x+a的图象如图,则方程kx+b=x+a的解是.
三、解答题(共26分)
7.(8分)(2013·绍兴中考)某市出租车计费方法如图所示,x(km)表示行驶里
程,y(元)表示车费,请根据图象回答下面的问题:
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数解析式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
8.(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=x的图象的交点为C(m,4).
(1)求一次函数y=kx+b的解析式.
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,求点D的坐标.
【拓展延伸】
9.(10分)有一个一次函数的图象,小华和小云分别说出了它的两个特征.
小华:图象与x轴交于点(6,0).
小云:图象与x轴、y轴围成的三角形的面积是9.
你知道这个一次函数的关系式吗?
答案解析
1.【解析】选C.∵一次函数y=kx+b的图象与x轴的交点为(-1,0),∴当kx+b=0时,x=-1.
2.【解析】选D.由题意知对于函数y=4x-b,当x=2时,y=5.
3.【解析】选C.根据进球总数为49个得:2x+3y=49-5-3×4-2×5=22,
整理得:y=-x+,
∵20人一组进行足球比赛,
∴1+5+x+y+3+2=20,整理得:y=-x+9.
4.【解析】关于x的方程ax-5=7(即ax-12=0)的解即为一次函数y=ax-12的图象与x轴交点的横坐标. 答案:(1,0)
5.【解析】ax-1=b可变形为ax-b=1,即所求的x为函数值y=1时x对应的值,由图象知其对应x=4.
答案:4
6.【解析】一次函数y1=kx+b与y2=x+a的图象的交点的横坐标是3,故方程的解是:x=3.
答案:x=3
7.【解析】(1)由图象得:出租车的起步价是8元;
设当x>3时,y与x的函数解析式为y=kx+b,
由函数图象,得解得:。
