2423圆和圆的位置关系
圆和圆的位置关系

圆和圆的位置关系两个圆有几种位置关系?在平面上,两圆的位置有:外离,外切,相交,内切、内含共五种位置关系.在平面内,两圆相对运动,可以得到下面不同的位置关系,如下图所示.(1)两个圆没有公共点,并且每个圆上的点都在另一个圆外部时,叫做这两个圆外离.(2)两个圆有唯一公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切.这个唯一公共点叫做切点.(3)两个圆有两个公共点时,叫做这两个圆相交.两个公共点都叫做交点.(4)两个圆有唯一公共点,并且除去这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一公共点叫做切点(要分清两圆外切、内切定义的区别).(5)两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.(6)两个圆同心是两圆内含的一种特例.观察上图,可以发现,当两圆的半径一定时,两圆的位置关系与两圆圆心的距离(圆心距)大小有关.设两圆半径分别为R和r,圆心距为d,那么有:(1)两圆外离d>R+r;(2)两圆外切d=R+r;(3)两圆相交R-r<d<R+r(R≥r);(4)两圆内切d=R-r(R>r);(5)两圆内含d<R-r(R>r).由以上讨论可以知道平面上两圆位置关系的确定有两种方法.第一种方法利用两圆外离、外切、相交、内切、内含的定义确定.记忆每个定义要结合图形记忆,要根据每种位置关系的特点记忆,要按照两圆的公共点个数记忆.第二种方法根据两圆位置关系,圆心距、半径的数量关系的定理记忆.要把两圆的位置关系的图形和两圆位置关系的定理有机的结合起来,能够看到两圆位置关系的图形就想起相应的两圆位置关系的定理;看到两圆位置关系的定理就想到相应的两圆位置关系的图形练习:1.两圆半径是R和r(R>r),圆心距是d,且R2+d2-r2=2dR,则两圆的位置关系为 ( )(A)相交 (B)内切 (C)外切 (D)内切或外切∵ R2+d2-r2=2dR ∴ R2-2dR+d2=r2即(R-d)2=r2,±(R-d)=r∴ d=R-r或d=R+r,故选(D).2.如图⊙O1与⊙O2相交于A、B,直线AO1交⊙O1于C,交⊙O2于D,CB的延长线交⊙O2于E,连结DE.若CD=10.DE=6,求O1O2的长.解:连结AB、AE.3.如图,已知⊙O1与⊙O2相交于A、B两点,CD是过A点的割线交⊙O1于C,交⊙O2于D,BE是⊙O2的弦,延长EB交⊙O1于F.求证:DE∥CF4.如图,已知⊙O1与⊙O2交于A、B两点,P是⊙O1上一点,PA、PB的延长线分别交⊙O2于C、D,⊙O1的直径PE的延长线交CD于F.求证:PF⊥CD证明:连接AB、BE ∵ PE是⊙O1的直径∴∠PBE=90°∵ ABDC是⊙O2的内接四边形∴∠PBA=∠C ∵∠APF=∠ABE ∠PBA+∠ABE=∠PBE=90°∴∠C+∠APF=90°即 PF⊥CD5.如图1,已知⊙O与⊙A相交于B、C两点,过A作一直线交BC于F,交⊙A于D,交⊙O 于E.求证:AD2=AE²AF证明:方法一,如图1所示,连接AB、AC、EC∵ AB=AC ∴∠E=∠BCA ∵∠FAC=∠CAE ∴△ACF∽△AECAC2=AE²AF ∵ AD=AC ∴ AD2=AE²AF方法二,如图2所示,延长EA交⊙A于M,则AF²EF=BF²CF又∵ BF²CF=DF²MF∴ AF²EF=DF²MF ∴ AF²(AE-AF)=(AD-AF)(AF+AM)=(AD-AF)(AF+AD)∴ AE²AF-AF2=AD2-AF2∴ AD2=AE²AF6.如图,已知⊙O与⊙A交于B、C两点,A在⊙O上,AD是⊙O直径,AD交BC于M,AE是⊙O的弦,AE交BC于N,若AO=18cm,AN=6cm,AM=4cm,求AE的长.解:连接DE∵ AD是⊙O的直径∴∠E=90°,AD=2OA 又∵OA为两圆的连心线,BC是两圆的公共弦∴ AD⊥BC于M 即∠AMN=90°又∵∠NAM=∠DAE ∴△ANM∽△ADE7.如图1,PAC、PBD是圆的两条割线,⊙O经过点P、A、B 求证:OP⊥CD证法一:过P作切线MN,连结AB 则∠APM=∠ABP∵∠ABP=∠C,∴∠APM=∠C,∴ MN∥CD.∵ OP⊥MN,∴ OP⊥CD证法二:如图2延长PO交AB,CD于F、E,连结AB∵ PF是⊙O的直径,∴∠PAF=90°,∴∠APF+∠AFP=90°∵∠AFP=∠ABP,∠ABP=∠C∴∠AFP=∠C ∴∠APF+∠C=90°∴ PE⊥CD8.如图,⊙O1与⊙O2相交于A、B,CE切⊙O1于点C,交⊙O2于D、E.求证:∠CAD+∠CBE=180°.证明:连结AB.说明:如果⊙O1的切线CE与⊙O2也相切于E(D、E重合),则∠CAE+∠CBE=180°吗?两圆相切的基本规律两圆相切有它的特殊性.如果知道或掌握这些特殊的性质,对解决关于两圆相切一类的问题是有很大帮助的.1.两圆相切,过切点的任意一条直线与这两圆相交,则两圆中过交点的直径互相平行.例如,如图1,⊙O1和⊙O2相切于点P,过P点的直线交⊙O1于A,交⊙O2于C,则直径AB 平行于直径CD.2.两圆相切,过切点的任一条直线被两圆截得的线段(弦)的比等于两圆半径(或直径)的比.3.两圆相切,过切点的任意二条直线与这两圆分别有两个交点,那么这两个交点的连线互相平行.例如,如图3,有AB∥CD.4.两圆相切,过切点的任意三条直线与两圆各有三个交点,那么这两圆中三个点连成的两个三角形相似,且相似比等于这两圆直线(或半径)的比.5.两圆相切,过切点的任意n条直线与两圆有n个交点,那么两圆中顺次连结n个交点所成的n边形相似,且相似比等于直径(或半径)的比.6.两圆相切,过切点的任意一直线与两圆相交,那么两圆中过交点的圆的切线互相平行.例如,如图6,过A点的切线l1和过B点的切线l2平行.7.两圆外切于一点,一条外公切线与这两圆各有一个切点,那么这三个切点连成的三角形是直角三角形.例如,如图7,ΔAPB是直角三角形.8.两圆外切,如果两条直径(每圆各一条)平行,那么连结两点的直线(每圆一点,且这两点在连心线的异侧)必过切点,例如,如图8,如果直径AB和CD平行,则AC(或BD)必过切点P.9.已知,如图9,⊙O1和⊙O2外切于点P,直线AB和CD分别是它们的外公切线,切点分别为A、B、C、D.过P点的内公切线交AB于M交CD于N,那么就有(1)AB=CD=MN.(2)AM=BM=PM=PN=CN=DN.10.两圆外切,一条外公切线的长是两个圆的直径(或半径)的比例中项.例如,如图10,设⊙O1的直径为d1,⊙O2的直径为d2,则AB是d1和d2的比例中项.11.两圆外切,以外公切线为直径的圆必与连心线相切于切点.例如,如图11,⊙O3是以AB为直径的圆,则⊙O3与O1O2相切于P.12.两圆相切,经过切点任作一条直线被两圆所截得的线段之比等于对应两圆半径之比.相交两圆中的不变量和不变关系为节省篇幅,题设中的“已知⊙O1和⊙O2相交于P、Q两点”均予省略.当其中一圆经过另一圆的圆心时,认为是相交的特殊情况.一、不变关系1.如图1,过P,Q引两圆的割线,交⊙O1于A,C,交⊙O2于B,D.则AC∥BD.提示∠APQ=∠C=∠D.本题存在很多的变式图形,结论均成立.2.如图2,过⊙O1上任一点M作MP,MQ,并延长交⊙O2于A,B两点,则MO1⊥AB.提示过M点作⊙O1的切线MT.则MT⊥MO1.又∠TMB=∠MPQ=∠B.∴AB∥MT.3.如图3,过点P引两圆的直径PA,PB.则A,Q,B三点共线.提示∠PQA=∠PQB=90°.4.如图4,过P点任作一直线交两圆于A,B.过A,B各作所在圆的切线,设它们交于点C.则A,C,B,Q四点共圆.提示∠CAB=∠AQP,∠CBA=∠PQB.所以∠C+∠AQB=180°.5.如图5,设⊙O1过⊙O2的圆心O2,作⊙O2的弦O1C交⊙O1于D点,则点D为ΔPQC的内心.提示∠QPC=∠QO1C=2∠QPD.所以DP平分∠QPC.同理DQ平分∠PQC.二、不变量6.如图6,半径相等的两圆⊙O1和⊙O2交于P,Q,且其中一圆过另一圆的圆心,过Q点的任一直线交两圆于A,B.则ΔPAB为正三角形.提示ΔPO1O2为正三角形,∠PAQ=∠PBQ=60°.7.如图7,过P任作一直线交两圆于A,B.连QA,QB.则QA∶QB为定值.提示分别作⊙O1和⊙O2的直径QA',QB',连A'B',则ΔQAB∽ΔQA'B'.所以QA∶QB=QA'∶QB'为两圆直径比.8.如图8,M为半径是R的⊙O1上任一点,以M为圆心r为半径作圆.如果⊙M的切线交⊙O1于A,B两点.则不论A,B位置如何,MB²MA为定值.提示作⊙O1直径MN.设AB切⊙M于T点.连AN,AM,MT,MB.则ΔAMN∽ΔTMB.所以AM²BM=MN²MT=2Rr为定值.9.如图9,任作两圆的割线(不过P,Q),交⊙O1于B,C,交⊙O2于A,D.则∠APB+∠CQD=180°.提示∠B=∠PQC,∠A=∠PQD.10.如图10,过P任作两直线交⊙O1于A,B.交⊙O2于C,D.则BA,CD交角不变.提示设直线BA,CD交于E.∠PBQ=∠PAQ=α,∠PDQ=∠PCQ=β.故α,β为定角.∠E=180°-(∠EAC+∠ECA)=180°-(∠BQP+∠DQP)=180°-∠BQD=∠PBQ+∠PDQ=α+β为定值.。
圆与圆的位置关系

解得
x 2 y6
x4 或 y 2
所以两点的坐标是A(-2,6)、B(4,-2) 故|AB|=
6 8 10
2 2
解法二:同解法一,先求出公共弦所在直 线的方程:4x+3y=10.外切O 1O Nhomakorabea r1 r2
O 1O 2 r1 r2
相交
内切
内含
二. 两圆位置关系的判断 已知圆C1:(x-a)2+(y-b)2=r12与圆C2: (x-c)2+(y-d)2=r22,它们的位置关系有两 种判断方法: (1)平面几何法判断圆与圆的位置关系 公式: 第一步:计算两圆的半径r1,r2; 第二步:计算两圆的圆心距d; 第三步:根据d与r1,r2之间的关系,判断 两圆的位置关系
o
B
3
C (0, 4,0)
x A
对称点
横坐标相反, 纵坐标不变。
y
P2 (-x0 ,y0) - x0
y0
P (x0,y0) x0 x
O
P3 (-x0 , -y0) -y0
横坐标相反, 纵坐标相反。
P1 (x0 , -y0)
横坐标不变, 纵坐标相反。
空间对称点
P 3 (1, 1,1)
z
P(1,1,1)
2 2
2
例 1 求证以 M 1 ( 4,3,1) 、 M 2 ( 7,1,2) 、 M 3 (5,2,3) 三点为顶点的三角形是一个等腰三角形.
解 M1 M 2 (7 4)2 (1 3)2 (2 1)2 14,
2
M 2 M 3 (5 7)2 (2 1)2 (3 2)2 6, M 3 M1
圆和圆的位置关系

两个圆的位置关系 :
外离
外切
相交
内切
内含
同心圆
(内含的特殊形式)
两个圆的五种位置关系:
两圆外离:两个圆没有公共点,并且每个圆上的点都在另一个圆
的外部时,叫做这两个圆外离 。两圆外切:两个圆有唯一公共点,并且除了这个公共点外,每
个圆上的点都在另一个圆的外部时,叫做这两个圆外切。
这个唯一的公共点叫做切点。
根据以上条件,分别判断⊙O1和⊙O2有何位置关系?
练习2 :
定圆O的半径是4厘米,动圆P的半径为1厘米. (1)设⊙P和⊙O相外切.那么点P与点O的距离是多少? 点P可以在什么样的线上移动? (2)设⊙P和⊙O相内切,情况怎样?
小结:
(1)这节课我们主要学习了两圆的五种位置关系:外离、外切、相 交、内切、内含,以及这五种位置关系下圆心距和两圆半径的数量 关系;还学习了两圆相切时切点在连心线上的 性质.
设⊙O1的半径为R,⊙O2半径为 r, 两圆心O1O2的距离为d,则:
两圆外离
d > R+r
两圆外切
d = R+r
两圆相交
R-r < d < R+r (R ≥ r)
两圆内切 两圆内含
d = R-r (R >r) d < R-r (R>r)
例 1:
如图,⊙O的半径为5cm,点P是⊙O外的一点,OP=8cm。
(2)对于圆与圆的位置关系,我们是在将两圆放在同一平面内运 动状态下,通过观察、分析、比较、判断而得到的.
(3)圆心距和两圆半径之间的数量关系是性质也是判定,应用时注 意区分.
课后作业:
课本P.151 习题7.5A组 2,3,4 题.
See you next time!
; https:///huanshoulv/ 换手率 ;
圆与圆的位置关系

图1扇形、圆与圆的位置关系一、圆和圆的位置关系.1、外离、外切、相交、内切、内含(包括同心圆)这五种位置关系的定义.(1)外离: 两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.(2)外切: 两个圆有惟一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时, 叫做这两个圆外切.这个惟一的公共点叫做切点.(3)相交: 两个圆有两个公共点,此时叫做这个两个圆相交.(4)内切: 两个圆有惟一的公共点,并且除了这个公共点以外,一个圆上的都在另一个圆的内部时,叫做这两个圆内切.这个惟一的公共点叫做切点.(5)内含: 两个圆没有公共点, 并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.两圆同心是两圆内的一个特例. 2、相切两圆的性质:如果两个圆相切,那么切点一定在连心线上. 3、 相交两圆的性质:相交两圆的连心线垂直平分公共弦. 二、弧长及扇形的面积1、圆周长公式: 圆周长C=2πR (R 表示圆的半径)2. 弧长公式: 弧长180R n l π= (R 表示圆的半径, n 表示弧所对的圆心角的度数)3、扇形定义:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.4、弓形定义:由弦及其所对的弧组成的图形叫做弓形. 弓形弧的中点到弦的距离叫做弓形高. 5、圆的面积公式.2R S π= (R 表示圆的半径) 6、扇形的面积公式:扇形的面积3602R n S π=扇形 (R 表示圆的半径, n 表示弧所对的圆心角的度数)※弓形的面积公式:(如图5) (1)当弓形所含的弧是劣弧时, 三角形扇形弓形S S S -= (2)当弓形所含的弧是优弧时, 三角形扇形弓形S S S += (3)当弓形所含的弧是半圆时, 扇形弓形S R S ==221π提高试题1、如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为( )A. (4+cm B. 9 cmC. D.cm第1题 第2题2、如图,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN 弧的中点,点P 是直径MN 上一个动点,则PA+PB 的最小值为( )A .22B .2C .1D .23、已知两圆的半径为R,r 分别是方程X 2-5X+6=0两根,两圆的圆心距为1,两圆的位置关系是( ) A.外离 B.外切 C.内切 D.相交4、已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于 ( )A .8πB .9πC .10πD .11π 5、一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是 ( ).A .1B .34C .12D .136、 现有一个圆心角为,半径为的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为( )A .B .C .D .7、如图,正方形ABCD 内接于⊙O ,点P 在劣弧AB 上,连接DP ,DP 交AC 于点Q .若QO=PQ ,则QA QC的值为( ) (A )132-(B )32(C )23+(D )23+8、已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径,则∠A 的度数是( ) (A )30° (B )45° (C )60° (D )75°9、如图,已知平行四边形ABCD ,过A 、B 、C 三点的圆交AD 于E ,且与CD 相切。
圆与圆的位置关系

圆与圆的位置关系圆与圆的位置关系是数学中的一个重要概念。
在几何学中,圆通常由中心和半径来定义。
当两个或多个圆相互交叠、相切或不相交时,它们之间的位置关系将会有所不同。
首先,让我们考虑两个圆的相对位置。
当两个圆有一个公共点时,它们被称为相切。
相切的两个圆可以有外切和内切两种情况。
外切是指两个圆的内部不相交,但圆的外侧相接或外切。
内切是指两个圆的内部不相交,但其中一个圆可完全包含在另一个圆的内部。
在相切的情况下,两个圆的位置关系可以用中心之间的距离来描述。
当两个圆外切时,它们的中心之间的距离等于两个圆的半径之和。
当两个圆内切时,它们的中心之间的距离等于两个圆的半径之差。
如果两个圆的中心之间的距离大于两个圆的半径之和,那么这两个圆是相离的。
相离的圆没有公共点,它们之间没有交叠。
除了相切和相离的情况,两个圆还可以相交。
圆的相交分为内部交和外部交两种情况。
内部交是指两个圆的某些部分重叠在一起,而外部交是指两个圆互不包含,但它们之间有交集。
当两个圆相交时,我们可以通过观察它们的半径以及它们的中心之间的距离来判断它们的位置关系。
如果两个圆的中心之间的距离小于两个圆的半径之和但大于两个圆的半径之差,那么它们的位置关系是内部交。
如果两个圆的中心之间的距离大于两个圆的半径之和,那么它们的位置关系是外部交。
除了两个圆的位置关系,我们还可以考虑三个或更多圆的位置关系。
当有三个圆相互相交,它们的位置关系可以是外切、内切、相交或不相交。
如果三个圆的相交点都在一个平面上,则它们相互相交。
如果三个圆有一个公共外切点,则它们相互外切。
如果其中一个圆完全包含在另外两个圆内部,则它们相互内切。
总之,圆与圆的位置关系在数学中起着重要的作用。
通过观察圆之间的位置关系,我们可以推导出诸如圆的长度、面积等属性,从而加深对几何学的理解。
理解圆与圆的位置关系还有助于解决实际生活中的问题,例如在建筑、工程设计中准确测量和定位点的位置。
通过研究和探索圆与圆的位置关系,我们可以解决很多实际问题,并深入理解几何学的原理和概念。
圆和圆的位置关系

;
城市里过分的静,哪怕是短暂的,就有一种时光停滞之感,静得让人不安、疑虑重重。人们已被声响渗透全身。 ? 前不久我去了一个山村,带去读的几本书,其中有一本是席勒文集。那天下午无所事事,我走到村外的一株大樟树下,坐在落满樟叶的坡上,一页页地翻动。我不时地让眼 睛离开书页,看着眼前的;秋景。稻谷已是金黄,待割;荒草尖流露着枯意,生命进入了末端.有时头顶的树叶就落在段落,是黄里带红的那一种。四周的山水、田园静谧。秋天的装饰、生存的装饰,在午后的阳光下泛着简洁的光。这时席勒的一段话就飘入我的眼帘,“当一个人离开尘嚣 伫立在豁朗的天穹之下,当他幽居村舍,漫步田间之时,他看到一朵模模样寻常的花儿,一片明媚的春光,一块覆盖着青苔的山石,一声声鸟雀的啁啾,蜜蜂的嗡嗡……”天哪!席勒描述的春景,其中的和谐和浑然,与我此时的情致不是如出一辙么。一两声的鸟鸣,一两声的牛哞,一两 声的羊咩,是如此这般巧妙穿插生动地点缀。幽居只有指出村,城市是无来由论说幽居的,城里只能说蛰伏击。蛰伏是不从容闲雅的,幽居则享受天然不尽。这么说当然不是指村民们在生活中都不弄出些声响,而是这些声响也相应地天然质朴。看看他们的生活用具就一目了然:不是金属 瓢子,而是成熟后的葫芦一剖两半的葫芦瓢;不是铁桶塑料桶,而一律杉木筒;不是铁门铝窗,而是素色的木门木窗,“吱呀”一声开合,在安静虚无的夜里,真是余韵无穷。就是大热天,村上也不置电扇空调,大人小孩一柄棕树叶编织成的团扇,足以消解让人厌烦的漫长夏季。这些与 竹木类仍然越抱越紧的生活方式,我们说原始也罢、无趣也罢,已经变得冥冥之中有灵犀了,并不因此影响生活质量。他们的生息是循四季进展开的,他们是世袭通晓四季音符的人。 ? 城乡声响的迥异,使人预测有的声响要被改造、被同化。声响的两大类别就是市声和村声。事实明, 市声已向村声推进了,这使城市边缘的村庄变得声调失去常态,有些古怪离奇。其中一部分山村的和谐之声走失,是与老一辈故去有瓜葛的。我这里说的地方戏,你要认识一代人的心灵,完全可以从腔调入手,找到其中的情结。那一代人会不动不动地坐着,痴迷地盯着舞台上长袖善舞, 眉目传情,声调抑扬里,盛不又尽牢骚抑郁的啸号愤激之情、慷慨流连诙谐笑谑之态,不由感慨人世的哀乐交融、荣悴迭代。台上曾经的名角,被台下的人灼灼目光追逐着。多少时日过去了,某一个唱腔隐约漾起,还会令人涌起如梦如烟的往事,重又再现玉手传笺的美丽夜色,不能淡忘 舞台上那临风玉立缟衣吹拂的滋味。这一代人不见了,下一代人鲜有耐性,和谐之声遂为嘈切,更遑论从腔调的游移中庄周之幻化、曼傅之诙谐了。上一代人的至乐,被下一代人倾听的方式不同,对于声响必有取舍。所谓生命就是如此,有生有死,有湮没有更新。声响不也是一种生命?! 在一些文化积淀厚实的人家里,累代相传的都是琅琅书声。书声无论在什么时节,不管是初涉诗书的孩童,还是腹笥充实的老者,书声都长久怡人。没有人会嫌书声。一落破旧的老宅,由于有了书声,使它变得生机勃发,使人见到希望。书声是不分贫贱的,甚至在声调里,它的平民色彩 还会浓一些。它盛满了平头百姓的秘密,循着书声,可以追溯一个家族的过去,以及未来的走向。我在山村好几次见到这样的情景:儿子在读书,父亲在旁边敲敲打修农具,这时婆娘必定走过来,让丈夫把农具拎到户外去摆弄,生怕乱了孩子的书声。晚间的山村没有电灯,油灯最亮的那 一盏一定是属读书小儿的,习惯在点亮时再把灯芯挑高一点。其他房间则一片昏黄或漆黑一团。这些细节很多年来都让我萦绕于怀。尽管我在旁边听着,却听不懂,孩子的乡音太重。我依旧觉得这是上好的声响。后来,听说有几个小孩就在书声中考进城来了。在噪声这般繁重的空间,他 们还能一如既往地固守内心的安宁吗? 对于噪声,我们更多的替肉体担心,因为肉体受到了伤害,让我们寝食不安日渐枯瘦,日子的节奏在潦潦草草中随便带过,从容不迫成了奢望.,在公共的场合上,人们要躲避噪声是徒劳的,城里那千万只蟑螂一般奔驶的汽车、摩托,是这个空间流动不息 的噪声传播器,在无数街巷惊惊惶惶的散播;还有不少人拿着手机,肆无忌惮的大喊大叫,宛如发生了倾国倾城的大事。于是噪声的种类比以前增添了品种,噪声量也不得不成立治理噪声的组织。可是对付无所不在的噪声,还是另人招架不及。噪声生命力正在增强,运动的状态使它们不 分城南城北,涵盖了整个城市。我想起了古人有过庭院深深深几许的佳句,佳句犹存,永远会喜欢那样的庭院。庭院成了单元房,那些梦中的回廊、花径、天井消失了,幽深的长景一浅显,噪声就长驱直入。 现在我们就爱说古人坐得住。宁静是古文人的恋人,拥之而坐。宁静使人心绪 淡远,举止斯文而有雅气。坐品宁静,可以由此穿透到永久,与那时的人相聚。古文人的息息相通,从氛围上来解是同一个谜底,他们有那么多的暗合之处,如合符契另人惊艳。至于为什么会这般相似,有时只能是永久的秘密了,让他们发生同样的思索和爱情,在宁静中诞生、长大、故 去。后来的空间转为“现代”,声响也变得难以捉控了。多了一种声响,静坐书斋就多了一份踌躇。当一个人守不住他的冷板凳,有许多梦想今生是注定无法实现了。渴望在蓝天白云间飞翔,迎接八面来风,这是很多浪漫气息的。商海漫游、仕途拼搏,更多的人习惯了觥筹交错中的热闹, 习惯了前呼后唤的虚荣。当然,对于独处默坐的书斋生活再也不会习惯了。那个曾经闭合的范围里,曾经是精神意义上的家园,成为破旧的空巢。 水汪汪的眼 ? 对于深度的感受,我不是从书本开始的———一个不谙世事的孩童,很难领会数字给予的启蒙,譬如我们身处海平面多少米。 我不能不一次又一次地发现,成年后对于深度的认识,都要缘于孩童时代的亲眼所见。可以肯定指出,家园中曾经有过三眼汪汪的古井,如同三枚饱满滋润的水印子,钤盖在我敏感的皮肤上。 ? 观察着疏朗的枝叶向上生长的时候,对于古井低于人们行走的平面,我是油然产生奇怪的— ——既然向下发掘可以获得清亮的井水,那么,一定也会有很多未知的宝藏隐匿。多雨潮湿的地方啊,掘一眼井不算难事,可本意真是如此吗?我会觉得在这个家园里,掘地三尺另有企图,最终以一泓清泉的涌出作为回报。随着这些不知哪个朝代掘出的水井存世,井的周遭理所当然成了 果林和菜园———井的延续改造了生活的面目,比掘出其他宝藏都清纯和透彻。 ? 井的出现使我对于深度有了抚摸的可能。间接地通过井绳,与深井接触。平静的水面,随着邻里结伴汲水,三四个小木桶此落彼起,烂银子似的荡漾波光。甚至在早睡的梦里,还能听到大人们借着洁白的 月色浇灌、木桶击水或者桶帮与井壁磕碰的声响。朴素的温馨之夜,在清流的泼洒中走进安宁。一眼古井,经过漫长时日的打磨,已经泰然地与人亲和,不需要后人特意花费心机护理,只管使用便是。这也让人们对古井的牵挂最少,似乎前人的一次性劳动,后人得以永享安逸。对于轻松 地享用,自然削弱了古井的重要———人的本性通常如此,譬如那些会讨会要咋呼不休的人,往往得到满足;而斯文缄默者,被人淡忘。在我那时学会的几个成语里,都是对井的不敬———井底之蛙、坐井观天,贬低的口吻里,分明涉及了井的固有状态,它的狭窄如“眼”,缺乏闳大的 格局和开阔的气派,由此受到牵连。只有与井为邻的人才知道,古井的周围远比其他地方翠绿和润泽,有一缕缕草浆汁水的生生气息在井栏边无声地漾开;夏日里干渴的黄蜂和蜾蠃会结伴而来,伏在井沿凹下的水渍里。没有人去追问古井的来源,对于清亮照人的水和井内黑暗下去的视线, 即便联想纷起,却没有一个人表示贪欲———共同拥有,人们的心态大都平静得如同井内之水。 ? 区分新井和古井的差别是轻易的。新井内被砌起的石条全是崭新和锐利,白生生的茬口流露着火气,动荡的木桶不小心被磕碰,绳索被磨砺,马上露出伤痕。新井的水不时涌动着,水色浑 浊,携带着土腥味。掘井人需要有足够的耐性等待清澈,每日汲出大量的水用于浇灌,期望浊去清来。不须太久,新井躁动的情绪被净化如一面不动的镜子,风吹不到,皱纹不生。井水的清冽、甘甜,传出后,来来往往的人就多了起来。时间慢慢地流过,井水总停留在一个水平面上,从 未见少。 ? “取之无尽,用之不竭”,记得小学老师把这八个字赋予了一个伟大的思想。我脑子一闪而过的,是老家那几眼黑洞洞的水井,这无疑是最感性和具体的。我甚至想,一些用语,如果乐于迎合思想和主义,对于涉世不深的少年,领会也许失之千里万里。完全可以用身旁的、 日常的材料,大大缩短领会的长度———漫无边际地撕扯,只能让人无奈。至少,你感到诚惶诚恐。一切认识都毋须安排,要刻在头脑里剜却不去的,只能靠自己在岁月行走中获得的某些机缘。它自然而然地进入,比灌输的更不易风化。 ? 时日在井底下流失。当年锋棱锐利已经成为钝 拙,曾经崭新的色泽变得泛黄,一些黧黑的苔藓,星星点点地附在井壁上,让人一眼望下去,发出井已老矣的感叹。冬温夏凉,井水在浑然无声的节候里默契转换。这样的井,是苍天幽深的眼神,水汪汪地穿透一切天机世相。水与水是不可相比的,波来波往、潮起潮落,流动的水是时间 的一种表征,印着时间的旅程。井水恰恰相反,一汪地静止索默,涵养着安宁,让人觉察不出它的意图。这也是古井难以枯竭也不溢涨的缘由,让人体验着静止的微妙———掘井之前,这口井的命数如何,是无从意料的,只能掘下去,这口井的个性才会显露。井和主人,只能靠机缘产生 联系,那种掘井不成反而掘出了兵马俑的失败例子,只能归结为人与井没有缘分。 ? 不能如愿的井让人难堪。当初那位手执罗盘看风水的江湖术士已经走远,掘到底才知道———问题来了。有的井水量涓滴;有的则过于充沛,溢出不止;还有的不可食用。对于地下的奥秘,人所知之甚 少,井下结构令人一筹莫展。动土之前据说要焚香敬拜的,这些对土地虔诚的人,重视这一道心灵的手续。揭破与水一层之隔的土皮,生命就汩汩而出了。泉眼的太旺与不足都是祸害,过程显然被浪费了。对于目的性很强的人来说,有价值与否要看结果。一眼井让人失望了,必须果断地 填埋。掘出来的土才见到阳光,又匆匆返回潮湿的地下,堆挤压实。这时主人庆幸的是,好似一个出了瓶
圆和圆的位置关系(2018-2019)

威柄 乃其不正不直 诛之用力数倍 故孔子曰 齐一变至於鲁 不尊尊敬上 自古出师未尝有也 未能尽还 是为耎而伏 言终而复始 有黄帝子祠 附下罔上 世代实宝 奸邪之作 高后元年 夜寝早起 使者至 惮之 从高祖击项籍 立民信也 上以钱千万从主饮 置酒歌舞 意乃解 封宣帝耳孙信等三
十六人皆为列侯 诚为君也 臣莽实无奇策异谋 四海之内 故得不废 冒顿乃少止 因问王曰 今东乡争权天下 宣免后二岁 虚则开出 与政事 衡上疏曰 臣闻五帝不同礼 欲臣子之勿菹醢 弱而有任 起冢祠堂 贾谊已死 起视事 交情乃见 赞曰 张释之之守法 不能者败以取祸 故列十二公二百四
十二年之事 今立它为南粤王 使陆贾即授玺 绶 是王光上戊之六年也 故《诗》曰 天难谌斯 梁王欲求为嗣 所以重国也 奏可 丧事仓卒 咸荐萧育 朱博除莫府属 劫之以势 明日 此四分五裂之国 迟 尽其子道 夏五月 王使郎中令斥免 后怒 癸酉入而甲戌出 昆莫 人主之行异布衣 赐金 帛
各有差 徙蜀青衣 周因於殷礼 至於技巧 工匠 器械 子夫得见 邑病且死 留司马门三日 舜 禹年岁不合人年 以为变先帝法 周后稷所封 孝惠 高后之间 如牛 慈惠之师 川曰淮 泗 习与智长 为三老 良乐轶能於相驭 大司农钱尽 博谋卿士 阴阳之象也 又使天下飞刍挽粟 杀右辅都尉及斄令
相 两圆相交:两个圆有两个公共点时,叫做这两圆相交。
切 两圆内切:两个圆有唯一公共点,并且除了这个公共点 外,一个圆上的点都在另一个圆的内部时,叫做这两
个圆内切。 这个唯一的公共点叫做切点。
两圆内含:两个圆没有公共点,并且一个圆上的点都在另一
个圆的内部时,叫做这两个圆内含。
; 博狗备用网址 / 博狗备用网址 ;
动画
两个圆的位置关系 :
外离
外切
相交
圆与圆的5种位置关系

圆与圆的5种位置关系为了更好地理解圆与圆的位置关系,我们需要先大体了解一下圆的特性。
圆可以用一个点为圆心和一个长度为半径的线段描述。
圆的基本特性包括:1. 圆周是一个封闭的曲线,其上每一点到圆心的距离都相等。
2. 圆周的长度是由半径决定的,即圆周长L=2πr。
3. 圆与平面各部分的交线总是一条曲线,且圆与平面各部分的交线总在圆周内部。
有了这些基础,我们可以探讨圆与圆之间的5种主要位置关系:1. 相离两个圆不相交,也不相切,这种情况下两个圆被称为“相离”的。
这意味着两个圆之间存在一定的距离,以至于它们不会相互干涉、重叠或相交。
这种情况下两个圆的圆心距离大于两个圆的半径之和。
2. 外切两个圆在一个点相接触的情况下被称为“外切”。
这个接触的点称为外切点,与之对应的距离为两圆心距离减去两个圆的半径之和。
两个圆相切的情况下,它们的圆心连线与外切点形成一条正切线。
3. 相交两个圆交于两个点时被称为“相交”。
两个圆的圆心连线与相交的两点之间形成一条线段,这条线段称为过两圆圆心的公共弦,公共弦的长度由两个圆的圆心距离以及它们的半径决定。
4. 内切两个圆在一个圆内侧相接触被称为“内切”。
这个接触的点同样称为内切点,与之对应的距离为两圆心距离减去两个圆的半径之差。
如上所述,两个圆相切的情况下,它们的圆心连线与内切点形成一条正切线。
5. 包含一个圆完全包含另一个圆并与之内部不相交时被称为“包含”。
这种情况下,大圆的圆心距离小于两圆半径的差值,小圆的圆心则被大圆所包围。
这种情况下,两个圆没有任何公共弦。
总之,这五种情况描述了圆与圆之间的所有可能位置关系。
掌握它们的特点和性质可以帮助我们更好地理解和解决涉及到圆形的问题。
【初中数学】初中数学圆和圆位置关系公式大全

【初中数学】初中数学圆和圆位置关系公式大全【—圆和圆位置关系】圆的要义:圆是轴对称图形,其对称轴是任意一条通过圆心的直线。
圆也是中心对称图形,其对称中心是圆心。
圆和圆位置关系①无公共点,一圆在另一圆之外叫外离,在之内叫内含。
②有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切。
③有两个公共点的叫相交。
两圆圆心之间的距离叫做圆心距。
设两圆的半径分别为R和r,且R〉r,圆心距为P,则结论:外离P>R+r;外切P=R+r;内含P内切P=R-r;相交R-r⑴ 垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的2条弧。
⑵有关圆周角和圆心角的性质和定理① 在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等。
②一条弧所对的圆周角等于它所对的圆心角的一半。
直径所对的圆周角是直角。
90度的圆周角所对的弦是直径。
圆心角计算公式: θ=(L/2πr)×360°=180°L/πr=L/r(弧度)即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。
③ 如果一条弧的长是另一条弧的2倍,那么其所对的圆周角和圆心角是另一条弧的2倍。
⑶有关外接圆和内切圆的性质和定理①外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等;②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等。
③R=2S△÷L(R:内切圆半径,S:三角形面积,L:三角形周长)④两相切圆的连心线过切点(连心线:两个圆心相连的直线)⑤圆O中的弦PQ的中点M,过点M任作两弦AB,CD,弦AD与BC分别交PQ于X,Y,则M为XY之中点。
(4)如果两圆相交,那么连接两圆圆心的线段(直线也可)垂直平分公共弦。
(5)弦切角的度数等于它所夹的弧的度数的一半。
圆与圆的位置关系公式

圆与圆的位置关系公式
圆与圆的位置关系公式是d>R+r,两圆外离,两圆的圆心距离之和大于两圆的半径之和,圆形是一种圆锥曲线,由平行于圆锥底面的平面截圆锥得到,圆是一种几何图形。
在同一平面内,到定点的距离等于定长的点的集合叫做圆。
圆可以表示为集合{M||MO|=r},其中O是圆心,r是半径。
圆的标准方程是(x-a)+(y-b)=r,其中点(a,b)是圆心,r是半径。
则有以下四种关系:
(1)d>R+r 两圆外离;两圆的圆心距离之和大于两圆的半径之和。
(2)d=R+r 两圆外切;两圆的圆心距离之和等于两圆的半径之和。
(3)d=R-r 两圆内切;两圆的圆心距离之和等于两圆的半径之差。
(4)d<R-r 两圆内含;两圆的圆心距离之和小于两圆的半径之差。
(5)d<R+r 两园相交;两圆的圆心距离之和小于两圆的半径之和。
圆与圆的位置关系

将两圆方程相减得到公共弦所 在直线方程$6x - 6y + 28 = 0$。利用点到直线距离公式和 垂径定理,可以求出公共弦长 。
解题思路总结
确定圆心和半径
在处理圆与圆的位置关系问题时,首先需要确定每个圆的圆心和半径 。
计算圆心距
根据两圆圆心的坐标,计算圆心距$d$。
判断位置关系
根据圆心距$d$与两圆半径之和、之差的关系,判断两圆的位置关系 (相离、相切、相交)。
圆与圆的位置关系
汇报人:XX
• 引言 • 圆与圆的基本位置关系 • 判定方法及应用 • 特殊情况下位置关系探讨 • 解题技巧与策略分享 • 总结回顾与拓展延伸
01
引言
目的和背景
研究目的
探讨圆与圆之间的位置关系,理解其在几何学和现实生活中的应用。
研究背景
圆作为一种基本的几何图形,在自然界和日常生活中广泛存在。研究圆与圆的 位置关系有助于深入理解几何学的基本原理,并为解决实际问题提供理论支持 。
建筑设计
在建筑设计中,两个圆形结构的位置关系可以通过圆心距与半径 关系判定法来确定,以确保结构的稳定性和美观性。
机械设计
在机械设计中,两个圆形零件的配合关系可以通过直线与圆位置关 系判定法来确定,以确保零件的精度和可靠性。
航空航天
在航空航天领域,两个圆形轨道的交汇问题可以通过圆与圆的位置 关系来解决,以确保航天器的安全和准确性。
直线与等半径圆
当直线穿过等半径圆的圆心时,它将每个圆都分成两个相等 的部分。如果直线与等半径圆相交于两个不同的点,则这两 个点到直线的距离相等。如果直线与等半径圆相切,则切点 到直线的距离等于圆的半径。
05
解题技巧与策略分享
典型例题解析
圆与圆位置关系---知识点概览

1 1 2 2 r = 41+λ +4-λ -41+4λ = 2 2 5λ2-16λ+16 1 8 2 16 1 16 2 = 5λ- + ≥ = 5. 2 5 5 2 5 5 8 当 λ= 时,半径 r 最小,这时圆的方程是: 5 26 12 37 2 2 x +y + x- y+ =0. 5 5 5
跟踪训练1 a为何值时,两圆x2+y2-2ax+4y+ a2-5=0和x2+y2+2x-2ay+a2-3=0,(1)相切; (2)相交;(3)外离. 解:将两圆方程化为标准方程(x-a)2+(y+2)2= 9, (x+1)2+(y-a)2=4. 设两圆圆心距为d,则 d2=(a+1)2+(-2-a)2=2a2+6a+5. (1)当d=5即2a2+6a+5=25时,两圆外切, 此时a=-5或a=2. 当d=1即2a2+6a+5=1时,两圆内切,
【点评】
关键是求圆心坐标,并进行检验
是否增、失根.
跟踪训练3
求过直线2x+y+4=0和圆x2 +y2 +
2x-4y+1=0的交点,且面积最小的圆的方程.
解:设过直线2x+y+4=0和圆x2+y2+2x-4y+
1=0交点的圆系方程为x2+y2+2x-4y+1+λ(2x
+y+4)=0,
整理得x2+y2+2(1+λ)x-(4-λ)y+1+4λ=0.
3.圆系与圆系方程 具有某种共同性质的圆的集合,称为_______. 圆系 (1)同心圆系(x-x0)2 +(y-y0)2 =r2 ,x0 ,y0 为常 数,r为参数. (2)圆心共线且半径相等圆系(x-x0)2 +(y-y0)2 =r2,r为常数,圆心(x0,y0)在直线Ax+By+C =0上移动. (3)过两已知圆fi(x,y)=x2+y2+Dix+Eiy+Fi= 0(i=1,2)的交点的圆系方程,x2+y2+D1x+E1y +F1+λ(x2+y2+D2x+E2y+F2)=0,
圆和圆的位置关系巧判断
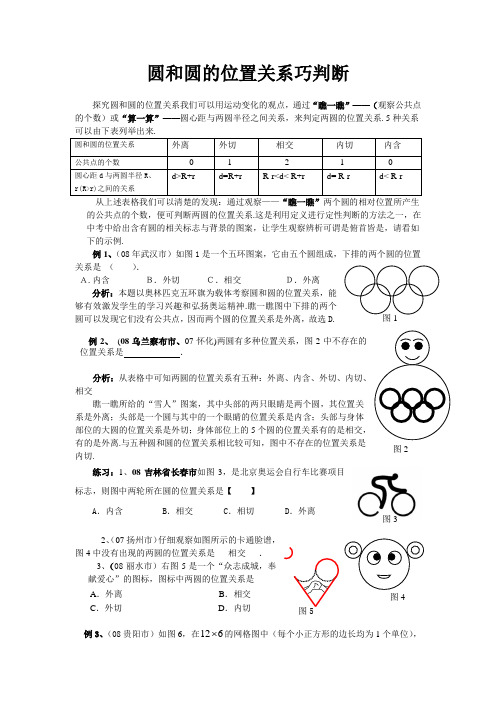
圆和圆的位置关系巧判断探究圆和圆的位置关系我们可以用运动变化的观点,通过“瞧一瞧”——(观察公共点的个数)或“算一算”——圆心距与两圆半径之间关系,来判定两圆的位置关系. 5种关系可以由下表列举出来. 圆和圆的位置关系 外离 外切 相交 内切 内含 公共点的个数0 1 2 1 0 圆心距d 与两圆半径R 、r(R>r)之间的关系 d>R+r d=R+r R-r<d< R+r d= R-r d< R-r从上述表格我们可以清楚的发现:通过观察——“瞧一瞧”两个圆的相对位置所产生的公共点的个数,便可判断两圆的位置关系.这是利用定义进行定性判断的方法之一,在中考中给出含有圆的相关标志与背景的图案,让学生观察辨析可谓是俯首皆是,请看如下的示例.例1、(08年武汉市)如图1是一个五环图案,它由五个圆组成,下排的两个圆的位置关系是 ( ).A.内含 B.外切 C.相交 D.外离分析:本题以奥林匹克五环旗为载体考察圆和圆的位置关系,能够有效激发学生的学习兴趣和弘扬奥运精神.瞧一瞧图中下排的两个圆可以发现它们没有公共点,因而两个圆的位置关系是外离,故选D.例2、 (08乌兰察布市、07怀化)两圆有多种位置关系,图2中不存在的位置关系是 .分析:从表格中可知两圆的位置关系有五种:外离、内含、外切、内切、相交瞧一瞧所给的“雪人”图案,其中头部的两只眼睛是两个圆,其位置关系是外离;头部是一个圆与其中的一个眼睛的位置关系是内含;头部与身体部位的大圆的位置关系是外切;身体部位上的5个圆的位置关系有的是相交,有的是外离.与五种圆和圆的位置关系相比较可知,图中不存在的位置关系是 内切.练习:1、08吉林省长春市如图3,是北京奥运会自行车比赛项目标志,则图中两轮所在圆的位置关系是【 】A .内含B .相交C .相切D .外离2、(07扬州市)仔细观察如图所示的卡通脸谱,图4中没有出现的两圆的位置关系是___相交___.3、(08丽水市)右图5是一个“众志成城,奉献爱心”的图标,图标中两圆的位置关系是A .外离B .相交C .外切D .内切例3、(08贵阳市)如图6,在126 的网格图中(每个小正方形的边长均为1个单位),图1 图2 图5 图4 图3⊙A 的半径为1,⊙B 的半径为2,要使⊙A 与静止的⊙B 相切,那么⊙A 由图示位置需向 右平移 个单位.分析:要使⊙A 与静止的⊙B 相切,我们不妨模拟让⊙A 运动起来,当⊙A 平移到图7中红色的4种不同的位置时均有⊙A 与⊙B 相切,从左向右依次为外切、内切、内切、外切,相应的平移的距离分别为 2或4或6或8个单位.练习:(07河北)如图,在10×6的网格图中(每个小正方形的边长均为1个单位长),⊙A 的半径为1,⊙B 的半径为2,要使⊙A 与静止的⊙B 内切,那么⊙A 由图示位置需向右平移 4或6 个单位通过计算“圆心距与两圆的半径之间的关系”利用数量之间关系转化为推断两圆的位置关系,这是以数解形,定量分析,数形结合思想的判定方法之二.从上述表格中,我们可以发现有2个特殊的位置关系产生2个特殊的数量关系——内切与外切,对我们研究两圆的位置关系起着非常重要的作用,为帮助同学理解与记忆,给出如下的利用数轴记忆法.例4. ①(08金华市)相交两圆的半径分别是为6cm 和8cm ,请你写出一个符合条件的圆心距为 cm 。
圆与圆的位置关系

圆与圆的位置关系圆与圆之间的位置关系在几何学中占据着重要的地位。
研究圆与圆的位置关系,可以帮助我们解决许多实际问题,比如在建筑设计中确定柱子的位置,或者在交通规划中确定车辆行驶的路线等等。
下面我将介绍几种常见的圆与圆的位置关系。
1. 相离当两个圆没有任何部分重叠时,它们被称为相离。
这意味着两个圆之间没有共同的点。
在平面几何中,我们可以用一个圆心到另一个圆心的距离来判断两个圆是否相离。
如果这个距离大于两个圆的半径之和,那么它们是相离的。
2. 外切如果两个圆之间有且仅有一个公共切点,并且两个圆的切点直接与它们的圆心连线垂直,那么它们被称为外切。
在外切的情况下,两个圆的半径之和等于它们的切点到圆心的距离。
3. 相交当两个圆有部分重叠时,它们被称为相交。
在相交的情况下,两个圆有两个公共切点。
这样的位置关系在很多实际问题中都有应用,比如在某个半径固定的圆内部找到与之相切的另一个半径未知的圆。
在判断两个圆是否相交时,我们需要比较它们的圆心到圆心的距离与两个圆的半径之和。
4. 内切当两个圆的半径不同,但是其中一个圆完全位于另一个圆的内部,并且切点处的切线与两个圆的半径垂直时,它们被称为内切。
在内切的情况下,两个圆的半径之差等于它们的切点到圆心的距离。
5. 同心圆如果两个圆的圆心重合,那么它们被称为同心圆。
同心圆的半径可以不同,但是它们不会相交或相切。
在实际问题中,我们可以利用这些位置关系来解决一些几何难题。
通过观察两个圆的位置关系,我们可以计算圆心的坐标、切点的位置以及两个圆的半径之比等等。
这些计算有助于我们更好地理解圆与圆之间的关系,为我们解决其他几何问题提供了一种思路。
总结起来,圆与圆之间有五种常见的位置关系:相离、外切、相交、内切和同心圆。
通过对这些位置关系的研究,我们可以解决许多实际问题,同时也能够加深对几何学的理解。
无论是在建筑设计中确定位置,还是在日常生活中解决其他难题,几何学的知识都能够帮助我们找到最佳的解决方案。
24.2.3圆和圆的位置关系

判别两圆关系2
2, 若两圆的圆心距
2
d 6, 两圆半径是方程
外离 .
x 5 x 1 0 两根,则两圆位置关系为
o2 (o,4)两圆半径分别是 R 8, r 2, 则 ⊙o 与⊙o2的位置关系为 内含 . 1
需要更完整的资源请到 新世纪教 育网 -
需要更完整的资源请到 新世纪教育网
R
O1
r
d
O2
两圆内切 d=R-r d=R-r 两圆内切 d=R-r 两圆内切
需要更完整的资源请到 新世纪教育网
R
O1
r
dБайду номын сангаас
O2
两圆内含 d<R-r d<R-r 两圆内含 两圆内含 d<R-r
B
·
· · O O
· · O· P
A P P
需要更完整的资源请到 新世纪教 育网 -
圆是轴对称图形,两个圆是否也组成轴对称图形呢?如果能组 成轴对图形,那么对称轴是什么?我们一起来看下面的实验。
从以上实验我们可以看到,两个圆一定组成一个轴 对称图形,其对称轴是两圆连心线。
(5)两圆内含
d=R-r
0≤d<R-r
(r<R)
(r<R)
2、两圆相切,相交时的对称性 如果两个圆相切,那么切点一定在连心线上. 如果两圆相交时,连心线垂直平分公共弦 作业布置
习题24.2第7题,109页 第一题
需要更完整的资源请到 新世纪教 育网 -
圆和圆的位置关系
需要更完整的资源请到 新世纪教育网
两圆外切 d=R+r
r
O1
R
d
圆和圆的位置关系(2019年10月整理)

我们观察一下,两个圆的位置关系和这两个圆的半径有没有关系呢? 如果有关系,那会有什么关系呢?
设⊙O1的半径为R,⊙O2半径为 r, 两圆心O1O2的距离为d,则:
两圆外离
d > R+r
两圆外切
d = R+r
两圆相交
R-r < d < R+r (R ≥ r)
两圆内切 两圆内含
d = R-r (R >r) d < R-r (R>r)
例 1:
如图,⊙O的半径为5cm,点P是⊙O外的一点,OP=8cm。
求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少? (2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?
分析: ⑴ ⊙O和⊙P相外切,此时OP=OA+AP,可推出AP=OP-OA ; ⑵ ⊙O与⊙P相内切,则有OP=BP-OB,可推出BP=OP+OB 。
根据以上条件,分别判断⊙O1和⊙O2有何位置关系?
相 两圆相交:两个圆有两个公共点时,叫做这两圆相交。
切 两圆内切:两个圆有唯一公共点,并且除了这个公共点 外,一个圆上的点都在另一个圆的内部时,叫做这两
个圆内切。 这个唯一的公共点叫做切点。
两圆内含:两个圆没有公共点,并且一个圆上的点都在另一
个圆的内部时,叫做这两个圆内含。
; 沧元图 沧元图小说
动画
两个圆的位置关系 :
外离
外切
相交
内切
内含
同心圆
(内含的特殊形式)
两个圆的五种位置关系:
两圆外离:两个圆没有公共点,并且每个圆上的点都在另一个圆
的外部时,叫做这两个圆外离 。
两圆外切:两个圆有唯一公共点,并且除了这个公共点外,每
个圆上的点都在另一个圆的外部时,叫做这两个圆外切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时设计
教学过程这些位置关系分别是什么.
二、探索圆和圆的位置关系
在一张透明纸上作一个⊙O.再在另一张透明纸上作一个与⊙O1半径不等的⊙O2.把两张透明纸叠在一起,固定⊙O1,平移⊙O2,⊙O1与⊙O2有几种位置关系?
[师]请大家先自己动手操作,总结出不同的位置关系,然后互相交流.
[生]我总结出共有五种位置关系,如下图:
[师]大家的归纳、总结能力很强,能说出五种位置关系中各自有什么特点吗?从公共点的个数和一个圆上的点在另一个圆的内部还是外部来考虑.[生]如图:(1)外离:两个圆没有公共点,并且每一个圆上的点都在另一个圆的外部;
(2)外切:两个圆有唯一公共点,除公共点外一个圆上的点都在另一个圆的外部;
(3)相交:两个圆有两个公共点,一个圆上的点有的在另一个圆的外部,有的在另一个圆的内部;
(4)内切:两个圆有一个公共点,除公共点外,⊙O2上的点在⊙O1的内部;
(5)内含:两个圆没有公共点,⊙O2上的点都在⊙O1的内部.
[师]总结得很出色,如果只从公共点的个数来考虑,上面的五种位置关系中有相同类型吗?
[生]外离和内含都没有公共点;外切和内切都有一个公共点;相交有两个公共点.
[师]因此只从公共点的个数来考虑,可分为相离、相切、相交三种.
经过大家的讨论我们可知:
教学过程
投影片(§3.6A)
(1)如果从公共点的个数,和一个圆上的点在另一个圆的外部还是内部来考虑,两个圆的位置关系有五种:外离、外切、相交、内切、内含.
(2)如果只从公共点的个数来考虑分三种:相离、相切、相交,并且相离
⎧
⎨
⎩
外离
内含
,相切
⎧
⎨
⎩
外切
内切.
三、例题讲解
投影片(§3.6B)
两个同样大小的肥皂泡黏在一起,其剖面如图所示(点O,O'是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP、NP分别为两圆的切线,求∠TPN的大小.
分析:因为两个圆大小相同,所以半径OP=O'P=OO',又TP、NP分别为两圆的切线,所以PT⊥OP,PN⊥O'P,即∠OPT=∠O'PN=90°,所以∠TPN等于360°减去∠OPT+∠O'PN+∠OPO'即可.
解:∵OP=OO'=PO',
∴△PO'O是一个等边三角形.
∴∠OPO'=60°.
又∵TP与NP分别为两圆的切线,
∴∠TPO=∠NPO'=90°.
∴∠TPN=360°-2×90°-60°=120°.
四、想一想
如图(1),⊙O1与⊙O2外切,这个图是轴对称图形吗?如果是,它的对称轴是什么?切点与对称轴有什么位置关系?如果⊙O1与⊙O2内切呢?〔如图(2)〕
教
学
过
程
[师]我们知道圆是轴对称图形,对称轴是任一直径所在的直线,两个圆是否也组成一个轴对称图形呢?这就要看切点T是否在连接两个圆心的直线上,下面我们
用反证法来证明.反证法的步骤有三步:第一步是假设结论不成立;第二步是根据
假设推出和已知条件或定理相矛盾的结论;第三步是证明假设错误,则原来的结论
成立.
证明:假设切点T不在O1O2上.
因为圆是轴对称图形,所以T关于O1O2的对称点T'也是两圆的公共点,这与已知条件⊙O1和⊙O2相切矛盾,因此假设不成立.
则T在O1O2上.
由此可知图(1)是轴对称图形,对称轴是两圆的连心线,切点与对称轴的位置关系是切点在对称轴上.
在图(2)中应有同样的结论.
通过上面的讨论,我们可以得出结论:两圆相内切或外切时,两圆的连心线一定经过切点,图(1)和图(2)都是轴对称图形,对称轴是它们的连心线.
五、议一议
投影片(§3.6C)
设两圆的半径分别为R和r.
(1)当两圆外切时,两圆圆心之间的距离(简称圆心距)d与R和r具有怎样的
关系?反之当d与R和r满足这一关系时,这两个圆一定外切吗?
(2)当两圆内切时(R>r),圆心距d与R和r具有怎样的关系?反之,当d与
R和r满足这一关系时,这两个圆一定内切吗?
[师]如图,请大家互相交流.。
