第三章动量和能量守恒定律
大学物理 第三章 动量守恒定律和能量守恒定律 3-5 保守力与非保守力
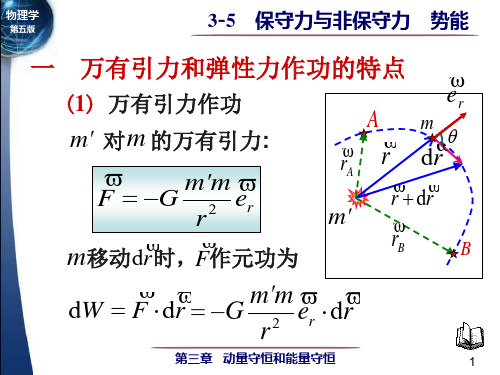
m' m m' m 引力的功 引力的功 WAB = −(−G r ) − (−G r ) B A
A点势能: 点势能: 且令E 设B点为无限远 即rB=∞ 且令 PB=0 点为无限远
m' m WAB = −G rA
= − ( E pB − E pA ) = E pA
功与路径无关,只决定于初末位置。 功与路径无关,只决定于初末位置。 第三章 动量守恒和能量守恒
4
} ⇒ dW
物理学
第五版
3-5 保守力与非保守力 势能 -
F
dW
O
x1
x2
dx
x2 x
W = ∫ Fdx = ∫
x1
x2
x1
1 2 1 2 − kxdx = −( kx2 − kx1 ) 2 2
5
第三章 动量守恒和能量守恒
W p → p0 = −( Ep0 − Ep ) = −∆Ep
E p ( x, y, z) =
∫
E p0 = 0
( x, y,z )
F ⋅ dr
任意一点的势能等于在保守力作用下 从该点到势能零点保守力所作的功
第三章 动量守恒和能量守恒 10
物理学
第五版
3-5 保守力与非保守力 势能 -
W AB = − ( E pB − E pA ) = − ∆ E P
引力的功 引力的功
m' m m' m WAB = −(−G ) − (−G ) rB rA
引力势能 引力势能
m' m Ep = −G r
弹性势能 弹性势能
弹力的功 弹力的功
W AB 1 1 2 2 = − ( kx B − kx A ) 2 2
动量守恒和能量守恒定律

第三章 动量守恒和能量守恒定律§1-1质点和质点系的动量定理一、质点的动量定理 1、动量质点的质量m 与其速度v的乘积称为质点的动量,记为P。
(3-1)说明:⑴P是矢量,方向与v相同⑵P是瞬时量 ⑶P 是相对量⑷坐标和动量是描述物体状态的参量2、冲量牛顿第二定律原始形式)(v m dtd F =由此有)(v m d dt F= 积分:122121p p P d dt F p p t t -==⎰⎰(3-2)定义:⎰21t t dt F称为在21t t -时间内力F对质点的冲量。
记为(3-3)说明:⑴I是矢量⑵I是过程量 ⑶I是力对时间的积累效应 ⑷I的分量式⎪⎪⎩⎪⎪⎨⎧===⎰⎰⎰212121t t z z t t y y t t x x dtF I dt F I dt F I∵⎪⎪⎩⎪⎪⎨⎧=-=-=-⎰⎰⎰212121)()()(121212t t z z t t y y t t x x dtF t t F dt F t t F dt F t t F (3-4)∴分量式(3—4)可写成⎪⎩⎪⎨⎧-=-=-=)()()(121212t t F I t t F I t t F I z zy y x x (3-5)x F 、y F 、zF 是在21t t -时间内x F 、y F 、z F 平均值。
3、质点的动量定理由上知12p p I -=(3-6)结论:质点所受合力的冲量=质点动量的增量,称此为质点的动量定理。
说明:⑴I 与12p p-同方向⑵分量式⎪⎩⎪⎨⎧-=-=-=z 1z 2zy 1y 2y x 1x 2x pp I p p I p p I (3-7)⑶过程量可用状态量表示,使问题得到简化 ⑷成立条件:惯性系⑸动量原理对碰撞问题很有用二、质点系的动量定理概念:系统:指一组质点内力:系统内质点间作用力外力:系统外物体对系统内质点作用力设系统含n 个质点,第i 个质点的质量和速度分别为i m 、i v,对于第i 个质点受合内力为内i F ,受合外力为外i F,由牛顿第二定律有dtv m d F F i i i i )(=+内外对上式求和,有∑∑∑∑======+n1i i i n1i i i n1i i n1i i )v m (dtd dt)v m (d F F 内外因为内力是一对一对的作用力与反作用力组成,故0=合内力F, 有Pdtd F =合外力 (3-8)结论:系统受的合外力等于系统动量的变化,这就是质点系的动量定理。
大学物理动量守恒定律和能量守恒定律

04
动量守恒定律和能量守恒定 律的意义与影响
在物理学中的地位
基础定律
动量守恒定律和能量守恒定律是物理学中的两个基础定律,它们 在理论物理学和实验物理学中都占据着重要的地位。
理论基石
这两个定律为物理学理论体系提供了基石,许多物理理论和公式都 是基于这两个定律推导出来的。
验证实验
许多实验通过验证动量守恒定律和能量守恒定律的正确性,来检验 实验的准确性和可靠性。
适用条件
系统不受外力或外力合力为零
动量守恒定律只有在系统不受外力或外力合力为零的情况下才成立。如果系统受到外力作 用,则总动量将发生变化。
系统内力的作用相互抵消
系统内力的作用只会改变系统内各物体的速度,而不会改变系统的总动量。如果系统内力 的作用相互抵消,则总动量保持不变。
理想气体和刚体的动量守恒
未来能源利用的发展需要解决环 境问题和能源短缺问题,动量守 恒定律和能量守恒定律将在新能 源技术、节能技术等领域发挥关
键作用。
感谢您的观看
THANKS
在理想气体和刚体的研究中,由于气体分子之间的相互作用力和刚体之间的碰撞力都可以 忽略不计,因此它们的动量守恒。
实例分析
弹性碰撞
当两个小球发生弹性碰撞时,根据动量守恒定律,它们碰撞后 的速度满足m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'。由于弹性碰撞中能 量没有损失,因此碰撞前后两小球的速度变化量相等。
动量与能量的关系
动量是质量与速度的乘积,表 示物体的运动状态;能量是物 体运动状态的度量,包括动能
和势能。
动量和能量都是矢量,具有 方向性,遵循矢量合成法则。
动量和能量可以相互转化,但 总量保持不变,这是动量守恒 和能量守恒定律的内在联系。
动量守恒和能量守恒公式

动量守恒和能量守恒公式动量守恒(momentum conservation)和能量守恒(energy conservation)是物理学中两个非常重要的定律。
首先,我们来了解一下动量守恒。
动量是描述物体运动状态的物理量,它是质量(m)乘以速度(v),即p=mv。
根据牛顿第二定律,物体的动量变化率等于作用在物体上的力产生的冲量,即F=dp/dt,其中F是力,dp/dt是动量的变化率。
根据动量守恒定律,当物体间的外力为零时,物体的总动量保持不变。
当有两个物体发生碰撞时,这个系统的总动量在碰撞前后是守恒的。
换句话说,如果一个物体的动量增加,那么另一个物体的动量必然减小,这就是动量守恒的基本原理。
这个原理被广泛应用在各个领域,例如交通事故、运动中的球类运动和飞行器的设计等。
接下来,我们来讨论能量守恒。
能量是物体进行工作或引起变化的能力,是物理系统的基本属性。
根据能量守恒定律,一个系统的总能量在任意时刻都是保持不变的。
能量可以分为各种形式,包括动能、势能、热能等。
动能是物体运动的能量,由于速度和质量的平方成正比。
势能是物体由于位置而具有的能量,如重力势能和弹性势能。
热能是物体内部粒子运动产生的能量。
在一个封闭系统中,能量守恒定律表明,系统的总能量是一个恒定值,一旦系统能量从一种形式转化为另一种形式,总能量保持不变,只是能量在不同形式之间的转化。
例如,考虑一个物体自由下落的情况。
当物体下落时,势能转化为动能。
当物体触地时,物体的动能转化为热能和声能,但总能量不变。
总结一下,动量守恒和能量守恒是物理学中的两个重要定律。
动量守恒表明在一个封闭系统中,系统的总动量在任意时刻都保持不变。
能量守恒表明系统的总能量在各种能量形式之间转化时保持不变。
这些定律在解释和预测物理现象和事件方面起着关键的作用,并在许多领域的科学研究和技术应用中发挥着重要作用。
动量与能量守恒

动量与能量守恒动量和能量是物理学中两个重要的守恒量,它们对于理解和描述各种物理现象都具有重要作用。
本文将介绍动量和能量守恒的概念、原理以及在实际应用中的重要性。
一、动量守恒动量是物体运动中的基本物理量,定义为物体的质量乘以其速度。
动量的大小和方向与物体的质量和速度有关。
当一个物体不受外力作用时,它的动量保持不变,这就是动量守恒的基本原理。
动量守恒定律可以用数学公式表示如下:\[ m_{1}v_{1}+m_{2}v_{2}=m_{1}v'_{1}+m_{2}v'_{2} \]其中,m和v分别代表物体的质量和速度。
这个公式表示了两个物体碰撞前后动量的守恒关系。
根据动量守恒定律,系统内外力的合力为零时,系统的总动量保持不变。
动量守恒在许多物理问题中都有广泛的应用,例如汽车碰撞、弹道学、运动物体的跳跃等。
通过分析动量守恒,可以预测物体运动的轨迹和速度变化。
二、能量守恒能量是物体运动和变化的基本原因,它存在于各种物理系统中。
能量守恒定律指出,在一个封闭系统中,能量既不能被创造也不能被消灭,只能从一种形式转化为另一种形式,总能量保持不变。
能量守恒定律可以用数学公式表示如下:\[ E_{i} = E_{f} \]其中,\(E_{i}\)代表系统的初始能量,\(E_{f}\)代表系统的最终能量。
这个公式表明,在一个封闭系统中,能量总量在时间上保持不变。
能量守恒在物理学中起着重要的作用,它可以解释和预测各种物理现象,例如机械能守恒、热能守恒和化学能守恒等。
通过分析能量守恒,可以计算物体的动能、势能和热能的变化。
三、动量与能量守恒的关系动量和能量守恒是物理学中两个独立但相互联系的概念。
它们在某些情况下可以相互转化,但在大多数情况下是独立守恒的。
例如,在完全弹性碰撞中,动量守恒和能量守恒同时成立。
动量守恒可以用来确定碰撞物体的速度变化,而能量守恒可以用来确定碰撞物体的动能变化。
在这种情况下,动量和能量都守恒,并且可以相互转化。
大学物理第三章-动量守恒定律和能量守恒定律-习题及答案

即:作用在两质点组成的系统的合外力的冲量等于系统内两质点动量之和的增 量,即系统动量的增量。 2.推广:n 个质点的情况
t2 t2 n n n n F d t + F d t m v mi vi 0 i外 i内 i i i 1 i 1 i 1 i 1 t1 t1
yv 2
同乘以 ydy,得
y 2 gdty y
积分 得
y
0
y
gdty
yvdt( yv)
0
1 3 1 gy ( yv) 2 3 2
因而链条下落的速度和落下的距离的关系为
2 v gy 3
1/ 2
7
第4讲
动量和冲量
考虑到内力总是成对出现的,且大小相等,方向相反,故其矢量和必为零, 即
F
i 0
n
i内
0
设作用在系统上的合外力用 F外力 表示,且系统的初动量和末动量分别用
5
第4讲
动量和冲量
P0 和 P 表示,则
t2 n n F d t m v mi vi 0 i i 外力 t1
F外 dt=dPFra bibliotek力的效果 关系 适用对象 适用范围 解题分析
*动量定理与牛顿定律的关系 牛顿定律 动量定理 力的瞬时效果 力对时间的积累效果 牛顿定律是动量定理的 动量定理是牛顿定律的 微分形式 积分形式 质点 质点、质点系 惯性系 惯性系 必须研究质点在每时刻 只需研究质点(系)始末 的运动情况 两状态的变化
1
第4讲
动量和冲量
§3-1 质点和质点系的动量定理
实际上,力对物体的作用总要延续一段时间,在这段时间内,力的作用将 积累起来产生一个总效果。下面我们从力对时间的累积效应出发,介绍冲量、 动量的概念以及有关的规律,即动量守恒定律。 一、冲量 质点的动量定理 1.动量:Momentum——表示运动状态的物理量 1)引入:质量相同的物体,速度不同,速度大难停下来,速度小容易停下;速 度相同的物体,质量不同,质量大难停下来,质量小容易停下。 2)定义:物体的质量 m 与速度 v 的乘积叫做物体的动量,用 P 来表示 P=mv 3)说明:动量是矢量,大小为 mv,方向就是速度的方向;动量表征了物体的 运动状态 -1 4)单位:kg.m.s 5)牛顿第二定律的另外一种表示方法 F=dP/dt 2.冲量:Impulse 1)引入:使具有一定动量 P 的物体停下,所用的时间Δt 与所加的外力有关, 外力大,Δt 小;反之外力小,Δt 大。 2)定义: 作用在物体外力与力作用的时间Δt 的乘积叫做力对物体的冲量, 用 I 来表 示 I= FΔt 在一般情况下,冲量定义为
第三章 动量守恒定律与能量守恒定律

第三章 动量守恒定律和能量守恒定律3-1 一架以12ms 100.3-⨯的速率水平飞行的飞机,与一只身长为0.20m 、质量为0.50kg 的飞鸟相碰。
设碰撞后飞鸟的尸体与飞机具有同样的速度,而原来飞鸟对于地面的速率很小,可以忽略不计。
估计飞鸟对飞机的冲击力,根据本题的计算结果,你对高速运动的物体与通常情况下不足以引起危害的物体相碰后产生后果的问题有什么体会?解:以飞鸟为研究对象,其初速为0,末速为飞机的速度,由动量定理。
vlt mv t =∆-=∆ ,0F 联立两式可得: N lmv F 521025.2⨯==飞鸟的平均冲力N F F 51025.2'⨯-=-=式中的负号表示飞机受到的冲击力与飞机的运动速度方向相反。
从计算结果可知N F F 51025.2'⨯-=-=大于鸟所受重力的4.5万倍。
可见,冲击力是相当大的。
因此告诉运动的物体与通常情况下不足以引起危险的物体相碰,可能造成严重的后果。
3-2 质量为m 的物体,由水平面上点O 以初速为0v 抛出,0v 与水平面成仰角α。
若不计空气阻力。
求:(1)物体从发射点O 到最高点的过程中,重力的冲量;(2)物体从发射点到落回至同一水平面的过程中,重力的冲量。
解:(1)在垂直方向上,物体m 到达最高点时的动量的变化量是:αsin 01mv P -=∆而重力的冲击力等于物体在垂直方向的动量变化量:ααsin sin 0011mv mv P I -=-=∆=(2)同理,物体从发射点到落回至同一水平面的过程中,重力的冲力等于物体竖直方向上的动量变化量αααsin 2sin sin 1222mv mv mv mv mv P I -=--=-=∆=负号表示冲量的方向向下。
3-3 高空作业时系安全带是非常必要的。
假如一质量为51.0kg 的人,在操作时不慎从高空跌落下来,由于安全带保护,最终使他悬挂起来。
已知此时人离原处的距离为 2.0m ,安全带弹性缓冲作用时间为0.50s 。
动量守恒定律和能量守恒定律解析

第三章 动量守恒定律和能量守恒定律概述:1、牛顿第二定律描述了力对物体作用的瞬间关系,物体瞬间获得响应的加速度,物体的运动状态已经开始发生变化,要使物体的运动状态继续变化,需要力的作用有一个过程。
本章从力的空间累积效应和时间累积效应出发,用动量和能量对机械运动进行分析。
2、由对一个质点的研究过渡到质点系的研究。
3、守恒定律是完美、和谐的自然界的体现。
动量守恒和能量守恒源于牛顿力学,但在牛顿定律不适用的领域,例如微观粒子及高能物理领域仍然适用,故它是自然界的一条基本定律。
3-1质点和质点系的动量定理一、 冲量 质点的动量定理牛顿第二定律的微分形式d d t =pF d d t =F p 22112121d t d t t m m ==-⎰⎰p p F p p p =υ-υ1.冲量:力对时间的积分,常以I 表示,并称⎰=21d t t t F I为在1t ~2t 时间内、力F 对质点的冲量,或简单说成F 的冲量。
说明:(1).冲量,是一个矢量,大小为21d t t t =⎰I F ,方向是速度或动量的变化方向。
(2).由于冲量是作用力的时间积分,必须知道力在这段时间中的全部情况,才能求出冲量。
实际上要知道力的大小和方向随时间变化是很困难的,必须采取近似处理。
F 为恒力(方向也不变)时,t =∆I F ;(高中的冲量定义) F 作用时间很短时,可用力的平均值F 来代替。
211d t t t t =∆⎰F F ,21t t t ∆=-2.动量(p )是描述物体运动状态的物理量,有大小和方向,是一个矢量。
方向和运动速度的方向相同。
单位:㎏·m/s量纲:MLT -1。
3.质点的动量定理:在给定的时间间隔内,质点所受合力的冲量,等于该质点动量的增量。
22112121d t d t t m m ==-⎰⎰p p F p p p =υ-υ在直角坐标系中,质点的动量定理的分量形式:212121212121---t x x x xt t y y y y t t z zz zt I F dt m υm υI F dt m υm υI F dt m υm υ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩⎰⎰⎰动量定理在打击和碰撞等情形中特别有用。
大学物理第三章动量守恒定律和能量守恒定律

动量守恒定律的表述
总结词
动量守恒定律表述为系统不受外力或所 受外力之和为零时,系统总动量保持不 变。
VS
详细描述
动量守恒定律是自然界中最基本的定律之 一,它表述为在一个封闭系统中,如果没 有外力作用或者外力之和为零,则系统总 动量保持不变。也就是说,系统的初始动 量和最终动量是相等的。
动量守恒定律的适用条件
能量守恒定律可以通过电磁学 的基本公式推导出来。
能量守恒定律可以通过相对论 的质能方程推导出来。
能量守恒定律的应用实例
01
02
03
04
机械能守恒
在无外力作用的系统中,动能 和势能可以相互转化,但总和
保持不变。
热能守恒
在一个孤立系统中,热量只能 从高温物体传递到低温物体,
最终达到热平衡状态。
电磁能守恒
详细描述
根据牛顿第三定律,作用力和反作用力大小相等、方向相反。如果将一个物体施加一个力F,则该力会产生一个 加速度a,进而改变物体的速度v。由于力的作用是相互的,反作用力也会对另一个物体产生相同大小、相反方向 的加速度和速度变化。因此,在系统内力的相互作用下,系统总动量保持不变。
02
能量守恒定律
能量守恒定律的表述
感谢观看
01
能量守恒定律表述为:在一个封闭系统中,能量不能被创造或消灭, 只能从一种形式转化为另一种形式。
02
能量守恒定律是自然界的基本定律之一,适用于宇宙中的一切物理过 程。
03
能量守恒定律是定量的,可以用数学公式表示。
04
能量守恒定律是绝对的,不受任何物理定律的限制。
能量守恒定律的适用条件
能量守恒定律适用于孤立系统,即系统与外界没有能量 交换。
大学物理 第三章 动量守恒定律和能量守恒定律 3-9 质心 质心运动定律
第五版
3-9 质心 -
质心运动定律
一 质心
1 质心的概念
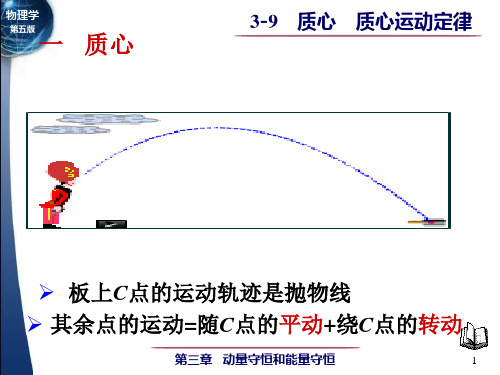
板上C点的运动轨迹是抛物线 板上 点的运动轨迹是抛物线 其余点的运动=随 点的平动+绕 点的 点的平动 点的转动 其余点的运动 随C点的平动 绕C点的转动
第三章 动量守恒和能量守恒
1
物理学
第五版
3-9 质心 -
质心运动定律
2 质心的位置 由n个质点组成 个质点组成 的质点系, 的质点系,其质心 的位置: 的位置:
13
物理学
第五版
3-9 质心 n n v v v m'vC = ∑ mi vi = ∑ pi = p i =1 i =1
质心运动定律
求一阶导数, 再对时间 t 求一阶导数,得
质心加速度
dp v m'aC = dt v v dp ex 根据质点系动量定理 = Fi dt
第三章 动量守恒和能量守恒
}⇒
x2 = 2 xC
17
第三章 动量守恒和能量守恒
物理学
第五版
3-9 质心 -
质心运动定律
例4 用质心运动定律 y F 来讨论以下问题. 来讨论以下问题. 一长为l 一长为 、密度均匀的 y 柔软链条, 柔软链条,其单位长度的质 c yC 量为 λ .将其卷成一堆放在 地面. 若手提链条的一端, 地面. 若手提链条的一端, o 以匀速v 将其上提.当一端 以匀速 将其上提. 被提离地面高度为 y 时,求手的提力. 求手的提力.
竖直方向作用于链条的合外力为 F − λyg
第三章 动量守恒和能量守恒
20
物理学
第五版
3-9 质心 -
质心运动定律
v 得到 F − yλg = lλ ⋅ l
动力学的基本定律质点系统的动量守恒与动能守恒

动力学的基本定律质点系统的动量守恒与动能守恒动力学的基本定律:质点系统的动量守恒与动能守恒动力学是研究物体运动的力学分支,通过运用基本定律来描述和解释物体运动的规律。
在动力学中,有两个重要的定律,即动量守恒定律和动能守恒定律。
本文将详细介绍这两个定律以及它们在质点系统中的应用。
一、动量守恒定律动量是物体运动的重要属性,定义为物体的质量乘以其速度。
动量守恒定律表明,在没有外力作用的情况下,质点的动量保持不变。
具体而言,对于一个孤立系统(也称为自由系统),质点在相互作用力的作用下,其动量的代数和保持不变。
这意味着在系统内发生的各种碰撞和相互作用过程中,质点的总动量始终保持不变。
动量守恒定律可以用数学表达式表示为:∑m1v1 = ∑m2v2其中,m1和m2分别是碰撞或相互作用前后各个质点的质量,v1和v2分别是其对应的速度。
通过使用动量守恒定律,可以推导出各种碰撞类型(如弹性碰撞和非弹性碰撞)的动量守恒方程式。
二、动能守恒定律动能是物体运动的能量形式,定义为物体的质量乘以速度的平方的一半。
动能守恒定律表明,在没有非弹性碰撞和其他形式的能量转化的情况下,质点的总动能保持不变。
同样地,对于一个孤立系统,质点在相互作用力的作用下,其总动能保持不变。
这意味着在碰撞和相互作用中,质点的动能可以从一个物体转移到另一个物体,但是系统的总动能保持不变。
动能守恒定律可以用数学表达式表示为:∑(1/2)mv1^2 = ∑(1/2)mv2^2其中,m为质点的质量,v1和v2为其相应的速度。
通过使用动能守恒定律,我们可以推导出各种碰撞类型(如完全弹性碰撞和部分非弹性碰撞)的动能守恒方程式。
三、质点系统中的定律应用在质点系统中,动量守恒定律和动能守恒定律都可以用来解释和描述质点之间的相互作用。
比如,在多个质点组成的系统中,当发生碰撞或相互作用时,动量守恒定律可以帮助我们计算各个质点的速度变化。
例如,考虑两个质点A和B之间的弹性碰撞。
大学物理第三章动量守恒定律和能量守恒定律

探索其他守恒定律
鼓励了对其他守恒定律的探索,如角动量守恒定律、电荷守恒定律等。
THANKS
感谢观看
探索性实验:动量与能量的关系研究
实验目的
研究动量与能量的关系,探索两者之间的联系和 区别。
实验步骤
选择合适的实验器材,如弹性碰撞器、非弹性碰 撞器等,设计不同的碰撞条件,记录实验数据。
实验原理
动量和能量是描述物体运动状态的物理量,两者 之间存在一定的关系。通过研究不同运动状态下 物体的动量和能量变化,可以深入理解两者之间 的关系。
05
实验验证与探索
动量守恒定律的实验验证
实验目的
通过实验验证动量守恒定律, 加深对动量守恒定律的理解。
实验原理
动量守恒定律指出,在没有外 力作用的情况下,系统的总动 量保持不变。
实验步骤
选择合适的实验器材,如滑轨、 滑块、碰撞器等,按照实验要求 进行操作,记录实验数据。
实验结果
通过分析实验数据,验证动量 守恒定律的正确性。
动量守恒定律的应用实例
总结词:举例说明
详细描述:应用动量守恒定律的实例包括行星运动、碰撞、火箭推进等。例如,在行星运动中,行星绕太阳旋转时动量守恒 ;在碰撞过程中,两物体相互作用时的动量变化遵循动量守恒定律;火箭推进则是通过燃料燃烧产生高速气体,利用反作用 力推动火箭升空,这一过程中动量守恒。
03
守恒定律的意义
强调了守恒定律在物理学中的重要地位,以及在解决实际问题中的应 用价值。
对动量守恒定律和能量守恒定律的思考
守恒的哲学思考
探讨了守恒定律在哲学上的意义,以及它们 对宇宙观的影响。
动量与能量的守恒定律

动量与能量的守恒定律动量守恒定律和能量守恒定律是物理学中两个基本的守恒定律。
本文将从概念、原理和应用等方面阐述动量与能量的守恒定律。
一、动量守恒定律动量是物体运动的量度,与物体的质量和速度有关。
动量守恒定律指出,在没有外力作用时,一个系统的总动量保持不变。
动量守恒定律的数学表达式为:对于一个孤立系统,其初态和末态动量之间的差等于系统内部作用力的冲量。
动量守恒定律可以应用于众多实际问题,例如碰撞、爆炸等。
在碰撞问题中,如果系统内部没有外力作用,那么两个物体的总动量在碰撞前后保持不变。
这意味着一个物体的速度增加,另一个物体的速度必然减小。
二、能量守恒定律能量是物体或系统进行工作或产生热的能力。
能量守恒定律指出,在一个封闭系统中,能量不会凭空产生或消失,只会从一种形式转化为另一种形式。
能量守恒定律的数学表达式为:对于一个封闭系统,其初态和末态的能量之差等于系统所做的功与系统所接受的热之和。
能量守恒定律适用于各种能量转化的过程,包括机械能转化、热能转化和化学能转化等。
例如,一个物体从高处自由下落,其势能逐渐转化为动能,而且在空气阻力下逐渐转化为热能。
三、动量守恒与能量守恒的关系动量守恒和能量守恒是物理世界中两个独立而又相互关联的守恒定律。
动量守恒定律和能量守恒定律都描述了物理系统在各种变化中某一物理量的守恒情况,但两者关注的物理量不同。
动量守恒侧重于物体的运动状态,而能量守恒则侧重于物体的能量变化。
在某些情况下,动量守恒和能量守恒可以相互影响和转化。
例如,在完全弹性碰撞中,动能守恒和动量守恒同时适用。
在这种碰撞中,物体之间没有能量损失,同时总动量也保持不变。
四、应用举例动量守恒和能量守恒定律在实际问题中有广泛的应用。
下面以两个具体例子作进一步说明。
例一:弹性碰撞考虑两个质量分别为m1和m2的物体碰撞的情况。
由于没有外力作用,根据动量守恒定律,我们可以得到:m1v1i + m2v2i = m1v1f + m2v2f其中,m1v1i和m2v2i分别表示碰撞前两个物体的动量,m1v1f和m2v2f表示碰撞后两个物体的动量。
第3章-动量守恒定律和能量守恒定律

质点的位移在力方向的分量和力的大小的乘积。
dW
F
cos
dr
F cos
ds
dW F dr
B
*
0 90, dW 0 90 180 , dW 0
dr
*A
F
90 F dr dW 0
20
3-4 动能定理
• 变力的功
W
B F dr
B
F
cos
ds
A
A
dri
i
B
*
端 , 绳的上端固定在天花板上 . 起初把绳子放在与竖
直线成 30 角处, 然后放手使小球沿圆弧下落 . 试求
绳解与: 竖d直W线成F
10角时 小球 的速率 d s FT d s P d s
.
P d s mgl d cos
mgl sin d
W mgl sin d 0
mgl (cos cos0 )
I
t2 t1
Fdt
p2
p1
mv2
mv1
问:冲量是矢量,它的方向就是力的方向吗 ?
分量形 式 I Ixi Iy j Izk
单位和量纲 1N·s = 1kgm/s dimI = M·L-1·T-1
Ix
t2 t1
Fxdt
mv2 x
mv1x
I y
t2 t1
Fydt
mv2 y
mv1y
Iz
14
3-2 动量守恒定律
例 1 设有一静止的原子核, 衰变辐射出一个电子和一
个中微子后成为一个新的原子核. 已知电子和中微子的
运动方向互相垂直, 电子动量为1.210-22 kg·m·s-1,中微
子的动量为 6.410-23 kg·m·s-1 . 问新的原子核的动量的
大学物理-第三章-动量守恒定律和能量守恒定律

20
★一对作用力与反作用力的功只与相对位移有关
f ji
ri
f ij
rij
rj
0
dW
jidWij
f
ji
dri
fij drj
f ji fij
fji f ji
(dd(rriidrrjj))
f ji
drij
S
S u
动量的相 对性和动量定 理的不变性
F(t)
t1 m
v1
光滑
v 2
m t2
参考系 t1 时刻 t2 时刻
动量定理
S系
S’系
mv1
mv2
m(v1 u) m(v2 u)
t2 t1
F (t )dt
mv2
mv1
5
例3-1: 作用在质量为1kg 的物体上的力 F=6t+3,如果物体在这
0=m1(v1+v2)+m2v2
v2
m1v1 m1 m2
x
t 0
v2dt
m1 m1 m2
t 0
v1dt
L
t
0 v1dt
x m1L 0.8m m1 m2
负号表示船移动的方向与人前进的方向相反。
17
3-4 动能定理
一、功的概念(work) 功率(power) 1、恒力的功
2、动能定理
2
1
或
F
dr
F
dr
1 2
mv22
大学物理动量守恒定律和能量守恒定律

注意:
1、计算势能必须规定零势能参考点。势能是相对量, 其量值与零势能点的选取有关。
2、势能函数的形式与保守力的性质相关,对应于一种 保守力的函数就可以引进一种相关的势能函数。
3、势能是属于以保守力形式相互作用的物体系统所共 有的。
第三章 动量守恒定律和能量守恒定律
守恒定律
动量守恒定律 机械能守恒定律 能量守恒定律
物理学大厦 的基石
3-1 质点和质点系的动量定理
一、冲量 质点的动量定理
F dpd(mv) dt dt
牛顿第二定律 动量 pm v
F d td pd(m v)
I t 1 t2 F d t p p 1 2 d p p 2 p 1 m v 2 m v 1
vv 21 vv 2m m 1v 1 rvm r 23 .1 2 7 .1 71 0 1 3 0m 3m /s /s
3-4 动能定理
一、功、功率
1、功
r
i
F
B
i
恒力功: W F s c o s F s
变力功
A
元功:
d W Fd r
取得有限位移 W dW r2Fdr r1
冲量: I t2 Fdt t1
力对时间的累积效应
作用于物体上的合外力的冲量等于物体动量的增量
——质点的动量定理
分量表示式
t1t2FxdtIx mv2xmv1x t1 t2FydtIymv2ymv1y t1t2FzdtIz mv2zmv1z
问题:动量增量方向?
o v0
x
冲量的方向?动量增量的 方向,一般与力的方向不一致。
功的单位:焦耳(J)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: 人和车组成的质点系,水平
方向不受力,动量守恒。
? ? L ?
tr u (t )dt
x?
tr v (t )dt
0
0
初态动量 p0 ? 0
? r
u(t) r v(t)
L0
x
末态动量 p ? Mv ? m(v ? u)
v? m u M?m
? ? x ?
t
r v (t ) dt
?
t
m
udt ?
mL
0
0M?m
计算力对物体做功时
必功须率说明P 是? 哪dW个力对P物?体F沿c哪os条?路d径rr ?所F做c的o功s?。v
dt
dt
P
?
r F
?vr
二、动能定理
? W合 AB ?
?
B A B
v F合
?drv
v F合
m dvv ?drv ?
? mav ? m dvv dt
m B (dvv) ?vv
21 代入
? ? ?
平速度 u 跳车 求:(1)同时跳后车速 v车=?
(2)一个一个跳后车速 v车=? 解:
r u m
无摩擦
M vr
x
相对同一惯性参考系“地面”列动量守恒式
(车和人系统水平方向不受外力)
(1) Mv 车对地 ? 2 mv 人对地 ? 0
v人对地 ? -u + v车对地
v1 ? v车对地
?
2m u
M ? 2m
u
dm
火箭质量变为M-dm,对地速度为 v? ? dv? (t)
(t ? dt)
动量守恒
Mv ? dm(v ? dv? u) ? (M ? dm)(v ? dv)
喷出气体的质量等于火箭质量的减少量,dm ? ? dM
Mv? dm(v ? dv ? u) ? (M ? dm)(v ? dv) dm ? ? dM15
——系统受到的合外力等于
系统动量对时间的变化率。
i? j, j?1
这就是质点系 的牛顿第二定律 系统只有一个质点时为
? ? ? 质点系Ft1tv2外F的v合?外动dt?d量?t ?定dprpr理2 ?
r p1
?
i
v mivi2
?
中F?学外v所? 学d形(dm式t v?:) ?
? ma
mivi1
i
内力能使系统内各个质点的动量发生改变,但它们对系统的
2
一、冲量 质点的动量定理
v F外
?
dpv dt
?
r
d (mv) ?
dt
r ma
考虑力的时 间积累效应
力的时间积累 力的冲量
质点的动量定理:
动量定理是牛顿
第二定律变形。
v F外
?dt
?
dpv
动量定理微分形式
质点受合外力的冲量等于同一时间内该质点动量的增量。
t2
? ? t1
v F合外?dt
v
? ? 冲量 I ?
n
? ? ? ? Wi外 ?
Wi内 ?
E ikB ?
E ikA
i?1
i?1
i?1
i?1
所有外力对质点系做的功和内力对质点系做的功之和等于质
mu M ?m
v1 ? v车对地
?
2m u
M ? 2m
v 2 ? v1
3-3* 系统内质量移动问题
14
选地面作参照系 选向上为正向
(1它) 们t 时对刻地:的火速箭度+为燃料v? = M
v
v? dv M? dm
M
(2)v经 dt 时间后,质量为dm的燃料喷出
u 称为喷气速度
(喷出燃料相对火箭速度)
?
t2 t1
p2 dvp ? vp1 F合外 ?dt
v p2
?
v p1
v I合外力 ?
pv2
?
pv1
t2 t1
v F合外?dt
?
v mv2
?
v mv1
动量定理 积分形式
冲击力下
F
3
? v
I?
t2
v Fdt
?
v F?t
v t1
F
F
v F?
? t 时间内的平均力
v I
?
v p2
?
v p1
? ? t
r I合外力 ?
v 2. v ? ln M0 , M0 大
大
MM
这对燃料的携带来说不合适,用多级火箭可避免这一困难。
火箭在燃料燃烧时所获推力
17
以喷出的气体dm为研究对象,它在dt 时间内的动量变化率为
dm?(v ? dv ? u) ? v?? ? u dm 由牛二定律,该变化率即为喷
dt
dt 出气体所受推力,有
总动量没有任何影响。
? ? 3-2 动量守恒定律
当系统所受的合外力为
r dp ? 0
或
r p
?
dt
v 0, 即 F外 ? 0
v F外
?
r dp dt
v pi
?
mivvi ? 常矢量
i
i
7
当一个 质点系 受的合外力为零时,该系统总动量保 持不变。
动量守恒定律
分量式
8
当 Fx=0,则 px= 恒量
即 m1v1x ? m2v2x ? ? ? mivix ? ? ? 恒量
dm
dt
v F外
当
当 当
? d ?mvv ??
u?
?
dt
0
uvrv???00
uv?dm d?t
F外
? F外 v F外
? m dv? ? ma?
?
dt
d ?m
v?
?
dt
?
?
r u
dm
dt
3-4 动能定理
一、功
v ? Fdrv
19
1.物dW体作?直F线c运os动?,?|恒d力rv |做? 功Fr
?drv?
3.质点系的动能定理
23
对n个质点组成的质点系: 每个质点分别使用动能定理
m1: W1合 ? W1外 ? W1内 ? E1kB ? E1kA
m2: W2合 ? W2外 ? W2内 ? E 2 kB ? E 2 kA
……………
mn:
n
Wn合 ? Wn外 ? Wn内 ? E nkB ? E nkA
n
n
t2 t1
t2v? t1 F合外 ?dt
?
v p2
?
v p1
O t1
矢量式
?t
t2 t
? Ix ?
t2 t1
Fx
?dt
?
px2
?
px1
? Iy ?
t2 t1
Fy ?dt ?
py2
?
py1
?t 2
Iz ? t1 Fz ?dt ? pz2 ? pz1
逆风行船
v f船对风 ??t
?
pv2
?
pv1
?
? pv
M?m
例2.桌面有一小孔质量M的软绳,软绳下垂部分的长度为lo, 10 放手绳子下落,求:t 时刻下垂长度为y 时绳子下端的速率。
解:研究对象:整条绳子
设 t 时刻绳下垂质量为m,桌面质量为M- m,
桌面绳受重力和支持力相互抵消,由动量定理
mg ? d[(M ? m) ?0 ? mv] ? d (mv)
当 Fy=0, 则 Py= 恒量
即 m1v1y ? m2v2 y ? ? ? miviy ? ? ? 恒量
当 Fz=0, 则 Py= 恒量
即 m1v1z ? m2v2z ? ? ? miv3z ? ? ? 恒量
讨论
1.当某一方向外力为零时该方向动量守恒,
2.当内力 >> 外力时,动量守恒。
例1.人质量m,站在质量M,长度L的小车上。小车开始时 9 静止,地面光滑。 求:人从车的一端走到另一端时,车移动的距离。
相当于4000 吨海轮所受浮力!
动量定理与牛顿定律 (以火箭为例受推力)F ? u dm 18
火由F箭v外u受v?力?muvd?dv?tvFv?外vv??uv得uv??ddmvvt ??ddmmt
dvv dt
?m
v F外
dvv ? dt
? m dvv ? uv dt
dm
v v
?
uv?dm
dt
dt
dt
r u
m
M vr13
(2)
无摩擦
x
( M ? m ) v车对地 1 ? mv 人对地 ? 0
v人对地 ? - u + v车对地 1
v车对地
1?
M
mu ? 2m
Mv 车对地 2 ? mv 人对地 ? ( M ? m ) v车对地 1
v人对地 ? - u + v车对地 2
v2
?
v 车对地
2
?
M
m u? ? 2m
B A
v F合
?drv
2.质点的动能定理
W合 AB
?
E kB
?
E kA
?
? Ek?
1 2
mv
2 B
?
1 2
mv
2 A
合外力 对质点 所做的功 (其它物体对它所做的总功)等于 质
点动能的增量。
3.讨论:
(1)功是标量,反映了能量的变化。
(2)功是过程量,某一时刻的功没有意义。
(3)功是相对量,与位移和参考系的选择有关。
v
