数字推理题的解题技巧大全
数字推理答题技巧(公开版)

数字推理答题技巧施久亮解题突破五大要诀――抓住数列的阿喀琉斯之踵一、先加减,后乘除,根据数字大小变化的规律判断属于何种数列类型1、数字快速增减的2、数字平稳增减的3、数字高低起伏的4、数字非常接近的二、分析项数,确定关键项,注意项与项之间关系,注意数列的级数(确定是几项关联、几级数列或组合还是间隔)1、项数低于或等于5项的2、项数为6项的3、项数大于6项的4、项数超多的三、抓住关键项,分析敏感数字1、平方数、立方数及其相邻数2、0、1及其相邻数以及常见变化3、基本数列4、分数题注意通分后的变化,关注小分子分母项四、找准起步点1、特别注意1、2项之间的关系五、寻找薄弱环节,确定关键数字,一举突破1、数列的不和谐部分、与众不同部分2、敏感数字,如0或1及其附近数3、从选项中找突破口基本功练习一、心算练习二、数字基础三、熟练基本数列四、中央及浙江真题练习数字推理基础一、基本数列(加减乘除)1、加减法数列差的几种形式:等差(常数):3例1:2 5 8 11 14自然顺序数:1、2、3、4、5例1:2 3 5 8 12 17平方数或立方数例1:5 6 10 19 45 70加减法单项数列1、2、3、4、5加减法双项数列2 3 5 8 13 21 例1:56,79,129,202,325 ()例2:3,-1,5,1,()A.3B.7.C.25D.64加减法三项数列例1:1 2 4 7 13 24 ()例2:1 4 3 5 2 6 4 7 ()2、乘除法数列乘除法单项数列乘除法双项数列例1:3,4,12,48,()A 96B 36C 192D 5763、加减法和乘除法混合数列例1:16 17 36 111 448 ( )例2:5,( ),39,60,105.A.10B.14C.25D.30例3:-2 ,-1, 1, 5 () 29A.17B.15C.13D.11例4:172,84,40,18,()例5:-1,0,1,2,9,()A.11B.82C.729D.730例6:3, 7, 16, 107,()A.1707B.1704C.1086D.1072二、数列的组合和延伸一级数列二级数列三级数列间隔组合数列分段组合数列对称组合数列三、题目类型1、单项数列例1:27 16 5 ()1/7例2:1\7 1\26 1\63 1\124 ( )例3:-1,0,27,()。
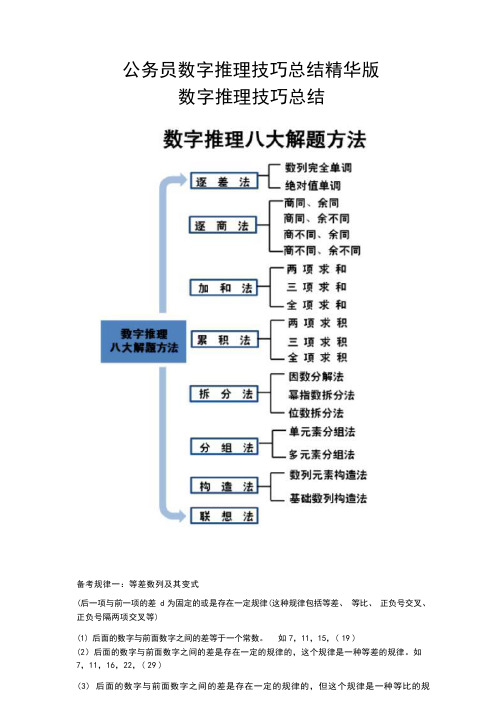
数字推理八大解题方法

数字推理八大解题方法逐差法:指原数列相邻两项逐级做差。
、逐商法是指原数列相邻两项逐级做商,进而推出数列规律的方法。
对于单调性明显,倍数关系明显或者增幅较大的数列,应当优先采用逐商法。
其中,单调性明显,即可以表现为通常意义上所指的单调性,也可以表现为正负交替出现,但是绝对值具有单调性。
使用逐商法之后,需要重点注意做商后得到的商值数列和余数数列的规律。
根据其表现形式的不同可以分为如下四种情况:商同、余同,商同、余不同,商不同、余同和商不同、余不同。
【核心矢口识】商同、余不同是指对原数列做商后得到的商信歡列为當数列,於救刃则呈现出一定的亲见障.其中,杀数数列可以是當见的基就敌列,也可以是基刊数列的变形.乩闾不同、冷同【核心知识】崗不同、金同罡指对原煎列徴裔后得到册發数数列淘常第勿裔值数列则呈现出一定的规律•其中裔值数列可収是常见的基础数列•也可以是基础数列的变形.【核心知识】丽同余雨是指賤列噓后輕胸商数列和余狀不是常敎列,各白呈现出某沖规律耳口商值数列和余数数列即可漩常见谑臟称也可以是基臓列的变啟【按I阑识】加和法是指对碟数列进匸求利从而得到数叨规律胶方丸对于(1}負關关系不胡呈;住倍葩关系不朋显;(3擞字差别幅度不犬的数列;应勃诜使用兀和扯-对于符细]和法奠用原則的数列,优;先对其进行匹项求和,两项求和后无日胆规萍时,再对其进行三互哀和阪全项求和.【核硼】两项求和,是指对原数列相緬项进行逐次求和,从而得到数列的规衛具中,得到的和值数列既可以是基鹼列,也可以是与殿列相关B®列.【檢谀识]三或乩是指対质数列馆邻三龜行逐玄沏9从而得到数列的规淳【核谀识】全项求和,是指依次对软列每-项之前的所有赃行求和,从而得到数列的规律.【核心知识】累枳法是指求取融列各项的乘积,进而得到数列规律的方法•对于(1庠调关系明显;(2賂数关系明显;(3蘇积倾向册数列;应该优先采用累积法•对干符合累积法使用觌的数列,优删船砸项求积,两项求躺元明魏律时,再对其进行三项求积以能项求积.【核悯识】两匝求积,是指逐谀求取原数列相邻两项的乘积,从而得到数列的规律•乘积后得到的数列既可以是基础数列,也可以是与原数列相关的数列.L三銅【骯赧】三顶求和是指徹桶藤则E邻三项娠祝从碉驗列帧箒【核朋识】全项求积,是指依次求顋数列每-项之前的所有项的乘积,从而得到数船规律.【松沁】拆分法是指将数列的甸项分解成两韶分或考多部分的乘积或加和的形轧根据分解后的各部分对应元養之间的规律来寻求数列关系的方法.具中,在公务员考翩字推理部分常黜讖拆分法和位数拆分法.【帥识】因数分解法,是指对霖列中的每一个元素都由因数分解将其分解为两琳通过分析分【核心知识】对于具有明显指数特征(基于数字敏感和数形敬感)或看幅度变化校快的数列,优先考解霜指数拆分法,将其化为多次方式aXb-+加如22 = 2X3*4)的形式,通过寻a、b、m、n 之间的关系进行求解•拆分时主要是绕多次方数的和、差、倍数的形式展的,通常数列中会有两个或多个指数特征非常明显怖数字,一般都是以这些数字为突破口的数字推理部分而言,在使用该方法时,主要从以下两个方面进行考虑.数列的各顼均与基础的多欢方敦比做近对于数列中各项均与基础的多次方数比较接近的题U,解题的关键是首先要确定出修m的变化规律•所谓基础凶多次方数,即可以化为扩形式的数字.【核心知识】位数拆分法,解思义,就是指将狮原数列每一项的数字分拆成若干纵通过拆分后各酬应数字之间的规律来寻求原数列规律的方法•对于多位数(位数不少于三位)酸出现’或馥列的幅度觌无明显规律的数列,可以考虑使用位数拆分法•拆分后,各软i应数字之间的关系一腿过加和或看倍姒系表则来.【核测】分组法,解思义,就是将原数列按照-定K)分组方式分为两部分或多盼,根据分组后各那分内部或各部分之间的关系来推求数列关系的一种方法。
行测数字推理题技巧

行测数字推理题技巧
1.规律分析:首先看给出的数字序列是否存在其中一种规律,例如递增、递减、交替等。
通过观察规律,可以将下一个数字或者数字序列进行
推理。
2.数字运算:在数字推理题中,经常出现的是数字的运算关系。
可以
通过加减乘除等简单的运算符号,对给出的数字进行运算,从而得出新的
数字或者数字序列。
3.数字特征:观察给出的数字是否有一些特殊的特征,例如是否为质数、完全平方数、斐波那契数列等,可以通过这些特征进行逻辑推理。
4.数字拆分:有些数字推理题给出的数字较大,可以将其拆分成小的
数字,然后再进行运算或者找规律。
5.条件限制:有些数字推理题在给出的数字序列中存在一些限制条件,例如数字的位数、数字之间差距等。
可以通过这些限制条件进行推理。
6.平均数:在有些数字推理题中,给出的数字序列的平均数可能有特
殊的含义,通过计算平均数,可以得到下一个数字或者数字序列。
7.数字替换:有些数字推理题中,给出的数字序列中存在一些数字可
以进行替换,通过替换数字,可以发现其中一种规律。
公考数字推理攻略汇总
公务员数字推理技巧总结精华版数字推理技巧总结备考规律一:等差数列及其变式(后一项与前一项的差 d 为固定的或是存在一定规律(这种规律包括等差、等比、正负号交叉、正负号隔两项交叉等)(1) 后面的数字与前面数字之间的差等于一个常数。
如7,11,15,( 19 ) (2)后面的数字与前面数字之间的差是存在一定的规律的,这个规律是一种等差的规律。
如7,11,16,22,( 29 )(3)后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种等比的规律。
如7,11,13,14,( 14.5 )(4)后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号进行交叉变换的规律。
【例题】7,11,6,12,( 5 )(5) 后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号每“相隔两项”进行交叉变换的规律。
【例题】7,11,16,10,3,11,(20 )备考规律二:等比数列及其变式(后一项与除以前一项的倍数 q 为固定的或是存在一定规律(这种规律包括等差、等比、幂字方等)(1)“后面的数字”除以“前面数字”所得的值等于一个常数。
【例题】4,8,16,32,( 64 )(2)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数加1。
【例题】4,8,24,96,( 480 )(3)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数乘 2【例题】4,8,32,256,( 4096 )(4)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数为 3 的n 次方。
【例题】2,6,54,1428,( 118098 )(5)后面的数字与前面数字之间的倍数是存在一定的规律的,“倍数”之间形成了一个新的等差数列。
【例题】2,-4,-12,48,(240 )备考规律三:“平方数”数列及其变式(an=n2+d,其中d为常数或存在一定规律)(1) “平方数”的数列【例题】1,4,9,16,25,36 ,49,64,81,100,121,144,169,196(2)每一个平方数减去或加上一个常数【例题】 0,3,8,15,24,(35 )【例题变形】2,5,10,17,26,(37 )(3) 每一个平方数加去一个数值,而这个数值本身就是有一定规律的。
数字推理之解题技巧(精华版)

数字推理之解题技巧(精华版)(1)等差,等比这种最简单的不用多说,深一点就是在等差,等比上再加、减一个数列,如24,70,208,622,规律为a*3-2=b(注:a、b为前后数)(2)深一层次的,①各数之间的差有规律,如 1、2、5、10、17。
它们之间的差为1、3、5、7,成等差数列。
这些规律还有差之间成等比之类。
②各数之间的和有规律,如1、2、3、5、8、13,前两个数相加等于后一个数。
(注:前一就是高中数学常说的差后等差数列或等比数列)(3)看各数的大小组合规律,作出合理的分组。
如 7,9,40,74,1526,5436,可以划分为7和9,40和74,1526和5436三组,这三组各自是大致处于同一大小和位数级别,那规律就要从组方面考虑,即不把它们看作6个数,而应该看作3个小组。
而组和组之间的差距不是很大,用乘法就能从一个组过渡到另一个组。
所以7*7-9=40 , 9*9-7=74 ,40*40-74=1526 ,74*74-40=5436,这就是规律。
(4)如根据大小不能分组的,①,看首尾关系,如7,10,9,12,11,14,这组数 7+14=10+11=9+12。
首尾关系经常被忽略,但又是很简单的规律。
②,数的大小排列看似无序的,可以看它们之间的差与和有没有顺序关系。
(5)各数间相差较大,但又不相差大得离谱,就要考虑乘方,这里就要看各位对数字敏感程度如何了。
如6、24、60、 120、210,感觉它们之间的差越来越大,但这组数又看着比较舒服(个人感觉,嘿嘿),它们的规律就是2^3-2=6、3^3-3=24、4^3-4=60、5^3-5=120、6^3-6=210。
(注意,这组数比较巧的是都是6的倍数,大家容易导入歧途。
)6)看大小不能看出来的,就要看数的特征了。
如21、31、47、56、69、72,它们的十位数就是递增关系;如 25、58、811、1114 ,这些数相邻两个数首尾相接,且2、5、8、11、14的差为3;如论坛上fjjngs所解答的一道题:256,269,286,302,(),2+5+6=132+6+9=17 2+8+6=16 3+0+2=5,∵256+13=269 269+17=286 286+16=302 ∴下一个数为302+5=307。
数字推理九大解题法

目前总结了九大种方法,解数字推理问题最关键的是第一步,大部分人的做题习惯是:如果一眼看不出规律,首先会选择前后项做差的方法,来判断差之间的关系。
而事实上我在总结的过程中也发现,利用做差关系来命题占了很大一部分。
诸如此类的规律在解题当中很有帮助!本文主要列举一些例子,总结一些方法,希望能给各位起到抛砖引玉的作用,大家一起总结规律。
数字推理第一步解题法一、做差3,5,8,13,20,做差得到:2,3,5,7,11为质数34,47,62,79,98,(做差得到:13,15,17,19,21 等差-5,1,8,16,(25)做差得到:6,7,8,912,13,17,26,42,(67)做差得到:1,4,9,16,2522,17,23,20,28,27,(37)做差得到:5,-6,3,-8,1,-10 奇偶分开1,3,5,7,8,(10)两个一组做差是21,4,7,19,40,()做差跟前项比较3*1+4=7,3*4+7=19,3*7+19=40,3*19+40=9712,18,24,33,45,()12/2+18=24,18/2+24=33,24/2+33=45,33/2+45=61.55,6,8,10,14,(19)A.16 B.18 C.19 D.20C-A=3,4,6,9 隔项差,二次等差4,11,31,64,110,(169)做差得到:7,20,33,46,(59)做差得到:13,13,13,13456,567,678,789,(900)A8910,B. 890 C. 900 D.989做差得到:111,111,111,1112. 3,7,22,45,() A.58 B.73 C.94 D.116三级等差数列45+28=73二、分解各项因式8,12,16,18,20,(除以2得到:4,6,8,9,10,12素数2,12,36,80,()2*1,3*4,4*9,5*16,6*25=1500,4,18,48,100,()0*1,1*4,2*9,3*16,4*258,18,40,63,110,()A.140 B.144 C.150 D.1562*4=8,3*6=18,5*8=40,7*9=63,11*10=110,13*12=156质数*素数7,8,9,24,100,(216)A.190 B.216 C.153 D.200能被1,2,3,4,5,6整除1,24,135,448,() A.1125 B 1104 C 1060 D 985被1 8 27 64 125 整数三、A+B=C4,3,7,10,178,7,5,2,7,(9)A+B取个位得到C1,1,3,5,11,(21)1*2+1=3,1*2+3=5,3*2+5=11,5*2+11=21四、A+B+C=D1,0,2,3,5,10,五、通分1/2,4/7,5/8,2/3,(3/6,4/7,5/8,6/9,7/10六、A*B7,8,6,8,8,4,(2)A*B取个位得到C4,3,11,32,()4*3-1=11,3*11-1=32,11*32-1=351七、B/A4,4,6,12,30,B/A=1,1.5,2,2.5,34,7,12,10,36,13,(108),16 A.72 B.49 C.98 D.108 奇数项:4,12,36,108 偶数项:7,10,131/3,1/2,3/4,9/8,A*3/2=B6,2,15,5,21,7,(36),12 A.28 B.36 C.42 D.486/2=15/5=21/7=36/12分组同商4,7,8,14,16,(28)A.22 B.24 C.26 D.28奇数项:4,8,16 偶数项:7,14,28八、常数的乘方-1,0,3,80^2-1=-1,1^2-1=0,2^2-1=3,3^2-1=8,4^2-1=15 3,8,24,48,()2^2-1=3,3^2-1=8,5^2-1=24,7^2-1=48,11^2-1=120 32,81,64,25,(),12^5,3^4,4^3,5^2,6^1=6,7^00,0,1,4,() A.10 B.11 C.12 D.132^0-1 2^1-2 2^2-3 2^3-4 2^4-5=1114,20,54,76,()A.104B.116C.144D.1263^2+5 5^2-5 7^2+5 9^2-5 11^2+5=126九、个位和十位35,44,53,80,(71)A.71 B.91 C.102 D.993+5=4+4=5+3=8+0=7+1=8134,532,426,615,(628)A.844 B.734 C.628 D.3481+3=4,3+2=5,4+2=6,1+5=6,6+2=8,1/2,1/5,4/5,5/7,( 4/11) A.12/13 B.4/11 C.7/11 D.7/13分子+分母得到:3,6,9,12,1547,58,71,79,(95)A.95 B.100 C.87 D.9247+4+7=58,58+5+8=71,71+7+1=79,79+7+9=95十、1十一、 1十二、 1十三、 1图形推理的50项规律1.大小变化2.方向旋转3.笔画增减(数字,线条数)4.图形求同5.相同部份去掉6.图形叠加(简单叠加,合并叠加,去同叠加)7.图形组合变化(如:首尾两个图形中都包含中间图形)8.对应位置阴影变化(两图相同或不同则第三图对应位置变阴影或变空白)9.顺时针或逆时针旋转10.总笔画成等差数列11.由内向外逐步包含12.相同部件,上下,左右组合13.类似组合(如平行,图形个数一样等)14.横竖线条之比有规律(如横线3条竖线4条,横线4条竖线5条等)15.缺口相似或变化趋势相似(如逐步远离或靠近)16.图形运动变化(同一个图形从各个角度看的不同样子)17.图形拆分(有三个图构成,后两个图为第一个图的构成部件)18.线条交点数有规律19.方向规律(上,下,左,右)20.相隔一个图形分别对称(如:以第三个图为中心,1和5对称,2和4对称)21.含义依据条件而变(如一个错号,可以表"划",也可以表示"两划")22.图形趋势明显(点或图形从左到右,从上到下变化等)23.图形的上,中,下部分分别变化(求同,重叠,或去同叠加)24.相似类(包含,平行,覆盖,相交,不同图形组成,含同一图形等)25.上,中,下各部分别翻转变化26.角的度数有规律27.阴影重合变空白28.翻转,叠加,再翻转30.与特定线的交点数相同(如:与折线的交点数有规律,有直线的交点数不用考虑)31.图形有多条对称轴,且有共同交点,轴对称图形(如正三角形,正方形)32.平行,上下移动33.图形翻转对称34.图形边上角的个数增多或减少35.不同图形叠加形成新图36.图形中某条线均为长线或短线(寻找共同部分)37.线段间距离共性.(如:直线上有几个点,分成几条线段,上部覆盖有另一个图形,如圆,三角形等,但是上面的图形占的位置都不大于最外面两点间的距离)38.图形外围,内部分别顺或逆时针旋转(内外部变化相反)39.特殊位置变化有规律(如当水平时,垂直时图形有一规律)40.各图形组成部件属于同一类(如:均为三条曲线相交)41.以第几幅图为中心进行变化(如:旋转,走近,相反等)42.求共同部分再加点变化(如:提出共同部分,然后让共同部分都变黑什么的)43.除去共同部分有规律44.数线段出头数,有规律(成等差数列,或有明显规律)45.图形每行图形被分割成的空间数相同46.以中间图形为中心,上下,对角分别成对称47.先递增再递减规律48.整套图形横着看,或竖着看,分别有规律.49.注意考虑图形部分变化(如:分别为上下不变中间变化,然后上中下一起变化,左右分别变化,左右一起变化等)50.顺着次序变化.(如:原来在内部的放大变为外部图形,内部图形相应变化.左右组成的图,上一个右边图等于下个左边图,右边再加个新图,如此循环)。
数字推理技巧总结

数字推理技巧总结
数字推理是一种基于数字和数学知识的推理方法,通过对数字的组合、转换和计算,得出一些结论或规律。
数字推理技巧是指在数字推理过程中可以使用的一些方法和策略,以下是一些数字推理技巧的总结:
1.观察数字的规律:在数字推理题目中,往往会出现一些数字的规律,例如数列的增长规律、数字的排列顺序等等,要仔细观察这些规律,并将其应用到题目中。
2.利用数据的对称性:在数字推理题目中,往往会出现一些对称的数字或图形,这时可以利用对称性来推导出一些结论。
3.进行逆向推理:有时候可以从题目给出的答案中逆推出一些关键的数字或规律,然后再根据这些数字或规律来推导出正确的答案。
4.应用数学公式:有些数字推理题目中会涉及到一些数学公式,例如平均数、标准差等等,要熟练掌握这些公式,并能够灵活应用。
5.运用逻辑思维:数字推理也涉及到逻辑思维,要善于运用逻辑思维来推导出正确的答案。
6.学会多种解题方法:在数字推理题目中,有时候会有多种解题方法,要学会多种解题方法,并根据实际情况选择合适的方法来解题。
以上是一些数字推理技巧的总结,希望对大家有所帮助。
- 1 -。
行测数字推理八大解题技巧

数字推理八大解题方法【真题精析】例1.2,5,8,11,14,( )A.15 B.16 C.17 D.18[答案]C[解析]数列特征明显单调且倍数关系不明显,优先采用逐差法。
差值数列是常数列。
如图所示,因此,选C。
【真题精析】例1、(2006·国考A类)102,96,108,84,132,( )A.36 B.64 C.70 D.72[答案]A[解析]数列特征明显不单调,但相邻两项差值的绝对值呈递增趋势,尝试采用逐差法。
差值数列是公比为-2的等比数列。
如图所示,因此,选A。
【真题精析】例1.(2009·江西)160,80,40,20,( )A.B.1 C.10 D.5[答案]C[解析]数列特征明显单调且倍数关系明显,优先采用逐商法。
商值数列是常数列。
如图所示,因此,选C【真题精析】例1、2,5,13,35,97,( )A.214 B.275 C.312 D.336[答案]B[解析]数列特征明显单调且倍数关系明显,优先采用逐商法。
商值数列是数值为2的常数列,余数数列是J2-I:h为3的等比数列。
如图所示,因此,选B。
【真题精析】例1、(2009·福建)7,21,14,21,63,( ),63A.35 B.42 C.40 D.56[答案]B[解析]数列特征明显单调且倍数关系明显,优先采用逐商法。
商值数列是以为周期的周期数列。
如图所示,因此,选B。
【真题精析】例1.8,8,12,24,60,( )A.90 B.120 C.180 D.240[答案]C[解析]逐商法,做商后商值数列是公差为0.5的等差数列。
【真题精析】例1. -3,3,0,3,3,( )A.6 B.7 C.8 D.9[答案]A[解析]数列特征:(1)单调关系不明显;(2)倍数关系不明显;(3)数字差别幅度不大。
优先采用加和法。
【真题精析】例1、(2008·湖北B类)2,3,5,10,20,( )A.30 B.35 C 40 D.45[答案]C[解析]数列特征明显单调且倍数关系不明显,优先做差后得到结果选项中不存在;则考虑数列特征:(1)倍数关系不明显;(2)数字差别幅度不大,采用加和法。
数字推理技巧总结

数字推理技巧总结
数字推理是一种常见的思考方法,同时也是非常实用的技巧。
以下是一些数字推理的技巧总结:
1. 观察数字之间的关系。
数字可以按照大小、倍数、时间、空间等不同的关系进行比较。
了解数字之间的关系对于进行数字推理很有帮助。
2. 进行变量替换。
将数字转化成不同的变量,有助于更好地理解数字之间的关系。
同时,也可以更直接地运用数字进行推理。
3. 使用辅助工具。
数字推理可以用图表、表格、图像等方式进行辅助。
这些辅助工具可以帮助我们更直观地观察数字之间的关系。
4. 利用数学公式和运算符。
数字推理往往需要进行加减乘除等运算,数学公式和运算符是进行数字推理的常见工具。
5. 细心观察条件。
数字推理往往需要根据条件进行推理解题,因此细心观察条件是十分重要的。
同时,也需要注意条件中的排除性关系等细节问题。
总之,数字推理是一种灵活运用数字的思考方法,需要我们不断练习。
通过观察数字之间的关系,进行变量替换,使用辅助工具,利用数学公式和运算符,以及细心观察条件,我们可以更快、更准确地进行数字推理解题。
公务员考试数字推理题解题技巧大全

公务员考试数字推理题解题技巧大全公务员考试是一项重要的选拔机制,而数字推理题是其中的一项难点。
在数字推理题中,考生需要通过数字、图表等信息,寻找一定的规律和推理思路,从而解决问题。
为了帮助考生顺利应对数字推理题,本文将为大家介绍一些解题技巧和思路。
一、理解题目和数据在做数字推理题时,首先需要认真阅读题目和给出的数据,了解题目的背景和要求。
在阅读中要注意对数据进行分类和总结,分析数字间的关系和规律。
二、寻找常见数字规律数字推理题中存在着许多常见的数字规律,例如:相邻数的关系、乘法和除法关系、平方、倒数等规律。
若能找出这些规律,便能够轻松解决此类推理题。
三、寻找图形规律数字推理题中,常常会配有一些图形数据。
对于这些图形,我们可以通过寻找它们的共性和特点,来发现其中的规律。
例如,周期性图形的规律常常是循环或对称性;封闭型图形的规律常常是不变性或连通性。
通过这些规律,我们可以迅速地推断出答案。
四、确定类型和答案数字推理题大致可以分为数列和图形两类。
对于数列题,我们可以看其中的差值和倍数规律,以及数列的加和、中位数、众数等;对于图形题,我们可以寻找变化和相似性规律,以及图形的方向、角度、面积和比例等。
同时,我们也可以先推断出答案,然后再用已有的数据进行验证,验证结果。
五、注意隐形陷阱在数字推理题中,经常会隐藏着一些陷阱,这些陷阱可能会导致我们犯错。
例如,数据中可能存在重复数字、相同数字或相同图形,这就需要我们仔细分辨;同时也要注意看清题目要求,不要遗漏信息或多读信息。
总之,数字推理题是公务员考试中的难点之一,但是只要我们掌握题目信息,查找数字和图形规律,注意隐形陷阱,便能够较为轻松地应对此类题目。
希望以上简单的技巧和思路能够对大家在公务员考试中取得好成绩有所帮助。
数字推理技巧总结

数字推理技巧总结数字推理技巧是一种通过观察数字之间的关系和规律来推断答案的方法。
在解决问题和推理推断过程中,数字推理技巧可以帮助我们更加准确地得出结论。
本文将从数字序列、数学运算、逻辑推理和概率统计等方面总结数字推理技巧。
一、数字序列推理数字序列是数字按一定顺序排列而形成的序列,通过观察数字序列中的规律可以推断出下一个数字或者找出隐藏的规律。
常见的数字序列包括等差数列、等比数列和斐波那契数列等。
1. 等差数列:等差数列是指相邻两个数之间差值相等的数列。
观察数字序列中相邻数字的差值,如果差值相等,则可以判断为等差数列。
根据已知数字序列的首项和公差,可以推算出下一个数字。
2. 等比数列:等比数列是指相邻两个数之间比值相等的数列。
观察数字序列中相邻数字的比值,如果比值相等,则可以判断为等比数列。
根据已知数字序列的首项和公比,可以推算出下一个数字。
3. 斐波那契数列:斐波那契数列是指每个数都是前两个数之和的数列。
观察数字序列中的数字之间的相加关系,如果每个数字都是前两个数字之和,则可以判断为斐波那契数列。
根据已知数字序列的前两个数字,可以推算出下一个数字。
二、数学运算推理数学运算是通过对数字进行加减乘除等运算,推导出结果的过程。
在数学运算推理中,常见的技巧包括逆运算、代入法和重复运算法等。
1. 逆运算:逆运算是指对已知的数学运算进行反向操作,从结果推算出原始的数字。
例如,已知两个数的和,可以通过减去其中一个数,得到另一个数。
2. 代入法:代入法是指将已知的数字代入到数学公式或方程中,通过计算得到结果。
例如,已知一个等式中的一部分数字,可以将这些数字代入到等式中,求解未知的数字。
3. 重复运算法:重复运算法是指通过多次进行相同的数学运算,逐步逼近目标结果。
例如,已知一个数字进行重复的加法运算,每次加上相同的数,直到达到目标结果。
三、逻辑推理逻辑推理是通过观察数字之间的逻辑关系,推断出隐藏的规律或者答案。
在逻辑推理中,常见的技巧包括排除法、归纳法和演绎法等。
行测解答数字推理的四种思维方式

行测解答数字推理的四种思维方式数字推理是行政职业能力测验(简称行测)中常见的题型之一,它主要考察考生对于数字关系的分析和推理能力。
在数字推理题中,做题者需要根据给定的数字关系、规律或模式,找出其中的规律并应用于后续的题目。
为了帮助考生更好地解答数字推理题,本文将介绍四种常见的思维方式。
1. 递增递减法递增递减法是最常见也是最基础的数字推理思维方式。
通过观察数字序列的增减规律,可以推断出后续数字的变化规律。
常见的递增递减法包括等差数列、等比数列等。
例如,给定一个数字序列1,3,5,7,问下一个数字是多少?通过观察可知,该数字序列是一个等差数列,公差为2,因此下一个数字是9。
2. 交替排列法交替排列法是指数字序列中数字的交替排列规律。
交替排列可以按照顺序进行,也可以按照特定的排列顺序进行。
例如,给定一个数字序列2,4,1,3,6,问下一个数字是多少?观察可知,该数字序列是按照奇偶递增排列的,因此下一个数字应是5。
3. 分组对比法分组对比法主要通过将数字序列进行分组,观察每组数字之间的关系,从而找出规律。
例如,给定一个数字序列1,2,4;3,6,12;4,8,16;问下一个数字是多少?通过观察可知,数字序列每组数字第一个数字是后续数字的一半,第二个数字是后续数字的相同倍数,因此下一个数字应该是8,16。
4. 乘积和差法乘积和差法是通过数字序列中数字间的乘积和差的规律来推断后续数字的变化规律。
例如,给定一个数字序列2,6,18,54,问下一个数字是多少?通过观察可知,该数字序列的每个数字都是前一个数字乘以3得到的,因此下一个数字应该是162。
以上是数字推理题常见的四种思维方式,通过掌握这些思维方式,考生可以更好地解答数字推理题。
在实际解题过程中,考生还应注意对题目进行综合分析,灵活运用多种思维方式,并进行逻辑。
数字推理十大题型秒杀技巧

数字推理十大题型秒杀技巧
1. 数字推理里的等差数列题型,那简直就是送分题呀!比如说1,3,5,7,这不是很明显的等差数列嘛,公差为2,下一个数不就是9 嘛!
2. 等比数列题型,哇塞,一旦发现规律就超简单的!像2,4,8,16,这倍数关系多明显呀,下一个肯定是 32 啦!
3. 平方数列题型,这可得瞪大眼睛找呀!像 1,4,9,16,不就是平方数嘛,下一个就是 25 咯!
4. 立方数列题型,这个有点难度哦,但找到了就很有成就感呀!比如1,8,27,64,那下一个就是 125 呀!
5. 组合数列题型,就像玩拼图一样有趣呢!比如奇数项和偶数项各有规律,找到就轻松解题啦!
6. 数字拆分题型,把数字拆开来分析,哎呀,真的很有意思!像34 可以拆成 3 和 4 嘛,然后再找规律。
7. 分数数列题型,这可不能被分数吓到呀!比如1/2,2/3,3/4,那下一个不就是 4/5 嘛!
8. 根式数列题型,虽然看着有点复杂,但找到了根号里的规律就迎刃而解啦!
9. 周期数列题型,就像循环播放的音乐一样有规律呀!比如1,2,
3,1,2,3,那下一个当然还是 1 啦!
10. 递推数列题型,一环扣一环的,多有意思呀!像前面两个数相加等于后面一个数,找到这个关系就好办啦!
我觉得呀,掌握了这些数字推理的秒杀技巧,就像是拥有了一把打开数字世界大门的钥匙,能让我们在数字的海洋里畅游无阻!。
行测数字推理题技巧

行测数字推理题技巧数字推理题是公务员考试中常见的题型之一,包含数字序列、数字关系、数字分类等多种形式。
数字推理题不仅考察了考生的数学能力,更重要的是考察了考生的逻辑思维和推理能力。
本文将从四个方面为大家介绍数字推理题的技巧和方法。
一、数字序列题数字序列题是指给出一组数字序列,要求考生根据规律推断出下一个数字或者缺失的数字。
数字序列题考察的是考生的数学能力和逻辑推理能力。
下面介绍一些数字序列题的常见规律和解题方法。
1.等差数列等差数列是指每一项与前一项之差相等的数列,例如1、3、5、7、9……。
在等差数列中,每一项与前一项之差都相等,这个差值称为公差。
在数字序列题中,等差数列的规律通常是给出前几项,要求考生推断出下一项或者缺失的项。
解题方法是求出公差,然后根据公差推断出下一项或者缺失的项。
2.等比数列等比数列是指每一项与前一项之比相等的数列,例如1、2、4、8、16……。
在等比数列中,每一项与前一项之比都相等,这个比值称为公比。
在数字序列题中,等比数列的规律通常是给出前几项,要求考生推断出下一项或者缺失的项。
解题方法是求出公比,然后根据公比推断出下一项或者缺失的项。
3.斐波那契数列斐波那契数列是指第一项和第二项都为1,从第三项开始,每一项都是前两项之和的数列,例如1、1、2、3、5、8……。
在斐波那契数列中,每一项都是前两项之和,这个规律称为递推关系。
在数字序列题中,斐波那契数列的规律通常是给出前几项,要求考生推断出下一项或者缺失的项。
解题方法是根据递推关系推断出下一项或者缺失的项。
二、数字关系题数字关系题是指给出一组数字之间的关系,要求考生根据这些关系推断出其他数字之间的关系。
数字关系题考察的是考生的逻辑推理能力和数学能力。
下面介绍一些数字关系题的常见关系和解题方法。
1.加减乘除加减乘除是数字关系题中最为常见的关系,例如1+2=3,2-1=1,2×3=6,6÷2=3等。
在数字关系题中,加减乘除的规律通常是给出部分数字和运算符号,要求考生推断出其他数字和运算符号。
行测数字推理方法总结

行测数字推理方法总结数字推理是行政职业能力测验(简称行测)中的重要一部分,对于备考者来说,掌握数字推理方法是提高得分的关键。
本文将系统总结数字推理方法,以帮助读者更好地应对此类题型。
一、分类思维法分类思维法是数字推理中常用的方法之一。
这种方法通过将一组数字按照一定的规则进行分类,然后再寻找一个规则与之不符的数字,以此来得出正确答案。
例如,给定一组数字序列:2、4、6、8、10,第一个分类可能是偶数,但是最后一个数字10是一个偶数,与之前的分类规则不符,因此正确答案是另外一种分类规则,即数字逐渐增加2。
二、数列规律法数列规律法是数字推理中常见的方法之一,尤其适用于给定一组数字序列,要求推理下一个数字。
首先观察数字间的间隔关系,即找出相邻数字之间的规律,例如1、3、5、7,可以看出每个数字都比前一个数字大2。
其次,观察数字的增长规律,即数字序列整体的增长关系,例如2、4、8、16,可以看出每个数字都是前一个数字乘以2。
通过观察数字间的间隔关系和数字的增长规律,可以推理出下一个数字是什么。
三、替换法替换法是处理数字推理题目时常用的方法之一。
它通过观察数字序列中的某个数字是否可以通过替换来得到下一个数字。
例如,给定一组数字序列:3、6、9、12,观察可以发现每个数字都是前一个数字加上3得到的,因此,可以推断下一个数字是15。
四、逻辑推理法逻辑推理法是数字推理中较为复杂的方法之一,它要求考生根据已知条件,通过逻辑思维找出数字序列的规律。
这种方法需要考生具备较强的思辨能力和逻辑分析能力。
例如,给定一组数字序列:1、4、9、16,观察可以发现每个数字都是前一个数字的平方,因此,可以推断下一个数字是25。
五、倒推法倒推法是数字推理中常用的方法之一。
它通过观察数字序列的规律,从已知的最后一个数字开始,一步一步地往前推理,最终找到第一个数字是什么。
例如,给定一组数字序列:36、25、16、9,观察可以发现每个数字都是前一个数字的平方,因此,可以推断第一个数字是6。
数字推理题的解题技巧大全

第一部分:数字推理题的解题技巧一、解题前的准备1.熟记各种数字的运算关系。
如各种数字的平方、立方以及它们的邻居,做到看到某个数字就有感觉。
这是迅速准确解好数字推理题材的前提。
常见的需记住的数字关系如下:(1)平方关系:2-4,3-9,4-16,5-25,6-36,7-49,8-64,9-81,10-100,11-121,12-144 13-169,14-196,15-225,16-256,17-289,18-324,19-361,20-400(2)立方关系:2-8,3-27,4-64,5-125,6-216,7-343,8-512,9-729,10-1000(3)质数关系:2,3,5,7,11,13,17,19,23,29......(4)开方关系:4-2,9-3,16-4......以上四种,特别是前两种关系,每次考试必有。
所以,对这些平方立方后的数字,及这些数字的邻居(如,64,63,65等)要有足够的敏感。
当看到这些数字时,立刻就能想到平方立方的可能性。
熟悉这些数字,对解题有很大的帮助,有时候,一个数字就能提供你一个正确的解题思路。
如 216 ,125,64()如果上述关系烂熟于胸,一眼就可看出答案但一般考试题不会如此弱智,实际可能会这样 215,124,63,()或是217,124,65,()即是以它们的邻居(加减1),这也不难,一般这种题5秒内搞定。
2.熟练掌握各种简单运算,一般加减乘除大家都会,值得注意的是带根号的运算。
根号运算掌握简单规律则可,也不难。
3.对中等难度以下的题,建议大家练习使用心算,可以节省不少时间,在考试时有很大效果。
二、解题方法按数字之间的关系,可将数字推理题分为以下十种类型:1.和差关系。
又分为等差、移动求和或差两种。
(1)等差关系。
这种题属于比较简单的,不经练习也能在短时间内做出。
建议解这种题时,用口算。
12,20,30,42,()127,112,97,82,()3,4,7,12,(),28(2)移动求和或差。
破解数字推理题的12个实用小技巧

(1)等差,等比这种最简单的不用多说,深一点就是在等差,等比上再加、减一个数列,如24,70,208,622,规律为a*3-2=b (2)深一点模式,各数之间的差有规律,如1、2、5、10、17。
它们之间的差为1、3、5、7,成等差数列。
这些规律还有差之间成等比之类。
B,各数之间的和有规律,如1、2、3、5、8、13,前两个数相加等于后一个数。
(3)看各数的大小组合规律,做出合理的分组。
如7,9,40,74,1526,5436,7和9,40和74,1526和5436这三组各自是大致处于同一大小级,那规律就要从组方面考虑,即不把它们看作6个数,而应该看作3个组。
而组和组之间的差距不是很大,用乘法就能从一个组过渡到另一个组。
所以7*7-9=40 , 9*9-7=74 , 40*40-74=1526 , 74*74-40=5436,这就是规律。
(4)如根据大小不能分组的,A,看首尾关系,如7,10,9,12,11,14,这组数; 7+14=10+11=9+12。
首尾关系经常被忽略,但又是很简单的规律。
B,数的大小排列看似无序的,可以看它们之间的差与和有没有顺序关系。
(5)各数间相差较大,但又不相差大得离谱,就要考虑乘方,这就要看各位对数字敏感程度了。
如6、24、60、120、210,感觉它们之间的差越来越大,但这组数又看着比较舒服,它们的规律就是2^3-2=6、3^3-3=24、4^3-4=60、5^3-5=120、6^3-6=210。
这组数比较巧的是都是6的倍数,容易导入歧途。
(6)看大小不能看出来的,就要看数的特征了。
如21、31、47、56、69、72,它们的十位数就是递增关系,如25、58、811、1114 ,这些数相邻两个数首尾相接,且2、5、8、11、14的差为3,如论坛上答:256,269,286,302,(),2+5+6=13 2+6+9=172+8+6=163+0+2=5,∵256+13=269 269+17=286286+16=302 ∴下一个数为302+5=307。
数字推理题的解题方法

数字推理题的解题方法数字推理题是一类需要根据一定的规律或模式来推断或填充数字的问题。
这类题目常见于智力测试、数学竞赛等场合。
解决数字推理题通常需要观察数字序列中的规律,并据此找到正确的解法。
以下是一些常见的数字推理题的解题方法:1. 找规律:仔细观察数字序列,寻找其中的规律或模式。
这可能涉及到数字之间的运算、递增规律、几何形状等。
2. 算术运算:检查数字序列中相邻数字之间是否存在某种算术运算关系,如加法、减法、乘法、除法等。
这些运算关系可以用于推测下一个数字或填充缺失的数字。
3. 几何形状:数字序列有时可能构成一些几何形状,如等差数列、等比数列、斐波那契数列等。
找到这些几何形状有助于推断下一个数字。
4. 奇偶性:观察数字的奇偶性,有时可以发现一些规律。
例如,每两个数字之和是偶数,或者奇数和偶数交替出现等。
5. 位数和数字之和:考虑数字的位数和各位数字之和。
有时规律可能与这些因素有关,例如数字之和是某个特定值,或者数字的位数遵循某种规律。
6. 填空法:如果有多个数字序列,可以尝试在其中的一个序列中找到规律,然后应用相同的规律到其他序列中。
7. 找出特殊模式:有时数字序列中可能存在一些特殊的模式,例如重复、对称、交替等,这些模式可以帮助你找到规律。
8. 试错法:如果找不到明显的规律,可以尝试一些常见的数学运算和规律,并检查是否满足给定的条件。
例子:给定数字序列:2, 4, 8, 16, __观察到每个数字是前一个数字的两倍,因此下一个数字应为16 的两倍,即 32。
这只是数字推理题的一种解法,具体的方法可能因题目而异。
在解决这类问题时,耐心观察、灵活思维和多角度思考都是很有帮助的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
! ts_ljm 编辑,请各位朋友多多支持 编辑,请各位朋友多多支持! ! ! ! !
(2)移动求和或差。从第三项起,每一项都是前两项之和或差,这种题初次做稍有难度,做多 了也就简单了。 1,2,3,5, () ,13 A9 B 11 C8 D7 选 C。1+2=3,2+3=5,3+5=8,5+8=13 2,5,7, () ,19,31,50 A 12 选A 0,1,1,2,4,7,13, () A 22 B 23 C 24 D 25 选 C。注意此题为前三项之和等于下一项。一般考试中不会变态到要你求前四项之和,所 以个人感觉这属于移动求和或差中最难的。 5,3,2,1,1, () A-3 B-2 选 C。 2.乘除关系。又分为等比、移动求积或商两种 (1)等比。从第二项起,每一项与它前一项的比等于一个常数或一个等差数列。 8,12,18,27, (40.5)后项与前项之比为 1.5。 6,6,9,18,45, (135)后项与前项之比为等差数列,分别为 1,1.5,2,2.5,3 (2)移动求积或商关系。从第三项起,每一项都是前两项之积或商。 2,5,10,50, (500) 此题稍有难度,从第三项起,第项为前两项之积除以 2 后项为前两项之积+1 100,50,2,25, (2/25) 3,4,6,12,36, (216) 1,7,8,57, (457) 3.平方关系 1,4,9,16,25, (36) ,49 66,83,102,123, (146) 4.立方关系 1,8,27, (81) ,125 3,10,29, (83) ,127 0,1,2,9, (730) 行简单的通分,则可得出答案 1/2 2/3 4/3 1/2 9/4 2/5 16/5 25/6 (36/7) 分子为等比,分母为等差 将 1/2 化为 2/4,1/3 化为 2/6,可知 1/3 (1/4) 立方后+2 有难度,后项为前项的立方+1 8,9,10,11,12 的平方后+2 C0 D2 B 13 C 10 D11
二、解题方法
按数字之间的关系,可将数字推理题分为以下十种类型: 1.和差关系。又分为等差、移动求和或差两种。 (1)等差关系。这种题属于比较简单的,不经练习也能在短时间内做出。建议解这种题时,用 口算。 12,20,30,42, () 127,112,97,82, () 3,4,7,12, () ,28
! 本题典说明如下:本题典的所有题都适用 本题典说明如下:本题典的所有题都适用! 1) 题目部分用黑体字 2) 解答部分用红体字 3) 先给出的是题目,解答在题目后。 . 4) 如果一个题目有多种思路,一并写出 如果一个题目有多种思路,一并写出. 5) 由于制作仓促,题目可能有错的地方, !!! 请谅解 请谅解!!!
! ts_ljm 编辑,请各位朋友多多支持 编辑,请各位朋友多多支持! ! ! ! !
目录:单击进入相应的页面☺ F·························································· 1 目录: 目录:F 第一部分:数字推理题的解题技巧············ 2 第二部分:数学运算题型及讲解················ 6 : 数字推理题的各种规律············ 8 第三部分 第三部分: :数字推理题典 ! 第四部分 第四部分: 数字推理题典! !······················ 16 )·····················62 (数字的整除特性 数字的整除特性) 继续题典···································· 65
第各位朋友多多支持 编辑,请各位朋友多多支持! ! ! ! !
依次相减,得 3,4,6,10,18, () 再相减,得 1,2,4,8, () ,此为等比数列,下一个为 16,倒推可知选 A。 10.其他数列。 2,6,12,20, () A 40 B 32 C 30 D 28 选 C。2=1*2,6=2*3,12=3*4,20=4*5,下一个为 5*6=30 1,1,2,6,24, () A 48 B 96 C 120 D 144 选 C。后项=前项*递增数列。1=1*1,2=1*2,6=2*3,24=6*4,下一个为 120=24*5 1,4,8,13,16,20, () A20 B 25 C 27 D28 选 B。每三项为一重复,依次相减得 3,4,5。下个重复也为 3,4,5,推知得 25。 27,16,5, () ,1/7 A 16 B1 C0 D2 选 B。依次为 3 的 3 次方,4 的 2 次方,5 的 1 次方,6 的 0 次方,7 的-1 次方。 这些数列部分也属于组合数列,但由于与前面所讲的和差,乘除,平方等关系不同,故在此列为 其他数列。这种数列一般难题也较多。 综上所述,行政推理题大致就这些类型。至于经验,我想,要在熟练掌握各种简单运算关系 的基础上,多做练习,对各种常见数字形成一种知觉定势,或者可以说是条件反射。看到这些数 字时,就能立即大致想到思路,达到这种程度,一般的数字推理题是难不了你了,考试时十道数 字推理在最短的时间内正确完成 7 道是没有问题的。但如果想百尺竿头更进一步,还请继续多 做难题。强烈建议继续关注我们的清风百合江苏公务员,在下次公务员考试之前,复习冲刺的时 候,我们会把一些难题汇总并做解答,对大家一定会有更多的帮助的。 讲了这么多, 自我感觉差不多了。 这篇文章主要是写给没有经过公务员考试且还未开始准备公务 员考试的版友看的属于入门基础篇,高手见笑了。仓促完成,难免有不妥之处,欢迎版友们提出 让我改善。目前准备江苏省公务员考试时间很充裕,有兴趣的朋友可以先开始看书准备。也欢迎 有对推理题有不懂的朋友把题目帖出来,大家讨论。我不可能解出所有题,但我们清风版上人才 众多,潜水者不计其数,肯定会有高手帮助大家。
ts_ljm 06-3-7 中午
第 1 页 共 77 页
! ts_ljm 编辑,请各位朋友多多支持 编辑,请各位朋友多多支持! ! ! ! !
第一部分:数字推理题的解题技巧
行政能力倾向测试是公务员(civil servant)考试必考的一科,数字推理题又是行政测试中一直 以来的固定题型。如果给予足够的时间,数字推理并不难;但由于行政试卷整体量大,时间短, 很少有人能在规定的考试时间内做完,尤其是对于文科的版友们来说,数字推理、数字运算(应 用题)以及最后的资料分析是阻碍他们行政拿高分的关卡。并且,由于数字推理处于行政 A 类 的第一项, B 类的第二项,开头做不好,对以后的考试有着较大的影响。应广大版友,特别 是 MM 版友的要求,甘蔗结合杨猛 80 元书上的习题,把自己的数字推理题解题心得总结出来。如 果能使各位备考的版友对数字推理有所了解,我在网吧花了 7 块钱打的这篇文章也就值了。 数字推理考察的是数字之间的联系,对运算能力的要求并不高。所以,文科的朋友不必担心 数学知识不够用或是以前学的不好。只要经过足够的练习,这部分是可以拿高分的,至少不会拖 你的后腿。抽根烟,下面开始聊聊。
一、解题前的准备
1.熟记各种数字的运算关系。 如各种数字的平方、立方以及它们的邻居,做到看到某个数字就有感觉。这是迅速准确解好数 字推理题材的前提。常见的需记住的数字关系如下: (1)平方关系:2-4,3-9,4-16,5-25,6-36,7-49,8-64,9-81,10-100,11-121,12-144 13-169,14-196,15-225,16-256,17-289,18-324,19-361,20-400 (2)立方关系:2-8,3-27,4-64,5-125,6-216,7-343,8-512,9-729,10-1000 (3)质数关系:2,3,5,7,11,13,17,19,23,29...... (4)开方关系:4-2,9-3,16-4...... 以上四种,特别是前两种关系,每次考试必有。所以,对这些平方立方后的数字,及这些数 字的邻居(如,64,63,65 等)要有足够的敏感。当看到这些数字时,立刻就能想到平方立 方的可能性。熟悉这些数字,对解题有很大的帮助,有时候,一个数字就能提供你一个正确的解 题思路。如 216 ,125,64()如果上述关系烂熟于胸,一眼就可看出答案但一般考试题不 会如此弱智,实际可能会这样 215,124,63, () 或是 217,124,65, ()即是以它们的 邻居(加减 1) ,这也不难,一般这种题 5 秒内搞定。 2.熟练掌握各种简单运算,一般加减乘除大家都会,值得注意的是带根号的运算。根号运算掌 握简单规律则可,也不难。 3.对中等难度以下的题,建议大家练习使用心算,可以节省不少时间,在考试时有很大效果。
5.分数数列。一般这种数列出难题较少,关键是把分子和分母看作两个不同的数列,有的还需进
下一个为 2/8 6.带根号的数列。这种题难度一般也不大,掌握根号的简单运算则可。限于计算机水平比较烂, 打不出根号,无法列题。 7.质数数列 2,3,5, (7) ,11 4,6,10,14,22, (26) 8.双重数列。又分为三种: (1)每两项为一组,如 质数数列除以 2 20,22,25,30,37, (48) 后项与前项相减得质数数列。
第 3 页 共 77 页
! ts_ljm 编辑,请各位朋友多多支持 编辑,请各位朋友多多支持! ! ! ! !
1,3,3,9,5,15,7, (21) 第一与第二,第三与第四等每两项后项与前项之比为 3
2,5,7,10,9,12,10, (13)每两项之差为 3 1/7,14,1/21,42,1/36,72,1/52, () 两项为一组,每组的后项等于前项倒数*2 (2)两个数列相隔,其中一个数列可能无任何规律,但只要把握有规律变化的数列就可得出结 果。 22,39,25,38,31,37,40,36, (52) 由两个数列,22,25,31,40, ()和 39, 38,37,36 组成,相互隔开,均为等差。 34,36,35,35, (36) ,34,37, (33) 由两个数列相隔而成,一个递增,一个递减 (3)数列中的数字带小数,其中整数部分为一个数列,小数部分为另一个数列。 2.01, 4.03, 8.04, 16.07, (32.11) 整数部分为等比,小数部分为移动求和 数列。双重数列难题也较少。能看出是双重数列,题目一般已经解出。特别是前两种,当数字的 个数超过 7 个时,为双重数列的可能性相当大。 9.组合数列。 此种数列最难。前面 8 种数列,单独出题几乎没有难题,也出不了难题,但 8 种数列关系两两 组合,变态的甚至三种关系组合,就形成了比较难解的题目了。最常见的是和差关系与乘除关系 组合、和差关系与平方立方关系组合。只有在熟悉前面所述 8 种关系的基础上,才能较好较快 地解决这类题。 1,1,3,7,17,41() A 89 B 99 C 109 D 119 选 B。此为移动求和与乘除关系组合。第三项为第二项*2+第一项 65,35,17,3,() A1 B2 C 0 D 4 选 A。平方关系与和差关系组合,分别为 8 的平方+1,6 的平方-1,4 的平方+1,2 的平方-1, 下一个应为 0 的平方+1=1 4,6,10,18,34, () A 50 B 64 C 66 D 68 选 C。 各差关系与等比关系组合。 依次相减, 得 2, 4, 8, 16 () , 可推知下一个为 32, 32+34=66 6,15,35,77, () A 106 B 117 C 136 D 163 选 D。等差与等比组合。前项*2+3,5,7 依次得后项,得出下一个应为 77*2+9=163 2,8,24,64, () A 160 B 512 C 124 D 164 选 A。此题较复杂,幂数列与等差数列组合。2=1*2 的 1 次方,8=2*2 的平方,24=3*2 的 3 次方,64=4*2 的 4 次方,下一个则为 5*2 的 5 次方=160 0,6,24,60,120, () A 186 B 210 C 220 D 226 选 B。和差与立方关系组合。0=1 的 3 次方-1,6=2 的 3 次方-2,24=3 的 3 次方-3,60=4 的 3 次方-4,120=5 的 3 次方-5。 1,4,8,14,24,42, () A 76 B 66 C 64 D68 选 A。两个等差与一个等比数列组合
