陕西省定边县安边中学2016-2017学年高一下学期中期数学试题
2017年定州市高一数学下期末考试题(有答案和解释)

2017年定州市高一数学下期末考试题(有答案和解释)河北定州2016—2017学年度第二学期期末考试高一年级承智班数学试卷一、选择题1 已知点和在直线的两侧,则实数的取值范围为()A BD【答案】A【解析】试题分析:由题意可知考点:直线方程2 设为不重合的平面,为不重合的直线,则下列命题正确的是()A 若,则B 若,则若,则D 若,则【答案】D【解析】试题分析:A的结论可能是,B的结论可能是,的结论可能是,因此A、B、均错误,故选D考点:空间点线面的位置关系3 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为()A B【答案】B【解析】由已知可得该几何体是由一个四棱锥和半个圆锥组成的,故其体积为,故选B【点睛】本题主要考查三视图,属于较易题型应注意把握三个视图的位置和尺寸:主视图在图纸的左上方,左视图在主视图的右方,俯视图在主视图的下方;主视图与俯视图长应对正(简称长对正),主视图与左视图高度保持平齐(简称高平齐),左视图与俯视图宽度应相等(简称宽相等),若不按上述顺序放置,则应注明三个视图名称4 下图画出的是某几何体的三视图,网格纸上小正方形的边长为,则该几何体的体积为()A B D【答案】D【解析】由已知中的三视图可得,该几何体是一个长方体挖掉两个圆锥所得的组合体,所以几何体的体积为: ,故选D点睛:本题考查立体几何三视图的直观图,以及还原几何体后求出相应的体积和表面积三视图的长度特征:“长对正、宽相等,高平齐”,即正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.直线在轴上的截距是,且它的倾斜角是直线的倾斜角的2倍,则()D【答案】B【解析】根据题意,设直线为直线l,另一直线的方程为,变形可得,其斜率= ,则其倾斜角为60∘,而直线l的倾斜角是直线的倾斜角的2倍,则直线l的倾斜角为120∘,且斜率=tan120∘=− ,又由l在轴上的截距是−1,则其方程为=− x−1;又由其一般式方程为x+ −1=0,分析可得:=− ,n=−2;故选:A点睛:直线在轴上的截距即为令x=0,解得的的值,也称为纵截距,截距不同于距离,截距可正可负可为0,在直线中还有横截距,即令=0,解出x即是6 若直线与直线的交点位于第一象限,则直线的倾斜角的取值范围是()A BD【答案】B【解析】试题分析:画出图象如下图所示,直线过定点,由图可知,斜率最小值为,此时直线的倾斜角为,故倾斜角的取值范围是.考点:两条直线的位置关系7 如图,在正三棱锥中,、分别是棱、的中点,且,若,则此正三棱锥外接球的体积是()A BD【答案】B【解析】试题分析:三棱锥为正棱锥, 对棱互相垂直, ,又,而,,即, ,将此三棱锥补成正方体,则它们有相同的外接球侧棱长为, , 正三棱锥外接球的体积是选B.考点:球的组合体8 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:),可得这个几何体的体积为()A B D【答案】D【解析】由三视图可知此几何体为四棱锥,底面是边长为2的正方形,面积为4,高为3,所以四棱锥的体积,故选D9 某四棱锥的三视图如图所示,该四棱锥外接球的体积为()A B D 【答案】D【解析】该四棱锥的底面是正方形,其中一条侧棱与底面垂直,所以该四棱锥的外接球就是它所在的长方体的外接球,半径,所以体积,故选D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.10 若过点的直线与圆相较于两点,且为弦的中点,则为()A B 4 D 2【答案】A【解析】圆心坐标为,半径为,。
陕西省定边县安边中学2016-2017学年高一下学期期中考

安边中学2017年春高一物理期中试卷考号:姓名:班级:一、单选题(共40分)1.关于曲线运动下列叙述正确的是()A.曲线运动的物体不受外力作用B.物体只有受到一个方向不断改变的力,才可能作曲线运动C.曲线运动的加速度为0D.平抛运动是一种匀变速曲线运动2.若已知物体的速度方向和它所受合力的方向,如图所示,可能的运动轨迹是()A.B.C.D.3.某河流宽420m,船在静水中的航速为4m/s,水流速度是3m/s,则船渡过该河流的最短时间()A.140 s B.105 s C.84 s D.60 s4.物体受到几个外力的作用而做匀速直线运动,如果撤掉其中的一个力而其它力不变,它不可能做()A.匀加速直线运动B.匀减速直线运动C.变加速曲线运动D.匀加速曲线运动5.下列关于平抛运动说法正确的是()A.在日常生活中,我们将物体以水平速度抛出后物体在空气中一定做平抛运动B.做平抛运动的物体水平位移越大,则说明物体的初速度越大C.做平抛运动的物体运动时间越长,则说明物体做平抛运动的竖直高度越大D.做平抛运动的物体落地时速度方向与水平方向夹角的正弦值与时间成正比6.如图所示在皮带传动中,两轮半径不等,下列说法正确的是()A.两轮角速度相等B.两轮边缘线速度的大小相等C.大轮边缘一点的向心加速度大于小轮边缘一点的向心加速度D.同一轮上各点的向心加速度大小相等7.小船以恒定速率渡河,船头方向始终垂直河岸,当河水流速突然增大时,对小船渡河经历的路程、时间发生的影响是()A.路程增加、时间增加B.路程增加、时间缩短C.路程增加、时间不变D.路程、时间均与水速无关8.从同一高度、同时水平抛出五个质量不同的小球,它们初速度分别为v,2v,3v,4v,5v.在小球落地前的某个时刻,小球在空中的位置关系是()A.五个小球的连线为一条直线,且连线与水平地面平行B.五个小球的连线为一条直线,且连线与水平地面垂直C.五个小球的连线为一条直线,且连线与水平地面既不平行,也不垂直D.五个小球的连线为一条曲线9.如图所示,在匀速转动的圆筒内壁上紧靠着一个物体与圆筒一起运动,物体相对桶壁静止.则()A.物体受到4个力的作用B.物体所受向心力是物体所受的重力提供的C.物体所受向心力是物体所受的弹力提供的D.物体所受向心力是物体所受的静摩擦力提供的10.一物体做平抛运动,在两个不同时刻的速度分别为v1和v2,时间间隔为△t,以下说法错误的是()A.v1和v2的方向一定不同B.若v2是后一时刻的速度,则v1<v2C.由v1到v2的速度变化量△v的方向是不断变化的D.由v1到v2的速度变化量△v的大小为g△t二、多选题(共16分)11.关于物体的运动状态与受力关系,下列说法中正确的是()A.物体的运动状态发生变化,物体的受力情况一定变化B.物体在恒力作用下,一定做匀变速直线运动C.物体的运动状态保持不变,说明物体所受的合外力为零D.物体做曲线运动时,受到的合外力可以是恒力12.关于斜抛运动,忽略空气阻力.下列说法中正确的是()A.斜抛运动是曲线运动B.斜抛运动的初速度是水平的C.斜抛运动在最高点速度不为零D.斜抛运动的加速度是恒定的13.如图所示,汽车以恒定速率通过半圆形拱桥,下列关于汽车在顶点处受力情况(空气阻力不计)的说法中,正确的是()A.汽车受重力、支持力和摩擦力的作用B.汽车受重力、支持力、牵引力、摩擦力和向心力的作用C.汽车所受的向心力就是重力D.汽车所受的重力和支持力的合力充当向心力14.如图所示,甲、乙两球作匀速圆周运动,向心加速度随半径变化.由图象可以知道()A.甲球运动时,线速度大小保持不变B.甲球运动时,角速度大小保持不变C.乙球运动时,线速度大小保持不变D.乙球运动时,角速度大小保持不变三.实验题(共16分)15.某同学在“探究平抛运动的规律”时做了以下操作.(1)先采用图甲所示装置,用小锤打击弹性金属片,金属片把球A沿水平方向弹出,同时B 球被松开自由下落,观察到两球同时落地.改变小锤打击力的大小,即可改变球A被弹出时的速度,两球仍然同时落地,这说明.(2)接着他用频闪照相机得到小球做平抛运动的闪光照片,图乙是照片的一部分,正方形小方格每边长L=1.0cm,闪光的快慢是每秒30次,则可以计算出小球做平抛运动的初速度是m/s.16.在做“研究平抛物体的运动”的实验时,通过描点法画出小球平抛运动轨迹,并求出平抛运动初速度.实验装置如图所示.(1)实验时将固定在斜槽的木板放在实验桌上,实验前要检查木板是否水平,请简述你的检查方法:.(2)关于这个实验,①除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是.A.秒表 B.坐标纸 C.天平 D.弹簧秤 E.重垂纸②引起实验误差的原因是A.安装斜槽时,斜槽末端切线方向不水平B.确定Oy轴时,没有用重垂线C.斜槽不是绝对光滑的,有一定摩擦D.根据曲线计算平抛运动的初速度时,在曲线上取作计算的点离原点O较近③某同学用如图所示的装置,进行了“探究平抛运动规律”的实验:两个相同的弧形轨道M、N,分别用于发射小铁球 P、Q,其中N的末端与可看作光滑的水平板相切;两轨道上端分别装有电磁铁C、D;调节电磁铁C、D的高度,使AC=BD,从而保证小铁球P、Q在轨道出口处的水平初速度v0相等,现将小铁球P、Q分别吸在电磁铁C、D上,然后切断电源,使两小球能以相同的初速度v0同时分别从轨道M、N的下端射出.仅仅改变弧形轨道M的高度,重复上述实验,仍能观察到相同的现象,这说明.(3)某同学采用频闪摄影的方法拍摄到如图所示的“小球做平抛运动”的闪光照片的一部分.图中每个背景方格的边长均为4.90cm,那么拍摄照片时所用闪光频率是Hz,小球运动到b点的速度为m/s(g=9.8m/s2).四、解答题(共3小题,满分28分)17.如图所示,轻杆OA长L=0.5m,在A端固定一小球,小球质量m=0.5kg,以O点为轴使小球在竖直平面内做圆周运动,当小球到达最高点时,小球的速度大小为V=0.4m/s,求在此位置时杆对小球的作用力.(g取10m/s2)18.从某高度处以12m/s的初速度水平抛出一物体,经2s落地,g取10m/s2,求:(1)物体抛出时的高度;(2)物体抛出点与落地点的水平距离;(3)落地时速度方向与水平方向的夹角θ的正切tanθ.19.球m=10kg,在水平面内沿半径R=20cm的圆形轨道做匀速圆周运动,线速度v=0.2m/s,那么,它的向心加速度为多少m/s2,它的周期为多少秒?它受到的向心力多大?安边中学2017年春高一物理期中试题答题卡考号:姓名:班级:总分:一、二、单选与多选三.实验题15、16、四、解答题17、18、19、。
数学高一下期中经典测试卷(含答案解析)(1)

一、选择题1.(0分)[ID :12425]设曲线31x y x +=-在点25(,)处的切线与直线10ax y +-=平行,则a=( )A .-4B .14-C .14D .42.(0分)[ID :12421]设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( ) A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥3.(0分)[ID :12416]水平放置的ABC 的斜二测直观图如图所示,若112A C =,111A B C △的面积为22,则AB 的长为( )A .2B .217C .2D .84.(0分)[ID :12398]已知定义在R 上的函数()21()x m f x m -=-为实数为偶函数,记0.5(log 3),a f 2b (log 5),c (2)f f m ,则,,a b c ,的大小关系为( )A .a b c <<B .c a b <<C .a c b <<D .c b a << 5.(0分)[ID :12377]<九章算术>中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑,PA ⊥平面,2,4ABC PA AB AC ===,三棱锥P ABC -的四个顶点都在球O 的球面上,则球O 的表面积为( )A .8πB .12πC .20πD .24π6.(0分)[ID :12356]在我国古代数学名著 九章算术 中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD 中, AB ⊥平面BCD ,且AB BC CD ==,则异面直线AC 与BD 所成角的余弦值为( )A .12B .12-C 3D .3 7.(0分)[ID :12344]用一个平面去截正方体,则截面不可能是( )A .直角三角形B .等边三角形C .正方形D .正六边形 8.(0分)[ID :12396]若a >b >0,0<c <1,则A .log a c <log b cB .log c a <log c bC .a c <b cD .c a >c b9.(0分)[ID :12395]正方体ABCD ﹣A 1B 1C 1D 1中,E ,F 分别是AD ,DD 1的中点,AB =4,则过B ,E ,F 的平面截该正方体所得的截面周长为( )A .62+45B .62+25C .32+45D .32+25 10.(0分)[ID :12387]α,β为两个不同的平面,m ,n 为两条不同的直线,下列命题中正确的是( )①若α//β,m ⊂α,则m//β; ②若m//α,n ⊂α,则m//n ;③若α⊥β,α∩β=n ,m ⊥n ,则m ⊥β ④若n ⊥α,n ⊥β,m ⊥α,则m ⊥β. A .①③ B .①④ C .②③ D .②④ 11.(0分)[ID :12371]若方程21424x kx k +-=-+ 有两个相异的实根,则实数k 的取值范围是( )A .13,34⎛⎤ ⎥⎝⎦ B .13,34⎛⎫ ⎪⎝⎭ C .53,124⎛⎫ ⎪⎝⎭ D .53,124 12.(0分)[ID :12369]某锥体的三视图如图所示(单位:cm ),则该锥体的体积(单位:cm 3)是( )A .13 B .12 C .16 D .113.(0分)[ID :12410]已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( ) A 2 B 3C 2 D 2 14.(0分)[ID :12397]若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( )A .9,34⎛⎫ ⎪⎝⎭B .9,34⎡⎫⎪⎢⎣⎭C .()1,3D .()2,3 15.(0分)[ID :12360]如图,网格纸上小正方形的边长为1,粗实(虚)线画出的是某多面体的三视图,则该多面体的体积为( )A .64B .643C .16D .163二、填空题16.(0分)[ID :12478]在棱长为1的正方体1111ABCD A B C D -中,BD AC O ⋂=,M 是线段1D O 上的动点,过M 做平面1ACD 的垂线交平面1111D C B A 于点N ,则点N 到点A 的距离最小值是___________.17.(0分)[ID :12463]已知圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是22,则圆M 与圆22:(1)(1)1N x y -+-=的位置关系是_________.18.(0分)[ID :12462]若一个圆柱的侧面展开图是边长为2的正方形,则此圆柱的体积为 .19.(0分)[ID :12522]在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,3AB =,4BC =,5PA =,则三棱锥P ABC -的外接球的表面积为__________20.(0分)[ID :12508]已知P 是抛物线24y x =上的动点,点Q 是圆22:(3)(3)1C x y ++-=上的动点,点R 是点P 在y 轴上的射影,则PQ PR +的最小值是____________.21.(0分)[ID :12443]已知B 与点()1,2,3A 关于点()0,1,2M -对称,则点B 的坐标是______.22.(0分)[ID :12431]已知棱长等于23的正方体1111ABCD A B C D -,它的外接球的球心为O ﹐点E 是AB 的中点,则过点E 的平面截球O 的截面面积的最小值为________.23.(0分)[ID :12430]若直线:20l kx y --=与曲线()2:111C y x --=-有两个不同的交点,则实数k 的取值范围________.24.(0分)[ID :12432]如图所示,二面角l αβ--为60,,A B 是棱l 上的两点,,AC BD 分别在半平面内,αβ,且AC l ⊥,,4,6,8AB AC BD ===,则CD 的长______.25.(0分)[ID :12450]已知球的表面积为20π,球面上有A 、B 、C 三点.如果2AB AC ==,22BC =,则球心到平面ABC 的距离为__________.三、解答题26.(0分)[ID :12628]已知点()1,0P ,圆22:6440C x y x y +-++=.(1)若直线l 过点P 且到圆心C 的距离为2,求直线l 的方程;(2)设过点()0,1Q -的直线m 与圆C 交于A 、B 两点(m 的斜率为负),当||4AB =时,求以线段AB 为直径的圆的方程.27.(0分)[ID :12597]已知点(3,3)M ,圆22:(1)(2)4C x y -+-=.(1)求过点M 且与圆C 相切的直线方程;(2)若直线40()ax y a -+=∈R 与圆C 相交于A ,B 两点,且弦AB 的长为23,求实数a 的值.28.(0分)[ID :12545]如图所示,已知四棱锥P ABCD -中,底面ABCD 为菱形,PA ⊥平面ABCD ,60,,ABC E F ∠=分别是,BC PB 的中点.(1)证明:AE ⊥平面PAD ;(2)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值为3,求二面角B AF C --的正切值.29.(0分)[ID :12622]已知圆22C (4)4x y +-=:,直线:(31)(1)40l m x m y ++--=.(1)求直线l 所过定点A 的坐标;(2)求直线l 被圆C 所截得的弦长最短时直线l 的方程及最短弦长;(3)已知点M (-3,4),在直线MC 上(C 为圆心),存在定点N (异于点M ),满足:对于圆C 上任一点P ,都有||||PM PN 为一常数, 试求所有满足条件的点N 的坐标及该常数.30.(0分)[ID :12542]如图,将棱长为2的正方体1111ABCD A B C D -沿着相邻的三个面的对角线切去四个棱锥后得一四面体11A CB D -.(Ⅰ)求该四面体的体积;(Ⅱ)求该四面体外接球的表面积.【参考答案】2016-2017年度第*次考试试卷参考答案 **科目模拟测试一、选择题1.D2.B3.B4.B5.C6.A7.A8.B9.A10.B11.D12.A13.A14.B15.D二、填空题16.【解析】连结易知面面而即在面内且点的轨迹是线段连结易知是等边三角形则当为中点时距离最小易知最小值为17.相交【解析】【分析】根据直线与圆相交的弦长公式求出的值结合两圆的位置关系进行判断即可【详解】解:圆的标准方程为则圆心为半径圆心到直线的距离圆截直线所得线段的长度是即则圆心为半径圆的圆心为半径则即两个18.2π【解析】试题分析:设圆柱的底面半径为r高为h底面积为S体积为V则有2πr=2⇒r=1π故底面面积S=πr2=π×(1π)2=1π故圆柱的体积V=Sh=1π×2=2π考点:圆柱的体积19.【解析】【分析】以为长宽高构建长方体则长方体的外接球是三棱锥的外接球由此能求出三棱锥的外接球的表面积【详解】由题意在三棱锥中平面以为长宽高构建长方体则长方体的外接球是三棱锥的外接球所以三棱锥的外接球20.【解析】根据抛物线的定义可知而的最小值是所以的最小值就是的最小值当三点共线时此时最小最小值是所以的最小值是3【点睛】本题考查了点和圆的位置关系以及抛物线的几何性质和最值问题考查了转化与化归能力圆外的21.【解析】【分析】根据空间直角坐标系中点坐标公式求结果【详解】设B则所以所以的坐标为【点睛】本题考查空间直角坐标系中点坐标公式考查基本分析求解能力属基础题22.【解析】【分析】当过球内一点的截面与垂直时截面面积最小可求截面半径即可求出过点的平面截球的截面面积的最小值【详解】解:棱长等于的正方体它的外接球的半径为3当过点的平面与垂直时截面面积最小故答案为:【23.【解析】【分析】由题意可知曲线为圆的右半圆作出直线与曲线的图象可知直线是过点且斜率为的直线求出当直线与曲线相切时k的值利用数形结合思想可得出当直线与曲线有两个公共点时实数的取值范围【详解】对于直线则24.【解析】【分析】推导出两边平方可得的长【详解】二面角为是棱上的两点分别在半平面内且的长故答案为:【点睛】本题考查线段长的求法考查空间中线线线面面面间的位置关系等基础知识考查运算求解能力考查函数与方程25.【解析】设球的半径为表面积解得∵在中∴从圆心作平面的垂线垂足在斜边的中点处∴球心到平面的距离故答案为点睛:本题考查的知识点是空间点线面之间的距离计算其中根据球心距球半径解三角形我们可以求出所在平面截三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题1.D解析:D【解析】【分析】求出原函数的导函数,得到函数在2x =时的导数,再由两直线平行与斜率的关系求得a 值.【详解】 解:由31x y x +=-,得()()2213411x x y x x ---=---'=, ∴2'|4x y ==-,又曲线31x y x +=-在点25(,)处的切线与直线10ax y +-=平行, ∴4a -=-,即4a =.故选D .【点睛】本题考查利用导数研究过曲线上某点处的切线方程,考查两直线平行与斜率的关系,是中档题.2.B解析:B【解析】A 中,,αβ也可能相交;B 中,垂直与同一条直线的两个平面平行,故正确;C 中,,αβ也可能相交;D 中,l 也可能在平面β内.【考点定位】点线面的位置关系3.B解析:B【解析】【分析】依题意由111A B C △的面积为114B C =,所以8BC =,2AC =,根据勾股定理即可求AB .【详解】依题意,因为111A B C △的面积为所以11111sin 452AC B C ︒=⨯⋅=11122B C ⨯⨯,解得114B C =, 所以8BC =,2AC =,又因为AC BC ⊥,由勾股定理得:AB ====故选B .【点睛】本题考查直观图还原几何图形,属于简单题. 利用斜二测画法作直观图,主要注意两点:一是与x 轴平行的线段仍然与x '轴平行且相等;二是与y 轴平行的线段仍然与y '轴平行且长度减半. 4.B解析:B【解析】由()f x 为偶函数得0m =,所以0,52log 3log 32121312,a =-=-=-=2log 521514b =-=-=,0210c =-=,所以c a b <<,故选B.考点:本题主要考查函数奇偶性及对数运算.5.C解析:C【解析】【分析】先作出三棱锥P ABC -的图像,根据P ABC -四个面都为直角三角形和PA ⊥平面ABC ,可知PC 中点即为球心,利用边的关系求出球的半径,再由24S R π=计算即得.【详解】三棱锥P ABC -如图所示,由于P ABC -四个面都为直角三角形,则ABC 是直角三角形,且2ABC π∠=,2223BC AC AB ∴=-=,又PA ⊥平面ABC ,且PAC 是直角三角形,∴球O 的直径2222PC R PA AB BC ==++2025==,5R ∴=,则球O 的表面积2420S R ππ==.故选:C【点睛】本题考查多面体外接球的表面积,是常考题型.6.A解析:A【解析】如图,分别取,,,BC CD AD BD 的中点,,,M N P Q ,连,,,MN NP PM PQ ,则,MN BD NP AC ,∴PNM ∠即为异面直线AC 和BD 所成的角(或其补角).又由题意得PQ MQ ⊥,11,22PQ AB MQ CD ==. 设2AB BC CD ===,则2PM =又112,222MN BD NP AC ====, ∴PNM ∆为等边三角形,∴60PNM =︒∠,∴异面直线AC 与BD 所成角为60︒,其余弦值为12.选A . 点睛:用几何法求空间角时遵循“一找、二证、三计算”的步骤,即首先根据题意作出所求的角,并给出证明,然后将所求的角转化为三角形的内角.解题时要注意空间角的范围,并结合解三角形的知识得到所求角的大小或其三角函数值. 7.A解析:A【解析】【分析】【详解】画出截面图形如图显然A 正三角形C 正方形:D 正六边形可以画出三角形但不是直角三角形;故选A .用一个平面去截正方体,则截面的情况为:①截面为三角形时,可以是锐角三角形、等腰三角形、等边三角形,但不可能是钝角三角形、直角三角形;②截面为四边形时,可以是梯形(等腰梯形)、平行四边形、菱形、矩形,但不可能是直角梯形;③截面为五边形时,不可能是正五边形;④截面为六边形时,可以是正六边形.故可选A .8.B解析:B【解析】试题分析:对于选项A ,a b 1gc 1gc log c ,log c lg a lg b==,01c <<,10gc ∴<,而0a b >>,所以lg lg a b >,但不能确定lg lg a b 、的正负,所以它们的大小不能确定;对于选项B ,c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >,两边同乘以一个负数1lg c改变不等号方向,所以选项B 正确;对于选项C ,利用c y x =在第一象限内是增函数即可得到c c a b >,所以C 错误;对于选项D ,利用xy c =在R 上为减函数易得a b c c <,所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较;若底数不同,可考虑利用中间量进行比较. 9.A解析:A【解析】【分析】利用线面平行的判定与性质证明直线1BC 为过直线EF 且过点B 的平面与平面11BCC B 的交线,从而证得1,,,B E F C 四点共面,然后在正方体中求等腰梯形1BEFC 的周长即可.【详解】作图如下:因为,E F 是棱1,AD DD 的中点,所以11////EF AD BC ,因为EF ⊄平面11BCC B ,1BC ⊂平面11BCC B ,所以//EF 平面11BCC B ,由线面平行的性质定理知,过直线EF 且过点B 的平面与平面11BCC B 的交线l 平行于直线EF ,结合图形知,l 即为直线1BC ,过B ,E ,F 的平面截该正方体所得的截面即为等腰梯形1BEFC ,因为正方体的棱长AB =4,所以11EF BE C F BC ====所以所求截面的周长为+故选:A【点睛】本题主要考查多面体的截面问题和线面平行的判定定理和性质定理;重点考查学生的空间想象能力;属于中档题.10.B解析:B【解析】【分析】在①中,由面面平行的性质定理得m ∥β;在②中,m 与n 平行或异面;在③中,m 与β相交、平行或m ⊂β;在④中,由n ⊥α,m ⊥α,得m ∥n ,由n ⊥β,得m ⊥β.【详解】由α,β为两个不同的平面,m ,n 为两条不同的直线,知:在①中,若α∥β,m ⊂α,则由面面平行的性质定理得m ∥β,故①正确;在②中,若m ∥α,n ⊂α,则m 与n 平行或异面,故②错误;在③中,若α⊥β,α∩β=n ,m ⊥n ,则m 与β相交、平行或m ⊂β,故③错误; 在④中,若n ⊥α,m ⊥α,则m ∥n ,由n ⊥β,得m ⊥β,故④正确.故选:B .【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想,是中档题.11.D解析:D【解析】【分析】由题意可得,曲线22(1)4(1)x y y +-=与直线4(2)y k x -=-有2个交点,数形结合求得k 的范围.【详解】如图所示,化简曲线得到22(1)4(1)x y y +-=,表示以(0,1)为圆心,以2为半径的上半圆,直线化为4(2)y k x -=-,过定点(2,4)A ,设直线与半圆的切线为AD ,半圆的左端点为(2,1)B -,当AD AB k k k <,直线与半圆有两个交点,AD 与半圆相切时,2|124|21k k --+=+,解得512AD k =, 4132(2)4AB k -==--,所以53,124k ⎛⎤∈ ⎥⎝⎦. 故选:D【点睛】本题考查直线与圆的位置关系,属于中档题.12.A解析:A【解析】【分析】根据三视图知该几何体对应的三棱锥,结合图中数据求得三棱锥的体积.【详解】由题意可知三棱锥的直观图如图:三棱锥的体积为:111211323⨯⨯⨯⨯=. 故选:A .【点睛】本题考查了利用三视图求几何体体积的应用问题,考查了空间想象能力,是基础题.13.A解析:A【解析】【分析】【详解】根据题意作出图形:设球心为O ,过ABC 三点的小圆的圆心为O 1,则OO 1⊥平面ABC ,延长CO 1交球于点D ,则SD ⊥平面ABC .∵CO 1=233323⨯=, ∴116133OO =-=, ∴高SD=2OO 1=263,∵△ABC 是边长为1的正三角形,∴S △ABC =34, ∴132623436S ABC V -=⨯⨯=三棱锥.考点:棱锥与外接球,体积.【名师点睛】本题考查棱锥与外接球问题,首先我们要熟记一些特殊的几何体与外接球(内切球)的关系,如正方体(长方体)的外接球(内切球)球心是对角线的交点,正棱锥的外接球(内切球)球心在棱锥的高上,对一般棱锥来讲,外接球球心到名顶点距离相等,当问题难以考虑时,可减少点的个数,如先考虑到三个顶点的距离相等的点是三角形的外心,球心一定在过此点与此平面垂直的直线上.如直角三角形斜边中点到三顶点距离相等等等.14.B解析:B【解析】【分析】利用函数的单调性,判断指数函数底数的取值范围,以及一次函数的单调性,及端点处函数值的大小关系列出不等式求解即可【详解】解:函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩单调递增,()301373a a a a ⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤< 所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭.故选:B .【点睛】本题考查分段函数的应用,指数函数的性质,考查学生的计算能力,属于中档题. 15.D 解析:D【解析】根据三视图知几何体是:三棱锥D ABC -为棱长为4的正方体一部分,直观图如图所示:B 是棱的中点,由正方体的性质得,CD ⊥平面,ABC ABC ∆的面积12442S =⨯⨯=,所以该多面体的体积1164433V =⨯⨯=,故选D.二、填空题16.【解析】连结易知面面而即在面内且点的轨迹是线段连结易知是等边三角形则当为中点时距离最小易知最小值为6【解析】连结11B D ,易知面1ACD ⊥面11BDD B ,而1MN ACD ⊥,即1NM D O ⊥,NM 在面11BDD B 内,且点N 的轨迹是线段11B D ,连结1AB ,易知11AB D 是等边三角形,则当N 为11B D 中点时,NA 6 17.相交【解析】【分析】根据直线与圆相交的弦长公式求出的值结合两圆的位置关系进行判断即可【详解】解:圆的标准方程为则圆心为半径圆心到直线的距离圆截直线所得线段的长度是即则圆心为半径圆的圆心为半径则即两个【解析】【分析】根据直线与圆相交的弦长公式,求出a 的值,结合两圆的位置关系进行判断即可.【详解】解:圆的标准方程为222:()(0)M x y a a a +-=>,则圆心为(0,)a ,半径R a =,圆心到直线0x y +=的距离d =,圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是∴即24a =,2a =,则圆心为(0,2)M ,半径2R =,圆22:(1)(1)1N x y -+-=的圆心为(1,1)N ,半径1r =,则MN =3R r +=,1R r -=,R r MN R r ∴-<<+,即两个圆相交.故答案为:相交.【点睛】本题主要考查直线和圆相交的应用,以及两圆位置关系的判断,根据相交弦长公式求出a 的值是解决本题的关键.18.2π【解析】试题分析:设圆柱的底面半径为r 高为h 底面积为S 体积为V 则有2πr=2⇒r=1π故底面面积S=πr2=π×(1π)2=1π故圆柱的体积V=Sh=1π×2=2π考点:圆柱的体积解析:2π【解析】试题分析:设圆柱的底面半径为r ,高为h ,底面积为S ,体积为V ,则有2πr =2⇒r =1π,故底面面积S =πr 2=π×(1π)2=1π,故圆柱的体积V =Sh =1π×2=2π. 考点:圆柱的体积 19.【解析】【分析】以为长宽高构建长方体则长方体的外接球是三棱锥的外接球由此能求出三棱锥的外接球的表面积【详解】由题意在三棱锥中平面以为长宽高构建长方体则长方体的外接球是三棱锥的外接球所以三棱锥的外接球 解析:50π【解析】以,,AB BC PA 为长宽高构建长方体,则长方体的外接球是三棱锥P ABC -的外接球,由此能求出三棱锥P ABC -的外接球的表面积.【详解】由题意,在三棱锥P ABC -中,PA ⊥平面,,3,4,5ABC AB BC AB BC PA ⊥===, 以,,AB BC PA 为长宽高构建长方体,则长方体的外接球是三棱锥P ABC -的外接球, 所以三棱锥P ABC -的外接球的半径为22215234522R =++=, 所以三棱锥P ABC -的外接球的表面积为225244()502S R πππ==⨯=. 【点睛】 本题主要考查了三棱锥的外接球的表面积的计算问题,其中解答中根据几何体的结构特征,以,,AB BC PA 为长宽高构建长方体,得到长方体的外接球是三棱锥P ABC -的外接球是解答的关键,着重考查了数形结合思想,以及推理与运算能力.20.【解析】根据抛物线的定义可知而的最小值是所以的最小值就是的最小值当三点共线时此时最小最小值是所以的最小值是3【点睛】本题考查了点和圆的位置关系以及抛物线的几何性质和最值问题考查了转化与化归能力圆外的 解析:【解析】根据抛物线的定义,可知1PR PF =-,而PQ 的最小值是1PC -,所以PQ PR +的最小值就是2PF PC +-的最小值,当,,C P F 三点共线时,此时PF FC +最小,最小值是()()2231305CF =--+-= ,所以PQ PR +的最小值是3.【点睛】本题考查了点和圆的位置关系以及抛物线的几何性质和最值问题,考查了转化与化归能力,圆外的点和圆上的点最小值是点与圆心的距离减半径,最大值是距离加半径,抛物线上的点到焦点的距离和到准线的距离相等,这样转化后为抛物线上的点到两个定点的距离和的最小值,即三点共线时距离最小.21.【解析】【分析】根据空间直角坐标系中点坐标公式求结果【详解】设B则所以所以的坐标为【点睛】本题考查空间直角坐标系中点坐标公式考查基本分析求解能力属基础题解析:()1,4,1--【解析】【分析】根据空间直角坐标系中点坐标公式求结果.【详解】设B (),,x y z ,则1230,1,2222x y z +++=-==,所以1,4,1x y z =-=-=,所以B 的坐标为()1,4,1--.【点睛】本题考查空间直角坐标系中点坐标公式,考查基本分析求解能力,属基础题. 22.【解析】【分析】当过球内一点的截面与垂直时截面面积最小可求截面半径即可求出过点的平面截球的截面面积的最小值【详解】解:棱长等于的正方体它的外接球的半径为3当过点的平面与垂直时截面面积最小故答案为:【 解析:3π.【解析】【分析】当过球内一点E 的截面与OE 垂直时,截面面积最小可求截面半径,即可求出过点E 的平面截球O 的截面面积的最小值.【详解】解:棱长等于1111ABCD A B C D -,它的外接球的半径为3,||OE =当过点E 的平面与OE 垂直时,截面面积最小,r 33S ππ=⨯=, 故答案为:3π.【点睛】本题考查过点E 的平面截球O 的截面面积的最小值及接体问题,找准量化关系是关键,属于中档题.23.【解析】【分析】由题意可知曲线为圆的右半圆作出直线与曲线的图象可知直线是过点且斜率为的直线求出当直线与曲线相切时k 的值利用数形结合思想可得出当直线与曲线有两个公共点时实数的取值范围【详解】对于直线则 解析:4,23⎛⎤ ⎥⎝⎦【解析】【分析】由题意可知,曲线C 为圆()()22111x y -+-=的右半圆,作出直线l 与曲线C 的图象,可知直线l 是过点()0,2-且斜率为k 的直线,求出当直线l 与曲线C 相切时k 的值,利用数形结合思想可得出当直线l 与曲线C 有两个公共点时实数k 的取值范围.【详解】对于直线:2l y kx =-,则直线l 是过点()0,2P -且斜率为k 的直线,对于曲线()2:111C y x --=-,则101x x -≥⇒≥,曲线C 的方程两边平方并整理得()()22111x y -+-=,则曲线C 为圆()()22111x y -+-=的右半圆,如下图所示:当直线l 与曲线C 相切时,0k >()222123111k k k k ---==++-,解得43k =, 当直线l 过点()1,0A 时,则有20k -=,解得2k =.结合图象可知,当4,23k ⎛⎤∈ ⎥⎝⎦时,直线l 与曲线C 有两个交点. 故答案为:4,23⎛⎤ ⎥⎝⎦. 【点睛】本题考查利用直线与曲线的交点个数求参数,解题的关键就是将曲线C 化为半圆,利用数形结合思想求解,同时要找出直线与曲线相切时的临界位置,考查数形结合思想的应用,属于中等题.24.【解析】【分析】推导出两边平方可得的长【详解】二面角为是棱上的两点分别在半平面内且的长故答案为:【点睛】本题考查线段长的求法考查空间中线线线面面面间的位置关系等基础知识考查运算求解能力考查函数与方程 解析:217【解析】【分析】推导出CD CA AB BD =++,两边平方可得CD 的长.【详解】二面角l αβ--为60︒,A 、B 是棱l 上的两点,AC 、BD 分别在半平面α、β内, 且AC l ⊥,BD l ⊥,4AB =,6AC =,8BD =,∴CD CA AB BD =++,∴22()CD CA AB BD =++2222CA AB BD CA BD =+++361664268cos12068=+++⨯⨯⨯︒=,CD ∴的长||68217CD ==.故答案为:217.【点睛】本题考查线段长的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.25.【解析】设球的半径为表面积解得∵在中∴从圆心作平面的垂线垂足在斜边的中点处∴球心到平面的距离故答案为点睛:本题考查的知识点是空间点线面之间的距离计算其中根据球心距球半径解三角形我们可以求出所在平面截 3【解析】设球的半径为r ,表面积24π20πS r ==,解得5r =ABC 中,2AB AC ==,22BC =222AB AC BC +=,∴90BAC ∠=︒,从圆心作平面ABC 的垂线,垂足在斜边BC 的中点处,∴球心到平面ABC 的距离22132d r BC ⎛⎫=-= ⎪⎝⎭3 点睛:本题考查的知识点是空间点、线、面之间的距离计算,其中根据球心距d ,球半径R ,解三角形我们可以求出ABC 所在平面截球所得圆(即ABC 的外接圆半径),构造直角三角形,满足勾股定理,我们即可求出球心到平面ABC 的距离是与球相关的距离问题常用方法.三、解答题26.(1)1x =或0y =;(2)()()22134x y -++=.【解析】【分析】(1)对直线l 的斜率是否存在进行分类讨论,利用圆心到直线l 的距离等于2可求得直线l 的方程;(2)先通过点到直线的距离及勾股定理可解得直线m 的斜率,然后将直线m 的方程与圆的方程联立,求出线段AB 的中点,作为圆心,并求出所求圆的半径,进而可得出所求圆的方程.【详解】(1)由题意知,圆C 的标准方程为()()22329x y -++=,∴圆心()3,2C -,半径3r =,①当直线l 的斜率k 存在时,设直线的方程为()01y k x -=-,即kx y k 0--=, 则圆心到直线l的距离为2d ==,0k ∴=.∴直线l 的方程为0y =;②当直线l 的斜率不存在时,直线l 的方程为1x =,此时圆心C 到直线l 的距离为2,符合题意.综上所述,直线l 的方程为1x =或0y =;(2)依题意可设直线m 的方程为1y kx =-,即()100kx y k --=<,则圆心()3,2C -到直线m的距离d === 22320k k ∴+-=,解得12k =或2k =-, 又0k <,2k ∴=-,∴直线m 的方程为210x y ---=即210x y ++=,设点()11,A x y 、()22,B x y ,联立直线m 与圆C 的方程得()()22210329x y x y ++=⎧⎪⎨-++=⎪⎩, 消去y 得251010x x -+=,122x x ∴+=,则线段AB 的中点的横坐标为1212x x +=,把1x =代入直线m 中得3y =-, 所以,线段AB 的中点的坐标为()1,3-, 由题意知,所求圆的半径为:122AB =, ∴以线段AB 为直径的圆的方程为:()()22134x y -++=.【点睛】本题考查利用圆心到直线的距离求直线方程,同时也考查了圆的方程的求解,涉及利用直线截圆所得弦长求参数,考查计算能力,属于中等题.27.(1)3x =或34210x y +-=;(2)34-. 【解析】【分析】(1)考虑切线的斜率是否存在,结合直线与圆相切的的条件d=r ,直接求解圆的切线方程即可.(2)利用圆的圆心距、半径及半弦长的关系,列出方程,求解a 即可.【详解】(1)由圆的方程得到圆心(1,2),半径2r .当直线斜率不存在时,直线3x =与圆C 显然相切;当直线斜率存在时,设所求直线方程为3(3)y k x -=-,即330kx y k -+-=,2=,解得34k =-, ∴ 方程为33(3)4y x -=--,即34210x y +-=. 故过点M 且与圆C 相切的直线方程为3x =或34210x y +-=. (2)∵ 弦长AB为 2.圆心到直线40ax y -+=的距离d =∴2242⎛⎛⎫+= ⎝⎭, 解得34a =-. 【点睛】本题考查直线与圆的位置关系的综合应用,考查切线方程的求法,考查了垂径定理的应用,考查计算能力. 28.(1)见证明;(2) 【解析】【分析】(1)由PA ⊥面ABCD 可知PA AE ⊥,又可证AE BC ⊥,根据线面垂直的判定即可证明(2) 取AB 中点M ,作MN AF ⊥于N ,连CN ,可证MNC ∠是二面角B AF C --的平面角,解三角形即可求解.【详解】(1)PA ⊥面ABCD ,AE ⊂面ABCD ,PA AE ∴⊥; 又底面ABCD 为菱形,60ABC ∠=,E 为BC 中点,,//,,AE BC AD BC AE AD ∴⊥∴⊥AE ∴⊥面PAD ;(2)AE 面PAD ,AHE ∴∠是EH 与面PAD 所成角,tan ,AE AHE AH PO AH∠=⊥时,AH 最小,tan AHE ∠最大,AHE ∠最大, 令2AB =,则3,1AE AH ==,在Rt AHD ∆中,2,30AD ADH =∠=, 在Rt PAD ∆中,233PA = PA ⊥面ABCD ,∴面PAB ⊥面ABCD ,且交线为AB ,取AB 中点M ,正ABC ∆中,,CM AB CM ⊥∴⊥面PAB ,作MN AF ⊥于N ,连CN ,由三垂线定理得CN AF ⊥,MNC ∠是二面角B AF C --的平面角.3CM =.在PAB ∆中,23,2,3BF AF AB ===边AF 上的高11,2BG MN ==, tan 23CM MNC MN∠==【点睛】 本题主要考查了线面垂直的判定,线面垂直的性质,二面角的求法,属于难题. 29.(1)A (1,3);(2)直线l 方程为20x y -+=,最短弦长为223)在直线MC 上存在定点4,43N ⎛⎫-⎪⎝⎭,使得||||PM PN 为常数32. 【解析】【分析】(1)利用直线系方程的特征,直接求解直线l 过定点A 的坐标;(2)当AC ⊥l 时,所截得弦长最短,由题知C (0,4),2r,求出AC 的斜率,利用点到直线的距离,转化求解即可;(3)由题知,直线MC 的方程为4y =,假设存在定点N (t ,4)满足题意,则设。
陕西省定边县安边中学2016-2017学年高一上学期第三次月考数学试题

安边中学2016年秋高一数学第三次数学月考试题 班级: 姓名: 一、选择题(共60分)1.函数65)(2+-=x x f x 的零点是 ( ) A 、-2,3 B 、-2,-3 C 、2,3 D 、2,-3 2.()833-+=x x f x ,且()()(),0)2(,025.1,05.1,01><><f f f f则函数()f x 的零点落在区间( )A .(1,1.25)B .(1.25,1.5)C .(1.5,2)D .不能确定 3.分别在两个平面内的两条直线间的位置关系是( )A.异面B.平行C.相交D.以上都有可能 4.已知函数()2log ,0,3,0x x x f x x >⎧=⎨≤⎩则18ff ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦( ) A .9 B .19C .127D . 275.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )6.三个数60.7、0.76、log 0.76的大小顺序是… ( ) A.0.76<log 0.76<60.7B.0.76<60.7<log 0.76C.log 0.76<60.7<0.76D.log 0.76<0.76<60.77.函数()39xf x =-的零点是( )A .(2,0)B .(3,0)C .2D .38.若函数()1f x ax =+在区间(1,1)-上存在一个零点,则实数a 的取值范围是( ) A.1a > B.1a <- C..1a <-或1a > D.11a -<< 9.若函数()y f x =是函数()1xy a a a =>≠0,且的反函数,且()42f =-, 则()f x =( ) A .B .C .x 2logD .2x10、如果一条直线与两个平行平面中的一个平行,那么这条直线与另外一个平面的位置关系( )A 、平行B 、相交C 、在平面内D 、平行或在平面内11.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如下左图,图中四边形是为体现其直观性所作的辅助线.其实际直观图中四边形不存在,当其正视图和侧视图完全相同时,它的正视图和俯视图分别可能是( )A .a ,bB .a ,cC .c ,bD .b ,d12.一个锥体的正视图和左视图如下图,下面选项中,不可能是该锥体的俯视图的是( )答 题 卡一、选择题(共5⨯12=60分)二、填空题(共20分) 13、函数xy -=12log 的定义域是 .14、已知幂函数()a f x x =的图象过点1124⎛⎫⎪⎝⎭,,则log 8a = . 15、已知AB//PQ,BC//QR,30︒=∠ABC ,则=∠PQR .16、以下命题(其中a b ,表示直线, a 表示平面):①若//a b ,b α⊂,则//a α; ②若//a α,b α⊂,则//a b ;③若//a b ,//b α,则//a α;其中正确命题的是 。
2016-2017学年高一(承智班)下学期期中考试数学试题 含答案

河北定州中学2016—2017学年度第二学期期中考试高一年级承智班数学试卷第I 卷(选择题)一、选择题(每小题5分,共60分)1.在ABC ∆中,a ,b,c 分别为A 、B 、C 的对边,若23,3,cos 4bac a c B =+==,C. 3 D 。
—3 则.AB BC =( )A. 32B 。
- 32( )2.若sin cos cos A B Ca b c==,则ABC是 A. 等腰直角三角形 B 。
有一内角是30的直角三角形 C. 等边三角形 D 。
有一内角是30的等腰三角形3.一海轮从A 处出发,以每小时40海里的速度沿南偏东40的方向直线航行,30分钟后到达B 处,在C 处有一座灯塔,海伦在A处观察灯塔,其方向是南偏东70,在B 处观察灯塔,其方向是北偏东65,那么,B C 两点间的距离是( )A.海里 B。
C。
D.4.数列{}n a 满足211233332n n n a a a a -++++=,则n a =( )A. 1132n -⋅ B. 1123n -⋅ C 。
12nD.3nn 5.(福建省漳州市八校2017届高三下学期2月联考数学文第8题) 大衍数列,来源于《乾坤谱》中对易传“大衍之数五十"的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和。
是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0、2、4、8、12、18、24、32、40、50…… ,则此数列第20项为( )A. 180 B 。
200 C. 128 D 。
162 6.定义为个正数的“均倒数”。
若已知数列的前项的“均倒数”为,又,则…( )A 。
B. C 。
D.7.已知01c <<,1a b >>,下列不等式成立的是A.a b c c >B.a ba cb c>-- C.c c ba ab >D 。
2016-2017学年陕西省西安市高一数学下期中试卷(理科)

2016-2017 学年陕西省西安市高一 (下)期中数学试卷(理科)一、选择题:在每小题给出的四个选项中,只有一项符合题目要求(本大题共 12小题,每小题4分,共48分)21 .已知集合 M={x| - 1 v x v 3}, N={x|x +2x - 3V 0},则集合 M n N 等于( )A . {x| - 1v x v 3}B . {x| - 3v x v 1}C . {x| - 1 v x v 1}D . {x| - 3v x v 3}2. 如图所示,在三棱台 A ' B ' -ABC 中,沿A ' B(截去三棱锥 A'- ABC ,则剩余的部分是4. 在等比数列{a n }中,a 1= - 16, a 4=8,C .5.若a , b , c 为实数,则下列命题错误的是()A .若 ac 2>be 2,则 a > bB .若 a v b v 0,则 a 2v b 21 1C .若 a >b >0,贝V v .D .若 a v b v 0, c >d >0,贝ac v bd 6. 一个水平放置的平面图形的斜二测直观图是一个底角为 45 °腰和上底均为1的等腰梯形,则这个平面图形的面积为()1 V2V2心V2A .二 +B . 1+C . 1+D . 2+] 107. 数列{a n }的通项公式是a n =、胡](n € N* ),若前n 项的和为• •,则项数为( )C .三棱柱D •组合体3. 在△ ABC 中,,则C=C . 77T 则 a 7=(A .三棱锥B .四棱锥A . 12B .C . 1011。
陕西省定边县安边中学2016-2017学年高二下学期中期考试数学(文)试题
安边中学2017年春中期高二数学文科试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题 1.下列四个函数中,在()0,+∞上为增函数的是()A. ()3f x x =-B. ()23f x x x =-C. ()11f x x =-+ D.()f x x =-2.执行如图所示的程序框图,若输入的5n =,则输出的结果为()A. 4B. 5C. 6D. 73.复数()z a i a R =+∈的虚部为()A. 1B. iC. -1D. i -4.若集合{}2,1,0,1,2A =--,集合(){|30}B x x x =+<,则A B ⋂等于()A. {}1,0,1,2-B. {}2,1--C. {}1,2D. {}0,1,25.设集合2{|230},{|33}M x x x N x x =--≥=-<<,则()A. M N ⊆B. N M ⊆C. M N R ⋃=D. M N ⋂=∅6.已知集合{}0,1A =,{},,B x y z =,则从集合A 到集合B 的映射可能有()种A .6B .8C .9D .127.若函数()21f x x ax x =++在1,2⎛⎫+∞ ⎪⎝⎭是增函数,则a 的取值范围是() A. []1,0- B. [)1,-+∞ C. []0,3 D. [)3,+∞ 8.已知复数2i 1iz +=-(i 为虚数单位),那么z 的共轭复数为() A. 33i 22+ B. 13i 22- C. 13i 22+ D. 33i 22- 9.下列说法正确的是()A .0与}0{的意义相同B .高一(1)班个子比较高的同学可以形成一个集合C .集合N}x 2,y 3x |y){(x,A ∈=+=是有限集D .方程0122=++x x 的解集只有一个元素10.已知z 满足()1i z i -=(i 为虚数单位),则z =()C. 2D. 1 11.函数)1lg(3++-=x x y 的定义域是()A .)3,1(- B.)3,1[- C.]3,1(- D.),3(+∞12.当4n =时,执行如图所示的程序框图,输出的S 值为()A. 6B. 8C. 14D. 30第II 卷(非选择题)二、填空题13.已知集合{}0,1,2A =,则A 的子集个数为__________.14.函数()1f x x =-的定义域为__________. 15.如果框图所给的程序运行结果为35S =,那么判断框中整数m 的值为__________.16.若函数()22f x x mx m =-++是偶函数,则m =____________.三、解答题17.已知全集UR =,集合{|30},{|14}M x x N x x =-≥=-≤<. (1)求集合,M N M N ;(2)求集合U C N .(3)求集合()U C N M .18.计算:(1)()()1223029279.6 1.548--⎛⎫⎛⎫---+ ⎪ ⎪⎝⎭⎝⎭; (2)122i i +-;(12)(2)i i +⋅- (3)121111333424(3)(4)(2)xy x y x y -----19.设集合{|12}A x x =-<<,{|2123}B x a x a =-<<+. (1)若A B ⊆,求a 的取值范围;(2)若A B =∅ ,求a 的取值范围.20.当实数m 为何值时,复数()()221z m m m i =++-是: (1)实数;(2)虚数;(3)纯虚数21.已知函数()321313f x x x x =--+. (1)求()y f x =在1x =处的切线方程;(2)求()y f x =的极值点.22.已知函数2()21f x x ax =--(1)当1a =-,求()f x 在[2,1]-上的最大值和最小值;(2)求()f x 在区间[]1,2-的最小值.。
2016-2017年陕西师大附中高一(下)期中数学试卷和答案

2016-2017学年陕西师大附中高一(下)期中数学试卷一、选择题(本大题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(4分)已知向量=(1,m),=(m,2),若∥,则实数m等于()A.﹣B.C.﹣或D.02.(4分)若角α与β的终边垂直,则α与β的关系是()A.β=α+90°B.β=α±90°C.β=k•360°+α+90°,k∈ZD D.β=k•360°+α±90°,k∈Z3.(4分)函数f(x)=2sinxcosx是()A.最小正周期为2π的奇函数B.最小正周期为2π的偶函数C.最小正周期为π的奇函数D.最小正周期为π的偶函数4.(4分)已知为两个单位向量,下列四个命题中正确的是()A.如果与平行,那么与相等B.与相等C.如果与平行,那么或D.与共线5.(4分)的值是()A.B.C.0D.16.(4分)设,,且、夹角为,则等于()A.2B.4C.12D.7.(4分)设a=sin33°,b=cos55°,c=tan35°,则()A.a>b>c B.b>c>a C.c>b>a D.c>a>b 8.(4分)已知△ABC和点M满足.若存在实数m使得成立,则m=()A.2B.3C.4D.59.(4分)已知非零向量,满足(+)•=0,且•=,则△ABC的形状是()A.三边均不相等的三角形B.直角三角形C.等腰(非等边)三角形D.等边三角形10.(4分)若sin2α=,sin(β﹣α)=,且α∈[,π],β∈[π,],则α+β的值是()A.B.C.或D.或11.(4分)定义在R上的偶函数f(x)满足f(2﹣x)=f(x),且在[﹣3,﹣2]上是减函数,α,β是钝角三角形的两个锐角,且α<β,则下列不等式关系中正确的是()A.f(sinα)>f(cosβ)B.f(cosα)<f(cosβ)C.f(cosα)>f(cosβ)D.f(sinα)<f(cosβ)12.(4分)如图,边长为1的正方形ABCD的顶点A,D分别在x轴、y轴正半轴上移动,则的最大值是()A.2B.C.πD.4二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)若角θ的终边经过点P(﹣1,﹣2),则cosθ=.14.(5分)若扇形的周长是16cm,圆心角是2弧度,则扇形的面积是.15.(5分)已知(tanα+3)(tanα﹣2)=0,且α为第三象限角,则的值为.16.(5分)有以下关于三角函数的命题:(1)存在φ,使函数f(x)=sin(x+φ)是偶函数;(2)sin15°+cos15°>sin16°+cos16°;(3)对任意的x∈[0,π],都有;(4)函数的零点个数为5.其中真命题的序号是.三、解答题(本大题共5小题,共52分,解答应写出文字说明、证明过程或推演步骤)17.(10分)已知函数f(x)=﹣sin(2x+)+6sinxcosx﹣2cos2x+1,x∈R.(Ⅰ)求f(x)的最小正周期;(Ⅱ)求f(x)在区间上的最大值和最小值.18.(10分)试用向量方法证明“平行四边形的对角线互相平分”.19.(10分)海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:经长期观测,这个港口的水深与时间的关系,可近似用函数f(t)=Asin(ωt+ϕ)+b来描述.(1)根据以上数据,求出函数f(t)=Asin(ωt+ϕ)+b的表达式;(2)一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口然后离开港口?每次在港口能停留多久?20.(10分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g (x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.21.(12分)已知,,若函数,且.(1)计算g(1)+g(2)+g(3)+…+g(2017)的值;(2)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.2016-2017学年陕西师大附中高一(下)期中数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(4分)已知向量=(1,m),=(m,2),若∥,则实数m等于()A.﹣B.C.﹣或D.0【解答】解:∵=(1,m),=(m,2),且,所以1•2=m•m,解得m=或m=.故选:C.2.(4分)若角α与β的终边垂直,则α与β的关系是()A.β=α+90°B.β=α±90°C.β=k•360°+α+90°,k∈ZD D.β=k•360°+α±90°,k∈Z【解答】解:若角α与β的终边垂直,则β﹣α=k•360°±90°,k∈Z,∴β=k•360°+α±90°,k∈Z.故选:D.3.(4分)函数f(x)=2sinxcosx是()A.最小正周期为2π的奇函数B.最小正周期为2π的偶函数C.最小正周期为π的奇函数D.最小正周期为π的偶函数【解答】解:∵f(x)=2sinxcosx=sin2x,∴f(x)为周期为π的奇函数,故选:C.4.(4分)已知为两个单位向量,下列四个命题中正确的是()A.如果与平行,那么与相等B.与相等C.如果与平行,那么或D.与共线【解答】解:∵为两个单位向量,∴如果与平行,那么或,故A不正确,C正确;因为两向量相等的充要条件是模相等且方向相同,所以B不正确;∵为两个单位向量,∴为两个向量不一定平行,故D不正确.故选:C.5.(4分)的值是()A.B.C.0D.1【解答】解:因为tan30=tan(11+19)==,所以(tan11°+tan19°)=1﹣tan11°tan19°则原式==1﹣tan11°•tan19°+tan11°•tan19°=1.故选:D.6.(4分)设,,且、夹角为,则等于()A.2B.4C.12D.【解答】解:∵=1,=2,、夹角为,∴=(2+)•(2+)=4+4•+=4+4•||cos+4=4+4×1×2×(﹣)+4=4,∴|2+|=2.故选:A.7.(4分)设a=sin33°,b=cos55°,c=tan35°,则()A.a>b>c B.b>c>a C.c>b>a D.c>a>b【解答】解:由诱导公式可得b=cos55°=cos(90°﹣35°)=sin35°,由正弦函数的单调性可知b>a,而c=tan35°=>sin35°=b,∴c>b>a故选:C.8.(4分)已知△ABC和点M满足.若存在实数m使得成立,则m=()A.2B.3C.4D.5【解答】解:由知,点M为△ABC的重心,设点D为底边BC的中点,则==,所以有,故m=3,故选:B.9.(4分)已知非零向量,满足(+)•=0,且•=,则△ABC的形状是()A.三边均不相等的三角形B.直角三角形C.等腰(非等边)三角形D.等边三角形【解答】解:∵(+)•=0,,分别为单位向量,∴∠A的角平分线与BC垂直,∴AB=AC,∵cosA=•=,∴∠A=,∴∠B=∠C=∠A=,∴三角形为等边三角形.故选:D.10.(4分)若sin2α=,sin(β﹣α)=,且α∈[,π],β∈[π,],则α+β的值是()A.B.C.或D.或【解答】解:∵α∈[,π],β∈[π,],∴2α∈[,2π],又0<sin2α=<,∴2α∈(,π),即α∈(,),∴β﹣α∈(,),∴cos2α=﹣=﹣;又sin(β﹣α)=,∴β﹣α∈(,π),∴cos(β﹣α)=﹣=﹣,∴cos(α+β)=cos[2α+(β﹣α)]=cos2αcos(β﹣α)﹣sin2αsin(β﹣α)=﹣×(﹣)﹣×=.又α∈(,),β∈[π,],∴(α+β)∈(,2π),∴α+β=,故选:A.11.(4分)定义在R上的偶函数f(x)满足f(2﹣x)=f(x),且在[﹣3,﹣2]上是减函数,α,β是钝角三角形的两个锐角,且α<β,则下列不等式关系中正确的是()A.f(sinα)>f(cosβ)B.f(cosα)<f(cosβ)C.f(cosα)>f(cosβ)D.f(sinα)<f(cosβ)【解答】解:∵偶函数f(x)在[﹣3,﹣2]上是减函数,∴f(x)在[2,3]上是增函数,又∵偶函数f(x)满足f(2﹣x)=f(x),∴f(x)=f(x﹣2),即f(x+2)=f(x),函数的周期T=2,∴f(x)在[0,1]上是增函数,∵α,β是钝角三角形的两个锐角,且α<β,∴根据余弦函数在(0,π)上递减得,0<cosβ<cosα<1,则f(cosα)>f(cosβ),故选:C.12.(4分)如图,边长为1的正方形ABCD的顶点A,D分别在x轴、y轴正半轴上移动,则的最大值是()A.2B.C.πD.4【解答】解:如图令∠OAD=θ,由于AD=1故0A=cosθ,OD=sinθ,如图∠BA x=﹣θ,AB=1,故x B=cosθ+cos(﹣θ)=cosθ+sinθ,y B=sin(﹣θ)=cosθ,故=(cosθ+sinθ,cosθ),同理可求得C(sinθ,cosθ+sinθ),即=(sinθ,cosθ+sinθ),∴•=(cosθ+sinθ,cosθ)•(sinθ,cosθ+sinθ)=1+sin2θ,=1+sin2θ 的最大值是2,故选:A.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)若角θ的终边经过点P(﹣1,﹣2),则cosθ=﹣.【解答】解:∵角θ的终边经过点P(﹣1,﹣2),∴x=﹣1,y=﹣2,r=|OP|==,∴cosθ==﹣,故答案为:﹣.14.(5分)若扇形的周长是16cm,圆心角是2弧度,则扇形的面积是16cm2;.【解答】解:设扇形半径为r,面积为s,圆心角是α,则α=2,弧长为αr,则周长16=2r+α r=2r+2r=4r,∴r=4,扇形的面积为:s=α r2=×2×16=16 (cm2),故答案为16 cm2.15.(5分)已知(tanα+3)(tanα﹣2)=0,且α为第三象限角,则的值为﹣3.【解答】解:由(tanα+3)(tanα﹣2)=0,得tanα=﹣3或tanα=2.∵α为第三象限角,∴tanα=2.则==.故答案为:﹣3.16.(5分)有以下关于三角函数的命题:(1)存在φ,使函数f(x)=sin(x+φ)是偶函数;(2)sin15°+cos15°>sin16°+cos16°;(3)对任意的x∈[0,π],都有;(4)函数的零点个数为5.其中真命题的序号是(1)、(4).【解答】解:对于(1),当φ=+kπ,k∈Z时,函数f(x)=sin(x+φ)是偶函数,(1)正确;对于(2),sin15°+cos15°=sin(15°+45°)=sin60°,sin16°+cos16°=sin(16°+45°)=sin61°,sin60°<sin61°,∴sin15°+cos15°<sin16°+cos16°,(2)错误;对于(3),对任意的x∈[0,π],sinx≥0,∴==|sinx|=sinx,(3)正确;对于(4),函数的零点,是函数y=x与y=cosx图象交点的横坐标,在同一坐标系内画出两函数的图象,如图所示,由图象知,y=x与y=cosx的图象有5个交点,∴f(x)的零点有5个,(4)正确;综上,真命题的序号是(1)、(4).故答案为:(1)、(4).三、解答题(本大题共5小题,共52分,解答应写出文字说明、证明过程或推演步骤)17.(10分)已知函数f(x)=﹣sin(2x+)+6sinxcosx﹣2cos2x+1,x∈R.(Ⅰ)求f(x)的最小正周期;(Ⅱ)求f(x)在区间上的最大值和最小值.【解答】解:(I)∵sinxcosx=sin2x,cos2x=(1+cos2x)∴f(x)=﹣sin(2x+)+6sinxcosx﹣2cos2x+1=﹣sin2x﹣cos2x+3sin2x﹣(1+cos2x)+1=2sin2x﹣2cos2x=2sin(2x﹣)因此,f(x)的最小正周期T==π;(II)∵0≤x≤,∴﹣≤2x﹣≤∴当x=0时,sin(2x﹣)取得最小值﹣;当x=时,sin(2x﹣)取得最大值1由此可得,f(x)在区间上的最大值为f()=2;最小值为f(0)=﹣2.18.(10分)试用向量方法证明“平行四边形的对角线互相平分”.【解答】证明:设O为平行四边形ABCD对角线的交点,如图所示;则=,﹣=﹣,∴+=+=,即=﹣,=﹣,∴||=||,||=||,即AC、BD互相平分;故“平行四边形的对角线互相平分”.19.(10分)海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:经长期观测,这个港口的水深与时间的关系,可近似用函数f(t)=Asin(ωt+ϕ)+b来描述.(1)根据以上数据,求出函数f(t)=Asin(ωt+ϕ)+b的表达式;(2)一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口然后离开港口?每次在港口能停留多久?【解答】(本题满分12分)解:(1)由表格知f max=7.5,f min=2.5,…(1分),…(2分)T=12,∴,…(4分)即当t=2时,,解得,又,∴…(6分)∴.(2)货船需要的安全水深为4.25+2=6.25米,∴当f(t)≥6.25时就可以进港.…(7分)令,得…(8分)∴,…(9分)解得12k≤t≤4+12k,…(10分)又t∈[0,24),故k=0时,t∈[0,4];k=1时,t∈[12,16]…(11分)即货船可以在0时进港,早晨4时出港;或在中午12时进港,下午16时出港,每次可以在港口停留4小时左右.…(12分)20.(10分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g (x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.【解答】解:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.数据补全如下表:且函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)知f(x)=5sin(2x﹣),得g(x)=5sin(2x+2θ﹣).因为y=sinx的对称中心为(kπ,0),k∈Z.令2x+2θ﹣=kπ,解得x=,k∈Z.由于函数y=g(x)的图象关于点(,0)成中心对称,令=,解得θ=,k∈Z.由θ>0可知,当K=1时,θ取得最小值.21.(12分)已知,,若函数,且.(1)计算g(1)+g(2)+g(3)+…+g(2017)的值;(2)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.【解答】解:(1)∵,,函数,且.∴f(x)=2sinxsin(x﹣)+2sinxcosx=sin2x+sin2x=sin2x﹣cos2x+=sin(2x﹣)+,∴g(x)=f()=sin(x﹣)+.T=4,∴g(1)+g(2)+g(3)+g(4)=g(5)+g(6)+g(7)+g(8)=…=g(2009)+g(2010)+g(2011)+g(2012).g(1)+g(2)+g(3)+g(4)=2,g(1)+g(2)+g(3)+…+g(2014)=503×2+g(1)+g(2)=1006+=.(2)g(x)在[t,t+2]上零点的个数等价于y=sin(x﹣)与y=﹣两图象交点个数.在同一直角坐标系内作出这两个数的图象.当4k<t<+4k,k∈Z时,由图象可知,y=sin(x﹣)与y=﹣两图象无交点,g(x)无零点,当+4k≤t<2+4k或+4k<t≤4+4k时,y=sin(x﹣)与y=﹣两图象1个交点,g(x)1个零点当2+4k≤t≤+4k时,y=sin(x﹣)与y=﹣两图象2个交点,∴g(x)在[t,t+2]上零点的个数是2.。
2016-2017年陕西省西安中学高一(下)期中数学试卷和答案

2016-2017学年陕西省西安中学高一(下)期中数学试卷一、选择题(共12小题)1.(5分)412°角的终边在()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)点A(x,y)是300°角终边上异于原点的一点,则值为()A.B.﹣C.D.﹣3.(5分)根据如下样本数据,得到回归方程=bx+a,则()A.a>0,b>0B.a>0,b<0C.a<0,b>0D.a<0,b<0 4.(5分)阅读如图所示的程序框图,运行相应的程序,输出的S的值等于()A.18B.20C.21D.405.(5分)某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是()A.B.C.D.6.(5分)已知sina=,cosa=﹣,则角a所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限7.(5分)从长度分别为2,3,4,5的四条线段中任意取出三条线段,则以这三条线段为边可以构成三角形的概率是()A.B.C.D.8.(5分)下列函数中,既是以π为周期的奇函数,又是上的增函数的是()A.y=tanx B.y=cosx C.D.y=|sinx| 9.(5分)根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml(不含80)之间,属于酒后驾车,处暂扣一个月以上三个月以下驾驶证,并处200元以上500元以下罚款;血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,处十五日以下拘留和暂扣三个月以上六个月以下驾驶证,并处500元以上2000元以下罚款.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为()A.2160B.2880C.4320D.864010.(5分)方程|x|=cosx在(﹣∞,+∞)内()A.没有根B.有且仅有一个根C.有且仅有两个根D.有无穷多个根11.(5分)已知sin(α+75°)=,则cos(α﹣15°)=()A.B.﹣C.D.﹣12.(5分)从区间[0,1]随机抽取2n个数x1,x2,…,x n,y1,y2,…,y n构成n 个数对(x1,y1),(x2,y2)…(x n,y n),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为()A.B.C.D.二.填空题(共5小题)13.(5分)已知样本数据x1,x2,…,x n的均值=5,则样本数据2x1+1,2x2+1,…,2x n+1 的均值为.14.(5分)点P(﹣1,2)在角α的终边上,则=.15.(5分)从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离小于该正方形边长的概率为.16.(5分)函数y=cos2x﹣3cosx+2的最小值为.17.(5分)(必做题)为调查长沙市中学生平均每人每天参加体育锻炼时间(单位:分钟),按锻炼时间分下一列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有l0000名中学生参加了此项活动,如图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是.三.解答题(共4小题)18.(15分)已知角α的终边过点P(4,﹣3)(1)求sinα,cosα,tanα的值.(2)求的值.19.(15分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:甲:82,81,79,78,95,88,93,84乙:92,95,80,75,83,80,90,85(1)用茎叶图表示这两组数据;(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.20.(17分)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.(Ⅰ)求取出的两个球上标号为相邻整数的概率;(Ⅱ)求取出的两个球上标号之和能被3整除的概率.21.(18分)20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:(Ⅰ)求频率分布直方图中a的值;(Ⅱ)分别求出成绩落在[50,60)与[60,70)中的学生人数;(Ⅲ)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.2016-2017学年陕西省西安中学高一(下)期中数学试卷参考答案与试题解析一、选择题(共12小题)1.(5分)412°角的终边在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:412°=360°+52°,∴412°与52°终边相同.故选:A.2.(5分)点A(x,y)是300°角终边上异于原点的一点,则值为()A.B.﹣C.D.﹣【解答】解:点A(x,y)是300°角终边上异于原点的一点,则=tan300°=tan (180°+120°)=tan120°=tan(180°﹣60°)=﹣tan60°=﹣,故选:B.3.(5分)根据如下样本数据,得到回归方程=bx+a,则()A.a>0,b>0B.a>0,b<0C.a<0,b>0D.a<0,b<0【解答】解:由题意可知:回归方程经过的样本数据对应的点附近,是减函数,所以b<0,且回归方程经过(3,4)与(4,2.5)附近,所以a>0.故选:B.4.(5分)阅读如图所示的程序框图,运行相应的程序,输出的S的值等于()A.18B.20C.21D.40【解答】解:由程序框图知:算法的功能是求S=21+22+…+2n+1+2+…+n的值,∵S=21+22+1+2=2+4+1+2=9<15,S=21+22+23+1+2+3=2+4+8+1+2+3=20≥15.∴输出S=20.故选:B.5.(5分)某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是()A.B.C.D.【解答】解:设小明到达时间为y,当y在7:50至8:00,或8:20至8:30时,小明等车时间不超过10分钟,故P==,故选:B.6.(5分)已知sina=,cosa=﹣,则角a所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:由sina=>0得,角a的终边在第一、或第二象限;再由cosa=﹣<0得,角a的终边在第二、或第三象限,综上,角a所在的象限是第二象限.7.(5分)从长度分别为2,3,4,5的四条线段中任意取出三条线段,则以这三条线段为边可以构成三角形的概率是()A.B.C.D.【解答】解:由题意知,本题是一个古典概率,∵试验发生包含的基本事件为(2,3,4);(2,3,5);(2,4,5);(3,4,5),共4种;而满足条件的事件是可以构成三角形的事件为(2,3,4);(2,4,5);(3,4,5),共3种;∴以这三条线段为边可以构成三角形的概率是,故选:D.8.(5分)下列函数中,既是以π为周期的奇函数,又是上的增函数的是()A.y=tanx B.y=cosx C.D.y=|sinx|【解答】解:函数是以π为周期的奇函数,选项A正确,B是偶函数不正确;C 的周期是2π,D是偶函数,y=tanx在上的增函数正确;故选:A.9.(5分)根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml(不含80)之间,属于酒后驾车,处暂扣一个月以上三个月以下驾驶证,并处200元以上500元以下罚款;血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,处十五日以下拘留和暂扣三个月以上六个月以下驾驶证,并处500元以上2000元以下罚款.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为()A.2160B.2880C.4320D.8640【解答】解:∵血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,通过频率分步直方图知道属于醉驾的频率是(0.005+0.01)×10=0.15,∵样本容量是28800,∴醉驾的人数有28800×0.15=4320故选:C.10.(5分)方程|x|=cosx在(﹣∞,+∞)内()A.没有根B.有且仅有一个根C.有且仅有两个根D.有无穷多个根【解答】解:方程|x|=cosx在(﹣∞,+∞)内根的个数,就是函数y=|x|,y=cosx 在(﹣∞,+∞)内交点的个数,如图,可知只有2个交点.故选:C.11.(5分)已知sin(α+75°)=,则cos(α﹣15°)=()A.B.﹣C.D.﹣【解答】解:∵sin(α+75°)=,则cos(α﹣15°)=sin[90°﹣(α﹣15°)]=sin (α+75°)=,故选:C.12.(5分)从区间[0,1]随机抽取2n个数x1,x2,…,x n,y1,y2,…,y n构成n 个数对(x1,y1),(x2,y2)…(x n,y n),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为()A.B.C.D.【解答】解:由题意,两数的平方和小于1,对应的区域的面积为π•12,从区间[0,1】随机抽取2n个数x1,x2,…,x n,y1,y2,…,y n,构成n个数对(x1,y1),(x2,y2),…,(x n,y n),对应的区域的面积为12.∴=∴π=.故选:C.二.填空题(共5小题)13.(5分)已知样本数据x1,x2,…,x n的均值=5,则样本数据2x1+1,2x2+1,…,2x n+1 的均值为11.【解答】解:∵数据x1,x2,…,x n的平均数为均值=5,则样本数据2x1+1,2x2+1,…,2x n+1 的均值为:=5×2+1=11;故答案为:11.14.(5分)点P(﹣1,2)在角α的终边上,则=﹣10.【解答】解:∵角α的终边经过点P(﹣1,2),∴x=﹣1,y=2,则tanα=﹣2,cosα=﹣∴=﹣10.故答案为:﹣10.15.(5分)从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离小于该正方形边长的概率为.【解答】解:设正方形边长为1,则从正方形四个顶点及其中心这5个点中任取2个点,共有10条线段,4条长度为1,4条长度为,两条长度为,∴这2个点的距离小于该正方形边长的概率为:p==.故答案为:.16.(5分)函数y=cos2x﹣3cosx+2的最小值为0.【解答】解:令cosx=t,则t∈[﹣1,1],换元可得y=t2﹣3t+2,由二次函数的知识可知:函数y=t2﹣3t+2在t∈[﹣1,1]单调递减,∴当t=1时,函数取最小值y min=1﹣3+2=0故答案为:017.(5分)(必做题)为调查长沙市中学生平均每人每天参加体育锻炼时间(单位:分钟),按锻炼时间分下一列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有l0000名中学生参加了此项活动,如图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是0.38.【解答】解:由图知输出的S的值是运动时间超过20分钟的学生人数,由于统计总人数是10000,又输出的S=6200,故运动时间不超过20分钟的学生人数是3800事件“平均每天参加体育锻炼时间在0~20分钟内的学生的”频率是=0.38故答案为:0.38.三.解答题(共4小题)18.(15分)已知角α的终边过点P(4,﹣3)(1)求sinα,cosα,tanα的值.(2)求的值.【解答】解:(1)∵角α的终边过点P(4,﹣3),∴;,.(2)由三角函数的定义知,,,∴原式=.19.(15分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:甲:82,81,79,78,95,88,93,84乙:92,95,80,75,83,80,90,85(1)用茎叶图表示这两组数据;(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.【解答】解:(2)根据所给的数据得到(88﹣85)2+(93﹣85)2+(95﹣85)2]=35.5(90﹣85)2+(92﹣85)2+(95﹣85)2]=41∵=,s甲2<s乙2,∴甲的成绩较稳定,派甲参赛比较合适20.(17分)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.(Ⅰ)求取出的两个球上标号为相邻整数的概率;(Ⅱ)求取出的两个球上标号之和能被3整除的概率.【解答】解:设从甲、乙两个盒子中各取1个球,其数字分别为x,y,用(x,y)表示抽取结果,则所有可能有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16种.(Ⅰ)所取两个小球上的数字为相邻整数的结果有(1,2),(2,1),(2,3),(3,2),(3,4),(4,3),共6种.故所求概率.即取出的两个小球上的标号为相邻整数的概率为.(Ⅱ)所取两个球上的数字和能被3整除的结果有(1,2),(2,1),(2,4),(3,3),(4,2),共5种.故所求概率为.即取出的两个小球上的标号之和能被3整除的概率为.21.(18分)20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:(Ⅰ)求频率分布直方图中a的值;(Ⅱ)分别求出成绩落在[50,60)与[60,70)中的学生人数;(Ⅲ)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.【解答】解:(Ⅰ)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.(Ⅱ)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,成绩落在[60,70)中的学生人数为3×0.005×10×20=3.(Ⅲ)记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,故所求概率为P=.。
陕西省榆林市定边县安边中学2017-2018学年高一下学期

2018年春高一物理期中考试试题班级_________姓名__________考号__________一、选择题(其中1-16为单选题,每题3分,17-18为多选题,每题4分,共56分) 1.物体做匀速圆周运动时,一定不变的物理量是( ) A. 速度 B. 周期 C. 加速度 D. 合外力2.如图所示,a 、b 是地球赤道上的两点,b 、c 是地球表面上不同纬度同一经度上的两个点,下列说法中正确的是( )A. a 、b 、c 三点的角速度相同B. b 、c 两点的线速度大小相同C. a 、b 两点的线速度大小不相同D. b 、c 两点的角速度不相同3.如图所示,门上有 A 、B 两点,在开门的过程中,A 、B 两点的角速 度和线速度的大小关系为( )A. A B ωω>B. A B ωω<C. A B v v >D. A B v v <4.如图所示,自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样,它们的边缘上有三个点A ,B ,C .下列关于它们的线速度大小、角速度、周期、向心加速度大小关系式中正确的是( )A. v A >v B >v CB. ωA <ωB <ωCC. T A >T B >T CD. a A <a B <a C5.物体在水平恒力F 的作用下,在光滑的水平面上由静止前进了路程S .再进入一个粗糙水平面.又继续前进了路程S.设F在第一段路程中对物体做功为W1,在第二段路程中对物体做功为W2.则()A. W1>W2B. W1<W2C. W1=W2D. 无法判断6.如图所示,在水平地面上,一物块在与水平方向成θ角的恒力F作用下,水平向右运动了一段位移x.在此过程中,恒力F对物体所做的功为()A. FxcosθB. 错误!未找到引用源。
C. FxsinθD. 错误!未找到引用源。
7.下列哪些情况中力做的功为零()A. 向上抛出一物体上升过程中,重力对物体做的功B. 卫星做匀速圆周运动时,卫星受到的引力对卫星所做的功C. 汽车匀加速上坡时,合力对货物所做的功D. 汽车匀速上坡时,车厢底部摩擦力对货物所做的功8.如图所示,物体m沿不同的路径Ⅰ和Ⅱ从A滑到B,重力所做的功为()A. 沿路径Ⅰ和Ⅱ重力做功一样大。
陕西省定边县安边中学高一下学期中期数学试题

安边中学2017年春中期高一数学试卷一、选择题 :(本大题共12小题 ,每小题5分,共60分)1、已知下列各角:①-120°;②-240°;③180°;④495°, 其中是第二象限内角的是( ) A.①② B.①③ C.②③ D.②④2、若β是第四象限角,则180°-β是第( )象限角 A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限3、与600°角终边相同的角可表示为( ) A.k ·360°+220°(k ∈Z) B.k ·360°+240°(k ∈Z) C.k ·360°+60°(k ∈Z) D.k ·360°+260°(k ∈Z)4、把53πrad 化成度数 ( ) A 、︒108 B 、︒54 C 、︒36 D 、︒1505、已知角α的终边过点P (-6,8),则cos α 的值是( ) A. 35- B.35 C. 45- D. 456、化简0sin 690的值是( )A .0.5B .0.5-C .7、1sin -=x y 的值域为( )A 、]0,2[-B 、]1,1[-C 、 ]0,1[-D 、]1,2[-8、已知扇形所在圆半径为5,圆心角为︒135,扇形面积为() A 、875π B 、825π C 、475π D 、425π9、下列关系式中正确的是( ) A .210sin 120sin 45sin << B . 120sin 45sin 210sin <<C .120sin 210sin 45sin << D .45sin 120sin 210sin <<10、化简()θπθπ-+⎪⎭⎫⎝⎛+cos 2sin = ( )A 、1B 、-1C 、0D 、2θcos 11、当],[ππ-∈x 时,函数x y sin 3= ( ) A 、在区间]0,[π-上是增加的,在区间],0[π是减少的。
陕西省定边县安边中学2016-2017学年高一下学期月考数学试题缺答案

安边中学2017年春高一数学月考试题一、选择题 :(本大题共12小题 ,每小题5分,共60分)1、 在如图所示的“茎叶图”表示的数据中,众数和中位数分别 ( )A.31与26B .23与26C .24与30D .26与302、把红、黑、白4张纸牌随机地分发给甲、乙、丙、丁,1个人,每人分得1张,事件“甲分得红牌”与事件“乙分得红牌”是( )A .不可能事件B .互斥但不对立事件C .对立事件D .以上答案都不对3、某大学中文系共有本科生5000人,其中一、二、三、四年级的学生的比为5:4:3:1,要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本,则 应抽二年级的学生( )A 、100人B 、60人C 、80人D 、20人4、200辆汽车通过某一段公路时,时速的频率分布直方图如右图所示,则时速在[50,70)的汽车大约有( )。
12 42 03 5 6 3 0 1 14 1 2时速(km ) 0.010.02 0.03 0.04 频率 组距40 50 60 70 80A.60辆B.80辆C.70辆D.140辆5、执行下列算法语句后输出的结果()a=2D0a=a2+Loop while 10≤a输出aA、12B、10C、14D、86、设一组数据的方差是s2,将这组数据的每个数都乘以10,所得到的一组新数据的方差是()A. 0。
12S B.2S C.102S D.1002S7、该算法输出的S和T是多少( )S=0T=1For i=1 T0 3S=S+iT=T*iNext输出S输出TA 、3和2B 、1和1C 、6和6D 、5和68、为了在运行下面的程序之后输入的x 值为16,则输出的y 值应该是 ( )。
INPUT xIF x 〈0 THENy=(x+1)(x+1) ELSEy=(x —1)(x-1)END IFPRINT yA. 289 B . 225 C.256或289 D.2569、同时掷2枚硬币,至少有1枚正面向上的概率是 ( )A.41B. 21 C.43D.8110、高一(1)班学生50人,学号从01~50,学校举行某项活动,要求高一(1)班选出5人参加,班主任老师运用随机数表法选了5名学生,首先被选定的是第21行第15个数码,为26,然后依次选出,那么被选出的5个学生是( )附随机数表的第21行第11个数开始到第22行第10个数如下: …44 22 78 84 26 04 33 46 09 5268 07 97 06 57 74 57 25 65 76 5929 97 68 60 …A .26、22、44、40、07B .26、10、29、02、41C .26、04、33、46、09D .26、49、09、47、3811、从分别写有A ,B ,C ,D ,F ,的五张卡片中任取两张,这两张卡片上的字母顺序恰好相邻的概率为( )A .103B .51C .52D .10712、执行如图所示的程序框图,输出的S 是 ( )A 、2B 、6C 、22、D 、278答题卡 题号 1 2 3 4 5 6 7 8 9 10 11 12答案二、填空题:(共4小题,每题5分,共20分)13、已知一组数据为20、30、40、50、60、60、70,则这组数据的众数、中位数、平均数分别为、、、14。
陕西省定边县安边中学2016_2017学年高一化学下学期月考试题(无答案)

陕西省定边县安边中学2016-2017学年高一化学下学期月考试题(无答案)考试时间:100分钟注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)一、选择题(45分)1.下列有关物质用途的说法正确的是A. 碳酸钠用于治疗胃酸过多B. 稀硫酸用于除铁锈C. 晶体硅用于制造光导纤维D. 硫酸钡用于制作石膏绷带2.下列有关浓硝酸的说法中错误..的是A. 浓HNO3能与碳反应,说明其具有强氧化性B. 浓HNO3能溶解金属铜,说明其具有强酸性C. 浓HNO3不稳定易分解,需要避光保存D. 常温下浓HNO3能使金属铝钝化,可以用铝槽车运输浓HNO33.下列陈述Ⅰ、Ⅱ正确并且有因果关系的是4.下列叙述不正确...的是A. 氨气极易溶解于水且溶解的快,因此可用来做喷泉实验B. 实验室可用氢氧化钠溶液处理含有二氧化硫或氯气的尾气C. 铵盐受热易分解,因此贮存铵态氮肥时要密封保存,并放在阴凉通风处D.与金属反应时,稀HNO3被还原为更低价态,则稀HNO3氧化性强于浓HNO35.下列物质间的转化只通过一步化学反应不能实现的是A. SiO2-H2SiO3B. Fe-FeCl3C. NO2-NOD. S-SO26.下列关于Na2CO3、NaHCO3说法正确的是A. 受热时NaHCO3较Na2CO3更不稳定,更易分解产生CO2B. 等质量的Na2CO3、NaHCO3与足量盐酸反应,前者产生的CO2更多C. Na2CO3和NaHCO3都既能与酸反应,又能与氢氧化钠溶液反应D. 向Na2CO3、NaHCO3溶液中分别滴加澄清石灰水,前者产生白色沉淀,后者无沉淀7.将3.84 g铜粉与一定量浓硝酸反应,当铜粉完全作用时,收集到标况下气体2.24 L,则所消耗硝酸的物质的量是A. 0.24 molB. 0.22 molC. 0.18 molD. 0.16 mol8.取碘水四份于试管中,编号为Ⅰ、Ⅱ、Ⅲ、Ⅳ分别加入汽油、CCl4、酒精、NaCl溶液,振荡后静置,现象正确的是A. Ⅰ中溶液分层,下层呈紫红色B. Ⅱ中溶液分层,下层呈紫红色C. Ⅲ中溶液分层,下层呈棕黄色D. Ⅳ中溶液不分层,溶液由棕黄色变成黄绿色9.用右图所示实验装置(夹持仪器己略去)探究铜丝与过量浓硫酸的反应。
陕西省定边县安边中学2016-2017学年高一下学期中期化学试题缺答案

绝密★启用前安边中学2017年春中期高一化学试卷考试时间:90分钟;第I卷(选择题)一、选择题(共45分)1.下列有关13C的说法不正确的是()A. 13C的质量数是13,有6个电子B。
13C 与12C是两种不同的核素C. 13C 与12C互为同位素D。
13C 与12C 的化学性质有很大的差别2.下列物质中,既能跟盐酸反应,又能跟NaOH溶液反应的化合物是()①Al ②Al2O3③Al(OH)3④NaHCO3 ⑤Fe(OH)3⑥Fe2O3 A。
①②③④B。
②③④ C. ①③④⑤D。
①②④⑥3.下列装置所示的实验中,能达到实验目的的是()A.分离碘和酒精B.除去CO2中的HClC.实验室制氨气D.排水法收集NO4.实验室用NH4Cl固体和Ca(OH)2固体反应制备NH3,下列装置能达到相应实验目的的是()A。
装置甲:制备NH3 B. 装置乙:干燥NH3C。
装置丙:收集NH3D。
装置丁:吸收多余NH35.下列反应中,既表现硝酸的氧化性,又表现了硝酸的酸性的是( )A. CuO+HNO3B. Cu+HNO3(浓)C。
Fe(OH)3+HNO3 D. C+HNO3(浓)6.下列各组物质中,不能进行喷泉实验的是()A。
NH3和H2O B. NO和H2O C。
CO2和NaOH溶液 D. HCl和H2O7.下列离子在溶液中能够大量共存的是()A. Fe3+、NH4+、SCN-、Cl—B. Fe3+、H+、NO3—、SO42-C. K+、H+、NO3-、[Al(OH)4]-D。
Na+、NH4+、Cl—、OH—8.下列说法不正确的是()A. 晶体硅可用作半导体材料和光导纤维B。
水泥、玻璃、陶瓷是硅酸盐材料,它们是三大传统无机非金属材料C. Na2SiO3可用作防火材料,其水溶液俗称为水玻璃D。
实验室存放碱性溶液的试剂瓶要用橡胶塞而不能用玻璃塞9.下列物质的转化在给定条件下能实现的是()A 。
SiO 22H O→加热H 2SiO 3(aq )a aq N OH →()Na 2SiO 3 B.C 。
陕西省定边县安边中学2016-2017学年高一下学期期中考试化学试题缺答案

2016年春高一化学期中化学试题姓名:班级:座位号:(时间:90分钟满分:100分)一、选择题(本题包括16个小题,每小题3分,共48分,每小题只有一个选项符合题意)1.下列有关210 84Po的说法正确的是( )A.Po原子核外电子数是126B.Po原子核内中子数与质子数之差是42C.Po是金属元素,最外层电子数小于4D.Po元素的相对原子质量是2102.下列说法中错误的是()A.原子及其离子的核外电子层数等于该元素所在的周期数B.元素周期表中从ⅢB族到ⅡB族10个纵列的元素都是金属元素C.除氦外的稀有气体原子的最外层电子数都是8D.同一元素的各种同位素化学性质几乎完全相同3.下列说法正确的是( )A.第2周期元素从左到右,最高正化合价从+1递增到+7 B.在周期表中的过渡元素中寻找半导体材料C.元素周期表中元素的性质与元素在周期表中的位置有关D.同种元素的原子均有相同的质子数和中子数4.下列说法不正确的是()A.I的原子半径大于Br,HI比HBr的热稳定性强B.P的非金属性强于Si,H3PO4比H4SiO4的酸性强C.原子半径:Na>MgD.同主族元素的简单阴离子还原性从上到下依次增强5.根据原子结构及元素周期律的知识,下列推断正确的是() A.同主族元素含氧酸的酸性随核电荷数的增加而减弱B.核外电子排布相同的微粒化学性质也相同C.Cl-、S2-、Ca2+、K+半径逐渐减小D.错误!Cl与错误!Cl得电子能力相同6.有下列结论:①微粒半径:S2->Cl>S>F;②氢化物的稳定性:HF>HCl>H2S>H2Se;③离子的还原性:S2->Cl->Br->I-;④氧化性:Cl2>S>Se>Te;⑤酸性:H2SO4>HClO4>H2SeO4;⑥非金属性:F>Cl>S>Se。
其中正确的是()A.②④⑥ B.①③④C.只有① D.只有⑥7.下列叙述中,正确的是( )A.C、N、O元素的单质与氢气化合越来越难B.Li、Na、K的氧化物的水化物的碱性依次减弱C.Na、Mg、Al的简单离子的氧化性依次增强D.P、S、Cl元素的最高正价依次升高,其对应的气态氢化物的稳定性依次减弱8.某元素X的气态氢化物的化学式为XH3,则下列叙述中不正确的是()A.该元素原子的最外电子层上有5个电子B.该元素最高价氧化物的化学式为X2O5C.该元素在元素周期表中位于ⅤA族D.该元素最高价氧化物对应的水化物的化学式H2XO39.下列事实不能用元素周期律解释的只有()A.碱性:KOH〉NaOH B.相对原子质量:Ar> KC.酸性:HClO4〉H2SO4D.元素的金属性:Mg>Al10.短周期元素R、T、Q、W在元素周期表中的相对位置如图所示,其中T所处的周期序数与族序数相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安边中学2017年春中期高一数学试卷
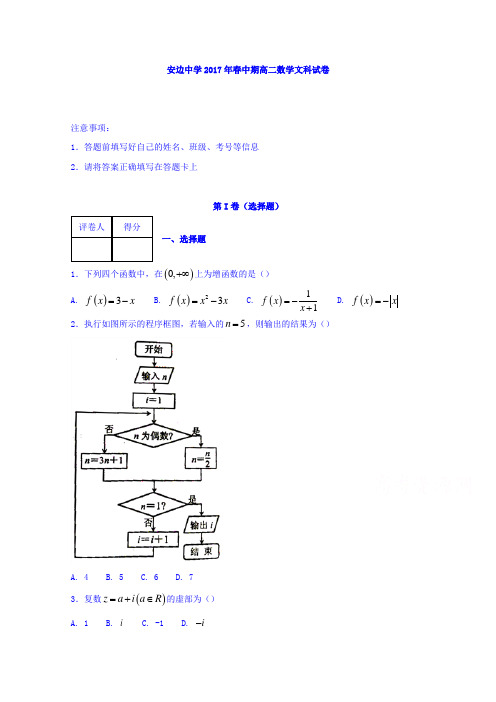
一、选择题 :(本大题共12小题 ,每小题5分,共60分)
1、已知下列各角:①-120°;②-240°;③180°;④495°, 其中是第二象限内角的是( ) A.①② B.①③ C.②③ D.②④
2、若β是第四象限角,则180°-β是第( )象限角 A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限
3、与600°角终边相同的角可表示为( ) A.k ·360°+220°(k ∈Z) B.k ·360°+240°(k ∈Z) C.k ·360°+60°(k ∈Z) D.k ·360°+260°(k ∈Z)
4、把
5
3π
rad 化成度数 ( ) A 、︒108 B 、︒54 C 、︒36 D 、︒150
5、已知角α的终边过点P (-6,8),则cos α 的值是( ) A. 35-
B. 35
C. 45-
D. 45
6、化简0
sin 690的值是( )
A .0.5
B .0.5-
C .7、1sin -=x y 的值域为( )
A 、]0,2[-
B 、]1,1[-
C 、 ]0,1[-
D 、]1,2[-
8、已知扇形所在圆半径为5,圆心角为︒135,扇形面积为() A 、
875π B 、825π C 、475π D 、4
25π
9、下列关系式中正确的是( ) A .
210sin 120sin 45
sin << B . 120sin 45sin 210sin <<
C .
120sin 210sin 45sin << D .
45sin 120sin 210sin <<
10、化简()θπθπ-+⎪⎭
⎫
⎝⎛+cos 2sin = ( )
A 、1
B 、-1
C 、0
D 、2θcos 11、当],[ππ-∈x 时,函数x y sin 3= ( ) A 、在区间]0,[π-上是增加的,在区间],0[π是减少的。
B 、在区间]2,2[π
π-
上是增加的,在区间]2,[ππ--、],2
[ππ
是减少的。
C 、在区间]0,[π-上是减少的,在区间],0[π是增加的。
D 、在区间]2
,[ππ--,],2[ππ上是增加的,在区间]2,2[π
π-是减少的。
12、在]2,0[π上满足2
1
sin ≥x 的x 的取值范围是( )
A 、]6,0[π
B 、]65,
6[ππ C 、]32,6[ππ D 、],6
5[ππ
答题卡
二、填空题:(共4小题,每题5分,共20分) 13、求4
9cos
π
的函数值 。
14、化简)2sin(απ-= .
15、判断1sin -=x y 是奇函数还是偶函数? 16、下列语句正确的是 .
①终边在x 轴负半轴上的角是零角②第一象限的角只有锐角 ③不相等的角的终边一定不相同④若0
•360k βα=+(k Z ∈),则α与β终边相同
三、解答题: (解答题应书写合理的解答或推理过程.)
17、(10分)判定下列各角是第几象限的角,并判断每个角正弦值的正负。
①︒-60 ②︒606 ③423π ④611π ⑤4
3π
18、(14分)已知角α的终边经过下列各点,求角α的正弦值、余弦值。
(1)(2,5) (2)(-3,4) (3)(1,3--) (4)(,512-)
19、(10分)用诱导公式计算下列各角函数值:)316cos(π-
3
19sin π
︒300cos )611sin(π-
4
3sin π
20、(12分)计算、化简
(1)︒+︒-︒+︒180sin 10270sin 390sin 50sin 2 (2)2
3sin
3
sin
34
sin
26
sin
π
π
π
π
++- (3))
2
9sin()sin()3sin()cos()
211cos()2cos()cos()2sin(απ
απαπαπαπ
απαπαπ+-----++-
21、(12分)画出下列函数在区间]2,0[π上的简图,并简单分析函数的定义域、值域、单调性、奇偶性、对称轴
(1)x y sin 2-= (2)1sin 3+=x y
22、(12分)已知扇形AOB 的圆心角为120°,半径长为6,求:
(I )弧
的长;
(II )扇形所含弓形的面积 (即阴影面积).。
