二元一次方程4doc
二元一次方程教案

一、教材的地位与作用《二元一次方程》是九年义务教育人教版教材七年级下册第四章《二元一次方程组》的第一节。
在此之前学生已经学习了一元一次方程,这为本节的学习起了铺垫的作用。
本节内容是二元一次方程的起始部分,因此,在本章的教学中,起着承上启下的地位。
二、教学目标(一)知识与技能:1.了解二元一次方程概念;2.了解二元一次方程的解的概念和解的不唯一性;3.会将一个二元一次方程变形成用关于一个未知数的代数式表示另一个未知数的形式。
(二)数学思考:体会学习二元一次方程的必要性,学会独立思考,体会数学的转化思想和主元思想。
(三)问题解决:初步学会利用二元一次方程来解决实际问题,感受二元一次方程解的不唯一性。
获得求二元一次方程解的思路方法。
(四)情感态度:培养学生发现意识和能力,使其具有强烈的好奇心和求知欲。
三、教学重点与难点教学重点:二元一次方程及其解的概念。
教学难点:二元一次方程的概念里“含未知数的项的次数”的理解;把一个二元一次方程变形成用关于一个未知数的代数式表示另一个未知数的形式。
四、教法与学法分析教法:情境教学法、比较教学法、阅读教学法。
学法:阅读、比较、探究的学习方式。
五、教学过程1.创设情境,引入新课从学生熟悉的姚明受伤事件引入。
师:火箭队最近取得了20连胜,姚明参加了前面的12场比赛,是球队的顶梁柱。
(1)连胜的第12场,火箭对公牛,在这场比赛中,姚明得了12分,其中罚球得了2分,你知道姚明投中了几个两分球?(本场比赛姚明没投中三分球)师:能用方程解决吗?列出来的方程是什么方程?(2)连胜的第1场,火箭对勇士,在这场比赛中,姚明得了36分,你知道姚明投中了几个两分球,罚进了几个球吗?(罚进1球得1分,本场比赛姚明没投中三分球)师:这个问题能用一元一次方程解决吗?,你能列出方程吗?设姚明投进了x个两分球,罚进了y个球,可列出方程______。
(3)在雄鹿队与火箭队的比赛中易建联全场总共得了19分,其中罚球得了3分。
二元一次方程10道题带过程

二元一次方程10道题带过程【原创版3篇】篇1 目录1.引言:二元一次方程的概述2.二元一次方程的求解方法3.例题一:解一个简单的二元一次方程组4.例题二:解一个含有分数的二元一次方程组5.例题三:解一个含有绝对值的二元一次方程组6.例题四:解一个含有平方项的二元一次方程组7.例题五:解一个含有两个未知数的二次项的二元一次方程组8.例题六:解一个含有参数的二元一次方程组9.例题七:解一个含有矩阵的二元一次方程组10.例题八:解一个含有行列式的二元一次方程组11.例题九:解一个含有高次项的二元一次方程组12.例题十:解一个含有多个方程的二元一次方程组13.结论:二元一次方程的求解技巧和注意事项篇1正文二元一次方程是由两个含有两个未知数的一次方程组成的方程组,是代数学中的基本内容之一。
在解决实际问题中,我们常常会遇到需要解决二元一次方程的问题。
本文将通过十个例子,详细讲解如何解决二元一次方程。
首先,我们需要了解二元一次方程的求解方法。
一般地,我们可以通过以下步骤求解:1.列出方程组;2.消元,将方程组化为一个一元一次方程;3.解出一个未知数;4.将已知数代入原方程,解出另一个未知数。
下面,我们将通过十个具体的例子,详细讲解如何运用以上方法解决二元一次方程。
例题一:解一个简单的二元一次方程组。
方程组:x + y = 6, x - y = 2。
解:通过消元法,我们可以将方程组化为一个一元一次方程:2x = 8,解得 x = 4,代入原方程解得 y = 2。
例题二:解一个含有分数的二元一次方程组。
方程组:x + y = 6, x - y = 1/2。
解:通过消元法,我们可以将方程组化为一个一元一次方程:2x = 15/2,解得 x = 15/4,代入原方程解得 y = 11/4。
例题三:解一个含有绝对值的二元一次方程组。
方程组:x + y = 6, |x - y| = 2。
解:通过消元法,我们可以将方程组化为一个一元一次方程:x - y = 2 或 x - y = -2,解得两组解:x = 4, y = 2 或 x = 2, y = 4。
(word完整版)二元一次方程组的概念和解法-教师版

(word 完整版)二元一次方程组的概念和解法-教师版二元一次方程的基本概念1。
含有两个未知数,并且含未知数项的最高次数是1的方程叫二元一次方程。
判定一个方程是二元一次方程必须同时满足三个条件: ①方程两边的代数式都是整式——整式方程; ②含有两个未知数——“二元”;③含有未知数的项的次数为1——“一次”。
2。
二元一次方程的一般形式:0ax by c ++=(0a ≠,0b ≠)3。
二元一次方程的解:使二元一次方程左、右两边的值相等的两个未知数的值,叫做二元一次方程的解。
一般情况下,一个二元一次方程有无数个解。
【例1】 下列各式是二元一次方程的是( )A 。
30x y z -+=B 。
30xy y x -+=C 。
12023x y -= D 。
210y x+-=【解析】根据二元一次方程的定义,从二元一次方程的未知数的个数和次数方面辨别. 【答案】故本题选C .【巩固】下列方程是二元一次方程的是( )A.31x xy -= B 。
2430x x += C.23y += D.3x y =【答案】D .【例2】 若32125m n x y ---=是二元一次方程,则求m 、n 的值.【答案】由定义知:321m -=,11n -=,所以:1m =,2n =.【巩固】已知方程11(2)2m n m x y m ---+=是关于x 、y 的二元一次方程,求m 、n 的值。
【答案】根据题意可得:20m -≠,11n -=,11m -=,所以2n =,0m =.二元一次方程组的概念和解法同步练习知识讲解(word 完整版)二元一次方程组的概念和解法-教师版【例3】 若32125m n x y ---=是二元一次方程,则求m 、n 的值。
【答案】由定义知:321m -=,11n -=,所以:1m =,2n =。
【巩固】已知方程11(2)2m n m x y m ---+=是关于x 、y 的二元一次方程,求m 、n 的值。
二元一次方程

教学内容【新课导入】二元一次方程的定义:含有两个未知数,并且未知数的项的次数都是1,像这样的方程叫做二元一次方程。
二元一次方程的一般形式是0(0,0,,,++=≠≠均为常数)ax by c a b a b c★注意:定义包含以下三点:①具有两个未知数②未知项的次数是1③等号两边的代数式是整式④方程需要化简后再判断二元一次方程的一个解:适合一个二元一次方程的一组_______的值,叫做这个二元一次方程的解。
二元一次方程的解的求法:用含有一个未知数的代数式表示___________________,然后求出它的一个解。
知识点21..二元一次方程组的定义:把具有相同未知数的两个二元一次方程合在一起,就组成了一个二元一次方程组。
1、二元一次方程组的解:一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解,二元一次方程有无数个解。
2、二元一次方程组的解:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。
3、代入消元法解二元一次方程组:(1)基本思路:未知数又多变少。
(2)消元法的基本方法:将二元一次方程组转化为一元一次方程。
(3)代入消元法:把二元一次方程组中一个方程的未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。
这个方法叫做代入消元法,简称代入法。
(4)代入法解二元一次方程组的一般步骤:1、从方程组中选出一个系数比较简单的方程,将这个方程中的一个未知数(例如y)用含另一个未知数(例如x)的代数式表示出来,即写成y=ax+b的形式,即“变”2、将y=ax+b代入到另一个方程中,消去y,得到一个关于x的一元一次方程,即“代”。
3、解出这个一元一次方程,求出x的值,即“解”。
4、把求得的x值代入y=ax+b中求出y的值,即“回代”5、把x、y的值用{联立起来即“联”4、加减消元法解二元一次方程组(1)两个二元一次方程中同一个未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法。
【初中数学】二元一次方程8种典型例题详解

【初中数学】二元一次方程8种典型例题详解1.列方程组解应用题的基本思想列方程组解应用题,是把“未知”转换成“已知”的重要方法,它的关键是把已知量和未知量联系起来,找出题目中的等量关系。
一般来说,有几个未知量就必须列出几个方程,所列方程必须满足:①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数要相等。
2.列二元一次方程组解应用题的一般步骤设:用两个字母表示问题中的两个未知数;列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);解:解方程组,求出未知数的值;答:写出答案。
3.要点诠释(1)“设”、“答”两步,都要写清单位名称;(2)一般来说,设几个未知数就应该列出几个方程并组成方程组。
1.和差倍数问题知识梳理和差问题是已知两个数的和或这两个数的差,以及这两个数之间的倍数关系,求这两个数各是多少。
典型例题:【思路点拨】由甲乙两人2分钟共打了240个字可以得到第一个等量关系式2(x+y)=240,再由甲每分钟比乙多打10个字可以得到第二个等量关系式x-y=10,组成方程组求解即可。
变式拓展:【思路点拨】由甲组学生人数是乙组的3倍可以得到第一个等量关系式x=3y,由乙组的学生人数比甲组的3倍少40人可以得到第二个等量关系式3x-y=40,组成方程组求解即可。
2.产品配套问题知识梳理总人数等于生产各个产品的人数之和;各个产品数量之间的比例符合整体要求。
典型例题:【思路点拨】本题的第一个等量关系比较容易得出:生产螺钉和螺母的工人共有22名;第二个等量关系的得出要弄清螺钉与螺母是如何配套的,即螺母的数量是螺钉的数量的2倍(注意:别把2倍的关系写反)。
变式拓展:【思路点拨】根据共有170名学生可得出第一个等量关系x+y=170,根据每个树坑对应一棵树可得第二个等量关系3x=7y,组成方程组求解即可。
3.工作量问题知识梳理我们在解决工程问题时通常把工作总量看成1;工作量=工作效率×工作时间;总工作量=每个个体工作量之和;工作效率=工作量÷工作时间(即单位时间的工作量);工作效率=1÷完成工作的总时间。
二元一次方程组讲义

二元一次方程组知识点1:解方程一、考点讲解:1.二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.2.二元一次方程组:含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.3.二元一次方程组的解:二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.4.二元一次方程组的解法.(1)代人消元法:解方程组的基本思路是“消元”一把“二元”变为“一元”,主要步骤是,将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代人另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代人消元法,简称代人法.(2)减消无法:通过方程两边分别相加(减)消去其中一个未知数,这种解二元一次方程组的方法叫做加减消元法,简称加减法.5.整体思想解方程组.(1)整体代入.如解方程组3(1) 5 5(1)3(5) x y y x -=+⎧⎨-=+⎩①②,方程①的左边可化为3(x+5)-18=y+5③,把②中的 3(x+5)看作一个整体代入③中,可简化计算过程,求得y .然后求出方程组的解.(2)整体加减,如1+3y 19 313x+y 11 3x ⎧=⎪⎪⎨⎪=⎪⎩①②因为方程①和②的未知数x 、y 的系数正好对调,所以可采用两个方程整体相加减求解.利用①+②,得x+y=9③,利用②-①得x -y=3④,可使③、④组成简单的方程组求得x ,y .二、经典考题剖析:【考题1-1】(2004、汉中)若x+y+4则 3x+2y =_______【考题1-2】(2004、北碚,5分)解方程组:x-y=42x+y=5⎧⎨⎩三、针对性训练:( 20分钟) (答案:242 )1、对方程组4x+7y=-19 4x-5y=17 ⎧⎨⎩①②,用加减法消去x ,得到的方程为( )A 、2y=-2 B.2y=-36C. 12y=-2D.12y=-362.二元一次方程组x+y=102x-y=-1⎧⎨⎩的解是( ) A .11x=x=2x=73 C. D.19y=8y=3y=3x=3 B.y=7⎧⎪⎧⎧⎪⎪⎪⎨⎨⎨⎪⎪⎩⎩⎪⎪⎩⎧⎨⎩ 3.若x=-2y=1⎧⎨⎩ 是方程组ax+by=1bx+ay=7⎧⎨⎩的解,则() (a -b )的值为( ) A. -353 B. 353 C. -16 D.16 4.解方程组:⑴2x+5y=53x+2y=5 3x-5y=102x+5y=7⎧⎧⎨⎨⎩⎩⑵5.已知方程组ax+5y=15 4x-by=-2 ⎧⎨⎩①②由于甲看错了方程①中的a 得到的方程组的解为x=-3y=-1⎧⎨⎩乙看错了方程②中的b ,得到方程组的解为x=5y=4⎧⎨⎩若按正确的a 、b 为计算,求原方程组的解x 与y 的差.6.若a+b 4b 与3a+b 是同类二次根式,求a 、b 的值.7.已知关于x ,y 的方程组2x-y=32kx+(k+1)y=10⎧⎨⎩的解互为相反数,则k 的值是多少?8.甲、乙两人解同一个二元一次方程组,甲正确地得出解x=3,y =-2,乙因把这个方程组中的第二个方程X 的系数抄错了,得到一个错误的解为x =-2,y=2.他们解先后,原方程组的三个系数又被污染而看不清楚,变成下面的形式:请你把原方程组的三个被污染的系数填上.知识点2:方程组的实际应用一、考点讲解:方程组解决实际问题:应用方程组解决实际问题的关键在于正确找出问题中的两个等量关系,列出方程并组成方程组,同时注意检验解的合理性.二、经典考题剖析:【考题2-1】(2004、宁安)某商品按进价的100%加价后出售.经过一段时间,商家为了减少库存,决定5折销售,这时每件商品( )A .赚50%B .赔50%C .赔25%D .不赔不赚解:D 点拨:利润=销售价-进价.【考题2-2】(2004、南山区正题3分)如图1-7-1,AB ⊥BC ,∠ABD 的度数比∠DBC 的度数的两倍少15°,设∠ABD 和∠DBC 的度数分别为x 、y ,那么下面可以求出这两个角的度数的方程组是( )A .9015x y x y +=⎧⎨=-⎩ B .90215x y x y +=⎧⎨=-⎩ C .90152x y x y +=⎧⎨=-⎩ D .290215x x y =⎧⎨=-⎩【考题2-3】(2004、宁安)如图,如果横行上的两个数字之和相等,竖列上的两个数字之和相等,那么a 、b 、c 、d 依次可为 。
二元一次方程

二元一次方程二元一次方程,又称二元线性方程,是指包含两个未知数的一次方程。
本文将从解的求解方法、应用实例等方面进行探讨。
一、解的求解方法二元一次方程可以通过以下几种方法求解。
1. 代入法:将其中一个未知数表示成另一个未知数的函数,然后代入到另一个方程中求解。
2. 消元法:通过消元将其中一个未知数消去,得到一个只包含一个未知数的一次方程,然后求解。
3. Cramer法则:通过构建系数矩阵和常数向量,利用行列式的求解方法得到未知数的解。
二、应用实例二元一次方程在实际问题中具有广泛的应用,下面以几个例子进行说明。
1. 人头与鸡兔问题:假设有一群动物,其中有若干只鸡和兔,总共有若干个头和脚。
已知鸡的头和脚的总数分别为c1和c2,兔的头和脚的总数分别为r1和r2。
则可以建立如下方程组:2c1 + 4r1 = 总头数2c2 + 4r2 = 总脚数通过求解这个方程组,可以得到鸡和兔的数量。
2. 配对问题:小明和小红一起做对练习,已知小明做对的套数和错的套数的总和为m,小红做对的套数和错的套数的总和为n。
每个人的对数和错数都是整数。
则可以建立如下方程组:a +b = mc +d = n其中a、b、c、d分别表示小明做对的套数、小明错的套数、小红做对的套数、小红错的套数。
通过求解这个方程组,可以得到每个人的对、错的数量。
3. 投资问题:某人在两个项目上投资了一定金额,已知两个项目的年收益率分别为r1和r2,总收益为m。
如果假设第一个项目的投资金额为x,第二个项目的投资金额为y,则可以建立如下方程组: rx + ry = mx + y = 总投资金额通过求解这个方程组,可以得到每个项目的投资金额。
三、总结二元一次方程是数学中常见的一种方程形式,可以通过代入法、消元法和Cramer法则等方法求解。
它在实际问题中具有广泛的应用,在人头与鸡兔问题、配对问题和投资问题等方面可以帮助我们解决实际的数学难题。
通过掌握解的求解方法和应用实例,我们可以更好地理解和应用二元一次方程。
二元一次方程计算题

二元一次方程计算题1.2x+9y=813x+y=342.9x+4y=358x+3y=303.7x+2y=527x+4y=624.4x+6y=549x+2y=875.2x+y=72x+5y=196.x+2y=213x+5y=567.5x+7y=525x+2y=22 8.5x+5y=657x+7y=2039. 8x+4y=56x+4y=21 10.5x+7y=415x+8y=44 11.7x+5y=543x+4y=38 12.x+8y=154x+y=29 13.3x+6y=249x+5y=46 14.9x+2y=62 4x+3y=36 15.9x+4y=46 7x+4y=42 16.9x+7y=135 4x+y=41 17.3x+8y=51 x+6y=27 18.9x+3y=99 4x+7y=95 19.9x+2y=38 3x+6y=18 20.5x+5y=45 7x+9y=6921.8x+2y=28 7x+8y=62 22.x+6y=14 3x+3y=27 23.7x+4y=67 2x+8y=26 24.5x+4y=52 7x+6y=74 25.7x+y=9 4x+6y=16 26.6x+6y=48 6x+3y=42 27.8x+2y=167x+y=1128.4x+9y=778x+6y=9429.6x+8y=687x+6y=6630.2x+2y=227x+2y=47(1) 66x+17y=3967 25x+y=1200谜底:x=48 y=47 (2) 18x+23y=2303 74x-y=1998谜底:x=27 y=79 (3) 44x+90y=7796 44x+y=3476答案:x=79 y=48 (4) 76x-66y=408230x-y=2940答案:x=98 y=51 (5) 67x+54y=854671x-y=5680谜底:x=80 y=59(6) 42x-95y=-141021x-y=1575答案:x=75 y=48(7) 47x-40y=85334x-y=2006答案:x=59 y=48(8) 19x-32y=-178675x+y=4950答案:x=66 y=95(9) 97x+24y=720258x-y=2900答案:x=50 y=98(10) 42x+85y=636263x-y=1638答案:x=26 y=62(11) 85x-XXX-251827x-y=486答案:x=18 y=44 (12) 79x+40y=2419 56x-y=1176答案:x=21 y=19 (13) 80x-87y=2156 22x-y=880谜底:x=40 y=12 (14) 32x+62y=5134 57x+y=2850答案:x=50 y=57 (15) 83x-XXX59x+y=2183答案:x=37 y=61 (16) 91x+70y=5845 95x-y=4275答案:x=45 y=25 (17) 29x+44y=5281 88x-y=3608谜底:x=41 y=93(18) 25x-XXX-4355 40x-y=2000答案:x=50 y=59 (19) 54x+68y=3284 78x+y=1404答案:x=18 y=34 (20) 70x+13y=3520 52x+y=2132答案:x=41 y=50 (21) 48x-54y=-3186 24x+y=1080答案:x=45 y=99 (22) 36x+77y=7619 47x-y=799谜底:x=17 y=91 (23) 13x-42y=-2717 31x-y=1333答案:x=43 y=78 (24) 28x+28y=3332 52x-y=4628答案:x=89 y=30 (25) 62x-XXX-2564 46x-y=2024答案:x=44 y=54 (26) 79x-XXX-4388 26x-y=832答案:x=32 y=91 (27) 63x-40y=-821 42x-y=546答案:x=13 y=41 (28) 69x-XXX-1209 42x+y=3822答案:x=91 y=78 (29) 85x+67y=7338 11x+y=308谜底:x=28 y=74 (30) 78x+74y=14x+y=1218谜底:x=87 y=83 (31) 39x+42y=533159x-y=5841答案:x=99 y=35 (32) 29x+18y=191658x+y=2320答案:x=40 y=42 (33) 40x+31y=604345x-y=3555答案:x=79 y=93 (34) 47x+50y=859845x+y=3780答案:x=84 y=93 (35) 45x-30y=-145529x-y=725谜底:x=25 y=86 (36) 11x-43y=-136147x+y=799答案:x=17 y=36 (37) 33x+59y=3254 XXX答案:x=11 y=49 (38) 89x-74y=-273568x+y=1020答案:x=15 y=55 (39) 94x+71y=7517 78x+y=3822答案:x=49 y=41 (40) 28x-62y=-4934 46x+y=552答案:x=12 y=85 (41) 75x+43y=8472 17x-y=1394谜底:x=82 y=54 (42) 41x-XXX-1180 29x+y=1450答案:x=50 y=85 (43) 22x-59y=824 63x+y=4725谜底:x=75 y=14 (44) 95x-56y=-401 90x+y=1530谜底:x=17 y=36(45) 93x-52y=-852 29x+y=464答案:x=16 y=45 (46) 93x+12y=8823 54x+y=4914答案:x=91 y=30 (47) 21x-63y=84 20x+y=1880谜底:x=94 y=30 (48) 48x+93y=9756 38x-y=950谜底:x=25 y=92 (49) 99x-67y=4011 75x-y=5475答案:x=73 y=48 (50) 83x+64y=9291 90x-y=3690谜底:x=41 y=92 (51) 17x+62y=3216 75x-y=7350答案:x=98 y=25 (52) 77x+67y=2739 14x-y=364答案:x=26 y=11 (53) 20x-68y=-4596 14x-y=924答案:x=66 y=87 (54) 23x+87y=4110 83x-y=5727答案:x=69 y=29 (55) 22x-XXX86x+y=6708谜底:x=78 y=24 (56) 20x-45y=-3520 56x+y=728谜底:x=13 y=84 (57) 46x+37y=7085 61x-y=4636答案:x=76 y=97 (58) 17x+61y=408871x+y=5609答案:x=79 y=45 (59) 51x-61y=-1907 89x-y=2314答案:x=26 y=53 (60) 69x-XXX-2404 21x+y=1386谜底:x=66 y=71 (61) 15x-41y=754 74x-y=6956谜底:x=94 y=16 (62) 78x-55y=656 89x+y=5518谜底:x=62 y=76 (63) 29x+21y=1633 31x-y=713答案:x=23 y=46 (64) 58x-28y=2724 35x+y=3080答案:x=88 y=85(65) 28x-63y=-225488x-y=2024谜底:x=23 y=46(66) 43x+50y=706485x+y=8330谜底:x=98 y=57(67) 58x-77y=117038x-y=2280谜底:x=60 y=30(68) 92x+83y=43x+y=3010答案:x=70 y=62(69) 99x+82y=605552x-y=1716答案:x=33 y=34(70) 15x+26y=172994x+y=8554答案:x=91 y=14 (71) 64x+32y=355256x-y=2296答案:x=41 y=29(72) 94x+66y=84x-y=7812谜底:x=93 y=27 (73) 65x-79y=-5815 89x+y=2314答案:x=26 y=95 (74) 96x+54y=6216 63x-y=1953谜底:x=31 y=60 (75) 60x-44y=-352 33x-y=1452答案:x=44 y=68 (76) 79x-45y=510 14x-y=840谜底:x=60 y=94 (77) 29x-35y=-218 59x-y=4897答案:x=83 y=75 (78) 33x-24y=1905 30x+y=2670答案:x=89 y=43 (79) 61x+94y=93x+y=5952答案:x=64 y=84 (80) 61x+90y=5001 48x+y=2448答案:x=51 y=21 (81) 93x-19y=286x-y=1548答案:x=18 y=88 (82) 19x-XXX-5910 30x-y=2340答案:x=78 y=77 (83) 80x+74y=8088 96x-y=8640答案:x=90 y=12 (84) 53x-XXX45x+y=2610答案:x=58 y=12 (85) 93x+12y=911728x-y=2492答案:x=89 y=70 (86) 66x-71y=-1673 99x-y=7821谜底:x=79 y=97 (87) 43x-52y=-1742 XXX1976谜底:x=26 y=55 (88) 70x+35y=8295 40x+y=2920答案:x=73 y=91 (89) 43x+82y=4757 11x+y=231答案:x=21 y=47 (90) 12x-19y=236 95x-y=7885答案:x=83 y=40 (91) 51x+99y=8031 71x-y=2911谜底:x=41 y=60(92) 37x+74y=4403 69x-y=6003答案:x=87 y=16 (93) 46x+34y=4820 71x-y=5183答案:x=73 y=43 (94) 47x+98y=5861 55x-y=4565谜底:x=83 y=20 (95) 30x-17y=239 28x+y=1064谜底:x=38 y=53 (96) 55x-12y=4112 79x-y=7268答案:x=92 y=79 (97) 27x-24y=-450 67x-y=3886答案:x=58 y=84 (98) 97x+23y=8119 14x+y=966答案:x=69 y=62 (99) 84x+53y=70x+y=6790谜底:x=97 y=59 (100) 51x-97y=297 19x-y=1520。
二元一次方程

1.基本概念二元一次方程:方程中含有两个未知数,并且所含未知数的项的次数都是1.二元一次方程组:含有两个未知数的两个一次方程所组成的一组方程. 二元一次方程的一个解:适合一个二元一次方程的一组未知数的值.二元一次方程组的解:二元一次方程组中各个方程的公共解.2.二元一次方程组的解法:(1)代入消元法(简称“代入法” ):代入法的主要步骤:将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元二次方程.(2)加减消元法(简称“加减法” ):加减法的主要步骤:通过两式相加(减)消去其中一个未知数,让二元一次方程组为一元一次方程求解.3.二元一次方程组的应用:利用二元一次方程组解决实际问题的过程:主要分为“鸡兔同笼”问题、“增收节支”问题、“数字问题”.列方程组解应用题的步骤:(1)设出未知数;(2)找出相等关系;(3)根据相等关系列方程组;(4)解方程组;(5)作答.一、选择题1.方程x+y=5的解有( )A .1个B .2个C .3个D .无数个2.下列方程组中,不是二元一次方程组的是( )A .112x y =⎧⎨-=⎩,B .13x y x y +=⎧⎨-=⎩,C .2104x y xy +=⎧⎨=⎩,D .21x y x y =⎧⎨-=⎩,3.解二元一次方程组的基本思路是( )A .代入法B .加减法C .代入法和加减法D .将二元一次方程组转化为一元一次方程4.方程5x+4y=17的一个解是( )A .13x y =⎧⎨=⎩, B .21x y =⎧⎨=⎩, C .32x y =⎧⎨=⎩, D .41x y =⎧⎨=⎩, 5.方程组5(1)210(2)x y x y +=⎧⎨+=⎩,,由②—①得 ( )A .3x=10B .x=5C .3x =-5D .x=-56.若关于x 、y 的方程2211a b a b x y -++-=是二元一次方程,那么a 、b 的值分别是( )A .1、0B .0、-1C .2、1D .2、-37.有一个两位数,它的十位数字与个位数字之和为5,则符合条件的两位数有 ( )A .4个B .5个C .6个D .7个8.若x :y=3:2,且3x+2y=13,则x 、y 的值分别为( )A .3、2B .2、3C .4、1D .1、49.若二元一次方程3x -y=7,2x+3y=1,y=kx -9有公共解,则k 的值为( )A .3B .-3C .-4D .410.某班共有学生49人.一天,该班某男生因事请假,当天的男生人数恰为女生人数的一半.若设该班男生人数为x ,女生人数为y ,则下列方程组中,能正确计算出x 、y 的是( )A .()4921x y y x -=⎧⎪⎨=+⎪⎩,B .()4921x y y x +=⎧⎪⎨=+⎪⎩,C .()4921x y y x -=⎧⎪⎨=-⎪⎩,D .()4921x y y x +=⎧⎪⎨=-⎪⎩, 11.“五一”黄金周,某人民商场“女装部”推出“全部服装八折”.男装部推出“全部服装八五折”的优惠活动,某顾客在女装部购买了原价x 元、男装部购买了原价为y 元的服装各一套,优惠前需付700元,而他实际付款580元,则可列方程组为 ( )A .5800.80.85700x y x y +=⎧⎨+=⎩,B .7000.850.8580x y x y +=⎧⎨+=⎩, C .7000.80.85700580x y x y +=⎧⎨+=-⎩, D .7000.80.85580x y x y +=⎧⎨+=⎩, 12.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:“(1)班与(5)班得分比为6:5.”乙同学说:“(1)班得分比(5)班得分的2倍少40分.”若设(1)班得x 分,(5)班得y 分,根据题意所列的方程组应为( )A .65240x y x y =⎧⎨=-⎩,B .65240x y x y =⎧⎨=+⎩,C .56240x y x y =⎧⎨=+⎩,D .56240x y x y =⎧⎨=-⎩, 二、填空题13.在方程2x -y=1中,若x=-4,则y=________;若y=-3,则x=________.14.写出满足二元一次方程x+2y=9的一对整数解_____________.15.已知12x y =⎧⎨=⎩,是方程a x -3y=5的一个解,则a =____________.16.若x -y=5,则14-3x+3y=______________.17.若一个二元一次方程的一个解为21x y =⎧⎨=-⎩,,则这个方程可以是_______.(只要求写出一个)18.方程组3520x y x y +=⎧⎨-=⎩,的解是____________. 19.若二元一次方程组23521x y x y +=⎧⎨-=⎩,的解是方程8x -2y=k 的解,则k=___________.20.若12x y =⎧⎨=⎩,和24x y =-⎧⎨=-⎩,都是某二元一次方程的解,则这个二元一次方程是_______.21.在y=kx+b 中,当x=1时,y=4:当x=2时,y=10,则k=______,b=________.22.有一个两位数,它的两个数字之和为11,把这个两位数的个位数字与十位数字对调,所得的新数比原数大63,设原两位数的个位数字为x ,十位数字为y ,则用代数式表示原两位数为_________,根据题意得方程组____________________________.⎧⎨⎩, 三、解答题23.解下列方程组:(1)4519323m n m n +=-⎧⎨-=⎩,; (2)32123x y x y ++==24.已知二元一次方程:(1)x+y=4;(2)2x -y=2;(3)x -2y=1.请从这三个方程中选择你喜欢的两个方程,组成一个方程组,并求出这方程组的解.25.若关于x 、y 的二元一次方程组3522718x y x y m +=⎧⎨+=-⎩,的解x 、y 互为相反数,求m 的值.26.已知方程组44ax y -=⎧⎨⎩,(1)2x+by=14,(2)由于甲看错了方程①中的a 得到方程组的解为26x y =-⎧⎨=⎩,, 乙看错了方程②中的b 得到方程组的解为44.x y =-⎧⎨=-⎩,若按正确的a 、b 计算,求原方程组的解.二元一次方程组解应用题题型一、列二元一次方程组解决生产中的配套问题1、某服装厂生产一批某种款式的秋装,已知每2米的某种布料可做上衣的衣身3个或衣袖5只,贤计划用132米这样布料生产这批秋装(不考虑布料的损耗),应分别用多少布料才能使做的衣身和衣袖恰好配套题型二、列二元一次方程组解决行程问题2、甲、乙两地相距160千米,一辆汽车和一辆拖拉机同时由甲、乙两地相向而行,1小时20分相遇。
专题07二元一次方程(组)(含解析).docx
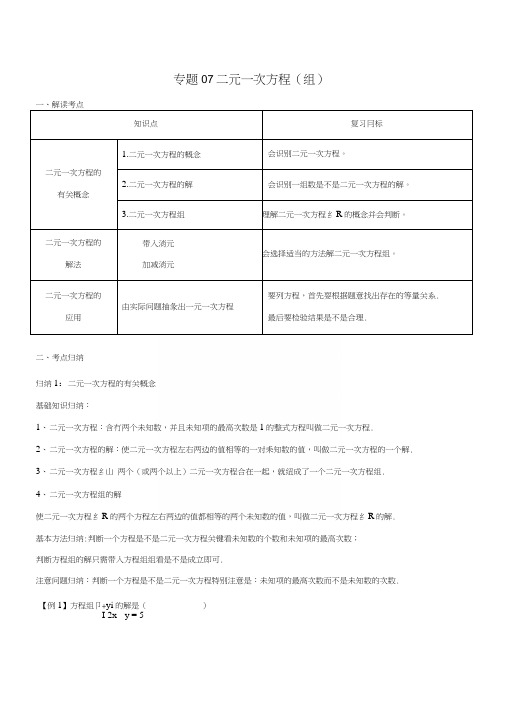
专题07二元一次方程(组)一、解读考点知识点复习冃标二元一次方程的有关概念1.二元一次方程的概念会识别二元一次方程。
2.二元一次方程的解会识别一组数是不是二元一次方程的解。
3.二元一次方程组理解二元一次方程纟R的概念并会判断。
二元一次方程的解法带入消元加减消元会选择适当的方法解二元一次方程组。
二元一次方程的应用由实际问题抽彖出一元一次方程要列方程,首先耍根据题意找出存在的等量关系.最后要检验结果是不是合理.二、考点归纳归纳1:二元一次方程的有关概念基础知识归纳:1、二元一次方程:含冇两个未知数,并且未知项的最高次数是1的整式方程叫做二元一次方程.2、二元一次方程的解:使二元一次方程左右两边的值相等的一对耒知数的值,叫做二元一次方程的一个解.3、二元一次方程纟山两个(或两个以上)二元一次方程合在一起,就纽成了一个二元一次方程组.4、二元一次方程组的解使二元一次方程纟R的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程纟R的解.基本方法归纳:判断一个方程是不是二元一次方程关键看未知数的个数和未知项的最高次数;判断方程组的解只需带入方程组组看是不是成立即可.注意问题归纳:判断一个方程是不是二元一次方程特别注意是:未知项的最髙次数而不是未知数的次数. 【例1】方程组卩+yi的解是()I 2x - y = 5【答案】D. 【解析】试题分析:根据方程组的解的意义,将各选项分别代入方程组验算作出选择:丘:不满足2x-y = 5,故它不是方程组的解;3. {X = ;2不满^2x-y = 5,故它不是方程组的解;iy = 3c. 'X = ;不满足X-y = 1,故它不是方程组的解;.V =1|\ = ?D. <、满足x-y=l 和2x-y = 5>故它是方程组的解•i v = —1故选D ・ 考点:方程组的解.归纳2:二元一次方程的解法基础知识归纳:解一元二次方程组的方法(1)代入法(2)加减法基本方法归纳:解一元二次方程组的方法关键是消元。
二元一次方程解法大全

二元一次方程解法大全1、直接开平方法:直接开平方法就是用直接开平方求解二元一次方程的方法。
用直接开平方法解形如(x-m)2=n(n ≥0)的方程,其解为x=±根号下n+m.例1.解方程(1)(3x+1)2=7(2)9x2-24x+16=11分析:(1)此方程显然用直接开平方法好做,(2)方程左边是完全平方式(3x-4)2,右边=11>0,所以此方程也可用直接开平方法解。
(1)解:(3x+1)2=7×∴(3x+1)2=5∴3x+1=±(注意不要丢解)∴x=∴原方程的解为x1=,x2=(2)解:9x2-24x+16=11∴(3x-4)2=11∴3x-4=±∴x=∴原方程的解为x1=,x2=2.配方法:用配方法解方程ax2+bx+c=0(a≠0)先将常数c移到方程右边:ax2+bx=-c将二次项系数化为1:x2+x=-方程两边分别加上一次项系数的一半的平方:x2+x+()2=-+()2方程左边成为一个完全平方式:(x+)2=当b^2-4ac≥0时,x+=±∴x=(这就是求根公式)例2.用配方法解方程3x^2-4x-2=0(注:X^2是X的平方)解:将常数项移到方程右边3x^2-4x=2将二次项系数化为1:x2-x=方程两边都加上一次项系数一半的平方:x2-x+()2=+()2配方:(x-)2=直接开平方得:x-=±∴x=∴原方程的解为x1=,x2=.3.公式法:把一元二次方程化成一般形式,然后计算判别式△=b2-4ac的值,当b2-4ac≥0时,把各项系数a,b,c的值代入求根公式x=[-b±(b^2-4ac)^(1/2)]/(2a),(b^2-4ac≥0)就可得到方程的根。
例3.用公式法解方程2x2-8x=-5解:将方程化为一般形式:2x2-8x+5=0∴a=2,b=-8,c=5b^2-4ac=(-8)2-4×2×5=64-40=24>0∴x=[(-b±(b^2-4ac)^(1/2)]/(2a)∴原方程的解为x1=,x2=.4.因式分解法:把方程变形为一边是零,把另一边的二次三项式分解成两个一次因式的积的形式,让两个一次因式分别等于零,得到两个一元一次方程,解这两个一元一次方程所得到的根,就是原方程的两个根。
二元一次方程组知识点归纳及解题技巧汇总

二元一次方程组知识点归纳及解题技巧汇总二元一次方程组知识点归纳及解题技巧汇总1、二元一次方程:含有两个未知数,并且未知数的项的次数都是1,像这样的方程叫做二元一次方程。
2、二元一次方程组:把具有相同未知数的两个二元一次方程合在一起。
3、二元一次方程组的解:一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解,二元一次方程有无数个解。
4、二元一次方程组的解:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。
5、消元法解二元一次方程组:(1) 基本思路:未知数又多变少。
(2) 消元法的基本方法:将二元一次方程组转化为一元一次方程。
6.解法:通过“代入”消去一个未知数,从而求出方程组的解的方法叫做代入消元法(elimination by substitution),简称代入法。
例:解方程组x+y=5①6x+13y=89②解:由①得x=5-y ③把③带入②,得6(5-y)+13y=89y=59/7把y=59/7带入③,得x=5-59/7即x=-24/7∴x=-24/7y=59/7 为方程组的解加减消元法:例:解方程组x+y=9①x-y=5②解:①+② 2x=14即 x=7把x=7带入①得7+y=9解得y=-2∴x=7y=-2 为方程组的解7. 二元一次方程组的解有三种情况:1.有一组解如方程组x+y=5① 6x+13y=89② x=-24/7 y=59/7 为方程组的解2.有无数组解如方程组x+y=6① 2x+2y=12②因为这两个方程实际上是一个方程(亦称作“方程有两个相等的实数根”),所以此类方程组有无数组解。
3.无解如方程组x+y=4① 2x+2y=10②,因为方程②化简后为x+y=5 这与方程①相矛盾,所以此类方程组无解。
注意:用加减法或者用代入消元法解决问题时,应注意用哪种方法简单,避免计算麻烦或导致计算错误。
教科书中没有的几种解法(一)加减-代入混合使用的方法.例1, 13x+14y=41 (1)14x+13y=40 (2)解:(2)-(1)得x-y=-1 x=y-1 (3)把(3)代入(1)得13(y-1)+14y=4113y-13+14y=4127y=54y=2把y=2代入(3)得x=1所以:x=1,y=2特点:两方程相加减,单个x或单个y,这样就适用接下来的代入消元.(二)换元法例2, (x+5)+(y-4)=8(x+5)-(y-4)=4令x+5=m,y-4=n原方程可写为m+n=8m-n=4解得m=6,n=2所以x+5=6,y-4=2所以x=1,y=6特点:两方程中都含有相同的代数式,如题中的x+5,y-4之类,换元后可简化方程也是主要原因。
二元一次方程

二元一次方程
二元一次方程是指含有两个未知数和以1次为最高次数的方程。
一般形式为ax + by + c = 0,其中a、b、c为已知数,并且a和b不能同时等于0。
解二元一次方程的方法有代入法、消元法和Cramer法。
在代入法中,我们将其中一个未知数用另一个未知数表示,并代入另一个方程中,从而得到只含有一个未知数的一元一次方程,从而解得这个未知数的值,再代入原方程中求得另一个未知数的值。
消元法主要是利用不同方程中同一未知数的系数之比进行消去。
通过适当调整两个方程中同一未知数的系数,使其相乘之后可以得到一个相等的式子,然后通过加减法进行消元,得到一个只含有一个未知数的一元一次方程,进而求解。
Cramer法则是利用二阶行列式的计算来解二元一次方程。
首先使用Cramer法需要求解系数行列式的值,然后将未知数的系数用结果行列式来替换原方程组中的系数,从而得到一个只含有一个未知数的一元一次方程,进而求解。
以上是解二元一次方程的几种常见方法。
根据具体方程的形式和问题的要求,选择适当的方法进行计算求解。
(word完整版)二元一次方程组 习题及答案100道

二元一次方程组习题及答案100道1。
2x+9y=813x+y=342.9x+4y=358x+3y=303.7x+2y=527x+4y=624。
4x+6y=549x+2y=875。
2x+y=72x+5y=196。
x+2y=213x+5y=567.5x+7y=525x+2y=228。
5x+5y=657x+7y=203 9.8x+4y=56x+4y=2110.5x+7y=41 5x+8y=44 11。
7x+5y=54 3x+4y=38 12.x+8y=154x+y=2913。
3x+6y=24 9x+5y=46 14。
9x+2y=62 4x+3y=36 15.9x+4y=46 7x+4y=42 16.9x+7y=135 4x+y=4117.3x+8y=51 x+6y=2718。
9x+3y=99 4x+7y=95 19。
9x+2y=38 3x+6y=18 20.5x+5y=45 7x+9y=69 21。
8x+2y=28 7x+8y=62 22.x+6y=143x+3y=27 23。
7x+4y=67 2x+8y=26 24.5x+4y=52 7x+6y=74 25。
7x+y=94x+6y=1626.6x+6y=486x+3y=4227。
8x+2y=167x+y=1128。
4x+9y=778x+6y=9429.6x+8y=687x+6y=6630.2x+2y=227x+2y=471)66x+17y=396725x+y=1200答案:x=48y=47(2)18x+23y=2303 74x—y=1998答案:x=27y=79(3)44x+90y=779644x+y=3476答案:x=79y=48(4)76x—66y=408230x—y=2940答案:x=98y=51(5)67x+54y=854671x—y=5680答案:x=80y=59(6)42x—95y=-1410 21x—y=1575答案:x=75y=48(7)47x-40y=85334x-y=2006答案:x=59y=48(8)19x—32y=—1786 75x+y=4950答案:x=66y=95(9)97x+24y=720258x—y=2900答案:x=50y=98(10)42x+85y=636263x—y=1638答案:x=26y=62(11)85x-92y=—2518 27x—y=486答案:x=18y=44 (12)79x+40y=241956x-y=1176答案:x=21y=19 (13)80x-87y=215622x—y=880答案:x=40y=12 (14)32x+62y=513457x+y=2850答案:x=50y=57(15)83x-49y=8259x+y=2183答案:x=37y=61(16)91x+70y=584595x-y=4275答案:x=45y=25(17)29x+44y=528188x-y=3608答案:x=41y=93(18)25x—95y=—4355 40x-y=2000答案:x=50y=59(19)54x+68y=328478x+y=1404答案:x=18y=34(20)70x+13y=3520 52x+y=2132答案:x=41y=50(21)48x—54y=-3186 24x+y=1080答案:x=45y=99(22)36x+77y=7619 47x—y=799答案:x=17y=91(23)13x-42y=-2717 31x-y=1333答案:x=43y=78(24)28x+28y=333252x—y=4628答案:x=89y=30 (25)62x-98y=—2564 46x-y=2024答案:x=44y=54 (26)79x—76y=-4388 26x—y=832答案:x=32y=91(27)63x-40y=—821 42x-y=546答案:x=13y=41 (28)69x—96y=-1209 42x+y=3822答案:x=91y=78(29)85x+67y=7338 11x+y=308答案:x=28y=74 (30)78x+74y=12928 14x+y=1218答案:x=87y=83(31)39x+42y=533159x—y=5841答案:x=99y=35 (32)29x+18y=191658x+y=2320答案:x=40y=42(33)40x+31y=604345x—y=3555答案:x=79y=93(34)47x+50y=8598 45x+y=3780答案:x=84y=93(35)45x-30y=-145529x-y=725答案:x=25y=86(36)11x-43y=—1361 47x+y=799答案:x=17y=36(37)33x+59y=3254 94x+y=1034答案:x=11y=49(38)89x—74y=-2735 68x+y=1020答案:x=15y=55(39)94x+71y=7517 78x+y=3822答案:x=49y=41(40)28x—62y=-4934 46x+y=552答案:x=12y=85 (41)75x+43y=8472 17x—y=1394答案:x=82y=54 (42)41x-38y=-1180 29x+y=1450答案:x=50y=85(43)22x—59y=824 63x+y=4725答案:x=75y=14(44)95x—56y=-401 90x+y=1530答案:x=17y=36(45)93x-52y=—852 29x+y=464答案:x=16y=45(46)93x+12y=8823 54x+y=4914答案:x=91y=30(47)21x-63y=84 20x+y=1880答案:x=94y=30 (48)48x+93y=975638x—y=950答案:x=25y=92 (49)99x-67y=4011 75x-y=5475答案:x=73y=48 (50)83x+64y=9291 90x—y=3690答案:x=41y=92(51)17x+62y=3216 75x—y=7350答案:x=98y=25(52)77x+67y=2739 14x—y=364答案:x=26y=11 (53)20x-68y=—4596 14x-y=924答案:x=66y=87(54)23x+87y=4110 83x-y=5727答案:x=69y=29(55)22x—38y=804 86x+y=6708答案:x=78y=24(56)20x-45y=-3520 56x+y=728答案:x=13y=84 (57)46x+37y=708561x-y=4636答案:x=76y=97(58)17x+61y=4088 71x+y=5609答案:x=79y=45 (59)51x—61y=-1907 89x—y=2314答案:x=26y=53 (60)69x—98y=—2404 21x+y=1386答案:x=66y=71(61)15x-41y=754 74x-y=6956答案:x=94y=16 (62)78x-55y=65689x+y=5518答案:x=62y=76 (63)29x+21y=163331x-y=713答案:x=23y=46(64)58x—28y=2724 35x+y=3080答案:x=88y=85 (65)28x—63y=-225488x-y=2024答案:x=23y=46(66)43x+50y=7064 85x+y=8330答案:x=98y=57 (67)58x—77y=1170 38x-y=2280答案:x=60y=30(68)92x+83y=11586 43x+y=3010答案:x=70y=62(69)99x+82y=6055 52x-y=1716答案:x=33y=34(70)15x+26y=1729 94x+y=8554答案:x=91y=14(71)64x+32y=355256x-y=2296答案:x=41y=29 (72)94x+66y=1052484x-y=7812答案:x=93y=27(73)65x—79y=—5815 89x+y=2314答案:x=26y=95 (74)96x+54y=621663x—y=1953答案:x=31y=60(75)60x—44y=—352 33x—y=1452答案:x=44y=68(76)79x—45y=51014x-y=840答案:x=60y=94 (77)29x-35y=-21859x-y=4897答案:x=83y=75 (78)33x-24y=1905 30x+y=2670答案:x=89y=43(79)61x+94y=11800 93x+y=5952答案:x=64y=84 (80)61x+90y=5001 48x+y=2448答案:x=51y=21 (81)93x-19y=286x—y=1548答案:x=18y=88(82)19x-96y=-591030x-y=2340答案:x=78y=77 (83)80x+74y=8088 96x-y=8640答案:x=90y=12(84)53x—94y=1946 45x+y=2610答案:x=58y=12 (85)93x+12y=911728x-y=2492答案:x=89y=70(86)66x-71y=—1673 99x-y=7821答案:x=79y=97(87)43x—52y=-1742 76x+y=1976答案:x=26y=55(88)70x+35y=8295 40x+y=2920答案:x=73y=91(89)43x+82y=4757 11x+y=231答案:x=21y=47 (90)12x—19y=236 95x—y=7885答案:x=83y=40(91)51x+99y=8031 71x—y=2911答案:x=41y=60 (92)37x+74y=4403 69x-y=6003答案:x=87y=16(93)46x+34y=4820 71x-y=5183答案:x=73y=43 (94)47x+98y=586155x-y=4565答案:x=83y=20 (95)30x—17y=239 28x+y=1064答案:x=38y=53 (96)55x—12y=4112 79x-y=7268答案:x=92y=79(97)27x—24y=-450 67x—y=3886答案:x=58y=84 (98)97x+23y=8119 14x+y=966答案:x=69y=62(99)84x+53y=1127570x+y=6790答案:x=97y=59 (100)51x-97y=297 19x—y=1520答案:x=80y=39。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑴ ⑵
⑶ ⑷
⑸ ⑹
(1)
4、如果(5a-7b+3)2+ =0,求a与b的值。
5、若方程组 与 有公共的解,求a来自b.6、当k=______时,方程组 的解中x与y的值相等。
7、已知二元一次方程3x+4y=6,当x、y互为相反数时,x=_____,y=______;当x、y相等时,x=______,y= _______。
课题名
8.2二元一次方程组的解法(2)
课时
1
备课时间
授课时间
教学目标
会运用代入消元法解二元一次方程组.
教学重点
会运用代入消元法解二元一次方程组.
教学难点
会运用代入消元法解二元一次方程组.
主备人:唐精
【检学】
1、方程组 的解是()
A. B. C. D.
2、若2ay+5b3x与-4a2xb2-4y是同类项,则a=______,b=_______。
8、对于关于x、y的方程y=kx+b,k比b大1,且当x= 时,y= ,则k、b的值分别是()
A. B.2,1 C.-2,1 D.-1,0
教
学
后
记
