5平面桁架习题课
李廉锟《结构力学》(上册)课后习题详解(5-7章)【圣才出品】

第5章静定平面桁架复习思考题1.桁架的计算简图作了哪些假设?它与实际的桁架有哪些差别?答:(1)桁架的计算简图假设①各结点都是无摩擦的理想铰;②各杆轴都是直线,并在同一平面内且通过铰的中心;③荷载只作用在结点上并在桁架的平面内。
(2)桁架的计算简图与实际桁架的差别①结点的刚性。
②各杆轴线不可能绝对平直,在结点处也不可能准确交于一点。
③非结点荷载(例如杆件自重、风荷载等)。
④结构的空间作用,等等。
2.如何根据桁架的几何构造特点来选择计算顺序?答:根据桁架的几何构造特点来选择计算顺序的方法(1)找出零杆根据节点的几何特征和外部受力特点判断出零杆。
(2)选择合适的方法求解桁架①用节点法解简单桁架时,在求出支座反力后,可按与几何组成相反的顺序,从最后的结点开始,依次倒算回去,便能顺利地用结点法求出所有杆件的内力。
②求解联合桁架时,用结点法将会遇到未知力超过两个的结点,可以先用截面法将联合杆件的内力求出,再用结点法求解其它杆件的内力。
③求解复杂桁架时,根据桁架的几何构造特点看,可先算出截面单杆的内力,再选择合适的计算方法求解剩余杆的内力。
3.在结点法和截面法中,怎样尽量避免解联立方程?答:在结点法和截面法中,尽量避免解联立方程的方法:(1)采用结点法时,为避免解联立方程,可改选投影轴方向或者改用力矩平衡方程(向力的汇交点取矩)。
(2)采用截面法时,使用力矩法的关键在于选取合理的力矩中心,因此应尽量选取多力汇交点作为力矩中心;使用投影法的过程中,应尽量选择多个力所在方向作为力分解的坐标轴。
4.零杆既然不受力,为何在实际结构中不把它去掉?答:在实际结构中不把零杆去掉的原因:(1)在实际结构中,工况更复杂,荷载不是一成不变的,荷载改变后,“零杆”可能变为非零杆。
因此,为了保证结构的几何形状在任何载荷作用下都不会改变,零杆不能从桁架中除去。
(2)在理想桁架(做了诸多假设)中“零杆”才是零杆,而实际结构中,零杆的内力也不是零,只是较小而已。
第二节平面桁架问题
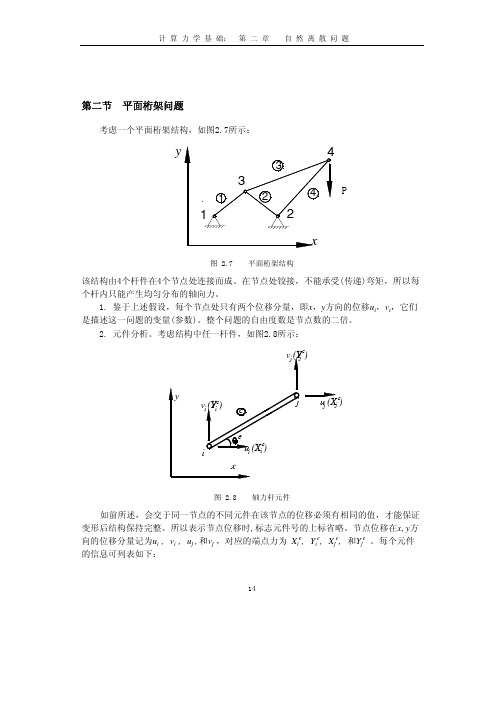
第二节 平面桁架问题考虑一个平面桁架结构,如图2.7所示:图 2.7 平面桁架结构该结构由4个杆件在4个节点处连接而成。
在节点处铰接,不能承受(传递)弯矩,所以每个杆内只能产生均匀分布的轴向力。
1. 鉴于上述假设,每个节点处只有两个位移分量,即x,y方向的位移u i,v i,它们1415元件号 节点号 节点坐标 弹性模量 横截面积 e i , j ( x i , y i );(x j , y j ) E e A e杆件的长度可由下式计算()()L x y x x y y e eej i j i =+=−+−∆∆2222()()ij i j e x x y y tg −−=θ其中e θ是杆件的轴向与x 轴正方向的夹角。
对于图2.8所示的结构,每个元件的节点号如下所示:424433322311j i e杆件产生节点位移u i ,v i ,u j ,v j 后,杆的长度变化为(以受拉为正,受压为负) ))sin cos (sin cos (e i e i e j e j e v u v u L θθθθ+−+=∆ 在节点 j 处的端点轴向力为ee ee e e e e eee jL L LA E L L A E F ∆=∆=∆=κ 其中e ee eLA E =κ 该力在x , y 方向的分量就是X j e 和Y j e ,其表达式为:ee e e e j e j L F X θκθcos cos ∆== j e e e j e e i e e e i e e v u v u θθκθκθθκθκsin cos cos cos sin cos 22++−−=e e e e e j e j L F Y θκθsin sin ∆== j e e j e e e i e e i e e e v u v u θκθθκθκθθκ22sin cos sin sin sin cos ++−−=由杆件本身的平衡得到 F i e = -F j e 即(2.11)(2.14a)(2.12)(2.14b)(2.13)16j eeej eei eeei eee je i v u v u X X θθκθκθθκθκsin cos cos cos sin cos 22−−+=−=j eej eeei eei eeeej e i v u v u Y Y θκθθκθκθθκ22sin cos sin sin sin cos −−+=−=把以上4式合并起来,写成矩阵形式如下⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡−−−−−−−−=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧j j i i e ee ee e e e e ee ee e e ee e e e e ee e e e j e j e i e i v u v u Y X Y X θθθθθθθθθθθθθθθθθθθθθθθθκ22222222sin cos sin sin cos sin cos sin cos cos sin cos sin cos sin sin cos sin cos sin cos cos sin cos 上式写成分块形式为F F k k k k d d i ej e ii eijejie jj e i j ⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪=⎡⎣⎢⎢⎤⎦⎥⎥⎧⎨⎩⎫⎬⎭上式中各子矩阵,各子向量的意义是很明确的。
理论力学桁架网络练习题

理论力学桁架网络练习题一、基本概念题1. 请简述桁架结构的特点。
2. 桁架中的杆件主要承受哪种类型的载荷?3. 什么是节点?桁架中的节点有哪些类型?4. 简述静定桁架与超静定桁架的区别。
5. 桁架结构中的零杆具有什么性质?二、计算题1. 已知一简单桁架,各杆件的长度和材料相同,求各杆件的内力。
2. 计算如下图所示桁架结构中各杆件的内力(图中已给出各杆件长度和载荷)。
3. 有一静定桁架,部分杆件长度和载荷已知,求剩余杆件的长度。
4. 已知一超静定桁架,求各杆件的内力。
5. 分析下图所示桁架结构,判断其是否为静定桁架,并说明理由。
三、分析题1. 分析桁架结构在不同载荷作用下的受力特点。
2. 论述桁架结构在工程中的应用及其优缺点。
3. 比较分析不同材料桁架的受力性能。
4. 针对一个实际桁架工程案例,分析其设计合理性。
5. 讨论桁架结构在地震作用下的稳定性问题。
四、作图题1. 根据给定条件,绘制一个静定桁架的受力图。
2. 绘制一个超静定桁架的受力图,并标明各杆件的内力。
3. 根据下图所示桁架结构,绘制其节点载荷图。
4. 绘制一个桁架结构的弯矩图和剪力图。
5. 请绘制一个简支桁架在均布载荷作用下的受力图。
五、综合题2. 分析一个实际桁架结构,提出改进措施,使其受力更加合理。
3. 针对一个超静定桁架,采用力法求解各杆件的内力。
4. 讨论桁架结构在温度变化影响下的受力特点。
5. 结合工程实际,论述桁架结构在施工过程中的注意事项。
六、判断题1. 桁架结构中的杆件只能承受轴向力。
()2. 所有桁架结构都必须是静定的。
()3. 在桁架结构中,节点载荷可以分解为各杆件的轴力。
()4. 超静定桁架的杆件内力可以通过静力平衡方程直接求出。
()5. 桁架结构的稳定性只与杆件长度有关。
()七、选择题A. 受拉杆件B. 受压杆件C. 零杆D. 弯曲杆件2. 桁架中的节点是:A. 杆件连接处B. 载荷作用点C. 支撑点D. 所有上述选项A. 杆件数量等于节点数减去支撑数B. 杆件数量等于节点数加上支撑数C. 载荷作用点等于节点数D. 支撑数等于节点数A. 力法B. 位移法C. 力矩分配法D. 直接平衡法5. 桁架结构的优化设计主要目的是:A. 减轻结构重量B. 提高结构稳定性C. 降低材料成本D. 所有上述选项八、填空题1. 桁架结构主要由______、______和______组成。
工程力学平面桁架问题课件PPT

本节只讨论平面简单桁架内力的计算。
15
注意
工 1、一般要求所有杆件的内力时,采用节点法;只需要 程 求桁架中某一根或某几根杆件的内力时,采用截面法。 力 学 2、两种方法一般都是先要取整体为研究对象,根据平
面力系平衡 方程求出支座约束反力。 下面通过例子说明两种方法的应用。
16
例一
工 程 力 学
FBy
C
31
例三 已知P1,P2,P3, 尺寸如图。求1,2,3杆所受力。
工
程 力
若再求4,5杆受力
FAy
FBy
学 取节点D考虑
Fx 0 F5 Fy 0 F4
32
零杆:
工 程 力 学
所谓“零杆”,即是内力为零的杆。 当荷载改变后,“零杆”可以变为非零杆。因此,为 了保证结构的几何形状在任何荷载作用下都不会改变, 零杆不能从桁架中除去。
工 程 力 学
A
B
如果两支承点是简支的,很容易证明此桁架是静定的。
13
关于平面理想桁架的基本假设
组成桁架的杆件的轴线都在同一平面内的桁架称为平面桁架。 只需要求桁架中某一根或某几根杆件的内力时,采用截面法。
关 所于谓平“零面杆理”,想即桁是架内的(力1基为本)零假各的设杆杆。 在端点用光滑铰链相连接,连接点称为节点
已知:静止的桁架如图所示,AD=DE=EH=HB=a。
已请知指P出1图,中P2桁,架P内3,力(尺2为寸零)如的图杆杆。件的? 自重相对载荷可以忽略不计
一节点上有三根杆件,如果节点上无外力的作用,其中两根共线,则另一杆为零杆.
工 (2) 杆的自重相对载荷可以忽略不计
(3) 载荷及支座反力均作用在节点上。 否则,称之为空间桁架。
第五章 桁架及组合布局习题解答

I
3m
3m
C
P
0 0
N CD
10 10
Nb
3 3
N
4 5
FE
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
5平面桁架习题课

N CB 3a
a O' a
P
D b E O K
N KBB
例5:求图示桁架结构中 a, b 和 c杆的内力. 解: [ 分析 ] 这是一个上,下两层三铰刚 架构成的桁架 结构. 取上部三铰刚架为隔离体.
P
J
F cGaH Nc Na
A N JA
∑ M O' = 0
1.5 1.5 1.5 1.5
2m 1m 2m 1m
Ne
H
5 P 3
Na
P P
a a F a
P
P
P
4P
P
E
[ 分析 ] 截面法计算 将杆件EG,FH和BC三根 联系杆件截断,取任一边 为隔离体进行计算.
A
B 3a
C
D
3a
5 P 3 Nc
P
N GE
a
Na
∑ Mo = 0
2 2 Pa + N a × 5a = 0 2
Na
2 2 Na = P 5
O a
例1:试用结点法计算图示桁架结构各杆内力. 解: 1)首先判断零杆: 依次观察结点2,7,3,8, 4,9,10,可发现链杆27, 73,38,84,49,95和10-5 均为零杆. 2)取结点1为隔离体
6 15m
N 56
1 2 7 45kN 45kN 3 60 4 5
N 511
8 9 10 4m×5=20m 11 11
A
b 3m
B K 1.5m 1.5m 3m
N AG
5 = P 4
A
5 P 4
∑X =0
1 Nb ' ' = P 4
P 2
Nb
2m
07.桁架与习题课

§2-6 平面简单桁架的内力计算§3-4 平面简单桁架的内力计算桁架——一种由杆件彼此在两端用铰链连接而成的几何形状不变的结构平面桁架——所有杆件都在同一平面内的桁架节点——桁架中杆件的铰接接头桁架的优点:杆件主要承受拉力或压力,可以充分发挥材料的作用,节约材料,减轻结构的重量桁架计算中的通用假设:●桁架的杆件都是直杆●杆件用光滑铰链连接●桁架所受的力(载荷)都作用在节点上●忽略杆重,或平均分配到杆件两端的节点上手工计算桁架杆件内力的方法:●节点法:逐个节点地研究节点平衡,由已知力逐步求出全部未知的杆件内力。
●截面法:选取一适当截面,假想地将桁架截分为二,考察其中任一部分的平衡,以被截断杆件的内力代替另一部分对此部分的作用,由平衡方程求出这些内力。
例:节点法和截面法求桁架内力图示桁架,已知P 1= P 7= P ,P 2= P 3= P 4= P 5= P 6= 2P 。
用节点法求第1 至第6 各杆内力,用截面法求第14 杆内力。
P 1P 2P 3P 4P 5P 6P 72a 2a 2a 2a 2a2a 3a AB C D E F G H I K L1234567891011121314161718192021解:1. 求约束反力以整体为对象,画受力图。
A J15F LyF Ax F Ay列平衡方程0:0==∑Ax F X :0=∑AM ()021086421212=⋅⋅++++-⋅-⋅P a P a a F Ly 得:F Ly = 6P:0=∑LM()021086421212-=⋅⋅+++++⋅+⋅P a P a a F Ay 得:F Ay = 6P校核:()07654321=++++++-+=∑P P P P P P P F FY Ly Ay2. 节点法求各杆内力P 1P 2P 3P 4P 5P 6P 72a2a2a2a2a2a3aA B C D E F G H I J K L123456789101112131415161718192021F LyF Ax F Ay研究A 点平衡,设各杆均受拉力。
静定平面桁架(5-2-6-1)
ɑ
F
F
F FN2 FN3 FN1
FN4
FN2 = -0.417F= -4.17KN FN3= 0.417F=4.17KN
4、四杆结点无荷载。
1 4 3 2 N1=N2 N3=N4
1
F2 F1
2
N1=F1 N2=F2 3 F1 2 N3= –F1 N1≠N2
5、四杆结点无荷载。
3 1 4 2
1
N3= –N4 N1≠N2
判别结构中的零杆
F F F
P
由力矩平衡方程得 N1= N2= N3=0 N1
Ⅰ
P
Ⅰ
N3
N2
▲ 利用结构的对称性 由于结构对称,荷载对称, 由于结构对称,荷载对称,其内力和反力一定对 结构反对称,荷载反对称, 称。结构反对称,荷载反对称,其内力和反力一定 也反对称。利用这个规律可以进行零杆的判断。 也反对称。利用这个规律可以进行零杆的判断。
有些情况下, 结点法求解不方便, 有些情况下,用结点法求解不方便,如: 求解不方便
开始没法用结点法
用结点法计算量大
A.定义: A.定义: 定义 截面法是截取桁架一部分作为研究对 截面法是截取桁架一部分作为研究对 象计算桁架内力的方法。 象计算桁架内力的方法。 B.要求 要求: B.要求: 截面法将桁架截成二部分, 截面法将桁架截成二部分,每一部分至少有 一根完整的杆件(否则为结点法 结点法)。 一根完整的杆件(否则为结点法)。 C.要点 要点: C.要点: 一个截面将桁架截成二部分, 一个截面将桁架截成二部分,取一部分作为研 究对象时。隔离体上的力是一个平面任意力系, 究对象时。隔离体上的力是一个平面任意力系, 可列出三个独立的平衡方程。取隔离体时一般 可列出三个独立的平衡方程。取隔离体时一般 切断的未知轴力的杆件不多余三根。 切断的未知轴力的杆件不多余三根。
静力学-5平面桁架

4 4 FDB 0 ; FDB 2.5kN; 5 5
FAD
FDA
FDB
3 3 FDA FDE 0 ; FDE 3kN; 5 5
[D]
FDE
[B]
4 4 Fiy 0, FBD FBE 0 ; FBE 2.5kN; A 5 5
FR
左螺旋
当空间力系简化为一合力时,合力矩定理仍然成立。 空间一般力系的平衡条件 空间一般力系平衡 的充分和必要条件:
FR Fi 0
M O M Oi 0
FR Fi 0
M O M Oi 0
——空间一般力系的平衡方程
刚体系的平衡
刚体系平衡 系统中每个刚体平衡 平面任意力系的平衡方程
F2 F1
F3
解: 1、选取截面
2、画出研究对象受力图 3、建立平衡方程 研究整体:
FB
研究部分桁架
M
A
0 FB
F
y
0 F1
例: 求图示结构中, CB杆上C端的约束力和杆1的内力 已知:M, P, AE=EC=CD=DB=DH=EG=L 解: 1、研究整体
FAy F Ax
A
E
C
F
P
一、节点法:将每个节点视为平面汇交力系平衡对 像,逐个节点求解内力。 二、截面法:截取桁架每一部份视为平面力系平衡 对像,应用三个平衡方程求解内力。
二、平面桁架内力的计算方法
1、节点法: 以节点为研究对象计算杆件内力的方法 A D 4 例: 在图示桁架中,已知水平杆 1 和铅垂杆等长, 节点E上作用有 7 3 5 铅垂力P, 求各杆内力. E 6 C 2 B 节点法的特点: P 研究节点E->杆1、2的内力 研究节点C->杆3、6的内力 研究节点D->杆4、5的内力 研究节点B->杆7内力和B处的约束力
第五章静定平面桁架

1 F [ F 2 dF dFd ] x E F A 1 2 2 H
M H
0 D
(压力)
结论:可证简支桁架,竖直向下荷载作用 下弦杆受拉力,上弦杆受压力 —— 对应梁,受竖直向下荷载的下、上边缘
(3)斜杆FNED EF、CD交点O,Σm0=0,FNED平移到D分解
桁架各部分名称
弦杆:上、下弦杆 腹杆:斜杆、竖杆 节间:弦杆上, 相邻结点区间 跨度、桁髙
桁架类型
(外形) a)平行弦 b)折弦 c)三角形 (是否有推力) a,b,c)无推力 d)有推力(拱式)
(几何组成方式)——与求解方法有关 (1)简单桁架(a,b,c)——二元体 (2)联合桁架(d,e)——三、二刚片规则 (3)复杂桁架(f)——非基本组成规则方式
1 F [ F aF ( ad ) ] Y E D A 1aF 2 a 2 d
(可能+、-)
2.投影(方程)法 (上、下弦杆平行) (1)求斜杆DG Ⅱ—Ⅱ截面(左) ∑Y=0 FYDG=-(FA-F1-F2-F3) =-F0SDG ——剪力法
F0SDG
截面法: ①所截杆件一般不超过三根 ——三个独立平衡方程可解 ②截面多于三个未知力, 如其中除一根外,其余均交于一点、或平行 ——可解此杆——截面单杆 ③几何组成相反次序求解
§5-6 组 合 结 构 计 算
组合结构——链杆与梁式杆,组合而成结构 (轴力杆:FN)(受弯杆件:M、FS、FN) 计算顺序:反力—链杆—梁式杆 【例5-3】 ①几何组成 ②求解次序 ③反力 FAV=5kN, FBV=3kN ④链杆 FNDE: ⑤梁式杆:受荷载、 链杆的作用力FN ⑥校核结点A/B,F/G
桁架求解的几种方法PPT课件

§ 组合结构的计算
组合结构是指由链杆和受弯为主的梁式杆组成的结 构。链杆只受轴力作用,梁式杆除受轴力外,还要受弯 矩、剪力的作用。用截面法计算组合结构内力时,为了使 隔离体上的未知力不致过多,应尽量避免截断受弯杆件。 因此,计算组合结构的步骤一般是先求支座反力,然后计 算各链杆的轴力,最后计算受弯杆的内力。
ΣFy = 0, ΣFx = 0,
FFNANEAD+22FN4AE×0 2
FNAE = -24 /2 = 0
FNAD = -(-42 )×2 /2 = 4 kN
(2) 取结点D为隔离体,如图5-7(c)所示。
= -5.66 kN
ΣFx = 0, FNDC = 4 kN; ΣFy = 0, FNDE = 2 kN (3) 取结点E为隔离体,如图5-7(d)所示。
FNa×d + F×d = 0 FNa = -F
(2) 取结点G为隔离体,由ΣFy = 0,得 FNc = -F
由ΣFx = 0,得 FNFG = FNa = -F
(3) 作截面2 Ⅱ-Ⅱ,取左部分为隔离体,由ΣMA=0,得 •Page 17 FNb× d+F×d-F×d = 0, FNb = 0
例5-4 求图5-12所示桁架中
(a)
I C
(b )
a A
II
b
II
F
F
B
F IF
F
F
F
图5-9
I F
FC F F
A B
D
E
I
图5-10
•Page 16
§截面法和结点法的联合应用
结点法和截面法是计算桁架内力的两种基本方法。两 种方法各有所长,应根据具体情况灵活选用。
理论力学课件(桁架计算)

刚度矩阵法
总结词
通过建立刚度矩阵,将节点位移和杆件内力之间的关系进行数学描述,方便进行数值计 算。
详细描述
刚度矩阵法是理论力学中常用的方法之一,它通过建立刚度矩阵来描述节点位移和杆件 内力之间的关系。在桁架计算中,根据杆件的几何特性和材料属性,可以建立相应的刚 度矩阵。通过求解线性方程组,可以得到节点位移和杆件内力的数值解。这种方法适用
实例分析
以一个简单的组合结构为例,通过分 析其受力情况,可以计算出各结构形 式的内力和变形,从而判断结构的稳 定性和安全性。
谢谢聆听
于求解大型复杂结构的静力和动力问题。
桁架的应力与稳定性
05
应力计算
01
节点应力
根据力的平衡原理,计算节点处的应力,包括拉应力和 压应力。
02
杆件应力
根据杆件受力情况,采用截面法或能量法计算杆件内部 的应力分布。
03
应力分布规律
分析不同类型桁架的应力分布规律,如三角形、四边形 、多边形等。
稳定性分析
虚功原理
总结词
基于虚功原理,通过分析力和位移的关系,推导出节点位移和杆件内力的关系。
详细描述
虚功原理是理论力学中的基本原理之一,它指出在理想约束条件下,一个系统处于平衡状态时,任何一个虚位移 都不会对任何外力做功。在桁架计算中,利用虚功原理可以推导出节点位移和杆件内力的关系,为后续的位移计 算和内力分析提供基础。
02
截面法适用于任何形式的桁架,包括三角形、矩形、梯 形等。
03
在使用截面法时,需要特别注意截面的选择,因为不同 的截面会导致不同的结果。
节点法
节点法是通过分析节点之间的相 互作用力和外力,从而求出整个
桁架的内力。
第5章 静定平面桁架

- 23/85页 -
FP
FP 1
D
FP
C
3FP
E
1.5FP -
2
1m B 1m
A
3FP F
G
H
2m 2m 2m 2m
1.5FP
1.5FP
FP C
3FP A
F
即
FNAC
1.5FP
可由比例关系求得
Fy1
FN1
D Fx1
G
Fx2
Fy2
FN2
24
《 第5章 静定平面桁架 》
- 24/85页 -
【例】 用结点法求AC、AB杆轴力。
F6=120kN
6
4
3
F7H=120kN 7
F7V=45kN
4m
5 15kN 4m
2 15kN 4m
3m
1 15kN
按结点1,2,…,6依次计算各结点相关杆件轴力 。
结点7用于校核。
17
《 第5章 静定平面桁架 》
- 17/85页 -
2. 零杆和等力杆
(1) 关于零杆的判断 在给定荷载作用下,桁架中轴力为零的杆件, 称为零杆。 1) L形结点:成L形汇交的两杆结点无荷载作 用,则这两杆皆为零杆。
FyAC
FyAB
4m
2m
1 2
3 2
27
《 第5章 静定平面桁架 》
- 27/85页 -
【例】用结点法求各杆轴力。 解: 1)支座反力
FAy=FBy=30kN(↑)
FAx=0
2)判断零杆
3)求各杆轴力 取结点隔离体顺序为:A、E、D、C。 结构对称,荷载对称,只需计算半边结构。
28
《 第5章 静定平面桁架 》
理论力学课件 平面简单桁架。摩擦

动摩擦
Fd = fFN
f称为动摩擦因数,和物体相对运动速度有关。
3.5 摩擦
静摩擦力 大小:是一个范围
0 ≤ F ≤ Fmax = fs FN
只有临界的情况才能引用 Fmax = fs FN 而且摩擦力方向不能假设
方向:与相对运动 摩擦
MA
FAy
∑Fx = 0
FBy FBx
∑Fy = 0
∑MA =0
FAx − FBx = 0 FAx = 8kN
FAy − FBy = 0 FAy = 4kN
M A + M + FBx × 2a − FBy × a = 0
M A = −22kN ⋅ m
3.3 简单物体系平衡问题
思考题:人重W,板重P,若人有足够大的力量。 1、可能维持平衡的是? 2、哪种情况人更费力?
注意: 平面静定桁架的零力杆只是在特定载荷下内力为零, 所以它绝不是多余的杆件。
3.4 平面简单桁架
判断0杆
0 0 0 0
0 0
0 0
0 0
0
0
3.4 平面简单桁架
3、截面法
用适当的截面将桁架截开,取其中一部分为研究对 象,建立平衡方程,求解被切断杆件内力的一种方法。
截取的部分上的力系是平面任意力系
∑ Fx = 0 ∑ Fy = 0
FP
E
FP
FP
FP
H
C
FP
2 I
30° 30°
2
30° 30° A
G
D
B
FIy
a
a
a
a
FA
FP
FCE
C
y FCD x
《平面桁架习题》课件

04 平面桁架的优化 设计
平面桁架的尺寸优化
总结词
尺寸优化是平面桁架优化设计的重要环节,主要涉及对杆件长度、截面尺寸等参 数的调整,以达到更好的力学性能和经济效益。
详细描述
在平面桁架的尺寸优化过程中,通常采用数学模型和计算机模拟技术,通过对杆 件长度、截面面积等参数的调整,使整个结构在满足承载能力的前提下,具有更 小的重量和成本。同时,尺寸优化还可以改善结构的稳定性和振动性能。
平面桁架习题
目 录
• 平面桁架的基本概念 • 平面桁架的内力分析 • 平面桁架的位移分析 • 平面桁架的优化设计 • 平面桁架的应用实例
01 平面桁架的基本 概念
平面桁架的定义
总结词
平面桁架是一种由杆件组成的结 构,其所有杆件都在同一平面内 相互连接。
详细描述
平面桁架是由若干直杆在端点以 铰链连接组成的结构,所有杆件 都在同一平面内,形成了一个几 何不变体系。
总结词
高层建筑中,平面桁架用于连接高层建筑竖 向结构和水平楼板,提高整体稳定性。
详细描述
在高层建筑中,平面桁架被广泛应用于连接 高层建筑的竖向结构和水平楼板。通过合理 设计平面桁架的结构形式和尺寸,可以有效 地提高高层建筑的整体稳定性,增强结构的 承载能力和抗风能力,确保高层建筑的安全 性和稳定性。
05 平面桁架的应用 实例
桥梁工程中的平面桁架
总结词
桥梁工程中,平面桁架常被用于主梁和桥墩的连接,以承受和传递荷载。
详细描述
在桥梁工程中,平面桁架结构因其高强度的承载能力和稳定性而被广泛应用。 通过合理设计平面桁架的结构形式和尺寸,可以有效地将桥面荷载传递到桥墩 上,确保桥梁的整体稳定性和安全性。
平面桁架的结构优化
教学课件第五章静定平面桁架

60
40
20
-
A
-120 C -20 F -20
15kN 15kN
4m
4m
4m
G
15kN
结点分析时把所有杆内力均画成拉力(含已求得的压力)并代 入方程,然后是拉力的得正值,是压力的得负值。结果为正说 明该杆受拉,结果为负说明该杆受压,这样做不易出错。
§5-2 结点法
小结
• 以结点作为平衡对象,结点承受汇交力 系作用;
2.对称结构受对称荷载作用, 内力和反力均为对称: 受反对称荷载作用, 内力和反力均为反对称。
E 点无荷载,红色杆对不称受轴力处垂的直杆对不称受轴的力杆不受力
FFAAyy
FFBBy y
§5-2 结点法
2.对称结构受对称荷载作用, 内力和反力均为对称: 受反对称荷载作用, 内力和反力均为反对称。 对称结构:几何形状和支座对某轴对称的结构.
FP
§5-2 结点法
关于零杆的判断
桁架中的零杆虽然不受力,但却是保持 结构坚固性所必需的。因为桁架中的载荷往 往是变化的。在一种载荷工况下的零杆,在 另种载荷工况下就有可能承载。如果缺少了 它,就不能保证桁架的坚固性。
分析桁架内力时,如首先确定其中的零杆, 这对后续分析往往有利。
§5-2 结点法
• 按与“组成顺序相反”的原则,逐次建 立各结点的平衡方程,则桁架各结点未 知内力数目一定不超过独立平衡方程数;
• 由结点平衡方程可求得桁架各杆内力。
§5-2 结点法 二、结点法计算简化的途径
1. 对于一些特殊的结点,可以应用平衡条件直 接判断该结点的某些杆件内力为零。 零杆
(1) L型结点:两杆交于一点,若结点无荷载,则两杆 的内力都为零。
理论力学桁架计算 ppt课件

MD0, 求出杆1的内力F1。
2F
F
a
a
D 3
m
B
3P 3
(拉)
截面法求解要点 假想用一截面截取出桁架的某一部分 作为研究对象,此时被截杆件的内力作为研究对象的外力, 可应用一般力系的平衡条件列平衡方程求出被截杆件的未 知内力。
思考题
C
用截面法求杆1,2,3的内力。 m a1
用截面m,并取上半部分。
E a
Fx 0, 求出杆2的内力F2。
A
a
MC0, 求出杆3的内力F3。
理想桁架
桁架中每根杆件均为二力杆
三、简单理想桁架的内力计算
对于简单理想桁架,各杆所传递的力均可通过力系的 平衡方程来计算。 节点法—— 应用平面汇交力系平衡条件,逐一研究桁架上
每个节点的平衡。 截面法—— 应用平面任意力系的平衡条件,研究桁架由截
面切出的某些部分的平衡。
注意
1.无论采用哪种方法,往往都应先求支座的约束反力。
由平面力系平衡条件列平衡方程
Fx 0 FAx 0
MB 0 2lP3lFAy0
FAy
2 3
P
节点法 依次取节点A,C,E为研究对象
对节点A由平面汇交力系平衡条件列平衡方程
F y 0 , F A y F A s C 6 i n 0
F x 0 , F A E F A c C 6 o 0 s
焊接
铆接
螺栓连接
实际建筑 中的桁架
结构
各杆件轴线不在同一平面内的桁架,称为空间桁架。 各杆件轴线都在同一平面内的桁架,称为平面桁架。
空间桁架
平面桁架
二、建立平面桁架力学模型
考虑如下几点假设:
1.各杆件为直杆,各杆轴线位于同一平面内。 2.杆件与杆件间均用光滑铰链连接。 3.外力都作用在节点上。 4.各杆件自重不计或平均分布在节点上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H
P
a
Na
P P P P 4P
[ 分析 ]
a
E
F
截面法计算
a
A
B
C
3a
将杆件EG、FH和BC三根 联系杆件截断,取任一边 D 为隔离体进行计算。
P
NGE
Na
a
Mo 0
2 Pa
2 2
Na
5a
0
2m 1m 2m 1m
O
N CB
a
3a
例5:求图示桁架结构中 a、 b 和 c杆的内力。
D
a
解法 I:利用对称性简化计算
1)正对称荷载作用下
C
G
EP
a
判断零杆
D
C
P
G
2
A
B
F
E
P
a
a
2
A
B
F
用结点法按照E、D、G、B顺序,分别取结点隔离体图,利 用平面汇交力系的平衡条件,逐步计算各杆内力。
D
1)反对称荷载作用下
C
P
G
2
E
P
2
A
B
F
解法 II:截面法求解关键杆内力
a
判断零杆 用结点法分别取E、F结点 为隔离体,逐步计算各杆 内力。
静定平面桁架习题课
一、桁架 简单桁架:通过逐步增加二元体可构成的桁架;
分类 联合桁架:由两个(或三个)刚片组成的桁架; 复杂桁架:
二、计算 结点法:以宜单用个于结简点单为桁隔架离的体计,算利用平面汇交力系平
方法
衡条件为依据计算杆件内力;
截面法:以宜包用含于两联个合及桁两架个计以算上刚结片点间部联分系为杆隔件离的体内,力
截面单杆内力可直接由力矩平衡方程求出。
例1:试用结点法计算图示桁架结构各杆内力。
解: 1)首先判断零杆:
6
依次观察结点2,7,3,8,
15m
3m5=15m
4,9,10,可发现链杆27,
73,38,84,49,95和10-5 1 均为零杆。
2 3 604 5
2)取结点1为隔离体
Y 0
3 45 N17 5 0 45
N17 75 kN
7 N12 4455kkNN 8
9
N17
10
4m5=20m
N 56 N511
1111
X 0
N12
75
4 5
0
N12 60 kN
3)取结点5为隔离体 X 0
2a a
例2:求图示桁架中指定杆件的内力。
解: 1)先判断零杆
PP
2)求支反力
O
22PP b
OO
O a
a OO
O
O
3)计算 a杆内力 结点法:
O O
O
O
OOO
取结点B计算 a杆内力;
截面法:
13 P
b
b
a
6a 6a
B 5P
MA 0
6
2P
P
6
Na
2a a
2 2
Na
3a
13 6
P
3a
4 Pa
0
52 Na 6 P
4)计算 b杆内力
13 P
Nb A 6a
3a 2a a
结点单杆:如果在同利一用结平点衡的条所件有计内算力某未些知关的键各杆杆件中的,内除力某;一杆 外,其余各杆都共线,则该杆称为该结点的结点单杆
结点单杆内力可直接根据静力平衡条件计算得到;
截面单杆:如果在同一截面所截取的所有内力未知的各杆中,除 某一杆外,其余各杆都汇交于一点,则该杆称为该截
面的截面单杆。
P
P
取结点 F为隔离体
P
C
2 Na
F
2
2a
D
E
F
2m 4m
G
计算得: N FB
N FB
5P 4
N
a
1 4
P
A
b 3m
根据对称性可得: N EA
5P 4
取结点 A为隔离体,
X 0
Nb ''
1 4
P
H
B K 1.5m 1.5m 3m
N AG
A
5 P
4
Nb P 2
例7:求桁架结构各杆的内力。
3m 1.5m 1.5m 3m
1)正对称荷载作用下 取结点 A为隔离体
P
P
2
2
N AE A
E
F
2m 4m
Nb P
2
A
B
Y 0
b
K
N AE
2 P0 52
3m 1.5m 1.5m 3m
P
P
2
2
5 N AE 4 P
X 0
Nb '
5 P 4
1 0 5
Nb '
1 4
P
2)反对称荷载作用下
结构本身的几何构造分析入手。
例6:求桁架结构中 a、b杆的内力。
2m222mmm 4m444mmm
PPPP
PPPP
CC C
2P222P
2 EEE
2P222 a a
F2FF a
DD D
E
F
GG
HH
G
H
AAA A
bbb KKK
BBB B
3m33mmb 1.151.m5.5mmK1.151.m5.5mm 3m33mm
P
Nc
1 6
P
X 0
Na
1 P P 0 P
6
Na
5 6
P
下面计算杆 b的轴力
C D
b
F
NGba
H E
J H
A 5P
E
K B
MK 0
6
K
Nb
3 3 5 P1 0
10
6
1.5 1.5 1.5 1.5 1.5 1.5 B
Nb
5 10 36
P
注意: 对于较为复杂的平面桁架,指定杆件内力的计算往往是从
D
对右半部分隔离体,取CD、
AG和EF杆法线方向力的平
C
a
衡方程,首先计算杆FB的
轴力,然后按B、E、D、C、 A
A顺序用结点法逐步计算各
P
杆轴力。
2
G
EP
B F
a
aP
2
解法 III:用截面法计算关键杆件内力
取隔离体图如下: D
f DD
a
a
N DC
N DC N DE
G
EP
C
GG
EP
a
a
N GA
N EF
解: [ 分析 ] 这是一个上、下两层三铰刚
架构成的桁架 结构。
取上部三铰刚架为隔离体。
a
Na O’
Na
2 2 5
P
a D
P
J
P
C
bE
F cGaH O
Nc Na
K
A N JA
N
B
KB
MO' 0
1.5 1.5 1.5 1.5
2m 1m 2m 1m 2m 1m 2m 1m
Nc 6 4P 3P 0
NGA NGB f
MF 0
BA
B
F N BF
F
a
X
a
f
f
0
a
2 2
N DC
2a
2 2
NGA
a
Pa
0
NDC NGA 0
联立方程计算杆件DC和GA的轴力,然后用结点法逐步计算其它
所有杆件的内力。
MC 0
Nb
2a
5 6
P
4a
0
C
Nb
5 3
P
例3:试求图示桁架指定杆的内力。
Nb
6a
e
H
5P 6
d
cF Eb
A
G Ca D
B
4P P P P P P P P P 4P
9a
3a
Na
11 P 3
Ne
11 3
P
Nc 0
Ne
H
5P 3
Nc
5P 3
例4:求桁架 a杆内力。 G
G
