一元二次方程的应用(动点问题)精编版
一元二次方程的应用3 动点问题

练习
1、某农场要建一个长方形的养鸡场, 鸡场的一边靠墙,墙长25m,另三边用 总长40m的木栏围成。 (1)试通过计算说明鸡场的面积能达 到180m2; (2)鸡场的面积能达到250m2吗?为什 么?
2、将一块长比宽多3cm的长方形铁皮 四角各剪去一个边长为4cm的小正方形, • 做成一个无盖的盒子.已知盒子的体 积是280cm3,求原铁皮的边长.
的速度移动,与此同时,点Q从点B 开始沿边BC向点C以2cm/s的速度移 动。如果P、Q分别 从A、B同时出发, 经过几秒,三角形 PBQ的面积等于8cm2? (AB=6cm,BC=8cm)
s
练习: 1、如图,在矩形ABCD中, AB=6cm,BC=3cm。点P沿边AB从点 A开始向点B以2cm/s的速度移动,点Q 沿边DA从点D开始向点A以1cm/s的速 度移动。如果P、Q同时出发,用t(s) 表示移动的时间(0≤t≤3)。那么,当t 为何值时, △QAP的面积 等于2cm2?
2、用长为100 cm的金属丝制作一 个矩形框子。框子各边多长时,框 子的面积是600 cm2?能制成面积 是800 cm2的矩形框子吗?
3、据新华网报道,2000年我国共有 荒漠化、沙化土地216.5万平方千米, 2002年初增长到267.4万平方千米。 从2000年初到2002年初的两年间, 我国荒漠化、沙化土地面积的年平 均增长率是多少?
一元二次方程的应用3
动点问题
例1、矩形ABCD中,点P从点A沿AB 向B点以每秒2cm的速度移动,点Q从 点B开始沿BC向C点以每秒1cm的速度 移动,AB=6cm,BC=4cm, 若P、Q两点分别从A、B 同时出发,问几秒钟后P、 Q两点之间的距离为 cm2
例2、 如图,在
ABC中, B 90, 点p从点A开始沿边AB向点B以1cm
一元二次方程-动点问题

D
C
整理,得 x262x80
解这个方程,得 x1 2,x2 4
Q
0x6所以2秒或4秒后⊿ PBQ的面
积等于8cm2
A
B
P
A
R
P
例2:等腰直角⊿ ABC
中,AB=BC=8cm,动点P从A点出发,
解:设AP=x,则PR=x,PB沿B=C8A,A-BC向x的B直移线动与,通A过C点,BPC引分平别行交于于R、
四边形DFCE的面积为20cm2?
C
F E
A
D
B
添加标题
01 经过多少时间后,S△PCQ的面积为 15cm2?
添加标题
02 请用配方法说明,何时△PCQ的面积 最大,最大面积是多少?
单击此处添加 大标题内容
如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截 去四个相同的小正方形,设小正方形的边长为xcm. 底面的长AB=_______cm,宽BC=__________cm(用含x的代数式表示) 当做成盒子的底面积为300cm2时,求该盒子的容积. 该盒子的侧面积S是否存在最大的情况?若存在,求出x的值及最大值是多少?若不存在,说明 理由.
5.如图所示,已知在△ABC中,∠B=90°,AB=5,点Q 从点A开始沿AB边向点B以1cm/s的速度移动,点P从点 B开始沿BC边向点C以2cm/s的速度移动. (1)如果P、Q分别从A、B两点出发,那么几秒后, △PBQ的面积等于4cm2? (2)在(1)中,△PBQ的面积能否等于7cm2?试说明 理由.
3、如图,已知A、B、C、D为矩形的四个顶
点,AB=16㎝,AD=6㎝,动点P、Q分别从点A、C同时 出发,点P以3㎝/s的速度向点B移动,一直到点B为止,
(完整版)一元二次方程动点问题讲解

1)设⊿ ABC位于直线L左侧部分的面积为S,写出S与x之间的函 数关系式; 2)当x为何值时,直线L平分⊿ ABC的面积?
(1)解:∠ BAC=45°,AP=x,
∴当L位于CD的右侧时,与
BC交于点Q
L
AP=X,PB=3-X
C
Q
CD=2,PQ=?
p
由小学学习的比例计算PQ 即:CD:DB=PQ:BQ
∴450=½×(2X-50)×3X
Q
X²-25X-30=0
C
解得:X₁=-5(舍去);X₂=30
解得:综合以上情况在10S,15S,30S时,△OPQ的面积为450
例2 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始 以1cm/s的速度沿AB边向点B移动,点Q从点B开始以 2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B 同时出发,几秒后⊿ PBQ的面积等于8cm2?
C
通过观察,有两种情况:(1)蚂蚁未爬完OA这段距离
(2)蚂蚁爬完OA这段距离后,再由O点向B爬行
例1 如图OA=OB=50cm,OC是一条射线,OC⊥AB,一
只蚂蚁由点A以2cm/s的速度向B处爬行,同时另一只蚂
蚁由O点以3cm/s的速度沿oc方向爬行,则是否存在这样
的时刻,使两只蚂蚁所在位置与O点组成的三角形的面积
·ALeabharlann RP∴S◇=S△ABC-S△BPQ-S△APQ
∴16=32-½(8-X)²-½×(X)²
整理:x²-8x+16=0
整理:x₁=x₂=4
CQ
B
∴当AP=4cm时,平行四边形PQCR的面积等于16cm2
例4:⊿ABC中,AB=3, ∠ BAC=45°,CD⊥ AB,垂足为D,CD=2,P 是AB上的一动点(不与A,B重合),且AP=x,过点P作直线L与AB垂直.
一元二次方程与动点及答案精编版.doc

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1、如图,在△ ABC 中,∠ B = 90°, BC = 12cm, AB = 6cm,点 P 从点 A 开始沿 AB 边向点 B 以 1cm/s 的速度移动,点 Q 从点 B 开始沿 BC 边向点 C 以 2cm/s 的速度移动,如果 P、Q 分别从 A 、 B 同时出发,几秒后△PBQ 的面积等于8cm2?CQ↑B P ← A2. △ ABC 中,∠ B=90 °, AB=5cm ,BC=6cm ,点 P 从点 A 开始沿边 AB 向终点 B 以 1cm/s 的速度移动,与此同时,点 Q 从点 B 开始沿边 BC 向终点 C 以 2cm/s 的速度移动.如果P、 Q 分别从 A、 B 同时出发,当点 Q 运动到点 C 时,两点停止运动.设运动时间为 t 秒.( 1)填空: BQ=,PB=(用含t的代数式表示);(2)当 t 为何值时, PQ 的长度等于 5cm ?(3)是否存在 t 的值,使得△ PBQ 的面积等于 4cm 2?若存在,请求出此时 t 的值;若不存在,请说明理由.3. 如图,在△ ABC中,∠B=90°,AB=6,BC=8.点P从点A开始沿边AB向点 B以 1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.设 P、 Q 分别从 A 、 B 同时出发,运动时间为 t ,当其中一点先到达终点时,另一点也停止运动.解答下列问题:(1)经过几秒,△ PBQ 的面积等于 8cm 2?(2)是否存在这样的时刻 t ,使线段 PQ 恰好平分△ ABC 的面积?若存在,求出运动时间 t ;若不存在,请说明理由.4.如图所示,△ ABC 中,∠ B=90 °,点 P 从点 A 开始沿 AB 边向 B 以 1cm/s 的速度移动,点 Q从 B 点开始沿 BC 边向点 C 以 2cm/s 的速度移动.(1)如果 P, Q 分别从 A , B 同时出发,经几秒,使△PBQ 的面积等于8cm2?(2)如果 P, Q 分别从 A , B 同时出发,并且 P 到 B 后又继续在 BC 边上前进, Q 到 C 后又继续在 CA 边上前进,经过几秒,使△ PCQ 的面积等于 12.6cm 2?5. 如图, A 、 B 、 C 、 D 为矩形的 4 个顶点, AB=16cm , BC=6cm ,动点 P、 Q 分别从 A 、C 同时出发,点 P 以 3 厘米每秒的速度向点 B 移动,一直到达点 B 为止.点 Q 以 2 厘米每秒的速度向点D 移动,经过多长时间 P 、Q 两点之间的距离是 10 厘米?6.如图, A 、 B、C、D 为矩形的 4 个顶点, AB = 16cm, BC = 6cm,动点 P、Q 分别从点 A 、 C 同时出发,点 P 以 3cm/s 的速度向点 B 移动,一直到达点 B 为止;点 Q 以 2cm/s 的速度向点 B 移动,经过多长时间 P、 Q 两点之间的距离是 10cm?C DQBP A7.如图,有一边长为 5cm 的正方形 ABCD 和等腰 △ PQR ,PQ=PR=5cm ,QR=8cm ,点 B 、C 、Q 、 R 在同一条直线 l 上,当 C 、Q 两点重合时,等腰 △PQR 以 1cm/秒的速度沿直线 l 按箭头所示方向开始匀速运动, t 秒后正方形 ABCD 与等腰 △ PQR 重合部分的面积为 Scm 2.解答下列问题:( 1)当 t=3 秒时,求 S 的值; ( 2)当 t=5 秒时,求 S 的值;( 3)当 5 秒 ≤t ≤8 秒时,求 S 与 t 的函数关系式.8.2012?重庆模拟)如图,已知正方形ABCD 的边长与Rt△ PQR 的直角边PQ 的长均为6cm,QR=12cm ,AB 与 QR 在同一条直线l 上.开始时点 Q 与点 B 重合,让△ PQR 以 1cm/s 速度在直线 l 上运动,直至点R 与点 A 重合为止,设运动时间为t( s), t> 0.(1)点 P 与点 D 重合时,令PR 与 BC 交于 M 点,求 PM 的长度;(2)设△PQR 与正方形ABCD 重叠部分的面积为Scm 2,直接写出S 与 t 之间的函数关系式和相应的自变量t 的取值范围;(3)在运动的过程中,令线段PR 与线段 AD 的交点为N(若无交点则不考虑),则是否存在 t 的值,使△NQR 为等腰三角形?若存在,求出相应的t 的值;若不存在,请说明理由.9.( 2012?市南区模拟)如图,已知正方形 ABCD 的边长与 Rt △ PQR 的直角边 PQ 的长均为4cm ,QR=8cm , AB 与 QR 在同一直线 l 上,开始时点 Q 与点 A 重合,让 △ PQR 以 1cm/s 的速度在直线 l 上运动,同时 M 点从点 Q 出发以 1cm/s 沿 QP 运动,直至点 Q 与点 B 重合时,都停止运动,设运动的时间为t ( s ),四边形 PMBN 的面积为 S( c m 2).( 1)当 t=1s 时,求 S 的值;(2)求 S 与 t 之间的函数关系式,并写出自变量 t 的取值范围(不考虑端点) ;(3)是否存在某一时刻t ,使得四边形 PMBN 的面积?若存在,求出此时t 的值;若不存在,说明理由; (4)是否存在某一时刻 t ,使得四边形 PMBN 为平行四边形?若存在,求出此时t 的值;若不存在,说明理由.10.如图 1,在长为 44,宽为 12 的矩形 PQRS 中,将一张直角三角形纸片 ABC 和一张正方形纸片DEFG 如图放置,其中边 AB 、DE 在 PQ 上,边 EF 在 QR 上,边 BC、DG 在同一直线上,且 Rt△ ABC 两直角边BC=6 , AB=8 ,正方形 DEFG 的边长为4.从初始时刻开始,三角形纸片ABC ,沿 AP 方向以每秒 1 个单位长度的速度向左平移;同时正方形纸片DEFG ,沿 QR 方向以每秒 2 个单位长度的速度向上平移,当边GF 落在 SR 上时,纸片DEFG 立即沿RS 方向以原速度向左平移,直至 G 点与 S 点重合时,两张纸片同时停止移动.设平移时间为 x 秒.(1)请填空:当 x=2 时, CD= 2,DQ=4,此时CD+DQ=CQ(请填“<”、“=”、“>”);(2)如图 2,当纸片 DEFG 沿 QR 方向平移时,连接 CD、DQ 和 CQ,求平移过程中△CDQ 的面积 S 与 x 的函数关系式,并写出自变量x 的取值范围(这里规定线段的面积为零);(3)如图 3,当纸片DEFG 沿 RS 方向平移时,是否存在这样的时刻x,使以 A 、 C、 D 为顶点的三角形是等腰三角形?若存在,求出对应x 的值;若不存在,请说明理由.11.(2013?长春)如图①,在 ?ABCD 中, AB=13 ,BC=50 , BC 边上的高为12.点 P 从点B 出发,沿 B ﹣A ﹣D ﹣A 运动,沿 B﹣ A 运动时的速度为每秒 13 个单位长度,沿 A ﹣ D﹣A 运动时的速度为每秒 8 个单位长度.点 Q 从点 B 出发沿 BC 方向运动,速度为每秒 5 个单位长度. P、 Q 两点同时出发,当点 Q 到达点 C 时, P、 Q 两点同时停止运动.设点P 的运动时间为 t (秒).连结 PQ.(1)当点 P 沿 A ﹣ D﹣ A 运动时,求 AP 的长(用含 t 的代数式表示).(2)连结 AQ ,在点 P 沿 B﹣ A ﹣ D 运动过程中,当点P 与点 B、点 A 不重合时,记△ APQ 的面积为 S.求 S 与 t 之间的函数关系式.(3)过点 Q 作 QR∥ AB ,交 AD 于点 R,连结 BR ,如图② .在点 P 沿 B﹣ A ﹣ D﹣ A 运动过程中,当线段 PQ 扫过的图形(阴影部分)被线段BR 分成面积相等的两部分时t 的值.(4)设点 C、 D 关于直线 PQ 的对称点分别为 C′、 D ′,直接写出 C′D′∥BC 时 t 的值.12.(2006?青岛)如图①,有两个形状完全相同的直角三角形ABC 和 EFG 叠放在一起(点A 与点 E 重合),已知 AC=8cm , BC=6cm ,∠ C=90 °, EG=4cm ,∠ EGF=90 °, O 是△EFG 斜边上的中点.如图②,若整个△ EFG 从图①的位置出发,以 1cm/s 的速度沿射线 AB 方向平移,在△ EFG 平移的同时,点 P 从△ EFG 的顶点 G 出发,以 1cm/s 的速度在直角边 GF 上向点 F 运动,当点 P 到达点 F 时,点 P 停止运动,△ EFG 也随之停止平移.设运动时间为 x( s), FG 的延长线交 AC 于 H,四边形 OAHP 的面积为 y( cm 2)(不考虑点 P 与 G、 F 重合的情况).(1)当 x 为何值时, OP∥ AC ;(2)求 y 与 x 之间的函数关系式,并确定自变量x 的取值范围;(3)是否存在某一时刻,使四边形OAHP 面积与△ABC 面积的比为13: 24?若存在,求出 x 的值;若不存在,说明理由.(参考数据:2 2 2或114 =12996, 115 =13225, 116 =134562 2 24.4 =19.36 , 4.5 =20.25 , 4.6 =21.16)1.解:设 x 秒钟后,△ PBQ 的面积等于 8cm 2,由题意可得:2x ( 6-x )÷ 2=8解得 x 1 =2 , x 2 =4 .经检验均是原方程的解.答: 2 或 4 秒钟后,△ PBQ 的面积等于 8cm 2.2.解:( 1 )由题意,得BQ=2t , PB=5-t.故答案为: 2t , 5-t.(2)在 Rt △ PBQ 中,由勾股定理,得4t 2 +( 5-t )2 =25 ,解得:t 1 =0 , t 2 =2 .( 3)由题意,得2t (5 - t )2=4 ,解得:t 1 =1 , t 2 =4 (不符合题意,舍去),∴当 t=1时,△PBQ的面积等于4cm2.3.解:( 1 )设经过 x 秒,△ PBQ 的面积等于 8cm 2则:BP=6-x , BQ=2x ,所以 S△P BQ =12×( 6-x )× 2x=8 ,即 x 2 -6x+8=0,可得: x=2 或 4(舍去),即经过 2 秒,△ PBQ 的面积等于 8cm 2.( 2)设经过 y 秒,线段 PQ 恰好平分△ ABC 的面积,△ PBQ 的面积等于 12cm 2,S△P BQ = 12×( 6-y )× 2y=12 ,即 y 2-6y+12=0,因为△ =b 2 -4ac=36-4× 12=-12<0,所以△PBQ的面积不会等于12cm2,则线段PQ不能平分△ ABC 的面积.4.相似三角形的判定与性质;一元二次方程的应用.几何动点问题.(1)设 x 秒时.由三角形的面积公式列出关于x 的方程, ( 6﹣ x )?2x=8 ,通过解方程求得 x 1=2, x 2=4;(2)过 Q 作 QD ⊥ CB ,垂足为 D ,构建相似三角形△ CQD ∽△ CAB ,由该相似三角形的对应边成比例得到,即 QD=;然后由三角形的面积公式列出关于x 的方程( 14﹣ x ) ?=12.6 ,解之得 x 1=7,x 2=11 .由实际情况出发,来对方程的解进行取舍.解:( 1)设 x 秒时,点 P 在 AB 上,点 Q 在 BC 上,且使△ PBQ 面积为 8cm 2,由题意得 ( 6﹣ x ) ?2x=8,解之,得 x 1=2 ,x 2=4,经过 2 秒时,点 P 到距离 B 点 4cm 处,点 Q 到距离 B 点 4cm 处;或经 4 秒,点 P 到距离 B 点 2cm 处,点 Q 到距离 B 点 8cm 处,△ PBQ 的面积为 8cm 2,综上所述,经过 2 秒或 4 秒,△ PBQ 的面积为 8cm 2;(2)当 P 在 AB 上时,经 x 秒,△ PCQ 的面积为: ×PB ×CQ=×( 6﹣ x )(8﹣ 2x ) =12.6,解得: x 1=(不合题意舍去) , x 2= ,经 x 秒,点 P 移动到 BC 上,且有 CP=( 14﹣ x ) cm ,点 Q 移动到 CA 上,且使 CQ= ( 2x﹣ 8) cm ,过 Q 作 QD ⊥ CB ,垂足为 D ,由△ CQD ∽△ CAB 得,即QD= ,由题意得( 14﹣x ) ?=12.6,解之得 x 1=7, x 2=11.经 7 秒,点 P 在 BC 上距离 C 点 7cm 处,点 Q 在 CA 上距离 C 点 6cm 处,使△ PCQ 的面积等于12.6cm 2.经 11 秒,点 P 在 BC 上距离 C 点 3cm 处,点 Q 在 CA 上距离 C 点 14cm 处, 14> 10,点 Q 已超出 CA 的范围,此解不存在.综上所述,经过 7 秒和秒时△ PCQ 的面积等于 12.6cm 2.5. 解 : 设 P , Q 两 点 从 出 发 经 过 t 秒 时 , 点 P , Q 间 的 距 离 是 10cm ,作 PH ⊥ CD , 垂 足 为 H ,则 PH=AD=6 , PQ=10 , HQ=CD-AP-CQ=16-5t ,∵ PH 2 +HQ 2 =PQ 2可 得 :( 16-5t ) 2 +6 2 =10 2 ,答 : P , Q 两 点 从 出 发 经 过 1.6 或 4.8 秒 时 , 点 P , Q 间 的 距 离 是 10cm .6.答案略分析:7.( 1)当 t=3 时, CQ=3,过 P 作 PE⊥QR 于 E,易求得 PE 的长和△ QPE 的面积,设PQ 交 CD 于 G,由于 CG∥PE,可证得△ CQG∽△ EQP,根据相似三角形的面积比等于相似比的平方即可得到S 的值.( 2)当 t=5 时,Q、B 重合,线段 PR 与 CD 相交,设 PR 与 CD 相交于 G,可仿照( 1)的方法求得△ RCG 的面积,从而由△RPQ、△RCG的面积差求得阴影部分的面积.(3)当 5≤t≤8 时, AB 与 PQ 相交, RP 与 CD 相交,仿照( 1)的方法,可求得正方形外部的两个小三角形的面积,进而可参照(2)的方法求得阴影部分的面积表达式,由此可得到关于S、 t 的函数关系式,根据函数的性质即可得到S 的最大值.解答:解:( 1)作 PE⊥ QR, E 为垂足.∵ PQ=PR,∴QE=RE= QR=4 ,在Rt△ PEQ 中∴ PE==3;( 1 分)当t=3 时, QC=3,设 PQ 与 DC 交于点G.∵ PE∥ DC ,∴△ QCG∽△ QEP.( 2 分)∴,∵S△QEP= ×4×3=6 ,∴ S=×6=(cm2).(3分)(2)当 t=5 时, CR=3 .设PR 与 DC 交于 G,由△ RCG∽△ REP,可求出 CG= ,所以, S△RCG= ×3× = ( cm 2),( 5 分)S=12 ﹣ = ( cm 2).( 6 分)(3)当 5≤t≤8 时, QB=t ﹣ 5, RC=8 ﹣ t,设 PQ 交 AB 于点H,由△ QBH ∽△ QEP, EQ=4 ,∴ BQ: EQ= ( t﹣ 5): 4,∴S△BQH: S△PEQ=( t﹣ 5)2: 42,又 S△PEQ=6,∴S△QBH= ( t﹣5)2( 7 分)由△ RCG∽△ REP,同理得 S△RCG=(8﹣t)2(8分)∴ S=12﹣(t ﹣ 5)2﹣( 8﹣ t)2.即 S=﹣( 9 分)当 t=﹣=时,S最大,S的最大值==(cm2).(10分)考8. 相似形综合题.点:分析:( 1)由正方形的性质可以得出DC ∥AB ,就有∠ CDR= ∠ARD ,在 Rt△ PQR 中,由PQ=6cm , QR=12cm 有 tan∠ ARD=,就可以得出MC ,再根据勾股定理就可以求出PM 的值;(2)分情况求出当当 0< t≤6 时,当 6< t≤12 时, 12< t≤18 时,根据三角函数和梯形的面积公式三角形的面积公式就可以表示出S 的解析式;(3)根据等腰三角形的条件分三种情况进行计算,先运用勾股定理将三角形的三边表示出来,由等腰三角形的边的平方相等建立的等量关系求出其解就可以了.解答:解:( 1)∵四边形ABCD 是正方形,∴ CD=BC , CD ∥AB ,∠C=90 °, ∴∠ CDR= ∠ ARD , ∵ PQ=6cm , QR=12cm , ∴ tan ∠ ARD= ,∴ tan ∠ CDR= = ,∵ CD=6 ,∴ CM=3 ,在 Rt △ CPM 中,由勾股定理,得 PM==3 .( 2)如图 1,当 0< t ≤6 时,∵ QB=t ,QR=12 , ∴ BR=12 ﹣ t ,∴ BM=6 ﹣ 0.5t ,∴ S=,∴ S=﹣ t 2+6t ,如图 2,当 6< t ≤12 时,∵ AR=12 ﹣t+6=18 ﹣ t , BR=12 ﹣ t , ∴ SA=9 ﹣ 0.5t , MB=6 ﹣ 0.5t∴ S=,=3t+45 ,如图 3,12< t ≤18 时,AR=6 ﹣( t ﹣ 12)=18 ﹣ t , AS=9 ﹣ 0.5t ,∴ S=,= t 2﹣ 9t+81 ;( 3)当 6< t ≤12 时,由图象得:222222﹣ 21t+117,QN =AQ +AN =( t ﹣6) +( 9﹣ 0.5t ) = t 22 2 2 2 t 2﹣45t+405NR =AN +AR =(9﹣ 0.5t ) +( 18﹣ t ) =2RQ =144① 如图 4,当 QR 2=NR 2时,t 2﹣ 45t+405=144 ,解得: t 1=18+t >12(舍去), t 2 =18﹣ ;② 如图 5,当 QN 2 =QR 2时, t 2﹣ 21t+117=144 ,解得: t 1=﹣ 1.2(舍去), t 2=18(舍去),③ 如图 6,当 QN 2 =RN 2时, t2﹣ 21t+117= t 2﹣45t+405 , 解得: t=12,12 < t ≤18 与 6< t ≤12 时一致,而 t=18 时△ NQR 不存在, ∴ t=12 或 t=18 ﹣.9.( 1)当 t=1 时, AQ=MQ=1 , AB=PQ=4 ,∴MP=QB=4 ﹣1=3 .∵Q R=8 ,∴B R=8 ﹣ 3=5.∵在 Rt△ PQR 中, PQ=4,QR=8 ,∴t an∠PRQ= = .∴,∴,∴B N=2.5 .S 四边形PMBN ==(0≤t≤4);(2)由题意,得AQ=MQ=t , PM=BQ=4 ﹣ t, BR=8 ﹣( 4﹣ t) =4+t ,∴B N=2+ t,∴S 四边形PMBN =,2=t ﹣ 4t+12( 0≤t≤4);(3)由题意,得2t ﹣ 4t+12=×4×8,解得: t1=8+4 (舍去), t2=8﹣ 4 ,∴t 的值为 8﹣ 4 ;(4)∵四边形 PMBN 是平行四边形,∴PM=BN .∵P M=4 ﹣ t, BN=2+ t,∴4﹣ t=2+ t ,∴t=∴t=时,四边形PMBN 为平行四边形.10.分析:( 1)当 x=2 时,延长ED 交 BC 于 H ,延长 GD 交 PQ 于点 K,就有 EQ=DK=2x ,BK=HD=x ,BQ=4+x ,就可以求出 CH=6 ﹣ 2x,再根据勾股定理就可以求出 CD 、 DQ 及CQ 的值;(2)由图形观察可以得出 S△CDQ=S△CBQ﹣S△CHD﹣ S 梯形 HBQD ,只要根据条件分别表示出 =S△CBQ、 S△CHD、 S 梯形HBQD的面积即可;( 3)根据数学分类讨论思想,从不同的时间进行计算.如图6,当 CD=AC 时,作CH ⊥ GD 的延长线于点 H,解直角三角形 CHD ;如图 7,当 AD=AC 时,作 DH ⊥ PQ 于点H,解直角三角形 ADH ;如图 8,当 AD=CD 时,作 DK ⊥BC 于 BC 延长线于点K ,作 DH ⊥ PQ 于点 H ,解直角三角形 DCK 和直角三角形 DHA ;如图 9,当 CD=AC 时,作 DK ⊥ BC 于 BC 延长线于点 K ,解直角三角形 DKC ;如图 10,当 AD=AC 时,作 DH ⊥PQ 于点,解直角三角形DHA .结合各图形运动的不同位置表示出相应线段的长度,根据勾股定理建立方程求出x 的值即可.解答:解:( 1)延长 ED 交 BC 于 H,延长 GD 交 PQ 于点 K ,∴EQ=DK=2x , BK=HD=x , BQ=4+x ,∵ x=2, BC=6 , DE=4 ,∴EQ=DK=HB=4 , BK=HD=2 , BQ=6 ,∴ CH=2 .在 Rt △ CHD 、 Rt △DKQ 、 Rt △ CBQ 中,由勾股定理得: CD=2, DQ=4, CQ=6.∴ CD+DQ=6,∴ CD+DQ=CQ .故答案为: 2 , 4 ,=;( 2)当 0≤x ≤2 时,如图 2,∵ EQ=DK=2x , BK=HD=x , BQ=4+x ,CH=6 ﹣ 2x ,∴ S △CDQ =,=﹣ x 2﹣ 4x+12当 2< x ≤3 时,如图 5,作 CH ⊥ DG 于 H , DK ⊥ BC 于 K , ∴ EQ=BK=2x , CK=HD=6 ﹣ 2x , BQ=4+x , CH=x ,∴ S △CDQ =CK ?KD+KB ?BQ ﹣ ﹣ ﹣ ,=( 6﹣ 2x ) x+2x (4+x )﹣﹣﹣,2=x +4x ﹣ 12;当 3< x ≤4 时,如图 3,作 DH ⊥ BC 的延长线于 H ,∴ EQ=HB=2x , HD=x , BQ=4+x , CH=2x ﹣ 6,∴ S △CDQ =HB ?QB ﹣ ﹣ ﹣ ,=2x ( 4+x )﹣﹣﹣,=8x+2x 2﹣x 2+3x ﹣ 4x ﹣ 12﹣ 3x ,2=x +4x ﹣ 12. ∴ S=,( 3)∵纸片 DEFG 沿 RS 方向平移, ∴ 4≤x ≤24.如图 6,当 CD=AC 时,作 CH ⊥ GD 的延长线于点 H ,∴ GR=2x ﹣4, BQ=x+4 ,∴ DH=12 ﹣ 6﹣ 4=2 ,CH= ( x+4 )﹣( 2x ﹣4) =8﹣ x , ∵ AB=8 , BC=6 , ∴ AC==10在 Rt △ CHD 中,由勾股定理,得22( 8﹣ x ) +2 =100 , 解得: x 1=8+4 , x 2=8﹣ 4 < 4(舍去); 如图 7,当 AD=AC时,作 DH ⊥PQ 于点 H ,∴ GR=2x ﹣4, BQ=x+4 ,∴ DH=12 ﹣ 4=8 , AH= ( x+4+8 )﹣( 2x ﹣ 4) =16 ﹣x ,在 Rt △ ADH 中,由勾股定理,得22( 16﹣ x ) +8 =100,解得: x1=22 , x2=10;如图 8,当 AD=CD 时,作 DK ⊥BC 于 BC 延长线于点K ,作 DH ⊥ PQ 于点 H,∴GR=2x ﹣4, BQ=x+4 ,∴DK=2x ﹣ 4﹣( x+4) =x ﹣8, KC=12 ﹣4﹣ 6=2 ,AH=x+4+8 ﹣( 2x﹣4) =16 ﹣x, DH=12 ﹣ 4=8 .2 2∴( x﹣ 8)+4= ( 16﹣ x) +64,∴x=15 ;综上所述:纸片 DEFG 沿 RS 方向平移,当x 的值为: 22,10, 15 , 8+4 时,以 A 、 C、D 为顶点的三角形是等腰三角形.11.分析:( 1)分情况讨论,当点P 沿 A ﹣ D 运动时,当点P 沿 D ﹣A 运动时分别可以表示出AP 的值;( 2)分类讨论,当0< t< 1 时,当 1< t<时,根据三角形的面积公式分别求出S 与 t 的函数关系式;( 3)分情况讨论,当0< t< 1 时,当 1< t<时,当<t<时,利用三角形的面积相等建立方程求出其解即可;( 4)分情况讨论当P 在 A ﹣ D 之间或 D ﹣A 之间时,如图⑥,根据轴对称的性质可以知道四边形QCOC ′为菱形,根据其性质建立方程求出其解,当P在D﹣A之间如图⑦ ,根据菱形的性质建立方程求出其解即可.解答:解:( 1)当点 P 沿 A ﹣D 运动时, AP=8 ( t﹣ 1)=8t﹣ 8.当点 P 沿 D ﹣A 运动时, AP=50 ×2﹣ 8( t﹣ 1) =108﹣ 8t.( 2 分)(2)当点 P 与点 A 重合时, BP=AB ,t=1.当点 P 与点 D 重合时, AP=AD , 8t﹣ 8=50, t=.当0< t< 1 时,如图① .过点 Q 作 QE⊥ AB 于点 E.S△ABQ ==,∴ QE===.2∴ S=﹣ 30t +30t.当 1< t≤时,如图② .S==,∴S=48t﹣ 48;( 3)当点 P 与点 R 重合时,AP=BQ , 8t﹣ 8=5t, t=.当 0< t≤1 时,如图③ .∵S△BPM=S△BQM,∴PM=QM .∵ AB ∥ QR,∴∠ PBM= ∠ QRM ,∠ BPM= ∠ MQR ,在△ BPM 和△ RQM 中,∴△ BPM ≌△ RQM .∴BP=RQ ,∵ RQ=AB ,∴BP=AB∴13t=13 ,解得: t=1当1< t≤时,如图④ .∵BR 平分阴影部分面积,∴ P 与点 R 重合.∴t= .当<t≤时,如图⑤ .∵S△ABR =S△QBR,∴S△ABR< S 四边形BQPR.∴BR 不能把四边形 ABQP 分成面积相等的两部分.综上所述,当t=1 或时,线段PQ扫过的图形(阴影部分)被线段BR 分成面积相等的两部分.( 4)如图⑥,当 P 在 A ﹣ D 之间或 D﹣ A 之间时, C′D′在 BC 上方且 C′D′∥ BC 时,∴∠ C′OQ=∠ OQC .∵△ C′OQ≌△ COQ,∴∠ C′OQ=∠ COQ ,∴∠ CQO= ∠ COQ,∴QC=OC ,∴50﹣ 5t=50 ﹣8( t﹣ 1) +13,或 50﹣ 5t=8( t﹣ 1)﹣ 50+13 ,解得: t=7 或 t=.当 P 在 A ﹣D 之间或 D﹣ A 之间, C′D′在 BC 下方且 C′D ′∥ BC 时,如图⑦ .同理由菱形的性质可以得出:OD=PD ,∴50﹣ 5t+13=8 ( t﹣ 1)﹣ 50,解得: t=.∴当 t=7 ,t=,t=时,点C、D关于直线P Q 的对称点分别为C′、D ′,且 C′D′∥ BC.分析:( 1)由于 O 是 EF 中点,因此当 P 为 FG 中点时, OP∥ EG∥ AC ,据此可求出x 的值.( 2)由于四边形 AHPO 形状不规则,可根据三角形AFH 和三角形 OPF 的面积差来得出四边形 AHPO 的面积.三角形AHF 中, AH 的长可用AF 的长和∠ FAH 的余弦值求出,同理可求出 FH 的表达式(也可用相似三角形来得出AH 、 FH 的长).三角形 OFP 中,可过 O 作 OD⊥ FP 于 D , PF 的长易知,而 OD 的长,可根据 OF 的长和∠ FOD 的余弦值得出.由此可求得y、 x 的函数关系式.(3)先求出三角形 ABC 和四边形 OAHP 的面积,然后将其代入( 2)的函数式中即可得出x 的值.解答:解:( 1)∵ Rt△ EFG∽ Rt△ ABC∴,∴ FG==3cm∵当 P 为 FG 的中点时, OP∥ EG, EG∥AC∴OP∥ AC∴x== ×3=1.5 ( s)∴当 x 为 1.5s 时, OP∥AC .(2)在 Rt△ EFG 中,由勾股定理得 EF=5cm∵EG∥ AH∴△ EFG∽△ AFH∴∴ AH= ( x+5), FH= ( x+5 )过点 O 作 OD ⊥FP ,垂足为 D∵点 O 为 EF 中点∴ OD= EG=2cm∵ FP=3﹣ x∴S四边形OAHP =S △ AFH ﹣ S △OFP= ?AH ?FH ﹣ ?OD?FP= ? ( x+5) ? ( x+5)﹣ ×2×( 3﹣x )2=x +x+3( 0< x <3).( 3)假设存在某一时刻 x ,使得四边形 OAHP 面积与 △ ABC 面积的比为 13:24则S四边形 OAHP =×S △ ABC2∴ x +x+3=× ×6×82∴ 6x +85x ﹣ 250=0解得 x 1=, x 2=﹣ (舍去)∵ 0< x <3∴当 x=( s )时,四边形 OAHP 面积与 △ ABC 面积的比为 13: 24.。
一元二次方程中的动点问题

B 90 , AB 5 cm, BC 7 cm
点P从A点开始沿AB边向点B以1cm/s的速度移动, 点Q从点B开始沿BC边向点C以2cm/s的速度移 动. • (2)如果P,Q分别从A,B同时出发,那么几秒后, PQ的长度等于5cm?
• 1、已知:如图3-9-3所示,在△ABC中,
其它类型应用题:
5.在直角梯形ABCD中,AD∥BC,∠C=90°, BC=16,AD=21,DC=12,动点P从点D出发,沿 线段DA方向以每秒2个单位长度的速度运动, 动点Q从点C出发,沿线段CB 以每秒1个单位 长度的速度向点B运动. 点P、Q分别从点D、C 同时出发,当点P运动到点A时,点Q随之停止 运动,设运动时间为t秒. 问:当t为何值时,△BPQ是等腰三角形? P D A 分类讨论思想
• 点P从A点开始沿AB边向点B以1cm/s的速度移动,
你还行吗
• 1、已知,如图所示,在三角形ABC中, B 90 , AB 5 cm, BC 7 cm • 点P从A点开始沿AB边向点B以每秒1cm的速度移动,点Q从点 B开始沿BC边向点C 以每秒2cm的速度移动。 • (3) 如果P、Q分别从A、B同时出发,那么几秒后,PQ的长 等于5cm.
Q C
B
2、如图,A、B、C、D为矩形的四个顶点, AB=16cn,AD=6cm,动点P、Q分别从点A、C 同时出发,点P以3cm/s的速度向点B移动,一 直到达B为止,点Q以2cm/s的速度向D移动。 (2)P、Q两点从出发开始到几秒时,点P和点Q 的距离是10cm?
A P D
Q
B
C
B 90 , AB 5 cm, BC 7 cm
点P从A点开始沿AB边向点B以1cm/s的速度移动, 点Q从点B开始沿BC边向点C以2cm/s的速度移 动. • 在(1)中,△PQB的面积能否等于7?说明理由
一元二次方程的应用面积和动点问题

一元二次方程的应用面积和动点问题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(一元二次方程的应用面积和动点问题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为一元二次方程的应用面积和动点问题的全部内容。
青云学校九年级上册数学学科教案 总第7课时一、引入回顾列一元二次方程解决实际问题的基本步骤有哪些? 审、设、列、解、答二、教师精讲:(只列方程,不解方程)1、在长为60cm,宽为40cm 的矩形的四个角上截去四个全等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800,求所截去小正方形的边长。
2、校生物小组有一块长32m ,宽20m 的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道.要使种植面积为540,小道的宽应是多少?3、如图,有一面积为的长方形鸡场,鸡场的一边靠墙(墙长),另三边用竹篱笆围成,如果竹篱笆的长为,求鸡场的长与宽各为多少米?三、合作探究: 专题一:如图,有长为24m 的篱笆,一面利用墙(墙的最大可用长度a 为10m 中间隔有一道篱笆的长方形花圃,设花圃的宽AB 为x (m ),求: (1)如果要围成面积为45m 2的花圃,AB 的长度是多少? (2)花圃的面积能否达到50m 2 ?2cm 2m 2150m m 18m 35青云学校九年级上册数学学科教案总第8课时一、教师精讲1、以P52例4讲解解决动点问题的基本思路:以静制动(动态问题静态处理)(1)设未知数,设运动时间为t,(2)用代数式表示运动长度(3)据面积或长度公式列出方程(4)解方程(5)检验作答,特别注意求出的解是否符合实际问题2、变式训练:变式1:△PCQ的面积能否为10平方厘米?42变式2:P,Q出发几秒后,PQ的长度为cm?二、合作探究:专题一:学法大视野P34探究一及变式练习专题二:在△ABC中, AC=50cm,CB=40cm, ∠C=90°,点P从点A 开始沿AC边向点C以2cm/s的速度移动, 同时另一点Q由C点以3cm/s的速度沿着CB边移动,几秒钟后, 四边形APQB的面积等于550cm²?。
(完整版)一元二次方程解决动点问题

24.4 一元二次方程的应用(6)班级:姓名:小组:【学习目标】1. 通过回忆旧知,学生能准确说出几何图形中动点的行走路程;2. 通过认真审题,学生能准确找出其中的等量关系;3. 借助等量关系,学生能准确列出关于动点的一元二次方程;4. 根据一元二次方程的特点,学生能灵活选用适当的方法解一元二次方程;5. 根据具体题意,学生能合理舍掉其中一个根.【重点难点】重点:用一元二次方程解决动点问题;难点:分析动点的运动,列出一元二次方程.【导学流程】(一)了解感知:认真阅读下面一段话,然后完成练习1. 一般动态问题的解法是“动中求静”,即按题意确定动点的一个基本位置,然后按照这个这个基本位置作出恰当的图形,再按照题意逐步探索和求解。
2. 完成课本56页C组1题(写在书上)(二)深入学习:分析下列题目的等量关系,列一元二次方程求解:1.等腰直角△ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm²? 2.如图所示,已知在△ABC中,∠B=90°,AB=BC=5cm,点P从点A开始沿AB边向点B 以1cm/s的速度移动,点Q从B开始沿边BC向点C以2cm/s的速度移动,若一动点运动到终点,则另一个也随之停止。
(1)如果P、Q分别从A、B两点同时出发,那么几秒后,△PBQ的面积等于4cm²?(2)在(1)中,△PBQ的面积能否等于7cm²?说明理由。
(三)迁移运用:用一元二次方程的相关知识解决下列问题:1.在矩形ABCD中,AB=5cm,BC=7cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发了t秒,直至两动点中某一点到达端点后停止(即0<t<3.5)(1)经过几秒后,PQ的长度等于5?(2)经过几秒后,△BPQ的面积等于4?(3)经过几秒后,DP=DQ?QPD CBA。
专题八:一元二次方程应用类型中的动点问题(有答案)

专题八:一元二次方程应用类型中的动点问题(有答案)➢知识指引所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类问题.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.解题时要注意动点的起始位置和终止位置、运动方向,有时还要关注动点的运动速度,注意在运动过程中寻找等量关系.动点问题思路剖析问题1:动点问题的处理框架是什么?答:读题标注,整合信息(即明确所研究的背景图形)问题2:分析运动过程需要关注四要素是什么?答:①起点、终点、速度:标注到图形中,以示说明②时间范围根据路程、时间和速度的公式s=vt,已知动点的速度,结合基本图形中线段长的研究,可以确定动点的运动时间③状态转折状态转折即点的运协发生变化的时刻,常体现在动点的运动方向,运动速度发生了改变④目标或结论导向根据题意作出图形,有序操作(分段作图并求解)问题3:在分析几何特征,表达时,常见表达线段长的方式有哪些?答:①路程即线段长,可根据s=vt直接进行表达已走路程或未走路程②根据研究几何特征的需求进行表达,即要利用动点的运动情况,又要结合背景图形信息➢知识点睛由点的运动产生的几何问题称为动点问题.动点问题的解决方法:1.研究背景图形并标注;;2.分析运动过程,并适时分段;3.表达线段长,建等式和方程.➢典型例题【例1】如图,在△ABC中,∠B=90°,AB=9,BC=12,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:(1)填空:BQ= ,PB= (用含t的代数式表示)(2)经过几秒,PQ的长为6√2cm?(3)经过几秒,△PBQ的面积等于8cm2?【解答】(1)根据题意得:BQ=2t,PB=9-t.故答案为:2t;9-t.(2)根据题意得:(9-t)2+(2t)2=72,,t2=3,解得:t1=35秒或3秒,PQ的长为6√2cm.∴经过35×(9-t)×2t=8,(3)根据题意得:12解得:t1=8,t2=1.∵0≤t≤6,∴t=1.答:经过1秒,△PBQ的面积等于8cm2.【例2】如图,在四边形ABCD中,AD∥BC ,∠C=90°, BC=16,DC=12 ,AD=21 ,动点P从点D出发,沿线段 DA的方向以每秒2个单位长的速度运动;动点Q从点 C出发,在线段 CB 上以每秒1个单位长的速度向点B运动;点P,Q 分别从点D,C同时出发,当点P运动到点 A 时,点Q随之停止运动,设运动的时间为t秒).(1)当t=2时,求△BPQ的面积;(2)若四边形ABQP为平行四边形,求运动时间t.(3)当t为何值时,以 B,P,Q为顶点的三角形是等腰三角形?备用图【解答】(1)如图,过点P 作PM ⊥BC 于M ,则四边形PDCM 为矩形,∴PM=DC=12.∵QB=16-t ,当t=2时,则BQ=14,则S=12QB ⋅PM =12×14×12=84;(2)当四边形ABQP 是平行四边形时,AP=BQ,即21-2t=16-t .解得t=5. ∴当t=5时,四边形ABQP 是平行四边形.(3)由图可知,CM=PD=2t ,CQ=t ,若以B 、P 、Q 为顶点的三角形是等腰三角形,可以分为以下三种情况:①若PQ=BQ ,在Rt △PMQ 中,PQ 2=t 2+122,由PQ 2= BQ 2, 得t 2+ 122= (16-t)2 解得t=72;②若BP=BQ ,在Rt △PMB 中,PB 2=(16-2t)2+122,由PB 2= BQ 2得(16-2t)2+ 122= (16-t)2,即3t 2+-32t+144= 0.此时,Δ= (-32)2 -4×3×144= -704<0, 所以此方程无解,所以PB ≠BQ ;③若PB=PA ,由PB 2= PQ 2,得t 2+ 122= (16-2t)2 + 122 , 解得t 1=163,t 2=16,(不合题意,舍去);综上所述,当t=72或163时,以B ,P ,Q 为顶点的三角形是等腰三角形.➢ 跟踪训练1.如图,在△ABC 中,AC=50cm ,BC=40 cm ,∠C =90°,点P 从点A 开始沿AC 边向点C 以每秒2 cm 的速度匀速移动,同时另一点Q 由C 点开始以每秒3 cm 的速度沿着射线CB 匀速移动,当△PCQ 的面积等于300 cm 2运动时间为( ).A. 5秒B. 20秒C. 5秒或20秒D. 不确定【解答】由题意,得AP=2t ,CQ=3t ,∴PC=50-2t ,∴12•PC•CQ=300,∴12•(50-2t )•3t=300,解得t=20或5,∴t=20s 或5s 时,△PCQ 的面积为300m 2.故选:C .2.如图,在△ABC 中,∠B=90°,AB=6cm ,BC=8cm .点P 从点A 开始沿AB 边向点B 以1cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以2cm/s 的速度移动.若P 、Q 两点同时出发,当点P 运动到点B 时,P ,Q 两点同时停止运动,当三角形PQB 的面积是三角形ABC 的面积的三分之一时,所需时间为( )A .4 sB .2 sC .2或4sD .3或4s【解答】设经过x 秒,三角形PQB 的面积是三角形ABC 的面积的三分之一.∵P 、Q 移动t 秒时,AP=t ,BQ=2t ,则PB=AB-AP=6-t ,∴S △P B Q =13,由S △A B C =12AB•BC=12×6×8=24,当S △P B Q =13S △A B C 时,则12•2t(6-t )=13×24,整理,得t 2-6t+8=0,解得t 1=2,t 2=4,即当t=2或4时,△PBQ 的面积等于△ABC 的面积的三分之一. 故选:C .3.如图,在Rt △ABC 中,∠B =90°,AB =BC =12 cm ,点D 从点A 开始沿边AB 以2 cm/s 的速度向点B 移动,移动过程中始终保持四边形DFCE (点E ,F 分别在AC ,BC 上)为平行四边形,则出发________s 时,四边形DFCE 的面积为20 cm 2.【解答】设点D从点A出发x s时,四边形DFCE的面积为20 cm2.由题意,得12×12×12−4x22−(12−2x)22=20,解得x1=1,x2=5,故答案为:1或5.4.某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系l=t2+3t(t≥0),乙以8cm/s的速度匀速运动,半圆的长度为42cm.(1)甲运动4s后的路程是多少?(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?【解答】(1)当t=4s 时,l=t2+3t=16+12=28(cm).答:甲运动4s后的路程是28cm.(2)由图可知,甲乙第一次相遇时走过的路程为半圆21cm,甲走过的路程为t2+3t,乙走过的路程为4t,则t2+3t+8t=42,解得:t1=3,t2=-14(不合题意,舍去).答:甲、乙从开始运动到第一次相遇时,它们运动了3s.(3)由图可知,甲乙第一次相遇时走过的路程为三个半圆3×42=126cm,则t2+3t+8t=126,解得:t=7或t=-18(不合题意,舍去).答:甲、乙从开始运动到第二次相遇时,它们运动了7s .5.如图,在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点A 开始以1cm/s 的速度沿AB 边向B 移动,点Q 从点B 开始以2cm/s 的速度沿BC 边向点C 移动.如果P 、Q 分别从A 、B 同时出发,当点Q 运动到点C 时,P 、Q 两点同时停止运动. (1)是否存在某一时刻使得△PQD 的面积等于8cm 2?若存在,求出运动的时间;若不存在,说明理由.(2)几秒后,△PQD 是以DP 为斜边的直角三角形.【解答】(1)不存在,理由如下:设出发秒x 时△DPQ 的面积等于8cm 2. ∵S 矩形A B C D -S △A P D -S △B P Q -S △C D Q =S △D P Q ,∴6×12-12×12×x -12×(6-x )•2x -12(12-2x )×6=8,∴x 2-6x+28=0,∵∆=b 2-4ac=36-4×28=-76<0,∴原方程无实数根,即不存在某一时刻使得△PQD 的面积等于8cm 2. (2)∵∠A=∠B=∠C=90°,∴PD 2=t 2+122,PQ 2=(6-t )2+(2t )2,QD 2=(12-2t )2+62, ∵△PQD 是以DP 为斜边的直角三角形,∴PD 2=PQ 2+QD 2,即t 2+122=(6-t )2+(2t )2+(12-2t )2+62, 整理得2t 2-15t+18=0,解之得t 1=6,t 2=32,即当t 为32秒或6秒时,△PQD 是以PD 为斜边的直角三角形.6.如图,在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点B 出发沿线段BC 、CD 以2cm/s 的速度向终点D 运动;同时,点Q 从点C 出发沿线段CD 、DA 以1cm/s 的速度向终点A 运动(P 、Q 两点中,只要有一点到达终点,则另一点运动立即停止).(1)运动停止后,哪一点先到终点?另一点离终点还有多远?(2)在运动过程中,△APQ 的面积能否等于22cm 2?若能,需运动多长时间?若不能,请说明理由【解答】(1)点P 从开始到运动停止用的时间为:(12+6)÷2=9s,点Q 从开始到运动停止用的时间为:(6+12)÷1=18s, ∵9<18,只要有一点到达终点,则另一点运动立即停止,∴点P 先到终点,此时点Q 离终点的距离是:(6+12)-1×9=9cm, 答:点P 先到终点,此时点Q 离终点的距离是9cm ;(2)在运动过程中,△APQ 的面积能等于22cm 2,当P 从点B 运动到点C 的过程中,设点P 运动时间为as ,∵△APQ 的面积能否等于22cm 2, ∴12×6-2a×62−(12−2a)×a2−(6−a)×122=22,解得,此方程无解;当点P 从C 到D 的过程中,设点P 运动的时间为(b+6)s ,∵△APQ 的面积能否等于22cm 2, ∴12×6-(6+2b)×122−b(6−2b)2=22,解得,b 1=1,b 2=14(舍去),即需运动6+1=7s ,△APQ 的面积能等于22cm 2.7.如图,在矩形ABCD 中,AB=5cm ,BC=6cm ,点P 从点A 开始沿边AB 向终点B 以1cm/s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向终点C 以2cm/s 的速度移动.如果P ,Q 分别从A ,B 同时出发,当点Q 运动到点C 时,两点停止运动,设运动时间为t 秒. (1)填空:BQ=__________,PB=_________;(用含t 的代数式表示) (2)当t 为何值时,PQ 的长度等于5cm ?(3)是否存在t 的值,使得五边形APQCD 的面积等于26cm 2?若存在,请求出此时t 的值;若不存在,请说明理由.【解答】(1)∵P从点A开始沿边AB向终点B以1cm/s的速度移动,∴AP=tcm.∵AB=5cm,∴PB=(5-t)cm.∵点Q从点B开始沿边BC向终点C以2cm/s的速度移动,∴BQ=2tcm;(2)由题意,得(5-t)2+(2t)2=52.解得t1=0(不合题意,舍去),t2=2.所以当t=2秒时,PQ的长度等于5cm.(3)存在,t=1秒时,能够使得五边形APQCD的面积等于26cm2.由矩形ABCD的面积是5×6=30cm2,若五边形APQCD的面积等于26cm2,则△PBG的面积为30-26=4 cm2,=4.解得t1=4(不合题意,舍去),t2=1.即(5-t)×2t×12即当t=1秒时,五边形APQCD的面积等于26cm2.8. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动,到达点C停止运动.点Q在射线PC上,且PQ =2AP,以线段PQ为边向上作正方形PQNM.在运动过程中,设运动时间为t秒,(1)当N点落在BC上时,t= 秒;(2)若设正方形PQNM与△ABC重叠部分的面积为8,求t的值.备用图【解答】(1)当N 落在BC 上时,Q 点在C 处,此时CP+AP=2t+t=6,∴t=2,.故填:2(2)∵AP =t ,PQ =2AP ,∴PQ =2t ,①如图1,当0≤t ≤2时,S =(2t )2﹣12t 2=72t 2=8, 解得:t 1=47√7,t 2=﹣47√7(不合题意,舍去),②如图2,当2≤t ≤3时,S =12×6×6﹣12t 2﹣12(6﹣2t )2=12t ﹣25t 2=8, 解得:t 1=4(不合题意,舍去),t 2=45(不合题意,舍去), ③如图3,当3≤t ≤6时,S =12×6×6﹣12t 2=8,解得:t 1=2√5,t 2=﹣2√5(不合题意,舍去), 综上,t 的值为47√7或2√5时,重叠面积为8.9.等腰△ABC 的直角边AB=BC=10cm ,点P 、Q 分别从A 、C 两点同时出发,均以1cm/秒的相同速度作直线运动,已知P 沿射线AB 运动,Q 沿边BC 的延长线运动,PQ 与直线AC 相交于点D .设P 点运动时间为t ,△PCQ 的面积为S . (1)当点P 运动几秒时,S △PCQ =S △ABC ?(2)作PE ⊥AC 于点E ,当点P 、Q 运动时,线段DE 的长度是否改变?证明你的结论.【解答】(1)由S △ABC =12AB •BC =12×10×10=50.当t <10秒时,P 在线段AB 上,此时CQ=t ,PB=10-t. ∴S △PCQ =12×t×(10−t)=12 (10t −t 2) =50.整理得t 2-10t+100=0无解.当t >10秒时,P 在线段AB 得延长线上,此时CQ=t ,PB=t-10. ∴S △PCQ =12×t×(t −10)=12(t 2−10t) =50.整理得t 2-10t-100=0解得t=5±5√5(舍去负值). ∴当点P 运动5+5√5秒时,S △PCQ =S △ABC .(2)当点P,Q 运动时,线段DE 的长度不会改变. 证明:过Q 作QM ⊥AC ,交直线AC 于点M 易证△APE ≌△QCM ,∴AE=PE=CM=QM=√22t ,∴四边形PEQM 是平行四边形,且DE 是对角线EM 的一半. 又∵EM=AC=10√2,∴DE=5√2.∴当点P 、Q 运动时,线段DE 的长度不会改变. 同理,当点P 在点B 右侧时,DE=5√2。
一元二次方程动点应用

一元二次方程应用------方程与图形例1、如图,在△ABC 中∠B=90°,AB=7cm ,BC=6cm ,点P 从点A 开始沿线段AB 向点B 以2cm/s 的速度运动,点Q 从点C 开始沿线段CB 向点B 以1cm/s 的速度运动.设时间为t ;如果P 、Q 分别从A 、C 同时出发,请在图中标出运动方向和运动速度,用含t 的代数式表示PB= ,BQ= ,问经过多少秒时,PQ=10变式1:若以B 为原点,AB 所在直线为x 轴,BC 所在直线为y 轴,并且P 从A 点沿x 轴正方向运动,Q 从C 点沿y 轴正方向运动,其他条件不变,请在图中建立坐标系,并直接写出A 点坐标( , ),C 点坐标( , );当t 为何值时,△BPQ 面积为23,并写出此时P ,Q 的坐标;变式2:一轮船在A 点以30km/h 的速度由西向东航行(如图),在途中接到台风警报,台风中心C 以20km/h 的速度由南向北移动.已知距台风中心200km 的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得CA=500km,BC=300km.(1)轮船不改变航向,轮船会不会进入台风影响区?(2)若会,请求出船受台风影响的时间有多长?拓展:如图,在直角梯形ABCD中,AD//BC,∠C=90°,BC=16,DC=12,AD=31。
动点P从点D出发沿线段DA以每秒2个单位长的速度向A运动,设运动时间为t,当t为何值时,BP=BC?思考:在原题基础上又出现动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动。
当t为何值时,以B,P,Q三点为顶点并且以BP为一腰的三角形为等腰三角形?感谢您的阅读,祝您生活愉快。
DB CD。
一元二次方程与动点及答案精编版

1 如图,在△ ABC中,/ B = 90°, BC = 12cm, AB = 6cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,几秒后厶PBQ的面积等于8cm2?2. △ ABC 中,/ B=90 ° , AB=5cm , BC=6cm,点P 从点A 开始沿边AB 向终点B 以1cm/s 的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动•如果P、Q分别从A、B同时岀发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.(3)是否存在t的值,使得△P B Q的面积等于4c m2?若存在,请求岀此时t的值;若不存在,请说明理由.3.如图,在△ ABC 中,/ B=90 ° , AB=6 , BC=8 .点P从点A开始沿边AB向点B 以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.设P、Q分别从A、B同时岀发,运动时间为t,当其中一点先到达终点时,另一点也停止运动.解答下列问题:(1)经过几秒,△ PBQ的面积等于8cm 2?(2)是否存在这样的时刻t,使线段PQ恰好平分△ ABC的面积?若存在,求岀运动时间t;若不存在,请说明理由.4•如图所示,△ ABC中,/ B=90 °,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC 边向点C以2cm/s的速度移动.(1)如果P,Q分别从A,B同时出发,经几秒,使△ PBQ的面积等于8cm2?(2)如果P,Q分别从A,B同时出发,并且P到B后又继续在BC边上前进,Q到C后又继续在CA边上前进,经过几秒,使△ PCQ的面积等于12.6cm2?5.如图,A、B、C、D为矩形的4个顶点,AB=16cm , BC=6cm ,动点P、Q分别从A、C同时岀发,点P以3厘米每秒的速度向点B移动,一直到达点B为止•点Q 以2厘米每秒的速度向点D移动,经过多长时间P、Q两点之间的距离是10厘米?6•如图,A、B、C、D为矩形的4个顶点,AB = 16cm,BC = 6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止;点Q以2cm/s的速度7•如图,有一边长为5cm的正方形ABCD和等腰△ PQR, PQ=PR=5cm , QR=8cm ,点B、C、Q、R在同一条直线I上,当C、Q两点重合时,等腰△ PQR以1cm/秒的速度沿直线I按箭头所示方向开始匀速运动,t秒后正方形ABCD与等腰△ PQR重合部分的面积为Scm2.解答下列问题:(1 )当t=3秒时,求S的值;(2 )当t=5秒时,求S的值;(3)当5秒E詣秒时,求S与t的函数关系式.A DQ ------- C R IQR在同一条直线I 上.开始时点Q与点B重合,让厶PQR以1cm/s速度在直线I上运动,直至点R与点A 重合为止,设运动时间为t (s), t> 0.(1 )点P与点D重合时,令PR与BC交于M点,求PM的长度;(2 )设厶PQR与正方形ABCD重叠部分的面积为Scm2,直接写出S与t之间的函数关系式和相应的自变量t的取值范围;(3)在运动的过程中,令线段PR与线段AD 的交点为N (若无交点则不考虑),则是否存在t的值,使△ NQR为等腰三角形?若存在,求出相应的t的值;若不存在,请说明理由.AB与QR在同一直线I上,开始时点Q与点A重合,让△ PQR以1cm/s 的速度在直线I上运动,同时M点从点Q出发以1cm/s沿QP运动,直至点Q与点B重合时,都停止运动,设运动的时间为t( s),四边形PMBN的面积为SD(P) CA(Q) B R I(cm2). 图(1 )(1 )当t=1s时,求S的值;(2)求S与t之间的函数关系式,并写出自变量(3)是否存在某一时刻t,使得四边形PMBN 值;若不存在,说明理由;(4)是否存在某一时刻t,使得四边形PMBN 若不存在,说明理由.t的取值范围(不考虑端点);的面积* 若存在,求出此时t的为平行四边形?若存在,求出此时t的值;10.如图1,在长为44,宽为12的矩形PQRS中,将一张直角三角形纸片ABC和一张正方形纸片DEFG如图放置,其中边AB、DE在PQ上,边EF在QR上,边BC、DG在同一直线上,且Rt△ ABC两直角边BC=6,AB=8,正方形DEFG的边长为4.从初始时刻开始,三角形纸片ABC,沿AP方向以每秒1个单位长度的速度向左平移;同时正方形纸片DEFG , 沿QR方向以每秒2个单位长度的速度向上平移,当边GF落在SR上时,纸片DEFG立即沿RS方向以原速度向左平移,直至G点与S点重合时,两张纸片同时停止移动. 设平移时间为x秒.(1)请填空:当x=2 时,CD= 「_, DQ= ,此时CD+DQ = CQ(请填N ”、的面积S与x的函数关系式,并写出自变量x的取值范围(这里规定线段的面积为零)(3)如图3,当纸片DEFG沿RS方向平移时,是否存在这样的时刻x,使以A、C、D为顶点的三角形是等腰三角形?若存在,求出对应x的值;若不存在,请说明理由.11. (2013?长春)如图①,在?ABCD中,AB=13 , BC=50 , BC边上的高为12.点P从点B出发,沿B - A - (2)如图2,当纸片DEFG沿QR方向平移时, 连接CD、DQ和CQ,求平移过程中△ CDQS G F RP A BD - A运动,沿B - A运动时的速度为每秒13个单位长度,沿A - D - A运动时的速度为每秒8个单位长度.点Q从点B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动•设点P的运动时间为t (秒).连结PQ.(1)当点P沿A - D - A运动时,求AP的长(用含t的代数式表示).(2)连结AQ,在点P沿B - A - D运动过程中,当点P与点B、点A不重合时,记△ APQ 的面积为S.求S 与t之间的函数关系式.(3)过点Q作QR // AB,交AD于点R,连结BR,如图②.在点P沿B - A - D - A运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.12. (2006?青岛)如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A 与点E 重合),已知AC=8cm,BC=6cm,/ C=90 ° EG=4cm,/ EGF=90 ° O 是厶EFG 斜边上的中点.如图②,若整个△ EFG从图① 的位置出发,以1cm/s的速度沿射线AB方向平移,在厶EFG 平移的同时,点P从厶EFG的顶点G出发,以1cm/s的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△ EFG也随之停止平移.设运动时间为x ( s) , FG的2延长线交AC于H,四边形OAHP的面积为y (cm )(不考虑点P与G、F重合的情况).图①图②(1 )当x为何值时,OP// AC ;(2)求y与x之间的函数关系式,并确定自变量x的取值范围;(3)是否存在某一时刻,使四边形OAHP面积与△ ABC面积的比为13: 24?若存在,求2 2 2出x的值;若不存在,说明理由. (参考数据:114 =12996, 115 =13225, 116 =13456或2 2 24.4 =19.36 , 4.5 =20.25 , 4.6 =21.16)1.解:设x秒钟后,△ PBQ的面积等于8cm 2,由题意可得:2x ( 6-x) + 2=8解得x i =2 , X2=4 .经检验均是原方程的解.答:2或4秒钟后,△ PBQ的面积等于8cm 2.2.解:(1 )由题意,得BQ=2t , PB=5-t . 故答案为:2t , 5-t .(2)在Rt △ PBQ中,由勾股定理,得4t 2+ ( 5-t ) 2=25,解得:t i=0,t 2=2.(3)由题意,得2t(5-t)2=4,解得:t=1,t=4 (不符合题意,舍去),•••当t=1时,△ PBQ的面积等于4cm2.3.解:(1 )设经过x秒,△ PBQ的面积等于8cm2则:BP=6-x ,BQ=2x,所以S△ P BQ =12X( 6-x ) X 2x=8,即X2-6X+8=0,可得:x=2或4 (舍去),即经过2秒,△ PBQ的面积等于8cm2.(2)设经过y秒,线段PQ恰好平分△ ABC的面积,△ PBQ的面积等于12cm2,S △ PBQ =2X( 6-y ) X 2y=1, 即2,y2-6y+12=0 ,因为△ =b2-4ac=36-4 X 12=-12 v 0,所以△ PBQ的面积不会等于12cm2,则线段PQ不能平分△ ABC的面积.4•相似三角形的判定与性质;一元二次方程的应用. 几何动点问题.(1 )设x秒时.由三角形的面积公式列出关于x的方程,—(6 - x) ?2x=8,通过解方程求2得x i=2, x2=4;(2)过Q作QD丄CB,垂足为D,构建相似三角形△ CQD CAB,由该相似三角形的对应边成比例得到一:即QD= ;;2i _8 AC 10然后由三角形的面积公式列出关于x的方程一 (14 -x) ? :■=12.6,解之得x i=7,2 丄。
一元二次方程应用(动点问题)
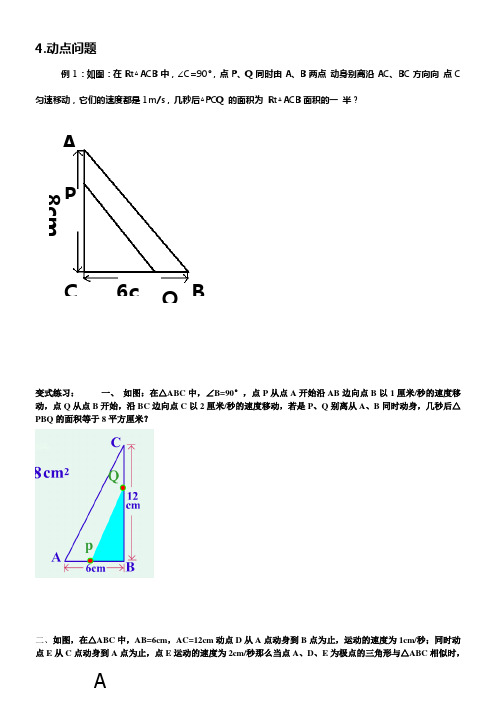
4.动点问题例1:如图:在Rt △ACB 中,∠C=90°,点P 、Q 同时由A 、B 两点 动身别离沿AC 、BC 方向向 点C 匀速移动,它们的速度都是1m/s ,几秒后△PCQ 的面积为 Rt △ACB 面积的一 半?变式练习: 一、 如图:在△ABC 中,∠B=90°,点P 从点A 开始沿AB 边向点B 以1厘米/秒的速度移动,点Q 从点B 开始,沿BC 边向点C 以2厘米/秒的速度移动,若是P 、Q 别离从A 、B 同时动身,几秒后△PBQ 的面积等于8平方厘米?二、如图,在△ABC 中,AB=6cm ,AC=12cm 动点D 从A 点动身到B 点为止,运动的速度为1cm/秒;同时动点E 从C 点动身到A 点为止,点E 运动的速度为2cm/秒那么当点A 、D 、E 为极点的三角形与△ABC 相似时,ABC P Q 6c 8cmA运动的时刻是( )3.如图,在矩形ABCD 中,AB=3,BC=4,点P 以每秒2个单位长度的速度从点C 动身,沿CA 向点A 运动;点Q 同时以每秒1个单位长度的速度从点A 动身,沿AB 向点B 运动,设P 、Q 两点移动t 秒(1)求△APQ 与△ABC 相似时t 的值(2)求四边形BCPQ 面积S 与时刻t 的关系式(3)求△APQ 为等腰三角形时t 的值例2:一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20 海里的圆形区域(包括边界)都属台风区.当轮船到A 处时,测得台风中心移到位于点A 正南方向B 处,且AB=100海里.若这艘轮船自A 处按原速度继续航行,在途中会可不能碰到台风?若会,试求轮船最初碰到台风的时刻;若可不能,请说明理由.BCE D 10变式练习:某军舰以20节的速度由西向东航行,一艘电子侦查船以30节的速度由南向北航行,它能侦查出周围50海里(包括50海里)范围内的目标。
4.27 8.6一元二次方程的应用——动点问题

动点问题需要注意几个问题: 1、有几个动点? 2、怎样运动?即向哪儿运动?
3、运动的速度、时间、距离分别是多少?
例题赏析
如图,某海军基地位于点A处,在其正南方向200海里处有一重要
目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC
的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰从A
例2:在Rt△ABC中,∠C=90°,AC=30cm, BC=25cm,动点P沿CA方向运动,速度是 2cm⁄s;动点Q从B点出发,沿BC方向运动, 速度是1cm⁄s,几秒后P、Q两点相距25cm?
设时间为x,, 则可表示出CP=2x,BQ=x,QC=25-x
等量关系:P、Q两点相距25cm
解:设x秒后P、Q两点相距25cm.
在Rt△QCP中 QC2+PC2=PQ2
(25-x)2+(2x)2=252 5x2-50x=0
x1=0 (舍),x2=10
答:10秒后PQ相距25cm。
出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向
匀速直线航行,欲将一批物品送达军舰.
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船
相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到
0.1海里,其中6 2.449 00
BE F
C
200
例题赏析
练习1
练习2:在Rt△ABC中,∠C=90°,AC=8,BC=6. 点P由A点出发沿AC方向向点C匀速移动,点Q 由B点出发沿BC方向向点C匀速移动,它们的速 度都是1cm⁄s,几秒后△PCQ的面积为 △ABC面积的一半?
一元二次方程的应用(动点问题)

二实验中学西校九年级数学组
1.如图 所示, 在直角坐标系中,四边形OACB 为矩形, C点的坐标为(3,6),若点P 从 O点沿 OA向点A 以1㎝/s 的 速度运动,点Q 从点 A沿 AC以2cm/s 的速度运动,如 果P,Q 分别从O,A 同时出发 ,问 (1)经过多长时间△PAQ 的面积为2平方厘米? (2) △PAQ的面积能否达到3平方厘米? (3)经过多长时间P,Q两点间的距离是 2 2 厘米?
3.如图所示 ,△ABC中,∠B=900,AB=BC=6cm。点 P从A点开始沿AB边向点B以每秒1cm的速度移动, 点Q从点B开始沿BC边向点C以每秒2cm的速度移动. (1)P、Q两点分别从A,B同时出发,经过几秒钟,使 △PBQ的面积等于8平方厘米? (2)如果P、Q两点分别从A,B出发,并且P到B点后 继续在BC边上前进,点Q到点C后又继续在CA边上 前进,从开始经过几秒钟,使△PCQ的面积等于 10 2 平方厘米? (P在BC上,Q在AC上) C C Q A Q P
P
B
A
BLeabharlann yB CQ
O
P
A
x
2.如图所示 AO=OB=50厘米,OC是一条射线, OC⊥AB,一只蚂蚁由A点以2厘米每秒的速度沿 AB方向向B点爬行,同时另一只蚂蚁由O点以3厘 米每秒的速度沿OC方向爬行,是否存在这样的时 刻,使两只蚂蚁所在的位置与O点组成的三角形面 积为450平方厘米? A P O B
Q C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
△PCQ的面积能为10cm2?
(3)当点P、Q出发几秒后,
PQ的长度为 4 2 cm?
有关“动点”的运动问题”
1)关键—— 以静代动把动的点进行转换,
变为线段的长度,
2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点 的运动路程”,也是求线段的长度;
拓展提升:
P54 T7
(4)当x为何值时,四边形PQMN 为直角梯形?
几秒后△ PQD的面积等于28cm2?
D
C
Q
A
B
P
牛刀小试
2、在直角三角形ABC 中,AB=BC=12cm,点D从点A开始以 2cm/s的速度沿AB边向点B移动,过 点D做DE平行于BC,DF平行于AC,点 E.F分别在AC,BC上,问:点D出发 C 几秒后四边形DFCE的面积为20cm2?
F
E
A
3)常找的数量关系——面积,勾股定理等;
由此,学会把动点的问题转化为静点的问题, 是解这类问题的关键.
习题速练:
P53 练习 T2
牛,点P
从点A开始以1cm/s的速度沿AB边向点B移
动,点Q从点B开始以2cm/s的速度沿BC边
向点C移动,如果P、Q分别从A、B同时出发,
动点问题
合作交流
例1 如图,在△ABC 中,∠C=90°,AC=6 cm,BC=8 cm. 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s的速度移动;同时点 Q沿 CB 边从点 C 向 终点 B 以 2 cm/s的速度移动,且当其中一点到达 终点时,另一点也随之停止移动. 问:(1)点 P,Q 出发几秒后, △PCQ 为等腰三角形?
D
B
一个长为10m的梯子斜靠在墙上, 梯子的顶端距地面的垂直距离为8m, 如果梯子的顶端下滑1m,梯子的底端 滑动xm,可列方程为:__________
已知:如图,△ABC是边长3cm的等边三 角形,动点P、Q同时从A、B两点出发,分别 沿AB、BC方向匀速移动,点P的速度为 1cm/s,点Q的速度为2cm/s,当点Q到达点C时, P、Q两点停止运动,设点P的运动时间为t (s),解答下列问题: (1)当t为何值时,△PBQ是直角三角形? (2)△PBQ能否为等边三角形?若能,请求出t的 值,若不能,说明理由.
