除法器设计方法

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
entity divider is
Port ( dividend_in : in std_logic_vector(7 downto 0); --被除数
remainder<=dividend(7 downto 4); --分离出余数
quotient<=dividend(3 downto 0); --分离出商
state_graph:process(state,st,c)
--状态控制器
begin
load<='0';overflow<='0';sh<='0';su<='0';
update:process(clk)
--同步数据更新进程
begin
if(clk='1'and clk'event) then
state<=nextstate;
if load='1' then
dividend<='0'&dividend_in;
end if;
if su='1' then
dividend(8 downto 4)<=subout;
divisor : in std_logic_vector(3 downto 0); --除数
st : in std_logic;
--除法启动控制信号
clk : in std_logic;
--时钟信号
quotient : out std_logic_vector(3 downto 0); --商
remainder : out std_logic_vector(3 downto 0); --余数
w Function
R3in R3out 控制器
ALU
G
Ain Gin
Gout
AddSub
Extern
Done
简易CPU的基本操作及功能
操作 Load Rx，Data Move Rx，Ry Add Rx，Ry
Sub Rx，Ry
功能 Rx←Data Rx←[Ry] Rx←[Rx]+[Ry] Ry←[Rx]-[Ry]
else sh<='1';nextstate<=2;
end if;
when 2|3|4=>
--状态2、3、4：实现除法运算
if(c='1')then su<='1';nextstate<=state;
else sh<='1';nextstate<=state+1;
end if;
when 5=>
--状态5：结束运算过程，返回初始态
overflow : out std_logic);
--溢出标志
end divider;
architecture Behavioral of divider is
signal state,nextstate:integer range 0 to 5;
signal c,load,su,sh:std_logic;
设计控制电路至少需要有四个状态T0、T1、T2、T3，其中 T0状态表示没有任何操作的状态，即初始状态。T1对应各 种操作的第一步，T2、T3则分别对应加法和减法器的第二 步和第三步。为了实现这样的状态控制，可以用如图8-14 所示的电路实现。图8-14中包括一个4进制计数器和一个24译码器。用4进制计数器实现4个状态转换控制，用2-4译 码器对这4个状态进行译码，产生相应的控制信号。
dividend(0)<='1';
end if;
if sh='1' then
dividend<=dividend(7 downto 0)&'0';
end if;
end if;
end process update;
end Behavioral;
简易CPU的设计
Data
Bus
Clock
R0
R3
A
B
R0in R0out
C’/Sh
S5
S4
S3
C/Su
C/Su
当启动信号St=1时，启动除法器工作，产生Load信号，装 载被除数寄存器和除数寄存器。如果C=1，除法溢出，除 法器停止工作，溢出标志OV输出有效；如果C=0，将发生 第一次移位操作，控制电路转到状态S2。然后，如果C=1， 执行减法操作，减法操作完成后，C将保持为“0”，保证在 下一次时钟有效时产生移位操作。这个过程将直到完成4次 移位操作结束，控制状态转到S5。最后，如果C=1，执行 最后一次减法运算，否则，不做减法运算。这时没有移位 操作要求，控制电路回到停止状态S0。在这里假设启动信 号St为高有效，并且仅持续一个时钟周期，在完成全部操 作前，启动信号St将一直保持为低电平。
if(c='1') then su<='1';
end if;
nextstate<=0;
end if;
when 5=>
--状态5：结束运算过程，返回初始态
if(c='1') then su<='1';
end if;
nextstate<=0;
end case;
end process state_graph;
signal subout:std_logic_vector(4 downto 0);
signal dividend:std_logic_vector(8 downto 0);
begin
subout<=dividend(8 downto 4)-('0'&divisor); --减法器
c<=not subout(4);
remainder<=dividend(7 downto 4); --分离出余数
quotient<=dividend(3 downto 0); --分离出商
begin
subout<=dividend(8 downto 4)-('0'&divisor); --减法器
c<=not subout(4);
case state is
when 0=>
--状态0 ：启动除法运算
if(st='1') then load<='1';nextstate<=1;
else nextstate<=0;
end if;
when 1=>
--状态1 ：溢出判断
if(c='1')then overflow<='1';nextstate<=0;
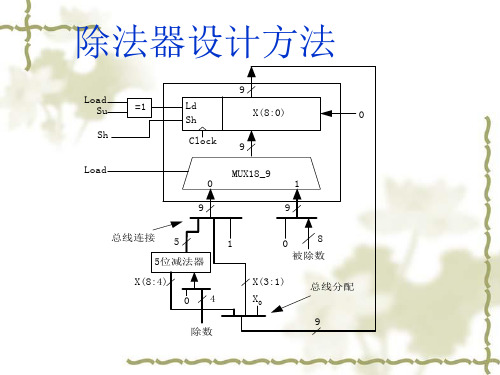
除法器设计方法
9
Load Su
=1
Ld
Sh
X(8:0)
0
Sh
Clock
9
Load
MUX18_9
0
1
9
9
总线连接 5
1
5位减法器
X(8:4)
04
除数
0
8
被除数
X(3:1) X0
总线分配 9
St’/0
S0 (停止)
St/Load
C’/Sh S1
S2
C/OV
C/Su
C/Su C’/0
C’/Sh
பைடு நூலகம்
C’/Sh