32位除法器的设计
电路中的除法器设计

电路中的除法器设计在电路设计中,除法器是一种十分重要的组件。
它可以将输入的数字进行除法运算,将商和余数输出。
除法器在计算机和数字信号处理器等电子设备中被广泛使用,因此其设计和优化具有重要意义。
一、除法器的基本原理除法运算是一种复杂的运算,要实现除法器的设计,首先需要了解其基本原理。
除法器的基本原理是通过移位和减法实现的。
在将被除数和除数输入除法器后,除法器将被除数和除数进行比较,并开始迭代过程。
在每一次迭代中,被除数的位数向左移动,直到其高位与除数相等或超过除数。
然后,除法器进行减法操作,将除数减去被除数,结果作为商的一位。
此后,商持续左移,被减数保持不变,重复上述过程,直到所有的商位都得出。
二、除法器的设计策略在除法器的设计中,有几种常见的策略可以考虑。
1. 组合逻辑除法器:这种类型的除法器使用组合逻辑电路实现,通过减法器、比较器和移位器等组件的组合来实现除法运算。
组合逻辑除法器的优点是速度较快,但缺点是占用较多的电路资源。
2. 串行逻辑除法器:与组合逻辑除法器相反,串行逻辑除法器使用顺序逻辑电路实现。
它通过一个时钟信号,逐位地进行计算,因此典型的串行逻辑除法器速度较慢。
但串行逻辑除法器更节省电路资源,因此在一些资源有限的场景中得到了广泛应用。
3. 重复系列除法器:这种除法器通过多个并行的子除法器实现,并行计算多个位的商。
重复系列除法器具有较高的性能,但需要更多的电路资源和功耗。
三、除法器的优化方法为了提高除法器的性能和效率,可以采用一些优化方法。
1. 位级并行思路:通过将除法器分解为多位的子除法器,并行计算多个子除法器,可以大幅提高除法器的速度。
这种方法在重复系列除法器中得到了广泛应用。
2. 乘法相关技巧:利用乘法器计算除法运算,可以加速除法器的运算速度。
通过将除数进行逆运算,转化为乘法操作,可以利用乘法器的高速性能,提升除法器的效率。
3. 进制转换思想:将数字进行二进制到十进制的转换,然后进行简单的除法运算,可以减少运算的复杂程度,提高除法器的运算速度。
32位算术逻辑运算单元

32位算术逻辑运算单元32位算术逻辑运算单元(ALU)是计算机体系结构中的一个关键组件,它执行计算机中的算术和逻辑运算。
它通常由多个逻辑门和寄存器组成,用于执行加法、减法、逻辑与、逻辑或等运算。
在本文中,我将详细介绍32位ALU的工作原理和设计。
首先,让我们了解一下什么是32位ALU。
它是一种具有32个位的数据运算单元,用于处理32位的二进制数据。
每个位都可以表示0或1,并且可以进行各种二进制运算。
这些运算可以是算术运算,如加法和减法,也可以是逻辑运算,如逻辑与、逻辑或和逻辑非等。
32位ALU的核心部分是一组逻辑门,包括与门、或门、非门等。
这些逻辑门通过电路连接在一起,实现了不同的运算。
例如,对于算术加法运算,ALU使用一组全加器电路来执行。
每个全加器将输入的两个位和进位位相加,并生成和位和进位位。
这些和位和进位位将传递给下一个全加器,直到所有位都被加起来。
最后,将得到的和位作为结果输出。
除了算术运算,32位ALU还可以执行逻辑运算。
例如,对于逻辑与运算,ALU使用一组与门来执行。
它将输入的两个位分别与对应的两个位进行逻辑与运算,并得到一个结果位。
这些结果位将传递给下一个与门,直到所有位都被运算。
最后,得到的结果位将作为运算结果输出。
在32位ALU中,还有一些其他重要的组件。
其中之一是寄存器,用于存储运算结果和其他中间结果。
寄存器是一种能够存储和读取数据的高速存储器。
它通常由触发器组成,可以在时钟信号的作用下保持数据的稳定性。
寄存器在ALU中用于存储运算结果,并将其传递给其他部分进行处理。
另一个重要的组件是控制单元。
控制单元负责控制ALU的操作和流程。
它接收指令和数据,并根据指令的类型和操作码来决定执行何种运算。
控制单元还可以控制ALU的时钟信号和寄存器的读写操作。
它基于计算机指令的解码和执行机制来实现这些功能。
在设计32位ALU时,需要考虑的因素有很多。
首先是电路的优化和性能。
ALU需要在非常短的时间内完成运算,并且需要具有高的稳定性和可靠性。
32位加减法器设计2010012107季涛

带有溢出标志的32位加减法器的设计2010012107 季涛加法器是一个非常基本的数字运算电路,经常出现在数字电路的关键路径中。
本次作业实现的加减法器一共要实现五个基本功能:1)求补2)无符号数的加法3)无符号数的减法4)有符号数的加法5)有符号数的减法,同时对应每种功能还要给出对应的溢出标志。
虽然看起来功能有五种,但是核心的模块还是一个32位的加法器。
现在比较流行的加法器结构有很多,从最基本的一位半加器、全加器,到多位的行波进位加法器,曼彻斯特进位链加法器,旁路进位加法器,超前进位加法器,选择进位加法器,到更复杂的更多位的树结构表示的加法器,如Brent-Kung树、Kogge-Stone树等等。
由于想要实现一个速度较快的加法器,所以一般会选择后几种类型的结构,然后我之前的课程里已经实现过了超前进位加法器、Brent-Kung树结构前置进位加法器,所以本次作业我选择了Kogge-Stone树。
它的主要特点是:能获得log2N的级数,每级的扇出为2,代价是级间布线有很多的长线,PG单元更多。
Kogge-Stone树结构图如下:结构框图如下:设计的思路是这样的,求补的话就是对操作数进行取反然后+1,令加法器的一个输入为1,另一个输入为~a即可;无符号数和有符号数的加法的输入是一样的;减法的时候只要对第二个操作数求补即可。
然后溢出标志的获取我是对四种功能分别考虑,无符号数的加法,只有在最高位的进位信号为1的时候表示超过了数的表示范围,溢出信号为1,其余情况都为0;无符号数的减法只有在第一个操作数比第二个操作数小的时候溢出信号为1,其余为0;有符号数的加法只有在两个操作数的符号相同而和的最高位符号与他们不同时为1.其余为0;有符号数的减法只有在两个操作数的符号位不同而差的最高位和第二个操作数符号位相同时为1,其余为0。
这样就基本实现了功能。
总结:第一次作业主要让我又回顾了modelsom、DC等软件的使用方法,时隔一年没用有些东西确实都生疏了,甚至安装modelsim软件、DC综合的过程中也产生了不少问题,好在在同学和助教姐姐的帮助下都克服了困难。
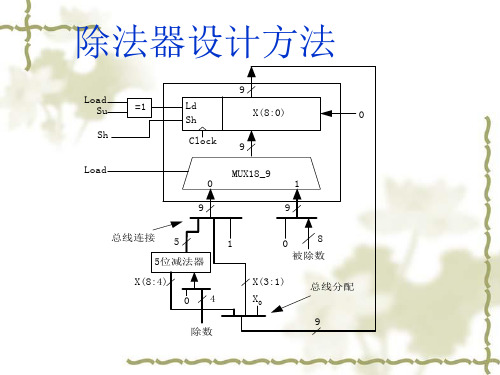
除法器设计方法
controlsignals:process(T,I,X,Y)
--状态控制进程
begin
Extern<='0';Done<='0';Ain<='0';Gin<='0';
Gout<='0';AddSub<='0';Rin<="0000";Rout<="0000";
case T is
when "00"=>
update:process(clk)
--同步数据更新进程
begin
if(clk='1'and clk'event) then
state<=nextstate;
if load='1' then
dividend<='0'÷nd_in;
end if;
if su='1' then
dividend(8 downto 4)<=subout;
end proc;
architecture Behavioral of proc is
component upcount
--计数器元件声明
Port ( Clear,Clock : in std_logic;
Q : buffer std_logic_vector(1 downto 0));
end component;
signal subout:std_logic_vector(4 downto 0);
signal dividend:std_logic_vector(8 downto 0);
基于 FPGA的32位除法器设计

目录摘要 (1)第1章绪论 (2)第2章设计原理 (3)2.1 除法运算分析 (3)2.2 除法器算法的实现 (3)2.2.1除法器无符号数的除法 (3)2.2.2除法器有符号数的除法 (3)第3章软件介绍及设计过程 (4)3.1 Quartus II简介 (4)3.2 程序设计过程 (4)3.3 仿真结果 (6)结论 (7)参考文献 (8)附录1 源程序 (9)摘要介绍了一种使用可编程逻辑器件FPGA和VHDL语言实现32位除法器的设计方法。
该除法器不仅可以实现有符号数运算,也可以实现无符号数的运算。
除法器采用节省FPGA逻辑资源的时序方式设计,主要由移位、比较和减法三种操作构成。
由于优化了程序结构,因此程序浅显易懂,算法简单,不需要分层次分模块进行。
并使用Altera公司的QuartusⅡ软件对该除法器进行编译、仿真,得到了完全正确的结果。
关键词:FPGA;VHDL;除法器;减法;移位第1章绪论EDA 技术就是以计算机为工具,设计者在 EDA 软件平台上,用硬件描述语言 VHDL完成设计文件,然后由计算机自动地完成逻辑编译、化简、分割、综合、优化、布局、布线和仿真,直至对于特定目标芯片的适配编译、逻辑映射和编程下载等工作。
EDA 技术的出现,极大地提高了电路设计的效率和可操作性,减轻了设计者的劳动强度。
VHDL是一种全方位的硬件描述语言,包括系统行为级、寄存器传输级和逻辑门级多个设计层次,支持结构、数据流和行为 3 种描述形式的混合描述,因此 VHDL几乎覆盖了以往各种硬件描述语言的功能,整个自顶向下或自底向上的电路设计过程都可以用 VHDL来完成。
另外,VHDL还有以下优点:VHDL的宽范围描述能力使它成为高层次设计的核心,将设计人员的工作重心转移到了系统功能的实现和调试上,只需要花较少的精力用于物理实现;VHDL可以用简洁明确的代码描述来进行复杂控制逻辑的设计,灵活且方便,而且也便于设计结果的交流、保存和重用;VHDL的设计不依赖于特定的器件,方便了工艺的转换。
数字系统设计32位进位选择加法器设计

1、12进位选择加法器原理图32位进位选择加法器原理图仅仅是将12位进位选择加法器原理图中虚线框内的模块再向后重复5次,这就构成了32位进位选择加法器原理图。
2、Verilog模块根据上图可以将进位选择加法器在结构上分为四个模块:①四位先行进位加法器adder_4bits②四位数据选择器mux_2to1③高四位选择加法器(虚线框内部分)adder_high_4bits④顶层设计32位进位选择加法器adder_32_bits3、Verilog代码# 四位先行进位加法器module adder_4bits(a,b,s,ci,co);parameter N=4;input[N-1:0] a;input[N-1:0] b;input ci;output[N-1:0] s;output co;wire [N-1:0] c;wire [N-1:0] g;wire [N-1:0] p;assign g=a&b;assign p=a|b;assign c[0]=g[0]||(p[0]&&ci);assign c[1]=g[1]||(p[1]&&g[0])||(p[1]&&p[0]&&ci);assign c[2]=g[2]||(p[2]&&g[1])||(p[2]&&p[1]&&g[0])||(p[2]&&p[1]&&p[0]&&ci);assignc[3]=g[3]||(p[3]&&g[2])||(p[3]&&p[2]&&g[1])||(p[3]&&p[2]&&p[1]&&g[0])||(p[3]&&p[2]&&p[1]&&p[0]&&ci);assign s[0]=p[0]&~g[0]^ci;assign s[1]=p[1]&~g[1]^c[0];assign s[2]=p[2]&~g[2]^c[1];assign s[3]=p[3]&~g[3]^c[2];assign co=c[3];endmodule# 四位数据选择器module mux_2to1 (out,in0,in1,sel);parameter N=4;output[N:1] out;input[N:1] in0,in1;input sel;assign out=sel?in1:in0;endmodule# 高四位选择加法器module adder_high_4bits(a,b,ci,co,s);parameter N=4;input[N-1:0] a;input[N-1:0] b;input ci;output[N-1:0] s;output co;wire [N-1:0] sum1,sum0;wire co1,co0,cand;adder_4bits #(4) adder_1(.a(a),.b(b),.s(sum1),.ci(1'b1),.co(co1)); adder_4bits #(4) adder_2(.a(a),.b(b),.s(sum0),.ci(1'b0),.co(co0)); mux_2to1 #(4) mux1(.in0(sum0),.in1(sum1),.sel(ci),.out(s)); and G1(cand,ci,co1);or G2(co,cand,co0);endmodule# 顶层设计32位进位选择加法器module adder_32bits(a,b,s,ci,co);parameter N=32;input [N-1:0] a;input [N-1:0] b;input ci;output [N-1:0] s;output co;wire co1,co2,co3,co4,co5,co6,co7;adder_4bits #(4) adder1(.a(a[3:0]),.b(b[3:0]),.ci(ci),.s(s[3:0]),.co(co1));adder_high_4bits #(4) adder2(.a(a[7:4]),.b(b[7:4]),.ci(co1),.s(s[7:4]),.co(co2));adder_high_4bits #(4) adder3(.a(a[11:8]),.b(b[11:8]),.ci(co2),.s(s[11:8]),.co(co3));adder_high_4bits #(4) adder4(.a(a[15:12]),.b(b[15:12]),.ci(co3),.s(s[15:12]),.co(co4));adder_high_4bits #(4) adder5(.a(a[19:16]),.b(b[19:16]),.ci(co4),.s(s[19:16]),.co(co5));adder_high_4bits #(4) adder6(.a(a[23:20]),.b(b[23:20]),.ci(co5),.s(s[23:20]),.co(co6));adder_high_4bits #(4) adder7(.a(a[27:24]),.b(b[27:24]),.ci(co6),.s(s[27:24]),.co(co7));adder_high_4bits #(4) adder8(.a(a[31:28]),.b(b[31:28]),.ci(co7),.s(s[31:28]),.co(co)); endmodule4、仿真结果①四位先行进位加法器进行仿真,结果如下如图所示,a=0101,b=1010,ci=1;sum=0000,cout=1;仿真正确。
位可控加减法器设计32位算术逻辑运算单元

位可控加减法器设计32位算术逻辑运算单元标题:深入探讨位可控加减法器设计中的32位算术逻辑运算单元一、引言在计算机系统中,算术逻辑运算单元(ALU)是至关重要的部件,用于执行数字运算和逻辑运算。
而在ALU中,位可控加减法器设计是其中的重要部分,尤其在32位算术逻辑运算单元中更是不可或缺。
本文将深入探讨位可控加减法器设计在32位算术逻辑运算单元中的重要性,结构特点以及个人观点和理解。
二、位可控加减法器设计的重要性位可控加减法器是ALU中的重要组成部分,它具有对加法和减法操作进行控制的能力,可以根据输入信号来实现不同的运算操作。
在32位算术逻辑运算单元中,位可控加减法器的设计要考虑到对每一位进行并行操作,并且要保证高速、低功耗和稳定性。
位可控加减法器设计在32位算术逻辑运算单元中具有非常重要的意义。
三、位可控加减法器设计的结构特点在32位算术逻辑运算单元中,位可控加减法器的设计需要考虑到以下几个结构特点:1. 并行运算:位可控加减法器需要能够实现对32位数据的并行运算,以提高运算速度。
2. 控制信号:设计需要合理的控制信号输入,来实现不同的运算模式和操作类型。
3. 进位传递:保证进位信号能够正确传递和计算,以确保运算的准确性。
4. 低功耗:设计需要考虑到低功耗的特点,以满足现代计算机系统对能源的需求。
四、个人观点和理解在我看来,位可控加减法器设计在32位算术逻辑运算单元中扮演着十分重要的角色。
它不仅需要具备高速、稳定和精确的运算能力,还需要考虑到功耗和控制信号的合理设计。
只有兼具这些特点,才能更好地满足现代计算机系统对于高效、可靠和低功耗的需求。
五、总结和回顾通过本文对位可控加减法器设计在32位算术逻辑运算单元中的深入探讨,我们可以看到它在计算机系统中的重要性和结构特点。
而个人观点也表明了它需要具备高速、低功耗和稳定性等特点,才能更好地满足现代计算机系统的需求。
在写作过程中,我对位可控加减法器设计在32位算术逻辑运算单元中的重要性和结构特点进行了深入探讨,并分享了个人观点和理解。
基于 FPGA的32位除法器设计汇总

目录摘要 (1)第1章绪论 (2)第2章设计原理 (3)2.1 除法运算分析 (3)2.2 除法器算法的实现 (3)2.2.1除法器无符号数的除法 (3)2.2.2除法器有符号数的除法 (3)第3章软件介绍及设计过程 (4)3.1 Quartus II简介 (4)3.2 程序设计过程 (4)3.3 仿真结果 (6)结论 (7)参考文献 (8)附录1 源程序 (9)摘要介绍了一种使用可编程逻辑器件FPGA和VHDL语言实现32位除法器的设计方法。
该除法器不仅可以实现有符号数运算,也可以实现无符号数的运算。
除法器采用节省FPGA逻辑资源的时序方式设计,主要由移位、比较和减法三种操作构成。
由于优化了程序结构,因此程序浅显易懂,算法简单,不需要分层次分模块进行。
并使用Altera公司的QuartusⅡ软件对该除法器进行编译、仿真,得到了完全正确的结果。
关键词:FPGA;VHDL;除法器;减法;移位第1章绪论EDA 技术就是以计算机为工具,设计者在 EDA 软件平台上,用硬件描述语言 VHDL完成设计文件,然后由计算机自动地完成逻辑编译、化简、分割、综合、优化、布局、布线和仿真,直至对于特定目标芯片的适配编译、逻辑映射和编程下载等工作。
EDA 技术的出现,极大地提高了电路设计的效率和可操作性,减轻了设计者的劳动强度。
VHDL是一种全方位的硬件描述语言,包括系统行为级、寄存器传输级和逻辑门级多个设计层次,支持结构、数据流和行为 3 种描述形式的混合描述,因此 VHDL几乎覆盖了以往各种硬件描述语言的功能,整个自顶向下或自底向上的电路设计过程都可以用 VHDL来完成。
另外,VHDL还有以下优点:VHDL的宽范围描述能力使它成为高层次设计的核心,将设计人员的工作重心转移到了系统功能的实现和调试上,只需要花较少的精力用于物理实现;VHDL可以用简洁明确的代码描述来进行复杂控制逻辑的设计,灵活且方便,而且也便于设计结果的交流、保存和重用;VHDL的设计不依赖于特定的器件,方便了工艺的转换。
基于FPGA的32位循环型除法器设计

基于FPGA的32位循环型除法器设计作者:李文彬陈金鹰王惟洁任小强来源:《物联网技术》2014年第11期摘要:借助于硬件描述语言Verilog HDL语言和FPGA,提出了一种32位循环型除法器的实现方法。
该除法器通过改善程序结构,优化了时序,提高了除法运算速度,克服了传统除法器“吃时钟”的弊端。
且该除法器的移位、相减和比较操作都在一个程序下完成,无需模块划分,节约逻辑资源。
该设计并顺利通过Quartus II编译、综合和仿真工具Modelsim的仿真,达到了预期的结果。
关键词:Verilog HDL;FPGA;循环;除法器中图分类号:TP393 文献标志码:A 文章编号:2095-1302(2014)11-00-020 引言在数据处理过程中,除法是经常用但也是最复杂的四则运算。
特别是针对含有除法器的FPGA设计中,除法器的运算速度,运算精度和占用逻辑资源大小对系统的整体性能具有很大影响[1]。
现有的EDA软件提供的除法模块时钟消耗多,占有逻辑资源量大,且除数受限,只能是2的次幂。
因此,设计一种由Verilog HDL[2]编写的可综合的,可以是任意除数的,运算速度快,逻辑资源占用量小[3,4]的除法器在FPGA数据处理中就显得尤为必要。
1 循环型除法器原理与设计循环性除法器也叫位操作除法器,主要通过移位、相减和比较三种操作实现求商和得余[5]。
无论是乘法器还是除法器都有操作空间,典型的循环型除法器又可分为操作空间可恢复性和不可恢复性,这里采用易于控制,逻辑清晰的操作空间不可恢复型算法。
在上述所采用算法中,首先保证被除数为正值,若为负值,则对被除数正值化,然后进行相应的移位、减法和比较操作,最后再对结果进行调整。
具体实现过程如下:假设除数和被除数都是N位,那么操作空间P的位宽就是2*N,其中P[N-1:0]用来填充被除数,P[2*N-1:N-1]是用来与除数进行递减操作。
此外,为了保证运算结果正确性,还要考虑同步操作,P[2*N-1:N-1]和除数的递减操作应该发生在别的空间,此处命名为D空间,D空间具有和P 空间同样的位宽。
基于FPGA的32位除法器设计

基于FPGA的32位除法器设计FPGA(Field-Programmable Gate Array)是一种可编程逻辑器件,可以通过编程来实现特定功能。
在设计一个基于FPGA的32位除法器时,我们需要考虑如下几个方面:1.硬件资源分配:32位除法器需要大量的逻辑门和寄存器资源。
我们需要确定所使用的FPGA型号,并评估所需资源量,以确保设计能够适应硬件资源的限制。
2.算法选择:除法的计算是一种复杂的任务,需要使用有效且高效的算法来实现。
在选择算法时,我们需要考虑计算的精度、执行时间、资源消耗等因素。
在32位除法器设计中,最常用的算法是非恢复余数法(Non-Restoring Division),该算法采用二进制除法的方法,可以高效地进行除法计算。
3.状态机设计:除法过程包括初始化、迭代计算、判断结果等多个阶段。
我们可以使用状态机的方式来设计整个除法器,以确保每个阶段的正确顺序和相应控制信号的生成。
4.数据通路设计:设计数据通路时,需要包括输入寄存器、输出寄存器、除法器控制单元(CU)等。
CU负责控制数据的传输和状态的转换,输入寄存器和输出寄存器用于保存输入和输出数据。
5.时序优化:除法计算的正确性依赖于时序的准确控制。
时钟频率的选择和信号的传输路径都会对时序造成影响。
我们需要进行时序分析和优化,以保证计算的准确性和速度。
6.验证和测试:在设计完成后,我们需要对除法器进行验证和测试,以确保它能够正确地计算出结果。
可以使用仿真工具对设计进行功能验证,并使用实际数据进行硬件测试。
除此之外,为了提高除法计算的效率和性能,还可以考虑采用流水线和并行计算等技术,以加速计算过程。
总结:。
位可控加减法器设计32位算术逻辑运算单元

【位可控加减法器设计32位算术逻辑运算单元】1. 引言位可控加减法器是现代计算机中十分重要的组成部分,它可以在逻辑电路中实现对算术运算的功能。
其中,32位算术逻辑运算单元是计算机中非常常见的一个部件,它可以用来进行32位数据的加法、减法和逻辑运算。
本文将就位可控加减法器的设计和32位算术逻辑运算单元进行全面评估,并给出深度和广度兼具的解析。
2. 什么是位可控加减法器位可控加减法器是一种灵活的算术逻辑电路,它可以根据控制信号来选择进行加法运算或减法运算。
这种设计可以大大提高电路的灵活性和适用性,使得算术运算单元可以在不同的情况下实现不同的运算需求。
3. 32位算术逻辑运算单元的设计原理32位算术逻辑运算单元是计算机中进行32位数据运算的核心部件,它通常包括加法器、减法器、逻辑门等组件。
在设计中,需要考虑到加法器和减法器的位宽、进位和溢出等问题,同时还需要考虑逻辑门的多功能性和灵活性。
通过合理的组合和控制,可以实现对32位数据进行高效的算术逻辑运算。
4. 位可控加减法器设计在32位算术逻辑运算单元中的运用位可控加减法器的设计可以很好地应用在32位算术逻辑运算单元中,通过控制信号来选择进行加法或减法运算,从而满足不同情况下对数据的处理需求。
这种设计不仅能简化电路结构和控制逻辑,还能提高算术逻辑运算单元的灵活性和效率,使其更适用于不同的场景和运算需求。
5. 个人观点和理解从我个人的理解来看,位可控加减法器设计在32位算术逻辑运算单元中的应用,可以很好地提高计算机的运算效率和灵活性。
通过合理的设计和控制,可以使得算术逻辑运算单元在不同的情况下具有不同的功能,从而更好地满足计算机对于数据处理的需求。
这种设计也为计算机的设计和优化提供了很好的思路和方法。
6. 总结通过本文的评估和解析,我们对于位可控加减法器的设计以及在32位算术逻辑运算单元中的应用有了更深入的理解。
通过灵活的控制信号,可以实现算术逻辑运算单元在不同情况下对数据进行不同的处理,从而提高了计算机的运算效率和灵活性。
毕业设计--32位不恢复替代算法除法器设计[管理资料]
![毕业设计--32位不恢复替代算法除法器设计[管理资料]](https://img.taocdn.com/s3/m/48439dd3482fb4daa48d4b0c.png)
32位不恢复替代算法除法器设计摘要CPU的核心功能之一是实现基本算术运算。
在四则基本运算中,除法在技术实现上具有较高的复杂性,所以硬件除法器的设计一般会成为CPU设计中的重点与难点。
对于嵌入式CPU来说,其设计目标更加关心成本的降低,使得其算术运算单元在性能设计指标上需要有较大的灵活性,从而使硬件占用较小的面积。
本文根据不恢复替代算法,实现了32位不恢复替代算法除法器。
本文首先介绍了除法器在CPU设计中的地位、设计所面临的挑战。
然后简单说明了Digit Recurrence算法基本理论和除法器的基本算法,即:恢复迭代算法及其电路、不恢复迭代算法及其电路、基数-4SRT算法、Newton-Raphson除法算法。
然后用半定制方法对32不恢复替代算法除法器器进行了设计和分析。
最后进行了硬件电路的综合。
综合结果表明,无论从资源占用方面还是从最高工作频率方面。
基于ALTERA Stratix II 的综合结果显示,基于掩码的数据反转的桶形移位器的最高工作频率可以达到30MHz。
关键词:除法器;不恢复替代算法;半定制设计;Verilog HDLDesign of 32-bits Not Resume AlternativeAlgorithm DividerAbstractArithmetic computation is a key function of Central Processor Unit (CPU).Among basic arithmetic operation, division is the most difficult one to implement. Therefore the design of dedicate hardware divider is usually the vital part in CPU development. Since the design of an embedded CPU is more concerned about cost reduction, its ALU design usually emphasizes on flexibility rather than performance. This orientation demands solutions that consume minimum die area.This article does not resume under an alternative method to achieve a 32-bit replacement algorithm does not restore divider. This paper introduces the divider position in the CPU design, design challenges and research significance.Then a brief description of the basic theory and algorithm Digit Recurrence divider the basic algorithm, that is: restore iterative algorithm and its circuit, not to resume iterative algorithm and its circuit, the base -4 SRT algorithm, Newton-Raphson division algorithm. Then the paper designs and analyses The Divider in the semi- custom approach.Finally, I completed to integrate the circuit hardware .The result of systhesis based on the ALTERA Stratix II indicates that the mask-based data- reversal barrel shifter can work in the 30MHz.Keywords: Divider;Not Resume Alternative Algorithm;Semi-custom Approach;Verilog HDL目录 (1) (1) (3) (6) (7) (8)2. 除法器的基本算法 (9)Recurrence算法基本理论 (9) (9)数学表述 (11)基数 (13) (13) (14) (16)SRT算法 (19)Newton-Raphson 除法算法 (23) (24) (24)硬件时序结构的优化方法 (26) (29)3. 32位不恢复替代算法除法器设计 (33)Verilog HDL (33) (34) (38)HDL的设计与验让流程 (38)综合仿真图形 (41) (43) (44) (44)致谢 (45)参考文献 (46)附录 (48)外文资料翻译及原文 (54)微电子技术是随着集成电路,尤其是超大规模集成电路而发展起来的一门新的技术。
8位单片机 32位除法

8位单片机 32位除法8位单片机是一种常见的嵌入式微控制器,它具有8位的数据总线,可以处理8位宽的二进制数据。
而32位除法是一种数学运算,用于将一个32位的整数除以另一个整数。
今天,我们将探讨如何在8位单片机上进行32位除法,并谈谈相关的应用和意义。
首先,理解什么是8位单片机很重要。
它是一种微型计算机芯片,能够集成处理器核心、内存和外设接口等功能于一个芯片上。
8位单片机在嵌入式系统中得到广泛应用,例如家电、汽车等领域。
它的低成本、低功耗和易于处理简单任务的特点使得它成为许多小型电子设备的理想选择。
而32位除法则是一种复杂的运算,用于将一个32位的整数除以另一个整数,并给出商和余数。
32位除法可以解决一些实际问题,例如计算机网络中的IP地址划分,图形处理中的像素计算等。
这种除法运算需要更强大的处理能力和更大的数据宽度,因此往往在高性能计算机和处理器中使用。
然而,在一些特殊应用场景中,我们需要在8位单片机上实现32位除法,这就需要我们深入研究并合理设计算法。
在处理32位除法时,需要注意的是,8位单片机的数据宽度有限,无法直接进行32位运算。
因此,我们需要采用一些特定的算法来完成这个任务。
其中一个常见的算法是采用二进制长除法。
这种算法将32位整数划分为若干个8位部分,并逐位进行除法运算,最终给出商和余数。
实现32位除法需要考虑到多个方面的问题,例如数据存储、算法设计和性能优化。
在数据存储方面,我们需要明确如何将32位整数分解为8位部分,以及如何存储和操作这些部分。
在算法设计方面,我们需要选择合适的除法算法,并合理利用8位单片机的有限资源,以提高运算效率。
在性能优化方面,我们可以通过优化算法、减少不必要的计算和合理规划程序结构等手段来提高程序的执行速度和资源利用率。
掌握在8位单片机上实现32位除法的技术在嵌入式系统开发中具有重要的意义。
它可以帮助我们深入理解单片机的底层原理和运算机制,并为我们提供更多的自主开发和创新空间。
pic单片机32位除法

pic单片机32位除法pic单片机是一种常用的32位单片机,其具有高性能和强大的计算能力。
在pic单片机中,除法是一项常见的运算操作。
本文将探讨pic单片机32位除法的原理和实现方式。
我们需要了解32位除法的基本原理。
除法是一种数学运算,用于将一个数(被除数)除以另一个数(除数),得到商和余数。
在32位除法中,被除数和除数都是32位的二进制数。
在pic单片机中,除法操作可以通过软件算法或硬件模块来实现。
软件算法是通过编写程序来进行除法运算,而硬件模块则是通过专门的电路来实现除法运算。
对于软件算法来说,一种常见的方法是使用循环来逐位进行除法运算。
具体步骤如下:1. 将被除数和除数加载到寄存器中。
2. 将商寄存器清零。
3. 从高位开始,逐位进行除法运算,直到最低位。
4. 每次运算中,将被除数左移一位,并与除数进行比较。
5. 如果被除数大于或等于除数,则将商寄存器的对应位设置为1,并将被除数减去除数。
6. 如果被除数小于除数,则将商寄存器的对应位设置为0。
7. 重复步骤4至6,直到所有位都计算完毕。
8. 最后得到的商就是除法的结果。
这种软件算法的实现简单,但运算速度相对较慢。
如果需要进行大量的除法运算,可能会影响系统的性能。
因此,在一些对性能要求较高的应用中,可以使用硬件模块来实现32位除法运算。
pic单片机中的硬件模块通常是由专门的除法器实现的。
这种除法器可以通过硬件电路来进行除法运算,具有快速、高效的特点。
在进行除法运算时,只需要将被除数和除数输入到除法器中,然后通过特定的指令来触发除法运算。
除法器会自动完成除法运算,并将结果存储在指定的寄存器中。
pic单片机的32位除法器通常具有高精度和高速度的特点,可以满足各种应用的需求。
除法器的性能主要取决于硬件电路的设计和实现方式。
一些高端的pic单片机还可以支持并行计算和流水线技术,进一步提高除法运算的效率。
总结起来,pic单片机32位除法是一项常见的运算操作,可以通过软件算法或硬件模块来实现。
快速加法器与32位ALU设计

实验二快速加法器与32位ALU设计实验1.1设计要求1. 掌握串行加法器逻辑实现原理。
1) 能设计8 位可控加减法电路。
2. 掌握快速加法中先行进位的原理。
1) 能设计4 位先行进位电路。
2) 能设计4 位快速加法器。
3. 掌握组内先行,组间先行的基本原理。
1) 利用4 位快速加法器构建16 位、32 位快速加法器。
2) 能分析相关电路延迟。
1. 掌握定点数加减法溢出检测方法。
2. 理解算术逻辑运算单元ALU 的基本构成。
3. 掌握Logisim 中各种运算组件的使用方法:1) 逻辑运算:与、或、非、异或2) 算术运算:乘法器、除法器、求补器、比较器3) 移位器4. 熟练掌握多路选择器的使用方法。
5. 能利用前述实验完成的32 位加法器(禁止使用Logisim 自带的加法器/减法器组件)和Logisim 的运算组件构造指定规格的ALU 单元。
运算器功能以及输入输出引脚见下表表 0.1 片引脚与功能描述引脚输入/输出位宽功能描述X 输入32 操作数XY 输入32 操作数YALU_OP 输入 4 运算器功能码,具体功能见下表Result 输出32 ALU运算结果Result2 输出32 ALU结果第二部分,用于乘法指令结果高位或除法指令的余数位,其他操作为零OF 输出 1 有符号加减溢出标记,其他操作为零CF 输出 1 无符号加减溢出标记,其他操作为零Equal 输出 1 Equal=(x==y)?1:0, 对所有操作有效表 0.2 运算符功能ALU OP 十进制运算功能0000 0 Result = X << Y 逻辑左移(Y取低五位)Result2=00001 1 Result = X >>>Y 算术右移(Y取低五位)Result2=00010 2 Result = X >> Y 逻辑右移(Y取低五位)Result2=00011 3 Result = (X * Y)[31:0]; Result2 = (X *Y)[63:32] 有符号0100 4 Result = X/Y; Result2 = X%Y 无符号0101 5 Result = X + Y Result2=0 (Set OF/CF)0110 6 Result = X - Y Result2=0 (Set OF/CF)0111 7 Result = X & Y Result2=01000 8 Result = X | Y Result2=01001 9 Result = X⊕Y Result2=01010 10 Result = ~(X |Y) Result2=01011 11 Result = (X < Y) ? 1 : 0 Signed Result2=01100 12 Result = (X < Y) ? 1 : 0 Unsigned Result2=01101 13 Result = Result2=01110 14 Result = Result2=01111 15 Result = Result2=01.2方案设计1.2.1 八位可控加减法器原理:补码减法变加法原理减法变加法原因:负数的减法运算也要设法化为加法来做,其所以使用这种方法而不使用直接减法,是因为它可以和常规的加法运算使用同一加法器电路,从而简化了计算机的设计。
计算机组成原理--除法器原理及c代码

计算机组成原理--除法器原理及c代码除法器是计算机中的一种重要的算术逻辑单元,用于实现除法运算。
除法器的设计是计算机组成原理中的重要内容之一,本文将从除法器的原理和相关的C代码实现两个方面进行介绍。
一、除法器原理除法器的原理主要包括除法算法和硬件实现两个方面。
1.除法算法在计算机中,除法可以采用多种算法实现,其中最常用的算法是连续除法和恢复余数法。
连续除法是将除数逐位地与被除数相减,判断余数的大小来进行下一步的操作。
具体操作如下:1)将被除数置于一边,余数和商置于另一边;2)被除数减去除数,得到当前位上的余数;3)余数进行左移,并加上下一位的被除数;4)重复上述操作直到计算完所有位。
恢复余数法是将除法过程中的余数加上除数,然后与被除数进行比较,得到商和下一位的余数。
具体操作如下:1)将被除数放在寄存器的高位,余数和商放在低位;2)将寄存器与除数进行比较,若寄存器大于等于除数,说明商的该位为1,余数等于当前寄存器减去除数;3)将寄存器进行左移,并加上下一位的被除数;4)重复上述操作直到计算完所有位。
2.硬件实现硬件实现除法器可以采用著名的Restoring、Non-Restoring和SRT 等算法。
其中Restoring算法是最常用的硬件实现方式。
Restoring算法中,通过比较、左移、减法等操作进行计算。
具体操作如下:1)将除数和被除数放入寄存器的高位和低位,商和余数置零;2)将寄存器与除数进行比较,若寄存器大于等于除数,说明商的该位为1,余数等于当前寄存器减去除数;3)将寄存器逻辑左移一位;4)循环执行2-3步,直到计算完所有位。
二、C代码实现以下是C语言中使用Restoring算法实现的除法器代码:```c#include <stdio.h>unsigned int divide(unsigned int dividend, unsigned int divisor)unsigned int quotient = 0;unsigned int remainder = 0;//32位无符号整数除法for (int i = 31; i >= 0; i--)remainder = (remainder << 1) , ((dividend >> i) & 1); // 将被除数逻辑左移一位,并加上下一位的被除数if (remainder >= divisor) // 判断余数是否大于等于除数remainder -= divisor; // 余数减去除数quotient ,= (1u << i); // 商的该位为1}}return quotient;int mainunsigned int dividend = 53;unsigned int divisor = 5;unsigned int result = divide(dividend, divisor);printf("%u / %u = %u\n", dividend, divisor, result);return 0;```以上的代码实现了一个32位无符号整数的除法操作,通过Restoring算法将除法运算转化为逐位比较、逻辑左移和减法等操作,最终得到商。
stm32除法运算

stm32除法运算STM32是一款广泛应用于嵌入式系统开发的微控制器系列,其中的除法运算在嵌入式系统的开发中起到了重要的作用。
本文将从STM32除法运算的原理、应用场景和注意事项等方面进行介绍。
我们来了解一下STM32除法运算的原理。
在STM32中,除法运算是通过硬件模块实现的,这个硬件模块被称为除法器。
除法器实际上是一个专门用于执行除法运算的电路,它能够以非常高的速度进行除法运算。
在进行除法运算时,STM32将被除数和除数输入到除法器中,经过计算后得到商和余数。
这种硬件实现的除法运算速度非常快,可以满足嵌入式系统对高效运算的需求。
接下来,我们来看一下STM32除法运算的应用场景。
除法运算在嵌入式系统的开发中非常常见,它可以用于各种需要进行数据处理和计算的场景。
例如,在控制系统中,可以通过除法运算来计算传感器数据的比例,从而实现对系统的精确控制;在通信系统中,可以利用除法运算来计算数据的传输速率;在图像处理中,可以通过除法运算来实现图像的缩放、旋转等操作。
总之,STM32的除法运算在嵌入式系统的开发中扮演着重要的角色。
在使用STM32进行除法运算时,还需要注意一些事项。
首先,除数不能为0,否则会导致除法运算错误。
其次,除法运算可能会存在精度丢失的问题,特别是在进行浮点数除法运算时,结果可能会存在舍入误差。
因此,在进行除法运算时,需要根据具体的应用需求来选择适当的数据类型和算法,以保证计算结果的准确性。
此外,还需要注意除法运算的性能消耗,尽量避免在嵌入式系统中频繁地进行大量的除法运算,以免影响系统的实时性能。
STM32除法运算在嵌入式系统的开发中具有重要的作用。
通过硬件实现的除法器,能够以高效的速度进行除法运算,满足嵌入式系统对高效运算的需求。
除法运算在各种数据处理和计算场景中都有广泛的应用,但在使用过程中需要注意除数不能为0、精度丢失的问题以及性能消耗等事项。
只有正确应用和合理使用STM32的除法运算功能,才能更好地完成嵌入式系统的开发任务。
stc32g 硬件乘除法

stc32g 硬件乘除法摘要:1.STC32G 简介2.硬件乘法器3.硬件除法器4.应用实例正文:【1.STC32G 简介】STC32G 是一款高性能、低功耗的32 位单片机,广泛应用于各种嵌入式系统中。
它内部集成了丰富的硬件功能,如硬件乘除法器等,为开发者提供了极大的便利。
【2.硬件乘法器】STC32G 硬件乘法器可以实现两个16 位数据的乘法运算,其运算结果为32 位。
使用硬件乘法器可以大大提高乘法运算的速度,减轻CPU 的负担。
要使用硬件乘法器,需要先设置相应的控制和状态寄存器(CSSR),然后通过指针寄存器(PTR)指向待乘数据。
在完成乘法运算后,结果会自动存储在指定的寄存器中。
【3.硬件除法器】STC32G 硬件除法器可以实现两个16 位数据的除法运算,其运算结果为32 位。
使用硬件除法器同样可以提高除法运算的速度,减轻CPU 的负担。
要使用硬件除法器,需要先设置相应的控制和状态寄存器(CSSR),然后通过指针寄存器(PTR)指向待除数据和商寄存器。
在完成除法运算后,商和余数会自动存储在指定的寄存器中。
【4.应用实例】假设我们要计算两个16 位整数相乘的结果,我们可以按照以下步骤使用STC32G 的硬件乘法器:1.设置CSSR 寄存器,使能硬件乘法器。
2.将待乘数1 和待乘数2 分别存储在指定的寄存器中。
3.设置PTR 寄存器,使其指向待乘数1 和待乘数2。
4.启动硬件乘法器。
5.硬件乘法器完成运算后,结果会自动存储在指定的寄存器中。
通过以上步骤,我们可以轻松地实现硬件乘法器的使用。
同样地,对于硬件除法器,我们也可以按照类似的步骤进行操作。
