串联超前校正课程设计
实验用频率法设计串联超前校正网络备课讲稿

串联超前校正网络对系统性能的影响
,%,c,ts
三、实验内容
系统结构图
设 G0(s)0.2s(0K.3s1) , Gc (s)为超前校正网络。
试设计惯性环节和一个无源串联超前校正装置,要
求系ቤተ መጻሕፍቲ ባይዱ校正后满足下列指标:当r(t)t 时,稳态误
差
ess 0.05
' 55
,相角裕度
四、实验步骤
1. 根据稳态指标的要求确定开环增益K
6. 从两阶系统频率特性表中读取校正后系统的时
域性能指标及截止频率 w c ' 和相角裕度 ' 。
五、实验报告要求
1.根据校正网络的设计要求,写出设计过程及设计 结果。
2.给出经实验调试后的校正装置参数(惯性环节和 校正网络的R、C值)。
3.在同一坐标系上画出系统校正前后的开环Bode图, 分析超前校正的作用及特点。
2.校正方式: ① 串联校正:超前校正、滞后校正、滞后-超 前校正 ② 反馈校正 ③ 前馈校正 ④ 复合校正
3.无源超前校正网络
图1 无源超前网络
超前网络的传递函数为: GC(S)a111aTTSS
式中: a R4 R5 1
R5
T
R4R5 R4 R5
C3
10loga 10loga
' c
m
'
按下图连接超前校正网络电路图 注意:无源串联超前校正网络的增益为1/a,
故应将惯性环节的增益增大为原来a倍,即R3变 为原来的1/a。
超前校正网络电路图
5. 对校正后的系统进行频域特性测试 把设计好的校正网络串联在原系统的A1与
A5之间,测试校证后系统的频域特性。若此时 满足指标要求则记录相应的性能指标,方法同 第二次实验中所述,若不满足要求重新设计校 正网络。
串联超前校正课程设计

串联超前校正课程设计一、课程目标知识目标:1. 让学生掌握串联超前校正的基本概念,理解其在控制系统中的应用和作用。
2. 学会运用数学公式和电路图表达串联超前校正环节,并分析其对系统性能的影响。
3. 掌握串联超前校正参数的设计方法,能够根据特定性能指标完成校正参数的计算。
技能目标:1. 培养学生运用仿真软件进行串联超前校正电路搭建和测试的能力。
2. 提高学生分析控制系统性能、提出改进方案并实施的能力。
3. 培养学生团队协作、沟通表达的能力,能够在小组讨论中分享观点和倾听他人意见。
情感态度价值观目标:1. 激发学生对自动化控制技术的兴趣,培养其探究精神和创新意识。
2. 引导学生认识到科技进步对国家发展的重要性,树立正确的价值观。
3. 培养学生严谨、务实的科学态度,养成良好的学习习惯。
本课程针对高年级学生的认知水平和学习特点,注重理论知识与实践操作的相结合,培养学生的动手能力和创新能力。
通过本课程的学习,使学生能够更好地理解和应用串联超前校正技术,为后续专业课程打下坚实基础。
同时,注重培养学生的团队协作能力和沟通表达能力,提升其综合素质。
1. 理论知识:- 串联超前校正的基本原理及其在自动控制系统的应用。
- 串联超前校正的数学模型及传递函数推导。
- 串联超前校正对系统稳定性、快速性、平稳性等性能的影响。
- 校正参数的设计方法及步骤。
2. 实践操作:- 使用仿真软件(如MATLAB)搭建串联超前校正电路。
- 对搭建的校正电路进行仿真测试,分析校正效果。
- 根据性能指标要求,调整校正参数,优化系统性能。
3. 教学安排与进度:- 理论知识部分:共4课时,分两个阶段进行。
第一阶段(2课时)主要介绍串联超前校正的基本原理、数学模型及传递函数;第二阶段(2课时)讲解校正参数设计方法及性能分析。
- 实践操作部分:共4课时,与理论知识部分同步进行。
学生分小组进行仿真软件操作,教师指导并解答疑问。
4. 教材章节与内容:- 教材第五章:自动控制系统中的校正方法。
自动控制原理课程设计 超前校正

自动控制原理课程设计一. 设计题目1.掌握控制系统的设计与校正方法、步骤。
2.掌握对控制系统的相角裕度、稳态误差、截止频率和动态性能分析。
3.掌握利用matlab 对控制理论内容进行分析。
4.提高大家分析问题解决问题的能力。
二. 题目任务及要求题目1:已知单位负反馈系统被控制对象的开环传递函数()()10+=s s K s G 用串联校正的频率域方法对系统进行串联校正设计。
任务:用串联校正的频率域方法对系统进行串联校正设计,使系统满足如下动态及静态性能指标:(1)在单位斜坡信号作用下,系统的稳态误差rad e ss 151<; (2)系统校正后,相位裕量 45≥γ。
(3)截止频率s rad c /5.7≥ω。
设单位负反馈系统的开环传递函数为)1()(+=s s K s G用相应的频率域校正方法对系统进行校正设计,使系统满足如下动态和静态性能:(1) 相角裕度045≥γ;(2) 在单位斜坡输入下的稳态误差为1.0=sse ; (3) 系统的剪切频率wc <4.4rad/s 。
(4)模值余度h ≥10dBk=10;num1=[1];den1=conv([1 0],[1 1]); sys1=tf(k*num1,den1); figure(1);Margin(sys1);hold onfigure(2);sys=feedback(sys1,1) step(sys)Transfer function:10-------s^2 + s未校正前的Bode图未校正前的的阶跃响应曲线由图可以看出未经校正的Bode图及其性能指标,还有如图(-2)所示的未校正的系统的阶跃响应曲线。
由图(-1)可以看出系统的:模值稳定余度; h=∞dB; -pi穿越频率:Wg=∞dB;相角稳定余度为γ=180剪切频率:Wc=3.08rad/s;由图(-1)可以知道,系统校正前,相角稳定余度=18<45。
为满足要求,开环系剪切频率wc=3.08rad/s<4.4rad/s。
自动控制原理课程设计串联超前滞后校正装置

自动控制原理课程设计报告一、设计目的(1)掌握控制系统设计与校正的步骤和方法。
(2)掌握对控制系统相角裕度、稳态误差、剪切频率、相角穿越频率以及增益裕度的求取方法。
(3)掌握利用Matlab对控制系统分析的技能。
熟悉MATLAB这一解决具体工程问题的标准软件,能熟练地应用MATLAB软件解决控制理论中的复杂和工程实际问题,并给以后的模糊控制理论、最优控制理论和多变量控制理论等奠定基础。
(4)提高控制系统设计和分析能力。
(5)所谓校正就是在系统不可变部分的基础上,加入适当的校正元部件,使系统满足给定的性能指标。
校正方案主要有串联校正、并联校正、反馈校正和前馈校正。
确定校正装置的结构和参数的方法主要有两类,分析法和综合法。
分析法是针对被校正系统的性能和给定的性能指标,首先选择合适的校正环节的结构,然后用校正方法确定校正环节的参数。
在用分析法进行串联校正时,校正环节的结构通常采用超前校正、滞后校正和滞后-超前校正这三种类型。
超前校正通常可以改善控制系统的快速性和超调量,但增加了带宽,而滞后校正可以改善超调量及相对稳定度,但往往会因带宽减小而使快速性下降。
滞后-超前校正兼用两者优点,并在结构设计时设法限制它们的缺点。
二、设计要求(姬松)1.前期基础知识,主要包括MATLAB系统要素,MATLAB语言的变量与语句,MATLAB的矩阵和矩阵元素,数值输入与输出格式,MATLAB系统工作空间信息,以及MATLAB的在线帮助功能等。
2.控制系统模型,主要包括模型建立、模型变换、模型简化,Laplace变换等等。
3.控制系统的时域分析,主要包括系统的各种响应、性能指标的获取、零极点对系统性能的影响、高阶系统的近似研究,控制系统的稳定性分析,控制系统的稳态误差的求取。
4.控制系统的根轨迹分析,主要包括多回路系统的根轨迹、零度根轨迹、纯迟延系统根轨迹和控制系统的根轨迹分析。
5.控制系统的频域分析,主要包括系统Bode 图、Nyquist 图、稳定性判据和系统的频域响应。
实验四:连续系统串联超前校正

实验目的
1. 加深理解串联校正装置对系统动态性 能的校正作用。 2. 对给定系统进行串联校正设计,并通 过模拟实验检验设计的正确性。
实验内容
串联超前校正
系统模拟电路图(含结构图)如下,图中开关S断开对应未校正 情况, 接通对应超前校正:
实验步骤
1.连接被测量典型环节的模拟电路。电路的输入U1接A/D、 D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入。检 查无误后接通电源。
2.开关S放在断开位置。 3.选中 [实验课题→ 连续系统串联校正→超前校正] 菜单项,鼠 标单击将弹出参数设置窗口。系统加入阶跃信号。参数设置完成 后鼠标单击确认测量系统阶跃响应,并记录最大超调量Mp和调节 时间ts。
4.开关S接通,重复步骤3,将两次所测的波形进行比较。 并将测量结 果记入下表中:
超前校正系统 指标
阶跃响应曲线
Mp tp(秒) ts(秒)
校正前
校正后
实验报告
1.计算串联校正装置的传递函数 Gc(s)和校正 网络参数。
2.画出校正后系统的对数坐标图,并求出校 正后系统的ωc及γ 。
3.比较校正前后系统的阶跃响应曲线及性能 指标,说明校正装置的作用。
付出总有回报
祝愿大家不断ቤተ መጻሕፍቲ ባይዱ步!
自控课程设计实验报告串联超前校正滞后装置

课题:串联超前校正滞后装置专业:电气工程及其自动化班级:组长:组员:指导教师:设计日期:成绩:超前校正课程设计报告一、设计目的(1)把握操纵系统设计与校正的步骤和方式。
(2)把握对操纵系统相角裕度、稳态误差、剪切频率、相角穿越频率和增益裕度的求取方式。
(3)把握利用Matlab 对操纵系统分析的技术。
熟悉MATLAB 这一解决具体工程问题的标准软件,能熟练地应用MATLAB 软件解决操纵理论中的复杂和工程实际问题,并给以后的模糊操纵理论、最优操纵理论和多变量操纵理论等奠定基础。
(4)提高操纵系统设计和分析能力。
二、设计要求与内容已知单位负反馈系统的开环传递函数0()(1)(0.251)K G S S S S =++,试用频率法设计串联校正装置,要求校正后系统的静态速度误差系数1v K 5s -≥,系统的相角裕度045γ≥,校正后的剪切频率2C rad s ω≥已知参数和设计要求:1.前期基础知识,要紧包括MATLAB 系统要素,MATLAB 语言的变量与语句,MATLAB 的矩阵和矩阵元素,数值输入与输出格式,MATLAB 系统工作空间信息,和MATLAB 的在线帮忙功能等。
2.操纵系统模型,要紧包括模型成立、模型变换、模型简化,Laplace 变换等等。
3.操纵系统的时域分析,要紧包括系统的各类响应、性能指标的获取、零极点对系统性能的阻碍、高阶系统的近似研究,操纵系统的稳固性分析,操纵系统的稳态误差的求取。
4.操纵系统的根轨迹分析,要紧包括多回路系统的根轨迹、零度根轨迹、纯迟延系统根轨迹和操纵系统的根轨迹分析。
5.操纵系统的频域分析,要紧包括系统Bode图、Nyquist图、稳固性判据和系统的频域响应。
6.操纵系统的校正,要紧包括根轨迹法超前校正、频域法超前校正、频域法滞后校正和校正前后的性能分析。
三、实现进程1、系统概述所谓校正,确实是在系统中加入一些其参数能够依照需要而改变的机构或装置,使系统整个特性发生转变,从而知足给定的各项性能指标。
串联超前校正装置的课程设计

目录一、绪论 (1)二、原系统分析 (1)2.1原系统的单位阶跃响应曲线 (1)2.2原系统的Bode图 (2)2.3原系统的Nyquist曲线 (4)2.4原系统根轨迹 (5)三、校正装置设计 (6)3.1校正装置参数的确定 (6)3.2校正装置的波特图 (7)四、校正后系统的分析 (8)4.1校正后系统的单位阶跃响应曲线 (8)4.2校正后系统的波特图 (9)4.3校正后系统的Nyquist曲线 (10)4.4校正后系统的根轨迹 (11)五、总结 (13)六、参考文献 (13)一、绪论在系统中,往往需要加入一些校正装置来增加系统的灵活性,使系统发生变化,从而满足给定的各项性能指标。
按照校正装置的特性不同,可分为PID 校正、超前校正、滞后校正和滞后-超前校正。
我们在这里讨论串联超前校正。
在直流控制系统中,由于传递直流电压信号,适于采用串联校正。
串联超前校正的基本原理:利用超前网络的相角超前特性。
只要正确的将超前网络的交接频率1/aT 和1/T 选择在带校正系统截止频率的两旁,并适当选取参数a 和T ,就可以校正系统的截止频率和相角裕度满足性能指标的要求,从而改善系统的动态性能。
串联超前校正的优点:保证低频段满足稳态误差,改善中频段,使截止频率增大,相角裕度变大,动态性能提高,高频段提高使其抗噪声干扰能力降低。
有些情况下采用串联超前校正是无效的,它受到以下两个因素的限制: 1.闭环宽带要求。
若待校正系统不稳定的话,为了得到规定的相角裕度,需要超前网络提供很大的相角超前量。
这样的话,超前网络的a 值必须选取的很大,从而造成已校正系统带宽过大,使得通过系统的高频噪声电平很高,很可能使系统失控。
2.在截至频率附近相角迅速减小的待校正系统,一般不宜采用串联超前校J 卜。
因为随着截止频率的增大,待校正系统相角迅速减小,使已校正系统的相角裕度改善不大,很难得到足够的相角超前量,在一般情况下,产生这种相角迅速减小的原因是,在待校正系统的截止频率附近,或有交接频率彼此靠近的惯性环节;或由两个交接频率彼此相等的惯性环节;或有一个震荡环节。
自动控制课程设计--频率法串联超前校正

自动控制课程设计报告题目频率法串联超前校正院系机电工程系专业测控技术与仪器二零一二年十一月目录摘要 (3)1课程设计目的内容及要求................. 错误!未定义书签。
1.1设计目的 ......................... 错误!未定义书签。
1.2设计内容与要求.................... 错误!未定义书签。
1.3课程设计条件...................... 错误!未定义书签。
2系统设计步骤 .......................... 错误!未定义书签。
2.1系统计算 ......................... 错误!未定义书签。
2.2matlab程序运用.................... 错误!未定义书签。
2.3校正前系统bode图及分析........... 错误!未定义书签。
2.4一次校正后的bode图............... 错误!未定义书签。
2.5二次校正后的bode图分析........... 错误!未定义书签。
3小结 .................................. 错误!未定义书签。
参考文献................................ 错误!未定义书签。
摘要利用频率法串联超前校正,可以根据已知传递函数,分析系统是否稳定。
当一个或某些系统参数的变化时,确定闭环极点随参数变化的轨迹,进而研究闭环系统极点分布变化的规律。
应用matlab 仿真,只需进行简单计算就可得知系统一个或某些系统参数变化对闭环极点的影响趋势。
这种定性分析在研究系统性能和提出改善系统性能的合理途径方面具有重要意义。
【关键词】:闭环特征方程,根轨迹,零极点分布,mtlab 仿真一、设计目的:1、了解控制系统设计的一般方法、步骤。
2、掌握对系统进行稳定性分析、稳态误差分析以及动态特性分析的方法。
3、掌握利用MATLAB 对控制理论内容进行分析和研究的技能。
基于频率法串联超前校正课程设计

基于频率法串联超前校正课程设计一、课程标准与设计理念频率法串联超前校正课程是针对电气工程中普遍存在的问题——电气传输中的频率漂移,并采用现代控制理论的超前校正方法来进行纠正的课程。
其设计目的是为了帮助学生掌握电气传输中的关键问题,并提高其在实际应用中的能力。
该课程的核心内容包括频率法的原理、频率漂移的影响、超前校正方法的基本原理、算法设计和实现等。
旨在培养电气工程学生掌握频率法和超前校正技术应用的能力,让其具备在电气工程领域中研究和解决类似问题的能力。
该课程的教学目标主要包括以下几点:1、理解频率漂移及其影响。
通过教学让学生了解频率漂移的概念和机理,及其在电气传输过程中的影响,从而认识到该问题对电气系统运行的重要性。
2、了解频率法的原理和应用。
通过教学使学生了解频率法在电气工程中的基本原理和实际应用,并了解频率法在解决频率漂移问题方面的优势和局限性。
3、掌握超前校正技术的原理和方法。
通过教学使学生了解超前校正技术的基本原理和实现方法,在此基础上逐步掌握频率法串联超前校正方法的基本思路和具体实现过程。
4、培养学生分析问题、设计解决方案的能力。
通过教学帮助学生掌握电气系统中频率漂移问题发生的原因和机理,培养学生在理论和实践中设计和应用超前校正技术解决问题的能力。
二、教学内容与方法1、教学内容:(1)频率漂移的概念和意义。
(2)频率法在电气工程中的基本原理和实际应用。
(3)超前校正技术的基本原理和方法。
(4)频率法串联超前校正技术的设计和实现。
(5)案例分析与实践操作。
2、教学方法:本课程采用课堂讲授、案例分析、练习、模拟实验与实际实验相结合的教学方法。
其中,课堂讲授重点讲述频率法、超前校正技术的基本原理和方法;案例分析和练习则让学生通过具体问题和仿真练习任务,逐步了解和掌握具体应用过程;模拟实验和实际实验则是让学生积累实际操作和实验数据处理的能力,以便于对理论内容进行深入理解和应用。
三、课程评估与改进通过考试、公开报告、教学效果调查等方式,对课程的教学效果进行评估和改进。
串联超前校正系统分析自动控制原理课程设计
一、设计目的1、 通过课程设计进一步掌握自动控制原理课程的相关知识,加深对所学内容的理解,提高解决实际问题的能力。
2、 理解在自动控制系统中对不同的系统选用不同的校正方式,以保证得到最佳的系统;3、 理解相角裕量、稳态误差、穿越频率等参数的含义;4、 学习MATLAB 在自动控制中的应用,会利用MATLAB 提供的函数求出所需要得到的实验结果;5、 从总体上把握对系统进行校正的思路,能够将理论与实际相结合。
二、设计内容与要求 设计内容:1、阅读有关资料。
2、对系统进行稳定性分析、稳态误差分析以及动态特性分析。
3、绘制根轨迹图、Bode 图。
4、设计校正系统,满足工作要求。
设计条件:⊗则已知单位负反馈系统被控制对象的开环传递函数为:()()0.110.011S kG s s s =⨯++对系统进行串联校正任务: (1)()r t t=时,0.004ss e ≤;(2)校正后,相角裕量45r >; (3)30/c w rad s>。
sR设计要求1、能用MATLAB 解复杂的自动控制理论题目;2、能用MATLAB 设计控制系统以满足具体的性能指标;3、能灵活应用MATLAB 的SIMULINK 仿真软件,分析系统的性能。
三、设计原理校正方式的选择,按照校正装置在系统中的链接方式,控制系统校正方式分为串联校正、反馈校正、前馈校正、和复合校正4种。
串联校正是最常见的一种校正方式。
串联校正方式是校正器与受控对象进行串联连接的。
可分为串联超前校正、串联滞后校正和滞后-超前校正。
其一般设计步骤如下:(1)根据静态性能指标,计算开环系统的增益。
之后求取校正前系统的频率特性指标,并与设计要求进行比较;(2)确定校正后期望的穿越频率,具体值得选取与所选择的校正方式相适应; (3)根据待设计的校正环节的形式和转折频率,计算相关参数,进而确定校正环节; (4)得出校正后系统。
检验系统满足设计要求。
四、设计步骤1、校正前的系统分析 时域分析: 其中已知21()R s s =---------------------------------------------------------------------------------①()1H s = ---------------------------------------------------------------------------------②()()()0.110.011kG s s s s =⨯⨯+⨯+ --------------------------------------------------------③根据稳态误差公式1lim ()1()()ss s e R s s G s H s →=⨯⨯+⨯ -------------------------------------------------------④③将①②③带入④式得()211lim1(0.11)0.011ss s e s ks s s s →=⨯⨯+⨯⨯+⨯+化简得出1ss e k =又有题目0.004ss e ≤最后得250k ≥此时取250k =进行分析。
串联超前校正电子教案
上式表明,m 仅与a 值有关,a 值选得越大,则超前网络的微分效应越强。
实际选用的a 值必须 考虑到网络物理结构的限制及附加放大器的放大系数等原因,一般取值不大于20。
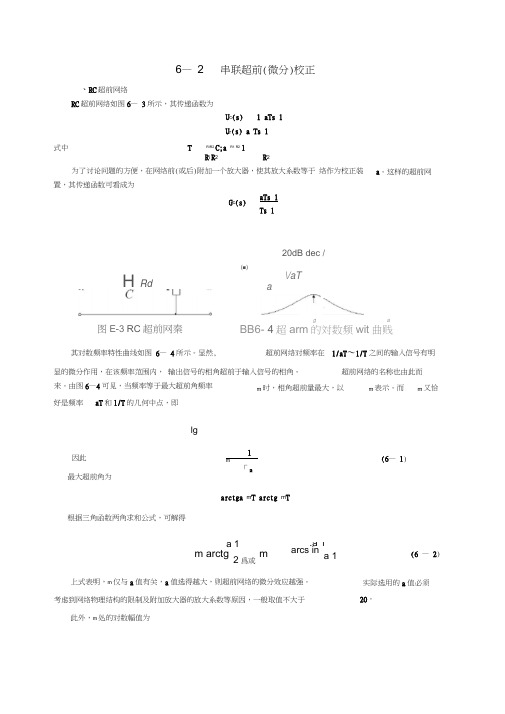
此外,m 处的对数幅值为6— 2串联超前(微分)校正、RC 超前网络RC 超前网络如图6— 3所示,其传递函数为U c (s) 1 aTs 1U r (s) a Ts 1式中TRlR2C;a R1 R2 1R i R 2R 2为了讨论问题的方便,在网络前(或后)附加一个放大器,使其放大系数等于 络作为校正装置,其传递函数可看成为20dB dec /(■)超前网络对频率在 1/aT 〜1/T 之间的输入信号有明显的微分作用,在该频率范围内, 输出信号的相角超前于输入信号的相角。
超前网络的名称也由此而好是频率 aT 和1/T 的几何中点,即lg最大超前角为arctga m T arctg m T根据三角函数两角求和公式,可解得G c (s)aTs 1 Ts 1a 。
这样的超前网\/aT a图E-3 RC 超前网秦g aBB6- 4超arm 的対数频wit 曲贱其对数频率特性曲线如图 6— 4所示。
显然,来。
由图6—4可见,当频率等于最大超前角频率m 时,相角超前量最大,以m 表示。
而m 又恰因此 1m「a(6— 1)a 1m arctg2爲或 m.a 1 arcs ina 1(6 — 2)H Rd裕量G 17。
(3)为了满足指标要求(G 50 ° ),至少需要加入相角超前量 33。
L m 20lg |G c (j m )| 10lgaa 与m 和Iga 的关系曲线如图6- 5所示。
二、串联超前校正利用超前网络进行串联校正的基本原理, 乃是利用超前网络相角超前特性。
只要正确地将超前网络的交接频率1/aT 和1/T 设置在待校正系统截 止频率 c 的两边,就可以使已校正系统的截止 频率c 和相裕量满足性能指标要求,从而达到 改善系统动态性能的目的。
自动控制理论课程设计超前串联校正设计

一.题目004已知单位负反馈系统的开环传递函数为)5.0(4)(0+=S S S G ,试对系统进行超前串联校正设计,使之满足:(1)闭环主导极点的阻尼比ζ=0.5; (2)自然振荡角频率wn=5rad/s ; (3)静态速度误差系数Kv=50rad/s 。
二.校正前系统分析编程绘制其单位阶跃响应曲线,根轨迹,奈氏图如下: num=4;den=conv([1,0],[1,0.5]); G0=tf(num,den); G=feedback(G0,1); figure(1); step(G); figure(2); rlocus(G0); figure(3); nyquist(G0)2.1单位阶跃响应图1..校正前单位阶跃响应由图可知上升时间tr=0.567s,峰值时间tp=1.61s,超调量σ%=67..2%,调节时间ts=14.7s( 2%的允许误差),系统稳态误差ess=0。
2.2根轨迹图图2 闭环根轨迹使系统稳定的根轨迹增益范围为k>0。
3.3奈氏图奈氏图不包括(-1,0),所以系统稳定。
应用Matlab绘制出开环系统Bode图,程序如下:4.4开环波特图num=4;den=conv([1,0],[1,0.5]);w=logspace(-2,3,100);bode(num,den,w);grid on;[mag,phase,w]=bode(num,den,w);magdB=20*log10(mag);[Gm,Pm,Wcg,Wcp]=margin(mag,phase,w) %求系统的幅值裕量、相角裕量及其所对应的频率mr=max(mag) %求谐振峰值wr=spline(mag,w,mr) %求谐振频率运行结果:幅值裕量:Gm = 1.6482e+006幅值裕量:Pm =14.2694穿越频率:Wcg =2.5676e+003剪切频率:Wcp =1.9688谐振峰值:mr = 799.8400谐振频率:wr =0.0100图3 开环波特图校正前系统的相角裕量γ=14.2694°,幅值裕量20lgkg=1.6482*10^6。
用频率法设计串联超前校正

频率法设计串联超前校正河南科技大学课程设计说明书课程名称控制理论课程设计题目用频率法设计串联超前校正学院班级学生姓名指导教师时间控制理论课程设计任务书班级: 姓名: 学号:设计题目: 用频率法设计串联超前校正一、设计目的控制理论课程设计是综合性与实践性较强的教学环节。
其目的要进一步巩固自动控制理论知识,培养所学理论知识在实际中的应用能力;掌握自动控制系统分析、设计和校正的方法;掌握应用MATLAB 语言分析、设计和校正控制系统的方法;培养查阅图书资料的能力;培养使用MATLAB 语言软件应用的能力、培养书写技术报告的能力。
使学生初步掌握控制系统数字仿真的基本方法,同时学会利用MATLAB 语言进行控制系统仿真和辅助设计的基本技能,为今后从事控制系统研究工作打下较好的基础。
二、设计任务及要求应用时域法、频域法或根轨迹法设计校正系统,根据控制要求,制定合理的设计校正方案;编写相关MATLAB 程序,绘制校正前后系统相应图形,求出校正前后系统相关性能指标;比较校正前后系统的性能指标;编制设计说明书。
三、控制要求 设单位负反馈系统的开环传递函数为()(0.11)K G s s s =+,试用频率法设计串联超前校正装置,是系统的相对裕度°45γ≥,静态速度误差系数Kv=200,截止频率不低于15rad/s 。
四、设计时间安排查找相关资料(1天);编写相关MATLAB 程序,设计、确定校正环节、校正(2天);编写设计报告(1天);答辩修改(1天)。
五、主要参考文献[1] 胡寿松. 自动控制原理(第五版), 科学出版社.[2]黄永安,李文成等.Matlab7.0/Simulink6.0应用实例仿真与高效算法开发.北京:清华大学出版社,2008[3] 黄坚主. 自动控制原理及其应用. 北京:高等教育出版社 2004[4].黄忠霖,自动控制原理的MATLAB 实现,国防工业出版社.指导教师签字: 年 月 日摘要通过自动控制原理的学习,我们知道了分析系统的基本方法。
串联超前校正课程设计..

天津城市建设学院课程设计任务书2010 —2011 学年第 2 学期电子与信息工程 系 电气工程及其自动化 专业 08-1 班级课程设计名称: 自动控制原理课程设计设计题目: 串联超前校正装置的设计完成期限:自 2011 年5 月 30 日至 2011 年 6 月 3 日共 1 周设计依据、要求及主要内容: 已知单位反馈系统的开环传递函数为:)104.0(100)(+=s s K s G 要求校正后系统对单位斜坡输入信号的稳态误差01.0≤ss e ,相角裕度 45≥γ,试设计串联超前校正装置。
基本要求:1、对原系统进行分析,绘制原系统的单位阶跃响应曲线,2、绘制原系统的Bode 图,确定原系统的幅值裕度和相角裕度。
3、绘制原系统的Nyquist 曲线。
4、绘制原系统的根轨迹。
5、设计校正装置,绘制校正装置的Bode 图。
6、绘制校正后系统的Bode 图、确定校正后系统的幅值裕度和相角裕度。
7、绘制校正后系统的单位阶跃响应曲线。
8、绘制校正后系统的Nyquist 曲线。
9、绘制校正后系统的根轨迹。
指导教师(签字):教研室主任(签字):批准日期:2011年5月28日目录一、绪论 (2)二、对原系统进行分析 (3)1)绘制原系统的单位阶跃曲线 (3)2)绘制原系统bode图 (3)3)绘制原系统奈式曲线 (4)4)绘制原系统根轨迹 (4)三、校正系统的确定 (5)四、对校正后的装置进行分析 (5)1)绘制校正后系统bode图 (5)2)绘制校正后系统单位阶跃响应曲线 (6)3)绘制校正后的奈式曲线 (7)4)绘制校正后的根轨迹 (7)五、总结 (8)六、附图 (9)参考文献 (15)一绪论所谓校正,就是在系统中加入一些其参数可以根据需要而改变的机构或装置,使系统整个特性发生变化,从而满足给定的各项性能指标。
系统校正的常用方法是附加校正装置。
按校正装置在系统中的位置不同,系统校正分为串联校正、反馈校正和复合校正。
串联超前校正.

R2 (1 R1Curs) R2 R1 R1R2Cs
C R2
R2
R2 R1
1
(1
uRc1RR1C2 s)Cs
1 a
1 aTs 1 Ts
R2 R1
其中
a R1 R2 R2
T R1R2C R1 R2
由:
1 1 aTs Gc (s) a 1 Ts
arcsin
a a
1 1
注:ɑ值选的越大,超前网络的微分效应越强,
但为保持较高的信噪比, ɑ值一般不超过20
ωm 处的对数幅频特性:
Lc () 20log Gc ( jm) 10log a
ɑ与 m 及10lg ɑ的关系曲线
60
50
40
mm ( ) 30
m
10 lg
12
3.串联滞后校正
(2)无源滞后网络
a.无源滞后-超前网络的电路
图
R1
R2
U1
U2
C
b.无源滞后网络的传递函数 两个假设:①输入信号源的内阻为零,②输出
端负载阻抗为无穷大,则其传递函数:
U2 (s) U1 ( s)
Gc (s)
R2
1 sC
R1
R2
1 sC
1 R2Cs 1 (R2 R1)Cs
(c) c (c) c (c) 是根据校正后系统的截止频率的计算值 。
(3)串联滞后校正设计实例
例6-4: 设控制系统如图所示,若要求校正后系统 的 静 态 速 度 误 差 系 数 等 于 30s-1 , 相 角 裕
度 40o ,幅值裕度 hdB 10dB 截止频 率 c 2.3rad / s ,试设计串联无源校正装置。
串联超前校正的设计步骤

串联超前校正的设计步骤引言在工程领域中,为了确保系统的稳定性和性能,需要对系统进行校正。
其中一种常见的校正方法是串联超前校正。
本文将介绍串联超前校正的设计步骤,并详细讨论每个步骤的目标、方法和注意事项。
步骤一:系统分析和建模在进行任何形式的校正之前,首先需要对待校正系统进行全面的分析和建模。
该分析包括确定系统结构、参数和性能指标等。
目标:•理解待校正系统的结构和工作原理。
•理解各个组件之间的相互关系。
•确定待校正系统的参数和性能指标。
方法:1.收集有关待校正系统的技术规格说明书、原理图等资料。
2.绘制待校正系统的框图,标明各个组件之间的连接关系。
3.研究待校正系统中各个组件的功能和特性。
4.测试待校正系统以获取基本性能数据。
注意事项:•对于复杂的系统,可能需要使用计算机辅助设计(CAD)软件来绘制框图。
•在测试期间,确保使用准确和可靠的测试设备和方法。
步骤二:确定校正目标和要求在进行超前校正之前,需要明确校正的目标和要求。
这些目标和要求通常包括系统的稳定性、响应速度、抗干扰能力等。
目标:•确定校正的具体目标和要求。
•确定校正后系统应满足的性能指标。
方法:1.与系统设计人员和用户进行沟通,了解他们对系统性能的期望。
2.根据系统分析结果,确定校正目标和要求。
3.将校正目标和要求以清晰明确的方式记录下来。
注意事项:•在与设计人员和用户沟通时,需要充分理解他们的需求,并将其转化为具体的性能指标。
步骤三:设计串联超前校正器在完成系统分析、建模以及确定校正目标之后,可以开始设计串联超前校正器了。
串联超前校正器是一种用于改善系统响应速度和稳定性的控制器。
目标:•设计一个满足校正目标和要求的串联超前校正器。
•改善系统响应速度和稳定性。
方法:1.根据系统分析结果,选择合适的串联超前校正器类型。
2.根据校正目标和要求,设计串联超前校正器的传递函数。
3.使用数学工具(如MATLAB)进行仿真和优化。
4.根据仿真结果,进一步优化串联超前校正器的设计。
串联超前校正课程设计

电子与电气工程学院课程设计报告课程名称自动控制原理设计题目串联超前校正装置的设计所学专业名称自动化班级自动化133学号2013211269学生姓名指导教师华贵山2015年12月26日电气学院 自动控制原理 课程设计任 务 书设计名称: 串联超前校正装置的设计 学生姓名: 指导教师: 华贵山 起止时间:自 2015 年 12 月 13 日起 至 2015 年 12 月 26 日止一、课程设计目的1、通过课程设计进一步掌握自动控制原理课程的有关知识,加深对所学内容的理解,提高解决实际问题的能力。
2、理解在自动控制系统中对不同的系统选用不同的校正方式,以保证得到最佳的系统。
3、了解控制系统设计的一般方法、步骤。
4、从总体上把握对系统进行校正的思路,能够将理论运用于实际。
二、课程设计任务和基本要求 设计任务:已知单位反馈系统的开环传递函数为:)104.0(100)(+=s s Ks G要求校正后系统对单位斜坡输入信号的稳态误差01.0≤ss e ,相角裕度o 45≥γ,试设计串联超前校正装置。
基本要求:1、对原系统进行分析,绘制原系统的单位阶跃响应曲线,2、绘制原系统的Bode图,确定原系统的幅值裕度和相角裕度。
3、绘制原系统的Nyquist曲线。
4、绘制原系统的根轨迹。
5、设计校正装置,绘制校正装置的Bode图。
6、绘制校正后系统的Bode图、确定校正后系统的幅值裕度和相角裕度。
7、绘制校正后系统的单位阶跃响应曲线。
8、绘制校正后系统的Nyquist曲线。
9、绘制校正后系统的根轨迹。
电气学院自动控制原理课程设计指导老师评价表目录摘要与关键字 (1)1 校正前系统分析 (2)1.1绘制原系统的单位阶跃响应 (2)1.2原系统BODE图的绘制 (3)1.3奈氏曲线 (4)1.4根轨迹 (5)2设计校正装置 (7)2.1校正装置的设计 (7)2.2绘制校正装置的bode图 (7)3对校正后的系统进行分析分析 (9)3.1校正后系统的bode图 (9)3.2校正后的单位阶跃响应 (10)3.3校正后的奈式曲线 (11)3.4绘制校正后的根轨迹 (13)总结 (15)参考文献 (15)串联超前校正装置的设计摘要与关键字摘要:所谓校正,就是在系统中加入一些其参数可以根据需要而改变的机构或装置,使系统整个特性发生变化,从而满足给定的各项性能指标。
串联超前校正设计

目录绪论 (3)1设计题目和设计要求 (4)1.1设计题目 (4)1.1.1题目 (4)1.1.2初始条件 (4)1.1.3设计要求 (4)1.1.4主要任务 (4)2设计原理 (5)2.1滞后-超前校正原理 (5)3设计方案 (7)3.1校正前系统分析 (7)3.1.1确定未校正系统的传递函数 (7)3.1.2未校正系统的伯德图和单位阶跃响应曲线和根轨迹 (7)3.2 未校正系统性能分析 (10)3.2.1未校正系统的相角裕度和幅值裕度 (10)3.2.2分析系统稳定时参数K的取值范围 (10)3.2.3系统的动态性能 (10)3.3方案选择 (10)4设计分析与计算 (11)4.1校正环节参数计算 (11)4.1.1确定系统的开环增益K (11)ϕ (11)4.1.2确定需要增加的超前相角c4.1.3确定校正装置的参数α (11)4.1.1确定校正传递函数 (11)4.2已校正系统传递函数 (11)5已校正系统的仿真波形及仿真程序 (12)5.1已校正系统的根轨迹 (12)5.2已校正系统的伯德图 (13)5.3已校正系统的单位阶跃响应曲线 (14)6系统校正前后图形对比 (15)6.1对比图与程序 (15)6.1.1系统校正前后伯德图 (15)6.1.2系统校正前后阶跃响应曲线 (16)结论 (17)参考文献 (18)附录 (20)总程序 (20)绪论《自动控制原理》在工程应用中有了不可缺少作用,拥有非常重要的地位,一个理想的控制系统更是重要。
然而,理想的控制系统是难以实现的。
要想拥有一个近乎理想的控制系统,就得对设计的控制系统进行校正设计。
对于一个控制系统,要想知道其的性能是否满足工程应用的要求,就得对系统进行分析。
对性能指标不满足要求的系统必须对其校正,目前常用的无源串联校正方法有超前校正、滞后校正和滞后-超前校正。
滞后-超前校正方法融合了超前和滞后校正的特点,具有更好的校正性能。
在校正设计过程中需要利用仿真软件MATLAB绘制系统的伯德图、根轨迹和单位阶跃响应曲线以获得系统的相关参数。
两次串联超前校正

课程设计任务书2012 —2013学年第1学期电子与信息工程系电气工程及其自动化专业 10-1班级课程设计名称:自动控制原理课程设计设计题目:串联超前校正装置的设计完成期限:自 2012年12—月日至2012年12月14日共1周设计依据、要求及主要内容:设单位反馈系统的开环传递函数为:G(s):s(s+1)(0.6s + 1)(0.001s + 1) 要求校正后系统的幅值裕度大于10dB,相角裕度 _40,试设计串联超前校正装置。
基本要求:1、对原系统进行分析,绘制原系统的单位阶跃响应曲线,2、绘制原系统的Bode图,确定原系统的幅值裕度和相角裕度。
3、绘制原系统的Nyquist曲线。
4、绘制原系统的根轨迹。
5、设计校正装置,绘制校正装置的 Bode图。
&绘制校正后系统的Bode图、确定校正后系统的幅值裕度和相角裕度。
7、绘制校正后系统的单位阶跃响应曲线。
8、绘制校正后系统的Nyquist曲线。
9、绘制校正后系统的根轨迹。
指导教师(签字): ____________________________教研室主任(签字):________________________ 批准日期:2012年12月8日目录一、绪论 (3)二、原系统分析 (5)2.1原系统的单位阶跃响应曲线 (5)2.2原系统的Bode图 (5)2.3原系统的Nyquist 曲线 (6)2.4原系统的根轨迹 (6)三、校正装置设计 (7)3.1校正装置参数的确定 (7)3.2校正装置的Bode图 (7)四、校正后系统的分析 (7)4.1 校正后系统的Bode图 (8)4.2二次校正系统分析 (8)五、二次校正后系统的分析 (8)5.1二次校正后系统的Bode图 (9)5.2校正后系统的单位阶跃响应曲线 (9)5.3校正后系统的Nyquist 曲线 (9)5.4校正后系统的根轨迹 (10)六、总结 (10)七、附图 (11)七、参考文献 (16)、绪论完成一个控制系统的设计任务,往往需要经过理论和实践的反复比较才可以 得到比较合理的结构形式和满意的性能,在用分析法进行串联校正时,校正环节的结构通常采用超前校正、滞后校正、滞后超前校正这三种类型,也就是工程上 常用的PID 调节器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津城市建设学院课程设计任务书2010 —2011 学年第 2 学期电子与信息工程 系 电气工程及其自动化 专业 08-1 班级课程设计名称: 自动控制原理课程设计设计题目: 串联超前校正装置的设计完成期限:自 2011 年5 月 30 日至 2011 年 6 月 3 日共 1 周设计依据、要求及主要内容: 已知单位反馈系统的开环传递函数为:)104.0(100)(+=s s K s G 要求校正后系统对单位斜坡输入信号的稳态误差01.0≤ss e ,相角裕度 45≥γ,试设计串联超前校正装置。
基本要求:1、对原系统进行分析,绘制原系统的单位阶跃响应曲线,2、绘制原系统的Bode 图,确定原系统的幅值裕度和相角裕度。
3、绘制原系统的Nyquist 曲线。
4、绘制原系统的根轨迹。
5、设计校正装置,绘制校正装置的Bode 图。
6、绘制校正后系统的Bode 图、确定校正后系统的幅值裕度和相角裕度。
7、绘制校正后系统的单位阶跃响应曲线。
8、绘制校正后系统的Nyquist 曲线。
9、绘制校正后系统的根轨迹。
指导教师(签字):教研室主任(签字):批准日期:2011年5月28日目录一、绪论 (2)二、对原系统进行分析 (3)1)绘制原系统的单位阶跃曲线 (3)2)绘制原系统bode图 (3)3)绘制原系统奈式曲线 (4)4)绘制原系统根轨迹 (4)三、校正系统的确定 (5)四、对校正后的装置进行分析 (5)1)绘制校正后系统bode图 (5)2)绘制校正后系统单位阶跃响应曲线 (6)3)绘制校正后的奈式曲线 (7)4)绘制校正后的根轨迹 (7)五、总结 (8)六、附图 (9)参考文献 (15)一绪论所谓校正,就是在系统中加入一些其参数可以根据需要而改变的机构或装置,使系统整个特性发生变化,从而满足给定的各项性能指标。
系统校正的常用方法是附加校正装置。
按校正装置在系统中的位置不同,系统校正分为串联校正、反馈校正和复合校正。
按校正装置的特性不同,又可分为PID校正、超前校正、滞后校正和滞后-超前校正。
利用超前网络或PD控制器进行串联校正的基本原理,是利用超前网络或PD控制器的相角超前特性采用串联校正装置的优点采用串联超前校正可使开环系统截止频率增大,从而闭环系统带宽也增大,使响应速度加快适用范围应当指出,在有些情况下采用超前校正是无效的,它受以下两个因素的限制:1)闭环带宽要求。
若待校正系统不稳定,为了得到规定的相角裕度,需要超前网络提供很大的相角超前量。
这样,超前网络的a值必须选的很大,从而造成已校正系统带宽过大,使得通过系统的高噪声电平很高,很可能是系统失控。
2)在截止频率附近相角迅速减小的待校正系统,一般不宜采用串联超前校正。
因为随着截止频率的增大,带校正系统相角迅速减小,是以矫正系统的相角裕度改善不大,很难得到足够的相角超前量二对原系统进行分析Ⅰ绘制原系统的单位阶跃响应 已知单位反馈系统的开环传递函数为:)104.0(100)(+=s s K s G 要求校正后系统对单位斜坡输入信号的稳态误差01.0≤ss e ,相角裕度 45≥γ,试设计串联超前校正装置。
Ⅰ对原系统进行分析,绘制原系统的单位阶跃响应曲线由题意可得:e ss =k1001=0.01 取k=1 则原开环传递函数)104.0(100)(+=s s s G ……………………. ① 应用MATLAB 仿真绘制响应图如图(1)所示。
MATLAB 文本如下:校正前单位阶跃响应:num=[100];den=[0.04 1 0];sys=tf(num,den);sys1=feedback(sys,1);t=0:0.01:3;step(sys1,t)hold ongridhold offⅡ原系统BODE 图的绘制)104.0(100)(+=s s s G 典型环节分解;惯性环节 :104.01+s W=04.01=25rad由系统BODE 图得系统截止频率:c w =47 radγ=c w 04.0arctan 90180-︒-︒=︒28 w ϕ=0-x w arctan 90-︒=-180=h ∞;经MATLAB 仿真后的图如图2所示。
其仿真文本为:num=[100];den=[0.04 1 0];sys=tf(num,den);margin(sys)hold ongridhold offⅢ奈氏曲线系统开环传递函数标准形式为G (s )=2500/s(s+25)。
分析:起点:A(w 0→)=∞,Φ(w 0→)=-900终点:A(w ∞→)=0,Φ(w ∞→)=-1800。
与实轴的交点:经计算得G(jw)=-2500J(Jw-25)/[w(w 2+625)]所以与实轴无交点应用MATLAB 仿真绘制Nyquist 曲线如图3所示。
其仿真文本为:num=[100];den=[0.04 1 0];sys=tf(num,den);nyquist(sys)v=[-100,100,-80,80];axis(v)hold onplot([-1],[0],'o')gtext('-1')hold offⅣ根轨迹由公式①可得开环传递函数的标准形式: G s =2500/[s(s+25)]1. 根的起点和终点。
起于开环极点止于开环零点。
2. 根轨迹的分支数n=2,关于实轴对称。
3. 根轨迹的渐近线和交点为:Фa =900,-900,()2/250-=a ϕ=-12.54. 根轨迹在实轴上的分布:(-25,0),x=-12.5。
应用MATLAB 仿真绘制根轨迹图如图2-4所示。
其仿其仿真文本为:根据式①可得MATLAB 文本如下:num=[100];den=[0.04 1 0];sys=tf(num,den);rlocus(sys)hold onplot([0],[0])gtext('0')plot([-2],[0])gtext('-2')plot([-5],[0])gtext('-5')hold off 得根轨迹 零极点分布 如图4所示:V 设计校正装置,绘制校正装置bode 图1)校正装置的设计根据题意:校正后的相角裕度 45≥γ确定需要对系统增加的相位超前量m θ=*γ-γ+(5~12)= ︒45-︒28+︒12=29︒ 11arcsin +-=a a m θ ; 得 a=2.85;计算校正后的截止频率 )('C W L +10log3.76=0; ⇒=c w ''62.6rad ; T a w w m c 1''==;得T=0.0095;应用MATLAB 仿真也能球a=2.85和T=0.0095。
其仿其仿真文本为:num=[100];den=[0.04 1 0];sys=tf(num,den);wm=62.6;l=bode(sys,wm);lwc=20*log10(l);a=10^(-0.1*lwc)T=1/(wm*sqrt(a))确定超前校正网络的传递函数: 10095.01027.010095.010095.0*85.211)(++=++=++=s s s s Ts aT s G C 2)绘制校正装置的bode 图应用MATLAB 仿真绘制根轨迹图如图5所示。
其仿其仿真文本为:um=[0.027 1];den=[0.0095 1];sys=tf(num,den);bode(sys)grid四校正后的系统分析串联校正后的开环传递函数: 10095.01027.0)104.0(100)()(++⨯+=s s s s s G s G C =)10095.0)(104.0()1027.0(100+++s s s s 五校正后系统的bode 图对校正后的开环传递函数的典型环节的分解:①阶微分环节0.027s+1 …………04.3711==Tw rad …………dec db k /20= ②惯性环节 104.01+s ……………2512==Tw rad ………… dec db k /20-= 10095.01+s …………26.10513==Tw rad ………dec db k /20-= 应用MATLAB 仿真绘图,得校正后的bode 图如图6所示,matlab 文本如下: num=[100];den=[0.04 1 0];sys1=tf(num,den);num1=[0.027 1];den1=[0.0095 1];sys2=tf(num1,den1);sys3=sys1*sys2;margin(sys3)grid由bode 图可得:相角裕度:rad w c 6.62==--︒-+︒=c c c w w w 0095.0arctan 04.0arctan 90027.0arctan 180'γ︒≥︒454.50 幅值裕度:设穿越频率为x w ,则有πϕ)12(0074.0arctan 04.0arctan 90028.0arctan +=--︒-=k w w w c c x w ; 得 x w = 10074.01028.0)104.0(100)()(++⨯+=s s s s s G s G C =)10074.0)(104.0()1028.0(100+++s s s s Ⅶ校正后的单位阶跃响应应用MATLAB 仿真绘制阶跃响应如图7: matlab 文本如下 num=[100];den=[0.04 1 0];sys1=tf(num,den);num1=[0.027 1];den1=[0.0095 1];sys2=tf(num1,den1);sys3=sys1*sys2;sys4=feedback(sys3 ,1);t=0:0.01:1;step(sys4,t)Ⅷ校正后的奈式曲线10095.01027.0)104.0(100)()(++⨯+=s s s s s G s G C =)10095.0)(104.0()1027.0(100+++s s s s 对校正后的开环传递函数进行系统分析:起点 ∞==SA 100)0( ︒-=90)0(ϕ 终点 000038.01003)(==∞SA ︒-=∞180)(ϕ与实轴的交点:0对原传递函数化简得)10095.0)(104.0()10095.0)(104.0)(10275.0(100)()(22--+-+=s s s s s s s G s G C 化成频率特性有)10095.0)(104.0()10095.0)(104.0)(1027.0(1002222)(----+=w w w j jw jw jw G W 应用MATLAB 仿真绘图,如图8,matlab 文本如下: num=[100];den=[0.04 1 0];sys1=tf(num,den);num1=[0.027 1];den1=[0.0095 1];sys2=tf(num1,den1);sys3=sys1*sys2;nyquist(sys3)v=[-100,100,-80,80];axis(v)hold onplot([-1],[0],'o')gtext('-1')hold offⅨ绘制校正后的根轨迹=)('s G )10095.0)(104.0()1027.0(100+++s s s s ; 对系统分析如下:开环零点 s=-37 m=1开环极点 s=-105 s=-24.9 s=0 n=3根轨迹数为3渐近线角度 ︒±=-+=9013)12(πϕk 渐近线与实轴交点 45.4613379.24105-=--+-=σ 分离点坐标 3719.2411051+=+++d d d得1.d=15-应用MATLAB绘制根轨迹,如图8所示,matlab文本如下:num=[100];den=[0.04 1 0];sys1=tf(num,den);num1=[0.027 1];den1=[0.0095 1];sys2=tf(num1,den1);sys3=sys1*sys2;rlocus(sys3)六、附图图1 单位阶跃响应曲线图2 原系统bode图图3 原系统奈式曲线零极点分布图4 根轨迹分布图5 校正装置的bode图图6校正后系统bode图图7 校正后的单位阶跃响应图8 校正后的奈式曲线图 9校正后的根轨迹七、总结这次课设的完成是我在最短时间内把真本书浏览一遍,感慨学习动力---只要用心做,我们可以比玩魔兽还沉迷!言归正传,实话说这课设是在两天之内外加半个通宵,回头看还是很有成就感的,从开始的连软件都不会用,到后来的大型复杂的运算,怎么说呢,收获很大。
