奥数-鸡兔同笼问题的四种题型

合集下载

小学四年级上册鸡兔同笼问题数学问题奥数问题

一、判断题：请在正确的说法后面打“√”，在错误的说法后面打“X”。

(1)一个笼子里面有10只鸡，共有20条腿。

（）(2)一个笼子里面有10只兔，一共有40条腿。

（）(3)一个笼子里面有5只鸡和5只兔，-共有30条腿。

（）(4)一个笼子里面有4只鸡和6只兔，一共有28条腿。

（）二、应用题1、有鸡和兔共20只，一共有50只脚,求鸡和兔各有多少只？2.一队猎手一队狗,两队并着-起走，数头共-百六，数脚一共三百九。

求有多少位猎手和多少只狗？3.停车场上汽车和摩托车共有24辆，其中每辆汽车有4个轮子，每辆摩托车有两个轮子，所有车辆共有68个轮子。

那么摩托车和汽车各有多少辆?4、大油瓶一瓶装5千克油。

小油瓶两瓶装一干克油，现有100千克油装了110个瓶，那么大小油瓶各有多少个?5.农场工人上山植树，晴天时每人每天植树20棵，雨天时每人每天植树12棵，工人张宁接连几天共植树112棵，平均每天植树14棵。

张宁植树这些天一共有几个雨天？已知次数学竞赛一共有五题,答对一题得10分，答错一题倒扣5 分，请在下列正确的说法后面打“√”，错误的说法后面打“X"。

(1)答对三题，齐错两题共得30分。

（）(2)答对三题，答错两题共得20分。

（）(3)答对四题，答错一题共得35分。

（）1、一次口算比赛中，规定:答对一题得8分,答错一题扣5分,张华答了18道题,得了92分。

张华在此次比赛中答错了几道题?2.一个生日宴会上，主人订了100箱啤酒，和托运方协商好每箱运费20元如损坏一箱除不给运费外,还要赔偿损失100元，结果托运方只得到了1400元的运费，求损坏了几箱啤酒。

3.某物流公司运800个花瓶，每个花瓶100元,按合同每个运费5元，每损坏一个除不给运费外,还要赔偿花瓶价格的一半,实收运费3780元。

求损坏了几个花瓶。

4.某数学竞赛一-共有10道题。

每做对一题得10分，每做错一题倒扣两分。

小明得64分。

他做错了多少题?5.小毛参加智力竞赛,共20细题。

“鸡兔同笼”问题最常用的四种解题方法练习题(含答案和解析)

“鸡兔同笼”问题最常用的四种解题方法练习题（含答案和解析）鸡兔同笼问题早在1500年前，《孙子算经》中就记载了，小学奥数及小升初考试中经常出现，甚至公务员考试中也会出现。

现面我们就鸡兔同笼相关解法作一简单介绍。

题目：现有一笼子，里面有鸡和兔子若干只，数一数，共有头15个，腿40条，球鸡和兔子各有多少只？（请用尽量多的方法解答）1、金鸡独立法分析：让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即20只脚。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从20里减去头数15，剩下来的就是兔的头数20－15=5只，鸡有20－5=15只。

2、吹哨法分析：假设鸡和兔接受过特种部队训练，吹一声哨，它们抬起一只脚，还有40-15=15只腿在站着，再吹一声哨，它们又抬起一只脚，这时鸡都一屁股坐地上了，兔子还有两只脚立着。

这时还有25-15=10只腿在站着，而这10只腿全部是兔子的，所以兔子有10÷2=5只，鸡有15-5=10只。

3、假设法（1）分析：假设全部是鸡，则有15×2=30条腿，比实际少40-30=10只，一只鸡变成一只兔子腿增加2条，10÷2=5只，所以需要5只鸡变成兔子，即兔子为5只，鸡为15-5=10只。

（2）分析：假设全部是兔子，则有15×4=60条腿，比实际多60-40=20只，一只兔子变成一只鸡腿减少2条，20÷2=10只，所以需要10只兔子变成鸡，即鸡为10只，兔子为15-10=5只。

4、方程法（1）分析：设鸡的数量为x只，则兔子有（15-x）只，有2x+4（15-x）=40，解出x=10，所以有鸡10只，兔子15-10=5只。

（2）分析：设兔子的数量为x只，则鸡有（15-x）只，有4x+2（15-x）=40.解得x=5，所以兔子有5只，鸡有15-5=10只。

试题答案：第1题：正确答案：B 答案解析：第2题：正确答案：C 答案解析：第3题：正确答案：D 答案解析：第4题：正确答案：D 答案解析：第5题：正确答案：A 答案解析：第6题：正确答案：C 答案解析：。

奥数-鸡兔同笼问题的四种题型

鸡兔同笼问题的四种题型（一）常规题例如：有鸡、兔共36只，它们共有脚100只，鸡、兔各是多少只？解一（100-2×36）÷（4-2）=14（只）………兔； 36-14=22（只）………鸡。

解二（4×36-100）÷（4-2）=22（只）………鸡； 36-22=14（只）………兔。

练习与提高：1、现有鸡和兔共35只，合计腿数共100只。

鸡和兔各有多少只？2、2、21枚5分和2分的硬币共6角，其中5分、2分硬币各几枚？3、某人购买1元、8角、4角的邮票20张，共计15元，其中1元与8角邮票的张数相等。

三种邮票各几张？（二）得失问题（鸡兔问题的推广题）：例如：某小学举行一次数学竞赛，共15道题，每做对一题得8分，每做错一题倒扣4分，小明共得了72分。

他做对了几道题？解一（72+4×15）÷（8+4）=11（道）……对题数； 15-11=4（道）……………错题数。

解二（8×15-72）÷（8+4）=4（道）………错题数； 15-4=11（道）……………对题数。

练习与提高：1、一次智力测验有10道题，每答对一道得3分，每答错一道扣2分，小红答完了10道题，只得了20分。

她答对了几道题？2、南城区举行小学数学竞赛共15道题，每做对一题得8分，做错一题倒扣4分，李明共得84分，他做对了几道题？3、给商店运货，规定每件商品运费是4元，如果搬运时损坏商品，每损坏一件不但不给运费还要罚款5元。

结果运了100件商品，得运费220元。

问损坏了多少件商品？（三）巧用和倍解“头和腿差的问题“（总头数和鸡兔脚数的差）：例如：鸡兔同笼，它们一共有100只，而鸡足比兔足多80只。

鸡兔各有多少只？解一：80÷2=40（只）（100-40）÷（2+1）=20（只）…………………………兔； 100-20=80（只）…………………………鸡。

小学奥数鸡兔同笼问题题库学生版

鸡兔同笼问题板块一、两个对象的“鸡兔同笼”【例 1】鸡兔同笼，头共46，足共128，鸡兔各几只？【巩固】点点家养了一些鸡和兔子，同时养在一个笼子里，点点数了数，它们共有35个头，94只脚．问：点点家养的鸡和兔各有多少只？【巩固】鸡兔共有45只，关在同一个笼子中．每只鸡有两条腿，每只兔子有四条腿，笼中共有100条腿．试计算，笼中有鸡多少只？兔子多少只？【巩固】动物园里有一群鸵鸟和大象,它们共有36只眼睛和52只脚，问：鸵鸟和大象各有多少？【巩固】鸡兔同笼，上有35头，下有94足，求笼中鸡兔各几只？【例 2】动物园里养了一些梅花鹿和鸵鸟，共有脚208只，鸵鸟比梅花鹿多20只，梅花鹿和鸵鸟各有多少只？【巩固】一个养殖园内，鸡比兔多36只，共有脚792只，鸡兔各几只？【巩固】鸡兔同笼，鸡、兔共有107只，兔的脚数比鸡的脚数多56只，问鸡、兔各多少只？【巩固】鸡、兔共100只，鸡脚比兔脚多20只.问：鸡、兔各多少只?【巩固】鸡、兔共60只，鸡脚比兔脚多60只．问：鸡、兔各多少只？【巩固】鸡、兔同笼，鸡比兔多26只，足数共274只，问鸡、兔各几只？【巩固】鸡与兔共100只,鸡的脚数比兔的脚数少28.问鸡与兔各几只？【例 3】在一个停车场上，现有车辆41辆，其中汽车有4个轮子，摩托车有3个轮子，这些车共有127个轮子，那么三轮摩托车有多少辆？【巩固】体育老师买了运动服上衣和裤子共21件，共用了439元，其中上衣每件24元、裤子每件19元，问老师买上衣和裤子各多少件？【巩固】小建和小雷做仰卧起坐，小建先做了3分钟，然后两人各做了5分钟，一共做仰卧起坐136次．已知每分钟小建比小雷平均多做4次，那么小建比小雷多做了多少次？【例 4】（中国古代僧粥问题）一百个和尚刚好喝一百碗粥，一个大和尚喝三碗粥，三个小和尚喝一碗粥，那么大和尚有多少个，小和尚有多少个？【巩固】100个和尚140个馍，大和尚1人分3个馍，小和尚1人分1个馍．问：大、小和尚各有多少人？【巩固】100个和尚160个馍，大和尚1人分3个馍，小和尚1人分1个馍．问：大、小和尚各有多少人？【解析】从前有座山，山里有个庙，庙里有许多小和尚，两个小和尚用一根扁担一个桶抬水，一个小和尚用一根扁担两个桶挑水，共用了38根扁担和58个桶，那么有多少个小和尚抬水？多少个挑水？【例 5】工人运青瓷花瓶250个，规定完整运到目的地一个给运费20元，损坏一个倒赔100元．运完这批花瓶后，工人共得4400元，则损坏了多少个？【巩固】乐乐百货商店委托搬运站运送100只花瓶．双方商定每只运费1元，但如果发生损坏，那么每打破一只不仅不给运费，而且还要赔偿1元，结果搬运站共得运费92元．问：搬运过程中共打破了几只花瓶？【巩固】有一辆货车运输2000只玻璃瓶,运费按到达时完好的瓶子数目计算,每只2角,如有破损,破损瓶子不给运费,还要每只赔偿1元.结果得到运费379.6元,问这次搬运中玻璃瓶破损了几只【例 6】（2008年第八届“春蕾杯”小学数学邀请赛决赛）甲、乙两人进行射击比赛，约定每中一发得20分，脱靶一发扣12分，两人各打10发，共得208分，最后甲比乙多得64分，乙打中发。

鸡兔同笼问题的四种题型

鸡兔同笼问题的四种题型各种名称的含意（在鸡兔同笼问题的题目中）高价——兔子的腿数低价——鸡的腿数总物——鸡和兔子的总只数原钱数——鸡和兔子的总腿数低价物——鸡的只数（一）高价物与低价物问题：（高价×总物－原钱数）÷（高价－低价）＝低价物（原钱数－低价×总物）÷（高价－低价）＝高价物例如：有鸡、兔共36只，它们共有脚100只，鸡、兔各是多少只？解一（100-2×36）÷（4-2）=14（只）………兔； 36-14=22（只）………鸡。

解二（4×36-100）÷（4-2）=22（只）………鸡； 36-22=14（只）………兔。

练习与提高：1、现有鸡和兔共35只，合计腿数共100只。

鸡和兔各有多少只？2、21枚5分和2分的硬币共6角，其中5分、2分硬币各几枚？3、一辆汽车从甲地到乙地再开往丙地，共用25小时，甲、丙两地相距900千米，这辆车从甲地到乙地以每小时30千米的速度行驶，从乙地到丙地以每小时40千米的速度行驶，乙地到丙地是多少千米？4、小军要翻过一座山，上午7点上山，每小时行2千米，到达山顶玩了1小时，下山比上山每小时多行3千米。

中午12点到达山下，全程共行了11千米，问上山、下山各行了多少千米？5、一个机关里有14张办公桌，其中有的是一屉桌，有的是二屉桌，有的是三屉桌，这些桌子一共有25个抽屉，一屉桌的张数等于二屉桌和三屉桌的和，三屉桌有多少张？6、某人购买1元、8角、4角的邮票20张，共计15元，其中1元与8角邮票的张数相等。

三种邮票各几张？ 7、某人买四种物品共36件，总共花了100元，这四种物品的单价分别是1元、2元、3元、5元，已知单价1元的物品的件数等于5元的件数，单价2元的件数等于3元的件数。

问买四种物品各几件？8、蜘蛛有8条腿，没有翅膀；蝉有6条腿，1对翅膀；蜻蜓有6条腿，2对翅膀。

现在这三种昆虫共有36只，236条腿和40对翅膀。

鸡兔同笼问题全汇总

鸡兔同笼问题全汇总“鸡兔同笼”是一个古老而有趣的数学问题，常常出现在小学奥数和数学教材中。

它看似简单，却蕴含着丰富的数学思维和解题方法。

接下来，让我们对鸡兔同笼问题来个全面的汇总。

一、鸡兔同笼问题的基本形式通常，鸡兔同笼问题会这样描述：在一个笼子里，有若干只鸡和兔。

从上面数，有若干个头；从下面数，有若干只脚。

问鸡和兔各有多少只？例如：笼子里有若干只鸡和兔，从上面数有 8 个头，从下面数有 26 只脚。

问鸡和兔各有几只？二、常见的解题方法1、假设法假设全是鸡，那么脚的总数就应该是头的数量乘以 2。

如果总脚数比这个假设的脚数多，多出来的就是兔子比鸡多的脚数。

因为每只兔子比每只鸡多2 只脚，所以用多出来的脚数除以2 就得到兔子的数量，再用总数减去兔子的数量就是鸡的数量。

以刚才的例子来说，假设 8 个头全是鸡，那么脚应该有 8×2 ＝ 16 只。

但实际有 26 只脚，多出来 26 16 ＝ 10 只脚。

这 10 只脚就是兔子多出来的，每只兔子比鸡多 2 只脚，所以兔子有 10÷2 ＝ 5 只，鸡就有8 5 ＝ 3 只。

假设全是兔的方法也是类似的，先算出假设全是兔时的脚数，与实际脚数比较，少的部分除以 2 就是鸡的数量。

2、方程法设鸡的数量为 x 只，兔的数量为 y 只。

根据头的数量和脚的数量可以列出两个方程：x ＋ y ＝ 8 （头的总数）2x ＋ 4y ＝ 26 （脚的总数）通过解方程组，可以求出 x 和 y 的值，从而得到鸡和兔的数量。

3、列表法依次列举鸡和兔可能的数量组合，计算对应的脚数，直到找到符合条件的组合。

这种方法比较繁琐，但对于数量较小的情况还是可行的。

三、鸡兔同笼问题的变形1、已知头和脚的数量差比如：笼子里鸡和兔共有 30 个头，鸡脚比兔脚少 20 只，问鸡和兔各有多少只？这种情况下，可以先假设鸡和兔的脚数一样多，然后根据脚数差逐步调整鸡和兔的数量。

2、已知脚和头的数量比例如：笼子里鸡和兔的脚数比是 2:3，头共有 20 个，问鸡和兔各有多少只？可以根据脚数比得出鸡和兔数量的关系，再结合头的数量求解。

六年级奥数——鸡兔同笼(从基础到培优)

3.新思维家教数学竞赛，共有20道题，做对一题得8分，做错一题倒扣4分，维维做完所有题目后最终得112分，他做对多少题目？
4.狗蛋去工地搬运花瓶，共有100个，搬一个花瓶可得运费3 角，但打碎一个花瓶要赔5角，搬运完后，狗蛋共得搬运费 260元。问狗蛋打碎多少个花瓶？
5.狗蛋去灯泡厂上班，工资计件，生产一个合格的灯泡得4元，如果灯泡不合格要扣除15元。狗蛋生产了1000只灯泡，共得 3525元，狗蛋生产了多少个灯泡不合格？
6.一队猎手一队狗，两队并着一起走。数头一共一百六，数脚一共三百九。则有多少猎手多少狗？
三、分组法（腿和）
1.鸡和兔一样多，共有30条腿，那么鸡兔各有几只？
2.鸡和兔一样多，共有48条腿，鸡兔各有几只？
3.鸡兔一样多，共有120条腿，鸡兔各有几只？
分组法（头倍腿和）
4.鸡的数量是兔的2倍，共有80条腿，鸡兔各有多少只？
分组法（头倍‘多或少’腿和）
10.锦鸡是梅花鹿的3倍多2只，数腿共有74条，锦鸡和梅花鹿各有多少只？
11.鸡比兔的2倍多3只，数腿共有78条，鸡兔各有多少只？
12.兔比鸡的2倍多1只，数腿共有94条，鸡兔各有多少只？
分组法（头和腿同）
13.鸡腿和兔腿一样多，鸡和兔共有30只，鸡兔各多少只？
14.鸡腿和兔腿一样多，鸡和兔有24只。鸡兔各有多少只？
15.鸡腿和兔腿一样多，鸡兔共有21只，那么兔有多少只？
分组法（腿倍头和）
16.兔腿是鸡腿的2倍，鸡和兔有40只，鸡兔各有多少只？
17.兔腿是鸡腿的2倍，鸡和兔共有20个头，鸡兔各有多少只？
18.兔腿是鸡腿的4倍，鸡和兔共有30个头，鸡兔各有多少只？
新思维家教
小学奥数--鸡兔同笼

奥数鸡兔同笼问题

奥数鸡兔同笼问题1、有若干只鸡和兔子，它们共有88个头，244只脚，鸡和兔各有多少只？解：我们设想，每只鸡都是“金鸡独立”，一只脚站着；而每只兔子都用两条后腿，像人一样用两只脚站着.现在，地面上出现脚的总数的一半，•也就是244 + 2=122 （只）.在122这个数里，鸡的头数算了一次，兔子的头数相当于算了两次.因此从122减去总头数88,剩下的就是兔子头数122-88=34,有34只兔子.当然鸡就有54只.答：有兔子34只，鸡54只.上面的计算，可以归结为下面算式：总脚数+ 2-总头数二兔子数.2、红铅笔每支0.19元，蓝铅笔每支0.11元，两种铅笔共买了 16支，花了 2.80元.问红、蓝铅笔各买几支？解：以“分”作为钱的单位.我们设想，一种“鸡”有11只脚，一种“兔子”有19只脚，它们共有16个头，280只脚.现在已经把买铅笔问题，转化成“鸡兔同笼”问题了.利用上面算兔数公式，就有蓝笔数=（19x 16-280） + （19-11）=24 + 8=3 （支）.红笔数=16-3=13 （支）.答：买了13支红铅笔和3支蓝铅笔.3、一份稿件，甲单独打字需6小时完成.乙单独打字需10小时完成, 现在甲单独打若干小时后，因有事由乙接着打完，共用了7小时.甲打字用了多少小时？解：我们把这份稿件平均分成30份（30是6和10的最小公倍数），甲每小时打30 + 6=5 （份），乙每小时打30 + 10=3 （份）.现在把甲打字的时间看成“兔”头数，乙打字的时间看成“鸡” 头数，总头数是7.“兔”的脚数是5,“鸡”的脚数是3,总脚数是30,就把问题转化成“鸡兔同笼”问题了.根据前面的公式“兔”数二（30-3X7）・（5-3）=4.5,“鸡”数=7-4.5=2.5,也就是甲打字用了 4.5小时，乙打字用了 2.5小时.答：甲打字用了 4小时30分.4.今年是1998年，父母年龄（整数）和是78岁，兄弟的年龄和是17岁.四年后（2002年）父的年龄是弟的年龄的4倍，母的年龄是兄的年龄的3倍.那么当父的年龄是兄的年龄的3倍时，是公元哪一年？解：4年后，两人年龄和都要加8.此时兄弟年龄之和是17+8=25,父母年龄之和是78+8=86.我们可以把兄的年龄看作“鸡”头数，弟的年龄看作“兔”头数.25是“总头数”.86是“总脚数”.根据公式，兄的年龄是（25X4-86） + （4-3） =14 （岁）.1998年，兄年龄是14-4=10 （岁）.父年龄是(25-14)X4-4=40 (岁).因此，当父的年龄是兄的年龄的3倍时，兄的年龄是(40-10) + (3-1) =15 (岁).这是2003年.答：公元2003年时，父年龄是兄年龄的3倍.5.蜘蛛有8条腿，蜻蜓有6条腿和2对翅膀，蝉有6条腿和1对翅膀.现在这三种小虫共18只，有118条腿和20对翅膀.每种小虫各几只？解：因为蜻蜓和蝉都有6条腿，所以从腿的数目来考虑，可以把小虫分成“8条腿”与“6条腿”两种.利用公式就可以算出8条腿的蜘蛛数二(118-6X18)0(8-6)=5 (只).因此就知道6条腿的小虫共18-5=13 (只).也就是蜻蜓和蝉共有13只，它们共有20对翅膀.再利用一次公式蝉数二（13X2-20）0（2-1） =6 （只）.因此蜻蜓数是13-6=7 （只）.答：有5只蜘蛛，7只蜻蜓，6只蝉.6.某次数学考试考五道题，全班52人参加，共做对181道题，已知每人至少做对1道题，做对1道的有7人，5道全对的有6人，做对7道和3道的人数一样多，那么做对4道的人数有多少人？解：对2道、3道、4道题的人共有52-7-6=39 （人）.他们共做对181Tx7-5X6=144 （道）.由于对2道和3道题的人数一样多，我们就可以把他们看作是对2.5道题的人（（2+3）+2=2.5）.这样兔脚数=4,鸡脚数=2.5,总脚数=144,总头数=39.对4道题的有（144-2.5X39） + （4-1.5） =31 （人）.答：做对4道题的有31人.7.买一些4分和8分的邮票，共花6元8角.已知8分的邮票比4分------------------------------------------------ 百度文库 ---------------------------------------------- 的邮票多40张，那么两种邮票各买了多少张？解一：如果拿出40张8分的邮票，余下的邮票中8分与4分的张数就一样多.（680-8X40） + （8+4） =30 （张），这就知道，余下的邮票中，8分和4分的各有30张.因此8分邮票有40+30=70 （张）.答：买了 8分的邮票70张，4分的邮票30张.也可以用任意假设一个数的办法.解二：譬如，假设有20张4分，根据条件“8分比4分多40张”，那么应有60张8分.以“分”作为计算单位，此时邮票总值是4X20+8X60=560.比680少，因此还要增加邮票.为了保持“差”是40,每增加1 张4分，就要增加1张8分，每种要增加的张数是（680-4X20-8X60） + （4+8） =10 （张）.因此4分有20+10=30 （张），8分有60+10=70 （张）.------------------------------------------------ 百度文库 ----------------------------------------------- 8.一项工程，如果全是晴天，15天可以完成.倘若下雨，雨天一天工程要多少天才能完成？解：类似于例3,我们设工程的全部工作量是150份，晴天每天完成10份，雨天每天完成8份.用上一例题解一的方法，晴天有(150-8X3) + (10+8) = 7 (天).雨天是7+3=10天，总共7+10=17 (天).答：这项工程17天完成.。

[奥数方法]鸡兔同笼问题

一、鸡兔同笼问题例1 笼中有若干只鸡和兔，它们共有50个头和140只脚，问鸡兔各有多少只？兔：鸡：解法1 假设法假设一个未知数是已知的，比如假定50个头全是兔，则共有脚（4×50=）200（只），这与题中已知140只不符，多出（200-140=）60（只），多的原因是鸡当兔后每只鸡多算了2只脚，所以鸡的只数是（60÷2=）30（只），则兔的只数为（50-30＝）20（只）。

这种解法，思路清晰，但较复杂，不便操作。

能不能形象地画个图呢？让我们试试。

解法2 图形法从图中看ACDF的面积＝4×50＝200（只脚），比实际多出GHEF的面积＝200-140＝60（只脚），AB=GH=60÷2=30（只鸡），BC=AC-AB=50-30＝20（只兔）解法2比解法1高级，算理是一样的。

这里答案是图上算出的，显然这两种解法都要用纸和笔。

不用纸和笔肯定是用口诀或易记的公式，这是老公公的传家宝。

解法3 公式法老公公讲：只要用哨子一吹，并喊一声口令：“全体肃立”。

这时每只鸡呈金鸡独立之状，每只兔呈玉兔拜月状，着地的脚数之和有（140÷2＝）70（只），其中鸡的头数与脚数相等，由于每只兔的脚比头数多1，因此兔的头数为（70－50＝）20（个），即兔有20只，则鸡有（50－20＝）30（只）。

这个故事实际上老公公用了如下的公式。

脚数和÷2-头数和=兔子数。

小孙子们听了兴趣为之大增，纷纷叫老公公再出几道题。

老公公又出了（1）30个头，80只脚……。

（兔10，鸡20）。

（2）100只脚，40个头……。

（兔10，鸡30）。

（3）80个头，200只脚……。

（兔20，鸡60）小孙子们个个都愉快地答出来了。

这个公式简洁好用，它是祖代传下来的还是老公公想出来的呢？我们中华文化博大精深，这两种可能性都是有的。

这个公式是碰巧做对还是符合算理的呢？这是十分重要的。

数学家高斯说过：“数学中许多方法与定理是靠归纳发现的，证明只是补行的手续而已。

奥数-鸡兔同笼

鸡兔同笼（17年1月19日）题目一(简单):鸡兔共笼，鸡和兔子总共60只，共有脚160只，鸡兔各几只？题目二(中等难度)鸡兔共笼，鸡比兔子多20只，共有脚160只.问鸡与兔各几只？题目三（进阶思考）有一辆货车运输1000只玻璃瓶,运费计算方式为：完好的瓶子每只2角,如有破损,破损瓶子不仅不给运费,还要每只赔偿1元.结果得到运费176元,问这次搬运中玻璃瓶破损了几只?鸡兔同笼问题（17年12月25日）今天的目标是不用方程解如下问题:足球比赛中，赢一场得3分，平一场得1分，负1场得0分。

有一只足球队，比赛了20场，得分45分，已知该队平的场次和负的场次一样多。

请问：该队赢了多少场？答案：14分析：该问题不用方程很难思考，但由于平和负的场次一样多，问题中其实是两个因素，赢的场次和平的场次。

让人想起鸡兔问题，其实，这道题实质也是鸡兔问题。

先看最原始的鸡兔同笼问题：一个笼子里有一些兔和鸡，共有20个头，56只脚。

请问鸡和兔各有多少只？一个经典的解法是这样的：步骤1：让鸡和兔全部抬起2只脚，共抬起了40只脚；步骤2：剩下16只脚，全部是兔子的，且每个兔子剩2只；所以，兔子有8只，鸡12只。

这个经典的解法中，第一步的实质是假设全部是鸡；第二步的实质是差额部分是兔子造成的。

因此，所有鸡兔问题的解法是这样的：第一步假设全部是其中一个；第二步计算差额部分；最后对照差额做除法。

回到文章开始的题目：考虑赢与平两个种类，第一步：假设全部赢了，得分应是60分；第二步：实际得分45分，差额是15分；由于每平1场就伴随着负1场，得分为1，如果这2场都赢了，得分就是6，因此每平1场，总得分就减少5。

故，平的场次是3=15/5，所以，赢的场次是20-3-3=14。

鸡兔问题（18年2月1日）某商场打折，单价4元的钢笔买3支送1支，单价5元的笔记本买4本送1本。

小明花了400元，得到钢笔和笔记本共118件。

请问其中钢笔和笔记本各多少？答案：钢笔73支，笔记本45本。

鸡兔同笼的9种解法

鸡兔同笼是我国古代著名趣题之一，记载于《孙子算经》之中。

鸡兔同笼问题，是小学奥数的常见题型。

是指已知鸡与兔的总头数和总足数，求鸡和兔各是多少只的应用题。

1、列表法。

2、画图法，画图法也是低年级小朋友很好接受的一个方法，呵呵，画图还可以让数学变得形象化，而且经常画图还有助于创造力的培养！假设14只全部是鸡，先把鸡给画好。

3、金鸡独立法，让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即19只脚。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍。

4、吹哨法。

5、假设法，假设全部是鸡。

6、假设法，假设全部是兔子。

7、特异功能法，鸡有2条腿，比兔子少2条腿，这不公平，但是鸡有2只翅膀，兔子却没有。

假设鸡有特级功能，把两只翅膀变成2条腿，那么鸡也有4条腿。

8、特异功能法，假设每只鸡兔都具有“特异功能”，鸡飞起来，兔立起来，这时立在地上的脚全是兔的。

9、特异功能法，假设孙悟空变成兔子，说“变”，每只兔子又长出一个头来，然后对妖精说“将它劈开”，变成“一头两脚”的两只“半兔”，半兔与鸡都是两只脚。

10、砍足法，假如把每只砍掉1只脚、每只兔砍掉3只脚，则每只鸡就变成了“独角鸡”，每只兔就变成了“双脚兔”。

基本概念：鸡饭同笼问题又称为置换问题、假设问题，就是把假设错的那部分置换出来：基本思路：①假设，即假设某种现象存在（甲和乙一样或者乙和甲•样）：②假设后，发生了和题目条件不同的差，找出这个差是多少：③每个事物造成的差是固定的，从而找出出现这个差的原因：④再根据这两个差作适当的调整，消去出现的差。

基本公式：①把所有鸡假设成兔子：鸡数=（兔脚数X总头数一总脚数）子（兔脚数一鸡脚数）②把所有兔子假设成鸡：兔数=（总脚数一鸡脚数X总头数）子（兔脚数一鸡脚数）关犍问题：找出总量的差与单位量的差。

解决鸡兔同笼一般用“假设法”来求解。

即假设全是鸡或是全是兔，然后根据出现的足数差，推算出鸡或兔的只数。

鸡兔同笼问题4种解题方法

鸡兔同笼问题4种解题方法鸡兔同笼解题方法：1，假设法设全是鸡，则兔的只数为：（总头数×2--总脚数）÷2设全是兔，则鸡的只数为：（总头数x4--总脚数）÷2总只数--鸡只数=兔只数基本原理：总头数x2如果=总脚数，说明全是鸡，如果<总脚数，说明其中有兔，每少2只脚就有1只兔。

总头数×4=总脚数，说明全是兔，如果>总脚数，说明其中有鸡，每多2只就有1只鸡。

2，公式法：总脚数÷2--总头数=兔只数总只数--兔只数=鸡只数基本原理：原来的头总量是鸡头和兔头的总量，脚总量也是鸡脚和兔脚的总量。

用脚总数÷2是按全是鸡来计算的，如果商=总头数，说明全是鸡，如果商>总头数，说明其中有兔。

每多1个头就是1只兔。

因为1只兔有4只脚，前面÷的是2，1只兔就变成2个头，也就多了1个头，所以总脚数÷2--总头数的差是多少就有多少只兔。

3，排除法：（脚总量--总头数x2）÷2=兔只数：总只数--兔只数=鸡只数基本原理：先让每只鸡兔各抬起2只脚，这时鸡无剩下的脚，排除鸡后剩下的脚都是兔的。

前面抬起2只脚，现在每只兔还剩下2只脚。

所以用总脚数--总头数×2的差再÷2就是兔的只数。

4，分组法（1）鸡兔共有100只，鸡脚比兔脚多20只，问鸡兔各有多少只？20÷2=10只100--10=90只兔：90÷（1+2）=30只100--30=70只验算：70×2--30×4=20（2）鸡兔共有90只，鸡的脚比兔的脚少60只，问有鸡兔各几只？60÷4=15只90--15=75只免：75÷（1+2）=25只鸡：75--25=50只验算：50×2=100（25+15）x4=160160--100=60只5，方程法可用一元一次和二元一次方程直接解题。

奥数-鸡兔同笼问题的四种题型

解二（4×36-100）÷（4-2）=22（只）………鸡； 36-22=14（只）………兔。

练习与提高：1、现有鸡和兔共35只，合计腿数共100只。

他做对了几道题？解一（72+4×15）÷（8+4）=11（道）……对题数； 15-11=4（道）……………错题数。

解二（8×15-72）÷（8+4）=4（道）………错题数； 15-4=11（道）……………对题数。

练习与提高：1、一次智力测验有10道题，每答对一道得3分，每答错一道扣2分，小红答完了10道题，只得了20分。

结果运了100件商品，得运费220元。

问损坏了多少件商品？（三）巧用和倍解“头和腿差的问题“（总头数和鸡兔脚数的差）：例如：鸡兔同笼，它们一共有100只，而鸡足比兔足多80只。

鸡兔各有多少只？解一：80÷2=40（只）（100-40）÷（2+1）=20（只）…………………………兔； 100-20=80（只）…………………………鸡。

三年级奥数--鸡兔同笼问题

鸡兔同笼问题1、有鸡兔共20只，脚44只，鸡兔各几只？2、鸡兔同笼，共5个头，16条腿，鸡兔各多少只？3、鸡兔共有14个头，38条腿，有几只鸡？有几只兔？4、蛐蛐和蜘蛛共有12只，腿有82条，蛐蛐和蜘蛛各有几只？5、小强爱好集邮，他用1元钱买了4分和8分的两种邮票，共20张。

那么他买了4分邮票多少张6、刘老师带了51名同学去北海公园划船，共租了10条船．每条大船坐7人，每条小船坐4人，问大船、小船各租几条？7、三年级举行一次数学竞赛，共16道题，每做对一题得6分，每做错一题倒扣3分，小文得了78分，他做对多少道题？8、曾老师带了43名同学去北海公园划船，共租了8条船。

每条大船坐7人，每条小船坐4人，问大船、小船各租几条？所有小船共坐了多少人？9、数学智力题共10道题，每做对一道得10分，做错一道倒扣5分，小兰得了70分，她做对了多少道题？10、曾老师带三年（二）班43名同学栽树，曾老师栽14棵，男生每人栽5棵，女生每人栽2棵，总共栽树160棵，问三年（二）班男生、女生各多少人？11、小红的储钱罐里有面值2元和5元的人民币共65张，总钱数为205元，两种面值的人民币各多少张？12、150个桃子35个猴子吃，大猴子每只吃了6个，小猴子每只吃3个。

大猴子、小猴子各有多少只？大猴子共吃了多少个桃子？13、30枚硬币，由2分和5分组成，共值9角9分，2分硬币有枚，5分有枚。

14、松鼠妈妈采松子，晴天每天可以采9个，雨天每天只能采2个。

她一连23天采了130个松子，这23天有几天晴天，几天雨天？15、小强买回8分邮票和3分邮票共78张，共付出5.59无。

求小强买回这两种邮票各多少张？各付出多少钱？16、二小有象棋、跳棋共28副，恰好可供120个学生同时进行活动。

2人下一副象棋，6人下一副跳棋。

那么象棋和跳棋各有多少副？17、蜘蛛有8条腿，蝴蝶有6条腿和2对翅膀，蝉有6条腿和一对翅膀，现有这三种动物共21只，共140条腿和23对翅膀，问蜘蛛、蝴蝶、蝉各有几只?18、某人买了甲乙两种戏票共30张，付了195元，甲种票每张7元，乙种票每张6张。

小学生奥数鸡兔同笼问题(精选)

1.小学生奥数鸡兔同笼问题1、鸡兔同笼，鸡兔共35个头，94条腿，问鸡兔各多少只？2、鸡兔同笼，鸡比兔多15只，鸡兔共有脚132只，问鸡兔各多少只？3、鸡兔同笼，鸡兔共40个头，鸡脚比兔脚共多32只，问鸡兔各多少只？4、鸡兔同笼，鸡比兔多10只，但脚却比兔子少60只，问鸡兔各多少只？5、鸡兔同笼，鸡比兔多10只，鸡脚比兔脚多10只，问鸡兔各多少只？6、在一个停车场内，汽车、摩托车共停了48辆，其中每辆汽车有4个轮子，每辆摩托车有3个轮子，这些车共有172个轮子，停车场内有汽车、摩托车各多少辆？7、张大妈养鸡兔共200只，鸡兔足数共560只，求鸡兔各有多少只？8、张大妈家养的鸡比兔多13只，兔足比鸡足少16只，求鸡兔各有多少只？9、鹤龟同池，鹤比龟多12只，鹤龟足共72只，求鹤龟各有多少只？10、小刚买回8分邮票和4分邮票共100张，共付出6.8元，问，小刚买回这两种邮票个多少张？各付出多少元？2.小学生奥数鸡兔同笼问题1、鸡兔同笼，共有头30个，足86只，求鸡兔各有多少只？2、有20张5元和10元的人民币，一共是175元，5元和10元的人民币各有多少张？3、王老师圆珠笔和钢笔共买了15枝，圆珠笔每枝1.5元，钢笔每枝4.5元，共花了49.5元，圆珠笔和钢笔各买了多少枝？4、鸡兔同笼，鸡兔共35个头，94条腿，问鸡兔各多少只？5、在一个停车场内，汽车、摩托车共停了48辆，其中每辆汽车有4个轮子，每辆摩托车有3个轮子，这些车共有172个轮子，停车场内有汽车摩托车各多少辆？6、小刚买回8分邮票和4分邮票共100张，共付出6.8元，问，小刚买回这两种邮票各多少张？7、在知识竞赛中，有10道判断题，评分规定：每答对一道题的两分，答错一道题要倒扣一分。

小明答了全部题目，但最后只得了14分，他答错几题？8、某运输队为超市运送暖瓶500箱，每箱装有6个暖瓶。

已知每10个暖瓶的运费为5元，损坏一个不但不给运费还要赔10元，运后结算时，运输队共得1350元的运费。

四年级奥数鸡兔同笼考点类型全包括

四年级奥数鸡兔同笼考点类型考点1：常规考法方法总结：1、砍腿法：假如把每一只动物都砍掉两条腿，那么此时还剩下的腿都是兔子的腿，每只兔子剩两条腿。

那么，兔的数量=剩下的腿➗2 鸡的数量=总头数➖兔的数量2、假设法：基本关系式是（1）如果假设全是兔，那么鸡的数量=（每只兔子的脚数×鸡兔总数➖实际的脚数）➗（每只兔子的脚数➖每只鸡的脚数）（2）如果假设全是鸡，那么兔的数量=（实际脚数➖每只鸡脚数×鸡兔总数）➗（每只兔子脚数➖每只鸡的脚数）例1 张大伯养鸡和兔一共有20只，脚一共有62只，求鸡和兔各有多少只？例2 鹤龟同池，一共有35个头，94只脚，问鹤与龟各多少只？例3 在一个停车场，共有车辆30辆，其中汽车有4个轮胎，摩托车有3个轮胎，这些车辆一共有110个轮胎，问摩托车有多少辆？例4 小松鼠采松果，晴天每天可以采10个，雨天每天只能采6个，它连着几天一共采了80个松果，平均每天采8个，那么其中有几天是晴天？练1：鸡兔共有36只，它们共有脚100只，鸡、兔各有多少只？练2：人民中学一共有30间宿舍，大宿舍每间住6人，小宿舍每间住4人，已知这些宿舍中一共住了168名同学，那么其中有多少间大宿舍？练3：童童家有8分的邮票和4分的邮票共有100张，总共价值6.8元，问，童童有这两种邮票各多少张？练4：小浩计划用几天的时间把112页字帖全部写完，这样下来平均每天要写14页，妹妹不在家的时间小浩一天可以写20页，妹妹在家的时候小浩每天只能写14页，那么其中有几天妹妹在家呢？考点2：“倒扣”问题例1：新世界百货超市委托搬运公司搬运泥罐，双方约定每只运费0.24元，但是如果发生损坏，那么每打破一只不仅不给运费，而且还要赔偿1.26元，结果搬运公司一共获得运费115.5元。

问：搬运过程中共打破了几只花瓶？例2：天台小学有3名同学参加灯谜比赛，一共有10道题，猜对一道得10分，猜错一道不但不得分，反而还要扣3分，这3名同学都猜了所有的题，小童得了74分，浩浩得了22分，丽丽得了87分，请问他们三人各猜对了多少道题？练1：在一次数学比赛中，有10道判断题，规定：每答对一道题得2分，答错或不答要倒扣一分，浩浩最后只得了14分，请问浩浩答错了几道题？练2：灯泡厂生产灯泡的工人，按得分的多少给工资，每生产一个合格品得4分，每生产一个不合格的产品不仅不得分，还要倒扣15分，某工人生产了1000只灯泡，共得3525分，请问这个工人生产的灯泡中有多少个不合格？练3：一次数学禁赛共有20道题。

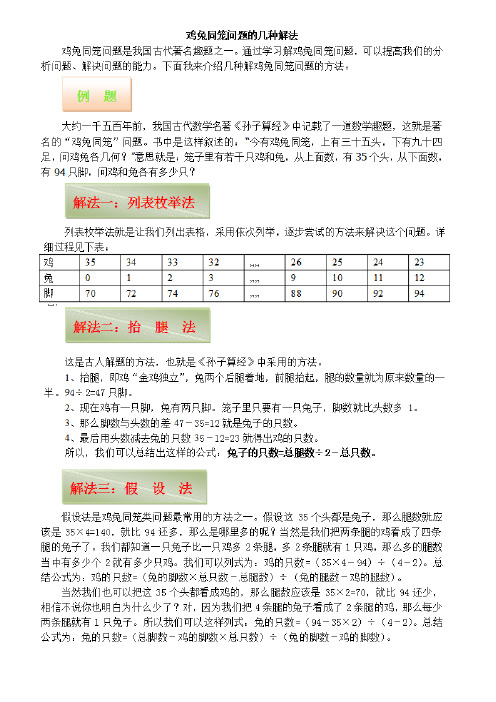
奥数-鸡兔同笼问题的四种题型

小学四年级上册鸡兔同笼问题数学问题奥数问题

“鸡兔同笼”问题最常用的四种解题方法 练习题(含答案和解析)

奥数-鸡兔同笼问题的四种题型

小学奥数鸡兔同笼问题题库学生版

鸡兔同笼问题的四种题型

鸡兔同笼问题全汇总

六年级奥数——鸡兔同笼(从基础到培优)

奥数鸡兔同笼问题

[奥数方法]鸡兔同笼问题

奥数-鸡兔同笼

鸡兔同笼的9种解法

鸡兔同笼问题4种解题方法

奥数-鸡兔同笼问题的四种题型

三年级奥数--鸡兔同笼问题

小学生奥数鸡兔同笼问题(精选)

四年级奥数鸡兔同笼考点类型全包括

“鸡兔同笼”问题最常用的四种解题方法练习题(含答案和解析)