(完整word版)湘教版七年级数学下第四章《相交线与平行线》基础卷含答案,推荐文档
湘教版七年级下册数学第4章 相交线与平行线含答案【参考答案】
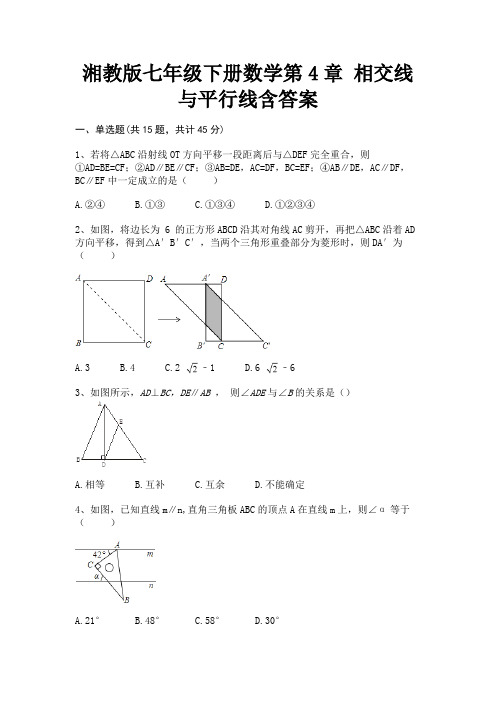
湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题,共计45分)1、若将△ABC沿射线OT方向平移一段距离后与△DEF完全重合,则①AD=BE=CF;②AD∥BE∥CF;③AB=DE,AC=DF,BC=EF;④AB∥DE,AC∥DF,BC∥EF中一定成立的是()A.②④B.①③C.①③④D.①②③④2、如图,将边长为 6 的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD 方向平移,得到△A′B′C′,当两个三角形重叠部分为菱形时,则DA′为()A.3B.4C.2 ﹣1D.6 ﹣63、如图所示,AD⊥BC,DE∥AB,则∠ADE与∠B的关系是()A.相等B.互补C.互余D.不能确定4、如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α等于()A.21°B.48°C.58°D.30°5、如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则()A.点B到AO的距离为sin54°B.点B到AO的距离为tan36°C.点A到OC的距离为sin36°sin54°D.点A到OC的距离为cos36°sin54°6、如图,下列不能判定AB∥CD的条件是()A.∠B+∠BCD=180°B.∠1=∠2C.∠3=∠4D.∠B=∠57、如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=()A.30°B.60°C.90°D.120°8、如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=27°,则∠2的度数是()A.53°B.63°C.73°D.83°9、直线AB上有一点O,OM⊥AB于O,另有直角∠COD在平角∠AOB内绕O点左右摆动(OC与OA,OD与OB不重合),在摆动时,始终与∠MOD保持相等的角是()A.∠BODB.∠AOCC.∠COMD.没有10、如图中直线l1, l2被l3所截,则同位角有()对.A.1对B.2对C.3对D.4对11、有下列命题:①两点之间,线段最短;②相等的角是对顶角;③当a≥0时,|a|=a;④内错角互补,两直线平行.其中是真命题的有()A.1个B.2个C.3个D.4个12、如图,某天然气公司的主输气管道从A市的北偏东方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东方向,测绘员由A 处沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西方向,试在主输气管道上寻找支管道连接点N,使点N到该小区铺设的管道最短,此时铺设的管道的最短距离约是().(参考数据:,)A.366米B.650米C.634米D.700米13、如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠AOF=25°,求∠CDO 的度数()A.50°B.45°C.35°D.65°14、如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于()A.40°B.45°C.50°D.55°15、下列命题:①对顶角相等;②垂直于同一条直线的两条直线平行;③过一点只有一条直线与已知直线平行;④过一点只有一条直线与已知直线垂直;⑤垂线段最短.正确的个数有()A.1 个B.2 个C.3 个D.4 个二、填空题(共10题,共计30分)16、如图,在四边形ABCD中,∠B=120°,∠B与∠ADC互为补角,点E在BC 上,将△DCE沿DE翻折,得到△DC′E,若AB∥C′E,DC′平分∠ADE,则∠A 的度数为________°.17、如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是________18、如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.若∠En=1度,那∠BEC等于________度19、如图,a∥b,∠1=76°,∠3=72°,则∠2的度数是________.20、如图,,点E在线段BC上.若,,则的度数为________.21、如图,已知矩形纸片的一条边经过一个含30°角的直角三角尺的直角顶点,矩形纸片的一组对边分别与直角三角尺的两边相交,∠2=115°,则∠1的度数是________.22、如图所示,若FE∥ON,OE平分∠MON,∠FEO = 28°,则∠MFE =________.23、如图,两个直角三角板ABC与CDE按如图所示的方式摆放,其中∠B=∠D=30°,∠ACB=∠ECD=30°,,且、、共线,将沿DC方向平移得到,若点落在上,则平移的距离为________.24、如图,已知AE//BD,∠1=3∠2,∠2=26°,则∠C=________25、如图所示,已知∠C=100°,若增加一个条件,使得AB∥CD,试写出符合要求的一个条件________.三、解答题(共5题,共计25分)26、如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.27、如图,,,试说明:.28、如图,∠ABC=∠ADE,∠1+∠2=180°, ∠BEC=80°,将求∠CGF的过程填写完整.解:因为∠ABC=∠ADE,所以BC∥①(②).所以∠2=③又因为∠1+∠2=180°,所以∠1+④=180°.所以BE∥GF(⑤).所以∠CGF=⑥(⑦).因为CEB=80°,所以∠CGF=⑧.29、对于同一平面内的三条直线abc给出下列五个判断(1)a‖b;(2)b‖c ;(3)a⊥b ;(4)a∥c ;(5)a⊥c,以其中两个论断为条件,一个论断为结论,组成一个正确的命题。
湘教版七年级下册数学第4章 相交线与平行线含答案

湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题,共计45分)1、下列命题正确的是( )A.两直线与第三条直线相交,同位角相等B.两直线与第三条直线相交,内错角相等C.两直线平行,内错角相等D.两直线平行,同旁内角相等2、如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于()A.75B.100C.120D.1253、将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为()A.3cmB.6cmC.3 cmD.6 cm4、下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是()A. B. C. D.5、如图,如果AB∥DE,那么∠BCD=( )A.∠2=∠1B.∠1+∠2C.180°+∠1-∠2D.180°+∠2-2∠16、在同一平面内,不重合的两条直线的位置关系有()A.平行和相交B.平行和垂直C.平行、垂直和相交D.垂直和相交7、如图,AB∥CD,直线l分别与AB、CD相交,若∠1=120°,则∠2=()A.30°B.50°C.60°D.120°8、如图,在矩形ABCD中,AB=10, BC=5 .若点M、N分别是线段ACAB上的两个动点,则BM+MN的最小值为()A.10B.8C.5D.69、如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠4B.∠D=∠DCEC.∠1=∠2D.∠D+∠ACD=180°10、如图,在平行线l1, l2之间放置一块直角三角板,三角板的锐角顶点A,B分别在直线l1, l2上,若∠1=55°,则∠2的度数是()A.25°B.30°C.35°D.40°11、如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE与AD相交于点F,∠EDF=38°,则∠DBE的度数是()A.25°B.26°C.27°D.38°12、已知三角形的三个顶点坐标分别是,把运动到一个确定位置,在下列各点坐标中,()是平移得到的.A. B. C.D.13、如图,已知直线a、b被直线c所截,那么∠1的同位角是()A.∠4B.∠3C.∠2D.∠514、下列说法正确的是( )A.两条平行线之间的距离是两平行线上任意两点之间的距离B.平行线中一条直线上的任一点到另一条上任意一点的距离都相等C.两条平行线间的距离是定值,等于其中一条直线上的点到另一条直线的距离D.平移已知直线,使所得像与已知直线的距离为3cm,这样的像只有1个15、如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为()A.30°B.35°C.40°D.45°二、填空题(共10题,共计30分)16、如图,CE是△ABC外角的平分线,且AB∥CE,若∠ACB=36°,则∠A等于________度.17、如图,在中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD 和AC上的动点,则PC+PQ的最小值是________.18、如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=3cm,则PC的长为________cm.19、如图,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,则∠BOE=________度,∠AOG=________度.20、如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为________ .21、把一个直角三角板(,)如图放置,已知∥ ,平分,则=________22、∵a∥b,a∥c(已知)∴b∥c理由是________.23、如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2=________.24、如图,如果∠________=∠________,可得AD∥BC.25、如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD的度数为________.三、解答题(共5题,共计25分)26、如图,将△ABC绕点C顺时针旋转90°后得△DEC,若BC∥DE,求∠B的度数.27、已知:如图,a//b,∠1=55°,∠2=40°,求∠3和∠4的度数.28、如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BF=DE. 求证:AE∥CF.29、如图,AB∥CD,E为AC上一点,∠ABE=∠AEB,∠CDE=∠CED.求证:BE⊥DE.30、已知,如图,,垂足分别为、,,试说明.将下面的解答过程补充完整,并填空(理由或数学式)解:∵ ,(_▲_),∴ _▲_(__▲_),∴ __▲_(_▲_)又∵ (已知),∴ _▲_(_▲_),∴ _▲_(__▲_),∴ (_▲__)参考答案一、单选题(共15题,共计45分)1、C2、B3、D4、A5、C6、A7、C8、B9、C10、C11、B12、D13、C14、C15、B二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
湘教版七年级下《相交线与平行线》单元测试卷含答案

第 4 章订交线与平行线单元测试卷一、选择题 ( 每题 2 分, 共 20 分)1. 如图 , 直线 a,b 被直线 c 所截 , ∠ 1 与∠ 2 的地点关系是 ()A. 同位角B. 内错角C.同旁内角D.对顶角2. 如图 ,AB∥CD,AD均分∠ BAC,若∠ BAD=65°, 那么∠ ACD的度数为 ()A.40°B.35°C.50°D.45°3.如图 ,AB∥EC,以下说法不正确的选项是 ()A. ∠B=∠ECDB.∠A=∠ECDC. ∠B+∠ECB=180°D. ∠A+∠ B+∠ACB=180°4.如图 , 在俄罗斯方块游戏中 , 出现一小方块拼图向下运动 , 经过平移运动拼成一个完好的图案 , 最后全部图案消逝 , 则对小方块进行的操作为 ()A. 向右平移 1 格再向下B. 向右平移 3 格再向下C.向右平移 2 格再向下D. 以上答案均可5.以下图 ,3 块同样的三角尺拼成一个图形 , 图中有好多对平行线 , 此中不可以由下边的依据得出两直线平行的是 ()A. 同位角相等 , 两直线平行B. 内错角相等 , 两直线平行C.平行于同向来线的两直线平行D.垂直于同向来线的两直线平行6.如图 , 直线 AB∥CD,AE均分∠ CAB,AE与 CD订交于点 E, ∠ACD=40°, 则∠ BAE的度数是()A.40°B.70°C.80°D.140°7. 同一平面内的四条互不重合的直线知足a⊥ b,b ⊥c,c⊥d, 则以下各选项中关系能建立的是()A.a ∥dB.a⊥ cC.a⊥dD.b⊥d8. 如图 ,AB∥EF,CD⊥ EF,∠BAC=50°, 则∠ ACD=()A.120°B.130°C.140°D.150°9. 如图 ,AD 是∠ EAC的均分线 ,AD∥ BC,∠B=30°, 则∠ C为()A.30°B.60°C.80°D.120°10.如图 , 把一块含有 45°角的直角三角尺的两个极点放在直尺的对边上 . 假如∠1=20°, 那么∠ 2 的度数是 ()A.30°B.25°C.20°D.15°二、填空题 ( 每题 3 分, 共 21 分)11.以下图 , 某地一条小河的两岸都是直的 , 小明和小亮分别在河的两岸 , 他们拉紧了一根细绳 , 当测出∠ 1 和∠ 2 知足关系 ________时 , 河岸的两边才是平行的. 12.同一个平面内的三条直线两两订交 , 最多有 a 个交点 , 最罕有 b 个交点 , 则a+b=________.13.在丈量跳远成绩时 , 从落地址到起跳线所拉的皮尺应该与起跳线 ________.14.如图 , 在三角形 ABC中,BC=5 cm,将三角形 ABC沿 BC方向平移至三角形 A'B'C' 的地点时 ,B'C=3 cm, 则三角形 ABC平移的距离为cm.15.如图是我们常用的折叠式小刀, 刀柄外形是一个长方形挖去一个小半圆, 此中刀片的两条边沿线可当作两条平行的线段 , 转动刀片刻会形成以下图的∠ 1 与∠2, 则∠1 与∠ 2 的度数和是度.16. 如图 , 直线 l 1∥ l 2, ∠α =∠β , ∠1=40°, 则∠ 2=°.17. 以下图 , 第 1 个图案是由黑白两种颜色的六边形地面砖构成的 , 第 2 个, 第 3 个图案能够当作是第 1 个图案经过平移而得 , 那么第 2015 个图案中有白色六边形地面砖块.三、解答题 (22~24 题每题 9 分, 其他每题 8 分, 共 59 分)18.如图 , 在一条公路 l 的双侧有 A,B 两个乡村 .(1)此刻镇政府为民服务 , 沿公路开通公共汽车 , 同时修筑 A,B 两个乡村到公路的道路 , 要使两个乡村村民搭车最为方便 , 请你设计道路路线 , 在图中画出 ( 注明① ), 并标出公共汽车停靠点的地点 , 说出你这样设计的原因 ;(2)为方便两村物流互通 ,A,B 两村计划合资修筑一条由 A 村抵达 B 村的道路 , 要使两个乡村物流、通行最为方便 , 请你设计道路路线 , 在图中画出 ( 注明② ), 说出你这样设计的原因 .19. 以下图 ,AB∥ CD,AE交 CD于点 C,DE⊥AE,垂足为 E, ∠A=37°, 求∠ D的度数 .20. 如图 ,CD⊥ AB,EF⊥AB,∠ E=∠EMC,说明 :CD 是∠ ACB的均分线 .21.如图 , 已知点 A,O,B 在同向来线上 ,OC 是从点 O出发的随意一条射线 ,OD 是∠AOC的均分线 ,OE 是∠ COB的均分线 , 试确立 OD和 OE的地点关系 , 并说明原因 .22. 如图 , ∠E=∠3, ∠ 1=∠2, 试说明 : ∠ 4+∠BAP =180°.23.以下图 , 潜望镜中的两个镜子是相互平行搁置的 , 光芒经过镜子反射时 , 入射光芒与平面镜的夹角等于反射光芒与平面镜的夹角 ( ∠ 1=∠2, ∠ 3=∠ 4). 请说明为何进入潜望镜的光芒和走开潜望镜的光芒是平行的 .24.如图 , 直线 AC∥ BD,连结 AB,直线 AC,BD及线段 AB把平面分红①②③④四个部分, 规定 : 线上各点不属于任何部分 . 当动点 P 落在某个部分时 , 连结 PA,PB,构成∠PAC,∠APB,∠PBD三个角 .(1) 当动点 P 落在第①部分时 , 如图① , 试说明 : ∠ APB=∠PAC+∠PBD;(2) 当动点 P 落在第②部分时 , 如图② , ∠APB=∠PAC+∠PBD能否建立 ?若不建立 , 请说明原因 .参照答案一、 1. 【答案】 B 2. 【答案】 C3.【答案】 B解:依据两直线平行 , 同位角相等 , 得出 A 正确 ; 依据两直线平行 , 同旁内角互补 , 得出 C 正确 ; 依据两直线平行 , 内错角相等 , 得出∠ A=∠ ACE,而∠ ACE+∠ B+∠ACB=180°, 则∠ A+∠ B+∠ACB=180°. 得出 D 正确 . 应选 B.4.【答案】 C5. 【答案】 C6. 【答案】 B7.【答案】 C 8. 【答案】 C 9. 【答案】 A 10. 【答案】 B 二、11. 【答案】∠ 1=∠ 212.【答案】 4解: a=3,b=1.13. 【答案】垂直16. 【答案】 14014. 【答案】 215. 【答案】17. 【答案】 806290三、18. 解 :(1) 绘图如图图, 两点之间 , 线段最短 .,P,Q即为公共汽车停靠点的地点垂线段最短;(2)绘图如19.解: 由于 AB∥ CD,因此∠ ECD=∠A=37°, 又由于 DE⊥AE,因此∠ CED=90°, 因此∠D=180° - 90° - 37°=53°.20.解: 由于 CD⊥AB,EF⊥AB,因此 CD∥ EF(垂直于同向来线的两直线平行 ).因此∠ E=∠ BCD(两直线平行 , 同位角相等 ), ∠ EMC=∠ACD(两直线平行 , 内错角相等), 又由于∠ E=∠ EMC,因此∠ BCD=∠ ACD(等量代换 ).因此 CD是∠ ACB的均分线 ( 角均分线定义 ).21. 解:OD 和 OE相互垂直 , 即 OD⊥OE.原因以下 : 由于点 A,O,B 在同向来线上 , 因此∠ AOB=180°. 又由于 OD是∠ AOC的均分线 ,OE 是∠ COB的均分线 , 因此∠ DOC= ∠AOC,∠COE= ∠COB所.以∠ DOE=∠DOC+∠COE= ( ∠AOC+∠COB)= ∠AOB= ×180°=90°, 因此 OD⊥ OE.22.解: 由于∠ ENM=∠ 3( 对顶角相等 ), ∠E=∠3( 已知 ),因此∠ ENM=∠ E(等量代换 ),因此 AE∥ HM(内错角相等 , 两直线平行 ).因此∠ EAM=∠ AMH(两直线平行 , 内错角相等 ).又由于∠ 1=∠ 2,因此∠ EAM+∠ 1=∠ AMH+∠2( 等式性质 ),即∠ BAM=∠AMC.因此 AB∥ CD(内错角相等 , 两直线平行 ).因此∠ AMD+∠BAP=180°( 两直线平行 , 同旁内角互补 ).由于∠ 4=∠AMD(对顶角相等 ),因此∠ 4+∠BAP=180°( 等量代换 ).23.解: 依据题意 , 作出以下图的几何图形 , 已知 :AB∥ CD,∠1=∠ 2, ∠3=∠4.试说明 :EF∥GH.说明过程 : 由于 AB∥CD(已知 ),因此∠ 2=∠3( 两直线平行 , 内错角相等 ).又由于∠ 1=∠ 2, ∠ 3=∠4, 因此∠ 1=∠ 2=∠ 3=∠ 4. 由于∠ 5=180° -( ∠ 1+∠ 2), ∠ 6=180° -( ∠3+∠ 4),因此∠ 5=∠6, 因此 EF∥GH(内错角相等 , 两直线平行 ).即进入潜望镜的光芒和走开潜望镜的光芒是平行的.24.解:(1) 如图① : 过点 P 作 MP∥ AC,则MP∥BD, 由于 MP∥ AC,因此∠ APM=∠PAC,由于 MP∥ BD,因此∠ BPM=∠PBD,因此∠ APM+∠ BPM =∠PAC+∠PBD,即: ∠APB=∠PAC+∠PBD.因此∠ APB=∠ PAC+∠ PBD不建立 .①②(2)不建立 .原因以下 : 如图② , 过点 P 作 MP∥ AC,则MP∥BD, 由于 MP∥ AC,因此∠ APM=∠PAC,由于 MP∥ BD,因此∠ BPM=∠PBD,因此∠ APM+∠ BPM =∠PAC+∠PBD,即:360 °- ∠APB=∠PAC+∠PBD.因此∠ APB=∠ PAC+∠ PBD不建立 .。
湘教版数学七年级下册第4章 相交线与平行线 达标测试卷(含答案)

第4章相交线与平行线达标测试卷一、选择题(共6题,每题3分,共18分)1. 下列图形中,能将其中一个三角形平移得到另一个三角形的是()A B C D2. 如图,对于图中标记的各角,下列条件能够推理得到a∥b的是()A.∠1=∠2B.∠2=∠4C.∠3=∠4D.∠1+∠4=180°(第2题)(第3题)(第4题)3. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为()A.30°B.60°C.80°D.120°4. 在体育课上某同学立定跳远的情况如图所示,l表示起跳线,在测量该同学的实际立定跳远成绩时,应测量的线段及理由是()A.BP,经过一点有且只有一条直线垂直于已知直线B.CP,垂线段最短C.DP,两点之间,线段最短D.BD,两平行线间的公垂线段相等5. 如图,已知正方形ABCD的面积为4,则三角形EBC的面积为()A.4 B.3 C.2 D.1(第5题)(第6题)(第7题)(第8题)6. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120°B.130°C.140°D.150°二、填空题(共6题,每题4分,共24分)7. 如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE=______°.8. 如图,a∥b,点P在直线a上,点A在直线b上,P A⊥b,P A=2 cm,则点A到直线a的距离为________cm.9. 如图,AB∥CD,EF分别交AB,CD于G,H两点,若∠1=50°,则∠EGB=________.(第9题) (第10题)10. 如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西________.11. 如图,若直线EF⊥MN于F,且∠1=140°,则当∠2=________时,AB∥CD.(第11题) (第12题)12. 如图,直线AB,CD交于点O,∠BOC=70°,现作射线OE⊥CD,则∠AOE的大小为__________.三、解答题(共6题,共58分)13. (8分)如图,要把水渠中的水引到C点,在渠岸AB的什么地方开沟,才能使沟最短?画出图形,并说明理由.14. (8分)如图,直线AB、CD相交于点O, OD垂直于OE,∠BOE=18°.求∠AOC的度数.15. (8分)如图,已知AD∥BC,AC=15 cm,BC=12 cm,BE⊥AC于点E,BE=10 cm,求AD与BC之间的距离.16. (10分)如图,已知∠ABC=180°-∠A,BD⊥CD于点D,EF⊥CD于点F.(1)试说明:AD∥BC.(2)若∠1=36°,求∠2的度数.317. (10分)如图,将周长为18 cm的三角形ABC沿BC方向平移得到三角形DEF.如果四边形ABFD的周长是21 cm,求平移的距离.18. (14分)问题情境:如图①,AB∥CD,∠P AB=130°,∠PCD=120°,求∠APC的度数.小明的解题思路:如图②,过P作PE∥AB,通过平行线的性质,可得∠APC =50°+60°=110°.问题迁移:(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A,B两点外侧运动(点P与A,B,O三点不重合),请你直接写出∠CPD,∠α,∠β之间的数量关系.答案一、1.A 2.D 3.A 4.B 5.C 6.C二、7.258.2【点拨】因为a∥b,P A⊥b,P A=2 cm,所以AP⊥a,所以点A到直线a 的距离=P A=2 cm.9.50°10.48°【点拨】如图,因为AC∥BD,∠1=48°,所以∠2=∠1=48°,根据方向角的概念可知,乙地所修公路的走向是南偏西48°.11.50°【点拨】如图,因为AB∥CD,所以∠3=∠4(两直线平行,同位角相等).又因为∠1+∠3=180°,∠1=140°,所以∠3=∠4=40°.因为EF⊥MN,所以∠2+∠4=90°,所以∠2=50°.12.20°或160°【点拨】因为OE⊥DC,所以∠DOE=90°.因为∠AOD=∠BOC,∠BOC=70°,所以∠AOD=70°.①当OE在DC的左侧时,∠AOE=∠DOE-∠AOD=90°-70°=20°;②当OE在DC的右侧时,∠AOE=∠DOE+∠AOD=90°+70°=160°.综上,∠AOE=20°或160°.5三、13.解:图略.过C作CD⊥AB,垂足为D,在D处开沟,则沟最短.因为直线外一点与直线上各点连线的所有线段中,垂线段最短.14.解:因为OD⊥OE,所以∠BOD+∠EOB=90°.因为∠BOE=18°,所以∠BOD=90°-18°=72°,所以∠AOC=∠BOD=72°.15.解:过点A作BC的垂线,交BC于点P,三角形ABC的面积为12×AC×BE=12×15×10=75(cm2),又因为三角形ABC的面积为12×BC×AP=75(cm2),所以AP=12.5 cm,因此AD与BC之间的距离为12.5 cm.16.解:(1)因为∠ABC=180°-∠A,所以∠ABC+∠A=180°,所以AD∥BC.(2)因为AD∥BC,∠1=36°,所以∠3=∠1=36°.因为BD⊥CD,EF⊥CD,所以∠BDC=∠EFC=90°.所以BD∥EF.所以∠2=∠3=36°.17.解:因为三角形DEF是由三角形ABC沿BC方向平移得到的,所以AD=CF,AC=DF.所以四边形ABFD的周长为AD+AB+BF+DF=AD+AB+BC+AC+CF=2AD+(AB+BC+AC)=21 cm.因为AB+BC+AC=18 cm,所以2AD=3 cm,解得AD=1.5 cm.答:平移的距离为1.5 cm.18.解:(1)∠CPD=∠α+∠β.理由如下:如图①,过P作PE∥AD交CD于E,因为AD∥BC,所以AD∥PE∥BC.所以∠α=∠DPE,∠β=∠CPE.所以∠CPD=∠DPE+∠CPE=∠α+∠β.(2)当点P在线段BA的延长线上时,如图②.∠CPD=∠β-∠α.当点P在线段AB的延长线上时,如图③. ∠CPD=∠α-∠β.7。
湘教版七年级下册数学第4章 相交线与平行线含答案(含解析)

湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题,共计45分)1、如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为()A.50°B.45°C.30°D.40°2、将点向右平移个单位长度得到点,且点在轴上,那么点的坐标是()A. B. C. D.3、点P为直线l外一点,点A,B,C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm,那么点P到直线l的距离是()A.2cmB.小于2cmC.不大于2cmD.大于2cm,且小于5cm4、如图三角形ABC平移后得到三角形DEF.若AE=11,DB=5,则平移的距离是().A.6B.3C.5D.115、如图,直线∥ ,直线与直线、分别交于点A,点B,AC⊥AB 于点A,交直线于点C.如果∠1 = 34°,那么∠2的度数为()A.34°B.56°C.66°D.146°6、将一直角三角板和直尺如图摆放,则∠1+∠2等于()A.30°B.60°C.90°D.180°7、小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为()A.38°B.42°C.48°D.52°8、过一点画已知直线的平行线()A.有且只有一条B.不存在C.有两条D.不存在或有且只有一条9、如图,若点为函数图象上的一动点,表示点到原点的距离,则下列图象中,能表示与点的横坐标的函数关系的图象大致是().A. B. C. D.10、如图,,要使,则的大小是()A. B. C. D.11、如图,直线,,,则的度数为( )A. B. C. D.12、如图,与∠1是内错角的是()A.∠2B.∠3C.∠4D.∠513、已知,如图,AB∥CD,∠A=70°,则∠ACD=()A.55°B.70°C.40°D.110°14、如图,用19颗心组成的“大”字图案中不包含的变换是()A.位似B.旋转C.平移D.轴对称15、如图,已知a∥b,将直角三角形如图放置,若∠2=50°,则∠1为()A.120°B.130°C.140°D.150°二、填空题(共10题,共计30分)16、如图所示,已知AB、CD相交与O,OE平分∠AOD,OF⊥CD于O,∠1=40°,则∠2=________;∠3=________.17、如图,平移△ABC可得到△DEF,若∠A=45°,∠C=65°,则∠E=________,∠EDF=________,∠DOB=________.18、如图,a∥b,∠1=40°,∠2=80°,则∠3=________度.19、如图,当风车的一片叶子AB旋转到与地面MN平行时,叶子CD与地面MN________ ,理由是________ .20、如图,AC⊥BC,垂足为C,且BC=5,AC=12,AB=13,则点A到BC的距离是________,点B到点A的距离是________.21、如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=58°,则∠2=________.22、如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为________.23、平面直角坐标系中,将点A(﹣1,2)先向左平移2个单位,再向上平移1个单位后得到的点A的坐标为________.124、在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,且两弦在圆心O的异侧,若AB=24,则CD的长为________.25、如图所示,请写出能判定CE∥AB的一个条件________.三、解答题(共5题,共计25分)26、如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.27、完成下面推理过程:如图所示,直线AD与AB、CD分别相交于点A、D,与EC、BF分别相交于点H、G,已知:∠1=∠2,∠B=∠C.求证:∠A=∠D.证明:∵∠1=∠2(已知),∠2=∠AGB(对顶角相等)∴∠1=∠AGB(________)∴EC∥BF(________)∴∠B=∠AEC(________)又∵∠B=∠C(已知)∴∠AEC=________(________)∴________(________)∴∠A=∠D(________)28、如图所示,已知:BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.29、如图,矩形ABCD中,E为BC上一点,连接AE,过顶点D作DF⊥AE,垂足为F,求证:△ABE∽△DFA.30、如图,已知∠A=∠C,AB∥CD.那么∠E与∠F相等吗?请说明理由.参考答案一、单选题(共15题,共计45分)1、D2、C3、C4、B6、C7、B8、D9、C10、D11、A12、B13、B14、C15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、30、。
(基础题)湘教版七年级下册数学第4章 相交线与平行线含答案
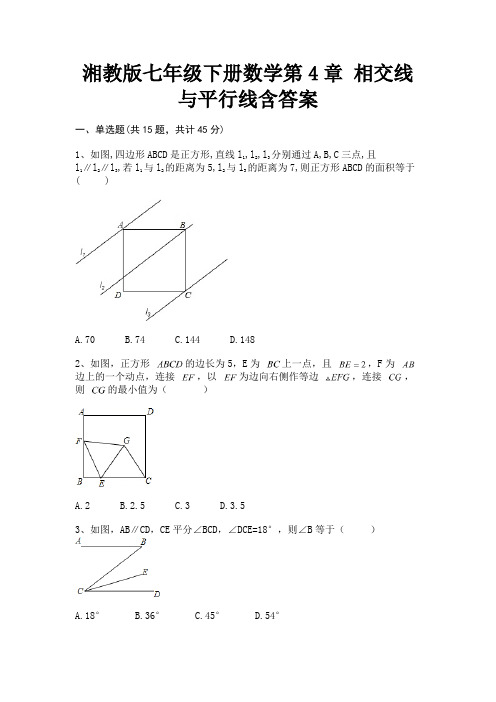
湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题,共计45分)1、如图,四边形ABCD是正方形,直线l1,l2,l3分别通过A,B,C三点,且l 1∥l2∥l3,若l1与l2的距离为5,l2与l3的距离为7,则正方形ABCD的面积等于( )A.70B.74C.144D.1482、如图,正方形的边长为5,E为上一点,且,F为边上的一个动点,连接,以为边向右侧作等边,连接,则的最小值为()A.2B.2.5C.3D.3.53、如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B等于()A.18°B.36°C.45°D.54°4、如图,中,,AC=3,,点P是BC边上的动点,则AP长不可能是()A.3.5B.4.2C.5.8D.75、如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为()A.①②B.①③C.②③D.以上都错6、如图,,则()A.20°B.60°C.80°D.100°7、如图,AB∥EF,CD⊥EF,∠ACD=130°,则∠BAC=()A.40°B.50°C.60°D.70°8、如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是( )A.α+β=180°B.α+β=90°C.β=3αD.α﹣β=90°9、如图,直线 AB交∠DCE的边 CE于点 F,则∠1 与∠2 是()A.对顶角B.同旁内角C.同位角D.内错角10、如图,在平行四边形ABCD中,BC=7厘米,CD=5厘米,∠D=50°,BE平分∠ABC,下列结论中错误的是()A.∠C=130°B.∠BED=130°C.AE=5厘米D.ED=2厘米11、在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都加上3,则所得图形与原图形的关系是:将原图形()A.向左平移3个单位B.向右平移3个单位C.向上平移3个单位 D.向下平移3个单位12、下列命题是假命题的是()A.两条直线被第三条直线所截,内错角相等B.在同一平面内,垂直于同一条直线的两条直线互相平行C.不相等的角不是对顶角;D.若一个角的两边分别与另一个角的两边平行,那么这两个角相等或互补13、在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是()A.(3,﹣3)B.(﹣3,3)C.(3,3)或(﹣3,﹣3)D.(3,﹣3)或(﹣3,3)14、如图,△DEF是由△ABC经过平移后得到的,则平移的距离是()A.线段BC的长度B.线段EC的长度C.线段BE的长度D.线段EF的长度15、如图,已知直线l1∥l2,∠1=50°,∠2=80°,那么∠3的大小为()A.40°B.50°C.60°D.70°二、填空题(共10题,共计30分)16、如图,直线AB、CD被直线EF所截,当满足条件________ 时(只需写出一个你认为合适的条件),AB∥CD.17、如图,直线AB的解析式y= x+3,交x轴于点A,交y轴于点B,点P为线段AB上一个动点,作PE⊥x轴于点E,PF⊥y轴于点F,则线段EF的最短长度为________。
湘教版七年级下册数学第4章 相交线与平行线含答案

湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题,共计45分)1、下列说法中,正确的是()A.在同一平面内,经过已知一点有且只有一条直线与已知直线平行B.两个相等的角是对顶角C.互补的两个角一定是邻补角D.直线外一点与直线上各点连接的所有线段中,垂线段最短2、下列说法正确的有()①两点之间的所有连线中,线段最短;②相等的角叫对顶角;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤两点之间的距离是两点间的线段;⑥在同一平面内的两直线位置关系只有两种:平行或相交.A.1个B.2个C.3个D.4个3、如图,已知,直线a∥b,1=50°,2= 3,则2的度数为()A.75°B.65°C.60°D.50°4、如图,AB∥DF,AC⊥BC于C,BC与DF交于点E,若∠A=20°,则∠CEF等于()A.110°B.100°C.80°D.70°5、如图,已知直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3=()A.40°B.50°C.60°D.70°6、如图,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD相等的角有( )A.1个B.2个C.3个D.4个7、如图,已知l1∥l2∥l3∥l4,相邻两条平行直线间的距离相等.若等腰直角的三个顶点分别在三条平行直线上,则∠α的正弦值是()A. B. C. D.8、如图,将边长为的正方形ABCD沿对角线AC平移,使点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是()A. B. C.1 D.9、如图,在下列四组条件中,能得到AB∥CD的是()A.∠ABD=∠BDCB.∠3=∠4C.∠BAD+∠ABC=180°D.∠1=∠210、下列命题中,其逆命题是真命题的是()A.对顶角相等B.两直线平行,同位角相等C.全等三角形的对应角相等D.如果,那么11、如图,直线,直线与,分别交于A,B两点,若,则( )A.65°B.75°C.115°D.125°12、如图,四边形中,点,分别在,上,,,将沿翻折,得,若,,则的度数为()A. B. C. D.13、如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是()A. B. C. D.14、如图,已知点A 的坐标为(-1,0 ),点B在直线y=x上运动,当线段AB 最短时,点B的坐标为()A.(0,0)B.(, - )C.(-,-)D.(-,-)15、如图,把河AB中的水引到C,拟修水渠中最短的是()A.CM C.CPD.CQ二、填空题(共10题,共计30分)16、如图,直角△ABC中,∠C=90°,AC=5,BC=12则内部五个小直角三角形的周长的和为________.17、如图,在▱ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是________.18、如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动________格.19、如图,在△ABC中,AB=AC,DE∥BC,∠1=65°,则∠2=________°20、若直线a∥b,a∥c,则直线b与c的位置关系是________.21、小张同学观察如图1所示的北斗七星图,小张同学把北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A、B、C、D、E、F、G,然后将点A、B、C、D、E、F、G顺次首尾连接,发现AG恰好经过点C,且∠B-∠DCG=115°,∠B-∠D=10°,若AG//EF,则∠E=m°,这里的m=________.22、如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=________度.23、把一个直角三角板(,)如图放置,已知∥,平分,则=________24、如图,在中,,,为边上一动点,作如图所示的使得,且,连接,则的最小值为________.25、如图是一个探照灯的剖面,位于点O处的灯泡发出的两束光线OB,OC经反射后平行射出,若∠ABO=α,∠DCO=β,则∠BOC=________.三、解答题(共5题,共计25分)26、如图所示,直线AB、CD、EF相交于点O,CD⊥AB,∠AOE:∠AOD=3:5,求∠BOF与∠DOF的度数.27、在数学活动课上,李老师让同学们试着用角尺平分∠AOB(如图所示),有两组同学设计了如下方案:方案①将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度位于OA,OB上,且交点分别为M,N,即PM=PN,过角尺顶点P的射线OP 就是∠AOB的平分线。
湘教版七年级下册数学第4章 相交线与平行线含答案

湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题,共计45分)1、已知图①~④,图①图②图③图④在上述四个图中,∠1与∠2是同位角的有( ).A.①②③④B.①②③C.①③D.①2、直线y=kx沿y轴向下平移4个单位长度后与x轴的交点坐标是(-3,0),以下各点在直线y=kx上的是()A.(-4,0)B.(0,3)C.(3,-4)D.(-4,3)3、下列说法中正确的有()①等角的余角相等;②两直线平行,同旁内角相等;③相等的角是对顶角;④同位角相等;⑤直角三角形中两锐角互余.A.1个B.2个C.3个D.4个4、如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是()A.35°B.70°C.90°D.110°5、如图,直线L1∥L2,则∠α为().A.150°B.140°C.130°D.120°6、下列说法中,正确的是()A.对顶角相等B.补角相等C.锐角相等D.同位角相等7、如图,CD⊥AB于D.且BC=4,AC=3, CD=2.4.则点C到直线AB 的距离等于()A.4B.3C.2.4D.28、在数学活动课上, 小明提出这样一个问题: 如图, ∠B =∠C = 90°, E 是BC的中点, DE平分∠ADC,∠CED = 35°, 则∠EAB的度数是()A.35°B.45°C.55°D.65°9、如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是()A.AB∥CDB.AD∥BCC.∠B=∠DD.∠DCA=∠DAC10、同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是()A. a∥bB. b⊥dC. a⊥dD.b∥c11、如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个12、给出下列说法:(1)两条直线被第三条直线所截,同位角相等;(2)不相等的两个角不是同位角;(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(4)从直线外一点到这条直线的垂线段,叫做该点到直线的距离;(5)过一点作已知直线的平行线,有且只有一条。
(黄金题型)湘教版七年级下册数学第4章 相交线与平行线含答案
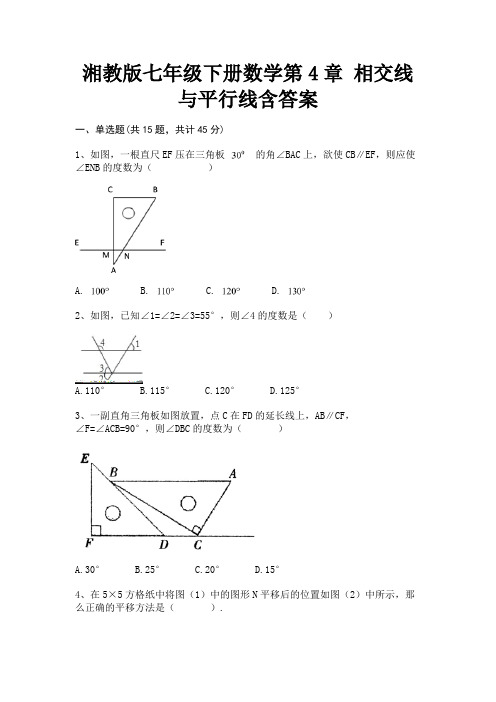
湘教版七年级下册数学第4章相交线与平行线含答案一、单选题(共15题,共计45分)1、如图,一根直尺EF压在三角板的角∠BAC上,欲使CB∥EF,则应使∠ENB的度数为()A. B. C. D.2、如图,已知∠1=∠2=∠3=55°,则∠4的度数是()A.110°B.115°C.120°D.125°3、一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为()A.30°B.25°C.20°D.15°4、在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是().A.先向下移动1格,再向左移动1格B.先向下移动1格,再向左移动2格C.先向下移动2格,再向左移动1格D.先向下移动2格,再向左移动2格5、点P为直线l外一点,点A,B,C在直线l上,若PA=4cm,PB=5cm,PC=6cm,则点P到直线l的距离为()A.4 cmB.小于或等于4 cmC.大于4 cmD.5 cm6、如图1,将正方形ABCD按图1所示置于平面直角坐标系中,AD边与x轴重合,顶点B,C位于x轴上方,将直线l:y=x﹣3沿x轴向左以每秒1个单位长度的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t秒,m与t的函数图象如图2所示,则a,b的值分别是()A.6,6B.6,4C.7,7D.7,57、在平面直角坐标系中,点)平移后能与原来的位置关于轴对称,则应把点()A.向右平移个单位B.向左平移个单位C.向右平移个单位 D.向左平移个单位8、下列语句叙述正确的有( )①如果两个角有公共顶点且没有公共边,那么这两个角是对顶角;②如果两个角相等,那么这两个角是对顶角;③连接两点的线段长度叫做两点间的距离;④直线外一点到这条直线的垂线段叫做这点到直线的距离.A.0个B.1个C.2个D.3个9、如图,直线l1∥l2, l3∥l4,∠1=45°,∠2=55°,则∠3等于A.100°B.90°C.80°D.70°10、如图,直线AB交CD于O,OE⊥AB,且∠DOE=50°,则∠AOC等于()A.40°B.45°C.50°D.60°11、如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有()A.1个B.2个C.3个D.4个12、如图所示,等边三角形沿射线向右平移到的位置,连接、,则下列结论:(1)(2)与互相平分(3)四边形是菱形(4),其中正确的个数是()A.1B.2C.3D.413、如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=63°,则∠2=( )A.63°B.53°C.37°D.27°14、在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线y=上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为()A.3B.2C.D.15、下列说法错误的是()A.对顶角相等B.两点之间所有连线中,线段最短C.等角的补角相等D.过任意一点P,都能画一条直线与已知直线平行二、填空题(共10题,共计30分)16、如图,∠1,∠2,∠3均是五边形ABCDE的外角,AE∥BC,则∠1+∠2+∠3=________°.17、如图,要把池中的水引到D处,可过D点引DC⊥AB于C,然后沿DC开渠,可使所开渠道最短,试说明设计的依据:________ .18、如图,四边形ABCD中,∠A=100°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B =________度.19、如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为________ .20、在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是________.21、把一张对边互相平行的纸条折成如图所示,是折痕,若,则下列结论:① ;② ;③;④ 正确的序号为________.22、如图所示,大正方形ABCD内有一小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D'E'BG',则大正方形ABCD的面积为________.23、如图所示,∠1的内错角是________ ,∠B的同旁内角有________ (只写一个)24、探照灯、锅形天线、汽车灯以及其它很多灯具都可以反射光线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湘教版七年级数学(下)第四章《相交线与平行线》基础卷(含答案)
一、选择题(30分)
1、如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A. 同位角相等,两直线平行;
B. 内错角相等,两直线平行;
C. 同旁内角互补,两直线平行;
D.两直线平行,同位角相等;
2、下列四个说法中,正确的是( )
A. 相等的角是对顶角;
B. 和为180°的两个角互为邻补角;
C. 两条直线被第三条直线所截,内错角相等;
D.两直线相交形成的四个角相等,则这两条直线互相垂直;
3、如图,直线a ∥b ,
直线c 分别与a 、b 相交,∠1=50°,则∠2的度数为( )
A. 150°;
B. 130°;
C. 100°;
D. 50°;
4、如图,直线AB ∥CD ,AF 交CD 于点E ,∠CEF=140°,则∠A 等于( )
A. 35°;
B. 40°;
C. 45°;
D. 50°;
5、在下列实例中, ①时针运转过程;②火箭升空过程;③地球自转过程;④飞机从起跑到离开地面的过程;不属于平移过程的有( )
A. 1个;
B. 2个;
C. 3个;
D. 4个;
6、如图,能判断直线ABCD 的条件是( )
A. ∠1=∠2;
B. ∠3=∠4;
C. ∠1+∠3=180°;
D. ∠3+∠4=180°;
7、如图,P O ⊥OR ,O Q ⊥PR ,则点O 到PR 所在直线的距离是线段( )的长。
A. OQ ;
B. RO ;
C. PO ;
D. PQ ;
8、如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数为( )
A. 30°;
B. 25°;
C. 20°;
D. 15°; 9、如图,已知AB ∥CD ,∠DFE=135°,
则∠ABE 的度数为( ) A. 30°; B. 45°; C. 60°; D. 90°;
A B C D E F a b c 1 2 (第1题) (第3题) (第4题) A B C D 1 3 2
4 1 2 第6题 第7题 第8题 A B
C D E F 第9题
10、如图,已知l ∥m ,等腰直角三角形ABC 直角顶点C 在直线m 上,若∠β=20°, 则∠α的度数是( )
A. 25°;
B. 30°;
C. 20°;
D. 35°; 二、填空题(24分) 11、如图,当剪刀口∠AOB 增大21时, ∠COD ,(填“增大”或“减少”) 度。
12、两条平行线被第三条直线所截,
同旁内角的比是7:11,则这两个角 的度数分别是 。
13、设a 、b 、l 为平面内三条不同直线,若a ∥b ,l ⊥a ,则l 与b 的位置关系是 。
若l ⊥a ,l ⊥b ,则a 与b 的位置关系是 。
若a ∥b ,l ∥a ,则l 与b 的位置关系是 。
14、同一平面内,两相交直线构成的 相等。
15、如图,用4根木棒可拼成大写字母“M ”,平移其中一根木棒,就能得到另一个大写字母,请写出这个英文字母 。
16、如图,按角的位置关系填空:∠A 与∠1是 ,∠A 与∠3是 ,∠2与∠3是 .
17、如图,∠1=∠2,∠A=60°,则∠ADC= 度。
18、某宾馆重新装修时,准备在大厅主
楼梯铺设地毯,已知这种地毯每平方米的
售价50元,主楼梯宽2m ,其侧面如图, 则购买地毯至少要 元。
三、解答题(46分)
19、(8分)(1)如图,一辆汽车在直线形 公路AB 上由A 向B 行驶,M 、N 分别是位于
公路AB 两侧的村庄,设汽车行驶到P 点时,离 村庄M 最近;汽车行驶到Q 点时,离村庄N 最近;
请在图中公路AB 上分别画出点P 、Q 的位置。
·
· A B C l m β α
第10题
第11题 第15题 1 2 3 A B C A 第16题 1 2 B C D 第17题
2.6第18题
A B
M N
(2)把下图中的小船向右平移,使得小船上的点A 向右平移5cm 到A′,请在图中画出A′的位置。
26、(6分)如图,∠5=∠CDA=∠ABC ,∠1=∠4,∠2=∠3,
∠BAD+∠CDA=180°,填空:
因为∠5=∠CDA (已知)
所以 ∥ ( )
因为∠5=∠ABC (已知) 所以 ∥ ( )
因为∠2=∠3,(已知)
所以 ∥ ( ) 因为∠BAD+∠CDA=180°(已知)
所以 ∥ ( ) 因为∠5=∠CDA (已知)
又因为∠5与∠BCD 互补( ),
∠CDA 与 互补(邻补角定义)
所以∠BCD=∠6,所以 ∥ ( )
21、(8分)如图所示,AB ,CD 相交于点O ,OE 平分∠AOD ,∠AOC=120° 求∠BOD ,∠AOE 的度数。
A B A C D E 第20题 A B C D E O
22、(8分)如图所示,AB ∥CD ,∠A=128°,∠D=32°,
求∠AED 的度数。
23、(8分)如图,已知OA ⊥OB ,∠1与∠2互补,
试说明:OC ⊥OD.
24、(8分)如图,直线m ⊥l ,n ⊥l ,∠1=∠2, 试说明:∠3=∠4.
A B C D E O A C B D 2 1 l m n 1 2 3 4
参考答案:一、1、A;2、D;3、B;4、B;5、B;
6、D;
7、A;
8、B;
9、B;10、A;
二、11、21°;12、,70°,110°;13、l⊥b,a∥b,l∥b;
14、对顶角;15、W;
16、同旁内角,同位角,内错角;17、120;18、840;
三、19、略;
20、BE,AD,内错角相等,两直线平行;AB,CD,同位角相等,两直线平行;
AB,CD,内错角相等,两直线平行;AB,CD,同旁内角互补,两直线平行;
邻补角定义,∠6,等角的补角相等;BE,AD,同位角相等,两直线平行;
21、因为∠BOD=∠AOC,∠AOC=120°,所以∠BOD=120°,
又因为∠AOC+∠AOD=180°,∠AOC=120°,所以∠AOD=60°,
∠AOD=30°
因为OE平分∠AOD,所以∠AOE=1
2
22、过点E作EF∥AB;
因为AB∥CD,所以EF∥CD(平行于同一直线的两直线平行)
所以∠A+∠AEF=180°,∠FED=∠D,
因为∠A=128°,∠D=32°,所以∠AEF=180°-128°=52°
所以∠AED=52°+32°=84°;
23、证明:因为∠1与∠2互补,所以∠1+∠2=180°;
因为∠1+∠2+∠AOB+∠COD=360°;
所以∠AOB+∠COD=180°,又因为OA⊥OB,所以∠AOB =90°;所以∠COD =90°;即:OC⊥OD
24、因为直线m⊥l,n⊥l,所以m∥n
所以∠1=∠4,∠2=∠3
又因为∠1=∠2,所以∠3=∠4。
