相似三角形经典模型总结
相似三角形几种基本模型
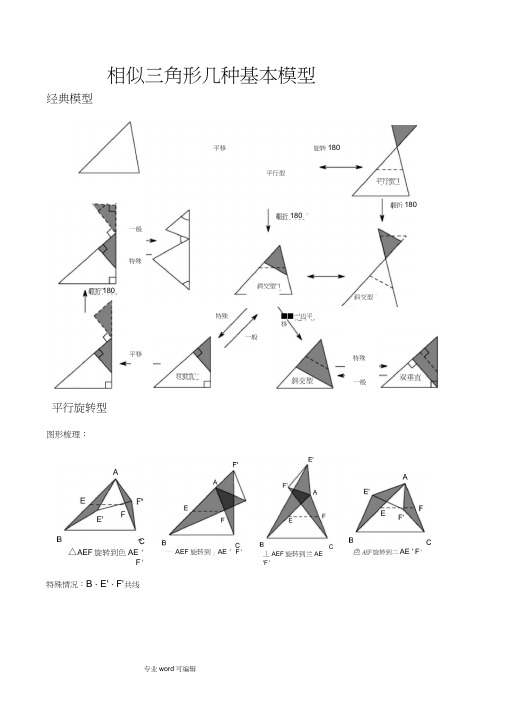
相似三角形几种基本模型经典模型平行旋转型图形梳理:特殊情况:B 、E'、F'共线平移一般平移特殊翻折180°旋转180°平行型平行型翻折180°翻折180°斜交型斜交型■■一边平移双垂直特殊一般特殊一般C△AEF 旋转到色AE 'F 'F'一 AEF 旋转到」AE ' F '丄AEF 旋转到兰AE 'F '色AEF 旋转到二AE ' F 'C , E', F'共线相似三角形有以下几种基本类型 :①平行线型常见的有如下两种 ,DE//BC ,则厶ADE S MBC②相交线型常见的有如下四种情形 ,如图,已知/仁/B ,则由公共角ZA 得,△ ADE s^ABCA B C△ AEF 旋转到厶AE‘ F 'A△ AEF 旋转至U 厶AE‘ F '八BC 一AEF 旋转至U 仝AE ‘ F 'AAEF 旋转到 A AE ‘ F 'E'A如下左图,已知Z1= ZB,则由公共角Z A 得,△ADC s^ACBZ1= Z得,△ ADE s^ABC 已知ZBAD= /CAE,Z B= ZD ,则厶ADE^A ABC,下图为常见的基本图形④母子型已知Z ACB=90 ° ,AB 丄CD ,则厶CBD ^A ABC^A ACD .如下右图,已知ZB= ZD,则由对顶角③旋转型相似三角形常见的图形1、下面我们来看一看相似三角形的几种基本图形(1)如图:称为平行线型”的相似三角形(有A 型”与X 型”图)反A 共角共边型”、蝶型”)⑷如图:/仁Z2,/B= ZD ,则厶ADE ^A ABC ,称为 旋转型”的相似三角形2、几种基本图形的具体应用(1)若 DE//BC (A 型和 X 型)则厶 ADE S ^ABC(2)射影定理 若CD 为Rt △ ABC 斜边上的高(双直角图形)(3) 如图:称为 垂直型”有 双垂直共角型 型”)EC双垂直共角共边型 (也称 射影定理型 ”)”三垂直如图:其中/仁Z2 ,则厶ADE S ^ABC 称为 斜交型”的相似三角形(有反A 共角型ED则Rt△ ABC^Rt△ ACD^Rt △ CBD 且AC2=AD AB , CD2=AD BD , BC2=BD AB ;(3) 满足1、AC2=AD AB, 2、/ACD= ZB, 3、/ACB= Z ADC ,都可判定△ ADC ^A ACB ./ ⑴AD AE亠亠(4) 当或AD AB=AC AE 时,△ ADE ^△ACB .AC AB。
相似三角形经典模型总结及例题分类

相似三角形经典模型总结经典模型【精选例题】 “平行型”【例 1】 如图,EEJ / FFJ / MM 1,若 AE=EF=FM=MB ,贝V S.A E ® : S 四边形EE 1F 1F : S 四边形FF 1M 1M : S 四边形MM QB 二翻折180°翻折180°V平行型斜交型斜交型平行型斜交型双垂直双垂直特殊平移翻折180°一般平移旋转180°一般一般特殊特殊C1[例2】如图,AD// EF M/N BC若AD =9 , BC =18 , AE :EM :MB = 2:3: 4,则EF = _____ , MN = ______长线,AB的延长线分别相交于点E,F,G,H求证:PE PH PF 一PG【例3】已知, P为平行四边形ABCD对角线,AC上一点,过点P的直线与AD , BC , CD的延【例4】已知:在ABC中,D为AB中点, 求目匸的值EF E为AC上一点,且Ah2,BE、CD相交于点F ,NCWORD整理版1 1【例引已知:在ABC中,AD AB,延长BC到F,使CF BC ,连接FD交AC于点E2 3AE =2CE求证: ① DE 二EF ②【例6】已知:D , E为三角形ABC中AB、BC边上的点,连接DE并延长交AC的延长线于点F , BD: DE 二AB:AC求证::CEF为等腰三角形【例7】如图,已知AB//EF / /CD,若AB =a,CD = b,EF = c,求证:1 =——cab【例8】如图,找出S.ABD、S BED、S.BCD之间的关系,并证明你的结论【例9】如图,四边形ABCD中,B=/D =90,M是AC上一点,ME _ AD于点E , MF _ BC于占JF 求证: MF ME ,1AB CDC【例10】如图,在ABC中,D是AC边的中点,过D作直线EF交AB于E,交BC的延长线于F 求证:AE BF 二BE CF【例11】如图,在线段AB上,取一点C,以AC,CB为底在AB同侧作两个顶角相等的等腰三角形ADC和CEB,AE交CD于点P,BD交CE于点Q,求证:CP =CQ【例12】阅读并解答问题.在给定的锐角三角形ABC中,求作一个正方形DEFG,使D,E落在BC边上,F , G分别落在AC , AB边上,作法如下:第一步:画一个有三个顶点落在ABC两边上的正方形D'E'F'G'如图,第二步:连接BF'并延长交AC于点F第三步:过F点作FE _ BC ,垂足为点E 第四步:过F点作FG // BC交AB于点G 第五步:过G点作GD _ BC,垂足为点D 四边形DEFG即为所求作的正方形问题:⑴证明上述所作的四边形DEFG为正方形⑵在ABC中,如果BC =6「3 , ABC =45 , • BAC = 75 ,求上述正方形DEFG的边长B D' E' D E C“平行旋转型”图形梳理:C , E', F'共线【例13】已知梯形ABCD , AD // BC,对角线AC、BD互相垂直,则①证明:AD2 BC2二AB2 CD2色AEF旋转到公AE 一AEF旋转到一AE ' F' AAEF旋转到至AE ''二AEF旋转到二AE 'F' △AEF旋转至U色AE ' F'△AEF旋转至U色AE ' F' △AEF旋转至U色AE ' F'【例14】当 MOD ,以点O 为旋转中心,逆时针旋转 日度(0£日<90),问上面的结论是否成立,请 说明理由D【例15】(全国初中数学联赛武汉选拔赛试题)如图,四边形AG : DF : CE = ___________ .“斜交型”【例16】如图,.:ABC 中,D 在AB 上,且DE // BC 交AC 于E , F 在AD 上,且AD^AF AB , 求证:AEF L ACD【例17】如图,等边三角形 ABC 中,D , E 分别在BC , AB 上,且CE 二BE , AD , CE 相交于M , 求证:EAM L ECAABCD 和BEFG 均为正方形,求GFBEDCD【例18】如图,四边形 ABCD 的对角线相交于点 O , . BAC — CDB ,求证:.DAC = . CBDAB BC CA【例佃】如图,设伴二CA ,则.仁.2吗?AD DE EA等于18和2,DE =2,求AC 边上的高BD 1【例21】如图,在等边 ABC 的边BC 上取点D ,使 ,作CH _AD ,H 为垂足,连结BH 。
((完整版))相似三角形模型分析大全(非常全面-经典),推荐文档

A
E
F
B
D
C
例 2:(1)在 ABC 中, AB AC 5 , BC 8 ,点 P 、 Q 分别在射线 CB 、 AC 上(点 P 不与点
C 、点 B 重合),且保持 APQ ABC .
①若点 P 在线段 CB 上(如图),且 BP 6 ,求线段 CQ 的长;
②若 BP x , CQ y ,求 y 与 x 之间的函数关系式,并写出函数的定义域;
12
相关练习:
1、如图,在△ABC 中, AB AC 8 , BC 10 , D 是 BC 边上的一个动点,点 E 在 AC 边上,且
ADE C .
(1) 求证:△ABD∽△DCE;
A
(2) 如果 BD x , AE y ,求 y 与 x 的函数解析式,并写出自变量 x 的定义域;
(3) 当点 D 是 BC 的中点时,试说明△ADE 是什么三角形,并说明理由.
A、P 两点的距离为 x,△BEP 的面积为 y.
(1)求证:AE=2PE; (2)求 y 关于 x 的函数解析式,并写出它的定义域; (3)当△BEP 与△ABC 相似时,求△BEP 的面积.
P
A
DE
C
(第 25 题图)
双垂型
1、如图,在△ABC 中,∠A=60°,BD、CE 分别是 AC、AB 上的高
A Q
B
P
C
A
A
B
C
B
C
备用图
备用图
(2)正方形 ABCD 的边长为 5 (如下图),点 P 、 Q 分别在直线 CB 、 DC 上(点 P 不与点 C 、点
B 重合),且保持 APQ 90 .当 CQ 1时,求出线段 BP 的长.
初中数学相似三角形模型总结

初中数学相似三角形模型总结数学这门学科,说简单也简单,说难也难。
有时候,一些看似抽象的概念一旦掌握了,就会觉得它们其实挺有趣的。
今天,我们要聊的就是相似三角形这个话题。
别着急,听我慢慢说,相信我,搞懂它们其实比你想象的要容易得多。
1. 相似三角形的基本概念1.1 什么是相似三角形?大家都知道,三角形有各种各样的样子,有的胖,有的瘦,有的高,有的矮。
但不管它们的外形如何,只要它们的角度相同,比例也保持一致,那它们就是相似三角形。
换句话说,就是这些三角形看起来像是放大或缩小版的关系。
1.2 为什么要学习相似三角形?可能有同学会问,这些三角形和我们的生活有什么关系?其实,了解相似三角形能帮助我们解决很多实际问题,比如测量远处物体的高度或距离,甚至能帮助我们设计一些简单的模型。
相似三角形的知识不仅能帮我们在考试中得高分,还能在生活中找到实际的应用。
2. 相似三角形的判定条件2.1 角角相似(AA)这是最基本的相似三角形判定方法。
只要两个三角形的两个角相等,那这两个三角形就是相似的。
这就像两个镜子前的自己,只要你转身的角度一样,镜子中的影像也会一样。
用公式来讲,角角相似就是:如果 (angle A = angle A') 和 (angle B = angle B'),那么△ABC ~ △A'B'C'。
2.2 边角边相似(SAS)另一种情况是,一个三角形的两边分别和另一个三角形的两边成比例,同时夹角也相等。
那么这两个三角形也是相似的。
简单来说,就像你用尺子量了一下两个三角形的边,再确认它们之间的夹角也是一致的,那么这两个三角形就是相似的。
2.3 边边边相似(SSS)如果两个三角形的三边分别成比例,那这两个三角形也是相似的。
想象一下,你有两个相同的形状的三角形,但是一个比另一个大,那它们之间的边的长度比例也应该是一样的。
这种情况下,三角形之间的相似性就完全取决于边的比例关系了。
(完整版)相似三角形模型分析大全(精).doc

第一部分相似三角形知识要点大全知识点 1. .相似图形的含义把形状相同的图形叫做相似图形。
(即对应角相等、对应边的比也相等的图形)解读 :( 1)两个图形相似,其中一个图形可以看做由另一个图形放大或缩小得到.( 2)全等形可以看成是一种特殊的相似,即不仅形状相同,大小也相同.( 3)判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.例 1.放大镜中的正方形与原正方形具有怎样的关系呢?分析:要注意镜中的正方形与原正方形的形状没有改变. 解:是相似图形。
因为它们的形状相同,大小不一定相同.例 2.下列各组图形:①两个平行四边形;②两个圆;③两个矩形;④有一个内角 80°的两个等腰三角形;⑤两个正五边形;⑥有一个内角是 100°的两个等腰三角形,其中一定是相似图形的是_________( 填序号 ) .解析:根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,而平行四边形、矩形、等腰三角形都属于形状不唯一的图形, 而圆、正多边形、 顶角为 100°的等腰三角形的形状不唯一, 它们都相似. 答案:②⑤⑥.知识点 2.比例线段对于四条线段 a,b,c,d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即a c(或a:b=c:d )那么这四条线段叫做成比例线段,简称比例线段.bd解读 :( 1)四条线段 a,b,c,d成比例,记作a c(或 a:b=c:d ),不能写成其他形式,即比例线段b d有顺序性.( 2)在比例式a c(或 a:b=c:d )中,比例的项为 a,b,c,d,其中 a,d 为比例外项, b,c 为比例内项, dbd是第四比例项.( 3)如果比例内项是相同的线段,即a bb或 a:b=b:c ,那么线段 b 叫做线段和的比例中项。
c(4) 通常四条线段 a,b,c,d 的单位应一致,但有时为了计算方便, a 和 b 统一为一个单位,c 和d 统一为另一个单位也可以,因为整体表示两个比相等.例 3.已知线段 a=2cm, b=6mm, 求 a. b分析:求a即求与长度的比,与的单位不同,先统一单位,再求比.b例 4.已知 a,b,c,d成比例,且 a=6cm,b=3dm,d= 3dm ,求 c 的长度.2分析:由 a,b,c,d成比例,写出比例式a:b=c:d ,再把所给各线段a,b,,d统一单位后代入求c .知识点 3.相似多边形的性质相似多边形的性质:相似多边形的对应角相等,对应边的比相等.解读 :( 1)正确理解相似多边形的定义,明确“对应”关系. ( 2)明确相似多边形的“对应”来自于书写,且要明确相似比具有顺序性.例 5.若四边形 ABCD 的四边长分别是 4, 6,8, 10,与四边形 ABCD 相似的四边形 A 1B 1C 1D 1 的最大边长为 30,则四边形 A 1B 1C 1D 1 的最小边长是多少?分析:四边形 ABCD 与四边形 A 1B 1C 1D 1 相似,且它们的相似比为对应的最大边长的比,即为1,再根据相似3多边形对应边成比例的性质,利用方程思想求出最小边的长. 知识点 4.相似三角形的概念对应角相等,对应边之比相等的三角形叫做相似三角形.解读 :( 1)相似三角形是相似多边形中的一种;( 2)应结合相似多边形的性质来理解相似三角形; ( 3)相似三角形应满足形状一样,但大小可以不同; ( 4)相似用“∽”表示,读作“相似于” ;( 5)相似三角形的对应边之比叫做相似比.注意 :①相似比是有顺序的,比如△ABC ∽△ A 1B 1C 1,相似比为 k, 若△ A 1B 1C 1∽△ABC ,则相似比为1。
相似三角形的基本模型归纳总结

相似三角形的基本模型归纳总结
相似三角形是指拥有相似的形状但大小不同的三角形。
在相似三角形中,对应角度相等,而对应边长之间存在比例关系。
以下是一些基本的相似三角形模型:
1. 比例模型:在两个相似三角形中,对应边长之比相等。
例如,若∆ABC与∆DEF相似,则有AB/DE = BC/EF = AC/DF。
2. 三角形高度模型:在两个相似三角形中,对应高度之比等于对应边长之比。
例如,若∆ABC与∆DEF相似,则有h_1/h_2 = AB/DE = BC/EF = AC/DF,其中h_1和h_2分别为∆ABC和
∆DEF的高度。
3. 角平分线模型:在两个相似三角形中,对应角的平分线所延伸的比例相等。
例如,若∆ABC与∆DEF相似,角A和角D相等,则有BD/CE = AB/DE = AC/DF。
4. 底角模型:在两个相似三角形中,底角对应相等。
例如,若∆ABC与∆DEF相似,并且∠A = ∠D,则有∠B = ∠E和∠C
= ∠F。
5. 周长模型:在两个相似三角形中,对应边长之比等于相似三角形的周长比。
例如,若∆ABC与∆DEF相似,则有
(A+B+C)/(D+E+F) = AB/DE = BC/EF = AC/DF。
这些是常见的相似三角形模型,可以根据具体问题选择适合的模型进行求解。
但需要注意的是,在相似三角形中,只有形状
相似,而边长比例相等,因此,对于三角形中角度的求解通常更加重要。
归纳相似三角形的模型

课例研究新教师教学与相似三角形有关的几何证明题是初高中数学学习的难点。
相似三角形变化多样,尤其当题目图示中有超过三个三角形时,就无法一眼看出谁和谁相似,更别说证明让人眼花缭乱的边长关系了。
本文意在介绍几个简单常见的相似三角形模型。
有了这些内容的积累,学生的记忆不再停留在两个三角形相似的情况。
我们知道,一些复杂的几何题,正是由基本的三角形模型组合起来的。
有了这些相似三角形模型,学生对复杂的三角形几何图形便有了“整体分拆”的意识。
这对我们处理复杂问题,和快速解决问题有帮助。
同时学生对相似三角形图形的应用、认知会有新的认识。
一、基本相似三角形模型A 字型 8字型对于这两个模型,简单叙述一下就行。
已知条件是两直线平行,于是得到各个图中的两个三角形相似。
斜A 字型母子型双垂直对于斜A 字型,已知条件是∠1=∠2,于是得到图中的两个三角形相似。
若将线段CD 向下移动,使点C 到三角形的一顶点处,便得到经典的“母子型”模型。
对于“母子型”,前提条件依旧是∠1=∠2,于是得到图中ΔABC ∽ΔACD ,即在这三个三角形中,上面的三角形与大三角形相似(与下三角形无关)。
再由相似的性质知AC 2=AD•AB ,即AC 为比例中项。
对于AC 2=AD•AB 这个式子,可以用一句话来记忆:两相似三角形的公共边长度的平方=两相似三角形由公共角的顶点发射的两条线段长的乘积。
有了这句话,同学们可以比较容易地写出AC 2=AD•AB 。
对于这个式子:AC 2=AD•AB ,有些同学似乎想到了射影定理。
没错,我只要稍加改变就可以联系到射影定理,那就是增加两个垂直条件,从而演化成“双垂直”型(如图所示)。
由“母子型”模型可以知“双垂直”中三个三角形均相似,又由两相似三角形的公共边长度的平方=两相似三角形公共角的顶点发射的两条线段长的乘积知:AC 2=AD•AB ,BC 2=BD•AB ,CD 2=AD•BD 。
这就是射影定理。
用一句话便可记住,以后便可灵活运用。
三角形相似模型总结

三角形相似模型总结
嘿,朋友们!今天咱就来好好唠唠三角形相似模型总结。
你们看啊,就说那相似三角形,不就好比是一对双胞胎嘛!两个三角形长得有点像,但又不完全一样。
比如说,咱有两个三角形,一个大的,一个小的,嘿,它们的角都一样大!这就叫相似呀!
就像一次数学测验里,有这样一道题,给你两个三角形,让你判断是不是相似。
你就得瞪大眼睛,瞅瞅它们的角,再看看它们边的比例是不是一样。
要是角相等,边的比例也对得上,那它们就是相似三角形没跑啦!
还有啊,相似三角形的性质也超级重要呢!比如对应边是成比例的,对应角相等。
这就好像两个小伙伴,有很多相同的地方,但又有各自的特点。
记得有次和同学一起做练习题,看到个三角形,我们很快就发现了它和另一个相似三角形的关系,那种感觉,哇,太爽了!
再来想想,相似三角形的判定也很有意思呀!就像要给三角形贴上一个“相似”的标签一样,得满足那些条件才行。
像是三边对应成比例,两角对应相等,这不就好比是进入一个秘密社团的密码嘛!
相似三角形在生活中也有很多用处呢!好比建筑师要盖房子,就得用相似三角形的知识来确保结构稳固。
咱平时看到的那些高楼大厦,说不定就有相似三角形在里面帮忙呢!
哎呀呀,三角形相似模型真的是太有趣太有用啦!总结起来就是,它就像一把神奇的钥匙,能打开好多数学难题的大门,能让我们发现生活中那些隐藏的数学奥秘。
大家一定要好好掌握它呀!。
相似三角形”A“字模型(含详细问题详解)-经典

教师辅导教案授课日期:年月日授课课时:课时ABC △与A B C '''△相似,AD 是ABC △中BAC ∠的角平分线,A D ''是A B C '''△中B A C '''∠的角平分线,则有AB BC AC AD k A B B C A C A D ====''''''''(k 为相似比). 4.相似三角形周长的比等于相似比. ABC △与A B C '''△相似,则有AB BC ACk A B B C A C ===''''''(k 为相似比).应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C++====''''''''''''++. 5.相似三角形面积的比等于相似比的平方.ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AH k A B B C A C A H ====''''''''(k 为相似比).进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△.二、相似三角形的判定1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可简单说成:两角对应相等,两个三角形相似.3.如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似. 4.如果一个三角形的三条边与另一个三角形的你对应成比例,那么这两个三角形相似.可简单地说成:三边对应成比例,两个三角形相似.5.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.6.直角三角形被斜边上的高分成的两个直角三角形相似(常用但要证明)7.如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等,那么这两个等腰三角形相似;如果它们的腰和底对应成比例,那么这两个等腰三角形也相似. 三、相似证明中的基本模型A 字形图①A 字型,DE//BC ;结论:AD AE DEAB AC BC==, 【例1】李老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,你能帮他调整过来吗?证明步骤正确的顺序是( )已知:如图,在△ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,且DE ∥BC ,DF ∥AC ,求证:△ADE∽△DBF.证明:①又∵DF∥AC,②∵DE∥BC,③∴∠A=∠BDF,④∴∠ADE=∠B,∴△ADE∽△DBF.A.③②④① B.②④①③ C.③①④② D.②③④①【解答】证明:②∵DE∥BC,④∴∠ADE=∠B,①又∵DF∥AC,③∴∠A=∠BDF,∴△ADE∽△DBF.故选:B.【练1】如图,在△ABC中,∠ACB=90°,BC=16cm,AC=12cm,点P从点B出发,以2cm/秒的速度向点C移动,同时点Q从点C出发,以1cm/秒的速度向点A移动,设运动时间为t秒,当t= 4.8或秒时,△CPQ与△ABC相似.【解答】解:CP和CB是对应边时,△CPQ∽△CBA,所以,,即,解得t=4.8;CP和CA是对应边时,△CPQ∽△CAB,所以,,即,解得t=.综上所述,当t=4.8或时,△CPQ与△CBA相似.故答案为4.8或.图②反A字型,∠ADE=∠B或∠1=∠B结论:AE AD DE==AC AB BC【例2】如同,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是()A.=B.=C.∠ADE=∠C D.∠AED=∠B【解答】解:∵∠DAE=∠CAB,∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;当=即=时,△ABC∽△AED.故选:A.【例3】如图,P是△ABC的边AB上的一点.(不与A、B重合)当∠ACP=∠ B 时,△APC与△ABC是否相似;当AC、AP、AB满足时,△ACP与△ABC相似.【解答】解:∵∠A=∠A,∠ACP=∠B,∴△ACP∽△ABC;∵,∠A=∠A,∴△ACP与△ABC;故答案为:B;.【练习1】如图,D、E为△ABC的边AC、AB上的点,当∠ADE=∠B 时,△ADE∽△ABC.其中D、E分别对应B、C.(填一个条件).【解答】解:当∠ADE=∠B,∵∠EAD=∠CAB,∴△ADE∽△ABC.故答案为∠ADE=∠B.【练习2】如图,在△ABC中,D、E分别在AB与AC上,且AD=5,DB=7,AE=6,EC=4.求证:△ADE∽△ACB.【解答】证明:∵AD=5,DB=7,AE=6,EC=4,∴AB=5+7=12,AC=6+4=10,∴====,∴=,又∵∠A=∠A,∴△ADE∽△ACB.【练习3】如图,AB=AC,∠A=36°,BD是∠ABC的角平分线,求证:△ABC∽△BCD.【解答】证明:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD是角平分线,∴∠ABD=∠DBC=36°,∴∠A=∠CBD,又∵∠C=∠C,∴△ABC∽△BCD.【练习4】已知:如图,△ABC中,∠ACD=∠B,求证:△ABC∽△ACD.【解答】证明:∵∠ACD=∠B,∠A=∠A,∴△ABC∽△ACD.【练习5】如图,已知AD•AC=AB•AE.求证:△ADE∽△ABC.【解答】证明:∵AD•AC=AE•AB,∴=在△ABC与△ADE 中∵=,∠A=∠A,∴△ABC∽△ADE.【练习6】已知:如图,在△ABC中,D,E分别为AB、AC边上的点,且AD=AE,连接DE.若AC=4,AB=5.求证:△ADE∽△ACB.【解答】证明:∵AC=3,AB=5,AD=,∴,∵∠A=∠A,∴△ADE∽△ACB.图③双A字型【例4】如图,在△ABC中,D,E分别是AB,AC上的点,∠AED=∠ABC,∠BAC 的平分线AF交DE于点G,交BC于点F.(1)试写出图中所有的相似三角形,并说明理由(2)若=,求的值.【解答】解:(1)∵∠AED=∠ABC,∠EAD=∠BAC,∴△ABC∽△AED.∵∠AED=∠ABC,∠EAG=∠BAF,∴△AEG∽△ABF.∵∠EDG=∠ACF,∠DAG=∠CAF,∴△ADG∽△ACF.(2)∵=,∴=,∵△ADG∽△ACF,∴==.【练习1】如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.(1)请你直接写出图中所有的相似三角形;(2)求AG与GF的比.【解答】解:(1)△ADG∽△ACF,△AGE∽△AFB,△ADE∽△ACB;(2)∵==,=,∴=,又∵∠DAE=∠CAB,∴△ADE∽△ACB,∴∠ADG=∠C,∵AF为角平分线,∴∠DAG=∠FAE∴△ADG ∽△ACF , ∴==,∴=2.图④内含正方形A 字形,结论AH a aAH BC-=(a 为正方形边长)【例5】如图,△ABC ,是一张锐角三角形的硬纸片,AD 是边BC 上的高,BC=40cm ,AD=30cm ,从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ,使它的一边EF 在BC 上,顶点G 、H 分别在AC ,AB 上,AD 与HG 的交点为M . (1)求证:=;(2)求这个矩形EFGH 的周长;(3)是否存在一个实数a ,当HE=a 时从三角形硬纸片上剪下的矩形面积最大?若存在,试求出a ;若不存在,请说明理由.【解答】(1)证明:∵四边形HEFG 为矩形, ∴HG ∥EF , 而AD ⊥BC , ∴AM ⊥BC ,。
初二超经典相似三角形模型分析大全
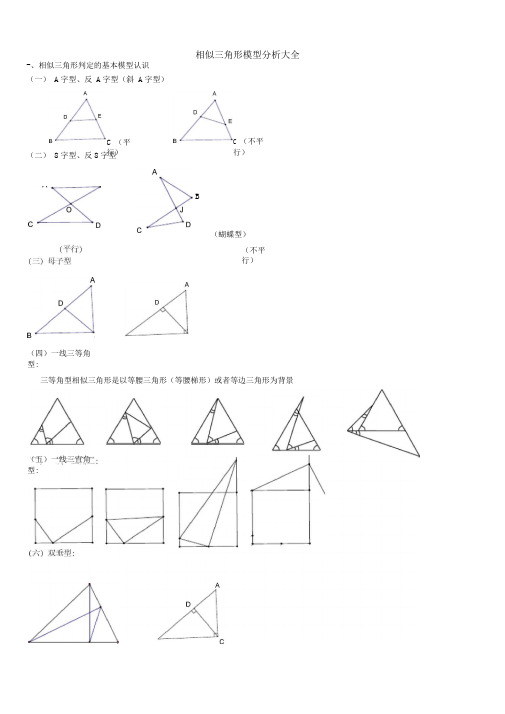
相似三角形模型分析大全-、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)(二)8字型、反8字型C (平行)C (不平行)B(蝴蝶型)(不平行)(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:、相似三角形判定的变化模型母子型相似三角形:例1:如图,梯形ABCD中,AD // BC,对角线AC、BD交于点0, BE // CD交CA延长线于E.求证:0C2 0A 0E .旋转型: 由A字型旋转得到-- 1 - =—a h c8字型拓展EB共享性线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解等腰△ ABC 中,AB = AC , AD 丄 BC 于 D , CG // AB , BG 分另交 AD 、AC 于 E 、F .相关练习:1、如图,已知 AD 为^ ABC 的角平分线,EF 为AD 的垂直平分线•求证:FD 2FB FC .AD 是Rt △ ABC 中/ A 的平分线,/ C=90°, EF 是AD 的垂直平分线交 AD 于M EF 、BC 的延长线交于一点 N 。
2△ AM 0A NMD; (2)ND =NC- NB已知:如图, △ ABC 中,点E 在中线AD 上,DEB求证: (1) DB2DE DA ; (2) DCE求证: BE 2 EFEG .已知:如图, 2、已知: 求证:⑴A3、已知:如图,在△ ABC中,/ ACB=90 , CD! AB于D, E是AC上一点,CF丄BE于F。
求证:EB- DF=AE- DB/I4.在ABC中,AB=AC高AD与BE交于H EF BC,垂足为F,延长AD到G,使DG=EF M是AH勺中点。
求证:GBM 905.已知:如图,在Rt△ ABC中,/ C=90°,BC=2, AC=4, P是斜边AB上的一个动点,PDLAB,交边AC于点D (点D 与点A C都不重合),E是射线DC上一点,且/ EPD/ A.设A、P两点的距离为X, △ BEP的面积为y.(1)求证:AE=2PE求y关于X的函数解析式,并写出它的定义域;当^ BEP与△ ABC相似时,求△ BEP的面积.双垂型:1、如图,在△ ABC 中,/ A=60°, BD CE 分别是 AC AB 上的高2、如图,已知锐角△ ABC , AD 、CE 分别是BC 、AB 边上的高,△ ABC 和^ BDE 的面积分别是 27和3, DE=6 J 2 ,1 >△ ABC 是等边三角形,D 、B 、C E 在一条直线上,/ DAE=12O ,已知BD=1, CE=3 ,求等边三角形的边长.2、已知:如图,在 Rt △ ABC 中,AB=AC ,/ DAE =45°求证:(〔)△ AB»A ACE (2)A AD0AABC (3)BC=2ED求证:(1) △ ABE sA ACD ;(2) BC 22BE CD.求:点B 到直线AC 的距离。
相似三角形的性质及判定知识点总结+经典题型总结

相似三角形的性质及判定知识点总结+经典题型总结(总16页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除板块 考试要求 A 级要求B 级要求C 级要求相似三角形了解相似三角形掌握相似三角形的概念,判定及性质,以及掌握相关的模型会运用相似三角形相关的知识解决有关问题一、相似的有关概念1.相似形具有相同形状的图形叫做相似形.相似形仅是形状相同,大小不一定相同.相似图形之间的互相变换称为相似变换. 2.相似图形的特性两个相似图形的对应边成比例,对应角相等. 3.相似比两个相似图形的对应角相等,对应边成比例.二、相似三角形的概念1.相似三角形的定义对应角相等,对应边成比例的三角形叫做相似三角形.如图,ABC △与A B C '''△相似,记作ABC A B C '''△∽△,符号∽读作“相似于”.A 'B 'C 'CB A2.相似比相似三角形对应边的比叫做相似比.全等三角形的相似比是1.“全等三角形”一定是“相似形”,“相似形”不一定是“全等形”.三、相似三角形的性质1.相似三角形的对应角相等知识点睛 中考要求 相似三角形的性质及判定如图,ABC △与A B C '''△相似,则有A A B B C C '''∠=∠∠=∠∠=∠,,.A 'B 'C 'CB A2.相似三角形的对应边成比例ABC △与A B C '''△相似,则有AB BC ACk A B B C A C ===''''''(k 为相似比).3.相似三角形的对应边上的中线,高线和对应角的平分线成比例,都等于相似比.如图1,ABC △与A B C '''△相似,AM 是ABC △中BC 边上的中线,A M ''是A B C '''△中B C ''边上的中线,则有AB BC AC AMk A B B C A C A M ====''''''''(k 为相似比). M 'MA 'B 'C 'C BA图1如图2,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AHk A B B C A C A H ====''''''''(k 为相似比).H 'H AB C C 'B 'A '图2如图3,ABC △与A B C '''△相似,AD 是ABC △中BAC ∠的角平分线,A D ''是A B C '''△中B A C '''∠的角平分线,则有AB BC AC ADk A B B C A C A D====''''''''(k 为相似比).D 'D A 'B C 'C B A图34.相似三角形周长的比等于相似比.如图4,ABC △与A B C '''△相似,则有AB BC ACk A B B C A C ===''''''(k 为相似比).应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++.A 'B 'C 'CB A图45.相似三角形面积的比等于相似比的平方.如图5,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AHk A B B C A C A H ====''''''''(k 为相似比).进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△.H 'H AB C C 'B 'A '图5四、相似三角形的判定1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可简单说成:两角对应相等,两个三角形相似.3.如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.4.如果一个三角形的三条边与另一个三角形的你对应成比例,那么这两个三角形相似.可简单地说成:三边对应成比例,两个三角形相似.5.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.6.直角三角形被斜边上的高分成的两个直角三角形相似(常用但要证明)7.如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等,那么这两个等腰三角形相似;如果它们的腰和底对应成比例,那么这两个等腰三角形也相似.五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有“三点定形法”.1.横向定型法 欲证AB BCBE BF=,横向观察,比例式中的分子的两条线段是AB 和BC ,三个字母A B C ,,恰为ABC △的顶点;分母的两条线段是BE 和BF ,三个字母B E F ,,恰为BEF △的三个顶点.因此只需证ABC EBF △∽△. 2.纵向定型法欲证AB DEBC EF=,纵向观察,比例式左边的比AB 和BC 中的三个字母A B C ,,恰为ABC △的顶点;右边的比两条线段是DE 和EF 中的三个字母D E F ,,恰为DEF △的三个顶点.因此只需证ABC DEF △∽△. 3.中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况,此时可考虑运用等线,等比或等积进行变换后,再考虑运用三点定形法寻找相似三角形.这种方法就是等量代换法.在证明比例式时,常用到中间比.比例中项式的证明,通常涉及到与公共边有关的相似问题。
(完整版)相似三角形模型分析大全(非常全面-经典)
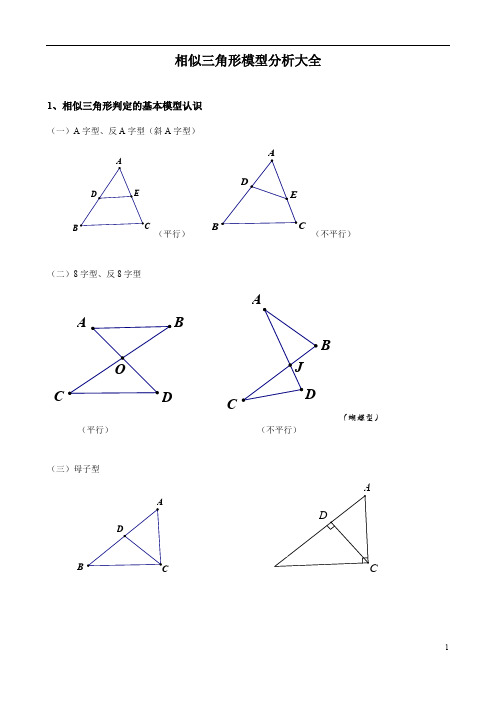
相似三角形模型分析大全1、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)B(平行)B(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(6)双垂型:2、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展B一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E .求证:.OE OA OC ⋅=2例2:已知:如图,△ABC 中,点E 在中线AD 上, .ABC DEB ∠=∠求证:(1); (2).DA DE DB ⋅=2DAC DCE ∠=∠ACDEB例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:.EG EF BE ⋅=2相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:.FC FB FD ⋅=22、已知:AD 是Rt△ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME∽△NMD; (2)ND =NC·NB23、已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F。
求证:EB·DF=AE·DB⊥,垂足为F,延长AD到G,使DG=EF,M是AH的中点。
4.在∆ABC中,AB=AC,高AD与BE交于H,EF BCGBM90求证:∠=︒5.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt△ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ;(2)求y 关于x 的函数解析式,并写出它的定义域;(3)当△BEP 与△ABC 相似时,求△BEP 的面积.双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高A(第25题图)求证:(1)△ABD∽△ACE;(2)△ADE∽△ABC;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=6,求:点B 到直线AC 的距离。
相似三角形模型分析大全(精)

第一部分相似三角形知识要点大全知识点1..相似图形的含义把形状相同的图形叫做相似图形。
(即对应角相等、对应边的比也相等的图形)解读:(1)两个图形相似,其中一个图形可以看做由另一个图形放大或缩小得到.(2)全等形可以看成是一种特殊的相似,即不仅形状相同,大小也相同.(3)判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.例1.放大镜中的正方形与原正方形具有怎样的关系呢?分析:要注意镜中的正方形与原正方形的形状没有改变.解:是相似图形。
因为它们的形状相同,大小不一定相同.例2.下列各组图形:①两个平行四边形;②两个圆;③两个矩形;④有一个内角80°的两个等腰三角形;⑤两个正五边形;⑥有一个内角是100°的两个等腰三角形,其中一定是相似图形的是_________(填序号).解析:根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,而平行四边形、矩形、等腰三角形都属于形状不唯一的图形,而圆、正多边形、顶角为100°的等腰三角形的形状不唯一,它们都相似.答案:②⑤⑥.知识点2.比例线段对于四条线段a,b,c,d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即a cb d=(或a:b=c:d)那么这四条线段叫做成比例线段,简称比例线段.解读:(1)四条线段a,b,c,d成比例,记作a cb d=(或a:b=c:d),不能写成其他形式,即比例线段有顺序性.(2)在比例式a cb d=(或a:b=c:d)中,比例的项为a,b,c,d,其中a,d为比例外项,b,c为比例内项,d是第四比例项.(3)如果比例内项是相同的线段,即a bb c=或a:b=b:c,那么线段b叫做线段和的比例中项。
(4)通常四条线段a,b,c,d的单位应一致,但有时为了计算方便,a和b统一为一个单位,c和d统一为另一个单位也可以,因为整体表示两个比相等.例3.已知线段a=2cm, b=6mm, 求ab.分析:求ab即求与长度的比,与的单位不同,先统一单位,再求比.例4.已知a,b,c,d成比例,且a=6cm,b=3dm,d=32dm,求c的长度.分析:由a,b,c,d成比例,写出比例式a:b=c:d,再把所给各线段a,b,,d统一单位后代入求c.知识点3.相似多边形的性质相似多边形的性质:相似多边形的对应角相等,对应边的比相等.解读:(1)正确理解相似多边形的定义,明确“对应”关系.(2)明确相似多边形的“对应”来自于书写,且要明确相似比具有顺序性.例5.若四边形ABCD的四边长分别是4,6,8,10,与四边形ABCD相似的四边形A1B1C1D1的最大边长为30,则四边形A1B1C1D1的最小边长是多少?分析:四边形ABCD与四边形A1B1C1D1相似,且它们的相似比为对应的最大边长的比,即为13,再根据相似多边形对应边成比例的性质,利用方程思想求出最小边的长.知识点4.相似三角形的概念对应角相等,对应边之比相等的三角形叫做相似三角形.解读:(1)相似三角形是相似多边形中的一种; (2)应结合相似多边形的性质来理解相似三角形; (3)相似三角形应满足形状一样,但大小可以不同; (4)相似用“∽”表示,读作“相似于”; (5)相似三角形的对应边之比叫做相似比.注意:①相似比是有顺序的,比如△ABC ∽△A 1B 1C 1,相似比为k,若△A 1B 1C 1∽△ABC ,则相似比为1k。
相似三角形模型(全)

面积比等于相似比的平方
如果两个三角形相似,则它们的对应 角相等。
如果两个三角形相似,则它们的面积 比等于它们的相似比的平方。
对应边成比例
如果两个三角形相似,则它们的对应 边成比例。
相似三角形的判定条件
两个三角形对应角相等,则这两个三角形相似。
两个三角形对应边成比例,则这两个三角形相似。
两个三角形有一个对应的角相等,且这个角所对的两边成比例,则这两个三角形相 似。
射影定理还涉及到角度的关系,即 $angle A_1 = angle A_2, angle B_1 = angle B_2, angle C_1 = angle C_2$ 。
在两个相似三角形中,对应边的比例 相等,即$frac{a_1}{a_2} = frac{b_1}{b_2} = frac{c_1}{c_2}$。
03
相似三角形的应用
在几何作图中的应用
利用相似三角形确定未知长度
01
通过已知的边长比例关系,利用相似三角形来求解未知的边长
或角度。
确定未知角度
02
通过相似三角形的性质,可以确定未知的角度。
证明定理和性质
03
相似三角形在几何作图中常被用来证明定理和性质,如角平分
线定理、中线定理等。
在解决实际问题中的应用
泰勒斯定理还可以表述为:在任何三 角形中,半周长与内切圆半径之和等 于从三角形一边上的一点到另两边的 垂直距离之和。
THANK YOU
测量问题
在测量中,可以利用相似三角形 的性质来计算难以直接测量的距
离和高度。
建筑设计
在建筑设计中,可以利用相似三角 形来计算建筑物的尺寸和比例。
物理学应用
在物理学中,可以利用相似三角形 来解释和计算光学、力学等问题。
相似三角形的九大模型

相似三角形的九大模型相似三角形是几何学中一类重要的图形,它具有一些独特的性质和模型。
这些模型可以用来解决各种实际问题,从简单的长度关系到复杂的空间结构。
本文将介绍相似三角形的九大模型,并给出相应的例子和应用场景。
相似三角形是指两个三角形形状相同,大小成比例。
相似三角形的对应边成比例,对应角相等。
相似三角形还有一些其他的性质,例如,相似三角形的中线、角平分线、高的比等于它们的相似比。
平行线模型:两个三角形分别在两条平行线上,它们的对应边平行且成比例。
这种模型经常用于解决一些与长度和角度相关的问题。
共顶点模型:两个三角形有一个共同的顶点,且它们的对应边成比例。
这种模型常用于证明两个三角形相似,以及求解一些角度问题。
角平分线模型:一个三角形的角平分线将这个三角形分成两个小的相似三角形。
这种模型可以用于证明两个三角形相似,以及求解一些角度问题。
平行四边形模型:一个平行四边形被它的两条对角线分成四个小的相似三角形。
这种模型可以用于解决一些与面积和长度相关的问题。
位似模型:一个相似变换将一个三角形映射到另一个三角形,这种变换称为位似变换。
这种模型可以用于解决一些与长度、角度和面积相关的问题。
旋转模型:一个三角形绕着它的一个顶点旋转一定的角度后得到另一个三角形,这两个三角形是相似的。
这种模型可以用于解决一些与角度和长度相关的问题。
镜像模型:一个三角形沿一条直线翻折后得到另一个三角形,这两个三角形是相似的。
这种模型可以用于解决一些与长度和角度相关的问题。
传递模型:如果一个三角形与另一个三角形相似,那么这个三角形的每一个部分都与另一个三角形的对应部分相似。
这种模型可以用于解决一些与长度和角度相关的问题。
扩展模型:如果一个三角形与另一个三角形相似,那么这个三角形的每一个部分都与另一个三角形的对应部分成比例。
这种模型可以用于解决一些与长度和角度相关的问题。
相似三角形的九创作者是几何学中一类重要的模型,它们具有广泛的应用价值。
相似三角形”8“字模型(含详细答案)-经典
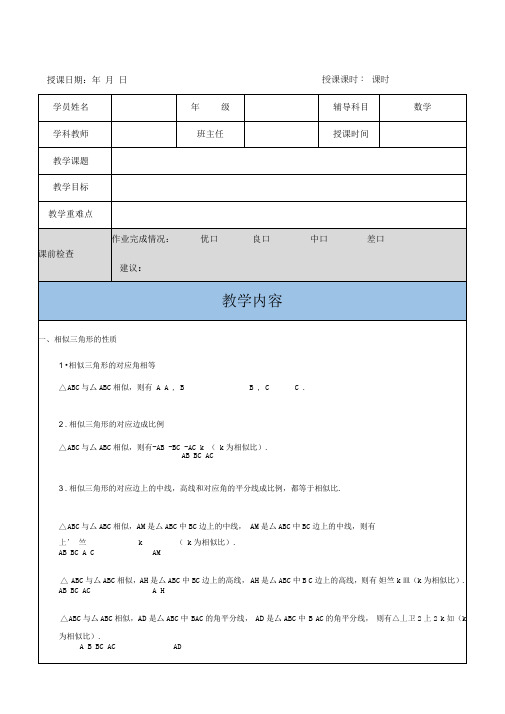
授课日期:年月日授课课时:课时是△ ABC中BC边上的高线,则有AB BC ACAB BC ACAHk ---------A H(k为相似比)•进而可得ABCABC1BC AH21BC AH2BC AHB C AHk2•那么8字形图①8字型,结论:AO BO ABOD CO CD4 •相似三角形周长的比等于相似比.AB BC AC△ ABC与厶ABC相似,则有————---- k( k为相似比)•应用比例的等比性质有AB BC ACAB BC AC AB BC AC--- ------ ------ ------------------ k •AB BC AC AB B C AC5 •相似三角形面积的比等于相似比的平方.△ ABC与厶ABC相似,AH是厶ABC中BC边上的高线,AH、相似三角形的判定1 •平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.2 •如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可简单说成: 两角对应相等,两个三角形相似.3 •如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.4 .如果一个三角形的三条边与另一个三角形的你对应成比例,那么这两个三角形相似.可简单地说成: 三边对应成比例,两个三角形相似.5 •如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,这两个直角三角形相似.6 •直角三角形被斜边上的高分成的两个直角三角形相似(常用但要证明)7 •如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等,那么这两个等腰三角形相似; 如果它们的腰和底对应成比例,那么这两个等腰三角形也相似.三、相似证明中的基本模型【例1】.如图,在?ABCD中,F是AD延长线上一点,连接BF交DC于点E,则图中相似三角形共有()AE ,交BC 于点F ,•••念EF 与△ADC 只有一个角相等,•••念EF 与△ACD 不一定相似,故选项 D 错误,符合题意.故选:D.【练习1】.如图,E 为?ABCD 的DC 边延长线上一点,连 则图中与厶ABF 相似的三角形共有 2 个. 【解答】解:•••四边形 ABCD 是平行四边形,•••AB //CD , AD //BC,z.^ABF S ©EF ,A CEFS 念ED ,z.^ABF s 念ED .•••图中与A ABF 相似的三角形是:△ CEF,^AED .故答案为:2【练习2】.如图,在?ABCD 中,AC , BD 相交于点0,点E 是OA 的中点,连接 BE 并延长交AD 于点F, 已知S ZAEF =4,则下列结论:① △ACD ,其中一定正确的是 ①②③ (填序号) 【解答】解:/•在?ABCD 中,A0= =AC,② S ZBCE =36; •••点E 是0A 的中点,•••AE 亠E, '/AD //BC, z.^AFE s©BE , •丄』二 •BC = □= 3,BC 的延长线于P ,求证:••AD=BC ,•••AF= AD ,3•••丄二;故①正确;FD 2•••S*=4, 「=(二)2=_,.••S ZBCE =36;故②正确;..坠臺丄 .%AE F =1_S AABE 3,•••S ZABE =12,故③正确; ••BF 不平行于CD , •••念EF 与A ADC 只有一个角相等, •••念EF 与△ACD 不一定相似,故④错误, 故答案为:①②③.【练习3】.如图,在平行四边形 ABCD 中,E 、F 分别是AD 、CD 边上的点,连接 BE 、AF ,他们相交于 G,延长BE 交CD 的延长线于点 H ,则图中的相似三角形共有4 对.【解答】解:.四边形 ABCD 是平行四边形,•••AB //CD , AD //BC,•••念BG S /FH G , A ABE s/DHE ^ZCHB ,•••图中的相似三角形共有 4对.故答案为:4.【练习4】.在厶ABC 中,DB=CE , DE 的延长线交【解答】解:过点 C 作CG//DP 交AB 于G, .AD _AE BD _BP……订,.一-,8AD?BP=AE ?CP .AO DF AD a"CO _ AC"2V5a ,,DF= —-5 5PF= —a ,所以 tan /BPC =4 q.•.PC —上一理,过D 作DF 丄AC,垂足为F ,设AD=a ,贝U A0=4a ,••OA=0B,点C 为OB 中点, • C0=2a ,在 RtSCO 中,AC=小「 「| _「=2 ,a,又 r Rt A ADF s Rt △XCO ,PF=AC - AF - PC=2 L ;%(3 )与( 2)的方法相同,设AD =a ,求出DF = J a ,【练习7】.已知线段 OA 丄OB ,C 为OB 上中点,D 为AO 上一点,连AC 、BD 交于P 点. (1 )如图1,当OA=OB 且D 为AO 中点时,求話的值;AD 1(2)如图2,当OA=OB ,时,求△ BPC 与△ACO 的面积之比.A0 4【解答】解:(1 )过C 作CE //OA 交BD 于E ,• ZBCEs/BOD ,…而麺••C 为OB 上中点,1•••CE= —OD ,DF 1PF = 2tan ZBPC=tan ZFPD= •••D 为AO 中点,•AF =•••ZECP S/DAP ,.AP 二ACL?;■pc=cir ;(2)过C作CE//OA交BD于E,过P作PF丄OB交OB于F,••QD=3x ,•••/BCE S/BQD , C 为 OB 上中点,vZECP S/D AP ,Is由勾股定理可知 BD=5x , DE=—x,• PD二2,•琏-PD百'PD=AD=x ,_ |1212 2PF=K S A BPC=5S ZACO=4X2,弘BPC』S AACO '图②反8字型,结论:AO BO △旦、四点共圆CO DO CD【例3】•如图,不能判定△AOB 和ADOC相似的条件是A . AO?CO=BO?DOB .二-二C ./A= ZD D ./B= ZCEO CD【解答】解:A、能判定•利用两边成比例夹角相等.B、不能判定.C、能判定•两角对应相等的两个三角形相似.D、能判定•两角对应相等的两个三角形相似.故选:B.【练习1】.如图,在四边形 ABCD中,对角线 AC与BD相交于点O, AC平分Z DAB,且Z DAC= ZDBC , 那么下列结论不一定正确的是()A . A AOD s/BOCB . A AOB ^ZDOC C . CD=BCD . BC?CD=AC ?OA【解答】解:A '•••/DAC= ZDBC , ZAOD= ZBOC ,•••@0D s/Boc,故此选项正确,不合题意;B、TZAOD s/BOC ,A0_0D|B0= CO,AO B0|0D= CO,又 v/AOB= Z COD ,S/DOC,故此选项正确,不合题意;C、TZAOB s/DOC , •••ZBAO= ZODC , •/AC 平分Z DAB ,•••ZDAC= ZBAC , •••ZBAC= ZBDC , •/ZDAC= ZDBC , •••zCDB= Z CBD ,则△ABC s 公EF ; (2 )若/E= ZB ,则△ABC s^\EF .故答案为:AF : AC ,Z B .•••CD=BC,故此选项正确,不合题意;D 、无法得出BC?CD=AC ?0A ,故此选项错误,符合题意.故选:D.【练习 2】.如图,(1 )若 AE : AB= AF : AC ,则△ ABC s 公EF ; (2 )若Z E= ZB ,则△ABC s 念EF.【解答】解:(1 )若AE : AB=AF : AC ,图③双8字型,结论:【例4】如图,AB//CD,点E为AB上一点,点F为CD上一点,求证:【例5】.如图,在平行四边形 ABCD中(AB M BC),直线EF经过其对角线的交点0,且分别交 AD、BC于点M、N,交BA、DC的延长线于点 E、F,下列结论:① AO=BO :②OE=OF ;③厶EAM S/EBN:④"AO也/CNO,其中正确的是( )A .①②B.②③C .②④D .③④【解答】解:①平行四边形中邻边垂直则该平行四边形为矩形,故本题中AC M BD,即AO MBO,故①错误;②T AB //CD ,•••ZE= ZF,又•••/EOA= ZFOC , AO=CO• △DE 也zCOF ,•••OE=OF,故②正确;③T AD //BC,z.ZEAM S/EB N,故③正确;④•••△AOE也zCOF,且△ FCO和加“。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形经典模型总结
经典模型
【精选例题】 “平行型”
【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===,
则1
11
1
1
1
:::_________AEE EE F F FF M M MM CB S S S S ∆=四边形四边形四边形
M 1F 1E 1M E F A B
C
【例2】 如图,AD EF MN BC ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则
_____EF =,_____MN =
M N A B
C
D E F
【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延
长线,AB 的延长线分别相交于点E ,F ,G ,H
求证:
PE PH
PF PG
= P
H
G
F
E
D
C
B
A
【例4】 已知:在ABC ∆中,D 为AB 中点,E 为AC 上一点,且
2AE
EC
=,BE 、CD 相交于点F , 求
BF
EF
的值
【例5】 已知:在ABC ∆中,AB=3AD ,延长BC 到F ,使1
3
CF BC =
,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE
=F
E D
C
B
A
B
C
D
F
E
【例6】 已知:D ,E 为三角形ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,
::BD DE AB AC =
求证:CEF ∆为等腰三角形
F
E
D
C
B
A
【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111
c a b
=+.
F
E D
C
B
A
【例8】 如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.
F
E D
C
B
A
【例9】 如图,四边形ABCD 中,90B D ∠=∠=︒,M 是AC 上一点,ME AD ⊥于点E ,MF BC
⊥于点F
求证:
1MF ME
AB CD
+=
A
B
C
E
F M
【例10】 如图,在ABC ∆中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F
求证:AE BF BE CF ⋅=⋅
F
E
D
C B
A
【例11】 如图,在线段AB 上,取一点C ,以AC ,CB 为底在AB 同侧作两个顶角相等的等腰三角形
ADC ∆和CEB ∆,AE 交CD 于点P ,BD 交CE 于点Q ,
求证:CP CQ =
Q
P
E
D
C B
A
【例12】 阅读并解答问题.
在给定的锐角三角形ABC 中,求作一个正方形DEFG ,使D ,E 落在BC 边上,F ,G 分别落在AC ,AB 边上,作法如下:
第一步:画一个有三个顶点落在ABC ∆两边上的正方形''''D E F G 如图, 第二步:连接'BF 并延长交AC 于点F 第三步:过F 点作FE BC ⊥,垂足为点E 第四步:过F 点作FG BC ∥交AB 于点G 第五步:过G 点作GD BC ⊥,垂足为点D
四边形DEFG 即为所求作的正方形
问题:⑴证明上述所作的四边形DEFG 为正方形
⑵在ABC ∆
中,如果6BC =+45ABC ∠=︒,75BAC ∠=︒,求上述正方形DEFG 的边长
“平行旋转型”
图形梳理:
AEF 旋转到AE‘F’
C
B
A
AEF 旋转到AE‘F’
C
B
B
C
AEF 旋转到
AE‘F’
A
B
C
AEF 旋转到AE‘F’
特殊情况:B 、'E 、'F 共线
AEF 旋转到AE‘F’C
B
A
A
B C
E
F E'
F'
AEF 旋转到AE‘F’
C ,'E ,'F 共线
AEF 旋转到AE‘F’
C
B
A
AEF 旋转到AE‘F’
C
B
A G'
F'
E'D'A
B C
D
E
F
G
【例13】 已知梯形ABCD ,AD BC ∥,对角线AC 、BD 互相垂直,则
1.证明:2
2
2
2
AD BC AB CD +=+
O
A
B C
D
2.当AOD ∆,以点O 为旋转中心,逆时针旋转θ度(090θ<<),问上面的结论是否成立,请说明理由
D
C
B A
O
【例14】 (全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和BEFG 均为正方形,求
::AG DF CE =_________.
A
B
E
F G
G
F
E
D
C
B
A
“斜交型”
【例15】 如图,ABC ∆中,D 在AB 上,且DE BC ∥交AC 于E ,F 在AD 上,且2
AD AF AB =⋅,
求证:AEF
ACD ∆∆
F E
D C
B
A
【例16】 如图,四边形ABCD 的对角线相交于点O ,BAC CDB ∠=∠,求证:DAC CBD ∠=∠
O
D
C
B
A
【例17】 如图,设
AB BC CA
AD DE EA
==,则12∠=∠吗? 21A
B
C
D
E
【例18】 在锐角三角形ABC 中,AD ,CE 分别为BC ,AB 边上的高,ABC ∆和BDE ∆的面积分别
等于18和2,2DE =,求AC 边上的高
A
B
C
D
E
【例19】 如图,在等边ABC ∆的边BC 上取点D ,使2
1
=CD BD ,作CH AD ⊥,H 为垂足,连结BH 。
求证:DBH DAB
∠=∠
【例20】 已知:在正三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD CE =,直线CD
与AE 相交于点F
求证:①DC AE =,②2
AD DC DF =⋅
A
B C
D
E
F
“斜交特殊型”(隐含三垂直)
【例21】 已知,如图,ABC ∆中,AD BC ⊥于点D ,DE AC ⊥于点E ,DF AB ⊥于点F ,求证:
AEF B ∠=∠
A
B
C
D
E
F
【例22】 已知:如图,CE 是直角三角形斜边AB 上的高,在EC 的延长线上任取一点P ,连结AP ,BG
⊥AP ,垂足为G ,交CE 于D ,求证:DE PE CE ⋅=2。
G
P
A
B
C
D
E
【例23】 如图,E 、G 、F 、H 分别是矩形ABCD 四条边上的点,EF GH ⊥,若2AB =,3BC =,
则:EF GH 等于( )
A. 2:3
B. 3:2
C. 4:9
D.无法确定
A
B
C
D E F
G H
【例24】 如图,已知:正方形ABCD 中,点M 、N 分别在AB 、BC 上,且BM BN =,BP MC
⊥于点P
求证:DP NP ⊥
P
A
B C
D
M
N
【例25】 如图,Rt ABC ∆中,90BAC ∠=︒,2AB AC ==,点D 在BC 上运动(不经过B ,C ),过
点D 作45ADE ∠=︒,DE 交AC 于E
①图中有无与ABD ∆一定相似的三角形,若有,请指出来并加以证明
②设BD x =,AE y =,求y 与x 的函数关系,并写出其定义域; ③若ADE ∆恰为等腰三角形,求AE 的长
E
D C
B
A 友情提示:本资料代表个人观点,如有帮助请下载,谢谢您的浏览!。
