相似三角形总复习模型总结

相似三角形题型归纳总结非常全面

相似三角形题型归纳一、比例的性质：二、成比例线段的概念： 1．比例的项：在比例式::a b c d =（即a cb d =）中，a ，d 称为比例外项，b ，c 称为比例内项．特别地，在比例式::a b b c =（即a bb c=）中，b 称为a ，c 的比例中项，满足b ac 2=．2．成比例线段：四条线段a ，b ，c ，d 中，如果a 和b 的比等于c 和d 的比，即a cb d=，那么这四条线段a ，b ，c ，d 叫做成比例线段，简称比例线段．3．黄金分割：如图，若线段AB 上一点C ，把线段AB 分成两条线段AC 和BC （AC BC >），且使AC 是AB 和BC 的比例中项（即AC AB BC 2=⋅），则称线段AB 被点C 黄金分割，点C 叫线段AB 的黄金分割点，其中.AC AB AB ≈0618，BC AB =.AB ≈0382，AC 与AB 的比叫做黄金比．（注意：对于线段AB 而言，黄金分割点有两个．）三、平行线分线段成比例定理 1．平行线分线段成比例定理A两条直线被三条平行线所截，所得的对应线段成比例，简称为平行线分线段成比例定理．如图：如果123////l l l ，则AB DE BC EF =，AB DE AC DF =，BC EFAC DF=．AD BE CF1l 2l 3lA D BE CF 1l 2l 3l【小结】若将所截出的小线段位置靠上的（如AB ）称为上，位置靠下的称为下，两条线段合成的线段称为全，则可以形象的表示为=上上下下，=上上全全，=下下全全．2．平行线分线段成比例定理的推论平行于三角形一边的直线，截其它两边（或两边的延长线），所得的对应线段成比例．如图：如果EF//BC ，则AE AF EB FC =，AE AF AB AC =，BE CFAB AC=． ABC E FFEC BA平行线分线段成比例定理的推论的逆定理若AE AF EB FC =或AE AF AB AC =或BE CF AB AC=，则有EF//BC ．【注意】对于一般形式的平行线分线段成比例的逆定理不成立，反例：任意四边形中一对对边的中点的连线与剩下两条边，这三条直线满足分线段成比例，但是它们并不平行．【小结】推论也简称“A ”和“8”，逆定理的证明可以通过同一法，做'//EF BC 交AC 于'F 点，再证明'F 与F 重合即可．四、相似三角形的定义、性质和判定 1．相似图形①定义：对应角相等，对应边成比例的图形叫做相似图形．对应边的比例叫做相似比．相似图形是形状相同，大小不一定相同．相似图形间的互相变换称为相似变换．②性质：两个相似图形的对应角相等，对应边成比例．2．相似三角形的定义3．相似三角形的性质 ①相似三角形的对应角相等．如图，∽△△ABC A B C '''，则有 A A '∠=∠，B B C C ''∠=∠∠=∠，．②相似三角形的对应边成比例．如图，∽△△ABC A B C '''，则有AB BC ACk A B B C A C ===''''''（k 为相似比）． ③相似三角形的对应边上的中线，高线和对应角的平分线成比例，都等于相似比．如图，△ABC ∽△A B C '''，AM AH 、和AD 是△ABC 中BC 边上的中线、高线和角平分线，A M ''、A H ''和A D ''是△ABC '''中B C ''边上的中线、高线和角平分线，则有AB BC AC AM AH ADk A B B C A C A M A H A D ======''''''''''''④相似三角形周长的比等于相似比．如图，△ABC ∽△A B C '''，则有AB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++． ⑤相似三角形面积的比等于相似比的平方．如图，△ABC ∽△A B C '''，则有 △△ABC A B C BC AHS BC AH k S B C A H B C A H 2'''1⋅⋅2==⋅=1''''''''⋅⋅24．相似三角形的判定判定定理判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．简称为两角对应相等，两个三角形相似．如图，如果'A A ∠=∠，'B B ∠=∠，则△∽△ABC A B C '''．判定定理2：如果两个三角形的三组对应边成比例，那么这两个三角形相似．简称为三边对应成比例，两个三角形相似．如图，如果AB BC ACA B B C A C ==''''''，则 △∽△ABC A B C '''．判定定理3：如果两个三角形的两组对应边成比例，并且对应的夹角相等，那么这两个三角形相似．简称为两边对应成比例且夹角相等，两个三角形相似．如图，如果AB ACA B A C =''''，'A A ∠=∠，则△∽△ABC A B C '''．五、“A ”字和“8”字模型六、与内接矩形的有关的相似问题如图，已知四边形DEFG 是△ABC 的内接矩形，E 、F 在BC 边上，D 、G 分别在AB 、AC 边上，则有：△∽△ADG ABC ，DG ANBC AM=．特别地，当BAC ∠=90︒时，有△∽△∽△∽△ADG EBD FGC ABC ．NM GFE DCB AGFEDCBA七、“A ”字和“8”字模型的构造“A ”字和“8”字模型的构造常常作平行线，常见的作平行线的方法：G EDCAGFEDCBA G FE DC B ADEFCBAGA HDFBECAGDF BEC八、斜“8”模型九、斜“A”模型十、射影定理十一、三平行模型十一二、三垂直模型十三、角平分线定理十四、线束模型题型一比例的性质和成比例线段的概念例题1 （1）已知::::x y z =135，则x y zx y z+3--3+的值是_______．（2）若x y z 234==．则x y z x y-+3=3-_______．（3）若a b c 2=3=4，且abc ≠0，则a bc b+-2的值是_______．解析（1）设x k =，y k =3，z k =5．∴x y z k k k x y z k k k +3-+9-55==--3+-9-53；（2）113；（3）-2 巩固1：（1）如果:2:3x y =，则下列各式不成立的是（） A ．53x y y += B ．13y x y -= C ．123x y = D ．1314x y +=+ （2）已知：23a c e b d f ===，求值：①a cb d++；②2323a c e b d f -+-+．（3）已知b c a c a b a b c a b c +-+-+-==，求()()()a b b c a c abc+++的值．解析：（1）A 为合比性质，B 为分比性质，C 显然正确，D 错误，由于11x y ≠，不能用等比定理．故答案为D ．（2）由等比性质直接可以得到23a c b d +=+；232233a c eb d f -+=-+．（3）当0a bc ++≠时，()()()b c a c a b a b c b c a c a b a b c a b c a b c+-+-+-+-++-++-====1++ 于是：2,2,2b c a a c b a b c +=+=+=，()()()a b b c a c abc+++=8．当0a b c ++=时，()()()()()()a b b c a c c a b abc abc+++-⋅-⋅-==-1．本题答案为1-或8．题型二平行线分线段成比例定理例题2（1）如图2-1，已知∥∥l l l 123，用面积法证明：AB DEBC EF=．（2）如图2-2，∥∥AD BE CF ，若AB =4，AC =10，DE =5，则DF =______．（3）如图2-3，∥∥l l l 123，AB =3，BC =5，DF =12，则_______DE =，______EF =．A D BECF l 12l 3lAD B ECFA DBECF l 12l l 3图2-1 图2-2 图2-3（1）如图所示，连接AE ，BD ，BF ，CE ．△△ABECBES AB BC S =∴． ∥AD BE ∵，∥BE CF ，△△ABE DEB S S =∴，△△CBE FEB S S =．△△△△ABE EDB CBE EFB S S AB DEBC S S EF===∴．（2）252；（3）92，152．巩固2：（1）如图2-1，直线∥∥l l l 123，已知.cm AG =06，.cm BG =12，.cm CD =15，CH =_____．（2）如图2-2，在△ABC 中，D 、E 分别为AB 、AC 边上的点，若AD BD 2=3，AE =3，则AC =______（3）如图2-3，AB ∥DE ，AE 与DB 交于C ，AC =3，BD =3，CD =2，则CE =______A CH GDBl 1l 2l 3B ADEABC图2-1 图2-2 图2-3解析：（1）0.5cm ；（2）152；（3）6 题型三相似三角形的定义、性质和判定例题3如图，直角梯形ABCD 中，∠ADC =90︒，∥AD BC ，点E 在BC 上，点F 在AC上，∠∠DFC AEB =．（1）求证：△∽△ADF CAE ．（2）当AD =8，DC =6，点E 、F 分别是BC 、AC 的中点时，求直角梯形ABCD 的面积．解析：（1）∵∥AD BC ，∴∠∠DAF ACE =，∵∠∠DFC AEB =，∴DFA AEC ∠=∠，∴△∽△ADF CAE（2）∵AD =8，DC =6，∴AC =10，又∵F 是AC 的中点，∴AF =5 ∵△∽△ADF CAE ，∴AD AF CA CE =，∴CE 85=10，∴CE 25=4，∵E 是BC 的中点， ∴BC 25=2，∴直角梯形ABCD 的面积125123⎛⎫=⨯+8⨯6= ⎪222⎝⎭A D BECF l 12l 3l F EDCBA巩固3：（1）下列所给条件中，可以判断△ABC 与△DEF 相似的是（） A ．90A ∠=︒，90F ∠=︒，5AC =，13BC =，10DF =，26EF = B ．85C ∠=︒，85E ∠=︒，AC DEBC DF=C ．1AB =， 1.5AC =，2BC =，8EF =，10DE =，16FD = D ．46A ∠=︒，80B ∠=︒，45E ∠=︒，80F ∠=︒（2）如图1，在△ABC 中，点D 是BC 边上的中点，且AD AC =，DE BC ⊥，交BA 于点E ，EC 与AD 相交于点F ．求证：△∽△ABC FCD ．（3）如图2，△ABC 为等腰直角三角形，BD CE BC 21⋅=2，求证：△∽△ACE DBA ．AEF DADB CE图1 图2解析：（1）D ；（2）AD AC =∵，FDC ACB ∠=∠∴；DE ∵垂直平分BC ，EB EC =∴， ∴ABC FCD ∠=∠，△∽△ABC FCD ∴.（3）由等腰直角三角形得到BC =条件变为BD CE AB AB AC 2221⋅=⋅2==2，条件变为比例形式：BD BAAC CE=，由于DBA ACE ∠=180︒-45︒=∠，∴△∽△ACE DBA ．题型四 “A ”字和“8”字模型例题4 （1）如图4-1，已知□ABCD 中，过点B 的直线顺次与AC 、AD 及CD 的延长线相交于点E 、F 、G ，若BE =5，EF =2，则FG 的长为____________．（2）如图4-2，已知在□ABCD 中，M 、N 为AB 的三等分点，DM 、DN 分别交AC 于P 、Q 两点，则AP:PQ:QC =____________．G BAF DC EC AD M N PQ图4-1 图4-2解析：（1）∵四边形ABCD 为平行四边形，∴//AD BC ∴△∽△AEF CEB ，△∽△GFD GBC ，∴AF EF CB EB 2==5，∴DF AD AF CB CB -3==5∴FG DF BG CB 3==5，即FG FG 3=+75．得.FG =105．（2）由DC ∥AB ，得AP AM PC AB 1==3，AP AC 1=4，同理AQ AC 2=5，PQ AC 2=51-4AC =AC 320，QC =AC 35，故1::::::4AP PQ QC 33==5312205．巩固4：（1）如图4-1，在ABC △中，M 、E 把AC 边三等分，MN//EF//BC ，MN 、EF 把ABC △分成三部分，则自上而下部分的面积比为．（2）如图4-2，AB 、CD 、EF 都与BD 垂直，垂足分别是B 、D 、F ，且1AB =，3CD =，则:EF CD 的值为__________．（3）如图4-3，已知在平行四边形ABCD 中，M 为AB 的中点，DM ，DB 分别交AC 于P ，Q 两点，则::AP PQ QC =___________．NM FE C BAAB CEF DA CBQPD图4-1 图4-2 图4-3解析：（1）1:3:5；（2）14；（3）AQ CQ AC 1==2∵，又AP AM PC CD 1==2，AP AC 1=3∴ PQ AC AC 111⎛⎫=1--= ⎪236⎝⎭∴，::::AP PQ QC =213∴．题型五与内接矩形有关的相似问题例题5（1）如图5-1，△ABC 中，正方形EFGH 的两个顶点E 、F 在BC 上，另两个顶点G 、H 分别在AC 、AB 上，BC =15，BC 边上的高AD =10，求正方形EFGH S ．（2）如图5-2，已知△ABC 中，四边形DEGF 为正方形，D ，E 在线段AC ，BC 上，F ，G 在AB 上，如果ADF CDE S S ∆∆==1，BEG S ∆=3，求△ABC 的面积．HAB C D E FGACDEGB图5-1 图5-2解析：（1）设正方形EFGH 的边长为x ，AD 、HG 的交点为M ，则有AM HG AD BC =，即x x10-=1015，解得，x =6，故EFGH S 2=6=36正方形（2）设正方形边长为x ，则AF x 2=，CI x 2=，BG x6=．由△∽△CDE CAB ，得CI DE CH AB =，∴xxx x x x2=28++，解得x =2， ∴AB =6，CH =3，∴ABC S AB CH ∆1=⋅=92巩固5：如图，已知ABC △中，AC =3，BC =4，C ∠=90︒，四边形DEGF 为正方形，其中D 、E 在边AC 、BC 上，F 、G 在AB 上，求正方形的边长．GF EDC B A H IDC EGF ABGFED CBA H MACDEG BIHHPED CB A解析：法一：由勾股定理可求得AB =5，由AB CH AC BC ⋅=⋅可得.CH =24．由CDE CAB △∽△可得DE CI AB CH =，设正方形的边长为x ，则..x x 24-=524，解得x 60=37．法二：设CE k =4，则DE k =5，∴GE k =5，BE k 25=3． ∴CE BE +=4，即k k 254+=43，解得k 12=37，∴DE k 60=5=37．题型六 “A 字和“8”字模型的构造例题6如图，ABC △中，D 为BC 边的中点，延长AD 至E ，延长AB 交CE 的延长线于P ．若AD DE =2，求证：3AP AB =．解析：如图，过点D 作PC 的平行线，交AB 于点H ． ∵HD PC ∥，AH ADAD DE AH PH PH DE=2⇒==2⇒=2， HD PC ∥，BH BDBD CD BH PH PH CD=⇒==1⇒=， ∴AP AH PH PH =+=3，AH BH AB PH BH =+=2=2， ∴AB BH PH ==，∴AP PH AB =3=3．还可用如下辅助线来证此题：A BCD EKPABCDEK P PKED CBA巩固6：如图，已知线段AB ∥CD ，AD 与BC 相交于点K ，E 是线段AD 上一动点．（1）若BK KC 5=2，求CDAB的值；（2）连接BE ，若BE 平分∠ABC ，则当AE AD 1=2时，猜想线段AB 、BC 、CD 三者之间有怎样等量关系？请写出你的结论并予以证明．再探究：当AE AD n1=()n >2，而其余条件不变时，线段AB 、BC 、CD 三者之间又有怎样的等量关系？请直接写出你的结论，不必证明．解析：（1）∵BK KC 5=2，∴CK BK 2=5，又∵CD ∥AB ，∴KCD KBA △∽△，∴CD CK AB BK 2==5（2）当BE 平分ABC ∠，AE AD 1=2时，AB BC CD =+；证明：取BD 的中点为F ，连接EF 交BC 于G 点，由中位线定理，得EF//AB//CD ，∴G 为BC 的中点，GEB EBA ∠=∠，又∵EBA GBE ∠=∠，∴GEB GBE ∠=∠，∴EG BG BC 1==2，ABDECC DEKBA而GF CD 1=2，EF AB 1=2，EF EG GF =+，即：AB BC CD 111=+222；AB BC CD ∴=+；当AE AD n1=(n >2)时，(1)BC CD n AB +=-．题型七斜“A ”和斜“8”模型例题7如图，在ABC △中，AD BC ⊥于D ，CE AB ⊥于E ，ABC △的面积是BDE △面积的4倍，6AC =，求DE 的长．解析：∵AD BC ⊥，CE AB ⊥，ABD CBE ∠=∠， ∴ABD CBE △∽△， ∴BE BCBD AB =，∵EBD CBA ∠=∠，∴BED BCA △∽△，∴11322DEDE AC AC===⇒==．巩固7：（1）如图，ABC △是等边三角形，点D ，E 分别在BC ，AC 上，且BD CE =，AD 与BE 相交于点F ．求证：①BD AD DF 2=⋅；②AF AD AE AC ⋅=⋅；③BF BE BD BC ⋅=⋅．（2）如图，四边形ABCD 是菱形，AF AD ⊥交BD 于E ，交BC 于F ．求证：AD DE DB 21=⋅2．FECDBAA DEF C解析：（1）∵等边ABC △，∴AB BC =，ABC ACB BAC ∠=∠=∠=60︒ ∵BD CE = ∴ABD BCE △≌△．∴BAD CBE ∠=∠，∴BFD BAD ABE CBE ABE ABC ∠=∠+∠=∠+∠=∠ ∴ABD BFD △∽△ ∴BD DFAD BD=，∴BD AD DF 2=⋅． ②证明AFE ACD △∽△即可． ③证明BFD BCE △∽△即可．（2）方法一：取DE 中点M ，连接AM ， ∵AF AD ⊥，M 为DE 中点∴MA MD DE 1==2，∴∠1=∠2，又∵AB AC =，∴∠2=∠3，∴∠1=∠3，∴DAM DBA △∽△，∴DA DM DB 2=⋅，∴AD DE DB 21=⋅2．方法二：取BD 中点N ，连接AN ．由等腰三角形的性质可知：AN BD ⊥，又∵EAD ∠=90︒，∴AND EAD △∽△，∴AD DN DE 2=⋅，又∵DN BD 1=2，∴AD DE BD 21=⋅2．总结：考查斜“A ”和斜“8”常见结论，看到比例乘积想到斜“A ”和斜“8”，也要会找ADEF CM123ED CAB巩固8：在等边ABC △中，点D 为AC 上一点，连结BD ，直线l 与AB ，BD ，BC 分别相交于点E 、P 、F ，且BPF ∠=60︒．（1）如图8-1，写出图中所有与BPF △相似的三角形，并选择其中一对给予证明．（2）若直线l 向右平移到图8-2、图8-3的位置时（其它条件不变），（1）中的结论是否仍然成立？若成立，请写出来（不证明），若不成立，请说明理由．（3）探究：如图8-1，当BD 满足什么条件时（其它条件不变），PF PE 1=2？请写出探究结果，并说明理由．（说明：结论中不得含有未标识的字母）图3图2图1lP FEDCB AFP EDC BAlFPEDCBA 图3图2l P F E D CB A l FPEDC BA图3lPFED CB A 图8-1 图8-2 图8-3 解析：（1）BPF EBF △∽△与BPF BCD △∽△，以BPF EBF △∽△为例，证明如下： ∵BPF EBF ∠=∠=60，BFP BFE ∠=∠，∴BPF EBF △∽△．（2）均成立，均为BPF EBF △∽△，BPF BCD △∽△．（3）BD 平分ABC ∠时，PF PE 1=2．证明：∵BD 平分ABC ∠，∴ABP PBF ∠=∠=30∵BPF ∠=60，∴BFP ∠=90，∴PF PB 1=2，又BEF ABP ∠=60-30=30=∠，∴BP EP =，∴PF PE 1=2．题型八射影定理例题8如图，已知AD 、CF 是ABC △的两条高，EF AC ⊥与E ，交CB 延长线于G ，交AD 于H ，求证：EF EH EG 2=⋅．解析：∵CF AB ⊥，EF AC ⊥，∴EF AE CE 2=⋅，又由AD BC ⊥可知，AEH CEG ∠=∠=90︒，EAH EGC ∠=∠，∴AEH GEC △∽△，∴EH EAEC EG=， ∴EH EG EA EC ⋅=⋅，∴EF EH EG 2=⋅．巩固9：（1）如图9-1，在ABC △中，CD AB ⊥于D ，DE AC ⊥于E ，DF BC ⊥于F ．求证：CEF CBA △∽△．（2）如图9-2，在Rt ABC △中，AD 是斜边BC 上的高，DE AC ⊥于E ，DF AB ⊥于F ，求证：AB FB FD AC EC ED44⋅=⋅． GHFED CB ACAEFDBBAEDC F图9-1 图9-2解析：（1）分别在ADC △与CDB △中由射影定理得到：2CD CE CA =⋅，2CD CF CB =⋅， CE CA CF CB ⋅=⋅∴，即CE CFCB CA=，ECF BCA ∠=∠∵，ECF BCA ∴△∽△．（2）由射影定理可以依次得到422422AB BD BC BF ABAC DC BC EC AC⋅⋅==⋅⋅，于是仅需证明AB FDAC ED=，由于BDA ADC △∽△，DF DE 、分别是AB 与AC 上的高，所以有AB DFAC DE=，得证．题型九三垂直模型例题9如图，M 为线段AB 的中点，AE 与BD 交于点C ，DME A B α∠=∠=∠=，且DM交AC 于F ，ME 交BC 于G ．（1）求证：AMF BGM △∽△．（2）连接FG ，如果45α=︒，42AB =，3AF =，求FG 的长．解析：（1）由题意得，DME A B α∠=∠=∠=， ∴180AMF BMG α∠+∠=︒-，180AMF AFM α∠+∠=︒-，∴BMG AFM ∠=∠，又E A B α∠=∠=∠=，∴△AMF ∽△BGM ．（2）∵AMF BGM △∽△，∴AM AF BG BM =∴，∵M 为AB 的中点，∴12AM BM AB ==∴， ∵42AB =，3AF =，∴83BG =∴， ∵45α=︒∵，∴90ACB ∠=︒∴，4AC BC ==，∴1CF AC AF =-=∴，43CG BC BG =-=， ∴2253FG CF CG =+=．巩固10：（1）如图10-1，矩形ABCD 中，由8个面积均为1的小正方形组成的L 型模板如图放置，则矩形ABCD 的周长为____________．（2）如图10-2，在直角坐标系中，矩形ABCO 的边OA 在x 轴上，边OC 在y 轴上，点B 的坐标为(1,3)，将矩形沿对角线AC 翻折，使得B 点落在D 点的位置，且AD 交y 轴于点E ，则D 点坐标为___________．GFE DCB AByD E OAxC图10-1 图10-2EDCG FBM A解析：（1）ABE ECF FDG △∽△∽△，2AB AEFD FG==， ∴2AB DF =，∴2AB CF =，1AB AE BEEC EF CF===， ∴AB CE =，BE CF =，∴2CE CF =，又∵4EF =，∴CE =，CF =BC，AB ， ∴矩形ABCD的周长为（2）过D 点做DF x ⊥轴于F 点，BC 与FD 的延长线交于G 点则CGD DFA △∽△，∴13CG GD CD DF AF AD ===，设CG x =，则3DF x =，1AF x =+，33GD x =-，由于3AF GD =，列得方程：()1333x x +=-，解得45x =，故45CG =，125DF =，求得D 点坐标为41255⎛⎫- ⎪⎝⎭，．巩固11：如图11-1，ABC △和DEF △是两个全等的等腰直角三角形，90BAC EDF ∠=∠=︒，DEF △的顶点E 与ABC △的斜边BC 的中点重合．将DEF △绕点E 旋转到如图11-2，线段DE 与线段AB 相交于点P ，线段EF 与线段CA 的延长线相交于点Q ．（1）求证：BPE CEQ △∽△．（2）已知BP a =，92CQ a =，求P 、Q 两点间的距离（用含a 的代数式表示）．B DFA PQECBDFAP Q图11-1 图11-2解析：（1）∵ABC △和DEF △是两个全等的等腰直角三角形，∴45B C DEF ∠=∠=∠=︒， ∴135BEP CEQ ∠+∠=︒，135CQE CEQ ∠+∠=︒，∴BEP CQE ∠=∠，又∵45B C ∠=∠=︒，∴BPE CEQ △∽△．（2）连接PQ ，∵BPE CEQ △∽△，∴BP BECE CQ=， ∵BP a =，92CQ a =，BE CE =，∴BE CE ==，∴BC =，∴3AB AC a ==，∴32AQ a =，2PAa =，在Rt APQ △中，52PQ a =．题型十三平行模型例题10 已知：如图，在梯形ABCD 中，AB//CD ，M 是AB 的中点，分别连接AC 、BD 、MD 、MC ，且AC 与MD 交于点E ，DB 与MC 交于F ．（1）求证：EF//CD ；（2）若AB a =，CD b =，求EF 的长．DFAPQFEMDCBA解析：（1）∵AB CD ∥，∴ME AM ED CD =，MF BMFC CD=， ∵AM BM =，∴AM BM CD CD =（中间过渡量），∴ME MF EF CD ED FC=⇒∥．（2）∵AM EF CD ∥∥，∴111EF AM CD =+，∴2abEF a b=+．巩固12：如图所示，在ABC △中，120BAC ∠=︒，AD 平分BAC ∠交BC 于点D ．求证：111AD AB AC=+．ABDABCEF解析：分别过B 、C 两点做AD 的平行线，分别交CA 、BA 的延长线于E 、F 两点．由于EB//AD//FC ，有111AD BE FC=+；由于60EBA BAD ∠=∠=︒，18060EAB BAC ∠=︒-∠=︒所以EAB △为正三角形，同理FAC △亦为正三角形．BE AB =∴，FC AC =．故111AD AB AC=+．题型十一角平分线定理例题11 在ABC △中，B ∠的平分线交AC 于D ，C ∠的平分线交AB 于E ，且BE CD =．求证：AB AC =．解析：由角平分线定理得到AB AD BC DC =，AC AEBC BE=， ∵BE CD =∵，∴AD DC BE AE AB BC BC AC===∴ 即AD AEAB AC=，∴AD AC CD =-∴，AE AB BE =- ∴()()AC AC CD AB AB CD -=-，整理得到()()0AC AB AC AB CD -+-= 明显0AC AB CD +-≠，故AC AB =．巩固13：（1）如图13-1，在ABC △中，C ∠=90︒，CA =3，CB =4，且CD 是C ∠的平分线．则AD 的长为__________．（2）如图13-2，I 是ABC △内角平分线的交点，AI 交对应边于D 点，求证：AI AB ACID BC+=．CADBIAD B C图13-1 图13-2解析：（1）由角平分线定理34AD ACDB BC ==，由于5AB ==，31577AD AB ==∴ B AED（2）由角平分线定理得到AI AB AC ID BD CD ==，由等比性质得到：AI AB AC AB AC ID BD CD BC++==+．巩固14：若AP PB =，2APB ACB ∠=∠，AC 与PB 相交于点D ，且4PB =，3PD =．求AD DC ⋅的值．P DCBAEA BCDP解析：过P 点做APB ∠的角平分线PE ，交AD 于E 点．∵EPD APE C ∠=∠=∠∵，且PDE CDB ∠=∠，∴PDE CDB ∴△∽△，∴3ED DC PD DB ⋅=⋅=∴，又由于PE 是角平分线，∴PA AE PD ED =∴，∵4PA PB ==∵，∴43AE ED =∴，∴73AD ED =∴， 773AD DC ED DC ⋅=⋅=∴．题型十二线束模型例题12 如图，M 、N 为ABC △边BC 上的两点，且满足BM MN NC ==，一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F ．求证：3EF DE =．法一：如下左图，过D 作DG BC ∥交AC 于G ，交AM 、AN 于P 、Q ，由线束定理可知DP PQ QG ==，∵DF AC ∥，∴DE DP AG PG 1==2，DF DQ AG QG ==2， ∴DE DF 1=4，∴EF DE =3．过E 点或F 点作BC 的平行线也可得到类似的证法．法二：如下右图，过M 作PQ DF ∥，交AB 于P ，交AF 延长线于Q ，则有AC DF PQ ∥∥， ∴PM BM AC BC 1==3，QM MNAC NC==1， ∴PM QM 1=3，由线束定理可知DE PM EF QM 1==3，即EF DE =3．过B 点或N 点作DF 的平行线也可得到类似的证法．QPABCMN DEFQP GABCMNDEF巩固15：（1）如图15-1，AB ∥CD ，AD 与BC 交于点P ，过P 点的直线与AB 、CD 分别交于E ，F ．求证：AE DFBE CF=． FED NMCBA（2）如图15-2，AB ∥CD ，AD 与BC 交于点P ，连接CA 、DB 并延长相交于O ，连接OP 并延长交CD 于M ，求证：点M 为CD 的中点．（3）如图15-3，在图15-2中，若点G 从D 点向左移动（不与C 点重合），AG 与BC 交于点P ，连OP 并延长交CD 于M ，直接写出MC 、MG 、MD 之间的关系式．AC FDE B POABCM D POAB CM D P G图15-1 图15-2 图15-3解析：（1）证明：如图1，∵AB //CD ，AD 与BC 交于点P ， ∴AEP DFP △∽△，BFP CFP △∽△， ∴AE EP DF FP =,BE EP CF FP =，∴AE BE DF CF =，∴AE DFBE CF=；（2）证明：如图2，设OM 交AB 于点N ．∵AB //CD ，∴AON COM △∽△，BON DOM △∽△，AOB COD △∽△， ∴OA AN OC CM =，OB BN OD DM =，OA OB OC OD =，∴AN BNCM DM=①， ∵ANP DMP △∽△，BNP CMP △∽△，APB DPC △∽△， ∴AN AP DM DP =，DN BP CM CP =，AP BP DP CP =，∴AN BNDM CM=②， ①÷②，DM CMCM DM=，∴CM =DM ，即点M 为CD 的中点；（3）解：MC 2=MG •MD ，理由如下：如图3，设OM 交AB 于点N ． ∵AB //CD ，∴MCP NBP △∽△，NAP MGP △∽△，∴MC MP NB NP =①，NA NPMG MP=②， ①×②，得MC NA MP NP NB MG NP MP ⨯=⨯=1，∴MC NB MG NA=． ∵AON COM △∽△，BON DOM △∽△，∴NA ON MC OM =，NB ONMD OM=， ∴NA NB MC MD =，∴MD NB MC NA =，∴MC MDMG MC=，∴MC MG MD 2=⋅．题型十三相似综合例题13 如图，点A 的坐标为(2,2)，点C 是线段OA 上的一个动点（不与O 、A 两点重合），过点C 作CDx 轴，垂足为D ，以CD 为边在右侧作正方形CDEF ．连接AF 并延长交x轴的正半轴于点B ，连接OF ．若以B 、E 、F 为顶点的三角形与OFE △相似，则点B 的坐标是．解析：要使BEF △与OFE △相似， ∵FEO FEB ∠=∠=90︒ ∴只要OE EF EB EF =或OE EF EF EB =，即BE t =2或EB t 1=2． ② 当BE t =2时，BO t =4， ∴t t t 2=42-，∴t =0（舍去）或t 3=2，∴(,)B 60． ②当EB t 1=2时，（i ）当B 在E 的左侧时，OB OE EB t 3=-=2，∴tt t23=2-2，∴t=0（舍去）或t2=3，∴(,)B10．（ii）当B在E的右侧时，OB OE EB t5=+=2，∴ttt25=2-2，∴t=0（舍去）或t6=5，∴(,)B30．巩固16：如图，Rt ABC△中，ACB∠=90︒，CD AB⊥于D，过点D作DE BC⊥，BDE△边DE上的中线BF延长线交AC于点G．（1）求证：AD BD CE CB⋅=⋅；（2）若AG FG=，求:BF GF；（3）在（2）的条件下，若BC=62BD的长度．AFECDGAFECDG P解析：（1）证明：∵CD AB⊥，∴BCD△是直角三角形．∵DE BC⊥，∴CD CE CB2=⋅．∵ABC△是直角三角形，CD AB⊥，∴CD AD BD2=⋅，∴AD BD CE CB⋅=⋅；（2）解：过G作GP DF⊥交DF于P，连结DG，∵AC BC⊥，DE BC⊥，GF DE⊥，∴四边形CEPG是矩形，∴CG EP=在Rt ADC△中，∵G是边AC中点，∴AG DG CG==．又∵AG FG=，∴DG FG=，∴GFD△是等腰三角形．∴GP是FD的中线，DP FP=，即FP DF EF1=1=22．∵CG EP=，FP EF=12，∴::PF CG=13，∴::PF FG=13．∵PFG EFB CGB△△△∽∽，∴::::CG BG EF BF PF GF===13，∴::FG BG=13，::BF GF=21；（3）解：∵BC=62:::CE BE GF BF==12，∴CE=22，BE=42∵::EF BF=13，设EF x=，则BF x=3，∴()x x222+2=9，解得x=2，∴BF=6，GF=3，AC=6，∴()AB AC BC2222+6+6263BD=43。

相似三角形常见模型(总结材料)

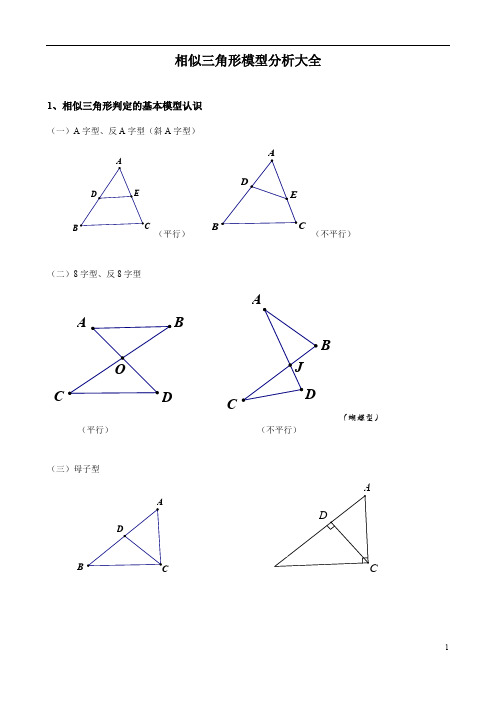
第一部分相似三角形模型分析一、相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）ABCDE（平行）CBA DE（不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行）（不平行）（三）母子型ABCDCAD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：CAD二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：OE OA OC ⋅=2．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2；（2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：EG EF BE ⋅=2．相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．AC D E B2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。

中考数学几何专项——相似模型(相似三角形)

中考数学几何专项——相似模型(相似三角形)相似模型相似模型一：A字型特征：DE∥BC模型结论：根据A字型相似模型，可以得出以下结论：C∠B=∠XXXAC²=AD×AB相似模型二：X型特征：AC∥BD模型结论：根据X型相似模型，可以得出以下结论：AO×OB=OC×ODBOC∽△DOACAOC∽△DOB相似模型三：旋转相似特征：成比例线，段共端点模型结论：根据旋转相似模型，可以得出以下结论：BEF∽△BCDDEF∽△DABAEB∽△DEC相似模型四：三平行模型特征：AB∥EF∥CD模型结论：根据三平行模型，可以得出以下结论：ABE∽△CDF相似模型五：半角模型特征：90度，45度；120度，60度模型结论：根据半角模型，可以得出以下结论：ABN∽△MAN∽△MCAABD∽△CAE∽△CBA相似模型六：三角形内接矩形模型特征：矩形EFGH或正方形EFGH内接与三角形模型结论：根据三角形内接矩形模型，可以得出以下结论：ABC∽△EFH相似模型七：十字模型特征：正方形HDGB模型结论：根据十字模型，可以得出以下结论：若AF=BE，则AF⊥BE，且为长方形若AF⊥BE，则AF=BEBDBC平行四边形，且△GME∽△HNF，△MED≌△BFA。

下面给出几个几何问题。

1.在△ABC中，AB＝AC，且有以下七个结论：①D为AC中点；②AE⊥BD；③BE：EC＝2：1；④∠ADB＝∠CDE；⑤∠AEB＝∠CED；⑥∠BMC＝135°；⑦BM：MC＝2：1.求AC和CD的比值。

2.在平行四边形ABCD中，AB∥CD，线段BC，AD相交于点F，点E是线段AF上一点且满足∠BEF=∠C，其中AF=6，DF=3，CF=2，求AE的长度。

3.在Rt△ABD中，过点D作CD⊥BD，垂足为D，连接XXX于点E，过点E作EF⊥BD于点F，若AB=15，CD=10，求4.在□ABCD中，E为BC的中点，连接AE，AC，分别交BD于M，N，求5.在平行四边形ABCD中，AB∥CD，AD，BC相交于点E，过E作EF∥AB交BD于点F。

相似三角形知识点归纳(全)

《相似三角形》—中考考点归纳与典型例题知识点1 有关相似形的概念(1)形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形．相似多边形对应边长度的比叫做相似比(相似系数)．知识点2 比例线段的相关概念、比例的性质（1）定义：在四条线段d c b a ,,,中，如果b a 和的比等于d c 和的比，那么这四条线段d c b a ,,,叫做成比例线段，简称比例线段．注：①比例线段是有顺序的，如果说a 是d c b ,,的第四比例项，那么应得比例式为：ad c b =． ②()()()a bc d a c d c b d b ad bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩，交换内项，交换外项．同时交换内外项核心内容：bc ad = （2）黄金分割：把线段AB 分成两条线段)(,BC AC BC AC >，且使AC 是BC AB 和的比例中项，即2AC AB BC =⋅，叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AB AC 215-=≈0.618AB．即12AC BC AB AC ==简记为：长短＝全长注：①黄金三角形：顶角是360的等腰三角形②黄金矩形：宽与长的比等于黄金数的矩形（3）合、分比性质：a c abcd b d b d±±=⇔=．注：实际上，比例的合比性质可扩展为：比例式中等号左右两个比的前项，后项之间发生同样和差变化比例仍成立．如：⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a 等等．（4）等比性质：如果)0(≠++++====n f d b nmf e d c b a那么ban f d b m e c a =++++++++ ．知识点3 比例线段的有关定理平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例. 已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE =====或或或或等. 特别在三角形中：由DE ∥BC 可得：ACAEAB AD EA EC AD BD EC AE DB AD ===或或知识点4 相似三角形的概念（1）定义：对应角相等，对应边成比例的三角形，叫做相似三角形．相似用符号“∽”表示，读作“相似于” ．相似三角形对应边的比叫做相似比(或相似系数)．相似三角形对应角相等，对应边成比例．注：①对应性：即把表示对应顶点的字母写在对应位置上 ②顺序性：相似三角形的相似比是有顺序的．③两个三角形形状一样，但大小不一定一样． ④全等三角形是相似比为1的相似三角形．（2）三角形相似的判定方法1、平行法：（图上）平行于三角形一边的直线和其它两边(或两边的延长线)相交，所构成的三角形与原三角形相似.2、判定定理1：简述为：两角对应相等，两三角形相似．AA3、判定定理2：简述为：两边对应成比例且夹角相等，两三角形相似．SAS4、判定定理3：简述为：三边对应成比例，两三角形相似．SSS5、判定定理4：直角三角形中，“HL ” 全等与相似的比较：三角形全等三角形相似两角夹一边对应相等(ASA) 两角一对边对应相等(AAS) 两边及夹角对应相等(SAS) 三边对应相等(SSS)、(HL ）两角对应相等两边对应成比例，且夹角相等三边对应成比例“HL ”如图，Rt △ABC 中，∠BAC=90°，AD 是斜边BC 上的高，则∽＝＝＞AD 2=BD ·DC ，∽＝＝＞AB 2=BD ·BC ，∽＝＝＞AC 2=CD ·BC .知识点5 相似三角形的性质(1)相似三角形对应角相等，对应边成比例．(2)相似三角形周长的比等于相似比．E BD DB C(3)相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比． (4)相似三角形面积的比等于相似比的平方．知识点6 相似三角形的几种基本图形：（1）如图：称为“平行线型”的相似三角形（有“A 型”与“X 型”图）(2) 如图：其中∠1=∠2，则△ADE ∽△ABC 称为“斜交型”的相似三角形。

相似三角形模型总结2(比例式、等积式的常见证明方法)

相似三角形模型总结2(比例式、等积式的常见证明方法)XXX∠XXX，∴△AEB∽△CEB，∴AE/AC＝EB/EC.又∵△ADB∽△ACB，∴AD/AC＝DB/BC.∴AE/AD＝EB/DB，∴AE/AC＝EB/EC＝EB/(EB+DB)。

ACADAE＝AC·EB/(EB+DB)＝AC·EB/AB.又∵△ABE∽△CDE，∴EB/DE＝AB/CD，∴EB＝AB·DE/CD.∴AE＝AC·AB·DE/(AB·DE+CD·EB)＝AC·AB·DE/(AB·DE+CD·AB·DE/CD)＝AC·AB·DE/(AB+DB)＝AC·DE/AD.又∵△ADE∽△ACB，∴DE/AC＝AD/AB，∴DE＝AC·AD/AB.∴AE＝AC·DE/AD＝AC·AC·AD/(AB·AD)＝AC2/AB，∴AE/AC＝AC/AB＝AC/AD。

AE/AC＝AD/AC，即AE/AC＝AE/AD-∵AC=AD，∴AE/AC＝AE/AE-DE，∴AE/AC＝DE/AE，∴AE2＝AC·DE，∴AE/AC＝DE/AE＝AE2/AC·AE＝AE/AD，即AE＝AC·AD/AB＝AC2/AB。

XXX，∴＝.1.由于文章中没有明显的格式错误，直接删除明显有问题的段落。

2.将原文中的符号改为中文，重新表述如下：已知在三角形ABE和ACB中，∠BAE=∠CAB，因此△ABE∽△ACB。

根据相似三角形的性质，可以得到AE/AB=AC/AE，所以AE²=AB×AC。

又因为AB=AD，所以AE²=AD×AC。

因此，DE²=AE²-BE²=AD×AC-BE²=BE×CE。

相似三角形典型模型及例题

1：相似三角形模型一：相似三角形判定的根本模型〔一〕 A 字型、反 A 字型〔斜 A 字型〕〔平行〕〔不平行〕〔二〕 8 字型、反 8 字型AA BBO JC DC D〔蝴蝶型〕〔平行〕〔不平行〕〔三〕母子型〔四〕一线三等角型：三等角型相似三角形是以等腰三角形〔等腰梯形〕或者等边三角形为背景，一个与等腰三角形的底角相等的顶点在底边所在的直线上，角的两边分别与等腰三角形的两边相交如下图：〔五〕一线三直角型：三直角相似可以看着是“一线三等角〞中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的根本图形如下：当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。

〔六〕双垂型：二：相似三角形判定的变化模型旋转型：由 A 字型旋转得到8 字型拓展AE FGB C共享性一线三等角的变形一线三直角的变形2：相似三角形典型例题〔 1〕母子型相似三角形例 1：如图，梯形ABCD 中， AD ∥ BC，对角线 AC、 BD 交于点 O， BE∥ CD 交 CA 延长线于 E．求证： OC 2OA OE．例 2：：如图，△ABC 中，点 E 在中线 AD 上 ,DEBABC ．求证：〔 1〕DB2DE DA ；〔2〕 DCE DAC ．BDEA C例 3：：如图，等腰△ABC 中， AB＝ AC，AD⊥ BC 于 D， CG∥ AB， BG 分别交 AD 、 AC 于 E、 F．求证： BE 2EF EG ．1、如图，AD 为△ABC 的角平分线， EF 为 AD 的垂直平分线．求证：FD2FB FC．2、： AD 是 Rt△ABC 中∠ A 的平分线，∠ C=90°，EF 是 AD 的垂直平分线交AD 于 M ，EF、BC 的延长线交于一点 N。

相似三角形经典总复习(含知识点习题)

第23章:相似三角形第一节:比例线段知识点:1、相似多边形：从几何直观上来说，两个图形如果形状一致，而大小不同，则称这两个图形相似，具体到多边形，称之为相似多边形。

从严谨定义上来说，如果两个多边形各边成比例，各角相等，则称这两个多边形为相似多边形。

2、比例线段：一、线段的比：如果用同一长度单位量得两条线段a 、b 的长度分别为m ，n ，则m ∶n 就是线段a ，b 的比，记作a ∶b ＝m ∶n 或a mb n=，其中a 叫做比例前项，b 叫做比例后项。

二、比例线段：四条线段，如果其中两条线段的比与另外两条线段的比相同，则称这四条线段成比例线段，简称比例线段。

例如线段a 、b 、c 、d ，如果a cb d=或者（::a b c d =）a 、b 、c 、d 成比例线段，这里要注意，a 、b 、c 、d 必须按顺序写出，不能写成b c a d =或a d b c=。

三、比例外项、比例内项、第四比例项、比例中项：若a cb d=，则称a 、d 为比例外项，b 、c 、为比例内项，d 为第四比例项，如果b ＝c ，则称b 为a 、c 的比例中项，可记做（2b ac =）3、比例性质： 1、基本性质：如果a cb d=，则根据等式的基本性质，两边同时乘以bd 得ad bc =。

2、合比性质：如果a cb d=，则根据等式的基本性质，两边同时加上1或－1得a b c d b d ±±=。

在此处键入公式。

a b c db d±±=3、等比性质：如果a c mb d n===（0b d n +++≠），则a c m a c mb d n b d n+++====+++，运用这个性质时，一定要注意0b d n +++≠的条件。

4、黄金分割：把线段AB 分成两条线段AP 、PB （AP ＞PB ），如果AP 是线段PB 和AB 的比例中项，则线段AP 把线段AB 黄金分割，点P 叫做线段AB 的黄金分割点。

相似三角形12种基本模型证明

相似三角形12种基本模型证明相似三角形是指拥有相同形状但不同大小的三角形。

在三角形中，如果它们的对应角度相等，那么它们就是相似三角形。

相似三角形一般用比例关系表示。

下面是相似三角形12种基本模型的证明：1. AAA相似模型如果两个三角形的三个角分别相等，则它们是相似的。

证明：三角形的三个角之和为180度。

如果两个三角形的三个角分别相等，那么它们的三个角和也相等，即这两个三角形的三个角和相等，因此它们是相似的。

2. AA相似模型如果两个三角形中有两个对应角相等，则它们是相似的。

证明：假设两个三角形的对应角分别为A和A’，B和B’，C和C’。

由于A和A’相等，B和B’相等，那么它们的第三个对应角C和C’也必须相等。

因此，这两个三角形的三个角分别相等，它们是相似的。

3. SSS相似模型如果两个三角形的三条边分别成比例，则它们是相似的。

证明：假设两个三角形的三条边为a, b, c和a’, b’, c’。

由于它们是成比例的，即a/a’= b/b’= c/c’，那么它们的三边比例相等，即它们是相似的。

4. SAS相似模型如果两个三角形中有两条边成比例，且夹角相等，则它们是相似的。

证明：假设两个三角形的两条边为a, b和a’, b’，夹角为C和C’。

由于它们是成比例的，即a/a’= b/b’，那么它们的三边比例相等。

又由于它们的夹角相等，即C = C’，因此它们是相似的。

5. ASA相似模型如果两个三角形中有两个角相等，且它们对应的两条边成比例，则它们是相似的。

证明：假设两个三角形的两个对应角分别为A和A’，B和B’，且对应的两条边分别为a, a’和b, b’。

由于它们的两条边成比例，即a/a’= b/b’，那么它们的三边比例相等。

又由于它们的两个角相等，即A = A’，因此它们是相似的。

6. HL相似模型如果两个三角形中有一条边和一条斜边分别成比例，且这两条边夹角相等，则它们是相似的。

证明：假设两个三角形的一条边为b，斜边为c，且夹角为C，另一个三角形的一条边为b’，斜边为c’，且夹角为C’。

(完整word版)相似五大模型总结老师,推荐文档

学科教师辅导讲义学员编号：年级：初三课时数：3学员姓名：辅导科目：数学学科教师：吴猛授课类型T(同步知识主题) C （专题方法主题）T （学法与能力主题）授课日期及时段2016-07-27相似三角形模型总结模型一：A型或反A型1．（2011•河北模拟）将三角形纸片△ABC按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．已知AB=AC=6，BC=8，若以点B′，F，C为顶点的三角形与△ABC相似，那么BF的长度是（）A．B．4 C．或2 D．4或考点：相似三角形的性质；解一元一次方程；翻折变换（折叠问题）．专题：计算题；压轴题．分析：根据折叠得到BF=B′F，根据相似三角形的性质得到=，设BF=x，则CF=8﹣x，即可求出x的长，得到BF的长，即可选出答案．解答：解：∵△ABC沿EF折叠B和B′重合，∴BF=B′F，设BF=x，则CF=8﹣x，∵当△B′FC∽△ABC，∴=，∵AB=6，BC=8，∴=，解得：x=，即：BF=，当△FB′C∽△ABC，，，解得：x=4，当△ABC∽△CB′F时，同法可求B′F=4，故BF=4或，故选：D．点评：本题主要考查了相似三角形的性质，折叠问题，解一元一次方程等知识点，解此题的关键是设BF=x，能正确列出方程．1、如图：△ABC中，D是AB上一点，AD=AC，BC边上的中线AE交CD于F。

2、求证：3、BDA CFE答案：证明：（方法一）如图延长AE到M使得EM=AE，连接CM∵BE=CE，∠AEB=∠MEC ∴△BEA≌△CEM ∴CM=AB，∠1=∠B ∴AB∥CM∴∠M=∠MAD，∠MCF=∠ADF∴△MCF∽△ADF ∴∵CM=AB，AD=AC ∴（方法二）过D作DG∥BC交AE于G则△ABE∽△ADG，△CEF∽△DGF∴，∵AD=AC，BE=CE ∴模型二：X型和反X型1．（2012•朝阳）如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，并且AE=4，EF=8，FC=12，则正方形与其外接圆形成的阴影部分的面积为80π﹣160．考点：相似三角形的判定与性质；勾股定理；正方形的性质；正多边形和圆．专题：压轴题．分析：首先连接AC，则可证得△AEM∽△CFM，根据相似三角形的对应边成比例，即可求得EM与FM的长，然后由勾股定理求得AM与CM的长，则可求得正方形与圆的面积，则问题得解．解答：解：连接AC，∵AE丄EF，EF丄FC，∴∠E=∠F=90°，∵∠AME=∠CMF（对顶角相等），∴△AEM∽△CFM，∴，∵AE=4，FC=12，∴，∴EM=2，FM=6，在Rt△AEM中，AM==2，在Rt△FCM中，CM==6，∴AC=8，在Rt△ABC中，AB=AC•sin45°=8×=4，∴S正方形ABCD=AB2=160，圆的面积为：π•（）2=80π，∴正方形与其外接圆之间形成的阴影部分的面积为80π﹣160．故答案为：80π﹣160．点评：此题考查了相似三角形的判定与性质，正方形与圆的面积的求解方法，以及勾股定理的应用．此题综合性较强，解题时要注意数形结合思想的应用．2、如图，弦和弦相交于内一点，求证：.思路点拨：题目中求证的是等积式，我们可以转化为比例式，从而找到应证哪两个三角形相似.同时圆当中同弧或等弧所对的圆周角相等要会灵活应用.证明：连接，.在∴∽∴.3．如图，△ABC≌△ADE且∠ABC=∠ADE，∠ACB=∠AED，BC．DE交于点O．则下列四个结论中，①∠1=∠2；②BC=DE；③△ABD∽△ACE；④A．O、C．E四点在同一个圆上，一定成立的有（）A． 1个B． 2个C． 3个D． 4个【答案】D模型三：字母型1．如图，点A ，B ，C ，D 为⊙O 上的四个点，AC 平分∠BAD，AC 交BD 于点E ，CE=2，CD=3，则AE 的长为（）A ．2B ．2.5C ．3D ．3.5 【答案】B. 2．（2015•南通）如图，AB 为⊙O 的直径，C 为⊙O 上一点，弦AD 平分∠BAC ，交BC 于点E ，AB=6，AD=5，则AE 的长为（）A ．2.5B ．2.8C ．3D ．3.2考点：相似三角形的判定与性质；勾股定理；圆周角定理．专题：压轴题．分析：连接BD 、CD ，由勾股定理先求出BD 的长，再利用△ABD ∽△BED ，得出=，可解得DE 的长，由AE=AD﹣DE 求解即可得出答案．解答：解：如图1，连接BD 、CD ，，∵AB 为⊙O 的直径，∴∠ADB=90°，∴BD=，∵弦AD 平分∠BAC ，∴CD=BD=，∴∠CBD=∠DAB ，在△ABD 和△BED 中，∴△ABD ∽△BED ，∴=，即=，解得DE=， ∴AE=AD ﹣DE=5﹣=2.8．故选：B点评：此题主要考查了三角形相似的判定和性质及圆周角定理，解答此题的关键是得出△ABD ∽△BED ．3、已知如图，CD 是Rt △ABC 斜边AB 上的高，E 为BC 的中点，ED 的延长线交CA 于F 。

相似三角形题型归纳总结非常全面

相似三角形题型归纳一、比例的性质：二、成比例线段的概念： 1．比例的项：在比例式::a b c d =（即a cb d =）中，a ，d 称为比例外项，b ，c 称为比例内项．特别地，在比例式::a b b c =（即a bb c=）中，b 称为a ，c 的比例中项，满足b ac 2=．2．成比例线段：四条线段a ，b ，c ，d 中，如果a 和b 的比等于c 和d 的比，即a cb d=，那么这四条线段a ，b ，c ，d 叫做成比例线段，简称比例线段．3．黄金分割：如图，若线段AB 上一点C ，把线段AB 分成两条线段AC 和BC （AC BC >），且使AC 是AB 和BC 的比例中项（即AC AB BC 2=⋅），则称线段AB 被点C 黄金分割，点C 叫线段AB 的黄金分割点，其中.AC AB AB ≈0618，BC AB =.AB ≈0382，AC 与AB 的比叫做黄金比．（注意：对于线段AB 而言，黄金分割点有两个．）三、平行线分线段成比例定理 1．平行线分线段成比例定理A两条直线被三条平行线所截，所得的对应线段成比例，简称为平行线分线段成比例定理．如图：如果123////l l l ，则AB DE BC EF =，AB DE AC DF =，BC EFAC DF=．AD BE CF1l 2l 3lA D BE CF 1l 2l 3l【小结】若将所截出的小线段位置靠上的（如AB ）称为上，位置靠下的称为下，两条线段合成的线段称为全，则可以形象的表示为=上上下下，=上上全全，=下下全全．2．平行线分线段成比例定理的推论平行于三角形一边的直线，截其它两边（或两边的延长线），所得的对应线段成比例．如图：如果EF//BC ，则AE AF EB FC =，AE AF AB AC =，BE CFAB AC=． ABC E FFEC BA平行线分线段成比例定理的推论的逆定理若AE AF EB FC =或AE AF AB AC =或BE CF AB AC=，则有EF//BC ．【注意】对于一般形式的平行线分线段成比例的逆定理不成立，反例：任意四边形中一对对边的中点的连线与剩下两条边，这三条直线满足分线段成比例，但是它们并不平行．【小结】推论也简称“A ”和“8”，逆定理的证明可以通过同一法，做'//EF BC 交AC 于'F 点，再证明'F 与F 重合即可．四、相似三角形的定义、性质和判定 1．相似图形①定义：对应角相等，对应边成比例的图形叫做相似图形．对应边的比例叫做相似比．相似图形是形状相同，大小不一定相同．相似图形间的互相变换称为相似变换．②性质：两个相似图形的对应角相等，对应边成比例．2．相似三角形的定义3．相似三角形的性质 ①相似三角形的对应角相等．如图，∽△△ABC A B C '''，则有 A A '∠=∠，B B C C ''∠=∠∠=∠，．②相似三角形的对应边成比例．如图，∽△△ABC A B C '''，则有AB BC ACk A B B C A C ===''''''（k 为相似比）． ③相似三角形的对应边上的中线，高线和对应角的平分线成比例，都等于相似比．如图，△ABC ∽△A B C '''，AM AH 、和AD 是△ABC 中BC 边上的中线、高线和角平分线，A M ''、A H ''和A D ''是△ABC '''中B C ''边上的中线、高线和角平分线，则有AB BC AC AM AH ADk A B B C A C A M A H A D ======''''''''''''④相似三角形周长的比等于相似比．如图，△ABC ∽△A B C '''，则有AB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++． ⑤相似三角形面积的比等于相似比的平方．如图，△ABC ∽△A B C '''，则有 △△ABC A B C BC AHS BC AH k S B C A H B C A H 2'''1⋅⋅2==⋅=1''''''''⋅⋅24．相似三角形的判定判定定理判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．简称为两角对应相等，两个三角形相似．如图，如果'A A ∠=∠，'B B ∠=∠，则△∽△ABC A B C '''．判定定理2：如果两个三角形的三组对应边成比例，那么这两个三角形相似．简称为三边对应成比例，两个三角形相似．如图，如果AB BC ACA B B C A C ==''''''，则 △∽△ABC A B C '''．判定定理3：如果两个三角形的两组对应边成比例，并且对应的夹角相等，那么这两个三角形相似．简称为两边对应成比例且夹角相等，两个三角形相似．如图，如果AB ACA B A C =''''，'A A ∠=∠，则△∽△ABC A B C '''．五、“A ”字和“8”字模型六、与内接矩形的有关的相似问题如图，已知四边形DEFG 是△ABC 的内接矩形，E 、F 在BC 边上，D 、G 分别在AB 、AC 边上，则有：△∽△ADG ABC ，DG ANBC AM=．特别地，当BAC ∠=90︒时，有△∽△∽△∽△ADG EBD FGC ABC ．NM GFE DCB AGFEDCBA七、“A ”字和“8”字模型的构造“A ”字和“8”字模型的构造常常作平行线，常见的作平行线的方法：G EDCAGFEDCBA G FE DC B ADEFCBAGA HDFBECAGDF BEC八、斜“8”模型九、斜“A”模型十、射影定理十一、三平行模型十一二、三垂直模型十三、角平分线定理十四、线束模型题型一比例的性质和成比例线段的概念例题1 （1）已知::::x y z =135，则x y zx y z+3--3+的值是_______．（2）若x y z 234==．则x y z x y-+3=3-_______．（3）若a b c 2=3=4，且abc ≠0，则a bc b+-2的值是_______．解析（1）设x k =，y k =3，z k =5．∴x y z k k k x y z k k k +3-+9-55==--3+-9-53；（2）113；（3）-2 巩固1：（1）如果:2:3x y =，则下列各式不成立的是（） A ．53x y y += B ．13y x y -= C ．123x y = D ．1314x y +=+ （2）已知：23a c e b d f ===，求值：①a cb d++；②2323a c e b d f -+-+．（3）已知b c a c a b a b c a b c +-+-+-==，求()()()a b b c a c abc+++的值．解析：（1）A 为合比性质，B 为分比性质，C 显然正确，D 错误，由于11x y ≠，不能用等比定理．故答案为D ．（2）由等比性质直接可以得到23a c b d +=+；232233a c eb d f -+=-+．（3）当0a bc ++≠时，()()()b c a c a b a b c b c a c a b a b c a b c a b c+-+-+-+-++-++-====1++ 于是：2,2,2b c a a c b a b c +=+=+=，()()()a b b c a c abc+++=8．当0a b c ++=时，()()()()()()a b b c a c c a b abc abc+++-⋅-⋅-==-1．本题答案为1-或8．题型二平行线分线段成比例定理例题2（1）如图2-1，已知∥∥l l l 123，用面积法证明：AB DEBC EF=．（2）如图2-2，∥∥AD BE CF ，若AB =4，AC =10，DE =5，则DF =______．（3）如图2-3，∥∥l l l 123，AB =3，BC =5，DF =12，则_______DE =，______EF =．A D BECF l 12l 3lAD B ECFA DBECF l 12l l 3图2-1 图2-2 图2-3（1）如图所示，连接AE ，BD ，BF ，CE ．△△ABECBES AB BC S =∴． ∥AD BE ∵，∥BE CF ，△△ABE DEB S S =∴，△△CBE FEB S S =．△△△△ABE EDB CBE EFB S S AB DEBC S S EF===∴．（2）252；（3）92，152．巩固2：（1）如图2-1，直线∥∥l l l 123，已知.cm AG =06，.cm BG =12，.cm CD =15，CH =_____．（2）如图2-2，在△ABC 中，D 、E 分别为AB 、AC 边上的点，若AD BD 2=3，AE =3，则AC =______（3）如图2-3，AB ∥DE ，AE 与DB 交于C ，AC =3，BD =3，CD =2，则CE =______A CH GDBl 1l 2l 3B ADEABC图2-1 图2-2 图2-3解析：（1）0.5cm ；（2）152；（3）6 题型三相似三角形的定义、性质和判定例题3如图，直角梯形ABCD 中，∠ADC =90︒，∥AD BC ，点E 在BC 上，点F 在AC上，∠∠DFC AEB =．（1）求证：△∽△ADF CAE ．（2）当AD =8，DC =6，点E 、F 分别是BC 、AC 的中点时，求直角梯形ABCD 的面积．解析：（1）∵∥AD BC ，∴∠∠DAF ACE =，∵∠∠DFC AEB =，∴DFA AEC ∠=∠，∴△∽△ADF CAE（2）∵AD =8，DC =6，∴AC =10，又∵F 是AC 的中点，∴AF =5 ∵△∽△ADF CAE ，∴AD AF CA CE =，∴CE 85=10，∴CE 25=4，∵E 是BC 的中点， ∴BC 25=2，∴直角梯形ABCD 的面积125123⎛⎫=⨯+8⨯6= ⎪222⎝⎭A D BECF l 12l 3l F EDCBA巩固3：（1）下列所给条件中，可以判断△ABC 与△DEF 相似的是（） A ．90A ∠=︒，90F ∠=︒，5AC =，13BC =，10DF =，26EF = B ．85C ∠=︒，85E ∠=︒，AC DEBC DF=C ．1AB =， 1.5AC =，2BC =，8EF =，10DE =，16FD = D ．46A ∠=︒，80B ∠=︒，45E ∠=︒，80F ∠=︒（2）如图1，在△ABC 中，点D 是BC 边上的中点，且AD AC =，DE BC ⊥，交BA 于点E ，EC 与AD 相交于点F ．求证：△∽△ABC FCD ．（3）如图2，△ABC 为等腰直角三角形，BD CE BC 21⋅=2，求证：△∽△ACE DBA ．AEF DADB CE图1 图2解析：（1）D ；（2）AD AC =∵，FDC ACB ∠=∠∴；DE ∵垂直平分BC ，EB EC =∴， ∴ABC FCD ∠=∠，△∽△ABC FCD ∴.（3）由等腰直角三角形得到BC =条件变为BD CE AB AB AC 2221⋅=⋅2==2，条件变为比例形式：BD BAAC CE=，由于DBA ACE ∠=180︒-45︒=∠，∴△∽△ACE DBA ．题型四 “A ”字和“8”字模型例题4 （1）如图4-1，已知□ABCD 中，过点B 的直线顺次与AC 、AD 及CD 的延长线相交于点E 、F 、G ，若BE =5，EF =2，则FG 的长为____________．（2）如图4-2，已知在□ABCD 中，M 、N 为AB 的三等分点，DM 、DN 分别交AC 于P 、Q 两点，则AP:PQ:QC =____________．G BAF DC EC AD M N PQ图4-1 图4-2解析：（1）∵四边形ABCD 为平行四边形，∴//AD BC ∴△∽△AEF CEB ，△∽△GFD GBC ，∴AF EF CB EB 2==5，∴DF AD AF CB CB -3==5∴FG DF BG CB 3==5，即FG FG 3=+75．得.FG =105．（2）由DC ∥AB ，得AP AM PC AB 1==3，AP AC 1=4，同理AQ AC 2=5，PQ AC 2=51-4AC =AC 320，QC =AC 35，故1::::::4AP PQ QC 33==5312205．巩固4：（1）如图4-1，在ABC △中，M 、E 把AC 边三等分，MN//EF//BC ，MN 、EF 把ABC △分成三部分，则自上而下部分的面积比为．（2）如图4-2，AB 、CD 、EF 都与BD 垂直，垂足分别是B 、D 、F ，且1AB =，3CD =，则:EF CD 的值为__________．（3）如图4-3，已知在平行四边形ABCD 中，M 为AB 的中点，DM ，DB 分别交AC 于P ，Q 两点，则::AP PQ QC =___________．NM FE C BAAB CEF DA CBQPD图4-1 图4-2 图4-3解析：（1）1:3:5；（2）14；（3）AQ CQ AC 1==2∵，又AP AM PC CD 1==2，AP AC 1=3∴ PQ AC AC 111⎛⎫=1--= ⎪236⎝⎭∴，::::AP PQ QC =213∴．题型五与内接矩形有关的相似问题例题5（1）如图5-1，△ABC 中，正方形EFGH 的两个顶点E 、F 在BC 上，另两个顶点G 、H 分别在AC 、AB 上，BC =15，BC 边上的高AD =10，求正方形EFGH S ．（2）如图5-2，已知△ABC 中，四边形DEGF 为正方形，D ，E 在线段AC ，BC 上，F ，G 在AB 上，如果ADF CDE S S ∆∆==1，BEG S ∆=3，求△ABC 的面积．HAB C D E FGACDEGB图5-1 图5-2解析：（1）设正方形EFGH 的边长为x ，AD 、HG 的交点为M ，则有AM HG AD BC =，即x x10-=1015，解得，x =6，故EFGH S 2=6=36正方形（2）设正方形边长为x ，则AF x 2=，CI x 2=，BG x6=．由△∽△CDE CAB ，得CI DE CH AB =，∴xxx x x x2=28++，解得x =2， ∴AB =6，CH =3，∴ABC S AB CH ∆1=⋅=92巩固5：如图，已知ABC △中，AC =3，BC =4，C ∠=90︒，四边形DEGF 为正方形，其中D 、E 在边AC 、BC 上，F 、G 在AB 上，求正方形的边长．GF EDC B A H IDC EGF ABGFED CBA H MACDEG BIHHPED CB A解析：法一：由勾股定理可求得AB =5，由AB CH AC BC ⋅=⋅可得.CH =24．由CDE CAB △∽△可得DE CI AB CH =，设正方形的边长为x ，则..x x 24-=524，解得x 60=37．法二：设CE k =4，则DE k =5，∴GE k =5，BE k 25=3． ∴CE BE +=4，即k k 254+=43，解得k 12=37，∴DE k 60=5=37．题型六 “A 字和“8”字模型的构造例题6如图，ABC △中，D 为BC 边的中点，延长AD 至E ，延长AB 交CE 的延长线于P ．若AD DE =2，求证：3AP AB =．解析：如图，过点D 作PC 的平行线，交AB 于点H ． ∵HD PC ∥，AH ADAD DE AH PH PH DE=2⇒==2⇒=2， HD PC ∥，BH BDBD CD BH PH PH CD=⇒==1⇒=， ∴AP AH PH PH =+=3，AH BH AB PH BH =+=2=2， ∴AB BH PH ==，∴AP PH AB =3=3．还可用如下辅助线来证此题：A BCD EKPABCDEK P PKED CBA巩固6：如图，已知线段AB ∥CD ，AD 与BC 相交于点K ，E 是线段AD 上一动点．（1）若BK KC 5=2，求CDAB的值；（2）连接BE ，若BE 平分∠ABC ，则当AE AD 1=2时，猜想线段AB 、BC 、CD 三者之间有怎样等量关系？请写出你的结论并予以证明．再探究：当AE AD n1=()n >2，而其余条件不变时，线段AB 、BC 、CD 三者之间又有怎样的等量关系？请直接写出你的结论，不必证明．解析：（1）∵BK KC 5=2，∴CK BK 2=5，又∵CD ∥AB ，∴KCD KBA △∽△，∴CD CK AB BK 2==5（2）当BE 平分ABC ∠，AE AD 1=2时，AB BC CD =+；证明：取BD 的中点为F ，连接EF 交BC 于G 点，由中位线定理，得EF//AB//CD ，∴G 为BC 的中点，GEB EBA ∠=∠，又∵EBA GBE ∠=∠，∴GEB GBE ∠=∠，∴EG BG BC 1==2，ABDECC DEKBA而GF CD 1=2，EF AB 1=2，EF EG GF =+，即：AB BC CD 111=+222；AB BC CD ∴=+；当AE AD n1=(n >2)时，(1)BC CD n AB +=-．题型七斜“A ”和斜“8”模型例题7如图，在ABC △中，AD BC ⊥于D ，CE AB ⊥于E ，ABC △的面积是BDE △面积的4倍，6AC =，求DE 的长．解析：∵AD BC ⊥，CE AB ⊥，ABD CBE ∠=∠， ∴ABD CBE △∽△， ∴BE BCBD AB =，∵EBD CBA ∠=∠，∴BED BCA △∽△，∴11322DEDE AC AC===⇒==．巩固7：（1）如图，ABC △是等边三角形，点D ，E 分别在BC ，AC 上，且BD CE =，AD 与BE 相交于点F ．求证：①BD AD DF 2=⋅；②AF AD AE AC ⋅=⋅；③BF BE BD BC ⋅=⋅．（2）如图，四边形ABCD 是菱形，AF AD ⊥交BD 于E ，交BC 于F ．求证：AD DE DB 21=⋅2．FECDBAA DEF C解析：（1）∵等边ABC △，∴AB BC =，ABC ACB BAC ∠=∠=∠=60︒ ∵BD CE = ∴ABD BCE △≌△．∴BAD CBE ∠=∠，∴BFD BAD ABE CBE ABE ABC ∠=∠+∠=∠+∠=∠ ∴ABD BFD △∽△ ∴BD DFAD BD=，∴BD AD DF 2=⋅． ②证明AFE ACD △∽△即可． ③证明BFD BCE △∽△即可．（2）方法一：取DE 中点M ，连接AM ， ∵AF AD ⊥，M 为DE 中点∴MA MD DE 1==2，∴∠1=∠2，又∵AB AC =，∴∠2=∠3，∴∠1=∠3，∴DAM DBA △∽△，∴DA DM DB 2=⋅，∴AD DE DB 21=⋅2．方法二：取BD 中点N ，连接AN ．由等腰三角形的性质可知：AN BD ⊥，又∵EAD ∠=90︒，∴AND EAD △∽△，∴AD DN DE 2=⋅，又∵DN BD 1=2，∴AD DE BD 21=⋅2．总结：考查斜“A ”和斜“8”常见结论，看到比例乘积想到斜“A ”和斜“8”，也要会找ADEF CM123ED CAB巩固8：在等边ABC △中，点D 为AC 上一点，连结BD ，直线l 与AB ，BD ，BC 分别相交于点E 、P 、F ，且BPF ∠=60︒．（1）如图8-1，写出图中所有与BPF △相似的三角形，并选择其中一对给予证明．（2）若直线l 向右平移到图8-2、图8-3的位置时（其它条件不变），（1）中的结论是否仍然成立？若成立，请写出来（不证明），若不成立，请说明理由．（3）探究：如图8-1，当BD 满足什么条件时（其它条件不变），PF PE 1=2？请写出探究结果，并说明理由．（说明：结论中不得含有未标识的字母）图3图2图1lP FEDCB AFP EDC BAlFPEDCBA 图3图2l P F E D CB A l FPEDC BA图3lPFED CB A 图8-1 图8-2 图8-3 解析：（1）BPF EBF △∽△与BPF BCD △∽△，以BPF EBF △∽△为例，证明如下： ∵BPF EBF ∠=∠=60，BFP BFE ∠=∠，∴BPF EBF △∽△．（2）均成立，均为BPF EBF △∽△，BPF BCD △∽△．（3）BD 平分ABC ∠时，PF PE 1=2．证明：∵BD 平分ABC ∠，∴ABP PBF ∠=∠=30∵BPF ∠=60，∴BFP ∠=90，∴PF PB 1=2，又BEF ABP ∠=60-30=30=∠，∴BP EP =，∴PF PE 1=2．题型八射影定理例题8如图，已知AD 、CF 是ABC △的两条高，EF AC ⊥与E ，交CB 延长线于G ，交AD 于H ，求证：EF EH EG 2=⋅．解析：∵CF AB ⊥，EF AC ⊥，∴EF AE CE 2=⋅，又由AD BC ⊥可知，AEH CEG ∠=∠=90︒，EAH EGC ∠=∠，∴AEH GEC △∽△，∴EH EAEC EG=， ∴EH EG EA EC ⋅=⋅，∴EF EH EG 2=⋅．巩固9：（1）如图9-1，在ABC △中，CD AB ⊥于D ，DE AC ⊥于E ，DF BC ⊥于F ．求证：CEF CBA △∽△．（2）如图9-2，在Rt ABC △中，AD 是斜边BC 上的高，DE AC ⊥于E ，DF AB ⊥于F ，求证：AB FB FD AC EC ED44⋅=⋅． GHFED CB ACAEFDBBAEDC F图9-1 图9-2解析：（1）分别在ADC △与CDB △中由射影定理得到：2CD CE CA =⋅，2CD CF CB =⋅， CE CA CF CB ⋅=⋅∴，即CE CFCB CA=，ECF BCA ∠=∠∵，ECF BCA ∴△∽△．（2）由射影定理可以依次得到422422AB BD BC BF ABAC DC BC EC AC⋅⋅==⋅⋅，于是仅需证明AB FDAC ED=，由于BDA ADC △∽△，DF DE 、分别是AB 与AC 上的高，所以有AB DFAC DE=，得证．题型九三垂直模型例题9如图，M 为线段AB 的中点，AE 与BD 交于点C ，DME A B α∠=∠=∠=，且DM交AC 于F ，ME 交BC 于G ．（1）求证：AMF BGM △∽△．（2）连接FG ，如果45α=︒，42AB =，3AF =，求FG 的长．解析：（1）由题意得，DME A B α∠=∠=∠=， ∴180AMF BMG α∠+∠=︒-，180AMF AFM α∠+∠=︒-，∴BMG AFM ∠=∠，又E A B α∠=∠=∠=，∴△AMF ∽△BGM ．（2）∵AMF BGM △∽△，∴AM AF BG BM =∴，∵M 为AB 的中点，∴12AM BM AB ==∴， ∵42AB =，3AF =，∴83BG =∴， ∵45α=︒∵，∴90ACB ∠=︒∴，4AC BC ==，∴1CF AC AF =-=∴，43CG BC BG =-=， ∴2253FG CF CG =+=．巩固10：（1）如图10-1，矩形ABCD 中，由8个面积均为1的小正方形组成的L 型模板如图放置，则矩形ABCD 的周长为____________．（2）如图10-2，在直角坐标系中，矩形ABCO 的边OA 在x 轴上，边OC 在y 轴上，点B 的坐标为(1,3)，将矩形沿对角线AC 翻折，使得B 点落在D 点的位置，且AD 交y 轴于点E ，则D 点坐标为___________．GFE DCB AByD E OAxC图10-1 图10-2EDCG FBM A解析：（1）ABE ECF FDG △∽△∽△，2AB AEFD FG==， ∴2AB DF =，∴2AB CF =，1AB AE BEEC EF CF===， ∴AB CE =，BE CF =，∴2CE CF =，又∵4EF =，∴CE =，CF =BC，AB ， ∴矩形ABCD的周长为（2）过D 点做DF x ⊥轴于F 点，BC 与FD 的延长线交于G 点则CGD DFA △∽△，∴13CG GD CD DF AF AD ===，设CG x =，则3DF x =，1AF x =+，33GD x =-，由于3AF GD =，列得方程：()1333x x +=-，解得45x =，故45CG =，125DF =，求得D 点坐标为41255⎛⎫- ⎪⎝⎭，．巩固11：如图11-1，ABC △和DEF △是两个全等的等腰直角三角形，90BAC EDF ∠=∠=︒，DEF △的顶点E 与ABC △的斜边BC 的中点重合．将DEF △绕点E 旋转到如图11-2，线段DE 与线段AB 相交于点P ，线段EF 与线段CA 的延长线相交于点Q ．（1）求证：BPE CEQ △∽△．（2）已知BP a =，92CQ a =，求P 、Q 两点间的距离（用含a 的代数式表示）．B DFA PQECBDFAP Q图11-1 图11-2解析：（1）∵ABC △和DEF △是两个全等的等腰直角三角形，∴45B C DEF ∠=∠=∠=︒， ∴135BEP CEQ ∠+∠=︒，135CQE CEQ ∠+∠=︒，∴BEP CQE ∠=∠，又∵45B C ∠=∠=︒，∴BPE CEQ △∽△．（2）连接PQ ，∵BPE CEQ △∽△，∴BP BECE CQ=， ∵BP a =，92CQ a =，BE CE =，∴BE CE ==，∴BC =，∴3AB AC a ==，∴32AQ a =，2PAa =，在Rt APQ △中，52PQ a =．题型十三平行模型例题10 已知：如图，在梯形ABCD 中，AB//CD ，M 是AB 的中点，分别连接AC 、BD 、MD 、MC ，且AC 与MD 交于点E ，DB 与MC 交于F ．（1）求证：EF//CD ；（2）若AB a =，CD b =，求EF 的长．DFAPQFEMDCBA解析：（1）∵AB CD ∥，∴ME AM ED CD =，MF BMFC CD=， ∵AM BM =，∴AM BM CD CD =（中间过渡量），∴ME MF EF CD ED FC=⇒∥．（2）∵AM EF CD ∥∥，∴111EF AM CD =+，∴2abEF a b=+．巩固12：如图所示，在ABC △中，120BAC ∠=︒，AD 平分BAC ∠交BC 于点D ．求证：111AD AB AC=+．ABDABCEF解析：分别过B 、C 两点做AD 的平行线，分别交CA 、BA 的延长线于E 、F 两点．由于EB//AD//FC ，有111AD BE FC=+；由于60EBA BAD ∠=∠=︒，18060EAB BAC ∠=︒-∠=︒所以EAB △为正三角形，同理FAC △亦为正三角形．BE AB =∴，FC AC =．故111AD AB AC=+．题型十一角平分线定理例题11 在ABC △中，B ∠的平分线交AC 于D ，C ∠的平分线交AB 于E ，且BE CD =．求证：AB AC =．解析：由角平分线定理得到AB AD BC DC =，AC AEBC BE=， ∵BE CD =∵，∴AD DC BE AE AB BC BC AC===∴ 即AD AEAB AC=，∴AD AC CD =-∴，AE AB BE =- ∴()()AC AC CD AB AB CD -=-，整理得到()()0AC AB AC AB CD -+-= 明显0AC AB CD +-≠，故AC AB =．巩固13：（1）如图13-1，在ABC △中，C ∠=90︒，CA =3，CB =4，且CD 是C ∠的平分线．则AD 的长为__________．（2）如图13-2，I 是ABC △内角平分线的交点，AI 交对应边于D 点，求证：AI AB ACID BC+=．CADBIAD B C图13-1 图13-2解析：（1）由角平分线定理34AD ACDB BC ==，由于5AB ==，31577AD AB ==∴ B AED（2）由角平分线定理得到AI AB AC ID BD CD ==，由等比性质得到：AI AB AC AB AC ID BD CD BC++==+．巩固14：若AP PB =，2APB ACB ∠=∠，AC 与PB 相交于点D ，且4PB =，3PD =．求AD DC ⋅的值．P DCBAEA BCDP解析：过P 点做APB ∠的角平分线PE ，交AD 于E 点．∵EPD APE C ∠=∠=∠∵，且PDE CDB ∠=∠，∴PDE CDB ∴△∽△，∴3ED DC PD DB ⋅=⋅=∴，又由于PE 是角平分线，∴PA AE PD ED =∴，∵4PA PB ==∵，∴43AE ED =∴，∴73AD ED =∴， 773AD DC ED DC ⋅=⋅=∴．题型十二线束模型例题12 如图，M 、N 为ABC △边BC 上的两点，且满足BM MN NC ==，一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F ．求证：3EF DE =．法一：如下左图，过D 作DG BC ∥交AC 于G ，交AM 、AN 于P 、Q ，由线束定理可知DP PQ QG ==，∵DF AC ∥，∴DE DP AG PG 1==2，DF DQ AG QG ==2， ∴DE DF 1=4，∴EF DE =3．过E 点或F 点作BC 的平行线也可得到类似的证法．法二：如下右图，过M 作PQ DF ∥，交AB 于P ，交AF 延长线于Q ，则有AC DF PQ ∥∥， ∴PM BM AC BC 1==3，QM MNAC NC==1， ∴PM QM 1=3，由线束定理可知DE PM EF QM 1==3，即EF DE =3．过B 点或N 点作DF 的平行线也可得到类似的证法．QPABCMN DEFQP GABCMNDEF巩固15：（1）如图15-1，AB ∥CD ，AD 与BC 交于点P ，过P 点的直线与AB 、CD 分别交于E ，F ．求证：AE DFBE CF=． FED NMCBA（2）如图15-2，AB ∥CD ，AD 与BC 交于点P ，连接CA 、DB 并延长相交于O ，连接OP 并延长交CD 于M ，求证：点M 为CD 的中点．（3）如图15-3，在图15-2中，若点G 从D 点向左移动（不与C 点重合），AG 与BC 交于点P ，连OP 并延长交CD 于M ，直接写出MC 、MG 、MD 之间的关系式．AC FDE B POABCM D POAB CM D P G图15-1 图15-2 图15-3解析：（1）证明：如图1，∵AB //CD ，AD 与BC 交于点P ， ∴AEP DFP △∽△，BFP CFP △∽△， ∴AE EP DF FP =,BE EP CF FP =，∴AE BE DF CF =，∴AE DFBE CF=；（2）证明：如图2，设OM 交AB 于点N ．∵AB //CD ，∴AON COM △∽△，BON DOM △∽△，AOB COD △∽△， ∴OA AN OC CM =，OB BN OD DM =，OA OB OC OD =，∴AN BNCM DM=①， ∵ANP DMP △∽△，BNP CMP △∽△，APB DPC △∽△， ∴AN AP DM DP =，DN BP CM CP =，AP BP DP CP =，∴AN BNDM CM=②， ①÷②，DM CMCM DM=，∴CM =DM ，即点M 为CD 的中点；（3）解：MC 2=MG •MD ，理由如下：如图3，设OM 交AB 于点N ． ∵AB //CD ，∴MCP NBP △∽△，NAP MGP △∽△，∴MC MP NB NP =①，NA NPMG MP=②， ①×②，得MC NA MP NP NB MG NP MP ⨯=⨯=1，∴MC NB MG NA=． ∵AON COM △∽△，BON DOM △∽△，∴NA ON MC OM =，NB ONMD OM=， ∴NA NB MC MD =，∴MD NB MC NA =，∴MC MDMG MC=，∴MC MG MD 2=⋅．题型十三相似综合例题13 如图，点A 的坐标为(2,2)，点C 是线段OA 上的一个动点（不与O 、A 两点重合），过点C 作CDx 轴，垂足为D ，以CD 为边在右侧作正方形CDEF ．连接AF 并延长交x轴的正半轴于点B ，连接OF ．若以B 、E 、F 为顶点的三角形与OFE △相似，则点B 的坐标是．解析：要使BEF △与OFE △相似， ∵FEO FEB ∠=∠=90︒ ∴只要OE EF EB EF =或OE EF EF EB =，即BE t =2或EB t 1=2． ② 当BE t =2时，BO t =4， ∴t t t 2=42-，∴t =0（舍去）或t 3=2，∴(,)B 60． ②当EB t 1=2时，（i ）当B 在E 的左侧时，OB OE EB t 3=-=2，∴tt t23=2-2，∴t=0（舍去）或t2=3，∴(,)B10．（ii）当B在E的右侧时，OB OE EB t5=+=2，∴ttt25=2-2，∴t=0（舍去）或t6=5，∴(,)B30．巩固16：如图，Rt ABC△中，ACB∠=90︒，CD AB⊥于D，过点D作DE BC⊥，BDE△边DE上的中线BF延长线交AC于点G．（1）求证：AD BD CE CB⋅=⋅；（2）若AG FG=，求:BF GF；（3）在（2）的条件下，若BC=62BD的长度．AFECDGAFECDG P解析：（1）证明：∵CD AB⊥，∴BCD△是直角三角形．∵DE BC⊥，∴CD CE CB2=⋅．∵ABC△是直角三角形，CD AB⊥，∴CD AD BD2=⋅，∴AD BD CE CB⋅=⋅；（2）解：过G作GP DF⊥交DF于P，连结DG，∵AC BC⊥，DE BC⊥，GF DE⊥，∴四边形CEPG是矩形，∴CG EP=在Rt ADC△中，∵G是边AC中点，∴AG DG CG==．又∵AG FG=，∴DG FG=，∴GFD△是等腰三角形．∴GP是FD的中线，DP FP=，即FP DF EF1=1=22．∵CG EP=，FP EF=12，∴::PF CG=13，∴::PF FG=13．∵PFG EFB CGB△△△∽∽，∴::::CG BG EF BF PF GF===13，∴::FG BG=13，::BF GF=21；（3）解：∵BC=62:::CE BE GF BF==12，∴CE=22，BE=42∵::EF BF=13，设EF x=，则BF x=3，∴()x x222+2=9，解得x=2，∴BF=6，GF=3，AC=6，∴()AB AC BC2222+6+6263BD=43。

模型总结：相似三角形模型解析及辅助线作法梳理

相似三角形（模型-辅助线）一、本章概述相似作为几何学习的一个重要内容，大量的出现在中考试卷中，它与勾股定理和锐角三角形函数并列为初中几何计算三大工具。

本章重点讲解相似的几个模型，如A字形，8字形，一线三等角等模型。

二、知识回顾1、图形的相似（1）相似图形：形状相同的图形叫做相似图形（2）相似多边形：对应角相等，对应边的比相等。

相似多边形对应边的比为相似比。

2.相似三角形（3）平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段的比相等。

（4）相似三角形的判定①预备定理：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段的比相等。

②判定定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。

如果两个三角形的三组对应边的比相等，那么这两个三角形相似。

如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。

③传递性定理：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

（5）相似三角形的性质①相似三角形的对应角相等，对应边成比例②相似三角形的周长的比等于相似比；对应线段的比等于相似比；面积比等于相似比的平方。

3.位似（6）多边形不仅相似，而且对应顶点的连线相交于一点，对应边互相平行，像这样的两个图形叫做位似图形，这个点叫做位似中心。

（7）在平面直角坐标系中，如果位似是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k。

1.相似基本模型一、本节概述本节重点讲解“A”字形和“8”字形的应用和构造方法，这两个模型是相似三角形中最为基础的两个模型，但应用十分广泛。

1.“A”字形相似2. ”8”字形相似二、典例精析能力目标：1.熟练掌握正A型相似和正8型相似模型：2.借助平行线构造正A型相似和正8型相似模型解决相关问题。

【例1】已知：图下图，AD（1）若E为AD的中点，射线CE交AB于F，则（2）若E为AD上一点，且,射线CE交AB于F，则思维探究：方法一：通过平行线构造相似解析：过A点作A P//BC交CF于点P,“8”字模型A P CD方法二：过A作A H//CF交BC延长线于H，则方法三：作DK//CF交AB于K,则方法四：作DM//AB交CF于M，则AF=DM,( 2 ) 构造平行线，通过线段比解决问题作B P//AD交CF于点P,大家可尝试过其他点作平行线，解答中用了A点和D点，其它的同学们自己尝试。

初中相似三角形知识点总结

初中相似三角形知识点总结
相似三角形是指两个或多个三角形的对应角相等，对应边成比例的关系。

以下是初中相似三角形的知识点总结：
1. 相似三角形的定义：两个或多个三角形的对应角相等，对应边成比例。

2. 相似三角形的性质：
- 对应角相等：两个相似三角形的对应角相等，即角A = 角D，角B = 角E，角C = 角F。

- 对应边成比例：两个相似三角形的对应边成比例，即 AB/DE = BC/EF = AC/DF。

3. 相似三角形的判定：
- AA相似定理：如果两个三角形的两个角分别相等，则这两个三角形相似。

- SAS相似定理：如果两个三角形的两个边成比例，并且夹角相等，则这两个三角形相似。

4. 相似三角形的应用：
- 求比例关系：根据相似三角形的性质，可以利用已知的比例关系来求解未知的边长或角度。

- 利用相似三角形求高度：在一个相似三角形中，可以利用已知的比例关系来求解未知的高度。

5. 相似三角形的注意事项：
- 只有对应角相等和对应边成比例的三角形才是相似三角形。

- 相似三角形的比例关系可以用来计算边长，但不能用来计算面积。

相似三角形是初中数学中的重要概念，它在几何形状的比较和计算中有着广泛的应用。

理解相似三角形的性质和应用方法，对于解决与三角形相关的问题具有重要意义。

相似三角形题型归纳总结非常全面

相似三角形题型归纳一、比例的性质:二、成比例线段的概念：1.比例的项：在比例式cr.b = c：d（即纟=上）中，a, d称为比例外项，b, c称为比例内项.特别地，h d在比例式a\b = b.c（即上=?）中，b称为a, c的比例中项，满足b2=ac・b c2.成比例线段：四条线段6 b, G d中，如果Q和b的比等于C和d的比，即- = 那么这四条线b d段a, b, c, d叫做成比例线段，简称比例线段.3.黄金分割：如图，若线段M上一点C,把线段朋分成两条线段AC和BC （AC >BC）,且使AC是和BC的比例中项（即AC2 =AB BC）,则称线段AB被点C黄金分割，点C叫线段&8 的黄金分割点，其中AC = ^1AB^Q.61SAB , = Q0.382AB, AC AB2 2的比叫做黄金比.（注意：对于线段A3而言，黄金分割点有两个.）•••A C B4三.平行线分线段成比例定理1.平行线分线段成比例定理两条直线被三条平行线所截.所得的对应线段成比例.简称为平行线分线段成比例立【小结】若将所截出的小线段位置靠上的（如&B ）称为上，位置靠下的称为下，两条线段合成的线段称为全，则可以形象的表示为二=二，空=刍 r r 全全2.平行线分线段成比例定理的推论平行于三角形一边的直线，截其它两边（或两边的延长线），所得的对应线段成比例.如AE AF AE EF --- = ---- ----△ABCsMBC ZB = ZB', ZC = ZC rZA = ZA\AB _ BC _ AC A^ = WC = A^CAB DEBC EF如AF BEAC ABAE _AF AE _AF EB^FC AB^AC—=SL EFT/BC & FAA'EB FC ABAABC △A'B'C' AM、AH AD AABC BC A!M f A!H rA!D9AA0C B f C AB _ BC _ AC AM _ AH _ AD 7^ = ^C = A^C= =A^r = A7T=WD;AABC /\A!B f C AB BC AC AB + BC + AC ;而一而一而一A® + B'C' + AC 一△ △>△ = Z4‘ ZZ? = ZZT AABC s MBC砂B'C' A'C'SC S MBCAB ACA® AC ZA_ZA△ABCs/WBC4DE // BC oHADE sAABC o A° - AE - DE AB AC BCA BA AB 〃CD o'AOB s HCOD O 竺=竺=竺CD OC ODDG _ AN△ABC AADG S^ABC BC ZBAC = 90° /\ADGsHEBDs&GCsMBCE MF CAE4A A A A3/AABD ^ACADZB = ZCADZC = ZBADAB 2 =AD 2+BD 2 AC 2 = AD 2 + CD 2 BC 2 ==AB 2 + AC 2C CE//AD BAE CE//AD Z1 = Z£ Z2 = Z3 AD ZBAC Z1 =Z2AE = ACCE 〃AD^ =竺竺=竺AE CD AC CDAB1.BDAABC S MDEAB DE = BC CDED 丄 BD AC 丄 ECBDAABC s*DE s AACEZABC = ZCDE = ZACE Z^ABC sMDE AB DE = BC CDAB BC AC CD^^DE^CE CBDAABC s*DE s AACEAD ACMBCMCDE & =忑 C BD BJCDAB ACZABC = ZACEAABC ZA4CAB BD AC = CDEAB BCAD C3/A F；VEAw/nBMCBMCEN BM .EN BM EF // BCEF // BC 一NF MC NF MCAABC ABACAB BD AC = CD条件变为比例形式: 走気，由于妙心180。

相似三角形复习(较全)

相似三角形知识点汇总【知识要点】1. 比例线段的有关概念：在比例式：：中，、叫外项，、叫内项，、叫前项，a b cda b c d a d b c a c ==()b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC ，使AC 2=AB ²BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质： ①基本性质：a b c dad bc =⇔= ②合比性质：±±a b c d a b b c dd =⇒= ③等比性质：……≠……a b c d m n b d n a c m b d n ab===+++⇒++++++=()03. 平行线分线段成比例定理：①定理：三条平行线截两条直线，所得的对应线段成比例，如图：l 1∥l 2∥l 3。

则，，，…AB BC DE EF AB AC DE DF BC AC EFDF=== ②推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例。

③定理：如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边。

二、有关知识点：1.相似三角形定义：对应角相等，对应边成比例的三角形，叫做相似三角形。

2.相似三角形的表示方法：用符号“∽”表示，读作“相似于”。

3.相似三角形的相似比：相似三角形的对应边的比叫做相似比。

4.相似三角形的预备定理：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所截成的三角形与原三角形相似。

5.相似三角形的判定定理：(1)三角形相似的判定方法与全等的判定方法的联系列表如下：从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理，这就是我们数学中的用类比的方法，在旧知识的基础上找出新知识并从中探究新知识掌握的方法。

相似三角形常见模型(总结)1

相似三角形第一部分相似三角形模型分析一、相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）BDE（平行）BDE（不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行）（不平行）（三）母子型BDD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：ADC 二、相似三角形判定的变化模型旋转型：由A字型旋转得到。

8字型拓展CB EDA共享性GABEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD中，AD∥BC，对角线AC、BD交于点O，BE∥CD交CA延长线于E．求证：OEOAOC⋅=2．例2：已知：如图，△ABC中，点E在中线AD上, ABCDEB∠=∠．求证：（1）DADEDB⋅=2；（2）DACDCE∠=∠．例3：已知：如图，等腰△ABC中，AB＝AC，AD⊥BC于D，CG∥AB，BG分别交AD、AC于E、F．求证：EGEFBE⋅=2．相关练习：1、如图，已知AD为△ABC的角平分线，EF为AD的垂直平分线．求证：FCFBFD⋅=2．A CDEBGMF EHDCBA2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。

求证：∠=︒GBM 905．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt △ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边AC 于点D （点D 与点A 、C 都不重合），E 是射线DC 上一点，且∠EPD =∠A ．设A 、P 两点的距离为x ，△BEP 的面积为y ．（1）求证：AE =2PE ；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）当△BEP 与△ABC 相似时，求△BEP 的面积．双垂型1、如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高求证：（1）△ABD ∽△ACE ；（2）△ADE ∽△ABC ；(3)BC=2ED2、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=62，求：点B 到直线AC 的距离。

(完整版)相似三角形模型分析大全(非常全面-经典)

相似三角形模型分析大全1、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）B（平行）B（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（6）双垂型：2、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展B一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：．OE OA OC ⋅=2例2：已知：如图，△ABC 中，点E 在中线AD 上, ．ABC DEB ∠=∠求证：（1）；（2）．DA DE DB ⋅=2DAC DCE ∠=∠ACDEB例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：．EG EF BE ⋅=2相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：．FC FB FD ⋅=22、已知：AD 是Rt△ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME∽△NMD; (2)ND =NC·NB23、已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于D，E是AC上一点，CF⊥BE于F。

求证：EB·DF=AE·DB⊥，垂足为F，延长AD到G，使DG=EF，M是AH的中点。

4.在∆ABC中，AB=AC，高AD与BE交于H，EF BCGBM90求证：∠=︒5．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt△ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边AC于点D （点D 与点A 、C 都不重合），E 是射线DC 上一点，且∠EPD =∠A ．设A 、P 两点的距离为x ，△BEP 的面积为y ．（1）求证：AE =2PE ；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）当△BEP 与△ABC 相似时，求△BEP 的面积．双垂型1、如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高A（第25题图）求证：（1）△ABD∽△ACE；（2）△ADE∽△ABC；(3)BC=2ED2、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=6，求：点B 到直线AC 的距离。

2023年中考数学常见几何模型全归纳之模相似模型-母子型(共角共边模型)和A(X)字型(解析版)

（1）证明∶∵∠ACB=90°，AC=BC，CD是中线，
∴∠BCD=∠ACD=45°，∠BCE=∠ACF= 90°，∴∠DCE=∠DCF= 135°
∵在△DCE与△DCF中，
，∴ ，∴DE=DF；
（2）证明∶∵∠DCE= ∠DCF= 135°∴∠CDF+∠F=180°-135°=45°，
∵∠CDF+∠CDE=45°，∴∠F=∠CDE，
【详解】∵∠B=∠ACD，∠A=∠A，
∴△ACD∽△ABC，∴ ，
∵ ，∴ ，
∴ ，
∴△ADC与△ACB的周长比1:2，故选：B．
【点睛】本题主要考查了相似三角形的判定与性质，证明△ACD∽△ABC是解答本题的关键．
2．（2022·陕西汉中·九年级期末）如图，是等腰直角斜边的中线，以点为顶点的绕点旋转，角的两边分别与、的延长线相交，交点分别为点、，与交于点，与交于点，且．(1)如图1，若，求证：；(2)如图2，若，求证：；
1．（2022·湖南怀化·中考真题）如图，△ABC中，点D、E分别是AB、AC的中点，若S△ADE＝2，则S△ABC＝_____．
【答案】8
【分析】根据三角形中位线定理求得DE∥BC，，从而求得△ADE∽△ABC，然后利用相似三角形的性质求解．
【详解】解：∵D、E分别是AB、AC的中点，则DE为中位线，
∴ ，∴ ∴ ，
∵ ，DE=BF，∴ ，
∴ ，∴ ，
∵ ，，∴ ，
∵ ，∴ ，
∴ ．
【点睛】本题考查了相似三角形，熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键．
3．（2022·浙江宁波·中考真题）(1)如图1，在中，D，E，F分别为上的点，交于点G，求证：．

2024年中考数学复习(全国版)重难点09 相似三角形8种模型(解析版)

∴△ 퐶퐴 ∽△ 퐶 ，
∴ ∠퐶퐴 = ∠퐶 ，
∵ ∠퐶퐴 = ∠퐶퐵 ，
∴ ∠퐶 퐵 = ∠퐶퐵 ，
∴ 퐵퐶 = 퐶，
∴ 퐶 = 퐶퐵， ∴ ∠퐵 퐶 = ∠퐵퐴 ，
∴ 퐶//퐴 ，
∴
푃퐶 퐶
=
푃 퐴
=
2� �
=
2，
∴ 푃퐶 = 2퐶 = 4 2，
∵ ∠푃퐶퐵 = ∠푃퐴 ，∠퐶푃퐵 = ∠퐴푃 ，
．
【答案】2 【分析】过 D 作垂直퐴퐶于 H 点，过 D 作 ∥퐴 交 BC 于 G 点，先利用解直角三角形求出퐶 的长，其次利用△ 퐶 ∽△ 퐶퐵 ，求出퐶 的长，得出퐵 的长，最后利用△ 퐵 ∽△ 퐵퐴 ，求出퐵 的长，最后得出答案．【详解】解：如图：过 D 作垂直퐴퐶于 H 点，过 D 作 ∥퐴 交퐵퐶于 G 点，
∴퐴
= 퐴�，即
퐴 �+
�
=
� 퐴
∴2
2+
�
=
� 2
解得 � = 5 − 1 或 � =− 5 − 1 < 0（不符题意，舍去）
则퐵 = � = 5 − 1
故答案为：2， 5 − 1．【点睛】本题考查了矩形的性质、折叠的性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点，根据矩形与折叠的性质，正确找出两个相似三角形是解题关键． 3．（2020·山东济宁·中考真题）如图,在四边形 ABCD 中，以 AB 为直径的半圆 O 经过点 C,D．AC 与 BD 相
BC=DC，证明
OC∥AD，利用平行线分线段成比例定理得到퐶푃퐶
=
푃 퐴
=
2，则푃퐶
=
2퐶
= 4 2，然后证

相似三角形总复习模型总结

相似三角形题型归纳总结非常全面

相似三角形常见模型(总结材料)

中考数学几何专项——相似模型(相似三角形)

相似三角形知识点归纳(全)

相似三角形模型总结2(比例式、等积式的常见证明方法)

相似三角形典型模型及例题

相似三角形经典总复习(含知识点习题)

相似三角形12种基本模型证明

(完整word版)相似五大模型总结老师,推荐文档

相似三角形题型归纳总结非常全面

模型总结： 相似三角形模型解析及辅助线作法梳理

初中相似三角形知识点总结

相似三角形题型归纳总结非常全面

相似三角形复习(较全)

相似三角形常见模型(总结)1

(完整版)相似三角形模型分析大全(非常全面-经典)

2023年中考数学常见几何模型全归纳之模 相似模型-母子型(共角共边模型)和A(X)字型(解析版)

2024年中考数学复习(全国版)重难点09 相似三角形8种模型(解析版)

模型总结：相似三角形模型解析及辅助线作法梳理

2023年中考数学常见几何模型全归纳之模相似模型-母子型(共角共边模型)和A(X)字型(解析版)