刘徽和割圆术
刘徽割圆术精品PPT课件

第五,刘徽指出:“割之弥细,所失 弥少。割之又割,以至于不可割,则与 圆周合体而无所失矣。”(《九章算术》 方田章圆田术刘徽注)这就是说,圆内 接正多边形的边数无限增加的时候,它 的周长的极限是圆周长,它的面积的极 限是圆面积。
发,求得正十二边形的边长。根据勾股 定理,从圆内接正n边形每边的长,可以 求出圆内接正2n边形每边的长。
第三,从圆内接正n边形每边的长, 可以直接求出圆内接正2n边形面积。如 图所示,四边形OADB的面积等于半径 OD和正n边形边长AB乘积的一半。
第四,圆面积S满足不等式 S2n<S<S2n+(S2n-Sn)。
因为《缀术》失传了,祖冲之究竟是用什么方法将π算 到小数点后第七位,又是怎样找到既精确又方便的密 率的呢?这至今仍是困惑数学家的一个谜。
祖冲之曾写过一本数学著作《缀术》,记录了他 对圆周率的研究和成果。但当时“学官莫能究其 深奥,是故废而不理”,以致后来失传。
很多人都知道用密率355/113表示π的近似值,是 一项了不起的贡献。密率355/113传到了日本后, 1913年日本数学史家三上一夫建议将祖冲之圆周 率的密率数值命名为“祖率”,得到一致赞同。 祖冲之对圆周率的求索,超过了世界水平整整 1000年!直到16世纪德国人V·奥托和荷兰人A·安 托尼斯才发现了圆周率的密率355/113。 但是 “祖率”的妙处,和给今人留下的困惑,不少人 却说不出来。
(二)圆周率的定义
指平面上圆的周长与直径之比。早 在一千四百多年以前,我国古代著名 的数学家祖冲之,就精密地计算出圆 的周长是它直径的3.1415926--3.1415927倍之间。这是当时世界上 算得最精确的数值----圆周率。
[精华]割圆术——刘徽《九章算术注》
![[精华]割圆术——刘徽《九章算术注》](https://img.taocdn.com/s3/m/16d6ebfe846a561252d380eb6294dd88d1d23d59.png)
割圆术——刘徽《九章算术注》割圆术(cyclotomic method)所谓“割圆术”,是用圆内接正多边形的周长去无限逼近圆周并以此求取圆周率的方法。
这个方法,是刘徽在批判总结了数学史上各种旧的计算方法之后,经过深思熟虑才创造出来的一种崭新的方法。
中国古代从先秦时期开始,一直是取“周三径一”(即圆周周长与直径的比率为三比一)的数值来进行有关圆的计算。
但用这个数值进行计算的结果,往往误差很大。
正如刘徽所说,用“周三径一”计算出来的圆周长,实际上不是圆的周长而是圆内接正六边形的周长,其数值要比实际的圆周长小得多。
东汉的张衡不满足于这个结果,他从研究圆与它的外切正方形的关系着手得到圆周率。
这个数值比“周三径一”要好些,但刘徽认为其计算出来的圆周长必然要大于实际的圆周长,也不精确。
刘徽以极限思想为指导,提出用“割圆术”来求圆周率,既大胆创新,又严密论证,从而为圆周率的计算指出了一条科学的道路。
在刘徽看来,既然用“周三径一”计算出来的圆周长实际上是圆内接正六边形的周长,与圆周长相差很多;那么我们可以在圆内接正六边形把圆周等分为六条弧的基础上,再继续等分,把每段弧再分割为二,做出一个圆内接正十二边形,这个正十二边形的周长不就要比正六边形的周长更接近圆周了吗?如果把圆周再继续分割,做成一个圆内接正二十四边形,那么这个正二十四边形的周长必然又比正十二边形的周长更接近圆周。
这就表明,越是把圆周分割得细,误差就越少,其内接正多边形的周长就越是接近圆周。
如此不断地分割下去,一直到圆周无法再分割为止,也就是到了圆内接正多边形的边数无限多的时候,它的周长就与圆周“合体”而完全一致了。
按照这样的思路,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.14和 3.1416这两个近似数值。
这个结果是当时世界上圆周率计算的最精确的数据。
刘徽对自己创造的这个“割圆术”新方法非常自信,把它推广到有关圆形计算的各个方面,从而使汉代以来的数学发展大大向前推进了一步。
刘徽与割圆术

▪ 刘徽由正六邊形開始,不斷倍增正多邊形的邊數。
正6邊形
正12邊形
正24邊形
邊數愈多,正多邊形愈接近圓形。 最後,劉徽求得π≈ 3.1416。 BG
正48邊形
7
谢谢观看
BG
8
BGΒιβλιοθήκη 4②刘徽原理在《九章算术•阳马术》注中,他在用无限分割的方法解决锥体体积时, 提出了关于多面体体积计算的刘徽原理。
③“牟合方盖”说 在《九章算术•开立圆术》注中,他指出了球体积公式V=9D3/16(D为球直径) 的不精确性,并引入了“牟合方盖”这一著名的几何模型。“牟合方盖”是 指正方体的两个轴互相垂直的内切圆柱体的贯交部分。
▪ 成就
▪ 刘徽的成就大致为两方面:
一是清理中国古代数学体系并奠定了它的理论基础。这方面集中体现在《九章算
术注》中。它实已形成为一个比较完整的理论体系: ①在数系理论方面 用数的同类与异类阐述了通分、约分、四则运算,以及繁分数化简等的
运算法则;在开方术的注释中,他从开方不尽的意义出发,论述了无理方根 的存在,并引进了新数,创造了用十B进G 分数无限逼近无理根的方法。 3
④方程新术 在《九章算术•方程术》注中,他提出了解线性方程组的新方法,运用了 比率算法的思想。 ⑤重差术 在白撰《海岛算经》中,他提出了重差术,采用了重表、连索和累矩等 测高测远方法。他还运用“类推衍化”的方法,使重差术由两次测望,发展 为“三望”、“四望”。而印度在7世纪,欧洲在15~16世纪才开始研究两次 测望的问题。
二是在继承的基础上提出了自己的创见。这方面主要体现为以下几项有代表性的
创见: ①割圆术与圆周率 他在《九章算术•圆田术》注中,用割圆术证明了圆面积的精确公式,并
刘徽割圆术

(四)建议将3月14日定为祖冲之纪念日 建议将 月 日定为祖冲之纪念日
美国麻省理工学院首先倡议将3日 日 寓意3﹒ ) 美国麻省理工学院首先倡议将 日14日(寓意 ﹒14)定为国际 圆周率日(National p Day)。1736年,瑞士数学家歐拉 (Euler, 圆周率日 。 年 , 1707 – 1783) 提倡以希腊字母 p (音:pi) 来表示圓周率,p是圓周 来表示圓周率, 是圓周 音 的字頭。直到現在, 的希腊文 perijereia (英文为 periphery) 的字頭。直到現在,p 已 英文为 成为圓周率的专用符號。在这一天,学生们会彼此祝福“ 成为圓周率的专用符號。在这一天,学生们会彼此祝福“圆周率日 快乐! 快乐!”用大家熟悉的生日歌旋律唱起 happy pi day to you!学 ! 院众多对圆周率有兴趣的人聚在一起讨论圆周率问题,吃馅饼(英 院众多对圆周率有兴趣的人聚在一起讨论圆周率问题,吃馅饼 英 同音)以及其他各种以圆周率为主题的食物 文pie,与圆周率英文 同音 以及其他各种以圆周率为主题的食物, ,与圆周率英文pi同音 以及其他各种以圆周率为主题的食物, 举行圆周率背诵比赛。 举行圆周率背诵比赛。 全球各地的一些著名大学的数学系,也在3月 日举行 日举行Party庆 全球各地的一些著名大学的数学系,也在 月14日举行 庆 在圓周率日當天, 祝。在圓周率日當天,加拿大滑铁庐大学还会以供應免費的餡餅来 庆祝。而3月14日恰好又是著名的物理学家爱因斯坦 (Albert 庆祝。 月 日恰好又是著名的物理学家爱因斯坦 Einstein,1879 – 1955) 的生日。所以他们还会「择时辰」以庆祝 的生日。所以他们还会「择时辰」 , 圆周率日:选择在下午1時 分开始庆祝 分开始庆祝, 圆周率日:选择在下午 時59分开始庆祝,它代表 3.14159 (准确至 准确至 六位小数) 的圓周率近似值。 六位小数 的圓周率近似值。
刘徽和割圆术

刘徽和割圆术中国向来以文明古国自称,谈到中国古代文明,我们一定会说起以“经世致用”为信条,以筹算为主的中国古代数学史。
在这段曲折发展的历史中,我们的古代数学跟其他古文明一样,在一定程度上获得了发展,特别是在算法的深度和广度上有着卓越的发展。
但我们不得不提及,在中国古代长达2000多年的封建制度统治下,数学研究一直停留在计算层面,理论的严谨和系统却不尽如人意,这同时也导致了一些错误的结果的出现。
在这样的数学背景下,刘徽可谓是中国数学史上的一朵奇葩,他有着“为数学而数学”的价值观,曾令中国古代数学的严谨与系统达到前所未有的高度。
下面我将主要介绍刘徽及其最耐人寻味的一段成就——割圆术。
刘徽,生于公元250年左右,是魏晋时人。
他的一生为数学刻苦探求,虽然地位低下,但人格高尚。
他所撰的《九章算术注》是中国最宝贵的数学遗产。
刘徽思想敏捷,方法灵活,既提倡推理又主张直观,是中国最早明确主张用逻辑推理的方式来论证数学命题的人。
他不是沽名钓誉的庸人,而是学而不厌的伟人。
由于篇幅有限,对刘徽卓越的成就不能一一介绍,只能介绍其最耐人寻味的割圆术。
割圆术可谓是中国古代数学的奇迹,在后面与阿基米德求圆面积方法的比较中,您将发现割圆术的精妙与美丽。
在《九章算术》中曾提到“圆田术”---半周半径相乘得积步。
这就是著名的圆面积公式:(1) 其中S 表示圆面积,C 表示周长,R 表示半径。
我们今天可以得出这个公式是正确的,但在《九章算术》中只是提到了这一结论,却未给出严谨的证明。
在刘徽之前人们以圆内接正六边形的周长代替圆周长C ,以圆内接正十二边形的面积代替圆面积S ,用出入相补原理将正十二边形拼补成一个以正六边形的周长的一半作为长,以圆半径作为宽的长方形来推证上述公式。
在今天,我们可以看出用圆内12S CR接正六边形和圆内接正十二边形来近似代替圆是相当粗糙的,但在当时很少有人能指出这一算法的不严谨性,而刘徽却说此方法“合径率一而外周率三也”,一针见血的指出了这一方法的不严格性。
刘徽与割圆术

他沿着割圆术的思 路,从圆内接正六 边形算起,边数依 次加倍,相继算出 正12边形,正24边 形……直到正192边 形的面积,得到圆 周率兀的近似值为 157/50 (3.14);后 来,他又算出圆内 接正3 072边形的面 积,从而得到更精 确的圆周率近似值: 兀≈3927/1 250(3.1416)。
刘徽首创“割圆术” 的方法,可以说他是中国古 代极限思想思想的杰出代表,不仅为200年后祖 冲之圆周率的计算提供了思想方法与理论依据, 也对中国古代的数学研究产生了很大影响。
在生活中,我们也要善于观察、勤于思考, 养成爱动脑的好习惯。你们也有可能成为数 学家哦!
ቤተ መጻሕፍቲ ባይዱ刘徽与割圆术
刘徽是公元三世纪世 界上最杰出的数学家, 他在公元263年撰写 的著作《九章算术注》 以及后来的《海岛算 经》,是我国最宝贵 的数学遗产,从而奠 定了他在中国数学史 上的不朽地位。
我国古代的刘徽他为了圆周率的计算一直 潜心钻研着。
一次,刘徽看到石匠在加工石头,觉得 很有趣就仔细观察了起来。
“哇!原本一块 方石,经石匠师 傅凿去四角,就 变成了八角形的 石头。再去八个 角,又变成了十 六边形。”
一斧一斧地凿下去,一块方形石料就被加工成了一根圆柱。
谁会想到,在一般人看来非常普通的事情,却触发 了刘徽智慧的火花。他想:“石匠加工石料的方法, 可不可以用在圆周率的研究上呢?”
于是,刘徽采用这个方法,把圆逐渐分割下去, 一试果然有效。他发明了亘古未有的“割圆术”。
《刘徽割圆术》课件

割圆术与极限思想的关系
极限思想是数学中一个重要的 概念,它描述了当某量变化时 ,其极限的存在性。
割圆术体现了极限思想的应用 ,即通过不断增加多边形的边 数,使得多边形的周长无限接 近于圆的周长。
这种极限思想的应用使得刘徽 能够利用有限的手段来逼近无 限的数值,从而得到圆周率的 近似值。
感谢您的观看
THANKS
计算机图形学
在现代计算机图形学中,刘徽割圆术 的思想被广泛应用于生成平滑的曲线 和曲面,例如在制作动画、游戏、电 影等领域。
数值分析
刘徽割圆术中的数值计算方法也被广 泛应用于现代科学中的数值分析领域 ,例如在计算物理、工程等领域中, 可以利用刘徽割圆术的方法进行数值 模拟和计算。
04
刘徽割圆术的局限性与挑战
在数学史上的地位
推动了中国古代数学的发展
刘徽割圆术是中国古代数学发展史上的重要里程碑,它的出现标志着中国古代数学从经验型向理论型的转变。
对世界数学史的影响
刘徽割圆术的提出和应用,不仅对中国古代数学产生了深远影响,也对世界数学史的发展产生了重要影响,为后 来的数学家提供了宝贵的启示和借鉴。
在现代科学中的应用
古代科学技术的局限性
缺乏精确的测量工具
古代科学技术的限制使得刘徽在进行 割圆术时无法获得精确的数值和比例 。
缺乏数学理论支持
受限于经验和实践
由于历史背景和知识体系的限制,刘 徽只能通过直观和实践来验证割圆术 ,这使得其结果的可靠性和准确性存 在一定问题。
当时的数学理论尚未发展到能够完全 支撑刘徽割圆术的证明,这使得该方 法在理论上的可靠性受到质疑。
刘徽割圆术在现代科学中的应用前景
数学建模
刘徽割圆术的基本思想和技巧可以应用 于数学建模中,为解决实际问题提供新 的思路和方法。例如,在物理、工程、 经济等领域中,可以利用刘徽割圆术的 思想来建立数学模型,解决复杂的问题 。
刘徽割圆术求圆面积的过程

刘徽割圆术求圆面积的过程
刘徽首先从圆的内接正六边形开始割圆,然后将边数逐渐增加,照这样一直分割下去,等到不可割的时候,圆的内接正多边形就和圆合二为一了。
然后他将这个正多边形分割成以圆心为原点,以每条边为底的等腰三角形,这些等腰三角形的高和底相乘得出的结果,是它本身面积的两倍。
因此将他们全部相加便是圆的面积的两倍,而这些等腰三角形的底边之和便是圆的周长,因此圆的面积等于圆的周长的一半乘以半径。
《刘徽割圆术》课件

刘徽割圆术在中国数学史上具有重要的地位,它不仅为后来 的数学家提供了研究圆周率的方法,而且对整个数学的发展 产生了深远的影响。
刘徽割圆术的提出标志着中国古代数学的发展达到了一个新 的高度,为后来的数学家提供了研究数学的新思路和新方法 。
01
刘徽割圆术的数学 原理
圆周率的定义
圆周率:圆的周长与其直径的比值,记作π。 圆周率在数学和科学中具有广泛的应用,是研究圆和其他几何图形的基础。
传承价值
刘徽割圆术的传承价值不仅在于其数学成果,更在于其背 后所蕴含的数学思想和智慧,对于中国古代数学的发展和 现代数学的研究都具有重要的意义。
刘徽割圆术的发展现状
学术研究
现代学者对刘徽割圆术的研究主 要集中在对其数学思想和方法的 探讨,以及其在现代数学中的应
用等方面。
普及教育
刘徽割圆术作为中国古代数学的瑰 宝,已经被纳入到中小学数学教材 中,成为学生了解中国古代数学的 重要内容。
国际影响
随着中国数学文化的传播,刘徽割 圆术也逐渐受到国际数学界的关注 和认可,成为世界数学史上的重要 篇章。
刘徽割圆术的未来展望
学术研究深化
随着数加深入,有望在数 学史和数学思想方面取得更多的
突破。
文化传承与创新
刘徽割圆术作为中国传统文化的 重要组成部分,未来需要在传承 的基础上进行创新,以适应现代
03
刘徽割圆术的提出,使得中国数学在当时的国际数学界获得了
高度评价和认可。
对世界数学的影响
丰富了世界数学文化宝库
刘徽割圆术作为一种独特的数学思想和算法,为世界数学的发展 做出了重要贡献,丰富了世界数学文化宝库。
促进了东西方数学的交流
刘徽割圆术的传播,使得东西方数学在圆周率研究方面得以相互借 鉴和交流,推动了数学的发展。
中国古代数学家刘徽的小故事

中国古代数学家刘徽的小故事
数学家刘徽有一个小故事,那就是他发现“割圆术”的过程。
有一天,刘徽偶然看到石匠在切割石头,看着看着竟觉得十分有趣,就站在一边,细细地观察起来。
刘徽看
到,一块方形的石头,先由石匠切去了四个角,四角的石头瞬间就有了八个角,然后再把这八个角切去,以此类推,石匠一直在把这些角一个一个地切去,直到无角可切为止。
到最后,刘徽就发现,本来呈现方形的石块,早在不知不觉中变
成了一个圆滑的柱子。
石匠打磨石块的事情,每天都在发生,但就是这样的一件小事,让刘徽瞬间茅塞顿开,看到了别人没有看到的事情。
刘徽就像石匠所做的那样,把圆不断分割,终于发明了“割圆术”,为计算圆周率提供了一套严密的理论和完
善的算法。
刘徽和割圆术

刘徽和割圆术中国向来以文明古国自称,谈到中国古代文明,我们一定会说起以“经世致用”为信条,以筹算为主的中国古代数学史。
在这段曲折发展的历史中,我们的古代数学跟其他古文明一样,在一定程度上获得了发展,特别是在算法的深度和广度上有着卓越的发展。
但我们不得不提及,在中国古代长达2000多年的封建制度统治下,数学研究一直停留在计算层面,理论的严谨和系统却不尽如人意,这同时也导致了一些错误的结果的出现。
在这样的数学背景下,刘徽可谓是中国数学史上的一朵奇葩,他有着“为数学而数学”的价值观,曾令中国古代数学的严谨与系统达到前所未有的高度。
下面我将主要介绍刘徽及其最耐人寻味的一段成就——割圆术。
刘徽,生于公元250年左右,是魏晋时人。
他的一生为数学刻苦探求,虽然地位低下,但人格高尚。
他所撰的《九章算术注》是中国最宝贵的数学遗产。
刘徽思想敏捷,方法灵活,既提倡推理又主张直观,是中国最早明确主张用逻辑推理的方式来论证数学命题的人。
他不是沽名钓誉的庸人,而是学而不厌的伟人。
由于篇幅有限,对刘徽卓越的成就不能一一介绍,只能介绍其最耐人寻味的割圆术。
割圆术可谓是中国古代数学的奇迹,在后面与阿基米德求圆面积方法的比较中,您将发现割圆术的精妙与美丽。
在《九章算术》中曾提到“圆田术”---半周半径相乘得积步。
这就是著名的圆面积公式:(1) 其中S 表示圆面积,C 表示周长,R 表示半径。
我们今天可以得出这个公式是正确的,但在《九章算术》中只是提到了这一结论,却未给出严谨的证明。
在刘徽之前人们以圆内接正六边形的周长代替圆周长C ,以圆内接正十二边形的面积代替圆面积S ,用出入相补原理将正十二边形拼补成一个以正六边形的周长的一半作为长,以圆半径作为宽的长方形来推证上述公式。
在今天,我们可以看出用圆内接正六边形和圆内接正十二边形来近似代替圆是相当粗糙的,但在当时很少有人能指出这一算法的不严谨性,而刘徽却说此方法“合径率一而外周率三也”,一针见血的指出了这一方法的不严格性。
关于刘徽的割圆术

关于刘徽的割圆术关键词九章算术, 刘徽, 割圆术, 圆周率1 刘徽割圆术的内容刘徽的割圆术, 是刘徽在为《九章算术》第一卷方田中的圆田术所作的注中提出来的[ 1] , 包括如下内容:1) 刘徽首先解释了圆田术求圆面积的方法, 然后指出“周三径一”是不对的, 他说: 以半周乘半径而为圆幂, “此以周径谓至然之数, 非周三径一之率也. 周三者, 从其六觚之环耳, 以推圆规多少之较, 乃弓之与弦也. ”2) 刘徽提出用割圆内接正六边形为正十二边形等步骤, 使圆内接正多边形的面积逐次逼近圆的面积. 进而又指出: “割之弥细, 所失弥少. 割之又割, 以至于不可割, 则与圆周合体而无失矣. 觚面之外, 又有余径. 以面乘余径则幂出弧表. 若夫觚之细者, 与圆合体, 则表无余径. 表无余径, 则幂不外出矣. ”3) 刘徽详述了割圆的算法, 例如, 关于割圆内接正六边形为正十二边形, 他说: “令半径一尺为弦, 半面五寸为勾, 为之求股. 以勾幂二十五寸减弦幂, 余七十五寸, 开方除之, 下至秒忽, 又一退法求其微数, 微数无名者以为分子, 以下为分母, 约为五分忽之二, 故得股八寸六分六厘二秒五忽五分忽之二. 以减半径, 余一寸三分三厘九毫七秒四忽五分忽之三, 谓之小股, 为之求弦, 其幂二千六百七十九亿四千九百一十九万三千四百四十五忽, 余分弃之, 开方除之, 即十二觚之一面也. ”4) 刘徽在计算了圆内接正一百九十二边形的面积后, 对圆面积进行了大胆推断, 从而获得了当时世界上最精确的圆周率的值. 他说: “差幂六百二十五分寸之一百五, 以十二觚之幂为率消息, 当取此分寸之三十六以增于一百九十二觚之幂( 即三百一十四寸六百二十五分寸之六十四) , 以为圆幂三百一十四寸二十五分寸之四. ”5) 刘徽验证了自己获得的结果的正确性, 为此, 他继续用割圆术, 直到求出圆内接正三千零七十二边形的面积. 他说: “当求一千五百三十六觚之一面, 得三千七十二觚之幂, 而裁其微分, 数亦宜然, 重其验耳. ”2 刘徽割圆术的历史地位2. 1古希腊已有割圆思想古希腊巧辩学派的学者Ant iphon ( 约公元前五世纪) 提出用边数不断增加的圆内接正多边形来接近圆, 并提出把圆看作是无穷多边的正多边形; 另一个古希腊巧辩学派的学者Br yso n( 约公元前五世纪) 类似地提出用边数不断增加的圆外切正多边形来接近圆; 而古希腊的一位大数学家Eudox us( 约公元前四世纪) 则依据这一思想创立了穷竭法这种著名的获取定理和证明定理的方法.虽然刘徽不是人类历史上第一个提出割圆思想的人, 但是, 他没有简单地重复任何人, 而是独立地、完整地、创造性地提出了割圆术, 和古希腊的数学家们一样, 刘徽的思想同样是辉煌的.2. 2刘徽用割圆术获得了当时世界上最精确的圆周率值古希腊的Ant iphon, Br yso n, Eudo xus 虽然先于刘徽提出割圆思想, 但他们都没有用它去求圆周率的值. 然而, Archimedes[ 3] ( 公元前287~公元前212年) 继承了割圆思想, 并根据圆周长大于圆内接正多边形周长而小于圆外切正多边形周长, 得到圆周率P满足223/ 71 < P< 22/ 7 的结果. 古希腊的Ptolemy[ 2] ( 公元?~168年) 并没有专门研究圆周率的值, 他依据他的定理( Ptolemy 定理) 提出一种特殊的割圆技巧, 求出了各圆心角所对的弦长的六十进制数值, 其中1/ 2度圆心角所对弦长的数值为31′2 5″,相当于求得P的值为P≈377/ 120. 这是刘徽以前有据可考的圆周率的最好结果.我国古代很早就知道“周三径一”误差很大, 需要改进, 不少人在这方面作过工作[ 4] :汉代的刘歆( 约公元前50~公元23年) 所用圆周率的值为P≈3. 1547; 汉代的张衡( 公元78~139年) 所用圆周率的值为P≈3. 1623; 三国的王蕃( 公元219~257年) 所用圆周率的值为P≈3. 1556. 这些P的近似值都不如Archimedes 和Ptolemy 的结果好, 并且都未提供出正确的算法, 缺乏理论根据.而刘徽根据他所提出的割圆术, 运用勾股定理, 设计出一个完整的求圆周率P近似值的算法.设n= 6 ( 术曰: 割六觚以为十二觚) , 又设r= 1, 则有s= 1( 术曰: 置圆径二尺, 半之为一尺, 即六觚之面也) , 算法步骤如下:¹设弦为r , 勾为s/ 2, 求股, 赋予a( 此为小股, 术曰: 令半径为弦, 半面为勾, 为之求股) ;º将r - a 赋予b( 此为余径, 术曰: 觚面之外, 又有余径, 又曰: 以减半径, 谓之小股) ; » 设勾仍为s/ 2, 股为b, 求弦, 赋予s( 实为圆内接正2n 边形的边长, 术曰: 为之求小弦, 即十二( 2n) 觚之一面也) ;¼求S n= nõs 圆周率的近似值( 实为圆内接正2n 边形的半周长, 亦为圆内接正4n 边形的面积, 术曰: 得二十四( 4n) 觚之幂) ;½将2n 赋予向¹ .上述算法为计算出更精确的圆周率值奠定了基础. 刘徽所获得的“圆幂三百一十四寸二十五分寸之四”,即P≈3. 1416, 这是当时世界上最精确的圆周率的值.顺便指出, 祖冲之[ 5] ( 公元429~500年) 研究过刘徽的割圆术, 再加上自己的创造, 他获得了当时世界上最精确的圆周率的值: 3. 1415926 < P< 3. 1415927. 此外, 他还用最佳近似分数给出所谓疏率和密率: P≈22/ 7, 这一结果与Archimedes[ 3] 的上限结果相同; P ≈355/ 113, 这一结果在西方迟至1573年才由Otho 重新获得.2. 3在中国刘徽首次比较准确地描述了极限概念在中国战国时代的著作《庄子》中记录了名家惠施的话: “一尺之棰, 日取其半, 万世不竭. ”这段话已经有了极限思想的雏形[ 5] . 但名家所表现出的极限思想是不自觉的、模糊的. 名家的目的仅仅是为了在辩论中强调名词概念的相对性, 因而不可能形成数学上的清晰的极限概念.但是, 刘徽在割圆术中比较准确地描述了极限概念. 他说: “割之弥细, 所失弥少. 割之又割, 以至于不可割, 则与圆周合体而无失矣. ”这明确地肯定了lim S n= P. 这里S n是圆内接正2n 边形的半周长, 亦为圆内接正4n 边形的面积.他又说: “觚面之外, 又有余径. 以面乘余径则幂出弧表. ”这表明刘徽实际上建立了不等式S 2n< P< S2n+ e n, 其中e n= S2n- S n, 此即刘徽所说的“差幂”.刘徽的这一不等式明显地优于Archimedes 的不等式, 这是因为: 第一, Archimedes 既要用到圆内接正多边形, 也要用到圆外切正多边形, 而刘徽用“差幂”,只需要用圆内接正多边形, 可以减少大约一半运算次数; 第二, 由于S 2n等于圆内接正4n 边形的半周长, 并且容易证明, S2n+ e n小于圆外切正4n 边形的半周长, 因而, 刘徽的这一不等式比Archimedes 的不等式更精确. 刘徽显然和Archimedes 一样, 已经意识到这里存在类似夹逼定理这样的极限性质, 由此既可以推断极限的存在, 还可以确定极限值各数位上的准确的有效数字. 刘徽正是这样做的, 他用圆内接正一千五百三十六边形和圆内接正三千零七十二边形的面积, 依据他的不等式, 验证了他的结果直到第四位小数都是正确的.刘徽接着说: “觚之细者, 与圆合体, 则表无余径, 表无余径, 则幂不外出矣. ”他正是根据这一点, 解释了圆田术求圆面积的方法( 半周半径相乘得积步) . 刘徽的解释方法, 与Eudox us 证明圆面积之比等于半径平方比的穷竭法如出一辙.3 刘徽割圆术的局限性刘徽的极限概念是不彻底的刘徽的割圆术虽然比较准确地描述了极限概念, 而且, 很可能进行了真正的极限运算, 但刘徽的数学素养还不足以完整地描述这个无限的趋向过程. 他采用了“割之又割, 以至于不可割, 则与圆周合体而无失矣”,“觚之细者, 与圆合体, 则表无余径”等绝对的、不准确的言词. 实际上, 刘徽的思想陷入了矛盾之中, 一方面, 他像惠施那样意识到割圆的过程是无限的, 是万世不竭的, 另一方面, 他又竭力回避无限, 不愿意正视无限, 相信总有“不可割”,“表无余径”,“幂不外出”,“与圆周合体而无失”之时. 这就足以说明刘徽的极限概念是不彻底的. 事实上, 我国古代还有不少学者虽具有极限思想的雏形, 但在描述中都毫无例外地不得不采用绝对的、不准确的言词. 极限概念的不彻底, 限制了刘徽对极限概念的挖掘和应用, 也限制了刘徽在数学上的创造性. 纵观刘徽在数学上的工作可以看出, 虽然他在圆周率的计算等方面取得了令世人瞩目的成果, 但是, 刘徽在整个数学史上的地位, 则不可能超过Ar chimedes 等人.参考文献1 刘徽注. 九章算术. 上海: 上海古籍出版社, 19902 Morris Kl ine 著; 张理京, 张锦炎译. 古今数学思想. 上海: 上海科学技术出版社, 19793 How ard Eves . An In tr od uct ion to the His tory of Mathemat ics. New York: Saunders Coll ege Pub lish ing, 19834 李俨. 中算史论丛. 北京: 中国科学院出版, 19545 钱宝琮. 中国数学史. 北京: 科学出版社, 19816 邓建中, 葛仁杰, 程正兴. 计算方法. 西安: 西安交通大学出版社, 19857 王乃信,王树林,西北农业大学学报,1997年8月。
刘徽与割圆术

劉徽﹝約公元3世紀﹞關於劉徽的生卒年代和身世履歷不詳,他可能是現今山東省臨淄或淄川一帶人。
劉徽注《九章算術》,同時又撰有《重差》一卷,《重差》後來印成單行本改稱為《海島算經》,在注文中,劉徽用語言來講清道理,用圖形來解釋問題﹝析理以辭,解體用圖﹞。
他不是只停留在對《九章》的注釋上,而是更上一層樓,在注釋的同時提出了許多創造性見解,例如為闡述幾何命題,証明幾何定理,創造了「以盈補虛法」,更為計算圓周率提出了「割圓術」:劉徽從最簡單的正六邊形開始,由正192邊形的面積得到π=151/50或3.14。
不過他更進一步算出3.14<π<3.14,後來在另一個地方,劉徽用他的方法,繼續演算到3072邊形,並且得到他的最佳值──一個相當於3.14159的數。
「割圓術」是我國數學史上首次將極限概念用於近似計算。
此外,劉徽的「齊同術」和「方程新術」等,是對《九章算術》方法的進一步闡述與補充。
在注釋《九章》的同時,劉徽深感有創立新的測量方法的必要,於是提出了重差術,撰《重差》一卷。
劉徽創立了割圓術,給出了「割圓」的一般法則,後世的割圓家可能在π 的近似值上估計得比他精密,但若論及創始的功勞,則他的地位是無人可以替代的。
劉徽是魏人,經歷可能延長到晉朝,這是史家根據《隋書》記載的「魏陳留王景元四年(263 A.D.)劉徽注九章」的文句推斷出來的。
除此之外,我們對他的身世一無所知。
晉朝算學博士王孝通(《緝古算經》的作者)稱讚他「思極毫芒」,推許他的著作「一時獨步」。
他那極富原創性的《九章算術注》(附於現傳本的《九章算術》內),及《重差術》(即現傳的《海島算經》)二部著作,的確是他不朽聲名的最佳註腳。
劉徽的割圓術記載在九章算術第一卷方田章的第32題關於圓面積計算的注文裏。
我們把它歸納為下列幾點來加以說明。
一、劉徽首先指出利用π=3 這一數值算得的結果不是圓面積,而是圓內接正十二邊形的面積,這個結果比π 的真值少。
刘徽与割圆术ppt课件

▪ 刘徽断言“割之弥细,所失弥少,割之又割,以至于不可割,则
与圆合体,而无所失矣”。其思想与古希腊穷竭法不谋而合。割 圆术在圆周率计算史上曾长期使用。1610年德国数学家柯伦用 2^62边形将圆周率计算到小数点后35位。1630年格林贝尔格利 用改进的方法计算到小数点后39位,成为割圆术计算圆周率的最 好结果。分析方法发明后逐渐取代了割圆术,但割圆术作为计算
二是在继承的基础上提出了自己的创见。这方面主要体现为以下几项有代表性的
创见: ①割圆术与圆周率 他在《九章算术•圆田术》注中,用割圆术证明了圆面积的精确公式,并
给出了计算圆周率的科学方法。他首先从圆内接六边形开始割圆,每次边数 倍增,算到192边形的面积,得到π=157/50=3.14,又算到3072边形的面积, 得到π=3927/1250=3.14▪ 刘徽由正六邊形開始,不斷倍增正多邊形的邊數。
正6邊形
正12邊形
正24邊形
邊數愈多,正多邊形愈接近圓形。 最後,劉徽求得π≈ 3.1416。
正48邊形
7
谢谢观看
8
4
②刘徽原理 在《九章算术•阳马术》注中,他在用无限分割的方法解决锥体体积时, 提出了关于多面体体积计算的刘徽原理。 ③“牟合方盖”说 在《九章算术•开立圆术》注中,他指出了球体积公式V=9D3/16(D为球直径) 的不精确性,并引入了“牟合方盖”这一著名的几何模型。“牟合方盖”是 指正方体的两个轴互相垂直的内切圆柱体的贯交部分。 ④方程新术 在《九章算术•方程术》注中,他提出了解线性方程组的新方法,运用了 比率算法的思想。 ⑤重差术 在白撰《海岛算经》中,他提出了重差术,采用了重表、连索和累矩等 测高测远方法。他还运用“类推衍化”的方法,使重差术由两次测望,发展 为“三望”、“四望”。而印度在7世纪,欧洲在15~16世纪才开始研究两次 测望的问题。
刘徽与割圆术

摘要:刘徽是公元三世纪世界上最杰出的数学家,他在公元263年撰写的著作《九章算术注》以及后来的《海岛算经》,是我国最宝贵的数学遗产,从而奠定了他在中国数学史上的不朽地位。
他通过割圆术中极限思想,进而引入数列极限的描述定义。
刘徽借“割圆术”方法,凭借其高超的对无限问题的理解和致用的处理方式,以“不可分量可积”前提、“夹逼准则”等知识证明了圆的面积公式,运算中包含着微积分的思想。
关键词:刘徽割圆术极限微积分徽率英文题目Abstract:Liu Hui is the third Century the world's most eminent mathematician,in the year 263writings" arithmetic in nine sections。
" and later" island art",is China's most valuable mathematical legacy,and laid him in Chinese history of mathematics in the immortal status。
He by cutting a circle limit thought in the limit of a sequence,and then introduce the definition。
Liu Hui" by cutting a circle" method,with its superb to infinite problem understanding and using manner,with " notcomponent integrable" premise," squeeze rule" knowledge that the area of a circle formula,computing contains calculus ideas。
刘徽与“割圆术”

O
r
A
刘徽提出的“ 割圆术” 发展而来 的。刘徽曾为《 九 章算术》 作注 ,割 圆术 ” “ 是他为《 九章算术》 中的 《 田章》 方 里的“ 圆田术” 一文写的注疏 。 在这篇注 疏 中, 刘徽提出了一个计算 圆周率 的算法 。下面 将会看到该算法 中包含了许多创造性 的思想 , 在 今 天看 来仍有 很 大的启发 意义 。
切
洛 : 徽 与 “ 圆术 刘 割
周率 的 。那 么如 何 估 计逼 近 误 差 呢 ? 里刘 徽 又 这
出奇招 , 参见下图 , A 以 B为一边作矩形A D , B E 使
,_ 、
D E与 A B相 切 于 M。
D
表 l 是用算法 I 进行计算得到的 , 可见 当割到 圆的 内接正 12 形 时 , 得 到通 常所 用 的 1的 9边 就 T 近似值 31。一直计算下去 , . 4 可以知道当割到圆
维普资讯
第l 9卷第 1 期
V 1 91 o. . 1
青海师范大学 民族师范学 院学报
Junlf nri eces o ee f i hi ec e nvri o rao oie T ahr C fg n a T ah rU i sy Mi ts i oQ g s e t
被 阿拉伯 人 阿尔 ・ 西打破 。祖 冲之 生活 的时期 , 卡 计 算工 具极 其 落后 , 么他 是用 什 么 方法 计 算 出 那
来 的呢? 据史实记 载 , 祖冲之用 了一种称为 “ 缀 术” 的方法 , 惜 “ 可 缀术 ” 己失传 。现 在许 多人认 早
为 “ 术 ” 从 我 国魏 晋 时期 另 一 杰 出 的数 学 家 缀 是
求得 的数据进行简单 的修正 , 就大大提高了逼近
刘徽与割圆术
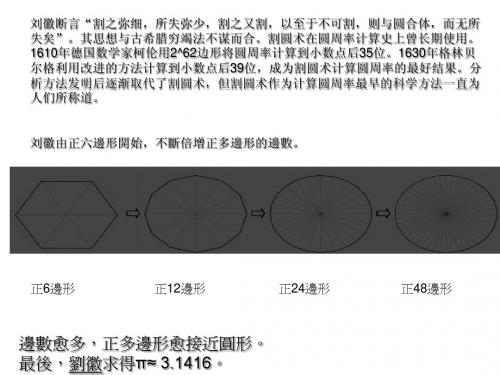
刘徽由正六邊形開始,不斷倍增正多邊形的邊數。
ቤተ መጻሕፍቲ ባይዱ正6邊形
正12邊形
正24邊形
正48邊形
邊數愈多,正多邊形愈接近圓形。 最後,劉徽求得π≈ 3.1416。
刘徽断言“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所 失矣”。其思想与古希腊穷竭法不谋而合。割圆术在圆周率计算史上曾长期使用。 1610年德国数学家柯伦用2^62边形将圆周率计算到小数点后35位。1630年格林贝 尔格利用改进的方法计算到小数点后39位,成为割圆术计算圆周率的最好结果。分 析方法发明后逐渐取代了割圆术,但割圆术作为计算圆周率最早的科学方法一直为 人们所称道。
刘徽割圆术的数学原理

刘徽割圆术,又称为“徽割圆术”或“刘徽圆周率计算法”,是中国古代数学家刘徽在《九章算术》中提出的一种计算圆周率的方法。
这个方法的数学原理涉及到对圆的割线和三角函数的概念。
刘徽的割圆术基于圆周率与圆的直径的关系,即π(圆周率)等于圆的周长与直径的比值。
他提出了一种通过割圆得到近似值的方法,主要涉及到正多边形的内接和外接。
具体步骤如下:
1. 内接正六边形的构造:在圆内作一个正六边形,使其顶点分别位于圆的周上,这个六边形的直径等于圆的直径。
2. 内接正十二边形的构造:在内接正六边形的每个边上取一点,连接这些点,得到一个内接正十二边形。
3. 内接正二十四边形的构造:在内接正十二边形的每个边上再取一点,连接这些点,得到一个内接正二十四边形。
4. 迭代过程:重复上述步骤,每次构造的多边形边数翻倍,从而逐渐逼近圆。
5. 圆周率的逼近:当多边形的边数越来越多时,多边形的周长将逐渐接近圆的周长。
刘徽认为,当多边形的边数非常大时,多边形的周长与圆的周长的比值即为π。
这个方法虽然在原理上是正确的,但是在实际计算中,随着多边形边数的增加,计算的复杂性也增加,所以其实用性相对有限。
现代数学中,我们更常用其他方法如莱布尼茨级数、无穷级数等来计算圆周率π。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刘徽和割圆术
中国向来以文明古国自称,谈到中国古代文明,我们一定会说起以“经世致用”为信条,以筹算为主的中国古代数学史。
在这段曲折发展的历史中,我们的古代数学跟其他古文明一样,在一定程度上获得了发展,特别是在算法的深度和广度上有着卓越的发展。
但我们不得不提及,在中国古代长达2000多年的封建制度统治下,数学研究一直停留在计算层面,理论的严谨和系统却不尽如人意,这同时也导致了一些错误的结果的出现。
在这样的数学背景下,刘徽可谓是中国数学史上的一朵奇葩,他有着“为数学而数学”的价值观,曾令中国古代数学的严谨与系统达到前所未有的高度。
下面我将主要介绍刘徽及其最耐人寻味的一段成就——割圆术。
刘徽,生于公元250年左右,是魏晋时人。
他的一生为数学刻苦探求,虽然地位低下,但人格高尚。
他所撰的《九章算术注》是中国最宝贵的数学遗产。
刘徽思想敏捷,方法灵活,既提倡推理又主张直观,是中国最早明确主张用逻辑推理的方式来论证数学命题的人。
他不是沽名钓誉的庸人,而是学而不厌的伟人。
由于篇幅有限,对刘徽卓越的成就不能一一介绍,只能介绍其最耐人寻味的割圆术。
割圆术可谓是中国古代数学的奇迹,在后面与阿基米德求圆面积方法的比较中,您将发现割圆术的精妙与美丽。
在《九章算术》中曾提到“圆田术”---半周半径相乘得积步。
这就是著名的圆面积公式:
(1) 其中S 表示圆面积,C 表示周长,R 表示半径。
我们今天可以得出这个公式是正确
的,但在《九章算术》中只是提到了这一结论,却未给出严谨的证明。
在刘徽之前人们以圆内接正六边形的周长代替圆周长C ,以圆内接正十二边形的面积代替圆面积S ,用出入相补原理将正十二边形拼补成一个以正六边形的周长的一半作为长,以圆半径作为宽的长方形来推证上述公式。
在今天,我们可以看出用圆内接正六边形和圆内接正十二边形来近似代替圆是相当粗糙的,但在当时很少有人能指出这一算法的不严谨性,而刘徽却说此方法“合径率一而外周率三也”,一针见血的指出了这一方法的不严格性。
为了给出这一公式的严格证明方法,刘徽发明了割圆术。
所谓割圆术其实就是现代微积分中的极限的思想,即用圆内接正多边形的面积来逼近圆的面积。
正如他在《九章算术注》中所说“割之弥细,所失弥少。
割之又割以至于不可割则与圆合体而无所失矣”。
在利用这一方法证明这一公式的过程中,刘徽还计算出了当时最精确的圆周率近似值---徽率( ),
这一结果要早西方很多年。
同时,我们了解割圆术后会发现利用这种方法我们可
以将圆周率计算到任意精确程度,但当时计算能力有限,只能依靠手工验算,
所以刘徽能算到
,已是很了不起了。
下面我们看一下刘徽割圆术的具体做法。
12S CR 1575015750
首先,刘徽从圆内接正六边形出发,开始割圆。
利用迭代的计算方法依次得到圆内接正62⨯,262⨯,……边形。
我们记圆内接正62n ⨯边形的面积为n S ,0,1,2,3,...n =,记圆的面积为S ,则有
n S S <
而随着分割次数的增多,n S S -越来越小,到不可再割时,n S 与S 重合,也就有了
lim n n S S →∞
= 然后,圆内接正62n ⨯边形的每边和圆周之间有一段距离n r ,如下图CD ,称之为余径。
记正62n ⨯边形的边长为n a ,将n a 乘n r ,其总和便是()12n n S S +-(这在下图中可以很显然的得到)。
而()12n n S S +-正是下图中矩形''AA B B 的面积,将它加到n S 上,则有
()12n n n S S S S +<+-
然而到不可割时,正62n ⨯边形与圆周合体,则有余径为0,即
lim 0n n r →∞
= 于是有 lim 0n n n r a →∞
= 因此
()1lim 2n n n n S S S S +→∞
+-=⎡⎤⎣⎦ 这就证明了圆面积的上界序列与下界序列的极限都是圆面积。
最后便是求出圆的周长。
刘徽把不可再割时与圆周合体的正多边形分割成无穷多个以圆心为顶点,以
B'
A'
D
C B A O
正多边形每边长为底的小等腰三角形,以圆半径乘这个多边形的边长是每个小等腰三角形面积的2 倍,也就是刘徽所说的“觚而裁之,每辄自倍”。
显然,所有这些小等腰三角形的底边之和就是圆周长,并且所有这些小等腰三角形面积的总和, 就是圆的面积。
于是就有了,圆半径乘圆周长,就是圆面积的2 倍,即
2CR S =
这样就证明了《九章算术》中著名的圆面积公式,即公式(1).
说到刘徽的割圆术,我们不得不提到古希腊数学家阿基米德计算圆面积的方法。
阿基米德是分别用圆的内接正多边形和圆的外切正多边形来作为圆的上界序列和圆的下界序列来逼近圆的。
这样就要进行两次来分别得到圆的内接正多边形和外切正多边形的面积,在古代的计算能力范围内,这无疑是增加了难度。
比较下来,我们发现刘徽的割圆术可谓是事半功倍。
从割圆术的巧妙中我们看到了刘徽的智慧与严谨,这在中国古代数学中是难能可贵的。
另外,割圆术中还包含了许多我们现在还在利用的数学方法和数学思想:
(1) 数形结合的的思想方法
在割圆的过程中刘徽一面画出图形,一面进行计算,这正是我们现代
数学中经常提到的数形结合的方法。
在数形结合的过程中,让他的计算方法更为直观,易于后人的理解领悟。
(2) 极限的思想方法
割圆的不断进行,越割多边形的边数越多,越来越接近于圆,这样不断分割逼近圆的思想这是我们现代数学中所讲的极限思想。
在刘徽的时代,他就能运用极限这是令人惊叹的。
(3) 数列极限的两面夹思想方法
在求数列极限的时候我们经常会用到两面夹准则。
刘徽在割圆的过程
中就是利用了两面夹的方法。
分别用n S 和n n+1n 2S S S +(-)从小大两个方向来
夹逼圆,两个数列极限一致,从而得出圆的面积公式。
不管是从数学本身还是文化层面来看割圆术,我们都能看到它的价值,它是中国古代数学的奇葩。
至今仍是值得我们研究学习的。
而刘徽的严谨治学的态度和精妙的解决方法至今也是值得我们后人效仿和学习的。
