七下期末复习

合集下载

七年级语文下学期期末复习诗歌鉴赏试题含答案

七年级语文下学期期末复习诗歌鉴赏试题含答案一、七年级下册诗歌鉴赏1．古诗阅读江夏送倩公归汉东[唐]李白彼美汉东国，川藏明月①辉。

宁知②丧乱③后，更有一珠归。

【注释】①明月：传说中的“随侯明珠”，与“和氏璧”齐名。

②宁知：谁也没有想到。

③丧乱：安史之乱。

（1）简要赏析“更有一珠归”中“珠”字的妙处。

（2）这首诗抒发了诗人怎样的思想感情？2．阅读下面古诗，完成下题。

约客【宋·赵师秀】黄梅时节①家家雨，青草池塘处处蛙。

有约不来过夜半，闲敲棋子落灯花②。

①黄梅时节：农历四、五月间，江南梅子黄了、熟了，大都是阴雨连绵的时候，所以称“黄梅时节”为江南雨季。

②落灯花：旧时以灯油照明，灯芯烧残，落下来时好像一朵闪亮的小花。

（1）诗歌前两句哪些词语交代了环境和时令？找出词语并说明环境和时令。

（2）诗人通过对撩人思绪的环境描写及“闲敲棋子”这一细节动作的渲染，表现了自己怎样的心情？3．阅读下面一首诗，完成问题。

登飞来峰[宋] 王安石飞来山上千寻塔，闻说鸡鸣见日升。

不畏浮云遮望眼，自缘身在最高层。

（1）请从描写方法的角度，赏析“飞来山上千寻塔，闻说鸡鸣见日升”。

（2）这首诗表达了诗人怎样的思想感情?4．阅读下面这首宋诗，完成后面小题。

南溪早春①杨万里还家五度见春容，长被春容恼病翁。

高柳下来垂处绿，小桃上去末梢红。

卷帘亭馆酣酣日，放杖溪山款款风。

更入新年足新雨，去年未当好时丰。

【注】①本诗是作者晚退职家居期间所作。

（1）诗人通过写柳树和桃树的什么特点来表现南溪早春的？（2）这首诗歌蕴含着诗人丰富的情感，请作赏析。

5．阅读诗歌，回答问题。

如梦令·春思①（北宋）苏轼手种堂前桃李，无限绿阴青子。

帘外百舌儿②，惊起五更春睡。

居士③，居士，莫忘小桥流水。

【注】①这首词是苏轼离开黄州多年后，回想起当年的生活情景而写的。

②百舌儿：鸟名。

③居士：苏轼自号“东坡居士”，这是作者的自成。

（1）第二句“无限”一词写出景物怎样的特点？（2）你从“莫忘小桥流水”中读出苏轼怎样的情怀？6．阅读下面两首诗歌，完成下面小题望岳(唐)杜甫岱宗夫如何?齐鲁青未了。

期末复习(压轴题49题)—2023-2024学年七年级数学下学期期末考点(北师大版)(解析版)

z 期末复习（压轴题49题20个考点）一．规律型：数字的变化类（共1小题）1．为了求1+2+22+23+…+22011+22012的值，可令S ＝1+2+22+23+…+22011+22012，则2S ＝2+22+23+24+…+22012+22013，因此2S ﹣S ＝22013﹣1，所以1+22+23+…+22012＝22013﹣1．仿照以上方法计算1+5+52+53+…+52012的值是（）A ．52013﹣1B ．52013+1C ．D ．【答案】D【解答】解：令S ＝1+5+52+53+ (52012)则5S ＝5+52+53+…+52012+52013，5S ﹣S ＝﹣1+52013，4S ＝52013﹣1，则S ＝．故选：D ．二．同底数幂的乘法（共1小题） 2．阅读材料：求1+2+22+23+24+…+22013的值．解：设S ＝1+2+22+23+24+…+22012+22013，将等式两边同时乘2得：2S ＝2+22+23+24+25+…+22013+22014 将下式减去上式得2S ﹣S ＝22014﹣1即S ＝22014﹣1即1+2+22+23+24+…+22013＝22014﹣1请你仿照此法计算：（1）1+2+22+23+24+…+210（2）1+3+32+33+34+…+3n （其中n 为正整数）．【答案】见试题解答内容【解答】解：（1）设S ＝1+2+22+23+24+ (210)将等式两边同时乘2得：2S ＝2+22+23+24+…+210+211，将下式减去上式得：2S ﹣S ＝211﹣1，即S ＝211﹣1，则1+2+22+23+24+…+210＝211﹣1；z （2）设S ＝1+3+32+33+34+…+3n ①，两边同时乘3得：3S ＝3+32+33+34+…+3n +3n +1②，②﹣①得：3S ﹣S ＝3n +1﹣1，即S ＝（3n +1﹣1），则1+3+32+33+34+…+3n ＝（3n +1﹣1）．三．多项式乘多项式（共1小题）3．如图，正方形卡片A 类，B 类和长方形卡片C 类若干张，如果要拼一个长为（a +2b ），宽为（a +b ）的大长方形，则需要C 类卡片张．【答案】见试题解答内容【解答】解：（a +2b ）（a +b ）＝a 2+3ab +2b 2．则需要C 类卡片3张．故答案为：3．四．完全平方公式（共3小题）4．已知a ﹣b ＝b ﹣c ＝，a 2+b 2+c 2＝1，则ab +bc +ca 的值等于．【答案】见试题解答内容【解答】解：∵a ﹣b ＝b ﹣c ＝，∴（a ﹣b ）2＝，（b ﹣c ）2＝，a ﹣c ＝， ∴a 2+b 2﹣2ab ＝，b 2+c 2﹣2bc ＝，a 2+c 2﹣2ac ＝， ∴2（a 2+b 2+c 2）﹣2（ab +bc +ca ）＝++＝， ∴2﹣2（ab +bc +ca ）＝， ∴1﹣（ab +bc +ca ）＝， ∴ab +bc +ca ＝﹣＝﹣．故答案为：﹣．z 5．请看杨辉三角（1），并观察下列等式（2）：根据前面各式的规律，则（a +b ）6＝．【答案】见试题解答内容【解答】解：（a +b ）6＝a 6+6a 5b +15a 4b 2+20a 3b 3+15a 2b 4+6ab 5+b 6故本题答案为：a 6+6a 5b +15a 4b 2+20a 3b 3+15a 2b 4+6ab 5+b 66．回答下列问题（1）填空：x 2+＝（x +）2﹣ ＝（x ﹣）2+（2）若a +＝5，则a 2+＝；（3）若a 2﹣3a +1＝0，求a 2+的值．【答案】见试题解答内容【解答】解：（1）2、2．（2）23．（3）∵a ＝0时方程不成立，∴a ≠0，∵a 2﹣3a +1＝0两边同除a 得：a ﹣3+＝0，移项得：a +＝3，∴a 2+＝（a +）2﹣2＝7．五．平方差公式的几何背景（共1小题）7．如图，边长为m +4的正方形纸片剪出一个边长为m 的正方形之后，剩余部分可剪拼成一个矩形，若拼成的矩形一边长为4，则另一边长为．z【答案】见试题解答内容【解答】解：设拼成的矩形的另一边长为x ，则4x ＝（m +4）2﹣m 2＝（m +4+m ）（m +4﹣m ），解得x ＝2m +4．故答案为：2m +4．六．整式的混合运算（共1小题）8．7张如图1的长为a ，宽为b （a ＞b ）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD 内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S ，当BC 的长度变化时，按照同样的放置方式，S 始终保持不变，则a ，b 满足（）A ．a ＝bB ．a ＝3bC ．a ＝bD ．a ＝4b 【答案】B 【解答】解：左上角阴影部分的长为AE ，宽为AF ＝3b ，右下角阴影部分的长为PC ，宽为a ，∵AD ＝BC ，即AE +ED ＝AE +a ，BC ＝BP +PC ＝4b +PC ，∴AE +a ＝4b +PC ，即AE ﹣PC ＝4b ﹣a ，∴阴影部分面积之差S ＝AE •AF ﹣PC •CG ＝3bAE ﹣aPC ＝3b （PC +4b ﹣a ）﹣aPC ＝（3b ﹣a ）PC +12b 2﹣3ab ，则3b ﹣a ＝0，即a ＝3b ．解法二：既然BC 是变化的，当点P 与点C 重合开始，然后BC 向右伸展，设向右伸展长度为X ，左上阴影增加的是3bX ，右下阴影增加的是aX ，因为S 不变，∴增加的面积相等，z ∴3bX ＝aX ，∴a ＝3b ．故选：B ．七．函数的图象（共4小题）9．如图，某电信公司提供了A ，B 两种方案的移动通讯费用y （元）与通话时间x （分）之间的关系，则下列结论中正确的有（）（1）若通话时间少于120分，则A 方案比B 方案便宜20元；（2）若通话时间超过200分，则B 方案比A 方案便宜12元；（3）若通讯费用为60元，则B 方案比A 方案的通话时间多；（4）若两种方案通讯费用相差10元，则通话时间是145分或185分．A ．1个B ．2个C ．3个D ．4个【答案】C【解答】解：依题意得A ：（1）当0≤x ≤120，y A ＝30，（2）当x ＞120，y A ＝30+（x ﹣120）×[（50﹣30）÷（170﹣120）]＝0.4x ﹣18；B ：（1）当0≤x ＜200，y B ＝50，当x ＞200，y B ＝50+[（70﹣50）÷（250﹣200）]（x ﹣200）＝0.4x ﹣30，所以当x ≤120时，A 方案比B 方案便宜20元，故（1）正确；当x ≥200时，B 方案比A 方案便宜12元，故（2）正确；z 当y ＝60时，A ：60＝0.4x ﹣18，∴x ＝195，B ：60＝0.4x ﹣30，∴x ＝225，故（3）正确；当B 方案为50元，A 方案是40元或者60元时，两种方案通讯费用相差10元，将y A ＝40或60代入，得x ＝145分或195分，故（4）错误；故选：C ．10．在物理实验课上，小明用弹簧秤将铁块A 悬于盛有水的水槽中，然后匀速向上提起（不考虑水的阻力），直至铁块完全露出水面一定高度，则下图能反映弹簧秤的读数y （单位N ）与铁块被提起的高度x （单位cm ）之间的函数关系的大致图象是（）A ．B ．C ．D ．【答案】C 【解答】解：因为小明用弹簧秤将铁块A 悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度．则露出水面前读数y 不变，出水面后y 逐渐增大，离开水面后y 不变．故选：C ．11．“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事（x 表示乌龟从起点出发所行的时间，y 1表示乌龟所行的路程，y 2表示兔子所行的路程）．有下列说法：①“龟兔再次赛跑”的路程为1000米；②兔子和乌龟同时从起点出发；③乌龟在途中休息了10分钟；z ④兔子在途中750米处追上乌龟．其中正确的说法是．（把你认为正确说法的序号都填上）【答案】见试题解答内容【解答】解：根据图象可知：龟兔再次赛跑的路程为1000米，故①正确；兔子在乌龟跑了40分钟之后开始跑，故②错误；乌龟在30﹣﹣40分钟时的路程为0，故这10分钟乌龟没有跑在休息，故③正确；y 1＝20x ﹣200（40≤x ≤60），y 2＝100x ﹣4000（40≤x ≤50），当y 1＝y 2时，兔子追上乌龟，此时20x ﹣200＝100x ﹣4000，解得：x ＝47.5，y 1＝y 2＝750米，即兔子在途中750米处追上乌龟，故④正确．综上可得①③④正确．故答案为：①③④．12．小高从家门口骑车去单位上班，先走平路到达点A ，再走上坡路到达点B ，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是分钟．【答案】见试题解答内容【解答】解：先算出平路、上坡路和下坡路的速度分别为、和（千米/分），z 所以他从单位到家门口需要的时间是（分钟）．故答案为：15．八．二次函数的图象（共1小题） 13．如图，正方形ABCD 的边长为4，点P 、Q 分别是CD 、AD 的中点，动点E 从点A 向点B 运动，到点B 时停止运动；同时，动点F 从点P 出发，沿P →D →Q 运动，点E 、F 的运动速度相同．设点E 的运动路程为x ，△AEF 的面积为y ，能大致刻画y 与x 的函数关系的图象是（）A ．B ．C ．D ．【答案】A 【解答】解：当F 在PD 上运动时，△AEF 的面积为y ＝AE •AD ＝2x （0≤x ≤2），当F 在AD 上运动时，△AEF 的面积为y ＝AE •AF ＝x （6﹣x ）＝﹣x 2+3x （2＜x ≤4），图象为：故选：A ．z 九．平行线的性质（共2小题）14．如图，将长方形ABCD 沿线段EF 折叠到EB 'C 'F 的位置，若∠EFC '＝100°，则∠DFC '的度数为（）A ．20°B ．30°C ．40°D ．50°【答案】A【解答】解：由翻折知，∠EFC ＝∠EFC '＝100°，∴∠EFC +∠EFC '＝200°，∴∠DFC '＝∠EFC +∠EFC '﹣180°＝200°﹣180°＝20°，故选：A ．15．珠江流域某江段江水流向经过B 、C 、D 三点拐弯后与原来相同，如图，若∠ABC ＝120°，∠BCD ＝80°，则∠CDE ＝度．【答案】见试题解答内容【解答】解：过点C 作CF ∥AB ，已知珠江流域某江段江水流向经过B 、C 、D 三点拐弯后与原来相同，∴AB ∥DE ，∴CF ∥DE ，∴∠BCF +∠ABC ＝180°，∴∠BCF ＝60°，∴∠DCF ＝20°，∴∠CDE ＝∠DCF ＝20°．故答案为：20．z十．三角形的面积（共4小题）16．在如图的方格纸中，每个小方格都是边长为1的正方形，点A 、B 是方格纸中的两个格点（即正方形的顶点），在这个5×5的方格纸中，找出格点C 使△ABC 的面积为2个平方单位，则满足条件的格点C 的个数是（）A ．5B ．4C ．3D ．2【答案】A【解答】解：满足条件的C 点有5个，如图平行于AB 的直线上，与网格的所有交点就是．故选：A ． 17．如图，△ABC 三边的中线AD 、BE 、CF 的公共点为G ，若S △ABC ＝12，则图中阴影部分的面积是．【答案】见试题解答内容【解答】方法1解：∵△ABC 的三条中线AD 、BE ，CF 交于点G ，∴S △CGE ＝S △AGE ＝S △ACF ，S △BGF ＝S △BGD ＝S △BCF ，∵S △ACF ＝S △BCF ＝S△ABC＝×12＝6，z ∴S △CGE ＝S △ACF ＝×6＝2，S △BGF ＝S △BCF ＝×6＝2，∴S 阴影＝S △CGE +S △BGF ＝4．故答案为4．方法2设△AFG ，△BFG ，△BDG ，△CDG ，△CEG ，△AEG 的面积分别为S 1，S 2，S 3，S 4，S 5，S 6，根据中线平分三角形面积可得：S 1＝S 2，S 3＝S 4，S 5＝S 6，S 1+S 2+S 3＝S 4+S 5+S 6①，S 2+S 3+S 4＝S 1+S 5+S 6② 由①﹣②可得S 1＝S 4，所以S 1＝S 2＝S 3＝S 4＝S 5＝S 6＝2，故阴影部分的面积为4．故答案为：4．18．如图，A 、B 、C 分别是线段A 1B ，B 1C ，C 1A 的中点，若△ABC 的面积是1，那么△A 1B 1C 1的面积．【答案】见试题解答内容【解答】解：如图，连接AB 1，BC 1，CA 1，∵A 、B 分别是线段A 1B ，B 1C 的中点，∴S △ABB 1＝S △ABC ＝1，S △A 1AB 1＝S △ABB 1＝1，∴S △A 1BB 1＝S △A 1AB 1+S △ABB 1＝1+1＝2，同理：S △B 1CC 1＝2，S △A 1AC 1＝2，∴△A 1B 1C 1的面积＝S △A 1BB 1+S △B 1CC 1+S △A 1AC 1+S △ABC ＝2+2+2+1＝7．故答案为：7．z 19．如图，对面积为s 的△ABC 逐次进行以下操作：第一次操作，分别延长AB 、BC 、CA 至点A 1、B 1、C 1，使得A 1B ＝2AB ，B 1C ＝2BC ，C 1A ＝2CA ，顺次连接A 1、B 1、C 1，得到△A 1B 1C 1，记其面积为S 1；第二次操作，分别延长A 1B 1、B 1C 1、C 1A 1至点A 2、B 2、C 2，使得A 2B 1＝2A 1B 1，B 2C 1＝2B 1C 1，C 2A 1＝2C 1A 1顺次连接A 2、B 2、C 2，得到△A 2B 2C 2，记其面积为S 2；…；按此规律继续下去，可得到△A n B n ∁n ，则其面积S n ＝．【答案】见试题解答内容【解答】解：连接A 1C ；S △AA 1C ＝3S △ABC ＝3S ，S △AA 1C 1＝2S △AA 1C ＝6S ，所以S △A 1B 1C 1＝6S ×3+1S ＝19S ；同理得S △A 2B 2C 2＝19S ×19＝361S ； S △A 3B 3C 3＝361S ×19＝6859S ，S △A 4B 4C 4＝6859S ×19＝130321S ， S △A 5B 5C 5＝130321S ×19＝2476099S ，从中可以得出一个规律，延长各边后得到的三角形是原三角形的19倍，所以延长第n 次后，得到△A n B n ∁n ，则其面积Sn ＝19n •S ．十一．三角形内角和定理（共3小题）20．已知△ABC，（1）如图1，若P点是∠ABC和∠ACB的角平分线的交点，则∠P＝90°+∠A；（2）如图2，若P点是∠ABC和外角∠ACE的角平分线的交点，则∠P＝90°﹣∠A；（3）如图3，若P点是外角∠CBF和∠BCE的角平分线的交点，则∠P＝90°﹣∠A．上述说法正确的个数是（）A．0个B．1个C．2个D．3个【答案】C【解答】解：（1）若P点是∠ABC和∠ACB的角平分线的交点，则∠PBC＝∠ABC，∠PCB＝∠ACB则∠PBC+∠PCB＝（∠ABC+∠ACB）＝（180°﹣∠A）z在△BCP中利用内角和定理得到：∠P＝180﹣（∠PBC+∠PCB）＝180﹣（180°﹣∠A）＝90°+∠A，故成立；（2）当△ABC是等腰直角三角形，∠A＝90°时，结论不成立；（3）若P点是外角∠CBF和∠BCE的角平分线的交点，则∠PBC＝∠FBC＝（180°﹣∠ABC）＝90°﹣∠ABC，∠BCP＝∠BCE＝90°﹣∠ACB∴∠PBC+∠BCP＝180°﹣（∠ABC+∠ACB）又∵∠ABC+∠ACB＝180°﹣∠Az 在△BCP 中利用内角和定理得到：∠P ＝180﹣（∠PBC +∠PCB ）＝180﹣（180°+∠A ）＝90°﹣∠A ，故成立．∴说法正确的个数是2个．故选：C ．21．已知△ABC 中，∠A ＝α．在图（1）中∠B 、∠C 的角平分线交于点O 1，则可计算得∠BO 1C ＝90°+；在图（2）中，设∠B 、∠C 的两条三等分角线分别对应交于O 1、O 2，则∠BO 2C ＝；请你猜想，当∠B 、∠C 同时n 等分时，（n ﹣1）条等分角线分别对应交于O 1、O 2，…，O n ﹣1，如图（3），则∠BO n ﹣1C ＝（用含n 和α的代数式表示）．【答案】见试题解答内容【解答】解：在△ABC 中，∵∠A ＝α，∴∠ABC +∠ACB ＝180°﹣α，∵O 2B 和O 2C 分别是∠B 、∠C 的三等分线，∴∠O 2BC +∠O 2CB ＝（∠ABC +∠ACB ）＝（180°﹣α）＝120°﹣α；∴∠BO 2C ＝180°﹣（∠O 2BC +∠O 2CB ）＝180°﹣（120°﹣α）＝60°+α；在△ABC 中，∵∠A ＝α，∴∠ABC +∠ACB ＝180°﹣α，∵O n ﹣1B 和O n ﹣1C 分别是∠B 、∠C 的n 等分线，∴∠O n ﹣1BC +∠O n ﹣1CB ＝（∠ABC +∠ACB ）＝（180°﹣α）＝﹣． ∴∠BO n ﹣1C ＝180°﹣（∠O n ﹣1BC +∠O n ﹣1CB ）＝180°﹣（﹣）＝+．z 故答案为：60°+α；+．22．如图，在△ABC 中，∠A ＝m °，∠ABC 和∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 和∠A 1CD 的平分线交于点A 2，得∠A 2；…∠A 2012BC 和∠A 2012CD 的平分线交于点A 2013，则∠A 2013＝度．【答案】见试题解答内容【解答】解：∵A 1B 平分∠ABC ，A 1C 平分∠ACD ，∴∠A 1BC ＝∠ABC ，∠A 1CA ＝∠ACD ，∵∠A 1CD ＝∠A 1+∠A 1BC ，即∠ACD ＝∠A 1+∠ABC ，∴∠A 1＝（∠ACD ﹣∠ABC ），∵∠A +∠ABC ＝∠ACD ，∴∠A ＝∠ACD ﹣∠ABC ，∴∠A 1＝∠A ，∴∠A 1＝m °，∵∠A 1＝∠A ，∠A 2＝∠A 1＝∠A ， …以此类推∠A 2013＝∠A ＝°．故答案为：．十二．全等图形（共1小题）23．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（）A．150°B．180°C．210°D．225°【答案】B【解答】解：在△ABC与△EDC中，，∴△ABC≌△EDC（SAS），∴∠BAC＝∠1，∠1+∠2＝180°．故选：B．z十三．全等三角形的判定（共3小题）24．如图，△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是（）A．1对B．2对C．3对D．4对【答案】D【解答】解：∵AB＝AC，D为BC中点，在△ABD和△ACD中，，∴△ABD≌△ACD；（SSS）∵EF垂直平分AC，∴OA＝OC，AE＝CE，在△AOE和△COE中，，∴△AOE≌△COE（SSS；在△BOD和△COD中，，∴△BOD≌△COD（SAS）；在△AOC和△AOB中，，∴△AOC≌△AOB（SSS）；故选：D．25．如图EB交AC于M，交FC于D，AB交FC于N，∠E＝∠F＝90°，∠B＝∠C，AE＝AF．给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN．其中正确的结论有 ①②③（填序z号）．【答案】见试题解答内容【解答】解：∵∠B+∠BAE＝90°，∠C+∠CAF＝90°，∠B＝∠C∴∠1＝∠2（①正确）∵∠E＝∠F＝90°，∠B＝∠C，AE＝AF∴△ABE≌△ACF（ASA）∴AB＝AC，BE＝CF（②正确）z ∴△ACN ≌△ABM （ASA ）（③正确）∴CN ＝BM （④不正确）．所以正确结论有①②③．故填①②③．26．如图所示，在△ABC 中，D 、E 分别是AB 、AC 上的点，DE ∥BC ，如图①，然后将△ADE 绕A 点顺时针旋转一定角度，得到图②，然后将BD 、CE 分别延长至M 、N ，使DM ＝BD ，EN ＝CE ，得到图③，请解答下列问题：（1）若AB ＝AC ，请探究下列数量关系：①在图②中，BD 与CE 的数量关系是；②在图③中，猜想AM 与AN 的数量关系、∠MAN 与∠BAC 的数量关系，并证明你的猜想；【答案】见试题解答内容【解答】解：（1）①BD ＝CE ；②AM ＝AN ，∠MAN ＝∠BAC ，∵∠DAE ＝∠BAC ，∴∠CAE ＝∠BAD ，在△BAD 和△CAE 中∵∴△CAE ≌△BAD （SAS ），∴∠ACE ＝∠ABD ，z ∵DM ＝BD ，EN ＝CE ，∴BM ＝CN ，在△ABM 和△ACN 中，∵∴△ABM ≌△ACN （SAS ），∴AM ＝AN ，∴∠BAM ＝∠CAN ，即∠MAN ＝∠BAC ；十四．全等三角形的判定与性质（共12小题） 27．如图，AE ⊥AB 且AE ＝AB ，BC ⊥CD 且BC ＝CD ，请按照图中所标注的数据，计算图中实线所围成的图形的面积S 是（）A ．50B ．62C ．65D ．68 【答案】A【解答】解：∵AE ⊥AB 且AE ＝AB ，EF ⊥FH ，BG ⊥FH ，∴∠EAB ＝∠EF A ＝∠BGA ＝90°，∵∠EAF +∠BAG ＝90°，∠ABG+∠BAG＝90°，z ∴∠EAF ＝∠ABG ，在△EF A 和△AGB 中，，∴△EF A ≌△AGB （AAS ），∴AF ＝BG ，AG ＝EF ．同理证得△BGC ≌△CHD 得GC ＝DH ，CH ＝BG ．故FH ＝F A +AG +GC +CH ＝3+6+4+3＝16故S ＝（6+4）×16﹣3×4﹣6×3＝50．故选：A ．28．如图，点E 在正方形ABCD 的对角线AC 上，且EC ＝2AE ，直角三角形FEG 的两直角边EF 、EG 分别交BC 、DC 于点M 、N ．若正方形ABCD 的边长为a ，则重叠部分四边形EMCN 的面积为（）A ．a 2B ．a 2C ．a 2D ．a 2【答案】D【解答】解：过E 作EP ⊥BC 于点P ，EQ⊥CD 于点Q ，∵四边形ABCD是正方形，∴∠BCD＝90°，又∵∠EPM＝∠EQN＝90°，∴∠PEQ＝90°，∴∠PEM+∠MEQ＝90°，∵三角形FEG是直角三角形，∴∠NEF＝∠NEQ+∠MEQ＝90°，∴∠PEM＝∠NEQ，∵AC是∠BCD的角平分线，∠EPC＝∠EQC＝90°，∴EP＝EQ，四边形PCQE是正方形，在△EPM和△EQN中，，∴△EPM≌△EQN（ASA）∴S△EQN＝S△EPM，∴四边形EMCN的面积等于正方形PCQE的面积，∵正方形ABCD的边长为a，∴AC＝a，z∵EC＝2AE，∴EC＝a，∴EP＝PC＝a，∴正方形PCQE的面积＝a×a＝a2，∴四边形EMCN的面积＝a2，故选：D．29．如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形；④MB 平分∠AMC ，其中结论正确的有（）zA ．1个B ．2个C ．3个D ．4个【答案】D【解答】解：∵△ABD 、△BCE 为等边三角形，∴AB ＝DB ，∠ABD ＝∠CBE ＝60°，BE ＝BC ，∴∠ABE ＝∠DBC ，∠PBQ ＝60°，在△ABE 和△DBC 中，， ∴△ABE ≌△DBC （SAS ），∴①正确；∵△ABE ≌△DBC ，∴∠BAE ＝∠BDC ，∵∠BDC +∠BCD ＝180°﹣60°﹣60°＝60°，∴∠DMA ＝∠BAE +∠BCD ＝∠BDC +∠BCD ＝60°，∴②正确；在△ABP 和△DBQ 中，， ∴△ABP ≌△DBQ （ASA ），∴BP ＝BQ ，∴△BPQ 为等边三角形，∴③正确；∵∠DMA ＝60°，∴∠AMC ＝120°，∴∠AMC +∠PBQ ＝180°，∴P 、B 、Q 、M 四点共圆，z ∵BP ＝BQ ，∴，∴∠BMP ＝∠BMQ ，即MB 平分∠AMC ；∴④正确；综上所述：正确的结论有4个；故选：D ．30．如图，在正方形ABCD 中，如果AF ＝BE ，那么∠AOD 的度数是．【答案】见试题解答内容【解答】解：由ABCD 是正方形，得AD ＝AB ，∠DAB ＝∠B ＝90°．在△ABE 和△DAF 中，， ∴△ABE ≌△DAF （SAS ），∴∠BAE ＝∠ADF ．∵∠BAE +∠EAD ＝90°，∴∠OAD +∠ADO ＝90°，∴∠AOD ＝90°，故答案为：90°．31．如图，△ABC 和△EBD 中，∠ABC ＝∠DBE ＝90°，AB ＝CB ，BE ＝BD ，连接AE ，CD ，AE 与CD 交于点M ，AE 与BC 交于点N ．（1）求证：AE ＝CD ；（2）求证：AE ⊥CD ；（3）连接BM ，有以下两个结论：①BM 平分∠CBE ；②MB 平分∠AMD ．其中正确的有 ② （请写序号，少选、错选均不得分）．z【答案】见试题解答内容【解答】（1）证明：∵∠ABC ＝∠DBE ，∴∠ABC +∠CBE ＝∠DBE +∠CBE ，即∠ABE ＝∠CBD ，在△ABE 和△CBD 中，，∴△ABE ≌△CBD ，∴AE ＝CD ．（2）∵△ABE ≌△CBD ，∴∠BAE ＝∠BCD ， ∵∠NMC ＝180°﹣∠BCD ﹣∠CNM ，∠ABC ＝180°﹣∠BAE ﹣∠ANB ，又∠CNM ＝∠ANB ，∵∠ABC ＝90°，∴∠NMC ＝90°，∴AE ⊥CD ．（3）结论：②理由：作BK ⊥AE 于K ，BJ ⊥CD 于J ．z∵△ABE ≌△CBD ，∴AE ＝CD ，S △ABE ＝S △CDB ，∴•AE •BK ＝•CD •BJ ，∴BK ＝BJ ，∵作BK ⊥AE 于K ，BJ ⊥CD 于J ，∴BM 平分∠AMD ．不妨设①成立，则△CBM ≌△EBM ，则AB ＝BD ，显然不可能，故①错误．故答案为②．32．（1）如图1，在四边形ABCD 中，AB ＝AD ，∠B ＝∠D ＝90°，E 、F 分别是边BC 、CD 上的点，且∠EAF ＝∠BAD ．求证：EF ＝BE +FD ；（2）如图2，在四边形ABCD 中，AB ＝AD ，∠B +∠D ＝180°，E 、F 分别是边BC 、CD 上的点，且∠EAF ＝∠BAD ，（1）中的结论是否仍然成立？（3）如图3，在四边形ABCD 中，AB ＝AD ，∠B +∠ADC ＝180°，E 、F 分别是边BC 、CD 延长线上的点，且∠EAF ＝∠BAD ，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．【答案】见试题解答内容【解答】证明：（1）延长EB 到G ，使BG ＝DF ，连接AG ．z∵∠ABG ＝∠ABC ＝∠D ＝90°，AB ＝AD ，∴△ABG ≌△ADF ．∴AG ＝AF ，∠1＝∠2．∴∠1+∠3＝∠2+∠3＝∠EAF ＝∠BAD ．∴∠GAE ＝∠EAF ．又∵AE ＝AE ，∴△AEG ≌△AEF ．∴EG ＝EF ．∵EG ＝BE +BG ．∴EF ＝BE +FD（2）（1）中的结论EF ＝BE +FD 仍然成立．（3）结论EF ＝BE +FD 不成立，应当是EF ＝BE ﹣FD ．证明：在BE 上截取BG ，使BG ＝DF ，连接AG ．∵∠B +∠ADC ＝180°，∠ADF +∠ADC ＝180°，∴∠B ＝∠ADF ．∵AB ＝AD ，∴△ABG≌△ADF．∴∠BAG＝∠DAF，AG＝AF．∴∠BAG+∠EAD＝∠DAF+∠EAD＝∠EAF＝∠BAD．∴∠GAE＝∠EAF．∵AE＝AE，∴△AEG≌△AEF．∴EG＝EF∵EG＝BE﹣BG∴EF＝BE﹣FD．33．如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．（1）如果AB＝AC，∠BAC＝90°，①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD所在直线的位置关系为，线段CF、BD的数量关系为；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；（2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F不重合），并说明理由．【答案】见试题解答内容【解答】证明：（1）①正方形ADEF中，AD＝AF，∵∠BAC＝∠DAF＝90°，∴∠BAD＝∠CAF，又∵AB＝AC ，∴△DAB≌△F AC，∴CF＝BD，∠B＝∠ACF，∴∠ACB+∠ACF＝90°，即CF⊥BD．②当点D在BC的延长线上时①的结论仍成立．由正方形ADEF得AD＝AF，∠DAF＝90度．∵∠BAC＝90°，∴∠DAF＝∠BAC，∴∠DAB＝∠F AC，又∵AB＝AC，∴△DAB≌△F AC，∴CF＝BD，∠ACF＝∠ABD．∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∴∠ACF＝45°，∴∠BCF＝∠ACB+∠ACF＝90度．即CF⊥BD．（2）当∠ACB＝45°时，CF⊥BD（如图）．理由：过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，∵∠ACB＝45°，∠AGC＝90°﹣∠ACB，∴∠AGC＝90°﹣45°＝45°，∴∠ACB＝∠AGC＝45°，∴AC＝AG，∵∠DAG＝∠F AC（同角的余角相等），AD＝AF，∴△GAD≌△CAF，∴∠ACF＝∠AGC＝45°，∠BCF＝∠ACB+∠ACF＝45°+45°＝90°，即CF⊥BC．z34．（本题有3小题，第（1）小题为必答题，满分5分；第（2）、（3）小题为选答题，其中，第（2）小题满分3分，第（3）小题满分6分，请从中任选1小题作答，如两题都答，以第（2）小题评分．）在△ABC 中，∠ACB ＝90°，AC ＝BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E ．（1）当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE ＝AD +BE ；（2）当直线MN 绕点C 旋转到图2的位置时，求证：DE ＝AD ﹣BE ；（3）当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．【答案】见试题解答内容【解答】证明：（1）①∵∠ADC ＝∠ACB ＝∠BEC ＝90°，∴∠CAD +∠ACD ＝90°，∠BCE +∠CBE ＝90°，∠ACD +∠BCE ＝90°． ∴∠CAD ＝∠BCE ．∵AC ＝BC ，∴△ADC ≌△CEB （AAS ）．②∵△ADC ≌△CEB ，∴CE ＝AD ，CD ＝BE ．∴DE ＝CE +CD ＝AD +BE ．解：（2）∵∠ADC ＝∠CEB ＝∠ACB ＝90°，∴∠ACD ＝∠CBE．又∵AC ＝BC ，∴△ACD ≌△CBE （AAS ）．∴CE ＝AD ，CD ＝BE ．∴DE ＝CE ﹣CD ＝AD ﹣BE ．（3）当MN 旋转到图3的位置时，AD 、DE 、BE 所满足的等量关系是DE ＝BE ﹣AD （或AD ＝BE ﹣DE ，BE ＝AD +DE 等）．∵∠ADC ＝∠CEB ＝∠ACB ＝90°，∴∠ACD ＝∠CBE ，又∵AC ＝BC ，∴△ACD ≌△CBE （AAS ），∴AD ＝CE ，CD ＝BE ，∴DE ＝CD ﹣CE ＝BE ﹣AD ．35．（1）如图1，已知：在△ABC 中，∠BAC ＝90°，AB ＝AC ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E ．证明：DE ＝BD +CE ．（2）如图2，将（1）中的条件改为：在△ABC 中，AB ＝AC ，D 、A 、E 三点都在直线m 上，并且有∠BDA ＝∠AEC ＝∠BAC ＝α，其中α为任意锐角或钝角．请问结论DE ＝BD +CE 是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图3，D 、E 是D 、A 、E 三点所在直线m 上的两动点（D 、A 、E 三点互不重合），点F 为∠BAC 平分线上的一点，且△ABF 和△ACF 均为等边三角形，连接BD 、CE ，若∠BDA ＝∠AEC ＝∠BAC ，试判断△DEF 的形状．【答案】见试题解答内容【解答】证明：（1）∵BD ⊥直线m ，CE ⊥直线m ，∴∠BDA ＝∠CEA ＝90°，∵∠BAC ＝90°，∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（2）成立．∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，z∴DE＝AE+AD＝BD+CE；（3）△DEF是等边三角形．由（2）知，△ADB≌△CEA，BD＝AE，∠DBA＝∠CAE，∵△ABF和△ACF均为等边三角形，∴∠ABF＝∠CAF＝60°，∴∠DBA+∠ABF＝∠CAE+∠CAF，∴∠DBF＝∠F AE，∵BF＝AF在△DBF和△EAF中，，∴△DBF≌△EAF（SAS），∴DF＝EF，∠BFD＝∠AFE，∴∠DFE＝∠DF A+∠AFE＝∠DF A+∠BFD＝60°，∴△DEF为等边三角形．36．在课外小组活动时，小慧拿来一道题（原问题）和小东、小明交流．原问题：如图1，已知△ABC，∠ACB＝90°，∠ABC＝45°，分别以AB、BC为边向外作△ABD与△BCE，且DA＝DB，EB＝EC，∠ADB＝∠BEC＝90°，连接DE交AB于点F．探究线段DF与EF的数量关系．小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解．小东同学说：我做过一道类似的题目，不同的是∠ABC＝30°，∠ADB＝∠BEC＝60°．小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况．请你参考小慧同学的思路，探究并解决这三位同学提出的问题：（1）写出原问题中DF与EF的数量关系；（2）如图2，若∠ABC＝30°，∠ADB＝∠BEC＝60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；（3）如图3，若∠ADB＝∠BEC＝2∠ABC，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明．【答案】见试题解答内容【解答】解：（1）DF＝EF．（2）猜想：DF＝FE．证明：过点D作DG⊥AB于G，则∠DGB＝90°．∵DA＝DB，∠ADB＝60°．∴AG＝BG，△DBA是等边三角形．z ∴DB ＝BA ．∵∠ACB ＝90°，∠ABC ＝30°，∴AC ＝AB ＝BG ．在Rt △DBG 和Rt △BAC 中，∴Rt △DBG ≌Rt △BAC （HL ）．∴DG ＝BC ．∵BE ＝EC ，∠BEC ＝60°，∴△EBC 是等边三角形．∴BC ＝BE ，∠CBE ＝60°．∴DG ＝BE ，∠ABE ＝∠ABC +∠CBE ＝90°．∵∠DFG ＝∠EFB ，∠DGF ＝∠EBF ，在△DFG 和△EFB 中，∴△DFG ≌△EFB （AAS ）．∴DF ＝EF ．（3）猜想：DF ＝FE ．过点D 作DH ⊥AB 于H ，连接HC ，HE ，HE 交CB 于K ，则∠DHB ＝90°．∵DA ＝DB ， ∴AH ＝BH ，∠1＝∠HDB ．∵∠ACB ＝90°，∴HC ＝HB ．在△HBE 和△HCE 中，∴△HBE ≌△HCE （SSS ）．∴∠2＝∠3，∠4＝∠BEH ．∴HK ⊥BC ．∴∠BKE ＝90°．∵∠ADB ＝∠BEC ＝2∠ABC ，z ∴∠HDB ＝∠BEH ＝∠ABC ．∴∠DBC ＝∠DBH +∠ABC ＝∠DBH +∠HDB ＝90°，∠EBH ＝∠EBK +∠ABC ＝∠EBK +∠BEK ＝90°．∴DB ∥HE ，DH ∥BE ．∴四边形DHEB 是平行四边形．∴DF ＝EF ．37．（1）操作发现：如图①，D 是等边△ABC 边BA 上一动点（点D 与点B 不重合），连接DC ，以DC 为边在BC 上方作等边△DCF ，连接AF ．你能发现线段AF 与BD 之间的数量关系吗？并证明你发现的结论．（2）类比猜想：如图②，当动点D 运动至等边△ABC 边BA 的延长线上时，其他作法与（1）相同，猜想AF 与BD 在（1）中的结论是否仍然成立？（3）深入探究：Ⅰ．如图③，当动点D 在等边△ABC 边BA 上运动时（点D 与点B 不重合）连接DC ，以DC 为边在BC上方、下方分别作等边△DCF 和等边△DCF ′，连接AF 、BF ′，探究AF 、BF ′与AB 有何数量关系？并证明你探究的结论．Ⅱ．如图④，当动点D 在等边△ABC 边BA 的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．【答案】见试题解答内容z 【解答】解：（1）AF ＝BD ；证明如下：∵△ABC 是等边三角形（已知），∴BC ＝AC ，∠BCA ＝60°（等边三角形的性质）；同理知，DC ＝CF ，∠DCF ＝60°；∴∠BCA ﹣∠DCA ＝∠DCF ﹣∠DCA ，即∠BCD ＝∠ACF ；在△BCD 和△ACF 中，， ∴△BCD ≌△ACF （SAS ），∴BD ＝AF （全等三角形的对应边相等）；（2）证明过程同（1），证得△BCD ≌△ACF （SAS ），则AF ＝BD （全等三角形的对应边相等），所以，当动点D 运动至等边△ABC 边BA 的延长线上时，其他作法与（1）相同，AF ＝BD 仍然成立；（3）Ⅰ．AF +BF ′＝AB ；证明如下：由（1）知，△BCD ≌△ACF （SAS ），则BD ＝AF ；同理△BCF ′≌△ACD （SAS ），则BF ′＝AD ，∴AF +BF ′＝BD +AD ＝AB ；Ⅱ．Ⅰ中的结论不成立．新的结论是AF ＝AB +BF ′；证明如下：在△BCF ′和△ACD 中，，∴△BCF ′≌△ACD （SAS ）， ∴BF ′＝AD （全等三角形的对应边相等）；又由（2）知，AF ＝BD ；∴AF ＝BD ＝AB +AD ＝AB +BF ′，即AF ＝AB+BF ′．z 38．操作：如图①，△ABC 是正三角形，△BDC 是顶角∠BDC ＝120°的等腰三角形，以D 为顶点作一个60°角，角的两边分别交AB 、AC 边于M 、N 两点，连接MN ．探究：线段BM 、MN 、NC 之间的关系，并加以证明．说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．注意：选取①完成证明得10分；选取②完成证明得5分．AN ＝NC （如图②）；②DM ∥AC （如图③）．附加题：若点M 、N 分别是射线AB 、CA 上的点，其它条件不变，再探线段BM 、MN 、NC 之间的关系，在图④中画出图形，并说明理由．【答案】见试题解答内容【解答】解：（1）BM +CN ＝MN证明：如图，延长AC 至M 1，使CM 1＝BM ，连接DM 1由已知条件知：∠ABC ＝∠ACB ＝60°，∠DBC ＝∠DCB ＝30°，∴∠ABD ＝∠ACD ＝90°．∵BD ＝CD ，∴Rt △BDM ≌Rt △CDM 1，∴∠MDB ＝∠M 1DC ，DM ＝DM 1∴∠MDM 1＝（120°﹣∠MDB ）+∠M 1DC ＝120°．又∵∠MDN ＝60°，∴∠M 1DN ＝∠MDN ＝60°．∴△MDN ≌△M 1DN ．∴MN ＝NM 1＝NC+CM 1＝NC +MB ．z （2）附加题：CN ﹣BM ＝MN证明：如图，在CN 上截取CM 1，使CM 1＝BM ，连接MN ，DM 1∵∠ABC ＝∠ACB ＝60°，∠DBC ＝∠DCB ＝30°，∴∠DBM ＝∠DCM 1＝90°．∵BD ＝CD ，∴Rt △BDM ≌Rt △CDM 1，∴∠MDB ＝∠M 1DC ，DM ＝DM 1∵∠BDM +∠BDN ＝60°，∴∠CDM 1+∠BDN ＝60°．∴∠NDM 1＝∠BDC ﹣（∠M 1DC +∠BDN ）＝120°﹣60°＝60°．∴∠M 1DN ＝∠MDN ． ∵ND ＝ND ，∴△MDN ≌△M 1DN ． ∴MN ＝NM 1＝NC ﹣CM 1＝NC ﹣BM，即MN ＝NC ﹣BM ．z 十五．角平分线的性质（共1小题）39．如图，△ABC 的三边AB 、BC 、CA 长分别为40、50、60．其三条角平分线交于点O ，则S △ABO ：S △BCO ：S △CAO ＝．【答案】见试题解答内容【解答】解：过点O 作OD ⊥AB 于点D ，作OE ⊥AC 于点E ，作OF ⊥BC 于点F ，∵OA ，OB ，OC 是△ABC 的三条角平分线，∴OD ＝OE ＝OF ，∵△ABC 的三边AB 、BC 、CA 长分别为40、50、60，∴S △ABO ：S △BCO ：S △CAO ＝（AB •OD ）：（BC •OF ）：（AC •OE ）＝AB ：BC ：AC ＝40：50：60＝4：5：6．故答案为：4：5：6．十六．线段垂直平分线的性质（共1小题） 40．如图，△ABC 中，AB ＝AC ，∠BAC ＝54°，点D 为AB 中点，且OD ⊥AB ，∠BAC 的平分线与AB 的垂直平分线交于点O ，将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，则∠OEC 为度．【答案】见试题解答内容z 【解答】解：法一：如图，连接OB 、OC ，∵∠BAC ＝54°，AO 为∠BAC 的平分线，∴∠BAO ＝∠BAC ＝×54°＝27°，又∵AB ＝AC ，∴∠ABC ＝（180°﹣∠BAC ）＝（180°﹣54°）＝63°，∵DO 是AB 的垂直平分线，∴OA ＝OB ，∴∠ABO ＝∠BAO ＝27°，∴∠OBC ＝∠ABC ﹣∠ABO ＝63°﹣27°＝36°，∵AO 为∠BAC 的平分线，AB ＝AC ，∴△AOB ≌△AOC （SAS ），∴OB ＝OC ，∴点O 在BC 的垂直平分线上，又∵DO 是AB 的垂直平分线，∴点O 是△ABC 的外心，∴∠OCB ＝∠OBC ＝36°，∵将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，∴OE ＝CE ， ∴∠COE ＝∠OCB ＝36°，在△OCE 中，∠OEC ＝180°﹣∠COE ﹣∠OCB ＝180°﹣36°﹣36°＝108°．法二：证明点O 是△ABC 的外心，推出∠BOC ＝108°，根据OB ＝OC ，推出∠OCE ＝36°可得结论．故答案为：108．z 十七．等腰三角形的性质（共4小题）41．如图，在△ABC 中，AB ＝20cm ，AC ＝12cm ，点P 从点B 出发以每秒3cm 的速度向点A 运动，点Q 从点A 同时出发以每秒2cm 的速度向点C 运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ 是以PQ 为底的等腰三角形时，运动的时间是（）A ．2.5秒B ．3秒C ．3.5秒D ．4秒【答案】D【解答】解：设运动的时间为x cm ，在△ABC 中，AB ＝20cm ，AC ＝12cm ，点P 从点B 出发以每秒3cm 的速度向点A 运动，点Q 从点A 同时出发以每秒2cm 的速度向点C 运动，当△APQ 是等腰三角形时，AP ＝AQ ，AP ＝20﹣3x ，AQ ＝2x即20﹣3x ＝2x ，解得x ＝4（cm ）．故选：D ．42．如图，∠BOC ＝9°，点A 在OB 上，且OA ＝1，按下列要求画图：以A 为圆心，1为半径向右画弧交OC 于点A 1，得第1条线段AA 1；再以A 1为圆心，1为半径向右画弧交OB 于点A 2，得第2条线段A 1A 2；再以A 2为圆心，1为半径向右画弧交OC 于点A 3，得第3条线段A 2A 3；…这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n ＝ 9 ．【答案】见试题解答内容【解答】解：由题意可知：AO ＝A 1A ，A 1A ＝A 2A 1，…，则∠AOA 1＝∠OA 1A ，∠A 1AA 2＝∠A 1A 2A，…，∵∠BOC ＝9°，z ∴∠A 1AB ＝18°，∠A 2A 1C ＝27°，∠A 3A 2B ＝36°，∠A 4A 3C ＝45°，…，∴9°n ＜90°，解得n ＜10．由于n 为整数，故n ＝9．故答案为：9．43．如图所示，AOB 是一钢架，且∠AOB ＝10°，为了使钢架更加坚固，需在其内部添加一些钢管EF ，FG ，GH …，添加的钢管长度都与OE 相等，则最多能添加这样的钢管根．【答案】见试题解答内容【解答】解：∵添加的钢管长度都与OE 相等，∠AOB ＝10°，∴∠GEF ＝∠FGE ＝20°，…从图中我们会发现有好几个等腰三角形，即第一个等腰三角形的底角是10°，第二个是20°，第三个是30°，四个是40°，五个是50°，六个是60°，七个是70°，八个是80°，九个是90°就不存在了．所以一共有8个．故答案为：8．44．如图，△ABC 中AB ＝AC ，BC ＝6，点P 从点B 出发沿射线BA 移动，同时，点Q 从点C 出发沿线段AC 的延长线移动，已知点P 、Q 移动的速度相同，PQ 与直线BC 相交于点D ．（1）如图①，当点P 为AB 的中点时，求CD 的长；（2）如图②，过点P 作直线BC 的垂线垂足为E ，当点P 、Q 在移动的过程中，线段BE 、DE 、CD 中是否存在长度保持不变的线段？请说明理由．【答案】见试题解答内容【解答】解：（1）如图，过P 点作PF ∥AC 交BC 于F ，∵点P 和点Q 同时出发，且速度相同，∴BP ＝CQ ，∵PF∥AQ，∴∠PFB＝∠ACB，∠DPF＝∠CQD，又∵AB＝AC，∴∠B＝∠ACB，∴∠B＝∠PFB，∴BP＝PF，∴PF＝CQ，又∠PDF＝∠QDC，∴证得△PFD≌△QCD，∴DF＝CD＝CF，又因P是AB的中点，PF∥AQ，∴F是BC的中点，即FC＝BC＝3，∴CD＝CF＝；（2）分两种情况讨论，得ED为定值，是不变的线段，如图，如果点P在线段AB上，过点P作PF∥AC交BC于F，z∵△PBF为等腰三角形，∴PB＝PF，BE＝EF，∴PF＝CQ，∴FD＝DC，∴ED＝EF+FD＝BE+DC＝BC＝3，∴ED为定值，同理，如图，若P 在BA的延长线上，z作PM ∥AC 的延长线于M ，∴∠PMC ＝∠ACB ，又∵AB ＝AC ，∴∠B ＝∠ACB ，∴∠B ＝∠PMC ，∴PM ＝PB ，根据三线合一得BE ＝EM ，同理可得△PMD ≌△QCD ，所以CD ＝DM ，∵BE ＝EM ，CD ＝DM ，∴ED ＝EM ﹣DM ＝﹣DM ＝+﹣DM ＝3+DM ﹣DM ＝3，综上所述，线段ED 的长度保持不变．十八．等边三角形的性质（共1小题）45．图①是一块边长为1，周长记为P 1的正三角形纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉如图正三角形纸板边长的）后，得图③，④，…，记第n （n ≥3）块纸板的周长为P n ，则P n﹣P n ﹣1的值为（）zA ．B ．C ．D ．【答案】C【解答】解：P 1＝1+1+1＝3，P 2＝1+1+＝，P 3＝1+++×3＝，P 4＝1+++×2+×3＝， …∴P 3﹣P 2＝﹣＝＝， P 4﹣P 3＝﹣＝＝，则Pn ﹣Pn ﹣1＝＝．故选：C ．十九．轴对称-最短路线问题（共3小题）46．如图，点P 是∠AOB 内任意一点，OP ＝5cm ，点M 和点N 分别是射线OA 和射线OB 上的动点，△PMN 周长的最小值是5cm ，则∠AOB 的度数是（）。

七下册期末复习单元知识点总结

人教版七下英语1-12单元知识点总结Unit1:短语：1.play the guitar/drums/piano/violin（play+the+乐器）2.playchess/basketball/computergames（play+其他，无the）3.talkto...=talkWith…与…交谈PleasetalktoMr.Zhangafterclass.=PleasetalkwithMr.Zhangafterclass.4.do kungfu表演（中国）功夫，只能用doIdokungfueveryday.Hedoeskungfueveryday.5.tellstories讲故事6.thestorytellingclub讲故事俱乐部7.begoodatdoingsth.擅长做某事Heisgoodat telling stories.begoodtosb.对某人友好=befriendlytosb.=benicetosb=bekindtosb.beg。

OdWith…善于应付...；对...有办法begoodfor...对…有好处8.makefriends with sb.与...交朋友Shewantstomakefriendswithhernewclassmates.9.helpsbdosth帮助某人做某事helpsbwithsth在某方面帮助某人Bobhelpshismothermakebreakfasteveryday.IhelpMarywithherEnglishafterclass.10.ontheweekend=onweekends句子：1.Canyouswim?Yes,Ican./No,Ican't.2.Canheplaytheguitar?Yes,hecan./No z hecan't.3.Whatcanyoudo?Icandance.4.Whatcanhedo?Hecandraw.5.Whatclubdoyouwanttojoin?Iwanttojointhechessclub.作文：WewantsomenewmembersfortheSchoolMusicClub.Doyoulikemusic?Canyousinganddance?Areyougoodatplayingthe guitarortheviolin?Areyougoodwithpeopleorthings?Youneedtohavetimeontheweekend.Comeandjoinus!Youwanthavefunandlearnmoreaboutmusichere!Pleasecall1.iat564-8729Unit2短语：1.getupearly早起Ineedtogetupearly on schooldays.在上学日我需要早起。

七下期末字词专题复习(含答案)

七下期末字词专题复习1．下列字形和加点字注音全部正确的一项是()A．浊流(zhú) 取蒂颠沛流离(pèi) 酣然入梦B．亘古(gèng) 高梁深恶痛绝(wù) 苛捐杂税C．愧怍(zuō) 豁亮气冲斗牛(dǒu) 言外之义D．晌午(shǎng) 震悚沥尽心血(lì) 妇孺皆知2．下列加点词注音全部正确的一项是（）A．柠檬níng嗔怪chēn 倚靠yī懒惰duò拈轻怕重niān B．怂恿sǒng 倒坍tān 怅然chàng蜷伏quán 目光灼灼zhuó C．殉职xùn虐待nüè惩戒chěng干涸hé参差不齐cīD．狭隘ài 突兀wù热忱chén呻吟yín畏罪潜逃qián3．下列字形和加点字注音全部正确的一项是()A．卓越(zhuō) 祈祷锲而不舍(qì) 切切察察B．云鬓(bìn) 可汗兀兀穷年(wù) 锋芒毕露C．踱步(dú) 校对鲜为人知(xiān) 浩浩荡荡D．哺育(pǔ) 字贴群蚁排衙(yá) 迥乎不同4．下列字形和加点字注音全部正确的一项是()A．校补(xiào) 揩油颠沛流离(fèi) 忍俊不禁B．迸溅(bìng) 商酌气冲斗牛(dǒu) 千均重负C．鞠躬(jū) 招揽血气方刚(xuè) 毛骨悚然D．红晕(yūn) 派谴鞠躬尽瘁(cuì) 心有灵犀5．下列各组词语中划线字注音完全正确的一项是（）A．元勋（xūn）含蓄（xù）调羹（gēng）鲜为人知（xiǎn）B．选聘（pìng）筹（chóu）划赫（shè）然兀兀（wù）穷年C．疙（gē）痛署（shǔ）名绞（jiǎo）肉深恶（è）痛疾D．涉（shè）猎通宵（xiāo）澎湃（bài）气冲（dǒu）斗牛6．下列词语中书写无误的一项是（）A．潜心惯注心会神凝气冲斗牛家喻户晓B．慷慨淋漓锲而不舍历尽心血刮目相待C．搏学多识一反即往锋芒毕露目不窥园D．妇孺皆知马革裹尸警报迭起兽铤亡群7．下列词语没有错误的一项是（）A．山涧高粱亘古一泄万里B．薪金深宵选骋妇孺皆知C．惊骇摇篮斑澜合家欢乐D．咳嗽屏障谰语一反既往8．选出下列句中画线字注音正确的一项（）A．选聘（pìn）迭起（dié）澎湃（bài）义愤填膺（yīng）B．彷徨（páng）花圃（pǔ）深邃（suì）迥乎不同（jiǒng）C．字帖（tiě）胡骑（jì）徘徊（huái）烟雾缭绕（rào）D．校注（xiào）弄堂（nóng）倔强（jué）潜移默化（qián）9．下列词语中没有错别字的一项是（）A．斑澜叠起枯躁惊涛澎湃B．摇蓝险峻喧闹妇孺皆知C．署名屏障浊流马革裹尸D．深霄畴划慷慨兀兀穷年10．下列各组词语中没有错别字的一项是（）A．臆测穿带深宵饥肠辘辘B．暇疵装潢魄势悬崖绝壁C．坦荡景致翘首浊流宛转D．恫吓字贴蚱蜢警报迭起11．下面文中划线字的注音正确的一项是（）快乐而沉静的春雨，缓缓飘落，洗去一冬的污秽，把珍藏心间的欢乐吐成遍地的新绿。

2022学年部编版语文七年级下册期末复习检测卷(九) 部编人教版七年级下册

2022学年部编版语文七年级下册期末复习检测卷（九）部编人教版七年级下册部编语文七下期末复习检测卷（九）（含答案）一. 积累与运用（28分）1.下列词语中加点字的读音，全部正确的一项是（）（2分）A.选聘(pìn)毋宁(wú)重荷(hè)毛骨悚然(sǒnɡ)B.叱咤(chà)无垠(yín)磐石(bán)怏怏不乐(yànɡ)C.嗔视(chēn)冰雹(bào)轮廓(kuò)气冲斗牛(dǒu)D.吞噬(shì)嫉妒(jí)销蚀(shí)孜孜不倦(zī)2.下列词语中，没有错别字的一项是（）（2分）A.潜心贯注淋漓尽致摒气凝神谈笑自如B.如泣如诉俯拾皆是跃武扬威五体投地C.妇孺皆知时过境迁行云流水心不在焉D.恍然大悟咄咄逼人众目睽睽浑为一谈3.依次填入下列句中空缺处的词语恰当的一项是（）（2分）①70年前中华人民共和国的成立，彻底改变了近代以后100多年中国积贫积弱、受人的悲惨命运，中华民族走上了实现伟大复兴的壮阔道路。

②各地援鄂医疗队送行出征，以忘我投入和惊人业绩了医护人员不惧生死、敬佑生命、为民族担当高贵品格之内涵。

③线上学习令我们获得了应对学习困难的经验，历练了我们自主学习、自律自制的品质。

A.欺凌揭示反而B.凌辱揭示反而C.欺凌诠释而且D.凌辱诠释而且4.名著阅读。

（4分）（1）下面一段文字节选自《骆驼祥子》，读一读，指出A、B两处的人物是谁。

(2分)__A__心里有数儿。

他晓得祥子是把好手，即使不拉他的车，他也还愿意祥子在厂子里。

有祥子在这儿，先不提别的，院子与门口永远扫得干干净净。

__B__更喜欢这个傻大个儿，她说什么，祥子老用心听着，不和她争辩；别的车夫，因为受尽苦楚，说话总是横着来；她一点不怕他们，可是也不愿多搭理他们；她的话，所以，都留给祥子听。

A．__________ B．__________,（2）祥子前后有什么变化？你认为造成祥子这种变化的原因是什么？（2分）5.默写（每空1分，共8分）（1）马上相逢无纸笔，。

【情景试题】2022-2023学年(语文)七下期末复习：1

1.字音字形一、填空题1．（4分）根据拼音写汉字。

戈壁滩上常常风沙hū xiào，气温往往在零下三十多shè shì度。

核武器试验时大大小小突发的问题必层出不穷，稼先虽有“福将”之称，意外总是不能完全bì miǎn的。

1982 年，他做了核武器研究院院长以后，一次井下突然有一个信号测不到了，大家十分jiāo lǜ，人们劝他回去，他只说了一句话：“我不能走。

”2．（5分）给加点字选择正确的读音或根据拼音写出汉字。

（1）（1分）若有人说了什么可笑的话，鲁迅先生笑得连烟卷都拿不住了，常常是笑得咳sou()起来。

（2）（1分）鸡汤端到旁边用调羹()( A . gēng B . gēn)舀了一二下就算了事。

（3）（1分）青年人写信，写得太草率()(A . lǜ B . shuài)，鲁迅先生是深恶()(A . è B . wù)痛绝之的。

（4）（1分）保姆总是吩()(A . fēng B . fēn) 咐他说：“轻一点走，轻一点走。

”（5）（1分）若小细绳上有一个gē da()，也要随手把它解开的。

3．根据拼音写出相应的词语。

（1）像春蚕在jǔ jué()桑叶，像野马在平原上奔驰（2）钻之弥坚，越坚，钻得越qiè ér bù shě()。

（3）鲁迅先生笑得连烟卷都拿不住，常常是笑得ké sòu()起来（4）我们民族的伟大精神，将要在你的bǔ yù()下发扬滋长！二、综合题4．（6分）阅读下面选段，完成小题。

半夜里，忽然醒来，才觉得寒气逼人，刺入肌骨，浑身打着战，把毯子juǎn得更紧些，把身于quán起来，还是睡不着。

天上闪烁的星星好像黑色幕上缀着的宝石，它跟我们这样地接近哪！黑的山峰像巨人一样矗立在面前，四围的山把这山谷包围得像一口井。

上边和下边有几堆火没有熄，冻醒了的同志们围着火堆小声地谈着话，除此以外，就是寂静，耳朵里有不可捉摸的声响，极远的又是极近的，极洪大的又是极细切的，像春蚕在______桑叶，像野马在平原上______，像山泉在______，像波涛在______。

七年级语文下学期期末复习诗歌鉴赏试题答案

七年级语文下学期期末复习诗歌鉴赏试题答案一、七年级下册诗歌鉴赏1．诗歌鉴赏。

移家别湖上亭戎昱好是春风湖上亭，柳条藤蔓系离情。

黄莺久住浑相识，欲别频啼四五声。

（1）诗人“别湖上亭”时触动他情思的景物有哪些？（2）请赏析诗歌的三四句“黄莺久住浑相识，欲别频啼四五声”。

2．阅读下面两首古诗，完成两小题。

采莲曲唐·王昌龄荷叶罗裙一色裁，芙蓉向脸两边开。

乱入池中看不见，闻歌始觉有人来。

（1）诗歌第二句“芙蓉向脸两边开”用了衬托的手法，明写________，实则为了衬托出________之美。

（2）请赏析“乱”字的妙处。

3．诗歌鉴赏。

移家别湖上亭戎昱好是春风湖上亭，柳条藤蔓系离情。

黄莺久住浑相识，欲别频啼四五声。

（1）诗人“别湖上亭”时触动他情思的景物有哪些？（2）请赏析诗歌的三四句“黄莺久住浑相识，欲别频啼四五声”。

4．阅读诗歌，回答问题逢入京使岑参故园东望路漫漫，双袖龙钟泪不干。

马上相逢无纸笔，凭君传语报平安。

（1）作者用什么修辞手法写自己“龙钟泪不干”？“龙钟”是什么意思？（2）这首诗表达了作者怎样的思想感情？（3）展开联想与想象，描绘一下前两句所展现的画面。

5．阅读诗歌，回答问题。

桂源铺（宋）杨万里万山不许一溪奔，拦得溪声日夜喧。

到得前头山脚尽，堂堂①溪水出前村。

【注】①堂堂：形容阵容或力量壮大。

（1）从修辞手法的角度赏析第一，二句诗。

（2）朱光潜《诗论》说：“诗有说理的，但是它的‘理’融化在炽热的情感和灿烂的意象之中。

”这首哲理诗的第三，四句中能够表现“理”的意象是什么？从中告诉我们怎样的人生哲理？6．阅读下面的诗，完成各题。

夕次盱眙县韦应物落帆逗淮镇，停舫临孤驿。

浩浩风起波，冥冥日沉夕。

人归山郭暗，雁下芦洲白。

独夜忆秦关，听钟未眠客。

（1）请结合诗歌内容，分析诗句“浩浩风起波，冥冥日沉夕”中的叠字在写景中的表达效果。

（2）请结合全诗内容，说说诗人“未眠”的原因。

7．阅读下面这首诗，回答各题。

七年级数学下册期末复习每日一练

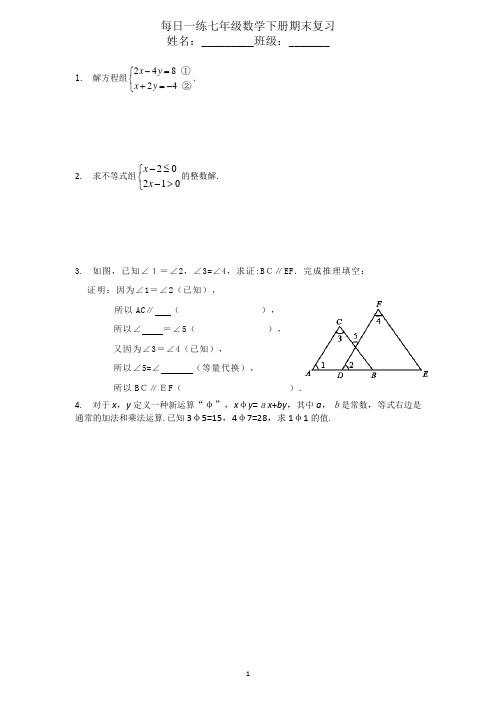
1.解方程组24824x yx y-=⎧⎨+=-⎩①②．2.求不等式组20210xx-≤⎧⎨->⎩的整数解.3.如图，已知∠１＝∠2，∠3=∠4，求证:BＣ∥EF．完成推理填空：证明：因为∠1＝∠2（已知），所以AC∥（），所以∠＝∠5（），又因为∠3＝∠4（已知），所以∠5=∠（等量代换），所以BＣ∥ＥF（）．4.对于x，y定义一种新运算“φ”，xφy=ａx+by，其中a，ｂ是常数，等式右边是通常的加法和乘法运算.已知3φ5=15，4φ7=28，求1φ1的值.1. 育人中学开展课外体育活动，决定开设A:篮球、B:乒乓球、C:踢毽子、Ｄ：跑步四种活动项目．为了解学生最喜欢哪一种活动项目（每人只选取一种），随机抽取了部分学生进行调查，并将调查结果绘成如甲、乙所示的统计图，请你结合图中信息解答下列问题.（1）样本中最喜欢A 项目的人数所占的百分比为，其所在扇形统计图中对应的圆心角度数是度;（2）请把条形统计图补充完整；（3）若该校有学生1000人，请根据样本估计全校最喜欢踢毽子的学生人数约是多少?2.在平面直角坐标系中，O为坐标原点，Ａ（—2，3），B（2，2）．（1）画出三角形OAB；（2）求三角形OＡB的面积;（3）若三角形OAB中任意一点P（x０，y０）经平移后对应点为Ｐ1（x0+4，ｙ0-3），请画出三角形OAＢ平移后得到的三角形O１A1Ｂ1，并写出点O１、Ａ1、Ｂ１的坐标.3.水果店以每千克4．5元进了一批香蕉，销售中估计有10％的香蕉正常损耗．水果店老板把售价至少定为多少，才能避免亏本？213456-1-21-3-41234-1-2-3y1.为了抓住集安国际枫叶旅游节的商机，某商店决定购进A、B两种旅游纪念品．若购进A种纪念品8件，B种纪念品3件，需要95０元；若购进A种纪念品５件，B种纪念品6件，需要80０元．（1）求购进Ａ、B两种纪念品每件各需多少元;（2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润3０元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？2.如图，点E在AC的延长线上，下列条件能判断AB∥CＤ的是（）①∠1＝∠2；②∠3＝∠４；③∠A=∠DCE；④∠D＋∠ABD=180°A ．①③④B．①②③C．①②④D ．②③④解析：2134ABCDE1.不等式组211420xx->⎧⎨-⎩，≤的解集在数轴上表示为（）解析：2.解方程组：{x2−y+13=13x+2y=103.用代入法解方程组：{2x−5y=−3−4x+y=−34.计算：(−1)2024+√−83+|1−√3|+√165.求x的值：8（x−1）3+27=01.若m，n为实数，且|m+√3|与√n−2互为相反数，求(mn)2的值.2.求下列各式中x的值:（1）2x3=-16; （2）4（x-1）2=64.3.如图，直线AB与CD相交于点O，OE平分∠AOD.若OF∠OE，试说明OF平分∠BOD.4.已知点P（2a-2，a+5），解答下列各题.（1）若点P在x轴上，求点P的坐标.（2）点Q的坐标为（4，5），直线PQ∠y轴，求点P的坐标.1. 某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费.为更好地决策，自来水公司的随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图（每组数据包括在右端点但不包括左端点），请你根据统计图解答下列问题:（1）此次抽样调查的样本容量是_____.（2）补全频数分布直方图，并求扇形图中“15吨~20吨”部分的圆心角的度数.（3）如果自来水公司将基本用水量定位每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格?2. 数学课上，老师出了一道题:比较√19-23与23的大小.小华的方法:因为√19 >4，所以√19-2 2，所以√19-2323（填“>”或“<”）.小英的方法:√19-23-23=√19-43.因为19>42=16，所以√19-4 0，所以√19-430，所以√19-2323（填“>”或“<”）.（1）根据上述材料填空;（2）请从小华和小英的方法中选择一种比较√6-14与12的大小.1.解下列不等式和不等式组，并把解集表示在数轴上.（1）2（x+3）-1≥3x+2 （2）{−3(x+1)−(x−3)<8 2x+13−1−x2≤12.把一部分书分给几名同学，如果每人分3本，则余8本;如果前面的每名同学分5本，那么最后一人就分不到3本（包含分不到书的情况），这些书有多少本?共有多少人?3.为更好的治理水质，保护环境，市治污办事处预购买10台污水处理设备，现有A、B:询问商家得知:购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元，根据以上条件.（1）求a、b的值;（2）市污水处理办公室由于资金缺乏，购买污水处理设备的资金最多105万元，你认为该有几种购买方案?（3）在（2）的情况下，若每月污水处理量要求不低于2040吨，为节约资金，请你帮污水处理办事处选取一种最省钱的方案?1.如图，若在中国象棋盘上建立平面直角坐标系，使“帅”位于点（-1，-1），“马”位于点（2，-1），则“兵”位于点（）A．（﹣1，2）B．（﹣3，2）C．（﹣3，1）D．（﹣2，3）2.郑州市某区为了解参加2021年中考的8900名学生的体重情况，随机抽查了其中1500名学生的体重进行统计分析，下列叙述正确的是（）A.8900名学生是总体B.每名学生是总体的一个个体C.1500名学生的体重是总体的一个样本D.以上调查是普查3.若﹣2x a y与5x3y b的和是单项式，求（a+b）2的平方根.4.在平面直角坐标系中，△ABC经过平移得到三角形△A`B`C`，位置如图所示:（1）分别写出点A、A`的坐标:A ，A` ;（2）若点M（m，n）是△ABC内部一点，则平移后对应点M的坐标为 ;（3）求△ABC的面积.5.已知5a+2的立方根是3，3a+b﹣1的算术平方根是4，c是√13的整数部分．（1）求a，b，c的值；（2）求3a﹣b+c的平方根．1. 某中学组织本校教师开展线上教学，为了解学生线上教学的学习效果，决定随机抽取八年级学生部分学生进行质量测评，根据测试的数学成绩绘制统计表和频数分布直方图．请根据所给信息，解答下列问题：（1）求a 和b ；（2）求此次抽样的样本容量，并补全频数分布直方图；（3）已知该年级有800名学生参加测试，请估计该年级数学成绩为优秀（80分及以上）的人数．2. 如图，已知直线AB 与CD 交于点O ，OM∠CD ，OA 平分∠MOE ，且∠BOD ＝28°，求∠AOM ，∠COE 的度数．3. 若关于x ，y 的方程组{x +3y =4m +1x −y =3 的解满足x+y=4，求m 的值．1.计算：−12024+√25−2×√−183−|3−π|2.用两种方法解二元一次方程组：{x−y=44x+2y=13.解不等式组，{2x≥5x−34x+23>x 并写出它的所有整数解.4.如图，在边长为1个单位长度的小正方形网格中建立平面直角坐标系，已知三角形ABC 的顶点A的坐标为A（-1，4），顶点B的坐标为（-4，3），顶点C的坐标为（-3，1）.（1）把三角形ABC向右平移5个单位长度，再向下平移4个单位长度得到三角形A'B'C'，请你画出三角形A'B'C';（2）请直接写出点A’，B'，C'的坐标;（3）求三角形ABC的面积.1.近日教育部正式印发《义务教育课程方案》并发布《义务教育劳动课程标准（2022年版）》，今秋开学起，劳动将正式成为中小学的一门独立课程。

部编人教版七年级下册语文期末复习试卷 4套(含答案+解析)

部编人教版七年级下册语文期末复习试卷11.下列加粗的字注音完全正确的一项是（）A.烧灼（zhuó）毡鞋（zhān）炽热（zhì）迟钝（dùn）B.暴涨（zhàng）鲁莽（mǎng）拖拽（zhuài）臆断（yì）C.模拟（nǐ）凛冽（lín）合拢（lǒng）辜负（gū）D.溯流（sù）吞噬（shì）俯瞰（kàn）拍摄（shè）2.下列词语中有错别字的一项是（）A.遗孀海市蜃楼毛骨悚然五脏六腑B.羸弱天崖海角耀武扬威千钧重负C.拯救不期而至广阔无垠耐人寻味D.闲暇心有灵犀风餐露宿坚持不懈3.下列加粗成语使用不恰当的一项是（）A.路上，一棵棵盘虬卧龙般的大树为我们遮挡了毒辣的太阳。

B.“六一”文艺会演中；小明滑稽的表演让大家忍俊不禁地大笑起来。

C.在沙漠里经历了整整四天的苦苦挣扎之后，他终于发现了一片水源，这对于他来说，真可以说是仙露琼浆啊。

D.不求高官厚禄，但求清正廉洁；不求轰轰烈烈，但求坦坦荡荡。

4.依次填入下面一段文字横线处的语句，衔接最恰当的一组是（）要说梅，我最偏爱的是白梅，它冷艳洁白，一尘不染，清香浓郁。

白得超凡脱俗，白得素雅纯净，白得如冰似雪。

_________________①但写梅写得最绝的还是林逋的“疏影横斜水清浅，暗香浮动月黄昏”。

②王冕也在《白梅》中写道：“冰雪林中著此身，不同桃李混芳尘。

忽然一夜清香发，散作乾坤万里春。

”③他的诗中不见一个梅字，却把梅的影子和暗香写得入木三分，写得俏丽可人，引起人们无数的联想。

④卢梅坡曾在《雪梅》中写道：“梅须逊雪三分白，雪却输梅一段香。

”A.③①②④B.④①②③C.④②①③D.②④①③5.诗文名句默写。

（1）可怜夜半虚前席，__________________。

（李商隐《贾生》）（2）__________________，青草池塘处处蛙。

七下语文期末复习专题一字音字形

七下语文(yǔwén)期末复习专题(zhuāntí)一字音字形一、词语(cíyǔ)积累第一(dìyī)单元确凿．（záo）:确实(quèshí)。

菜畦．（qí）：菜地。

攅．(cuán)：凑在一块儿。

人迹罕．(hǎn)至：少有人来。

迹：足迹，脚印。

罕：稀少。

秕．(bǐ)谷：长得不饱满的鼓励。

倜．(tì)傥．(tǎng)：洒脱，不拘束。

人声鼎．(dǐng)沸：形容人声喧闹。

叮嘱：再三嘱咐。

嫉．(jí)妒：忌妒。

骊．(lí)歌：告别的歌。

玉簪．(zān)花姊妹：姐妹。

静默：不出声。

木屐．(jī)：木头鞋。

讪．(shàn)笑：嘲笑。

沮．(jǔ)丧：灰心失望。

来势汹．(xiōng)汹：动物或事物到来的气势很猛烈。

盔（kuī）甲沼．(zhǎo)泽．(zé)地：水草茂密的泥泞地带。

伫．(zhù)立：长时间的站立。

萋．(qī)萋：形容草木长得茂盛。

瞬．(shùn)息：短时间。

第二单元巅．（diān）：山顶。

澎．(péng)湃．(pài)：波浪相互撞击。

狂澜．(lán)：巨大的波浪。

逼狭：狭窄。

哺．（bǔ）育：培养，喂养。

屏障．（zhàng）：像屏风那样遮挡着的东西。

诧．(chà)异：觉得奇怪。

踱．（duó）来踱．去：来回慢步行走。

亦复如是：也是这样。

祈．（qí）祷．(dǎo)：信仰宗教的人向神默告自己的愿望。

崎．（qí）岖．(qū)：形容山路不平，此处指处境艰难。

哽．（gěng）：声气阻塞。

炽．(chì)痛：热烈而深切。

嗥．(háo)鸣：嚎叫。

谰．（lán）语：没有根据的话。

怪诞．(dàn)：荒诞离奇。

斑斓．（lán）：灿烂多彩。

人教版七年级英语下学期期末总复习重点知识汇总-(共64张PPT)

His brother often makes him stay in the sun.
…To do/doing 两种用法பைடு நூலகம்
• find/see/ sb. do sth. → 观看/看见某人做某事 I saw you pick an apple just now. • find/see/sb. doing sth. → 观看/看见某人正在做某事 I saw you playing basketball with your classmates o
非谓语动词
• help sb. to do sth. →帮助某人做某事 Lucy often helps Lily to wash her clothes.
• help sb. do sth. →帮助某人做某事 He usually helps me learn English.
• help sb. with sth. →帮助某人做某事 I sometimes help my mother with the housework.
• take sb. to sp→带某人到某地 Mr. Wang took us to the Summer Palace last Sunday.
可跟双宾语的动词
• show sb. Sth→给某人看某物 Please show me the map. show sth. to sb. →把某物给某人看 Please show the map to me.
• buy sb. sth. →为某人买某物 Mother bought me a bike.
• buy sth. for sb. →为某人买某物 Mother bought a bike for me.
• give sb. sth →把某物给某人 Jim gave me an English dictionary.

2022学年部编版语文七年级下册期末复习检测试题及答案部编人教版七年级下册

2022学年部编版语文七年级下册期末复习检测试题及答案部编人教版七年级下册部编语文七下期末复习检测试题（含答案和解析）一.积累与运用（28分）1.下列加下划线的字注音全部正确的一项是（）（2分）A.伫立（zhù）萋萋（qī）酒酿（niàng）盘虬（qiú）B.服侍（Sì）执着（zhuò）矜持（jīn）瀑布（pù）C.瞬息（shùn）迸溅（bèng）挑逗（tiǎo）忏悔（qiàn）D.颤抖（chàn）忧郁（yù）叩门（kòu）赤裸（guǒ）2.下列各项中词语书写无误的一项是（）（2分）A.野马奔驰酣然入梦浑身紧张悬涯峭壁B.故弄玄虚不可捉摸刺入肌骨苛捐杂税C.荒山野岭大显身手勇敢无畏歪风斜气D.美好景致寒气逼人寒风凛洌扶危济困3.在下列句子的横线处填入的词语最恰当的一项是（）（2分）①对这一转变作出了巨大贡献的，有一位长期以来________的科学家：邓稼先。

②那是中华民族________的时代，是有亡国灭种危险的时代。

③邓稼先是中华民族核武器事业的奠基人和开拓者。

张爱萍将军称他为“两弹元勋”，他是________的。

④今天，一个世纪以后，中国人站起来了。

这是千千万万人努力的结果，是许许多多________的英雄人物创造出来的伟大胜利。

⑤1949年到1966年我在普林斯顿高等学术研究所工作，前后17年的时间里所长都是物理学家奥本海默。

当时他是美国________的人物。

A.①鲜为人知②任人宰割③当之无愧④可歌可泣⑤家喻户晓B.①当之无愧②任人宰割③家喻户晓④鲜为人知⑤可歌可泣C.①鲜为人知②任人宰割③当之无愧④家喻户晓⑤可歌可泣D.①可歌可泣②家喻户晓③任人宰割④鲜为人知⑤当之无愧4.对下列文句的修辞方法理解错误的一项是（）（2分）我的心也震颤了起来，一种悲壮的感觉攫住了我。

土埋了大半截了，还开花!土埋了大半截了，还开花!我跨过障碍，走进去看这朵从重压中挣扎出来的花。

语文七年级下学期期末复习文言文综合检测试卷带答案

语文七年级下学期期末复习文言文综合检测试卷带答案一、文言文1．阅读下面两则材料，回答问题。

【甲】水陆草木之花，可爱者甚蕃。

晋陶渊明独爱菊。

自李唐来，世人甚爱牡丹。

予独爱莲之出淤泥而不染，濯清涟而不妖，中通外直，不蔓不枝，香远益清，亭亭净植，可远观而不可亵玩焉。

予谓菊，花之隐逸者也；牡丹，花之富贵者也；莲，花之君子者也。

噫！菊之爱，陶后鲜有闻。

莲之爱，同予者何人？牡丹之爱，宜乎众矣。

（周敦颐《爱莲说》）【乙】周敦颐，字茂叔，为分宁主簿①。

有狱②久不决，敦颐至，一讯立辨。

邑人惊曰：“老吏不如也。

”有囚法不当死，转运使王逵欲深治之。

逵，酷悍吏也，众莫敢争。

敦颐独与之辩，不听，乃委手版③归，将弃官去，曰：“如此尚可仕乎！杀人以媚人，吾不为也。

”逵悟，囚得免。

（选自《宋史·周敦颐传》）【注】①主簿：官名。

②狱：案件。

③手版：笏板，是古时大臣上朝时手中所持的狭长板子，用以列出上奏的事项。

（1）《爱莲说》的作者周敦颐，是________时期的________家。

（2）解释下面句中划线的词语。

①可爱者甚蕃________②陶后鲜有闻________③转运使王逵欲深治之________④将弃官去________（3）用现代汉语翻译下面的语句。

①予独爱莲之出淤泥而不染，濯清涟而不妖。

②逵，酷悍吏也，众莫敢争。

（4）【甲】文中作者独爱莲花，认为莲才是花中君子。

请结合对莲的描写体会莲具有哪些君子品性？（5）黄庭坚称周敦颐“人品甚高，胸怀洒落，如光风霁月”。

阅读【乙】文，说说文中的周敦颐是个怎样的人？2．阅读下文，回答问题。

王冕者，诸暨人。

七八岁时，父命牧牛陇上，窃入学舍，听诸生诵书；听已，辄默记。

暮归，忘其牛，或①牵牛来责蹊田②者。

父怒，挞之，已而复如初。

母曰：“儿痴如此，曷不听其所为？”冕因去，依僧寺以居。

夜潜出，坐佛膝上，执策③映长明灯读之，琅琅达旦。

佛像多土偶，狞恶可怖；冕小儿，恬④若不见。

【注释】①或：有人，有的人。

七年级下学期期末复习文言文语文综合检测试卷带解析1

七年级下学期期末复习文言文语文综合检测试卷带解析1 一、文言文1．阅读下面的文段，回答问题。

（甲）沧州南一寺临河干，山门圮于河，二石兽并沉焉。

阅十余岁，僧募金重修，求二石兽于水中，竟不可得。

以为顺流下矣，棹数小舟，曳铁钯，寻十余里无迹。

一讲学家设帐寺中，闻之笑曰：“尔辈不能究物理，是非木杮，岂能为暴涨携之去？乃石性坚重，沙性松浮，湮于沙上，渐沉渐深耳。

沿河求之，不亦颠乎？”众服为确论。

一老河兵闻之，又笑曰：“凡河中失石，当求之于上流。

盖石性坚重，沙性松浮，水不能冲石，其反激之力，必于石下迎水处啮沙为坎穴，渐激渐深，至石之半，石必倒掷坎穴中。

如是再啮，石又再转。

转转不已，遂反溯流逆上矣。

求之下流，固颠；求之地中，不更颠乎？”如其言，果得于数里外。

然则天下之事，但知其一，不知其二者多矣，可据理臆断欤？（乙）刘羽冲偶得古兵书，伏读经年，自谓可将十万。

会有土寇，自练乡兵与之角，全队溃覆，几为所擒。

又得古水利书，伏读经年①，自谓可使千里成沃壤。

绘图列干②州官。

州官也好事，使试于一村。

沟洫③甫成，水大至，顺渠灌入，人几为鱼。

由是抑郁不自得，恒独步庭阶，摇首自语曰：“古人岂欺我哉!”如是日千百遍，惟此六字。

不久，发病死。

【注释】①经年：一年左右。

②干：求见。

③沟恤：沟渠。

（1）解释下列句中加下划线字①尔辈不能究物理 ________ ②自谓可将十万________③竟不可得________ ④恒独步庭阶________（2）下列加下划线字意义和用法不相同的一项是（）A.惟此六字惟手熟尔B.一老河兵闻之何陋之有C.几为所擒岂能为暴涨携之去D.古人岂欺我哉孤岂欲卿治经为博士耶（3）翻译下列句子①然则天下之事，但知其一，不知其二者多矣，可据理臆断欤？②又得古水利书，伏读经年，自谓可使千里成沃壤。

（4）（乙）文中刘羽冲失败的原因是什么？从讲学家和刘羽冲失败的经历中，你明白了什么？2．阅读下面的文段，回答问题。

甲水陆草木之花，可爱者甚蕃。

人教版七年级下册数学期末复习：动点问题压轴题

人教版七年级下册数学期末复习: 动点问题压轴题1. 如图, 点A在x轴的负半轴上, 点D在y轴的正半轴上, 将三角形AOD沿x轴向右平移, 平移后得到三角形BEC, 点A的对应点是点B. 已知点A的坐标为(a, 0), 点C 的坐标为(b, c), 且a, b, c满足.(1)求点B的坐标;(2)求证: ∠DAE=∠BCD；(3)点P是线段BC上一动点（不与点B、C重合）, 连接DP、AP, 在点P运动过程中, ∠CDP、∠DPA、∠PAE之间是否存在永远不变的数量关系？若存在, 写出它们之间的数量关系, 并请证明；若不存在, 请说明理由．2. 已知, 直线, 直线和, 分别交于C, D点, 点A, B分别在直线, 上, 且位于直线的左侧, 动点P在直线上, 且不和点C, D重合.(1)如图1, 当动点P在线段CD上运动时, 求证: ∠APB＝∠CAP＋∠DBP；(2)如图2, 当动点P在点C上方运动时（P, A, B不在同一直线上）, 请写出∠APB, ∠CAP, ∠DBP之间的数量关系, 并选择其中一种的数量关系说明理由．3. 如图①, 平直角坐标系中, 已知点A（a, 0）, B（0, b）, 其中a, b满足|2a﹣3b﹣39|＝0, 将点B向右平移24个单位长度得到点C.(1)点A和点C的坐标；(2)如图①, 点D为线段BC上一动点, 点D从点C以2个单位长度/秒的速度向点B运动, 同时点E为线段OA上一动点, 从点O以3个单位长度/秒的速度向点A运动, 设运动的时间为t秒（0＜t＜10）, 四边形BOED的面积记为S四边形BOED（以下同理表示）, 若S四边形BOEDS四边ACDE, 求t的取值范围；(3)如图②, 在（2）的条件下, 在点D, E运动的过程中, DE交OC于点F, 求证：S△OEF＞S△DCE总成立．4. 在平面直角坐标系中, O为原点, 点A（0, 2）, B（﹣2, 0）, C（4, 0）.(1)如图1, △ABC的面积为；(2)如图2, 将点B向右平移7个单位长度, 再向上平移4个单位长度, 得到对应点D．①求①ACD的面积；②点P是x轴上一动点, 若△PAO的面积等于3, 请求出点P的坐标.5. 在平面直角坐标系中, O为原点, 点A(0, −3), B(−2, 0).（1）如图①, 则三角形OAB的面积为_______；（2）如图②, 将线段AB向右平移5个单位长度, 再向上平移4个单位长度, 得到平移后的线段A′B′．连接OA′, OB′．①求三角形OA′B′的面积；②P(−1, m)（m>0）是一动点, 若SΔPOB′=10, 请直接写出点P坐标.6. 在平面直角坐标系中, , 满足.（1）直接写出、的值: ；；（2）如图1, 若点满足的面积等于6, 求的值；（3）设线段交轴于C, 动点E从点C出发, 在轴上以每秒1个单位长度的速度向下运动, 动点F从点出发, 在轴上以每秒2个单位长度的速度向右运动, 若它们同时出发, 运动时间为秒, 问为何值时, 有？请求出的值．7. 如图1, ABCD, 定点E, F分别在直线AB, CD上, 在平行线AB, CD之间有一动点P, 满足0°＜∠EPF＜180°.(1)试问∠AEP, ∠EPF, ∠PFC满足怎样的数量关系？解: 由于点P是平行线AB, CD之间有一动点, 因此需要对点P的位置进行分类讨论: 如图1, 当P点在EF的左侧时, ∠AEP, ∠EPF, ∠PFC满足数量关系为, 如图2, 当P点在EF的右侧时, ∠AEP, ∠EPF, ∠PFC满足数量关系为.(2)如图3, EQ, FQ分别平分∠PEB和∠PFD, 且点P在EF左侧.①若∠EPF＝60°, 则∠EQF＝.②猜想∠EPF与∠EQF的数量关系, 并说明理由；③如图4, 若∠BEQ与∠DFQ的角平分线交于点Q1, ∠BEQ1与∠DFQ1的角平分线交于点Q2, ∠BEQ2, 与∠DFQ2的角平分线交于点Q3；此次类推, 则∠EPF与∠EQ2021F满足怎样的数量关系？（直接写出结果）8. 已知直线、, 直线与直线、分别交于点C和点D, 在直线上有动点P（点P与点C.D 不重合）, 点A在直线上, 点B在直线上.(1)如图①, 如果点P在C.D之间运动时, 且满足∠1+∠3=∠2, 请写出与之间的位置关系并说明理由；(2)如图②, 如果, 点P在直线的上方运动时, 请写出∠1, ∠2与∠3之间的数量关系并说明理由；(3)如图③, 如果, 点P在直线的下方运动时, 请直接写出∠PAC、∠PBD、∠APB之间的关系（不需说明理由）．9. 如图, , 平分, 设为, 点E是射线上的一个动点.（1）若时, 且, 求的度数；（2）若点E运动到上方, 且满足, , 求的值；（3）若, 求的度数（用含n和的代数式表示）．10. 如图所示, 已知, 点P是射线AM上一动点（与点A不重合）, BC.BD分别平分和, 分别交射线AM于点C.D, 且（1）求的度数.（2）当点P运动时, 与之间的数量关系是否随之发生变化？若不变化, 请写出它们之间的关系, 并说明理由；若变化, 请写出变化规律.（3）当点P运动到使时, 求的度数．11. 已知点D在∠ABC内, E为射线BC上一点, 连接DE, CD. （1）如图1, 点E在线段BC上, 连接AE, ∠AED=∠A+∠D.①求证AB①CD；②过点A作AM∥ED交直线BC于点M, 请猜想∠BAM与∠CDE的数量关系, 并加以证明；（2）如图2, 点E在BC的延长线上, ∠AED=∠A﹣∠D．若M平面内一动点, MA∥ED, 请直接写出∠MAB与∠CDE的数量关系．12. 如图1, 在平面直角坐标系中, 点A, B的坐标分别为（1, 0）, （4, 0）, 现同时将点A, B分别向上平移3个单位长度, 再向左平移1个单位长度, 分别得到A, B的对应点C, D, 连接AC, BD, CD.图1图2（1）求点C, D的坐标.（2）P是x轴上（除去B点）的动点.①连接PC, BC, 使S△PBC=2S△ABC, 求符合条件的P点坐标.②如图2, Q是线段BD上一定点, 连接PQ, 请直接写出∠BPQ+∠PQB与∠CDB的数量关系．13. 如图, 在长方形ABCD中, AB=8cm, BC=6cm, 点E是CD边上的一点, 且DE=2cm, 动点P从A点出发, 以2cm/s的速度沿A→B→C→E运动, 最终到达点E. 设点P运动的时间为t秒.（1）请以A点为原点, AB所在直线为x轴, 1cm为单位长度, 建立一个平面直角坐标系, 并用t表示出点P在不同线段上的坐标.（2）在（1）相同条件得到的结论下, 是否存在P点使△APE的面积等于20cm2时,若存在, 请求出P点坐标；若不存在, 请说明理由．14. 如图, 直线PQ∥MN, 点C是PQ、MN之间（不在直线PQ, MN上）的一个动点.（1）若∠1与∠2都是锐角, 如图甲, 请直接写出∠C与∠1, ∠2之间的数量关系；（2）若把一块三角尺（∠A＝30°, ∠C＝90°）按如图乙方式放置, 点D, E, F是三角尺的边与平行线的交点, 若∠AEN＝∠A, 求∠BDF的度数；（3）将图乙中的三角尺进行适当转动, 如图丙, 直角顶点C始终在两条平行线之间, 点G在线段CD上, 连接EG, 且有∠CEG＝∠CEM, 求值．15. 如图,在直角坐标系中,点A. C分别在x轴、y轴上,CB∥OA, OA=8,若点B的坐标为.(1)直接写出点A, C的坐标；(2)动点P从原点O出发沿x轴以每秒2个单位的速度向右运动, 当直线PC把四边形OABC分成面积相等的两部分时停止运动, 求P点运动时间；(3)在(2)的条件下, 点P停止运动时, 在y轴上是否存在一点Q, 连接PQ, 使三角形CPQ的面积与四边形OABC的面积相等?若存在, 求点Q的坐标；若不存在, 请说明理由．16. 如图, 已知点, 且, 满足.过点分别作轴、轴, 垂足分别是点、.（1）求出点B的坐标；（2）点是边上的一个动点（不与点重合）, 的角平分线交射线于点, 在点运动过程中, 的值是否变化？若不变, 求出其值；若变化, 说明理由.（3）在四边形的边上是否存在点, 使得将四边形分成面积比为1：4的两部分？若存在, 请直接写出点的坐标；若不存在, 说明理由.17. 如图, 在平面直角坐标系中, 点A, B的坐标分别为A（0, a）, B（b, a）, 且a、b满足（a﹣2）2+|b﹣4|=0, 现同时将点A, B分别向下平移2个单位, 再向左平移1个单位, 分别得到点A, B的对应点C, D, 连接AC, BD, AB.（1）求点C, D的坐标及四边形ABDC的面积S四边形ABCD；（2）在y轴上是否存在一点M, 连接MC, MD, 使S△MCD=S四边形ABDC？若存在这样一点, 求出点M的坐标, 若不存在, 试说明理由；（3）点P是直线BD上的一个动点, 连接PA, PO, 当点P在BD上移动时（不与B, D 重合）, 直接写出∠BAP、∠DOP、∠APO之间满足的数量关系．18. 如图1, 在平面直角坐标系中, A（a, 0）是x轴正半轴上一点, C是第四象限内一点, CB⊥y轴交y轴负半轴于B（0, b）, 且|a﹣3|+（b+4）2＝0, S四边形AOBC＝16.（1）求点C的坐标.（2）如图2, 设D为线段OB上一动点, 当AD⊥AC时, ∠ODA的角平分线与∠CAE 的角平分线的反向延长线交于点P, 求∠APD的度数；（点E在x轴的正半轴）. （3）如图3, 当点D在线段OB上运动时, 作DM⊥AD交BC于M点, ∠BMD、∠DAO的平分线交于N点, 则点D在运动过程中, ∠N的大小是否会发生变化？若不变化, 求出其值；若变化, 请说明理由．19. 如图1, 在平面直角坐标系中, 点A为x轴负半轴上一点, 点B为x轴正半轴上一点, C(0, a), D(b, a), 其中a, b满足关系式: |a+3|+(b-a+1)2=0.（1）a=___, b=___, △BCD的面积为______；（2）如图2, 若AC⊥BC, 点P线段OC上一点, 连接BP, 延长BP交AC于点Q, 当∠CPQ=∠CQP时, 求证:BP平分∠ABC；（3）如图3, 若AC⊥BC, 点E是点A与点B之间一动点, 连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时, 的值是否变化？若不变, 求出其值；若变化, 请说明理由.20. 已知: 在平面直角坐标系中, 四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°, AB∥CD, AB=CD=8, AD=BC=6, D点与原点重合, 坐标为（0, 0）.（1）直接写出点B的坐标__________.（2）动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动, 若P, Q两点同时出发, 设运动时间为t秒, 当t为何值时, PQ∥y轴？（3）在Q的运动过程中, 当Q运动到什么位置时, 使△ADQ的面积为9？求出此时Q 点的坐标？。

期末复习测试题 2022-2023学年部编版语文七年级下册

2022-2023学年度下学期七年级语文期末复习题一、积累(30分)1.阅读下面的文字,完成(1)—(4)题。

(10分)父母的关爱无处不在。

每一次跌倒,他们都会拍去我们身上的泥土;每一次失利,他们都会甲(A.抚慰 B.抚摸)我们烦燥的内心……他们的爱是夏日的凉风,是冬日的暖阳,是风雨中的港湾,是黑暗中的烛光。

作为子女的我们,要充满感恩之心,用实际行动去报答父母。

比如锁碎家事勤做,不可疏懒．( )。

其实即便是一张粗拙．( )的贺卡,一个乙(A.呆滞 B.滞笨)的动作,也能让他们十分欣慰。

(1)给加点的字注音。

(2分)疏懒．( ) 粗拙．( )(2)文段中有两个错别字,请找出来并改正。

(4分)改为改为(3)从文段的括号内选择符合语境的词语分别填入甲、乙处。

(只填序号)(2分)甲: 乙:(4)文中画线句使用了、的修辞手法。

(2分)2.下面语段中加点的成语使用有误的一项是(2分) ( )2022年5月4日凌晨,中国科考队向着珠峰峰顶挺进。

科考设备沉重,天气瞬息万变．．．．,高海拔造成缺氧……困难络绎不绝．．．．。

但是科考队员们胸有成竹．．．．,不惧困难,最终在人迹罕至．．．．的峰顶圆满完成了综合科考任务。

A.瞬息万变B.络绎不绝C.胸有成竹D.人迹罕至3.下列句子没有语病．．．．的一项是(2分) ( ) A.一个班级能否形成良好的班级文化,对学生的健康成长起着至关重要的作用。

B.通过对宋代瓷器艺术的研究,展现了中国古代崇尚简朴、崇尚道德的社会风貌。

C.《标准汉语》的主要读者对象是为英语国家的中国留学生子女及汉语爱好者编写的一套汉语学习课本。

D.新中国在一代又一代领导人的带领下,从站起来到富起来再到强起来,正大步行走在民族复兴的道路上。

4.填入下面横线处的语句,与上下文衔接最恰当的一项是(2分)( )中国艺术的极境如空谷幽兰,似有若无,也无人注意。

在这个寂静的世界中,它自在开放,小小的花朵散发出淡淡的幽香,似淡若浓,沁人心脾。

2024年七年级语文下册期末复习检测试卷附答案解析

2024年七年级语文下册期末复习检测试卷（满分120分）一、语文积累与运用(20分)1、文段中给划线的字注音，或根据拼音写汉字都正确的是（）（2分）徜．（）徉在语文的天地里，我们感动于邓稼先“鞠躬尽cuì（），死而后已”的一生，领略到黄河伟大而又坚强的英雄气gài（），感受到端木蕻良在广大的关东原野上挚．（）痛的爱国情怀，也见证了杨绛作为一个幸运的人对一个不幸者的愧怍。

A.cáng瘁概zhìB.cháng瘁概zìC. cháng瘁概zhìD. cháng瘁慨zhì2．依次填入下面句子横线处的词语最恰当的一项是（）（2分）人生旅途，如果太过平坦顺利，反而会在______中虚度。

正如流水，有波折才会______美丽的浪花。

至于结局，并非是最重要的，______你享受了______的过程。

A．索然无味激起而且精致B．如释重负激扬况且精妙C．如释重负激扬因而精美D．索然无味激起因为精彩3．下列各句没有语病的一项是（）（2分）A．解放前，爸爸和哥哥两人挣来的钱还不够养活一家人的生活。

B．据统计，中学生大约有百分之七十左右的学生喜欢课外阅读。

C．黄河孕育了中华文明，哺育了华夏儿女。

D．为了提高同学们的语文素养，我校团委积极开展“读经典作品，建书香校园”。

4．给下列句子排序正确的一项是（）（2分）①与我国其他航天器命名思路一脉相承①体现着航天人的科学梦想和浪漫情怀，彰显着中国人的探索精神和文化自信①首辆火星车命名来自中国传统文化元素①例如：“嫦娥、墨子、悟空、北斗”等①以火神的名字命名中国第一辆火星车，是现代科学与传统文化的跨时空融合A．①①①①①B．①①①①①C．①①①①①D．①①①①①（2分）5．下列句子标点符号不正确．．的一项是（）A．他的那条大狗也像主人一样，安静，忠厚，不张扬。

B．不少的人对工作不负责任：拈轻怕重，把重担子推给人家，自己挑轻的。