人教版九级上册数学课件 第二十二章 二次函数 复习课
合集下载
九年级数学上册-第二十二章 二次函数 复习课件-人教版

例2
某商店销售一种销售成本为40元/千克的水产品,若按50元/ 千克销售,一个月可售出500千克,销售价每涨价1元,月销售量 就减少10千克。 (1)写出月销售利润y与售价x之间的函数关系式。 (2)销售单价定为55元时,计算月销售量与销售利润。 (3)商场想在月销售成本不超过3000元的情况下,使得月销售 利润达到8000元,销售单价应定为多少? (4)当售价定为多少元时,会获得最大利润?求出最大利润。
3 AD长度固定,只需找到点P使AP+PD最小即可,找到点A关于y轴的 对称点A',连接A'D,则A'D与y轴的交点即是点P的位置。
思维导图 例题示范
例1
如图,已知二次函数 y 1 x2 bx c 的图象经过A(2,0)、 2
B(0,-6)两点。
(3)若抛物线的顶点为D,在y轴上是否存在一点P,使得△PAD的周
接QE、OP、PQ,求OP+PQ+QE的最小值。
思维导图 例题示范
例3
如图,在平面直角坐标系中,已知抛物线 y 3 x2 3x 4 3 交
3
3
x轴于A,B两点,交y轴于点C,抛物线上一点D的横坐标为-5。
(1)求直线BD的解析式;
解:(1)令y=0,则 3 x2 3x 4 3 0 ,解得x=-4或1,
2
思维导图 例题示范
例1
如图,已知二次函数 y 1 x2 bx c 的图象经过A(2,0)、 2
B(0,-6)两点。
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求
△ABC的面积;
解:(2)∵ 二次函数的解析式为:y 1 x2 4x 6,
2
∴ 二次函数的对称轴为x=4,即OC=4,
某商店销售一种销售成本为40元/千克的水产品,若按50元/ 千克销售,一个月可售出500千克,销售价每涨价1元,月销售量 就减少10千克。 (1)写出月销售利润y与售价x之间的函数关系式。 (2)销售单价定为55元时,计算月销售量与销售利润。 (3)商场想在月销售成本不超过3000元的情况下,使得月销售 利润达到8000元,销售单价应定为多少? (4)当售价定为多少元时,会获得最大利润?求出最大利润。
3 AD长度固定,只需找到点P使AP+PD最小即可,找到点A关于y轴的 对称点A',连接A'D,则A'D与y轴的交点即是点P的位置。
思维导图 例题示范
例1
如图,已知二次函数 y 1 x2 bx c 的图象经过A(2,0)、 2
B(0,-6)两点。
(3)若抛物线的顶点为D,在y轴上是否存在一点P,使得△PAD的周
接QE、OP、PQ,求OP+PQ+QE的最小值。
思维导图 例题示范
例3
如图,在平面直角坐标系中,已知抛物线 y 3 x2 3x 4 3 交
3
3
x轴于A,B两点,交y轴于点C,抛物线上一点D的横坐标为-5。
(1)求直线BD的解析式;
解:(1)令y=0,则 3 x2 3x 4 3 0 ,解得x=-4或1,
2
思维导图 例题示范
例1
如图,已知二次函数 y 1 x2 bx c 的图象经过A(2,0)、 2
B(0,-6)两点。
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求
△ABC的面积;
解:(2)∵ 二次函数的解析式为:y 1 x2 4x 6,
2
∴ 二次函数的对称轴为x=4,即OC=4,
初中数学人教九年级上册第二十二章二次函数人教版初中数学二次函数复习课PPT

【答案】(1)由函数 y1 的图象经过点(1,-2),得(a+1)(-a) =-2, 解得 a1=-2,a2=1,代入 a1,a2 得到 y1 的解析式为 y1=x2-x -2; (2)当 y=0 时,(x+a)(x-a-1)=0,解得 x1=-a,x2=a+1, y1 的图象与 x 轴的交点是(-a,0),(a+1,0), 当 y2=ax+b 经过(-a,0)时,-a2+b=0,即 b=a2; 当 y2=ax+b 经过(a+1,0)时,a2+a+b=0,即 b=-a2-a; (3)当 P 在对称轴的左侧(含顶点)时,y 随 x 的增大而减小, (1,n)与(0,n)关于对称轴对称,
【例6】如图是二次函数
y图a象2 的x 部b分,x与c(xa 轴,的b,交c是 点A在点常 (2,a0)数 0) ,
和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a +b
m(am+b)(m为实数);⑤当-1<x<3时,y>0,其中正确的是( )
A.①②④
的图象叫做____. 3.每条抛物线都有对称轴.抛物线与对称轴的交点叫做抛物线的 _____是抛物线 最____或最_____点.
yax2bxca0
(一) 谁是控制图像的“幕后高手”
1. a决定开口方向:
a>0↔开口_______;向(上如图1) a<0↔开口_______;(如图2)
相同,抛物线的形状向_下____;
A.ya2xbxc B.2xy20
C.y2 ax2
D.2xy210
【针对练习】
1.若 y(m 是1二)x次m 函2 数1,则m m的 值x3是( )
A.1 B.-1
人教版九年级数学上册第22章二次函数复习课件共36张PPT

⑨在抛物线上是否存在点P,使得S∆ABP是∆ABC面积的2倍,若存在,请求出点P的坐标,若不存在, 请说明理由
(7)已知二次函数y=x2+bx+c的顶点坐标(1,-2),求b,c的值 (8)已知二次函数y=x2+4x+c的顶点坐标在x轴上,求c的值 (9)已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1上,求c的值
y 3.5m
2.5m
o 4m
3.05 m x
2.你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的 甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1 米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学 生丁的身高。
b ( , c) a
(1) y=2(x+2)2是由
向 平移 y=2个x2单位得到 左
2
(2) y=-2x2-2是由
向 平移y=-2x2 个单位得到下
2
(3) y=-2(x-2)2+3是由
向 平移 y=个-2单x2位
右
2
,再向
平移 上
个单位得到 3
(4) y=2x2+4x-5是由 下
向 平移 y=个2单x2 位,再向 左 平移 7
(50+x-40)元 (500-10x) 个 (50+x-40)(500-10x)元
7. 如图,已知直线 y= -x+3与X轴、y轴分别交于点B、C ,抛物线y= -x2+bx+c经过点B、C,点A是抛物线与x轴的另 一个交点。
(1)求抛物线的解析式;
人教版九级上册数学优质课件二次函数复习优质课件

人教版九级上册数学优质课件二次函 数复习 优质课 件
思维导图 例题示范
例1
如图,已知二次函数 y 1 x2 bx c 的图象经过A(2,0)、 2
B(0,-6)两点。
(1)求这个二次函数的解析式;
解:(1)将点A(2,0)、B(0,-6)代入得:c226b c 0 ,
解得:bc
4 6
解:(3)存在,点P的坐标为 (0, 2) 。 3
AD长度固定,只需找到点P使AP+PD最小即可,找到点A关于y轴的 对称点A',连接A'D,则A'D与y轴的交点即是点P的位置。
人教版九年 级级 上上 册册 数学数优学质课课件件二第次二函十数二复章习 优二质次课函件数 复习课件(共20张PPT)
人教版九年 级级 上上 册册 数学数优学质课课件件二第次二函十数二复章习 优二质次课函件数 复习课件(共20张PPT)
人教版九年 级级 上上 册册 数学数优学质课课件件二第次二函十数二复章习 优二质次课函件数 复习课件(共20张PPT)
人教版九年 级级 上上 册册 数学数优学质课课件件二第次二函十数二复章习 优二质次课函件数 复习课件(共20张PPT)
思维导图 例题示范
例2
某商店销售一种销售成本为40元/千克的水产品,若按50元/ 千克销售,一个月可售出500千克,销售价每涨价1元,月销售量 就减少10千克。 (1)写出月销售利润y与售价x之间的函数关系式。
人教版九年级上册 数学 课件 第二十二章 二次函数 复习课件(共20张PPT)
思维导图 例题示范
例2
某商店销售一种销售成本为40元/千克的水产品,若按50元/ 千克销售,一个月可售出500千克,销售价每涨价1元,月销售量 就减少10千克。 (2)销售单价定为55元时,计算月销售量与销售利润。
人教版数学九年级上第二十二章二次函数复习课(62张ppt)

当x b 时, y最大值为 4ac b2
2a
4a
1、抛物线 y 4x2 3 的对称轴及顶点坐标分
别是( D ) A、y轴,(0,-4) B、x=3,(0,4) C、x轴,(0,0) D、y轴, (0,3)
2、二次函数 y (x 1)2 2 图象的顶点坐
标和对称轴方程为( A ) A、(1,-2), x=1 B、(1,2),x=1 C、(-1,-2),x=-1 D、(-1,2),x=-1
即:y=-x2+1
练习1
根据下列条件,求二次函数的解析式。 (1)、图象经过(0,0), (1,-2) , (2,3) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ;
(3)、图象经过(0,0), (12,0) ,且最高点 的纵坐标是3 。
能力训练
1、选择合适的方法,求下列二次函数的解析式。
(3,0)x
当 x 1 时,y有最 小值,是 25
2
4
(1,-6) 函数值y的正负性:
(0,-6)(—12 ,-—245)
当 x<-2或x>3 时,y>0 当 x=-2或x=3 时,y=0
当 -2<x<3
时,y<0
2.复习二次函数的图象及性质
y
y
(0,c)
b 2a
,
4ac 4a
一般地,如果 y=ax2+bx+c(a,b,c 是常数, a≠0),那么,y叫做x的二次函数。
定义要点: (1)a≠0. (2)最高次数为2. (3)代数式一定是整式
练习: 1、y=-x²,y=2x²-2/x,y=100-5x²,
y=3x²-2x³+5,其中是二次函数的有__2__个。
人教版九年级上册第22章二次函数复习 课件(共19张PPT)

y<0
10. 当a>0, △<0时,抛物线y=ax2+bx+c与x 轴 无交点,即全部图象在x 轴的上方,一元二 次方程ax2+bx+c=0无实数根,无论x 取何值, 都有y>0; 无论 x 取何值,都不可能有y≤0。
y>0
11.当a<0, △<0时,抛物线y=ax2+bx+c与x 轴无交点,即全部图象在x 轴的下方,一 元二次方程ax2+bx+c=0无实数根,无论x 取何值,都有y<0 .
【例】已知某二次函数二的次图函象数过的(一1,1般0)式,。(1,4) , (2,7) 三点,求这个函数的解析式。
解:设所求函数解析式为 y ax2 bx c
由已知函数图象过(1,10),(1,4),(2,7) 三点得
a b c 10 a b c 4 4a 2b c 7 解这个方程组得a 2,b 3,c 5
∴所求得的函数解析式为 y 2x2 3x 5。
巩固练习1
已知某二次函数图象上有(1,3) ,(1,3) ,(2,6)三
个点,求它的函数解析式。
解:设函数解析式为 y ax2 bx c 由已知,函数图象上有 (1,3) ,(1,3) ,(2,6) 三个点,
得
a b c 3 a b c 3 4a 2b c 6
3. 当 a > 0 时,在对称轴的左侧,y 随 x 的增大而减小,
在对称轴的右侧,y 随 x 的增大而增大;当 a < 0 时,
在对称轴的左侧,y 随 x 的增大而增大,在对称轴的
右侧,y 随 x 的增大而减小。
4. y=a(x-h)2+k 的顶点坐标是(h, k) , 对称轴是直线 x㎝
10. 当a>0, △<0时,抛物线y=ax2+bx+c与x 轴 无交点,即全部图象在x 轴的上方,一元二 次方程ax2+bx+c=0无实数根,无论x 取何值, 都有y>0; 无论 x 取何值,都不可能有y≤0。
y>0
11.当a<0, △<0时,抛物线y=ax2+bx+c与x 轴无交点,即全部图象在x 轴的下方,一 元二次方程ax2+bx+c=0无实数根,无论x 取何值,都有y<0 .
【例】已知某二次函数二的次图函象数过的(一1,1般0)式,。(1,4) , (2,7) 三点,求这个函数的解析式。
解:设所求函数解析式为 y ax2 bx c
由已知函数图象过(1,10),(1,4),(2,7) 三点得
a b c 10 a b c 4 4a 2b c 7 解这个方程组得a 2,b 3,c 5
∴所求得的函数解析式为 y 2x2 3x 5。
巩固练习1
已知某二次函数图象上有(1,3) ,(1,3) ,(2,6)三
个点,求它的函数解析式。
解:设函数解析式为 y ax2 bx c 由已知,函数图象上有 (1,3) ,(1,3) ,(2,6) 三个点,
得
a b c 3 a b c 3 4a 2b c 6
3. 当 a > 0 时,在对称轴的左侧,y 随 x 的增大而减小,
在对称轴的右侧,y 随 x 的增大而增大;当 a < 0 时,
在对称轴的左侧,y 随 x 的增大而增大,在对称轴的
右侧,y 随 x 的增大而减小。
4. y=a(x-h)2+k 的顶点坐标是(h, k) , 对称轴是直线 x㎝
人教版九年级数学上册第22章二次函数章末复习课件 (共68张ppt)

(4)当图像与x轴 有两个交点时, b2-4ac>0;当图像与x轴只有一个 交点时, b2-4ac=0; 当图像与x轴没有交点时, b2-4ac<0. (5)图像过点(1, a+b+c)和点(-1, a-b+c), 再根据图像上的点的位置可 确定式子a+b+c和a-b+c的符号.
例1 已知二次函数y=ax2+bx+c的图像如图22-Z-1所示, 那么下
二次函数 的图像和
性质
开口方向
a>0, 图像开口向上 a<0, 图像开口向下
对称轴
a, b同号, 对称轴在y轴左侧 a, b异号, 对称轴在y轴右侧
烦烦烦鬼鬼鬼鬼 鬼鬼鬼鬼跟鬼鬼 鬼鬼鬼g鬼鬼
二次函数 的图像和
性质
a>0 增减性
a<0
最值
二次函数 的解析式
y=ax²+bx+c(a≠0)(一般式) y=a(x-h)²&#(a≠0)(交点式)
【要点指导】研究二次函数的图像的平移、轴对称变换过程, 实 际 就是确定变换后所得图像的二次函数解析式, 研究变换后的图 像和性质 的过程, 关键是找到变换后图像上的特殊点(如抛物线的 顶点), 从而得出 函数解析式, 最后利用二次函数的性质解答.
例4 如图22-Z-3, 在平面直角坐标系 xOy中, 将抛物线y=2x2沿y轴 向上平移1个单 位长度, 再沿x轴向右平移2个单位长度, 平移 后所 得抛物线的顶点记作A, 直线x=3与平移 后的抛物线相交于点B, 与 直线OA相交于点C. (1)求平移后的抛物线的函数解析式; (2)求点C的坐标及△ABC的面积.
例2 已知二次函数的图像以A(-1, 4)为顶点, 且过点B(2, -5). (1)求该函数的解析式; (2)求该函数图像与坐标轴的交点坐标.
九年级数学上册第二十二章二次函数复习课件(新版)新人教版
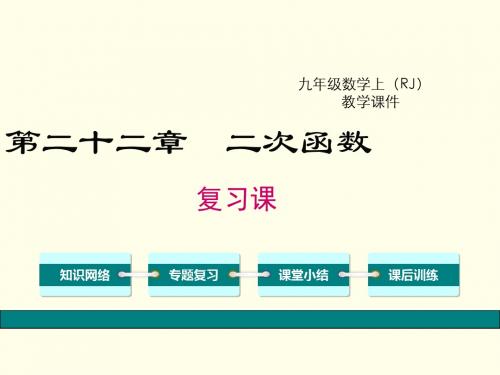
值范围.
丙
1m
丁
甲
1m
2.5m 4m 1<s<3
乙
课堂小结
二次函数的定 义
二次函数的图 象 及 性 质 二次函数的应 用
二次函数的概念及 图 象 特 征
二次函数
用数形结合 的方法去研 究 和 运 用
建立二次函数模型, 将实际问题数学化, 运用二次函数知识解 决 实 际 问 题
课后训练
1.对于抛物线y=-2(x-5)2+3 ,下列说法正确的是(
专题七 综合应用—呈抛物线形状实物的几何探究
例7 跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图,正在甩绳 的甲、乙两名同学拿绳的手间距为4米,距地面均为1米,丙、丁同学分别 站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处,刚好通过他 们的头顶,已知丙同学的身高是1.5米. (1)请你算一算丁同学的身高. 丁 丙(1,1.5)
九年级数学上(RJ) 教学课件
第二十二章 二次函数
复习课
知识网络 专题复习 课堂小结 课后训练
知识网络
二次函数的概念 图 二 次 函 数 象
y=ax2+bx+c 一般形式 (a,b,c是常数,a≠0) 自变量的取值范围 全体实数 一条抛物线 y=ax2+bx+c(a≠0) 一般式 顶点式 交点式 y=a(x-h)2+k y=a(x-x1)(x-x2)
b 2a
b 2a
x
b 2a
4ac b2 y最大值= 4a
专题二 二次函数图象的对称性
例2 抛物线y=ax2+bx+c (a≠0)与x轴的公共点是(-1,0), 直线x=1 (3,0),则这条抛物线的对称轴为_________. 解析 抛物线与x轴的两个交点是一对对称点.其实只要抛物线上两点( x1,y0)、(x2,y0)的纵坐标相等,这两点就是一对d对关于抛物线对称
丙
1m
丁
甲
1m
2.5m 4m 1<s<3
乙
课堂小结
二次函数的定 义
二次函数的图 象 及 性 质 二次函数的应 用
二次函数的概念及 图 象 特 征
二次函数
用数形结合 的方法去研 究 和 运 用
建立二次函数模型, 将实际问题数学化, 运用二次函数知识解 决 实 际 问 题
课后训练
1.对于抛物线y=-2(x-5)2+3 ,下列说法正确的是(
专题七 综合应用—呈抛物线形状实物的几何探究
例7 跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图,正在甩绳 的甲、乙两名同学拿绳的手间距为4米,距地面均为1米,丙、丁同学分别 站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处,刚好通过他 们的头顶,已知丙同学的身高是1.5米. (1)请你算一算丁同学的身高. 丁 丙(1,1.5)
九年级数学上(RJ) 教学课件
第二十二章 二次函数
复习课
知识网络 专题复习 课堂小结 课后训练
知识网络
二次函数的概念 图 二 次 函 数 象
y=ax2+bx+c 一般形式 (a,b,c是常数,a≠0) 自变量的取值范围 全体实数 一条抛物线 y=ax2+bx+c(a≠0) 一般式 顶点式 交点式 y=a(x-h)2+k y=a(x-x1)(x-x2)
b 2a
b 2a
x
b 2a
4ac b2 y最大值= 4a
专题二 二次函数图象的对称性
例2 抛物线y=ax2+bx+c (a≠0)与x轴的公共点是(-1,0), 直线x=1 (3,0),则这条抛物线的对称轴为_________. 解析 抛物线与x轴的两个交点是一对对称点.其实只要抛物线上两点( x1,y0)、(x2,y0)的纵坐标相等,这两点就是一对d对关于抛物线对称
第22章《二次函数》复习课PPT课件(人教版)
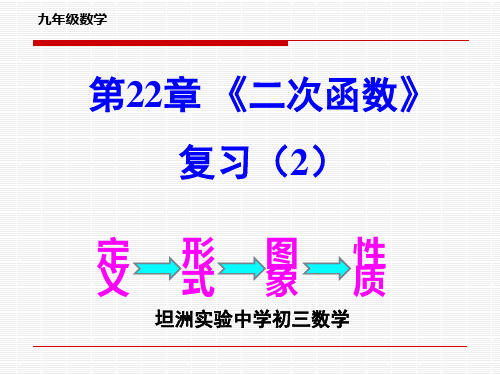
形?若存在,求点N的坐标;若不存在,请说明理由
三、课堂练习
N M
N
重视知识归纳; 重视基本概念; 重视典型题型; 重视每日小练; 重视错题整理; 避免盲目大意。
九年级数学
第22章 《二次函数》 复习(2)
定形图 性 义式象 质
坦洲实验中学初三数学
一、知识回顾
归纳知识:
(1)开a口的向符上号:由抛物a线>0的开口y 方向确定
开口向下
(2)c的符号:
a<0
o
x
由抛物线与y轴的交点位置确定.
交点在y轴正半轴
c>0
y
交点在y轴负半轴
c<0
交点是坐标原点
c=0
ox
∴ OE=DE=1.5 即D(1.5,-1.5)
设直线OD为y=kx,代入D点坐标得y= -x
令x2-2x-3 = -x
二、典型例题
证明: b2-4ac=[-(2m-1)]2-4×1×(m2-m-2) =4m2-4m+1-4m2+4m+8 =9
即b2-4ac >0 ∴ 抛物线与x轴有两个不同的交点
三、课堂练习
C
一次函数y=ax+b经过的象限与a, b符号关系 A选项,经过一二四象限, a<0, b>0 B选项,经过一二三象限,a>0, b>0 C选项,经过一三四象限, a>0, b<0 D选项,经过一三四象限,a>0, b<0
三、课堂练习
·B
A2
6
三、课堂练习
-1·
·5
与x,y轴交点
-5·
二、典型例题
解:令x=0,解得y=m2-m-2 令y=0,得x2-(2m-1) x+m2-m-2=0 [x-(m-2)][x-(m+1)]=0
三、课堂练习
N M
N
重视知识归纳; 重视基本概念; 重视典型题型; 重视每日小练; 重视错题整理; 避免盲目大意。
九年级数学
第22章 《二次函数》 复习(2)
定形图 性 义式象 质
坦洲实验中学初三数学
一、知识回顾
归纳知识:
(1)开a口的向符上号:由抛物a线>0的开口y 方向确定
开口向下
(2)c的符号:
a<0
o
x
由抛物线与y轴的交点位置确定.
交点在y轴正半轴
c>0
y
交点在y轴负半轴
c<0
交点是坐标原点
c=0
ox
∴ OE=DE=1.5 即D(1.5,-1.5)
设直线OD为y=kx,代入D点坐标得y= -x
令x2-2x-3 = -x
二、典型例题
证明: b2-4ac=[-(2m-1)]2-4×1×(m2-m-2) =4m2-4m+1-4m2+4m+8 =9
即b2-4ac >0 ∴ 抛物线与x轴有两个不同的交点
三、课堂练习
C
一次函数y=ax+b经过的象限与a, b符号关系 A选项,经过一二四象限, a<0, b>0 B选项,经过一二三象限,a>0, b>0 C选项,经过一三四象限, a>0, b<0 D选项,经过一三四象限,a>0, b<0
三、课堂练习
·B
A2
6
三、课堂练习
-1·
·5
与x,y轴交点
-5·
二、典型例题
解:令x=0,解得y=m2-m-2 令y=0,得x2-(2m-1) x+m2-m-2=0 [x-(m-2)][x-(m+1)]=0
人教版数学九年级上册第22章《二次函数》复习课件 (共12张PPT)

变型题: -3 -2 -1 在线段BC下方的 -1 1 2 3 4 5 6 X -2 抛物线上有一动点D, 1、知识要点梳理: C -3 二次函数图像和性质、极值 当△ BCD的面积最大 -4 D 2、方法技巧归纳: 时,求点D的坐标? 求极值问题,就是构建二次函数问题 -5
●
抛物线 只有一个交点, 求交点D的坐标? A
聪
谜语 耳朵听着,
眼睛看着, 嘴巴说着, 心里想着。
(答一汉字)
专题复习 教材典型题拓展
(孙悟空七十二变)
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关 知识解决下列问题。 y (1)将其转化为顶点式: 6 5 (2)将其转化为交点式: 4 (3)开口方向: 3 (4)对称轴: 2 1 (5)顶点坐标: -3 -2 -1 (6)与X轴的交点坐标 : -1 1 2 3 4 5 6 X -2 (7)与Y轴的交点坐标 : 1、知识要点梳理: -3 (8)根据已得的关键点, 一般式确定与 Y轴交点坐标,顶点式确定顶 -4 点坐标及对称轴,交点式确定与 X轴交点坐标。 画出其图像近似图: 2、方法技巧归纳: -5
-6 解函数问题,抓关键点坐标 3、解题步骤完善:
· · ···
例:已知二次函数y1=x2 -2x-3,根据已学的二次函数相关 知识解决下列问题。 ( 9 )关于X轴对称的 y 6 抛物线解析式 : 5 4 (10)关于Y轴对称的 3 抛物线解析式 : 2 1 (11)关于原点对称的 -3 -2 -1 -1 1 2 3 4 5 6 X 抛物线解析式 : -2 (12)向右平移3个单位, 1、知识要点梳理: -3 二次函数图像和性质、轴对称、中心对称 -4 再向上平移6个单 2、方法技巧归纳: -5 解图像变换问题,抓开口方向和顶点坐标 -6 3、解题步骤完善: 位后抛物线解析式:
人教版九年级上册数学第22章二次函数复习课件(36张)

[注意] (1)等号右边必须是整式;(2)自变量的 最高次数是2;(3)当b=0,c=0时,y=ax2是特 殊的二次函数.
注意:
开口方向与 a 的关系; 抛物线与 y 轴的交点与 c 的关系;
对称轴与 a,b 的关系; 抛物线与 x 轴交点数目与 b2-4ac 的符号关系。
抛物线 y=ax2 的图象 :
若抛物线 y=-7(x+4)2-1平移得到 y=-7x2,则可 能( B ) A.先向左平移4个单位,再向下平移1个单位 B.先向右平移4个单位,再向上平移1个单位 C.先向左平移1个单位,再向下平移4个单位 D.先向右平移1个单位,再向下平移4个单位
已知关于x的二次函数,当x=-1时,函数值为10,当x=1
∴当x=87时,W有最大值,此时W=-(87-
90)2+900=891.
一家电脑公司推出一款新型电脑,投放市场以来3个月的利 润情况如图所示,该图可以近似看作为抛物线的一部分,请结 合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式; (2)该公司在经营此款电脑过程中,第 几月的利润最大?最大利润是多少? (3)若照此经营下去,请你结合所学的 知识,对公司在此款电脑的经营状况 (是否亏损?何时亏损?)作预测分析.
中考热点
1. 二次函数的定义、图象、图象的 平移、性质、图象与系数的关系。
2. 二次函数解析式求法。 3. 二次函数图象与一元二次方程的 根的关系。
本章易错点
1. 二次函数的情势及结构特点。 2. 忽略自变量的取值范围,误认为二次 函数的最值点就是顶点。 3. 二次函数与一元二次方程的关系。 4. 点的坐标与距离的区分和联系。
顶点式y=a(x-h)2+k的情势,得到: 对称轴是直线x=h,最值为y=k,顶 点坐标为(h,k);
注意:
开口方向与 a 的关系; 抛物线与 y 轴的交点与 c 的关系;
对称轴与 a,b 的关系; 抛物线与 x 轴交点数目与 b2-4ac 的符号关系。
抛物线 y=ax2 的图象 :
若抛物线 y=-7(x+4)2-1平移得到 y=-7x2,则可 能( B ) A.先向左平移4个单位,再向下平移1个单位 B.先向右平移4个单位,再向上平移1个单位 C.先向左平移1个单位,再向下平移4个单位 D.先向右平移1个单位,再向下平移4个单位
已知关于x的二次函数,当x=-1时,函数值为10,当x=1
∴当x=87时,W有最大值,此时W=-(87-
90)2+900=891.
一家电脑公司推出一款新型电脑,投放市场以来3个月的利 润情况如图所示,该图可以近似看作为抛物线的一部分,请结 合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式; (2)该公司在经营此款电脑过程中,第 几月的利润最大?最大利润是多少? (3)若照此经营下去,请你结合所学的 知识,对公司在此款电脑的经营状况 (是否亏损?何时亏损?)作预测分析.
中考热点
1. 二次函数的定义、图象、图象的 平移、性质、图象与系数的关系。
2. 二次函数解析式求法。 3. 二次函数图象与一元二次方程的 根的关系。
本章易错点
1. 二次函数的情势及结构特点。 2. 忽略自变量的取值范围,误认为二次 函数的最值点就是顶点。 3. 二次函数与一元二次方程的关系。 4. 点的坐标与距离的区分和联系。
顶点式y=a(x-h)2+k的情势,得到: 对称轴是直线x=h,最值为y=k,顶 点坐标为(h,k);
人教版初三数学上册第二十二章《二次函数》复习课1PPT41页

拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
人教版初三数学上册第二十二章《二次 函数》复习课1
56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将圆。
Байду номын сангаас 56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
人教版初三数学上册第二十二章《二次 函数》复习课1
56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将圆。
Байду номын сангаас 56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
人教版九年级上册数学课件第二十二章二次函数复习课(共18张PPT)

C、x轴,(0,0) D、y轴, (0,3)
(1) 求抛物线的解析式;
= 1/2BF. 1、抛物线
y=-x²-2x+3 的对称轴及顶点坐标分别是( )
(0,3)
若不存在,请说明理由.
(2)在(1)中抛物线 ③b2 - 4ac 0;
形如 y=ax²+ bx + c ( a 、 b 、 c 是常数, a ≠ 0 )的函数叫做二次函数
2
左加右减 上加下减
综合题:如图①, 已知抛物线 y=ax²+bx+3
(a≠0)与 x轴交于点A(1,0)和点B (-3,0),与 y轴交于点C.
(1) 求抛物线的解析式; (2)在(1)中抛物线的对称轴上是否存在点Q,使得 △QAC的周长最小?若存在,求出Q点的坐标;若不存在, 请说明理由. (3) 设抛物线的对称轴与 x轴交于点M, 问在对称轴上是否 存在点P,使△CMP为等腰三角形?若存在,请直接写出 所有符合条件的点P的坐标;若不存在,请说明理由. (4) 如图②,若点E为第二象限抛物线上一动点,连接BE、 CE,求四边形BOCE面积的最大值,并求此时E点的坐 标.
•
(交点式)
二次函数y=ax² + bx + c图像与系数a b c的关系
•1. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号: •①a 0; •②c 0; •③b2 - 4ac 0; •④ b 0; •小结:a 决定开口方向,c决定与y轴交点位置,b2 - 4ac决 定与x轴交点个数,a,b结合决定对称轴;
复习课
教学目标
1系统的复习二次函数,学生自主 梳理知识并掌握复习方法。
2通过复习二次函数相关知识,加 深学生对二次函数知识的理解,提 高学生运用知识解决实际问题的能 力。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
讨论:二次函数y=ax²+bx+c的图象如下所示,则
在下列各不等式中成立的个数
①abc<0 ②a+b+c < 0 ③a+c > b ④2a+b=0 ⑤ b2 -4ac>0
复习课
教学目标
1系统的复习二次函数,学生自主 梳理知识并掌握复习方法。
2通过复习二次函数相关知识,加 深学生对二次函数知识的理解,提 高学生运用知识解决实际问题的能 力。
复习二次函数相关知识
确定函数 解析式
定义 二次函数
图像的 平移
图像特征 与系数的
关系
表达形 式
图像和性 质
二次函数定义
形如 y=ax² + bx + c ( a 、 b 、 c 是常数, a ≠ 0 )的函数叫做二次 函数
-1 01
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
确定函数解析式:
1抛物线经过(2,0)(0,-2)(-1,0)三点。求此函数 解析式
2抛物ห้องสมุดไป่ตู้的顶点坐标是(6,-2),且与 X轴的一个交点的横 坐标是8。求函数解析式
•
(交点式)
抛物线
二次函数的图像及性质
开口方向 顶点坐标
对称轴 增减性
最值
y = ax2
y = ax2 + k y = a(x – h )2 y = a( x – h )2 + k y=ax²+ bx + c
y=a(x-x1)(x-x2)
a>0 开口向上
a,<0 开口向下
(0,0)
y轴
(0,k)
y轴
A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
y=-x²-2x+3
(2)在(1)中抛物线
的对称轴上是否存在点
Q,使得△QAC的周长
(-3,0)
最小?若存在,求出Q
点的坐标;若不存在,
请说明理由.
2
左加右减 上加下减
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 年 级 级 上上 册册 数 数 学学 课课 件 件第第二二 十 十 二二 章章二 二 次 次函 函数数复复习习课课( 共18张 PPT)
综合题:如图①, 已知抛物线 y=ax²+bx+3
3. 抛物线 y 1 ( x 3 ) 2 2 对称轴是______, 顶 点坐标是_____2_ 4. 二次函数y=x2-x-6的图象顶点坐标________ 对称轴是____当x ___时y随x的增大而减少, 当x____时y随x的增大而增大.当x=____时 y有最____值,它是____
二次函数y=ax² + bx + c图像与系数a b c的关系
•1. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号: •①a 0; •②c 0; •③b2 - 4ac 0; •④ b 0; •小结:a 决定开口方向,c决定与y轴交点位置,b2 - 4ac决 定与x轴交点个数,a,b结合决定对称轴;
2、二次函数 y(x1)22图象的顶点坐
标和对称轴方程为( ) A、(1,-2), x=1 B、(1,2),x=1 C、(-1,-2),x=-1 D、(-1,2),x=-1
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 年 级 级 上上 册册 数 数 学学 课课 件 件第第二二 十 十 二二 章章二 二 次 次函 函数数复复习习课课( 共18张 PPT)
人 教 版 九 年 级上册 数学课 件 第 二 十二章 二 次 函数 复 习 课( 共18张 PPT)
.如图①, 已知抛物线y=ax²+bx+3 (a≠0)与 x轴交于点
(a≠0)与 x轴交于点A(1,0)和点B (-3,0),与 y轴交于点C.
(1) 求抛物线的解析式; (2)在(1)中抛物线的对称轴上是否存在点Q,使得 △QAC的周长最小?若存在,求出Q点的坐标;若不存在, 请说明理由. (3) 设抛物线的对称轴与 x轴交于点M, 问在对称轴上是否 存在点P,使△CMP为等腰三角形?若存在,请直接写出 所有符合条件的点P的坐标;若不存在,请说明理由. (4) 如图②,若点E为第二象限抛物线上一动点,连接BE、 CE,求四边形BOCE面积的最大值,并求此时E点的坐 标.
3图象经过(0,0), (12,0) ,且最高点 是3 。
的纵坐标
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
将 y 1 x 2 向左平移3个单位,再向下平移2个单位 后,所得2 的抛物线的关系式是 y 1 ( x 3 ) 2 2
定义要点:①a ≠ 0 ②最高次数为 2
③代数式一定是整式
二次函数y=ax² + bx + c几种不同的表达形 式
• y = ax2
• y = ax2 + k
• y = a(x – h )2
• y = a( x – h )2 + k (顶点式)
• y=ax²+ bx + c (一般式)
• y=a(x-x1)(x-x2)
(h,0)
X=h
(h,k)
X=h
(-b/2a,4ac-b²/4a) x=-b/2a
当a>0时 在对称轴左
边y随x增大 而减少,在
对称轴右边y 随x增大而增 大
当a<0时, 在对称轴左
边y随x增大 而增大,在
对称轴右边y 随x增大而减 少。
0 k 0 k 4ac-b²/4a
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
做一做:
1、抛物D线 y4x2 3的对称轴及顶点坐标分
别是( ) A、y轴,(0,-4) B、x=3,(0,4) C、x轴,(0,0) D、y轴, (0,3)
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
讨论:二次函数y=ax²+bx+c的图象如下所示,则
在下列各不等式中成立的个数
①abc<0 ②a+b+c < 0 ③a+c > b ④2a+b=0 ⑤ b2 -4ac>0
复习课
教学目标
1系统的复习二次函数,学生自主 梳理知识并掌握复习方法。
2通过复习二次函数相关知识,加 深学生对二次函数知识的理解,提 高学生运用知识解决实际问题的能 力。
复习二次函数相关知识
确定函数 解析式
定义 二次函数
图像的 平移
图像特征 与系数的
关系
表达形 式
图像和性 质
二次函数定义
形如 y=ax² + bx + c ( a 、 b 、 c 是常数, a ≠ 0 )的函数叫做二次 函数
-1 01
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
确定函数解析式:
1抛物线经过(2,0)(0,-2)(-1,0)三点。求此函数 解析式
2抛物ห้องสมุดไป่ตู้的顶点坐标是(6,-2),且与 X轴的一个交点的横 坐标是8。求函数解析式
•
(交点式)
抛物线
二次函数的图像及性质
开口方向 顶点坐标
对称轴 增减性
最值
y = ax2
y = ax2 + k y = a(x – h )2 y = a( x – h )2 + k y=ax²+ bx + c
y=a(x-x1)(x-x2)
a>0 开口向上
a,<0 开口向下
(0,0)
y轴
(0,k)
y轴
A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
y=-x²-2x+3
(2)在(1)中抛物线
的对称轴上是否存在点
Q,使得△QAC的周长
(-3,0)
最小?若存在,求出Q
点的坐标;若不存在,
请说明理由.
2
左加右减 上加下减
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 年 级 级 上上 册册 数 数 学学 课课 件 件第第二二 十 十 二二 章章二 二 次 次函 函数数复复习习课课( 共18张 PPT)
综合题:如图①, 已知抛物线 y=ax²+bx+3
3. 抛物线 y 1 ( x 3 ) 2 2 对称轴是______, 顶 点坐标是_____2_ 4. 二次函数y=x2-x-6的图象顶点坐标________ 对称轴是____当x ___时y随x的增大而减少, 当x____时y随x的增大而增大.当x=____时 y有最____值,它是____
二次函数y=ax² + bx + c图像与系数a b c的关系
•1. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号: •①a 0; •②c 0; •③b2 - 4ac 0; •④ b 0; •小结:a 决定开口方向,c决定与y轴交点位置,b2 - 4ac决 定与x轴交点个数,a,b结合决定对称轴;
2、二次函数 y(x1)22图象的顶点坐
标和对称轴方程为( ) A、(1,-2), x=1 B、(1,2),x=1 C、(-1,-2),x=-1 D、(-1,2),x=-1
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 年 级 级 上上 册册 数 数 学学 课课 件 件第第二二 十 十 二二 章章二 二 次 次函 函数数复复习习课课( 共18张 PPT)
人 教 版 九 年 级上册 数学课 件 第 二 十二章 二 次 函数 复 习 课( 共18张 PPT)
.如图①, 已知抛物线y=ax²+bx+3 (a≠0)与 x轴交于点
(a≠0)与 x轴交于点A(1,0)和点B (-3,0),与 y轴交于点C.
(1) 求抛物线的解析式; (2)在(1)中抛物线的对称轴上是否存在点Q,使得 △QAC的周长最小?若存在,求出Q点的坐标;若不存在, 请说明理由. (3) 设抛物线的对称轴与 x轴交于点M, 问在对称轴上是否 存在点P,使△CMP为等腰三角形?若存在,请直接写出 所有符合条件的点P的坐标;若不存在,请说明理由. (4) 如图②,若点E为第二象限抛物线上一动点,连接BE、 CE,求四边形BOCE面积的最大值,并求此时E点的坐 标.
3图象经过(0,0), (12,0) ,且最高点 是3 。
的纵坐标
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
将 y 1 x 2 向左平移3个单位,再向下平移2个单位 后,所得2 的抛物线的关系式是 y 1 ( x 3 ) 2 2
定义要点:①a ≠ 0 ②最高次数为 2
③代数式一定是整式
二次函数y=ax² + bx + c几种不同的表达形 式
• y = ax2
• y = ax2 + k
• y = a(x – h )2
• y = a( x – h )2 + k (顶点式)
• y=ax²+ bx + c (一般式)
• y=a(x-x1)(x-x2)
(h,0)
X=h
(h,k)
X=h
(-b/2a,4ac-b²/4a) x=-b/2a
当a>0时 在对称轴左
边y随x增大 而减少,在
对称轴右边y 随x增大而增 大
当a<0时, 在对称轴左
边y随x增大 而增大,在
对称轴右边y 随x增大而减 少。
0 k 0 k 4ac-b²/4a
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
人 教 版 九 级 上册数 学课件 第 二十 二章 二 次 函 数 复 习 课
做一做:
1、抛物D线 y4x2 3的对称轴及顶点坐标分
别是( ) A、y轴,(0,-4) B、x=3,(0,4) C、x轴,(0,0) D、y轴, (0,3)
