扩展有限元简介

扩展有限元法(XFEM)及其应用12

• 1999年，以美国西北大学Belytschko教授为代表的研究组首先提出了XFEM的思想[21]，2000年，他们正式提出了XFEM术语[22]。XFEM是迄今为止求解不连续力学问题的最有效的数值方法，它在标准有限元框架内研究问题，不需要对结构内存在的几何或物理界面进行剖分，保留了CFEM 的所有优点。XFEM与CFEM的最根本区别在于所使用的网格与结构内部的几何或物理界面无关，从而克服了在诸如裂纹尖端等高应力和变形集中区进行高密度网格剖分所带来的困难，当模拟裂纹扩展时也无需对网格进行重新剖分。XFEM在处理裂纹问题包括以下三个方面[23]：
• 2. 单位分解法（PUM） • 2.1 单位分解法的基本概念 • 1996年Melenk和Babuska[24]及Duarte和 Oden[25]先后提出了单位分解法（PUM），其基本思想是任意函数ψ(x)都可以用域内一组局部函数NI(x)ψ(x)表示，即 • ，, （1） • 其中，NI(x)为有限单元形状函数, 它形成一个单位分解。 N ( x) 1 • , (2） • 基于此，可以对有限元形状函数根据需要进行改进。
• 数值方法，如有限元、边界元、无单元法等，特别是有限元法（FEM）已被广泛用于处理不连续问题。有限元法具有其它数值方法无可比拟的优点，如适用于任意几何形状和边界条件、材料和几何非线性问题、各向异性问题、容易编程等，是数值分析裂纹问题的主要手段。这方面的工作很多，无法一一列举。Oritz等[1]及Belytschko等[2]通过使用多场变分原理，用可以横贯有限单元的“弱”（应变）间断模拟剪切带。Dvorkin等[3]通过修改虚功原理表达式考虑了“强”（位移）间断问题；Lotfi和Sheng[4]将HuWashizu变分原理推广至具有内部间断的物体中；通过考虑软化本构律和界面上的面力－位移关系，Simo及其同事[5，6]提出了分析强间断问题的统一框架，很多研究者 [7-12]将该法应用到变形局部化分析中。Borja[13]提出了分析强间断问题的标准Galerkin公式，并证明它与假定改进应变逼近等价。

扩展有限元法及其在结构开裂研究中的应用

* 国家自然科学基金项目（ 11372113 ）。 1975 年出生，第一作者：杨怡，男，副教授。电子信箱： yiyang@ scut． edu． cn 收稿日期： 2016 － 04 － 30
工业建筑 2016 年第 46 卷增刊 251
网格重划，这样会带来大量的网格划分工作，以及新旧网格之间状态变量的映射等问题。随着断裂力学的发展，为了解决网格依赖性等问题，学者们提出了不少的新方法，其中被认为最具应用前景的是 Belytschko 等基于单位分解法思想提［7 － 9 ］。它是以传统的有出的扩展有限元法（ XFEM ）在非裂缝区域采用标准的有限元法，限元法为基础，在不连续的裂缝区对位移函数进行修改，位移插值函数在裂纹面引入阶跃函数和在裂纹尖端引入渐进位移场附加函数，克服了弥散裂纹模型和分离裂纹模型的网格依赖问题，能够很好地模拟宏观裂纹的萌生和扩展。扩展有限元法的快速发展和广泛应用与其本身［10 ］的优越性密不可分，可以概括为以下几点： 1 ）克裂纹扩展时不需要考虑网格重新服了网格依赖性，剖分，允许裂纹贯穿单元，并与连续剖分的有限元相在剖分的不同单元之间不需要太多的映射； 2 ）比，引入两类特定的增强函数来构造非线性，对裂纹面满足和裂纹尖端附近的单元节点增加附加自由度，适当性质的形函数来捕捉裂纹尖端的奇异场，网格尺寸很大同样能获得较精确的解； 3 ）它适用于各种性质的材料和多介质问题以及空隙夹杂等，同样适应于几何非线性和接触非线性； 4 ）可以在有限元框目前在大型商业软件如 ABAQUS、架内并行计算， ANSYS、 LSDYNA 等中已经嵌入了 XFEM 分析模块，而边界元法和无网格法没有成熟的软件包，相比较而言扩展有限元法具有更大的优势。 1 扩展有限元法的基本思想扩展有限元法是基于单位分解法思想发展而成，在传统有限元框架下引入能反应位移间断性的［11 ］增强项，并使用水平集法（ LSM ）或快速推进法（ FMM）［12］描述几何间断性。对于混凝土材料，计算时通常还要加入相应的裂缝模型。 1. 1 单位分解法单位分解法

裂纹扩展的扩展有限元(xfem)模拟实例详解

基于ABAQUS 扩展有限元的裂纹模拟化工过程机械622080706010 李建1 引言1.1 ABAQUS 断裂力学问题模拟方法在abaqus中求解断裂问题有两种方法（途径）：一种是基于经典断裂力学的模型；一种是基于损伤力学的模型。

断裂力学模型就是基于线弹性断裂力学及其基础上发展的弹塑性断裂力学等。

如果不考虑裂纹的扩展，abaqus可采用seam型裂纹来分析(也可以不建seam，如notch型裂纹)，这就是基于断裂力学的方法。

这种方法可以计算裂纹的应力强度因子，J积分及T-应力等。

损伤力学模型是指基于损伤力学发展而来的方法，单元在达到失效的条件后，刚度不断折减，并可能达到完全失效，最后形成断裂带。

这两个模型是为解决不同的问题而提出来的，当然他们所处理的问题也有交叉的地方。

1.2 ABAQUS 裂纹扩展数值模拟方法考虑模拟裂纹扩展，目前abaqus有两种技术：一种是基于debond的技术（包括VCCT）；一种是基于cohesive技术。

debond即节点松绑，或者称为节点释放，当满足一定得释放条件后（COD 等，目前abaqus提供了5种断裂准则），节点释放即裂纹扩展，采用这种方法时也可以计算出围线积分。

cohesive有人把它译为粘聚区模型，或带屈曲模型，多用于模拟film、裂纹扩展及复合材料层间开裂等。

cohesive模型属于损伤力学模型，最先由Barenblatt 引入，使用拉伸-张开法则（traction-separation law）来模拟原子晶格的减聚力。

这样就避免了裂纹尖端的奇异性。

Cohesive 模型与有限元方法结合首先被用于混凝土计算和模拟，后来也被引入金属及复合材料。

Cohesive界面单元要服从cohesive 分离法则，法则范围可包括粘塑性、粘弹性、破裂、纤维断裂、动力学失效及循环载荷失效等行为。

此外，从abaqus6.9版本开始还引入了扩展有限元法（XFEM），它既可以模拟静态裂纹，计算应力强度因子和J积分等参量，也可以模拟裂纹的开裂过程。

扩展有限元的基本知识1

i 1
i
n { (x)} 覆盖 i 的单位分解函数。 i 1
设函数 Vi (x) 为函数u (x) 在子域i 内的近似函数，则函数u (x) 在求解域的全局近似可取为
u (x) i (x) Vi (x)
i 1 n
i 中逼近u (x) 在单位分解法中，任何能够在子域的函数都可以作为局部近似函数。
扩展有限元的基本知识
制作时间：2014.12.12
有限元在处理间断问Байду номын сангаас的缺陷
有限元采用的是连续性的位移近似函数，对于裂纹类强间断问题，为获得足够的计算精度，需要对网格进行足够的细分，计算量极大。采用拉格朗日法求解裂纹动态扩展、流固耦合、局部剪切等特大变形问题时，有限元网格可能会发生严重扭曲，使计算精度急剧下降甚至计算无法继续，因此，需要不断的进行网格重构、计算量极大，同时，也为了模拟裂纹的动态扩展过程，也需要不断的进行网格重构。
扩展有限元的提出
1999年，美国西北大belytschko 研究组提出的扩展有限元。借助于对研究问题的已有认识，在满足单位分解的前提下，在位移近似函数中增加更能反映实际间断特征的函数项（称为富集函数）提高了计算精度。采用水平集法（LSM）或快速推进法（FMM）描述间断界面，使间断的描述独立于有限元网格，避免了计算过程中的重构。
扩展有限元的概念
扩展有限元（XFEM）：是在标准有限元方法的框架下，提出来的一种用于解决裂纹、孔洞、夹杂等间断问题的数值方法。在有限元的近似函数中，增加能反映待求问题特性的附加函数项，采用水平集法（LSM）描述间断面的几何特征及其移动规律。
扩展有限元的优点
• 计算精度高 • 勿需网格重构

扩展有限元方法和裂纹扩展

扩展有限元方法和裂纹扩展1.1 扩展有限元方法（XFEM ）基本理论1999年，美国Northwestern University 的Belytschko 和Black 领导的研究小组提出了扩展有限元方法，为解决裂纹这类强不连续问题带来了曙光。

他们正式应用扩展有限元法（XFEM ）这一专业术语是在2000年，截止到目前，扩展有限元法（XFEM ）成为我们解决强不连续力学问题的最有效的数值计算方法，也成为计算断裂力学的重要分支。

XFEM 在有限元的框架下进行求解，无需对构件内部的物理界面进行网格划分，具有常规有限元方法的所有优点。

它最明显的特点是用已知的特征函数作为形函数来使传统有限元的位移得到逼近，进而克服了在裂纹尖端和变形集中处进行高密度网络划分产生的困难，方便地模拟裂纹的任意路径，而且计算精度和效率得到了显著的提高[6]。

扩展有限元方法是将已知解析解的特征函数作为插值函数增强传统有限元的位移逼近，来使得单元内的真实位移特性得以体现，裂纹尖端和物理或几何界面独立于有限元网格。

XFEM 主要包括以下三部分内容：首先是不考虑构件的任何内部细节，按照构件的几何外形尺寸生成有限元网格；其次，采用水平集方法跟踪裂纹的实际位置；根据已知解，改进影响区域的单元的形函数，来反映裂纹的扩展。

最后通过引入不连续位移模式来表示不连续几何界面的演化。

因为改进的插值函数在单元内部具有单元分解的特性，其刚度矩阵的特点与常规有限元法的刚度矩阵特性保持一致。

单元分解法(Partition Of Unity Method)和水平集法（Level Set Method ）、节点扩展函数构成了扩展有限元法的基本理论，其中，单元分解法是通过引入加强函数计算平面裂纹扩展问题，保证了XFEM 的收敛性；水平集法是跟踪裂纹的位置和模拟裂纹扩展的常用数值方法，任何内部几何界面位置都可用它的零水平集函数来表示。

(1)单元分解法的基本思想是任意函数()x φ都可以用子域内一组局部函数()()x x N I ϕ表示，满足如下等式：()()()x x N x II ϕφ∑= （1）其中，它们满足单位分解条件：f I Iåx ()=1 ()x N I 是有限元法中的形函数，根据上述理论，便可以根据需要对有限元的形函数进行改进。

扩展有限元的基本原理

1 引言
有限元法是科学研究和工程分析中使用最多的一种数值分析方法，其数学理论基础和误差估计理论都十分成熟。然而，有限元采用连续函数作为形函数，对于处理像裂纹这样的不连续问题时，需要将裂纹面设置为单元的边、裂尖设置为单元的结点、在裂尖附近不连续体的奇异场内进行高密度网格划分以及在模拟裂纹扩展时需要不断的进行网格的重新划分，使得有限元程序计算相当复杂，且效率极低[1]。边界元法研究裂纹扩展方面有较成熟的应用，但它不便于处理非线性、多介质等复杂问题。无单元法将整个求解域离散为独立的结点，无需将结点连成单元，因而在裂纹扩展数值模拟中得到了广泛的应用[2,3]。但是现有的各种无单元法存在缺少坚实的理论基础和严格的数学证明；计算时间长、效率低；存在一些未确定的参数，如插值域的大小，背景积分域的大小等；解决复杂的工程和科学问题的研究不够；没有成熟的商业软件包，限制了其实际应用和推广等不足。 1999 年，以美国西北大学 Belytschko 教授为代表的研究组首先提出用扩展有限元（XFEM）来解决不连续问题[4]。XFEM 是基于单位分解的方法（PUM）对单元的形函数加以改进，从而考虑所研究问题的不连续、奇异性和边界层等特性。XFEM 所使用的网格与结构内部几何或物理界面无关，从而克服了裂纹尖端等高应力和变形集中区网格划分的困难，使得模拟裂纹生长也无需对网格进行重新划分。自 XFEM 问世以来，在国际上得到了很快的发展和广泛的应用。在最初的 XFEM 中，位移模式中加进的是裂尖渐进位移场函数的主要项，且围绕裂尖加强结点的相应系数是相互独立的，这样加强位移场并不是真实的裂尖附近的渐进位移场，因此，局部位移场的精度仍不能令人满意，应力强度因子必须经过后处理才能求出。文[5][6]提出了一种改进的 XFEM，提高了局部位移场的精度，且不需要经过后处理就可以直接求出应力强度因子，从而为分析裂纹扩展提供了方便。文中首先简要介绍了改进扩展有限元的基本原理，然后详细分析了采用该方法分析不连续力学问题需要注意的问题，包括：积分方案、裂纹闭合时的接触问题和裂纹扩展的分析。

重力坝开裂过程扩展有限元数值模拟

重力坝开裂过程扩展有限元数值模拟靳旭;董羽蕙【摘要】扩展有限元法(XFEM)是一种求解不连续问题的数值方法.它继承了常规有限元法(CFEM)的所有优点,在模拟裂纹扩展、界面、复杂流体等不连续问题时特别有效,近十多年得到了快速发展.介绍了XFEM的基本原理,给出了进行混凝土裂纹扩展分析的方法.利用XFEM模拟混凝土重力坝裂纹扩展,通过对比有、无裂纹情况下的重力坝应力分布,分析裂纹存在对重力坝应力场分布的影响；分析裂纹扩展受网格疏密程度的影响；计算在不同岩基弹性模量下裂纹的扩展方向.%Extended finite element method(XFEM)is a numerical solution for analyzing discontimuity problem . It inherited all the advantages of the conventional finite element method (CFEM) , in the simulation of crack extension , interface, complex fluid and other discontinuities are particularly effective , in the past decade it has been rapid development. The basic theory of XFEM in introduced and the method of analyzing concrete fracture is presented. The XFEM is utilized to simulate the crack propagation in concrete gravity dam. By the contrast of stress distribution under no crack and crack circumstance of gravity dam the discipline of stress field distribution is analyzed; It is also used for influence of mesh density to crack propagation and is calculated the crack propagation direction in batholith elastic modulus.【期刊名称】《科学技术与工程》【年(卷),期】2012(012)033【总页数】6页(P9100-9104,9109)【关键词】重力坝;扩展有限元法;裂纹扩展;网格疏密;弹性模量【作者】靳旭;董羽蕙【作者单位】昆明理工大学建筑工程学院,昆明650500;昆明理工大学建筑工程学院,昆明650500【正文语种】中文【中图分类】TV313;TV642.3实际工程中，无论采用多么严格的裂缝控制措施，混凝土结构仍然会带裂缝工作。

扩展有限元法的研究

学位论文作者签名：谢海
日期： 2009 年 1 月 14 日
上海交通大学学位论文版权使用授权书
本学位论文作者完全了解学校有关保留、使用学位论文的规定，同意学校保留并向国家有关部门或机构送交论文的复印件和电子版，允许论文被查阅和借阅。本人授权上海交通大学可以将本学位论文的全部或部分内容编入有关数据库进行检索，可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
上海交通大学硕士学位论文扩展有限元法的研究姓名：谢海申请学位级别：硕士专业：固体力学指导教师：冯淼林 20090101
上海交通大学硕士学位论文
扩展有限元法的研究摘要
扩展有限元法(the extended finite element method, XFEM)是解决以裂纹问题为代表的不连续力学问题的有效方法，由于其在保留常规有限元(CFEM)所有优点的基础上，解决了常规有限元需在应力集中区高密度划分单元的所带来的困难，模拟裂纹生长时也无需网格重划分，而得到了快速的发展。本文介绍了扩展有限元的基本理论，并通过编写 ABAQUS 用户子程序 UEL ，在商业软件 ABAQUS 平台的基础上实现了线弹性扩展有限元功能。本文先介绍了有关单位分解法，水平集法的理论，然后论述了基于这两个方法的扩展有限元法；接着对 ABAQUS 用户子程序 UEL 进行简单的介绍，并阐述如果应用 UEL 在 ABAQUS 平台上实现 XFEM。最后，通过三个算例的比较可以看出 XFEM 能在较粗糙的网格前提下，实现了较高的精度和准确度。
保密□，在本学位论文属于不保密□。√ （请在以上方框内打“√” ）
年解密后适用本授权书。
学位论文作者签名：谢海
指导教师签名：冯淼林

ANSYS16.0新增扩展有限元XFEM裂纹扩展仿真简介

ANSYS16.0新增扩展有限元XFEM裂纹扩展仿真简介中国矿业大学, 师访, matmes@1 引言早在两年前，就听安世亚太的人说ANSYS15.0将加入XFEM，但结果令人失望。

左盼右盼，终于在ANSYS16.0中等来了扩展有限元（Extended Finite ElementMethod）XFEM 功能。

首先，对于不知道XFEM为何物的朋友们，建议看下这篇文献：断裂问题的扩展有限元法研究_茹忠亮_岩土力学_2011.pdf(834.69 KB, 下载次数: 0)欢迎联系我讨论关于XFEM断裂模拟的相关问题，QQ：15492217582 ANSYS16.0 XFEM简介ANSYS16.0发布时候关于结构分析的简介中并未提及XFEM，由此可见ANSYS中的XFEM功能也不会太让人满意，看了其帮助文档（ANSYS Mechanical APDL Fracture Analysis Guide.pdf(2.52 MB, 下载次数: 0)，3.2节）后发现，事实确实如此。

（1）基于虚拟节点法，与Abaqus一致。

（2）仅支持线弹性材料。

（3）不支持裂尖增强，同样与Abaqus一致，这就导致裂纹尖端不能落在单元内部，只能位于单元边界上。

（4）必须事先给定初始裂纹，即不支持裂纹的自动萌生。

鸡肋的是，初始裂纹的定义居然要通过给定水平集值的方法来实现：XFDATA,LSM,ELEMNUM,NODENUM,PHI（5）支持粘聚裂纹。

（6）支持PLANE182（4节点四边形单元，用于2D平面问题分析）及SOLID185（8节点正方形单元，用于3D问题分析）这两种单元。

（7）仅支持准静态分析，不支持动态断裂。

（8）裂纹每次只能扩展一个单元长度。

（9）仅支持两个裂纹扩展准则：STTMAX，最大周向应力准则（Maximum circumferential stress criterion）；PSMAX（Circumferential stress criterion）。

扩展有限元

an
ao
③Reeder law 2002年由Reeder提出，是对BK law的继承和发展：
G II G III G III G II G III G equivC G IC G IIC G IC G G IIIC IIC G G G II III I G II G III G I G II G III
Yes
No
Yes Yes Yes Yes
No Yes No No
VCCT基本假设是：裂纹扩展所释放的应变能等于让裂纹重新闭合所需要的能量。因此，采用的断裂判据如下：
f
G equiv G equivC
1.0
Gequiv为等效应变能释放率； GequivC为临界应变能释放率。
ห้องสมุดไป่ตู้
计算等效应变能释放率有三种方法： ①BK law 1996，Benzeggagh提出三种模式下等效应变能释放率可以表示为：
当上述断裂判据一旦满足，裂纹扩展，扩展方向可以选择为：①最大切应力方向（默认）②垂直于单元局部坐标系的1方向③平行于单元局部坐标系的1方向。
cracks based on the principles of linear elastic fracture mechanics (LEFM) and phantom nodes ）
基于线弹性断裂力学准则和虚拟节点的移动裂纹建模模拟断裂问题的断裂判据如下图，基于线弹性断裂力学准则和虚拟节点的移动裂纹建模可以采用虚拟裂纹闭合法（以下简称VCCT）
大型通用有限元分析软件Abaqus 中扩展有限元的实现原理
——李东
建模方法
“粘性片段方法及虚拟节点方法”以及“线弹性断裂力学准则和虚拟节点方法”是abaqus中扩展有限元对扩展裂纹的两种建模方法。这两种方法看似不同，实则相似。两种方法共同采用虚拟节点法，裂纹通过的单元都具有虚节点，当断裂判据满足时，虚节点断开，如下图所示。两种方法所不同的是他们的断裂判据不一样。方法一由粘性分离定律确定，而方法二为线弹性断裂力学准则。由于玻璃属于较为满意的线弹性材料，所以，我以下将采用方法二：基于线弹性断裂力学准则和虚拟节点的移动裂纹建模（Modeling moving

��
• 由于�� , ��, �� 的水平集�� , ��, �� 就是曲线�� , �� ，因此根据水平集定义，即（4），有�� , �� , �� =0，微分该式可得
= �� , �� , ��
（3）
• 方程3实质是材料界面演化变形的Lagrange描述，可采用格子类方法来求解，但在实际计算时常遇到精度低，甚至数值不稳定的困难，特别是当界面产生奇异和拓扑变化的时候,其数值处理更加困难。为了克服这些问题,这里将采用隐式形式描述材料界面,将方程3从Lagrange描述等价地转化为Euler描述,并导出标准的水平集方程。
2.2 水平集法（LSM）
• 水平集法是一种跟踪界面移动的数值技术，这种方法将界面的变化表示成比界面高一维的水平集曲线。 • 1988年Osher和Sethian提出水平集方法，并构造了水平集方程的高精度稳定数值解法。这种方法吧所跟踪界面表示为高维函数水平集，能方便地推广到任意维数空间，易于编程。这一方法的理论基础是Crandall和Lions建立的 Hamilton-Jacobi方程的粘性解理论。 • 例如，��2 中移动界面�� ⊂ ��2 可以表示成 �� = �� ∈ ��2 : �� , �� = 0 其中�� , �� 称为水平集函数。
有限元建模加边界条件有限元计算 �� 、 ��

基于扩展有限元(XFEM)裂缝扩展总结

基于扩展有限元（XFEM ）裂纹扩展总结通过四个算例总结了用ABAQUS 计算裂纹扩展应用情况。

算例1基于XFEM 使用虚拟裂缝闭合技术结合Cohesive 单元，实现混凝土基体断裂和钢筋混凝土界面脱层的混合失效模式；算例2基于XFEM 以VCCT 准则判断裂缝的开裂扩展，研究了偏荷载作用下不同配筋率对裂缝扩展方向的影响，并对比了考虑钢筋与混凝土粘结滑移与不考虑粘结滑移的裂缝扩展情况；算例3则是以粘聚力模型判断裂缝扩展,研究了裂缝扩展情况；算例4对比了Cohesive 和VCCT 两种开裂准则下钢筋混凝土（纵、箍筋组合）的裂缝扩展情况。

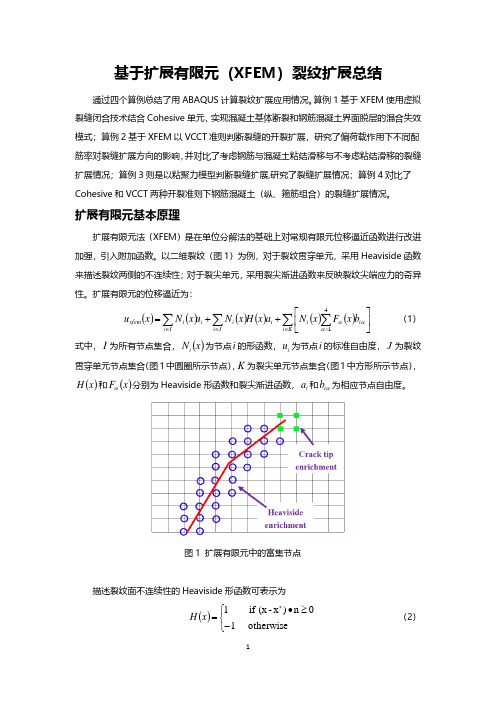
扩展有限元基本原理扩展有限元法（XFEM ）是在单位分解法的基础上对常规有限元位移逼近函数进行改进加强，引入附加函数。

以二维裂纹（图1）为例，对于裂纹贯穿单元，采用Heaviside 函数来描述裂纹两侧的不连续性；对于裂尖单元，采用裂尖渐进函数来反映裂纹尖端应力的奇异性。

扩展有限元的位移逼近为：()()()()()()∑∑∑∑∈=∈∈⎥⎦⎤⎢⎣⎡++=K i i i i J i i i I i i xfem b x F x N a x H x N u x N x u 41ααα （1）式中，I 为所有节点集合，()x N i 为节点i 的形函数，i u 为节点i 的标准自由度，J 为裂纹贯穿单元节点集合（图1中圆圈所示节点），K 为裂尖单元节点集合（图1中方形所示节点），()x H 和()x F α分别为Heaviside 形函数和裂尖渐进函数，i a 和αi b 为相应节点自由度。

图1 扩展有限元中的富集节点描述裂纹面不连续性的Heaviside 形函数可表示为 ()⎩⎨⎧−≥•=*otherwise 10n )x -(x if 1x H （2）式中，*x 为点x 到裂纹面最近处的投影，n 为*x 点处的单位外法线向量（如图2所示）。

可以看出，节点位于裂纹面上侧时()1=x H ，节点位于裂纹面下侧时()1−=x H ，Heaviside 形函数能较好的描述裂纹面两侧的不连续性。

扩展有限元法(XFEM)漫谈-我的XFEM学习经验分享

B
A
C
图 5. 折线裂纹示意图以图 5 中折线裂纹 AB 和 BC 为例说明通过映射法修改裂尖增强函数的过程。（1-2）式裂尖增强函数仅适用于图 5 虚线（线段 AB 在 B 点的垂线）右侧的高斯积分点，虚线左侧的增强函数需要进行修正。如图 6(a)所示，高斯点的坐标为(x, y)，α 为 BA 和 B 之间的夹角，θR 为 BA 和 BC 之间的夹角。定义夹角：
2.4 对于裂缝面承受载荷的裂缝，这些载荷是作用于增强自由度上的对于水力压裂分析（裂缝面承受水压）、爆破分析（裂缝面承受高压气体作用）、裂缝面接触滑动（法向和切向接触力作用于裂缝面）、粘聚裂纹模型（粘聚内力作用于裂尖附近的裂缝面上）等裂缝表面承受载荷的分析，注意：这些载荷是作用于增强自由度上的，而不是 FEM 自由度。这一点对于初学者来说或许是个易犯的错误。
3 / 14
A+
裂纹
A+
裂纹
i
i
A－
A－
(a)增强节点 i
(b)不增强节点 i
图 4. Heaviside 增强节点的选择
2.2 含折点的某些情况下必须要特殊处理（1-2）式中的裂尖增强函数仅适用于直线裂纹，对于带折点的裂纹，需要做特殊处理，否则将会因为裂纹面两侧 Heaviside 增强和裂尖增强的相互矛盾而导致计算出错。例如，图 2-4 为一折线裂纹，其中用“○”标记的是 Heaviside 增强节点，用“□”标记的是裂尖增强节点，对于阴影区域内的高斯积分点而言，位于裂纹片段 BC 的上侧，Heaviside 增强函数值为 1，但这些高斯点却位于裂纹片段 AB 延长线的下侧，二者是矛盾的。 Belytschko[4]采用映射法，给出了这一问题的解决办法。