裂纹扩展的扩展有限元(xfem)模拟实例详解
ABAQUS平台的扩展有限元方法模拟裂纹实现

ABAQUS平台的扩展有限元方法模拟裂纹实现1.1 扩展有限元方法(XFEM)在ABAQUS上的实现ABAQUS中XFEM的实现,两个步骤最为关键:1、选择模型中可能出现的裂纹区域,将其单元设为具有扩展有限元性质的enrichment element.2、其次重要的是选择恰当的破坏准则,使单元在达到给定的条件破坏,裂纹扩展。
在ABAQUS中模拟裂纹扩展的操作中,需要注意的是:1、在Property模块,添加损伤演化参数、破坏法则、损伤稳定性参数2、在Interaction模块,主菜单Special中创建XFEM的enrichment element对于固定的裂纹模型,采用ABAQUS/STANDARD中使用奇异渐进函数。
针对移动的裂纹问题,在XFEM中,有一种方法基于traction-separation cohesive behavior,即使用虚拟节点连续片段法进行移动裂纹建模,ABAQUS/STANDAR D 中用于计算脆性或韧性材料的裂纹初始化和扩展过程的模拟。
另外一种cohesive segments method (粘性片段方法)可用于bulk material中的任意路径的裂纹初始化模拟扩展过程,由于裂纹扩展不依赖于单元边界,在XFEM中,裂纹每扩展一次需要通过一个完整单元,避免尖端应力奇异性。
除此之外,ABAQUS为拥护提供了自定义子程序,来满足不同建模的需要。
ABAQUS/STANDARD中的任意力学本构模型均可用来模拟扩展裂纹的力学特性。
由于XFEM采用的形函数在求解过程中,很容易造成逼近线性相关,极大的增加了收敛难度,到目前为止,能够实现扩展有限元的商业软件只有ABAQUS,但是ABAQUS为了减少求解难度,做了大量简化,因此用ABAQUS 扩展有限元模拟裂纹扩展时,有一些局限[16]:1.扩展单元内不能同时存在两条裂纹,所以ABAQUS不能模拟分叉裂纹;2.在裂纹扩展分析过程中,每一个增量步的裂纹转角不允许超过90度;3.自适应的网格是不被支持的;4.固定裂纹中,只有各向同性材料的裂纹尖端渐进场才被考虑。
裂纹扩展的扩展有限元(xfem)模拟实例详解

基于ABAQUS 扩展有限元的裂纹模拟化工过程机械622080706010 李建1 引言1.1 ABAQUS 断裂力学问题模拟方法在abaqus中求解断裂问题有两种方法(途径):一种是基于经典断裂力学的模型;一种是基于损伤力学的模型。
断裂力学模型就是基于线弹性断裂力学及其基础上发展的弹塑性断裂力学等。
如果不考虑裂纹的扩展,abaqus可采用seam型裂纹来分析(也可以不建seam,如notch型裂纹),这就是基于断裂力学的方法。
这种方法可以计算裂纹的应力强度因子,J积分及T-应力等。
损伤力学模型是指基于损伤力学发展而来的方法,单元在达到失效的条件后,刚度不断折减,并可能达到完全失效,最后形成断裂带。
这两个模型是为解决不同的问题而提出来的,当然他们所处理的问题也有交叉的地方。
1.2 ABAQUS 裂纹扩展数值模拟方法考虑模拟裂纹扩展,目前abaqus有两种技术:一种是基于debond的技术(包括VCCT);一种是基于cohesive技术。
debond即节点松绑,或者称为节点释放,当满足一定得释放条件后(COD 等,目前abaqus提供了5种断裂准则),节点释放即裂纹扩展,采用这种方法时也可以计算出围线积分。
cohesive有人把它译为粘聚区模型,或带屈曲模型,多用于模拟film、裂纹扩展及复合材料层间开裂等。
cohesive模型属于损伤力学模型,最先由Barenblatt 引入,使用拉伸-张开法则(traction-separation law)来模拟原子晶格的减聚力。
这样就避免了裂纹尖端的奇异性。
Cohesive 模型与有限元方法结合首先被用于混凝土计算和模拟,后来也被引入金属及复合材料。
Cohesive界面单元要服从cohesive 分离法则,法则范围可包括粘塑性、粘弹性、破裂、纤维断裂、动力学失效及循环载荷失效等行为。
此外,从abaqus6.9版本开始还引入了扩展有限元法(XFEM),它既可以模拟静态裂纹,计算应力强度因子和J积分等参量,也可以模拟裂纹的开裂过程。
基于XFEM的膜盘联轴器裂纹扩展模拟

基于XFEM的膜盘联轴器裂纹扩展模拟引言膜盘联轴器是一种常见的传动装置,用于连接两个轴并传递扭矩。
由于受到工作环境的复杂性和工作参数的不确定性,联轴器在使用过程中可能会出现裂纹扩展的情况,严重影响其工作性能和安全性。
研究膜盘联轴器的裂纹扩展行为对于提高其使用寿命和可靠性具有重要意义。
本文将基于XFEM(扩展有限元方法)对膜盘联轴器的裂纹扩展行为进行模拟分析,探讨其裂纹扩展机理和影响因素,为设计和改进膜盘联轴器提供理论基础和参考依据。
1. 膜盘联轴器的结构和工作原理膜盘联轴器是由两个平行的轴、套柱、弹性膜盘、密封环、螺栓等组成的机械传动装置,广泛应用于工程机械、船舶、风力发电等领域。
其工作原理是通过弹性薄膜盘在两轴之间传递扭矩,使两轴实现相对转动,从而实现机械传动功能。
2. XFEM方法简介XFEM是一种用于处理裂纹和裂纹扩展问题的数值方法,相比传统的有限元方法,XFEM 可以更加准确地描述裂纹尖端的应力和位移场。
它通过引入裂纹增强函数和不连续性域的概念,实现裂纹的自适应建模和精确计算。
3. 膜盘联轴器裂纹扩展模拟① 模型建立:利用CAD软件建立膜盘联轴器的三维实体模型,并将其转换为有限元分析模型。
在模型中人为引入裂纹,确定裂纹的初始位置和方向。
② 材料参数:选取与实际膜盘联轴器相似的弹性材料参数,并确定裂纹的材料特性,包括裂纹扩展速率、裂纹尖端的应力强度因子等。
③ 裂纹扩展模拟:利用XFEM方法进行裂纹扩展的数值模拟,根据裂纹尖端附近的应力场和材料特性,计算裂纹的扩展路径和扩展速率。
④ 结果分析:分析裂纹扩展过程中的应力状态、位移场和裂纹尖端的变化规律,探讨裂纹扩展的机理和影响因素。
4. 结果与讨论通过膜盘联轴器的裂纹扩展模拟,可以得到裂纹扩展的路径、速率和受力状态等数据,从而分析裂纹扩展的机理和规律。
裂纹扩展路径:根据模拟结果可以得到裂纹扩展的路径和形态,研究裂纹扩展与联轴器结构的关系,探讨载荷大小和方向对裂纹扩展的影响。
基于XFEM的膜盘联轴器裂纹扩展模拟

基于XFEM的膜盘联轴器裂纹扩展模拟膜盘联轴器是一种常见的轴系传动装置,用于将两个轴连接起来,传递扭矩和运动。
由于在使用过程中会受到扭转和振动的作用,膜盘联轴器可能会发生裂纹,并且会随着使用时间的增长而逐渐扩展,最终导致设备损坏或者故障。
对膜盘联轴器的裂纹扩展行为进行模拟和分析是非常重要的。
基于扩展有限元法(XFEM),可以对膜盘联轴器的裂纹扩展行为进行模拟和分析。
XFEM 是传统有限元法的一种扩展,可以处理裂纹和接触问题。
相比传统有限元法,XFEM可以更好地模拟裂纹的扩展行为,减少计算网格对裂纹位置和形态的敏感性。
在进行膜盘联轴器裂纹扩展模拟之前,首先需要对膜盘联轴器的几何形状进行建模。
可以使用三维CAD软件进行建模,将联轴器的几何形状导入到有限元模型中。
然后,需要定义膜盘材料的力学性质,如弹性模量、泊松比等。
在建立有限元模型之后,可以开始进行裂纹的定义和初始化。
可以使用XFEM的裂纹初始化算法,在合适的位置和方向上设置初始裂纹,并将其添加到有限元模型中。
然后,通过施加适当的加载条件,例如扭矩加载或振动加载,模拟联轴器的工作状态,从而引起裂纹的扩展。
裂纹的扩展行为可以通过分析膜盘联轴器的应力和应变分布来研究。
通过在裂纹的前沿区域使用局部加密网格,可以更准确地描述裂纹扩展的细节。
使用XFEM的裂纹扩展算法,可以在模拟过程中动态地更新裂纹的位置和形态。
通过不断迭代模拟和分析,可以得到膜盘联轴器在不同工况下裂纹扩展的演化过程。
这样可以帮助工程师了解裂纹扩展的机理和趋势,为设计和使用膜盘联轴器提供参考和指导。
基于XFEM的膜盘联轴器裂纹扩展模拟可以帮助工程师更好地了解裂纹扩展的行为和机理,为联轴器的设计和使用提供指导。
需要注意的是,在进行模拟之前,需要准确地建立有限元模型,并选择合适的裂纹初始化算法和裂纹扩展算法,以获得准确的模拟结果。
XFEM实现裂纹扩展

---因为专注,所以卓越!
网格划分
焊缝在管道的上下起始位置,造成几何模型的急剧变化, 导致网格不容易划分,因此,使用专业的的前处理软件 ANSA进行网格划分,使得焊缝的网格密度大于其他位置 的网格密度。
初始裂纹在焊缝中的位置
---因为专注,所以卓越!
分析过程
---因为专注,所以卓越!
I型裂纹扩展过程的动画演示
---因为专注,所以卓越!
II型裂纹扩展过程的动画演示
---因为专注,所以卓越!
ABAQUS采用XFEM模 案例2 块实现压力容器的裂纹 过程的模拟,如果图所 示,压力容器与外部连 接的接口处存在初始微 裂纹,当容器内压力达 到一定程度,裂纹开始 启裂并扩展。 模型的建模与应用针对 工程实例,很好的展现 了XFEM强大的裂纹扩 展功能。
石油管道的裂纹扩展模拟
利用ABAQUS的XFEM方法实现石油管道的裂纹扩展,在 已知起始裂纹尺寸的情况下,根据外部载荷模拟裂纹的起 裂和扩展过程。 由于裂纹的尺寸较整体模型尺寸较小,因此采用用户子模 型的方法对局部进行更加细致的分析。
一、XFEM模块功能简述
ABAQUS V6.9及其以后的版本将拓展有限元方法引入到 其分析中,并增加了新的模块XFEM,该方法可以认为是 有限元方法处理不连续问题的革命性变革。这是第一个将 XFEM商用化的软件。 固体力学中存在两类典型的不连续问题,一类是因材料特 性突变引起的弱不连续问题,这类问题以双材料问题和夹 杂问题为代表,其复杂性由物理界面处的应变不连续性引 起;另一类是因物体内部几何突变引起的强不连续问题, 这类问题以裂纹问题为代表,其复杂性由几何界面处的位 移不连续性和端部的奇异性引起。物体内部物理界面的脱 粘或起裂,是上述两类问题的混合。
基于XFEM的膜盘联轴器裂纹扩展模拟

基于XFEM的膜盘联轴器裂纹扩展模拟引言膜盘联轴器是一种用于传递旋转动力的机械装置,广泛应用于机械传动系统中。
由于长期使用和外部载荷的影响,膜盘联轴器可能会发生裂纹扩展,进而导致设备损坏和安全事故。
对膜盘联轴器裂纹扩展行为进行模拟和研究具有重要意义。
本文将基于XFEM(扩展有限元法)对膜盘联轴器裂纹扩展过程进行模拟分析,以期为相关工程应用提供理论参考和技术支持。
膜盘联轴器裂纹扩展模拟原理XFEM是一种针对裂纹扩展问题的有限元分析方法,相比传统有限元方法,XFEM能够更准确地描述裂纹位置和形态,从而能够模拟更为真实的裂纹扩展过程。
在XFEM中,裂纹被视为一个额外的自由度,其位移场可以通过enriched shape functions来描述。
XFEM能够有效地模拟材料的裂纹扩展行为,对于工程中的裂纹扩展问题具有重要的应用价值。
1. 几何建模:首先进行膜盘联轴器的几何建模,包括模型的尺寸、形状和裂纹位置等信息。
2. 网格划分:将膜盘联轴器模型进行网格划分,生成有限元网格,确保裂纹位置的精确刻画。
3. 材料属性设定:设定膜盘联轴器的材料参数,包括弹性模量、泊松比和断裂韧度等。
4. 载荷和边界条件:给定膜盘联轴器的载荷情况和边界条件,模拟实际工况下的受力情况。
5. 裂纹初始化:在指定位置和方向初始化膜盘联轴器的裂纹,为裂纹扩展模拟做准备。
6. XFEM裂纹模拟:利用XFEM方法对膜盘联轴器裂纹的扩展过程进行模拟,观察裂纹形态和扩展路径。
7. 结果分析:对模拟结果进行分析,评估膜盘联轴器的裂纹扩展行为和结构性能。
以某型号膜盘联轴器为例,进行裂纹扩展模拟分析。
设定膜盘联轴器的材料为A3钢,载荷为周期性加载,裂纹初始化位置为膜盘联轴器轴向的内孔侧面。
通过XFEM方法进行裂纹扩展模拟,并得到裂纹扩展路径和载荷-位移曲线等结果。
模拟结果表明,在周期性加载的作用下,膜盘联轴器的裂纹将呈现出周期性扩展和闭合的行为,裂纹沿着内孔侧面逐渐扩展,并在载荷卸载阶段出现闭合现象。
扩展有限元法仿真混凝土裂纹扩展

扩展有限元法仿真混凝土裂纹扩展下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!扩展有限元法在混凝土裂纹扩展仿真中的应用研究一、引言混凝土结构在长期的荷载作用下,往往会产生裂纹,而裂纹的扩展将直接影响结构的安全性和耐久性。
裂纹扩展的扩展有限元(xfem)模拟实例详解

裂纹扩展的扩展有限元(xfem)模拟实例详解基于ABAQUS 扩展有限元的裂纹模拟化⼯过程机械622080706010 李建1 引⾔1.1 ABAQUS 断裂⼒学问题模拟⽅法在abaqus中求解断裂问题有两种⽅法(途径):⼀种是基于经典断裂⼒学的模型;⼀种是基于损伤⼒学的模型。
断裂⼒学模型就是基于线弹性断裂⼒学及其基础上发展的弹塑性断裂⼒学等。
如果不考虑裂纹的扩展,abaqus可采⽤seam型裂纹来分析(也可以不建seam,如notch型裂纹),这就是基于断裂⼒学的⽅法。
这种⽅法可以计算裂纹的应⼒强度因⼦,J积分及T-应⼒等。
损伤⼒学模型是指基于损伤⼒学发展⽽来的⽅法,单元在达到失效的条件后,刚度不断折减,并可能达到完全失效,最后形成断裂带。
这两个模型是为解决不同的问题⽽提出来的,当然他们所处理的问题也有交叉的地⽅。
1.2 ABAQUS 裂纹扩展数值模拟⽅法考虑模拟裂纹扩展,⽬前abaqus有两种技术:⼀种是基于debond的技术(包括VCCT);⼀种是基于cohesive技术。
debond即节点松绑,或者称为节点释放,当满⾜⼀定得释放条件后(COD 等,⽬前abaqus提供了5种断裂准则),节点释放即裂纹扩展,采⽤这种⽅法时也可以计算出围线积分。
cohesive有⼈把它译为粘聚区模型,或带屈曲模型,多⽤于模拟film、裂纹扩展及复合材料层间开裂等。
cohesive模型属于损伤⼒学模型,最先由Barenblatt 引⼊,使⽤拉伸-张开法则(traction-separation law)来模拟原⼦晶格的减聚⼒。
这样就避免了裂纹尖端的奇异性。
Cohesive 模型与有限元⽅法结合⾸先被⽤于混凝⼟计算和模拟,后来也被引⼊⾦属及复合材料。
Cohesive界⾯单元要服从cohesive 分离法则,法则范围可包括粘塑性、粘弹性、破裂、纤维断裂、动⼒学失效及循环载荷失效等⾏为。
此外,从abaqus6.9版本开始还引⼊了扩展有限元法(XFEM),它既可以模拟静态裂纹,计算应⼒强度因⼦和J积分等参量,也可以模拟裂纹的开裂过程。
扩展有限元法在疲劳裂纹扩展模拟中的应用

2019年18期创新前沿科技创新与应用Technology Innovation and Application扩展有限元法在疲劳裂纹扩展模拟中的应用张芮晨(中国直升机设计研究所,天津300000)前言目前,有限元仿真大量应用于疲劳问题分析计算中。
然而常规有限元法采用连续函数作为形状(插值)函数,在单元内部形状函数和材料性能必须保证连续,进行裂纹分析时,裂纹面需与网格边界重合,网格节点需与间断面的尖端重合[1-2]。
如Abaqus 中针对裂纹扩展分析的两种技术:基于debond 裂纹扩展技术和基于cohesive 裂纹扩展技术。
两种技术均需提前指定裂纹扩展区域与方向,对于网格的划分限制较大,工作量大,效率低。
而在扩展有限元法(Extended Finite Element Method ,XFEM )中,网格与结构内部的几何或物理界面无关,两者间相互独立,裂纹尖端应力场的计算与裂纹面扩展计算相互独立,避免了在裂纹尖端进行高密度网格划分的问题和网格重新划分的工作[3-5]。
本文采用扩展有限元法对疲劳裂纹扩展进行仿真分析,达到无需指定裂纹扩展路径、无需进行高密网格划分也可模拟裂纹扩展的目的,节省建模所需要的时间,大大减少工作量,同时又提高了裂纹扩展模拟的准确度。
1扩展有限元法理论基础1.1单位分解法(PUM )扩展有限元通过在常规有限元位移模式中加进跳跃函数和渐进裂尖位移场函数等一些特殊的函数,来有效地模拟类似裂纹一类的强不连续问题,而它的理论基础既为单位分解法。
在单位分解法中,认为任何函数φ(x)都可以用域内局部函数H Γ(x)φ(x)表示,即其中,H Γ(x)为有限单元形状函数,它形成一个单位分解(2)以此为基础,对有限元形状函数进行改进。
重叠分片{θi }构成研究区域M 的一个覆盖,{φi }为覆盖上的一个单位分解。
在每一分片上,函数空间V i 为区域M 的局部逼近,总体试探空间V 为(3)总体空间V 不但具有局部空间V i 的逼近特性,又有单位分解φi 和局部空间V i 的光滑性,只要单位分解φi 足够光滑,就能构造出足够光滑的试探空间。
基于XFEM的膜盘联轴器裂纹扩展模拟

基于XFEM的膜盘联轴器裂纹扩展模拟膜盘联轴器是一种常见的传动装置,其特点是具有较大的变形能力和轻质化结构。
但是由于使用环境的原因以及其自身的材料缺陷,膜盘联轴器在使用过程中可能会发生裂纹,对其使用寿命和安全性产生威胁。
因此,需要对膜盘联轴器的裂纹扩展进行预测和仿真分析。
传统的有限元方法在对裂纹扩展进行分析时存在一些缺陷,比如需要事先预测裂纹的形状和位置,忽略了裂纹的主动扩展过程等。
针对这些问题,基于扩展有限元方法(XFEM)的技术被广泛应用于裂纹扩展分析。
XFEM技术可以在有限元网格中自适应地加入裂纹扩展的路径,无需定义裂纹的几何形状,从而更加准确地模拟裂纹扩展过程。
此外,XFEM还可以考虑裂纹周围的应力场对裂纹扩展的影响,因此对于三维问题具有显著的优越性。
本文考虑了一种膜盘联轴器的裂纹扩展问题,并基于XFEM技术进行数值仿真研究。
具体来说,我们将环状膜盘联轴器建模为一个三维弹性体,在其内部引入一个初始裂纹,并通过控制载荷和边界条件模拟裂纹的扩展过程。
仿真结果显示,裂纹的扩展路径与实验结果相符合,证明了XFEM在膜盘联轴器的裂纹扩展分析中的有效性。
此外,我们还进一步分析了载荷、材料性质和裂纹形状对裂纹扩展路径的影响。
结果表明,载荷大小对于裂纹扩展路径有很大的影响。
当载荷大于一个临界值时,裂纹的扩展趋势将发生显著改变。
此外,材料的韧性和弹性模量也对裂纹扩展路径有影响,具有更韧性和较小弹性模量的材料会导致裂纹扩展路径更弯曲。
裂纹的初始形状对裂纹扩展路径的影响不如其他因素显著。
综上所述,本文基于XFEM技术,对膜盘联轴器的裂纹扩展进行了数值仿真研究,并探究了不同因素对裂纹扩展路径的影响。
研究结果为膜盘联轴器的设计和使用提供了一定的参考和指导,也为XFEM在裂纹扩展分析中的应用提供了一个具体案例。
应用XFEM模拟研究钻杆裂纹扩展过程

Simulation on crack growth of drill pipe with XFEM
LIN Tie-jun 1 , LIAN Zha ng-hua 1 , ZENG Xiao-jia n 2 , CHENG Yong 3 , LIU Xia o-feng 4
( 1. St at e Key L aborato ry of Oil and Gas Reservo ir Geolog y and Exploit at ion, So ut hw est Pet roleum Universit y, Chengdu 610500, P. R. China; 2. Branch of P et roleum Eng ineering Southw est Com pany, Deyang 618000, P . R. China; 3. Drilling T echno logy Research Inst itut e of Karamay, West ern Drilling Eng ineer ing Company , Karamay 834000, P. R. China; 4. Inst it ut e of Drilling Engineering, Sout hw est Branch, Dey ang 618000, P . R. China) Abstract: Crack gro wt h of drill pipe is a t ypical discont inuous pr oblem . It is diff icult t o simulat e w it h conventional f init e element method and ex tended finite elem ent method ( XFEM ) is developed in recent year s for t he problem. Wit h t he int roduction of XF EM, t he XFEM mo del of 5 inch drill pipe w as proposed w it h diff erent dept h init ial cracks under combined act io n betw een t orque and t ension. Based on t he simulat io n, It is f ound t hat t he sm aller cracks is not easy t o g row , w hilst the crack of dept h more t han 2mm could g row under relatively low er ext ernal load and larg er gr ow th surface, ev ent ually leads to pipe fracture f ailure. T hrough this sim ulat ion o n cr ack g row t h of drill pipe, it is show ed t hat t he XF EM is appropr iat e in analy sis of f ract ure f ailure. Key words: XF EM; crack g row t h; drill pipe; failure; dynam ic simulat ion
基于XFEM的膜盘联轴器裂纹扩展模拟

基于XFEM的膜盘联轴器裂纹扩展模拟膜盘联轴器是一种常见的传动装置,它由若干个相互连接的膜片组成。
在工作过程中,膜盘联轴器通常承受着较大的转矩和转速,在长时间的工作过程中,可能会出现裂纹扩展的问题。
为了对膜盘联轴器的裂纹扩展进行模拟分析,可以采用基于扩展有限元法(XFEM)的方法。
XFEM是一种能够建模材料内部裂纹扩展的有限元方法。
与传统的有限元方法相比,它能够准确地模拟裂纹的扩展行为,为工程师提供更加准确的断裂分析结果。
在膜盘联轴器的裂纹扩展模拟中,首先需要将裂纹引入到模型中。
由于膜盘联轴器是由多个膜片组成的,因此裂纹通常会发生在膜片之间的接头处。
引入裂纹后,需要对裂纹进行离散化,将裂纹划分为许多小的单元,以便进行有限元分析。
在裂纹扩展过程中,裂纹尖端会受到应力场的影响,从而导致裂纹扩展。
为了模拟这个过程,需要在有限元分析中引入裂纹扩展准则。
常用的裂纹扩展准则包括J-integral准则和应力强度因子准则。
通过这些准则,可以根据应力和应变场的变化来判断裂纹是否会继续扩展。
在裂纹扩展模拟中,使用XFEM可以有效地模拟裂纹的扩展行为。
XFEM采用了分片形函数的方法,能够在裂纹尖端的元素上引入裂纹影响函数,从而准确地模拟裂纹扩展过程。
与传统的有限元方法相比,XFEM能够更加准确地预测裂纹的扩展路径和扩展速率。
通过基于XFEM的膜盘联轴器裂纹扩展模拟,可以得到裂纹扩展的路径和速率,为工程师提供了重要的参考数据。
这对于设计更可靠的膜盘联轴器、预测其寿命和提高其工作性能具有重要意义。
还可以通过模拟分析来指导维修和保养过程,及时发现和修复潜在的裂纹问题,确保膜盘联轴器的正常运行。
ANSYS16.0新增扩展有限元XFEM裂纹扩展仿真简介

ANSYS16.0新增扩展有限元XFEM裂纹扩展仿真简介中国矿业大学, 师访, matmes@1 引言早在两年前,就听安世亚太的人说ANSYS15.0将加入XFEM,但结果令人失望。
左盼右盼,终于在ANSYS16.0中等来了扩展有限元(Extended Finite ElementMethod)XFEM 功能。
首先,对于不知道XFEM为何物的朋友们,建议看下这篇文献:断裂问题的扩展有限元法研究_茹忠亮_岩土力学_2011.pdf(834.69 KB, 下载次数: 0)欢迎联系我讨论关于XFEM断裂模拟的相关问题,QQ:15492217582 ANSYS16.0 XFEM简介ANSYS16.0发布时候关于结构分析的简介中并未提及XFEM,由此可见ANSYS中的XFEM功能也不会太让人满意,看了其帮助文档(ANSYS Mechanical APDL Fracture Analysis Guide.pdf(2.52 MB, 下载次数: 0),3.2节)后发现,事实确实如此。
(1)基于虚拟节点法,与Abaqus一致。
(2)仅支持线弹性材料。
(3)不支持裂尖增强,同样与Abaqus一致,这就导致裂纹尖端不能落在单元内部,只能位于单元边界上。
(4)必须事先给定初始裂纹,即不支持裂纹的自动萌生。
鸡肋的是,初始裂纹的定义居然要通过给定水平集值的方法来实现:XFDATA,LSM,ELEMNUM,NODENUM,PHI(5)支持粘聚裂纹。
(6)支持PLANE182(4节点四边形单元,用于2D平面问题分析)及SOLID185(8节点正方形单元,用于3D问题分析)这两种单元。
(7)仅支持准静态分析,不支持动态断裂。
(8)裂纹每次只能扩展一个单元长度。
(9)仅支持两个裂纹扩展准则:STTMAX,最大周向应力准则(Maximum circumferential stress criterion);PSMAX(Circumferential stress criterion)。
基于XFEM的膜盘联轴器裂纹扩展模拟

基于XFEM的膜盘联轴器裂纹扩展模拟膜盘联轴器是一种常用的机械传动装置,其主要用于传递两个轴的转矩。
在使用过程中,由于工作条件的复杂性以及材料的疲劳,裂纹的形成和扩展是不可避免的。
对膜盘联轴器裂纹扩展行为的研究具有重要的意义。
基于扩展有限元法(XFEM),可以模拟材料中裂纹的扩展行为。
XFEM是一种将数值分析方法与数学基础理论相结合的仿真方法。
通过加入扩展刚度场(ESF)和裂缝增长准则,XFEM可以模拟裂纹的扩展路径和速率。
需要建立膜盘联轴器的几何模型,并进行网格划分。
膜盘联轴器通常由圆盘和薄膜组成,所以在建模时需要考虑这两者的几何形状和尺寸。
对于圆盘部分,可以使用二维或三维的几何模型,而薄膜部分可以使用二维的模型。
接下来,需要定义材料的物理性质。
膜盘联轴器通常由金属材料制成,所以可以使用弹塑性或弹性模型来描述材料的力学行为。
还需要考虑到裂纹的存在,因此还需要定义裂纹初始位置和几何形状。
在建立模型和定义物理性质之后,可以进行裂纹扩展的模拟。
需要通过裂纹模式函数来描述裂纹的形状。
裂纹模式函数通常具有能量的形式,可以通过求解裂纹模式函数的极小值问题来确定裂纹的形状。
接着,需要定义扩展刚度场(ESF)。
ESF是一种包含了裂纹信息的场,用于模拟裂纹的扩展行为。
ESF可以根据裂纹的位置和形状被构建出来,并被添加到原始的有限元方程中。
通过裂纹增长准则来决定裂纹的扩展路径和速率。
裂纹增长准则通常基于能量释放率或位移场,在每个时间步中,通过计算裂纹增长准则来确定裂纹的扩展行为。
基于XFEM的膜盘联轴器裂纹扩展模拟可以提供有关裂纹形成和扩展行为的重要信息。
通过模拟,可以研究不同参数和工况对裂纹扩展的影响,为膜盘联轴器的设计和寿命评估提供依据。
该模拟方法还可以应用于其他材料和结构的裂纹扩展研究中。
【免费下载】裂纹扩展的扩展有限元(xfem)模拟实例详解

基于ABAQUS 扩展有限元的裂纹模拟化工过程机械 622080706010李建1 引言1.1 ABAQUS 断裂力学问题模拟方法在abaqus 中求解断裂问题有两种方法(途径):一种是基于经典断裂力学的模型;一种是基于损伤力学的模型。
断裂力学模型就是基于线弹性断裂力学及其基础上发展的弹塑性断裂力学等。
如果不考虑裂纹的扩展,abaqus 可采用seam 型裂纹来分析(也可以不建seam ,如notch 型裂纹),这就是基于断裂力学的方法。
这种方法可以计算裂纹的应力强度因子,J 积分及T-应力等。
损伤力学模型是指基于损伤力学发展而来的方法,单元在达到失效的条件后,刚度不断折减,并可能达到完全失效,最后形成断裂带。
这两个模型是为解决不同的问题而提出来的,当然他们所处理的问题也有交叉的地方。
1.2 ABAQUS 裂纹扩展数值模拟方法考虑模拟裂纹扩展,目前abaqus 有两种技术:一种是基于debond 的技术(包括VCCT );一种是基于cohesive 技术。
debond 即节点松绑,或者称为节点释放,当满足一定得释放条件后(COD 等,目前abaqus 提供了5种断裂准则),节点释放即裂纹扩展,采用这种方法时也可以计算出围线积分。
cohesive 有人把它译为粘聚区模型,或带屈曲模型,多用于模拟film 、裂纹扩展及复合材料层间开裂等。
cohesive 模型属于损伤力学模型,最先由Barenblatt 引入,使用拉伸-张开法则(traction-separation law )来模拟原子晶格的减聚力。
这样就避免了裂纹尖端的奇异性。
Cohesive 模型与有限元方法结合首先被用于混凝土计算和模拟,后来也被引入金属及复合材料。
Cohesive 界面单元要服从cohesive 分离法则,法则范围可包括粘塑性、粘弹性、破裂、纤维断裂、动力学失效及循环载荷失效等行为。
此外,从abaqus6.9版本开始还引入了扩展有限元法(XFEM ),它既可以模拟静态裂纹,计算应力强度因子和J 积分等参量,也可以模拟裂纹的开裂过程。
XFEM裂纹扩展范例

Add Weight Traditional Sensors Data Convert Data to Stress History Damage Growth on Digital Twin Life Estimate of Panel/Airplane
Uncertainty in Location/Size
In Development
Conditional Maintenance
1Black, 2Coppe,
Structural health monitoring: Composites get smart, 2008. Simplified damage growth models can still yield accurate prognosis, submitted. 3An, Experimental study on identifying cracks of increasing size using ultrasonic excitation, 2011. Structural & Multidisciplinary Optimization Group Mechanical and Aerospace Engineering Department
4/36
xx xy yy
N N
N
a or N
?
Structural & Multidisciplinary Optimization Group Mechanical and Aerospace Engineering Department
5/36
Overview
• Fatigue crack growth • Stress intensity factor evaluation – Extended Finite Element Method (XFEM) – Exact XFEM reanalysis algorithm • Integration of fatigue crack growth models – Surrogate models for high-order integration – Surrogate models for variable integration step size • Variable amplitude fatigue crack growth from flight data – Crack tip plasticity – Conversion of flight data to biaxial stress histories – Example problem and discussion • Conclusions
基于扩展有限元(XFEM)裂缝扩展总结
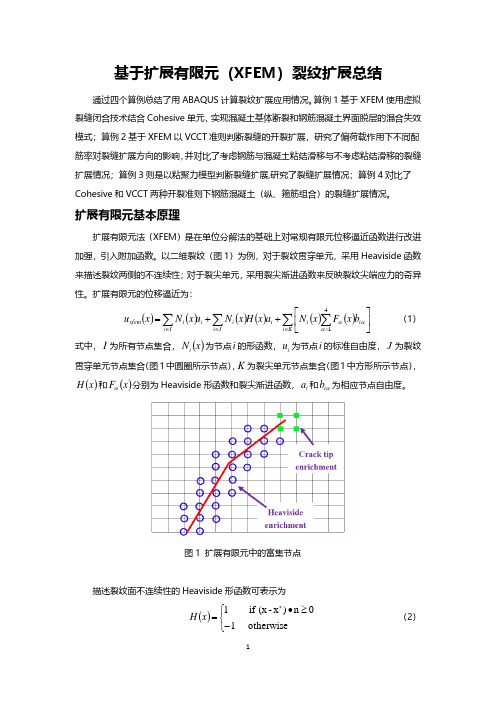
基于扩展有限元(XFEM )裂纹扩展总结通过四个算例总结了用ABAQUS 计算裂纹扩展应用情况。
算例1基于XFEM 使用虚拟裂缝闭合技术结合Cohesive 单元,实现混凝土基体断裂和钢筋混凝土界面脱层的混合失效模式;算例2基于XFEM 以VCCT 准则判断裂缝的开裂扩展,研究了偏荷载作用下不同配筋率对裂缝扩展方向的影响,并对比了考虑钢筋与混凝土粘结滑移与不考虑粘结滑移的裂缝扩展情况;算例3则是以粘聚力模型判断裂缝扩展,研究了裂缝扩展情况;算例4对比了Cohesive 和VCCT 两种开裂准则下钢筋混凝土(纵、箍筋组合)的裂缝扩展情况。
扩展有限元基本原理扩展有限元法(XFEM )是在单位分解法的基础上对常规有限元位移逼近函数进行改进加强,引入附加函数。
以二维裂纹(图1)为例,对于裂纹贯穿单元,采用Heaviside 函数来描述裂纹两侧的不连续性;对于裂尖单元,采用裂尖渐进函数来反映裂纹尖端应力的奇异性。
扩展有限元的位移逼近为:()()()()()()∑∑∑∑∈=∈∈⎥⎦⎤⎢⎣⎡++=K i i i i J i i i I i i xfem b x F x N a x H x N u x N x u 41ααα (1)式中,I 为所有节点集合,()x N i 为节点i 的形函数,i u 为节点i 的标准自由度,J 为裂纹贯穿单元节点集合(图1中圆圈所示节点),K 为裂尖单元节点集合(图1中方形所示节点),()x H 和()x F α分别为Heaviside 形函数和裂尖渐进函数,i a 和αi b 为相应节点自由度。
图1 扩展有限元中的富集节点描述裂纹面不连续性的Heaviside 形函数可表示为 ()⎩⎨⎧−≥•=*otherwise 10n )x -(x if 1x H (2)式中,*x 为点x 到裂纹面最近处的投影,n 为*x 点处的单位外法线向量(如图2所示)。
可以看出,节点位于裂纹面上侧时()1=x H ,节点位于裂纹面下侧时()1−=x H ,Heaviside 形函数能较好的描述裂纹面两侧的不连续性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于ABAQUS 扩展有限元的裂纹模拟化工过程机械622080706010 李建1 引言1.1 ABAQUS 断裂力学问题模拟方法在abaqus中求解断裂问题有两种方法(途径):一种是基于经典断裂力学的模型;一种是基于损伤力学的模型。
断裂力学模型就是基于线弹性断裂力学及其基础上发展的弹塑性断裂力学等。
如果不考虑裂纹的扩展,abaqus可采用seam型裂纹来分析(也可以不建seam,如notch型裂纹),这就是基于断裂力学的方法。
这种方法可以计算裂纹的应力强度因子,J积分及T-应力等。
损伤力学模型是指基于损伤力学发展而来的方法,单元在达到失效的条件后,刚度不断折减,并可能达到完全失效,最后形成断裂带。
这两个模型是为解决不同的问题而提出来的,当然他们所处理的问题也有交叉的地方。
1.2 ABAQUS 裂纹扩展数值模拟方法考虑模拟裂纹扩展,目前abaqus有两种技术:一种是基于debond的技术(包括VCCT);一种是基于cohesive技术。
debond即节点松绑,或者称为节点释放,当满足一定得释放条件后(COD 等,目前abaqus提供了5种断裂准则),节点释放即裂纹扩展,采用这种方法时也可以计算出围线积分。
cohesive有人把它译为粘聚区模型,或带屈曲模型,多用于模拟film、裂纹扩展及复合材料层间开裂等。
cohesive模型属于损伤力学模型,最先由Barenblatt 引入,使用拉伸-张开法则(traction-separation law)来模拟原子晶格的减聚力。
这样就避免了裂纹尖端的奇异性。
Cohesive 模型与有限元方法结合首先被用于混凝土计算和模拟,后来也被引入金属及复合材料。
Cohesive界面单元要服从cohesive 分离法则,法则范围可包括粘塑性、粘弹性、破裂、纤维断裂、动力学失效及循环载荷失效等行为。
此外,从abaqus6.9版本开始还引入了扩展有限元法(XFEM),它既可以模拟静态裂纹,计算应力强度因子和J积分等参量,也可以模拟裂纹的开裂过程。
被誉为最具有前途的裂纹数值模拟方法。
本文将利用abaqus6.9版本中的扩展有限元法功能模拟常见的Ⅰ型裂纹的扩展。
2 Ⅰ型裂纹的扩展有限元分析本文针对断裂力学中的平面Ⅰ型裂纹扩展问题用abaqus中的扩展有限元方法进行数值模拟,获得了裂纹扩展的整个过程,裂尖单元的应力变化曲线,以及裂纹尖端塑性区的形状。
在此基础上绘制裂纹扩展的能量历史曲线变化趋势图。
2.1 平面裂纹的几何模型几何模型的尺寸参数如图1所示,其中a=1.5m,b=3m,L=10m,厚度为1m。
上下两端分别承受25.32MPa的拉力。
图1 裂纹的几何示意图2.2 有限元模型有限元程序采用大型通用ABAQUS6.9软件,选用8节点六面体减缩单元(C3D8R)。
网格划分的模型如图2所示。
图2 网格图2.3 材料性能在有限元分析中假定材料为理想线弹性的,弹性模量E为2.1×105MPa,泊松比为0.3。
本文采用的是基于损伤力学演化的失效准则。
具体的参数设置如下。
损伤判据为最大主应力失效准则作为损伤起始的判据,最大主应力为84.4MPa。
损伤演化选取基于能量的、线性软化的、混合模式的指数损伤演化规律,有关参数为G1C= G2C= G3C=42200N/m,α=1。
2.4 边界条件和初始条件对于含有裂纹的平板,我们仅仅需要约束住它的刚体位移,保证在在平板两个断面施加应力载荷时,平板不会出现意外的刚体运动。
设置裂纹类型为扩展有限元裂纹,扩展区域是整个平板,扩展路径为任意路径。
由于计算裂纹扩展实际上是一个大变形问题,所以分析步骤的几何非线性一定要打开。
由于裂纹扩展本身是一个强烈的非连续问题,它将导致求解过程的迭代有可能出现不收敛的情况,另外,求解的增量步也会要求很小,这会导致求解时间很长。
因此非常有必要对求解过程做一些参数控制,以避免迭代不收敛导致的求解失败的情况的出现。
图3 裂纹体及其扩展区域图4 载荷及边界条件3 结果分析3.1 静态裂纹的应力强度因子及J积分的验证计算应力强度因子及J积分时,需要设置裂纹不能扩展,从而计算静态裂纹的应力强度因子,同时还要在历史变量输出中做相关的设置。
另外分析步也需要将几何非线性去除,因为裂纹没有扩展。
由此计算得到了裂尖在25.32MPa载荷下的Ⅰ型应力强度因子。
同时,我们根据断裂力学理论中关于此模型的理论解如公式(1),计算理论的应力强度因子。
最后得到的结果列于表1。
⎪⎭⎫⎝⎛=I b a F a K πσ (1)上式中a ,b 分别是裂纹体的几何尺寸,F 为关于a 和b 比值的函数,可以查表得到,本文中a 与b 的比值为0.5,查表得到F 的函数值为1.50。
表1 应力强度因子的对比表本文计算值 理论计算值 )(2/1m MPa K ⋅I58.6958.28由此可以计算相对误差为:1.06%,此误差显然属于5%的允许误差范围之内。
所以本文计算得到的应力强度因子是可信的。
此外,本文还利用此模型计算了静态裂纹的J 积分值,由于材料是理想线弹性的,所以J 积分与应力强度因子之间存在这样关系,如公式(2)。
EK J 2I = (2)本文在这里列出J 积分的变化趋势图,图中对比了公式(2)的理论解以及有限元结果。
从图中可以看出,两者是吻合的,说明了有限元模拟是正确的。
J 积分随加载的变化趋势图如图5所示。
红色实线表示的是理论结果,黑色点表示有限元结果。
0.02.0x1034.0x1036.0x1038.0x1031.0x1041.2x1041.4x1041.6x1041.8x104J 积分/N m -1Step time图5 J 积分历史曲线图3.2 裂纹扩展过程展示Step time=0.1143 Step time=0.3943 Step time=0.6743 Step time=0.7976 Step time=0.8708 Step time=0.9551Step time=0.9994 Step time=0.9998 Step time=1图6 裂纹扩展过程从上述的裂纹扩展过程的应力分布图,我们可以得到如下几点结论,证明我们的数值模拟具有一定的正确性。
首先,在裂纹尖端出现了应力集中,这是和断裂力学理论符合的。
其次,观察裂纹附近的应力分布,我们可以看到应力分布的趋势是与理论计算的塑性区的形状大致相同的,理论计算的塑性区形状如图7所示。
图7 理论上的塑形区形状图3.3 裂尖单元应力变化其次,考察裂尖单元的应力随载荷增加的变化。
实际上裂尖单元应力值的具体大小并没有意义,因为表征断裂韧强度的是应力强度因子和J 积分。
而单元应力随载荷增加导致的变化可以帮助我们理解裂尖单元在起裂到完全断裂的整个过程。
观察图8,我们可以大致得到这个裂尖单元参与断裂过程的整个历史。
首先,在应力加载的早些时候,裂尖单元的应力随着载荷的增加而增加,此时裂尖单元的应力并没有达到损伤判据的临界应力,所以单元没有起裂。
随着载荷的继续增加,应力值继续增加,当到大概0.7976左右时,裂尖的最大主应力达到了最大主应力损伤判据的临界值,于是裂纹起裂,直至完全裂开,单元的应力奇异性消失,裂尖单元转变为一个普通的非裂尖单元。
这个过程对应于图8中的右边应力增大后有急剧减小的曲线。
之后,由于载荷还没有完全加载完毕,所以裂尖单元在转变为普通单元之后随着载荷的继续增加,其单元应力又会随之在增加。
以上就是一个裂尖单元在整个加载过程中的单元应力历史变化的三个阶段。
最大主应力/M P aStep time图8 裂纹尖端单元应力历史曲线3.4 裂纹扩展分析如图9所示,载荷从零开始不断加载。
随着载荷的增加,裂尖处的单元应力也不断增加。
当裂尖处的最大主应力值达到临界值时,裂尖处的单元开始失效,裂纹开始穿过单元扩展,时间步大概是0.7976左右,此时裂尖处开始形成粘结裂纹(cohesive crack)。
从0-0.7976这个过程可以认为是裂纹孕育期。
之后随着裂尖处的能量释放率达到裂纹扩展阻力率G C 时,裂尖处的粘结裂纹开始扩展成真实裂纹,裂尖单元的XFEM值达到1。
裂尖处的单元损伤值达到临界值,时间步大概是0.9996左右。
此时认为这一结构开始失效,裂纹失去平衡,开始失稳扩展,真实裂纹开始形成并不断扩展。
从0.7976-0.9996这个过程可以认为是裂纹的萌生过程。
0.9996以后裂纹失稳扩展,结构失效。
从图中可以看出初始裂纹长度为12个单元距离,到最终加载结束时,真实裂纹长度为15个单元长度,粘结裂纹长度为7个单元长度。
图9 随加载历史扩展的动态裂纹图3.5 裂纹扩展的能量历史曲线绘出整个模型的总能量,动能,内能和外力功随计算过程的历史曲线如图10所示。
由图可以看出,总能量和动能在整个过程中并没有发生显著的增加,可以表明整个计算过程基本是稳定的。
而伪应变能在计算过程中有稍微的增长。
-1x101x102x103x104x105x106x107x108x109x10能量/N m -1Step time图10 裂纹扩展的能量历史曲线4 结论本文的工作是基于abaqus6.9版本的扩展有限元功能计算了Ⅰ型裂纹的扩展。
得到如下几点结论。
首先,本文计算了Ⅰ型裂纹的应力强度因子,结构表明计算值与理论值的误差在5%以内,结果可靠有效。
同时计算了裂纹的J 积分值,获得了J 积分的历史曲线,有限元结果与理论结果吻合。
裂纹的扩展过程与理论是吻合的,整个裂纹扩展的计算没有出现不稳定的情况。
裂尖出现了应力的奇异性,裂纹扩展平稳。
并通过研究裂尖单元的应力历史曲线,直观的获得了裂纹在一个单元上扩展的三个典型阶段。
其次,对裂纹扩展的过程进行了分析,指出了裂纹扩展的大概几个阶段以及具体的裂纹扩展过程。
最后,对裂纹扩展过程中的能量变化作了简单描述,说明了计算过程的稳定性,并验证了系统的能量守恒关系。
