历年全国中考数学压轴题全析全解(1)
数学中考压轴题大全(含答案、详细解析版)

【最新】中考数学压轴题大全(安徽)按右图所示的流程,输入一个数据x ,根据y 与x 的关系式就输出一个数据y ,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:(Ⅰ)新数据都在60~100(含60和100)之间;(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y 与x 的关系是y =x +p(100-x),请说明:当p =12时,这种变换满足上述两个要求;(2)若按关系式y=a(x -h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。
(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)【解】(1)当P=12时,y=x +()11002x -,即y=1502x +。
∴y 随着x 的增大而增大,即P=12时,满足条件(Ⅱ)……3分 又当x=20时,y=1100502⨯+=100。
而原数据都在20~100之间,所以新数据都在60~100之间,即满足条件(Ⅰ),综上可知,当P=12时,这种变换满足要求;……6分(2)本题是开放性问题,答案不唯一。
若所给出的关系式满足:(a )h ≤20;(b )若x=20,100时,y 的对应值m ,n 能落在60~100之间,则这样的关系式都符合要求。
如取h=20,y=()220a x k -+,……8分∵a >0,∴当20≤x ≤100时,y 随着x 的增大…10分 令x=20,y=60,得k=60 ① 令x=100,y=100,得a ×802+k=100 ②1由①②解得116060a k ⎧=⎪⎨⎪=⎩, ∴()212060160y x =-+。
………14分 2、(常州)已知(1)A m -,与(2B m +,是反比例函数ky x=图象上的两个点. (1)求k 的值;(2)若点(10)C -,,则在反比例函数ky x=图象上是否存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形?若存在,求出点D 的坐标;若不存在,请说明理由.解:(1)由(1)2(33)m m -=+,得m =-,因此k = ································ 2分(2)如图1,作BE x ⊥轴,E为垂足,则3CE =,BE =BC =30BCE =∠.由于点C 与点A 的横坐标相同,因此CA x ⊥轴,从而120ACB =∠. 当AC 为底时,由于过点B 且平行于AC 的直线与双曲线只有一个公共点B , 故不符题意. ······························ 3分 当BC 为底时,过点A 作BC 的平行线,交双曲线于点D , 过点A D ,分别作x 轴,y 轴的平行线,交于点F .由于30DAF =∠,设11(0)DFm m =>,则1AF ,12ADm =,由点(1A--,,得点11(1)D m --,.因此11(1)(23)m --+=2解之得1m =10m =舍去),因此点6D ⎛ ⎝⎭.5分D . 由于 则∠因此22(1)3m m -+=.解之得22m =(21m =-舍去),因此点(1D . 此时4CD =,与AB 的长度不相等,故四边形ABDC 是梯形. ········· 7分 如图3,当过点C 作AB 的平行线,与双曲线在第三象限内的交点为D 时,同理可得,点(2D -,,四边形ABCD 是梯形. ·············· 9分综上所述,函数y x=图象上存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形,点D 的坐标为:6D ⎛ ⎝⎭或(1D 或(2D --,. ··············· 10分3、(福建龙岩)如图,抛物线254y ax ax =-+经过ABC △在x 轴上,点C 在y 轴上,且AC BC =.(1)求抛物线的对称轴;(2)写出A B C ,,三点的坐标并求抛物线的解析式;图1图2图33(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.解:(1)抛物线的对称轴5522a x a -=-=………2分(2)(30)A -, (54)B ,(04)C ,…………5分 把点A 坐标代入254y ax ax =-+中,解得16a =-………6分 215466y x x ∴=-++…………………………………………7分(3)存在符合条件的点P 共有3个.以下分三类情形探索. 设抛物线对称轴与x 轴交于N ,与CB 交于M .过点B 作BQ x ⊥轴于Q ,易得4BQ =,8AQ =, 5.5AN =,52BM =① ········································································································ 以AB 为腰且顶角为角A 的PAB △有1个:1P AB △.222228480AB AQ BQ ∴=+=+= ················· 8分4在1Rt ANP △中,1PN ====152P ⎛∴ ⎝⎭, ························· 9分 ②以AB 为腰且顶角为角B 的PAB △有1个:2P AB △.在2Rt BMP △中,22MP ====10分252P ⎛∴ ⎝⎭······················· 11分③以AB 为底,顶角为角P 的PAB △有1个,即3P AB △.画AB 的垂直平分线交抛物线对称轴于3P ,此时平分线必过等腰ABC △的顶点C .过点3P 作3P K 垂直y 轴,垂足为K ,显然3Rt Rt PCK BAQ △∽△. 312P K BQ CK AQ ∴==. 3 2.5P K = 5CK ∴= 于是1OK = ··············· 13分3(2.51)P ∴-, ·························· 14分注:第(3)小题中,只写出点P 的坐标,无任何说明者不得分. 4、(福州)如图12,已知直线12y x =与双曲线(0)ky k x=>交于A B ,两点,且点A 的横坐标为4. (1)求k 的值; (2)若双曲线(0)ky k x=>上一点C 的纵坐标为8,求AOC △的面积; (3)过原点O 的另一条直线l 交双曲线(0)ky k x=>于P Q ,两点(P点在第图125一象限),若由点A B P Q ,,,为顶点组成的四边形面积为24,求点P 的坐标.解:(1)∵点A 横坐标为4 , ∴当 x = 4时,y = 2 .∴ 点A 的坐标为( 4,2 ).∵ 点A 是直线 与双曲线(k>0)的交点 , ∴ k = 4 ×2 = 8 . (2) 解法一:如图12-1,∵ 点C 在双曲线上,当y = 8时,x = 1∴ 点C 的坐标为 ( 1, 8 ) . 过点A 、C 分别做x 轴、y 轴的垂线,垂足为M 、N ,得矩形DMON . S 矩形ONDM = 32 , S △ONC = 4 , S △CDA = 9, S △OAM = 4 . S △AOC = S 矩形ONDM - S △ONC - S △CDA - S △OAM = 32 - 4 - 9 - 4 = 15 . 解法二:如图12-2,过点 C 、A 分别做x 轴的垂线,垂足为E 、F , ∵ 点C 在双曲线8y x=上,当y = 8时,x = 1 . ∴ 点C 的坐标为 ( 1, 8 ). ∵ 点C 、A 都在双曲线8y x=上 , ∴ S △COE = S △AOF = 4 。
中考数学【压轴题全揭秘(河南专版)】专题01_动点与函数图象(原卷版)_

专题01 动点与函数图象【例1】(2019·郑州外国语测试)如图所示,在矩形ABCD中,AB=8,AD=4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N的速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图象为()A B C D【变式1-1】(2019·洛阳二模)如图,点P是边长为2 cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设DP=x cm,则△POD的面积y(cm2)随x(cm)变化的关系图象为()A B C D【变式1-2】(2019·叶县一模)如图,在△ABC中,△ABC=60°,△C=45°,点D,E分别为边AB,AC上的点,且DE△BC,BD=DE=2,CE=52,BC=245.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ△BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为()A.B.C.D.【例2】(2019·省实验一模)如图,正方形ABCD,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是()A.B.C.D.【变式2-1】(2019·名校模考)如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF△BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的()A.线段BE B.线段EF C.线段CE D.线段DE【变式2-2】(2018·洛宁县模拟)如图1,正△ABC 的边长为4,点P 为BC 边上的任意一点,且△APD =60°,PD 交AC 于点D ,设线段PB 的长度为x ,图1中某线段的长度为y ,y 与x 的函数关系的大致图象如图2,则这条线段可能是图1中的( )图1 图2 A .线段ADB .线段APC .线段PDD .线段CD【例3】(2019·周口二模)如图1,E 为矩形ABCD 边AD 上的一点,点P 从点B 沿折线BE -ED -DC 运动到点C 时停止,点Q 从点B 沿BC 运动到点C 时停止,它们运动的速度都是2 cm /s .若P ,Q 同时开始运动,设运动时间为t (s ),△BPQ 的面积为y (cm 2),已知y 与t 的函数关系图象如图2,则CDBE的值为( ) ABCD图1 图2【变式3-1】(2019·枫杨外国语三模)如图 1,动点 K 从△ABC 的顶点 A 出发,沿 AB ﹣BC 匀速运动到点 C 停止.在动点 K 运动过程中,线段 AK 的长度 y 与运动时间 x 的函数关系如图 2 所示,其中点 Q 为曲线部分的最低点,若△ABC的面积是,则 a 的值为图1 图2图1图2【变式3-2】(2019·中原名校大联考)如图1,在矩形ABCD中,动点M从点A出发,沿A→B→C方向运动,当点M到达点C时停止运动,过点M作MN△AM交CD于点N,设点M的运动路程为x,CN=y,图2表示的是y与x的函数关系的大致图象,则矩形ABCD的面积是()A.20B.18C.10D.91. (2019·濮阳二模)如图,点A在x轴上,点B,C在反比例函数y=kx(k>0,x>0)的图象上.有一个动点P从点A出发,沿A→B→C→O的路线(图中“→”所示路线)匀速运动,过点P作PM△x轴,垂足为M,设△POM的面积为S,点P的运动时间为t,则S关于t的函数图象大致为()A.B.C.D.2.(2019·南阳模拟)如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE△AC,交BC于E点;过E点作EF△DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y 与x函数关系的图象是()A.B.C.D.3.(2019·平顶山三模)如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是()A.B.C.D.4.(2017·预测卷)如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ 的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:△当0<t≤5时,y=25t2 △tan△ABE=34△点H的坐标为(11,0)△△ABE与△QBP不可能相似.其中正确的是(把你认为正确结论的序号都填上)5.(2019·焦作二模)如图1,在等边△ABC中,点D是BC边的中点,点P为AB边上的一个动点,设xAP ,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则等边△ABC的面积为.6.(2019·三门峡一模)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x ,两个三角形重叠面积为y ,则y 关于x 的函数图象是( )ABCD7.(2019·许昌月考)如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ,动点P 从点A 出发,沿A →D →E →F →G →B 的路线绕多边形的边匀速运动到点B 时停止(不含点A 和点B ),则△ABP 的面积S 随着时间t 变化的函数图象大致是( )A .B .C .D .8.(2019·信阳模拟)如图1,在△ABC 中,△C =90°,动点P 从点C 出发,以1cm /s 的速度沿折线CA →AB 匀速运动,到达点B 时停止运动,点P 出发一段时间后动点Q 从点B 出发,以相同的速度沿BC 匀速运动,当点P 到达点B 时,点Q 恰好到达点C ,并停止运动,设点P 的运动时间为t s ,△PQC 的面积为S cm 2,S 关于t 的函数图象如图2所示(其中0<t ≤3,3≤t ≤4时,函数图象均为线段(不含点O ),4<t <8时,函数图象为抛物线的一部分)给出下列结论:△AC =3cm ;△当S =65时,t =35或6.下结论正确的是( )A .△△都对B .△△都错C .△对△错D .△错△对9.(2018·新乡一模)如图,平行四边形ABCD 中,ABcm ,BC =2cm ,△ABC =45°,点P 从点B 出发,以1cm /s 的速度沿折线BC →CD →DA 运动,到达点A 为止,设运动时间为t (s ),△ABP 的面积为S (cm 2),则S 与t 的函数表达式为.10.(2019·郑州外国语模拟)如图,在等腰△ABC 中,AB =AC =4cm ,△B =30°,点P 从点Bcm /s 的速度沿BC 方向运动到点C 停止,同时点Q 从点B 出发以2cm /s 的速度沿B →A →C 运动到点C 停止,若△BPQ 的面积为y ,运动时间为t (s ),则y 与t 的函数关系式为:.11.(2019·安阳一模)如图,在四边形ABCD 中,AD △BC ,DC △BC ,DC =4 cm ,BC =6 cm ,AD =3 cm ,动点P ,Q 同时从点B 出发,点P 以2 cm /s 的速度沿折线BA -AD -DC 运动到点C ,点Q 以1 cm /s 的速度沿BC 运动到点C ,设P ,Q 同时出发t s 时,△BPQ 的面积为y cm 2,则y 与t 的函数图象大致是( )ABCDBBC12.(2019·开封模拟)如图,菱形ABCD 的边长是4 cm ,△B =60°,动点P 以1 cm /s 的速度从点A 出发沿AB 方向运动至点B 停止,动点Q 以2 cm /s 的速度从点B 出发沿折线BCD 运动至点D 停止.若点P ,Q 同时出发,运动了t s ,记△BPQ 的面积为S cm 2,则下面图象中能表示S 与t 之间的函数关系的是( )A .B .C .D .13. 如图,矩形ABCD 中,AB =2AD =4cm ,动点P 从点A 出发,以lcm /s 的速度沿线段AB 向点B 运动,动点Q 同时从点A 出发,以2cm /s 的速度沿折线AD →DC →CB 向点B 运动,当一个点停止时另一个点也随之停止.设点P 的运动时间是x (s )时,△APQ 的面积是y (cm 2),则能够反映y 与x 之间函数关系的图象大致是()14.(2019·信阳一模)如图,锐角三角形ABC 中,BC =6,BC 边上的高为4,直线MN 交边AB 于点M ,交AC 于点N ,且MN △BC ,以MN 为边作正方形MNPQ ,设其边长为x (x >0),正方形MNPQ 与△ABC 公共部分的面积为y ,则y 与x 的函数图象大致是( )A B C D15.(2018·开封二模)如图,在平面直角坐标系中,已知A(0,1),B0),以线段AB为边向上作菱形ABCD,且点D在y轴上. 若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行,直至顶点D落在x轴上时停止.设菱形落在x轴下方部分的面积为S,则表示S与滑行时间t的函数关系的图象为()图1 图2A B C D。
全国中考数学压轴题全解

全国数学中考压轴题汇编(附答案)(一)1、(2009广西贺州).(本题满分10分) 如图,抛物线2124y x x =--+的顶点为A ,与y 轴交于点B .(1)求点A 、点B 的坐标.(2)若点P 是x 轴上任意一点,求证:PA PB AB -≤.(3)当PB PA -最大时,求点P 的坐标.解:(1)抛物线2124y x x=--+与y 轴的交于点B , 令x=0得y=2.∴B (0,2) ······································1分∵22112(2)344y x x x =--+=-++∴A (—2,3) ····································· 3分(2)当点P 是 AB 的延长线与x 轴交点时,AB PB PA =-. ······································ 5分当点P 在x 轴上又异于AB 的延长线与x 轴的交点时, 在点P 、A 、B 构成的三角形中,AB PB PA <-. 综合上述:PA PB AB -≤ ……… 7分 (3)作直线AB 交x 轴于点P ,由(2)可知:当P A —PB 最大时,点P 是所求的点 ··· 8分作AH ⊥OP 于H . ∵BO ⊥OP ,∴△BOP ∽△AHP ∴AH HPBO OP=······················································································· 9分 由(1)可知:AH=3、OH=2、OB=2, ∴OP=4,故P (4,0) 10分2、(2009龙岩)26、(14分)如图,抛物线n mx x y ++=221与x 轴交于A 、B 两点,与y 轴交于C 点,四边形OBHC 为矩形,CH 的延长线交抛物线于点D (5,2),连结BC 、AD .(1)求C 点的坐标及抛物线的解析式;(2)将△BCH 绕点B 按顺时针旋转90°后 再沿x 轴对折得到△BEF (点C 与点E 对应),判断点E 是否落在抛物线上,并说明理由;(3)设过点E 的直线交AB 边于点P ,交CD 边于点Q . 问是否存在点P ,使直线PQ 分梯形ABCD 的面积为1∶3两部分?若存在,求出P 点坐标;若不存在,请说明理由. 解:(1)∵四边形OBHC 为矩形,∴CD ∥AB , 又D (5,2),BOA·xy第28题图BO A·xy第(1)证明:PH∴C (0,2),OC =2 . …………………………… 2分∴⎪⎩⎪⎨⎧=+⋅+⋅=2552122n m n 解得⎪⎩⎪⎨⎧=-=225n m∴抛物线的解析式为:225212+-=x x y …… 4分(2)点E 落在抛物线上. 理由如下:……… 5分由y = 0,得0225212=+-x x . 解得x 1=1,x 2=4. ∴A (4,0),B (1,0). ……………………………… 6分 ∴OA =4,OB =1.由矩形性质知:CH =OB =1,BH =OC =2,∠BHC =90°, 由旋转、轴对称性质知:EF =1,BF =2,∠EFB =90°,∴点E 的坐标为(3,-1). ………………………………………………… 7分 把x =3代入225212+-=x x y ,得123253212-=+⋅-⋅=y , ∴点E 在抛物线上. …………………………………………………………… 8分(3)法一:存在点P (a ,0),延长EF 交CD 于点G ,易求OF =CG =3,PB =a -1.S 梯形BCGF = 5,S 梯形ADGF = 3,记S 梯形BCQP = S 1,S 梯形ADQP = S 2,下面分两种情形:①当S 1∶S 2 =1∶3时,52)35(411<=+=S ,此时点P 在点F (3,0)的左侧,则PF = 3-a ,由△EPF ∽△EQG ,得31==EG EF QG PF ,则QG =9-3a , ∴CQ =3-(9-3a ) =3a -6由S 1=2,得22)163(21=⋅-+-a a ,解得49=a ;………………… 11分②当S 1∶S 2=3∶1时,56)35(431>=+=S 此时点P 在点F (3,0)的右侧,则PF = a -3,由△EPF ∽△EQG ,得QG = 3a -9,∴CQ = 3 +(3 a -9)= 3 a -6, 由S 1= 6,得62)163(21=⋅-+-a a ,解得413=a .综上所述:所求点P 的坐标为(49,0)或(413,0)……… 14分 法二:存在点P (a ,0). 记S 梯形BCQP = S 1,S 梯形ADQP = S 2,易求S 梯形ABCD = 8.当PQ 经过点F (3,0)时,易求S 1=5,S 2 = 3, 此时S 1∶S 2不符合条件,故a ≠3.设直线PQ 的解析式为y = kx +b(k ≠0),则⎩⎨⎧=+-=+013b ak b k ,解得⎪⎪⎩⎪⎪⎨⎧--=-=331a a b a k ,∴331---=a ax a y . 由y = 2得x = 3a -6,∴Q (3a -6,2) ……… 10分 ∴CQ = 3a -6,BP = a -1,742)163(211-=⋅-+-=a a a S . 下面分两种情形:①当S 1∶S 2 = 1∶3时,841S 41ABCD 1⨯==梯形S = 2;∴4a -7 = 2,解得49=a ;……………………………………………… 12分 ②当S 1∶S 2 = 3∶1时,6843S 43ABCD 1=⨯==梯形S ; ∴4a -7 = 6,解得413=a ;综上所述:所求点P 的坐标为(49,0)或(413,0)………… 14分[说明:对于第(3)小题,只要考生能求出49=a 或413=a 两个答案,就给6分. ]3、(2009广东湛江)28.已知矩形纸片OABC 的长为4,宽为3,以长OA 所在的直线为x轴,O 为坐标原点建立平面直角坐标系;点P 是OA 边上的动点(与点O A 、不重合),现将POC △沿PC 翻折 得到PEC △,再在AB 边上选取适当的点D ,将PAD △沿PD 翻折,得到PFD △,使得 直线PE PF 、重合.(1)若点E 落在BC 边上,如图①,求点P C D 、、的坐标,并求过此三点的抛物线的函数关系式;(2)若点E 落在矩形纸片OABC 的内部,如图②,设OP x AD y ==,,当x 为何值时,y 取得最大值?(3)在(1)的情况下,过点P C D 、、三点的抛物线上是否存在点Q ,使PDQ △是以PD 为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标C y EBFDA PxO 图①A BD F ECO P xy图②第28题图解:(1)由题意知,POC PAD △、△均为等腰直角三角形, 可得(30)(03)(41)P C D ,、,、, ··········································································· 2分设过此三点的抛物线为2(0)y ax bx c a =++≠,则39301641c a b c a b c =⎧⎪++=⎨⎪++=⎩12523a b c ⎧=⎪⎪⎪=-∴⎨⎪⎪⎪=⎩∴过P C D 、、三点的抛物线的函数关系式为215322y x x =-+ ······························ 4分 (2)由已知PC 平分OPE PD ∠,平分APF ∠,且PE PF 、重合,则90CPD ∠=° 90OPC APD ∴∠+∠=°,又90APD ADP ∠+∠=° OPC ADP ∴∠=∠.Rt Rt POC DAP ∴△∽△.OP OC AD AP ∴=,即34x y x=- ·········································································· 6分 2211414(4)(2)(04)33333y x x x x x x =-=-+=--+<< ∴当2x =时,y 有最大值43. ······································································· 8分 (3)假设存在,分两种情况讨论:①当90DPQ ∠=°时,由题意可知90DPC ∠=°,且点C 在抛物线上,故点C 与点Q 重合,Cy EBFDA P xO图①A BDF ECO P xy图②第28题图yxBAOP 所求的点Q 为(0,3) ······················································································ 9分 ②当90DPQ ∠=°时,过点D 作平行于PC 的直线DQ ,假设直线DQ 交抛物线于另一点Q ,点(30)03P C ,、(,),∴直线PC 的方程为3y x =-+,将直线PC 向上平移2个单位与直线DQ 重合,∴直线DQ 的方程为5y x =-+ ·················································· 10分由2515322y x y x x =-+⎧⎪⎨=-+⎪⎩得16x y =-⎧⎨=⎩或41x y =⎧⎨=⎩ 又点(41)(16)D Q ∴-,,,. 故该抛物线上存在两点(03)(16)Q -,、,满足条件. ················································ 12分4、(2009年大兴安岭地区)28、(本小题满分10分)直线)0(≠+=k b kx y 与坐标轴分别交于A 、B 两点,OA 、OB 的长分别是方程048142=+-x x 的两根(OB OA >),动点P 从O 点出发,沿路线O →B →A 以每秒1个单位长度的速度运动,到达A 点时运动停止.(1)直接写出A 、B 两点的坐标; (2)设点P 的运动时间为t (秒),OPA ∆的面积为S ,求S 与t 之间的函数关系式(不必写出自变量的取值范围);(3)当12=S 时,直接写出点P 的坐标,此时,在坐标轴上是否存在点M ,使以O 、A 、P 、M 为顶点的四边形是梯形?若存在,请直接写出点M 的坐标;若不存在,请说明理由. 解:(1) )6,0(),0,8(B A ………………….各1分 (2)∵8=OA ,6=OB ,∴10=ABy xABEC QOP DF(Q )第28题图当点P 在OB 上运动时,t OP =1,t t OP OA S 4821211=⨯⨯=⨯=;..............1分 当点P 在BA 上运动时,作OA D P ⊥2于点D , 有ABAP BO D P 22= ∵t t AP -=-+=161062,∴53482tD P -=………………………1分 ∴51925125348821212+-=-⨯⨯=⨯⨯=t t D P OA S ……………………1分(3)当124=t 时,3=t ,)3,0(1P ,………………………………1分此时,过AOP ∆各顶点作对边的平行线,与坐标轴无第二个交点,所以点M 不存在;……………………………………………………………………………1分当125192512=+-t 时,11=t ,)3,4(2P ,........................1分 此时,)3,0(1M 、)6,0(2-M (1)5、(2009年辽宁省锦州市)26.如图14,抛物线与x 轴交于A(x 1,0),B(x 2,0)两点,且x 1>x 2,与y 轴交于点C(0,4),其中x 1,x 2是方程x 2-2x-8=0的两个根. (1)求这条抛物线的解析式;(2)点P 是线段AB 上的动点,过点P 作PE∥AC,交BC 于点E ,连接CP ,当△CPE 的面积最大时,求点P 的坐标;(3)探究:若点Q 是抛物线对称轴上的点,是否存在这样的点Q ,使△QBC 成为等腰三角形,若存在,请直接写出所有符合条件的点Q 的坐标;若不存在,请说明理由.26.解:(1) ∵x 2-2x-8=0 ,∴(x -4)(x+2)=0 .∴x 1=4,x 2=-2. ∴A(4,0) ,B(-2,0). ……1分又∵抛物线经过点A 、B 、C,设抛物线解析式为y=ax 2+bx+c (a≠0),∴ ∴ ……3分∴所求抛物线的解析式为. ……4分(2)设P 点坐标为(m,0),过点E 作EG⊥x 轴于点G. ∵点B 坐标为(-2,0),点A 坐标(4,0),∴AB=6, BP=m+2. ∵PE∥AC, ∴△BPE∽△BAC. ∴.∴. ∴S △CPE = S △CBP - S △EBP =.∴ .∴. ……7分又∵-2≤m≤4,∴当m=1时,S △CPE 有最大值3. 此时P 点的坐标为(1,0). ……9分(3)存在Q 点,其坐标为Q 1(1,1),, ,.……14分6、(2009年赤峰市)25、(14分)如图,R t △ABC 的顶点坐标分别为A (0, ),B (-1/2, ),C (1,0),∠ABC=90°,BC 与y 轴的交点为D ,D 点坐标为(0, ),以点D 为顶点、y 轴为对称轴的抛物线过点B 。
中考数学 中考数学压轴题(讲义及答案)及解析
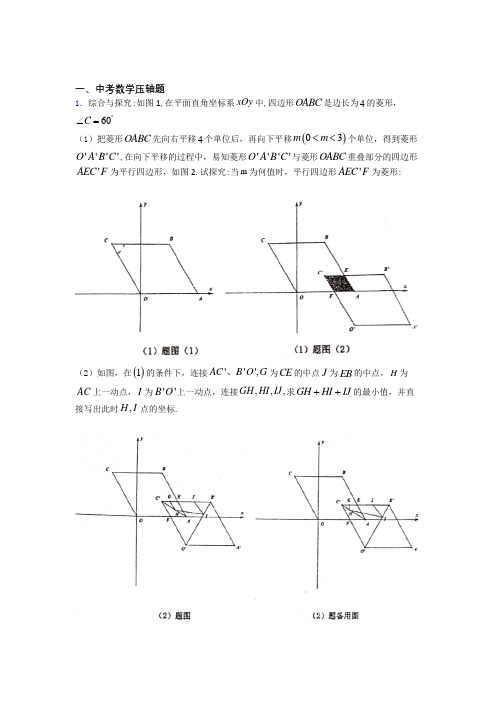
一、中考数学压轴题1.综合与探究:如图1,在平面直角坐标系xOy 中,四边形OABC 是边长为4的菱形,60C ︒∠=(1)把菱形OABC 先向右平移4个单位后,再向下平移()03m m <<个单位,得到菱形''''O A B C ,在向下平移的过程中,易知菱形''''O A B C 与菱形OABC 重叠部分的四边形'AEC F 为平行四边形,如图2.试探究:当m 为何值时,平行四边形'AEC F 为菱形:(2)如图,在()1的条件下,连接''',AC B O G 、为CE 的中点J 为EB 的中点,H 为AC 上一动点,I 为''B O 上一动点,连接,,,GH HI IJ 求GH HI IJ ++的最小值,并直接写出此时,H I 点的坐标.2.如图,已知抛物线y =2ax bx c ++与x 轴交于A 3,0-(),B 33,0()两点,与y 轴交于点C 0,3().(1)求抛物线的解析式及顶点M 坐标;(2)在抛物线的对称轴上找到点P ,使得PAC 的周长最小,并求出点P 的坐标; (3)在(2)的条件下,若点D 是线段OC 上的一个动点(不与点O 、C 重合).过点D 作DE //PC 交x 轴于点E .设CD 的长为m ,问当m 取何值时,PDE ABMC 1S S 9=四边形. 3.在平面直角坐标系中,抛物线24y mx mx n =-+(m >0)与x 轴交于A ,B 两点,点B在点A 的右侧,顶点为C ,抛物线与y 轴交于点D ,直线CA 交y 轴于E ,且:3:4∆∆=ABC BCE S S .(1)求点A ,点B 的坐标;(2)将△BCO 绕点C 逆时针旋转一定角度后,点B 与点A 重合,点O 恰好落在y 轴上, ①求直线CE 的解析式;②求抛物线的解析式.4.已知:如图,AB 为O 的直径,弦CD AB ⊥垂足为E ,点H 为弧AC 上一点.连接DH 交AB 于点F ,连接HA 、BD ,点G 为DH 上一点,连接AG ,HAG BDC ∠=∠. (1)如图1,求证:AG HD ⊥;(2)如图2,连接HC ,若HC HF =,求证:HC HA =;(3)如图3,连接HO 交AG 于点K ,若点F 为DG 的中点,HC 2HG =,求KG AK的值.5.如图1,抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),交x 轴于A 、B 两点,交y轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.(3)如图3,点M的坐标为(32,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.6.如图,在梯形ABCD中,AD//BC,AB=CD=AD=5,cos45B ,点O是边BC上的动点,以OB为半径的O与射线BA和边BC分别交于点E和点M,联结AM,作∠CMN=∠BAM,射线MN与边AD、射线CD分别交于点F、N.(1)当点E为边AB的中点时,求DF的长;(2)分别联结AN 、MD ,当AN//MD 时,求MN 的长;(3)将O 绕着点M 旋转180°得到'O ,如果以点N 为圆心的N 与'O 都内切,求O 的半径长.7.如图,在四边形ABCD 中,∠B=90°,AD//BC ,AD=16,BC=21,CD=13.(1)求直线AD 和BC 之间的距离;(2)动点P 从点B 出发,沿射线BC 以每秒2个单位长度的速度运动,动点Q 从点A 出发,在线段AD 上以每秒1个单位长度的速度运动,点P 、Q 同时出发,当点Q 运动到点D 时,两点同时停止运动,设运动时间为t 秒.试求当t 为何值时,以P 、Q 、D 、C 为顶点的四边形为平行四边形?(3)在(2)的条件下,是否存在点P ,使△PQD 为等腰三角形?若存在,请直接写出相应的t 值,若不存在,请说明理由.8.如图1,正方形CEFG 绕正方形ABCD 的顶点C 旋转,连接AF ,点M 是AF 中点. (1)当点G 在BC 上时,如图2,连接BM 、MG ,求证:BM =MG ;(2)在旋转过程中,当点B 、G 、F 三点在同一直线上,若AB =5,CE =3,则MF = ;(3)在旋转过程中,当点G 在对角线AC 上时,连接DG 、MG ,请你画出图形,探究DG 、MG 的数量关系,并说明理由.9.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,第一颗弹珠弹出后其速度1y (米/分钟)与时间x (分钟)前2分钟满足二次函数21y ax ,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.(1)求第一颗弹珠的速度1y (米/分钟)与时间x (分钟)之间的函数关系式;(2)第一颗弹珠弹出1分钟后,弹出第二颗弹珠,第二颗弹珠的运行情况与第一颗相同,直接写出第二颗弹珠的速度2y (米/分钟)与弹出第一颗弹珠后的时间x (分钟)之间的函数关系式;(3)当两颗弹珠同时在轨道上时,第____分钟末两颗弹珠的速度相差最大,最大相差______;(4)判断当两颗弹珠同时在轨道上时,是否存在某时刻速度相同?请说明理由,并指出可以通过解哪个方程求出这一时刻.10.综合与实践A纸是我们学习工作最常用的纸张之一,其长宽之比是2:1,我们定义:长宽之比是42:1的矩形纸片称为“标准纸”.操作判断:()1如图1所示,矩形纸片2=是一张“标准纸”,将纸片折叠一次,使点ABCD AD AB()AB=求CF的B与D重合,再展开,折痕EF交AD边于点,E交BC边于点F,若1,长,()2如图2,在()1的基础上,连接,BE判断四边形BD折痕EF交BD于点O,连接,BFDE的形状,并说明理由.探究发现:()3如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点A 与点C 重合,再展开,痕MN 交AD 边于点M ,BC 交边于点,N 交BD 也是点O .然后将四边形ENFM 剪下,探究纸片ENFM 是否为“标准纸”,说明理由.11.如图,在平面直角坐标中,点O 为坐标原点,ABC ∆的三个顶点坐标分别为()A O m ,,(),B m O -,(),C n O ,5AC =且OBA OAB ∠=∠,其中m ,n 满足725m n m n +=⎧⎨-=⎩.(1)求点A ,C 的坐标;(2)点P 从点A 出发,以每秒1个单位长度的速度沿y 轴负方向运动,设点P 的运动时间为t 秒.连接BP 、CP ,用含有t 的式子表示BPC ∆的面积为S (直接写出t 的取值范围);(3)在(2)的条件下,是否存在t 的值,使得ΔΔ32PAB POC S S =,若存在,请求出t 的值,并直接写出BP 中点Q 的坐标;若不存,请说明理由.12.注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.如图,将一个矩形纸片ABCD ,放置在平面直角坐标系中,()0,0A ,()4,0B ,()0,3D ,M 是边CD 上一点,将ADM 沿直线AM 折叠,得到ANM . (Ⅰ)当AN 平分MAB ∠时,求DAM ∠的度数和点M 的坐标;(Ⅱ)连接BN ,当1DM =时,求ABN 的面积;(Ⅲ)当射线BN 交线段CD 于点F 时,求DF 的最大值.(直接写出答案) 在研究第(Ⅱ)问时,师生有如下对话:师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题. 小明:我是这样想的,延长MN 与x 轴交于P 点,于是出现了Rt NAP △.小雨:我和你想的不一样,我过点N 作y 轴的平行线,出现了两个Rt NAP △.13.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a += (x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为__________________;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x=+>,请利用特征点求出该函数的最小值.14.如图①,在ABC ∆中,90C ∠=︒,10,8AB BC ==.点,D E 分别是边,AC BC 上的动点,连接DE .设CD x =(0x >),BE y =,y 与x 之间的函数关系如图②所示.(1)求出图②中线段PQ 所在直线的函数表达式;(2)将DCE 沿DE 翻折,得DME .①点M 是否可以落在ABC ∆的某条角平分线上?如果可以,求出相应x 的值;如果不可以,说明理由;②直接写出....DME 与ABC ∆重叠部分面积的最大值及相应x 的值.15.平面直角坐标系中,点A 、B 分别在x 轴正半轴、y 轴正半轴上,AO =BO ,△ABO 的面积为8.(1)求点A 的坐标;(2)点C 、D 分别在x 轴负半轴、y 轴正半轴上(D 在B 点上方),AB ⊥CD 于E ,设点D 纵坐标为t ,△BCE 的面积为S ,求S 与t 的函数关系;(3)在(2)的条件下,点F 为BE 中点,连接OF 交BC 于G ,当∠FOB +∠DAE =45°时,求点E 坐标.16.如图,在平面直角坐标系中,点(1,2)A ,(5,0)B ,抛物线22(0)y ax ax a =->交x 轴正半轴于点C ,连结AO ,AB .(1)求点C 的坐标;(2)求直线AB 的表达式;(3)设抛物线22(0)y ax ax a =->分别交边BA ,BA 延长线于点D ,E .①若2AE AO =,求抛物线表达式;②若CDB △与BOA △相似,则a 的值为 .(直接写出答案)17.已知:菱形 ABCD ,点 E 在线段 BC 上,连接 DE ,点 F 在线段 AB 上,连接 CF 、DF , CF 与 DE 交于点 G ,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.(1)求证:CD=CF ;(2)设∠CED = x ,∠DCF = y ,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围) (3)在(2)的条件下,当 x =45°时,以 CD 为底边作等腰△CDK ,顶角顶点 K 在菱形 ABCD 的内部,连接 GK ,若 GK ∥CD ,CD =4 时,求线段 KG 的长.18.在Rt ABC ∆中,6AB =,90B ∠=︒,8BC =,点P 从A 出发沿AC 方向在运动速度为3个单位/秒,点Q 从C 出发向点B 运动,速度为1个单位/秒,P 、Q 同时出发,点Q到点B 时两点同时停止运动.(1)点P 在线段AC 上运动,过P 作DP PQ ⊥交边AB 于D ,2t =时,求PD PQ 的值; (2)运动t 秒后,90BPQ ∠=︒,求此时t 的值;(3)t =________时,AQ QP =. 19.已知:AB 为⊙O 的直径,点C 为弧AB 的中点,点D 为⊙O 上一点,连接CD ,交AB 于点M ,AE 为∠DAM 的平分线,交CD 于点E .(1)如图1,连接BE ,若∠ACD=22°,求∠MBE 的度数;(2) 如图2,连接DO 并延长,交⊙O 于点F ,连接AF ,交CD 于点N .①求证:DM 2+CN 2=CM 2;②如图3,当AD=1,AB=10时,请直接写出....线段ME 的长. 20.如图,平面直角坐标系中,抛物线228y ax ax a =--与x 轴交于B 、C 两点(点B 在点C 右侧),与y 轴交于点A ,连接AB ,25AB =.(1)求抛物线的解析式;(2)点P 在第二象限的抛物线上,连接PB 交y 轴于D ,取PB 的中点E ,过点E 作EH x ⊥轴于点H ,连接DH ,设点P 的横坐标为t .ODH 的面积为S ,求S 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,作PF y ⊥轴于F ,连接CP 、CD ,CP CD =,点S 为PF 上一点,连接BS 交y 轴于点T ,连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒,在射线CS 上取点Q.连接QF ,QF RF =,求直线TQ 的解析式. 21.如图,直角梯形ABCD 中,1//,90,60,3,9,AD BC A C AD cm BC cm O ︒︒∠∠====的圆心1O 从点A 开始沿折线——A D C 以1/cm s 的速度向点C 运动,2O 的圆心2O 从点B 开始沿BA 边以3/cm s 的速度向点A 运动,1O 半径为22,cm O 的半径为4cm ,若12,O O 分别从点A 、点B 同时出发,运动的时间为ts(1)请求出2O 与腰CD 相切时t 的值;(2)在03s t s ≤<范围内,当t 为何值时,1O 与2O 外切?22.如图1,以AB 为直径作⊙O ,点C 是直径AB 上方半圆上的一点,连结AC ,BC ,过点C 作∠ACB 的平分线交⊙O 于点D ,过点D 作AB 的平行线交CB 的延长线于点E .(1)如图1,连结AD ,求证:∠ADC =∠DEC . (2)若⊙O 的半径为5,求CA •CE 的最大值. (3)如图2,连结AE ,设tan ∠ABC =x ,tan ∠AEC =y , ①求y 关于x 的函数解析式; ②若CB BE =45,求y 的值.23.在平面直角坐标系xOy 中,点A 、B 为反比例函数()4x 0xy =>的图像上两点,A 点的横坐标与B 点的纵坐标均为1,将()4x 0xy =>的图像绕原点O 顺时针旋转90°,A 点的对应点为A’,B 点的对应点为B’.(1)点A’的坐标是 ,点B’的坐标是 ;(2)在x 轴上取一点P ,使得PA+PB 的值最小,直接写出点P 的坐标. 此时在反比例函数()4x 0xy =>的图像上是否存在一点Q ,使△A’B’Q 的面积与△PAB 的面积相等,若存在,求出点Q 的横坐标;若不存在,请说明理由;(3)连接AB’,动点M 从A 点出发沿线段AB’以每秒1个单位长度的速度向终点B’运动;动点N 同时从B’点出发沿线段B’A’以每秒1个单位长度的速度向终点A’运动.当其中一个点停止运动时,另一个点也随之停止运动.设运动的时间为t 秒,试探究:是否存在使△MNB’为等腰直角三角形的t 值.若存在,求出t 的值;若不存在,说明理由.24.问题探究(1)如图1.在ABC 中,8BC =,D 为BC 上一点,6AD =.则ABC 面积的最大值是_______.(2)如图2,在ABC 中,60BAC ∠=︒,AG 为BC 边上的高,O 为ABC 的外接圆,若3AG =,试判断BC 是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.问题解决:如图3,王老先生有一块矩形地ABCD ,6212AB =,626BC =+,现在他想利用这块地建一个四边形鱼塘AMFN ,且满足点E 在CD 上,AD DE =,点F 在BC上,且6CF =,点M 在AE 上,点N 在AB 上,90MFN ∠=︒,这个四边形AMFN 的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由. 25.如图,直线y =12x ﹣2与x 轴交于点B ,与y 轴交于点A ,抛物线y =ax 2﹣32x+c 经过A ,B 两点,与x 轴的另一交点为C . (1)求抛物线的解析式;(2)M 为抛物线上一点,直线AM 与x 轴交于点N ,当32MN AN =时,求点M 的坐标; (3)P 为抛物线上的动点,连接AP ,当∠PAB 与△AOB 的一个内角相等时,直接写出点P 的坐标.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.H解析:(13221H(91413314,I(275235【解析】 【分析】(1)根据菱形性质,得到A 、B 、C 、O 四点坐标,然后根据平移得到对应点坐标,故可求得C E '和C F '的长,令它们相等可得m 的值;(2)点G 作以C A '为对称轴的点G ',交C F '于点G ',点J 作以O B ''为对称轴的点J ',交A B ''于点J ',G J ''与C A '、A B ''的交点便是点H 、I ;先利用对称的性质,求解得出点G '、J '的坐标,然后利用代入系数法求得线段对应函数解析式,最后联立方程得到点H 、I 的坐标. 【详解】(1)如下图,CB 与y 轴交于点M ,过点C 作x 轴的垂线,交x 轴于点N∵在菱形ABCO 中,∠C=60°,菱形边长为4 ∴在Rt △COM 中,CM=2,3∴O(0,0),A(4,0),B(2,3,C(-2,3∵将菱形OABC 先向右平移4个单位后,再向下平移() 03m m <<个单位,得到菱形''''O A B C∴O '(4,-m),A '(8,-m),B '(6,3m -),C '(2,3m -) ∴直线AB 的解析式为:y=343x +∵点E 的纵坐标为:3m -,代入解析式得:x=32+ ∴E(32+,3m -) 同理,F(34,0) ∵四边形AE C F '是菱形 ∴E F C C '=' E 33C m '=∵C '(2,3m -),F(34,0) ∴NF=32,∴23F 4C =-' 3234=- 解得:3(2)如下图,点G 作以C A '为对称轴的点G ',交C F '于点G ',过点C '作x 轴的垂线,交过点G '作y 轴的垂线于点K ,同样作点J '和点Q3C '(23),E(33 ∵点G 是C E '的中点,∴12C G '= ∴12C G ''=,∴14G K '=,3C K '=∴G '(94,334) 同理,J 32B J B '''== ∴34J Q '=,334QB '= ∴J '(274,3 ∴22279333214444G J ⎛⎫⎛⎫=-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭''21根据点A 、C '可得直线A C '的解析式为:35324y x =-+根据点O '、B '可得直线O B ''的解析式为:353y x =- 根据点G '、J '可得直线G J ''的解析式为:339y x = 联立G J ''和A C '得:x=914,y=13314,∴H(914,13314) 联立G J ''和O B ''得:x=275,2327523) 【点睛】本题考查了菱形的性质、一次函数与平面直角坐标系,在第(2)问中,解题关键是利用对称找出最短距离对应的点.2.C解析:(1)21y x 43=-+(,顶点M4;(2)P 2);(3)1m =2,2m =1【解析】 【分析】(1)由点C 的坐标,可求出c的值,再把()A、()B 代入解析式,即可求出a 、b 的值,即可求出抛物线的解析式,将解析式化为顶点式,即可求出顶点M 的坐标;(2)因为A 、B 关于抛物线的对称轴对称,连接BC 与抛物线对称轴交于一点,即为所求点P ,设对称轴与x 轴交于点H ,证明PHB COB ∽,即可求出PH 的长,从而求出点P 的 坐标;(3)根据点A 、B 、M 、C 的坐标,可求出ABMC S 四边形,从而求出PDES=OC =3,OB=OCB ∠=60,因为DE //PC ,推出 ODE ∠=60,从而得到OD =3m -,)OE 3m =-,根据PDEDOE PDOE SS S=-四边形,列出关于m 的方程,解方程即可. 【详解】(1)∵抛物线y =2ax bx c a 0++≠()过()A、()B ,()C 0,3三点, ∴c =3,∴3a 3027a 30⎧-+=⎪⎨++=⎪⎩,解得1a 3b 3⎧=-⎪⎪⎨⎪=⎪⎩.故抛物线的解析式为(2211y x x 3x 4333=-++=--+,故顶点M为)4.(2)如图1,∵点A 、B 关于抛物线的对称轴对称,∴连接BC 与抛物线对称轴交于一点,即为所求点P . 设对称轴与x 轴交于点H , ∵PH //y 轴, ∴PHB COB ∽. ∴PH BHCO BO=. 由题意得BH =23,CO =3,BO =33,∴PH 23333=, ∴PH =2. ∴()P3,2.(3)如图2,∵()A 3,0-、()B 33,0,()C 0,3,()M3,4,∴ABMC S 四边形=()AOC MHBCOHM 111SS S3334342393222++=⨯⨯++⨯⨯=梯形. ∵ABMC S 四边形=PDE9S ,∴PDES3=∵OC =3,OB =33∴OCB ∠=60. ∵DE //PC , ∴ODE ∠=60.∴OD =3m -,)OE 33m =-.∵PDOE S 四边形=))COE1S 33m 3m 22=⨯-=-,∴PDES=))2DOEPDOE S S3m 3m -=--=四边形20m +<<(.∴2+= 解得1m =2,2m =1. 【点睛】此题主要考查了待定系数法求二次函数解析式以及相似三角形的判定与性质和四边形面积求法等知识,熟练运用方程思想方法和转化思想是解题关键.3.A解析:(1) A (12,0) B (72,0);(2) ①33y x =-+,②2999y x x =-+【解析】 【分析】(1)根据抛物线的解析式可得对称轴为x =2,利用:3:4∆∆=ABC BCE S S 得出CA :CE =3:4,由△AOE ∽△AGC 可得13=AO AG ,进而求得OA 、OB 的长,即可求得点A 、点B 的坐标; (2)根据旋转的性质求出C 点坐标,利用C 点坐标和△AOE ∽△AGC 可求得E 点坐标,,分别利用待定系数法即可求得直线CE 和抛物线的解析式. 【详解】解:(1)∵抛物线的解析式为24(0)=-+>y mx mx n m ,∴对称轴为直线422-=-=mx m, 如图,设对称轴与x 轴交于G ,则//CG y 轴,2OG =,∴△AOE ∽△AGC , ∴=AO AEAG AC, ∵:3:4ABCBCES S=, ∴CA :CE =3:4 ,则31AE AC =, ∴13==AO AE AG AC , ∴1142==OA OG ,3342==AG OG , 则23==AB AG ,72=+=OB OA AB , ∴A (12,0), B (72,0); (2)如图,设O 旋转后落在点Q 处,过点C 作CP y ⊥轴于点P ,由旋转的性质得:△BCO ≌△ACQ , ∴BO =AQ =72,CO =CQ , ∴OQ====∵CP y ⊥轴,∴12==OP OQ ∴点C的坐标为(2,,则CG =由(1)得△AOE ∽△AGC ,13==OE AE CG AC ,∴3OE =,即点E的坐标为(0,3, ①设CE 的解析式为y kx b =+,分别代入C (2,,E 得:23k b b ⎧+=⎪⎨=⎪⎩,解得:k b ⎧=⎪⎪⎨⎪=⎪⎩, ∴CE的解析式为33y x =-+; ②将A (12,0),C (2,分别代入24y mx mx n =-+得:120448m m n m m n ⎧-+=⎪⎨⎪-+=⎩,解得:99m n ⎧=⎪⎪⎨⎪=⎪⎩,∴抛物线解析式为2999y x x =-+. 【点睛】本题考查了二次函数的综合、旋转的性质、相似三角形的性质和求一次函数的解析式,正确的理解题意,熟练运算“数形结合思想”是解题的关键.4.A解析:(1)详见解析;(2)详见解析;(3)15KG AK = 【解析】 【分析】(1)根据同弧所对的圆周角相等,进行角度计算,得90AHG HAG ∠+∠=︒,进而得到90AGH ∠=︒,即可证明AG HD ⊥;(2)连接AC 、AD 、CF ,根据同弧所对的圆周角相等,进行角度计算,得HFA HAF ∠=∠,进而得到HF HA =,再根据已知HC HF =,得到HC HA =; (3)在DH 上截取DT HC =,过点C 作CM HD ⊥于点M ,通过证明AHC ≌ATD 得到AH AT =,进而得到HG CH GD +=,再根据F 为DG 中点,得到GF DF =,通过勾股定理逆用,证明90HCF ∠=︒,再通过解ACE △得1tan 3CAB ∠=,解△CDH 得1tan 2CDF ∠=,求得OF 、OH ,逆用勾股定理证明90HOF ∠=︒,易求1tan 2KHG ∠=,1tan 3HAG ∠=,最后求得KG AK 的值. 【详解】(1)证明:如图,设HAG ∠为α,∵HAG BDC ∠=∠,∴HAG BDC α∠=∠=,∵CD AB ⊥,∴90BDC DBE ∠+∠=︒∴90DBE α∠=︒-, ∵AHG ∠与ABD ∠为同对弧AD 所对的圆周角,∴90AHG ABD α∠=∠=︒-,∴90AHG HAG ∠+∠=︒,∴18090AGH AHG HAG ∠=︒-∠-∠=︒∴AG HD ⊥(2)如图,连接AC 、AD 、CF ,∵AB 为直径,AB CD ⊥,∴CE DE =,∴AB 垂直平分CD ,∴AC AD =,FC FD =,∴ACD ADC ∠=∠,FCD FDC ∠=∠,∴ACD FCD ADC FDC ∠-∠=∠-∠,即ACF ADF ∠=∠,设FCD FDC α∠=∠=,ACF ADF β∠=∠=,∵ADH ∠与ACH ∠为同对弧AH 所对的圆周角,∴ADH ACH β∠=∠=,∴2HCF HCA ACF β∠=∠+∠=,∵HFC FCD FDC ∠=∠+∠,∴2HFC α∠=,∵HC HF =,∴HCF HFC ∠=∠,∴22αβ=,∴αβ=,∵AB 为直径,∴90ADB ∠=︒,∴90HDB β∠=︒-,∵HAB ∠与为HDB ∠同对弧BH 所对的圆周角,∴90HAB HDB β∠=∠=︒-,∵AB CD ⊥,∴9090BFD αβ∠=︒-=︒-,∵9090HFA BFD αβ∠=∠=︒-=︒-,∴HFA HAF ∠=∠,∴HF HA =,∴HC HA =;(3)如图,在DH 上截取DT HC =,∵ADH ∠与ACH ∠同对弧AH 所对的圆周角,∴ADH ACH ∠=∠,∵AB 为直径,且AB CD ⊥∴AC =AD ,∴AC AD =,∴AHC ≌ATD ,∴AH AT =,∵AG HT ⊥,∴HG TG =,∴HG CH GT DT GD +=+=,设2HG k =,则4CH k =,GD 6k =,∵F 为DG 中点,∴3GF DF k ==,∴5HF HG GF k =+=,FD =CF =3k ,在HCF 中,由勾股定理逆定理得90HCF ∠=︒,过点C 作CM HD ⊥于点M ,由△HCF 面积,可求CM =125k ,∴95MF k =, ∴1tan 2CM CM CDF MD MF FD ∠===+, 解ACE △得1tan 3CAB ∠=, 易求OF ,OH ,由勾股定理逆定理得90HOF ∠=︒, 易求1tan 2KHG ∠=,1tan 3HAG ∠=, ∴15KG AK =. 【点睛】本题考查圆与三角形综合,主要考查知识点有同弧所对的圆周角相等,垂径定理,三角形全等的判定与性质,勾股定理的逆用,解直角三角形,锐角三角函数等,知识点跨度大,计算量多;熟练掌握圆的性质和三角形相关知识是解决本题的关键.5.E解析:(1)2y x 2x 3=-++;(2)E (2,3)或(1,4);(3)P 点横坐标为【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),设抛物线的解析式为2(1)4y a x =-+,由抛物线过点B,(3,0),即可求出a 的值,即可求得解析式; (2)过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x xx -++,求出A 、D 点的坐标,得到OM=x ,则AM=x+1,由AF=2EF 得到22(1)33x AN AM +==,从而推出点F 的坐标21210(,)3333x x --+,由23FN EM =,列出关于x 的方程求解即可;(3)先根据待定系数法求出直线DM 的解析式为y=-2x+3,过点P 作PT ∥y 轴交直线DM 于点T ,过点F 作直线GH ⊥y 轴交PT 于点G ,交直线CE 于点H.证明△FGP ≌△FHQ ,得到FG=FH ,PT=45GH.设点P (m ,-m²+2m+3),则T (m ,-2m+3),则PT=m²-4m ,GH=1-m , 可得m²-4m=45(1-m ),解方程即可. 【详解】(1)∵抛物线的顶点为C (1,4),∴设抛物线的解析式为2(1)4y a x =-+,∵抛物线过点B,(3,0),∴20(31)4a =-+,解得a=-1,∴设抛物线的解析式为2(1)4y x =--+,即2y x 2x 3=-++;(2)如图,过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x x x -++,∵抛物线的解析式为2y x 2x 3=-++,当y=0时,2023x x =-++,解得x=-1或x=3,∴A (-1.0),∴点D (0,3),∴过点BD 的直线解析式为3y x =-+,点F 在直线BD 上,则OM=x ,AM=x+1,∴22(1)33xAN AM+==,∴2(1)2111333x xON AN+=-=-=-,∴21210(,)3333x xF--+,∴2210332233FNEM x xx+--++==,解得x=1或x=2,∴点E的坐标为(2,3)或(1,4);(3)设直线DM的解析式为y=kx+b,过点D(0,3),M(32,0),可得,323k bb⎧+=⎪⎨⎪=⎩,解得k=-2,b=3,∴直线DM的解析式为y=-2x+3,∴32OM=,3OD=,∴tan∠DMO=2,如图,过点P作PT∥y轴交直线DM于点T,过点F作直线GH⊥y轴交PT于点G,交直线CE于点H.∵PQ⊥MT,∴∠TFG=∠TPF,∴TG=2GF,GF=2PG,∴PT=25GF,∵PF=QF,∴△FGP≌△FHQ,∴FG=FH ,∴PT=45GH. 设点P (m ,-m²+2m+3),则T (m ,-2m+3),∴PT=m²-4m ,GH=1-m ,∴m²-4m=45(1-m ), 解得:1112018m -=,或2112018m +=(不合题意,舍去), ∴点P 的横坐标为11201-. 【点睛】本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识,解题的关键是学会用转化的思想思考问题,学会用数形结合的思想解决问题,有一定难度.6.D解析:(1)DF 的长为158;(2)MN 的长为5;(3)O 的半径长为258. 【解析】【分析】(1)作EH BM ⊥于H ,根据中位线定理得出四边形BMFA 是平行四边形,从而利用cos 45B =解直角三角形即可求算半径,再根据平行四边形的性质求FD 即可; (2)先证AMB CNM ∠=∠,再证MAD CNM ∠=∠,从而证明AFM NFD ∆~∆,得到AF MF AF DF NF MF NF DF=⇒=,再通过平行证明AFN DFM ∆~∆,从而得到AF NF AF MF NF DF DF MF=⇒=,通过两式相乘得出AF NF =再根据平行得出NF DF =, 从而得出答案.(3)通过图形得出MN 垂直平分'OO ,从而得出90BAM CMN ∠=∠=︒,再利用cos 45B =解三角函数即可得出答案. 【详解】(1)如图,作EH BM ⊥于H :∵E 为AB 中点,45,cos 5AB AD DC B ==== ∴52AE BE ==∴cos 45BH B BE == ∴2BH = ∴2253222EH ⎛⎫=-= ⎪⎝⎭设半径为r ,在Rt OEH ∆中: ()222322r r ⎛⎫=-+ ⎪⎝⎭ 解得:2516r =∵,E O 分别为,BA BM 中点 ∴BAM BEO OBE ∠=∠=∠又∵CMN BAM ∠=∠∴CMN OBE ∠=∠∴//MF AB∴四边形BMFA 是平行四边形∴2528AF BM r ===∴2515588FD AD AF =-=-= (2)如图:连接MD AN ,∵,B C BAM CMN ∠=∠∠=∠∴AMB CNM ∠=∠又∵AMB MAD ∠=∠∴MAD CNM ∠=∠又∵AFM NFD ∠=∠∴AFM NFD ∆~∆∴AF MF AF DF NF MF NF DF=⇒=① 又∵//MD AN∴AFN DFM ∆~∆ ∴AF NF AF MF NF DF DF MF=⇒=② 由①⨯②得; 22AF NF AF NF =⇒=∴NF DF =∴5MN AD ==故MN 的长为5;(3)作如图:∵圆O 与圆'O 外切且均与圆N 内切设圆N 半径为R ,圆O 半径为r∴'=NO R r NO -=∴N 在'OO 的中垂线上∴MN 垂直平分'OO∴90NMC ∠=︒∵90BAM CMN ∠=∠=︒∴A 点在圆上∴54cos 5AB B BM BM === 解得:254BM =O 的半径长为258【点睛】 本题是一道圆的综合题目,难度较大,掌握相似之间的关系转化以及相关线段角度的关系转化是解题关键.7.A解析:(1)12;(2)5s或373s;(3)163s或685s或72s【解析】【分析】(1)AD与BC之间的距离即AB的长,如下图,过点D作BC的垂线,交BC于点E,在RtDEC中可求得DE的长,即AB的长,即AD与BC间的距离;(2)四边形QDCP为平行四边形,只需QD=CP即可;(3)存在3大类情况,情况一:QP=PD,情况二:PD=QD,情况三:QP=QD,而每大类中,点P存在2种情况,一种为点P还未到达点C,另一种为点P从点C处返回.【详解】(1)如下图,过点D作BC的垂线,交BC于点E∵∠B=90°,AD∥BC∴AB⊥BC,AB⊥AD∴AB的长即为AD与BC之间的距离∵AD=16,BC=21,∴EC=5∵DC=13∴在Rt DEC中,DE=12同理,DE的长也是AD与BC之间的距离∴AD与BC之间的距离为12(2)∵AD∥BC∴只需QD=PC,则四边形QDCP是平行四边形QD=16-t,PC=21-2t或PC=2t-21∴16-t=21-2t或16-t=2t-21解得:t=5s或t=37 3s(3)情况一:QP=PD图形如下,过点P作AD的垂线,交AD于点F∵PQ=PD ,PF ⊥QD ,∴QF=FD∵AF ∥BP ,AB ∥FP ,∠B=90°∴四边形ABPF 是矩形,∴AF=BP由题意得:AQ=t ,则QD=16-t ,QF=8-2t ,AF=8+2t BP=2t 或BP=21-(2t -21)=42-2t∵AF=BP∴8+2t =2t 或8+2t =42-2t 解得:t=163或t=685情况二:PD=QD ,图形如下,过点P 作AD 的垂线,交AD 于点F同理QD=16-t ,PF=AB=12BP=2t 或21-(2t -21)=42-2t则FD=AD -AF=AD -BP=16-2t 或FD=16-(42-2t)=2t -26 ∴在Rt PFD 中,()22212162PD t =+-或()22212226PD t =+- ∵PD=QD ,∴22PD QD =∴()()22216t 12162t =+--或()()22216t 12226t =+-- 解得:2个方程都无解情况三:QP=QD ,图形如下,过点P 作AD 的垂线,交AD 于点F同理:QD=16-t ,FP=12BP=2t 或BP=42-2tQF=AF -AQ=BP -AQ=2t -t=t 或QF=42-2t -t=42-3t在Rt QFP 中,22212PQ t =+或()22212423PQ t =+- ∵PQ=QD ,∴22PQ QD =∴()22216t 12t =+-或()()22216t 12423t =+--第一个方程解得:t=72,第二个方程解得:无解 综上得:t=163或685或72 【点睛】本题考查四边形中的动点问题,用到了勾股定理、平行四边形的性质、矩形的性质,解题关键是根据点Q 运动的轨迹,得出BP 的长度. 8.D解析:(1)证明见解析;(2)29或5;(3)DG =2MG ,理由见解析.【解析】【分析】(1)连接MG 并延长交AB 于N 点,证明△ANM ≌△FGM 后得到MG=MN ,AN=CG ,进而得到BN=BG ,得到△ANG 为等腰直角三角形,即可证明MG=MB.(2)分两种情况画出图形再利用(1)中的思路结合勾股定理即可求解.(3)先画出图形,然后证明△ADG ≌△ABG ,得到DG=BG ,又△BMG 为等腰直角三角形,故而得到DG=BG=2MG.【详解】解:(1) 连接MG 并延长交AB 于N 点,如下图所示:∵GF ∥AN ,∴∠NAM=∠GFM在△ANM 和△FGM 中∠∠=⎧⎪=⎨⎪∠=∠⎩BAM GFM AM FMNMA GMF ,∴△ANM ≌△FGM(ASA)∴MG=MN ,CG=GF=AN∴AB-AN=BC-CG∴NB=GB∴△NBG 为等腰直角三角形又M 是NG 的中点∴由直角三角形斜边上的中线等于斜边的一半知:故有:MG=MB.(2)分类讨论:情况一:当B 、G 、F 三点在正方形ABCD 外同一直线上时延长MG 到N 点,并使得MG=MN ,连接AN ,BN∴∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ,∴△AMN ≌△FMG(SAS)∴AN=GF=GC ,∠NAM=∠GFM∴AN ∥GF∴∠NAB+∠ABG=180°又∠ABC=90°∴∠NAB+∠CBG=90°又在△BCG 中,∠BCG+∠CBG=90°∴∠NAB=∠BCG∴在△ABN 中和△CBG 中:∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ,∴△ABN ≌△CBG(SAS)∴BN=BG ,∠ABN=∠CBG∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形,且∠BGN=45°在Rt △BCG 中,2222=534-=-=BG BC CG过M 点作MH ⊥BG 于H 点,∴△MHB 为等腰直角三角形∴MH=BH=HG=12BG=2 在Rt △MFH 中,2222MF=2529+=+=MH HF情况二:当B 、G 、F 三点在正方形ABCD 内同一直线上时如下图所示,延长MG 到MN ,并使得MG=MN ,连接NA 、NB ,同情况一中证明思路,∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ,△AMN ≌△FMG(SAS)∴AN=GF=GC ,∠NAM=∠GFM∴AN ∥GF∴∠NAB=∠ABG又∠ABG+∠GBC=90°∠GBC+∠BIF=90°∴∠BIF=∠ABG又∠BIF=∠BCG ,∠ABC=∠NAB∴∠NAB=∠GCB∴在△ABN 中和△CBG 中:∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ,∴△ABN ≌△CBG(SAS)∴BN=BG ,∠ABN=∠CBG∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形,且∠BGN=45°在△BCG 中,2222=534-=-=BG BC CG过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形∴MH=BH=HG=12BG=2∴HF=HG-GF=2-1=1在Rt△MFH中,2222MF=215+=+=MH HF故答案为:29或 5.(3)由题意作出图形如下所示:DG、MG的数量关系为:2,理由如下:∵G点在AC上∴∠DAG=∠BAG=45°在△ADG和△ABG中:∠∠=⎧⎪=⎨⎪=⎩AD ABDAG BAGAG AG,∴△ADG≌△BAG(SAS)∴DG=BG又由(2)中的证明过程可知:△MBG为等腰直角三角形∴2MG∴2MG故答案为:2MG.【点睛】本题考查了正方形的旋转、三角形的全等、勾股定理等知识,难度很大,关键是要能正确做出图形,利用数形结合的思想,熟练的使用正方形的性质是解题的关键.9.(1)212(02)16(25)x xyxx⎧≤≤⎪=⎨≤≤⎪⎩;(2)220(01)2(1)(13)16(36)1xy x xxx⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)第2分钟末两颗弹珠速度相差最大,最大相差6米/分钟;(4)存在,理由详见解析【解析】【分析】(1)将(1,2)代入21y ax =,得2a =,从而得到212y x =,再代入2x =求出18y =,即可得到反比例函数解析式,即可得解;(2)当01x ≤≤时,第二颗弹珠未弹出,故第二颗弹珠的解析式为20y =;再分别根据(1)中的结论,即可求出当13x <≤和36x <≤时第二颗弹珠的解析式;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,则第2分钟末两颗弹珠速度相差最大,分别求出第2分钟末时两颗弹珠的速度,再相减即可的解;(4)第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟,第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同.可以根据速度相等时列方程求得时刻.【详解】(1)当02x ≤≤时,将(1,2)代入21y ax =,得2a =,212y x ∴=,∵当2x =时,18y =,∴当25x ≤≤时,116y x=, 1y ∴与x 的函数关系式为212(02)16(25)x x y x x⎧≤≤⎪=⎨≤≤⎪⎩; (2)当01x ≤≤时,第二颗弹珠未弹出,∴第二颗弹珠的解析式为20y =;当13x <≤时,第二颗弹珠的解析式为222(1)y x =-;当36x <≤时,第二颗弹珠的解析式为2161y x =-; ∴2y 与x 的函数关系式为220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,∴第2分钟末两颗弹珠速度相差最大,∵第一颗弹珠的速度为2218222y x =⨯==米/分钟,第二颗弹珠的速度为2122(1)212y x =⨯==-米/分钟,∴两颗弹珠的速度最大相差8-2=6米/分钟;(4)存在,理由如下:第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟, 第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同. 这个时刻可以通过解方程2162(1)x x =-求得. 【点睛】本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息,明确自变量的取值范围和图象所经过的点的坐标.10.(1) CF ;(2) 四边形BFDE 是菱形,理由见解析;(3) 纸片ENFM 是“标准纸",理由见解析【解析】【分析】(1)1AB =,则AD =ABCD 是矩形,得到1,CD AB BC AD ==-=FB FD =,设CF x =,则FB FD x ==,在Rt DCF △中,222+=CD CF DF ,可得)2221x x +=即可求解.(2)当顶点B 与点D 重合时,折痕EF 垂直平分BD ,可得OB OD =,90BOF DOE ∠=∠=,在矩形ABCD 中,//AD BC ,得到OBF ODE ∠=∠,在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,,可得BOF DOE ≅,OE OF =,再根据OB OD =,可得四边形BFDE 是平行四边形,最后根据EF BD ⊥,即可求证平行四边形BFDE 是菱形.(3)由()2可知,OE OF =,同理可知,OM ON =,可得四边形ENFM 是平行四边形,根据90DOE DAB ∠=∠=︒,得到DOE DAB ,再根据AD =,可得2OE AB OD AD ===,进而得到2OE OD =,2EF BD =,同理可得,2MN AC =,根据四边形ABCD 是矩形,可得AC BD =,EF MN =,四边形ENFM 是矩形,90EMF ∠=,MF OD tan FEM ME OE ∠===MF =,即可求证纸片ENFM 是“标准纸".【详解】解:()11,AB =则AD AB ==四边形ABCD 是矩形。
数学中考压轴题大全(含答案、详细解析版)

( 2) A( 3,0) B (5,4)
C (0,4) ………… 5 分
C
1
A 01
B x
把点 A 坐标代入 y ax2 5ax 4 中,解得 a
1
……… 6 分
6
y
1 x2
5 x
4 …………………………………………
7分
66
y
M
( 3)存在符合条件的点 P 共有 3 个.以下分三类情形探索.
A
1
N
令 x=20,y=60 ,得 k=60
①
令 x=100,y=100 ,得 a× 802+ k=100
②
由①②解得
1 a
160 , k 60
∴y
1
2
x 20 60 。……… 14 分
160
2 、(常州)已知 A( 1, m) 与 B(2, m 3 3) 是反比例函数
y
k
图象上的两个点.
x
( 1)求 k 的值;
( 3)过原点 O 的另一条直线 l 交双曲线 y k ( k 0) 于 P, Q 两 x
一象限),若由点 A, B, P, Q 为顶点组成的四边形面积为 24 ,求点
y A
解: (1) ∵点 A横坐标为 4 , ∴当 x = 4 时, y = 2 .
O B
点( P 点在第 P 的坐标. x
∴ 点 A的坐标为( 4 , 2 ) .
∴ S = S 梯形 PEFA △POA = 6 .
∴ 1 (2
8 ) (m 4)
6,
2m
解得 m = 8 , m = - 2 ( 舍去 ) .
∴ P(8, 1) .
∴ 点 P的坐标是 P( 2,4)或 P( 8, 1).
中考数学压轴题真题解析

中考数学压轴题真题解析中考数学压轴题往往是综合性最强、难度最大的题目,它不仅考查学生对基础知识的掌握程度,更考验学生的思维能力、解题技巧和应变能力。
下面,我们就来详细解析一道具有代表性的中考数学压轴题。
题目:如图,在平面直角坐标系中,抛物线 y = x²+ bx + c 与 x轴交于 A(-1,0)、B(3,0)两点,与 y 轴交于点 C,点 D 是抛物线的顶点。
(1)求抛物线的解析式及顶点 D 的坐标;(2)点 P 是抛物线上的动点,且位于对称轴的右侧,当△PAB 的面积等于△ABC 的面积时,求点 P 的坐标;(3)在抛物线的对称轴上是否存在点 M,使得以 A、B、M 为顶点的三角形是等腰三角形?若存在,求出点 M 的坐标;若不存在,请说明理由。
解析:(1)因为抛物线 y = x²+ bx + c 与 x 轴交于 A(-1,0)、B (3,0)两点,所以把 A、B 两点的坐标代入抛物线的解析式可得:\\begin{cases}(-1)² b + c = 0 \\(3)²+ 3b + c = 0\end{cases}\\\begin{cases}-1 b + c = 0 \\-9 + 3b + c = 0\end{cases}\用第二个方程减去第一个方程可得:\\begin{align}-9 + 3b + c (-1 b + c) &= 0 \\-9 + 3b + c + 1 + b c &= 0 \\4b 8 &= 0 \\4b &= 8 \\b &= 2\end{align}\把 b = 2 代入第一个方程可得:\\begin{align}-1 2 + c &= 0 \\c &= 3\end{align}\所以抛物线的解析式为 y = x²+ 2x + 3。
对于抛物线 y = x²+ 2x + 3,其对称轴为 x = b/2a =-2/(-2)= 1。
全国中考数学压轴题全析全解
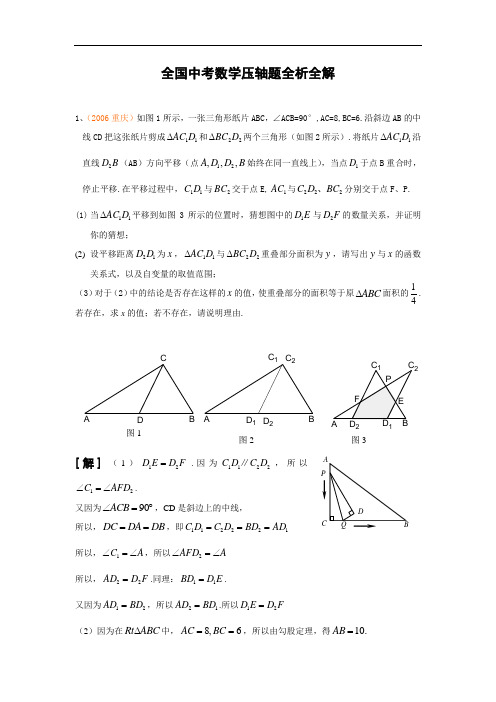
全国中考数学压轴题全析全解1、(2006重庆)如图1所示,一张三角形纸片ABC ,∠ACB=90°,AC=8,BC=6.沿斜边AB 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形(如图2所示).将纸片11AC D ∆沿直线2D B (AB )方向平移(点12,,,A D D B 始终在同一直线上),当点1D 于点B 重合时,停止平移.在平移过程中,11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P. (1) 当11AC D ∆平移到如图3所示的位置时,猜想图中的1D E 与2D F 的数量关系,并证明你的猜想;(2) 设平移距离21D D 为x ,11AC D ∆与22BC D ∆重叠部分面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;(3)对于(2)中的结论是否存在这样的x 的值,使重叠部分的面积等于原ABC ∆面积的14. 若存在,求x 的值;若不存在,请说明理由.[解](1)12D E D F =.因为1122C D C D ∥,所以12C AFD ∠=∠.又因为90ACB ∠=︒,CD 是斜边上的中线,所以,DC DA DB ==,即112221C D C D BD AD === 所以,1C A ∠=∠,所以2AFD A ∠=∠ 所以,22AD D F =.同理:11BD D E =.又因为12AD BD =,所以21AD BD =.所以12D E D F =(2)因为在Rt ABC ∆中,8,6AC BC ==,所以由勾股定理,得10.AB =CB D A 图1122图3C 2D 2C 1BD 1A 图2P即1211225AD BD C D C D ====又因为21D D x =,所以11225D E BD D F AD x ====-.所以21C F C E x == 在22BC D ∆中,2C 到2BD 的距离就是ABC ∆的AB 边上的高,为245. 设1BED ∆的1BD 边上的高为h ,由探究,得221BC D BED ∆∆∽,所以52455h x-=. 所以24(5)25x h -=.121112(5)225BED S BD h x ∆=⨯⨯=- 又因为1290C C ∠+∠=︒,所以290FPC ∠=︒.又因为2C B ∠=∠,43sin ,cos 55B B ==. 所以234,55PC x PF x == ,22216225FC P S PC PF x ∆=⨯=而2212221126(5)22525BC D BED FC P ABC y S S S S x x ∆∆∆∆=--=---所以21824(05)255y x x x =-+≤≤(3) 存在. 当14ABC y S ∆=时,即218246255x x -+=整理,得2320250.x x -+=解得,125,53x x ==.即当53x =或5x =时,重叠部分的面积等于原ABC ∆面积的142、(2006浙江金华)如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式; (2)若S 梯形OBCD,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的 三角形与△OBA 相似.若存在,请求出所有符合条件 的点P 的坐标;若不存在,请说明理由.[解] (1)直线AB 解析式为:y=33-x+3. (2)方法一:设点C坐标为(x ,33-x+3),那么OD =x ,CD =33-x+3.∴OBCD S 梯形=()2CD CD OB ⨯+=3632+-x . 由题意:3632+-x =334,解得4,221==x x (舍去) ∴ C(2,33) 方法二:∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形=334,∴63=∆ACD S . 由OA=3OB ,得∠BAO =30°,AD=3CD .∴ ACD S ∆=21CD ×AD =223CD =63.可得CD =33. ∴ AD=1,OD =2.∴C (2,33). (3)当∠OBP =Rt ∠时,如图①若△BOP ∽△OBA ,则∠BOP =∠BAO=30°,BP=3OB=3,∴1P (3,33). ②若△BPO ∽△OBA ,则∠BPO =∠BAO=30°,OP=33OB=1. ∴2P (1,3).当∠OPB =Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图),此时△PBO ∽△OBA ,∠BOP =∠BAO =30°过点P 作PM ⊥OA 于点M .方法一: 在Rt △PBO 中,BP =21OB =23,OP =3BP =23.∵ 在Rt △P MO 中,∠OPM =30°, ∴ OM =21OP =43;PM =3OM =433.∴3P (43,433).方法二:设P(x ,33-x+3),得OM =x ,PM =33-x+3由∠BOP =∠BAO,得∠POM =∠ABO .∵tan ∠POM==OMPM=x x 333+-,tan ∠ABOC=OBOA =3.∴33-x+3=3x ,解得x =43.此时,3P (43,433). ④若△POB ∽△OBA(如图),则∠OBP=∠BAO =30°,∠POM =30°. ∴ PM =33OM =43. ∴ 4P (43,43)(由对称性也可得到点4P 的坐标).当∠OPB =Rt ∠时,点P 在x轴上,不符合要求.综合得,符合条件的点有四个,分别是:1P (3,33),2P (1,3),3P (43,433),4P (43,43). 3、(2006山东济南)如图1,已知Rt ABC △中,30CAB ∠=,5BC =.过点A 作AE AB ⊥,且15AE =,连接BE 交AC 于点P .(1)求PA 的长;(2)以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由;(3)如图2,过点C 作CD AE ⊥,垂足为D .以点A 为圆心,r 为半径作⊙A ;以点C 为圆心,R 为半径作⊙C .若r 和R 的大小是可变化的,并且在变化过程中保持⊙A 和⊙C 相.切.,且使D 点在⊙A 的内部,B 点在⊙A 的外部,求r 和R 的变化范围.[解](1)在Rt ABC △中,305CAB BC ∠==,,210AC BC ∴==.CD图1图2AE BC ∥,APE CPB ∴△∽△. ::3:1PA PC AE BC ∴==. :3:4PA AC ∴=,3101542PA ⨯==. (2)BE 与⊙A 相切.在Rt ABE △中,AB =15AE =,tanAE ABE AB ∴∠===60ABE ∴∠=. 又30PAB ∠=,9090ABE PAB APB ∴∠+∠=∴∠=,, BE ∴与⊙A 相切.(3)因为5AD AB ==,,所以r 的变化范围为5r <<.当⊙A 与⊙C 外切时,10R r +=,所以R 的变化范围为105R -<<;当⊙A 与⊙C 内切时,10R r -=,所以R 的变化范围为1510R <<+ 4、(2006山东烟台)如图,已知抛物线L 1: y=x 2-4的图像与x 有交于A 、C 两点,(1)若抛物线l 2与l 1关于x 轴对称,求l 2的解析式; (2)若点B 是抛物线l 1上的一动点(B 不与A 、C 重合),以AC 为对角线,A 、B 、C 三点为顶点的平行四边形的第四个顶点定为D ,求证:点D 在l 2上;(3)探索:当点B 分别位于l 1在x 轴上、下两部分的图像上时,平行四边形ABCD 的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
数学f1初中数学2006年全国中考数学压轴题全解全析(1-14)

本文为自本人珍藏 版权所有 仅供参考 本文为自本人珍藏 版权所有 仅供参考2006年全国中考数学压轴题全解全析1、(北京课改B 卷)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;(2)探究:当等对角线四边形中两条对角线所夹锐角为60 时,这对60 角所对的两边之和与其中一条对角线的大小关系,并证明你的结论. [解] (1)答案不唯一,如正方形、矩形、等腰梯形等等.(2)结论:等对角线四边形中两条对角线所夹锐角为60 时,这对60 角所对的两边之和大于或等于一条对角线的长.已知:四边形A B C D 中,对角线A C ,B D 交于点O ,A C B D =, 且60AOD ∠= . 求证:B C A D A C +≥.证明:过点D 作D F AC ∥,在D F 上截取D E ,使D E AC =. 连结C E ,B E .故60EDO ∠= ,四边形A C E D 是平行四边形. 所以B D E △是等边三角形,C E A D =. 所以D E B E A C ==.①当B C 与C E 不在同一条直线上时(如图1), 在B C E △中,有B C C E B E +>.所以B C A D A C +>.②当B C 与C E 在同一条直线上时(如图2), 则BC C E BE +=.因此B C A D A C +=.综合①、②,得B C A D A C +≥.即等对角线四边形中两条对角线所夹角为60时,这对60角所对的两边之和大于或等于其中一条对角线的长.[点评]本题是一道探索题,是近年来中考命题的热点问题,在第2小题中要求学生先猜想可能的结论,再进行证明,这对学生的确有较高的能力要求,而在探索结论前可以自己先画几个草图,做到心中有数再去努力求证;很多学生往往会忽略特殊情况没有进行讨论,应当予以关注,总之这是一道新课标形势下的优秀压轴题。
全国中考数学压轴题全解全析

2006年全国中考数学压轴题全解全析31、(辽宁沈阳卷)如图,在平面直角坐标系中,直线13y x =-+分别与x 轴,y 轴交于点A ,点B .(1)以AB 为一边在第一象限内作等边ABC △及ABC △的外接圆M (用尺规作图,不要求写作法,但要保留作图痕迹);(2)若M 与x 轴的另一个交点为点D ,求A ,B ,C ,D 四点的坐标;(3)求经过A ,B ,D 三点的抛物线的解析式,并判断在抛物线上是否存在点P ,使A D P △的面积等于ADC △的面积?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.[解] (1)如图,正确作出图形,保留作图痕迹 (2)由直线13y x =-+,求得点A的坐标为),点B 的坐标为()01,∴在Rt AOB △中,OA =1OB =2AB ∴=,tan OAOBA OB==∠60OBA ∴=∠9030OAB OBA ∴=-=∠∠ABC △是等边三角形 2CA AB ∴==,60CAB =∠90CAD CAB OAB ∴=+=∠∠∠ ∴点C的坐标为)2,连结BMABC △是等边三角形 1302MBA ABC ∴==∠∠90OBM OBA MBA ∴=+=∠∠∠OB BM ∴⊥∴直线OB 是M 的切线 2OB OD OA ∴=213OD∴=OD ∴=点D的坐标为0⎫⎪⎪⎝⎭(3)设经过A ,B ,D 三点的抛物线的解析式是(y a x x ⎛=- ⎝⎭把()01B ,代入上式得1a =∴抛物线的解析式是21y x =+ 存在点P ,使ADP △的面积等于ADC △的面积点P 的坐标分别为12P ⎫⎪⎪⎝⎭,22P ⎫⎪⎪⎝⎭. [点评]本题是一道综合性很强的压轴题,主要考查二次函数、一次函数、圆、几何作图等大量知识,第3小题是比较常规的结论存在性问题,运用方程思想和数形结合思想可解决。
32、(山东滨州卷)已知:抛物线2:(1)(2)M y x m x m =+-+-与x 轴相交于12(0)(0)A x B x ,,,两点,且12x x <.(Ⅰ)若120x x <,且m 为正整数,求抛物线M 的解析式;(Ⅱ)若1211x x <>,,求m 的取值范围; (Ⅲ)试判断是否存在m ,使经过点A 和点B 的圆与y 轴相切于点(02)C ,,若存在,求出m 的值;若不存在,试说明理由;(Ⅳ)若直线:l y kx b =+过点(07)F ,,与(Ⅰ)中的抛物线M 相交于P Q ,两点,且使12PF FQ =,求直线l 的解析式. [解] (Ⅰ)解法一:由题意得, 1220x x m =-<. 解得,2m <.m 为正整数,1m ∴=.21y x ∴=-.解法二:由题意知,当0x =时,20(1)0(2)0y m m =+-⨯+-<. (以下同解法一) 解法三:22(1)4(2)(3)m m m ∆=---=-,12(1)(3)122m m x x x m --±-∴=∴=-=-,,.又122020x x x m <∴=->,. 2m ∴<.(以下同解法一.)解法四:令0y =,即2(1)(2)0x m x m +-+-=,12(1)(2)012x x m x x m∴++-=∴=-=-,,.(以下同解法三.) (Ⅱ)解法一:1212111010x x x x <>∴-<->,,,.12(1)(1)0x x ∴--<,即1212()10x x x x -++<.1212(1)2x x m x x m +=--=-,, (2)(1)10m m ∴-+-+<.解得 1m <.m ∴的取值范围是1m <.解法二:由题意知,当1x =时, 1(1)(2)0y m m =+-+-<. 解得:1m <.m ∴的取值范围是1m <.解法三:由(Ⅰ)的解法三、四知,1212x x m =-=-,.121121x x m <>∴->,,,1m ∴<.m ∴的取值范围是1m <. (Ⅲ)存在.解法一:因为过A B ,两点的圆与y 轴相切于点(02)C ,,所以A B ,两点在y 轴的同侧, 120x x ∴>.由切割线定理知,2OC OA OB =, 即2122x x =.124x x ∴=, 12 4.x x ∴=2 4.6m m ∴-=∴=.解法二:连接O B O C '',.圆心所在直线11222b m mx a --=-=-=, 设直线12mx -=与x 轴交于点D ,圆心为O ', 则122mO D OC O C OD -''====,.2132ABAB x x m BD =-==-=,, 32m BD -∴=. 在Rt O DB '△中, 222O D D B O B ''+=.即22231222m m --⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭.解得 6m =.(Ⅳ)设1122()()P x y Q x y ,,,,则22112211y x y x =-=-,. 过P Q ,分别向x 轴引垂线,垂足分别为112(0)(0)P x Q x ,,,.则11PP FO QQ ∥∥.所以由平行线分线段成比例定理知,11PO PF OQ FQ=. 因此,120102x x -=-,即212x x =-. 过P Q ,分别向y 轴引垂线,垂足分别为2122(0)(0)P y Q y ,,,, 则22PP QQ ∥.所以22FP P FQ Q △∽△.22P F FPFQ FQ∴=. 127172y y -∴=-.12212y y ∴-=.22122211212(1) 1.2324 1.x x x x ∴--=-∴-=-21142x x ∴=∴=,,或12x =-.当12x =时,点(23)P ,.直线l 过(23)(07)P F ,,,,7032.k b k b =⨯+⎧∴⎨=⨯+⎩, 解得72.b k =⎧⎨=-⎩,当12x =-时,点(23)P -,.直线l 过(23)(07)P F -,,,,703(2).k b k b =⨯+⎧∴⎨=⨯-+⎩, 解得72.b k =⎧⎨=⎩,故所求直线l 的解析式为:27y x =+,或27y x =-+.[点评]本题对学生有一定的能力要求,涉及了初中数学的大部分重点章节的重点知识,是一道选拔功能卓越的好题。
中考数学压轴题全解析

中考数学压轴题全解析中考数学压轴题,那可真是数学试卷里的“大魔王”啊。
咱就说这压轴题,那难度就像是让你去爬一座特别陡峭还云雾缭绕的高山,看着就有点吓人,但一旦征服了,那成就感也是满满的。
先说说这压轴题都有啥类型吧。
一种是函数综合题,这函数就像一个调皮的小精灵,一会儿是一次函数,一会儿是二次函数,它们还会和几何图形凑到一块儿玩。
比如说,给你个抛物线,再在旁边画个三角形,然后问你各种奇奇怪怪的问题,像这个点到那个点的距离最短是多少呀,这个三角形的面积什么时候最大之类的。
还有一种是几何探究题,那几何图形就像一个个小迷宫。
什么三角形旋转啦,四边形变形啦,让你去找出里面隐藏的规律。
就好比一个魔术师在变戏法,你得看穿他的把戏才行。
对于函数综合题的解法呢,你得先把函数的基本性质搞清楚。
一次函数的直线斜率,二次函数的对称轴、顶点坐标,这些都是你的武器。
当遇到和几何图形结合的题时,要善于把几何条件转化成数学表达式。
比如说,看到垂直,就想到斜率相乘等于 - 1;看到线段相等,就可以用两点间距离公式。
再看几何探究题,你得学会动手画草图。
很多时候,你画着画着就发现规律了。
而且要从特殊情况入手,比如先看看等边三角形、正方形这些特殊图形的情况,再慢慢推广到一般情况。
那这压轴题为啥这么难呢?一方面是它知识点涵盖得多,函数、几何、方程啥的都可能混在一起。
另一方面,它还考验你的思维能力,逻辑思维、空间想象思维都得跟上。
我还记得我初中的时候,看到压轴题也是头皮发麻。
但是我就不信邪,我一道一道地做,一道一道地研究。
我把做过的压轴题整理成一个小本子,没事就拿出来看看,看看自己当时是怎么想的,做错的地方是为啥错的。
慢慢地,我就发现这压轴题也不是那么可怕了。
所以啊,对于中考数学压轴题,大家不要害怕。
只要平时多下功夫,把基础打牢,再掌握一些解题的小技巧,就一定能战胜这个“大魔王”。
说不定还能在考试的时候,把压轴题当成是一个展示自己数学才华的舞台呢。
中考数学反比例函数-经典压轴题及答案解析

中考数学反比例函数-经典压轴题及答案解析一、反比例函数1.如图,点A在函数y= (x>0)图象上,过点A作x轴和y轴的平行线分别交函数y= 图象于点B,C,直线BC与坐标轴的交点为D,E.(1)当点C的横坐标为1时,求点B的坐标;(2)试问:当点A在函数y= (x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.(3)试说明:当点A在函数y= (x>0)图象上运动时,线段BD与CE的长始终相等.【答案】(1)解:∵点C在y= 的图象上,且C点横坐标为1,∴C(1,1),∵AC∥y轴,AB∥x轴,∴A点横坐标为1,∵A点在函数y= (x>0)图象上,∴A(1,4),∴B点纵坐标为4,∵点B在y= 的图象上,∴B点坐标为(,4);(2)解:设A(a,),则C(a,),B(,),∴AB=a﹣ = a,AC= ﹣ = ,∴S△ABC= AB•AC= × × = ,即△ABC的面积不发生变化,其面积为;(3)解:如图,设AB的延长线交y轴于点G,AC的延长线交x轴于点F,∵AB∥x轴,∴△ABC∽△EFC,∴ = ,即 = ,∴EF= a,由(2)可知BG= a,∴BG=EF,∵AE∥y轴,∴∠BDG=∠FCE,在△DBG和△CFE中∴△DBG≌△CEF(AAS),∴BD=EF.【解析】【分析】(1)由条件可先求得A点坐标,从而可求得B点纵坐标,再代入y= 可求得B点坐标;(2)可设出A点坐标,从而可表示出C、B的坐标,则可表示出AB和AC的长,可求得△ABC的面积;(3)可证明△ABC∽△EFC,利用(2)中,AB和AC的长可表示出EF,可得到BG=EF,从而可证明△DBG≌△CFE,可得到DB=CF.2.如图,一次函数y=x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A (﹣1,a),B(b,1)两点.(1)求反比例函数的表达式;(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;(3)求△PAB的面积.【答案】(1)解:当x=﹣1时,a=x+4=3,∴点A的坐标为(﹣1,3).将点A(﹣1,3)代入y= 中,3= ,解得:k=﹣3,∴反比例函数的表达式为y=﹣(2)解:当y=b+4=1时,b=﹣3,∴点B的坐标为(﹣3,1).作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小,如图所示.∵点B的坐标为(﹣3,1),∴点D的坐标为(﹣3,﹣1).设直线AD的函数表达式为y=mx+n,将点A(﹣1,3)、D(﹣3,﹣1)代入y=mx+n中,,解得:,∴直线AD的函数表达式为y=2x+5.当y=2x+5=0时,x=﹣,∴点P的坐标为(﹣,0)(3)解:S△PAB=S△ABD﹣S△BDP= ×2×2﹣ ×2× =【解析】【分析】(1)由一次函数图象上点的坐标特征可求出点A的坐标,根据点A的坐标利用待定系数法,即可求出反比例函数的表达式;(2)利用一次函数图象上点的坐标特征可求出点B的坐标,作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小,由点B的坐标可得出点D的坐标,根据点A、D的坐标利用待定系数法,即可求出直线AB的函数表达式,再由一次函数图象上点的坐标特征即可求出点P的坐标;(3)根据三角形的面积公式结合S△PAB=S△ABD﹣S△BDP,即可得出结论.3.如图,已知抛物线y=﹣x2+9的顶点为A,曲线DE是双曲线y= (3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2.(1)求双曲线的解析式;(2)设抛物线y=﹣x2+9与x轴的交点为B、C,且B在C的左侧,则线段BD的长为________;(3)点(6,n)为G1与G2的交点坐标,求a的值.(4)解:在移动过程中,若G1与G2有两个交点,设G2的对称轴分别交线段DE和G1于M、N两点,若MN<,直接写出a的取值范围.【答案】(1)把D(3,m)、E(12,m﹣3)代入y= 得,解得,所以双曲线的解析式为y= ;(2)2(3)解:把(6,n)代入y= 得6n=12,解得n=2,即交点坐标为(6,2),抛物线G2的解析式为y=﹣(x﹣a)2+9,把(6,2)代入y=﹣(x﹣a)2+9得﹣(6﹣a)2+9=2,解得a=6± ,即a的值为6± ;(4)抛物线G2的解析式为y=﹣(x﹣a)2+9,把D(3,4)代入y=﹣(x﹣a)2+9得﹣(3﹣a)2+9=4,解得a=3﹣或a=3+ ;把E(12,1)代入y=﹣(x﹣a)2+9得﹣(12﹣a)2+9=1,解得a=12﹣2 或a=12+2;∵G1与G2有两个交点,∴3+ ≤a≤12﹣2 ,设直线DE的解析式为y=px+q,把D(3,4),E(12,1)代入得,解得,∴直线DE的解析式为y=﹣ x+5,∵G2的对称轴分别交线段DE和G1于M、N两点,∴M(a,﹣ a+5),N(a,),∵MN<,∴﹣ a+5﹣<,整理得a2﹣13a+36>0,即(a﹣4)(a﹣9)>0,∴a<4或a>9,∴a的取值范围为9<a≤12﹣2 .【解析】【解答】解:(2)当y=0时,﹣x2+9=0,解得x1=﹣3,x2=3,则B(﹣3,0),而D(3,4),所以BE= =2 .故答案为2 ;【分析】(1)把D(3,m)、E(12,m﹣3)代入y= 得关于k、m的方程组,然后解方程组求出m、k,即可得到反比例函数解析式和D、E点坐标;(2)先解方程﹣x2+9=0得到B(﹣3,0),而D(3,4),然后利用两点间的距离公式计算DE的长;(3)先利用反比例函数图象上点的坐标特征确定交点坐标为(6,2),然后把(6,2)代入y=﹣(x ﹣a)2+9得a的值;(4)分别把D点和E点坐标代入y=﹣(x﹣a)2+9得a的值,则利用图象和G1与G2有两个交点可得到3+ ≤a≤12﹣2 ,再利用待定系数法求出直线DE的解析式为y=﹣ x+5,则M(a,﹣ a+5),N(a,),于是利用MN<得到﹣ a+5﹣<,然后解此不等式得到a<4或a>9,最后确定满足条件的a的取值范围.4.如图,已知直线y=ax+b与双曲线y= (x>0)交于A(x1, y1),B(x2, y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).【答案】(1)解:∵直线y=ax+b与双曲线y= (x>0)交于A(1,3),∴k=1×3=3,∴y= ,∵B(3,y2)在反比例函数的图象上,∴y2= =1,∴B(3,1),∵直线y=ax+b经过A、B两点,∴解得,∴直线为y=﹣x+4,令y=0,则x=4,∴P(4,O)(2)解:如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG 交于H,则AD∥BG∥x轴,AE∥BF∥y轴,∴= ,= = ,∵b=y1+1,AB=BP,∴= ,= = ,∴B(,y1)∵A,B两点都是反比例函数图象上的点,∴x1•y1= • y1,解得x1=2,代入= ,解得y1=2,∴A(2,2),B(4,1)(3)解:根据(1),(2)中的结果,猜想:x1, x2, x0之间的关系为x1+x2=x0【解析】【分析】(1)先把A(1,3)),B(3,y2)代入y= 求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出 = , = = ,根据题意得出 = , = = ,从而求得B(, y1),然后根据k=xy得出x1•y1= • y1,求得x1=2,代入 = ,解得y1=2,即可求得A、B的坐标;(3)合(1),(2)中的结果,猜想x1+x2=x0.5.抛物线y= +x+m的顶点在直线y=x+3上,过点F(﹣2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.(1)先通过配方求抛物线的顶点坐标(坐标可用含m的代数式表示),再求m的值;(2)设点N的横坐标为a,试用含a的代数式表示点N的纵坐标,并说明NF=NB;(3)若射线NM交x轴于点P,且PA•PB= ,求点M的坐标.【答案】(1)解:y= x2+x+m= (x+2)2+(m﹣1)∴顶点坐标为(﹣2,m﹣1)∵顶点在直线y=x+3上,∴﹣2+3=m﹣1,得m=2;(2)解:过点F作FC⊥NB于点C,∵点N在抛物线上,∴点N的纵坐标为: a2+a+2,即点N(a, a2+a+2)在Rt△FCN中,FC=a+2,NC=NB﹣CB= a2+a,∴NF2=NC2+FC2=( a2+a)2+(a+2)2,=( a2+a)2+(a2+4a)+4,而NB2=( a2+a+2)2,=( a2+a)2+(a2+4a)+4∴NF2=NB2,NF=NB(3)解:连接AF、BF,由NF=NB,得∠NFB=∠NBF,由(2)的思路知,MF=MA,∴∠MAF=∠MFA,∵MA⊥x轴,NB⊥x轴,∴MA∥NB,∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°,∴2∠MAF+2∠NBF=180°,∠MAF+∠NBF=90°,∵∠MAB+∠NBA=180°,∴∠FBA+∠FAB=90°,又∵∠FAB+∠MAF=90°,∴∠FBA=∠MAF=∠MFA,又∵∠FPA=∠BPF,∴△PFA∽△PBF,∴ = ,PF2=PA×PB= ,过点F作FG⊥x轴于点G,在Rt△PFG中,PG= = ,∴PO=PG+GO= ,∴P(﹣,0)设直线PF:y=kx+b,把点F(﹣2,2)、点P(﹣,0)代入y=kx+b,解得k= ,b= ,∴直线PF:y= x+ ,解方程 x2+x+2= x+ ,得x=﹣3或x=2(不合题意,舍去),当x=﹣3时,y= ,∴M(﹣3,).【解析】【分析】(1)利用配方法将二次函数化成顶点式,写出顶点坐标,由顶点再直线y=x+3上,建立方程求出m的值。
全国中考数学真题解析120考点汇编 压轴题1

全国中考数学真题解析120考点汇编 压轴题1一、选择题1. (2011•台湾34,4分)如图1,有两全等的正三角形ABC ,DEF ,且D ,A 分别为△ABC ,△DEF 的重心.固定D 点,将△DEF 逆时针旋转,使得A 落在上,如图2所示.求图1与图2中,两个三角形重迭区域的面积比为何( )A 、2:1B 、3:2C 、4:3D 、5:4考点:旋转的性质;等边三角形的性质。
分析:设三角形的边长是x ,则(1)中阴影部分是一个内角是60°的菱形,图(2)是个角是30°的直角三角形,分别求得两个图形的面积,即可求解.解答:解:设三角形的边长是x ,则高长是x 23. 图(1)中,阴影部分是一个内角是60°的菱形,AD=×x 23=x 33. 另一条对角线长是:2×21×x 33sin30°=31x . 则阴影部分的面积是:21×31x•63x=363x 2; 图(2)中,AD=×x 23=x 33. 是一个角是30°的直角三角形.则阴影部分的面积=21AD•sin30°•AD•cos30°=21×x•××x•23=363x 2. 两个三角形重迭区域的面积比为:363x 2:363x 2=4:3. 故选C .点评:本题主要考查了三角形的重心的性质,以及菱形、直角三角形面积的计算,正确计算两个图形的面积是解决本题的关键.2. (2011台湾,34,4分)如图1表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A ,且当钟面显示3点30分时,分针垂直于桌面,A 点距桌面的高度为10公分.如图2,若此钟面显示3点45分时,A 点距桌面的高度为16公分,则钟面显示3点50分时,A 点距桌面的高度为多少公分( )A .3322B .16+πC .18D .19考点:解直角三角形的应用;钟面角。
125--2021年全国中考数学压轴题解析汇编(1)及答案(京津沪渝地区)

【2021·北京·24题】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD。
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值。
解:(1)∵AB=AC∴∠ABC=∠ACB∵∠BAC+∠ABC+∠ACB=180°,∠BAC=α∴∠ABC=90°-1 2α∵∠ABC=∠ABD+∠DBC,且∠DBC=60°∴∠ABD=30°-1 2α(2)△ABE是等边三角形。
证明如下:连接AD、CD、ED。
∵BC=BD,∠DBC=60°∴△BCD是等边三角形∴BD=CD∵AB=AC,AD=AD∴△ABD≌△ACD∴∠BAD=∠CAD=12∠BAC=12α∠ACD=∠ABD=30°-1 2α∵∠ABE=∠DBC=60°∴∠DBE+∠ABD=∠DBE+∠CBE∴∠CBE=∠ABD=30°-1 2α∵∠BCE=150°∴∠BEC=180°-∠BCE-∠CBE=1 2α∴∠BEC=∠BAD=1 2α∵BC=BD∴△ABD≌△EBC(AAS)∴AB=EB∴△ABE是等腰三角形∵∠ABE=60°∴△ABE是等边三角形(3)∵∠BCE=150°,∠BCD=60°∴∠DCE=∠BCE-∠BCD=90°∵∠DEC=45°∴△DCE是等腰直角三角形∴CE=CD∵BC=CD∴BC=CE∴∠CBE=∠BEC∵由(2)知,∠CBE=30°-12α,∠BEC=12α∴30°-12α=12α∴α=30°【2013·北京·25题】对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:若⊙C 上存在两个点A 、B ,使得∠APB =60°,则称P 为⊙C 的关联点。
历届中考数学压轴(安徽考生试用)(含答案详解)
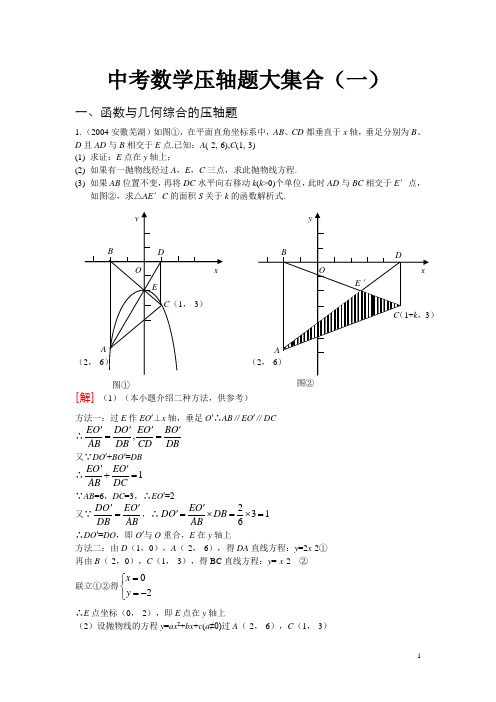
中考数学压轴题大集合(一)一、函数与几何综合的压轴题1.(2004安徽芜湖)如图①,在平面直角坐标系中,AB 、CD 都垂直于x 轴,垂足分别为B 、D 且AD 与B 相交于E 点.已知:A (-2,-6),C (1,-3) (1) 求证:E 点在y 轴上;(2) 如果有一抛物线经过A ,E ,C 三点,求此抛物线方程. (3) 如果AB 位置不变,再将DC 水平向右移动k (k >0)个单位,此时AD 与BC 相交于E ′点,如图②,求△AE ′C 的面积S 关于k 的函数解析式.[解] (1)(本小题介绍二种方法,供参考)方法一:过E 作EO ′⊥x 轴,垂足O ′∴AB ∥EO ′∥DC ∴,EO DO EO BO AB DB CD DB ''''==又∵DO ′+BO ′=DB ∴1EO EO AB DC''+=∵AB =6,DC =3,∴EO ′=2 又∵DO EO DB AB ''=,∴2316EO DO DB AB ''=⨯=⨯=∴DO ′=DO ,即O ′与O 重合,E 在y 轴上方法二:由D (1,0),A (-2,-6),得DA 直线方程:y =2x -2① 再由B (-2,0),C (1,-3),得BC 直线方程:y =-x -2 ②联立①②得02x y =⎧⎨=-⎩∴E 点坐标(0,-2),即E 点在y 轴上(2)设抛物线的方程y =ax 2+bx +c (a ≠0)过A (-2,-6),C (1,-3)图①图②E (0,-2)三点,得方程组42632a b c a b c c -+=-⎧⎪++=-⎨⎪=-⎩●解得a =-1,b =0,c =-2 ∴抛物线方程y =-x 2-2(3)(本小题给出三种方法,供参考)由(1)当DC 水平向右平移k 后,过AD 与BC 的交点E ′作E ′F ⊥x 轴垂足为F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006年全国中考数学压轴题全析全解1、(2006重庆)如图1所示,一张三角形纸片ABC ,∠ACB=90°,AC=8,BC=6.沿斜边AB 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形(如图2所示).将纸片11AC D ∆沿直线2D B (AB )方向平移(点12,,,A D D B 始终在同一直线上),当点1D 于点B 重合时,停止平移.在平移过程中,11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P. (1) 当11AC D ∆平移到如图3所示的位置时,猜想图中的1D E 与2D F 的数量关系,并证明你的猜想;(2) 设平移距离21D D 为x ,11AC D ∆与22BC D ∆重叠部分面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;(3)对于(2)中的结论是否存在这样的x 的值,使重叠部分的面积等于原ABC ∆面积的14. 若存在,求x 的值;若不存在,请说明理由.[解](1)12D E D F =.因为1122C D C D ∥,所以12C AFD ∠=∠.又因为90ACB ∠=︒,CD 是斜边上的中线,所以,DC DA DB ==,即112221C D C D BD AD === 所以,1C A ∠=∠,所以2AFD A ∠=∠ 所以,22AD D F =.同理:11BD D E =.又因为12AD BD =,所以21AD BD =.所以12D E D F =图1图3图2P(2)因为在Rt ABC ∆中,8,6AC BC ==,所以由勾股定理,得10.AB = 即1211225AD BD C D C D ====又因为21D D x =,所以11225D E BD D F AD x ====-.所以21C F C E x == 在22BC D ∆中,2C 到2BD 的距离就是ABC ∆的AB 边上的高,为245. 设1BED ∆的1BD 边上的高为h ,由探究,得221BC D BED ∆∆∽,所以52455h x-=. 所以24(5)25x h -=.121112(5)225BED S BD h x ∆=⨯⨯=- 又因为1290C C ∠+∠=︒,所以290FPC ∠=︒.又因为2C B ∠=∠,43sin ,cos 55B B ==. 所以234,55PC x PF x == ,22216225FC P S PC PF x ∆=⨯=而2212221126(5)22525BC D BED FC P ABC y S S S S x x ∆∆∆∆=--=---所以21824(05)255y x x x =-+≤≤(3) 存在. 当14ABC y S ∆=时,即218246255x x -+=整理,得2320250.x x -+=解得,125,53x x ==.即当53x =或5x =时,重叠部分的面积等于原ABC ∆面积的142、(2006浙江金华)如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式; (2)若S 梯形OBCD 43,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的 三角形与△OBA 相似.若存在,请求出所有符合条件 的点P 的坐标;若不存在,请说明理由.[解] (1)直线AB 解析式为:y=33-x+3.(2)方法一:设点C坐标为(x ,33-x+3),那么OD =x ,CD =33-x+3. ∴OBCD S 梯形=()2CD CD OB ⨯+=3632+-x . 由题意:3632+-x =334,解得4,221==x x (舍去) ∴ C(2,33) 方法二:∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形=334,∴63=∆ACD S . 由OA=3OB ,得∠BAO =30°,AD=3CD .∴ ACD S ∆=21CD ×AD =223CD =63.可得CD =33. ∴ AD=1,OD =2.∴C (2,33). (3)当∠OBP =Rt ∠时,如图①若△BOP ∽△OBA ,则∠BOP =∠BAO=30°,BP=3OB=3,∴1P (3,33). ②若△BPO ∽△OBA ,则∠BPO =∠BAO=30°,OP=33OB=1. ∴2P (1,3).当∠OPB =Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图),此时△PBO ∽△OBA ,∠BOP =∠BAO =30° 过点P 作PM ⊥OA 于点M .方法一: 在Rt △PBO 中,BP =21OB =23,OP =3BP =23.∵ 在Rt △P MO 中,∠OPM =30°, ∴ OM =21OP =43;PM =3OM =433.∴3P (43,433).方法二:设P(x ,33-x+3),得OM =x ,PM =33-x+3 由∠BOP =∠BAO,得∠POM =∠ABO .∵tan ∠POM==OMPM =x x 333+-,tan ∠ABOC=OBOA =3.∴33-x+3=3x ,解得x =43.此时,3P (43,433). ④若△POB ∽△OBA(如图),则∠OBP=∠BAO =30°,∠POM =30°. ∴ PM =33OM =43. ∴ 4P (43,43)(由对称性也可得到点4P 的坐标).当∠OPB =Rt ∠时,点P 在x轴上,不符合要求.综合得,符合条件的点有四个,分别是:1P (3,33),2P (1,3),3P (43,433),4P (43,43).3、(2006山东济南)如图1,已知Rt ABC △中,30CAB ∠=o,5BC =.过点A 作AE AB ⊥,且15AE =,连接BE 交AC 于点P .(1)求PA 的长;(2)以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由;(3)如图2,过点C 作CD AE ⊥,垂足为D .以点A 为圆心,r 为半径作⊙A ;以点C 为圆心,R 为半径作⊙C .若r 和R 的大小是可变化的,并且在变化过程中保持⊙A 和⊙C 相.切.,且使D 点在⊙A 的内部,B 点在⊙A 的外部,求r 和R 的变化范围.[解]CD图1图2(1)Q 在Rt ABC △中,305CAB BC ∠==o,, 210AC BC ∴==. AE BC Q ∥,APE CPB ∴△∽△. ::3:1PA PC AE BC ∴==. :3:4PA AC ∴=,3101542PA ⨯==. (2)BE 与⊙A 相切.Q 在Rt ABE △中,53AB =,15AE =, tan 353AE ABE AB ∴∠===,60ABE ∴∠=o . 又30PAB ∠=oQ ,9090ABE PAB APB ∴∠+∠=∴∠=oo,, BE ∴与⊙A 相切.(3)因为553AD AB ==,,所以r 的变化范围为553r <<.当⊙A 与⊙C 外切时,10R r +=,所以R 的变化范围为10535R -<<; 当⊙A 与⊙C 内切时,10R r -=,所以R 的变化范围为151053R <<+. 4、(2006山东烟台)如图,已知抛物线L 1: y=x 2-4的图像与x 有交于A 、C 两点,(1)若抛物线l 2与l 1关于x 轴对称,求l 2的解析式; (2)若点B 是抛物线l 1上的一动点(B 不与A 、C 重合),以AC 为对角线,A 、B 、C 三点为顶点的平行四边形的第四个顶点定为D ,求证:点D 在l 2上;(3)探索:当点B 分别位于l 1在x 轴上、下两部分的图像上时,平行四边形ABCD 的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
[解](1)设l 2的解析式为y=a(x-h)2+k∵l 2与x 轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l 1与l 2关于x 轴对称,∴l 2过A(-2,0),C(2,0),顶点坐标是(0,4)∴y=ax 2+4∴0=4a+4 得 a=-1∴l 2的解析式为y=-x 2+4 (2)设B(x 1 ,y 1) ∵点B 在l 1上∴B(x 1 ,x 12-4)∵四边形ABCD 是平行四边形,A 、C 关于O 对称 ∴B 、D 关于O 对称∴D(-x 1 ,-x 12+4).将D(-x 1 ,-x 12+4)的坐标代入l 2:y=-x 2+4 ∴左边=右边 ∴点D 在l 2上.(3)设平行四边形ABCD 的面积为S,则 S=2*S △ABC =AC*|y 1|=4|y 1|a.当点B 在x 轴上方时,y 1>0∴S=4y 1 ,它是关于y 1的正比例函数且S 随y 1的增大而增大, ∴S 既无最大值也无最小值b.当点B 在x 轴下方时,-4≤y 1<0∴S=-4y 1 ,它是关于y 1的正比例函数且S 随y 1的增大而减小, ∴当y 1 =-4时,S 由最大值16,但他没有最小值 此时B(0,-4)在y 轴上,它的对称点D 也在y 轴上. ∴AC ⊥BD∴平行四边形ABCD 是菱形 此时S 最大=16.5、(2006浙江嘉兴)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB 所在的抛物线以A 为顶点、开口向下,BC 所在的抛物线以C 为顶点、开口向上.以过山脚(点C )的水平线为x 轴、过山顶(点A )的铅垂线为y 轴建立平面直角坐标系如图(单位:百米).已知AB 所在抛物线的解析式为8412+-=x y ,BC 所在抛物线的解析式为2)8(41-=x y ,且已知)4,(m B . (1)设),(y x P 是山坡线AB 上任意一点,用y 表示x ,并求点B 的坐标;(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图). ①分别求出前三级台阶的长度(精确到厘米); ②这种台阶不能一直铺到山脚,为什么?(3)在山坡上的700米高度(点D )处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E 处,1600=OE (米).假设索道DE 可近似地看成一段以E 为顶点、开口向上的抛物线,解析式为2)16(281-=x y .试求索道的最大悬空..高度.[解] (1)∵),(y x P 是山坡线AB 上任意一点,∴8412+-=x y ,0≥x , ∴)8(42y x -=,y x -=82∵)4,(m B ,∴482-=m =4,∴)4,4(B (2)在山坡线AB 上,y x -=82,)8,0(A①令80=y ,得00=x ;令998.7002.081=-=y ,得08944.0002.021≈=x ∴第一级台阶的长度为08944.001=-x x (百米)894≈(厘米)同理,令002.0282⨯-=y 、002.0383⨯-=y ,可得12649.02≈x 、15492.03≈x ∴第二级台阶的长度为03705.012=-x x (百米)371≈(厘米) 第三级台阶的长度为02843.023=-x x (百米)284≈(厘米) ②取点)4,4(B ,又取002.04+=y ,则99900.3998.32≈=x∵002.0001.099900.34<=-∴这种台阶不能从山顶一直铺到点B ,从而就不能一直铺到山脚(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性) ②另解:连接任意一段台阶的两端点P 、Q ,如图 ∵这种台阶的长度不小于它的高度 ∴︒≤∠45PQR当其中有一级台阶的长大于它的高时,︒<∠45PQR在题设图中,作OA BH ⊥于H则︒=∠45ABH ,又第一级台阶的长大于它的高∴这种台阶不能从山顶一直铺到点B ,从而就不能一直铺到山脚 (3)PQR)7,2(D 、)0,16(E 、)4,4(B 、)0,8(C由图可知,只有当索道在BC 上方时,索道的悬空..高度才有可能取最大值 索道在BC 上方时,悬空..高度2)16(281-=x y 2)8(41--x )96403(1412-+-=x x 38)320(1432+--=x 当320=x 时,38max =y ∴索道的最大悬空..高度为3800米.6、(2006山东潍坊)已知二次函数图象的顶点在原点O ,对称轴为y 轴.一次函数1y kx =+的图象与二次函数的图象交于A B ,两点(A 在B 的左侧),且A 点坐标为()44-,.平行于x 轴的直线l 过()01-,点.(1)求一次函数与二次函数的解析式;(2)判断以线段AB 为直径的圆与直线l 的位置关系,并给出证明;(3)把二次函数的图象向右平移2个单位,再向下平移t 个单位()0t >,二次函数的图象与x 轴交于M N ,两点,一次函数图象交y 轴于F 点.当t 为何值时,过F M N ,,三点的圆的面积最小?最小面积是多少?[解](1)把(44)A -,代入1y kx =+得34k =-, ∴一次函数的解析式为314y x =-+;Q 二次函数图象的顶点在原点,对称轴为y 轴,∴ 设二次函数解析式为2y ax =,∴ ·······························································4∴二次函数解析式为214y x =.(2)由231414y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩解得44x y =-⎧⎨=⎩或114x y =⎧⎪⎨=⎪⎩,114B ⎛⎫∴ ⎪⎝⎭,,过AB ,点分别作直线l 的垂线,垂足为A B '',, 则15415144AA BB ''=+==+=,, ∴直角梯形AA B B ''的中位线长为5525428+=, 过B 作BH 垂直于直线AA '于点H ,则5BH A B ''==,115444AH =-=, 221525544AB ⎛⎫∴=+= ⎪⎝⎭,∴AB 的长等于AB 中点到直线l 的距离的2倍,∴以AB 为直径的圆与直线l 相切.(3)平移后二次函数解析式为2(2)y x t =--,令0y =,得2(2)0x t --=,12x t =22x t =,Q 过F M N ,,三点的圆的圆心一定在直线2x =上,点F 为定点, Q ····························· ∴要使圆面积最小,圆半径应等于点F 到直线2x =的距离, 此时,半径为2,面积为4π,设圆心为C MN ,中点为E ,连CE CM ,,则1CE =, 在三角形CEM 中,2213ME -=,23MN ∴=212MN x x t =-=,3t ∴=,∴ 当3t =时,过F M N ,,三点的圆面积最小,最小面积为4π.7、(2006江西)问题背景 某课外学习小组在一次学习研讨中,得到了如下两个命题:①如图1,在正三角形△ABC 中,M 、N 分别是AC 、AB 上的点,BM 与CN 相交于点O ,若∠BON =60º,则BM =CN ;②如图2,在正方形ABCD 中,M 、N 分别是CD 、AD 上的点,BM 与CN 相交于点O ,若∠BON =90º,则BM =CN ;然后运用类比的思想提出了如下命题:③如图3,在正五边形ABCDE 中,M 、N 分别是CD 、DE 上的点,BM 与CN 相交于点O ,若∠BON =108º,则BM =CN 。
