数字设计(Digital Design)习题解答5
数字设计(Digital Design)习题解答1

1INTRODUCTIONE X E R C I S E S O L U T I O N S1.2Three definitions of “bit”:(1) A binary digit (p. 1).(2)Past tense of “bite” (p. 1).(3) A small amount (pp. 6, 10).1.3ASIC Application-Specific Integrated CircuitCAD Computer-Aided DesignCD Compact DiscCO Central OfficeCPLD Complex Programmable Logic DeviceDAT Digital Audio TapeDIP Dual In-line PinDVD Digital Versatile DiscFPGA Field-Programmable Gate ArrayHDL Hardware Description LanguageIC Integrated CircuitIP Internet ProtocolLSI Large-Scale IntegrationMCM Multichip Module1–12DIGITAL CIRCUITSMSI Medium-Scale IntegrationNRE Nonrecurring EngineeringOK Although we use this word hundreds of times a week whether things are OK or not, we have probably rarely wondered about its history. That history is in fact a brief one, the word being first recorded in1839, though it was no doubt in circulation before then. Much scholarship has been expended on theorigins of OK, but Allen Walker Read has conclusively proved that OK is based on a sort of joke.Someone pronounced the phrase “all correct” as “oll (or orl) correct,” and the same person or someoneelse spelled it “oll korrect,” which abbreviated gives us OK. This term gained wide currency by beingused as a political slogan by the 1840 Democratic candidate Martin Van Buren, who was nicknamedOld Kinderhook because he was born in Kinderhook, New York. An editorial of the same year, refer-ring to the receipt of a pin with the slogan O.K., had this comment: “frightful letters . . . significant ofthe birth-place of Martin Van Buren, old Kinderhook, as also the rallying word of the Democracy of thelate election, ‘all correct’ .... Those who wear them should bear in mind that it will require their moststrenuous exertions ... to make all things O.K.” [From the American Heritage Electronic Dictionary(AHED), copyright 1992 by Houghton Mifflin Company]PBX Private Branch ExchangePCB Printed-Circuit BoardPLD Programmable Logic DevicePWB Printed-Wiring BoardSMT Surface-Mount TechnologySSI Small-Scale IntegrationVHDL VHSIC Hardware Description LanguageVLSI Very Large-Scale Integration1.4ABEL Advanced Boolean Equation LanguageCMOS Complementary Metal-Oxide SemiconductorJPEG Joint Photographic Experts GroupMPEG Moving Picture Experts GroupOK(see above)PERL According to some, it’s “Practical Extraction and Report Language.” But the relevant Perl FAQ entry, in perlfaq1.pod, says “never write ‘PERL’, because perl isn't really an acronym, apocryphal folkloreand post-facto expansions notwithstanding.” (Thanks to Anno Siegel for enlightening me on this.) VHDL VHSIC Hardware Description Language1.8In my book, “dice” is the plural of “die.”。
数字设计(Digital Design)习题解答6

119E X E R C I S E S O L U T I O N S SequentialLogic Design Principles77.27.3The latch oscillates if S and R are negated simultaneously. Many simulator programs will exhibit this same behavior when confronted with such input waveforms.S R Q QNS R QQN120DIGITAL CIRCUITS7.57.8Just tie the J and K inputs together and use as the D input. 7.9Excitation and output equations:Excitation/transition table; state/output table:7.15Excitation equations:Excitation/transition table; state table:7.18Excitation and output equations:QNQ Q QTEN J K CLKD1Q1′Q2+=D2Q2′X ⋅=Z Q1Q2′+=ENQ1Q201001011011010100001111010Q1*Q2*ENS1ZA C D 1BC C 0C A B 1DCC1S*D2Q (1Q0)Q1′Q2′⋅()⊕⊕=D1Q2=D0Q1=Q2Q1Q0Q2*Q1*Q0*000100001000010101011001100010101110110111111011S S*A E B A C F D B E C F G G H HDJ0K0EN ==J1K1Q0EN ⋅==MAX EN Q1Q0⋅⋅=EXERCISE SOLUTIONS 121Note that the characteristic equation for a J-K flip-flop is . Thus, we obtain the following transition equations:Transition/output table; state/output table:State diagram:Timing diagram:7.20This can be done algebraically. If all of the input combinations are covered, the logical sum of the expressionson all the transitions leaving a state must be 1. If the sum is not 1, it is 0 for all input combinations that are uncovered. For double-covered input combinations, we look at all possible pairs of transitions leaving a state.The product of a pair of transition equations is 1 for any double-covered input combinations.(a)State D , Y = 0 is uncovered.(b)State A , (X+Z ′) = 0 is uncovered. State B , W = 1 is double-covered; (W+X ) = 0 is uncovered. State C ,(W+X+Y+Z ) = 0 is uncovered; (W ⋅X + W ⋅Y + Z ⋅Y + Z ⋅X ) = 1 is double covered. State D , (X ⋅Y + ⋅X ′⋅Z + W ⋅Z ) = 0is uncovered; (W ⋅X ′⋅Z + W ⋅X ⋅Y ⋅Z ) = 1 is double-covered;Q ∗J Q ′⋅K ′Q ⋅+=Q0∗EN ′Q0⋅EN Q0′⋅+=Q1∗EN ′Q1⋅EN Q0⋅Q1′⋅EN Q0′Q1⋅⋅++=ENQ1Q2010000,001,00101,010,01010,011,01111,000,1Q1*Q2*, MAXENS1A A,0B,0B B,0C,0C C,0D,0DD,0A,1S*, MAXAENEN ENEN ′EN ′EN ′EN ′ENBCDCLK EN Q0Q1MAX122DIGITAL CIRCUITS7.21Table 9–4 on page 804 shows an output-coded state assignment. Here is a corresponding transition list:The excitation equations and circuit diagram follow directly from this transition list.7.25The minimum setup time is the clock period times the duty cycle. That is, the minimum setup time is the timethat the clock is 1.7.27As shown in Section 7.9.1, the excitation equation for the latch of Figure 7–72 is Below, we analyze Figure X7.27 in the same way:The feedback equation isThe feedback equations are the same, and so the circuits have identical steady-state behavior.The circuit in Figure X7.27 is better in two ways. It uses one less gate, and it has one less load on the D input. 7.29The AND gate in the original circuit is replaced with a NAND gate. As a result, the second flip-flop stores theopposite of the value stored in the original circuit; to compensate, swap connections to its Q and QN outputs.SL3Z L2Z L1Z R1Z R2Z R3ZTransition expression S*L3Z *L2Z *L1Z *R1Z *R2Z *R3Z *IDLE 000000(LEFT + RIGHT + HAZ)′IDLE 000000IDLE 000000LEFT ⋅HAZ ′⋅RIGHT ′L1001000IDLE 000000HAZ + LEFT ⋅RIGHT LR3111111IDLE 000000RIGHT ⋅HAZ ′⋅LEFT ′R1000100L1001000HAZ ′L2011000L1001000HAZ LR3111111L2011000HAZ ′L3111000L2011000HAZ LR3111111L31110001IDLE 000000R1000100HAZ ′R2000110R1000100HAZ LR3111111R2000110HAZ ′R3000111R2000110HAZ LR3111111R30001111IDLE 000000LR31111111IDLEY ∗C D ⋅C ′Y ⋅D Y⋅++=D C(C ⋅ D)′((C ⋅ D)′ ⋅ C) + Y ′C ⋅D + (((C ⋅ D)′ ⋅ C) + Y ′)′((C ⋅ D)′ ⋅ C)′QQNY ∗YY ∗C D ⋅C D ⋅()′C ⋅()Y ′+()′+=C D ⋅()C D ⋅()′C ⋅()′Y ⋅+=C D ⋅C D ⋅()(C ′)Y ⋅++=C D ⋅D C ′+()Y ⋅+=C D ⋅D Y ⋅C ′Y⋅++=EXERCISE SOLUTIONS 123The OR gates in the original circuit are also replaced with NAND gates. As a result, each input must be con-nected to a signal of the opposite polarity as before, that is, to the complementary flip-flop output. In the case of connections to the second flip-flop, we swapped outputs twice, so the connections remain the same.The final circuit below uses three 2-input NAND gates.7.45 A transition table corresponding to the state table is shown below:This table leads to the following Karnaugh maps for the excitation logic, assuming a “minimal cost” treatment of unused states.A BQ2Q1Q000011110Z0000010010100100001011011010010001000100110010000110110111100101100001101100100110101101111001011100011011001001Q2*Q1*Q0*D Q Q CLK D QQCLK XZCLK000111100001111000011110A BQ1 Q200011110A B A BA B A BA B A BA B A BABA BA BQ1Q2Q0=0Q1 Q2Q1Q2Q0=1100001111000011110Q1 Q200011110Q1Q2Q0=0Q1 Q2Q1Q2Q0=1000111100001111000011110Q1 Q200011110Q1Q2Q0=0Q1 Q2Q1Q2Q0=1D0D1D21100110011001100001100000000000011000000111111111111000001000010d d d d d d d d d d d d 0000011011101111111A ′0011Q1′⋅ Q2′ ⋅ A Q0Q0′ ⋅ Q1 ⋅ B 01Q0′ ⋅ Q2 ⋅ AQ0′ ⋅ Q1 ⋅ AQ1 ⋅ A ⋅ BQ2 ⋅ A ⋅ B124DIGITAL CIRCUITSThe resulting excitation equations areIgnoring inverters, a circuit realization with the new equations requires one 2-input gate, six 3-input gates, and one 5-input gate. This is more expensive than Figure 7–54, by four gates.7.49The new state assignment yields the followingtransition/excitation table and Karnaugh maps:This yields the following excitation equations:Compared with the results of original state assigment, these equations require two more 3-input AND gates,plus a 6-input OR gate inplace of a 4-input one. However, if we are not restricted to a sum-of-products realiza-tion, using the fact that might make this realization less expensive when discrete gates are used.D0A ′=D1Q1′Q2′⋅A ⋅Q0+=D2Q2A ⋅B ⋅Q0′Q2⋅A ⋅Q0′Q1⋅A ⋅Q1A ⋅B ⋅Q0′Q1⋅B⋅++++=X YQ1Q000011110Z0000011101 1 010******** 11111000100 1010000100Q2*Q1*or D1D20001100001111000011110X YQ1 Q200011110X YQ1Q2D1X YQ1 Q2X Q1Q2D21110101100000101010110101010010111Y Q1 ⋅ Q2′ ⋅ X ′Q1 ⋅ Q2′ ⋅ Y ′Q1′ ⋅ Q2 ⋅ Y Q1′ ⋅ X ⋅ YQ2 ⋅ X ′ ⋅ Y ′Q2 ⋅ X ⋅ YQ2′ ⋅ X ′ ⋅ Y Q2′ ⋅ X ⋅ Y ′Q1 ⋅ X ′ ⋅ Y ′Q1′ ⋅ Q2 ⋅ XD1Q1′Q2X ⋅⋅Q1′Q2Y ⋅⋅Q1′X Y ⋅⋅Q1Q2′X ′⋅⋅Q1Q2′Y ′⋅⋅Q1X ′Y ′⋅⋅+++++=D2Q2X Y ⋅⋅Q2′X Y ′⋅⋅Q2′X ′Y Q2X ′Y ′⋅⋅+⋅⋅++=D2Q2X Y ⊕⊕=EXERCISE SOLUTIONS 1257.57Here is the transition list:The transition/excitation and output equations below follow directly from the transition list.Starting from the IDLE state, the following transitions may be observed:For each input combination, the machine goes to the R1 state, because R1’s encoding is the logical OR of the encodings of the two or three next states that are specified by the ambiguous state diagram.SQ2Q1Q0Transition expressionS*Q2*Q1*Q0*IDLE000(LEFT+RIGHT+HAZ)′IDLE 000IDLE000LEFT L1001IDLE000HAZ LR3100IDLE 000RIGHTR1101L10011L2011L20111L3010L30101IDLE 000R1 1011R2111R2 1111R3110R31101IDLE 000LR311IDLESQ2Q1Q0LEFTRIGHTHAZQ2*Q1*Q0*S*IDLE000101101R1IDLE 000 011101R1IDLE 000 110101R1IDLE11111R1D2Q2∗Q2′Q1′Q0′HAZ ⋅⋅⋅== Q2′Q1′Q0′RIGHT⋅⋅⋅+ Q2Q1′Q0⋅⋅+ Q2Q1Q0⋅⋅+Q2′Q1′Q0′HAZ RIGHT +()⋅⋅⋅Q2Q0⋅+=D1Q1∗Q2′Q1′Q0⋅⋅== Q2′Q1Q0⋅⋅+ Q2Q1′Q0⋅⋅+ Q2Q1Q0⋅⋅+Q0=D0Q0∗Q2′Q1′Q0′LEFT⋅⋅⋅== Q2′Q1′Q0′RIGHT ⋅⋅⋅+ Q2′Q1′Q0⋅⋅+ Q2Q1′Q0⋅⋅+Q2′Q1′Q0′LEFT RIGHT +()⋅⋅⋅Q1′Q0⋅+=126DIGITAL CIRCUITSThe behavior aboveis not so good and is a result of synthesis choices—state encoding and logic synthesis method. If a different state encoding were used for R1, or if a different synthesis method were used (e.g., prod-uct-of-s-terms), then the results could be different. For example, starting with the transition list given earlier,we can obtain the following set of transition equations using the product-of-s-terms method:These equations yield the following transitions:This is obviously different and still not particularly good behavior.7.58Let E(SB), E(SC), and E(SD) be the binary encodings of states SB , SC , and SD respectively. Then, the bit-by-bit logical OR of E(SB) and E(SC). This is true because the synthesis method uses the logical OR of the next values for each state variable and, by extension, the logical OR of the encoded states.SQ2Q1Q0LEFTRIGHTHAZQ2*Q1*Q0*S*IDLE 000 000000IDLE IDLE 000 011100LR3IDLE 000 110001L1IDLE111IDLED2Q2∗Q2Q1Q0LEFT RIGHT HAZ +++++()== Q2Q1Q0LEFT ′+++()⋅ Q2Q1Q0′++()⋅ Q2Q1′Q0′++()⋅ Q2Q1′Q0++()⋅ Q2′Q1′Q0++()⋅ Q2′Q1Q0++()⋅Q2Q1RIGHT HAZ +++()Q2Q1LEFT ′++()Q2Q0′+()Q1′Q0+()Q2′Q0+()⋅⋅⋅⋅=D1Q1∗Q2Q1Q0LEFT RIGHT HAZ +++++()== Q2Q1Q0LEFT ′+++()⋅ Q2Q1Q0HAZ ′+++()⋅ Q2Q1Q0RIGHT ′+++()⋅ Q2Q1′Q0++()⋅ Q2′Q1′Q0++()⋅ Q2′Q1Q0++()⋅Q2Q1Q0++()Q1′Q0+()Q2′Q0+()⋅⋅=D0Q0∗Q2Q1Q0LEFT RIGHT HAZ +++++()== Q2Q1Q0HAZ ′+++()⋅ Q2Q1′Q0′++()⋅ Q2Q1′Q0++()⋅ Q2′Q1′Q0′++()⋅ Q2′Q1′Q0++()⋅ Q2′Q1Q0++()⋅Q2Q0LEFT RIGHT +++()Q2Q0HAZ ′++()Q1′()Q2′Q0+()⋅⋅⋅=E SD ()E SB ()E SC ()+=EXERCISE SOLUTIONS 1277.68As far as I know, I was the first person to propose BUT -flops, and Glenn Trewitt was the first person to analyzethem, in 1982. To analyze, we break the feedback loops as shown in the figure to the right.The excitation and output equations areThe corresponding transition/state table isThe two stable total states are circled. Notice that state 00 is unreachable.When X1 X2 = 00 or 11, the circuit generally goes to stable state 11, with Q1 Q2 = 11. The apparent oscillation between states 01 and 10 when X1 X2 = 11 may not occur in practice, because it contains a critical race that tends to force the circuit into stable state 11.When X1 X2 = 01 or 10, the Q output corresponding to the HIGH input will oscillate, while the other output remains HIGH .Whether this circuit is useful is a matter of opinion.7.71When X =1, the circuit was supposed to “count” through its eight states in Gray-code order. When X =0, itremains in the current state. If this were the case, I suppose it could be used as a 3-bit random number genera-tor. However, I messed up on the logic diagram and the circuit actually does something quite different and completely useless, compared to what I intended when I wrote the problem. Someday I’ll fix this problem.Also, metastability may occur when X is changed from 1 to 0. 7.79Figure X5.59 requires two “hops” for each input change. Figure 7–66 is faster, requiring only one hop for eachinput change. On the other hand, Figure 7–66 cannot be generalized for n >2.7.90Either this exercise is a joke, or a correct answer is much too dangerous to publish. Nevertheless, Earl Levineoffers two possible answers:(Stable output)Was the last answer to this question “yes”?(Oscillating output)Was the last answer to this question “no”?X2X1Q1Q2Y1∗Y2∗Y1Y2Y1X1Y1⋅()X2Y2⋅()′⋅[]′=X1′Y1′X2Y2⋅++=Y2X2Y2⋅()X1Y1⋅()′⋅[]′=X2′Y2′X1Y1⋅++=Q1Y1=Q2Y2=X1X2Y1Y2000111100011111111 0111101011 1111101101 1011110101Y1*Y2*。
数字媒体设计模拟试题答案

数字媒体设计模拟试题答案一、单项选择题1. 数字媒体设计中,以下哪种色彩模式最适用于网页设计?A. CMYKB. RGBC. HSBD. LAB答案:B2. 在Adobe Photoshop中,使用哪个工具可以快速选择图像中的相似颜色区域?A. 魔术棒工具B. 套索工具C. 快速选择工具D. 画笔工具答案:C3. HTML5中,用于定义文档结构的元素是:A. <head>B. <body>C. <header>D. <section>答案:D4. CSS中,哪个属性用于设置元素的背景图片?A. background-colorB. background-imageC. background-positionD. background-repeat答案:B5. 在数字媒体设计中,以下哪个术语描述的是用户界面的直观性和易用性?A. 可用性B. 可访问性C. 可读性D. 可扩展性答案:A二、多项选择题1. 在Adobe Illustrator中,以下哪些工具可以用于创建矢量图形?A. 钢笔工具B. 铅笔工具C. 画笔工具D. 形状工具答案:A、B、D2. 以下哪些原则是良好用户界面设计的关键要素?A. 一致性B. 反馈C. 容错性D. 简洁性答案:A、B、C、D3. 在数字媒体设计项目中,团队成员可能包括哪些角色?A. 项目经理B. 用户体验设计师C. 前端开发工程师D. 数据分析师答案:A、B、C三、判断题1. 所有的网页设计都应该优先考虑搜索引擎优化(SEO)。
答案:错误2. 动画在用户界面设计中仅用于娱乐目的。
答案:错误3. 用户体验(UX)设计专注于提高产品的功能性和性能。
答案:错误四、简答题1. 请简述响应式网页设计的基本原理及其对用户体验的影响。
答:响应式网页设计是一种设计方法,它使得网页能够根据不同的设备和屏幕尺寸自动调整布局。
其基本原理是通过使用流体网格、灵活的图片和媒体查询等技术,确保网页内容在任何设备上都能清晰、完整地展示。
数字设计原理与实践第四版课后习题答案

数字设计原理与实践 (第四版 )_课后习题答案数字设计原理与实践 (第四版) 是一本广泛使用于电子工程、计算机科学等领域的教材,它介绍了数字电路的基础知识和设计方法。
课后习题是巩固学习内容、提高理解能力的重要部分。
下面是一些课后习题的答案,供参考。
第一章绪论1. 什么是数字电路?数字电路是一种使用二进制数表示信息并通过逻辑门实现逻辑功能的电路。
2. 简述数字系统的设计过程。
数字系统的设计过程包括需求分析、系统规格说明、逻辑设计、电路设计、测试和验证等步骤。
3. 简述数字电路的分类。
数字电路可以分为组合逻辑电路和时序逻辑电路两类。
组合逻辑电路的输出只取决于当前输入,时序逻辑电路的输出还受到过去输入的影响。
4. 什么是门电路?门电路是由逻辑门组成的电路,逻辑门是实现逻辑运算的基本模块。
第二章组合逻辑电路设计基础1. 简述一下布尔代数的基本概念。
布尔代数是一种用于描述逻辑运算的数学系统。
它包括逻辑变量、逻辑表达式、逻辑运算等概念。
2. 简述编码器和译码器的功能和应用。
编码器用于将多个输入信号转换为较少的输出信号,译码器则将少量输入信号转换为多个输出信号。
它们常用于数据压缩、信号传输和地址译码等应用中。
3. 简述多路选择器的功能和应用。
多路选择器根据选择信号选择其中一个输入信号并输出,它可以实现多个输入信号的复用和选择。
它常用于数据选择、信号传输和地址译码等应用中。
第三章组合逻辑电路设计1. 简述组合逻辑电路的设计方法。
组合逻辑电路的设计方法包括确定逻辑功能、编写逻辑表达式、绘制逻辑图和验证电路正确性等步骤。
2. 请设计一个3位二进制加法器。
一个3位二进制加法器可以通过将两个2位二进制加法器和一个与门连接而成。
3. 简述半加器和全加器的功能和应用。
半加器用于实现两个二进制位的相加,它的输出包括和位和进位位。
全加器则用于实现三个二进制位的相加,它的输出包括和位和进位位。
它们常用于二进制加法器的设计。
第四章时序逻辑电路设计基础1. 简述触发器的功能和应用。
数字创意建模学习通课后章节答案期末考试题库2023年

数字创意建模学习通课后章节答案期末考试题库2023年1.视觉对简洁、完美的形象的追求被心理学家称之为“完形压强”。
( )参考答案:对2.在构成形态要素中,面是重要因素,它能决定形的方向,还可以作为形的骨架( )。
参考答案:对3.研究立体构成的意义不包括:( )参考答案:是平面造型艺术的基础4.立体主义的设计风格的特征是( )。
参考答案:分解与重构5.减法三原色不包括( )。
参考答案:蓝色6.立体构成中的空间关系是根据()的某些经验而确定的。
参考答案:人7.色彩的层次是指()。
参考答案:色彩表现上的前后距离和空间感,包括平面层次和实体层次两种8.金字塔造型可以看成是瓦楞折的变异构成。
( )参考答案:错9.立体的三种基本视图不包括:()。
参考答案:透视图10.光的三原色称之为( )。
参考答案:加法混合11.在Web上使用的图像格式有()。
参考答案:GIF/JPEG/PNG12.具象具备( )特性。
参考答案:明显的可识别性13.平面构成中,基本形或骨骼渐变构成至少要有()以上的变化才有渐变感。
参考答案:三个14.在立体构成中,线是具有长度、宽度和深度三度空间的实体线,不仅有粗细、长短的变化,它还有软与硬的区别。
( )参考答案:对15.使用RGB模式的图像中,呈现红色的组合是()。
参考答案:R200/G30/B3016.科学家们经过长期的探索和研究,认为能组合出各种色彩的最基本的色是( )。
参考答案:三原色17.加法指()群化组合构成的加工方法。
参考答案:单体18.在空间构成中可细分为()。
参考答案:二维空间的平面构成、色彩构成与三维空间的立体构成19.基本形是指构成图形的基本元素单位,是构成一个重复式彼此关联的符合形象的单位。
( )参考答案:对20.近似的表现是一种形体间的轻度差异。
( )参考答案:对21.近似的表现是一种()。
参考答案:轻微的差异22.美的表现形式,从总体可归纳为两大类:()和打破常规的美。
数字设计基础与应用第版第章习题解答完整版

数字设计基础与应用第版第章习题解答HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第1章 数字逻辑基础1-1 将下列二进制数转换为十进制数。
(1) 2(1101) (2) 2(10110110) (3) 2(0.1101) (4) 2(11011011.101) 解(1)3210210(1101)12120212(13)=⨯+⨯+⨯+⨯=(2)75421210(10110110)1212121212(182)=⨯+⨯+⨯+⨯+⨯=(3) 124210(0.1101)1212120.50.250.0625(0.8125)---=⨯+⨯+⨯=++= (4) 76431013210(11011011.101)22222222 12864168210.50.125 (219.625)--=+++++++=+++++++=1-2 将下列十进制数转换为二进制数和十六进制数(1) 10(39) (2) 10(0.625) (3) 10(0.24) (4) 10(237.375) 解(1)10216(39)(100111)(27)== (2) 10216(0.625)(0.101)(0.A)==(3)近似结果: 16210)3.0()00111101.0()24.0(D =≈ (4) 10216(237.375)(1110'1101.011)(0ED.6)==1-3 将下列十六进制数转换为二进制数和十进制数(1) 16(6F.8) (2) 16(10A.C) (3) 16(0C.24) (4) 16(37.4) 解(1) 16210(6F.8)(1101111.1)(111.5)==(2) 16210(10A.C)(1'0000'1010.11)(266.75)== (3) 16210(0C.24)(1100.0010'01)(12.140625)== (4) 16210(37.4)(11'0111.01)(55.25)== 1-4 求出下列各数的8位二进制原码和补码(1) 10(39)- (2) 10(0.625) (3) 16(5B) (4) 2(0.10011)- 解(1)10(39)(1'0100111)(1'1011001)-==原码补码 (2) (0.1010000)(0.1010000)==10原码补码(0.625) (3) 16(5B)(01011011)(01011011)==原码补码(4) 2(0.10011)(1.1001100)(1.0110100)-==原码补码1-5 已知10X (92)=-,10Y (42)=,利用补码计算X +Y 和X -Y 的数值。
数字设计:原理与实践第五版习题答案

数字设计:原理与实践第五版习题答案第一章:数字系统基础1. 哪些数学符号代表布尔逻辑运算?分别代表哪些逻辑操作?布尔逻辑运算包括与(AND)、或(OR)、非(NOT)、异或(XOR)等运算。
它们的对应数学符号表示如下:•与(AND):$\\cdot$ 或 $\\land$•或(OR):+或 $\\lor$•非(NOT):$\\overline{A}$ 或eee•异或(XOR):$\\oplus$2. 简述数字系统的信号表示和信号处理单元。
数字系统的信号表示使用离散量来表示连续或离散的信号,其中离散量指代具有离散数值的量。
信号处理单元是指对输入信号进行处理和操作的硬件模块,用于实现特定的功能或执行特定的任务。
3. 什么是布尔函数?它可以用哪些方法表示?布尔函数是指以布尔逻辑运算为基础,将一个或多个布尔变量映射为单一布尔值的函数。
布尔函数可以用真值表、逻辑表达式和逻辑图等方法表示。
4. 简述数字系统的设计方法。
数字系统的设计方法包括以下几个步骤:1.确定问题的需求和约束条件。
2.将问题抽象为逻辑功能的实现。
3.设计逻辑电路并进行仿真验证。
4.实现电路设计并进行实验验证。
5.优化电路设计并进行性能评估。
6.完成设计文档和报告。
第二章:组合逻辑电路设计1. 什么是组合逻辑电路?简述其基本特征。
组合逻辑电路是指将组合逻辑块进行组合形成的电路,其输出仅依赖于当前的输入。
它的基本特征包括:•输入输出之间无时序关系。
•只有组合逻辑块,没有存储元件。
•输出仅取决于当前输入。
2. 简述逻辑门的功能和特点。
逻辑门是实现布尔逻辑运算的基本构件,其功能和特点如下:•与门(AND):多个输入信号全部为高时,输出高;否则输出低。
•或门(OR):多个输入信号有一个为高时,输出高;否则输出低。
•非门(NOT):输入信号为高时,输出低;否则输出高。
•异或门(XOR):多个输入信号中奇数个为高时,输出高;否则输出低。
3. 什么是选择器和解码器?选择器是一种组合逻辑电路,根据选择信号将一组输入信号中的某一个作为输出。
数字设计(Digital Design)习题解答4

1 1 0 1 1 1 1 1 1 1 0 1 1 0 0 0
4.9 (a) F = X ′ ⋅ Y + Y ′ ⋅ X = ( X + Y ) ⋅ ( X ′ + Y ′ ) (b) F = A ⋅ B = ( A + B ) ⋅ ( A + B ′ ) ⋅ ( A ′ + B ) 4.12 (1) Including inverters makes the problem too difficult. (2) In modern PLD-based designs, inverters do cost nothing and really can be ignored. 4.13
XY Z 0 1 1 1 Y F=X⋅Y+Z (a) (b) 00 01 11 1 1 1 Z Z X 10 X⋅Y YZ W′ ⋅ Y′ ⋅ Z 00 01 11 Y 10 1 X F = W′ ⋅ X + X′ ⋅ Y′ ⋅ Z + X ⋅ Y 1 X⋅Y 1 WX 00 01 1 1 1 1 1 Z 11 W 10 W′ ⋅ X X′ ⋅ Y′ ⋅ Z′
Y+Z
Y
4.19
W′ ⋅ Y′ ⋅ Z (a) WX 00 YZ 00 01 11 Y 10 X F = W ′ ⋅ Y′ ⋅ Z + W ′ ⋅ X′ ⋅ Z + W ⋅ X ⋅ Y + W′ ⋅ X′ ⋅ Y′ or X′ ⋅ Y′ ⋅ Z′ 1 W⋅X⋅Y W′ ⋅ X′ 1 1 1 1 Z d Y 10 1 W⋅Y⋅Z X 11 d d 1 W 01 11 10 d X′ ⋅ Y′ ⋅ Z′ (b) WX 00 YZ 00 01 1 1 W 01 11 10 1 d Z X′ ⋅ Y′ X′ ⋅ Z
数字设计(Digital Design)习题解答3

3–1E X E R C I S E S O L U T I O N S DIGITAL CIRCUITS33.1The “probably” cases may cause damage to the gate if sustained.3.3A logic buffer is a non-linear amplifier that maps the entire set of possible analog input voltages into just two output votages, HIGH and LOW . An audio amplifier has a linear response over its specified operating range,mapping each input voltage into an output voltage that is directly proprtional to the input voltage.3.6From the American Heritage Electronic Dictionary (AHED), copyright 1992 by Houghton Mifflin Company:(1) A structure that can be swung, drawn, or lowered to block an entrance or a passageway.(2) a. An opening in a wall or fence for entrance or exit. b. The structure surrounding such an opening, such as the monumental or fortified entrance to a palace or walled city.(3) a. A means of access: the gate to riches. b. A passageway, as in an airport terminal, through which passen-gers proceed for embarkation.(4) A mountain pass.(5)The total paid attendance or admission receipts at a public event: a good gate at the football game.(6) A device for controlling the passage of water or gas through a dam or conduit.(7)The channel through which molten metal flows into a shaped cavity of a mold.(8)Sports. A passage between two upright poles through which a skier must go in a slalom race.(9)Electronics. A circuit with multiple inputs and one output that is energized only when a designated set of input pulses is received.(a)0(b)1(c)0(d)undefined (e)1(f)probably 1(g)probably 0(h)probably 03–2DIGITAL CIRCUITSWell, definition (9) is closest to one of the answers that I had in mind. The other answer I was looking for is the gate of a MOS transistor.3.14 A CMOS inverting gate has fewer transistors than a noninverting one, since an inversion comes “for free.” 3.15Simple, inverting CMOS gates generally have two transistors per input. Four examples that meet the require-ments of the problem are 4-input NAND , 4-input NOR , 2-in, 2-wide AND–OR–INVERT , and 2-in, 2-wide OR–AND–INVERT . 3.18One way is that a romance could be sparked, and the designers could end up with a lot less time to do theirwork. Another way is that the stray perfume in the IC production line could have contaminated the circuits used by the designers, leading to marginal operation, more debugging time by the deidicated designers, and less time for romance. By the way, the whole perfume story may be apocryphal. 3.20Using the maximum output current ratings in both states, the HIGH -state margin is 0.69V and the LOW -statemargin is 1.02V. With CMOS loads (output currents less than 20 µA), the margins improve to 1.349V and 1.25V, respectively. 3.21The first answer for each parameter below assumes commercial operation and that the device is used with themaximum allowable (TTL) load. The number in parentheses, if any, indicates the value obtained under a lesser but specified (CMOS) load.V OHmin 3.84V (4.4V )V IHmin 3.15V V ILmax 1.35V V OLmax 0.33V (0.1V)I Imax 1µA I OLmax 4 mA (20 µA)I OHmax-4 mA (-20 µA)3.22Current is positive if it flows into a node. Therefore, an output with negative current is sourcing current. 3.23The 74HC00 output drive is so weak, it’s not good for driving much:(a)Assume that in the LOW state the output pulls down to 0.33V (the maximum spec). Then the output current is , which is way more than the 4-mA commercial spec.(b)For this problem, you first have to find the Thévenin equivalent of the load, or in series with . In the HIGH state, the gate must pull the output up to 3.84V, a difference of 1.59V across ,requiring 10.7 mA, which is out of spec. In the LOW state, we have a voltage drop of across , so the output must sink 12.9mA, again out of spec.3.24(In the first printing, change “74FCT257T” to “74HC00.”) The specification for the 74HC00 shows a maxi-mum power-supply current of 10 µA when the inputs aree at 0 or 5V, but based on the discussion in Section 3.5.3 we would expect the current to be more when the inputs are at their worst-case values (1.35 or 3.15V). If we consider “nonlogic” input values, the maximum current will flow if the inputs are held right at the switching threshold, approximately V CC /2.3.26(In the first printing, change “74FCT257T” to “74HC00.”) Using the formulas on page 119, we can estimatethat or, using the higher value of in the spec, that . (The discrepancy shows that the output characteristic of this device is somewhat nonlinear.) We can also estimate . 3.29The purpose of decoupling capacitors is to provide the instantaneous power-supply current that is required dur-ing output transitions. Printed-circuit board traces have inductance, which acts as a barrier to current flow at high frequencies (fast transition rates). The farther the capacitor is from the device that needs decoupling, the larger is the instantaneous voltage drop across the connecting signal path, resulting in larger spike (up or down)in the device’s power-supply voltage.V OL 5.0V ()120Ω⁄41.7mA =148.5Ω2.25V 148.5Ω2.25V 0.33V –148.5ΩR p(on) 5.0 3.84–()0.004⁄290Ω==V OHmin R p(on) 5.0 4.4–()0.00002⁄30K Ω==R n(on)0.330.004⁄82.5Ω==EXERCISE SOLUTIONS 3–33.32(a) 5 ns.3.38Smaller resistors result in shorter rise times for LOW -to-HIGH transitions but higher power consumption in theLOW state. Stated another way, larger resistors result in lower power consumption in the LOW state but longer rise times (more ooze) for LOW -to-HIGH transitions. 3.39The resistor must drop with 5mA of current through it. Therefore; a good standard value would be . 3.41(The Secret of the Ooze .) The wired output has only passive pull-up to the HIGH state. Therefore, the time forLOW -to-HIGH transitions, an important component of total delay, depends on the amount of capacitive loading and the size of the pull-up resistor. A moderate capacitive load (say, 100pF) and even a very strong pull-up resistor (say, ) can still lead to time constants and transition times (15ns in this example) that are longer than the delay of an additional gate with active pull-up. 3.42The winner is 74FCT-T—48 mA in the LOW state and 15 mA in the HIGH state (see Table 3–8). TTL familiesdon’t come close. 3.46n diodes are required.3.49For each interfacing situation, we compute the fanout in the LOW state by dividing of the driving gateby of the driven gate. Similarly, the fanout in the HIGH state is computed by dividing of the driving gate by of the driven gate. The overall fanout is the lower of these two results.3.50For the pull-down, we must have at most a 0.5-V drop in order to create a that is no worse than a standardLS-TTL output driving the input. Since , we get and. (Alternatively, )For the pull-up, we must have at most a 2.3-V drop in order to create a that is no worse than a standardLS-TTL output driving the input. Since , we get and. (Alternatively, we could have calculated the result as.) The pull-up dissipates less power.3.52The main benefit of Schottky diodes is to prevent transistors from saturating, which allows them to switch morequickly. The main drawback is that they raise the collector-to-emitter drop across an almost-saturated transis-tor, which decreases LOW -state noise margin. 3.55Low-stateHigh-state Overall ExcessCaseRatio Fanout Ratio Fanout Fanout State Drive74LS driving 74LS 202020none74LS driving 74S484HIGHLOW -stateHIGH -stateOK?OK?470— 5.0470 4.59.57no <0—yes 3304702.9375193.8752.437512.57no<0—yes5.0 2.0–0.37– 2.63V =r 2.630.005⁄526Ω==510Ω150ΩI OLmax I ILmax I OLmax I IHmax 8mA 0.4mA ----------------400µA 20µA ----------------8mA 2mA-----------400µA 50µA----------------200µAV IL I ILmax 0.4mA =R pd 0.50.004⁄1250Ω==P pd V IL 2R pd ⁄0.5()21250⁄0.2mW ===P pd V IL I IL 0.50.0004⋅0.2mW ===V IH I IHmax 20µA =R pu 2.30.00002⁄115k Ω==P pu V IH 2R pu ⁄ 2.3()2115000⁄0.046mW ===P pu V IH I IH 2.30.00002⋅0.046mW ===R VCC Ω()R GND Ω()V Thev V ()R Thev Ω()V Thev V OLV ()–I OL mA ()V OH V Thev V ()–I OHµA ()3–4DIGITAL CIRCUITS3.563.57For each interfacing situation, we compute the fanout in the LOW state by dividing of the driving gateby of the driven gate. Similarly, the fanout in the HIGH state is computed by dividing of the driving gate by of the driven gate. The overall fanout is the lower of these two results.3.64TTL-compatible inputs have , and typical TTL outputs have . CMOS outputlevels are already high compared to these levels, so there’s no point in wasting silicon to make them any higher by lowering the voltage drop in the HIGH state. 3.68Including the DC load, a CMOS output’s rise and falltimes can be analyzed using the equivalent circuit shown to the right. This problem analyzes the fall time.Part (a) of the figure below shows the electrical condi-tions in the circuit when the output is in a steady HIGH state. Note that two resistors form a voltage divider, so the HIGH output is 4.583V, not quite 5.0V as it was in Section 3.6.1. At time the CMOS output changes to the LOW state, resulting in the situation depicted in (b). The output will eventually reach a steady LOW voltage of 0.227V, again determined by a voltage divider.At time , is still 4.583V, but the Thévenin equivalent of the voltage source and the two resistors in the LOW state is in series with a 0.227-V voltage source. At time , the capacitor will be dis-charged to the Thévenin-equivalent voltage and will be 0.227V. In between, the value of is gov-LOW -stateHIGH -stateCaseMargin Margin 74HCT driving 74LS0.8V0.33V0.47V2.0V3.84V1.84VLOW -stateHIGH -stateOverall ExcessCaseRatio Fanout Ratio Fanout Fanout StateDrive 74HCT driving 74LS1020010HIGHV ILmax V OLmax(T)V IHmin V OHmin(T)I OLmax I ILmax I OHmax I ILmax 4mA 0.4mA----------------4000µA 20µA-------------------3800µAV IHmin 2.0V =V OHmin 2.7V =V DD = +5.0 VV OUTV INR nR pCMOS inverterEquivalent load for transition-time analysis+–2.5 V1 k Ω100 pFt 0=AC load+–2.5 V1 k Ω100 pFV DD = +5.0 V V OUT = 4.583V I OUT = 0I OUTV IN> 1 M Ω200 ΩAC loadV DD = +5.0 VV OUT V IN(a)(b)100 Ω> 1 M Ω+–2.5 V1 k Ω100 pFt 0=V OUT 90.9Ωt ∞=V OUT V OUTEXERCISE SOLUTIONS 3–5erned by an exponential law:Because of the DC load resistance, the time constant is a little shorter than it was in Section 3.6.1, at 9.09ns.To obtain the fall time, we must solve the preceding equation for V OUT = 3.5 and V OUT = 1.5, yieldingThe fall time is the difference between these two numbers, or 7.7ns. This is slightly shorter than the 8.5nsresult in Section 3.6.1 because of the slightly shorter time constant.3.70The time constant is . We solve the rise-time equation for the point at which V OUT is1.5V, as on p. 118 of the text:3.77The LSB toggles at a rate of 16 MHz. It takes two clock ticks for the LSB to complete one cycle, so the transi-tion frequency is 8 MHz. The MSB’s frequency is 27 times slower, or 62.5 KHz. The LSB’s dynamic power is the most significant, but the sum of the transitions on the higher order bits, a binary series, is equivalent to almost another 8 MHz worth of transitions on a single output bit. Including the LSB, we have almost 16 MHz,but applied to the load capacitance on just a single output. If the different ouputs actually have different load capacitances, then a weighted average would have to be used.3.813.84In the situations shown in the figure, the diode with the lowest cathode voltage is forward biased, and the anode(signal C ) is 0.6V higher. However, under the conditions specified in the exercise, neither diode is forward biased, no current flows through , and is 5.0V.V OUT 0.227V 4.5830.227V –()+et R n C L ()⁄–⋅=4.356e t 90.91001012–⋅⋅()⁄–V⋅=4.356e t –()90.9109–⋅()⁄V⋅=t 9.09–109–VOUT 4.356-------------ln ⋅⋅=t 3.5 1.99 ns =t 1.59.69 ns=t f 1k Ω50 pF ⋅50 ns =t 1.550–109– 5.0 1.5–5.0--------------------ln ⋅⋅=t 1.517.83 ns=V CCAENOUTQ1Q2EN L L H H A L H L H B H H L L C H L H H DH L L LQ1on off off offQ2off on off off OUT L H Hi-Z Hi-ZEN AOUT(a)(b)(c)BCDR 2V C3–6DIGITAL CIRCUITS3.853.86In order to turn on Q2 fully, V A must be 1.2V , corresponding to the sum of the base-to-emitter drops of Q2 andQ5. This could happen if both X and Y are 0.95V or higher. In reality, a somewhat higher voltage is required,because the voltage divider consisting of R1, R3, and other components diverts current from the base of Q2from turning on fully until X and Y are about 1.1V or higher (at , according to the typical characteristics graphed in the TI TTL Data Book). 3.90When the output is HIGH , the relay coil will try to pull it to 12 volts. The high voltage will typically cause highcurrent to flow through the output structure back into the 5-V supply and will typically blow up the output.Open-collector TTL outputs theoretically should not have this problem, but most are not designed to withstand the 12-V potential and transistor breakdown will occur. A few TTL open-collector devices are designed with “high-voltage outputs” to solve this problem.3.92 F = W ⋅X + Y ⋅Z/* Transistor parameters */#define DIODEDROP 0.6 /* volts */#define BETA 10;#define VCE_SAT 0.2 /* volts */#define RCE_SAT 50 /* ohms */#define MAX_LEAK 0.00001 /* amperes */main(){float Vcc, Vin, R1, R2; /* circuit parameters */ float Ib, Ic, Vce; /* circuit conditions */if (Vin < DIODEDROP) { /* cut off */ Ib = 0.0;Ic = Vcc/R2; /* Tentative leakage current, limited by large R2 */ if (Ic > MAX_LEAK) Ic = MAX_LEAK; /* Limited by transistor */ Vce = Vcc - (Ic * R2); }else { /* active or saturated */ Ib = (Vin - DIODEDROP) / R1;if ((Vcc - ((BETA * Ib) * R2)) >= VCE_SAT) { /* active */ Ic = BETA * Ib;Vce = Vcc - (Ic * R2); }else { /* saturated */ Vce = VCE_SAT;Ic = (Vcc - Vce) / (R2 + RCE_SAT); } }}WXYZGFWXYZGF0000101000100001101001100010101010100011011011010100101100010111111125°CEXERCISE SOLUTIONS 3–73.96When one module is driving HIGH and the other modules are output-disabled, each disabled module hasa 74LS125 output sinking of leakage current. In addition, each of the n modules has a 74LS04 input sinking of leakage current. Thus, the total sink current is . The 74LS125 can source 2.6mA in the HIGH state, so we findWhen one module is driving LOW and the other modules are output-disabled, each disabled module has a 74LS125 output sourcing of leakage current. In addition, each of the n modules has a 74LS04 input sourcing 0.4mA. Thus, the total source current is . The 74LS125 can sink 24mA in the LOW state, so we findOverall, we require .0110101110010111111111W X Y Z G F W X Y Z G Fn 1–20µA 20µA n 1–n +()20µA ⋅n 1–n +()20µA ⋅ 2.6mA≤n 65≤n 1–20µA n 1)–()20µA ⋅n 0.4µA ⋅+n 1–()20µA ⋅n 0.4mA ⋅+24mA≤n 57≤n 57≤。
数字设计考试题及答案

数字设计考试题及答案一、选择题(每题2分,共20分)1. 以下哪个不是基本逻辑门?A. ANDB. ORC. XORD. NAND答案:D2. 一个4位二进制数可以表示的最大十进制数是多少?A. 15B. 16C. 255D. 256答案:C3. 一个D触发器的Q端在时钟脉冲上升沿触发时,其输出将:A. 保持不变B. 翻转C. 变为0D. 变为1答案:B...二、简答题(每题10分,共30分)1. 解释什么是同步计数器,并简述其工作原理。
答案:同步计数器是一种数字电路,它使用统一的时钟信号来同步各个触发器的触发时刻。
它的工作原理是,当时钟脉冲上升沿到来时,所有触发器同时接收输入信号,并更新其状态。
这样可以保证计数的准确性和同步性。
2. 描述一个简单的数字电路设计流程。
答案:一个简单的数字电路设计流程通常包括以下几个步骤:需求分析、逻辑设计、电路实现、仿真测试、版图设计、物理验证、制造和测试。
...三、计算题(每题15分,共30分)1. 设计一个4位二进制计数器,使用4个D触发器实现,画出电路图并说明其工作原理。
答案:4位二进制计数器可以使用4个D触发器串联实现。
每个D触发器的D输入端接前一个触发器的Q输出端,时钟输入端接统一的时钟信号。
这样,每个触发器在时钟脉冲上升沿时,将前一个触发器的输出作为自己的输入,并在下一个时钟脉冲上升沿时更新自己的输出。
电路图通常包括这些触发器的连接方式和时钟信号的引入。
2. 给定一个逻辑表达式:F = A'B + AB',使用与非门实现该逻辑表达式,并画出相应的逻辑电路图。
答案:首先,将逻辑表达式转换为与非形式:F = (A + B)'(A' +B')。
然后,使用与非门实现这个表达式,电路图将包括两个与门和两个非门,以及相应的输入和输出连接。
...四、论述题(20分)1. 论述数字电路设计中的错误检测和纠正技术,并给出至少两个实例。
数字设计(Digital Design)习题解答7

145E X E R C I S E S O L U T I O N S SequentialLogic Design Practices874x163CLR CLK LD QA QB 2141119ENP ENT710AB34C D 56QCQD15RCO13128.1In the first three printings, change “RAMBANK0” to “RAMBANK1” in the third line of the exercise. The results are the same. The new expression describes exactly the input combinations in which the 8 high-order bits of ABUS are 000000012, the same as the original expression using don’t-cares.8.2The 16-series devices have or 2048 fuses (see Figure 10–2). The 20-series devices have or 2560 fuses.8.3There are fuses in the AND array (see Figure 10–4). Each of the eight macrocells has one fuse to control the output polarity and one fuse to select registered vs. combinational configuration in the 16V8R, or to assert the output-enable in the 16V8S. There are also two global fuses to select the overall configuration (16V8C, 16V8R, or 16V8S). The total number of fuses is therefore .A real 16V8 (depending on the manufacturer) has at least 64 additional fuses to disable individual product terms, 64 user-programmable fuses that do nothing but store a user code, and a security fuse. (Once the security fuse is programmed, the rest of the fuse pattern can no longer be read.) 8.5The column below gives the answers in MHz.Part numbersSuffix PAL16L8, PAL16Rx, PAL20L8, PAL20Rx -5 5 4– 4.5 0117.7117.7PAL16L8, PAL16Rx, PAL20L8, PAL20Rx -7 7.5 6.5– 7 074.174.1PAL16L8, PAL16Rx, PAL20L8, PAL20Rx -10 10 8– 10 055.655.6GAL22V10-252515131533.335.76432×6440×6432×2048=2048162++2066=f maxE t PD t CO t CF t SU t H f maxE f maxI146DIGITAL CIRCUITS8.6The column above gives the answers in MHz. 8.7module Eight_Bit_Regtitle ’8-bit Edge-Triggered Register’Z74X374 device ’P16V8R’;" Input pinsCLK, !OE pin 1, 11;D1, D2, D3, D4, D5, D6, D7, D8 pin 2, 3, 4, 5, 6, 7, 8, 9;" Output pinsQ1, Q2, Q3, Q4, Q5, Q6, Q7, Q8 pin 19, 18, 17, 16, 15, 14, 13, 12;" Set definitionsD = [D1,D2,D3,D4,D5,D6,D7,D8]; Q = [Q1,Q2,Q3,Q4,Q5,Q6,Q7,Q8];equations Q := D;end Eight_Bit_Reg8.10If EN or CLK is 0, the output will be stable. If both are 1, the results are unpredictable, since they depend oncircuit timing. It is certain that the circuit’s output will be unstable as long as this condition is true.8.11The counter is modified to return to a count of 0 when count 9 is reached.8.13The counting direction is controlled by QD : count up when QD =1, count down when QD =0. A load occurswhen the counter is in the terminal state, 1111 when counting up, 0000 when counting down. The MSB is com-plemented during a load and the other bits are unchanged.Let us assume that the counter is initially in one of the states 0000–0111. Then the counter counts down (QD =0). Upon reaching state 0000, it loads 1000 and subsequently counts up (QD =1). Upon reaching state 1111, the counter loads 0111, and subsequently counts down, repeating the cycle.module Z74x162title '4-bit Decade Counter' "Z74X162 device 'P16V8R'; " Input pinsCLK, !OE pin 1, 11;A, B, C, D pin 2, 3, 4, 5; !LD, !CLR, ENP, ENT pin 6, 7, 8, 9; " Output pinsQA, QB, QC, QD pin 19, 18, 17, 16 istype 'reg';RCO pin 15; " Set definitionsINPUT = [ D, C, B, A ]; COUNT = [QD, QC, QB, QA ]; equationsCOUNT.CLK = CLK;COUNT := !CLR & ( LD & INPUT# !LD & (ENT & ENP) & (COUNT < 9) & (COUNT + 1) # !LD & (ENT & ENP) & (COUNT == 9) & 0 # !LD & !(ENT & ENP) & COUNT); RCO = (COUNT == 9) & ENT; end Z74x162f maxIEXERCISE SOLUTIONS147 If the counter is initially in one of the states 1000–1111, the same cyclic behavior is observed. The counting sequence has a period of 16 and is, in decimal,8, 9, 10, 11, 12, 13, 14, 15, 7, 6, 5, 4, 3, 2, 1, 0, 8, 9, ...If only the three LSBs are observed, the sequence is0, 1, 2, 3, 4, 5, 6, 7, 7, 6, 5, 4, 3, 2, 1, 0, 0, 1, ...8.14The only difference between a ’163 and a ’161 is that the CLR_L input of ’161 is asynchronous. Thus, thecounter will go from state 1010 to state 0000 immediately, before the next clock tick, and go from state 0000 to state 0001 at the clock tick. Observing the state just before each clock tick, it is therefore a modulo-10 counter, with the counting sequence 0, 1, ..., 9, 0, 1, ....Note that this type of operation is not recommended, because the width of the CLR_L pulse is not well con-trolled. That is, the NAND gate will negate the CLR_L pulse as soon as either one of its inputs goes to 0. If, say, the counter’s QB output clears quickly, and its QD output clears slowly, it is possible for CLR_L to be asserted long enough to clear QB but not QD, resulting in an unexpected next state of 1000, or possibly metastability of the QD output.8.17The path from the Q1 counter output (B decoder input) to the Y2_L output has 10ns more delay than the Q2 andQ0 (C and A) paths. Let us examine the possible Y2_L glitches in Figure 8–43 with this in mind:3→4 (011→100) Because of the delay in the Q1 path, this transition will actually look like 011→110→100.The Y6_L output will have a 10-ns glitch, but Y2_L will not.7→0 (111→000) Because of the delay in the Q1 path, this transition will actually look like 111→010→000.The Y2_L output will have a 10-ns glitch, but the others will not.8.19The delay calculation is different, depending on the starting state.In the INIT state, U7 and U8 take 21ns to propagate the CLEAR signal to the outputs. Then U6 requires 20ns setup time on its D inputs while U3 requires 20ns setup time on its RIN input. This implies a minimum clock period of 41ns, assuming zero delay from the control unit.In states M1–M8, the minimum clock period depends on the delay of the combinational logic in the control unit that asserts SELSUM when MPY0 is asserted. However, the most obvious way to do this is to connect MPY0 directly to SELSUM, creating a delay of 0ns. This assumption is made below. Also, it is assumed that MPY0 is1 to find the worst case. The figure on the next page shows the worst-case path, in heavy lines, to be 106ns.Since we would like to use the same clock for all states, the minimum clock period is 106ns.148DIGITAL CIRCUITSU6 Q outputs validU2, U3outputs valid U4 C4output validU5 C4output validU5 S outputs validU7 & U8outputs validU4 S outputs valid24ns16ns21ns16ns16ns24ns27ns39ns14ns14ns24nsU9 gate output valid27ns27nsU6 D inputs set up20ns20nsU3 RIN input set up 20nsReady for next clockClock edgeEXERCISE SOLUTIONS 1498.20The synchronizer fails if META has not settled by the beginning of the setup-time window for FF2, which is5ns before the clock edge. Since the clock period is 40ns, the available metastability resolution time is 35 ns.The MTBF formula isSubstituting the proper values of and for the ’F74, and of and for the problem, we calculate8.22Refer to the sample data sheet on page 169 of the text: “Not more than one output should be shorted at a time;duration of short-circuit should not exceed one second.” In the switch debounce circuit, the short lasts only for a few tens of nanoseconds , so it’s OK. 8.23CMOS outputs can “latch up” under certain conditions. According to the Motorola High-Speed CMOS LogicData book (1988 edition, pp. 4–10), a 74HCT output can latch up if a voltage outside the range is forced on the output by an external source. In a switch debounce circuit using 74HCT04s, the switch connection to ground is an external source, but the voltage (0V) is within the acceptable range and should not be a problem.Another potential problem is excessive short-circuit current, but again the data book indicates that shorting the output briefly is not a problem, as long as “the maximum package power dissipation is not violated” (i.e., the short is not maintained for a long time).Similar considerations apply to 74AC and 74ACT devices, but in the balance, such devices are not recom-mended in the switch-debounce application, as we’ll explain. On one hand, typical 74AC/74ACT devices are even less susceptible to latch-up than 74HCT devices. (For example, see the Motorola FACT Data book, 1988edition, pp. 2–9.) On the other hand, 74AC/74ACT’s high performance may create noise problems for other devices in a system. In particular, when the 74AC/74ACT HIGH output is shorted to ground, it may momen-tarily drag the local 5V power-supply rail down with it, especially if the decoupling capacitors are small, far away, or missing. This will in turn cause incorrect operation of the other, nearby logic devices.8.25TTL inputs require significant current, especially in the LOW state. The bus holder cannot supply enoughcurrent unless the series resistor is made much smaller, which then creates a significant load on the bus.MTBF t r ()t rτ⁄()exp T 0f ⋅a⋅------------------------=τT 0f a MTBF 35ns ()350.4⁄()exp 2.0104–106106⋅⋅⋅------------------------------------------21028s⋅≈=0.5–V out V CC 0.5V +≤≤150DIGITAL CIRCUITS8.26.8.28The maximum delay from clock to output of a 74HCT74 flip-flop is 44 ns. For a 4-bit ripple counter, the delayripples through four such stages for a total maximum delay of 176 ns. Similarly, the maximum delays using 74AHCT and 74LS74 flip-flops are 40 ns and 160 ns, respectively.8.32library IEEE;use IEEE.std_logic_1164.all;---- Exercise 8-26-- This code combines the address latch and -- and the decoder and its latch entity latch_decode is port (abus : in std_logic_vector ( 31 downto 0);avalid : in std_logic;la : out std_logic_vector ( 19 downto 0);romcs, ramcs0, ramcs1, ramcs2 : out std_logic);end entity latch_decode;architecture behave of latch_decode isbeginprocess (avalid, abus)beginif (avalid = '1') thenla <= abus (19 downto 0);end if;end process;process (abus, avalid)variable rom, ram1, ram2, ram0 : std_logic_vector (11 downto 0);beginrom := "111111111111";ram0 := "000000000000";ram1 := "000000010000";ram2 := "000000100000";If (avalid= '1') thenif (abus (31 downto 20) = rom ) then romcs <= '1'; else romcs <= '0'; end if; if (abus (31 downto 20) = ram0) then ramcs0 <= '1'; else ramcs0 <= '0'; end if; if (abus (31 downto 20) = ram1) then ramcs1 <= '1'; else ramcs1 <= '0'; end if; if (abus (31 downto 20) = ram2) then ramcs2 <= '1'; else ramcs2 <= '0'; end if;end if;end process;end behave;t period(min)t pTQ 3t AND t setup++=f max 1t period(min)⁄=EXERCISE SOLUTIONS1518.37Inputs Current state Next state CLR_L LD_L ENT ENP QD QC QB QA QD∗QC∗QB∗QA∗0x x x x x x x000010x x x x x x D C B A110x x x x x QD QC QB QA11x0x x x x QD QC QB QA111100000001111100010010111100100011111100110100111101000101111101010110111101100111111101111000111110001001111110010000111110101011111110110100111111001101111111010100111111101111111111110000152DIGITAL CIRCUITS8.3874LS163CLR CLK LD QA QB2141119ENP ENT710A B34C D 56QCQD 15RCOU1131274LS163CLR CLK LD QA QB 21411ENPENT10A B 34C D56QCQD 15RCOU2131274LS163CLR CLK LDQA QB 21411ENP ENT 10A B34C D56QC QD 15RCO U3131274LS163CLR CLK LDQA QB 21411ENP ENT 10A B34C D56QC QD 15RCO U91312CLOCK+5 VR12345611121243U18U1974LS3074LS0474LS00U1012321U1174LS04Note: This design assumes that largest available "AND" function is an 8-input NAND gate. Thus,cascading counters greater than 36 bits may require additional levels of delay.(Actually, we could make an equally fast counter with up to 100 bits by combining the outputs of three 74LS30s with a 74LS27, a 3-input NOR.)Q0Q1Q2Q3Q4Q5Q6Q7Q8Q9Q10Q11Q32Q33Q34Q35EXERCISE SOLUTIONS 153The minimum clock period is the sum of:(a)The delay from the clock edge to any RCO output (35ns).(b)The delay from any RCO output to any ENP input, that is, two gate delays ().(c)The setup time to the next clock edge required by the ENP inputs (20ns).Thus, the minimum clock period is 85 ns, and the corresponding maximum clock frequency is 11.76 MHz. 8.41To get even spacing, the strategy is for the MSB (N3) to select half the states, the ones where QA is 0. The nextbit down (N2) selects one-fourth of the states, the ones where QB is 0 and the less significant counter bits (i.e.,QA ) are all 1. Likewise, N1 selects the one-eighth of the states where QC is 0 and QB and QA are 1, and N0selects the state where QD is 0 and QC , QB , and QA are all 1. In this way, each non-1111 counter state is assigned to one input bit.215⋅30ns =1474LS163CLR ZCLK LDQA N3N2N1N0QB 21119ENP ENT 710A B34C D56QC QD 15RCO U11312CLOCK+5 VR74LS2012456U3121213U274LS103465U274LS1012U574LS0434U5U574LS045674LS04123456111212U474LS3091081213U374LS20U574LS04154DIGITAL CIRCUITS8.53--Chris Dunlap--Xilinx Applicationslibrary IEEE;use IEEE.std_logic_1164.all;use IEEE.std_logic_arith.all;use IEEE.std_logic_unsigned.all;entity v74x163s isgeneric(size : integer := 8); --added genericport (clk,clr_l,ld_l,enp,ent : in std_logic;d : in std_logic_vector (size-1 downto 0); --changes range of inputq : out std_logic_vector (size-1 downto 0); --changes range of outputrco : out std_logic);end v74x163s;architecture v74x163_arch of v74x163s iscomponent synsercell isport (clk, ldnoclr, di, coclrorld,cntenp,cnteni : in std_logic;qi,cnteni1 : out std_logic);end component;signal ldnoclr,noclrorld : std_logic;signal scnten : std_logic_vector (size downto 0); --creates a ranged temp with overflow room beginldnoclr <= (not ld_l) and clr_l;noclrorld <= ld_l and clr_l;scnten(0) <= ent;rco <= scnten(size);gi: for i in 0 to size-1 generate --counts for size of counterU1: synsercell port map (clk, ldnoclr, noclrorld, enp, d(i), scnten(i), scnten(i+1), q(i));end generate;end v74x163_arch;8.54--**********************************-- PROBLEM : WAKERLY - 8.54-- FILES :-- 8_54_top.vhd : top level file-- 8_54_par2ser.vhd : parallel to serial converter-- 8_54_control.vhd : control module-- 8_54_shift_synch.vhd : 8 bit shift register---- DESCRIPTION :-- Creates a parallel to serial converter.-- Data in is described as 8 x 8bit modules,-- with a single 8 bit data bus that carries-- data of the format given in Figure 8-55.-- Each serial link has its own SYNCH(i) line;-- the pulses should be staggered so SYNCH(i+1)-- occurs 1 clock cycle after SYNCH(i).---- Because of this, the load_synch line should-- also be staggered so the data transmitted-- over the serial link will correspond to its-- associated SYNCH line.--**********************************-- library declarationslibrary IEEE;use IEEE.std_logic_1164.all;-- top level entity declarationentity wak_8_54_top isport (data: in STD_LOGIC_VECTOR (63 downto 0);clock: in STD_LOGIC;synch: buffer STD_LOGIC_VECTOR (7 downto 0);sdata: out STD_LOGIC_VECTOR (7 downto 0));end wak_8_54_top;architecture wak_8_54_arch of wak_8_54_top issignal load_shift_master: std_logic;signal synch_master: std_logic;signal load_shift: std_logic_vector (7 downto 0);--component declarationscomponent par2ser isport (clock: in STD_LOGIC;data: in STD_LOGIC_VECTOR (7 downto 0);load_shift: in STD_LOGIC;sdata: out STD_LOGIC);end component;component control isport (clock: in STD_LOGIC;load_shift: out STD_LOGIC;synch: out STD_LOGIC);end component;component shift_synch isport (clock: in STD_LOGIC;synch_in: in STD_LOGIC;synch: buffer STD_LOGIC_VECTOR (7 downto 0));end component;begin--component instantiationsS1: shift_synch port map (clock=>clock, synch_in=>synch_master, synch=>synch);S2: shift_synch port map (clock=>clock, synch_in=>load_shift_master,synch=>load_shift);U1: par2ser port map (clock=>clock, data=>data(7 downto 0), load_shift=>load_shift(0), sdata=>sdata(0));U2: par2ser port map (clock=>clock, data=>data(15 downto 8),load_shift=>load_shift(1), sdata=>sdata(1));U3: par2ser port map (clock=>clock, data=>data(23 downto 16),load_shift=>load_shift(2), sdata=>sdata(2));U4: par2ser port map (clock=>clock, data=>data(31 downto 24),load_shift=>load_shift(3), sdata=>sdata(3));U5: par2ser port map (clock=>clock, data=>data(39 downto 32),load_shift=>load_shift(4), sdata=>sdata(4));U6: par2ser port map (clock=>clock, data=>data(47 downto 40),load_shift=>load_shift(5), sdata=>sdata(5));U7: par2ser port map (clock=>clock, data=>data(55 downto 48),load_shift=>load_shift(6), sdata=>sdata(6));U8: par2ser port map (clock=>clock, data=>data(63 downto 56),load_shift=>load_shift(7), sdata=>sdata(7));U9: control port map (clock=>clock, load_shift=>load_shift_master,synch=>synch_master);end wak_8_54_arch;--*************************************-- Basically an 8-bit shift register-- takes the synch_in signal as an-- input, and outputs an 8 bit signal,-- each consecutive bit delayed by one-- from the previous bit.-- library declarationlibrary IEEE;use IEEE.std_logic_1164.all;use IEEE.std_logic_arith.all;use IEEE.std_logic_unsigned.all;-- top level entity declarationentity shift_synch isport (clock: in STD_LOGIC;synch_in: in STD_LOGIC;synch: buffer STD_LOGIC_VECTOR (7 downto 0) );end shift_synch;architecture shift_synch_arch of shift_synch is begin-- low order synch signal is simply passed through -- to output. all others are delayed.synch(0) <= synch_in;process(clock)beginif clock'event and clock='1' thenfor I in 0 to 6 loopsynch(I+1) <= synch(I);end loop;end if;end process;end shift_synch_arch;--***************************************-- Parallel to serial converter-- Data is entered through 8 bit DATA bus-- It is loaded into the register when-- load_shift is low. If load_shift is-- high, shift data serially out through sdata -- library declarationslibrary IEEE;use IEEE.std_logic_1164.all;-- top level entity declarationentity par2ser isport (clock: in STD_LOGIC;data: in STD_LOGIC_VECTOR (7 downto 0); load_shift: in STD_LOGIC;sdata: out STD_LOGIC);end par2ser;architecture par2ser_arch of par2ser is-- internal signal declarationsignal REG: STD_LOGIC_VECTOR(7 downto 0); signal DIN: std_logic;begin-- DIN <= 0 will set the high order bit to be -- zero once data is loaded in.DIN <= '0';-- process to create shift register--accomplished by simply taking the DIN signal --and concatenating on the end the previous--6 high order bits.process (clock)beginif clock'event and clock='1' thenif load_shift = '0' thenREG <= data;elseREG <= DIN & REG(7 downto 1);end if;end if;sdata <= REG(0);end process;end par2ser_arch;--******************************-- Control logic-- controls the loading of the-- parallel to serial shift register-- through the load_shift signal.-- also, controls the synch word.-- this occurs every 256 clock cycles.--library declarationlibrary IEEE;use IEEE.std_logic_1164.all;use IEEE.std_logic_arith.all;use IEEE.std_logic_unsigned.all;--top level entity declarationentity control isport (clock: in STD_LOGIC;load_shift: out STD_LOGIC;synch: out STD_LOGIC);end control;architecture control_arch of control is--internal signal declarationsignal COUNT: STD_LOGIC_VECTOR(7 downto 0);signal load: STD_LOGIC;beginload <= '0'; --define constantprocess (clock)beginif clock'event and clock='1' thencount <= count + 1;if count(2 downto 0) = "110" thenload_shift <= load;elseload_shift <= not load;end if;if count = 254 thensynch <= '1';elsesynch <= '0';end if;end if;end process;end control_arch;8.55This is really the second paragraph of Exercise 8.54.8.62Regardless of the number of shift-register outputs connected to the odd-parity circuit, its output in state 00 (00)is 0, and the 00...00 state persists forever. However, suppose that an odd number of shift-register outputs are connected. Then the output of the odd-parity circuit in state 11...11 is 1, and the 11...11 state also persists for-ever. In this case, the number of states in the “maximum-length” sequence can be no more than , since two of the states persist forever. Therefore, if an LFSR counter generates a sequence of length , it must have an even number of shift-register outputs connected to the odd-parity circuit. 8.64The figure below shows the effect of physically changing the odd-parity circuit to an even-parity circuit (i.e.,inverting its output).From Exercise 9.32, we know that an even number of shift-register outputs are connected to the parity circuit,and we also know that complementing two inputs of an XOR gate does not change its output. Therefore, we can redraw the logic diagram as shown below.2n 2–2n 1–N-bit parallel-out shift registerPR CLK SERINQBQAQCQY QX QZCLOCK RESET_LXN_Lconnect to selected outputs (see table)even-parity circuitXN–1XN–2XN–3X2X1X0N-bit parallel-out shift registerPR CLK SERINQBQAQC QY QX QZCLOCK RESET_LXN_Lconnect to selected outputs (see table)even-parity circuitXN–1XN–2XN–3X2X1X0Finally, we can move the inversion bubbles as shown below.This circuit has exactly the same structure as Figure 8–68, except that the shift register stores complemented data. When we look at the external pins of the shift register in the first figure in this solution, we are looking at that complemented data. Therefore, each state in the counting sequence of the even-parity version (our first figure) is the complement of the corresponding state in the odd-parity version (Figure 8–68). The odd-parity version visits all states except 00...00, so the even-parity version visits all states except 11...11.N-bit parallel-out shift registerCLR CLK SERINQB QA QCQY QX QZCLOCK RESET_LXNconnect to selected outputs (see table)odd-parity circuitXN–1XN–2XN–3X2X1X08.68--Johnny West--Xilinx Applications--8.68 : Design an iterative circuit for checking the parity of a 16-bit data-- word with a single even-parity bit.--------------------------------------------------------------------------------------------------This portion of the code constructs the iterative module that will cascaded 16 --times in order to check the parity of a 16 bit word.------------------------------------------------------------------------------------------------library IEEE;use IEEE.std_logic_1164.all;--Generic Iterative Moduleentity Iterative_Module isport (carry_in, primary_in: in STD_LOGIC;carry_out: out STD_LOGIC);end Iterative_Module;--An XOR is performed on the current parity of a word (carry_in) and the--next bit in the word (boundary_in)--Even parity produces a 0 and odd parity produces a 1architecture Parity_Check of Iterative_Module isbegincarry_out <= carry_in xor primary_in;end Parity_Check;-------------------------------------------------------------------------------------This portion of the code cascades the interative module 16 times and connects the --modules together.-----------------------------------------------------------------------------------library IEEE;use IEEE.std_logic_1164.all;--Top level entity for checking the parity of a 16bit wordentity Parity_16bit isport (data_word: in STD_LOGIC_VECTOR (15 downto 0);parity: out STD_LOGIC );end Parity_16bit;--Architecture consists of 16 cascaded iterative modulesarchitecture Parity_16bit_arch of parity_16bit iscomponent Iterative_Moduleport (carry_in, primary_in: in STD_LOGIC;carry_out: out STD_LOGIC );end component;signal carry: STD_LOGIC_VECTOR (15 downto 0);signal cin0: STD_LOGIC;begincin0 <= '0';P0: Iterative_Module port map (cin0, data_word(0), carry(0));P1: Iterative_Module port map (carry(0), data_word(1), carry(1));P2: Iterative_Module port map (carry(1), data_word(2), carry(2));P3: Iterative_Module port map (carry(2), data_word(3), carry(3));P4: Iterative_Module port map (carry(3), data_word(4), carry(4));P5: Iterative_Module port map (carry(4), data_word(5), carry(5));P6: Iterative_Module port map (carry(5), data_word(6), carry(6));P7: Iterative_Module port map (carry(6), data_word(7), carry(7));P8: Iterative_Module port map (carry(7), data_word(8), carry(8));P9: Iterative_Module port map (carry(8), data_word(9), carry(9));P10: Iterative_Module port map (carry(9), data_word(10), carry(10));P11: Iterative_Module port map (carry(10), data_word(11), carry(11));P12: Iterative_Module port map (carry(11), data_word(12), carry(12));P13: Iterative_Module port map (carry(12), data_word(13), carry(13));P14: Iterative_Module port map (carry(13), data_word(14), carry(14));P15: Iterative_Module port map (carry(14), data_word(15), carry(15));parity <= carry(15); --parity = 0 is even parity and 1 if odd parityend parity_16bit_arch;8.75In the following design, RESET is not recognized until the end of phase 6. RESTART is still recognized at theend of any phase; otherwise it would have no real use (i.e., only going back to phase 1 after the end of phase 6,which happens anyway.) Presumably, RESTART would be used only with great care or in unusual circum-stances (e.g., during debugging).8.81This problem can be a bit confusing since the states in Table 7–14 have the same names as the ’163 data inputs.Therefore, we shall use the names SA , SB , and so on for the states.The idea is to normally allow the counter to count to the next state, but to force it to go to SA or SB when the wrong input is received. The CLR_L input is used to go to SA (0000), and the LD_L input is used to go to SB (0001; the counter’s A–D data inputs are tied LOW and HIGH accordingly).Inspecting the state table on page 582 of the text, we see that state A should be loaded when X =1 and the machine is in state SA , SD , or SH . Thus,All of the other next-states when X =1 are the natural successors obtained by counting.Similarly, state SB should be loaded when X =0 and the machine is in state SB , SC , SE , SF , or SH . In addition,notice that in state SG , the next state SE is required when X =0; the load input must be used in this case too, but a different value must be loaded. Thus, LD_L will be asserted in six of the eight states when X =0.Optionally, LD_L could be easily asserted in the remaining two states as well, since the required next states (SB and SE ) are ones that we must generate in other six cases anyway. Thus, we can connect X to the LD_L input, so we always load when X =0. Then, we load either SB (0010) or SE (0100) depending on the current state. There-fore, we can write the following equations for data inputs A –D :Alternatively, we could realize C as an AND -OR circuit and complement to get B :module TIMEGEN6title 'Six-phase Master Timing Generator'" Input and Output pinsMCLK, RESET, RUN, RESTART pin;T1, P1_L, P2_L, P3_L, P4_L, P5_L, P6_L pin istype 'reg'; " State definitionsPHASES = [P1_L, P2_L, P3_L, P4_L, P5_L, P6_L];NEXTPH = [P6_L, P1_L, P2_L, P3_L, P4_L, P5_L];SRESET = [1, 1, 1, 1, 1, 1];P1 = [0, 1, 1, 1, 1, 1];P6 = [1, 1, 1, 1, 1, 0];equationsT1.CLK = MCLK; PHASES.CLK = MCLK;WHEN (RESET & PHASES==P6 & !T1) THEN {T1 := 1; PHASES := SRESET;}ELSE WHEN (PHASES==SRESET) # RESTART THEN {T1 := 1; PHASES := P1;}ELSE WHEN RUN & T1 THEN {T1 := 0; PHASES := PHASES;}ELSE WHEN RUN & !T1 THEN {T1 := 1; PHASES := NEXTPH;}ELSE {T1 := T1; PHASES := PHASES;}end TIMEGEN6CLR_L X Q (C ′QB ′QA ′⋅⋅⋅QC ′QB QA ⋅⋅QC QB QA )⋅⋅++[]′=X Q (C ′QB ′QA ⋅⋅⋅QB QA )⋅+[]′=A 0=B SASB SC SE SF SH+++++=QB ′QC ′QA ′⋅QC QA ⋅++=C B ′=D 0=C QC ′QB QA ⋅⋅QC QB QA ′⋅⋅+=B C ′=。
数字集成电路分析与设计第五章答案

数字集成电路分析与设计第五章答案CHAPTER 5P5.1. For each problem, restate each Boolean equation into a form such that it can be translated into the p and n-complex of a CMOS gate.a. ()()Out ABC BD ABC BD A B C B D =+=+=+++b. ()()()Out AB AC BC AB AC BC A B A C B C =++=++=+++c. ()()Out A B CD A AB C D A A B CD A A B CD A =+++=++=+++=++AbVddVddAb BbAAbVddP5.2.AP5.3. First, convert the equation into its p and n-complex.()()()()()()()()()()()Out A B C BC AB AB C BC AB AB C BC AB AB C BC AB AB C BC AB AB C B C =⊕+=++=++=+=++=+++VddCbP5.4. The truth table is given below in terms of voltages. The function is F A B =The worse case V OH is V DD and the worse case V OL is 0V.P5.5. The first circuit is a NOR gate while the second is a NAND gate. The V OL and V OHcalculated are for the worst-case scenario. To find this, assume only one transistor turns on, this just reduces to a pseudo-NMOS/PMOS inverter, so the other transistors are not important.a. The V OL for the pseudo-NMOS (in 0.18µm) is:()()()2,1N N OXNSAT OX P GSP TPP SATOL W C L N DD TN GSP TP CP PDD TN SAT P N OX v C W V V I V k V V V V E L V V v W L C µ-==--+-=()2DD TP N N OX V V W C µ-()()()()()20.1DD TP CP P DD TN SAT P N DD TPDDN N DD TP CP P DD TN V V E L V V v W L V V V W V V E L V V µ-+--==-+-()()()()()()()()()()()()226440.18100.2100.210 1.80.50.14µm=1.40.11.8270 1.80.5240.2 1.80.5SAT P N DD TPN DD N DD TP CP P DD TN v W L V V W V V V E L V V µλ---=-+--==-+-Since the minimum width is 2λ, we make that the width. The V OH for the pseudo-PMOS (in 0.18µm) is:()()()()()()2221SDPSDP CP PN P V P OX P SGP TP SDP SAT OX N GSN TN V GSN TN CN N N SAT OX I sat I lin C W V V V v C W V V V V E L L v C µ=---= -++()2P OX N DD TN DD TN CN NC W V V V V E L µ-=-+()()()()(01DD OH DD OH CP PV V P DD TPDDOH V V P E L W V V VV L ------+()()()()()()20.1824620.184.8(70) 1.80.50.180.2(10)(810)1.80.51.80.5 1.21P P W L ----=-++4.2P W λ≈The pseudo-PMOS circuit will have bigger devices than the pseudo-NMOS.P5.6. The steps to solving this question are the same as the pseudo-NMOS question in Chapter4.a. For V OH , recognize that GS T V V >= for operation so the output can only be as high asDD T V V -. Since 0SB V ≠, body effect must be taken into account and the full equationis:()()()001.20.40.2OH DD T DDT V V V V Vγγ=-+=-+=-+ Iteration produces V OH =0.73V.b. For V OL , we must first recognize that the worst-case V OL occurs when only one of the pull-down transistors is on. Next we identify the regions of operation of the transistors. In this case, the pull-up transistor is always in saturation and the pull-down is most likely in the linear region since it will have a high input (high V GS ) and a low output (low V DS ). Then, we equate the two currents together and solve for V OL :()()()()2212222221111122460.61(1)(270)1.20.4(0.13)(10)(810)1.20.42(1.20.42)0.61DS DS CN OL OLV N OX GS T DS sat OX GS T V GS T CN E LV OL OL V OL I sat I lin W C V V V W v C V V V V E L L V V V µ-=---=-++--?--=--++ Using a programmable calculator or a spreadsheet program, V OL = 0.205V. The dc current with the output low is: ()()()()222222260.20520.2051(1)(270)(1.610)1.20.4(0.205)146.5DS DS CN V N OX GS T DS DS V ELW C V V V I L Aµµ---=+?--=+=The power with the output low is:(46.5)(1.2)55.8DS DD P I V A V W µµ===P5.7. See Example 5.2 which is based on the NAND gate. This question is the same except thatit addresses the NOR gate.With both inputs tied together, 88N P W W λλ==2χ=== ()()1.80.520.50.77V 112DD TP TNS V V V V χχIn the SPICE solution, the reason why the results vary for input A and B is due to body-effect.P5.8. The solution is shown below. Notice that there is no relevance with the lengths andwidths of the transistors when it comes to V OH , although they the do matter when calculating V OL .01.80.50.3 2.51Vout GG T GG out T V V V V V V γ=-=++=++=P5.9. For t PLH , we need to size the pull-up PMOS appropriately.()()()()15120.70.720.70.73010010845010PLH eqp LOAD p SQ LOAD PLHLt RC R C WL W R C k t λλ--====Ω?=?For V OL :()()()()()()()()()()()()()2246660.120.13 4.210810 1.610 1.20.4 1.08mA1.20.4240.1(270)(1.610)1.20.40.11138.577377232(3OLOL CN P sat OX GS T P GS T CP V N N OX OL TN OLN P V N N NW v C V V I sat V V E LW C V V V W I sat L L W W W stack L µλλλ-----===-+-+--?--==++===?=2)155(2)W stack λ=P5.10.The circuit is shown below:()()()()()()()()31512315120.720.70.7301075106350100.720.70.712.510751026.6275010PLH EQP LOAD P P EQPLOAD PLHPHL EQN LOAD NN EQNLOAD PHLLt RC R C W L W R C t Lt RC R C W L W R C t λλλλλ----====??=?====??=≈?Because the number of transistors in series is more than one, we must multiply the widths by the appropriate number. Here, all the NMOS transistors will have a width of 54λ. The PMOS transistors will have widths of 126λ and 190λ, respectively.P5.11. We estimate the dc power and dynamic switching power for this problem.a. The circuit’s dc power can be computed by computing the dc current when the output is low. This is given by I DS =550uA/um x 0.1um=55uA. Then P DC =66uW when the output is low.b. Its dynamic power can be calculated by simply using the equation 2dyn DD P CV f α=. Therefore, P dyn =(50fF)(V DD -V TN )(V DD )(100MHz)=4.4uW.P5.12. The pseudo-NMOS inverter has static current when the output is low. We can estimate itas:()()()()()()()()224660.110810 1.610 1.20.425.6A 1.20.4240.1P sat OX GS T P GS T CP W v C V V I sat V V E Lµ----===-+-+Then the average static power is P stat =(25.6uA)(1.2)/2 =15.4uW.The dynamic power is dyn DD swing avg P CV V f ==(50fF)(1.2)(1.1)f avg assuming that V OL is 0.1V.For the CMOS inverter, the static power is almost zero: P stat =I sub V DD . It is far less thanthe pseudo-NMOS case. The dynamic power dyn DD swing avg P CV V f ==(50fF)(1.2)2f avg is slightly larger than the pseudo-NMOS case.V VINCMOS InverterV V INPseudo-NMOSP5.13. Model development to compute αsc .P5.14. The energy delivered by the voltage source is:()()200202DDDDV C sourceDD DD L L DDC L DDV CDDcap C LC L C C LdvE i t V dt V C dt C V dv C V dt dv V E i t v dt C v dt C v dv C dt∞∞∞∞========As can be seen, only half the energy is stored in the capacitor. The other half was dissipated as heat through the resistor.P5.15. The average dynamic power does not depend on temperature if the frequency stays thesame. However, the short-circuit current will increase as temperature increases. In addition, the subthreshold current increases as temperature increases. So the overall power dissipation will be higher. P5.16. The circuit is shown below. The delay should incorporate both Q and Qb settling in400ps. All NMOS and PMOS devices are the same size in both NAND gates.()()()()()()()()15331220.70.70.70.720.71001030100.1212.5100.10.72400101µmN P P PHL PLH UP LOAD DOWN LOAD LOAD eqp eqn P N LOAD eqp eqn LOAD eqp eqn PL Lt t t R C R C C R R W W C R L R L WC R L R L W t --??=+=+=+ ?+=++==≈P5.17. The small glitch in J propagates through the flop even though it is small. This is due tothe fact that the JK-flop of Figure 5.20 has the 1’s catching problem. P5.18. The small glitch in J does not propagate through the flop since the edge-triggeredconfiguration does not have a 1’s catching problem.P5.19. The positive-edge triggered FF is as follows:QQDS(a) With CK=D=0 and S=R=1, the outputs are(b) Now CK=0。
数字设计-原理与实践课后习题答案

第1 章习题参考答案:1-6 一个电路含有一个2 输入与门(AND2),其每个输入/输出端上都连接了一个反相器;画出该电路的逻辑图,写出其真值表;能否将该电路简化?解:电路图和真值表如下:由真值表可以看出,该电路与一个2 输入或门(OR2)相同。
第2 章习题参考答案:将下面的八进制数转换成二进制数和十六进制数。
(a) 12348=1 010 011 1002=29C16(b) 1746378=1 111 100 110 011 1112=F99F16(c) 3655178=11 110 101 101 001 1112=1EB4F16(d) =10 101 011 101 011 010 0012=ABAD116(e) =111 100 011 0012=(f) =100 101 011 001 100 111 12=将下面的十六进制数转换为二进制数和八进制数。
(a) 102316=1 0000 0010 00112=100438(b) 7E6A16=111 1110 0110 10102=771528(c) ABCD16=1010 1011 1100 11012=1257158(d) C35016=1100 0011 0101 00002=1415208(e)=1001 1110 10102=(f)=1101 1110 1010 1110 1110 11112=将下面的数转换成十进制数。
(a) =107 (b) 1740038=63491 (c) 2=183(d) = (e)= (f)F3A516=62373(g) 120103=138 (h) AB3D16=43837 (i) 71568=3694(j) =完成下面的数制转换。
(a) 125= 1 111 1012 (b) 3489= 66418 (c) 209= 11 010 0012 (d) 9714= 227628 (e) 132= 10 000 1002 (f) 23851= 5D2B16 (g) 727= 104025 (h) 57190=DF6616 (i) 1435=26338(j) 65113=FE5916将下面的二进制数相加,指出所有的进位:(a) S:1001101 C:100100(b) S: 1010001 C: 1011100(c) S: 0 C: 0(d) S: C:利用减法而不是加法重复训练题,指出所有的借位而不是进位:(a) D:011 001 B:110000 (b) D:111 101 B:1110000 (c) D: B:00111000 (d) D:1101101 B:写出下面每个十进制数的8 位符号-数值,二进制补码,二进制反码表示。
数字视觉设计考试题及答案

数字视觉设计考试题及答案一、选择题(每题2分,共20分)1. 数字视觉设计中,以下哪种颜色模式不适用于网页设计?A. RGBB. CMYKC. HSBD. LAB答案:B2. 在Photoshop中,以下哪个工具用于创建选区?A. 画笔工具B. 套索工具C. 橡皮擦工具D. 钢笔工具答案:B3. 以下哪种文件格式是无损压缩的?A. JPEGB. PNGC. GIFD. TIFF答案:D4. 在数字视觉设计中,以下哪个术语指的是图像的清晰度?A. 分辨率B. 饱和度C. 对比度D. 色温答案:A5. 以下哪个选项不是数字视觉设计中常用的设计原则?A. 对齐B. 重复C. 接近D. 动态答案:D6. 在Adobe Illustrator中,以下哪个工具用于创建直线?A. 铅笔工具B. 画笔工具C. 直线工具D. 钢笔工具答案:C7. 以下哪种颜色模式适合用于印刷?A. RGBB. CMYKC. HSBD. LAB答案:B8. 在数字视觉设计中,以下哪个术语指的是颜色的纯度?A. 亮度B. 饱和度C. 对比度D. 色温答案:B9. 以下哪种文件格式适合用于网页设计中的图像?A. PSDB. AIC. SVGD. EPS答案:C10. 在数字视觉设计中,以下哪个术语指的是图像的明暗程度?A. 亮度B. 饱和度C. 对比度D. 色温答案:A二、填空题(每题2分,共20分)1. 在数字视觉设计中,______用于创建具有透明度的图像。
答案:PNG2. 在Photoshop中,______工具用于调整图像的亮度和对比度。
答案:曲线3. 在Adobe Illustrator中,______工具用于创建和编辑文本。
答案:文字工具4. 分辨率的单位是______。
答案:PPI(像素每英寸)5. 在数字视觉设计中,______原则有助于创建清晰、有序的布局。
答案:对齐6. 在Photoshop中,______工具用于调整图像的饱和度。
专科考试:2021数字媒体设计与制作真题模拟及答案(5)

专科考试:2021数字媒体设计与制作真题模拟及答案(5)1、下面关于图像窗口的说法中,正确的是:()(单选题)A. 用户可以同时打开多个图像窗口B. 用于显示图像文件C. 用于建立和编辑图像D. 以上都对试题答案:D2、按钮中加入的语句“on (release){ gotoAndPlay(120)} ”,该脚本语句的含义是()(单选题)A. 当双击该按钮后,动画停止在第120帧B. 当单击该按钮后,动画转到在第120帧播放C. 当双击该按钮后,动画转到在第120帧播放D. 当单击该按钮后,动画停止在第120帧试题答案:B3、Photoshop工作窗口的组成有:()(单选题)A. 标题栏、菜单栏、工具箱、调色板、状态栏B. 标题栏、菜单栏、工具选择条、工具箱、调色板C. 标题栏、菜单栏、工具选择条、工具箱、状态栏D. 以上都是试题答案:D4、下图的花瓶主要由哪几个基本形体构成?()(单选题)A. 圆柱体和圆球体B. 圆球体和长方体C. 长方体和正方体D. 正方体和圆锥体试题答案:A5、素描是指()。
(单选题)A. 以单色线条和块面来塑造物体的形象B. 用铅笔塑造物体的形象C. 用各种工具及颜色来塑造物体的形象D. 用铅笔及炭笔来塑造物体的形象试题答案:A6、如何复制一个图层()(单选题)A. 选择“编辑”→“复制”B. 选择“图像”→复制”C. 选择“文件”“复制图层”D. 将图层拖放到Layers调板下方创建新图层的图标上试题答案:D7、主点是指()。
(单选题)A. 眼睛观察物体所处的位置B. 画家眼睛正对视平线上的一点C. 画家眼睛看出去的假想线D. 画家眼睛看到的最远点试题答案:B8、当设计一个表现叶片旋转的动作动画时,假设设置了旋转1周,该动画共100帧。
若想使叶片的旋转速度慢1倍,下面哪个操作正确()。
(单选题)A. 将该动画的结束关键帧向右拖动,使动画达到200帧B. 将该动画的开始关键帧向右拖动,使动画达到200帧C. 将该动画的结束关键帧向左拖动,使动画达到50帧D. 将该动画的开始关键帧向左拖动,使动画达到50帧试题答案:A9、选项中()不是成角透视特点。
数字设计习题答案

数字设计习题答案数字设计习题答案数字设计是一门既有挑战性又有趣味性的学科。
通过解决习题,我们可以提高我们的思维能力和创造力。
在这篇文章中,我将为大家提供一些数字设计习题的答案,希望能够帮助大家更好地理解这门学科。
1. 习题:将数字1到9排列成一个3x3的矩阵,要求每行、每列以及对角线上的数字和都相等。
请给出一个解法。
答案:一个可能的解法是:8 1 63 5 74 9 2在这个解法中,每行、每列以及对角线上的数字和都是15。
2. 习题:有一个4位的数字,它的百位数字是2,十位数字比百位数字大1,个位数字比十位数字大1,千位数字比个位数字大1。
请问这个数字是多少?答案:这个数字是3210。
3. 习题:有一个6位的数字,它的百位数字是奇数,十位数字比百位数字大1,个位数字比十位数字大1,千位数字比个位数字大1,万位数字比千位数字大1,百万位数字比万位数字大1。
请问这个数字是多少?答案:这个数字是753210。
4. 习题:有一个4位的数字,它的百位数字是偶数,十位数字比百位数字大1,个位数字比十位数字大1,千位数字比个位数字大1。
请问这个数字是多少?答案:这个数字是8642。
通过以上的习题答案,我们可以看到数字设计的魅力所在。
通过巧妙的排列和组合,我们可以得到各种有趣的数字组合。
数字设计不仅仅是一种数学问题,更是一种锻炼思维和创造力的方式。
除了以上的习题,数字设计还可以涉及到更复杂的问题,如数独、迷宫设计等。
这些问题需要我们运用逻辑思维和创造力来解决。
通过解决这些问题,我们可以提高我们的问题解决能力和创造力,培养我们的耐心和毅力。
数字设计不仅仅是一门学科,更是一种思维方式。
通过数字设计,我们可以培养我们的逻辑思维和创造力,提高我们的问题解决能力。
希望以上的习题答案能够帮助大家更好地理解数字设计,并在解决问题的过程中得到乐趣。
让我们一起探索数字设计的无限魅力吧!。
数字设计 答案 第三章答案
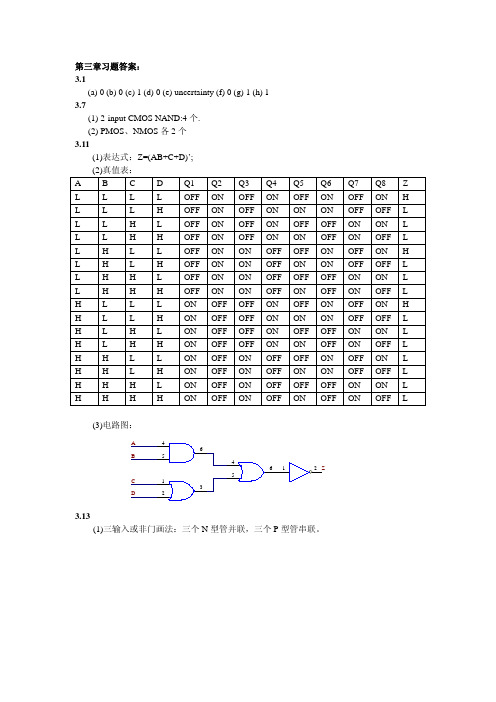
第三章习题答案: 3.1(a) 0 (b) 0 (c) 1 (d) 0 (e) uncertainty (f) 0 (g) 1 (h) 1 3.7(1) 2-input CMOS NAND:4个. (2) PMOS 、NMOS 各2个 3.11(1)表达式:Z=(AB+C+D)’; (2)真值表:A B C D Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Z L L L L OFF ON OFF ON OFF ON OFFON H L L L H OFF ON OFF ON ON ON OFF OFF L L L H L OFF ON OFF ON OFFOFFON ON L L L H H OFF ON OFFON ON OFFON OFF LL H L L OFF ON ON OFF OFF ON OFF ON H L H L H OFF ON ON OFF ON ON OFF OFF L L H H L OFF ON ON OFF OFFOFFON ON L L H H H OFF ON ON OFF ON OFFON OFF LH L L L ON OFF OFF ON OFF ON OFF ON H H L L H ON OFF OFF ON ON ON OFF OFF L H L H L ON OFF OFF ON OFFOFFON ON L H L H H ON OFF OFFON ON OFFON OFF LH H L L ON OFF ON OFF OFF ON OFF ON L H H L H ON OFF ON OFF ON ON OFF OFF L H H H L ON OFF ON OFF OFFOFFON ON L H H H H ON OFFON OFFON OFFON OFF L(3)电路图:3.13(1)三输入或非门画法:三个N 型管并联,三个P 型管串联。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5–1E X E R C I S E S O L U T I O N S COMBINATIONAL LOGIC DESIGN PRINCIPLES55.4READY ′ is an expression, with ′ being a unary operator. Use a name like READY_L or /READY instead.5.8Both LOW -to-HIGH and HIGH -to-LOW transitions cause positive transitions on the outputs of three gates (every second gate), and negative transitions on the other three. Thus, the total delay in either case isSince and for a 74LS00 are identical, the same result is obtained using a single worst-case delay of 15 ns.5.12The smallest typical delay through one ’LS86 for any set of conditions is 10 ns. Use the rule of thumb, “mini-mum equals one-fourth to one-third of typical,” we estimate 3 ns as the minimum delay through one gate.Therefore, the minimum delay through the four gates is estimated at 12 ns.The above estimate is conservative, as it does not take into account the actual transitions in the conditions shown. For a LOW -to-HIGH input transition, the four gates have typical delays of 13, 10, 10, and 20 ns, a total of 53 ns, so the minimum is estimated at one-fourth of this or 13 ns. For a HIGH -to-LOW input transition, the four gates have typical delays of 20, 12, 12, and 13 ns, a total of 57 ns, so the minimum is estimated at 14 ns.5.15 A decoder with active-low outputs ought to be faster, considering that this decoder structure can be imple-mented directly with inverting gates (which are faster than noninverting) as shown in Figures 5–35 and 5–37.5.16The worst-case ’138 output will have a transition in the same direction as the worst-case ’139 output, so we uset pHL numbers for both, which is the worst combination. The delay through the ’139 is 38 ns, and from thet p 3t pLH(LS00)3t pHL(LS00)+=315⋅315⋅+=90 ns=t pLH t pHL5–2DIGITAL CIRCUITSactive-low enable input of the ’138 is 32 ns, for a total delay of 70 ns. Using “worst-case” numbers for the parts and ignoring the structure of the circuit, an overly pessimistic result of 79 ns is obtained.We can also work the problem with 74HCT parts. Worst-case delay through the ’139 is 43 ns, and from the active-low enable input of the ’138 is 42 ns, for a total delay of 85 ns. Ignoring the structure of the circuit, an overly pessimistic result of 88 ns is obtained.We can also work the problem with 74FCT parts. Worst-case delay through the ’139 is 9 ns, and from the active-low enable input of the ’138 is 8 ns, for a total delay of 17 ns. Ignoring the structure of the circuit, a slightly pessimistic result of 18 ns is obtained.Finally, we can work the problem with 74AHCT parts. Worst-case delay through the ’139 is 10.5 ns, and fromthe active-low enable input of the ’138 is 12 ns, for a total delay of 22.5 ns. Ignoring the structure of the circuit,a slightly pessimistic result of 23.5 ns is obtained. 5.195.21Both halves of the ’139 are enabled simultaneously when EN_L is asserted. Therefore, two three-state driverswill be enabled to drive SDATA at the same time. Perhaps the designer forgot to put an extra inverter on the signal going to 1G or 2G , which would ensure that exactly one source drives SDATA at all times.5.22The total delay is the sum of the decoding delay through the 74LS139, enabling delay of a 74LS151, and delaythrough a 74LS20: .5.25The worst-case delay is the sum of the delays through an ’LS280, select-to-output through an ’LS138, andthrough an ’LS86: .5.30The worst-case delay is the sum of four numbers:•In U1, the worst-case delay from any input to C4 (22 ns).•In U2, the worst-case delay from C0 to C4 (22 ns).•In U3, the worst-case delay from C0 to C4 (22 ns).•In U4, the worst-case delay from C0 to any sum output (24 ns).Thus, the total worst-case delay is 90 ns.5.35With the stated input combination, Y5_L is LOW and the other outputs are HIGH . We have the following cases:(a)Negating G2A_L or G2B_L causes Y5_L to go HIGH within 18 ns.(b)Negating G1 causes Y5_L to go HIGH within 26 ns.(c)Changing A or C causes Y5_L to go HIGH within 27 ns (the change propagates through 3 levels of logic internally), and causes Y4_L or Y1_L respectively to go LOW within 41 ns (2 levels).(d)Changing B causes Y5_L to go HIGH within 20 ns (2 levels), and causes Y7_L to go LOW within 39 ns (3levels). The delays in the ’LS138 are very strange—the worst-case for 3 levels is shorter than for 2 levels!383015++83ns =504130++121 ns =t pHLEXERCISE SOLUTIONS5–3 5.395.46The inputs are active low and the outputs are active high in this design.5–4DIGITAL CIRCUITS 5.47EXERCISE SOLUTIONS5–5 5.54An internal logic diagram for the multiplexer is shown below.5–6DIGITAL CIRCUITSA truth table and pin assignment for the mux are shown below.The mux can be built using a single PLD, a PAL20L8 or GAL20V8; the pin assignment shown above is based on the PLD. The corresponding ABEL program, MUX3BY5.ABL , is shown below. module Mux_3x5title '5-Bit, 3-Input Multiplexer J. Wakerly, Marquette University'MUX3BY5 device 'P20L8';" Input pinsI1D0, I1D1, I1D2 pin 23, 1, 2;I2D0, I2D1, I2D2 pin 3, 4, 5;I3D0, I3D1, I3D2 pin 6, 7, 8;I4D0, I4D1, I4D2 pin 9, 10, 11;I5D0, I5D1, I5D2 pin 18, 17, 16;S0, S1 pin 13, 14;" Output pinsY1, Y2, Y3, Y4, Y5 pin 22, 21, 20, 19, 15;" Set definitionsBUS0 = [I1D0,I2D0,I3D0,I4D0,I5D0];BUS1 = [I1D1,I2D1,I3D1,I4D1,I5D1];BUS2 = [I1D2,I2D2,I3D2,I4D2,I5D2];OUT = [Y1, Y2, Y3, Y4, Y5 ];" ConstantsSEL0 = ([S1,S0]==[0,0]);SEL1 = ([S1,S0]==[0,1]);SEL2 = ([S1,S0]==[1,0]);IDLE = ([S1,S0]==[1,1]);equationsOUT = SEL0 & BUS0 # SEL1 & BUS1 # SEL2 & BUS2 # IDLE & 0;end Mux_3x5InputsOutputsS1S01Y 2Y 3Y 4Y 5Y 001D02D03D04D05D0011D12D13D14D15D1101D22D23D24D25D21100000EXERCISE SOLUTIONS5–7 5.55This is the actual circuit of a MUX21H 2-input multiplexer cell in LSI Logic’s LCA 10000 series of CMOSgate arrays. When S is 0, the output equals A; when S is 1, the output equals B.5.605.67The ’08 has the same pinout as the ’00, but its outputs are the opposite polarity. The change in level at pin 3 ofU1 is equivalent to a change at pin 4 of U2 (the input of an X OR tree), which is equivalent in turn to a change at pin 6 of U2 (the parity-generator output). Thus, the circuit simply generated and checked odd parity instead of even.The change in level at pin 6 of U1 changed the active level of the ERROR signal.5.69This problem is answered in Section 5.9.3 of the text, which makes it a silly question.5–8DIGITAL CIRCUITS5.755.79The function has 65 inputs, and the worst 65-input function (a 65-input parity circuit) has terms in theminimal sum-of-products expression. Our answer can’t be any worse than this, but we can do better.The expression for has 3 product terms: The expression for is If we substitute our previous expression for c1 in the equation above and “multiply out,” we get a result with product terms. Let us assume that no further reduction is possible.Continuing in this way, we would find that the expression for has product terms and, in general, the expression for has product terms.Thus, the number of terms in a sum-of-products expression for is no more than , fewer if minimiza-tion is possible.2651–c 1c 1c 0x 0⋅c 0y 0⋅x 0y 0⋅++=c 2c 2c 1x 1⋅c 1y 1⋅x 1y 1⋅++=331++7=c 3771++15=c i 2i 1+1–c 322331–EXERCISE SOLUTIONS5–9 5.805–10DIGITAL CIRCUITS5.825.915.93The obvious solution is to use a 74FCT682, which has a maximum delay of 11 ns to its output. How-ever, there are faster parts in Table 5–3. In particular, the 74FCT151 has a delay of only 9 ns from any select input to Y or . To take advantage of this, we use a ’138 to decode the SLOT inputs statically and apply the resulting eight signals to the data inputs of the ’151. By applying GRANT[2–0] to the select inputs of the ’151, we obtain the MATCH_L output (as well as an active-high MATCH, if we need it) in only 9 ns!。
