计量经济学课件第9章
9第九章 多维时间序列分析

DF检验假设了所检验的模型的随机扰动 项不存在自相关。对有自相关的模型, 需用ADF检验。 ADF检验:将DF检验的右边扩展为包含Yt 的滞后变量,其余同于DF检验。
构造统计量 查表、判断。
单位根检验: 单位根检验:ADF检验的方程式 检验的方程式
∆Yt= β0+β1t+δYt-1+αΣ ∆Yt-i + µt 其中i从1到m。 这一模型称为扩充的迪基-富勒检验。 因为ADF检验统计量和DF统计量有同样 的渐进分布,所以可以使用同样的临界 值。
模型形式
自回归条件异方差性模型 (Autoregressive Conditional Heteroscedasticity Model, ARCH) 简单形式
σt2 =α0 +α1εt2 1 −
即,εt的方差依赖于前一期误差的平方, 或者说,εt存在着以εt-1的变化信息为条件的 异方差。记成ARCH(1)
随机游走的比喻
一个醉汉的游走。醉汉离开酒吧后在时 刻t移动一个随机的距离ut,如果他无限 地继续游走下去,他将最终漂移到离酒 吧越来越远的地方。 股票的价格也是这样,今天的股价等于 昨天的股价加上一个随机冲击。
随机游走的表达式 Yt=ρYt-1+ µt (1) 等价于: Yt -Yt-1 =ρYt-1 -Yt-1 + µt 等价于: Yt -Yt-1 =(ρ-1)Yt-1 + µt 等价于: ∆Yt=δ Yt-1+ µt (2) “有单位根”=“ρ=1”=“δ=0”
1 Yt= 1 +(a11Yt−1 +⋯ 1mY −1) +⋯ (a11Yt−p +⋯ 1p Y −p ) +u1t c a1 mt + p1 a m mt 1 1
第9章 时间序列计量经济学模型的理论与方法-李子奈计量经济学课件

第九章时间序列计量经济学模型的理论与方法第一节 时间序列的平稳性及其检验第二节 随机时间序列模型的识别和估计第三节 协整分析与误差修正模型1§9.1 时间序列的平稳性及其检验一、问题的引出:非平稳变量与经典回归模型二、时间序列数据的平稳性三、平稳性的图示判断四、平稳性的单位根检验五、单整、趋势平稳与差分平稳随机过程2一、问题的引出:非平稳变量与经典回归模型3⒊ 数据非平稳,往往导致出现“虚假回归”问题表现在:两个本来没有任何因果关系的变量,却有很高的相关性(有较高的R2):例如:如果有两列时间序列数据表现出一致的变化趋势(非平稳的),即使它们没有任何有意义的关系,但进行回归也可表现出较高的可决系数。
在现实经济生活中:情况往往是实际的时间序列数据是非平稳的,而且主要的经济变量如消费、收入、价格往往表现为一致的上升或下降。
这样,仍然通过经典的因果关系模型进行分析,一般不会得到有意义的结果。
7时间序列分析模型方法就是在这样的情况下,以通过揭示时间序列自身的变化规律为主线而发展起来的全新的计量经济学方法论。
时间序列分析已组成现代计量经济学的重要内容,并广泛应用于经济分析与预测当中。
8二、时间序列数据的平稳性9时间序列分析中首先遇到的问题是关于时间序列数据的平稳性问题。
假定某个时间序列是由某一随机过程(stochastic process)生成的,即假定时间序列{X t}(t=1, 2,t=1, 2, ……)的每一个数值都是从一个概率分布中随机得到,如果满足下列条件:1)均值E(X t)=µ是与时间t 无关的常数;2)方差Var(X t)=σ2是与时间t 无关的常数;3)协方差Cov(X t,X t+k)=γk是只与时期间隔k有关,与时间t 无关的常数;则称该随机时间序列是平稳的(stationary),而该随机过程是一平稳随机过程(stationary stochastic process)。
第九章 JOHANSEN协整检验

(1 (1
ˆR i Ui
) )
~
2
(J
)
J h * (约束的行数)
弱外生检验
例如考虑货币需求m,p,y,r 检验p,y,r都是弱外生的 假设只有一个协整向量,检验的自由度是1*3=3
Yt1 0 1Yt1 ... p1Yt p1 Vt
ˆ UU
1 T
T
UtUt '
t 1
ˆ VU
1 T
T
VtU t '
t 1
ˆ VV
1 T
T
VtVt '
t 1
JOHANSEN检验步骤
矩阵的秩是该矩阵中不为0的特征值的个数,N计算 矩阵的特征值,假设从大到小排列
误差修正模型
2个误差修正模型的含义 yt 1xt1 r( yt1 xt1 ) t
Yt=Xt-1=0,系统维持均衡
yt 1xt1 r( yt1 xt1 ) t
Yt=Xt-1=/(1-1),系统均衡
多元系统的协整检验-JOHANSEN
JOHANSEN检验
模型
Yt1
Yt 2 2t '
1
1
1
t
1Yt1 ... Y p1 t p1 t
JOHANSEN 检验
实际应用中可以考虑3类模型 1)数据没有线性趋势。数据的一次差分均值是0,
长期模型中包括常数项 2)数据有线性趋势,短期和长期模型中都存在常
独立协整向量 该检验的功效比较低,一般使用迹检验更可靠。
例
假设三个变量:消费,收入和通货膨胀 1) 都是I(1) 2) VAR滞后长度 p=2 3) 检验结果 特征值 LR 5% 协整个数 0.5 37.04 29.68 0 0.3 13.64 15.41 最大1 0.04 1.413 3.76 最大2
计量经济学-9

2 2 2 Var (v e0 ) u 0 u,即误差方差比没有测量误差时更大,也导致
函数形式误设的一般检验(RESET) 基本思想:如果原模型y 0 1 x1 2 x2 L k xk u 满足假定(u∣x) 0 E 那么,在方程中添加自变量的非线性关系应该是不显著的。 不过,当解释变量很多时,添加自变量的平方和立方项会产生更多的 解释变量,损失了很大一部分自由度。一般会在模型中添加被解释变量 ˆ ˆ 的预测值的平方y 2及立方y 3: ˆ ˆ y 0 1 x1 2 x2 L k xk 1 y 2 2 y 3 u 检验H 0:1 0, 2 0 F 统计量渐近服从F2,nk 3分布。显著的F 统计量表明存在某种函数形式问题
(2)经典的含误差变量(CEV)假定:cov(x1 , e1 )=0 2 2 2 x1 x1 e1, cov( x1 , e1 ) E ( x1e1 ) E ( x1 e1 ) E (e1 ) 0 e1 e1 ,
自变量与测量误差肯定相关,因此自变量与合成误差u 1e1也必然
因变量测量误差问题 假设模型:y 0 1 x1 L k xk u,满足CLRM 假定 y是对y 观测到的度量,它们之间的误差为:e0 y y , 可估计的模型变成:y 0 1 x1 L k xk u e0 , 随机误差项变成了u e0
自变量测量误差问题
考虑一个简单回归模型:y 0 1 x1 u,假设满足CLRM 假定, 则参数估计是无偏的和一致的,但是x1 观测不到,我们只能观测到x1, 它们之间存在着一个测量误差:e1 x1 x1 假定E(e1 )=0,u与x1和x1 都不相关,此时将x1取代x1 放入原方程进行OLS
计量经济学第九章虚拟变量

虚拟变量的类型
季节虚拟变量
用于反映季节变动对经济活动的影响。
政策虚拟变量
用于反映某项政策实施前后对经济活 动的不同影响。
地区虚拟变量
用于反映不同地区之间经济活动的差 异。
行业虚拟变量
用于反映不同行业之间经济活动的差 异。
虚拟变量的引入原因
解决遗漏变量问题
01
当某些重要变量无法直接观测或获取时,可以通过引入虚拟变
在模型中引入虚拟变量与解释变量的交互项,通过 改变斜率的值来反映不同组别之间的差异。
斜率变动模型的应用
适用于研究不同组别之间在某一解释变量上 的边际效应差异,如不同教育水平对收入的 影响等。
含有多个虚拟变量的模型
含有多个虚拟变量的模型的定义
当模型中引入多个虚拟变量时,称为含有多个虚拟变量的模型。
含有多个虚拟变量的模型的设定
VS
使用计算变量功能
可以使用SPSS的计算变量功能手动创建虚 拟变量。在数据视图中,点击“转换”菜 单下的“计算变量”选项。在弹出的对话 框中,输入虚拟变量的名称和标签,并在 计算表达式中输入相应的逻辑表达式。例 如,对于分类变量`industry`,可以使用如 下表达式生成虚拟变量
SPSS中实现虚拟变量的方法
截距变动模型的设
定
在模型中引入虚拟变量,通过改 变截距项的值来反映不同组别之 间的差异。
截距变动模型的应
用
适用于研究不同组别之间在某一 解释变量上的平均差异,如不同 性别、不同地区等。
斜率变动模型
斜率变动模型的定义
当虚拟变量不仅影响模型的截距项,还影响 解释变量的斜率时,称为斜率变动模型。
斜率变动模型的设定
通过比较政策虚拟变量的系数,可以分析 出政策变动对市场需求的影响程度。
古扎拉蒂《计量经济学基础》第9章

虚拟变量数量的设置规则
1.若定性因素具有m(m≥2)个相互排斥
属性(或几个水平),当回归模型有截距项时, 只能引入m-1个虚拟变量;
2.当回归模型无截距项时,则可引入m个 虚拟变量;否则,就会陷入“虚拟变量陷阱”。 (为什么?)
若对两个相互排斥的属性 “性别属性”, 仍然引入m=2个虚拟变量,则有
E Yi | Di = 0 = 0
Yi ( 0 1) i 女 性
Yi 0 i
男性
(2)一个定性解释变量(两种属性)和一
个定量解释变量的情形
模型形式 Yi = f(Di,Xi )+μi 0 1Di
例如:Yi =0 1Di +Xi +μi
其中:Y-支出;X-收入;
Di
1 0
女性 支出
例:比较改革开放前、后我国居民(平 均)“储蓄-收入”总量关系是否发生了变 化?模型的设定形式为:
Yt 1 2 Dt 1X t 2 (Dt X t ) ut
其中 : Yt为储蓄总额,X t为收入总额。
D
1
0
改革开放后 改革开放前
回归方程:
改革开放后 EYt | Xt , D 1 (1 2)(1 2)Xt 改革开放前 EYt | Xt , D 0 1 1Xt
夏季、农村居民
E Yi | X i ,D1 = 1, D2 = 0 =( 0 + 1)+ X i
冬季、城市居民
E Yi | X i , D1 0, D2 1 (0 2 )+ X i
冬季、农村居民
E Yi | X i , D1 0, D2 0 0 X i
Y
D1 1,D2 1
基准:四季度
(4)两个定性解释变量(均为两种属性) 和一个定量解释变量的情形
《计量经济学》第九章 设定误差与测量误差

2
x22i
ቤተ መጻሕፍቲ ባይዱ
由Y = 1 + 2x2 + v 得
Var(ˆ2)
2
x22i (1-
x2i x22i
x3i x32i
)
2
x22i (1- r223 )
17
如果 X 3与 X 2相关,显然有 Var(ˆ2) Var(ˆ2)
对于是否误选无关变量的检验,只要针对无关变量系 数的期望值为零的假设,用t检验或F检验,对无关变 量系数作显著性检验即可。 对于遗漏变量设定误差的检验有多种方法,例如DW 检验、拉格朗日乘数检验、豪斯曼检验、RESET 一 般性检验等。 这里只讨论设定误差的一些最常用的检验方法。
29
一、 DW检验
计量经济学
第九章 设定误差与测量误差
1
引子:简单一定胜于复杂吗?
西方国家盛行“Occam`s razor”原则,意思是 “简单优于复杂”的节约性原则。经济模型永远 无法完全把握现实,在建立模型中一定的抽象和 简化是不可避免的。 在研究进口与国内生产总值的关系时,考虑到时 间趋势,建立并估计了以下模型
IM -217.186 0.173GDP
t (-0.5) (16.94)
(2)
R2 0.960 F 286.95 DW 0.735
进行比较:
两个方程的检验结果都较理想;
方程(2)GDP的t检验值似乎优于方程(1); 方程(2)函数形式也更为简单; 然而,能否根据“Occam’s razor”原则,判断方程(2)比 方程(1)好?
Yi 1 2 X 2i 3i X 3i ui
计量经济学第九章分布滞后和自回归模型

自回归模型的理论导出
适应性预期(Adaptive expectation)模型
在某些实际问题中,因变量 Yt 并不取决于解释变量的当
前实际值
X
t
,而取决于X
t
的“预期水平”或“长期均衡水X
* t
平” 。
例如,家庭本期消费水平,取决于本期收入的预期值;
❖ 为了解决滞后长度不确定的困难,可以依次估计滞 后效应变量的一期滞后、二期滞后…当发现滞后变 量(加入的最多期滞后)的回归系数在统计上开始 变得不显著,或至少有一个变量的系数改变符号 (由正变负或由负变正)时,就不再增加滞后期, 把此前一个模型作为分布滞后模型的形式,相应参 数估计作为模型的参数估计。
市场上某种商品供求量,决定于本期该商品价格的均衡值。
因此,适应性预期模型最初表现形式是
Yt
0
1
X
* t
t
由于预期变量是不可实际观测的,往往作如下 适应性预期假定:
X
* t
X* t 1
(Xt
X
* t 1
)
其中:r为预期系数(coefficient of expectation), 0r 1。
该式的经济含义为:“经济行为者将根据过去的 经验修改他们的预期”,即本期预期值的形成是一 个逐步调整过程,本期预期值的增量是本期实际值 与前一期预期值之差的一部分,其比例为r 。
这个假定还可写成:
X
* t
X t
(1
)
X
* t 1
将
X
* t
X t
(1
)
X
* t 1
代入
计量经济学第九章

计量经济学夏第九章联立方程模型第一节联立方程模型第二节联立方程模型的识别第三节递归系统模型第四节联立方程模型估计方法第五节联立方程模型估计方法的比较第六节联立方程模型的检验计量经济学夏引言⏹前面讨论的是单一方程模型,用一个变量描述一个经济变量与引起这个变量变化的各个因素之间的关系●解释变量X是被解释变量Y的原因,其因果关系是单向的⏹然而,经济现象是复杂的,因果关系可能是双向的,或者一果多因,或者一因多果●这时用一个单一方程很难完整的表达,需要用多个相互联系的方程,才能正确反映复杂的现实经济系统状况计量经济学夏第一节联立方程模型⏹变量⏹结构式模型⏹简化式模型计量经济学夏例子⏹[例9-1]农产品供需模型●⏹W:气候因素;Y:居民收入⏹[例9-2]简单国民收入决定模型●ttttttttttSDuWPSuYPD=+++=+++=221121βββαααttttttICYuYIuYC+=++=++=2111ββαα计量经济学夏例子(续)⏹[例9-3]三部门封闭经济的国内生产总值决定模型●⏹C:居民消费总额;I:投资总额⏹Y:国内生产总值;G:政府消费tttttttttttGICYuYYIuYC++=+++=++=-212111βββαα计联立方程模型的构成量经济学夏变量方程模型计量经济学夏变量⏹划分原因●联立方程模型中,因果关系是双向的,再将变量分成被解释变量和解释变量是不合适的⏹类别内生变量外生变量滞后内生变量先决变量变量计量经济学夏变量(续1)⏹内生变量●由模型系统决定,其参数是联立方程系统估计的元素⏹一般而言,内生变量既影响所在系统,又受所在系统影响●是具有某种概率分布的随机变量,并与随机扰动项相关⏹●一般为经济变量()()0,cov≠⇒≠ttttuYEuY计量经济学夏变量(续2)⏹外生变量●由模型系统外部因素决定,其参数不是模型系统研究的元素⏹外生变量影响系统,但本身不受系统的影响●是非随机变量,或具有临界概率分布的随机变量,与随机扰动项不相关⏹●一般是经济变量、条件变量、政策变量、虚变量()()0,cov=⇒=ttttuXEuX计量经济学夏变量(续3)⏹先决变量●也称前定变量或预定变量●包括:外生变量和滞后内生变量⏹滞后内生变量用以反映经济系统的动态性和连续性●与随机扰动项不相关⏹()()0,cov=⇒=--tsttstuYEuY计量经济学夏变量(续4)⏹比较●单方程模型中⏹内生变量作为被解释变量⏹外生变量与滞后内生变量作为解释变量●联立方程模型中⏹内生变量既作为被解释变量,又可以在不同的方程中作为解释变量计量经济学夏结构式模型⏹结构式模型●根据经济理论和行为规律建立的描述经济变量之间直接关系结构的计量经济学方程系统⏹模型中的每一个方程都是结构方程⏹各个结构方程的参数称为结构参数,表示解释变量对被解释变量的直接影响⏹解释变量可以出现内生变量⏹结构方程的正规形式●将一个内生变量表示为其他内生变量、先决变量和随机误差项的函数形式计量经济学夏结构式模型(续1) 结构方程的类型随机方程行为方程技术方程制度方程统计方程恒等方程定义方程平衡方程经验方程计量经济学夏结构式模型(续2)⏹习惯用法●Y:内生变量;X:先决变量;U:随机项●β:内生变量的结构参数●γ:先决变量的结构参数●X0:常数项⏹外生的虚变量,观测值始终取1⏹完备的结构式模型●独立结构方程的数目等于内生变量的数目⏹具有g个内生变量、k个先决变量、g个结构方程●每个内生变量都分别由一个方程来描述计量经济学夏结构式模型(续3)⏹矩阵形式●()UXYBUXBY=⎪⎪⎭⎫⎝⎛Γ=Γ+或⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=gnggnngyyyyyyyyyYYYY21222211121121⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=knkknnkxxxxxxxxxXXXX21222211121121⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=nnuuuuuuuuuUUUU222211121121计量经济学夏结构式模型(续4)⏹矩阵形式(续)●参数矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=ggggggBβββββββββ212222111211⎪⎪⎪⎪⎪⎭⎫⎝⎛=Γgkggkkγγγγγγγγγ212222111211计量经济学夏结构式模型(续5)⏹估计●OLS不适用于估计结构式模型中的单一方程⏹因为在该方程中有一个或多个解释变量与随机项相关,OLS估计量是非一致的,称为联立偏误●内生变量与随机项相关●由于联立偏误的存在,不能直接用OLS估计结构式模型计量经济学夏结构式模型(续6)[例9-4]将例9-3表示的宏观经济模型写成矩阵形式,各个矩阵为⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=nnntttYYYIIICCCYICY212121⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=--nnttGGGYYYGYX211111111⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=222211121121nnuuuuuuUUN()⎪⎪⎪⎭⎫----⎝⎛---=Γ111111211ββαβαB计量经济学夏简化式模型⏹简化式模型●用所有先决变量作为每个内生变量的解释变量所形成的模型⏹内生变量=f (先决变量,随机项)⏹每个方程称为简化式方程⏹方程的参数称为简化式参数(П)⏹特点●不反映经济系统中变量之间的直接关系●简化式参数表示方程中先决变量对内生变量的直接影响和间接影响的总度量●由于先决变量和随机项不相关,可以直接用计量经济学夏简化式模型(续1)⏹一般推导●结构式⏹●解出内生变量列向量Y⏹⏹参数关系体系●●描述了简化式参数与结构式参数之间的关系●称为参数关系体系UXBY=Γ+UBXBY11--+Γ-=Γ-=∏-1B计量经济学夏简化式模型(续2)⏹矩阵形式●E+∏=E+∏=XYXY或⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=gnggnngEEEEεεεεεεεεε21222211121121⎪⎪⎪⎪⎪⎭⎫⎝⎛=∏gkggkkπππππππππ212222111211计量经济学夏简化式模型(续3)⏹[例9-5]例9-3表示的宏观经济模型的简化式模型为●解出内生变量C、I、Y,得ttttttttttttGYYGYIGYC332131302221212011211110επππεπππεπππ+++=+++=+++=---1212111121211111121211111111211111111121112111111111111111βαβαβαββααββαβαβαββαβαββαβαβαββαβαβααβαβαβαβαβαα--++--+--+--+=--+-+--+---+--+-=---++--+--+--+-=----tttttttttttttttttuuGYYuuuGYIuuuGYC计量经济学夏简化式模型(续4)对比后得到简化式参数与结构式参数之间的关系体系为11321123111301112211212211111201111211211111211101111111111βαπβαβπβααβπβαβπβαβαβπβαβαβαβπβααπβαβαπβαβαβααπ--=--=--+=--=---=--+-=--=--=--+-=计量经济学夏简化式模型(续5)⏹●表示Y t-1对I t的影响●即Y t-1增加1个单位时对I t的影响●21π11212112122111βαββββαβαβπ--+=---=反映Yt-1对It的直接影响反映Yt-1对It的间接影响计量经济学夏第二节联立方程模型的识别⏹识别的概念⏹结构式识别条件⏹简化式识别条件⏹实际应用中的经验方法计量经济学夏识别的概念⏹识别的定义●如果联立方程模型中某个结构方程不具有确定的统计形式,则称该方程不可识别⏹统计形式●变量和方程关系式⏹具有确定的统计形式●模型系统中其他方程或所有方程的任意线性组合所构成的新的方程都不再具有这种统计形式●针对结构方程而言计量经济学夏识别的概念(续1)⏹模型的识别●如果一个模型中的所有随机方程都是可以识别的,则认为该联立方程模型系统是可识别的⏹恒等方程由于不存在参数的估计问题,则也不存在识别问题⏹但在判断随机方程的识别性时,应该将恒等方程考虑在内⏹恰好识别与过度识别●恰好识别⏹某一个随机方程具有一组参数估计量●过度识别某一个随机方程具有多组参数估计量计量经济学夏识别的概念(续2)⏹识别问题●即能否从所估计的简化式模型系数求出一个结构式方程的参数的数值估计值⏹如果能够,就说该方程是可识别的●如果求解结构参数值唯一,则称恰好识别●如果求解结构参数值不唯一,则称过度识别⏹如果不能,就说该方程是不可识别的●⏹能否从Π求出В和ГΓ-=∏-1B计量经济学夏结构式识别条件⏹结构式模型●⏹第i个方程中包含g i个内生变量(含被解释变量)和ki个先决变量(含常数项)⏹模型系统中内生变量和先决变量的数目仍用g和k表示⏹矩阵(В0Г0)表示第i个方程中未包含的变量(包括内生变量和先决变量)在其他g-1个方程中对应系数所组成的矩阵UXBY=Γ+计量经济学夏结构式识别条件(续1)⏹结构式条件●如果,则第i个结构方程不可识别●如果,则第i个结构方程可识别⏹如果,则第i个结构方程恰好识别⏹如果,则第i个结构方程过度识别()1-<ΓgBR()1-=ΓgBR1-=-iigkk1->-iigkk阶条件,用以判断结构方程恰好识别或过度识别秩条件,用以判断结构方程可否识别计量经济学夏结构式识别条件(续1)⏹[例9-10]判断模型是否可识别●结构参数矩阵为⎪⎩⎪⎨⎧+=+++=++++=---ttttttttttttICYuYYIuPCYC2121113121βββαααα()⎪⎪⎪⎭⎫⎝⎛---------=Γ1111121321βββααααBtCtItY1-tC1-tP1-tY1计量经济学夏结构式识别条件(续2)⏹对于第1个结构方程●⏹则该方程可识别●⏹则该方程为恰好识别的结构方程()()12112-==Γ⎪⎪⎭⎫⎝⎛--=ΓgBRBβ113411-==-=-gkk计量经济学夏结构式识别条件(续3)⏹对于第2个结构方程●⏹则该方程可识别●⏹则该方程为过度识别的结构方程⏹第3个方程是平衡方程,不存在识别问题⏹综上所述,该联立方程模型是可识别的()()121132-==Γ⎪⎪⎭⎫⎝⎛---=ΓgBRBαα1122422=->=-=-gkk计量经济学夏结构式识别条件(续4)⏹[例9-11]判断模型是否可识别●结构参数矩阵为⎪⎩⎪⎨⎧+=+++=++=-ttttttttttICYuYYIuYC212111βββαα()⎪⎪⎪⎭⎫⎝⎛-------=Γ11111211βββααBtCtItY1-tY1计量经济学夏结构式识别条件(续5)⏹对于第1个方程●⏹则该方程可识别●⏹则该方程为恰好识别的结构方程()()12112-==Γ⎪⎪⎭⎫⎝⎛--=ΓgBRBβ111211-==-=-gkk计量经济学夏结构式识别条件(续6)⏹对于第2个方程●⏹则该方程不可识别⏹综上所述,该联立方程模型不可识别()()1111-<=Γ⎪⎪⎭⎫⎝⎛-=ΓgBRB计量经济学夏简化式识别条件⏹简化式模型●⏹Π2是简化式参数矩阵Π中划去第i个结构方程所不包含的内生变量所对应的行和第i个结构方程中包含的先决变量所对应的列之后,剩下的参数按原次序组成的矩阵⏹简化式条件●如果,则第i个结构方程不可识别●如果,则第i个结构方程可识别⏹如果,则第i个结构方程恰好识别如果,则第i个结构方程过度识别E+∏=XY()12-<∏igR()12-=∏igR1-=-iigkk1->-gkk计量经济学夏简化式识别条件(续1)⏹[例9-12]有一联立方程模型,其结构式模型如下●已知其简化式模型参数矩阵如下,判断其可否识别⎪⎩⎪⎨⎧+++=++=+++=iiiiiiiiiiiiiiuxyyyuxyyuxxyy3332211323231212312211γγγββααα⎪⎪⎪⎭⎫⎝⎛---=∏12112324计量经济学夏简化式识别条件(续2)⏹对于第1个结构式方程●⏹则该方程可识别●⏹则该方程为恰好识别的结构方程()1113122-==∏⎪⎪⎭⎫⎝⎛∏gR=112311-==-=-gkk计量经济学夏简化式识别条件(续3)⏹对于第2个方程●⏹则该方程可识别●⏹则该方程为过度识别的结构方程()111212222-==∏⎪⎪⎭⎫⎝⎛--∏gR=1121322=->=-=-gkk计量经济学夏简化式识别条件(续4)⏹对于第3个方程●⏹则该方程不可识别⏹综上所述,该联立方程模型不可识别()211121224322=-<=∏⎪⎪⎪⎭⎫⎝⎛---∏gR=计量经济学夏实际应用中的经验方法⏹特点●不是建好模型后再考虑识别问题●而是在建模过程中,就保证模型的可识别⏹原则●在建立某个结构方程时,要使该方程包含前面每一个方程中都不包含的至少一个变量(内生或先决变量)⏹保证该方程的引入不破坏前面已有方程的可识别性●使前面每一个方程中都包含至少一个该方程所未包含的变量,并且互不相同⏹保证该新引入方程本身是可识别的实际应用中的经验方法(续)计量经济学夏计量第三节递归系统模型经济学夏⏹递归系统模型⏹递归系统模型的估计计量经济学夏递归系统模型⏹概念●联立方程模型⏹●如果●则称这类模型为递归系统模型UXBY=Γ+⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛------=1111321323121gggBββββββ⎪⎪⎪⎪⎪⎭⎫⎝⎛=Γgkggkkγγγγγγγγγ212222111211计量经济学夏递归系统模型(续)⏹递归系统模型●也称为三角型或因果型⏹B可化为下三角阵,主对角线为1●是单向因果依赖关系⏹⏹()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧====-gkggkkkuXXXYYYfYuXXXYYfYuXXXYfYuXXXfY,,,,,,,,,,,,,,,,,,,,,,,21121321213221121211ggYYYY→→→→-121←计量经济学夏递归系统模型的估计⏹估计方法●第1个方程的解释变量全部为先决变量⏹可以用单方程模型的估计方法直接估计其参数⏹并得到关于被解释变量的估计值●第2个方程的解释变量中,除了Y1之外,全部为先决变量,则有两种估计方法⏹以取代方程中Y1的,作为解释变量,用OLS等方法估计参数⏹以作为方程中Y1的工具变量,采用工具变量法估计参数●第3个方程的估计依此类推……即可完成模型系统的估计()nyyyY112111ˆ,,ˆ,ˆˆ=1ˆY1ˆY计量经济学夏递归系统模型的估计(续)⏹特点●递归模型在形式上属于联立方程模型●但可以采用单方程模型的估计方法估计每个方程计第四节联立方程模型估计方法量经济学夏⏹单方程估计方法⏹系统估计方法计量经济学夏基本概念⏹联立方程模型的估计方法●单方程估计方法⏹每次只估计模型系统中的一个方程⏹依次逐个估计●系统估计方法⏹同时对全部方程进行估计⏹同时得到所有方程的参数估计量。
计量经济学第九章完整课件

回归模型的应用案例
1 2 3
消费物价指数预测
通过建立回归模型,利用历史数据和相关解释变 量预测未来消费物价指数,为货币政策制定提供 依据。
股票价格预测
利用回归模型分析历史股票价格和相关解释变量 ,预测未来股票价格走势,为投资者提供决策参 考。
经济增长预测
通过建立回归模型,利用历史数据和相关解释变 量预测未来经济增长趋势,为政府和企业制定发 展计划提供依据。
多元线性回归模型
总结词
多元线性回归模型是一种扩展的回归模型,允许我们同时考虑多个自变量对因变 量的影响。
详细描述
多元线性回归模型通过引入多个自变量来扩展基本的回归模型。这种方法能够更 全面地描述因变量和自变量之间的关系,并提供更准确的预测。在经济学、金融 学和其他领域中,多元线性回归模型被广泛用于研究各种现象。
合度越好。
变量的显著性检验
t检验
用于检验单个解释变量对被解释 变量的影响是否显著,通过计算t 统计量并进行假设检验得出结论
。
F检验
用于检验多个解释变量整体上对被 解释变量的影响是否显著,通过计 算F统计量并进行假设检验得出结 论。
z检验
用于检验某个解释变量在两个或多 个总体中是否存在显著差异,通过 计算z统计量并进行假设检验得出结 论。
PART 02
回归模型的检验
模型的拟合度检验
决定系数(R-squared):衡量 模型解释变量变异程度的指标, 值越接近1表示模型拟合度越好
。
调整决定系数(Adjusted Rsquared):考虑了模型中自变 量的数量对R-squared的影响, 值越接近1表示模型拟合度越好
。
均方误差(Mean Squared Error,MSE):衡量模型预测 误差的指标,值越小表示模型拟
计量经济学联立方程模型

1 1
adj(A) = 1
1
1 1 1
1
1 1 1
1 = 1
1
1
1 11
1
1 1
。
1
的伴随矩阵是的代数余子式组成的矩阵的转置。
v = -1 u
v1 v2 v3
=
1
1 1
1
1 1
1
1
1 11
1
1 ut1
1 ut2
1
0
(第2版242页) (第3版208页)
有时由于两个变量之间存在双向因果关系,用单一方程模型就
3 3
联联不立立方方能程程模模完型型的的整识识别别的描述这两个变量之间的关系。有时为全面描述一项
经济活动只用单一方程模型是不够的。这时应该用多个方程的 Dt = 0 + 1 Pt + 2 It + u1 (需求函数)
对于第2个方程,被斥变量有3个 y1, x1, x2,(方程个数 – 1)= 2。
9.3 联立方程模型的识别(identification)
例:关于粮食的需求供给模型如下,
0 1 1 It = 2
1
1
1
yt
ห้องสมุดไป่ตู้
0
0
0
1
yt 1 Gt
+
ut1
ut2
0
用矩阵符号表示上式 Y = X + u ,则 Y = -1 X + -1u
结构参数和简化型参数有如下关系存在, = -1
简化型模型 Y = X + v
(第2版241页) (第3版207页)
⑵简化型模型(reduced-form equations)
第9章 虚拟变量回归

不同截距、斜率的组合图形
重合回归:截距斜率均相同
平行回归:截距不同斜率相同
共点回归:截距相同斜率不同
交叉(不同)回归:截距斜率均不同
33
三、虚拟解释变量综合应用
所谓综合应用是指将引入虚拟解释变量的加法方 式、乘法方式进行综合使用。 基本分析方式仍然是条件期望分析。 本课主要讨论
3
第八章 虚拟变量回归
本章主要讨论:
●虚拟变量
●虚拟解释变量的回归
●虚拟被解释变量的回归(选讲,不包括)
4
第一节 虚拟变量
本节基本内容:
●基本概念 ●虚拟变量设置规则
5
一、基本概念
定量因素:可直接测度、数值性的因素。 定性因素:属性因素,表征某种属性存在与否的 非数值性的因素。
基本思想:
直接在回归模型中加入定性因素存在诸多的困难 (那些困难?),是否可将这些定性因素进行量 化,以达到定性因素能与定量因素有着相同作用 之目的。
6
虚拟变量的定义
计量经济学中,将取值为0和1的人工变量称为虚 拟变量。虚拟变量也称:哑元变量、定性变量等 等。通常用字母D或DUM加以表示(英文中虚拟 或者哑元Dummy的缩写)。 对定性变量的量化可采用虚拟变量的方式实现。
7
二、虚拟变量设置规则
虚拟变量的设置规则涉及三个方面: 1.“0”和“1”选取原则 2.属性(状态、水平)因素与设置虚拟变量 数量的关系 3.虚拟变量在回归分析中的角色以及作用等 方面的问题
D1 0, D2 0
X
上述图形的前提条件是什么?
27
运用OLS得到回归结果,再用t检验讨论因素
是否对模型有影响。
加法方式引入虚拟变量的一般表达式:
计量经济学-詹姆斯斯托克-第9章-面板数据的处理ppt课件

35
.
FatalityRate v. BeerTax:
36
.
问题
在上述模型中,如果超过两期,即T>2, 怎么处理呢?
37
.
面板数据模型的一般理论
在模型的设定上,分为两大类: (一)“固定效应”模型; (二)“随机效应”模型;
38
.
(一) 固定效应的回归 Fixed Effects Regression
2
.
面板数据,简而言之是时间序列和截面数据的混合。 严格地讲是对一组个体(如居民、国家、公司等)连 续观察多期得到的资料。所以很多时候我们也称其为 “追踪资料”。近年来,由于面板数据资料的获得变 得相对容易,使其应用范围也不断扩大。
3
.
当描述截面数据时,我们用下标表示个体,如Yi表示 变量Y的第i个个体。当描述面板数据时,我们需要其 他符号同时表示个体和时期。为此我们采用双下标而 不是单下标,其中第一个下标i表示个体,第二个下 标t表示观测时间。
23
.
案例二:
啤酒税与交通死亡率
啤酒税与交通死亡率会是什么关系?
24
.
U.S. traffic death data for 1982:
$1982
较高的啤酒税,会导致更多的交通死亡吗?
25
.
U.S. traffic death data for 1988
较高的啤酒税,会导致更多的交通死亡吗?
16000
15000
14000
13000
INC
12000
11000
10000
9000
8000 10000
15000
20000
25000
计量经济学ppt9

一个单位时导致的产出量的增加量。用 于描述投入要素对产出量的影响程度。 MPK f / K MPL f / L 边际产量非负:MPK 0, MPL 0, 边际产量递减: 2 2 (MPK ) f (MPL ) f 0, 2 0, 2 K K L L
生产函数模型
二、一些重要的生产函数及其参数估计方法
一、几个常用概念
生产函数
描述生产过程中投入的生产要素的某种组
合同它可能的最大产出量之间的依存关系 的数学表达式,即
Y f ( A, K , L,)
其中,Y为产出量,A、K、L等表示技术、 资本、劳动等投入要素。
要素的边际产量
其它条件不变时,某一种投入要素增加
pj qi
替代品的需求互价格弹性:εij>0 互补品的需求互价格弹性:εij<0 独立品的需求互价格弹性:εij≈0
有收入补偿的价格弹性
当i≠j时,ij 0
qi qi p j qj ) ( I qi p j ij ( qi q qi ) pi i pi I qi
当b=0时,(1)式退化为CES形式
Y dk a k A exp A exp( ln ) 1 a k 1a L 1 a c k c( ) 1 1 a k a a a
1 a a
1 a 令 , Ae A, Aa a
1a
1 a
A
1 1 Y a ck 1 a 则 A( 1 a ) A(a k c) L a k 1 1 a K Y A(a ( ) c) L L
确定性边界生产函数的估计 取对数 ln Y ln f ( X ) u
应用计量经济学第9章PPT课件

序列相关性
Slides by Niels-Hugo Blunch Washington and Lee University
纯序列相关性
• 纯序列相关性破坏了古典假设 IV,古典假设 IV保证了在正确设定 的方程中各误差项观测值之间没有相关性
• 最被广泛假设的序列相关性是一阶序列相关性,在一阶序列相关 性中,随机误差项的当期值是上一期值的函数:
929neweywest标准误当然并丌是所有修正纯序列相关性的方法都广义最小二乘法glsneweywest标准误通过修正标准误来修正序列相关性而丌改变估计的回归系数如果序列相关性仅仅影响标准误而丌影响估计系数的无偏性那么修正序列相关性时调整估计系数的标准误即可而没有必要调整系数本身的估计值如果紧急医疗系统采用包括持续胸部按压的综合救治干预对于院外心脏骤停患者可以考虑在综合救治干预中使用被动通气技术
• 这也许是已知的最好的GLS方法
• 这是一种两步法,首先将估计出 ρ ,然后,使用该估计值进行GLS估计
• 这两步的具体步骤:
1. 对怀疑存在序列相关性的模型进行OLS估计,获得残差序列后,再估计方程:
et = ρet–1 + ut
(9.21)
此设处 的随et机是误对差怀项疑存在序列相关性的模型进行OLS估计后获得的鳌头, ut 是服从古典假
20
Figure 9.6 单边 Durbin–Watson
d 检验的例子
21
序列相关性的补救
• 修正自相关的第一步就是仔细检查可能引起不纯的序列相关性的模型设 定误差
– 函数形式正确吗? – 确定没有遗漏的变量了吗? – 只有仔细检查了模型的设定后,才有必要对纯序列相关性进行检验并修正 • 有两种主要的修正序列相关性的方法: 1. 广义最小二乘法(GLS:Generalized Least Squares) 2. Newey-West 标准误
第9章_异方差:如果误差方差不是常数会有什么结果
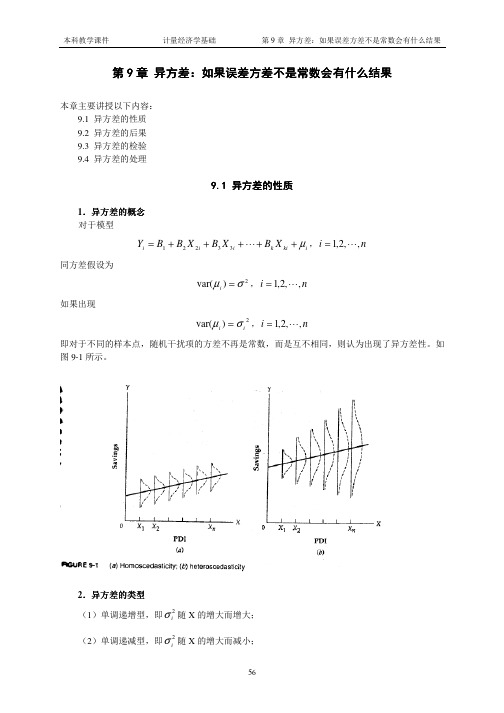
var(µ i ) = σ 2 , i = 1,2, ⋯, n
如果出现
var(µ i ) = σ i , i = 1,2, ⋯, n
2
即对于不同的样本点,随机干扰项的方差不再是常数,而是互不相同,则认为出现了异方差性。如 图 9-1 所示。
2.异方差的类型 (1)单调递增型,即 σ i 随 X 的增大而增大;
2
(2)单调递减型,即 σ i 随 X 的增大而减小;
2
56
本科教学课件
计量经济学基础
第 9 章 异方差:如果误差方差不是常数会有什么结果
(3)复杂型,即 σ i 与 X 的变化呈复杂形式。
2
如下图所示。
3.异方差产生的原因 (1)模型中遗漏了某些解释变量; (2)模型函数形式的设定误差; (3)样本数据的测量误差; (4)随机因素的影响。 经验表明,利用截面数据建立计量经济学模型时,由于不同样本点上解释变量以外的其他因素 的差异较大,所以往往存在异方差性。
本章主要讲授以下内容: 9.1 异方差的性质 9.2 异方差的后果 9.3 异方差的检验 9.4 异方差的处理
9.1 9.1 异方差的性质
1.异方差的概念 对于模型
Yi = B1 + B2 X 2i + B3 X 3i + ⋯ + Bk X ki + µ i , i = 1,2, ⋯, n
同方差假设为
Yi = B1 + B2 X i + µ i
(1)如果 var(ui)=σi2,且σi 已知,则可以进行下列变换:
1 = B1 σ σi i Yi
= B1 f (X i )
Yi
Xi + B 2 σ i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
地改变符号,而是相继若干个正的以后跟着几个负的。
表明存在正自相关。
et
et
t
(a)
et 1
20
如(b)图所示,扰动项的估计值呈锯齿状,随时间 逐次改变符号,表明存在负相关。
2、与
X
2
相比(依绝对值),
相对较小。
2
t
注意:由于由设定偏误引起,非纯序列相关可能导致有偏的估计系数。
如果设定偏误得以纠正,则估计的有偏性与非纯序列相关将同时被消除。
14
一个例子
P176
15
不正确的函数形式
假定真实的函数形式为多项式形式:
Yt
01 X1t
2
X
2 1t
t ,
t 是经典误差项。
却采用了线性回归的形式:
二、 模型设定误差。(表现为应变量不相关,误差项相关)
1、若回归模型中丢掉了应该列入模型的重要解释变量,那么它的影响必 然归并到误差项中,从而使误差项呈现序列相关。当然略去多个带有序 列相关的解释变量,也许因互相抵消并不使误差项呈现序列相关。
2、模型选择了错误的函数形式。若所用的数学模型与变量间的真实关系 不一致,误差项常表现出序列相关。比如平均成本与产量呈抛物线关系, 当用线性回归模型拟合时,误差项必存在序列相关。
非纯序列相关是由于真实的误差项不存在 序列相关,由于遗漏变量或不正确的函数形式, 导致新的误差项存在序列相关.
12
序列相关的修正方法取决于是纯序列相关 还是非纯序列相关;
对于非纯序列相关,补救措施:加入遗漏变 量或选择正确的函数形式;
在考虑纯序列相关之前,应尽可能保证其模 型设定是最优的.
13
遗漏一个解释变量
t
t4
t
10
高阶的序列相关
误差项观察值可能不仅仅是滞后一期误差项 观察值的函数,如二阶序列相关.
t
1 t 1
2 t2
t
11
9.1.2 非纯序列相关
非纯序列相关:由设定偏误,如遗漏变量或 不正确的函数形式,引起的序列相关.
纯序列相关是在方程正确设定时误差项的 潜在分布引起的序列相关.
假定真实的方程为:
Y X X ,
t
0
1 1t
2 2t
t
是经典误差项。 t
如果实际中估计了如下方程:
Y X * ,其中 * X ,
t
0
1 1t
t
t
2
2t
t
这时,新的误差项 *有可能序列相关,特别是在以下情况中: t
1、X 本身存在序列相关(时间序列很可能出现这种情况); 2t
第9章 序列相关性
4要求误差项的观察值互不相关。 序列相关:某期误差项的值以某种系统的方式 依赖于其他期误差项的值。
1
序列相关产生的原因
一、惯性。大多数经济时间序列都存在序列相关。其本期值往往受滞后
值影响。突出特征就是惯性与低灵敏度。如国民生产总值,固定资产投 资,国民消费,物价指数等随时间缓慢地变化,从而建立模型时导致误 差项序列相关。
,
t
t 1
t
其中, 0.
8
Hale Waihona Puke 负序列相关负序列相关:在相继的观察期内,误差项的符号从负到正, 然后由正变负,如此不断地转换.
例如:潜在的随机干扰项的抽取,存在某种循环. 在大多数时间序列中,负的序列相关较少. 图9-3
,
t
t 1
t
其中, 0.
9
季节的序列相关
在季节模型中,当前季节的误差项观察值可能与上 年同一季节的误差项观察值存在函数关系.
Yt
01 X1t
* t
,
其中
* t
2
X
2 1t
t ,
这时,新的误差项
*将表现为明显的序列相关模式。
t
P177
16
9.2 序列相关性的后果
1、纯序列相关不会导致对系数的有偏估计;但 由不正确设定产生的非纯序列相关,则可能导 致估计系数的偏误.
2、序列相关使OLS估计量不再是最小方差估 计量.序列相关增大了估计值分布的方差,增大 了任意给定的估计值可能异于真实值的数量.
3、解决办法:将略去的变量加入模型或改变模型的函数形式。
2
三、蛛网现象
许多农产品的供给表现出一种所谓的蛛网 现象。
例如,供给价格的反应要滞后一个时期。 今年种植的作物是受去年流行的价格影 响的,因此,相关的函数形式是:
St 1 P 2 t 1 t
这种现象就不能期望扰动项是随机的。
3
四、数据加工
9.1.1 纯序列相关性 误差项的两个任意观测值间的简单相关系数的期 望值不等于0,则称误差项是序列相关的。
E(r ) 0, (i j) i j
5
最常用的假定形式:一阶序列相关
误差项的当期值是其前一期值的函数。
t t1 t , 其中,是所研究方程的误差项,是参数,是经典误差项(无序列相关)。 上式又称一阶马尔可夫模式,称为一阶自相关系数。 的大小表明方程中序列相关的强度。若为0,则不存在序列相关,当在 绝对值上趋向于1时,误差项的前期值对于决定当期值 t就变得更加重要,
即存在高度序列相关。
若在绝对值上大于1,意味着误差项的绝对值具有随时间持续增加的趋势, 不合理,所以认为 1 1。
6
正序列相关
正序列相关:误差项从某一期到下一期倾向于有相同 的符号.
例如:外部冲击对经济系统的影响会延续到后面几期.
图9-1
,
t
t 1
t
其中, 0.
7
无序列相关
无序列相关:误差项的不同观测值之间完全不相关. 图9-2
在经验分析中,许多数据是经过加工而成的。 例如,在用到季度数据的时间序列回归中,季度数 据通常由月度数据加总而成。这种平均的计算减弱 了每月的波动而引进了数据的匀滑性。(内插与外 推等数据揉合技术)
注:序列相关也可能出现在横截面数据中,但更一 般出现在时间序列数据中。
4
9.1 纯序列相关与非纯序列相关
18
9.3 杜宾—沃森检验
❖ 图示法:首先用OLS估计方程,利用得到的 残差的图形来判断误差项是否存在自相关。
❖ 解析法:杜宾—沃森d检验和自回归模型的自 相关检验
19
一、图示法:
时间序列图(Time Sequence plot):将残差对时间描点。
如图(a)所示,扰动项的估计值呈循环形,并不频繁
17
9.2 序列相关的后果
3、序列相关导致OLS估计量的方差是有偏的,从而 导致不可靠的假设检验. 典型的是,OLS常常低估系数的标准误,从而高估t 统计值,导致拒绝虚拟假设的可能性增大,犯第一类 错误的可能性增加。
4、假设检验如t检验和F检验,在纯序列相关的情况 下变得有偏且不可靠。
5、降低预测精度。用依据普通最小二乘法得到的回 归方程去预测,预测是无效的。
