2018年江苏省高等数学竞赛本科一级试题与评分标准

合集下载

2018江苏数学高考真题及答案

2018年普通高等学校招生全国统一考试(江苏卷）

数学Ⅰ

参考公式：锥体的体积1

V Sh =，其中S 是锥体的底面积,h 是锥体的高．

一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1．已知集合{0,1,2,8}A =，{1,1,6,8}B =-，那么A

B = ▲ ．

2．若复数z 满足i 12i z ⋅=+，其中i 是虚数单位，则z 的实部为 ▲ ． 3．已知5位裁判给某运动员打出的分数的茎叶图如图所示，那么这5位裁判打出的分数的平均数为 ▲ ．

4．一个算法的伪代码如图所示，执行此算法,最后输出的S 的值为 ▲ ． 5．函数2()log 1f x x =-的定义域为 ▲ ．

6．某兴趣小组有2名男生和3名女生，现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 ▲ ． 7．已知函数sin(2)()22y x ϕϕππ=+-

x π

=对称,则ϕ的值是 ▲ ． 8．在平面直角坐标系xOy 中,若双曲线22221(0,0)x y a b a b

-=>>的右焦点(,0)F c 到一条渐近线的距离为3

2c ，则其离心

率的值是 ▲ ．

9．函数()f x 满足(4)()()f x f x x +=∈R ，且在区间(2,2]-上，cos ,02,2

()1||,20,2

x x f x x x π⎧

<≤⎪⎪=⎨⎪+<≤⎪⎩-

则((15))f f 的值为 ▲ ．

10．如图所示，正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 ▲ ．

11．若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点,则()f x 在[1,1]-上的最大值与最小值的和为 ▲ ． 12．在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，(5,0)B ，以AB 为直径的圆C 与直线l 交于另

2018年普通高等学校招生全国统一考试数学试题(江苏卷,含解析)

高考衣食住用行

衣：高考前这段时间，提醒同学们出门一定要看天气，否则淋雨感冒，就会影响考场发挥。穿着自己习惯的衣服，可以让人在紧张时产生亲切感和安全感，并能有效防止不良情绪产生。

食：清淡的饮食最适合考试，切忌吃太油腻或者刺激性强的食物。如果可能的话，每天吃一两个水果，补充维生素。另外，进考场前一定要少喝水！

住：考前休息很重要。好好休息并不意味着很早就要上床睡觉，根据以往考生的经验，太早上床反而容易失眠。考前按照你平时习惯的时间上床休息就可以了，但最迟不要超过十点半。

用：出门考试之前，一定要检查文具包。看看答题的工具是否准备齐全，应该带的证件是否都在，不要到了考场才想起来有什么工具没带，或者什么工具用着不顺手。

行：看考场的时候同学们要多留心，要仔细了解自己住的地方到考场可以坐哪些路线的公交车？有几种方式可以到达？大概要花多长时间？去考场的路上有没有修路堵车的情况？考试当天，应该保证至少提前20分钟到达考场。

2018年普通高等学校招生全国统一考试数学试题（江苏卷）

数学Ⅰ

注意事项

考生在答题前请认真阅读本注意事项及各题答题要求

1．本试卷共4页，均为非选择题(第1题~第20题，共20题)。本卷满分为160分，考试时间为120分钟。考试结束后，请将本试卷和答题卡一片交回。

2．答题前，请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3．请认真核对监考员从答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4．作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

2018年高考数学试题(江苏卷)含解析

一、填空题：本大题共 14 小题，每小题 5 分，共计 70 分．请把答案填写在答题卡相应位置上．

绝密★启用前

2018 年普通高等学校招生全国统一考试（江苏卷）

数学Ⅰ

注意事项

考生在答题前请认真阅读本注意事项及各题答题要求

1．本试卷共 4 页，均为非选择题(第 1 题~第 20 题，共 20 题)。本卷满分为 160 分，考试时间为 120

分钟。考试结束后，请将本试卷和答题卡一片交回。

2．答题前，请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定

位置。

3．请认真核对监考员从答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4．作答试题，必须用 0.5 毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无

效。

5．如需作图，须用 2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。

参考公式：

锥体的体积，其中是锥体的底面积，是锥体的高．

．．．．．．．．

1. 已知集合

【答案】{1，8}

，，那么 ________．

【解析】分析：根据交集定义

详解：由题设和交集的定义可知：

点睛：本题考查交集及其运算，考查基础知识，难度较小.

求结果.

2. 若复数满足，其中 i 是虚数单位，则的实部为________．

【答案】2

【解析】分析：先根据复数的除法运算进行化简，再根据复数实部概念求结果

详解：因为

，则，则的实部为 .

点睛：本题重点考查复数相关基本概念，如复数的实部为、虚部为、模为、对应点为、共轭复数为.

3.已知5位裁判给某运动员打出的分数的茎叶图如图所示，那么这5位裁判打出的分数的平均数为

2018年江苏数学高考试题(附答案)

绝密★启用前

2018年普通高等学校招生全国统一考试（江苏卷）

数学Ⅰ

参考公式：

锥体的体积

V Sh

=，其中S是锥体的底面积，h是锥体的高．

一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置

．．．．．．．上．．

1．已知集合{0,1,2,8}

A=，{1,1,6,8}

B=-，那么A B=▲ ．

2．若复数z满足i12i

z⋅=+，其中i是虚数单位，则z的实部为▲ ．

3．已知5位裁判给某运动员打出的分数的茎叶图如图所示，那么这5位裁判打出的分数的平均数为▲ ．

4．一个算法的伪代码如图所示，执行此算法，最后输出的S的值为▲ ．

．函数()f x 的定义域为 ▲ ．

6．某兴趣小组有2名男生和3名女生，现从中任选2名学生去参加活动，则恰好选中2名女生的概率为 ▲ ．

7．已知函数sin(2)()22y x ϕϕππ=+-<

x π

=对称，则ϕ的值是 ▲ ．

8．在平面直角坐标系xOy 中，若双曲线22

221(0,0)x y a b a b

-=>>的右焦点(,0)F c 到一条渐近

，则其离心率的值是 ▲ ． 9．函数()f x 满足(4)()()f x f x x +=∈R ，且在区间(2,2]-上，cos ,02,2()1||,20,2x x f x x x π⎧<≤⎪⎪=⎨⎪+<≤⎪⎩- 则

((15))f f 的值为

▲ ．

10．如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为 ▲ ．

11．若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点，则()f x 在[1,1]-上的

江苏省历届高等数学竞赛试卷(1991-2010)

江苏省第一届（1991年）高等数学竞赛

本科竞赛试题（有改动）

一、填空题（每小题5分，共50分）

1.函数

sin sin y x x

=（其中

2x π

≤

）的反函数为________________________。

2.当0→x 时，34sin sin cos x x x x -+x 与n

x 为同阶无穷小，则n =____________。

3.在1x =时有极大值6，在3x =时有极小值2的最低幂次多项式的表达式是 _____________________________________。

4.设(1)()n m n

n d x p x dx -=

，n m ,是正整数，则(1)p =________________。

[cos()]sin x x xdx π

π-+=

⎰_______________________________。

6. 若函数)(t x x =由

⎰=--x

t dt e t 1

所确定的隐函数，则

==0

2t dt x

d 。

7.已知微分方程()y y y x x ϕ'=+有特解ln x y x =，则()x ϕ=________________________。

8.直线21x z

y =⎧⎨

=⎩

绕z 轴旋转，得到的旋转面的方程为_______________________________。

9.已知a v 为单位向量，b a ϖϖ3+垂直于b a ϖϖ57-，b a ϖϖ4-垂直于b a ϖϖ27-，则向量b a ϖ

ϖ、的夹

角为____________。

10.

=⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝

2018年全国高中数学联赛江苏赛区复赛参考答案

O D
F
则 D，F，E，C 四点共圆．
A
……………………… 20 分
由点 P 是 CE，DF 的垂直平分线的交点，
故 PE＝PC，PF＝PD．
②
（第二题图）
从而∠PEC＝∠PCE，∠PFD＝∠PDF． ③
由 D，F，E，C 四点共圆得∠PEF＝180°－(∠PEC＋∠PDF)，
∠PFE＝180°－(∠PFD＋∠PCE)，
当 a＝3，b＝4.5 时，3a＋4b 取到最大值 27，即 3a＋4b 的取值范围为[24，27]．
6．如图，球 O 的内接八面体 PABCDQ 中，顶点 P，Q 分别在平面 ABCD 两侧，且四棱锥 P
－ABCD 与 Q－ABCD 都是正四棱锥．设二面角 P－AB－Q
P
的平面角的大小为 θ，则 tanθ 的取值范围是
x∈［0，1］．
所以 a＝－1，b＝12( 2＋1)．
……………………… 40 分
二、（本题满分 40 分）
如图，大圆和小圆为同心圆，其圆心为 O．过大圆上一点 A 作小圆的切线 AC，切点为
B，点 C 在大圆上，D 为 AB 的中点．△ACE 的顶点 E 在小圆上，AE 交小圆于 F．设 CE，
二、解答题（本题满分 16 分）
已知(sinα，sinβ) 是函数 f(x)＝ 3 x3 + t 3 和 g(x)＝3tx2＋(3t2＋1)x＋t 图象的公共点，求证：|t|≤1．

2018年高考数学江苏卷(含答案与解析)

数学试卷第1页（共42页）数学试卷第2页（共42页）

绝密★启用前

江苏省2018年普通高等学校招生全国统一考试

数学

本试卷共160分.考试时长120分钟.

参考公式：

锥形的体积公式13

V Sh =,其中S 是椎体的底面积,h 是椎体的高。一、填空题：本大题共14小题,每小题5分,共计70分. 1.已知集合{0,1,2,8}A =,{1,1,6,8}B =-,那么A

B = .

2.若复数z 满足i 12i z =+,其中i 是虚数单位,则z 的实部为 .

3.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 .

4.一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 .

函数()f x =的定义域为 .

6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 .

7.已知函数ππsin(2)()22y x ϕϕ=+-<

x =对称,则ϕ的值是 .

8.在平面直角坐标系xOy 中,若双曲线22

221(0)x y a b a b

-=>>0,的右焦点(,0)F c 到一条

渐近线的距离为2

,则其离心率的值是 . 9.函数()f x 满足(4)()()f x f x x +=∈R ,且在区间(2,2]-上,

()cos (2)2102x x f x x x π⎧⎪⎪

=⎨

⎪+⎪⎩

0＜≤，(-2＜≤)，,则((15))f f 的值为 . 10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .

11.若函数32

(完整版)2018年江苏省普通高校“专转本”统一考试《高等数学》试卷

2018年江苏省普通高校“专转本”统一考试

一、选择题（本大题共6小题，每小题4分，满分24分）

1、当0x →时，下列无穷小与()2sin f x x x =同阶的是（ )

A.2cos 1x -

1 C. 31x - D 。 ()32

11x +- 2、设函数2()x a f x x x b

-=++，若1x =为其可去间断点，则常数a ，b 的值分别为 ( ) A 。 1,2- B 。 1,2- C 。 1,2-- D. 1,2

3、设1()1x f x x ϕ-⎛⎫= ⎪+⎝⎭

,其中()x ϕ为可导函数，且()13ϕ'=，则()0f '等于 ( ） A.6- B 。 6 C.3- D. 3

4、设()2x F x e =是函数()f x 的一个原函数，则()xf x dx '=⎰ （） A. 2112x e x C ⎛⎫-+ ⎪⎝⎭ B. ()221x e x C -+ C. 2112x e x C ⎛⎫++ ⎪⎝⎭

D. ()221x e x C ++ 5、下列反常积分发散的是（ )

A 。 0x e dx -∞⎰

B 。 311dx x +∞⎰

C 。 211dx x +∞-∞+⎰

D 。 011dx x

+∞+⎰ 6、下列级数中绝对收敛的是( )

A. 1n n ∞=∑()1121n

n n ∞=+-∑ C. 21sin n n n ∞=∑ D 。 31(3)n n n ∞=-∑ 二、填空题（本大题共6小题,每小题4分，共24分）

7设()102lim 1lim sin x x x ax x x

江苏高等数学竞赛历年试题(本一)

2000年江苏省第五届高等数学竞赛试题（本科一级）

一、填空（每题3分，共15分） 1.设(

)f x =

()f f x =⎡⎤⎣⎦ .

2. 1lim

ln 1

x x x x

x x →-=-+ . 3.

()

1x dx x

=+⎰

4.通过直线122123:32;:312321x t x t L y t L y t z t z t =-=+⎧⎧⎪⎪

=+=-⎨⎨⎪⎪=-=+⎩⎩

的平面方程为 .

5.设(),z z x y =由方程,0y z F x x ⎛⎫

⎪⎝⎭

确定（F 为任意可微函数）

，则z z x y x y ∂∂+=∂∂ 二、选择题（每题3分，共15分）

1.对于函数11

2121

y -=

+，点0x =是( )

A. 连续点；

B. 第一类间断点；

C. 第二类间断点；D 可去间断点

2.设()f x 可导，()()()

1sin F x f x x =+，若欲使()F x 在0x =可导，则必有（） A. ()00f '=； B. ()00f =；C. ()()000f f '+=；D ()()000f f '-=

3. ()

sin lim

x y x y x y →→+=- （） A. 等于1； B. 等于0；C. 等于1-；D 不存在 4.若

()()0000,,,

x y x y f f x

∂∂∂∂都存在，则

(),f x y 在()00,x y ( )

A. 极限存在，但不一定连续；

B. 极限存在且连续；

C. 沿任意方向的方向导数存在； D 极限不一定存在，也不一定连续 5.设α

(完整版)2018江苏高考数学试题及答案word版

温馨提示：全屏查看效果更佳。

绝密★启用前

2018年普通高等学校招生全国统一考试（江苏卷）

数学I

注意事项

考生在答题前请认真阅读本注意事项及各题答题要求

1. 本试卷共4页，包含非选择题（第1题 ~ 第20题，共20题）.本卷满分为160分，考试时间为120分钟。考试结束后，请将本试卷和答题卡一并交回。

2. 答题前，请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3.请认真核对监考员在答题上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4.作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

5.如需改动，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗

一、填空题：本大题共14小题，每题5小分，共计70分。请把答案填写在答题卡相应位置上。

1.已知集合==-{0,1,2,8},{1,1,6,8}A B ,那么A B ⋂=__________.

2.若复数z 满足12i z i ⋅=+,其中i 是虚数单位,则z z 的实部为__________.

3.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为__________.

4.一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为__________.

5.函数()2log 1f x =-__________.

6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率是__________.

7.已知函数sin(2)()2

2018年10月自考00020高等数学一试题及答案含评分标准

2018 年10 月高等教育自学考试全国统一命题考试

高等数学（一）试卷

（课程代码00020）

本试卷共 4 页，满分 l00 分，考试时间 l50 分钟。考生答题注意事项：1．本卷所有试题必须在答题卡上作答。答在试卷上无效。试卷空白处和背面均可作草稿纸。

2．第一部分为选择题。必须对应试卷上的题号使用2B 铅笔将“答题卡”的相应代

码涂黑。

3．第二部分为非选择题。必须注明大、小题号，使用0．5 毫米黑色字迹签字笔作

答。

4．合理安排答题空间，超出答题区域无效。

第一部分选择题

一、单项选择题：本大题共 l0 小题，每小题 3 分，共 30分。在每小题列出的备选项中只有一项是最符合题目要求的，请将其选出。

1．若极限则常数 k=

A． 1 B ． 2

C． 3 D ． 4

A．高阶的无穷小量

B．低阶的无穷小量

C．是同阶无穷小量，但不是等价无穷小量

D．是等价无穷小量

3．下列函数中在点 x=0 处导数不存在的是

A．-2 B. -l C． 0 D ．1

8．设函数 f(x) 在区间【 a,b 】上连续，则下列等式正确的是

9．微分方程 sinxdx+cosydy=0 的通解为 A ． cos y+sin x=C B ．cos y-sin x=C C ．sin y+cos x=C D ．sin y-cos x=C

A．0 B ．1

C． 2 D ．3

第二部分非选择题

二、简单计算题：本大题共5 小题，每小题4 分，共20 分

三、计算题：本大题共 5 小题，每小题 5 分，共 25分。

16．求函数的定义域．

18．已知函数

19．求极限 20. 计算定积分

2018年江苏高考数学真题(word版)

精选

文档2018 年一般高等学校招生全国一致考试(江苏卷 )

数学Ⅰ

1．已知会合A 0,1,2,8 ， B 1,1,6,8 ，那么 A B _____

8 99 2．若复数 z 知足i z 1 2i ，此中i是虚数单位，则z 的实部为 _____ 9 011 3．已知 5 位裁判给某运动员打出的分数的茎叶图如下图，那么这 5 位(第3题) 裁判打出的分数的均匀数为 _____

4．一个算式的伪代码如下图，履行此算法，最后输出的S

I ← 1

的值为 ______

S← 1

5．函数f ( x) log 2 x 1 的定义域为 ______ While I<6

6．某兴趣小组有 2 名男生和 3 名女生，现从中选 2 名学生去参加，I←I+2 S← 2S

则恰巧有 2 名女生的概率为 _______

End While

7．已知函数y sin( 2x )( ) 的图象对于直线 x

3 Pnint S

2 2

(第 4 题 ) 对称，则的值是 ______

8．在平面直角坐标系xOy 中．若双曲线x2 y 2

1(a 0， b 0) 的右焦点F(c，0)到一a2 b 2

条渐近线的距离为3

c ，则其离心率的值是_____

cos

, 0 x 2,

9．函数 f(x) 知足 f(x ＋ 4)＝ f(x)(x ∈ R)，且在区间( 2, 2] 上， f ( x)

1 ,

x 2 x 0, 2

则 f ( f (15)) 的值为______

10．如下图，正方体的棱长为2，以其全部面的中心为极点的多面

体的体积为 _______

2018年江苏省高等数学竞赛本科二级试题与评分标准

1 2 ln x dy , x , y f x , 则 1 u x dx
.
x 1

.
(4)
0
1 x

x
2 3
dx
(5) 已知函数 F u , v 可微， Fu 0,0 1, Fv 0,0 2, 函数 z f x, y 由方程
0

1 cos 2 x 1 cos 4 x 2 2cos x 1 2sin 2 x d x （2 分） 2 2 0
1 4 1 2 2 sin 2 x sin 4 x 2sin x sin 3 x . （3 分） 2 4 8 3 0 2 3

.
(1) 求定积分
02 cos x cos 2 x
2

2
d x;
(2) 求极限 x lim
y
x y sin x 2 xy y 2 . 2 x xy y

解
(1) 原式 2 cos 2 x cos 2 2 x 2cos x cos 2 x d x
yn xn 1, 0 1, ( 2 分) 所以 yn xn yn xn
f 0 0 f 0 f 0 0 f 0 ( 3 分)

2018年江苏省高考数学试卷及答案(解析版)

2018年普通高等学校统一考试试题（江苏卷）

一、填空题：本大题共14小题，每小题5分，共计70分。请把答案填写在答题卡相印位置上。

1．函数)42sin(3π+

=x y 的最小正周期为．

【答案】π

【解析】T ＝|2πω |＝|2π2 |＝π．

2．设2)2(i z -=（i 为虚数单位），则复数z 的模为．

【答案】5

【解析】z ＝3－4i ，i 2＝－1，| z |＝＝5． 3．双曲线19

162

2=-y x 的两条渐近线的方程为．【答案】x y 4

3±= 【解析】令：091622=-y x ，得x x y 4

31692±=±=． 4．集合}1,0,1{-共有个子集．

【答案】8

【解析】23＝8．

5．右图是一个算法的流程图，则输出的n 的值是．

【答案】3

【解析】n ＝1，a ＝2，a ＝4，n ＝2；a ＝10，n ＝3；a ＝28，n ＝4．

则成绩较为稳定（方差较小）的那位运动员成绩的方差为．

【答案】2

【解析】易得乙较为稳定，乙的平均值为：9059288919089=++++=

x ．方差为：25

)9092()9088()9091()9090()9089(2

22222=-+-+-+-+-=S ． 7．现在某类病毒记作n m Y X ，其中正整数m ，n （7≤m ，9≤n ）可以任意选取，则n m ，都取到奇数的概率为．

【答案】63

20 【解析】m 取到奇数的有1，3，5，7共4种情况；n 取到奇数的有1，3，5，7，9共5种情况，则n m ，都取到奇数的概率为63209754=⨯⨯．

江苏省普通高等学校第十四届高等数学竞赛(本一)

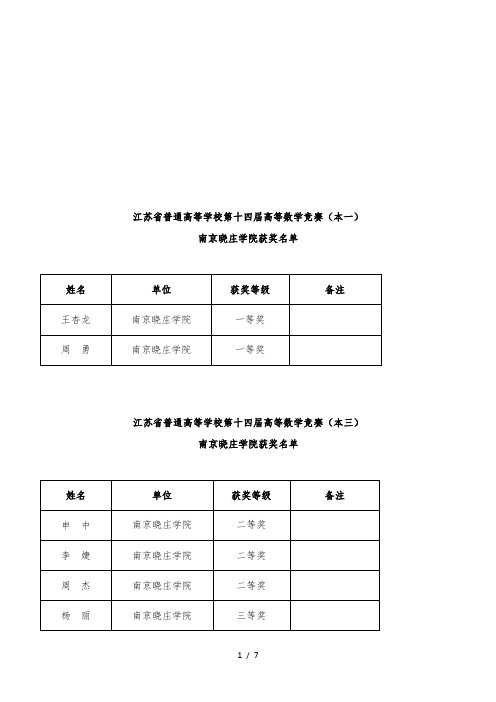
江苏省普通高等学校第十四届高等数学竞赛（本一）南京晓庄学院获奖名单
姓名王杏龙周勇
单位南京晓庄学院南京晓庄学院
获奖等级一等奖一等奖
备注
江苏省普通高等学校第十四届高等数学竞赛（本三）南京晓庄学院获奖名单
姓名申李周杨中婕杰丽
单位南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院
获奖等级二等奖二等奖二等奖三等奖
备注
1/7

贺韩
婕清
南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院南京晓庄学院
三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖三等奖
钱文慧黄董陈张叶颖源磊伟彤
谢敏寰陆晓蕾吴笑怡
2/7

3/7

4/7

5/7

6/7

7/7

2018年江苏省普通高校“专转本”统一考试《高等数学》试卷(2021年整理)

(完整)2018年江苏省普通高校“专转本”统一考试《高等数学》试卷(word 版可编辑修改)

编辑整理：

尊敬的读者朋友们：

这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整)2018年江苏省普通高校“专转本”统一考试《高等数学》试卷(word版可编辑修改)）的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整)2018年江苏省普通高校“专转本”统一考试《高等数学》试卷(word版可编辑修改)的全部内容。

2018年江苏省普通高校“专转本”统一考试

一、选择题(本大题共6小题，每小题4分，满分24分）

1、当0x →时,下列无穷小与()2sin f x x x =同阶的是 ( )

A.2cos 1x - B 。

1 C 。 31x - D 。 ()3

211x +- 2、设函数2()x a f x x x b

-=++，若1x =为其可去间断点，则常数a ，b 的值分别为 ( ） A. 1,2- B. 1,2- C 。 1,2-- D 。 1,2

3、设1()1x f x x ϕ-⎛⎫

= ⎪+⎝⎭，其中()x ϕ为可导函数，且()13ϕ'=，则()0f '等于（）

A 。6- B. 6 C.3- D. 3

4、设()2x F x e =是函数()f x 的一个原函数，则()xf x dx '=⎰ ( ）