结构位移计算(1)新
结构力学课件--5位移计算(1)

MP
EI
NP
EA
k
QP GA
k--为截面形状系数
1.2
10 9
(3) 荷载作用下的位移计算公式
MM P ds NNP ds kQ QP ds
2021/4/9
EI
EA
GA
二、各类结构的位移计算公式
21
(1)梁与刚架
MM P EI
ds
(2)桁架
NNP ds NNP ds NNPl
We =Wi
2021/4/9
§5-2 结构位移计算的一般公式 ——变形体的位移计算
18
d 1 ds ds d ds
R
d ds
K
t1 t2
c2
1
R1
K
c1
ds
ds R2 ds
M
N
Q
外虚功:We 1 Rk ck 内虚功:Wi M N Q ds
1 (RMkck N MQ N)dsQ Rdksck
9
刚体的虚功原理 刚体系处于平衡的必要和充分条件是:
对于任何可能的虚位移,作用于刚体 系的所有外力所做虚功之和为零。
2021/4/9
10
四、虚功原理的两种应用
1)虚功原理用于虚设的协调位移状态与实际的 平衡力状态之间。
例. 求 A 端的支座反力(Reaction at Support)。 直线
A
EA
EA
EA
(3)拱
MM P EI
ds
NNP EA
ds
2021/4/9
图乘§法5是-4V图er乘es法hag位in于移1计92算5年举提例出的,他当 22
时为莫斯科铁路运输学院的学生。
MiMk
结构力学 结构的位移计算

k
F Ndu
Md
F Q 0ds
F RC
只有荷载作用
无支座移动
k F Ndu Md FQ 0ds
由材料力学知
du
FNP d s EA
d
M Pds EI
d s
k FQP d s GA
10
1.2
9
k--为截面形状系数
A A1 [Al为腹板截面积]
FP
X
待分析平衡的力状态
(c)
直线
几点说明:
X C (1) 对静定结构,这里实际用的是刚体
虚设协调的位移状态
虚位移原理,实质上是实际受力状态 的平衡方程,即
由外力虚功总和为零,即:
X F 0
X
P
C
M 0 B
(2) 虚位移与实际力状态无关,故可设
1 x
X P b 0 (3) 求解时关键一步是找出虚位移状态的
计算结构的位移,就必须明确广义力与广义位移的对应关系。常见的对应有
以下几种情况:
基本原则
求哪个方向的位移就在要求位移的方向上施加相应的单位力。
A
B
位移方向未知
时无法直接虚
拟单位荷载!
求A点的 水平位移
P=1
m=1 求A截面 的转角
m=1
m=1
求AB两截面 的相对转角
P=1
P=1
求AB两点 的相对位移
位移与约束协调:位移函数在约束处的数值等于约束位移。
§4-2 虚功原理
一、虚功原理的三种形式
1、质点系的虚位移原理
具有理想约束的质点系,其平衡的必要和充分条件是:作用于质点系的主
第5章结构位移计算

1、结构材料服从“虎克定律”,即应力、应变成线形关系。
满足以上要求的体系为“线变形体系”。因位移与荷 载为线形关系,故求位移时可用叠加原理。
第5章
5.2
一、基本概念
虚功原理与位移计算一般公式
1、功:一般来说,力所作的功指力与力方向上位移乘积, 大小与作用点移动路线的形状、路程的长短有关。
i
Pi
i FR K CK
K
( M FQ 0 FN )ds
1)意义:虚功方程的每一项都是广义力与广义位移的 乘积。
2)虚位移原理:研究实际的平衡力系在虚设位移上的 功,以计算结构的未知力(如支座反力等)。 3)虚力原理:研究虚设的平衡力系在实际位移上的功, 以计算结构的未知位移(如挠度、转角等)。
MP EI
0 k
FQ P GA
FN P EA
于是:
FQ FQ P FF MMP cv ds k ds N NP ds EI GA EA
第5章
二、如何施加单位荷载(求线位移、角位移、相对位移) 求哪个方向的位移就在要求位移的方向上施加相应的单位力。
B P=1 C P=1 A B C M=1
α
Mk
x
ω dx
x0
Mi
y0
B
A
xMk dx
MK对 y 轴的静矩。
Mi=xtgα
y0=x0tgα x
w y0
EI
说明:
1)条件:AB杆为棱柱形直杆,即EI等于常数; Mi与Mk图形中有一个是直线图形。
2)y0与ω的取值: y0一定取自直线图形, ω则取 自另一个图形,且取ω的图形的形心位置是已知 的,不必另行求解。
第八章-结构的位移计算

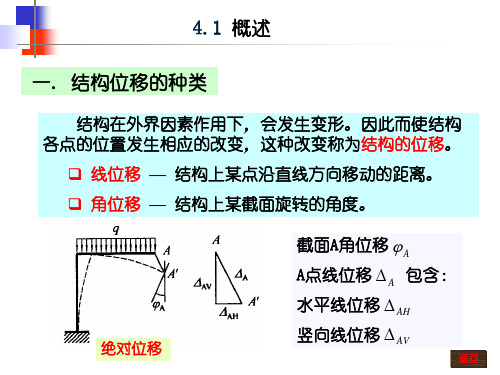
绝对位移
相对位移
截面A角位移A ,
A点线位移 A 包含: 水平线位移 AH 竖向线位移 AV
CD两点的水平相对线位移:
(CD )H C D
AB两截面的相对转角:AB A B
以上线位移、角位移及相对位移统称为广义位移
一.局部变形时的位移公式
如图所示,为一悬臂梁在B点附近有微段ds 有局部变形,结构其他部分没有变形,微
段 ds 局部变形包括三部分:
⑴ 轴向应变 ;⑵ 平均剪切应变 0 ;
⑶ 轴线曲率 ( 1 R,R 为轴线变形后
§8-2 结构位移计算的一般公式
—般情况下,结构发生位移在结构内部产生应变,因此,结构的位移计算 属于变形体体系的位移计算问题。计算变形体体系的位移采用的方法以虚 功原理最为普通。推导结构位移(变形体)计算的一般公式有两种途径:
一是根据变形体体系的虚功原理,然后由此导出变形体体系的位移公式, 另一种是先应用刚体体系的虚功原理导出局部变形时的位移公式,然后应 用叠加原理,导出整体变形时的位移公式。
第 六 章 结构位移计算
本章主要内容
➢ 应用虚功原理求刚体体系的位移 ➢ 结构位移计算的一般公式 ➢ 荷载作用下的位移计算 ➢ 图乘法 ➢ 温度作用及支座移动时的位移计算 ➢ 广义位移的计算 ➢ 互等定理
§8-1 应用虚功原理求刚体体系的位移
一.结构位移计算概述
◆结构位移的种类:结构在外界因素作用下发生变形。因此而使结构各点的 位置发生相应的改变,这种改变称为结构的位移。
在材料力学中,曾学过求梁的位移计算方法(如直接积分法等)。但这
些方法对于结构力学的研究对象,如多跨静定梁、桁架、刚架等结构,是
第6章 结构位移计算(1)

《 第6章 结构位移计算(1) 》
- 44/126页 -
正负号规则:
1) 不规定 和 的正负号,只规定乘积 的正负号。若 和 使杆件同一侧纤维受 拉伸长,则乘积为正,反之为负;
正
MP
MP
负
MP
《 第6章 结构位移计算(1) 》
- 45/126页 -
正
45
2) 和 以拉力为正,压力为负; 3) 和 的正负号见下图。
12
《 第6章 结构位移计算(1) 》
- 12/126页 -
§ 6-2 变形体系的虚功原理
一、 功、实功与虚功
1. 实功
外力(其值由零逐渐增加到最大值)在其自 身引起的位移上所作的功称为实功。
13
《 第6章 结构位移计算(1) 》
- 13/126页 -
2. 虚功
外力在其它原因(其它荷载、温度变化、支 座位移等)引起的位移上所作的功称为虚功。
略去高阶微量后,得杆件的变形虚功为:
16
《 第6章 结构位移计算(1) 》
- 16/126页 -
结构通常有若干根杆件,则对全部杆件求总 和得:
对于由直杆构成的结构:
17
《 第6章 结构位移计算(1) 》
- 17/126页 -
二、 刚体体系虚功原理
刚体体系处于平衡的必要和充分条件是,对于 符合约束条件的任意微小虚位移,刚体体系上所 有外力所做的虚功总和等于零 。
位移计算
§6-8 线弹性结构的互等定理
2
《 第6章 结构位移计算(1) 》
- 2/126页 -
§ 6-1 概 述
一、 结构的位移
在荷载等外因作用下结构都将产生形状的改变, 称为结构变形,结构变形引起结构上任一横截面 位置和方向的改变,称为位移。 1. 截面的位移(绝对位移)
01静定结构位移计算

§4.2 变形体虚功原理
五、直杆系虚功方程
q FPx p
δWe = δW =δWi q(s) 取任一单元
* FQj
* FNi
* FNj
M i* F i m(s) * Qi
j
p(s)
θ(s)
M* j
δWe 的计算:
δWei,j [ pδu qδv mδ ]d s
i 当无集中荷载时: δWe =Σ∫[pδu+qδv+mδθ]ds
l
M 2 ( x) FP 2l 3 dx 2 EI 6 EI
V FPl 3 FP 3EI
?
推导过程使用了互等定理,所以只适用线弹性结构
§4.0 理力材力相关内容回顾 四、摩尔定理(公式)
l
FN ( x)FN 0 ( x) T ( x)T 0 ( x) M ( x)M 0 ( x) dx dx dx EA GI p EI
l
l
FN ( x)、T ( x)、M ( x) - -结 构 在 原 载 荷 下 的 内 力 FN ( x)、T ( x)、M ( x) - -去 掉 原 载 荷 , 在 所 义 广 求 位移点,沿所求广移的方向加广义单时, 义位 位力 结构产生的内力
0 0 0
推导过程使用了两种力施加不同顺序得出结果相同, 所以只适用线弹性结构
X AΔ 0
YA
YB
§4.2 变形体虚功原理
一、虚位移、虚力
对一变形体
FP 力状态:平衡方程 FP/2 FP/2 满足平衡条件 FP 位移状态:协调方程 满足协调条件:光滑、连续、满足约束、微小
§4.2 变形体虚功原理
一、虚位移、虚力
结构力学-结构位移计算(1)新

δWe =Σ∫[pδu+qδv+mδθ]ds +Σ [FPxδu+FPyδv+Mδθ] i =Σ∫[FNδε+FQδγ+Mxδφ +Mδθ]ds = δWi
以上结论与材料物理性质及具体结构无关, 以上结论与材料物理性质及具体结构无关, 因此, 因此,虚功原理虚功方程既适用于一切线性结 构,也适用于一切非线性结构。
A
(a)
B a
b
FP C
解:去掉A端约束并代以反力 X,构造相 去掉 端约束并代以反力 , 应的虚位移状态如图(b)、 应的虚位移状态如图 、(c)
(b)
FP X
(c)
直线
∆C
∆X
待分析平衡的力状态
虚设协调的位移状态
由外力虚功总和为零, 由外力虚功总和为零,即:
X ⋅ ∆X + F ⋅ ∆C = 0 P b X ⋅ ∆X + FP ⋅ ∆X = 0 a b 计算 的计算:
取微段,其受力如下 取微段 其受力如下
变形可看成有如下几部分
微段受力
微段拉伸
微段剪切
微段扭转
微段弯曲
对于直杆体系,由于变形互不耦连, 对于直杆体系,由于变形互不耦连,所以 δWi =Σ∫[FNδε+FQδγ+Mxδφ+Mδθ]ds
杆系结构虚功方程
根据上述推证, 根据上述推证,可得杆系结构虚功方程如下
(虚)力状态
注意: 注意: 体系; (1)属同一体系;或两状态中的变形体 ) 同一体系 系只要外形相同,而材料、截面尺寸及约 系只要外形相同,而材料、截面尺寸及约 可以不同。 束可以不同。 (2)均为可能状态。即位移应满足变形 )均为可能状态。即位移应满足变形 协调条件;力状态应满足平衡条件 平衡条件。 协调条件;力状态应满足平衡条件。 完全无关; (3)位移状态与力状态完全无关; )位移状态与力状态完全无关
结构力学位移的计算

l
dl
l
的一半。
D
注意点:
(1)外力实功中,位移是由做功的力本身引起的,且外力是变化的 (由零开始逐渐增加到其最后数值)。
(2)计算外力实功时,力与位移必须相对应。
.
17
5-2 线性变形体系的功能原理 一、外力实功
计算外力实功时,力与位移必须相对应
P
D
MA
j
T 1 PΔ 2
T
1 2
M Aj
P
D
B
EA EI
GA
将式(2)代入(1),并在长度方向积分,得到一个杆件的实变形能
累加所有杆件的实变形能,得到体系的实变形能
j U U d d U U 1 2 ( F 2 N F 2 E N d d su A M M 2 2 E d d s I F Q F d 2 Q G 2 d ) s A
基础发生沉降 结构支座移动、转动 结构产生位移
4.其他因素
结构构件的尺寸制作误差、材料的干缩、混凝士凝结收缩等
.
7
5-1 概述 三、计算结构位移的目的 1.验算结构的刚度
结构要满足强度、刚度、稳定性要求。 结构的刚度:以其变形或位移来量度
(在验算结构刚度时,需计算结构位移)。 闸门:沿水流方向位移超过允许限度时,将使闸门的启闭受到阻碍,同 时影响止水效果。 结构设计规范中具体规定
1
P1
2
2
P2
.
21
5-2 线性变形体系的功能原理
1
1
P1
2
2
P2
b
a
1 1'
P1
1 1'
D1=Dl1
2 2'
2 2'
建筑结构力学位移计算

位移计算公式也是变形体虚功原理的一种表达式。
( M N Q ) ds R c k k
c2
K
K
ds
t1
1
R1
t2
c1
ds d ds ds ds
R2
ds
d
d
Q N 外虚功:W 内虚功:W 1 R c M N Q d e k k i
(2)由上面的内力计算应变,其表达式由材料力学知
M P
EI
N P
1.2
EA
Q kP
10 9
GA
A A1
k--为截面形状系数 (3) 荷载作用下的位移计算公式
M M N N k Q Q P P P ds ds ds EI EA GA
2019/2/27
建筑结构力学
20
。 例1. 试计算悬臂梁A点的竖向位移 ,EI C AV P=1 q x A x C C B A AV
B
l 2
1)列出两种状态
l 2
(a) 实际状态
l 2
l 2
(b) 虚设状态
N 0 M x Q 1
的内力方程:
l 0 x AC段 2
实功恒为正。
虚功是力在其它原因产生的位移上作的功。如T12, 如力与位移同向,虚功为正,反向时,虚功为负。 产生位移的原因 位移发生的位置
ΔKj
2、虚功原理
虚力原理:在给定的位移状态与虚设的力状态之间应用虚
3、虚功原理
功原理,这种虚功原理的形式称为虚力原理。 虚位移原理:在给定的力状态与虚设的位移状态之间应用
(最新整理)静定结构的位移计算

图乘法
2. 竖标yc必须取自直线图形,而不能从折线和曲 线中取值。
yc M图
ω
MP图
Δ
1 EI
ωyC
图乘法
若M图与MP图都是直线图形,则yc可以取自其中 任一图形。
ω1
y2
M图
y1
ω2
MP图
ΔE1Iω1y1E1Iω2y2
图乘法
3. 若与 y c 在杆件的同侧, y c取正值;反之,
取负值。
yc
k
k
du、d、dv
ds
位移状态
FPk=1 k
FN、M、FQ
ds
力状态
结构位移计算
外力虚功:
W F P K K F R 1 c 1 F R 2 c 2 F R 3 c 3 K F R c
内力虚功:
W ( i)lF N d u lM d lF Q Fd Qv d
由虚功原理W=W'有
MP图
l
yC
FP=1 M
(1)绘制MP图。
( 2)建立相应的虚拟 状态,绘制 M 图 。
( 3)图乘求位移。
1 ql2 l
22
yC
3 4
BE1I13q22ll4 3l
ql 4 8 EI
图乘法
例 求图示简支梁A端截面的转角 A 及跨中竖向位移 CV 。
q
解:1. 求A端截面的转角 A A
yc
M图
ω
MP图
ω
Δ
1 EI
ωyC
Δ
1 EI
ωyC
图乘法
4. 若Mp图是曲线图形,M 图是折线图形,则应
当从转折点分段图乘,然后叠加。
y1
y2
M图
结构位移的计算

A
A
p A
A
B
p B
AB
AB A B
4、上述各种位移统称为“广义位移”。与广义 位移相对应的力称为“广义力”。 二、计算结构位移的目的
1、刚度验算:电动吊车梁跨中挠度 fmax≤l/600. 高层建筑的最大位移< 1/1000 高度。 最大层间位移< 1/800 层高。
相邻微段k、j、i连续,变形协调,位移相等,而力为作用力 与反作用力, 虚功相互抵消,即W内=0,故:
全结构:W W外 (a)
18
A
B
力状态:静力平衡 位移状态:其它原因引起
ds
ds
(2) 按刚体虚功与变形虚功计算: 将ds虚位移分解为: 刚体虚位移: 变形虚位移: ABCD A'B'C'D' A'B'C'D' A''B''C''D''
——虚设力系求刚体体系位移
C B 已知 c1 求
?
A
设虚力状态
a
b
P=1
R1 a P b 0
虚功方程
R1
b a
A
C B a b
1 R1 c1 0
b c1 a
R1
小结: (1)形式是虚功方程,实质是几何方程; (2)在拟求位移方向虚设一单位力,利用平衡条件求出与已知位移相 应的支座反力。构造一个平衡力系;
1 cA 2l
1 3
A
2 3
B
C D
1
1 2l
2 l
3 2l
结构力学 第七章 结构位移计算

第七章 结构位移计算(Displacement)
五、位移计算中的基本假定
位移计算限定结构在线性弹性范围内工作。即,结构 的位移与荷载的大小成正比,且当荷载撤除后,结构的 位移也随之消失。并应满足如下基本假定: 1、应力和应变服从虎克定律(物理线性); 2、位移是微小位移(几何线性),即可用结构原尺寸 和叠加法计算其位移; 3、所有约束为理想约束,即约束力不作功。
刚体系处于平衡的充要条件是:在具有理想约束的
刚体体系中,若力状态中的力系满足静力平衡条件,位移状态 中的刚体位移与约束几何相容,则该力系在相应的刚体位移上 所作的外力虚功之和等于零,即 W12=0。
第七章 结构位移计算(Displacement)
2、静力实功 在静外力FP1作用下,变形体在力的作用点沿力的
方向发生位移△11 。静力实功为: 式中的“1/2” ?
W=(1/2)FP1△11
静力概念: 静力荷载加载到结构上是
有一个过程的,在这个加载 过程中,荷载从零增加到最 后值,结构的内力和位移也 达到最后值;
在整个加载过程中,外力 和内力始终保持静力平衡。第七章 结构移计算(Displacement)
A
0
B
位移与静力荷载
对于线弹性结构,在静力 荷载加载的过程中,结构 的位移和荷载成正比。
当结构的位移有一增量 d时,静力功有增量:
dW FP1 d
当静力达到最后值时,总 的静力功为:
W dW FP1 d
第七章 结构位移计算(Displacement)
一、变形与位移
§7-1 结构位移的概念与计算的目的
P
B'
△
K'
有形变有位移
有位移无形变
结构位移计算

[结构的位移]结构在荷载作用下产生应力和应变,以致结构的形状发生变化,即产生变形,由于这种变形,使结构上各点的位置产生位移,截面发生转动,这种移动和转动统称为位移。
位移有水平位移,竖向位移,即线位移;有角位移;又有相对位移和绝对位移;统称为广义位移。
除了荷载作用将引起位移外,温度改变,支座位移,材料收缩,制造误差等因素,虽不一定都产生应力和应变,但都将使结构产生位移。
[计算位移的目的](1)验算结构的刚度;(2)在结构的制作、架设和养护等过程中,需要进行位移计算,以便预先知道结构变形后的位置,采取一定的施工措施;(3)为超静定结构分析打下基础。
[计算位移的假设](1)材料线性假设:结构的材料服从虎克定律,应力与应变成线性关系;(2)几何线性假设:即小变形假设,结构的变形很小,应变与位移成线性关系;(3)弹性假设:结构在力的作用下发生变形,在力卸载之后,结构完全恢复原来的形状;(4)理想约束假设:结构的约束都为理想约束,不考虑摩擦的影响。
满足上述条件的变形体系,称之为线弹性变形体系。
它们的位移与荷载之间为线性关系,位移计算满足叠加原理。
§4-2 虚功原理[功的描述](1)简单的描述:功等于作用的力乘以所移动的距离;(2)进一步的描述:功等于力矢量与位移矢量的点积;(3)精确的描述:功等于力矢量与位移矢量点积的线积分。
[虚功的概念]作功的力与位移彼此独立无关,这种功称为虚功;在虚功中,力与位移分别属于同一体系的两种彼此独立无关的状态。
力所属的状态,称为力状态和第一状态;位移所属的状态,称为位移状态和第二状态。
力状态位移状态表示力状态的外力在位移状态相应位移上所作的虚功。
[变形直杆的平衡条件和力的边界条件]变形直杆,承受横向分布荷载,轴向分布荷载,分布力矩以及边界外力、、和、、的作用。
静力平衡条件为:力的边界条件为:证明:任意取一微段(略去高阶微量)[变形直杆的变形协调条件和位移边界条件]直杆变形后,以表示杆轴各点沿轴向的位移,表示杆轴各点沿轴竖向的位移。
结构位移计算

1/l
求AB两截面 的相对转角
1/l
求AB两点 连线的转角
例 1:已知图示梁的E 、G, 求A点的竖向位移。
解:构造虚设单位力状态.
q
A
h b
N ( x) 0, N P ( x) 0
l
Q ( x) 1, QP ( x) q(l x) M ( x) x l, M P ( x) q(l x)2 / 2
i k 1 1 2
a
2
ω1
l/3 c
y1
l/3
ω2
b
l/3
d
6
y2
b)非标准抛物线成直线形
例:求图示梁中点的挠度。
1 1 3a 3a Pa EI 2 4
P Pa Pa
P
?
P
MP
a
2 Pa a 2 a a 2 3a 4 a Pa EI 32 2 2 2 23Pa3 24 EI
P=1
l/6
M
求C点竖向位移。 q=625N/m 200 2.2 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ w1 220 C B A 2 2.2m 0.8m 2 0.8 y1 4Nm2 200 EI=3.6465 × 10 3 378 2 378 2.2 w2 555 ω1 ω 3
构;静定和超静定结构;
3. 材料性质:线性、非线性; 4. 变形类型:弯曲变形、拉(压)变形、剪切
变形;
5. 位移种类:线位移、角位移;相对线位移
和相对角位移。
荷载作用下的位移计算
注:(1)EI、EA、GA是杆件截面刚度; k是截面形状系数k矩=1.2, k圆=10/9。 真实 位移 (2)NP、QP、MP实际荷载引起的内力, 状态 是产生位移的原因;虚设单位荷载 引起的内力是 N , Q , M (3)公式右边各项分别是轴向、剪切、弯曲变形产生的位移。 NP ds = NN P l (4)梁和刚架 Δ= M MP ds (5)桁架 Δ= N EA EA EI MM NN 用于桁架杆 (6)桁梁混合结构 Δ= EI ds EA l
结构力学-6章 位移计算

例:求图示梁(EI=常数,跨长为l)B截面转角 B
q
A
1 2 ql 8 1 2
1
B
MP 图
M
图
解:
1 2 1 2 1 B [( l ql ) ] EI 3 8 2 3 1 ql ( ) 24 EI
三、图形分解
a
MP
1
a
1
2
b
2
b
Mi
c
d
M PMi 1 ds EI (M 1 M 2 )M i ds EI
2.桁架
ip
这些公式的适 用条件是什么?
3.组合结构
ip M PMi N Nl ds P i EI EI
例:求图示桁架(各杆EA相同)k点水平位移. 解:
kx N P Nil EA
P
P
1 P
0
a Pa 2 P 2 2a ] 2(1 2 ) ( ) EA
K 1
KC K
K
c1
c2 c3
R1
R3
R2
刚体虚功方程为:
δW =0
0 =1ΔkC+R1 C1 +R2 C2+R3 C3
计算公式为:
ic Ri Ci
例1:求 Cx ?
B C
解:构造虚设力状态
B C P=1
c3
A
l
A
XA 1
YC 1
c2
l
YA 1
c1
Cx (1 C1 1 C2 1 C3 ) (C1 C2 C3 )
Pl
EI
P
B
l
结构力学 位移计算

n1
h
C
(n 1)l n2
l n2
例:求图示梁(EI=常数,跨长为l)B截面转角 B
1
q
A
B
2
1
MP 图
解:
1 ql2
M图
8
B
1 EI
[(2 3
l
1 8
ql2 )
1] 2
1 ql3 ( )
24 EI
三、图形分解
求 B
20
40
A
B
MP
EI
20kN m10m40kN m
1
Mi
1/3 2/3
1
1 [(P)(1)a (P)(1)a EA
2P k
2P 2 2a] 2(1 2) Pa () a
2
Ni
1
EA
练习:求图示桁架(各杆EA相同)k点竖向位移.
P
2P
0 a NP
P
1
0a k
2 0
Ni
kx
NP Nil EA
1 1 [P 1 a ( 2P)( 2) 2a]
EA
1
(1 2
对于由线弹性直杆组成的结构,有:
P
NP EA
,
P
kQP GA
,
P
MP EI
适用于线弹性 直杆体系,
ip
[
NP N EA
i
kQP Qi GA
M P M i ]ds EI
例 1:已知图示粱的E 、G,
q
求A点的竖向位移。
解:构造虚设单位力状态.
Ah
Ni (x) 0, NP (x) 0
l
b
Qi (x) 1,QP (x) q(l x)
结构位移计算
1 A y0 EI
o
Mi = x tgα
y0 y0 = x0 tgα
Mi图 x
应用图乘法计算的注意点: ⑴ y0 与A 的取值: y0 一定取自直线图形,对应取A 图形的形心处。 A 则取 自另一个图形,且取A 的图形的形心位置是已知的。 ⑵ 若 y0 与A 在杆轴或基线的同一侧,则乘积A y0 取正号;若 y0 与A 不在杆轴 或基线的同一侧,则乘积A y0 取负号。
2、几种常见图形的面积和形心的位置
h
2l/3 三角形A = hl/2 l/3
顶点 FQ=0 h
l/2
l/2
标准二次抛物线A = 2hl/3 顶点 FQ=0
h h
顶点 FQ=0 3l/4 l/4
5l/8
3l/8
标准二次抛物线A = hl/3
标准二次抛物线A = 2hl/3
例:试求图示刚度为 EI 的简支梁 B 端截面的角位移。 解:⑴ 画出两种状态的弯矩图。 ⑵ 图乘计算 B :
l 2ac 2bd ad bc 6
式中同侧为正,异侧为负
3、应用图乘法时的几个具体问题
⑴ 如果两个图形都是直线图形,则 y0 可取自其中任一图形。
⑵ 如果EI 分段为常数或取 y0 的图形为折线时,应分段图乘再叠加。 ⑶ 如果图形比较复杂,则可将其分解为几个简单图形,分项图乘计算后
再进行叠加。
MP
A B C D
A2
b
A1
A B
A2
C
A3
D
a
A1
y2 l/3 l/3
M1
d
M
y1
y2
y3
c l/3
y1
y1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
将虚功原理用于实际协调位移和虚设平 衡力状态间已介绍过——单位荷载法。
下面从虚功方程入手,讨论杆系结构位 移计算的一般公式。杆系结构虚功方程为
δWe =Σ∫[pδu+qδv+mδθ]ds +Σ [FPxδu+FPyδv+Mδθ] i =Σ∫[FNδε+FQδγ+Mxδφ +Mδθ]ds = δWi
特点: 用几何法来解静力平衡问题。
2)虚功原理用于虚设的平衡力状态与实 际的协调位移状态之间。 例. 求 A 端支座发生竖向位移 c 时引起C点 的竖向位移 . 1
A
A
(b)
B C
c
A
(a)
B a
b
C
C
FA
解:首先构造出相应的虚设力状态。即, 在拟求位移之点(C点)沿拟求位移方向 (竖向)设置单位荷载。
(1)所建立的虚功方程,实质上是几何方程。
返回首页
(2)虚设的力状态与实际位移状态无关,故 可设单位广义力 P=1 (3)求解时关键一步是找出虚力状态的静力 平衡关系。
特点: 是用静力平衡法来解几何问题。 总的来讲,必须非常清楚的是:
单位位移法的虚功方程
单位荷载法的虚功方程
平衡方程
几何方程
3 单位荷载法 一、位移计算的一般公式
当变形体为杆件体系时,如:
C B
取任一单元 D
F
* Ni
q(s)
* FQj * FNj
A
M i* F i m(s) * Qi
j p(s)
M* j
δWe 的计算:
当无结点荷载时,δWe =Σ∫[pδu+qδv+mδθ]ds 当有结点荷载时 结点位移 δWe =Σ∫[pδu+qδv+mδθ]ds
+Σ [FPxδu+FPyδv+Mδθ] i 结点荷载
通常取
X 1 x
单位位移法(Unit-Displacement Method)
几点说明:
(1)对静定结构,这里实际用的是刚体虚 位移原理,实质上是实际受力状态的平衡 方程,即 M B 0 (2)虚位移与实际力状态无关,故可设 x
1
(3)求解时关键一步是找出虚位移状态的位 移关系。
(a)
B a
b
FP
C
解:去掉A端约束并代以反力 X,构造相 应的虚位移状态如图(b)、(c)
(b)
FP
X
(c)
直线
C
X
待分析平衡的力状态
虚设协调的位移状态
由外力虚功总和为零,即:
X X FP C 0 b X X FP X 0 a b X FP a
(2) 超静定、动力和稳定计算 (3)施工要求
返 首
三、 本章位移计算的假定
(1) 线弹性 (Linear Elastic), (2) 小变形 (Small Deformation), (3)理想联结 (Ideal Constraint)。
叠加原理适用(principle of superposition)
需要强调的几个问题
实际待分析的协调位移状态,虚设的平衡 力状态,将位移分析化为平衡问题来求解。
第一种应用一些文献称为“虚位移原理”, 而将第二种应用称为“虚力原理”。更确切 的说法为,两种应用的依据是上述两原理的 必要性命题。上述两原理都是充分、必要性 命题,它们和虚功原理是有区别的。
质点系是一个离散化体系,变形体是一个 连续体。我们认为,所谓将质点系虚位移原 → 理( Σf . → δri=0 )“应用于变形体”是不妥当 i 的。
δW =δWi
δWe =δWi
需要强调的几个问题
虚功原理里存在两个状态: 力状态必须满足平衡条件;位移状态必须满 足协调条件。因此原理仅是必要性命题。 原理的证明表明,原理适用于任何力学行 为(线性和非线性)的变形体,适用于任何结 构。 由于外力在变形虚位移上所作的功相对分 割面内力的虚变形功为高阶小量,因此许多 文献上称δWi为内力总虚功。 原理可有两种应用: 实际待分析的平衡力状态,虚设的协调位 移状态,将平衡问题化为几何问题来求解。
以上结论与材料物理性质及具体结构无关, 因此,虚功原理虚功方程既适用于一切线性结 构,也适用于一切非线性结构。
希望能很好理解,尽可能达到掌握!
三、虚功原理的两种应用
1)虚功原理用于虚设的协调位移状态与 实际的平衡力状态之间。 例. 求 A 端的支座反力(Reaction at Support)。
A
2 变形体虚功原理 (Principle of Virtual Work)
一、功(Work)、实功(Real Work)和虚功 (Virtual Work)
力状态 (虚力状态) 两种状态 位移状态 (虚位移状态)
FP q
FP /2
FP /2
无关
(虚)位移状态
(虚)力状态
注意: (1)属同一体系;或两状态中的变形体 系只要外形相同,而材料、截面尺寸及约 束可以不同。 (2)均为可能状态。即位移应满足变形 协调条件;力状态应满足平衡条件。 (3)位移状态与力状态完全无关;
δWi 的计算:
取微段,其受力如下
变形可看成有如下几部分
微段受力
微段拉伸
微段剪切
微段扭转
微段弯曲
对于直杆体系,由于变形互不耦连,所以
δWi =Σ∫[FNδε+FQδγ+Mxδφ+Mδθ]ds
杆系结构虚功方程
根据上述推证,可得杆系结构虚功方程如下
δWe =Σ∫[pδu+qδv+mδθ]ds +Σ [FPxδu+FPyδv+Mδθ] i =Σ3;Mδθ]ds = δWi
二、变形杆件的虚功原理
(1)质点系的虚位移原理 具有理想约束的质点系,在 某一位置处于平衡的必要和 充分条件是: 对于任何可能的虚位移, 作用于质点系的主动力所 F P2 做虚功之和为零。也即 →. → Σf δr =0
i i
FP1
FN1
m1 m2
FN 2
(2)刚体系的虚功原理
去掉约束而代以相应的 反力,该反力便可看成外 力。则有:刚体系处于平 衡的必要和充分条件是: 对于任何可能的虚 位移,作用于刚体系 的所有外力(主动力) 所做虚功之和为零。
由 M B 0 求得:
b FA a 虚功方程为:
b c a
1 FA c 0
这便是单位荷载法 (Dummy-Unit Load Method) 它是 Maxwell, 1864和Mohr, 1874提出, 故也称为Maxwell-Mohr Method 几点说明:
相对线位移
A
FP
A
y
C
C
C D
FP
D
D
x
相对角位移
线位移
线位移,角位移,相对线位移、角位移等统称广义位移
引起结构位移的原因
荷载、 温度改变 T、 制造误差 等 支座移动 c、
二、 计算位移的目的 (1) 刚度要求 如: 在工程上,吊车梁允许的挠度< 1/600 跨度; 高层建筑的最大位移< 1/1000 高度。 最大层间位移< 1/800 层高。 铁路工程技术规范规定: 桥梁在竖向活载下, 钢板桥梁和钢桁梁最大挠度 < 1/700 和1/900跨度
第三章 静定结构的位移计算
Displacement of Statically Determinate Structures
1. 2. 3. 4. 5. 6. 7.
弹性杆件的变形与变形能计算 变形体虚功原理 单位荷载法 图乘法 其他外因引起的位移计算 互等定理 结论与讨论
1 结构位移计算概述
一、结构的位移 (Displacement of Structures) 角位移
若结构有已知支座位移为ci ,与其对应 的由广义力 P 引起的支座反力为FRi 实际位移状态
B FP C
虚设的力状态
P B C
Bx ?
δε、δγ、δφ和 A δθ c
FN 、 FQ、 Mx和M
A
FR
则杆系结构虚功方程为 δWe =ΣFRi ci+PΔ =Σ∫[FNδε+FQδγ+Mxδφ +Mδθ]ds = δWi 虚功方程等式两边同除广义力 P ,并记 单位广义力(P/P=1)作用下,与之平衡的轴 力、剪力、扭矩和弯矩分别为FN 、 FQ、 Mx和M。单位广义力引起的,与已知位移 对应的反力为 FRi 。 位移计算的一般公式 则杆系结构虚功方程改写为 Δ =-ΣFRi ci+Σ∫[FNδε+FQδγ+Mxδφ +Mδθ]ds
设待求的实际广义位移为Δ ,与Δ对应 的广义力为P。 设仅在广义力P作用下,与之平衡的轴 力、剪力、扭矩和弯矩分别为FN 、 FQ、 Mx和M。 虚设的力状态 FP 实际位移状态 P
B C B C
Bx ?
A A
FN 、 FQ、 Mx和M
又设与内力FN 、 FQ、Mx和M对应的微 段实际变形分别为δε、δγ、δφ和δθ。
一些基本概念:
功:力×力方向位移之总和 广义力:功的表达式中,与广义位移对应的项 功:广义力×广义位移之总和 实功:广义力在自身所产生的位移上所作的功 虚功:广义力与广义位移无关时所作的功 变力功 W=FP1×Δ12 W=FP1×Δ11 /2 or W=FP2or 21 ×Δ W=FP2×Δ22 /2 W=FP×Δ/2
δ W = δ We
变形体虚功原理的证明
方案二:各部分外力不区分,虚位移区分 各部分的虚位移区分为:刚体虚位移和变 形虚位移两类。但必须注意,虚位移是光滑 连续的,可刚体和变形虚位移在分割面处一 般是不光滑、连续的。 变形体是平衡的,其各部分也必然平衡。 因此,各部分上的外力是平衡力系。 根据刚体虚位移原理,外力在刚体虚位移 上的总虚功等于零。因此各部分外力总虚功= 外力在变形虚位移上的总虚功 两方案计算同一内容,因此
