2019-2020年高三上学期期末数学文试题
2019-2020年高三上学期期末教学质量检测数学(文)试题 含答案

2019-2020年高三上学期期末教学质量检测数学(文)试题 含答案一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分. 1. 计算: . 2. 已知集合,,则 .3. 已知等差数列的首项为3,公差为4,则该数列的前项和 .4. 一个不透明袋中有10个不同颜色的同样大小的球,从中任意摸出2个,共有 种不同结果(用数值作答).5. 不等式的解集是 .6. 设8780178(1)x a a x a x a x -=++++,则0178||||||||a a a a ++++= .7. 已知圆锥底面的半径为1,侧面展开图是一个圆心角为的扇形,则该圆锥的侧面积是 .8. 已知角的顶点与直角坐标系的原点重合,始边在轴的正半轴上,终边在射线()上,则 .9. 已知两个向量,的夹角为,,为单位向量,,若,则 . 10. 已知两条直线的方程分别为:和:,则这两条直线的夹角大小为 (结果用反三角函数值表示).11. 若,是一二次方程的两根,则 .12. 直线经过点且点到直线的距离等于1,则直线的方程是 . 13. 已知实数、满足,则的取值范围是 .14. 一个无穷等比数列的首项为2,公比为负数,各项和为,则的取值范围是 .二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分. 15. 在下列幂函数中,是偶函数且在上是增函数的是( )A. B. C. D.16. 已知直线:与直线:,记3D k =A. 充分非必要条件C. 充要条件17. 则表示复数的点是( )18. A. 1个 B. 4个三、解答题(本大题满分74定区域内写出必要的步骤.19.(本题满分14分)本题共有2在锐角中,、、分别为内角、(1)求的大小;(2)若,的面积,求的值.B120.(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分.上海出租车的价格规定:起步费14元,可行3公里,3公里以后按每公里2.4元计算,可再行7公里;超过10公里按每公里3.6元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定.(1)小明乘出租车从学校到家,共8公里,请问他应付出租车费多少元?(本小题只需要回答最后结果)(2)求车费(元)与行车里程(公里)之间的函数关系式.21.(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.如图,正方体的棱长为2,点为面的对角线的中点.平面交与,于.(1)求异面直线与所成角的大小;(结果可用反三角函数值表示)(2)求三棱锥的体积.22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分.已知函数(其中).(1)判断函数的奇偶性,并说明理由;(2)求函数的反函数;(3)若两个函数与在闭区间上恒满足,则称函数与在闭区间上是分离的.试判断函数与在闭区间上是否分离?若分离,求出实数的取值范围;若不分离,请说明理由.23.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分7分.在数列中,已知,前项和为,且.(其中)(1)求;(2)求数列的通项公式;(3)设,问是否存在正整数、(其中),使得、、成等比数列?若存在,求出所有满足条件的数组;否则,说明理由.静安区xx第一学期期末教学质量检测高三年级数学(文科)试卷答案(试卷满分150分 考试时间120分钟) xx.12一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分. 1. 计算: . 解:.2. 已知集合,,则 . 解:.3. 已知等差数列的首项为3,公差为4,则该数列的前项和 . 解:.4. 一个不透明袋中有10个不同颜色的同样大小的球,从中任意摸出2个,共有 种不同结果(用数值作答). 解:45.5. 不等式的解集是 . 解:.6. 设8780178(1)x a a x a x a x -=++++,则0178||||||||a a a a ++++= .解:256.7. 已知圆锥底面的半径为1,侧面展开图是一个圆心角为的扇形,则该圆锥的侧面积是 . 解:.8. 已知角的顶点与直角坐标系的原点重合,始边在轴的正半轴上,终边在射线()上,则 . 解:.9. 已知两个向量,的夹角为,,为单位向量,,若,则 . 解:-2.10. 已知两条直线的方程分别为:和:,则这两条直线的夹角大小为 (结果用反三角函数值表示). 解:(或或).11. 若,是一二次方程的两根,则 . 解:-3.12. 直线经过点且点到直线的距离等于1,则直线的方程是 . 解:或.13. 已知实数、满足,则的取值范围是 . 解:.14. 一个无穷等比数列的首项为2,公比为负数,各项和为,则的取值范围是 . 解:.二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分. 15. 在下列幂函数中,是偶函数且在上是增函数的是( )A. B. C. D. 解:D.B 116. 已知直线:与直线:,记3D k =A. 充分非必要条件C. 充要条件解:B.17. 则表示复数的点是( )解:D.18. A. 1个 B. 4个解:C.三、解答题(本大题满分74定区域内写出必要的步骤.19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.在锐角中,、、分别为内角、、所对的边长,且满足. (1)求的大小;(2)若,的面积,求的值. 解:(1)由正弦定理:,得,∴ ,(4分) 又由为锐角,得.(6分)(2),又∵ ,∴ ,(8分)根据余弦定理:2222cos 7310b a c ac B =+-=+=,(12分) ∴ 222()216a c a c ac +=++=,从而.(14分)20.(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分.上海出租车的价格规定:起步费14元,可行3公里,3公里以后按每公里2.4元计算,可再行7公里;超过10公里按每公里3.6元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定.(1)小明乘出租车从学校到家,共8公里,请问他应付出租车费多少元?(本小题只需要回答最后结果)(2)求车费(元)与行车里程(公里)之间的函数关系式. 解:(1)他应付出出租车费26元.(4分)(2)14,03() 2.4 6.8,3103.6 5.2,10x f x x x x x <≤⎧⎪=+<≤⎨⎪->⎩ . 21.(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.如图,正方体的棱长为2,点为面的对角线的中点.平面交与,于.(1)求异面直线与所成角的大小;(结果可用反三角函数值表示)(2)求三棱锥的体积.解:(1)∵ 点为面的对角线的中点,且平面,∴ 为的中位线,得,又∵ ,∴ 22MN ND MD ===(2分) ∵ 在底面中,,,∴ ,又∵ ,为异面直线与所成角,(6分) 在中,为直角,,∴ .即异面直线与所成角的大小为.(8分) (2),(9分)1132P BMN V PM MN BN -=⋅⋅⋅⋅,(12分)22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分.已知函数(其中).(1)判断函数的奇偶性,并说明理由; (2)求函数的反函数;(3)若两个函数与在闭区间上恒满足,则称函数与在闭区间上是分离的.试判断函数与在闭区间上是否分离?若分离,求出实数的取值范围;若不分离,请说明理由. 解:(1)∵ ,∴ 函数的定义域为,(1分)又∵ ()()log )log )0a a f x f x x x +-=+=,∴ 函数是奇函数.(4分) (2)由,且当时,, 当时,,得的值域为实数集. 解得,.(8分)(3)在区间上恒成立,即, 即在区间上恒成立,(11分) 令,∵ ,∴ , 在上单调递增,∴ , 解得,∴ .(16分)23.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分7分.在数列中,已知,前项和为,且.(其中) (1)求;(2)求数列的通项公式; (3)设,问是否存在正整数、(其中),使得、、成等比数列?若存在,求出所有满足条件的数组;否则,说明理由. 解:(1)∵ ,令,得,∴ ,(3分)或者令,得,∴ .(2)当时,1111(1)()(1)22n n n n a a n a S ++++-+==,∴ 111(1)22n nn n n n a na a S S ++++=-=-,∴ , 推得,又∵ ,∴ ,∴ ,当时也成立,∴ ().(9分) (3)假设存在正整数、,使得、、成等比数列,则、、成等差数列,故(**)(11分) 由于右边大于,则,即, 考查数列的单调性,∵ ,∴ 数列为单调递减数列.(14分) 当时,,代入(**)式得,解得; 当时,(舍).综上得:满足条件的正整数组为.(16分)(说明:从不定方程以具体值代入求解也可参照上面步骤给分)温馨提示:最好仔细阅读后才下载使用,万分感谢!。
2019-2020年高三上学期期末考试数学(文)试题 含解析

2019-2020年高三上学期期末考试数学(文)试题 含解析注意事项:1、答卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上.2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上.3、不可以使用计算器.4、考试结束,将答题卡交回,试卷不用上交.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数113i z =-,21i z =-,则12z z +在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限2.设全集U 是实数集,R {}22,M x x =-≤≤,{}2430N x x x =-+>,则M N ⋂=( ) A .{|21}x x -≤< B .{|22}x x -≤≤ C .{|12}x x <≤D .{|2}x x <【答案】A 【解析】试题分析:{}{}{2430|(1)(3)03N x x x x x x x x =-+>=-->=>或}1x <, 则M N ⋂={|21}x x -≤<,故选A. 考点:1.一元二次不等式;2.集合的运算.3.已知平面向量()21=,a ,()2x =-,b ,若a ∥b ,则a+b 等于( ) A .()2,1--B .()2,1C .()3,1-D .()3,1-4.已知数列{}n a 为等差数列,若23a =,1612a a +=,则789a a a ++=( ) A .36B .42C .45D .635.在某次测量中得到的A 样本数据如下:82, 84, 84, 86, 86, 86, 88, 88, 88, 88.若B 样本数据恰好是A 样本数据都加2后所得数据,则A ,B 两样本的下列数字特征对应相同的是( ) A .众数B .平均数C .中位数D .标准差6.如图,设A 、B 两点在河的两岸,一测量者在A 的同侧所在的河岸边选定一点C ,测出AC 的距离为50m ,105,45=∠=∠CAB ACB 后,就可以计算出A 、B 两点的距离为( )A.m 2225B .m 225C .m 250D .m 3507.如图,定义某种运算a S b =⊗,运算原理如右图所示,则式子131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π的值为( )A .11B .13C .8D .4【答案】C 【解析】试题分析:根据算法程序框图可知该算法是一个分段函数(1),(1),a b a by a b a b +≥⎧=⎨-<⎩,根据新定义的运算故原式=131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π=2×(1+1)+2×(3-1)=8.故答案为C.考点:1.框图的运用;2.对数、三角函数运算.8.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则该棱柱的体积为( )A .123B .363C .273D .69.已知函数)(x f y =)(R x ∈满足(2)2()f x f x +=,且[1,1]x ∈-时,()1f x x =-+,则当(0,10]x ∈时,)(x f y =与4()log g x x =的图象的交点个数为( ) A .11B .10C .9D .8【答案】C10.对a ∀、b R ∈,运算“⊕”、“⊗”定义为:a b ⊕=,().()a a b b a b <⎧⎨≥⎩,a b ⊗=,().()a ab b a b ≥⎧⎨<⎩,则下列各式其中不恒成立的是( ) ⑴a b a b a b =+⊗+⊕ ⑵a b a b a b =-⊗-⊕ ⑶[][]a b a b a b =⋅⊗⋅⊕ ⑷[][]a b a b a b =÷⊗÷⊕ A .⑴、⑶B .⑵、⑷C .⑴、⑵、⑶D .⑴、⑵、⑶、⑷【答案】B 【解析】试题分析:由定义知若a b >,则a b b ⊕=,a b a ⊗=;所以a b a b a b ⊕+⊗=+;若a b <则a b a ⊕=,a b b ⊗=,所以a b a b a b ⊕+⊗=+;则⑴恒成立;若a b >,则a b b ⊕=,a b a ⊗=;所以[][]a b a b a b ⊕⊗=;若a b <则a b a ⊕=,a b b ⊗=,所以[][]a b a b a b ⊕⊗=;则⑶恒成立;若a b <则a b a ⊕=,a b b ⊗=,所以a b a b b a ⊗-⊕=-,[][]a b a b b a ⊗÷⊕=÷;则⑵⑷不恒成立; 故正确答案B.考点:新定义的一种运算性质.二、填空题(本大题共4小题,每小题5分,满分20分.) 11. 22cos 15sin 15-= .12.已知函数3log ,0()2,0x x x f x x >⎧=⎨≤⎩,则1(())9f f = .13.若变量,x y满足线性约束条件4325048010x yx yx+-≤⎧⎪-+≤⎨⎪-≥⎩,则2z x y=-的最大值为________.【答案】5【解析】试题分析:由约束条件4325048010x yx yx+-≤⎧⎪-+≤⎨⎪-≥⎩,得如下图所示的三角形区域,由8034425xx yy+-+==-⎧⎨⎩得(4,3)A直线2z x y=-过点(4,3)A时,z取得最大值为5.考点:线性规划.14.已知函数221,(20)()3,(0)ax x xf xax x⎧++-<≤=⎨->⎩有3个零点,则实数a的取值范围是.故答案为:3(,1)4.考点:1.函数零点的定义; 2.二次函数的性质应用.三、解答题( 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)15.(本题满分12分)设平面向量)sin ,(cos x x =,31(,)22b =,函数()1f x a b =⋅+. (Ⅰ)求函数)(x f 的值域和函数的单调递增区间; (Ⅱ)当9()5f α=,且263ππα<<时,求2sin(2)3πα+的值.(Ⅰ) 函数)(x f 的值域是[]0,2;………………………………………………(5分) 令πππππk x k 22322+≤+≤+-,解得52266k x k ππππ-+≤≤+………………(7分) 所以函数)(x f 的单调增区间为5[2,2]()66k k k Z ππππ-++∈.……………………(8分) (Ⅱ)由9()sin()1,35f παα=++=得4sin()35πα+=,因为2,63ππα<<所以,23ππαπ<+<得3cos()35πα+=-,………………………(10分)2sin(2+)sin 2()33ππαα=+ 432sin()cos()23355ππαα=++=-⨯⨯ 2425=-……………………………………………………………………(12分).考点:1.正弦函数的定义域和值域、正弦函数的单调性;2. 三角函数的恒等变换及化简求值;3.平面向量数量积的运算.16.(本题满分12分)某学校餐厅新推出A,B,C,D四款套餐,某一天四款套餐销售情况的条形图如下. 为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:满意一般不满意A套餐50% 25% 25%B套餐80% 0 20%C套餐50% 50% 0D套餐40% 20% 40%(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.【答案】(Ⅰ)0.1;(Ⅱ)5 6【解析】试题分析:(I)由条形图可得,选择A,B,C,D四款套餐的学生共有200人,其中选A款套餐的学生为40人,由分层抽样可得从A款套餐问卷中抽取的人数.17.(本题满分14分)如图所示,圆柱的高为27,AE、DF是圆柱的两条母线,过AD作圆柱的截面交下底面于BC, 四边形ABCD是正方形.;(Ⅰ)求证BC BE(Ⅱ)求四棱锥E-ABCD的体积.163【答案】(Ⅰ)详见解析;(Ⅱ【解析】⊥试题分析:(Ⅰ)根据AE是圆柱的母线,所以AE⊥下底面,又BC⊂下底面,则AE BC=∴BC⊥面ABE,又BE⊂面又截面ABCD是正方形,所以BC⊥AB,又AB AE AABE,即可得到BC⊥BE;18. (本小题满分14分)数列{n a }的前n 项和为n S ,2131(*)22n n S a n n n N +=--+∈. (I )设n n b a n =+,证明:数列{}n b 是等比数列;(II )求数列{}n nb 的前n 项和n T ;(Ⅲ)若12n n n c a ⎛⎫=- ⎪⎝⎭,22014211k k k k kc c P c c =++=+∑.求不超过P 的最大整数的值. 【答案】(Ⅰ)详见解析;(Ⅱ)222n n +-;(Ⅲ)2013. 【解析】考点:1.递推关系;2.等比数列的概念;3.数列求和.19.(本小题满分14分)已知函数()x f x e kx =-.(I )若0k >,且对于任意0)(,>∈x f R x 恒成立,试确定实数k 的取值范围;(II )设函数)()()(x f x f x F -+=,求证:1ln (1)ln (2)ln ()ln(2)()2n n F F F n e n N +*+++>+∈ 【答案】(I )0e k <<(Ⅱ)详见解析【解析】试题分析:(I )()f x 是偶函数,只需研究()0f x >对任意0x ≥成立即可,即当0x ≥时min ()0f x >由此可得,在[0)+∞,上,()(ln )ln f x f k k k k =-≥.依题意,ln 0k k k ->,又11e k k >∴<<,.综合①,②得,实数k 的取值范围是0e k <<. ……………………(7分)20.已知函数2()f x x x λλ=+,()ln g x x x λ=+,()()()h x f x g x =+,其中R λ∈,且0λ≠.⑴当1λ=-时,求函数()g x 的最大值; ⑵求函数()h x 的单调区间;⑶设函数(),0,()(),0.f x x xg x x ϕ≤⎧=⎨>⎩若对任意给定的非零实数x ,存在非零实数t (t x ≠),使得'()'()x t ϕϕ=成立,求实数λ的取值范围.【答案】⑴-1; ⑵详见解析; ⑶(,0)-∞【解析】试题分析:⑴令g ′(x )=0求出根1x =,判断g ′(x )在1x =左右两边的符号,得到g (x )在(0, 1)上单调递增,在(1, +)∞上单调递减,可知g (x )最大值为g (1),并求出最值;①当0x >时,∵'()x ϕ在(0,)+∞上是减函数,则在(0,)+∞上不存在实数t (t x ≠),使得'()'()x t ϕϕ=,则(,0)t ∈-∞,要在(,0)-∞上存在非零实数t (t x ≠),使得'()'()x t ϕϕ=成立,必定有A B ⊆,∴0λ<;②当0x <时,'()2x x ϕλλ=+在(,0)-∞时是单调函数,则(0,)t ∈+∞,要在(0,)+∞上存在非零实数t (t x ≠),使得'()'()x t ϕϕ=成立,必定有B A ⊆,∴0λ<.综上得,实数λ的取值范围为(,0)-∞. ……………(14分).考点:1.函数的最值、单调性;2.导数的应用.。
2019-2020年高三上学期数学文科期末考试试卷及答案

2019-2020年高三上学期数学文科期末考试试卷及答案本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120 分钟.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把答案涂在答题卡相应位置上......... 1.设全集U 是实数集,R 22{|4},{|1},1M x x N x x =>=≥- =N M I ( )A .{|21}x x -≤<B .{|22}x x -≤≤C .}32|{≤<x xD .{|2}x x < 2.下列结论正确的是( )A .当2lg 1lg ,10≥+≠>x x x x 时且B .21,0≥+>xx x 时当C .xx x 1,2+≥时当的最小值为2D .当(0,]2x π∈时,4()sin sin f x x x=+的最小值是4 3.已知正项数列{}n a 为等比数列,且4a 是22a 与33a 的等差中项,若22a =,则该数列的前5项的和为 ( )A .3312B .31C .314D .以上都不正确4.“a =3”是“直线ax -2y -1=0”与“直线6x -4y +c =0平行”的 ( )A .充分不必要条件B .必要不充分条件D .充要条件 D .既不充分也不必要条件5.若直线02=+-c y x 按向量)1,1(-=a 平移后与圆522=+y x 相切,则c 的值为( )A .8或-2B .6或-4C .4或-6D .2或-86.设双曲线)0,0(12222>>=-b a by a x 的离心率为3,且它的一条准线与抛物线x y 42=的准线重合,则此双曲线的方程为( )A .16322=-y x B .132322=-y xC .1964822=-y x D .1241222=-y x 7.设函数()sin()(0,0,||)2f x A x A πωϕωϕ=+≠><的图像关于直线23x π=对称,且它的最小正周期为π,则( )A .()f x 的图像经过点1(0,)2B .()f x 在区间52[,]123ππ上是减函数 C .()f x 的图像的一个对称中心是5(,0)12πD .()f x 的最大值为A8.已知||1,||3,0OA OB OA OB ==⋅=u u u r u u u r u u u r u u u r ,点C 在AOB ∠内, 且AOC ∠=30°,设 (),OC mOA nOB m n R =+∈u u u r u u u r u u u r ,则m n等于( )A .13B .3C .33D .39.如图所示,在棱长为1的正方体ABCD -A 1B 1C 1D 1中, E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一 点,且A 1G=λ(0≤λ≤1)则点G 到平面D 1EF 的距离 为 ( ) A .3B .2C .23λD .5510.设函数y=f (x )存在反函数y =1()f x -,且函数()y x f x =-的图象过点(1,2),则函数1()y f x x -=-的图象一定过点( )A .(-1,2)B .(2,0)C .(1,2)D .(2,1)11.直三棱柱111ABC A B C -中,若90BAC ∠=︒,1AB AC AA ==,则异面直线1BA 与1AC所成的角等于( )A .30°B .45°C .60°D .90°12.若x bx ax x f 2011)(20122010++=满足2)2011(='f ,则=-')2011(f( )A .-2010B .4020C .2011D .0第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.请把答案直接填写在答题卡相应位置上.13.若tan θ=2,则2sin 2θ-3sin θcos θ= .14. 设x ,y 满足约束条件24,1,20,x y x y x +≤⎧⎪-≤⎨⎪+≥⎩,则目标函数z =3x -y 的最大值为 .15.若直线20kx y --=21(1)||1y x --=-有两个不同的交点,则实数k 的取值范围是______________.16.若球O 的球面上共有三点A 、B 、C ,其中任意两点间的球面距离都等于大圆周长的1,6经过A 、B 、C 这三点的小圆周长为3π,则球O 的体积为 .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)已知向量2(3sin ,1),(cos ,cos )444x x xm n ==u r r .(1)若1m n ⋅=u r r ,求2cos()3x π-的值;(2)记x f ⋅=)(,在△ABC 中,角C B A ,,的对边分别是c b a ,,且满足C b B c a cos cos )2(=-,求函数f (A )的取值范围.18.(本小题满分12分)已知三棱柱111ABC A B C -的侧棱垂直于底面,90BAC ∠=o,12AB AA ==,B 1C 1A 1M1AC =,M ,N 分别是11A B ,BC 的中点.(1)证明:1AB AC ⊥;(2)证明:MN ∥平面11ACC A ; (3)求二面角M AN B --的余弦值.19.(本小题满分12分)已知圆C :224x y +=.(1)直线l 过点()1,2P ,且与圆C 交于A 、B 两点,若||AB =l 的方程; (2)过圆C 上一动点M 作平行于x 轴的直线m ,设m 与y 轴的交点为N ,若向量OQ OM ON =+u u u r u u u u r u u u r,求动点Q 的轨迹方程. 20.(本小题满分12分)设函数f (x )=x 3+ax 2-9x -1 (a <0),若曲线y=f (x )的斜率最小的切线与直线12x+y=6平行.(1)求a 的值;(2)求函数f (x )的单调区间.m21.(本小题满分12分)设数列{}n a 的前n 项和为,n S 已知11,a =142n n S a +=+.(1)设12n n n b a a +=-,证明:数列{}n b 是等比数列; (2)求数列{}n a 的通项公式;(3)若2(32)nn n c a n =+,n T 为{}n c 的前n 项和,求证:n T 23<.22.(本小题满分12分)已知椭圆C 1的方程为1422=+y x ,双曲线C 2的左、右焦点分别为C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点. (1)求双曲线C 2的方程; (2)若直线2:+=kx y l 与椭圆C 1及双曲线C 2都恒有两个不同的交点,且l 与C 2的两个交点A 和B 满足6<⋅OB OA (其中O 为原点),求k 的取值范围.参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把答案涂在答.题卡相应位置上....... 1 2 3 4 5 6 7 8 9 10 11 12 C B B B A A C B D A C B 二、填空题:本大题共4小题,每小题5分,共20分.请把答案直接填写在答题卡相应位置上. 13.5214.5, 15. 442,,233⎡⎫⎛⎤--⎪ ⎢⎥⎣⎭⎝⎦U 16. 288π 三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)已知向量2(3sin ,1),(cos ,cos )444x x xm n ==u r r .(1)若1m n ⋅=u r r ,求2cos()3x π-的值;(2)记n m x f ⋅=)(,在△ABC 中,角C B A ,,的对边分别是c b a ,,且满足C b B c a cos cos )2(=-,求函数f (A )的取值范围.解:(1)23sin cos cos 444x x x m n ⋅⋅+u r r 1sin()262x π=++∵1m n ⋅=u r r ∴1sin()262x π+=211cos()12sin ()23262x x ππ+=-+= 21cos()cos()332x x ππ-=-+=- ............5分 (2)∵(2a-c )cosB=bcosC由正弦定理得(2sinA-sinC)cosB=sinBcosC 2sinAcosB-sinCcosB=sinBcosC ∴2sinAcosB=sin(B+C) ∵A B C π++= ∴sin()sin 0B C A +=≠,∴1cos ,23B B π== ∴203A π<<∴1,sin()(,1)6262262A A ππππ<+<+∈........10分18.解法一:(Ⅰ)证明:因为1CC ⊥平面ABC ,所以AC 是1AC 在平面ABC 内的射影,…… 2 分 由条件可知AB ⊥AC ,所以1AB AC ⊥. ………………… 4 分 (Ⅱ)证明:设 AC 的中点为D , 连接DN ,1A D .因为D ,N 分别是AC ,BC 的中点, 所以DN //=12AB . 又1A M =1211A B ,11A B //=AB , 所以1A M //=DN . 所以四边形1A DNM 是平行四边形. 所以1A D ∥MN . …………………6 分因为1A D ⊂平面11ACC A ,MN ⊄平面11ACC A , 所以MN ∥平面11ACC A . …………… 8 分 (Ⅲ)如图,设AB 的中点为H ,连接MH , 所以MH ∥1BB . 因为1BB ⊥底面ABC , 所以MH ⊥底面ABC .在平面ABC 内,过点H 做HG ⊥AN ,垂足为G . 连接MG ,则MG ⊥AN .所以∠MGH 是二面角M AN B --的平面角. ……… 10 分 因为MH =1BB =2,由AGH ∆∽BAC ∆,得HG =5. DABB 1CC 1A 1 MNHG所以MG =22MH HG +=215. 所以cos MGH ∠=HG MG =2121. 二面角M AN B --的余弦值是2121. ………………… 12 分 解法二:依条件可知AB ,AC ,1AA 两两垂直. 如图,以点A 为原点建立空间直角坐标 系A xyz -.根据条件容易求出如下各点坐标:(0,0,0)A ,(0,2,0)B ,(1,0,0)C -,1(0,0,2)A ,1(0,2,2)B ,1(1,0,2)C -,(0,1,2)M ,1(,1,0)2N -.(Ⅰ)证明:因为(0,2,0)AB =u u u r,1(1,0,2)AC =-u u u u r,所以1AB AC ⋅=u u u r u u u u r0(1)20020⨯-+⨯+⨯=. …………… 2 分 所以1AB AC ⊥u u u r u u u u r .即1AB AC ⊥. ………………… 4 分(Ⅱ)证明:因为1(,0,2)2MN =--u u u u r ,(0,2,0)AB =u u u r 是平面11ACC A 的一个法向量,且MN AB ⋅=u u u u r u u u r 10022002-⨯+⨯-⨯=,所以MN AB ⊥u u u u r u u u r . ……………6 分又MN ⊄平面11ACC A ,所以MN ∥平面11ACC A . ………………… 8 分 (Ⅲ)设(,,)x y z =n 是平面AMN 的法向量,因为(0,1,2)AM =u u u u r ,1(,1,0)2AN =-u u u r ,A BB 1CC 1A 1MNxyz由=0,=0,AMAN⎧⋅⎪⎨⋅⎪⎩u u u u ru u u rnn得020,10.2y zx y++=⎧⎪⎨-+=⎪⎩解得平面AMN的一个法向量(4,2,1)=-n.由已知,平面ABC的一个法向量为(0,0,1)=-m.………………… 10 分设二面角M AN B--的大小为θ,则cos||||θ⋅=n mn m=211⨯=21.二面角M AN B--的余弦值是2121.………………… 12 分19.解(Ⅰ)①当直线l垂直于x轴时,则此时直线方程为1=x,l与圆的两个交点坐标为()3,1和()3,1-,其距离为32,满足题意………2分20.解(1)'()f x=3x2+2ax-9 …………………………………2分.3-9-)('42axfax取得最小值时,当-=因为斜率最小的切线与直线12x+y=6平行,即该切线的斜率为-12,所以9,123922=-=--a a 即 ,a =±3 又a <0, 所以a =-3……………………………6分 (2) 由(1)知a =-3,f(x)=x 3-3x 2-9x -1'()f x =3x 2-6x-9=3(x -3)(x +1)令'()f x =,解之得x 1=-1, x 2=3当x ∈(-∞,-1)时, '()f x >0, '()f x 在(-∞,-1)是增函数; 当x ∈(-1,3)时, '()f x <0, '()f x 在(-1,3)是减函数; 当x ∈(3,+∞)时, '()f x >0 , '()f x 在(3,+∞)是增函数;所以函数f(x)的单调递增区间为 (-∞,-1)和(3,+∞);单调递减区间为(-1,3). …………………………………12分 21.解:(I )由11,a =及142n n S a +=+,有12142,a a a +=+21121325,23a a b a a =+=∴=-=由142n n S a +=+,...① 则当2n ≥时,有142n n S a -=+.....② ②-①得111144,22(2)n n n n n n n a a a a a a a +-+-=-∴-=- 又12n n n b a a +=-Q ,12n n b b -∴={}n b ∴是首项13b =,公比为2的等比数列.…….4分(II )由(I )可得11232n n n n b a a -+=-=⋅,113224n n n n a a ++∴-= ∴数列{}2n n a 是首项为12,公差为34的等差数列. ∴1331(1)22444n na n n =+-=-,2(31)2n n a n -=-⋅ …….8分 (Ⅲ) 4(31)(32)n c n n =-+所以n T =111111141124(...)()32558313132313n n n ⋅-+-++-=-<-++ ………12分22.解:(Ⅰ)设双曲线C 2的方程为12222=-by ax ,则.1,31422222==+=-=b c b a a 得再由故C 2的方程为.1322=-y x ……………………………………………6分(II )将.0428)41(1422222=+++=++=kx x k y x kx y 得代入 由直线l 与椭圆C 1恒有两个不同的交点得,0)14(16)41(16)28(22221>-=+-=∆k k k即 .412>k ① 0926)31(1322222=---=-+=kx x k y x kx y 得代入将. 由直线l 与双曲线C 2恒有两个不同的交点A ,B 得.131.0)1(36)31(36)26(,0312222222<≠⎪⎩⎪⎨⎧>-=-+-=∆≠-k k k k k k 且即 )2)(2(,66319,3126),,(),,(22+++=+<+<⋅--=⋅-=+B A B A B A B A B A B A B A B A B B A A kx kx x x y y x x y y x x k x x k k x x y x B y x A 而得由则设 .1373231262319)1(2)(2)1(222222-+=+-⋅+--⋅+=++++=k k k k k k k x x k x x k B A B A .0131315,613732222>--<-+k k k k 即于是解此不等式得 .31151322<>k k 或 ③ 由①、②、③得.11513314122<<<<k k 或 故k 的取值范围为)1,1513()33,21()21,33()1513,1(Y Y Y ----………12分。
2019-2020年高三上学期期末考试数学(文)含答案

2019-2020年高三上学期期末考试数学(文)含答案2014.01本试卷共5页,分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试时间120分钟.第I 卷(选择题 共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再改涂其它答案标号.一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合()(){}{}2340,log 1,A x R x x B x R x A B =∈+-≤=∈≥⋂=则 A.[)2,4B.[]2,4C.()4,+∞D.[)4,+∞2.直线12,l l 平行的一个充分条件是 A.12,l l 都平行于同一个平面 B.12,l l 与同一个平面所成的角相等 C.12l l 平行与所在的平面D.12,l l 都垂直于同一个平面3.若(),0ln ,0x e x g x g x x ⎧≤=⎨>⎩,则(g (12))= A.ln 2-B.1C.12D.24.已知实数2,a ,8构成一个等比数列,则圆锥曲线221x y a+=的离心率为A.2B.2D.25.等差数列{}n a 满足1234345661525=a a a a a a a a S +++=+++=,,则 A.12B.30C.40D.256.已知不等式组51,0x y x y y +≤⎧⎪-≥⎨⎪≥⎩则目标函数2z y x =-的最大值是A.1B.1-C.5-D.47. 函数[]sin y x x ππ=-在,上的图象是8.M 是抛物线24y x =上一点,且在x 轴上方,F 是抛物线的焦点,若直线FM 的倾斜角为60,则FM = A.2B.3C.4D.69.某三棱锥的三视图如图所示,则该三棱锥的体积是 A.83B.4C.2D.4310.已知()()()1f x x x x m =--,满足()()01f f ''=,则函数()f x 的图象在点()(),m f m 处的切线方程为 A.2810x y +-= B.2810x y --= C.2810x y -+=D.2810x y ++=11.函数()()sin f x A x ωϕ=+(0,2A πϕ><其中)的部分图象如图所示,为了得到函数()cos2g x x =的图象,则只需将()f x 的图象A.向右平移6π个长度单位 B.向右平移12π个长度单位C.向左平移6π个长度单位D.向左平移12π个长度单位12.已知定义在R 上的函数()f x ,满足()()()(),3f x f x f x f x -=--=,当30,2x ⎛⎫∈ ⎪⎝⎭时,()()2ln 1f x x x =-+,则函数()f x 在区间[]0,6上的零点个数是A.3B.5C.7D.9第II 卷(非选择题 共90分)注意事项:1.将第II 卷答案用0.5mm 的黑色签字笔答在答题纸的相应位置上.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共4小题,每小题4分,共16分. 13.已知向量()()1,1,2,,a b a b λλ==⊥且则的值为__▲__.14.以双曲线221916x y -=的左焦点为圆心,并与其渐近线相切的圆的标准方程是__▲__. 15.已知()35cos ,sin 0051322ππαββαβ⎛⎫⎛⎫-==-∈∈- ⎪ ⎪⎝⎭⎝⎭,且,,,,则sin α=_▲_. 16.观察下列等式:()2331212+=+, ()2333123123,++=++()2333312341234+++=+++,… … … … … …根据以上规律,3333333312345678+++++++=___▲___.(结果用具体数字作答) 三、解答题:本大题共6小题,共74分.解答应写文字说明,证明过程或演算步骤.17.(本小题满分12分)已知等比数列{}13232423,2,n a a a a a a a +=+满足且是的等差中项. (I )求数列{}n a 的通项公式;(II )若212l ,,n n n n n n b a og a S b b b S =+=++⋅⋅⋅+求.18.(本小题满分12分)已知函数()223sin cos 2cos ,f x x x x x R =-∈.(I )求函数()f x 的最小正周期和最小值;(II )ABC ∆中,A,B,C 的对边分别为a,b,c ,已知()3,1,sin 2sin c f C B A ===,求a,b 的值.19.(本小题满分12分)如图,在四棱锥P-ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA PD ⊥,底面ABCD 是直角梯形,其中BC//AD ,90,3,BAD AD BC O ∠==是AD 上一点.(I )若AD=3OD ,求证:CD//平面PBO ; (II )求证:平面PAB ⊥平面PCD.20.(本小题满分12分)如图,两个工厂A,B (视为两个点)相距2km ,现要在以A,B 为焦点,长轴长为4km 的椭圆上某一点P 处建一幢办公楼.据测算此办公楼受工厂A 的“噪音影响度”与距离AP 成反比,办公楼受工厂B 的“噪音影响度”与距离BP 也成反比,且比例系数都为1.办公楼受A ,B 两厂的“总噪音影响度”y 是受A,B 两厂“噪音影响度”的和,设AP=.xkm(I )求“总噪音影响度”y 关于x 的函数关系式; (II )当AP 为多少时,“总噪音影响度”最小?21.(本小题满分13分)已知椭圆()222210x y C a b a b+=>>:的离心率为3,且经过点A (0,1-).(I )求椭圆的方程;(II )若过点30,5⎛⎫ ⎪⎝⎭的直线与椭圆交于M,N 两点(M,N 点与A 点不重合), 求证:以MN 为直径的圆恒过A 点;22.(本小题满分13分) 已知函数()()(),ln ,af x xg x f x x a R x=+=+∈. (I )当a=2时,求函数()g x 的单调区间; (II )当()()()()21002a h x g x x x b R b h x b==--∈≠时,记且,求在定义域内的极值点; (III )[)()()12121221,1,ln ln x x x x f x f x x x ∀∈+∞<-<-且,都有成立,求实数a 的取值范围.。
2019-2020年高三上学期期末考试 数学文试题 含答案
2019-2020年高三上学期期末考试数学文试题含答案一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知集合,集合,则=A. B. C. D.2.为了得到函数的图象,可以把函数的图象上所有的点A. 向右平行移动2个单位长度Array B.向右平行移动个单位长度C. 向左平行移动2个单位长度D. 向左平行移动个单位长度3. 执行如图所示的程序框图,输出的值为A. 6B. 24C.D.4.已知函数则是成立的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 若实数满足,则的最小值为A. B. C. D.6. 已知,且,则等于A. B. C. D.7. 若双曲线:与抛物线的准线交于两点,且,则的值是A. B. C. D.8. 函数的图象为曲线,函数的图象为曲线,过轴上的动点作垂直于轴的直线分别交曲线,于两点,则线段长度的最大值为A.2 B.4 C.5 D.第二部分(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9.已知数列为等差数列,若,,则公差 .10.已知三棱锥的三视图如图所示,则该三棱锥的体积是 ;表面积是 .11. 某校为了解高一学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在小时内的人数为_____.12.直线:被圆截得的弦的长是 .13.在△中, ,,则 ;的最小值是 . 14.用一个平面去截正方体,有可能截得的是以下平面图形中的 .(写出满足条件的图形序号) (1)正三角形 (2)梯形 (3)直角三角形 (4)矩形三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本题满分13分)已知函数. (Ⅰ)求的值;(Ⅱ)求函数的最小正周期及单调递增区间. 16. (本题满分13分)俯视图侧视图正视图甲、乙两名同学参加“汉字听写大赛”选拔性测试.在相同的测试条件下,两人5次测试的成绩(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算); (Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,求抽到的两个成绩中至少有一个高于90分的概率.17. (本题满分14分)如图,在三棱锥中,平面平面,,.设,分别为,中点. (Ⅰ)求证:∥平面; (Ⅱ)求证:平面;(Ⅲ)试问在线段上是否存在点,使得过三点 ,,的平面内的任一条直线都与平面平行?若存在,指出点的位置并证明;若不存在,请说明理由.18.(本题满分13分)已知函数,其中.(Ⅰ)若,求的值,并求此时曲线在点处的切线方程; (Ⅱ)求函数在区间上的最小值. 19.(本题满分14分)已知椭圆两焦点坐标分别为,,一个顶点为. (Ⅰ)求椭圆的标准方程;(Ⅱ)是否存在斜率为的直线,使直线与椭圆交于不同的两点,满足. 若存在,求出的取值范围;若不存在,说明理由. 20. (本题满分13分)已知数列的通项,. (Ⅰ)求;(Ⅱ)判断数列的增减性,并说明理由; (Ⅲ) 设,求数列的最大项和最小项.DEBAPC北京市朝阳区xx 学年度高三年级第一学期期末统一考试数学答案(文史类) xx.1二、填空题:三、解答题: 15.解:(Ⅰ)依题意.则. ………….7分(Ⅱ)的最小正周期.当时,即时,为增函数.则函数的单调增区间为,. ………….13分16 . 解:(Ⅰ)茎叶图如右图所示,由图可知,乙的平均成绩大于甲的平均成绩,且乙的方差小于甲的方差,因此应选派乙参赛更好. ……….6分(Ⅱ)设事件:抽到的成绩中至少有一个高于90分.从甲、乙两人5次的成绩中各随机抽取一个成绩,所有的基本事件如下:{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}58,65,58,82,58,87,58,85,58,95,55,65,55,82,55,87,55,85,55,95,76,65,76,82,76,87,76,85,76,95,88,65,88,82,88,87,88,85,88,95,92,65,92,82,92,87,92,85,92,95,共25个.事件包含的基本事件有{}{}{}{}{}{}{}{}{}58,95,55,95,76,95,88,95,92,65,92,82,92,87,92,85,92,95共9个.所以,即抽到的成绩中至少有一个高于90分的概率为. ……….13分 17. 证明:(Ⅰ)因为点是中点,点为的中点,所以∥.8 7 5 6 9826 甲 乙5 57 2 58 5又因为面,面,所以∥平面. ………….4分 (Ⅱ)因为平面面, 平面平面=,又平面,,所以面.所以. 又因为,且,所以面. ……….9分(Ⅲ)当点是线段中点时,过点,,的平面内的任一条直线都与平面平行. 取中点,连,连. 由(Ⅰ)可知∥平面. 因为点是中点,点为的中点, 所以∥.又因为平面,平面, 所以∥平面. 又因为, 所以平面∥平面,所以平面内的任一条直线都与平面平行.故当点是线段中点时,过点,,所在平面内的任一条直线都与平面平行. ……….14分 18. 解:(Ⅰ)已知函数,所以,, 又,所以. 又,所以曲线在点处的切线方程为. ………….…..…5分 (Ⅱ), 令,则.(1)当时,在上恒成立,所以函数在区间上单调递增,所以;(2)当时,在区间上,,在区间上,,所以函数在区间上单调递减,在区间上单调递增,且是上唯一极值点,所以;(3)当时,在区间上,(仅有当时),所以 在区间上单调递减 所以函数.综上所述,当时,函数的最小值为,时,函数的最小值为 ………………13分19.解:(Ⅰ)设椭圆方程为.则依题意 ,,所以于是椭圆的方程为 ……….4分DEAP CF(Ⅱ)存在这样的直线. 依题意,直线的斜率存在设直线的方程为,则 由得因为得……………… ① 设,线段中点为,则 于是因为,所以.若,则直线过原点,,不合题意. 若,由得,,整理得………………② 由①②知,, 所以又,所以. ……….14分 20.(Ⅰ),. ……….2分(Ⅱ)11(0.5)0.9(0.5)0.9n nn n a a n n ++-=+⋅--⋅.则当时,,则时,数列为递增数列,;当时,,数列为递减数列,. ……….7分 (Ⅲ)由上问可得,,.令,即求数列的最大项和最小项. 则.则数列在时递减,此时,即; 数列在 时递减,此时,即.因此数列的最大项为,最小项为. ……….….13分。
2019-2020年高三上学期期末考试数学文含答案

2019-2020年高三上学期期末考试数学文含答案xx .1本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,第I 卷1—2页,第II 卷3—4页,共150分,测试时间l20分钟.注意事项:选择题为四选一题目,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上.第I 卷(共60分)一、选择题:本大题共l2小题,每小题5分,共60分.把正确答案涂在答题卡上.1.若复数满足 (为虚数单位),则的共轭复数为A .B .C .D .2.已知集合M={},集合N={},则MN 为A .(-2,3)B .(-3,-2]C .[-2,2)D .(-3,3]3.已知a ,b ,c ,d 为实数,且c>d ,则“a>b ”是“a+c>b +d”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[l04,l06].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是A .90B .75C .60D .455.函数的零点所在的区间为A .(-2,-l)B .(-1,0)C .(0,1)D .(1,2)6.某算法的程序框图如图所示,如果输出的结果是26,则判断框内应为A .K>1B .K>2C .K>3D .K>47.函数y=sin2x 的图象向右平移个单位,得到的图象关于直线对称,则的最小值为A .B .C .D .8.已知平行四边形ABCD 中,AC 为一条对角线,若=(2,4),=(1,3),则=A .8B .6C .6D .89.设、是两个不重合的平面,m 、m 是两条不重合的直线,则以下结论错误..的是 A .若,则B .若,,//,//m n m n ααββ⊂⊂,则C .若,则D .若,则10.函数的图象的大致形状是11.已知双曲线C 1:22221(00)y x a b a b-=>>,的离心率为2,若抛物线C 2:的焦点到双曲线C 1的渐近线的距离是2,则抛物线C 2的方程是A .B .C .D .12.没函数在(0,+)内有定义,对于给定的正数K ,定义函数,取函数,恒有,则A .K 的最大值为B .K 的最小值为C .K 的最大值为2D .K 的最小值为2第Ⅱ卷(共90分)填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.13.设满足约束条件360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩,若,则实数的取值范围为 .14.某几何体的三视图(单位:cm)如下图,则这个几何体的表面积为 cm 2.15.已知圆的方程为.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为 .16.下列四个命题:①; ②23(0,),log log x x x ∃∈+∞<;③121(0,),()log 2x x x ∀∈+∞>;④. 其中正确命题的序号是 .三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.17.(本题满分l2分).某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人,将这l6人的数学成绩编成茎叶图,如图所示.(I)茎叶图中有一个数据污损不清(用△表示),若甲班抽出来的同学平均成绩为l22分,试推算这个污损的数据是多少?(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍,请将所有可能的结果列举出来,并求选出的两位同学不在同一个班的概率.18.(本题满分l2分)已知a ,b ,c 分别为ABC 的三个内角A ,B ,C 的对边, m =(sinA ,1),n =(cosA ,),且m //n .(I)求角A 的大小;(II)若a=2,b=2,求ABC 的面积.19.(本题满分l2分)如图,PA 平面ABCD ,四边形ABCD 为矩形,PA=AB=,AD=1,点F 是PB 的中点,点E 在边BC 上移动.(I)求三棱锥E —PAD 的体积;(II)试问当点E 在BC 的何处时,有EF//平面PAC ;(1lI)证明:无论点E 在边BC 的何处,都有PEAF .20.(本题满分l2分)已知数列{}中,a 1=1,前n 项和.(I)求a 2,a 3以及{}的通项公式;(II)设,求数列{}的前n 项和T n .21.(本题满分l3分)设函数2()(0)f x ax bx c a =++≠,曲线通过点(0,2a+3),且在处的切线垂直于y 轴.(I)用a 分别表示b 和c ;(II)当bc 取得最大值时,写出的解析式;(III)在(II)的条件下,若函数g(x ) 为偶函数,且当时, ,求当时g(x )的表达式,并求函数g(x )在R 上的最小值及相应的x 值.22.(本题满分l3分)给定椭圆C :,若椭圆C 的一个焦点为F(,0),其短轴上的一个端点到F 的距离为.(I)求椭圆C的方程;(II)已知斜率为k(k≠0)的直线l与椭圆C交于不同的两点A,B,点Q满足且=0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.。
2019-2020年高三上学期期末考试(数学文)

2019-2020年高三上学期期末考试(数学文)一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后括号内. 1.设集合=,=,则等于( )A .B .C .D . 2.“是偶数”是“与都是偶数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.函数的反函数是( )A .B .C .D .4.在中,,,,则的值是( )A .B .C .D . 5.不等式的解集是( )A .B .C .D .6.在各项都为正数的等比数列中,首项 ,前三项和为,则=( )A .B .C .D .7.设函数⎩⎨⎧>≤++=)0(2)0(24)(2x x x x x f ,则关于的方程的解的个数为( )A .B .C .D .8.计算机中常用的十六进制是逢进的记数制,采用数字和字母共个记数符号.这些符号与十进制的数的对应关系如下表:例如,用十六进制表示:,则( ) A .B .C .D .二、填空题:本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.9.对总数为的一批零件抽取一个容量为的样本,若每个零件被抽取的概率为,则的值是 .10.从名男生和名女生中选出人参加某个座谈会,若这人中必须既有男生又有女生,则不同的选法种数共有.(用数字作答)11.点按向量平移后的对应点的坐标是,则.12.已知的展开式中各项系数的和是,则;展开式中的系数是.(用数字作答)13.在半径为的球面上有、、三点,,,,则球心到平面的距离为.14.设函数的图象与直线,及轴所围成图形的面积称为函数在上的面积,已知函数在[0,]上的面积为(n∈N*),则(1)函数在[0,]上的面积为;(2)函数在[,]上的面积为.三、解答题:本大题共6个小题,共80分.解答题应写出文字说明,证明过程或演算步骤.15.(本题满分12分)在中,角、、的对边分别为、、,.(Ⅰ)求的值;(Ⅱ)若,且,求的长.16.(本题满分12分)已知函数的图象过点,且在处的切线斜率为.(Ⅰ)求函数的解析式;(Ⅱ)求函数的单调区间.17.(本题满分14分)如图,在三棱锥中,面面,是正三角形,,.(Ⅰ)求证:;A(Ⅱ)求二面角的大小;(Ⅲ)求异面直线与所成角的大小.18.(本题满分14分)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的;如果种子没有发芽,则称该次实验是失败的.(Ⅰ)第一小组做了三次实验,求至少两次实验成功的概率;(Ⅱ)第二小组进行试验,到成功了次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率.19.(本题满分14分)已知等差数列中,公差,其前项和为,且满足:,.(Ⅰ)求数列的通项公式;(Ⅱ)通过公式构造一个新的数列.若也是等差数列,求非零常数;(Ⅲ)求()的最大值.20.(本题满分14分)设(、为常数),方程的两个实数根为、,且满足,.(Ⅰ)求证:;(Ⅱ)设,比较与的大小.石景山区xx第一学期期末考试试卷高三数学(文科)参考答案一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只二、填空题:本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.注:第12、14题第1个空3分,第2个空2分.三、解答题:本大题共6个小题,共80分.解答题应写出文字说明,证明过程或演算步骤. 15.(本题满分12分) 解:(Ⅰ)∵ , ∴ . 又∵ , 解得 . ……………………3分 ∵ ,∴ 是锐角.∴ . ……………………6分 (Ⅱ)∵ ,∴ . 解得 . …………………8分 又∵ , ∴ .∴ 36cos 2222=-+=C ab b a c .∴ . ………………………12分16.(本题满分12分)解:(Ⅰ). ………………………2分由题意知,解得 . ………………5分∴ . ……………………6分(Ⅱ).令,即 .解得 . ………………………8分当0)(,21,21>'+>-<x f x x 时或;当0)(,2121<'+<<-x f x 时. ……………………10分∴ 的单调递增区间为:和,的单调递减区间为: . ……………12分17.(本题满分14分) 解法一:(Ⅰ)证明:∵ 面⊥面,,且面面,∴ 面. ……………2分 又∵ 面,∴ . ………………4分(Ⅱ)解:如图,过点作⊥于,连结. 由(Ⅰ)知面.∴ 是斜线在平面内的射影,∴ .(三垂线定理)∴ 是二面角的平面角. …………………6分 设,由,得,.∵ 是正三角形, ∴ . ∴ . ∴ . ∴二面角的大小为. …………………9分 (Ⅲ)解:如图,取三边、、的中点、、,连结、、、、, 则,;,.∴ 是异面直线与所成的角或其补角. ………………11分 ∵ 是正三角形,且平面平面, ∴ 面,是直角三角形,. 又∵ 面,故2222==+=ON AC DC AD .在中,,,.∴ 4321cos ==∠MN MOOMN . ∴ 异面直线和所成角为. ……………14分解法二:(Ⅰ)分别取、的中点、,连结、. ∵ 是正三角形,CBD∴ .∵ 面⊥面,且面面, ∴ 平面.∵ 是的中位线,且平面, ∴ 平面.以点为原点,所在直线为轴,所在直线为轴,所在直线为轴,建立空间 直角坐标系. ……………2分 设, 则,, , ,. ∴ ,. ……………………4分∴ 00)23(0)23(10=⨯-+⨯-+⨯=⋅CD AB .∴ ,即 . …………………6分(Ⅱ)∵ 平面,∴ 平面的法向量为. ……………………7分 设平面的法向量为, ∴ ,. ∴ 0)23()23(0=⨯-+⨯-+⨯=⋅z y x AB n ,即 . 0)23(231=⨯-+⨯+⨯=⋅z y x AD n ,即 . ∴ 令,则,.∴ . ……………………9分∴ 13133001)1()3()3(0)1(0313222222-=++⋅-++-⨯-+⨯+⨯-=. ∵ 二面角是锐角,∴ 二面角的大小为. ………………11分 (Ⅲ)∵ ,,∴AC BD >=<,cos 43)23()23(00)3(1)23(023301222222=-++⋅++-⨯+⨯+⨯=. ∴ 异面直线和所成角为. ……………14分y18.(本题满分14分)解:(Ⅰ)第一小组做了三次实验,至少两次实验成功的概率为277)31()311()31()(333223=⋅+-⋅⋅=C C A P . ……………………7分 (Ⅱ)第二小组在第次成功前,共进行了次试验,其中三次成功三次失败,且恰有两次连续失败,其各种可能的情况种数为.因此所求的概率为7293231)32()31(12)(33=⨯⨯⨯=B P . …………………14分 19.(本题满分14分)解:(Ⅰ)∵ 数列是等差数列,∴ .又 ,∴ ,或. ……………2分∵ 公差,∴ ,.∴ ,.∴ 34)1(1-=-+=n d n a a n . …………4分(Ⅱ)∵ n n n n n d n n na S n -=-+=-+=212)1(2)1(21, ∴ . ………………6分∵ 数列是等差数列,∴ .∴ cn n n c n n n c n n n +++-+++-=+++-+⋅)2()2()2(22)1()1()1(22222. 去分母,比较系数,得 . ……………9分∴ n n n n b n 22122=--=. ………………10分 (Ⅲ)2625125262++=++=nn n n n ≤. ……………12分 当且仅当,即时,取得最大值. ……………14分20.(本题满分14分)解:(Ⅰ)由,得 .∴ , . ………2分∴ 212212214)()(x x x x x x -+=-.∵ ,∴ .∴ ,即 . ……6分(Ⅱ))(1212c bx x c bt t ++-++=)())((111x t b x t x t -+-+=. ……………10分由,知.又∵ ,∴ ,011212<-+<-+x x x t . ∴ .∴ .………………14分注:若有其它解法,请酌情给分..。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
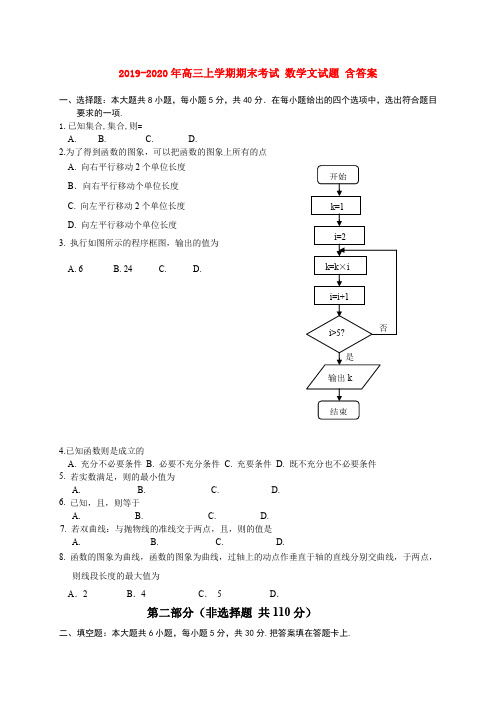
2019-2020年高三上学期期末数学文试题一、选择题(本大题共10小题,每小题5分,共50分;在每个小题列出的四个选项中,选出符合题目要求的一项). 1.设集合},02|{2R x x x x A ∈≤-=,}21,|{2≤≤--==x x y y B ,则A ∩B 等于( ) A . R B .}0,|{≠∈x R x x C . {0} D .φ 2.命题“,xx e x ∀∈>R ”的否定是( )A .,x x e x ∃∈<RB .,x x e x ∀∈<RC .,x x e x ∀∈≤RD .,xx e x ∃∈≤R 3.“m <14”是“一元二次方程x 2+x +m =0有实数解”的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.如果a ,b ,c 满足c <b <a 且ac <0,那么下列选项中不一定成立.....的是( ) A .ab >ac B .c (b -a )>0 C .ac (a -c )<0 D .cb 2<ab 25.若向量)1,1(),2,1(-==b a,且b a k +与b a -共线,则实数k 的值为( )A .1-B .1C .2D . 06.设{}n a 是公差为正数的等差数列,若12318a a a ++=,123120a a a =,则=++432a a a ( )A .18B .12C .30D .24 7.已知在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若,2cos2cosB b Aa =,222ab b a c -+=则△ABC 的形状是( )A .钝角三角形B .等边三角形C .直角三角形D .等腰直角三角形8.把函数cos y x x =-的图象向左平移m (m >0)个单位后,所得的图象关于y 轴对称,则m 的最小值是( )25A B C D 6336ππππ.... 9.已知()f x 为偶函数,且),4()(x f x f -=当02≤≤-x 时,xx f 3)(=,则=)2011(f ( )A .13 B . 3 C .3- D . 13- 10.定义方程()()f x f x '=的实数根0x 叫做函数()f x 的“新驻点”,如果函数()g x x =,()ln(1)h x x =+,()cos x x ϕ=(()x π∈π2,)的“新驻点”分别为α,β,γ,那么α, β,γ的大小关系是( )A .γβα<<B .βγα<<C .βαγ<<D .γαβ<<第Ⅱ卷 (非选择题 共100分)二、填空题(本大题共4小题,每小题5分,共20分).11.在等比数列{}n a 中,0>n a 且965=a a ,则=+9323log log a a __________. 12.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a=2,b=2,sinB+cosB=0,则角A 的大小为_____________.13.若点(1,0)在关于,x y 的不等式组0240331ax y b ax by bx y a +-≥⎧⎪--≤⎨⎪≥-+⎩所表示的平面区域内,则12b a -+的最小值为 .14. 在ABC ∆中,O 为中线AM 上一个动点,若AM=2,则)(OC OB OA +⋅的最小值是________.三、解答题(本大题共6小题,共80分;解答应写出文字说明,证明过程或演算步骤). 15.(本小题满分12分)设命题:p 函数3()()2x f x a =-是R 上的减函数,命题:q 函数2()43f x x x =-+在[]4,a 上递增.若“p 且q ”为假命题,“p 或q ”为真命题,求a 的取值范围.16.(本小题满分12分)设△ABC 三个角A ,B ,C 的对边分别为,,,c b a 若acA B 32tan tan 1=+. (1)求角B 的大小;(2)若)tan cos sin ,1(),cos ,(cos B A A n B A m -==,求⋅的取值范围.17.(本小题满分14分)已知函数22()log (23)f x ax x a =+-,(1)当1a =-时,求该函数的定义域和值域;(2)当.0≤a 时.,如果()f x ≥1在∈x [2,3]上恒成立,求实数a 的取值范围.18.(本小题满分14分)如图,2012年春节,摄影爱好者S 在某公园A 处,发现正前方B 处有一立柱,测得立柱顶端O 的仰角和立柱底部B 的俯角均为30︒,已知S(将眼睛距地面的距离按米处理)(1) 求摄影者到立柱的水平距离和立柱的高度;(2) 立柱的顶端有一长2米的彩杆MN 绕中点O 在S 与立柱所在的平面内旋转.摄影者有一视角范围为60︒的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.19.(本小题满分14分)设函数2113()424f x x x =+-,对于正数数列{}n a ,其前n 项和为n S ,且()n n S f a =,()n N *∈. (1)求数列{}n a 的通项公式;(2)是否存在等比数列{}n b ,使得2)12(212211+-=++++n b a b a b a n n n 对一切正整数n 都成立?若存在,请求出数列{}n b 的通项公式;若不存在,请说明理由.20.(本小题满分14分)已知函数2,ln )(,,0,,)2()(2=+=⎩⎨⎧≤>-=x b x c x g x bx x e ax x x f x 且是函数)(x f y =的极值点.(1)当0>x 时,求函数()f x 的单调区间;(2)若函数y =()f x m -有两个零点,求实数m b ,满足的条件;(3)直线l 是函数)(x f y =与函数)(x g y = 的图象在0x 处的公切线,若[]4,20∈x ,求cb的取值范围.汕头市金山中学2012~2013学年度第一学期期末考试高三文科数学 参考答案一、选择题(50分)题号 12 3 4 5 6 7 8 9 10 答案 CD ADACBCAD二、填空题(20分)11. 2 12. 30° 13. 23- 14. -2 三、解答题(80分)15. (本小题满分12分)解:由3012a <-<得3522a <<…2分2()(2)1f x x =--,在[]4,a 上递增,得42<≤a ……4分 p 且q 为假,p 或q 为真, ∴p 、q 一真一假. ……6分若p 真q 假得, 322a << , 若p 假q 真得,425<≤a . ……10分综上所得,a 的取值范围是322a <<或425<≤a . ……12分16、(本小题满分12分) 解 :(1)由acA B 32tan tan 1=+得 A C A A B B sin 3sin 2sin cos cos sin 1=+即A C A B C sin 3sin 2sin cos sin =),0(,π∈C A ,0sin ,0sin ≠≠∴A C23cos =∴B ……3分 ),0(π∈B得6π=B . …… 5分(2)由(1)知6π=B ,∴)cos 33sin ,1(),23,(cos A A A -==, ……6分 于是 )cos 33(sin 23cos A A A n m -+=⋅=A A sin 23cos 21+=)6sin(π+A . ……10分ππππ<+<∴<<66,650A A ∴1)6sin(21≤+<πA ,即121≤⋅<n m. …12分 17、(本小题满分14分)解:(1) 当1a =-时,22()log (23)f x x x =-++令2230x x -++>,解得13x -<<所以函数()f x 的定义域为(1,3)-. 3分 令2223(1)4t x x x =-++=--+,则04t <≤ 所以22()log log 42f x t =≤=因此函数()f x 的值域为(,2]-∞ 6分(2) 解法一:()1f x ≥在区间[2,3]上恒成立等价于22320ax x a +--≥在区间[2,3]上恒成立 ……7分 令2()232g x ax x a =+--当0a =时,()220g x x =-≥,所以0a =满足题意. 8分 当0<a 时,()g x 是二次函数,对称轴为1x a=-, 当205a -≤<时, 152a -≥,min ()(2)20g x g a ==+≥,解得2a ≥- 10分当25a <-时,1502a <-<,min ()(3)640g x g a ==+≥,解得23a ≥- 12分综上,a 的取值范围是⎥⎦⎤⎢⎣⎡-0,32 14分 解法二:()1f x ≥在区间[2,3]上恒成立等价于22320ax x a +--≥在区间[2,3]上恒成立由22320ax x a +--≥且[2,3]x ∈时,230x ->,得2223x a x -≥- 9分令222()3xh x x -=-,则222246()0(3)x x h x x -+'=>- 12分 所以()h x 在区间[2,3]上是增函数,所以max 2()(3)3h x h ==-因此a 的取值范围是⎥⎦⎤⎢⎣⎡-0,32. 14分18、(本小题满分14分)解:(1) 如图,不妨将摄影者眼部设为S 点,做SC 垂直OB 于C ,,60,30=∠=∠ASB CSB 又,3=SA 故在SAB Rt ∆中,可求得BA =3,即摄影者到立柱的水平距离为3米……… 3分由SC =3,,30=∠CSO 在SCO Rt ∆中,可求得,3=OC又,3==SA BC 故,32=OB 即立柱高为32米. ------------------------ 6分(2) (注:若直接写当SO MN ⊥时,MSN ∠最大,并且此时60<∠MSN ,得2分) 连结SM ,SN , 在△SON 和△SOM 中分别用余弦定理,13221)32(13221)32(222222⋅⋅-+-=⋅⋅-+a b 2622=+∴b a ……10分211311221122cos 22222>=+≥=-+=∠b a ab ab b a MSN60<∠∴MSN 故摄影者可以将彩杆全部摄入画面. ………………………………………………… 14分19、(本小题满分14分)解:(1)由2113()424f x x x =+-,()n n S f a = ,()n N *∈ 得2113424n n n S a a =+- ()n N *∈ ①2111113424n n n S a a +++=+- , ②即 221111111()422n n n n n n n a S S a a a a ++++=-=-+-,即 221111()()042n n n n a a a a ++--+= ,即 11()(2)0n n n n a a a a +++--= ……4分∵n a >0,∴12n n a a +-= ,即数列{}n a 是公差为2的等差数列,由①得,21111113424S a a a ==+-,解得13a = ……6分 因此 ,数列{}n a 的通项公式为21n a n =+. ……7分(2)假设存在等比数列{}n b ,使得对一切正整数n 都有111222(21)2n n n a b a b a b n ++++=-+ ③当2n ≥时,有1122112(23)2n n n a b a b a b n --+++=-+ ④③-④,得 2(21)n n n a b n =+,由21n a n =+得,2nn b = ……12分 又11162(211)a b ==⨯+满足条件, ……13分因此,存在等比数列{}2n ,使得111222(21)2n n n a b a b a b n ++++=-+对一切正整数n 都成立. ……14分 20、(本小题满分14分) 解:(1)20,()(2)x x f x x ax e >=-时, 22()(22)(2)[2(1)2]x x x f x x a e x ax e x a x a e '∴=-+-=+--.……1分由已知得,0,f=220,a ∴+-=解得a =1. ……2分∴x x e x x f e x x x f )2()(',)2()(22-=∴-=.当x ∈时,()0f x '<,当)x ∈+∞时,()0f x '>. ……3分 当0>x 时,()f x的递增区间为)+∞,递减区间为. ……4分 (2)由(1)知,当x ∈时,)(x f单调递减,()((2f x ∈-当)x ∈+∞时,)(x f单调递增,()((2)f x ∈-+∞. ……6分 要使函数y =()f x m -有两个零点,则函数)(x f y =的图象与直线m y =有两个不同的交点. ①当0>b 时,m=0或(2m = ……7分 ②当b=0时,((2m ∈-; ……8分 ③当0,((2)b m <∈-+∞时.……9分(3) 0>x 时,xxe x xf e x x x f )2()(',)2()(22-=∴-=0)2()(0200x e x x x f -=∴,0)2()(200/x e x x f -= 00)()2(:302020x x e x x x e x y l -+-=∴x cx g b x c x g =∴+=)(,ln )(/0/00)(,ln )(x cx g b x c x g =∴+=∴c b x c x x cy l -++=∴00ln :⎪⎩⎪⎨⎧-+=-=-∴cb xc e x x x c e x x x 03020020ln )()2(00两式相除得00203020ln 2x c cb xc x x x -+=--,整理得 020200ln 12x x x x c b -+--= …12分22000203040/)2(428)(---+--=x x x x x x c b令428)(02030400--+--=x x x x x h 则21634)(020300/-+--=x x x x h 23)4(420200----=x x x[]0)(,4,20/0<∴∈x h x)(0x h ∴在[]4,2递减 0)2()(=≤h x h 0)(/≤∴c b 仅在20=x 取等号, c b∴在[]4,2递减⎥⎦⎤⎢⎣⎡--∈∴2ln ,4ln 71c b ……14分。
