时间序列分析作业
我国人口出生率、死亡率和自然增长率数据入下表所示:

《应用时间序列分析》实验作业3班级:姓名:学号:习题5.5.4我国人口出生率、死亡率和自然增长率数据入下表所示:年份出生率死亡率自然增长率1980 18.21 6.34 11.87 1981 20.91 6.36 14.55 1982 22.28 6.6 15.68 1983 20.19 6.9 13.29 1984 19.9 6.82 13.08 1985 21.04 6.78 14.26 1986 22.43 6.86 15.57 1987 23.33 6.72 16.61 1988 22.37 6.64 15.73 1989 21.58 6.54 15.04 1990 21.06 6.67 14.39 1991 19.68 6.7 12.98 1992 18.24 6.64 11.61993 18.09 6.64 11.45 1994 17.7 6.49 11.21 1995 17.12 6.57 10.55 1996 16.98 6.56 10.42 1997 16.57 6.51 10.06 1998 15.64 6.5 9.14 年份出生率死亡率自然增长率1999 14.64 6.46 8.182000 14.03 6.45 7.582001 13.38 6.43 6.952002 12.86 6.41 6.452003 12.41 6.4 6.012004 12.29 6.42 5.872005 12.4 6.51 5.892006 12.09 6.81 5.282007 12.1 6.93 5.172008 12.14 7.06 5.082009 11.95 7.08 4.872010 11.9 7.11 4.792011 11.93 7.14 4.792012 12.1 7.15 4.952013 12.08 7.16 4.922014 12.37 7.16 5.212015 12.07 7.11 4.962016 12.95 7.09 5.862017 12.45 7.11 5.32(1)分析我国人口出生率、死亡率和自然增长率序列的平稳性。
统计学课后作业答案

f Me L
Mo L
2
S m1 fm
80 - 23.2 i 425 2 25 438.33公斤 = 31.5
1 31.5 10.7 i 425 25 437.53公斤 右偏 = 1 2 41.5
《描述统计》作业
STAT
[习题集P23第9题]某车间有两个小组,每组都是7人,每人日产 量数如下:第一组:20、40、60、70、80、100、120;第二组: 67、68、69、70、71、72、73。已知两组工人每人平均日产量件 数为70件,试计算:(1)R;(2)A.D;(3)S.D,并比较哪 个组的平均数代表性大? 解:(1)R1=120-20=100(件);R2=6(件)。 (2) x x 180 x x 12 A.D1 =25.71 A.D2 = 1.71 n 7 n 7
4000吨 1300 1400 500 7200
460 3000 420 1200 =421 / 吨 元 f 计 3000 1200 xf实 460 4000 420 1300 平均价格:x实 =426.25 / 吨 元 f 实 4000 1300 平均价格:x计
《描述统计》作业
资料整理,导出收获率(亩产量):
STAT
甲品种 播种面积 f 收获率 x 1. 2 亩 1000 斤/亩 1. 1 950 1. 0 1100 0. 9 900 0.8 1050 5.0 999
乙品种 播种面积 f 收获率 x 1. 5 亩 1120 斤/亩 1.3 1000 1. 3 900 1. 0 1220 0.9 700 6.0 1000
2071 172 .58 173 (台) 12
基于大数据的学生学习行为分析的方式

医学影像住院医师规范化培训体系的构建与影像教学改革的研究住院医师培训是临床医师必经的重要阶段,同时也是医学生成长为合格医师的有效途径,医学界对住院医师培养给予了高度重视。
随着现代医学影像设备的不断更新与完善,医学影像学涉及的内容复杂多样,为住院医师的学习增加了一定的难度[1]。
在影像教学过程中必须注重临床思维与影响知识的结合,培养学生的医学影像学基础知识与业务技能,因此,对医学影像住院医师规范化培训体系的构建与影像教学改革研究有着重要的实践意义与应用价值。
1 医学影像住院医师规范化培训体系的构建近年来,规范化培训在医学影像住院医师技能培训中得到了广泛的应用,其作为一种新型临床技能培训方法,坚持以自学为主、教师引导的原则,能够增强住院医师独立解决问题的能力,与此同时能够帮助住院医师充分利用网络资源进行自学,提高临床综合应用能力,满足影像学工作的需要,研究将从培训内容、培训方法以及培训效果评估三个方面对该培训体系进行阐述。
1.1 培训内容医学影像住院医师规范化培训体系结合学生的认知特点以及临床工作要求,遵循常见病到罕见症、简单病到复杂病、疑难病的特?c,共包括三个阶段。
第一个阶段1年,主要是对基础知识的讲解,培养住院医师对简单病、常见病以及多发病的诊断能力,使住院医师对基础疾病形成正确的认识。
第二个阶段2年,加强住院医师对常见病、多发病的深入认识,并能够对部分疑难病进行初步诊断[2]。
由于住院医师学习能力与学习进度的不同,对于学习能力强,掌握必备业务技能的住院医师,可提前进行第三个阶段的培训。
第三阶段2年,在该阶段中,住院医师深入到临床工作中,对日常临床事务进行处理,实现理论知识向实践能力的转化,其诊断报告需要由上级医师审核,在实践中提升业务技能。
1.2 培训方法对医学影像住院医师的培训主要包括以下几个方面:(1)日常工作培训。
日常工作培训主要针对的是第一、第二阶段。
在临床诊断过程中,要求住院医师参与其中,对病例的影像学特征进行观察与描述,并作出具体的分析,能够结合病例的临床表现,对患者进行鉴别诊断、诊断以及进一步检查等,在这一过程中,上级医师要做好跟踪,对住院医师的诊断结果进行修正、补充,使住院医师掌握基本的影像学技能;(2)晨间读片会培训。
时间序列分析ch3习题解答12-16

1 1 , 1 ,根据 ARMA(1,1) 模型 Green 函数的递推公式得: 4 2
G0 1 , G1 1G0 1 0.5 0.25 12 , Gk 1Gk 1 1k 1G1 1k 1 , k 2
0 1
2 E (12 )
Cov( yt , yt k ) Cov( yt , yt k )
k k
ˆt (k 1) y ˆt 1 (k ) y
解: (1)成立
(2)成立
(3)成立
(4)不成立。
16. 对于 AR(1)模型: xt 1 ( xt 1 ) t ,根据 t 个历史观
E ( xt )
0 3 12 。 1 1 2 1 1 0.25
14. 证明 ARMA(1,1)序列
xt 0.5xt 1 t 0.25 t 1 ,
t ~ WN (0, 2 ) 的自相关系数为:
1, k 0 k 0.27, k 1 0.5 , k 2 k 1
j 0
G0 1 , G1 1G0 1 0.6 0.3 0.3 , Gk 1Gk 1 1k 1G1 0.3 0.6k 1 , k 2
所以该模型可以等价表示为: xt t
0.3 0.6
k k 0
t k 1
。
13. 某 ARMA(2,2)模型为: ( B) xt 3 ( B) t ,求 E ( xt ) 。其中
时间序列分析00 3.5 习 题 12. 已知 ARMA(1,1)模型为: xt 0.6 xt 1 t 0.3 t 1 ,确定该模 型的 Green 函数,使该模型可以等价表示为无穷 MA 阶模型形式。 解:由模型,知: 1 0.6,1 0.3 Green 函数为:
时间序列作业VAR模型教学内容

一、案例分析的目的按国际货币基金组织的划分口径可以把货币供给划分为:M0 (现钞):是指流通于银行体系以外的现钞,即居民手中的现钞和企业单位的备用金,不包括商业银行的库存现金。
M1 (狭义货币):M0加上商业银行活期存款构成。
M2 (广义货币):由M1加上准货币构成。
准货币由银行的定期存款、储蓄存款、外币存款以及各种短期信用工具如银行承兑汇票、短期国库券等构成。
我国参照国际货币基金组织的划分口径,把货币供给层次划分如下:M0 =现金M1 =M0 +活期存款M2 = M1+城乡居民储蓄存款+定期存款+其他存款M3=M2+商业票据+大额可转让定期存单在这三个层次中,M0的流动性最强,M1次之,M2的流动性最差。
M0与消费变动密切相关,是最活跃的货币;M1反映居民和企业资金松紧变化,是经济周期波动的先行指标,流动性仅次于M0;M2流动性偏弱,但反映的是社会总需求的变化和未来通货膨胀的压力状况,通常所说的货币供应量,主要指M2。
1. M1反映着经济中的现实购买力;M2不仅反映现实的购买力,还反映潜在的购买力。
若M1增速较快,则消费和终端市场活跃;若M2增速较快,则投资和中间市场活跃。
中央银行和各商业银行可以据此判定货币政策。
M2过高而M1过低,表明投资过热、需求不旺,有危机风险;M1过高M2过低,表明需求强劲、投资不足,有涨价风险。
2. M1增加表示货币市场流通性增强,M2中包括了M1,因此,再排除M1变化因素后,M2的增减代表了储蓄的增加,货币流通性降低。
根据央行的数据,2009年9月份货币供应,M2余额58.5万亿,同比增长29.3%,比上年末加快11.5个百分点。
M1余额20.2万亿元,增长29.5%,加快20.5个百分点。
9月末M1与M2的同比与环比增速双双创出了新高。
与此同时,M1的同比增速已经超越了M2的同比增速,这意味着整个经济领域的活跃度已被有效激活,储蓄开始活期化。
本案例主要研究M1的数量与M2的数量关系。
时间序列分析作业

习题2.21975-1980年夏威夷岛莫那罗亚火山每月释放的co2数据如下330.45 330.97 331.64 332.87 333.61 333.55331.90 330.05 328.58 328.31 329.41 330.63331.63 332.46 333.36 334.45 334.82 334.32333.05 330.87 329.24 328.87 330.18 331.50332.81 333.23 334.55 335.82 336.44 335.99334.65 332.41 331.32 330.73 332.05 333.53334.66 335.07 336.33 337.39 337.65 337.57336.25 334.39 332.44 332.25 333.59 334.76335.89 336.44 337.63 338.54 339.06 338.95337.41 335.71 333.68 333.69 335.05 336.53337.81 338.16 339.88 340.57 341.19 340.87339.25 337.19 335.49 336.63 337.74 338.36程序如下:(1)绘制该序列时序图,并判断该序列是否平稳。
co2328329330331332333334335336337338339340341342time01JAN7501JUL7501JAN7601JUL7601JAN7701JUL7701JAN7801JUL7801JAN7901JUL7901JAN8001JUL8001JAN81时序图清晰地显示释放的co2的数量以月为周期呈现出规则的周期性,除此之外,还有明显的逐个周期递增的趋势。
显然该序列不是平稳序列。
(2) 计算该序列的样本自相关系数 由样本自相关图可知,序列自相关系数如下:1ˆ0.90751ρ=2ˆ0.72171ρ=3ˆ0.51252ρ=4ˆ0.34982ρ=5ˆ0.24690ρ=6ˆ0.20309ρ= 7ˆ0.21021ρ=8ˆ0.26429ρ=9ˆ0.36433ρ=10ˆ0.48472ρ=11ˆ0.58456ρ=12ˆ0.60198ρ= 13ˆ0.51841ρ=14ˆ0.36856ρ=15ˆ0.20671ρ=16ˆ0.08138ρ=17ˆ0.00135ρ=18ˆ0.03248ρ=-19ˆ0.02710ρ=-20ˆ0.01124ρ=21ˆ0.08275ρ=22ˆ0.17011ρ=23ˆ0.24320ρ= 24ˆ0.25252ρ= (3) 绘制该样本自相关图,并解释该图形。
第13章 时间序列分析和预测作业

计算该上店2000年上半年平均每月销售计划的完成程度
4.某工厂2000年下半年各月末工人数及其比重资料如下
月份
月末工人数 (人)
6
550
7
580
8
560
9
565
10
600
11
590
12
590
工人占全部 职工比%
80.0
86.0
81.0
80.0
90.0Biblioteka 87.085.0计算该工厂2000年下半年工人占全部职工人数的平均比重
3 354
4 311
5 280
6 290
10 330
12 368
1999年末定额流动资金为320万元。 根据上表资料分别计算该企业定额流动资金上半年平均占有额
下半年平均占有额和全年平均占有额。
3.某国有商店2000年上半年各月销售计划及其计划完成程度 如下 月份 计划销售额 (万元) 计划完成程度 (%) 1 45.0 104.0 2 40.0 98.0 3 46.0 95.0 4 50.0 102.0 5 55.0 106.0 6 60.0 101.0
时 间 数 列 作业
计算分析题
1.某自行车车库4月1日有自行车320辆,4月6日调出70辆, 4月18日进货120辆,4月26日调出80辆,直至月末再未 发生变动问该库4月份平均库存自行车多少辆?
2.某企业2000年定额流动资金占有的统计资料如下
月份 月末定额流动 资金(万元 )
1 298
2 300
预测第12年的粮食生产水平。
6.某地区年粮食总产量如下表 年份 1 2 3 4 5 产量(万吨) 230 236 241 246 252 年份 6 7 8 9 10 产量(万吨) 257 262 276 281 286
时间序列练习题

时间序列练习题时间序列分析是一种用于研究以时间为顺序的数据变动规律的方法。
它可以帮助我们理解和预测未来的趋势,对于决策和规划具有重要的意义。
本文将通过一些时间序列练习题,帮助读者更好地理解和应用时间序列分析。
练习题一:季度销售数据分析某公司的销售数据按照季度记录如下:季度销售额Q1 100Q2 200Q3 300Q4 400请你根据这些数据,进行以下的分析和预测:1. 绘制季度销售额的时间序列图。
2. 计算季度销售额的平均值。
3. 判断季度销售额是否存在趋势性,并进行趋势线的拟合。
4. 判断季度销售额是否存在季节性,如果存在,请进行季节性分解。
5. 使用你认为最适合的模型进行未来一年季度销售额的预测,并给出预测结果。
练习题二:月度股票收益率分析某股票连续12个月的收益率数据如下:月份收益率1 0.032 0.053 -0.024 0.025 -0.016 0.047 -0.038 0.019 0.0210 -0.0511 0.0112 0.03请你根据这些数据,进行以下的分析和预测:1. 绘制月度股票收益率的时间序列图。
2. 计算月度收益率的平均值和标准差。
3. 判断股票收益率是否存在趋势性,并进行趋势线的拟合。
4. 判断股票收益率是否存在季节性,如果存在,请进行季节性分解。
5. 使用你认为最适合的模型进行未来三个月股票收益率的预测,并给出预测结果。
练习题三:年度气温分析某城市过去10年(2011年至2020年)的年度平均气温数据如下:年份平均气温(摄氏度)2011 192012 212013 202014 182015 172016 182017 202018 222019 232020 21请你根据这些数据,进行以下的分析和预测:1. 绘制年度平均气温的时间序列图。
2. 计算年度平均气温的平均值、中位数和极差。
3. 判断气温是否存在趋势性,并进行趋势线的拟合。
4. 判断气温是否存在季节性,如果存在,请进行季节性分解。
时间序列分析范文

时间序列分析范文
时间序列分析是利用统计学和计算机技术来研究和预测未来时期观测
到的系列观测值的趋势,它是一种重要的风险管理工具,主要用于金融信
息的预测、量化投资、金融市场的异动检测以及过去的趋势推测和预测。
时间序列分析可以帮助企业和个人快速、准确地了解过去的行业动态,预
测未来的发展趋势。
时间序列分析的基本概念可以分为三个层次,宏观部分,定义有关系
统的趋势和变化的综述;微观部分,关注各种因素与变量之间的关系;趋
势部分,注重系统的演化过程,考虑未来变化的方向,可以通过回归模型
等方法来进行实证研究。
ARIMA模型是建立在自回归模型和移动平均模型之上的,自回归模型
可以用来描述和预测时间序列中残差序列的趋势,移动平均模型可以用来
描述和预测时间序列中的反复性,ARIMA模型集合了以上两种模型的优点,使其成为预测时间序列最常用的模型。
ARIMA模型可以在任何时期预测,如短期预测,如一个月内预测,中
期预测,如一年内预测,长期预测。
时间序列作业试题及答案

第六章动态数列-、判斷题若将某地区社会商品库存额按时间先后顺序排列,此种动态数二、1.列属于时期数列。
()定基发展速度反映了现象在一定时期内发展的总速度,环比发三、2.展速度反映了现象比前一期的增长程度。
()平均增长速度不是根据各期环比增长速度直接求得的,而是根四、3.据平均发展速度计算的。
()•用水平法计算的平均发展速度只取决于最初发展水平和最末发五、4展水平,与中间各期发展水平无关。
()平均发展速度是环比发展速度的平均数,也是一种序时平均六、5.数。
()1> X 2、X 3、J 4、V 5. Vo七、单项选择题•根据时期数列计算序时平均数应采用()。
八、1几何平均法 B.加权算术平均法C.简单九、 A.算术平均法 D.首末折半法十、2•下列数列中哪一个属于动态数列()。
十-、 A.学生按学习成绩分组形成的数列 B.工业企业按地区分组形成的数列十二、 C.职工按工资水平高低排列形成的数列 D.出口额按时间先后顺序排列形成的数列十三、3.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为()。
十四、心(190+195+193+201)4B.190+195 + 1933十五.(190/2)+195+193 + (201/2) 、[190/2)+195+193+(201/2)C・D・ ---------------------------------4-1 44.说明现象在较长时期内发展的总速度的指标是()。
A、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度5•已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计算方法为()。
A.(102%X105%X108%X107%) -100%B.102%X105%X108%X107%C.2%X5%X8%X7%D.(2%X5%X8%X7%) -100%6•定基增长速度与环比增长速度的关系是()。
时间序列作业
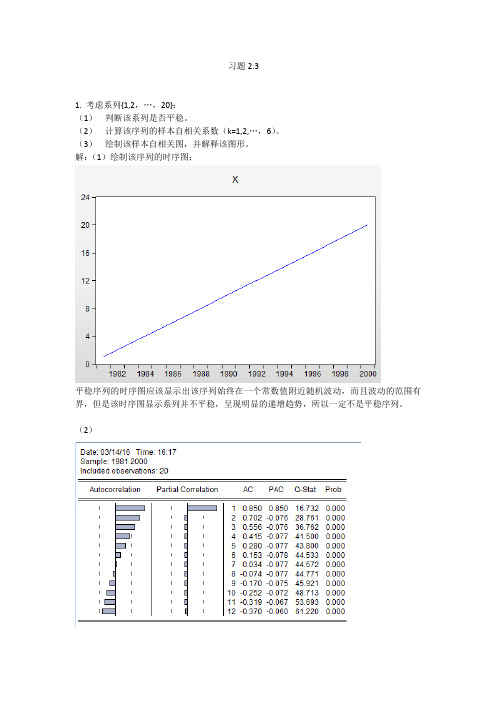
习题2.31. 考虑系列{1,2,…,20}:(1)判断该系列是否平稳。
(2)计算该序列的样本自相关系数(k=1,2,…,6)。
(3)绘制该样本自相关图,并解释该图形。
解:(1)绘制该序列的时序图;平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界,但是该时序图显示系列并不平稳,呈现明显的递增趋势,所以一定不是平稳序列。
(2)分析上图得; 1ρ=0.850 2ρ=0.702 3ρ=0.556 4ρ=0.415 5ρ=0.280 6ρ=0.153(3)考察该序列的自相关图,进一步检验该序列的平稳性。
从图中我们发现序列的自相关系数递减到零的速度相当缓慢,在很长的延迟时期里,自相关系数一直为正,而后又一直为负,在自相关图中显示三角对称性,这是具有单调趋势的非平稳序列的一种自相关图形式。
该序列并不平稳。
同时,由于Q 检验的P 值都非常小,所以有很大的把握,断定该序列属于非白噪声序列。
2、1975-1980年夏威夷岛莫纳罗亚火山(Mauna Loa )每月释放的CO 2 数据(单位:ppm )如表2-7所示(行数据)。
表2-7:(1) 绘制该序列的时序图,并判断该序列是否平稳。
(2) 计算该序列的样本自相关系数(k=1,2, (24)(3) 绘制该样本自相关图,并解释该图形。
2.解:(1)绘制时序图由该序列的时序图可知,夏威夷岛莫纳罗亚火山(Mauna Loa)平均每月释放的CO2 数据以年为周期呈现出规则的周期性,除此之外,还有明显的逐年递增趋势。
所以该序列一定不是平稳序列。
(2)由上图知,自相关系数ρ1=0.908 ρ2=0.722 ρ3=0.513 ρ4=0.350 ρ5=0.247ρ6=0.203 ρ7=0.210 ρ8=0.264 ρ9=0.364 ρ10=0.485 ρ11=0.585 ρ12=0.602ρ13=0.518ρ14=0.369ρ15=0.207 ρ16=0.081 ρ17=0.001 ρ18=-0.032ρ19=-0.027ρ20=0.011ρ21=0.083ρ22=0.170 ρ23=0.243 ρ24=0.253(3)该序列的样本自相关系数(k=1,2,…,24)长期位于零轴的一侧,这是具有单调趋势序列的典型特征,同时自相关图呈现出明显的正弦波动规律,这是具有周期变化规律的非平稳序列的典型特征。
应用时间序列分析实验我国人口出生率时序图

《应用时间序列分析》实验作业班级:姓名:学号:代码:setwd("C:/Users/(姓名)/Desktop/时间序列分析实验三") library(readxl)sy5_4<-read_excel("./E5_4.xlsx")library(tseries)x1<-ts(sy5_4$birth_rate,start = 1980)plot(x1,col=4,main="我国人口出生率时序图")dif_x1<-diff(x1)plot(dif_x1,type="o",main="我国人口出生率一阶差分时序图") library(aTSA)adf.test(dif_x1)for(k in 1:2)print(Box.test(dif_x1,lag=1*k,type = "Ljung-Box")) #模型假设par(mfrow=c(1,2))acf(dif_x1)pacf(dif_x1)#参数估计xfit11<-arima(x1,order = c(0,1,0))xfit11xfit12<-arima(x1,order = c(0,1,1))xfit12xfit13<-arima(x1,order = c(1,1,0))xfit13#模型有效性检验(残差序列主要看第三个白噪声检验)par("mar")par(mar=c(1,1,1,1))ts.diag(xfit11)ts.diag(xfit12)ts.diag(xfit13)#参数检验(精确)t=abs(xfit11$coef)/sqrt(diag(xfit11$var.coef))pt(t,length(x1)-length(xfit11$coed),lower.tail = F)t=abs(xfit12$coef)/sqrt(diag(xfit12$var.coef))pt(t,length(x1)-length(xfit12$coed),lower.tail = F)t=abs(xfit13$coef)/sqrt(diag(xfit13$var.coef))pt(t,length(x1)-length(xfit13$coed),lower.tail = F)#模型优化c(AIC(xfit11),AIC(xfit12),AIC(xfit13),BIC(xfit11),BIC(xfit12),BIC(xfit13))xfit12#预测library(forecast)fore1<-forecast(xfit12,h=10)#往后预测十个数据fore1plot(fore1,lty=2,main="未来10年的出生率预测情况",xlab="时间",ylab = "出生率")lines(fore1$fitted,col=4)#死亡率x2<-ts(sy5_4$mortality,start = 1980)plot(x2,col=4,main="我国人口死亡率时序图")dif_x2<-diff(x2)plot(dif_x2,type="o",main="我国人口死亡率一阶差分时序图")library(aTSA)adf.test(dif_x2)for(k in 1:6)print(Box.test(dif_x2,lag=1*k,type = "Ljung-Box"))#模型假设par(mfrow=c(1,2))acf(dif_x2)pacf(dif_x2)#参数估计xfit21<-arima(x2,order = c(0,1,0))xfit21xfit22<-arima(x2,order = c(0,1,1))xfit22xfit23<-arima(x2,order = c(1,1,0))xfit23#模型有效性检验(残差序列主要看第三个白噪声检验)par("mar")par(mar=c(1,1,1,1))ts.diag(xfit21)ts.diag(xfit22)ts.diag(xfit23)#参数检验(精确)t=abs(xfit21$coef)/sqrt(diag(xfit21$var.coef))pt(t,length(x2)-length(xfit21$coed),lower.tail = F)t=abs(xfit22$coef)/sqrt(diag(xfit22$var.coef))pt(t,length(x2)-length(xfit22$coed),lower.tail = F)t=abs(xfit23$coef)/sqrt(diag(xfit23$var.coef))pt(t,length(x2)-length(xfit23$coed),lower.tail = F)#模型优化c(AIC(xfit21),AIC(xfit22),AIC(xfit23),BIC(xfit21),BIC(xfit22),BIC(xfit23)) xfit21#预测library(forecast)fore2<-forecast(xfit21,h=10)#往后预测十个数据fore2plot(fore2,lty=2,main="未来10年的死亡率预测情况",xlab="时间",ylab = "死亡率")lines(fore2$fitted,col=4)#自然增长率x3<-ts(sy5_4$ngr,start = 1980)plot(x3,col=4,main="我国人口自然增长率时序图")dif_x3<-diff(x3)plot(dif_x3,type="o",main="我国人口自然增长率一阶差分时序图")library(aTSA)adf.test(dif_x3)for(k in 1:6)print(Box.test(dif_x3,lag=1*k,type = "Ljung-Box"))#模型假设par(mfrow=c(1,2))acf(dif_x3)pacf(dif_x3)#参数估计xfit31<-arima(x3,order = c(0,1,0))xfit31xfit32<-arima(x3,order = c(0,1,1))xfit32xfit33<-arima(x3,order = c(1,1,0))xfit33#模型有效性检验(残差序列主要看第三个白噪声检验)par("mar")par(mar=c(1,1,1,1))ts.diag(xfit31)ts.diag(xfit32)ts.diag(xfit33)#参数检验(精确)t=abs(xfit31$coef)/sqrt(diag(xfit31$var.coef))pt(t,length(x3)-length(xfit31$coed),lower.tail = F)t=abs(xfit32$coef)/sqrt(diag(xfit32$var.coef))pt(t,length(x3)-length(xfit32$coed),lower.tail = F)t=abs(xfit33$coef)/sqrt(diag(xfit33$var.coef))pt(t,length(x3)-length(xfit33$coed),lower.tail = F)#模型优化c(AIC(xfit31),AIC(xfit32),AIC(xfit33),BIC(xfit31),BIC(xfit32),BIC(xfit33))xfit32#预测library(forecast)fore3<-forecast(xfit32,h=10)#往后预测十个数据fore3plot(fore3,lty=2,main="未来10年的自然增长率预测情况",xlab="时间",ylab = "自然增长率")lines(fore3$fitted,col=4)截图与解释说明:从我国人口出生率时序图中可以看出该图有明显的趋势性,初步判断该序列是非平稳序列。
时间序列分析大学作业

基于时间序列模型对生鲜产品价格分析一、基于时间序列模型对生鲜产品价格分析 (2)(一)时间序列模型概念 (2)(二)模型构建理论 (3)2.1自相关函数 (3)2.2偏自相关函数 (4)2.3 ARIMA模型的参数确定 (4)(三)描述性统计分析 (6)(四)实证分析 (8)二、附录数据 (10)一、基于时间序列模型对生鲜产品价格分析(一)时间序列模型概念对于预测来说,在时间序列模型中,指数平滑法对于预测来说是非常有帮助的,而且它对时间序列上面连续的值之间相关性没有要求。
但是,如果你想使用指数平滑法计算出预测区间,那么预测误差必须是不相关的,而且必须是服从零均值、方差不变的正态分布。
即使指数平滑法对时间序列连续数值之间相关性没有要求,在某种情况下,我们可以通过考虑数据之间的相关性来创建更好的预测模型。
自回归移动平均模型(ARIMA)包含一个确定(explicit)的统计模型用于处理时间序列的不规则部分,它也允许不规则部分可以自相关。
一般我们使用arma模型,适用于平稳时序的三种基本模型:(1)模型(Auto regression Model)--自回归模型p阶自回归模型:式中,yt为时间序列第t时刻的观察值,即为因变量或称被解释变量;y t−1,y t−2,…,y t−p为时序yt的滞后序列,这里作为自变量或称为解释变量;et是随机误差项;c,∅1、∅2、…、∅p为待估的自回归参数。
(2)模型(Moving Average Model)--移动平均模型q阶移动平均模型:式中,u为时间序列的平均数,{y t}但当序列在0上下变动时,显然u=0,可删除此项;e1、e2、…、e t为模型在第1期,第2期,...,第t期的误差;θ1、θ2、…、θt为待估的移动平均参数。
(3)arma(p,q)模型--自回归移动平均模型(Auto regression Moving Average Model)模型的形式为:显然,arma模型为自回归模型和移动平均模型的混合模型。
数学建模B作业:非参数统计、灰色系统、时间序列分析010

2014年数学建模B作业:非参、灰色、时间序列分析非参数统计Ⅴ-1 某制造商想要比较两种不同的生产方法所花费的生产时间是否有差异。
随机地选取了11个工人,每一个工人都分别使用两种不同的生产方法来完成一项相同的任务,在样本中的每一个工人都做了观察。
数据见表,试用Wilcoxon秩和检解:提出原假设,这两组方法没有显著性差异,用配对实验的符号检验法,相应代码如下:data ex;input x1 x2@@;y=x1-x2;cards;10.2 9.59.6 9.89.2 8.810.6 10.19.9 10.310.2 9.310.6 10.510 1011.2 10.610.7 10.210.6 9.8;proc univariate;var y;run;运行结果如下:从结果中可以看出,sign统计量为3,其显著性为0.1094,大于0.05,故接受原假设,认为这两组方法没有显著性差异。
Ⅴ-2为培训大学生志愿者为社区服务,设计了4种培训方案,记作为A,B,C,D.将报名的30名大学生随机地分为4组,分别接受不同培训。
训练一周后,按规定的要求考试,评定的成绩如下,试用非参数检验方法检验这四种培训方案的有解:提出原假设,这四种培训方案方法没有显著性差异,相应代码如下:data ex;do a=1to4;input n@@;do i=1to n;input x@@;output;end;end;cards;7 60 75 62 76 73 98 867 72 52 68 82 74 64 878 61 85 78 66 70 59 69 798 63 58 65 71 84 77 80 89;proc npar1way wilcoxon;class a;var x;run;运行结果如下:从结果中可以看出,Chi-Square统计量为0.5537,其显著性为0.9069,大于0.05,故接受原假设,认为四种培训方案方法没有显著性差异。
时间序列作业 VECM模型

我国FDI与进出口和人民币实际有效汇率——基于协整的VECM分析一、案例分析背景外商直接投资已成为我国经济快速发展的主要推动力之一。
2007年,据联合国《世界投资报告》统计,2006年我国吸引的外国直接投资达694.68亿美元,占当年我国固定资产形成的8%。
影响外商直接投资的因素较多且作用机制比较复杂,本文试图通过对FDI,进口总额,出口总额和人民币实际有效汇率之间的相互关系,发现我国外商直接投资、进出口和人民币汇率等重要宏观变量之间的长期均衡关系及相互作用机制。
二、变量选择和数据来源本实验选取了外商直接投资中实际利用外资金额代表外商直接投资额并记为FDI,以及进口总额,出口总额,人民币实际有效汇率1998年5月至2011年12月月度数据进行分析,由于数据数量较多,具体数据见附录。
三、VECM模型的构建(一)数据处理1.外商直接投资额将外商直接投资额变量记为FDI,FDI经过X12季节性调整后的FDI_SA图形如图1所示。
图1 经季节性调整后FDI走势图为了平滑FDI的变动趋势,对FDI做对数处理记为LFDI。
LFDI的图形如图2所示。
图2 LFDI变动图2、出口总额将出口总额变量记为EX,对EX进行季节性调整,季节性调整后的EX_SA图形如图3所示。
图3 经季节性调整后EX走势图为了平滑EX的变动趋势,对EX做对数处理记为LEX。
LEX的图形如图4所示。
图4 LEX变动图3.进口总额将出口总额变量记为IM,对IM进行季节性调整,季节性调整后的IM_SA图形如图5所示。
图5 经季节性调整后IM走势图为了平滑IM的变动趋势,对IM做对数处理记为LIM。
LIM的图形如图6所示。
图6 Lim变动图4、人民币实际有效汇率将人民币实际有效汇率记为REER,为了减少异方差性,对REER进行取对数处理,并记为LREER,LREER的图形如图5所示。
图7 LREER变动图(二)单位根检验对LFDI,LEX,LIM,LREER四个变量选取相应的形式进行单位根检验。
时间序列案例分析作业

案例4 某专卖店销售额数量规律研究资料某专卖店为加强管理的科学化,采集了过去五年的销售量资料如下:年份季节实际销售额(1)(2)(万元)(3)2004冬26春31夏19秋282005冬25春30夏20秋282006冬27春34夏23秋322007冬27春35夏21秋312008冬28春36夏24秋35讨论大纲1.用哪些简单的描述性指标,可大致找到该专卖店销售额的一般规律?答:在不考虑不规则变化的情况下,用长期趋势、季节变动和周期波动这些描述性指标可以找到专卖店销售额的一般规律。
2.能否以一个近似的函数式描述出销售额的长期趋势?能否进行预测?答:可以用一个近似的函数式描述销售额的长期趋势,计算过程如下表所示A函数式为丫二24.87 0.298X ,可以进行预测,如预测2009年冬季的销售额,即将序号21作为自变量X的值代入上述函数式中求解相应的预测值。
A E C D I李节洪际销售额(万兀)SUMMARY OUTPUT 2126323143P5428 6525 7630 87r 209528 10927 11 10 34 1211 23 131232玩13 27 151435 1615 21 1716 31 18172S 191836 201924 2120 35Multiple0. 348286R Square0.121303Adjusted Q. 072487标准误差 4. 870812观测值20方差分析回归统计df祈归差计回残总89-11-58. 9533S427?0466BIS F5S. 9533S 2.48492SL 72481I nt ercepi 24.8736S季节0. 297M4标准误羞2. 2626460. 188882t Stat P-value10. 99319__2E-091. S76351 0.13243 •该数列是否存在明显的季节性变化,如何测定?4.该数列是否存在周期波动,如何测定?答:将3、4步合并进行分析,过程如下:第一步:计算上述时间序列的季节指数,利用移动平均比率法,计算过程如下表所示冬季节的季节指数分别为119.64%, 75.99%, 108.13%, 96.23%第二步:根据季节指数,可以得到消除季节影响的序列, 然后根据这一无季节影响的时间序列拟合趋势线,计算过程如下表AB C D 季节X 实际销售额(万兀) 季节指数 季节调整后销售额Y1 26 0. 9623 27.. 01860127 32 31 1.19&4 25.. 91106653 i 3 19 0. 7599 25.00328991 54 2S 1. 0813 25. 89475631 65 25 0. 9623 25, 9794:243 76 30 1.1964 25. 07522568 S7 20 0. 7599 26. 31925253 98 2S 1.0813 25. 89475631 109 27 0. 9623 28.. 05777824 11 10 34 1.1964 23. 4185891 12 11 23 0. 7599 30. 26714041 13 12 321.0813 29. 59400721 14 13 270. 9623 28.. 05777324 15 14 35 1.1964 29. 25442996 16 15 21 0. 7599 27. 63521516 17 16 31 1. 0813 28. 66919449 18 17 28 0. 9623 29. 09695521 19 18 36 1, 1964 30. 09027081 20 19 24 0. 7599 31.. 58310304 2120351.081332. 36844539A年份<1) 2 20043456 20057 3910 2Q0611 121314 200715 161718 200S19 2021冬春夏秋冬春夏秋冬春夏秋冬春夏秋冬春夏秋CDEG实际销售额(万兀)(3) 移动平均数移动平均比率 季平均 季节指数263119 25. B75 0. 734299517 Q* 75756 0.7599 2S 25. 625 1.092682927 1.07793 1.0813 25 25. 625 0. 975609756 0. 9593 0.9623 30 25. 75 1.165048544 1. 19271 1.1964 20 26 0.7692307692S 26. 75 1.04672897227 27. 625 0,97737556634 2氐5 1.19298245623 29 0. 79310344832 29.125 1.09871244627 29 0.93103448335 28. 625 1.22270742421 28. 625 6 73362445431 23. 875 1.07359307428 29. 375 0.9531914S93(5 30. 251.1900826452435E 季节<2)从季节指数的计算过程可以看出数列存在明显的季节性变化,用季节指数测定,春夏秋ASUOARY OUTPUT1516 Coefficien - 准误羞:t Stat value 17 Intercept 24.80064 0.536806 46.20039 3. 72E-2018 季节X0. 305602 0.044812 6. 819698 2. 2E-06所得趋势线为 Y =24.80 • 0.31X第三步:测定周期波动,将1-20这20个时间的序号分别代入第二步求解出的趋势A线丫 =24.80 0.31X 中,得到下表中的(3)列,然后用消除的季节影响的序列除以(3)列即可得到周期波动的成分,计算过程如下表所示:A B C D1 季节(1) 季节调整后销售额(2〉 销售额趋势值(3〉 周期波动(2) /2 r i 27.01860127 25. 11 1.0760096083 2 25.91106653 25. 42 1.0193131174 3 25.00328991 25. 73 0. 9717563125 r 4 25_ 89475631 26. 04 0,9944222856 r 5 25, 9794243 26. 35 0. 9859364067 r 6 25. 07522568 26. 66 鬣940556102 8 7 26.31925253 26. 97 0. 9758714329 r 3 25. 89475631 27. 28 0,949221272 10 r 9 28. 05777824 27. 59 1,01695463 11 10 28. 4185891 27. 9 1.018587423 12 11 36 26714041 28. 21 1.072922383 13 12 29. 59400721 28. 52 1.03765B037 14 13 28T 05777824 28. 88 0. 973214646 15 14 29. 25442996 29. 14 1.003926903 16 15 27. 63521516 29. 45 0. 938377425 17 16 28. 66919449 29. 76 0,963346589 18 17 29. 09695521 30, 07 0t 967640679 15 18 30. 09027081 30. 38 0. 99046316 20 19 31.58310304 30. 69 1.0291007832120 32, 36844539 31 1. 0441434 4 5 6 T 8g 1Multiple R Square Adjusted 标准饯差 观测值 0. 349097 0. 720966 0. 705464 1. 155586 20 方差分析 归差计 回残总2 3IX IX IX1 18 19 SS 62. 10615 24. 03681 86.14296MS 62. 10G15 1.335378 F 46. 508285.上述规律如何帮助该专卖店的经营决策?答:利用上述规律可以帮助专卖店预测下一年四个季度的销售额情况,如下表:A其中趋势值是将 21,22,23,24分别作为X 值代入 Y = 24.80 - 0.31X 中得到。
时间序列分析期末大作业GNP平减指数的季度序列分析

20XX级XX专业时间序列分析大作业20XX年X月X日某国佃60年第一季度-佃93年第四季度GNP平减指数的季度序列分析摘要附录中给出了某国1960年第一季度-1993年第四季度GNP平减指数的季度序列,本文旨在利用时间序列分析并结合Eviews来研究该时间序列,并给出该国GNP平减指数的时间序列方程式,从而对该国的GNP平减指数进行定性分析。
在进行时间序列分析时,先对数据进行平稳性检测,发现这个序列不平稳且具有季节性,故要用差分进行平稳化操作。
经过4阶普通差分,周期为4的季节差分后序列达到平稳。
平稳化后进行模型的识别。
首先要进行模型的识别与定阶,通过平稳后的序列的自相关系数和偏自相关系数图初步判定模型的种类,当模型都可以通过检验时,通过AIC准则进行模型的拟合度检验,模型的AIC值较小的拟合度较高。
拟合度检验后发现AR(4)SAR(4)的模型拟合度最高,故此序列的模型为AR(4)SAR(4)模型。
当模型定阶后,就要对模型参数T T: 」,;2,山p ,二- *狂,川入进行估计,这一步可以得到模型表达式。
定阶与参数估计完成后,还要对模型进行检验,即要检验弋是否为平稳白噪声,这里我们用检验法进行模型检验。
关键字:时间序列分析,Eviews,乘积季节模型1、平稳性和季节性检测1.1从序列的时序图可以初步判断样本序列是否平稳:根据平稳时间序列均值、方差为常数的性质,平稳时间序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界的特点。
如果观察序列的时序图显示出该序列有明显的趋势性或者周期性,则时间序列通常不是平稳的时间序列。
该时间序列的时序图如下图所示:该时序图存在明显的上升趋势,故可判定该时间序列非平稳。
1.2从序列的自相关系数和偏自相关系数图判断样本序列是否平稳:样本自相关函数与样本偏相关函数如果是截尾的或者是拖尾的 (即被负指数控制的),说明已服从ARMA 模型。
若自相关函数与偏相关函数至少有1个不是截尾的或拖尾的,说明序列不是平稳的,可以作1阶差分,并求其样本自相关函数与样本偏相关函数,再用上述方法讨论。
时间序列作业-单位根检验方法比较

单位根检验的几种方法比较一、引言单位根检验是时间序列进一步分析的基础。
传统的经济计量模型是根据某种经济理论和某些假设条件建立回归模型,描述各个经济变量之间相互依存、互为因果的关系。
其前提条件是回归时要求时序变量是平稳的,否则会产生伪回归现象。
现实经济中的变量儿乎都是非平稳的,直接运用变量的水平值研究经济现象之间的均衡关系容易导致谬论。
因此,建模前需对变量进行单位根检验。
二、文献综述随着计量经济学的发展,单位根检验理论不断得到完善和拓展,近30年來出现了多种检验单位根的方法,如DF和ADF检验法、PP检验法、KPSS检验法、DFOGLS 检验法、ERS检验法、NP检验法以及霍尔工具变量法等。
最常用的单位根检验方法是Fuller (1976)以及Dickey和Fuller (1979)提出的DF检验、ADF检验以及Phillips 和Perron (1988)提出的PP检验法。
然而,在现实经济环境下,由于受有限样本的影响,不同的检验方法存在着不同程度的检验水平畸变和检验功效损失。
虽然在大样本下,ADF、PP检验借助极限分布具有较好的功效,但是在小样本中,检验的功效明显下降。
为了提高时间序列单位根检验结果的可信性,应针对变量的数据生成特点采用多种单位根检验,并对其结果进行综合比较,若检验结果拒绝单位根过程,则可得出该序列是平稳序列;但若是非平稳的,还不能得出最终结论,因为检验研究假设前提是数据生成过程(DGP)无结构变化。
由于剧烈的外生冲击(如制度变迁,宏观经济政策等)可能会导致DGP具有结构突变,但若不考虑这种突变,用单位根检验时,将会把一个带水平突变或趋势突变的退势平稳过程误判为随机趋势非平稳过程,即进行单位根检验时不考虑结构突变会导致检验功效的降低。
Perron (1989)提出了结构突变的单位根检验,他利用此种方法对美国的14个经济变量重新进行平稳性检验发现,在Nelson和 Plosser检验的美国13个非平稳变量中,有10个变量是结构突变的趋势平稳,即分段平稳序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列分析作业
注意:为了尽量避免因个人尽量不足导致的模型识别问题,sas系统还提供了相对最有模型识别。
只要我们在identify命令中增加一个可选择命令minic,就可以获得一定范围内最优模型定阶。
即增加语句:identify var=x nlag=8 minic p=(0:5) q=(0:5)
作业:
第1题现有201个连续的生产纪录,如下
81.9 89.4 79.0 81.4 84.8 85.9 88.0 80.3 82.6
83.5 80.2 85.2 87.2 83.5 84.3 82.9 84.7 82.9
81.5 83.4 87.7 81.8 79.6 85.8 77.9 89.7 85.4
86.3 80.7 83.8 90.5 84.5 82.4 86.7 83.0 81.8
89.3 79.3 82.7 88.0 79.6 87.8 83.6 79.5 83.3
88.4 86.6 84.6 79.7 86.0 84.2 83.0 84.8 83.6
81.8 85.9 88.2 83.5 87.2 83.7 87.3 83.0 90.5
80.7 83.1 86.5 90.0 77.5 84.7 84.6 87.2 80.5
86.1 82.6 85.4 84.7 82.8 81.9 83.6 86.8 84.0
84.2 82.8 83.0 82.0 84.7 84.4 88.9 82.4 83.0
85.0 82.2 81.6 86.2 85.4 82.1 81.4 85.0 85.8
84.2 83.5 86.5 85.0 80.4 85.7 86.7 86.7 82.3
86.4 82.5 82.0 79.5 86.7 80.5 91.7 81.6 83.9
85.6 84.8 78.4 89.9 85.0 86.2 83.0 85.4 84.4
84.5 86.2 85.6 83.2 85.7 83.5 80.1 82.2 88.6
82.0 85.0 85.2 85.3 84.3 82.3 89.7 84.8 83.1
80.6 87.4 86.8 83.5 86.2 84.1 82.3 84.8 86.6
83.5 78.1 88.8 81.9 83.3 80.0 87.2 83.3 86.6
79.5 84.1 82.2 90.8 86.5 79.7 81.0 87.2 81.6
84.4 84.4 82.2 88.9 80.9 85.1 87.1 84.0 76.5
82.7 85.1 83.3 90.4 81.0 80.3 79.8 89.0 83.7
80.9 87.3 81.1 85.6 86.6 80.0 86.6 83.3 83.1
82.3 86.7 80.2
(1)判断该序列的平稳性
(2)如果该序列平稳且非白噪声。
选择适当模型拟合该序列的发展
(3)写出拟合模型,预测该序列后5年的95%预测的置信区间。
第2题某城市连续14年的月度婴儿出生率数据如下
26.663 23.598 26.931 24.740 25.806 24.364 24.477 23.901
23.175 23.227 21.672 21.870 21.439 21.089 23.709 21.669
21.752 20.761 23.479 23.824 23.105 23.110 21.759 22.073
21.937 20.035 23.590 21.672 22.222 22.123 23.950 23.504
22.238 23.142 21.059 21.573 21.548 20.000 22.424 20.615
21.761 22.874 24.104 23.748 23.262 22.907 21.519 22.025
22.604 20.894 24.677 23.673 25.320 23.583 24.671 24.454 24.122 24.252 22.084 22.991 23.287 23.049 25.076 24.037 24.430 24.667 26.451 25.618 25.014 25.110 22.964 23.981 23.798 22.270 24.775 22.646 23.988 24.737 26.276 25.816 25.210 25.199 23.162 24.707 24.364 22.644 25.565 24.062 25.431 24.635 27.009 26.606 26.268 26.462 25.246 25.180 24.657 23.304 26.982 26.199 27.210 26.122 26.706 26.878 26.152 26.379 24.712 25.688 24.990 24.239 26.721 23.475 24.767 26.219 28.361 28.599 27.914 27.784 25.693 26.881 26.217 24.218 27.914 26.975 28.527 27.139 28.982 28.169 28.056 29.136 26.291 26.987 26.589 24.848 27.543 26.896 28.878 27.390 28.065 28.141 29.048 28.484 26.634 27.735
27.132 24.924 28.963 26.589 27.931 28.009 29.229 28.759
28.405 27.945 25.912 26.619 26.076 25.286 27.660 25.951 26.398 25.565 28.865 30.000 29.261 29.012 26.992 27.897
(1)选择适当的模型拟合该序列的发展
(2)使用该拟合模型预测下一年度该城市月度婴儿出生率。
