《有理数的乘法运算律》课时练习含答案
2.3.2 有理数的乘法(含答案)

2.3.2 有理数的乘法◆教材知能精练知识点多个有理数相乘1. 下面乘积中符号为正的是()A.0×(-3)×(-4)×(-5) B.(-6)×(-15)×(-12)×13C.-2×(-12)×(+2) D.-1×(-5)×(-3)2. 4个有理数相乘,积的符号是负号,则这四个有理数中,正数有()个A.1个或3个B.1个或2个 C.2个或4个 D.3个或4个3. 互不相等的四个整数的积等于4,则这四个数的绝对值的和是()A.5 B.6 C.7 D.84. 五个有理数相乘,若积为负数,则其中负有理数的个数是()A.1 B.3 C.5 D.以上都有可能5. -38)×(+14.2)×0×(-935)=_______,-13×18+13×(-18)=________.6. 绝对值不小于2而小于5的所有负整数的积是__________. 知识点2 有理数的乘法运算律7. 计算(-1)×(-5)×(-15)的结果是().A.-1 B.1 C.-125D.-258.45-×1(1010.05)4-+=-8+1-0.04,这个运算应用了() A、加法结合律 B、乘法结合律 C、乘法交换律 D、分配律9.(-113)×(-115)×(-114)×(-116)=____________.10.计算:(-0.1)×(-0.001)×(-100)×1000=________.11. 计算:×18-28×(-47)12. (1)(-98)×(-0.125)+(-98)×18-98×(-47)(2)-12×(-13+14-16); (3)-92223×(-69);◆学科能力迁移13. 【易错题】计算下列各题:(1)(-413)×(-112)×34;(2)(-0.08)×(-2)×2×(-0.25);(3)(-34-156+78)×48.14.【易错题】计算:(-7)×(-227)+19×(-227)-5×(-227).15.【新情境题】讲完“有理数的乘法”后,老师在课堂上出了下面一道计算题:7115 16×(-8).不一会儿,不少同学算出了答案,老师把班上同学的解题归类写到黑板上:解法一:原式=-115116×8=-920816=-575.解法二:原式=(71+1516)×(-8)=71×(-8)+1516×(-8)=-57512.解法三:原式=(72-116)×(-8)=72×(-8)+116×(-8)=-57512.对这三种解法,大家议论纷纷,你认为哪种方法最好?________,理由是_______,本题对你有何启发?________16.【多变题】计算(1)(-8)×(-12)×(-0.125)×(-13)×(-0.01);(2)391415×(-11); (3)1.25×(-117)×(-3.2)×(-78);17.【开放题】x,y,z是三个有理数,若x<y,x+y=0,且xyz>0,试判断x+z的符号.◆课标能力提升18.【趣味题】一只小虫沿一条东西方向放着的木杆爬行,先以每分钟2.5米的速度向东爬行,后来又以这个速度向西爬行,试求它向东爬行3分钟,又向西爬行5•分钟后距出发点的距离.19.【学科内综合题】计算:1996×19951995-1995×19961996.20.【开放题】计算(1-12004)(1-12003)(1-12002) (1)13)(1-12).21.【探究题】1)计算:(-27131)×(-3)+(+27131)×(-5)+(-27131)×(-2);(2)已知|22m nm n-+|=3,求2(2)2m nm n-+-22m nm n-+-3的值.◆品味中考典题22. (2007黑龙江佳木斯课改,3分)某商店老板将一件进价为800元的商品先提价50%,再打8折卖出,则卖出这件商品所获利润是元.23.(2007.双柏)如果a,b是整数,且ab=6,那么a+b的最小值是_______.参考答案1.C2. A3. B 点拨:这四个数为±1,±2,所以绝对值之和为6.4. D5.0,-1126.-247. A8. D9. 1 10.-1011. 1612. (1)56 (2)3 (3)68713. (1)398(2)-0.08 (3)-82 点拨:注意运用乘法的运算律.14. -2215. 解法二与解法三;解法二与解法三巧妙地利用了拆分思想,把带分数拆成一个整数与一个真分数的和,再应用分配律,简化了计算过程;•我们在解题时要善于发现问题的特点.提示:711516=72-116=71+1516.16. (1)-0.04;(2)-439415(3)-417.x<0,y<0,z<0,则x+z为负号18. 分析:用正负数表示意义相反的量,向东爬行记为“+”,向西爬行记为“-”.解:3×2.5+5×(-2.5)=-5(米).因此,最后小虫距出发点的距离是5米19. 分析:此题用拆项法,使式中出现一些和为0的式子,便于化简.解:原式=1 996×(19 950 000+1 995)-1 995×(19 960 000+1 996)=1 996×19 950 000+1 996×1 995-1 995×19 960 000-1 995×1 996=1 996×1 995×10 000-1 995×1 996×10 000=0.20.1 200421. (1)分析:根据题意的特点,可逆用乘法分配律ab+ac=a(b+c),简化计算.•解:原式=27131×3+27131×(-5)+27131×2=27131×(3-5+2)=27131×0=0.点拨:此题在逆用乘法分配律时要注意符号.当符号不统一时,可先做整理,不要出现符号错误.(2)分析:此题把当作一个整体,用整体代入法求解.解:∵│22m nm n-+│=3,∴22m nm n-+=±3.当22m nm n-+=3时,2(2)2m nm n-+-22m nm n-+-3=2×3-3-3=0;当22m nm n-+=-3时,2(2)2m nm n-+-22m nm n-+-3=2×(-3)-(-3)-3=-6.∴2(2)2m nm n-+-22m nm n-+-3的值是0或-6.点拨:整体代入法是数学中一种常用的方法,要培养用整体的思想和观点解决某些特定的问题.22. 16023. -7。
最新【北师大版】七年级数学上册:2.7.2《有理数乘法的运算律》课时作业(含答案)

最新北师大版数学精品教学资料2.7.2 有理数乘法的运算律1.两个有理数的积是负数,和为零,那么这两个有理数( )A .一个为零,另一个为正数B .一个为零,另一个为负数C .一个为正数,另一个为负数D .互为相反数且都不为零2.若ab >0,则下列结论正确的是( )A .a >0,b >0B .a <0,b <0C .a ,b 同号D .以上答案都不对3.绝对值小于6的所有整数的积是________. 4.判断下列各个乘积的符号: ①(-2)×(-3)×4×(-5)×3;②4×(-2)×(-3.4)×(-6.7)×5×(-9)×3; ③4×7×(-5)×9×(-4.6)×9×13; ④(-2)×0×7×(-4);⑤(-2.1)×(-6)×(-9)×(-6.7)× (-5.8)×(-4.7).其中积为正数的有________,积为负数的有______,另外________的乘积既不是正数也不是负数(只填序号即可).5.计算(-2.5)×0.37×1.25×(-4)×(-8)的值为________. 6.计算:(1)(-4)×(-0.07)×(-25); (2)(47-118+314)×56.7.先阅读提供的材料,再解答相关问题: (1+12)×(1-13)=32×23=1.(1+12)×(1+14)×(1-13)×(1-15)=32×54×23×45=(32×23)×(54×45)=1×1=1.请你求(1+12)×(1+14)×(1+16)×(1-13)×(1-15)×(1-17)的结果.8.若a ,b 互为相反数,c ,d 互为倒数,m 的绝对值是1,求(a +b)cd -2 009m 的值.9.刘亮的妈妈每天早上要送新鲜蔬菜到市场去卖,下面是她一周送出的20筐菜的重量记录表,每筐以25 kg 为标准重量.(2013·台州模拟)计算(-1 00015)×(5-10)的值为( )A .1 000B .1 001C .1 999D .5 001课后作业1.D 两数互为相反数且不为0. 2.C 同号得正. 3.04.②③⑤ ① ④ 积的符号由负因数的个数决定 5.-37 6.解:(1)-7 原式=-4×25×0.07 =-100×0.07=-7;(2)-19 原式=47×56-98×56+314×56=32-63+12 =-19.7.解:原式=32×54×76×23×45×67=1.8.解:2 009或-2 009 ∵a,b 互为相反数,∴a+b =0,∵c,d 互为倒数,∴cd=1, ∵|m|=1,∴m=±1,当m =1时, (a +b)cd -2 009m =0×1-2 009×1 =-2 009;当m =-1时,原式=0×1-2 009×(-1)=2 009.9.解:501.3 kg 25×20+(-0.8×2+0.6×5-0.5×3+4×0.4+2×0.5+4×(-0.3) =500+(-1.6+3-1.5+1.6+1-1.2) =500+1.3 =501.3(kg ). 中考链接D 原式=-(1 000+15)×(-5)=(1 000+15)×5=1 000×5+15×5=5 000+1=5 001,所以选D .。
人教版七年级上册数学有理数乘除法练习题及答案

第1课时 有理数的乘法法则1.下列各组数中互为倒数的是( )A .4和-4B .-3和13C .-2和-12D .0和02.与-2的乘积为1的数是( )A .2B .-2 C.12 D .-123.下列算式中,积为正数的是( )A .-2×5B .-6×(-2)C .0×(-1)D .5×(-3)4.-12的倒数的相反数等于( )A .-2 B.12 C .-12 D .25.下列说法错误的是( )A .一个数同0相乘,仍得0B .一个数同1相乘,仍得原数C .一个数同-1相乘得原数的相反数D .互为相反数的两个数的积是16.对于式子-(-8),有以下理解:(1)可表示-8的相反数;(2)可表示-1与-8的乘积;(3)可表示-8的绝对值;(4)运算结果等于8.其中理解错误的个数是( )A .0个B .1个C .2个D .3个7.用字母表示有理数乘法的符号法则.(1)若a >0,b >0,则ab ____0,若a >0,b <0,则ab ____0;(2)若a <0,b >0,则ab ____0,若a <0,b <0,则ab ____0;(3)若a >0,b =0,则ab ____0.8.计算下列各题:(1)(-35)×(-1); (2)(-15)×24;(3)-4.8×(-45); (4)⎝ ⎛⎭⎪⎫-119×(-0.6).9.计算:(1)(-5)×(-6)-8×(-1.25);(2)⎝ ⎛⎭⎪⎫-32×16+⎝ ⎛⎭⎪⎫-35×⎝ ⎛⎭⎪⎫-53.10.已知实数a ,b 在数轴上对应的点如图所示,则下列式子正确的是()A.ab>0 B.a+b<0 C.|a|<|b| D.a-b>011.一辆出租车在一条东西走向的大街上行驶,这辆出租车连续送客20次,其中8次向东行驶,12次向西行驶,向东行驶每次的行程为10 km,向西行驶每次的行程为7 km.(1)该出租车连续20次送客后,停在何处?(2)该出租车一共行驶了多少路程?12.东东有5张写着不同数字的卡片:-4-50+3+2他想从中取出2张卡片,使这2张卡片上数字的乘积最大.你知道应该如何抽取吗?最大的乘积是多少?13. 规定运算,a b=ab+1,求下列各式的值:(1)(-2)3;(2)[(-1)2](-3).参考答案1.C 2.D 3.B 4.D 5.D 6.A7.(1)> < (2)< > (3)=8.(1)35 (2)-360 (3)216 (4)239.(1)40 (2)34 10.D11.(1)该出租车停在出发地西面4 km 处;(2)该出租车一共行驶了164 km .12.抽取-4和-5,乘积最大,最大的乘积是20.13.(1)-5 (2)41.4.1 第2课时 有理数乘法的运算律及运用1.计算⎝ ⎛⎭⎪⎫-531×⎝ ⎛⎭⎪⎫-92×⎝ ⎛⎭⎪⎫-3115×29的结果是( ) A .-3 B .-13 C .3 D.132.下列计算中错误的是( )A .-6×(-5)×(-3)×(-2)=180B .(-36)×⎝ ⎛⎭⎪⎫16-19-13=-6+4+12=10 C .(-15)×(-4)×⎝ ⎛⎭⎪⎫+15×⎝ ⎛⎭⎪⎫-12=6 D .-3×(+5)-3×(-1)-(-3)×2=-3×(5-1-2)=-63.利用运算律计算⎝ ⎛⎭⎪⎫-993233×33时,最恰当的方案是( ) A.⎝ ⎛⎭⎪⎫100-133×33 B.⎝ ⎛⎭⎪⎫-100-133×33 C .-⎝ ⎛⎭⎪⎫99+3233×33 D .-⎝ ⎛⎭⎪⎫100-133×33 4.计算:(-8)×(-12)×(-0.125)×⎝ ⎛⎭⎪⎫-13×(-0.001)=____. 5.-23与25的和的15倍是____,-23与25的15倍的和是________.6.运用运算律简便计算:(1)999×(-15);(2)999×11845+999×⎝ ⎛⎭⎪⎫-15-999×11835.7.运用简便方法计算:(1)(-125)×(-25)×(-5)×(-2)×(-4)×(-8);(2)(-36)×⎝ ⎛⎭⎪⎫-49+56-712; (3)9989×(-18).8.逆用乘法分配律计算:(1)17.48×37+174.8×1.9+8.74×88;(2)-13×23-0.34×27+13×(-13)-57×0.34.9.观察下列等式:第1个等式:a 1=11×3=12×⎝ ⎛⎭⎪⎫1-13; 第2个等式:a 2=13×5=12×⎝ ⎛⎭⎪⎫13-15; 第3个等式:a 3=15×7=12×⎝ ⎛⎭⎪⎫15-17; 第4个等式:a 4=17×9=12×⎝ ⎛⎭⎪⎫17-19. 请解答下列问题:(1)按以上规律列出第5个等式:a 5=__________=__________;(2)用含n 的式子表示第n 个等式:a n =__________=______________(n 为正整数);(3)求a 1+a 2+a 3+a 4+…+a 100的值.参考答案1.B 2.C 3.D 4.-0.004 5.-4 5136.(1)-14 985 (2)07.(1)1 000 000 (2)7 (3)-1 7988.(1)1 748 (2)-13.349.(1)19×11 12×⎝⎛⎭⎫19-111 (2)1(2n -1)(2n +1) 12×⎝⎛⎭⎫12n -1-12n +1 (3)100201 1.4.2 第1课时 有理数的除法法则1. 16的倒数是( )A .6B .-6 C.16 D .-162.下列计算正确的是( )A.⎝ ⎛⎭⎪⎫+12÷⎝ ⎛⎭⎪⎫-12=-1 B .-3÷⎝ ⎛⎭⎪⎫-13=1 C .(-5)×0÷0=0 D .2÷3×⎝ ⎛⎭⎪⎫-13=-2 3.如果一个数除以它的倒数,商是1,那么这个数是( )A .1B .2C .-1D .1或-14.倒数是它本身的数是___,相反数是它本身的数是____.5.计算:(1)(-15)÷(-3); (2)(-12)÷⎝ ⎛⎭⎪⎫-14;(3)(-12)÷⎝ ⎛⎭⎪⎫-12÷(-10).6.化简下列分数:(1)-162; (2)12-48; (3)-54-6; (4)-9-0.3.7.若a +b <0,b a >0,则下列结论成立的是( )A .a >0,b >0B .a <0,b <0C .a >0,b <0D .a <0,b >08.已知a 和b 一正一负,则|a |a +|b |b 的值为( )A .0B .2C .-2D .根据a ,b 的值确定9.计算:(1)⎝ ⎛⎭⎪⎫-23÷⎝ ⎛⎭⎪⎫-85÷(-0.25); (2)⎝ ⎛⎭⎪⎫-47÷⎝ ⎛⎭⎪⎫-314÷⎝ ⎛⎭⎪⎫-23;(3)(-2)÷13×(-3); (4)-2.5÷⎝ ⎛⎭⎪⎫-516×⎝ ⎛⎭⎪⎫-18÷(-4).10.若a ,b 互为相反数,c ,d 互为倒数,m 的倒数是2,求a +b -cd m的值.11.一列数a 1,a 2,a 3,…满足条件:a 1=12,a n =11-a n -1(n ≥2,且n 为整数),则a 2 016=____.参考答案1.A 2.A 3.D 4.±1 05.(1)5 (2)48 (3)-1256.(1)-8 (2)-14(3)9 (4)307.B 8.A 9.(1)-53 (2)-4 (3)18 (4)1410.-2 11.-11.4.2 第2课时 有理数的加、减、乘、除混合运算1.下列计算:①(-1)×(-2)×(-3)=6;②(-36)÷(-9)=-4;③23×⎝ ⎛⎭⎪⎫-94÷(-1)=32;④(-4)÷12×(-2)=16.其中计算正确的个数为( )A .4个B .3个C .2个D .1个2.计算⎝ ⎛⎭⎪⎫-14÷⎝ ⎛⎭⎪⎫-23÷⎝ ⎛⎭⎪⎫-58的结果是( )A .-53B .-35C .-56D .-653.计算4÷(-1.6)-74÷2.5的值为( )A .-1.1B .-1.8C .-3.2D .-3.94.在算式4-|-3□5|中的□所在位置,填入下列哪种运算符号,计算出来的值最小( )A .+B .-C .×D .÷5.计算⎝ ⎛⎭⎪⎫316-256×(-3)-145÷⎝ ⎛⎭⎪⎫-35的结果是( )A .4B .2C .-2D .-46.计算:(1)42×⎝ ⎛⎭⎪⎫-17+(-0.25)÷34;(2)-1-2.5÷⎝ ⎛⎭⎪⎫-114;(3)[12-4×(3-10)]÷4.7.计算:(1)-1÷⎝ ⎛⎭⎪⎫-18-3÷⎝ ⎛⎭⎪⎫-12; (2)-81÷13-13÷⎝ ⎛⎭⎪⎫-19; (3)-1+5÷⎝ ⎛⎭⎪⎫-16×(-6); (4)⎝ ⎛⎭⎪⎫13-12÷114÷110.8.[2016·杭州]计算6÷⎝ ⎛⎭⎪⎫-12+13时,方方同学的计算过程如下:原式=6÷⎝ ⎛⎭⎪⎫-12+6÷13=-12+18=6.请你判断方方的计算过程是否正确,若不正确,请你写出正确的计算过程.9.计算:(1)34×⎝ ⎛⎭⎪⎫-112÷⎝ ⎛⎭⎪⎫-214; (2)-34÷38×⎝ ⎛⎭⎪⎫-49÷⎝ ⎛⎭⎪⎫-23; (3)1÷⎝ ⎛⎭⎪⎫16-13×16; (4)-112÷34×(-0.2)×134÷1.4×⎝ ⎛⎭⎪⎫-35.10.如果规定符号“#”的意义是a #b =a +b ab ,试求2#(-3)#4的值.11.定义运算a ⊗b =a (1-b ),下面给出了关于这种运算的几个结论:①2⊗(-2)=6;②a ⊗b =b ⊗a ;③若a ⊗b =0,则a =0.其中正确结论的序号是____.参考答案1.C 2.B 3.C 4.C 5.B6.(1)-613(2)1 (3)10 7.(1)14 (2)-240 (3)179 (4)-438.方方同学的计算过程不正确,原式=-36,计算过程略.9.(1)12 (2)-43 (3)-1 (4)-31010.25411.①第6课时 利用计算器进行有理数的加减乘除混合运算1.在科学计算器上按顺序按3,8,×,1,5,+,3,2,=,最后屏幕上显示( )A .686B .602C .582D .5022.用计算器计算(-62.3)÷(-0.25)×940时,用带符号键(-)的计算器的按键顺序是_______________________________________________,用带符号转换键+/-的计算器的按键顺序是_____________________.3.(1)用计算器求 4.56+0.825,按键顺序及显示的结果是:4.56+________=________;(2)用计算器求(-2 184)÷14,按键顺序及显示的结果是:2 184________÷________=________.4.用计算器计算下列各题:(1)-98×(-32.7);(2)36÷7.2+(-48.6)÷2.4.5.在计算器上按如图1-4-2所示的程序进行操作,表中的x与y是分别输入的6个数及相应的计算结果:按键×3=输出y(计算结果)输入x――→图1-4-2上述操作程序中所按的第三个键和第四个键应是()A.“1”和“+” B.“+”和“1”C.“1”和“-” D.“+”和“-1”6.计算(本题可用计算器计算):(1)44×441+2+1=____;(2)666×6661+2+3+2+1=____;(3)8 888×8 8881+2+3+4+3+2+1=____.7.某粮食加工厂从生产的粮食中抽出20袋检查质量,以每袋50 kg为标准,将超过的千克数记为正数,不足的千克数记为负数,结果记录如下:这20袋大米共超重或不足多少千克?总质量为多少千克?8.利用计算器进行计算,将结果填写在横线上:99 999×11=____;99 999×12=____;99 999×13=____;99 999×14=____.(1)你发现了什么规律?(2)不用计算器,你能直接写出99 999×19的结果吗?参考答案1.B2.(-)62· 3÷(-)0· 25×940=62· 3+/-÷0· 25+/-×940=3.(1)0.825 5.385(2)+/-14-1564.(1)3 204.6(2)-15.25 5.B6.(1)484(2)49 284(3)4 937 2847.这20袋大米共超重0.4 kg,总质量为1 000.4 kg.8.1 099 989 1 199 988 1 299 987 1 399 986(1)(答案不唯一)规律①:第一个因数都是99 999不变,第二个因数由11逐渐加1,积的最高两位数随着第二个因数的增加由10逐渐加1,中间三位数都是999,末尾两位数由89逐渐减1;规律②:因数的规律同上,积的最高两位数比第二个因数少1,中间三位数都是999,末尾两位数与第二个因数的和为100;(2)1 899 981。
七年级数学有理数的乘法——运算律(基础)(含答案)

有理数的乘法——运算律(基础)一、单选题(共10道,每道9分)1.计算的结果是( )A.-50B.-200C.200D.答案:B解题思路:故选B.试题难度:三颗星知识点:有理数乘法运算2.计算的结果是( )A. B.C. D.答案:D解题思路:故选D.试题难度:三颗星知识点:有理数乘法运算3.计算的结果是( )A.-4B.-22C.6D.24答案:C解题思路:故选C.试题难度:三颗星知识点:有理数乘法运算4.计算的结果是( )A.0B.24C.40D.32答案:B解题思路:故选B.试题难度:三颗星知识点:有理数乘法运算5.计算的结果是( )A.-5B.-37C.1D.-1答案:D解题思路:故选D.试题难度:三颗星知识点:有理数乘法运算6.计算的结果是( )A.-22B.-10C.22D.14答案:A解题思路:故选A.试题难度:三颗星知识点:有理数乘法运算7.计算的结果是( )A.-7B.-14C.14D.7答案:C解题思路:故选C.试题难度:三颗星知识点:有理数乘法运算8.计算的结果是( )A. B.5C. D.-5答案:D解题思路:故选D.试题难度:三颗星知识点:有理数乘法运算9.计算的结果是( )A. B.C. D.答案:C故选C.试题难度:三颗星知识点:有理数乘法运算10.计算的结果是( )A. B.-27C. D.27答案:B解题思路:故选B.试题难度:三颗星知识点:有理数乘法运算二、填空题(共1道,每道10分)11.高度每增加1千米,气温就下降6℃,现在地面气温是10℃,那么7千米的高空的气温是____℃.解题思路:10+7×(﹣6)=10﹣42=﹣32℃.答:地面以上7千米的高空的气温是﹣32℃.试题难度:知识点:有理数乘法运算。
人教版数学七年级上册1.4.1《有理数的乘法运算律》训练(有答案)

人教版数学七年级上册 1.4.1《有理数的乘法运算律》训练(有答案)课时3 有理数的乘法运算律基础训练知识点(有理数的乘法运算律)1.(﹣12-14-16)×(﹣24)=(﹣12)×(﹣24)+(﹣14)×(﹣24)+(﹣16)×(﹣24)①=12+6+4②以上运算()A.运用了乘法结合律B.运用了乘法交换律C.①运用了分配律D.②运用了分配律2.用简便方法计算﹣6×(﹣12)×(﹣0.5)×(﹣4)的结果是()A.6B.3C.2D.13.下列变形不正确的是()A.5×(﹣6)=(﹣6)×5B.(14-12)×(﹣12)=(﹣12)×(14-12)C.(﹣16+13)×(﹣4)=(﹣4)×(﹣16)+13×4D.(﹣2.5)×(﹣16)×(﹣4)=[(﹣25)×(﹣4)]×(﹣16)4.下列计算正确的是()A.(﹣4)×(﹣3)×(﹣2)×(﹣2)=4×3×2×2=48B.(﹣12)×(13-14)=﹣4+3:=﹣1C.(﹣9)×5×(﹣4)×0=9×5×4=180D.﹣2×5﹣2×(﹣1)﹣(﹣2) ×2=﹣2×(5+1﹣2)=﹣85.﹣0.01×13×(﹣200)=13×[(﹣0.01)×______]=______.6.计算:(1)(﹣4)×(﹣7)×(﹣25);(2)(﹣16+34-112)×(﹣48)(3)(﹣273)×(﹣4)+(+273)×(﹣7)﹣(+273)×(﹣3).7.[2019山东枣庄峄城区期中]学习了有理数的乘法后,老师给同学们布置了这样=(50-125)×(﹣5)=50×(﹣5)-125×(﹣5)=﹣250+1 5=﹣2494 5(3)191516×(﹣8)=(20-116)×(﹣8)=20×(﹣8)-116×(﹣8)=﹣160+1 2=﹣15912课时3 有理数的乘法运算律提升训练1.[2019河北邯郸二十三中课时作业]用分配律计算(﹣3)×(4﹣12),下列计算过程正确的是()A.(﹣3)×4+(﹣3)×(﹣1 2 )B.(﹣3)×4-(﹣3)×(﹣12)C.3×4﹣(﹣3)×(﹣12)D.3×4×3×(﹣12)2.[2019陕西汉中市实验中学课时作业]在运用分配律计算3.96×(﹣99)时,下列变形较为简便的是()A.(3+0.96)×(﹣99)B.(4﹣0.04)×(﹣99)C.3.96×(﹣100+1)D.3.96×(﹣90﹣9)3.[2019河南南阳三中课时作业]计算下列各题:(1)(﹣12+23-14)×|24|(2)91718×(﹣54)(3)317×2122×(317-713)×(﹣722)(4)﹣1.53×0.75+0.53×34-3.4×0.754.[2019江西临川一中课时作业]阅读下面的材料:(1+12)×(1-13)=32×23=1,(1+12)×(1+14)×(1-13)×(1-15)=1×1=1根据以上信息,求出下式的结果.(1+12)×(1+14)×(1+16)×…×(1+120)×(1-13)×(1-15)×(1-17)×…×(1-121).5.[2019安徽合肥三十八中课时作业]已知x,y为有理数,如果规定一种新的运算※,定义x※y=xy+1.根据运算符号的意义完成下列各题.(1)求2※4的值;(2)求1※4※0的值;(3)任意选取两个有理数(至少有一个为负数)分别填入□※〇与〇※□的□与〇内,并比较两个运算结果,你能发现什么?(4)根据以上方法,设a,b,c为有理数,请与其他同学讨论a※(b—c)与a ※b+a※c的关系,并用式子把它表示出来.参考答案1.A2.C3.【解析】(1)(﹣12+23-14)×|24|=(﹣12+23-14)×24=(﹣12)×24+23×24-14×24=﹣12+16-6 =﹣2(2)91718×(﹣54)=(10-118)×(﹣54)=10×(﹣54)-118×(﹣54)=﹣540+3 =﹣537(3)317×2122×(317-713)×(﹣722)=﹣1×(2122×227-2122×223)=﹣1×(3-7)=﹣1×(﹣4)=4.(4)﹣1.53×0.75+0.53×34-3.4×0.75=﹣1.53×34+0.53×34-3.4×34=(﹣1.53+0.53-3.4)×3 4=(﹣4.4)×3 4=﹣3.34.【解析】(1+12)×(1+14)×(1+16)×…×(1+120)×(1-13)×(1-15)×(1-17)×…×(1-121)=1×1×1×…×1=15.【解析】(1)2※4=2×4+1=9. (2)1※4=1×4+1=5,(1※4)※0=5※0=5×0+1=1.(3)答案不唯一,如:选5和﹣1. ﹣1※5=﹣1×5+1=﹣4,5※(﹣1)=5×(﹣1)+1=﹣4,发现运算结果相等,即□※〇=〇※□.(4)a※(b+c) =a(b+c)+1=ab+ac+1,a※b+a※c=ab+1+ac+1.所以a※(b+c)+1=a※b+a※c.《有理数的乘法》拓展有理数乘法法则,实际上是一种规定(或说定义),要完全理解这样规定的科学性、合理性,怎样接受(或说承认,不拒绝)有理数乘法法则呢?乘数是正数的情况下是由实际问题得出的,乘数是负数时(所谓难就难在这里),则利用“把一个因数换成它的相反数,所得的积是原来的积的相反数”(本质是定义的另一种形式).这一结论所以比较容易为学生接受,是因为看起来,它好像是从实际中总结出来的.为什么说是“好像”呢?看下面的总结过程:由实际问题可以很容易得出:3×2=6①(-3)×2=-6②比较①,②就得到“把一个因数,换成它的相反数,所得的积是原来的积是相反数.”①,②确是由实际问题得出的,但是要得出上述法则有些牵强,举的例子是“被乘数”改变符号,而结论是“因数”改变符号.为了弥补这个不足之处,我们增加了有理数乘法的应用问题,验证法则的合理性.例1填空题:(1)五个数相乘,积为负,则其中正因数有____个.(2)四个各不相等的整数a,b,c,d,它们的积abcd=25,那么a+b+c+d=____.分析:(1)五个数相乘积为负,说明五个数中,负因数的个数是1个,3个或5个.(2)因为25=1×5×5,又a,b,c,d是四个各不相等的整数,所以这四个数只能是±1和±5.解:(1)五个数相乘积为负,说明五个数中,负因数的个数为奇数,即1个,3个或5个.∴正因数有4个,2个或0个.(2)∵a,b,c,d是四个各不相等的整数,且abcd=25=1×5×5,∴a,b,c,d只能是+1,-1,+5,-5这四个数.∴a+b+c+d=0.说明:几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.几个数相乘,有一个因数为0,积就为0.例2填空题:(1)(-0.001)×(-0.01)×(-0.1)×(-100)= __________;(2)2(16)(72.8)0(8)3-⨯-⨯⨯-=__________;(3)377(1)(24)4812--⨯-=__________.分析:(1)是4个不为0的数相乘,0.01×100=1,要注意小数点的位置;(2)是4个数相乘,其中有一个因数是0;(3)因为377777148124812--=--,三个分数的分子均为7,所以同时正用又逆用乘法分配律才是最佳的解题方法.解:(1)(-0.001)×(-0.01)×(-0.1)×(-100)=0.0001;(2)2 (16)(72.8)0(8)03-⨯-⨯⨯-=;(3)377(1)(24) 4812--⨯-例3计算:124 ( 1.4)(1)(1)( 5.5)()1137-⨯+⨯-⨯-⨯+.分析:这是5个非0的数相乘,其中有3个负因数,应当先确定积的符号,然后把绝对值相乘.绝对值相乘时,要注意运用乘法的交换律和结合律,此题把小数化为分数计算较简便.解:原式21214 (1)(1)(1)(5)()511327 =-⨯+⨯-⨯-⨯+=﹣8说明:几个不为0的数相乘时,确定积的符号是第一步,要使计算简便,关键在绝对值的计算.求积的绝对值时要注意运用乘法交换律和结合律;当因数是小数时,一般要化为分数再相乘;当因数是带分数时,要化为假分数再相乘;在化简时,能约分的要约分.例4计算2449(5)25⨯-.分析:此题若直接相乘很麻烦,根据它的特点:可以把被乘数拆成两项,然后用乘法分配律计算.解:2449(5)25⨯-说明:(1)此题利用分解思想把244925拆成15025-,然后运用分配律,可使运算简便,这是一个重要的方法技巧.(2)不要漏项,即可把乘数与括号内的每一项都相乘.(3)相乘时,符号不要弄错.。
1.4.1 第3课时 有理数的乘法运算律

1 -5752.
1.4.1 第3课时 有理数的乘法运算律
1
1
解 法 三 : 原 式 = (72 - 16 )×( - 8) = 72×( - 8) - 16 ×( - 8) = -
1 5752.
对这三种解法,大家议论纷纷,你认为哪种方法最好?________. 运用你认为最好的方法进行计算:
48 (1)949×(-7);
A.分配律 B.分配律和乘法结合律 C.乘法交换律和乘法结合律 D.乘法交换律和分配律
1.4.1 第3课时 有理数的乘法运算律
4. 下列变形不正确的是( C ) A.5×(-6)=(-6)×5 B.14-12×(-12)=(-12)×14-12 C.-16+13×(-4)=(-4)×-16+13×4 D.(-25)×(-16)×(-4)=[(-25)×(-4)]×(-16)
根据上述解答过程填空:
第①步,运用几个不为 0 的有理数的乘法法则,首先确定积的
符号,有三个负数,则积为____负____,再将四个因数的绝对值
___相_乘____,而第②步,将带分数化为假分数,小数化为分数,
5
7
故 的② 计中 算分 结别 果填 为____-__31__52__4______, .____3____,再计算括号内的值,最后
1.4.1 第3课时 有理数的乘法运算律 11. 计算: (1)3×105-(-5)×105+(-1)×105;
(2)317×2212×317-713×-272;
(3)(-3.61)×0.75+0.61×34+(-0.2)×75%;
(4)37×153-194-134×-1113-37×133.
1.4.1 第3课时 有理数的乘法运算律
1 (2)-2532×8.
《有理数的乘法运算律》课时练习含答案

《有理数的乘法运算律》课时练习含答案能力提升1.大于-3且小于4的所有整数的积为()A.-12B.12C.0D.-1442.3.125×(-23)-3.125×77=3.125×(-23-77)=3.125×(-100)=-312.5,这个运算运用了()A.加法结合律B.乘法结合律C.分配律D.分配律的逆用3.下列运算过程有错误的个数是()①×2=3-4×2②-4×(-7)×(-125)=-(4×125×7)③9×15=×15=150-④[3×(-25)]×(-2)=3×[(-25)×(-2)]=3×50A.1B.2C.3D.44.绝对值不大于2 015的所有整数的积是.5.在-6,-5,-1,3,4,7中任取三个数相乘,所得的积最小是,最大是.6.计算(-8)×(-2)+(-1)×(-8)-(-3)×(-8)的结果为.7.计算(1-2)×(2-3)×(3-4)×…×(2 014-2 015)×(2 015-2 016)的结果是.8.计算:(1)×8;(2)(-11)×+(-11)×+(-11)×.9.计算:×…×.10.已知|a+1|+|b+2|+|c+3|=0,求(a-1)×(b-2)×(c-3)的值.11.已知称为二阶行列式,规定的运算法则为=ad-bc,例如=3×4-5×2=2.根据上述内容计算的值.★12.观察下列等式(式子中的“!”是一种数学运算符号):1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…….求的值.创新应用★13.学习了有理数的运算后,王老师给同学们出了这样一道题: 计算71×(-8),看谁算得又对又快.下面是两位同学给出的不同解法:小强:原式=-×8=-=-575;小莉:原式=×(-8)=71×(-8)+×(-8)=-575.(1)以上两种解法,你认为谁的解法比较简便?(2)你还有其他解法吗?如果有,那么请写出解答过程;(3)你能用简便方法计算-99×198吗?如果能,那么请写出解答过程.参考答案能力提升1.C大于-3且小于4的所有整数中有一个为0,故乘积为0.2.D3.A①错误,3也应乘2;②③④正确.4.0符合条件的整数中有一个为0,所以它们的积为0.5.-1682106.0原式=(-8)×[(-2)+(-1)-(-3)]=(-8)×[(-2)+(-1)+(+3)]=(-8)×0=0.7.-1原式==-1.8.解:(1)原式=×8=-100×8+×8=-800+=-799.(2)原式=(-11)×=-11×2=-22.9.解:原式=×…×=-×…×=-.10.解:因为|a+1|+|b+2|+|c+3|=0,所以a+1=0,b+2=0,c+3=0,所以a=-1,b=-2,c=-3.所以原式=(-1-1)×(-2-2)×(-3-3)=(-2)×(-4)×(-6)=-48.11.解:×2=.12.解:=2016.创新应用13.解:(1)小莉的解法比较简便.(2)有,原式=×(-8)=72×(-8)-×(-8)=-575.(3)能,原式=-×198=-100×198+×198=-19800+2=-19798.。
有理数的乘除法(含答案)

1.4 有理数的乘除法●知识单一性训练1.4.1 有理数的乘法一、有理数的乘法法则及其运算律1.一个有理数和它的相反数相乘,积为()A.正数 B.负数 C.正数或0 D.负数或02.计算(-3)×(4-12),用分配律计算过程正确的是()A.(-3)×4+(-3)×(-12) B.(-3)×4-(-3)×(-12)C.3×4-(-3)×(-12) D.(-3)×4+3×(-12)3.下列说法正确的是()A.异号两数相乘,取绝对值较大的因数的符号; A.异号两数相乘,取绝对值较大的因数的符号;B.同号两数相乘,符号不变;C.两数相乘,如果积为负数,那么这两个因数异号;D.两数相乘,如果积为正数,那么这两个因数都为正数4.已知abc>0,a>c,ac<0,下列结论正确的是()A.a<0,b<0,c>0 B.a>0,b>0,c<0C.a>0,b<0,c<0 D.a<0,b>0,c>05.如果ab=0,那么一定有()A.a=b=0 B.a=0 C.b=0 D.a,b至少有一个为06.计算:(1)-2(m+3)+3(m-2);(2)5(y+1)-10×(y-110+15).7.若有理数m<n<0时,确定(m+n)(m-n)的符号.8.小林和小华二人骑自行车的速度分别为每小时12千米和每小时11千米,•若两人都行驶2小时,小林和小华谁走的路程长?长多少千米?9.登山队员攀登珠穆朗玛峰,在海拔3000m时,气温为-20℃,已知每登高1000m,•气温降低6℃,当海拔为5000m和8000m时,气温分别是多少?二、多个有理数相乘积的符号的确定10.三个数的积是正数,那么三个数中负数的个数是()A.1个 B.0个或2个 C.3个 D.1个或3个11.下面计算正确的是()A.-5×(-4)×(-2)×(-2)=80B.(-12)×(13-14-1)=0C.(-9)×5×(-4)×0=180D.-2×5-2×(-1)-(-2)×2=812.绝对值不大于4的整数的积是()A.6 B.-6 C.0 D.2413.在-2,3,4,-5这四个数中,任取两个数相乘,所得的积最大的是_______.14.若干个有理数相乘,其积是负数,则负因数的个数是_______.15.+(16)×5911×(-29.4)×0×(-757)=______.16.-4×125×(-25)×(-8)=________.17.计算:(1)(-10)×(-13)×(-0.1)×6;(2)-3×56×145×(-0.25).1.4.2 有理数的除法三、有理数的除法法则18.若两个有理数的商是正数,和为负数,则这两个数()A.一正一负 B.都是正数 C.都是负数 D.不能确定19.若两个数的商是2,被除数是-4,则除数是()A.2 B.-2 C.4 D.-420.一个非0的有理数与它的相反数的商是()A.-1 B.1 C.0 D.无法确定21.若ab>0,则的值是()A.大于0 B.小于0 C.大于或等于0 D.小于或等于022.两个不为零的有理数相除,如果交换被除数与除数的位置,它们的商不变,那么这两个数()A.一定相等 B.一定互为倒数C.一定互为相反数 D.相等或互为相反数23.当x=_______时,51x没有意义.24.若一个数与它的绝对值的商是1,则这个数是______数;若一个数与它的绝对值的商是-1,则这个数是_______数.25.两个因数的积为1,已知其中一个因数为-72,那么另一个因数是_______.26.若||mm=1,则m________0.27.某地探测气球的气象观测资料表明,高度每增加1千米,气温大约降低6℃,若该地面温度为21℃,高空某处温度为-39℃,求此处的高度是多少千米.四、有理数的乘除混合运算28.计算(-1)÷(-10)×110的结果是()A.1 B.-1 C.1100D.-110029.(-113)÷(-3)×(-13)的值是______.30.若ab<0,bc<0,则ac________0.31.计算:(1)-34×(-112)÷(-214);(2)15÷(-5)÷(-115);(3)(-3.5)÷78×(-34).五、有理数加减乘除混合运算32.计算(-12)÷[6+(-3)]的结果是()A.2 B.6 C.4 D.-4 33.计算:(1)(-1117)×15+(+517)×15+(-13713)÷5+(+11313)÷5;(2)-8-[-7+(1-23×0.6)÷(-3)].34.已知│3-y│+│x+y│=0,求x yxy的值.●能力提升性训练1.现有四个有理数3,4,-6,10,运用有理数的四则混合运算写出三种不同方法的运算式,使其结果等于24,运算如下:(1)______,(2)_____,(3)______,另有四个有理数,3,-5,7,-13时,可通过运算式(4)________,使其结果等于24.2.计算:(1)-3y+0.75y-0.25y;(2)5a-1.5a+2.4a.3.计算:(1)3(2m-13);(2)-7y+(2y-3)-2(3y+2).4.某班分小组举行知识竞赛,评分标准是:答对一道题加10分,•答错一道题扣10分,不答不得分.已知每个小组的基本分为100分,有一个小组共答20道题,•其中答对了10道题,不答的有2道题,结合你学过的有理数运算的知识,求该小组最后的得分是多少.5.已知a的相反数是123,b的相反数是-212,求代数式32a ba b+-的值.6.若定义一种新的运算为a*b=1abab-,计算[(3*2)]*16.7.若│a+1│+│b+2│=0,求:(1)a+b-ab;(2)ba+ab.8.已知a,b互为相反数,c,d互为倒数,且a≠0,那么3a+3b+ba-cd的值是多少?●针对性训练1.计算(-245)×(-2.5); 2.计算(-114)×(+45).3.计算-13×23-0.34×27+13×(-13)-57×0.34.4.计算37÷5×15; 5.计算(-112)×(-34)÷(-214).6.计算(-11223)()4267314÷-+-; 7.计算(213-312+1445)÷(-116).●中考全接触1.(2005,厦门)下列计算正确的是()A.-1+1=0 B.-1-1=0 C.3÷13=1 D.3=62.(2006,长春)化简m-n-(m+n)的结果是()A.0 B.2m C.-2n D.2m-2n3.(2006,浙江)若家用电冰箱冷藏室的温度是4℃,•冷冻室的温度比冷藏室的温度低22℃,则冷冻室的温度是()A.18℃ B.-26℃ C.-22℃ D.-18℃4.(2006,南昌)下列四个运算中,结果最小的是()A.1+(-2) B.1-(-2) C.1×(-2) D.1÷(-2)5.(2005,江西)计算(-2)×(-4)=_______.6.(2005,云南)计算(-12)×(-14)=________.7.(2005,陕西)5×(-4.8)+│-2.3│=________.8.(2006,温州)若x-y=3,则2x-2y=________.9.(2005,南通)计算(-12+23-14)×│-12│.答案:【知识单一性训练】1.D [提示:如1×(-1)=-1,一个正数和一个负数相乘,积为负数,但不要漏掉0的情况.]2.A [提示:(-3)×(4-12)=(-3)×[4+(-12)]=(-3)×4+(-3)×(-12),强调过程,而不是结果.]3.C [提示:根据有理数乘法法则,例如-2×4=-8,A错;(-2)×(-4)=8,B错;(-2)•×(-5)=10,D错.故C正确.]4.C [提示:由ac<0,得a与c异号,由a>c,得a>0,c<0.由abc>0,得b<0,故选C.] 5.D [提示:0同任何数相乘都得0.]6.解:(1)-2(m+3)+3(m-2)=-2m-6+3m-6=m-12.(2)5(y+1)-10×(y-110+15)=5y+5-10y+1-2=-5y+4.7.解:因为m<n<0,所以│m│>│n│,m+n<0,所以m-n<0,所以(m+n)(m-n)>0,•即(m+n)(m-n)的符号为正.8.解:小林走的路程为12×2=24(千米),小华走的路程为11×2=22(千米),• 因为24>22,所以小林走的路程比小华长,小林比小华多走24-22=2(千米),答:小林走的路程比小华长2千米.9.解:当海拔为5000m时,-20-500030001000-×6=-32(℃);当海拔为8000m时,-20-800030001000-×6=-50℃,•因此当海拔为5000m时,气温为-32℃,当海拔为8000m时,气温为-50℃.10.B [提示:几个不为零的有理数相乘,积的符号由负因数的个数决定,• 因为三个数的积是正数,所以负因数为偶数个或0个,故选B.]11.A [提示:(-12)×(13-14-1)=(-12)×13+(-12)×(-14)+(-12)×(-1)=-4+3+12=11;(-9)×5×(-4)×0=0;-2×5-2×(-1)-(-2)×2=-10+2+4=-4,故B,C,D都错,A对.]12.C [提示:绝对值不大于4的整数为0,±1,±2,±3,±4,所以它们的积为0,故选C.]13.12 [提示:3×4=12,其余积为负数和小于12.]14.奇数 [提示:由几个不为零的有理数相乘的法则可知.]15.0 [提示:任何有理数同0相乘都得0.]16.-100000 [提示:原式=-(4×125×25×8)=-100000.]17.解:(1)(-10)×(-13)×(-0.1)×6=-(10×13×110×6)=-2.(2)-3×56×145×(-0.25)=3×56×95×14=98.18.C [提示:从商为正数得出两个数同号,从和为负数得出两个数都为负数,• 若两个数都为正数,积只能为正数.]19.B [提示:分清除数、被除数的含义,用-4÷2=-2.]20.A [提示:可取特殊值计算,如:2的相反数是-2,那么2÷(-2)=-1,故选A.]21.A [提示:由ab>0可得a,b同号,则ab是正数.]22.D [提示:不要漏掉互为相反数这种情况.]23.1 [提示:当x=1时,x-1=0,除数为0,没意义.]24.正负 [提示:正数的绝对值是它本身,负数的绝对值是它的相反数.]25.-27[提示:另一个因数是1÷(-72)=-27.]26.> [提示:若m>0,│m│=m,则||mm=mm=1;若m<0,│m│=-m,则||mm=mm-=-1,m为分母,•不能等于0.]27.解:21(39)6--×1=10(千米),答:此处的高度是10千米.28.C [提示:(-1)÷(-10)×110=(-1)×(-110)×110=1100.故选C.]29.-427[提示:原式=(-43)×(-13)×(-13)=-427.]30.> [提示:因为ab<0,所以a,b异号,又因为bc<0,所以b,c异号,所以a,c同号,故ac>0.]31.解:(1)-34×(-112)÷(-214)=-34×(-32)×(-89)=-1.(2)-15÷(-5)÷(-115)=-15×(-15)•×(-56)=-52.(3)(-3.5)÷78×(-34)=(-72)×87×(-34)=3.32.D [提示:(-12)÷[6+(-3)]=(-12)÷3=-4,故选D.]33.解:(1)(-1117)×15+(+517)×15+(-13713)÷5+(+11313)÷5=(-1117)×15+(+517)×15+(-13713)×15+(+11313)×15=15×[(-1117)+(+517)+(-13713)+(+11313)]=15×[-6+(-24)]=15×(-30)=-6.(2)-8-[-7+(1-23×0.6)÷(-3)]=-8-[-7+(1-23×35)×(-13)]=-8-[-7+(1-25)×(-13)]=-8-[-7+35×(-13)]=-8-(-7-15)=-8+715=-45.34.解:│3-y│+│x+y│=0,且│3-y│≥,│x+y│≥0,所以3-y=0,x+y=0,•所以y=3,x=-3,所以330339x yxy+-+==-⨯-=0.【能力提升性训练】1.(1)4-(-6×10)÷3 (2)(10-6+4)×3 (3)10-[3×(-6)]-4 (4)[(-5)×(-13)+7]÷3 2.解:(1)-3y+0.75y-0.25y=(-3+0.75-0.25)y=-2.5y.(2)5a-1.5a+2.4a=(5-1.5+2.4)a=5.9a.3.解:(1)3(2m-13)=3×2m-3×13=6m-1.(2)-7y+(2y-3)-2(3y+2)=-7y+2y-3-2×3y+(-2)×2=-7y+2y-3-6y-4=(-7+2-•6)y-7=-11y-7.4.解:根据题意,得100+10×10+(20-10-2)×(-10)=100+100-80=120(分).答:该小组最后的得分是120分.5.解:因为a的相反数是123,则a=-123,因为b的倒数是-212,则b=1÷(-212)=-25.所以32a ba b+-=2213()352212()35-+⨯---⨯-=(-53-65)÷(-53+45)=(-251825124313431543)()()()151515151515151313-÷-+=-÷-=⨯=.6.解:因为a*b=1abab-,所以[(3*2)*16=32132⨯-⨯*16=(-65)*16=6115656111()1565-⨯-=--⨯+=-16.7.解:因为│a+1│+│b+2│=0,且│a+1│≥0,│b+2│≥0,所以a+1=0,b+2=0,• 所以a=-1,b=-2,所以,(1)a+b-ab=-1+(-2)-(-1)×(-2)=-3-2=-5.(2)ba+ab=2112--+--=2+12=52.8.解:因为a,b互为相反数,所以a+b=0,ba=-1.因为c,d互为倒数,所以c.d=1,•所以3a+3b+ba-cd=3(a+b)+ba-cd=3×0+(-1)-1=-2.【针对性训练】1.解:(-245)×(-2.5)=(-145)×(-52)=7.2.解:(-114)×(+45)=(-54)×(+45)=-1.3.解:-13×23-0.34×27+13×(-13)-57×0.34=-13×23+13×(-13)-0.34×27-57×0.34=-13×(23+13)-0.34×(27+57)=-13×1-0.34×1=-13-0.34=-13.34.4.解:37÷5×15=37×15×15=3725.5.解:(-112)×(-34)÷(-214)=(-32)×(-34)×(-94)=-(32×34×94)=-12.6.解:(-11223114245618 )()()() 42673144284-+-÷-+-=-÷1281841 ()().4284422814 =-÷=-⨯=-7.解:(213-312+1445)÷(-116)=(73-72+4945)×(-67)=73×(-67)+(-72)×(-67)+4945×(-67)=-2+3-141411151515=-=.【中考全接触】【中考全接触】1.A [提示:互为相反数的和为0.]2.C [提示:去括号时,要注意括号前的符号.] 3.D [提示:4-22=-18(℃).]4.C [提示:1+(-2)=-1,1-(-2)=1+2=3,1×(-2)=-2,1÷(-2)=-12,通过比较C最小.]5.8 [提示:同号相乘得正.] 6.1 87.-21.7 [提示:注意运算顺序.] 8.6 [提示:2x-2y=2(x-y)=2×3=6.]9.解:(-12+23-14)×│-12│=(-12+23-14)×12=(-12)×12+23×12+(-14)×12=-6+8-3=-1.。
人教版数学七年级上册:1.4.1 第2课时《有理数乘法的运算律及运用》练习课件(附答案)

(2)999×118 4 +999×(-1 )-999×18 3 .
5
5
5
解:原式=(118 4 - 1 -18 3 )×999=100×999= 55 5
99900.
16.某儿童服装店老板以 32 元的价格购进 30 件衣 服,针对不同的顾客,30 件衣服的售价不完全相 同.若以 47 元为标准,将超出的钱数记为正,不足 的钱数记为负,记录结果如下表: 售出件数 7 6 3 5 4 5
简便的是( C )
A.(2+ 1 )×(-98) B.(3-19 )×(-98)
20
20
C. 41×(-100+2) D. 41×(-90-8)
20
20
7.算式(-0.125)×7×(-8)的值为( D )
A.-7000 B.7000 C.-7 D.7
8.在算式每一步的后面填上该步运用的运算律:
(8
4.计算:
(1)(-4)×(-18)×(-25);
解:原式=-1800.
(2) 4 ×(- 25 )×(- 7 );
5
6
10
解:原式= 7 . 3
(3) 5 ×(-1.2)×(- 1 );
4
9
解:原式= 1 . 6
(4)-0.01× 1 ×(-15)×0×(-2019). 2016
解:原式=0.
快速对答案
1C
7D
乘法交换律
2C
8 乘法结合律
分配律
3
①④ ② 0
9 详细答案
点击题序
4
详细答案 点击题序
10 D
5D
11 D
6C
12 D
提示:点击 进入习题
13 -6
有理数的乘法及运算律练习

七年级数学上---《有理数的乘法的运算律》 乘法交换律: 字母表示:乘法结合律: 字母表示 乘法分配律: 字母表示: 练习:1、五个数相乘,积为负,那么其中负因数的个数是( ).A 、1B 、3C 、5D 、1或3或52、绝对值不大于4的所有整数的积是______________,和是_______.3、如果abcd <0,a +b =0,cd >0,那么这四个数中负因数的个数至少有( )A 、4个B 、3个C 、2个D 、1个4、计算下列各题:(1)5(6)()(4)4-⨯-⨯- (2)()2305⨯⨯- (3)11()()(2)26-⨯-⨯- (4) 114()30235-+-⨯5.计算:①(-8)×(-12)×(-0.125)×(- 31)×(-0.1) ②60×(1-21-31- 41)③(-43 )×(8-311-4 ) ④ 12216141⨯+)—(⑤ (-11)×(-52 )+(-11)×253 +(-11)×(- 51 )课后作业;计算:1. 76×(-3)+24×(-3)2. 86×(-491)+86×(-509)3. 2018 (-15)-18 (-15)4. 123 (-25)-377 255. (-426) 251-426 7496. 95 (-38)-95 88-95 (-26)7.54×(-95)+38×(-95)-8×95 8. ∣-99×73∣+205×73-4×73有理数乘法小测1、计算:⑴5×(-4)=_____ ⑵(-6)×4=____ ⑶(-7)×(-1)=____ ⑷(-5)×0=___⑸(-3)×(-0.3)=______ ⑹=-⨯-)32()61(____ ⑺(-3)×=-)31(____ ⑻=-⨯)23(94 _____ ⑼(-521)×(331)=____ ⑽(+32)×(-60.6)×0×(-931)=______ 2、填空:⑴-7的倒数是_____,它的相反数是______,它的绝对值是_____;522-的倒数是____; -2.5的倒数是_____;倒数等于它本身的有理数是_____;32-的倒数的相反数是________。
有理数的乘除乘方运算(含答案)

有理数的运算(乘、除、乘方)教学目的:1、 理解有理数的乘法法则;掌握异号两数的乘除运算的规律:2、 会进行有理数的乘法、除法、乘方的运算,能灵活运用运算律进行简化运算。
教学重点:1、 有理数的乘法、除法法则:2、 熟练的进行有理数乘法、除法、乘方运算。
教学难点:若干个有理数柑乘,积的符号的确定,乘方的符号确世。
有理数的乘法有理数的乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。
例题目的:掌握有理数的乘法法则。
有理数乘法法则的推广:(1) 几个不等于0的数相乘,积的符号由负因数的个数决定。
当负数的个数为奇数时,积为负,当负因数为偶数个时,积为正。
(2) 几个数相乘,有一个因数为0,积为0. ⑵ 1^X (-1)X (-2.5)X (-A) 3 9 25例®目的:会算两个以上有理数的乘法,并能判定积的符号。
有理数乘法的运算律:衽有理数运算中,乘法的交换律,结合律以及乘法对加法的分配律仍然成立。
乘法交换律:两个数相乘,交换因数的位S,积不变,用式子表示为a b=b a例1:计算⑴(-5)x(-3)⑵(一7)x41 7例 2: (I) -X(--)x(-4)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.用式子表示成(a ・b)・c=a ・(b ・c)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘. 用字母表示成-a(b+c)=a ・b+a ・c⑶7唏心)例題目的:掌握有理数乘法的运算律。
有理数的除法法则两个有理数相除,同号得正,异号向负,并把绝对值相除。
0除以任何非0的 数都得0。
倒数与负倒数的概念:乘积为1的两个有理数互为倒数,即若a, b 互为倒数,则ah = l ; 乘积为一1的两个有理数互为负倒数,即若互为负倒褻 则a b = -l法则2:除以一个数等于乘以这个数的倒数,即《4 ="・一0式0) b 例4: 1.求下列各■数的倒数,负倒数。
有理数的乘法及运算律练习
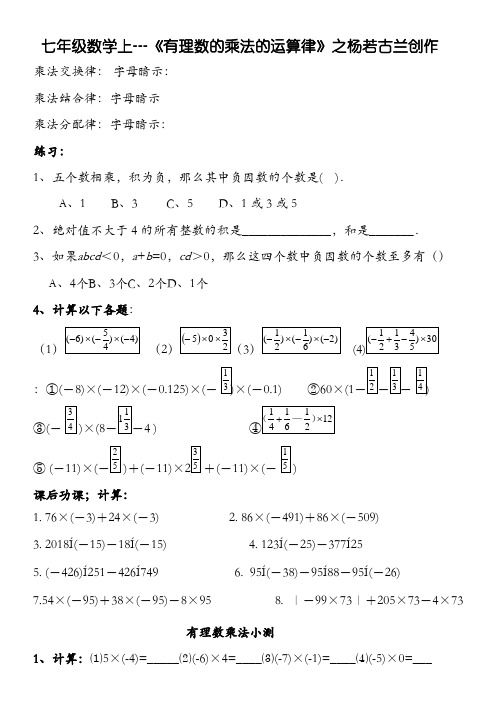
七年级数学上---《有理数的乘法的运算律》之杨若古兰创作乘法交换律:字母暗示:乘法结合律:字母暗示乘法分配律:字母暗示:练习:1、五个数相乘,积为负,那么其中负因数的个数是( ).A、1B、3C、5D、1或3或52、绝对值不大于4的所有整数的积是______________,和是_______.3、如果abcd<0,a+b=0,cd>0,那么这四个数中负因数的个数至多有()A、4个B、3个C、2个D、1个4、计算以下各题:(1(23:①(-8)×(-12)×(-0.125)×(-×(-0.1) ②60×(1③(-×(8 4 )⑤ (-11)×(+(-11)×+(-11)×(-课后功课;计算:1. 76×(-3)+24×(-3)2. 86×(-491)+86×(-509)3. 2018Í(-15)-18Í(-15)4. 123Í(-25)-377Í255. (-426)Í251-426Í7496. 95Í(-38)-95Í88-95Í(-26)7.54×(-95)+38×(-95)-8×95 8. ∣-99×73∣+205×73-4×73有理数乘法小测1、计算:⑴5×(-4)=_____⑵(-6)×4=____⑶(-7)×(-1)=____⑷(-5)×0=___⑸(-3)×(-0.3)=______⑺(-3)⑼(-____⑽(+32)×(-60.6)×0______2、填空:⑴-7的倒数是_____,它的相反数是______,它的绝对值是_____是____;-2.5的倒数是_____;倒数等于它本人的有理数是_____是________.⑵若|a|=5,b=-2,ab>0,则a+b=_____⑶绝对值大于1,小于4的所有整数的积是______;绝对值不大于5的所有负整数的积是_____3、选择:4、⑴一个有理数与其相反数的积()A、符号肯定为正B、符号肯定为负C、必定不大于零D、必定不小于零⑵以下说法错误的是()A、任何有理数都有倒数 B、互为倒数的两个数的积为1C、互为倒数的两个数同号D、1和-1互为负倒数⑶已知两个有理数a,b,如果ab<0,且a+b<0,那么()A、a>0,b>0B、a<0,b>0C、a,b异号D、a,b异号,且负数的绝对值较大⑷以下算式中,积为负数的是()A(-2)×(+5) B(-6)×(-2) C、0×(-1) D(+5)×(-2)⑸以下说法准确的是() A、异号两数相乘,取绝对值较大的因数的符号B.同号两数相乘,符号不变;C.两数相乘,如果积为负数,那么这两个因数异号D.两数相乘,如果积为负数,那么这两个因数都是负数⑹计算(-1)的结果是()A.-.-.-.⑺如果ab=0,那么必定有()A.a=b=0 B.a=0 C.a,b至多有一个为0 D.a,b最多有一个为0⑻上面计算准确的是() A、-5×(-4)×(-2)×(-2)=5×4×2×2=80B.12×(-5)=-50;C.(-9)×5×(-4)×0=9×5×4=180 D.(-36)×(-1)=-364、计算:56、若a,b互为相反数,c,d互为倒数,m的绝对值是1.。
有理数的乘法及运算律练习

七年级数学上---《有理数的乘法的运算律》之迟辟智美创作 乘法交换律: 字母暗示:乘法结合律:字母暗示乘法分配律:字母暗示:练习:1、五个数相乘,积为负,那么其中负因数的个数是( ).A 、1B 、3C 、5D 、1或3或52、绝对值不年夜于4的所有整数的积是______________,和是_______.3、如果abcd <0,a+b=0,cd >0,那么这四个数中负因数的个数至少有()A 、4个B 、3个C 、2个D 、1个4、计算下列各题:(1)5(6)()(4)4-⨯-⨯- (2)()2305⨯⨯-(3)11()()(2)26-⨯-⨯- (4)114()30235-+-⨯ 5.计算:①(-8)×(-12)×(-0.125)×(- 31)×(-0.1) ②60×(1-21-31- 41) ③(- 43 )×(8-311-4 ) ④12216141⨯+)—( ⑤ (-11)×(-52 )+(-11)×253 +(-11)×(- 51 ) 课后作业;计算:1. 76×(-3)+24×(-3)2. 86×(-491)+86×(-509)3. 2018(-15)-18(-15) 4. 123(-25)-377255. (-426)251-426749 6. 95(-38)-9588-95(-26)7.54×(-95)+38×(-95)-8×95 8. ∣-99×73∣+205×73-4×73有理数乘法小测1、计算:⑴5×(-4)=_____⑵(-6)×4=____⑶(-7)×(-1)=____⑷(-5)×0=___ ⑸(-3)×(-0.3)=______⑹=-⨯-)32()61(____⑺(-3)×=-)31(____⑻=-⨯)23(94 _____ ⑼(-521)×(331)=____⑽(+32)×(-60.6)×0×(-931)=______ 2、填空:⑴-7的倒数是_____,它的相反数是______,它的绝对值是_____;522-的倒数是____;-2.5的倒数是_____;倒数即是它自己的有理数是_____;32-的倒数的相反数是________.⑵若|a|=5,b=-2,ab>0,则a+b=_____⑶绝对值年夜于1,小于4的所有整数的积是______;绝对值不年夜于5的所有负整数的积是_____3、选择:4、⑴一个有理数与其相反数的积( )A 、符号肯定为正B 、符号肯定为负C 、一定不年夜于零D 、一定不小于零⑵下列说法毛病的是( )A 、任何有理数都有倒数 B 、互为倒数的两个数的积为1C 、互为倒数的两个数同号D 、1和-1互为负倒数⑶已知两个有理数a,b ,如果ab <0,且a+b <0,那么( )A 、a >0,b >0B 、a <0,b >0C 、a,b 异号D 、a,b 异号,且负数的绝对值较年夜⑷下列算式中,积为正数的是( )A(-2)×(+5) B(-6)×(-2) C 、0×(-1) D(+5)×(-2)⑸下列说法正确的是( ) A 、异号两数相乘,取绝对值较年夜的因数的符号B .同号两数相乘,符号不变;C .两数相乘,如果积为负数,那么这两个因数异号D .两数相乘,如果积为正数,那么这两个因数都是正数⑹计算(-221)×(-331)×(-1)的结果是( ) A .-661B .-551 C .-831D .565⑺如果ab =0,那么一定有( )A .a =b =0B .a =0C .a ,b 至少有一个为0D .a ,b 最多有一个为0 ⑻下面计算正确的是( ) A 、-5×(-4)×(-2)×(-2)=5×4×2×2=80B .12×(-5)=-50;C .(-9)×5×(-4)×0=9×5×4=180D .(-36)×(-1)=-364、计算: ⑴)5(252449-⨯⑵125)5.2()2.7()8(⨯-⨯-⨯-⑶6.190)1.8(8.7-⨯⨯-⨯- ⑷)251(4)5(25.0-⨯⨯-⨯--⑸)32()109(45)2(-⨯-⨯⨯-⑹(-6)×5×72)67(⨯- ⑺(-4)×7×(-1)×(-0.25) ⑿34.075)13(317234.03213⨯--⨯+⨯-⨯- ⑻41)23(158)245(⨯-⨯⨯-⑼)8141121()8(+-⨯- ⑾)543()411(-⨯-⑽)48()6143361121(-⨯-+--. 5、已知,032=-++y x 求xy y x 435212+--的值. 6、若a,b 互为相反数,c,d 互为倒数,m 的绝对值是1,求m cd b a 2009)(-+的值.。
人教版初中七年级上册数学《有理数乘法的运算律及运用》练习题

1.4 有理数的乘除法1.4.1 有理数的乘法第2课时 有理数乘法的运算律及运用1、已知两个有理数a,b ,如果ab <0,且a+b <0,那么( )A 、a >0,b >0B 、a <0,b >0C 、a,b 异号D 、a,b 异号,且负数的绝对值较大2、计算:(1))32()109(45)2(-⨯-⨯⨯-; (2)(-6)×5×72)67(⨯-;(3)(-4)×7×(-1)×(-0.25);(4)41)23(158)245(⨯-⨯⨯-3、计算:(1))5(252449-⨯; (2)125)5.2()2.7()8(⨯-⨯-⨯-;(3)6.190)1.8(8.7-⨯⨯-⨯-; (4))251(4)5(25.0-⨯⨯-⨯--。
4、已知,032=-++y x 求xy y x 435212+--的值。
5、若a,b 互为相反数,c,d 互为倒数,m 的绝对值是1,求m cd b a 2009)(-+的值。
参考答案1、D .ab <0,说明a,b 异号;又a+b <0,说明负数的绝对值较大2、(1)23)32109452()32()109(45)2(-=⨯⨯⨯-=-⨯-⨯⨯-;(2)(-6)×5×1072675672)67(=⨯⨯⨯=⨯-;(3)(-4)×7×(-1)×(-0.25)=7)41174(-=⨯⨯⨯-;(4)241412315824541)23(158)245(=⨯⨯⨯=⨯-⨯⨯-3、(1)54249)5(251)5(50)5()25150()5(252449-=-⨯--⨯=-⨯-=-⨯;(2)60)125255368(125)5.2()2.7()8(-=⨯⨯⨯-=⨯-⨯-⨯-;(3)06.190)1.8(8.7=-⨯⨯-⨯-;(4)51)251(4)5(25.0)251(4)5(25.0-=-⨯⨯-⨯-=-⨯⨯-⨯--。
有理数的乘法及运算律练习

七年级数学上--- 【2 】《有理数的乘法的运算律》乘法交流律: 字母表示:乘法联合律:字母表示乘法分派律:字母表示:演习:1.五个数相乘,积为负,那么个中负因数的个数是( ).A.1B.3C.5D.1或3或52.绝对值不大于4的所有整数的积是______________,和是_______.3.假如abcd <0,a +b =0,cd >0,那么这四个数中负因数的个数至少有()A.4个B.3个C.2个D.1个4.盘算下列各题:(1)5(6)()(4)4-⨯-⨯- (2)()2305⨯⨯-(3)11()()(2)26-⨯-⨯- (4)114()30235-+-⨯5.盘算:①(-8)×(-12)×(-0.125)×(- 31)×(-0.1) ②60×(1-21-31- 41)③(- 43 )×(8-311-4 ) ④12216141⨯+)—(⑤ (-11)×(-52 )+(-11)×253 +(-11)×(- 51)课后功课;盘算:1. 76×(-3)+24×(-3)2. 86×(-491)+86×(-509)3. 2018 (-15)-18 (-15)4. 123 (-25)-377 255. (-426) 251-426 7496. 95 (-38)-95 88-95 (-26)7.54×(-95)+38×(-95)-8×95 8. ∣-99×73∣+205×73-4×73有理数乘法小测⑸(-3)×(-0.3)=______⑹=-⨯-)32()61(____⑺(-3)×=-)31(____⑻=-⨯)23(94 _____ ⑼(-521)×(331)=____⑽(+32)×(-60.6)×0×(-931)=______ 2.填空:⑴-7的倒数是_____,它的相反数是______,它的绝对值是_____;522-的倒数是____; -2.5的倒数是_____;倒数等于它本身的有理数是_____;32-的倒数的相反数是________. ⑵若|a|=5,b=-2,ab>0,则a+b=_____⑶绝对值大于1,小于4的所有整数的积是______;绝对值不大于5的所有负整数的积是_____3、选择: 4.⑴一个有理数与其相反数的积( )A 、符号必定为正 B.符号必定为负 C.必定不大于零 D.必定不小于零⑵下列说法错误的是( )A.任何有理数都有倒数 B.互为倒数的两个数的积为1C.互为倒数的两个数同号D.1和-1互为负倒数⑶已知两个有理数a,b,假如ab <0,且a+b <0,那么( )A 、a >0,b >0 B.a <0,b >0 C.a,b 异号 D.a,b 异号,且负数的绝对值较大⑷下列算式中,积为正数的是( )A(-2)×(+5) B(-6)×(-2) C.0×(-1) D(+5)×(-2) ⑸下列说法准确的是( ) A.异号两数相乘,取绝对值较大的因数的符号B .同号两数相乘,符号不变;C .两数相乘,假如积为负数,那么这两个因数异号D .两数相乘,假如积为正数,那么这两个因数都是正数⑹盘算(-221)×(-331)×(-1)的成果是( ) A .-661B .-551 C .-831D .565 ⑺假如ab =0,那么必定有( )A .a =b =0B .a =0C .a,b 至少有一个为0D .a,b 最多有一个为0⑻下面盘算准确的是( ) A.-5×(-4)×(-2)×(-2)=5×4×2×2=80B .12×(-5)=-50;C .(-9)×5×(-4)×0=9×5×4=180D .(-36)×(-1)=-364.盘算: ⑴)5(252449-⨯⑵125)5.2()2.7()8(⨯-⨯-⨯-⑶6.190)1.8(8.7-⨯⨯-⨯- ⑷)251(4)5(25.0-⨯⨯-⨯--⑸)32()109(45)2(-⨯-⨯⨯-⑹(-6)×5×72)67(⨯- ⑺(-4)×7×(-1)×(-0.25) ⑿34.075)13(317234.03213⨯--⨯+⨯-⨯- ⑻41)23(158)245(⨯-⨯⨯-⑼)8141121()8(+-⨯- ⑾)543()411(-⨯-⑽)48()6143361121(-⨯-+--. 5.已知,032=-++y x 求xy y x 435212+--的值. 6.若a,b 互为相反数,c,d 互为倒数,m 的绝对值是1,求m cd b a 2009)(-+的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《有理数的乘法运算律》课时练习含答案
能力提升
1.大于-3且小于4的所有整数的积为()
A.-12
B.12
C.0
D.-144
2.3.125×(-23)-3.125×77=3.125×(-23-77)=3.125×(-100)=-312.5,那个运算运用了()
A.加法结合律
B.乘法结合律
C.分配律
D.分配律的逆用
3.下列运算过程有错误的个数是()
①×2=3-4×2
②-4×(-7)×(-125)=-(4×125×7)
③9×15=×15=150-
④[3×(-25)]×(-2)=3×[(-25)×(-2)]=3×50
A.1
B.2
C.3
D.4
4.绝对值不大于2 015的所有整数的积是.
5.在-6,-5,-1,3,4,7中任取三个数相乘,所得的积最小是,最大是.
6.运算(-8)×(-2)+(-1)×(-8)-(-3)×(-8)的结果为.
7.运算(1-2)×(2-3)×(3-4)×…×(2 014-2 015)×(2 015-2 016)的结果是.
8.运算:
(1)×8;
(2)(-11)×+(-11)×+(-11)×.
9.运算:×…×.
10.已知|a+1|+|b+2|+|c+3|=0,求(a-1)×(b-2)×(c-3)的值.
11.已知称为二阶行列式,规定的运算法则为=ad-bc,例如=3×4-5×2=2.依照上述内容运算的值.
★12.观看下列等式(式子中的“!”是一种数学运算符
号):1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…….求的值.
创新应用
★13.学习了有理数的运算后,王老师给同学们出了如此一道题: 运算71×(-8),看谁算得又对又快.
下面是两位同学给出的不同解法:
小强:原式=-×8=-=-575;
小莉:原式=×(-8)=71×(-8)+×(-8)=-575.
(1)以上两种解法,你认为谁的解法比较简便?
(2)你还有其他解法吗?假如有,那么请写出解答过程;
(3)你能用简便方法运算-99×198吗?假如能,那么请写出解答过程.
参考答案
能力提升
1.C大于-3且小于4的所有整数中有一个为0,故乘积为0.
2.D
3.A①错误,3也应乘2;②③④正确.
4.0符合条件的整数中有一个为0,因此它们的积为0.
5.-168210
6.0原式=(-8)×[(-2)+(-1)-(-3)]
=(-8)×[(-2)+(-1)+(+3)]
=(-8)×0=0.
7.-1原式=
=-1.
8.解:(1)原式=×8
=-100×8+×8
=-800+
=-799.
(2)原式=(-11)×
=-11×2=-22.
9.解:原式=×…×=-×…×=-.
10.解:因为|a+1|+|b+2|+|c+3|=0,
因此a+1=0,b+2=0,c+3=0,
因此a=-1,b=-2,c=-3.
因此原式=(-1-1)×(-2-2)×(-3-3)=(-2)×(-4)×(-6)=-48.
11.解:×2=.
12.解:=2021.
创新应用
13.解:(1)小莉的解法比较简便.
(2)有,原式=×(-8)=72×(-8)-×(-8)=-575.
(3)能,原式=-×198=-100×198+×198=-19800+2=-19798.。
