河北省沧州市第一中学2018届高三上学期第一次月考文数试题 含解析
河北省沧州一中2018届高三上学期第一次月考数学理试卷 含解析

2018-2018学年河北省沧州一中高三(上)第一次月考数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z满足z(2﹣i)=11+7i(i为虚数单位),则z为()A.3+5i B.3﹣5i C.﹣3+5i D.﹣3﹣5i2.下列叙述中正确的是()A.若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2﹣4ac≤0”B.若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c”C.命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0”D.l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β3.已知A={x|x≥k},B={{x|<1},若A⊆B,则k的范围是()A.k<﹣1 B.k≤﹣1 C.k>2 D.k≥24.某几何体的三视图如图所示则该几何体的表面积为()A.54 B.60 C.66 D.725.设函数f(x)=x3+x,x∈R.若当0<θ<时,不等式f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是()A.(﹣∞,1] B.6.已知函数f(x)=sin2x向左平移个单位后,得到函数y=g(x),下列关于y=g(x)的说法正确的是()A.图象关于点(﹣,0)中心对称B.图象关于x=﹣轴对称C.在区间单调递增D.在单调递减7.已知两个不同的平面α、β和两条不重合的直线,m、n,有下列四个命题:①若m∥n,m⊥α,则n⊥α②若m⊥α,m⊥β,则α∥β;③若m⊥α,m∥n,n⊂β,则α⊥β;④若m∥α,α∩β=n,则m∥n,其中不正确的命题的个数是()A.0个B.1个C.2个D.3个8.已知数列{a n}是等比数列,且a2018+a2018=dx,则a2018(a2018+2a2018+a2018)的值为()A.π2B.2πC.πD.4π29.已知函数y=log a(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则的最小值为()A.3 B.C.4 D.810.已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<e x的解集为()A.(﹣2,+∞)B.(0,+∞)C.(1,+∞)D.(4,+∞)11.已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,,则球O的表面积为()A.16π B.12π C.8πD.4π12.定义域为R的偶函数f(x)满足对任意x∈R,有f(x+2)=f(x)﹣f(1),且当x∈时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣log a(x+1)在(0,+∞)上至少有三个零点,则a的取值范围是()A.(0,)B.(0,)C.(0,)D.(0,)二、填空题:本大题共4小题,每小题5分.13.已知变量x,y满足约束条件,且有无穷多个点(x,y)使目标函数z=x+my 取得最小值,则m= .14.已知不等式f(x)=3sin cos+cos2﹣﹣m≤0,对于任意的﹣≤x≤恒成立,则实数m的取值范围是.15.观察下列等式:12=112﹣22=﹣312﹣22+32=612﹣22+32﹣42=﹣10…照此规律,第n个等式可为.16.在△ABC中,BO为边AC上的中线,=2,设∥,若=+λ,则λ的值为.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(10分)在数列{a n}中,a1=1,a n+1=a n+c(c为常数,n∈N*),且a1,a2,a5成公比不为1的等比数列.(1)求c的值;(2)设,求数列{b n}的前n项和S n.18.(12分)设f(x)=4cos(ωx﹣)sinωx﹣cos(2ωx+π),其中ω>0.(Ⅰ)求函数y=f(x)的值域(Ⅱ)若f(x)在区间上为增函数,求ω的最大值.19.(12分)已知各项均为正数的数列{a n}前n项和为S n,首项为a1,且,a n,S n成等差数列.(1)求数列{a n}的通项公式;(2)若a n2=,设c n=,求数列{c n}的前n项和T n.20.(12分)在△ABC中,角A、B、C的对边分别为a,b,c,a+=4cosC,b=1.(I)若A=90°,求△ABC的面积;(Ⅱ)若△ABC的面积为,求a,c.21.(12分)某种商品原来每件售价为25元,年销售量8万件.(Ⅰ)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收人不低于原收入,该商品每件定价最多为多少元?(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入(x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.22.(12分)已知函数f(x)=e x﹣ax2﹣bx﹣1,其中a,b∈R,e=2.718 28…为自然对数的底数.(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间上的最小值;(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,证明:e﹣2<a<1.2018-2018学年河北省沧州一中高三(上)第一次月考数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2018•山东)若复数z满足z(2﹣i)=11+7i(i为虚数单位),则z为()A.3+5i B.3﹣5i C.﹣3+5i D.﹣3﹣5i【考点】复数代数形式的乘除运算.【专题】数系的扩充和复数.【分析】等式两边同乘2+i,然后化简求出z即可.【解答】解:因为z(2﹣i)=11+7i(i为虚数单位),所以z(2﹣i)(2+i)=(11+7i)(2+i),即5z=15+25i,z=3+5i.故选A.【点评】本题考查复数代数形式的混合运算,考查计算能力.2.(2018•江西)下列叙述中正确的是()A.若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2﹣4ac≤0”B.若a,b,c∈R,则“a b2>cb2”的充要条件是“a>c”C.命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0”D.l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β【考点】命题的真假判断与应用;全称命题.【专题】简易逻辑.【分析】本题先用不等式的知识对选项A、B中命题的条件进行等价分析,得出它们的充要条件,再判断相应命题的真假;对选项以中的命题否定加以研究,判断其真假,在考虑全称量词的同时,要否定命题的结论;对选项D利用立体几何的位置关系,得出命题的真假,可知本题的正确答案.【解答】解:A、若a,b,c∈R,当“ax2+bx+c≥0”对于任意的x恒成立时,则有:①当a=0时,要使ax2+bx+c≥0恒成立,需要b=0,c≥0,此时b2﹣4ac=0,符合b2﹣4ac≤0;②当a≠0时,要使ax2+bx+c≥0恒成立,必须a>0且b2﹣4ac≤0.∴若a,b,c∈R,“ax2+bx+c≥0”是“b2﹣4ac≤0”充分不必要条件,“b2﹣4ac≤0”是“ax2+bx+c≥0”的必要条件,但不是充分条件,即必要不充分条件.故A错误;B、当ab2>cb2时,b2≠0,且a>c,∴“ab2>cb2”是“a>c”的充分条件.反之,当a>c时,若b=0,则ab2=cb2,不等式ab2>cb2不成立.∴“a>c”是“ab2>cb2”的必要不充分条件.故B错误;C、结论要否定,注意考虑到全称量词“任意”,命题“对任意x∈R,有x2≥0”的否定应该是“存在x∈R,有x2<0”.故C错误;D、命题“l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β.”是两个平面平行的一个判定定理.故D正确.故答案为:D.【点评】本题考查了命题、充要条件的知识,考查到了不等式、立体几何知识,有一定容量,总体难度不大,属于基础题.3.(2018秋•沧州校级月考)已知A={x|x≥k},B={{x|<1},若A⊆B,则k的范围是()A.k<﹣1 B.k≤﹣1 C.k>2 D.k≥2【考点】集合的包含关系判断及应用.【专题】计算题;方程思想;综合法;集合.【分析】化简集合A,B;再由A⊆B可求得实数k的取值范围.【解答】解:B={x|<1}=(﹣∞,﹣1)∪(2,+∞),A={x|x≥k}= B.【考点】其他不等式的解法.【专题】计算题;不等式的解法及应用.【分析】利用奇函数f(x)=x3+x单调递增的性质,可将不等式f(msinθ)+f(1﹣m)>0恒成立,转化为msinθ>m﹣1恒成立,由0<θ<,可求得实数m的取值范围.【解答】解:∵f(x)=x3+x,∴f(﹣x)=(﹣x)3+(﹣x)=﹣x3﹣x=﹣f(x),∴函数f(x)=x3+x为奇函数;又f′(x)=3x2+1>0,∴函数f(x)=x3+x为R上的单调递增函数.∴f(msinθ)+f(1﹣m)>0恒成立⇔f(msinθ)>﹣f(1﹣m)=f(m﹣1)恒成立,∴msinθ>m﹣1(0<θ<)恒成立⇔m(1﹣sinθ)<1恒成立,由0<θ<知,0<sinθ<1,0<1﹣sinθ<1,>1由m<恒成立知:m≤1.∴实数m的取值范围是(﹣∞,1].故选A.【点评】本题考查函数的奇偶性与单调性,突出考查转化思想与恒成立问题,属于中档题.6.(2018•潍坊模拟)已知函数f(x)=sin2x向左平移个单位后,得到函数y=g(x),下列关于y=g(x)的说法正确的是()A.图象关于点(﹣,0)中心对称B.图象关于x=﹣轴对称C.在区间单调递增D.在单调递减【考点】函数y=Asin(ωx+φ)的图象变换.【专题】三角函数的图像与性质;简易逻辑.【分析】根据函数图象的平移变换法则“左加右减,上加下减”,易得到函数y=sin2x的图象向左平移个单位后,得到的图象对应的函数解析式,然后利用函数的对称性,单调性判断选项即可.【解答】解:函数y=sin2x的图象向左平移个单位,得到的图象对应的函数为y=sin2(x+)=sin(2x+).对于A,当x=﹣时,y=sin(﹣)≠0.图象不关于点(﹣,0)中心对称,∴A不正确;对于B,当x=﹣时,y=sin0=0,图象不关于x=﹣轴对称,∴B不正确对于C,y=sin(2x+)的周期是π.当x=时,函数取得最大值,x=﹣时,函数取得最小值,∵⊂,∴在区间单调递增,∴C正确;对于D,y=sin(2x+)的周期是π.当x=时,函数取得最大值,∴在单调递减不正确,∴D不正确;故选:C.【点评】本题考查的知识点是函数图象的平移变换,其中熟练掌握图象的平移变换法则“左加右减,上加下减”,是解答本题的关键7.(2018•梅州二模)已知两个不同的平面α、β和两条不重合的直线,m、n,有下列四个命题:①若m∥n,m⊥α,则n⊥α②若m⊥α,m⊥β,则α∥β;③若m⊥α,m∥n,n⊂β,则α⊥β;④若m∥α,α∩β=n,则m∥n,其中不正确的命题的个数是()A.0个B.1个C.2个D.3个【考点】平面与平面平行的判定.【专题】综合题.【分析】从直线与平面平行和垂直的判定定理,以及性质定理,对四个选项逐一判断;判断时通过反例即可.【解答】解:真命题有①直线与平面垂直的判定定理之一;②两个平面平行的判定之一;③直线与平面垂直推出平面与平面垂直判定.④是假命题,m、n可以是异面直线.故选B.【点评】本题考查直线与平面平行与垂直,平面与平面垂直的判定,直线与直线平行的判定,是基础题.8.(2018•南昌模拟)已知数列{a n}是等比数列,且a2018+a2018=dx,则a2018(a2018+2a2018+a2018)的值为()A.π2B.2πC.πD.4π2【考点】等比数列的性质;定积分.【专题】等差数列与等比数列.【分析】求定积分可得a2018+a2018=π,由等比数列的性质变形可得a2018(a2018+2a2018+a2018)=(a2018+a2018)2,代值计算可得.【解答】解:由定积分的几何意义可得dx表示圆x2+y2=4在第一象限的图形的面积,即四分之一圆,故可得a2018+a2018=dx=×π×22=π,∴a2018(a2018+2a2018+a2018)=a2018•a2018+2a2018•a2018+a2018•a2018=+2a2018•a2018=(a2018+a2018)2=π2故选:A【点评】本题考查等比数列的性质,涉及定积分的求解,属中档题.9.(2018•泰安一模)已知函数y=log a(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则的最小值为()A.3 B.C.4 D.8【考点】基本不等式;对数函数的单调性与特殊点.【专题】计算题;综合题.【分析】根据对数函数的性质先求出A的坐标,代入直线方程可得m、n的关系,再利用1的代换结合均值不等式求解即可.【解答】解:∵x=﹣2时,y=log a1﹣1=﹣1,∴函数y=log a(x+3)﹣1(a>0,a≠1)的图象恒过定点(﹣2,﹣1)即A(﹣2,﹣1),∵点A在直线mx+ny+1=0上,∴﹣2m﹣n+1=0,即2m+n=1,∵mn>0,∴m>0,n>0,+=+=2+++2≥4+2•=8,当且仅当m=,n=时取等号.故选D.【点评】本题考查了对数函数的性质和均值不等式等知识点,运用了整体代换思想,是高考考查的重点内容.10.(2018•兰州一模)已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<e x的解集为()A.(﹣2,+∞)B.(0,+∞)C.(1,+∞)D.(4,+∞)【考点】利用导数研究函数的单调性;奇偶性与单调性的综合.【专题】综合题;函数的性质及应用.【分析】构造函数g(x)=(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,即可求解【解答】解:∵y=f(x+2)为偶函数,∴y=f(x+2)的图象关于x=0对称∴y=f(x)的图象关于x=2对称∴f(4)=f(0)又∵f(4)=1,∴f(0)=1设g(x)=(x∈R),则g′(x)==又∵f′(x)<f(x),∴f′(x)﹣f(x)<0∴g′(x)<0,∴y=g(x)在定义域上单调递减∵f(x)<e x∴g(x)<1又∵g(0)==1∴g(x)<g(0)∴x>0故选B.【点评】本题考查函数单调性与奇偶性的结合,结合已知条件构造函数,然后用导数判断函数的单调性是解题的关键.11.(2018春•钟祥市校级期中)已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,,则球O的表面积为()A.16π B.12π C.8πD.4π【考点】球的体积和表面积.【专题】计算题;空间位置关系与距离.【分析】由三棱锥S﹣ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,∠BAC=60°,知BC=,∠ABC=90°.故△ABC截球O所得的圆O′的半径r=AC=1,由此能求出球O的半径,从而能求出球O的表面积.【解答】解:如图,三棱锥S﹣ABC的所有顶点都在球O的球面上,∵SA⊥平面ABC,SA=2,AB=1,AC=2,∠BAC=60°,∴BC==,∴∠ABC=90°.∴△ABC截球O所得的圆O′的半径r=AC=1,∴球O的半径R==2,∴球O的表面积S=4πR2=16π.故选:A.【点评】本题考查球的表面积的求法,合理地作出图形,数形结合求出球半径,是解题的关键.12.(2018•河南模拟)定义域为R的偶函数f(x)满足对任意x∈R,有f(x+2)=f(x)﹣f (1),且当x∈时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣log a(x+1)在(0,+∞)上至少有三个零点,则a的取值范围是()A.(0,)B.(0,)C.(0,)D.(0,)【考点】根的存在性及根的个数判断.【专题】计算题;作图题;函数的性质及应用.【分析】由题意可判断函数f(x)是定义在R上的,周期为2的偶函数,令g(x)=log a(x+1),画出f(x)与g(x)在时,f(x)=﹣2x2+12x﹣18,令g(x)=log a(x+1),则f(x)与g(x)在=﹣,当n为奇数时,第n个等式左边=(12﹣22)+(32﹣42)+…++n2=﹣+n2=.综上,第n个等式为.故答案为:.【点评】本题考查规律型中的数字变化问题,找等式的规律时,既要分别看左右两边的规律,还要注意看左右两边之间的联系.16.(2018秋•沧州校级月考)在△ABC中,BO为边AC上的中线,=2,设∥,若=+λ,则λ的值为.【考点】平面向量的基本定理及其意义.【专题】方程思想;数形结合法;平面向量及应用.【分析】根据题意得出G是△ABC的重心,用、表示出向量,用表示出,写出的表达式,利用向量相等列出方程组求出λ的值.【解答】解:由已知得G是△ABC的重心,因此=(+),由于∥,因此设=k,所以=(+),那么=+=+(+1),=+λ,所以,解得λ=.故答案为:.【点评】本题考查了向量在几何中的应用问题,也考查平面向量的基本定理,是基础题目.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(10分)(2018•宜宾二模)在数列{a n}中,a1=1,a n+1=a n+c(c为常数,n∈N*),且a1,a2,a5成公比不为1的等比数列.(1)求c的值;(2)设,求数列{b n}的前n项和S n.【考点】数列的求和;等比数列的性质.【专题】计算题.【分析】(1)利用递推关系判断出数列{a n}为等差数列,将a1,a2,a5用公差表示,据此三项成等比数列列出方程,求出c.(2)写出b n,据其特点,利用裂项的方法求出数列{b n}的前n项和S n.【解答】解:(1)∵a n+1=a n+c∴a n+1﹣a n=c∴数列{a n}是以a1=1为首项,以c为公差的等差数列a2=1+c,a5=1+4c又a1,a2,a5成公比不为1的等比数列∴(1+c)2=1+4c解得c=2或c=0(舍)(2)由(1)知,a n=2n﹣1∴∴=【点评】求数列的前n项和时,应该先求出通项,根据通项的特点,选择合适的求和方法.18.(12分)(2018•重庆)设f(x)=4cos(ωx﹣)sinωx﹣cos(2ωx+π),其中ω>0.(Ⅰ)求函数y=f(x)的值域(Ⅱ)若f(x)在区间上为增函数,求ω的最大值.【考点】二倍角的余弦;两角和与差的正弦函数;二倍角的正弦;正弦函数的定义域和值域;正弦函数的单调性.【专题】计算题;转化思想.【分析】(I)由题意,可由三角函数的恒等变换公式对函数的解析式进行化简得到f(x)=sin2ωx+1,由此易求得函数的值域;(II)f(x)在区间上为增函数,此区间必为函数某一个单调区间的子集,由此可根据复合三角函数的单调性求出用参数表示的三角函数的单调递增区间,由集合的包含关系比较两个区间的端点即可得到参数ω所满足的不等式,由此不等式解出它的取值范围,即可得到它的最大值.【解答】解:f(x)=4cos(ωx﹣)sinωx﹣cos(2ωx+π)=4(cosωx+sinωx)sinωx+cos2ωx=2cosωxsinωx+2sin2ωx+cos2ωx﹣sin2ωx=sin2ωx+1,∵﹣1≤sin2ωx≤1,所以函数y=f(x)的值域是[](II)因y=sinx在每个区间[],k∈z上为增函数,令,又ω>0,所以,解不等式得≤x≤,即f(x)=sin2ωx+1,(ω>0)在每个闭区间[,],k∈z上是增函数又有题设f(x)在区间上为增函数所以⊆[,],对某个k∈z成立,于是有.解得ω≤,故ω的最大值是.【点评】本题考查三角恒等变换的运用及三角函数值域的求法,解题的关键是对所给的函数式进行化简,熟练掌握复合三角函数单调性的求法,本题考查了转化的思想,计算能力,属于中等难度的题19.(12分)(2018秋•桓台县校级期末)已知各项均为正数的数列{a n}前n项和为S n,首项为a1,且,a n,S n成等差数列.(1)求数列{a n}的通项公式;(2)若a n2=,设c n=,求数列{c n}的前n项和T n.【考点】数列的求和;等差数列的通项公式.【专题】综合题;等差数列与等比数列.【分析】(Ⅰ)由题意知,当n=1时,得a1=;当n≥2时,,两式相减得a n=S n﹣S n﹣1=2a n﹣2a n﹣1,由此能求出数列{a n}的通项公式.(Ⅱ)由,知b n=4﹣2n,故,由此利用错位相减法能求出数列{c n}的前n项和T n.【解答】(本小题满分12分)解:(Ⅰ)由题意知,…(1分)当n=1时,2a1=a1+,解得a1=,当n≥2时,,两式相减得a n=S n﹣S n﹣1=2a n﹣2a n﹣1…(3分)整理得:…(4分)∴数列{a n}是以为首项,2为公比的等比数列.∴.…(Ⅱ)∴b n=4﹣2n,…(6分)∴…①…②①﹣②得…(9分)=.…(11分)∴.…(12分)【点评】本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意迭代法和错位相减法的合理运用.20.(12分)(2018•武汉模拟)在△ABC中,角A、B、C的对边分别为a,b,c,a+=4cosC,b=1.(I)若A=90°,求△ABC的面积;(Ⅱ)若△ABC的面积为,求a,c.【考点】正弦定理;余弦定理.【专题】计算题;转化思想;综合法;解三角形.【分析】(I)由题意A=90°,可得cosC=,由a+==,解得a,利用勾股定理可求c,利用三角形面积公式即可得解.(Ⅱ)利用三角形面积公式可得sinC=,由a+=4cosC,可得cosC=,从而()2+()2=1,整理可得:a4﹣14a2+49=0,解得a,cosC,由余弦定理可得c的值.【解答】解:(I)在△ABC中,∵如图:A=90°,a+=4cosC,b=1,可得cosC=,∴a+==,解得:a=,∴c==,∴S△ABC=bc==.(Ⅱ)∵△ABC的面积为=absinC=asinC,可得:sinC=,①∵a+=4cosC,可得:cosC=,②∴()2+()2=1,整理可得:a4﹣14a2+49=0,解得:a=,∴cosC=,∴由余弦定理可得:c===2.【点评】本题主要考查了勾股定理,三角形面积公式,同角三角函数基本关系式,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.21.(12分)(2018秋•福州期末)某种商品原来每件售价为25元,年销售量8万件.(Ⅰ)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收人不低于原收入,该商品每件定价最多为多少元?(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入(x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.【考点】函数模型的选择与应用.【专题】应用题.【分析】(Ⅰ)设每件定价为x元,则提高价格后的销售量为,根据销售的总收人不低于原收入,建立不等式,解不等式可得每件最高定价;(Ⅱ)依题意,x>25时,不等式有解,等价于x>25时,有解,利用基本不等式,我们可以求得结论.【解答】解:(Ⅰ)设每件定价为x元,则提高价格后的销售量为,根据销售的总收人不低于原收入,有,(3分)整理得x2﹣65x+1000≤0,解得25≤x≤40.∴要使销售的总收入不低于原收入,每件定价最多为40元.(6分)(Ⅱ)依题意,x>25时,不等式有解,(8分)等价于x>25时,有解,(9分)∵(当且仅当x=30时,等号成立),(11分)∴a≥10.2.此时该商品的每件定价为30元(12分)∴当该商品明年的销售量a至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元.(13分)【点评】解决实际问题的关键是读懂题意,建立函数模型,同时应注意变量的取值应使实际问题有意义.22.(12分)(2018•成都校级二模)已知函数f(x)=e x﹣ax2﹣bx﹣1,其中a,b∈R,e=2.718 28…为自然对数的底数.(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间上的最小值;(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,证明:e﹣2<a<1.【考点】利用导数求闭区间上函数的最值;函数零点的判定定理;利用导数研究函数的单调性.【专题】导数的综合应用.【分析】(1)先求出函数f(x)的导数,通过讨论a的范围得出函数的单调区间,从而求出函数的最值;(2)设x0为f(x)在区间(0,1)内的一个零点,通过讨论a的范围,得出a的取值.【解答】解:(1)由f(x)=e x﹣ax2﹣bx﹣1,得g(x)=f′(x)=e x﹣2ax﹣b,所以g′(x)=e x﹣2a.当x∈时,g′(x)∈.当a≤时,g′(x)≥0,所以g(x)在上单调递增,因此g(x)在上的最小值是g(0)=1﹣b;当a ≥时,g′(x)≤0,所以g(x)在上单调递减,因此g(x)在上的最小值是g(1)=e﹣2a﹣b;当<a <时,令g′(x)=0,得x=ln(2a)∈(0,1),所以函数g(x)在区间上单调递减,在区间(ln(2a),1]上单调递增,于是,g(x)在上的最小值是g(ln(2a))=2a﹣2aln(2a)﹣b.综上所述,当a ≤时,g(x)在上的最小值是g(0)=1﹣b;当<a <时,g(x)在上的最小值是g(ln(2a))=2a﹣2aln(2a)﹣b;当a ≥时,g(x)在上的最小值是g(1)=e﹣2a﹣b.…(2)证明:设x0为f(x)在区间(0,1)内的一个零点,则由f(0)=f(x0)=0可知,f(x)在区间(0,x0)上不可能单调递增,也不可能单调递减.则g(x)不可能恒为正,也不可能恒为负.故g(x)在区间(0,x0)内存在零点x1.同理g(x)在区间(x0,1)内存在零点x2.故g(x)在区间(0,1)内至少有两个零点,由(1)知,当a ≤时,g(x)在递增,故g(x)在(0,1)内至多有1个零点,当a ≥时,g(x)在递减,故g(x)在(0,1)内至多有1个零点,都不合题意,所以<a <,此时,g(x)在区间递减,在区间(ln(2a),1)递增,因此x1∈(0,ln(2a)),x2∈(ln(2a),1),必有:g(0)=1﹣b>0,g(1)=e﹣2a﹣b>0,由f(1)=0,得a+b=e﹣1<2,有g(0)=a﹣e+2>0,g(1)=1﹣a>0,解得:e﹣2<a<1,所以函数f(x)在区间(0,1)内有零点时,e﹣2<a<1.【点评】本题考查了函数的单调性,函数的最值问题,考查导数的应用,考查分类讨论思想,是一道综合题.。
沧州市一中2018-2019学年上学期高三数学10月月考试题
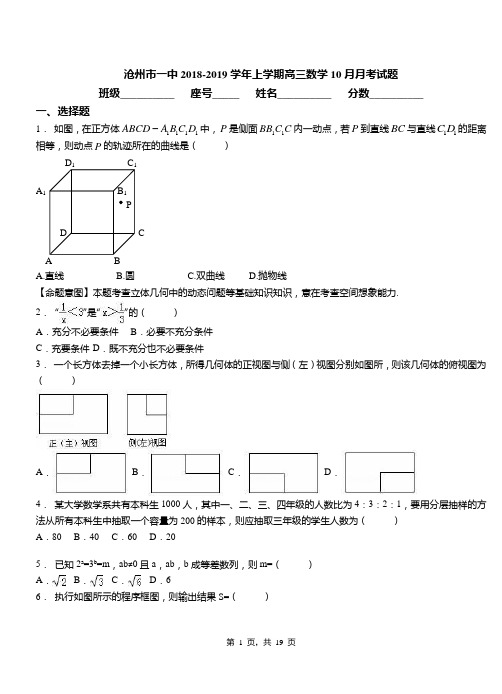
沧州市一中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. 如图,在正方体1111ABCD A B C D 中,P 是侧面11BB C C 内一动点,若P 到直线BC 与直线11C D 的距离相等,则动点P 的轨迹所在的曲线是( )A 1CA B A.直线 B.圆C.双曲线D.抛物线【命题意图】本题考查立体几何中的动态问题等基础知识知识,意在考查空间想象能力.2. “”是“”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3. 一个长方体去掉一个小长方体,所得几何体的正视图与侧(左)视图分别如图所,则该几何体的俯视图为( )A .B .C .D .4. 某大学数学系共有本科生1000人,其中一、二、三、四年级的人数比为4:3:2:1,要用分层抽样的方法从所有本科生中抽取一个容量为200的样本,则应抽取三年级的学生人数为( ) A .80 B .40 C .60 D .205. 已知2a =3b =m ,ab ≠0且a ,ab ,b 成等差数列,则m=( )A .B .C .D .66. 执行如图所示的程序框图,则输出结果S=( )A.15 B.25 C.50 D.1007.偶函数f(x)的定义域为R,若f(x+2)为奇函数,且f(1)=1,则f(89)+f(90)为()A.﹣2 B.﹣1 C.0 D.18.在数列{a n}中,a1=3,a n+1a n+2=2a n+1+2a n(n∈N+),则该数列的前2015项的和是()A.7049 B.7052 C.14098 D.14101x ,则输出的所有x的值的和为()9.执行如图所示的程序,若输入的3A.243B.363C.729D.1092【命题意图】本题考查程序框图的识别和运算,意在考查识图能力、简单的计算能力.10.奇函数()f x 满足()10f =,且()f x 在()0+∞,上是单调递减,则()()210x f x f x -<--的解集为( ) A .()11-, B .()()11-∞-+∞ ,, C .()1-∞-,D .()1+∞,11.如图,在等腰梯形ABCD 中,AB=2DC=2,∠DAB=60°,E 为AB 的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B 重合于点P ,则P ﹣DCE 三棱锥的外接球的体积为( )A. B. C. D.12.设函数()()21,141x x f x x ⎧+<⎪=⎨≥⎪⎩,则使得()1f x ≥的自变量的取值范围为( )A .(][],20,10-∞-B .(][],20,1-∞-C .(][],21,10-∞-D .[][]2,01,10-二、填空题13.设,y x 满足约束条件2110y x x y y ≤⎧⎪+≤⎨⎪+≥⎩,则3z x y =+的最大值是____________.14.已知集合{}|03,A x x x R =<∈≤,{}|12,B x x x R =-∈≤≤,则A ∪B = ▲ . 15.函数()2log f x x =在点()1,2A 处切线的斜率为 ▲ .16.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y (毫克)与时间t (小时)成正比;药物释放完毕后,y 与t 的函数关系式为y=()t ﹣a (a 为常数),如图所示,据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 小时后,学生才能回到教室.三、解答题17.(本题满分15分)已知抛物线C 的方程为22(0)y px p =>,点(1,2)R 在抛物线C 上.(1)求抛物线C 的方程;(2)过点(1,1)Q 作直线交抛物线C 于不同于R 的两点A ,B ,若直线AR ,BR 分别交直线:22l y x =+于M ,N 两点,求MN 最小时直线AB 的方程.【命题意图】本题主要考查抛物线的标准方程及其性质以及直线与抛物线的位置关系等基础知识,意在考查运算求解能力.18.(本小题满分13分) 已知函数32()31f x ax x =-+, (Ⅰ)讨论()f x 的单调性;(Ⅱ)证明:当2a <-时,()f x 有唯一的零点0x ,且01(0,)2x ∈.19.(本小题满分12分)已知平面向量(1,)a x = ,(23,)b x x =+-,()x R ∈.(1)若//a b ,求||a b -;(2)若与夹角为锐角,求的取值范围.20.(本小题满分12分)为了普及法律知识,达到“法在心中”的目的,某市法制办组织了普法知识竞赛.5名职工的成绩,成绩如下表:(1掌握更稳定;(2)用简单随机抽样法从乙单位5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的分数差至少是4的概率.21.已知S n为数列{a n}的前n项和,且满足S n=2a n﹣n2+3n+2(n∈N*)(Ⅰ)求证:数列{a n+2n}是等比数列;(Ⅱ)设b n=a n sinπ,求数列{b n}的前n项和;(Ⅲ)设C n=﹣,数列{C n}的前n项和为P n,求证:P n<.22.(本小题满分16分)在互联网时代,网校培训已经成为青年学习的一种趋势,假设某网校的套题每日的销售量()h x (单位:千套)与销售价格(单位:元/套)满足的关系式()()()h x f x g x =+(37x <<,m 为常数),其中()f x 与()3x -成反比,()g x 与()7x -的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套. (1) 求()h x 的表达式;(2) 假设网校的员工工资,办公等所有开销折合为每套题3元(只考虑销售出的套数),试确定销售价格的值,使网校每日销售套题所获得的利润最大.(保留1位小数)23.已知函数f (x )的定义域为{x|x ≠k π,k ∈Z},且对定义域内的任意x ,y 都有f (x ﹣y )=成立,且f (1)=1,当0<x <2时,f (x )>0. (1)证明:函数f (x )是奇函数;(2)试求f (2),f (3)的值,并求出函数f (x )在[2,3]上的最值.沧州市一中2018-2019学年上学期高三数学10月月考试题(参考答案)一、选择题1.【答案】D.第Ⅱ卷(共110分)2.【答案】B【解析】解:,解得或x<0,∴“”是“”的必要不充分条件.故选:B.3.【答案】C【解析】解:由正视图可知去掉的长方体在正视线的方向,从侧视图可以看出去掉的长方体在原长方体的左侧,由以上各视图的描述可知其俯视图符合C选项.故选:C.【点评】本题考查几何体的三视图之间的关系,要注意记忆和理解“长对正、高平齐、宽相等”的含义.4.【答案】B【解析】解:∵要用分层抽样的方法从该系所有本科生中抽取一个容量为200的样本,∴三年级要抽取的学生是×200=40,故选:B.【点评】本题考查分层抽样方法,本题解题的关键是看出三年级学生所占的比例,本题也可以先做出三年级学生数和每个个体被抽到的概率,得到结果.5.【答案】C.【解析】解:∵2a=3b=m,∴a=log2m,b=log3m,∵a,ab,b成等差数列,∴2ab=a+b,∵ab≠0,∴+=2,∴=log m2,=log m3,∴log m2+log m3=log m6=2,解得m=.故选C【点评】本题考查了指数与对数的运算的应用及等差数列的性质应用.6.【答案】C【解析】解:根据程序框图,S=(﹣1+3)+(﹣5+7)+…+(﹣97+99)=50,输出的S为50.故选:C.【点评】本题主要考查了循环结构的程序框图,模拟执行程序框图,正确得到程序框图的功能是解题的关键,属于基础题.7.【答案】D【解析】解:∵f(x+2)为奇函数,∴f(﹣x+2)=﹣f(x+2),∵f(x)是偶函数,∴f(﹣x+2)=﹣f(x+2)=f(x﹣2),即﹣f(x+4)=f(x),则f(x+4)=﹣f(x),f(x+8)=﹣f(x+4)=f(x),即函数f(x)是周期为8的周期函数,则f(89)=f(88+1)=f(1)=1,f(90)=f(88+2)=f(2),由﹣f(x+4)=f(x),得当x=﹣2时,﹣f(2)=f(﹣2)=f(2),则f (2)=0, 故f (89)+f (90)=0+1=1,故选:D .【点评】本题主要考查函数值的计算,利用函数奇偶性的性质,得到函数的对称轴是解决本题的关键.8. 【答案】B【解析】解:∵a n+1a n +2=2a n+1+2a n (n ∈N +),∴(a n+1﹣2)(a n ﹣2)=2,当n ≥2时,(a n ﹣2)(a n ﹣1﹣2)=2,∴,可得a n+1=a n ﹣1,因此数列{a n }是周期为2的周期数列. a 1=3,∴3a 2+2=2a 2+2×3,解得a 2=4, ∴S 2015=1007(3+4)+3=7052.【点评】本题考查了数列的周期性,考查了计算能力,属于中档题.9. 【答案】D【解析】当3x =时,y 是整数;当23x =时,y 是整数;依次类推可知当3(*)n x n N =∈时,y 是整数,则由31000nx =≥,得7n ≥,所以输出的所有x 的值为3,9,27,81,243,729,其和为1092,故选D .10.【答案】B 【解析】试题分析:由()()()()()212102102x x x f x f x f x f x --<⇒⇒-<--,即整式21x -的值与函数()f x 的值符号相反,当0x >时,210x ->;当0x <时,210x -<,结合图象即得()()11-∞-+∞ ,,.考点:1、函数的单调性;2、函数的奇偶性;3、不等式. 11.【答案】C【解析】解:易证所得三棱锥为正四面体,它的棱长为1,故外接球半径为,外接球的体积为,故选C .【点评】本题考查球的内接多面体,球的体积等知识,考查逻辑思维能力,是中档题.12.【答案】A 【解析】考点:分段函数的应用.【方法点晴】本题主要考查了分段函数的应用,其中解答中涉及到不等式的求解,集合的交集和集合的并集运算,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,属于中档试题,本题的解答中,根据分段函数的分段条件,列出相应的不等式,通过求解每个不等式的解集,利用集合的运算是解答的关键.二、填空题13.【答案】73【解析】试题分析:画出可行域如下图所示,由图可知目标函数在点12,33A ⎛⎫⎪⎝⎭处取得最大值为73.考点:线性规划. 14.【答案】1-1,3] 【解析】试题分析:A ∪B ={}{}|03,|12,x x x R x x x R <∈-∈ ≤≤≤=1-1,3] 考点:集合运算 【方法点睛】1.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其他的集合.2.求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解.3.在进行集合的运算时要尽可能地借助Venn 图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn 图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍.15.【答案】1ln 2【解析】试题分析:()()111ln 2ln 2f x k f x ''=∴== 考点:导数几何意义【思路点睛】(1)求曲线的切线要注意“过点P 的切线”与“在点P 处的切线”的差异,过点P 的切线中,点P 不一定是切点,点P 也不一定在已知曲线上,而在点P 处的切线,必以点P 为切点.(2)利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解. 16.【答案】0.6【解析】解:当t >0.1时,可得1=()0.1﹣a∴0.1﹣a=0 a=0.1由题意可得y ≤0.25=, 即()t ﹣0.1≤,即t ﹣0.1≥ 解得t ≥0.6,由题意至少需要经过0.6小时后,学生才能回到教室. 故答案为:0.6【点评】本题考查函数、不等式的实际应用,以及识图和理解能力.易错点:只单纯解不等式,而忽略题意,得到其他错误答案.三、解答题17.【答案】(1)24y x =;(2)20x y +-=.【解析】(1)∵点(1,2)R 在抛物线C 上,22212p p =⨯⇒=,…………2分即抛物线C 的方程为24y x =;…………5分18.【答案】(本小题满分13分)解:(Ⅰ)2()363(2)f x ax x x ax '=-=-, (1分)①当0a >时,解()0f x '>得2x a >或0x <,解()0f x '<得20x a <<, ∴()f x 的递增区间为(,0)-∞和2(,)a+∞,()f x 的递减区间为2(0,)a . (4分)②当0a =时,()f x 的递增区间为(,0)-∞,递减区间为(0,)+∞. (5分)③当0a <时,解()0f x '>得20x a<<,解()0f x '<得0x >或2x a <∴()f x 的递增区间为2(,0)a ,()f x 的递减区间为2(,)a-∞和(0,)+∞. (7分)(Ⅱ)当2a <-时,由(Ⅰ)知2(,)a -∞上递减,在2(,0)a上递增,在(0,)+∞上递减.∵22240a f a a -⎛⎫=> ⎪⎝⎭,∴()f x 在(,0)-∞没有零点. (9分) ∵()010f =>,11(2)028f a ⎛⎫=+< ⎪⎝⎭,()f x 在(0,)+∞上递减,∴在(0,)+∞上,存在唯一的0x ,使得()00f x =.且01(0,)2x ∈ (12分) 综上所述,当2a <-时,()f x 有唯一的零点0x ,且01(0,)2x ∈. (13分)19.【答案】(1)2或2)(1,0)(0,3)- .【解析】试题分析:(1)本题可由两向量平行求得参数,由坐标运算可得两向量的模,由于有两解,因此模有两个值;(2)两向量,a b 的夹角为锐角的充要条件是0a b ⋅> 且,a b不共线,由此可得范围.试题解析:(1)由//a b,得0x =或2x =-,当0x =时,(2,0)a b -=- ,||2a b -=,当2x =-时,(2,4)a b -=- ,||a b -=.(2)与夹角为锐角,0a b ∙> ,2230x x -++>,13x -<<,又因为0x =时,//a b,所以的取值范围是(1,0)(0,3)- .考点:向量平行的坐标运算,向量的模与数量积.【名师点睛】由向量的数量积cos a b a b θ⋅=可得向量的夹角公式,当为锐角时,cos 0θ>,但当cos 0θ>时,可能为锐角,也可能为0(此时两向量同向),因此两向量夹角为锐角的充要条件是0a ba b⋅>且,a b 不同向,同样两向量夹角为钝角的充要条件是0a ba b⋅<且,a b 不反向.20.【答案】(1)90=甲x ,90=乙x ,5242=甲s ,82=乙s ,甲单位对法律知识的掌握更稳定;(2)21. 【解析】试题分析:(1)先求出甲乙两个单位职工的考试成绩的平均数,以及他们的方差,则方差小的更稳定;(2)从乙单位抽取两名职工的成绩,所有基本事件用列举法得到共10种情况,抽取的两名职工的分数差至少是的事件用列举法求得共有种,由古典概型公式得出概率.试题解析:解:(1)90939191888751=++++=)(甲x ,90939291898551=++++=)(乙x 524])9093()9091()9091()9088()9087[(51222222=-+-+-+-+-=甲s 8])9093()9092()9091()9089()9085[(51222222=-+-+-+-+-=乙s∵8524<,∴甲单位的成绩比乙单位稳定,即甲单位对法律知识的掌握更稳定. (6分)考点:1.平均数与方差公式;2.古典概型.21.【答案】【解析】(I)证明:由S n=2a n﹣n2+3n+2(n∈N*),∴当n≥2时,,a n=S n﹣S n﹣1=2a n﹣2a n﹣1﹣2n+4,变形为a n+2n=2[a n﹣1+2(n﹣1)],当n=1时,a1=S1=2a1﹣1+3+2,解得a1=﹣4,∴a1+2=﹣2,∴数列{a n+2n}是等比数列,首项为﹣2,公比为2;(II)解:由(I)可得a n=﹣2×2n﹣1﹣2n=﹣2n﹣2n.∴b n=a n sinπ=﹣(2n+2n),∵==(﹣1)n,∴b n=(﹣1)n+1(2n+2n).设数列{b n}的前n项和为T n.当n=2k(k∈N*)时,T2k=(2﹣22+23﹣24+…+22k﹣1﹣22k)+2(1﹣2+3﹣4+…+2k﹣1﹣2k)=﹣2k=﹣n.当n=2k﹣1时,T2k﹣1=﹣2k﹣(﹣22k﹣4k)=+n+1+2n+1=+n+1.(III)证明:C n=﹣=,当n≥2时,c n.∴数列{C n}的前n项和为P n<==,当n=1时,c1=成立.综上可得:∀n∈N*,.【点评】本题考查了等差数列与等比数列的通项公式及其前n项和公式、“放缩法”、三角函数的诱导公式、递推式的应用,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.22.【答案】(1) ()()210473h x x x =+-- (37x <<)(2) 13 4.33x =≈ 试题解析:(1) 因为()f x 与3x -成反比,()g x 与7x -的平方成正比, 所以可设:()13k f x x =-,()()227g x k x =-,12.00k k ≠≠,,则()()()()21273k h x f x g x k x x =+=+--则 ………………………………………2分 因为销售价格为5元/套时,每日可售出套题21千套,销售价格为2.5元/套时,每日可售出套题69千套 所以,()()521, 3.569h h ==,即12124212492694k k k k ⎧+=⎪⎪⎨⎪+=⎪⎩,解得:12104k k =⎧⎨=⎩, ……………6分所以,()()210473h x x x =+-- (37x <<) ………………………………………8分 (2) 由(1)可知,套题每日的销售量()()210473h x x x =+--,答:当销售价格为4.3元/套时,网校每日销售套题所获得的利润最大.…………16分考点:利用导数求函数最值23.【答案】【解析】(1)证明:函数f(x)的定义域为{x|x≠kπ,k∈Z},关于原点对称.又f(x﹣y)=,所以f(﹣x)=f[(1﹣x)﹣1]======,故函数f(x)奇函数.(2)令x=1,y=﹣1,则f(2)=f[1﹣(﹣1)]==,令x=1,y=﹣2,则f(3)=f[1﹣(﹣2)]===,∵f(x﹣2)==,∴f(x﹣4)=,则函数的周期是4.先证明f(x)在[2,3]上单调递减,先证明当2<x<3时,f(x)<0,设2<x<3,则0<x﹣2<1,则f(x﹣2)=,即f(x)=﹣<0,设2≤x1≤x2≤3,则f(x1)<0,f(x2)<0,f(x2﹣x1)>0,则f(x1)﹣f(x2)=,∴f(x1)>f(x2),即函数f(x)在[2,3]上为减函数,则函数f(x)在[2,3]上的最大值为f(2)=0,最小值为f(3)=﹣1.【点评】本题主要考查了函数奇偶性的判断,以及函数的最值及其几何意义等有关知识,综合性较强,难度较大.。
2017-2018学年河北省沧州一中高考数学一模试卷(文科) Word版含解析

2017-2018学年河北省沧州一中高考数学一模试卷(文科)一、选择题1.设S n是等差数列{a n}的前n项和,若,则=()A.1 B.﹣1 C.2 D.2.已知F1(﹣1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线交于A、B两点,且|AB|=3,则C的方程为()A.B.C.D.3.若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=()A.5 B.4 C.3 D.24.设m>1,当实数x,y满足不等式组时,目标函数z=x+my的最大值等于2,则m的值是()A.2 B.3 C.D.5.如图是一几何体的三视图,则该几何体的体积是()A.9 B.10 C.12 D.186.已知函数,若方程f(x)﹣kx+k=0有两个实数根,则k的取值范围是()A. B.C.[﹣1,+∞)D.7.(理科)过抛物线y2=2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB 为直径的圆和该抛物线的准线l的位置关系是()A.相切B.相离C.相交D.不能确定8.若函数f(x)=x2+ax+b有两个零点cosα,cosβ,其中α,β∈(0,π),那么在f(﹣1),f(1)两个函数值中()A.只有一个小于1 B.至少有一个小于1C.都小于1 D.可能都大于19.已知抛物线C:y2=8x与点M(﹣2,2),过C的焦点,且斜率为k的直线与C交于A,B两点,若=0,则k=()A.B.C.D.210.已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC为球O的直径,且SC⊥OA,SC⊥OB,△OAB为等边三角形,三棱锥S﹣ABC的体积为,则球O的半径为()A.3 B.1 C.2 D.411.已知△ABC中,角A、B、C的对边分别为a、b、c,已知cos2A+cos2B=2cos2C,则cosC的最小值为()A.B.C.D.12.抛物线y2=12x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM 为等边三角形时,则△FPM的外接圆的方程为()A.(x﹣3)2+=5 B.C.(x﹣3)2+(y±3)2=9 D.二.填空题13.若正数x,y满足4x2+9y2+3xy=30,则xy的最大值是.14.定义在R上的奇函数f(x)满足:当x>0时,f(x)=2012x+log2012x,则在R上,函数f(x)零点的个数为.15.已知x,y均为正数,,且满足,,则的值为.16.已知数列{a n}的前n项和s n满足a n+3s n•s n﹣1=0(n≥2,n∈N*),a1=,则na n的最小值为.三.解答题17.在△ABC中,角A,B,C的对边分别是a,b,c.已知a=2c,且.(Ⅰ)求cosC的值;(Ⅱ)当b=1时,求△ABC的面积S的值.18.为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”(Ⅰ)若全校共有学生2000名,其中男生1100名,现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查,应抽取多少名女生?(Ⅱ)下表1,2分别为实行“传统式教学”与“三步式教学”后的数学成绩:表1数学成绩90分以下90﹣120分120﹣140分140分以上频数15 20 10 5表2数学成绩90分以下90﹣120分120﹣140分140分以上频数 5 40 3 2完成下面2×2列联表,并回答是否有99%的把握认为这两种教学法有差异.班次120分以下(人数)120分以上(人数)合计(人数)一班二班合计参考公式:K2=,其中n=a+b+c+d参考数据:P(K2≥k0)0.40 0.25 0.10 0.05 0.010 0.005k00.708 1.323 2.706 3.841 6.635 7.87919.在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρsin2θ=acosθ(a>0),过点P(﹣2,﹣4)的直线l的参数方程为(t为参数),直线l与曲线C相交于A,B两点.(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;(Ⅱ)若|PA|•|PB|=|AB|2,求a的值.20.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,CD⊥PA,DB平分∠ADC,E为PC 的中点,∠DAC=45°,AC=.(Ⅰ)证明:PA∥平面BDE;(Ⅱ)若PD=2,BD=2,求四棱锥E﹣ABCD的体积.21.已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为3,直线y=2与C的两个交点间的距离为.(I)求a,b;(II)设过F2的直线l与C的左、右两支分别相交于A、B两点,且|AF1|=|BF1|,证明:|AF2|、|AB|、|BF2|成等比数列.22.设函数f(x)=x2(e x﹣1)+ax3(1)当时,求f(x)的单调区间;(2)若当x≥0时,f(x)≥0恒成立,求a的取值范围.2015年河北省沧州一中高考数学一模试卷(文科)参考答案与试题解析一、选择题1.设S n是等差数列{a n}的前n项和,若,则=()A.1 B.﹣1 C.2 D.考点:等差数列的前n项和.分析:由等差数列的求和公式和性质可得=,代入已知可得.解答:解:由题意可得====1故选A点评:本题考查等差数列的求和公式,涉及等差数列的性质,属基础题.2.已知F1(﹣1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线交于A、B两点,且|AB|=3,则C的方程为()A.B.C.D.考点:椭圆的标准方程.专题:计算题;圆锥曲线的定义、性质与方程.分析:设椭圆的方程为,根据题意可得=1.再由AB经过右焦点F2且垂直于x轴且|AB|=3算出A、B的坐标,代入椭圆方程得,两式联解即可算出a2=4,b2=3,从而得到椭圆C的方程.解答:解:设椭圆的方程为,可得c==1,所以a2﹣b2=1…①∵AB经过右焦点F2且垂直于x轴,且|AB|=3∴可得A(1,),B(1,﹣),代入椭圆方程得,…②联解①②,可得a2=4,b2=3∴椭圆C的方程为故选:C点评:本题给出椭圆的焦距和通径长,求椭圆的方程.着重考查了椭圆的标准方程和椭圆的简单几何性质等知识,属于基础题.3.若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=()A.5 B.4 C.3 D.2考点:由y=Asin(ωx+φ)的部分图象确定其解析式;y=Asin(ωx+φ)中参数的物理意义.专题:计算题;三角函数的图像与性质.分析:利用函数图象已知的两点的横坐标的差值,求出函数的周期,然后求解ω.解答:解:由函数的图象可知,(x0,y0)与,纵坐标相反,而且不是相邻的对称点,所以函数的周期T=2()=,所以T==,所以ω==4.故选B.点评:本题考查三角函数解析式以及函数的周期的求法,考查学生的视图用图能力.4.设m>1,当实数x,y满足不等式组时,目标函数z=x+my的最大值等于2,则m的值是()A.2 B.3 C.D.考点:简单线性规划.专题:不等式的解法及应用.分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件画出满足约束条件的可行域,再用角点法,求出目标函数的最大值,从而建立关于m的等式,即可得出答案.解答:解:约束条件对应的平面区域如下图示:由得A(,),故当直线z=x+my过A(,)时,Z取得最大值2,∴+=2,m=.故选D.点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.5.如图是一几何体的三视图,则该几何体的体积是()A.9 B.10 C.12 D.18考点:由三视图求面积、体积.专题:探究型;空间位置关系与距离.分析:根据三视图确定空间几何体的结构,然后求几何体的体积即可.解答:解:由三视图可知该几何体是底面是直角梯形,侧棱和底面垂直的四棱锥,其中高为3,底面直角梯形的上底为2,下底为4,梯形的高为3,所以四棱锥的体积为.故选A.点评:本题主要考查三视图的识别和应用,利用三视图将几何体进行还原是解决三视图题目的关键.要求熟练掌握空间几何体的体积公式.6.已知函数,若方程f(x)﹣kx+k=0有两个实数根,则k的取值范围是()A. B.C.[﹣1,+∞)D.考点:根的存在性及根的个数判断.专题:函数的性质及应用.分析:求出函数f(x)的表达式,由f(x)﹣kx+k=0得f(x)=kx﹣k,然后分别作出y=f (x)和y=kx﹣k的图象,利用图象确定k的取值范围.解答:解:当0≤x<1时,﹣1≤x﹣1<0,所以f(x)=,由f(x)﹣kx+k=0得f(x)=kx﹣k,分别作出y=f(x)和y=kx﹣k=k(x﹣1)的图象,如图:由图象可知当直线y=kx﹣k经过点A(﹣1,1)时,两曲线有两个交点,又直线y=k(x﹣1)过定点B(1,0),所以过A,B两点的直线斜率k=.所以要使方程f(x)﹣kx+k=0有两个实数根,则≤k<0.故选B.点评:本题主要考查函数零点的应用,将方程转化为两个函数,利用数形结合,是解决本题的关键.7.(理科)过抛物线y2=2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB 为直径的圆和该抛物线的准线l的位置关系是()A.相切B.相离C.相交D.不能确定考点:圆与圆锥曲线的综合.专题:综合题.分析:设P为AB中点,A、B、P在准线l上射影分别为M、N、Q,根据抛物线的定义,可知AP+BP=AM+BN,从而,所以以AB为直径作圆则此圆与准线l相切.解答:解:设AB为过抛物线焦点F的弦,P为AB中点,A、B、P在准线l上射影分别为M、N、Q,∵AP+BP=AM+BN∴,∴以AB为直径作圆则此圆与准线l相切故选A.点评:本题以抛物线为载体,考查抛物线过焦点弦的性质,关键是正确运用抛物线的定义,合理转化,综合性强.8.若函数f(x)=x2+ax+b有两个零点cosα,cosβ,其中α,β∈(0,π),那么在f(﹣1),f(1)两个函数值中()A.只有一个小于1 B.至少有一个小于1C.都小于1 D.可能都大于1考点:二次函数的性质;函数的零点.专题:函数的性质及应用.分析:因为cosα,cosβ是函数f(x)=x2+ax+b有两个零点,所以可用cosα及cosβ表示f (1)、f(﹣1),再对α、β分①当时;②当时;③当0<α≤<β<π时,及当0时讨论即可.解答:解:∵函数f(x)=x2+ax+b有两个零点cosα,cosβ,∴cosα+cosβ=﹣a,cosα×cosβ=b.∴f(1)=1+a+b=1﹣cosα﹣cosβ+cosα cosβ=(1﹣cosα)(1﹣cosβ),f(﹣1)=1﹣a+b=1+cosα+cosβ+cosα cosβ=(1+cosα)(1+cosβ).∵α,β∈(0,π),下面对α,β分以下三种情况讨论(不妨设α<β).①当时,0≤cosβ<cosα<1,∴1>1﹣cosα>0,1≥1﹣cosβ>0,1+cosα>1,1+cosβ≥1,∴f(1)<1,f(﹣1)>1.②当时,﹣1<cosβ<cosα≤0,∴0<1+cosβ<1,0<1+cosα≤1,1﹣cosβ>1,1﹣cosα≥1,∴f(1)>1,f(﹣1)<1.③当0<α≤<β<π时,﹣1<cosβ<0≤cosα<1,cosαcosβ≤0.当cosα=0时,f(﹣1)=1+cosβ<1.下面对cosαcosβ<0用反证法证明f(1)、f(﹣1)必有一个小于1.假设f(1)≥1,f(﹣1)≥1,则1﹣cosα﹣cosβ+cosα cosβ≥1,1+cosα+cosβ+cosα cosβ≥1,∴cosαcosβ≥cosα+cosβ≥﹣cosαcosβ,∴cosαcosβ≥0,这与cosαcosβ<0矛盾,故f(1)与f(﹣1)中必有一个小于1.对0时,同理可得f(1)与f(﹣1)中必有一个小于1.综上①②③可知:f(1)与f(﹣1)中必有一个小于1.故选B.点评:本题综合考查了一元二次方程的根与系数的关系、函数的零点、三角函数的单调性及值域,分类讨论是解决此问题的关键.9.已知抛物线C:y2=8x与点M(﹣2,2),过C的焦点,且斜率为k的直线与C交于A,B两点,若=0,则k=()A.B.C.D.2考点:抛物线的简单性质;平面向量数量积的运算.专题:压轴题;圆锥曲线的定义、性质与方程.分析:由抛物线C:y2=8x得焦点(2,0),由题意可知:斜率k≠0,设直线AB为my=x﹣2,其中.与抛物线的方程联立可得根与系数的关系,再利用即可解出.解答:解:由抛物线C:y2=8x得焦点(2,0),由题意可知:斜率k≠0,设直线AB为my=x﹣2,其中.联立,得到y2﹣8my﹣16=0,△>0,设A(x1,y1),B(x2,y2).∴y1+y2=8m,y1y2=﹣16.又,,∴=(x1+2)(x2+2)+(y1﹣2)(y2﹣2)=(my1+4)(my2+4)+(y1﹣2)(y2﹣2)=(m2+1)y1y2+(4m﹣2)(y1+y2)+20=﹣16(m2+1)+(4m﹣2)×8m+20=4(2m﹣1)2由4(2m﹣1)2=0,解得.∴.故选D点评:本题综合考查了抛物线的性质、直线与抛物线相交转化为方程联立得到根与系数的关系、向量的数量积运算等基础知识,考查了推理能力、计算能力及分析问题和解决问题的能力.10.已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC为球O的直径,且SC⊥OA,SC⊥OB,△OAB为等边三角形,三棱锥S﹣ABC的体积为,则球O的半径为()A.3 B.1 C.2 D.4考点:球内接多面体;棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:根据题意作出图形,欲求球的半径r.利用截面的性质即可得到三棱锥S﹣ABC的体积可看成是两个小三棱锥S﹣ABO和C﹣ABO的体积和,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.解答:解:根据题意作出图形:设球心为O,球的半径r.∵SC⊥OA,SC⊥OB,∴SC⊥平面AOB,三棱锥S﹣ABC的体积可看成是两个小三棱锥S﹣ABO和C﹣ABO的体积和.∴V三棱锥S﹣ABC=V三棱锥S﹣ABO+V三棱锥C﹣ABO=××r2×r×2=,∴r=2.故选C.点评: 本题考查棱锥的体积,考查球内接多面体,解题的关键是确定将三棱锥S ﹣ABC 的体积看成是两个小三棱锥S ﹣ABO 和C ﹣ABO 的体积和.11.已知△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知cos2A+cos2B=2cos2C ,则cosC 的最小值为( )A .B .C .D .考点: 余弦定理;正弦定理. 专题: 解三角形. 分析: 利用倍角公式化为正弦形式,然后利用正弦定理化为边,用余弦定理化为cosC ,运用基本不等式可求得最小值.解答: 解:由cos2A+cos2B=2cos2C ,得1﹣2sin 2A+1﹣2sin 2B=2(1﹣2sin 2C ),即sin 2A+sin 2B=2sin 2C ,由正弦定理可得a 2+b 2=2c 2,由余弦定理可得c 2+2abcosC=2c 2,所以,所以cosC 的最小值为,故选C . 点评: 本题考查三角函数的恒等变换及其化简求值、正余弦定理,考查灵活运用公式解决问题的能力.12.抛物线y 2=12x 的焦点为F ,点P 为抛物线上的动点,点M 为其准线上的动点,当△FPM 为等边三角形时,则△FPM 的外接圆的方程为( )A . (x ﹣3)2+=5 B .C . (x ﹣3)2+(y ±3)2=9D .考点: 抛物线的简单性质;圆的标准方程. 专题: 圆锥曲线的定义、性质与方程.分析:利用抛物线的定义得出PM垂直于抛物线的准线,设M(﹣3,m),则P(9,m),求出△PMF的边长,写出有关点的坐标,得到外心Q的坐标,△FPM的外接圆的半径,从而求出其方程.解答:解:据题意知,△PMF为等边三角形,PF=PM,∴PM⊥抛物线的准线,F(3,0)设M(﹣3,m),则P(9,m),等边三角形边长为12,如图.在直角三角形APF中,PF=12,解得外心Q的坐标为(3,±4).则△FPM的外接圆的半径为4,∴则△FPM的外接圆的方程为.故选B.点评:本题主要考查了抛物线的简单性质,直线与抛物线的综合问题.考查了学生综合把握所学知识和基本的运算能力.二.填空题13.若正数x,y满足4x2+9y2+3xy=30,则xy的最大值是2.考点:基本不等式.专题:不等式的解法及应用.分析:由于4x2+9y2+3xy=30,配方可得30+9xy=(2x+3y)2,再利用基本不等式即可得出.解答:解:∵正数x,y满足4x2+9y2+3xy=30,∴30+9xy=(2x+3y)2≥4×2x×3y,∴15xy≤30,即xy≤2,当且仅当2x=3y=取等号.故答案为2.点评:变形利用基本不等式是解题的关键.14.定义在R上的奇函数f(x)满足:当x>0时,f(x)=2012x+log2012x,则在R上,函数f(x)零点的个数为3.考点:根的存在性及根的个数判断.专题:函数的性质及应用.分析:由题意先画出当x>0时,函数f1(x)=2012x,f2(x)=﹣log2012x的图象,由图象求出方程根的个数;再根据奇函数图象的对称性以及f(0)=0,求出方程所有根的个数.解答:解:当x>0时,令f(x)=0得,即2012x=﹣log2012x,在同一坐标系下分别画出函数f1(x)=2012x,f2(x)=﹣log2012x的图象,如下图可知,两个图象只有一个交点,即方程f(x)=0只有一个实根.∵f(x)是定义在R上的奇函数,∴当x<0时,方程f(x)=0也有一个实根,又由奇函数的性质可得f(0)=0,∴方程f(x)=0的实根的个数为3,故答案为:3.点评:本题的考点是奇(偶)函数图象的性质应用,即根据题意画出一部分函数的图象,由交点的个数求出对应方程根的个数,利用图象的对称性和“f(0)=0”求出方程根的个数,易漏f(0)=0,属于中档题.15.已知x,y均为正数,,且满足,,则的值为.考点:函数与方程的综合运用.专题:转化思想;三角函数的图像与性质.分析:由,两边同乘以x2+y2得到;把代入上式得,可化为,利用立方和公式可以把cos6θ+sin6θ化为1﹣3sin2θcos2θ,可化为,与sin2θ+cos2θ=1联立,即可解得sin2θ与cos2θ.再根据得,即可得出sinθ与cosθ,即可求出答案.解答:解:∵,∴,化为,(*)∵,∴,,代入(*)得,化为,∵cos6θ+sin6θ=(cos2θ+sin2θ)(cos4θ+sin4θ﹣sin2θcos2θ)=1×[(cos2θ+sin2θ)2﹣3sin2θcos2θ]=1﹣3sin2θcos2θ,∴,化为,与sin2θ+cos2θ=1联立,解得或.由得.故取.解得,∴.故答案为.点评:本题综合考查了三角函数的恒等变形、单调性、平方关系、立方和公式、配方法、方程思想等基础知识与基本方法,需要较强的推理能力和变形能力、计算能力.16.已知数列{a n}的前n项和s n满足a n+3s n•s n﹣1=0(n≥2,n∈N*),a1=,则na n的最小值为﹣.考点:数列递推式.专题:等差数列与等比数列.分析:利用n≥2时,a n=S n﹣S n﹣1,将a n+3s n•s n﹣1=0(n≥2,n∈N*),变形为S n﹣S n﹣1+3S n S n =0.﹣1进而得到.利用等差数列的通项公式即可得出S n.进而得到na n=n(S n﹣S n),利用其单调性即可得出.﹣1解答:解:∵a n+3s n•s n﹣1=0(n≥2,n∈N*),∴S n﹣S n﹣1+3S n S n﹣1=0.∴.∴数列{}是以为首项,3为公差的等差数列.∴,解得.n=1时也成立.∴na n=n(S n﹣S n﹣1)===.n≥2,单调递增,其最小值为,而,故na n的最小值为.故答案为.点评:熟练掌握a n与S n的相互转化、等差数列的通项公式及其数列的单调性即可得出.三.解答题17.在△ABC中,角A,B,C的对边分别是a,b,c.已知a=2c,且.(Ⅰ)求cosC的值;(Ⅱ)当b=1时,求△ABC的面积S的值.考点:正弦定理;三角形的面积公式;余弦定理.专题:计算题;解三角形.分析:(1)由已知及正弦定理可得,sinA=2sinC,结合及同角平方关系即可求解cosC(2)由已知可得B=π﹣(A+C)=,结合(1)及二倍角公式可求sinB,然后由正弦定理,可求c,代入三角形的面积公式可得,S=可求解答:解:(1)∵a=2c,由正弦定理可得,sinA=2sinC∵则C为锐角,cosC>0∴sinA=sin(C+)=cosC联立可得,2sinC=cosC∵sin2C+cos2C=1∴,cosC=(2)由A=C+可得B=π﹣(A+C)=∴sinB=cos2C=2cos2C﹣1=由正弦定理可得,即∴c=由三角形的面积公式可得,S===点评:本题主要考查了正弦定理、余弦定理同角平方关系及三角形的面积公式等知识的综合应用,解题的关键是灵活利用基本公式18.为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”(Ⅰ)若全校共有学生2000名,其中男生1100名,现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查,应抽取多少名女生?(Ⅱ)下表1,2分别为实行“传统式教学”与“三步式教学”后的数学成绩:表1数学成绩90分以下90﹣120分120﹣140分140分以上频数15 20 10 5表2数学成绩90分以下90﹣120分120﹣140分140分以上频数 5 40 3 2完成下面2×2列联表,并回答是否有99%的把握认为这两种教学法有差异.班次120分以下(人数)120分以上(人数)合计(人数)一班351550二班45550合计8020100参考公式:K2=,其中n=a+b+c+d参考数据:P(K2≥k0)0.40 0.25 0.10 0.05 0.010 0.005k00.708 1.323 2.706 3.841 6.635 7.879考点:独立性检验的应用.专题:概率与统计.分析:(Ⅰ)设女生为x可得,解方程可得;(Ⅱ)由已知数据易得列联表,计算K2的值可作出判断.解答:解:(Ⅰ)设女生为x,则,解得x=45名,∴女生抽取45人;(Ⅱ)列联表如下:班次1(20分)以下(人数)1(20分)以上(人数)合计(人数)1班35 15 502班45 5 50合计80 20 100计算可得K2=<6.635由此可知,没有99%的把握认为这两种教学法有差异.点评:本题考查独立检验,涉及抽样调查,快速计算是解决问题的关键,属基础题.19.在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρsin2θ=acosθ(a>0),过点P(﹣2,﹣4)的直线l的参数方程为(t为参数),直线l与曲线C相交于A,B两点.(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;(Ⅱ)若|PA|•|PB|=|AB|2,求a的值.考点:参数方程化成普通方程;点的极坐标和直角坐标的互化.专题:坐标系和参数方程.分析:(Ⅰ)把曲线C的极坐标方程、直线l的参数方程化为普通方程即可;(Ⅱ)把直线l的参数方程代入曲线C的直角坐标方程中,得关于t的一元二次方程,由根与系数的关系,求出t1、t2的关系式,结合参数的几何意义,求出a的值.解答:解:(Ⅰ)曲线C的极坐标方程ρsin2θ=acosθ(a>0),可化为ρ2sin2θ=aρcosθ(a>0),即y2=ax(a>0);(2分)直线l的参数方程为(t为参数),消去参数t,化为普通方程是y=x﹣2;(4分)(Ⅱ)将直线l的参数方程代入曲线C的直角坐标方程y2=ax(a>0)中,得;设A、B两点对应的参数分别为t1,t2,则;(6分)∵|PA|•|PB|=|AB|2,∴,即;(9分)∴,解得:a=2,或a=﹣8(舍去);∴a的值为2分)点评:本题考查了参数方程与极坐标的应用问题,也考查了直线与圆锥曲线的应用问题,解题时应先把参数方程与极坐标化为普通方程,再解答问题,是中档题.20.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,CD⊥PA,DB平分∠ADC,E为PC 的中点,∠DAC=45°,AC=.(Ⅰ)证明:PA∥平面BDE;(Ⅱ)若PD=2,BD=2,求四棱锥E﹣ABCD的体积.考点:直线与平面平行的判定;棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:(Ⅰ)设AC∩BD=F,证明CD⊥平面PAD,可得CD⊥AD.再由∠DAC=45°,DA=DC,可得△ADC为等腰直角三角形.根据DB平分∠ADC,可得F为AC中点,EF为△CPA的中位线,可得故有EF∥PA,再根据直线和平面平行的判定定理证得PA∥平面BDE.(Ⅱ)底面四边形ABCD的面积记为S,由于AC=,可得AD=DC=1,求得S=S△ADC+S△ABC=•AC•BD 的值,再根据点E为线段PC的中点,可得=×,运算求得结果.解答:解:(Ⅰ)设AC∩BD=F,连接EF,∵PD⊥平面ABCD,CD⊂平面ABCD,∴PD⊥CD.又∵CD⊥PA,PD∩PA=P,PD,PA⊂平面PAD,∴CD⊥平面PAD,∵AD⊂平面PAD,∴CD⊥AD.…(2分)∵∠DAC=45°,∴DA=DC,∴△ADC为等腰直角三角形.…(3分)∵DB平分∠ADC,故F为AC中点,EF为△CPA的中位线.…(4分)故有EF∥PA,而EF⊂平面BDE,PA不在平面BDE内,∴PA∥平面BDE.…(6分)(Ⅱ)底面四边形ABCD的面积记为S,由于AC=,∴AD=DC=1,则S=S△ADC+S△ABC=•AC•BD==2.…(9分)∵点E为线段PC的中点,∴=×==.…(12分)点评:本题主要考查直线和平面平行的判定定理的应用,求棱锥的体积,属于中档题.21.已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为3,直线y=2与C的两个交点间的距离为.(I)求a,b;(II)设过F2的直线l与C的左、右两支分别相交于A、B两点,且|AF1|=|BF1|,证明:|AF2|、|AB|、|BF2|成等比数列.考点:直线与圆锥曲线的关系;椭圆的简单性质.专题:证明题;综合题;压轴题;转化思想;圆锥曲线的定义、性质与方程.分析:(I)由题设,可由离心率为3得到参数a,b的关系,将双曲线的方程用参数a表示出来,再由直线建立方程求出参数a即可得到双曲线的方程;(II)由(I)的方程求出两焦点坐标,设出直线l的方程设A(x1,y1),B(x2,y2),将其与双曲线C的方程联立,得出x1+x2=,,再利用|AF1|=|BF1|建立关于A,B坐标的方程,得出两点横坐标的关系,由此方程求出k的值,得出直线的方程,从而可求得:|AF2|、|AB|、|BF2|,再利用等比数列的性质进行判断即可证明出结论.解答:解:(I)由题设知=3,即=9,故b2=8a2所以C的方程为8x2﹣y2=8a2将y=2代入上式,并求得x=±,由题设知,2=,解得a2=1所以a=1,b=2(II)由(I)知,F1(﹣3,0),F2(3,0),C的方程为8x2﹣y2=8 ①由题意,可设l的方程为y=k(x﹣3),|k|<2代入①并化简得(k2﹣8)x2﹣6k2x+9k2+8=0 设A(x1,y1),B(x2,y2),则x1≤﹣1,x2≥1,x1+x2=,,于是|AF1|==﹣(3x1+1),|BF1|==3x2+1,|AF1|=|BF1|得﹣(3x1+1)=3x2+1,即故=,解得,从而=﹣由于|AF2|==1﹣3x1,|BF2|==3x2﹣1,故|AB|=|AF2|﹣|BF2|=2﹣3(x1+x2)=4,|AF2||BF2|=3(x1+x2)﹣9x1x2﹣1=16因而|AF2||BF2|=|AB|2,所以|AF2|、|AB|、|BF2|成等比数列点评:本题考查直线与圆锥曲线的综合关系,考查了运算能力,题设条件的转化能力,方程的思想运用,此类题综合性强,但解答过程有其固有规律,一般需要把直线与曲线联立利用根系关系,解答中要注意提炼此类题解答过程中的共性,给以后解答此类题提供借鉴.22.设函数f(x)=x2(e x﹣1)+ax3(1)当时,求f(x)的单调区间;(2)若当x≥0时,f(x)≥0恒成立,求a的取值范围.考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性.专题:导数的综合应用.分析:(1)先确定函数的定义域然后求出函数的导涵数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间,(2)由于f(x)=x2(e x﹣1)+ax3=x2(e x﹣1+ax),令g(x)=e x﹣1+axx∈[0,+∞),求其导数g′(x)=e x+a,下面就a的值分类讨论,利用导数工具研究函数的单调性和最值,即可得a的取值范围.解答:解:(1)当时,f′(x)=2x(e x﹣1)+x2e x﹣x2=(2x+x2)(e x﹣1)令f′(x)>0,得x>0或﹣2<x<0;令f′(x)<0,得x<﹣2∴f(x)的单调递增区间为(﹣2,0),(0,+∞)f(x)的单调递减区间为(﹣∞,﹣2)…(4分)(2)f(x)=x2(e x﹣1)+ax3=x2(e x﹣1+ax)令g(x)=e x﹣1+axx∈[0,+∞)g′(x)=e x+a当a≥﹣1时,g′(x)=e x+a>0,g(x)在[0,+∞)上为增函数.而g(0)=0,从而当x≥0时,g(x)≥0,即f(x)≥0恒成立.若当a<﹣1时,令g′(x)=e x+a=0,得x=ln(﹣a)当x∈(0,ln(﹣a))时,g′(x)<0,g(x)在(0,ln(﹣a))上是减函数,而g(0)=0,从而当x∈(0,ln(﹣a))时,g(x)<0,即f(x)<0综上可得a的取值范围为[﹣1,+∞).…(12分)点评:本题主要考查了利用导数研究函数的最值,以及函数单调区间等有关基础知识,考查运算求解能力,属于中档题.。
河北省沧州市第一中学2017-2018学年高三暑假第一次周测考试语文试题 Word版含答案

一、基础知识1.下列词语中,加点字的读音全都正确的一组是()A.颤.抖(chàn)伫.立(chù)溘.然长逝(kè)所向披靡.(mǐ)B.踯.躅(zhí)变更.(gēng)不着.边际(zhuó)涸.辙之鲋(hé)C.悼.念(diào)纤.细(xiān)咎.由自取(jiù)锲.而不舍(qiè)D.湍.急(tuān)琴弦.(xián)惊魂甫.定(fǔ)载.歌载舞(zǎi)2.下列各组词语中,没有错别字的一组是()A.缅怀嬉戏没精打彩沧海一粟B.和谐凋弊崇山峻岭渡过难关C.飘渺脉搏文过饰非前倨后恭D.告诫宛然一泻千里目不遐接3.下列各句中,加点的成语使用恰当的一句是()A.《诗经》中的《卫风•氓》是一首以弃妇为题材的诗歌,该诗将弃妇的黍离之悲....写得淋漓尽致、感人至深。
B.网络给青少年的学习、生活带来了便利和乐趣,但一些青少年缺乏自制力,沉溺于网络游戏,夙兴夜寐....,身心健康受到危害。
C.为了参加“国之声”合唱比赛,我班文娱委员精心设计了不少演唱方法,虽屡试不爽....,但同学们仍旧以饱满的热情投入到排练中。
D.最近,金融、地产、汽车等行业纷纷爆发裁员危机,一叶知秋....,未来的就业环境不容乐观。
4.下列各句中,没有语病的一句是()A.“2011中国•都江堰放水节”开幕式围绕以“天上之水,天下人”为主题,表达“谢天、谢地、谢人”以及在大灾面前涌动大爱的感恩之心。
B.今年两会期间,代表们提出,只有走以最有效地利用资源和保护环境为基础的经济之路,提高人民的生活水平,才能实现可持续发展的目标。
C.王安石一直是中国古代历史上具有争议的人物之一,他的功过是非,在我国史学界也分为截然不同的两派。
D.遭遇地震袭击和核危机的日本东北部现有16万多灾民,其中一部分无法获得食物、饮用水、衣物、药品和生活必需品。
5.依次填入下面一段文字横线处的语句,衔接最恰当的一组是()月亮上来了,,,,,。
沧州市一中2018-2019学年高三上学期11月月考数学试卷含答案

沧州市一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 把函数y=cos (2x+φ)(|φ|<)的图象向左平移个单位,得到函数y=f (x )的图象关于直线x=对称,则φ的值为( )A.﹣B.﹣C.D.2. 若{}n a 为等差数列,n S 为其前项和,若10a >,0d <,48S S =,则0n S >成立的最大自 然数为( )A .11B .12C .13D .14 3. 从5名男生、1名女生中,随机抽取3人,检查他们的英语口语水平,在整个抽样过程中,若这名女生第一次、第二次均未被抽到,那么她第三次被抽到的概率是( ) A.B.C.D.4. 如图,四面体OABC 的三条棱OA ,OB ,OC 两两垂直,OA=OB=2,OC=3,D 为四面体OABC 外一点.给出下列命题.①不存在点D ,使四面体ABCD 有三个面是直角三角形 ②不存在点D ,使四面体ABCD 是正三棱锥 ③存在点D ,使CD 与AB 垂直并且相等④存在无数个点D ,使点O 在四面体ABCD 的外接球面上 其中真命题的序号是( )A .①②B .②③C .③D .③④5. 集合{}1,2,3的真子集共有( )A .个B .个C .个D .个 6. 已知函数1)1(')(2++=x x f x f ,则=⎰dx x f 1)(( )A .67-B .67C .65D .65- 【命题意图】本题考查了导数、积分的知识,重点突出对函数的求导及函数积分运算能力,有一定技巧性,难度中等.7. 设D 为△ABC所在平面内一点,,则( )A. B. C.D.8. 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形, 则该几何体的体积为( )班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A.64 B.32 C.643D.3239.已知复合命题p∧(¬q)是真命题,则下列命题中也是真命题的是()A.(¬p)∨q B.p∨q C.p∧q D.(¬p)∧(¬q)10.若偶函数f(x)在(﹣∞,0)内单调递减,则不等式f(﹣1)<f(lg x)的解集是()A.(0,10)B.(,10)C.(,+∞)D.(0,)∪(10,+∞)11.已知函数f(x)=x3+mx2+(2m+3)x(m∈R)存在两个极值点x1,x2,直线l经过点A(x1,x12),B(x2,x22),记圆(x+1)2+y2=上的点到直线l的最短距离为g(m),则g(m)的取值范围是()A.[0,2] B.[0,3] C.[0,)D.[0,)12.如果随机变量ξ~N (﹣1,σ2),且P(﹣3≤ξ≤﹣1)=0.4,则P(ξ≥1)等于()A.0.1 B.0.2 C.0.3 D.0.4二、填空题13.一质点从正四面体A﹣BCD的顶点A出发沿正四面体的棱运动,每经过一条棱称为一次运动.第1次运动经过棱AB由A到B,第2次运动经过棱BC由B到C,第3次运动经过棱CA由C到A,第4次经过棱AD由A到D,…对于N∈n*,第3n次运动回到点A,第3n+1次运动经过的棱与3n﹣1次运动经过的棱异面,第3n+2次运动经过的棱与第3n次运动经过的棱异面.按此运动规律,质点经过2015次运动到达的点为.14.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为小时.15.设全集U=R,集合M={x|2a﹣1<x<4a,a∈R},N={x|1<x<2},若N⊆M,则实数a的取值范围是.16.设x,y满足约束条件,则目标函数z=2x﹣3y的最小值是.17.设向量a=(1,-1),b=(0,t),若(2a+b)·a=2,则t=________.18.如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是.三、解答题19.已知椭圆E:+=1(a>b>0)的左、右焦点分别为F1,F2,离心率为,点(,)在椭圆E上.(1)求椭圆E的方程;(2)设过点P(2,1)的直线l与椭圆相交于A、B两点,若AB的中点恰好为点P,求直线l的方程.20.从某居民区随机抽取10个家庭,获得第i个家庭的月收入x i(单位:千元)与月储蓄y i(单位:千元)的数据资料,计算得x i=80,y i=20,x i y i=184,x i2=720.(1)求家庭的月储蓄对月收入的回归方程;(2)判断月收入与月储蓄之间是正相关还是负相关;(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.21.已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.(1)求椭圆C的方程;(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,说明理由.22.某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.(1)求n的值;(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b 至少有一人上台抽奖的概率.(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.23.已知等边三角形PAB的边长为2,四边形ABCD为矩形,AD=4,平面PAB⊥平面ABCD,E,F,G分别是线段AB,CD,PD上的点.(1)如图1,若G为线段PD的中点,BE=DF=,证明:PB∥平面EFG;(2)如图2,若E,F分别是线段AB,CD的中点,DG=2GP,试问:矩形ABCD内(包括边界)能否找到点H,使之同时满足下面两个条件,并说明理由.①点H到点F的距离与点H到直线AB的距离之差大于4;②GH⊥PD.24.已知椭圆的离心率,且点在椭圆上.(Ⅰ)求椭圆的方程;(Ⅱ)直线与椭圆交于、两点,且线段的垂直平分线经过点.求(为坐标原点)面积的最大值.沧州市一中2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题13.D.14.0.915.[,1].16.﹣6.17.18.0三、解答题19.20.21.22.23.24.。
河北省沧州市第一中学2018届高三上学期周练11.10数学

本卷分分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2018·湖北襄阳联考)函数11()2x f x +=的定义域是( )A .(-1,1)B .(,1)(1,)-∞--+∞C .(,1)(1,1)-∞--D .(,1)(1,1]-∞--2.(2018·湖南省株洲)函数21ln 2y x x =-的单调递减区间为( ) A .(1,1]- B .(0,1] C .[1,)+∞ D .(0,)+∞3.(2018·山东省枣庄月考)已知函数2log ,0()3,0,xx x f x x >⎧=⎨≤⎩则1(())4f f =( )A .19 B .9 C .-19D . -9 4.(2018·甘肃省会宁联考)已知0x >,0y >,lg 2lg8lg 2xy+=,则113x y+的最小值是( )A .2 B. C.4 D.5.(2018·福建省厦门期中)已知函数1222,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩,且()3f a =-,则(6)f a -=( )A .74-B .45- C.34- D .14- 6.(2018·海南省海口市模拟)函数5()3f x x x =+-零点所在的区间是( ) A .[0,1] B .[1,2] C.[2,3] D .[3,4]7.(2018·山东省师大附中模拟)函数3cos3()91x x x f x ⋅=-的图象大致为( )A .B .C.D .8.(2018·人大附中模拟)已知函数231,0()|41|,0x x f x x x x +≤⎧=⎨-+>⎩,若函数2()()()g x f x axf x =-恰有6个零点,则a 的取值范围是( )A .(0,3)B .(1,3) C.(2,3) D .(0,3)9.(2018·重庆市联考)已知函数y =的定义域为区间A ,值域为区间B ,则A C B =( )A .(1,2)B .(1,2] C.(0.1) D .(0,1]10.(20181.山东淄博邯郸市联考)下列函数中,既是偶函数又存在零点的是( ) A .cos y x = B .21y x =+ C.sin y x = D .ln y x = 11.(2018·河北省邯郸市联考)已知函数2|ln |,0()41,0x x f x x x x >⎧=⎨++≤⎩,若关于x 的方程2()()0f x bf x c -+=(,b c R ∈)有8个不同的实数根,则b c +的取值范围是( )A .(,3)-∞B .(0,3] C.[0,3] D .(0,3)12.(2018·河南省株洲市期末)已知函数3()sin 4f x a x bx =++(a R ∈,b R ∈),'()f x 为()f x 的导函数,则(2014)(2014)'(2015)'(2015)f f f f +-+--=( ) A .2018 B .2018 C.-2018 D .8第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在答题纸给定的)13.(2018·云南师大附中模拟)设函数()f x 是定义在R 上的周期为3的偶函数,当30,2x ⎡⎤∈⎢⎥⎣⎦时,()1f x x =+,则5()2f = .14.(2018·江西省南昌模拟)已知2ln 2()xx f x x +=,求'(1)f = .15.(2018·宁夏模拟)函数()1log a f x x =+(0a >,1a ≠)的图象恒过定点A ,若点A 在直线20mx ny +-=上,其中0mn >,则11m n+的最小值为 . 16.(2018·重庆模拟)已知函数()xf x x e =+,()lng x x x =+,()ln 1h x x =-的零点依次为a ,b ,c 从大到小的顺序为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17. (2018·黑龙江大庆铁人中学模拟)(本小题满分10分) 已知函数20()lg 10f x a x ⎛⎫=+⎪+⎝⎭为奇函数.(Ⅰ)求实数a 的值;(Ⅱ)求不等式()0f x >的解集.18. (2018·江西省南昌模拟)(本小题满分12分) 已知函数21()ln 2f x x a x =+ (Ⅰ)若1a =,求()f x 在点(1,(1))f 处的切线方程; (Ⅱ)若2a =-,求函数()f x 在[1,]e 上的最大值和最小值. 19. (2018·内蒙古赤峰模拟)(本小题满分12分) 已知函数()2421xxf x a =⋅--. (Ⅰ)当1a =时,求函数()f x 的零点; (Ⅱ)若函数()f x 有零点,求实数a 的取值范围. 20. (2018·山东联考)(本小题满分12分)已知二次函数()y f x =,当2x =时,函数取最小值-1,且(1)(4)3f f +=. (Ⅰ)求()f x 的解析式;(Ⅱ)若()()g x f x kx ==在区间[1,4]上不单调,求实数k 的取值范围.21. (2018·湖南省长沙模拟)(本小题满分12分)已知函数32()f x ax bx =+,()f x 在点(3,(3))f 处的切线方程为122270x y +-=. (Ⅰ)求函数()f x 的解析式;(Ⅱ)若对任意的[1,)x ∈+∞,'()ln f x k x ≤恒成立,求实数k 的取值范围. 22.(2018·浙江绍兴模拟)(本小题满分12分) 设函数2()ln f x a x bx =-,,a b R ∈ (Ⅰ)若函数()f x 在1x =处与直线12y =-相切; (ⅰ)求实数a ,b 的值;(ⅱ)求函数()f x 在1,e e⎡⎤⎢⎥⎣⎦上的最大值;(Ⅱ)当0b =时,若不等式()f x m x ≥+对任意的30,2a ⎡⎤∈⎢⎥⎣⎦,2(1,]x e ∈都成立,求实数m 的取值范围.专题三 函数与导数(文)一、选择题1-5:DBACA 6-10:BDCBA 11、12:DD二、填空题13.3214.2ln 23- 15.2 16.c b a >> 三、解答题17.解:(Ⅰ)由奇函数定义域关于原点对称得1a =-,经验证,此时()f x 的定义域为(-10,10),且有()()f x f x -=-,故实数1a =-.(5分) (Ⅱ)由(Ⅰ)()f x 定义域为(-10,10),故10()lglg(10)lg(10)10xf x x x x-==--++,(Ⅱ)由于函数()f x 的定义域为(0,)+∞,当2a =-时,2'()f x x x =-=,令'()0f x =,得x =或x =.(7分)当x ∈时,函数()f x 单调递减,当)x e ∈时,函数()f x 单调递增,所以()f x在x =1ln 2f =-,1()2f x =,24()2e f e -=,1ln 2f =-,(10分)∵24122e ->,∴min ()1ln 2f x f ==-,2max 4()()2e f x f e -==.(12分)19.解:(Ⅰ)1a =时,()2421x x f x =⋅--,令()0f x =,即22(2)210x x⋅--=,解得21x =或122x =-(舍) 所以0x =,所以函数()f x 的零点为0x =.(Ⅱ)若()f x 有零点,则方程24210x x a ⋅--=有解.于是221111112424224xxx xx a ⎡⎤+⎛⎫⎛⎫⎛⎫==+=+-⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,因为102x⎛⎫> ⎪⎝⎭,所以112044a >-=,即0a >.(12分)20.解:(Ⅰ)由题意得,设2()f x ax bx c =++(0a ≠),由题意可得:2212(1)(4)3b a b f a f f ⎧-=⎪⎪⎪⎛⎫-=-⎨ ⎪⎝⎭⎪⎪+=⎪⎩(3分)解得:143a b c =⎧⎪=-⎨⎪=⎩,所以2()43f x x x =-+.(6分)(Ⅱ)2()(4)3g x x k x =-++的对称轴为直线42kx +=, 因为()g x 在区间[1,4]上不单调, 故4142k+<<, (10分)解得,24k -<<,故k 的取值范围为(2,4)-. (12分)21.(Ⅰ)将3x =代入直线方程得92y =-,∴92792a b +=- ①2'()32f x ax bx =+,'(3)6f =-,∴2766a b +=-②①②联立,解得13a =-,12b =, ∴3211()32f x x x =-+. (4分)(Ⅱ)2'()f x x x =-+,∴2ln x x k x -+≤在[1,)x ∈+∞恒成立;即2ln 0x x k x -+≥在[1,)x ∈+∞恒成立;(6分) 设2()ln g x x x k x =-+,(1)0g =,∴只需证对任意[1,)x ∈+∞有()(1)g x g ≥.22'(2)21k x x kg x x x-+=-+=,[1,)x ∈+∞ 设2()2h x x x k =-+, ①当180k ∆=-≤,即18k ≥时,()0h x ≥,∴'()0g x ≥,()g x 在[1,)+∞上单调递增,∴()(1)g x g ≥;(9分) ②当180k ∆=->即18k <时,设1x ;2x 是方程220x x k -+=的两根且12x x <,由1212x x +=,可知11x <,分析题意可知当21x ≤时对任意[1,)x ∈+∞有()(1)g x g ≥;(11分)∴(1)10h k =+≥,1k ≥-,∴118k -≤≤, 综上分析,实数k 的取值范围为[1,)+∞.(12分)【方法点睛】对于含参数的函数在闭合区间上函数值恒大于等于或小于等于常数问题,可以求函数最值的方法,一般通过变量分离,将不等式恒成立问题转化为求函数的最值问题,然后再构造辅助函数()f x ,利用()f x m >恒成立min ()f x m ⇔>;()f x m <恒成立max ()f x m ⇔<,即可求出参数范围.22.解:(Ⅰ)(ⅰ)'()2a f x bx x =-,∵函数()f x 在1x =处于直线12y =-相切, '(1)201(1)2f a b f b =-=⎧⎪⎨=-=-⎪⎩,解得112a b =⎧⎪⎨=⎪⎩;(3分) (ⅱ)21()ln 2f x x x =-,211'()x f x x x x -=-=,当1x e e≤≤时,令'()0f x >,得11x e≤<; 令'()0f x <,得1x e <≤∴()f x 在1,1e ⎡⎤⎢⎥⎣⎦上单调递增,在[1,]e 上单调递减,∴max 1()(1)2f x f ==-; (6分)(Ⅱ)当0b =时,()ln f x a x =,∴问题等价于ln m a x x ≤-对所有的3[0,]2a ∈,2(1,]x e ∈都成立,(8分) 令()ln h a a x x =-,∵2(1,]x e ∈, ∴ln 0x >,故()h a 为关于a 的一次函数, ∴min ()(0)m h a h x ≤==-, ∴m x ≤-对多由的2(1,]x e ∈都成立.。
河北省沧州市第一中学2018届高三上学期第一次月考语文试题 含答案

一、现代文阅读。
(9分,每小题3分)阅读下面文字,完成1—3题唐人古体古体诗,亦名古诗、古风或往体诗,指的是产生于唐以前并和唐代新出现的近体诗(又今体诗)相对的一种试体。
它的特点是格律限制不太严格,篇幅可长可短,押韵比较自由灵活,不必拘守对偶、声律,有四言、五言、七言、杂言等多种形式。
不过唐人的古体以五言、七言为主,杂言也多以七言为主体。
五七言古诗自汉魏以来已经有了悠久的传统,至唐代又发生了新变。
唐代社会生活领域的扩展和人的思想感情的复杂化,要求诗歌作品在表现范围上有较大的开拓,加上篇幅短小、格律严整的近体诗走向定型化,更促使这种少受时空限制的古诗朝着发挥自己特长的道路迈进。
一般说来,较之魏晋六朝诗歌大多局限于比较单纯的抒情写景,唐人的古诗则趋向笔力驰骋、气象峥嵘、边幅开阔、语言明畅,不仅抒写波澜起伏的情感心理活动,还直接叙述事件,刻画人物,铺捧场景,发生议论,使诗歌表情达意的功能得到空前的发挥。
唐代诗人中也有接近于汉魏古诗含蓄淳厚作风的,如王、孟、韦、柳,但较为少见。
不构成唐人古诗的主流。
另外,在音节上,唐代古诗受今体诗的影响,或则吸取声律的和谐与对仗的工整,或则有意走上反律化的途径,皆不同于晋、宋以前诗歌韵调的纯任自然。
所以明代格调论者以唐人古诗为汉魏以来古诗的“变体”,并不算错。
只是他们从伸正黜变、荣古虐今的传统观念出发,贬抑唐人古诗的成就,甚至宣言“唐无五言古诗”(李攀龙《唐选诗序》),那就太过分了。
清王士禛《古诗选》在五言古诗部分选了一百多位汉魏六朝作家的作品,于唐人只取陈于昂、张九龄、李白、韦应物、柳宗元五家,还说是“四唐古诗之望,可以略暗焉”(《古诗选.五言诗凡例》),显示出同一偏见。
倒是明末许学灵在《》中强调指出“唐人五古自有唐体”,它以敷陈充畅为特色,不能拿汉魏古诗委婉含蓄的作风来硬加绳尺,可谓通达之见。
至于同属唐人古体,五言和七言又有所差别,这个问题比较微妙,须细心体察。
我们看五七言的区分,虽只在每句相差两个字上,但造成的节奏感和韵调感却很不一样。
2021届河北省沧州市泊头市一中2018级高三上学期第一次月考语文试卷及答案

河北省沧州市泊头一中高三年级上学期第一次月考语文试题一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
透视“李约瑟难题”:呼唤创新文化梁启东世界科技发展史上,曾经有一道著名的“李约瑟难题”。
英国历史学家李约瑟提出:“尽管中国古代对人类科技发展做出了很多重要贡献,但为什么科学和工业革命没有在近代的中国发生?”确实,元明以前,华夏大地在科技和经济很多领域都领先于世界。
但是到了近代,中国没有实现科技的突破和工业的崛起,中国的科技和经济却纷纷落伍了。
这其中的原因何在?比较近代世界科技发展的历史,18世纪以来,世界科技中心和工业中心从英国转到德国,再到美国,表面上是地理位置的更替,实质上是创新能力由弱向强的转移,是有利于创新的体制、机制和文化相互作用的结果。
英国是工业革命的发源地。
以蒸汽机的发明和广泛应用为标志的工业革命,推动了人类社会生产力的极大发展。
17、18世纪,那里有较为宽松的宗教背景,为牛顿等科学家提出超前的、有创见的理论提供了合适的气候和土壤;其先进的市场意识、商贸手段也为蒸汽机等技术发明和产业化创造了有利条件。
在相当长一段时间内,英国是世界科学中心、技术中心和产业中心。
我们再看看德国在近代为什么能够在迅速崛起。
德国的迅速崛起,要归功于德国哲学思想的活跃以及宗教改革以后的一系列政治、经济、社会方面政策措施的实施;归功于学校教育方面的创新,归功于将大学专业教学与专业研究结合起来,促使大批的青年人才直接参与科学前沿的探索活动,促成了科技创新和人力资本因素的长期积累。
这种新型模式催生了现代大学研究开发机构,为科研和创新营造了良好的文化环境,开辟了培养创新人才的先河。
现在世界科技和经济“超级大国”美国,也是通过文化创新后来居上的。
美国为什么能够成功?最大的因素,是有一个以市场机制为基础,不断营造和优化有利于创新的良好文化氛围。
古今中外的例子充分证明:一流的成果需要一流的人才,一流的人才的环境。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合{}{}2|,|lg 0M x x x N x x ===≤,则MN =( )A .[)0,1B .(]0,1C .[]0,1D .(],1-∞ 【答案】C考点:集合的运算. 2.若复数z 满足1zi i=-,其中i 为虚数单位, 则z =( ) A . 1i + B . 1i - C .1i -- D .1i -+ 【答案】B【解析】 试题分析:由1zi i=-,得()i i i z +=-=11,则i z -=1,故选项为B. 考点:复数的运算.3.设x R ∈,则“12x <<”是“21x -<”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .即不充分也不必要条件 【答案】A【解析】试题分析:由3112<<⇒<-x x ,又因为{}{}3121<<=⊆<<=x x B x x A ,故“12x <<”是“21x -<”的充分不必要条件,故选A. 考点:充要条件.4.已知命题:,23x x p x R ∀∈<;命题32:,1q x R x x ∃∈=-,则下列命题中为真命题的是( ) A .p q ∧ B .p q ⌝∧ C .p q ∧⌝ D .p q ⌝∧⌝ 【答案】B考点:复合命题的真假.5.函数()256lg 3x x f x x -+=-的定义域为( )A .()2,3B .(]2,4C .()(]4332,,⋃D .()(]1,33,6-【答案】C 【解析】试题分析:要使函数有意义需满足⎪⎩⎪⎨⎧>-+-≥-0365042x x x x ,解得()(]4332,,⋃∈x ,故选C. 考点:函数的定义域.6.设向量()()1,2,1,1,a b c a kb ===+,若b c ⊥,则实数k 的值等于( ) A .53 B .32 C .32-D .53-【答案】C 【解析】试题分析:由()()1,2,1,1,a b c a k b ===+,得()k k c ++=2,1,又由b c ⊥得021=+++k k ,解得23-=k ,故选项为C.考点:向量的坐标运算.7.已知数列{}n a 是公差为1的等差数列,n S 为数列{}n a 的前n 项和, 若844S S =,则10a =( ) A .172 B .192C .10D .12 【答案】B 【解析】试题分析:由题意得()⎩⎨⎧+⨯=⨯+=6441288111a a d ,解得211=a ,则219192110=⨯+=a ,故选B.考点:等差数列的性质.8.已知函数()()1222,1log 1,1x x f x x x -⎧-≤⎪=⎨-+>⎪⎩,且()3f a =-,则()6f a -=( )A .74-B .54-C .34- D .14-【答案】A 【解析】试题分析:由()3f a =-,得7=a ,则()()47221611=-=-=---f a f ,故选A. 考点:分段函数的性质.9.若函数()ln f x kx x ==-在区间()1,+∞上单调递增, 则实数k 的取值范围是( )A .(],2-∞-B .(],1-∞-C .[)2,+∞D .[)1,+∞ 【答案】D考点:利用导数研究函数的单调性.10.在平面直角坐标系中,O 为原点,()(()1,0,,3,0A B C -, 动点D 满足1CD =,则OA OB OD ++的取值范围是( )A .[]4,6B .1⎤⎦C .⎡⎣D .1⎤⎦【答案】D考点:向量的加法及其几何意义.【方法点睛】本题考查了向量的坐标运算、数量积性质、模的计算公式、三角函数的单调性等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.由于动点D 满足1CD =,()0,3C ,可设()θθsin ,cos 3+D []πθ20,∈.再利用向量的坐标运算、数量积性质、模的计算公式、三角函数的单调性即可得出.11.设函数()()21ln 11f x x x =+-+,则使()()21f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭ B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C .11,33⎛⎫- ⎪⎝⎭D .11,,33⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭【答案】A 【解析】试题分析:()()21ln 11f x x x =+-+,定义域为R ,∵()()x f x f =-,∴函数()x f 为偶函数,当0>x 时,()()2111ln x x x f +-+=函数单调递增,根据偶函数性质可知:得()()21f x f x >-成立,∴12->x x ,∴()2212->x x ,∴x 的范围为1,13⎛⎫ ⎪⎝⎭故答案为A.考点:抽象函数的不等式.【思路点晴】本题考查了偶函数的性质和利用偶函数图象的特点解决实际问题,属于基础题型,应牢记.根据函数的表达式可知函数()x f 为偶函数,根据初等函数的性质判断函数在x 大于零的单调性为递增,根据偶函数关于原点对称可知,距离原点越远的点,函数值越大,把()()21f x f x >-可转化为12->x x ,解绝对值不等式即可.12.已知函数()()22,0ln 1,0x x x f x x x ⎧-+≤⎪=⎨+>⎪⎩,若()f x ax ≥,则a 的取值范围是( )A .(],0-∞B .(],1-∞C .[]2,1-D .[]2,0- 【答案】D考点:不等式的解法.【方法点晴】本题考查其它不等式的解法,数形结合是解决问题的关键,属中档题.由函数图象的变换,结合基本初等函数的图象可作出函数()x f y =的图象,和函数ax y =的图象,把()f x ax ≥转化为()x f y =的图象始终在ax y =的图象的上方,直线介于l 和x 轴之间符合题意,由导数求切线斜率可得l 的斜率,进而数形结合可得a 的范围.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.若函数()22xf x b =--有两个零点, 则实数b 的取值范围是 .【答案】()0,2考点:函数的零点.【方法点晴】本题主要考查函数的零点以及数形结合方法,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.当涉及到零点的个数时主要转化为函数图象交点的个数,在该题中由函数()22xf x b =--有两个零点,可得b x =-22有两个零点,从而可得函数22-=x y 函数b y =的图象有两个交点,结合函数的图象可求b 的范围.14.设数列{}n a 满足:11a =,且()11n n a a n n N *+-=+∈,则数列1n a ⎧⎫⎨⎬⎩⎭的前10项和等于 . 【答案】1120 【解析】考点:(1)数列的递推式;(2)数列的求和.15.已知曲线ln y x x =+在点()1,1处的切线与曲线()221y ax a x =+++相切, 则a 的值为 . 【答案】8 【解析】试题分析:ln y x x =+的导数为xy 11+=',曲线ln y x x =+在1=x 处的切线斜率为2=k ,则曲线ln y x x =+在1=x 处的切线方程为221-=-x y ,即12-=x y .由于切线与曲线()221y ax a x =+++相切,故()221y ax a x =+++可联立12-=x y ,得022=++ax ax ,又0≠a ,两线相切有一切点,所以有082=-=∆a a ,解得8=a .故答案为:8.考点:利用导数研究曲线上某点切线方程.【方法点晴】本题考查导数的运用:求切线方程,主要考查导数的几何意义:函数在某点处的导数即为曲线在该点处的导数,设出切线方程运用两线相切的性质是解题的关键,难度中档.求出ln y x x =+的导数,求得切线的斜率,可得切线方程,再由于切线与曲线()221y ax a x =+++相切,有且只有一切点,进而可联立切线与曲线方程,根据0=∆得到a 的值.16.设x θ=时, 函数()sin 2cos f x x x =-取得最大值, 则cos θ= .【答案】5- 【解析】试题分析:()()α-=⎪⎪⎭⎫⎝⎛-=-=x x x x x x f sin 5cos 552sin 555cos 2sin (其中55cos =α,552sin =α),∵θ=x 时,函数()x f 取得最大值,∴()1sin =-αθ,即5cos 2sin =-θθ,又1cos sin 22=+θθ,联立得()1cos 5cos 222=++θθ,解得552cos -=θ.故答案为:5-.考点:(1)两角和与差的正弦函数;(2)正弦函数的定义域和值域.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分10分)在ABC ∆中, 已知2,3,60AB AC A ===. (1)求BC 的长; (2)求sin 2C 的值. 【答案】(1)7;(2)734. 考点:(1)余弦定理的应用;(2)二倍角的正弦.18.(本小题满分12分)在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,已知tan 24A π⎛⎫+= ⎪⎝⎭.(1)求2sin 2sin 2cos AA A+的值;(2)若 ,34B a π==,求ABC ∆的面积.【答案】(1)52;(2)9.考点:(1)三角恒等式;(2)三角形的面积公式.19.(本小题满分12分)已知{}n a 是递增的等差数列,23,a a 是方程2560x x -+=的两个实根.(1)求数列{}n a 的通项公式; (2)求数列{}2nn a 的前n 项和nS.【答案】(1)n a n =;(2)()2211+⋅-=+n n n S .【解析】试题分析:(1)利用{}n a 是递增的等差数列,23,a a 是方程2560x x -+=的根.得到2560x x -+=,再求首项和公差,进一步求通项公式;(2)利用错位相减法求和.试题解析:(1)方程2560x x -+=的两个实根为2,3,由题意得232,3a a ==,设数列{}n a 的公差为d ,则3232,1d a a =-=-=,从而11a =,所以数列{}n a 的通项公式n a n =. (2)由(1)知,12322,122232...2n n n n n a n S n =∴=⨯+⨯+⨯++ ①()23121222...122n n n S n n +∴⨯+⨯++-+ ②①-②得,()()2311212222 (22212)n n n n n S n n ++⨯--=++++-=--()111222122n n n n n +++=--=--,()1122n n S n +∴=-+.考点:(1)等差数列的通项公式;(2)数列求和.【方法点睛】本题主要考查了利用等差数列的性质求等差数列的通项公式,以及常见的利用错位相减法求数列的前n 项和,属于常规题,难度适中.首先通过解一元二次方程,得到等差数列中的两项,从而可以求得等差数列的通项公式;在求数列的前n 项和中,首先应求出该数列的通项公式,然后根据其特征,决定采用何种方法,当表示成等差数列n 和等比数列n2的乘积时,应采用错位相减法.20.(本小题满分12分)已知数列{}n a 是等差数列, 满足143,12a a ==,数列{}n b 满足144,20b b ==,且数列{}n n b a -为等比数列.(1)求数列{}n a 和{}n b 的通项公式; (2)求数列{}n b 的前n 项和n S .【答案】(1)n a n 3=,123-+=n n n b ;(2)()12132-++=n n n n S .(2)由(1)知,()132n n b n n N -*=+∈,()()231369 (3122)2...2n nS n -∴=++++++++++()()()1123331212122nn n n n n ⨯-+=+=++--.考点:(1)求数列的通项公式;(2)数列求和. 21.(本小题满分12分)已知函数()()24xf x e ax b x x =+--,曲线()y f x =在点()()0,0f 处的切线方程为44y x =+. (1)求,a b 的值;(2)讨论函数()f x 的单调性, 并求函数()f x 的极大值.【答案】(1)4,4a b ==;(2)()f x 在(),2-∞-和()ln 2,-+∞上单调递增, 在()2,ln 2--单调递减,函数()f x 的极大值为()()2241f e--=-.考点:(1)利用导数研究曲线上某点处切线方程;(2)利用导数研究函数的单调性. 22.(本小题满分12分)已知函数()()21ln 2x f x x -=-.(1)求函数()f x 的单调递增区间; (2)证明:当1x >时,()1f x x <-.【答案】(1)10,2⎛ ⎝⎭;(2)证明见解析.考点:(1)利用导数研究函数的单调性;(2)不等式的证明.【方法点睛】本题主要考查了利用导数研究函数的单调性,以及不等式的证明,注重对基础知识的考查,也是在高考中常见的考查形式,难度适中;利用导数求函数()f x 的单调性的步骤:①确定函数()f x 的定义域;②对()f x 求导;③求不等式()0>'x f 和()0<'x f 的解集,得单调区间;常见的证明不等式中,()()0>-x g x f ,令()()()x g x f x h -=,使得()0>x h 恒成立即可,转化为()0min >x h 即可,利用单调性得()min x h .。
