广东省13市2017届高三上学期期末考试数学理试题分类汇编：排列组合与二项式定理-Word版含答案

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省14市高三上学期期末考试数学理试题分类汇编排列组与二项式定理一、二项式定理1、（东莞市2019届高三上学期期末）二项式621()x x -的展开式的常数项为 A 、±15 B 、15 C 、±20 D 、－202、（广州市2019届高三12月调研考试）已知(4234012342x a a x a x a x a x +=++++，则()()2202413a a a a a ++-+=．3、（揭阳市2019届高三上学期期末）821)x 的展开式中1x 的系数为_______；4、（雷州市2019届高三上学期期末）已知5522105)1()1()1()1(x a x a x a a x -++-+-+=+ ，则=3aA ．40-B ．40C ．10D ．10-5、（茂名市2019届高三上期末）321()x x +的展开式中的常数项是． 6、（清远市2019届高三上期末）52)1)(13(x x+-的常数项是_____________ . 7、（汕尾市2019届高三上学期期末）522x x ⎛⎫- ⎪⎝⎭的展开式中1x 的系数是。

8、（肇庆市2019届高三上学期期末）()53221x x x ⎛⎫++ ⎪⎝⎭的展开式中4x 的系数为． 9、（佛山市2019届高三上学期期末）展开式中的系数为 A 、-40 B 、120 C 、160 D 、20010、（华附、省实、广雅、深中2019届高三上学期期末联考） 52431x xx ⎛⎛⎫-+- ⎪ ⎝⎭⎝的展开式中常数项为 A.30-B.30C.25-D.25参考答案一、1、B2、163、2244、A5、36、－77、－408、1209、B 10、C二、排列组合1、（汕头市2019届高三上学期期末）把分别写有1，2，3，4，5 的五张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么不同的分法种数为________(用数字作答)．2、（韶关市2019届高三上学期期末）某中学元旦晚会共由6个节目组成，演出顺序有如下要求：节目甲必须排在乙的前面，丙不能排在最后一位，该晚会节目演出顺序的编排方案共有A、720种B、360种C、300种D、600种3、（珠海市2019届高三上学期期末）将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（）A、12种B、24种C、36种D、48种4、（肇庆市2019届高三第一次统一检测）将甲、乙、丙、丁、戊共5人分配到A、B、C、D共4所学校，每所学校至少一人，且甲不去A学校，则不同的分配方法有A．72种B．108种C．180种D．360种5、（广东省七校2019届高三第一次联考）旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若甲景区不能最先旅游，乙景区和丁景区不能最后旅游，则小李旅游的方法数为（）A.24B.18C.16D.10、、、、五个数字任取三个数字，组成能被3整除的没有重6、（珠海市2019届高三摸底考试）由01234复数字的三位自然数，共有_____个．参考答案二、1、362、C3、C4、C5、D6、20。

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省14市高三上学期期末考试数学理试题分类汇编排列组与二项式定理一、二项式定理1、（东莞市2019届高三上学期期末）二项式621()x x -的展开式的常数项为 A 、±15 B 、15 C 、±20 D 、－202、（广州市2019届高三12月调研考试）已知(4234012342x a a x a x a x a x =++++，则()()2202413a a a a a ++-+=．3、（揭阳市2019届高三上学期期末）821)x 的展开式中1x 的系数为_______；4、（雷州市2019届高三上学期期末）已知5522105)1()1()1()1(x a x a x a a x -++-+-+=+ ，则=3aA ．40-B ．40C ．10D ．10-5、（茂名市2019届高三上期末）321()x x +的展开式中的常数项是． 6、（清远市2019届高三上期末）52)1)(13(x x+-的常数项是_____________ . 7、（汕尾市2019届高三上学期期末）522x x ⎛⎫- ⎪⎝⎭的展开式中1x 的系数是。

8、（肇庆市2019届高三上学期期末）()53221x x x ⎛⎫++ ⎪⎝⎭的展开式中4x 的系数为． 9、（佛山市2019届高三上学期期末）展开式中的系数为 A 、-40 B 、120 C 、160 D 、20010、（华附、省实、广雅、深中2019届高三上学期期末联考） 52431x xx ⎛⎛⎫-+- ⎪ ⎝⎭⎝的展开式中常数项为 A.30-B.30C.25-D.25参考答案一、1、B2、163、2244、A5、36、－77、－408、1209、B 10、C二、排列组合1、（汕头市2019届高三上学期期末）把分别写有1，2，3，4，5 的五张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么不同的分法种数为________(用数字作答)．2、（韶关市2019届高三上学期期末）某中学元旦晚会共由6个节目组成，演出顺序有如下要求：节目甲必须排在乙的前面，丙不能排在最后一位，该晚会节目演出顺序的编排方案共有A、720种B、360种C、300种D、600种3、（珠海市2019届高三上学期期末）将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（）A、12种B、24种C、36种D、48种4、（肇庆市2019届高三第一次统一检测）将甲、乙、丙、丁、戊共5人分配到A、B、C、D共4所学校，每所学校至少一人，且甲不去A学校，则不同的分配方法有A．72种B．108种C．180种D．360种5、（广东省七校2019届高三第一次联考）旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若甲景区不能最先旅游，乙景区和丁景区不能最后旅游，则小李旅游的方法数为（）A.24B.18C.16D.10、、、、五个数字任取三个数字，组成能被3整除的没有重6、（珠海市2019届高三摸底考试）由01234复数字的三位自然数，共有_____个．参考答案二、1、362、C3、C4、C5、D6、20。

广东省13市2017届高三上学期期末考试数学理试题分类汇编：排列组合与二项式定理(word版,附答案)

广东省13市2017届高三上学期期末考试数学理试题分类汇编排列组合与二项式定理一、排列组合1、（广州市2017届高三12月模拟）GZ 新闻台做“一校一特色”访谈节目, 分A, B, C 三期播出, A 期播出两间学校, B 期，C 期各播出1间学校, 现从8间候选学校中选出4间参与这三项任务, 不同的选法共有（A ）140种（B ）420种（C ）840种（D ）1680种2、（茂名市2017届高三第一次综合测试）学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座，每科一节课，每节至少有一科，且数学、理综不安排在同一节，则不同的安排方法共有( )A ． 6种B ．24种C ．30种D ．36种参考答案1、C2、 C 解：由于每科一节课，每节至少有一科，必有两科在同一节，先从4科中任选2科看作一个整体，然后做3个元素的全排列，共2343C A 种方法，再从中排除数学、理综安排在同一节的情形，共33A 种方法，故总的方法种数为2343C A -33A =36-6=30．二、二项式定理1、（潮州市2017届高三上学期期末）（x ++1）4展开式中常数项为（）A ．18B ．19C ．20D ．212、（东莞市2017届高三上学期期末）的展开式中含x 项的系数为－6，则常数a ＝_______．3、（佛山市2017届高三教学质量检测（一））二项式())(23*3N n x n ∈+展开式中只有一项的系数为有理数，则n 的可能取值为（） A ．6 B ．7 C ．8 D ．94、（惠州市2017届高三第三次调研）⎝⎛⎭⎫12x －2y 5的展开式中x 2y 3的系数是( ) （A ）－20 （B ）－5 （C ）5 （D ）205、（揭阳市2017届高三上学期期末）在8)1(xx -的展开式中，常数项是． 6、（茂名市2017届高三第一次综合测试）已知22cos a xdx ππ-=⎰，则二项式6()a x x+展开式中的常数项是 * ．7、（汕头市2017届高三上学期期末）将二项式6)2(x x +展开式各项重新排列，则其中无理项互不相邻的概率是（）A ．72B ．351 C. 358 D ．247 8、（韶关市2017届高三1月调研）在5(1)(12)x x +⋅+的展开式中，4x 的系数为（用数字作答）.9、（肇庆市2017届高三第二次模拟）若61()n x x x +的展开式中含有常数项，则n 的最小值等于（A ）3 （B ）4 （C ）5 （D ）610、（珠海市2017届高三上学期期末）若()na x x -展开式中所有二项式系数之和是64 ，常数项为15 ，则实数a 的值是．参考答案1、解：（x ++1）4展开式的T r +1=，（r=0，1，…，4）．的通项公式：T k +1==x r ﹣2k ，令r=2k ，可得：k=0时，r=0；k=1时，r=2，k=2时，r=4．∴（x ++1）4展开式中常数项=1++=19．故选：B ．2、33、B4、A5、706、解：22cos a xdx ππ-=⎰=22sin 2x ππ-=, 则二项式6(+)a x x ＝6)2(xx +展开式的通项公式为r r rr x C T 236612-+=，令0236=-r ，求得4=r ，所以二项式6()a x x+展开式中的常数项是46C ×24=240． 7、A8、【解析】在5(1)(12)x x +?的展开式中:当第一个因式取1时,则后一个因式取含4x 的项44445280C x x =. 当第一个因式取x 时,则后一个因式取含3x 的项33335280C x x =; 所以4x 的系数为160.9、C 10、±1。

广东省13市2017届高三上学期期末考试数学理试题分类汇编：不等式与不等式选讲含答案

广东省13市2017届高三上学期期末考试数学理试题分类汇编不等式与不等式选讲一、选择、填空题1、（潮州市2017届高三上学期期末）设实数x ，y 满足约束条件，则z=2x+y 的最大值为（）A ．10B ．8C ．D ．2、（东莞市2017届高三上学期期末）对于实数m ＞－3,若函数1()2xy =图象上存在点（x , y ）满足约束条件30230x y x y x m -+≥⎧⎪++≥⎨⎪≤⎩，则实数m的最小值为A ．12B. －1C.－32D 。

－23、（佛山市2017届高三教学质量检测（一)）量y x ,满足约束条件⎪⎩⎪⎨⎧≥≤--≥-+10202y y x y x ，则目标函数y x z 3+=的最小值为（） A ．2 B ．4 C ．5 D ．64、（广州市2017届高三12月模拟)已知,x y 满足约束条件220,220,20,x y x y x y -+≥⎧⎪--≤⎨⎪+-≤⎩若()0z x ay a =->的最大值为4，则a = 。

5、（惠州市2017届高三第三次调研）已知x ,y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩,若z ＝ax ＋y 的最大值为4，则a 等于( ）(A ）3 （B ）2 (C ）－2 （D ）－3 6、（江门市2017届高三12月调研）若x 、y 满足约束条件{y ≤x +15x +3y ≤152y ≥1,则 z =x +y 的最大值为M = ．7、（揭阳市2017届高三上学期期末）已知,a b R ∈、且2222290ab ab ++-=，若M 为22a b +的最小值，则约束条件⎩⎨⎧≤+≤+.2||||,322M y x M y x 所确定的平面区域内整点（横坐标纵坐标均为整数的点）的个数为（A)29(B ）25（C ）18 (D ）168、(茂名市2017届高三第一次综合测试）若圆2240xy x my +-+-=关于直线0=-y x 对称,动点P ()b a ,在不等式组2000x y x my y +-≤⎧⎪+≥⎨⎪≥⎩表示的平面区域内部及边界上运动，则21bz a -=-的取值范围是＊． 9、（清远市清城区2017届高三上学期期末）已知函数,)1ln()(2x x a x f -+=在区间（0、1）内任取两个实数P 、q ，且q P ≠，若不等式(1)(1)1f P f q P q+-+>-恒成立，则实数a 的取值范围为（）A. []∞+,11 B 。

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省14市高三上学期期末考试数学理试题分类汇编排列组与二项式定理一、二项式定理1、（东莞市2019届高三上学期期末）二项式621()x x -的展开式的常数项为 A 、±15 B 、15 C 、±20 D 、－202、（广州市2019届高三12月调研考试）已知(4234012342x a a x a x a x a x +=++++，则()()2202413a a a a a ++-+=．3、（揭阳市2019届高三上学期期末）821)x 的展开式中1x 的系数为_______；4、（雷州市2019届高三上学期期末）已知5522105)1()1()1()1(x a x a x a a x -++-+-+=+ ，则=3aA ．40-B ．40C ．10D ．10-5、（茂名市2019届高三上期末）321()x x +的展开式中的常数项是． 6、（清远市2019届高三上期末）52)1)(13(x x+-的常数项是_____________ . 7、（汕尾市2019届高三上学期期末）522x x ⎛⎫- ⎪⎝⎭的展开式中1x 的系数是。

8、（肇庆市2019届高三上学期期末）()53221x x x ⎛⎫++ ⎪⎝⎭的展开式中4x 的系数为． 9、（佛山市2019届高三上学期期末）展开式中的系数为 A 、-40 B 、120 C 、160 D 、20010、（华附、省实、广雅、深中2019届高三上学期期末联考） 52431x xx ⎛⎛⎫-+- ⎪ ⎝⎭⎝的展开式中常数项为 A.30-B.30C.25-D.25参考答案一、1、B2、163、2244、A5、36、－77、－408、1209、B 10、C二、排列组合1、（汕头市2019届高三上学期期末）把分别写有1，2，3，4，5 的五张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么不同的分法种数为________(用数字作答)．2、（韶关市2019届高三上学期期末）某中学元旦晚会共由6个节目组成，演出顺序有如下要求：节目甲必须排在乙的前面，丙不能排在最后一位，该晚会节目演出顺序的编排方案共有A、720种B、360种C、300种D、600种3、（珠海市2019届高三上学期期末）将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（）A、12种B、24种C、36种D、48种4、（肇庆市2019届高三第一次统一检测）将甲、乙、丙、丁、戊共5人分配到A、B、C、D共4所学校，每所学校至少一人，且甲不去A学校，则不同的分配方法有A．72种B．108种C．180种D．360种5、（广东省七校2019届高三第一次联考）旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若甲景区不能最先旅游，乙景区和丁景区不能最后旅游，则小李旅游的方法数为（）A.24B.18C.16D.10、、、、五个数字任取三个数字，组成能被3整除的没有重6、（珠海市2019届高三摸底考试）由01234复数字的三位自然数，共有_____个．参考答案二、1、362、C3、C4、C5、D6、20。

广东省13市2017届高三上学期期末考试数学理试题分类汇编：极坐标与参数方程 Word版含答案

广东省13市2017届高三上学期期末考试数学理试题分类汇编极坐标与参数方程1、（潮州市2017届高三上学期期末）已知直线l ：（t 为参数，α为l的倾斜角），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 为：ρ2﹣6ρcosθ+5=0．（1）若直线l 与曲线C 相切，求α的值；（2）设曲线C 上任意一点的直角坐标为（x ，y ），求x +y 的取值范围．2、（东莞市2017届高三上学期期末）已知曲线C的参数方程为21x y αα⎧=+⎪⎨=⎪⎩(α为参数)，以直角坐标系原点O 为极点，x 轴正半轴为极轴建立极坐标系. （Ⅰ）求曲线C 的极坐标方程；（Ⅱ）设，若l 1 、l 2与曲线C 相交于异于原点的两点 A 、B ，求△AOB 的面积.3、（佛山市2017届高三教学质量检测（一））在极坐标系中，射线6:πθ=l 与圆2:=ρC 交于点A ，椭圆Γ的方程为θρ22sin 213+=，以极点为原点，极轴为x 轴正半轴建立平面直角坐标系xOy（Ⅰ）求点A 的直角坐标和椭圆Γ的参数方程；（Ⅱ）若E 为椭圆Γ的下顶点，F 为椭圆Γ上任意一点，求AF AE ⋅的取值范围 4、（广州市2017届高三12月模拟）以直角坐标系的原点O 为极点,x 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线l 的参数方程为sin ,(1cos x t t y t ϕϕ=⎧⎨=+⎩为参数,0)ϕπ<<, 曲线C 的极坐标方程为2cos 4sin ρθθ=.(Ⅰ) 求直线l 的普通方程和曲线C 的直角坐标方程;（II ）设直线l 与曲线C 相交于,A B 两点, 当ϕ变化时, 求AB 的最小值.5、（惠州市2017届高三第三次调研）已知曲线C 的极坐标方程是4cos ρθ=．以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是1cos sin x t y t αα=+⎧⎨=⎩（t 为参数）．（Ⅰ）将曲线C 的极坐标方程化为直角坐标方程；（Ⅱ）若直线l 与曲线C 相交于A 、B 两点,且AB =求直线l 的倾斜角α的值．6、（珠海市2017届高三上学期期末）已知直线（ t 为参数），曲线为参数）．(1) 当r ＝1时，求C 1 与C 2的交点坐标；(2) 点P 为曲线 C 2上一动点，当r P 到直线C 1距离最大时点P 的坐标．7、（揭阳市2017届高三上学期期末）已知直线l 的参数方程为1cos 1sin x t y t αα=-+⎧⎨=+⎩学科网（t为参数）．以O 为极点，x 轴的非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos +=θρρ．(Ⅰ)写出直线l 经过的定点的直角坐标，并求曲线C 的普通方程； (Ⅱ)若4πα=，求直线l 的极坐标方程，以及直线l 与曲线C 的交点的极坐标．8、（茂名市2017届高三第一次综合测试）在直角坐标系xOy 中，曲线1C 的参数方程为,,x y α⎧=⎨=⎩(α为参数). 在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线22:4cos 2sin 40.C ρρθρθ+-+=（Ⅰ）写出曲线21C C ，的普通方程；（Ⅱ）过曲线1C 的左焦点且倾斜角为4π的直线l 交曲线2C 于B A ,两点，求AB .9、（清远市清城区2017届高三上学期期末）在直角坐标系xOy 中，曲线1C 的参数方程为2x y αα⎧=⎪⎨=+⎪⎩学科网（其中α为参数），曲线()222:11C x y -+=，以坐标原点O 为极点，x 轴的在半轴为极轴建立极坐标系. （Ⅰ）求曲线1C 的普通方程和曲线2C 的极坐标方程；（Ⅱ）若射线6πθ=()0ρ>与曲线12 C C ，分别交于A ，B 两点，求AB .10、（汕头市2017届高三上学期期末）在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为2cos ρθ=，0,2πθ⎡⎤∈⎢⎥⎣⎦.（1）求C 的参数方程；（2）设点D 在C 上，C 在D 处的切线与直线:2l y =+垂直，根据（1）中你得到的参数方程，确定D 的坐标.11、（韶关市2017届高三1月调研）在直角坐标系xOy 中，曲线C 的参数方程为cos ,(sin x y ααα⎧=⎪⎨=⎪⎩为参数).以点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为cos()4πρθ-=.(Ⅰ)将直线l 化为直角坐标方程；(Ⅱ)求曲线C 上的一点Q 到直线l 的距离的最大值及此时点Q 的坐标.12、（肇庆市2017届高三第二次模拟）在直角坐标系xOy 中，曲线1C 的参数方程为22cos 2sin x y θθ=-+⎧⎨=⎩（θ为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程是224sin =⎪⎭⎫⎝⎛+πθρ. （Ⅰ）直接写出1C 的普通方程和极坐标方程，直接写出2C 的普通方程；（Ⅱ）点A 在1C 上，点B 在2C 上，求AB 的最小值. 参考答案1、【解答】解：（1）曲线C 的直角坐标方程为x 2+y 2﹣6x +5=0即（x ﹣3）2+y 2=4曲线C 为圆心为（3，0），半径为2的圆．直线l 的方程为：xsinα﹣ycosα+sinα=0… ∵直线l 与曲线C 相切∴即…∵α∈[0，π）∴α=…（2）设x=3+2cosθ，y=2sinθ 则 x +y=3+2cosθ+2sinθ=…（9分） ∴x +y 的取值范围是．…（10分）2、(Ⅰ)∵曲线C 的参数方程为⎪⎩⎪⎨⎧+=+=ααsin 51cos 52y x (α为参数)∴曲线C 的普通方程为()()51222=-+-y x …………2分将⎩⎨⎧==θρθρsin cos y x 代入并化简得：θθρsin 2cos 4+=即曲线C 的极坐标方程为θθρsin 2cos 4+=. …………5分（Ⅱ）解法一：在极坐标系中，θθρsin 2cos 4+=：C∴由⎪⎩⎪⎨⎧+==θθρπθsin 2cos 46得到132+=OA …………7分同理32+=OB . ………… 9分又∵6π=∠AOB∴4358sin 21+=∠⋅=∆AOB OB OA S AOB . 即AOB ∆的面积为4358+. …………10分解法二：：在平面直角坐标系中，C ：()()51222=-+-y x x y l 331=：，x y l 32=： ∴由()()⎪⎩⎪⎨⎧=-+-=5123322y x x y得A 学科网 …………6分 ∴132+=OA …………7分同理⎪⎪⎭⎫⎝⎛++2332,232B …………8分∴132+=OA ，32+=OB …………9分又∵6π=∠AOB∴4358sin 21+=∠⋅=∆AOB OB OA S AOB 即AOB ∆的面积为4358+. …………10分 3、4、解: (Ⅰ) 由sin ,1cos ,x t y t ϕϕ=⎧⎨=+⎩消去t 得cos sin sin 0x y ϕϕϕ-+=, ……………………1分所以直线l 的普通方程为cos sin sin 0x y ϕϕϕ-+=. ……………………2分由2cos4sin =ρθθ, 得()2cos 4sin ρθρθ=, ……………………3分把cos ,sin x y ρθρθ==代入上式, 得y x 42=,所以曲线C 的直角坐标方程为y x 42=. …………………………………………5分 (II) 将直线l 的参数方程代入y x 42=, 得22sin4cos 40t t ϕϕ--=, ………………6分设A 、B 两点对应的参数分别为12,t t , 则122cos sin t t ϕϕ+=4, 122sin t t ϕ=-4, …………………………………………7分所以12AB t t =-==2sin ϕ=4. ……9分当2πϕ=时, AB 的最小值为4. …………………………………………10分5、解:（Ⅰ）由4cos ρθ=得24cos ρρθ=． ∵222x y ρ+=,cos x ρθ=,sin y ρθ=,∴曲线C 的直角坐标方程为2240x y x +-=,即()2224x y -+= ……4分（Ⅱ）将1cos ,sin x t y t αα=+⎧⎨=⎩代入圆的方程得()()22cos 1sin 4t t αα-+=,化简得22cos 30t t α--=． ……………5分设,A B 两点对应的参数分别为1t 、2t ,则12122cos ,3.t t t t α+=⎧⎨=-⎩ ……………6分∴12AB t t =-== ……………8分∴24cos 2α=,cos 2α=±,4πα=或34π．……………10分6、7、解：（Ⅰ）直线l 经过定点)1,1(-，-----------------------------------------------------------------2分由2cos +=θρρ得22)2cos (+=θρρ，得曲线C 的普通方程为222)2(+=+x y x ，化简得442+=x y ；---5分（Ⅱ）若4πα=，得⎪⎪⎩⎪⎪⎨⎧+=+-=t y tx 221221，的普通方程为2+=x y ，----------------------------------6分则直线l 的极坐标方程为2cos sin +=θρθρ，------------------------------------------------8分联立曲线C ：2cos +=θρρ．得1sin =θ，取2πθ=，得2=ρ，所以直线l 与曲线C 的交点为)2,2(π．------------10分8、解:（Ⅰ）2222()cos sin 122sin y x y αααα⎧=⎪⇒+=+=⎨=⎪⎩ ………………1分即曲线1C 的普通方程为221204x y+=…………………………………………………2分222,c o s ,s i n,x y x y ρρθρθ=+== 曲线2C 的方程可化为224240x y x y ++-+= (3)分即1)1()2(:222=-++y x C . ………………………………………………4分（Ⅱ）曲线1C 左焦点为（4-，0） ……………………………………………5分直线l 的倾斜角为4πα=, sin cos αα==…………………………………………6分所以直线l 的参数方程为：为参数）t t y t x (22224⎪⎪⎩⎪⎪⎨⎧=+-=………………………………7分将其代入曲线2C 整理可得：04232=+-t t ， ……………………………………8分设A,B 对应的参数分别为21,t t 则所以4,232121==+t t t t . ………………………9分所以12AB t t=-=== (10)分解法二：（Ⅰ）同解法一. ………………………………………………………………4分（Ⅱ）曲线1C左焦点为（4-，0）………………………………………………………5分直线l的斜率为tan14kπ==, ………………………………………………………6分直线l的普通方程为4y x=+. 即40x y-+=…………………………………7分圆2C的圆心坐标为：（-2，1）. ……………………………………………………8分圆心2C到直线l的距离2d==……………………………9分故AB===…………………………………………10分解法三：（Ⅰ）同解法一. …………………………………………4分（Ⅱ）曲线1C左焦点为（4-，0）…………………………………………5分直线l的斜率为tan14kπ==, ……………………………………………6分直线l的普通方程为4y x=+…………………………………………………7分2122212423560(2)(1)121y x x xx xx y y y=+⎧⎧⎧=-=-⇒++=⇒⎨⎨⎨++-===⎩⎩⎩或，…………9分AB=｜｜………………………………………10分9、解：（Ⅰ）由2xyαα⎧=⎪⎨=+⎪⎩得2xyαα⎧=⎪⎨-=⎪⎩，所以曲线1C的普通方程为()2227x y+-=.把cosxρθ=，sinyρθ=，代入()2211x y-+=，得()()22cos1sin1ρθρθ-+=，化简得，曲线2C的极坐标方程为2cosρθ=.（Ⅱ）依题意可设1266A Bππρρ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭，，，.因为曲线1C的极坐标方程为24sin30ρρθ--=，将()06πθρ=>代入曲线1C的极坐标方程得2230ρρ--=，解得13ρ=.同理将()06πθρ=>代入曲线2C的极坐标方程得2ρ=.所以123AB ρρ=-=10、解：（1）由题意知：θρcos 2=，]2,0[πθ∈，所以θρρcos 22=，]2,0[πθ∈，即0222=-+x y x ，可化为1)1(22=+-y x ，]1,0[∈y ，可得C 的参数方程为⎩⎨⎧=+=ty tx sin cos 1（t 为参数，π≤≤t 0）.（2）设)sin ,cos 1(t t D +，由（1）知C 是以)0,1(G 为圆心，1为半径的上半圆，因为C 在点D 处的切线与l 垂直，所以直线GD 与l 的斜率相同， ∴31)cos 1(0sin =-+-t t ，解得3tan =t ，即3π=t ，故D 的直角坐标为)3sin ,3cos 1(ππ+，即)23,23(. 11、解（Ⅰ）由cos()4πρθ-=，得cos cos sin sin 44ππρθθ⎛⎫+= ⎪⎝⎭ 化简得，cos sin 4ρθρθ+=， ………………………………………1分由 cos x ρθ=，sin y ρθ=∴直线l 的直角坐标方程为4x y +=. ………………………………………3分 (Ⅱ)由于点Q 是曲线C 上的点，则可设点Q的坐标为),sin αα……………4分点Q 到直线l的距离为d =………………………………5分=. …………………………7分当sin 13πα⎛⎫+=- ⎪⎝⎭时，即526k αππ=-max d ==……………………9分11此时，551cos cos()sin()6262απαπ=-=-=-=- ∴ 点Q 31(,)22--. ………………10分 12、解：（Ⅰ）1C 的普通方程是()2224x y ++= ，（2分）1C 的极坐标方程4cos ρθ=- ，（4分） 2C 的普通方程40x y +-=. （6分）（Ⅱ）方法一：1C 是以点()2,0-为圆心，半径为2的圆；2C 是直线. （7分）圆心到直线2C2=>，直线和圆相离. （8分）所以AB的最小值为2. （10分）方法二：设()22cos ,2sin A θθ-+，因为2C 是直线，（7分）所以AB 的最小值即点A 到直线的距离d的最小值，d ==，（9分）2=. （10分）。

广东省各地高三数学上学期期末考试试题分类汇编排列组二项式定

排列组合二项式定理1、（佛山市2014届高三教学质量检测（一））若420443322104,)1(a a a x a x a x a x a a x ++++++=-则的值为_______答案：82、（广州市2014届高三1月调研测试）有4名优秀学生A ，B ，C ，D 全部被保送到甲，乙，丙3所学校，每所学校至少去一名，则不同的保送方案共有种．答案：363、（增城市2014届高三上学期调研）二项式81x x ⎛⎫- ⎪⎝⎭的展开式中常数项是答案：704、（省华附、省实、广雅、深中四校2014届高三上学期期末）12(x -展开式中的常数项为A ．220B ．220-C ．1320D ．1320- 答案：B 5、（惠州市2014届高三第三次调研考）某班级要从4名男生、2名女生中选派4人参加社区服务，如果要求至少有1名女生，那么不同的选派方案种数为．（用数字作答）答案：146、（揭阳市2014届高三学业水平考试）10(1)x -的展开式中2x 的系数是．（用数字作答）答案：457、（汕头市2014届高三上学期期末教学质量监测）设6sin (a xdx,π=⎰则二项式的展开式中含有2x 的项于答案：2192x -8、（肇庆市2014届高三上学期期末质量评估）在1041x x ⎛⎫+ ⎪⎝⎭的展开式中常数项是____________.（用数字作答）答案：459、（肇庆市2014届高三上学期期末质量评估）平面内有4个红点,6个蓝点,其中只有一个红点和两个蓝点共线,其余任三点不共线,过这十个点中的任两点所确定的直线中,至少过一红点的直线的条数是( )A.28B.29C.30D.27答案：B10、（中山市2014届高三上学期期末考试）在二项式521xx⎛⎫-⎪⎝⎭的展开式中，含4x的项的系数是答案：1011、（东莞市2014届高三上学期期末调研测试）展开式中的系数是＿＿＿＿答案：21 212、（东莞市2014届高三上学期期末调研测试）将4个人（含甲、乙）分成两组，每组2人，则甲、乙分别同一组的概率为＿＿＿答案：1 3。

17年高考真题—理科数学9：排列组合与二项式定理

2017年高考真题分类汇编（理科）排列组合与二项式定理
第 1 页共 1 页
2017高考真题分类汇编：排列组合与二项式定理
1．【2017课标III 4】()()52x y x y +-的展开式中33x y 的系数为（）
（A ）80- （B ）40- （C ）40 （D ）80
2．【2017课标I 6】()62111x x ⎛
⎫++ ⎪⎝⎭
展开式中2x 的系数为（）（A ）15 （B ）20 （C ）30 （D ）35
3．【2017课标II 6】安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（）
（A ）12种（B ）18种（C ）24种（D ）36种
4．【2017山东 11】已知()13n
x +的展开式中含有2x 项的系数是54，则n = 。

5．【2017浙江 13】已知多项式()()
3254321234512x x x a x a x a x a x a ++=+++++，
则4a =___________，5a =___________。

6．【2017天津 14】用数字1,2,3,4,5,6,7,8,9组成没有重复数字，且至多有一个数字是偶数的四位数，这样的四位数一共有__________个。

（用数字作答）1080
7．【2017浙江 16】从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有种不同的选法。

（用数字填写答案）
附答案
CCD 4．4；5．16，4；6．1080；7．660。

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省14市高三上学期期末考试数学理试题分类汇编排列组与二项式定理一、二项式定理1、（东莞市2019届高三上学期期末）二项式621()x x -的展开式的常数项为 A 、±15 B 、15 C 、±20 D 、－202、（广州市2019届高三12月调研考试）已知(4234012342x a a x a x a x a x =++++，则()()2202413a a a a a ++-+=．3、（揭阳市2019届高三上学期期末）821)x 的展开式中1x 的系数为_______；4、（雷州市2019届高三上学期期末）已知5522105)1()1()1()1(x a x a x a a x -++-+-+=+ ，则=3aA ．40-B ．40C ．10D ．10-5、（茂名市2019届高三上期末）321()x x +的展开式中的常数项是． 6、（清远市2019届高三上期末）52)1)(13(x x+-的常数项是_____________ . 7、（汕尾市2019届高三上学期期末）522x x ⎛⎫- ⎪⎝⎭的展开式中1x 的系数是。

8、（肇庆市2019届高三上学期期末）()53221x x x ⎛⎫++ ⎪⎝⎭的展开式中4x 的系数为． 9、（佛山市2019届高三上学期期末）展开式中的系数为 A 、-40 B 、120 C 、160 D 、20010、（华附、省实、广雅、深中2019届高三上学期期末联考） 52431x xx ⎛⎛⎫-+- ⎪ ⎝⎭⎝的展开式中常数项为 A.30-B.30C.25-D.25参考答案一、1、B2、163、2244、A5、36、－77、－408、1209、B 10、C二、排列组合1、（汕头市2019届高三上学期期末）把分别写有1，2，3，4，5 的五张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么不同的分法种数为________(用数字作答)．2、（韶关市2019届高三上学期期末）某中学元旦晚会共由6个节目组成，演出顺序有如下要求：节目甲必须排在乙的前面，丙不能排在最后一位，该晚会节目演出顺序的编排方案共有A、720种B、360种C、300种D、600种3、（珠海市2019届高三上学期期末）将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（）A、12种B、24种C、36种D、48种4、（肇庆市2019届高三第一次统一检测）将甲、乙、丙、丁、戊共5人分配到A、B、C、D共4所学校，每所学校至少一人，且甲不去A学校，则不同的分配方法有A．72种B．108种C．180种D．360种5、（广东省七校2019届高三第一次联考）旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若甲景区不能最先旅游，乙景区和丁景区不能最后旅游，则小李旅游的方法数为（）A.24B.18C.16D.10、、、、五个数字任取三个数字，组成能被3整除的没有重6、（珠海市2019届高三摸底考试）由01234复数字的三位自然数，共有_____个．参考答案二、1、362、C3、C4、C5、D6、20。

2017届广东省珠海市高三上学期期末学业质量监测理科数学试题及答案精品

珠海市2013-2014学年度第一学期期末学生学业质量监测高三理科数学试题参考答案阅卷版一、选择题：本大题共8小题，每小题5分，满分40分．BBBCCCAA 二、填空题：本大题共7小题，每小题5分，满分30分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．请将答案填在答题卡相应位置. 9.（三角函数）已知1cos 3ϕ=-()0ϕπ<<,则sin 2ϕ=．9-10.（数列）已知数列{}n a 的前n 项和为n S ，且31n n S =+,则n a = ．141232n n n -=⎧⎨⋅≥⎩11.（线性规划）变量x y 、满足线性约束条件2200x y x y y +≤⎧⎪-≥⎨⎪≥⎩，则使目标函数(0)z ax y a =+>取得最大值的最优解有无数个，则a 的值为．2 12.（导数）曲线x e y x=在点2(2)2e ，处的切线方程为．240e x y -= 13.（函数）定义在R 上的函数()f x 满足3log (1)0()(1)(2)0x x f x f x f x x -≤⎧=⎨--->⎩，则(2014)f = ．3log 214．（坐标系与参数方程选做题）已知在平面直角坐标系xoy 中圆C 的参数方程为：3cos 13sin x y θθ⎧=⎪⎨=+⎪⎩，（θ为参数），以ox 为极轴建立极坐标系，直线极坐标方程为：,0)6cos(=+πθρ则圆C 截直线所得弦长为15．（几何证明选讲选做题）如右图，AB 是圆O 的直径，BC 是圆O 的切线，切点为B ，OC 平行于弦AD ，若3OB =，5OC =，则CD = . 4三、解答题:本题共有6个小题，12分+12分+14分+14分+14分+14分=80分．16.（三角函数）已知()2cos()cos 22f x x x x π=-，x R ∈(1) 求()6f π的值；(2)当∈x [0,]2π时，求()f x 的最值.解:(1)()2sin cos 2f x x x x =⋅- …………………………………………………………………1分sin 22x x =……………………………………………………………………………2分2sin(2)3x π=-…………………………………………………………………………………4分()2sin(2)2sin 00663f πππ=⋅-==……………………………………ODCBA…………………………6分(2)[0,]2x π∈Q ，22[,]333x πππ∴-∈-……………………………………………………………8分3sin(2)[32x π∴-∈-…………………………………………………………………………10分2sin(2)[3,2]3x π∴-∈-…………………………………………………………………………11分()2max f x ∴=，min ()3f x =-……12分17.（概率）PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可吸入肺颗粒物。

2017高考真题分类汇编——排列组合二项式定理

1、[2017.全国1]展开式中的系数为 A ．15B ．20C ．30D ．352、[2017.全国2]安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（）A ．12种B ．18种C ．24种D ．36种3、[2017.全国2]一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，X 表示抽到的二等品件数，则D X = ．4、[2017.全国3]5()(2)x y x y +-的展开式中33x y 的系数为（）A ．-80B ．-40C ．40D ．805、[2017.江苏]（5分）某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取件．6、[2017.天津]用数字1，2，3，4，5，6，7，8，9组成没有重复数字，且至多有一个数字是偶数的四位数，这样的四位数一共有___________个.（用数字作答）7、[2017.山东]为了研究某班学生的脚长x （单位：厘米）和身高y （单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y 与x 之间有线性相关关系，设其回归直线方程为ˆˆˆy bx a =+，已知101011ˆ225,1600,4i i i i x y b =====∑∑，该班某学生的脚长为24，据此估计其身高为（A ）160 （B ）163 （C ）166 （D ）708、9、[2017.山东]已知(13)n x + 的展开式中含有X 的系数是54，则n =____10、 621(1)(1)x x ++2x 211、12、[2017.浙江]。

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省14市高三上学期期末考试数学理试题分类汇编排列组与二项式定理一、二项式定理1、（东莞市2019届高三上学期期末）二项式621()x x -的展开式的常数项为 A 、±15 B 、15 C 、±20 D 、－202、（广州市2019届高三12月调研考试）已知(4234012342x a a x a x a x a x +=++++，则()()2202413a a a a a ++-+=．3、（揭阳市2019届高三上学期期末）821)x 的展开式中1x 的系数为_______；4、（雷州市2019届高三上学期期末）已知5522105)1()1()1()1(x a x a x a a x -++-+-+=+ ，则=3aA ．40-B ．40C ．10D ．10-5、（茂名市2019届高三上期末）321()x x +的展开式中的常数项是． 6、（清远市2019届高三上期末）52)1)(13(x x+-的常数项是_____________ . 7、（汕尾市2019届高三上学期期末）522x x ⎛⎫- ⎪⎝⎭的展开式中1x 的系数是。

8、（肇庆市2019届高三上学期期末）()53221x x x ⎛⎫++ ⎪⎝⎭的展开式中4x 的系数为． 9、（佛山市2019届高三上学期期末）展开式中的系数为 A 、-40 B 、120 C 、160 D 、20010、（华附、省实、广雅、深中2019届高三上学期期末联考） 52431x xx ⎛⎛⎫-+- ⎪ ⎝⎭⎝的展开式中常数项为 A.30-B.30C.25-D.25参考答案一、1、B2、163、2244、A5、36、－77、－408、1209、B 10、C二、排列组合1、（汕头市2019届高三上学期期末）把分别写有1，2，3，4，5 的五张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么不同的分法种数为________(用数字作答)．2、（韶关市2019届高三上学期期末）某中学元旦晚会共由6个节目组成，演出顺序有如下要求：节目甲必须排在乙的前面，丙不能排在最后一位，该晚会节目演出顺序的编排方案共有A、720种B、360种C、300种D、600种3、（珠海市2019届高三上学期期末）将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（）A、12种B、24种C、36种D、48种4、（肇庆市2019届高三第一次统一检测）将甲、乙、丙、丁、戊共5人分配到A、B、C、D共4所学校，每所学校至少一人，且甲不去A学校，则不同的分配方法有A．72种B．108种C．180种D．360种5、（广东省七校2019届高三第一次联考）旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若甲景区不能最先旅游，乙景区和丁景区不能最后旅游，则小李旅游的方法数为（）A.24B.18C.16D.10、、、、五个数字任取三个数字，组成能被3整除的没有重6、（珠海市2019届高三摸底考试）由01234复数字的三位自然数，共有_____个．参考答案二、1、362、C3、C4、C5、D6、20。

广东省13市高三上学期期末考试数学理试题分类汇编：统计与概率

2
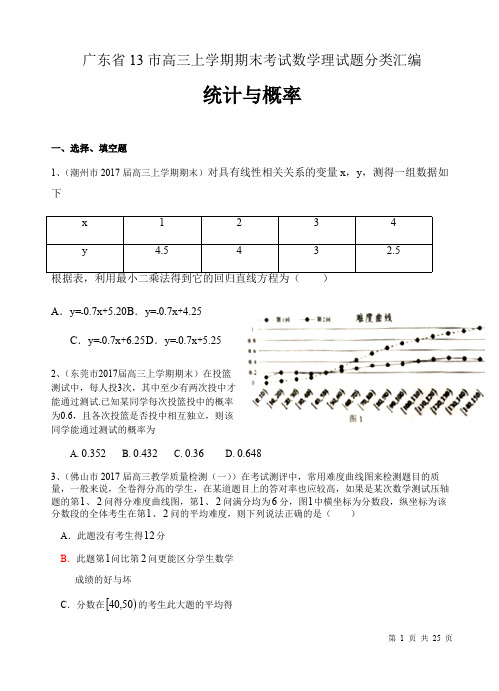
P ( 2 X 2 ) 0.9544 ．
（Ⅱ）某三位顾客各有一次 A 箱内摸奖机会，求其中中奖人数的分布列；（Ⅲ）某顾客消费额为 308 元，有两种摸奖方法，方法一：三次 A 箱内摸奖机会；方法二：一次 B 箱内摸奖机会．请问：这位顾客选哪一种方法所得奖金的期望值较大．
第 6 页共 25 页
研，用表示所抽取的3 名学生中为重本的人数，求随机变量的分布列和数学期望.
3、（佛山市 2017 届高三教学质量检测（一））我们国家正处于老龄化社会中，老有所依也是政府的民生工程．某市共有户籍人口 400 万，其中老人（年龄 60 岁及以上）人数约有 66 万，为了了解老人们的健康状况，政府从老人中随机抽取 600 人并委托医疗机构免费为他们进行健康评估，健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级，并以 80 岁为界限分成两个群体进行统计，样本分布被制作成如下图表：
2、（东莞市2017届高三上学期期末）在投篮测试中，每人投3次，其中至少有两次投中才能通过测试.已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学能通过测试的概率为 A. 0.352 B. 0.432 C. 0.36 D. 0.648
3、（佛山市 2017 届高三教学质量检测（一））在考试测评中，常用难度曲线图来检测题目的质量，一般来说，全卷得分高的学生，在某道题目上的答对率也应较高，如果是某次数学测试压轴题的第 1 、 2 问得分难度曲线图，第 1 、 2 问满分均为 6 分，图 1 中横坐标为分数段，纵坐标为该分数段的全体考生在第 1 、 2 问的平均难度，则下列说法正确的是（） A．此题没有考生得 12 分 B．此题第 1 问比第 2 问更能区分学生数学成绩的好与坏 C．分数在 40,50 的考生此大题的平均得

广东省13市2017届高三上学期期末考试数学理试题分类汇编：数列含答案

广东省13市2017届高三上学期期末考试数学理试题分类汇编数列一、选择、填空题1、（潮州市2017届高三上学期期末）设数列｛a n }是首项为1，公比为q(q ≠﹣1）的等比数列，若是等差数列，则=（）A ．4026B ．4028C ．4030D ．40322、（东莞市2017届高三上学期期末)《九章算术·均输》中有如下问题：“今有五人分五钱,令上二人所得与下三人等,问各得几何．”其意思为“已知甲、乙、丙、丁、戊五人分5 钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列，问五人各得多少钱？”(“钱”是古代的一种重量单位）．这个问题中,乙所得为（ ) A ．43钱 B ．54钱 C ．65钱 D ．76钱 3、（佛山市2017届高三教学质量检测（一））设等比数列{}n a 的公比为q ，前n 项和为n S ，则“1=q ”是“263S S =”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 4、（广州市2017届高三12月模拟）等比数列{}n a 的前n 项和为n S ，若230a S +=，则公比q = (A ） 1- （B ） 1 （C ） 2- (D) 25、(广州市2017届高三12月模拟）在数列{}n a 中,12a =,28a =,对所有正整数n 均有21n n n a a a +++=,则20171nn a==∑ 。

6、（江门市2017届高三12月调研）若等差数列{a n }满足a 1+a 2+a 2015+a 2016=3，则{a n }的前2016项之和S 2016=A ．1506B ．1508C ．1510D ．15127、（揭阳市2017届高三上学期期末)已知等差数列{}n a 的前n 项和为n S ,且322315S S -=,则数列{}n a 的公差为（A ）3（B)4（C ）5 （D ）68、（茂名市2017届高三第一次综合测试）我国古代数学著作《九章算术》有如下问题：“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，重二斤，问次一尺各重几何？”意思是：“现有一根金箠，一头粗，一头细，在粗的一端截下1尺，重4斤；在细的一端截下1尺，重2斤;问依次每一尺各重多少斤？”根据上题的已知条件，若金箠由粗到细的重量是均匀变化的,问第二尺与第四尺的重量之和为( ) A 。

广东省13市2017届高三上学期期末考试数学理试题分类汇编：程序框图 Word版含答案

广东省13市2017届高三上学期期末考试数学理试题分类汇编程序框图1、（潮州市2017届高三上学期期末）执行如图所示的程序，则输出的i的值为（）A．2 B．3 C．4 D．52、（东莞市2017届高三上学期期末）下方茎叶图为高三某班50名学生的数学考试成绩，算法框图中输入的i a为茎叶图中的学生成绩，则输出的m，n分别是( )A.m ＝38，n＝12mB.＝26，n ＝12C. m＝12，n＝12D. m＝24，n＝103、（佛山市2017届高三教学质量检测（一））如图2所示的程序框图，输出的值为（）A ．1615B ．1215C ．813D ．4134、（广州市2017届高三12月模拟）阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为(A) 7 (B) 9 (C) 10 (D) 115、（惠州市2017届高三第三次调研）执行如下图所示的程序框图，则输出的结果为( ) （A）7（B）9（C）10（D）116、（珠海市2017届高三上学期期末）某程序框图如图所示，若该程序运行后输出的值是25 13，则A. a＝11B. a＝12C. a＝13D. a＝147、（揭阳市2017届高三上学期期末）阅读如图1所示的程序框图，运行相应程序，输出的结果是（A）1234 （B）2017 （C）2258 （D）7228、（茂名市2017届高三第一次综合测试）执行如图1所示的程序框图，若输出的结果是31 32，则输入的a为（）A．3 B．4 C．5 D．69、（清远市清城区2017届高三上学期期末）执行如图所示的程序框图，则输出S的值是（）A.10B. 12C. 100D. 10210、（汕头市2017届高三上学期期末）中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的2=x ，2=n ，依次输入的a 为2，2，5，则输出的=s （）A ．7B ．12 C. 17 D ．3411、（韶关市2017届高三1月调研）执行如图所示的程序框图,则输出S =(A) 511 (B) 139 (C) 1611(D)17912、（肇庆市2017届高三第二次模拟）执行如图所示的程序框图，如果输入的[]2,2t ∈-，则输出的S 属于（A ）[-6，-2] （B ）[-5，-1] （C ）[-4，5] （D ）[-3，6]参考答案1、C2、B3、C4、B5、B6、B7、A 8、C 9、A 10、C11、【解析】框图中的S ，实际是计算2221111...2141101S =++++---，而21111()1211n n n =---+ 所以11111111161(1...)1(1)233591121111S =+-+-++-=+-=，选C 12、D。

(整理版)各地高三上期末考编排列组合与二项式定理

广东各地高三上期末考试题分类汇编—排列组合与二项式定理1、〔佛山普通高中高三教学质量检测〔一〕〕如果1()nxx 展开式中，第四项与第六项的系数相等，那么n = ，展开式中的常数项的值等于 .A ．130B ．110 C ．140 D ．1203、〔广州高三上期末调研测试〕922()2x x-展开式的常数项是 .〔结果用数值作答〕4、〔惠州高三第三次调研考试〕在二项式52a x x ⎛⎫- ⎪⎝⎭的展开式中， x 的一次项系数是10-，那么实数a 的值为．5、〔江门高三上期末调研测试〕62)2(-x x 展开式中，3x 的系数是． 6、〔揭阳市高三上学期学业水平考试〕假设2012(1)n n n x a a x a x a x +=++++〔n N *∈〕且1221a a +=，那么展开式的各项中系数的最大值为〔〕 A ．15 B ．20 C ．56 D ．70 7．〔揭阳市高三上学期学业水平考试〕从一个正方体的8个顶点中任取3个，那么以这3个点为顶点构成直角三角形的概率为〔〕A ．23B ．47C ．57D ．678、〔汕头10-11 普通高中毕业班教学质量监测〕设a 为函数)(cos 3sin R x x x y ∈+=的最大值，那么二项式6)1(xx a -的展开式中含2x 项的系数是( )A ．192B ．182C ．-192D ．-1829、〔广东省四校高三上期末联考〕在()()()347111x x x +++⋅⋅⋅++的展开式中，含x 项的系数是 *** ．〔用数字作答〕答案：1、8，702、C3、212-4、【解析】1；由二项式定理，()()5210355C C rrr rr rr a T x a xx --⎛⎫=-=-⋅ ⎪⎝⎭．当1031r -=时，3r =，于是x 的系数为()3335C 10a a -=-，从而1a =． 5、－1926．由1221a a +=得1221n n C C +=6n ⇒=，故各项中系数的最大值为3620C =,选 B ． 7．解法1：从正方体的8个顶点中任取3个有3856C =种取法，可构成的三角形有56种可能，正方体有6个外表和6个对角面，它们都是矩形〔包括正方形〕，每一个矩形中的任意3个顶点可构成4个直角三角形，共有12448⨯=个直角三角形，故所求的概率：486567P ==,选 D ．解法2：从正方体的8个顶点中任取3个有3856C =种取法，可构成的三角形有56种可能，所有可能的三角形分为直角三角形和正三角形两类，其中正三角形有8种可能〔每一个顶点对应一个〕，故所求的概率：5686567P -==,选 D ．8、因为)3sin(2cos 3sin π+=+x x x ，由题设知2a =.那么二项展开式的通项公式为r r rr r rrr x a C xx a C T ---+⋅⋅⋅-=-⋅=366661)1()1()(，令23=-r ，得1=r ，含2x 项的系数是1562192C -=-，选 C ；9、略。

【高中数学试题】高三上学期期末考试数学试题分类汇编-排列组合与二项式定理.doc

排列组合与二项式定理一、排列组合1、（崇明县2017届高三第一次模拟）将序号分别为1、2、3、4、5的5张参观券全部分给4人，每人至少[张，如果分给同一人的2张参观券连号，那么不同的分法种数是__________ •2、（黄浦区2017届高三上学期期终调研）若甲、乙两人从6门课程中各选修3门，则甲、乙所选修的课程屮至多有1门相同的选法种数为__________ .3、（静安区2017届向三上学期期质量检测）某班班会進备从含甲、乙的6名学生中选取4人发言，要求甲、乙两人至少有一人参加，那么不同的发言顺序有【 ]A. 336 种；B. 320 种；C. 192 种；D. 144 种.4、（闵行区2017届高三上学期质量调研）从单词“shadow"屮任意选取4个不同的字母排成一排，则其中含有的共有 ____________________ 种排法.（用数字作答）5、（徐汇区2017届高三上学期学习能力诊断）将6辆不同的小汽车和2辆不同的卡车驶入如图所示的10个车位中的某8个内，其中2辆卡车必须停在A与3的位置，那么不同的停车位置安排共有____________ 种？（结果用数值表示）第10題團6、（长亍、嘉定区2017届高三上学期期末质量调研）甲、乙两人从5门不同的选修课中各选修2 I'J,则甲、乙所选的课程中恰有1门相同的选法有_____________ 种.7、（金山区2017届高三上学期期末）从5名学生中任选3人分别担任语文、数学、英语课代表，其中学生甲不能担任数学课代表，共有 _______ 种不同的选法（结果用数值表示）排列组合参考答案：1、242、2003、A4、2405、403206、【解析】根据题意，采用间接法：①由题意可得，所有两人各选修2门的种数C52C52=100,②两人所选两门都相同的有为C52=10种，都不同的种数为C52C32=30, 故只恰好有1门相同的选法有100 - 10・30二60种.故答案为60.7、48二、二项式定理1、（宝山区2017届高三上学期期末）设常数。

广东省13市2017届高三上学期期末考试数学理试题分类汇编：排列组合与二项式定理-Word版含答案

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省13市2017届高三上学期期末考试数学理试题分类汇编：排列组合与二项式定理(word版,附答案)

广东省13市2017届高三上学期期末考试数学理试题分类汇编：不等式与不等式选讲含答案

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省13市2017届高三上学期期末考试数学理试题分类汇编：极坐标与参数方程 Word版含答案

广东省各地高三数学上学期 期末考试试题分类汇编 排列组二项式定

17年高考真题—理科数学9：排列组合与二项式定理

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

2017届广东省珠海市高三上学期期末学业质量监测理科数学试题及答案 精品

2017高考真题分类汇编——排列组合二项式定理

广东省14市高三上期末理试题分类汇编：排列组合与二项式定理

广东省13市高三上学期期末考试数学理试题分类汇编：统计与概率

广东省13市2017届高三上学期期末考试数学理试题分类汇编：数列含答案

广东省13市2017届高三上学期期末考试数学理试题分类汇编：程序框图 Word版含答案

(整理版)各地高三上期末考编排列组合与二项式定理

【高中数学试题】高三上学期期末考试数学试题分类汇编-排列组合与二项式定理.doc

广东省各地高三数学上学期期末考试试题分类汇编排列组二项式定

2017届广东省珠海市高三上学期期末学业质量监测理科数学试题及答案精品