动能定理PPT课件
合集下载
新人教版高一物理必修二 课件 7.7 动能和动能定理(共31张PPT)

25v2 S总 14g
易错点:
(1)动能是标量,E k
1 m v 2 对应于物
2
体的瞬时速度,使状态量,物体的运动
速度方向发生变化时,动能不变。
(2)当力做负功时,在动能定理的式中
应出现相应的负号。
的动能是 20 J。足球沿草地作直线运动,受
到的阻力是足球重力的0.2倍。当足球运动到距发
球点20m的后卫队员处时,速度为 20½ m/s
(g=10m/s2)
结论:
瞬间力做功直接转化为物体的初动能
求变力做功问题
在离地面高为h处竖直上抛一质量为m的物块,
抛出时的速度为V0,当它落到地面时速度为V,用 g表示重力加速度,则在此过程中物块克服空
B、速度不变,动能一定不变
C、动能变化,速度一定变化
D、动能不变,速度可能变化
二、动能定理
W=mv22/2-mv12/2
改 写
表达式:W=Ek2-Ek1
内容:力在一个过程中对物体 所做的功,等于物体在这个过程中 动能的变化。
对
动 问题3:如果物体受到几个力的作用,动
能 能定理中的W表示什么意义?
Ek
0
s
1 2
s
停在AB中点
多过程问题
(往复运动)
质量为m的物体以速度v竖直向上抛出,物 体落回地面时,速度大小为3v/4,设物体在运动 中所受空气阻力大小不变,求:
(1)物体运动中所受阻力大小; (2)物体以初速度2v竖直抛出时最大高度; (3)若物体与地面碰撞中无机械能损失,
求物体运动的总路程。
气阻力所做得功等于,( C )
1
A B
m-1g/2hm-1V/2²-m12 Vm²V- 02²-mmVg0h²
易错点:
(1)动能是标量,E k
1 m v 2 对应于物
2
体的瞬时速度,使状态量,物体的运动
速度方向发生变化时,动能不变。
(2)当力做负功时,在动能定理的式中
应出现相应的负号。
的动能是 20 J。足球沿草地作直线运动,受
到的阻力是足球重力的0.2倍。当足球运动到距发
球点20m的后卫队员处时,速度为 20½ m/s
(g=10m/s2)
结论:
瞬间力做功直接转化为物体的初动能
求变力做功问题
在离地面高为h处竖直上抛一质量为m的物块,
抛出时的速度为V0,当它落到地面时速度为V,用 g表示重力加速度,则在此过程中物块克服空
B、速度不变,动能一定不变
C、动能变化,速度一定变化
D、动能不变,速度可能变化
二、动能定理
W=mv22/2-mv12/2
改 写
表达式:W=Ek2-Ek1
内容:力在一个过程中对物体 所做的功,等于物体在这个过程中 动能的变化。
对
动 问题3:如果物体受到几个力的作用,动
能 能定理中的W表示什么意义?
Ek
0
s
1 2
s
停在AB中点
多过程问题
(往复运动)
质量为m的物体以速度v竖直向上抛出,物 体落回地面时,速度大小为3v/4,设物体在运动 中所受空气阻力大小不变,求:
(1)物体运动中所受阻力大小; (2)物体以初速度2v竖直抛出时最大高度; (3)若物体与地面碰撞中无机械能损失,
求物体运动的总路程。
气阻力所做得功等于,( C )
1
A B
m-1g/2hm-1V/2²-m12 Vm²V- 02²-mmVg0h²
第十三章 动能定理PPT课件

n
m
则 W (F i) W (Pj)W (F R)W (M O)
i1
j1
8
动力学篇
第十三章 动能定理
目录 上页 下页 例题库 习题集
四、质点系内力的元功
W F 1 • d r 1 F 2 • d r 2
F1 •dr1 F1 •dr2 F1 •d(r1 r2)
F1•dr1 2 F1dl
z A1
该位置的势能。基准点的势能为零。
12
动力学篇
第十三章 动能定理
目录 上页 下页 例题库 习题集
二、机械能守恒定理
条件:惯性参考系;做功的力为有势力
TUE
13
动力学篇
第十三章 动能定理
目录 三、势力场的特性
上页 设作用在质点上的有势力为:FF xiF yjF zk
下页 设质点的势能函数为:VV(x,y,z)则有关系式:
r
B
F
rdr
dr dxidyjdzk O
y
W F xd x F yd y F zd z
x
元功的解析表达式
力F在曲线上由A点到B点所作的功:
W A B (F )F • d r(F x d x F y d y F z d z )
A B
A B
6
动力学篇
第十三章 动能定理
目录 二、作用于刚体上力偶的元功
第十三章 动能定理
整体概况
01
概况二
点击此处输入 相关文本内容
02
概况三
点击此处输入 相关三章 动能定理
目录 §1 质点系的动能
上页
下页 例题库 习题集
一、质点系的动能
n
T
1 2
动能和动能定理 20张ppt

分析: V=60m/S
L 5.3102 m
(1)研究对象是什么?请描述其运动情景。 (2)该过程中,飞机受几个力?各力做功情况怎 样?
(3)飞机的初、末态动能的大小如何?
学习目标二
解: 以飞机为研究对象,根据动能定理
W
1 2
mV2
2
1 2
mV12
(F
f
)L
1 2
mv22
0
mv 2 F 0.02mg
300
h
学习目标二 动能定理的优越性
动能定理很简捷, 初态末态功连接, 曲线变力更优越。
巩固练习
1、改变汽车的质量和速度,都能使汽车的动能发 生变化,在下面几种情况中,汽车的动能是原来2倍 的是( )
A、质量不变,速度变为原来的2倍 B、质量和速度都变为原来的2倍 C、质量减半,速度变为原来的2倍 D、质量变为原来2倍,速度减半
动能和动能定理
学习目标一 理论推导
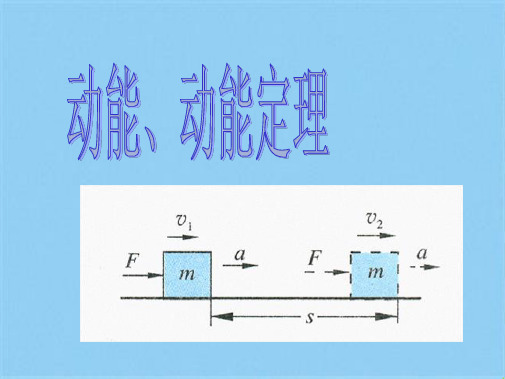
设某物体的质量m,在与运动方向相同 的推力的作用下发生一段位移,速度由 v1增加到v2,求这段位移推力做的功?
F
v1
v2
x
学习目标一 动能的表达式
1.定义:物体由于运动而具有的能。
2.表达式:
E 1 mv2
k2
v为物体对地 的瞬时速率
3.单位:焦耳。符号:J 4.标量
2L
F 1.8104 N
学习目标二 用动能定理解题的一般步骤
明确对象和过程, 过程分析找力功, 初态末态写动能, 讨论结果需完成 。
学习目标二 练习
如图所示,一人将质量为1kg的小球从h=
10m高处以与水平方向成30o角斜向上方抛出,
理论力学课件:动能定理

指标之一,一般机械效率η可由机械设计手册查得。
动能定理
【例12-8】 C618车床的主轴转速n=42r/min时,其切削力
P=14.3kN,若工件直径d=115mm,电动机到主轴的机械效率
η=0.76。求此时电动机的功率为多少?
解 由式(12-12)得切削力P 的功率:
动能定理
12.5 势力场 势能及机械能守恒定理
动能定理
动能定理
12.4 功率 功率方程
1.功率
在单位时间内力所做的功称为功率。它是衡量机器工作
能力的一个重要指标。
δW 是dt时间内力的元功,则功率为
动能定理
由于元功为δW =Ft·ds,因此
即,力的功率等于切向力与力作用点速度的乘积
力矩的元功为δW =M·dφ,则
即,力矩的功率等于力矩与物体转动角速度的乘积。
动能定理
动能定理
12.1 力的功
12.2 质点 质点系的动能
12.3 质点与质点系的动能定理
12.4 功率 功率方程
12.5 势力场 势能及机械能守恒定理
12.6 动力学普遍定理及综合应用
思考题
动能定理
12.1 力 的 功
工程实际中,一物体受力的作用所引起运动状态的变化,
不仅取决于力的大小和方向,而且与物体在力的作用下经过
的功。
动能定理
图12-15
动能定理பைடு நூலகம்
【例12-4】 在图12-16中,为测定摩擦系数f,把矿车置于
斜坡上的A 点处,让其无初速下滑。当它达到B 点时,靠惯性
又往前滑行一段路程,在C 点处停止。求摩擦系数f0,已知S1、
S2 和h。
图12-16
动能定理
动能定理
【例12-8】 C618车床的主轴转速n=42r/min时,其切削力
P=14.3kN,若工件直径d=115mm,电动机到主轴的机械效率
η=0.76。求此时电动机的功率为多少?
解 由式(12-12)得切削力P 的功率:
动能定理
12.5 势力场 势能及机械能守恒定理
动能定理
动能定理
12.4 功率 功率方程
1.功率
在单位时间内力所做的功称为功率。它是衡量机器工作
能力的一个重要指标。
δW 是dt时间内力的元功,则功率为
动能定理
由于元功为δW =Ft·ds,因此
即,力的功率等于切向力与力作用点速度的乘积
力矩的元功为δW =M·dφ,则
即,力矩的功率等于力矩与物体转动角速度的乘积。
动能定理
动能定理
12.1 力的功
12.2 质点 质点系的动能
12.3 质点与质点系的动能定理
12.4 功率 功率方程
12.5 势力场 势能及机械能守恒定理
12.6 动力学普遍定理及综合应用
思考题
动能定理
12.1 力 的 功
工程实际中,一物体受力的作用所引起运动状态的变化,
不仅取决于力的大小和方向,而且与物体在力的作用下经过
的功。
动能定理
图12-15
动能定理பைடு நூலகம்
【例12-4】 在图12-16中,为测定摩擦系数f,把矿车置于
斜坡上的A 点处,让其无初速下滑。当它达到B 点时,靠惯性
又往前滑行一段路程,在C 点处停止。求摩擦系数f0,已知S1、
S2 和h。
图12-16
动能定理
物理人教版(2019)必修第二册8.3动能和动能定理(共29张ppt)

典例解析
N
v0=0m/s f
F
v=80m/s
G l=2.5×103m
方法一:利用牛顿第二定律和运动学公式 解:设飞机做匀加速直线运动,受到重力、支持力、牵引力和阻力作用
根据牛顿第二定律:F合=F-kmg=ma 由v2-0=2al得:a=v2/2l 由以上两式得:F=1.04×105N
典例解析 v0=0m/s f
重力势能mgh 弹性势能kx2/2 动能表达式?
第一部分 动能的表达式
情景一
在光滑水平面上质量为m的物体,在与运动方向总相同的恒力F的作 用下发生一段位移l,速度由v1增加到v2,如图所示。试寻求这个过程中外 力做的功与v1、v2的关系?
v1
情景1
FN F
G
l
v2 F
情景一
W Fl
v1
情景1
动能定理
4.实质:动能定理从能量变化的角度反映了力改变运动的状态在空间上 的累积效果。
5.适用范围:动能定理是物体在恒力作用下,并且做直线运动的情况下 得到的,当物体受到变力作用,或者做曲线运动时,可以采用把整个过 程分成许多小段,也能得到动能定理。
典例解析
【例题1】一架喷气式飞机,质量m =7.0×104kg,起飞过程中从静止开始 滑跑.。当位移l达到2.5×103m时,速度达到起飞速度 v =80m/s,飞机受 到的平均阻力是飞机所受重力的1/50。g取10m/s2,求飞机受到的牵引力。
第二部分 动能定理
动能定理
1.内容:外力在一个过程中对物体做的功,等于物体在这个过程中动能 的变化。
2.公式:W=Ek2-Ek1 如果物体受到几个力的共同作用,W即为合力做的功,它等于各个
力做功的代数和。 3.物理意义:动能定理指出了合外力对物体所做的总功与物体动能变化 之间的关系,即若合外力做正功,物体的动能增加,若合外力做负功, 物体的动能减小,做了多少功,动能就变化多少。
动能和动能定理课件(共19张PPT)

功
2 5.310 2
1.8 10 4 N
升级题型:
例:如图,光滑的水平面AB与光滑的半圆形轨道相接触,直径BC 竖直,圆轨道半径为R一个质量为m的物体放在A处,AB=2R,物体 在水平恒力F的作用下由静止开始运动,当物体运动到B点时撤去 水平外力之后,物体恰好从圆轨道的顶点C水平抛出.物块运动过 程中空气阻力不计试求:
W=Ek2-Ek1 = △Ek
总功 末动能 初动能
• 动能定理说明了:做功的过程是能量转化的过程
• 等号并不意味着“功转化成动能”,而是“功引起动能 的变化”。体会“功是能量转化的量度”
• 合外力做正功(W>0)时,△Ek>0,即Ek2>Ek1,动能增加 • 合外力做负功(W<0)时,△Ek<0,即Ek2<Ek1,动能减少
升级题型: 5、运动员把质量是500g的足球踢出后,已知球 书P88 5 上升的最大高度是5m,到达最高点的速度为
10m/s,运动员踢球时对足球做的功。
升级题型:
例:一架喷气式飞机,质量m=5×103 kg,起飞过程 中从静止开始滑跑的路程为l=5.3×102m时,达到起 飞速度v=60m/s,在此过程中飞机受到的平均阻力是
基本题型:3、如图所示,质量为20g的子弹,以300m/s的
书P88 3
速度水平射入厚度是10cm的木板,射穿后的速 度是100m/s.子弹在射穿木板的过程中所受的
平均阻力是______N.
基本题型: 4、我们在第四章曾用牛顿运动定律解答过一
书P88 4
个问题:民航客机机舱紧急出口的气囊是一 个连接出口与地面的斜面,若斜面高3.2m,
8.3 动能和动能定理
末态
初态
理论力学课件 第十二章 动能定理

FRO
r1 r2 O
mg
解:取整体为研究对象,受力分析如图所示。 v1
A
v2
B
系统对O点的动量矩为
m1 g
m2 g
LO m1v1r1 m2v2r2 J0 (m1r12 m2r22 JO )
系统所受全部外力对O点的动量矩为
MO (F e ) m1gr1 m2gr2
质点系的动量矩定理为 dLO dt
WFN 0
WF F s fmgs cos 30 8.5 J
WF
1 2
k
(12
2 2
)
100 (0 0.52) 2
12.5 J
W Wi 24.5 0 8.512.5 3.5 J
12.2 质点和质点系的动能
12.2.1 质点的动能
设质量为m的质点,某瞬时的速度为v,则质点质量与其速度平方乘积的
路径无关。若质点下降,重力的功为正;若质点上升,重力的功为负。
对于质点系,重力的功等于各质点的重力功的和,即
上式也可写为
W12 mi g(zi1 zi2) W12 mg(zC1 zC2 )
2.弹力的功
设有一根刚度系数为k,自由长为l0的弹 簧, 一端固定于点O, 另一端与物体相连接,
如图所示。求物体由M1移动到M2过程中,弹 力F所做的功。
W12
M2 M1
(Fx
d
x
Fy
d
y
Fz
d
z)
12.1.3 常见力的功
1.重力的功
z M1 M
mg
设质点M的重力为mg,沿曲线由M1运动到
M2
M2,如图所示。因为重力在三个坐标轴上的
投影分别为Fx=Fy=0,Fz=-mg,故重力的功为
动能定理(共7张PPT)
(1)7.5×104N;(2)1.5× ×106W (3)16km
出,物体落地时的速度为13m/s,求物体在运动过程中克服空气
阻力做的功。
11.2J
例2、一架小型喷气式飞机的质量为5×103kg,在跑道上从静止开始滑 行时受到的发动机牵引力为1.8×104N,设运动中的阻力是它所受重力的 0.2倍,飞机离开跑道的起飞速度是60m/s,求飞机在跑道上滑行的距离.(g 取10米/秒2.)
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度 恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才
能到达斜面顶端?
V2 0
4gh
例8、质量为3000t的列车, 在恒定的额定功率下, 由静止开始出发, 运动 过程中受到的阻力大小恒定, 经过1000s速度达到最大行驶速度72km/h. 此时司机发现前方4km处的铁轨被洪水冲毁, 便立即紧急刹车, 结果列车 正好到达铁轨冲毁处停止, 若所加的制动力为7.5×104N. 求:(1) 列车在 行驶过程中所受阻力多大? (2) 列车的额定功率多大? (3) 列车的总行程 多长?
动能定理的解题步骤:
1125m
1、确定研究对象和研究过程
2、确定始末状态的动能
3、写出过程中合力的功或各力做的总功,明确各力做功的正负
4、利用动能定理,写出等式,左边写功(合力的功或各力的总功), 右边写末动能-初动能
例4、(1999广东高考)如图,一弹簧振子,物块的质量为m,它与
水平桌面间的动摩擦因数为μ,起初用手按住物块,弹簧的伸长量为x,
N
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才能到达斜面
出,物体落地时的速度为13m/s,求物体在运动过程中克服空气
阻力做的功。
11.2J
例2、一架小型喷气式飞机的质量为5×103kg,在跑道上从静止开始滑 行时受到的发动机牵引力为1.8×104N,设运动中的阻力是它所受重力的 0.2倍,飞机离开跑道的起飞速度是60m/s,求飞机在跑道上滑行的距离.(g 取10米/秒2.)
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度 恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才
能到达斜面顶端?
V2 0
4gh
例8、质量为3000t的列车, 在恒定的额定功率下, 由静止开始出发, 运动 过程中受到的阻力大小恒定, 经过1000s速度达到最大行驶速度72km/h. 此时司机发现前方4km处的铁轨被洪水冲毁, 便立即紧急刹车, 结果列车 正好到达铁轨冲毁处停止, 若所加的制动力为7.5×104N. 求:(1) 列车在 行驶过程中所受阻力多大? (2) 列车的额定功率多大? (3) 列车的总行程 多长?
动能定理的解题步骤:
1125m
1、确定研究对象和研究过程
2、确定始末状态的动能
3、写出过程中合力的功或各力做的总功,明确各力做功的正负
4、利用动能定理,写出等式,左边写功(合力的功或各力的总功), 右边写末动能-初动能
例4、(1999广东高考)如图,一弹簧振子,物块的质量为m,它与
水平桌面间的动摩擦因数为μ,起初用手按住物块,弹簧的伸长量为x,
N
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才能到达斜面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fτds=δW 代入得到
为Fτ在位移ds上所作的功,称为元功
d(mv2/2)=δW—质点动能定理的微分形式
质点动能的微分等于作用于质点上的力的元功。
如果质点自M1点到M2点作有限位移,相应 的坐标为s1和s2,相应的速度为v1和v2,对 上式积分
∫ v1 v2 d(mv2/ 2)= ∫ s1 s2 Fτds 得到:
质量的大小及其分布有关,与刚体的运动 无关。
刚体质量连续分布时,转动惯量可 以写成:
Jz=∫Mr2dm 通过积分可以求得质量均匀分布并
有规则几何形状的刚体的转动惯量。
几种常见刚体对过质心轴z的转动 惯量
1.质量为m,半径为R的均质圆盘 (圆柱),
Jz= m R2/2 2.质量为m,半径为R的均质圆环,
平移刚体的动能
刚体平移时各点速度相同,由T=∑mivi2/2得到 T=mv2/2
或写成T=mvc2/2 vc为刚体质心的速度。
定轴转动刚体的动能
设定轴转动刚体角速度为ω,其上任一点M 到转轴的距离为ri,其速度vi= ri ω,则刚 体的动能为
T=∑mivi2/2=∑mi (riω)2/2 = ∑mi ri2ω2/2=Jzω2/2 Jz =∑mi ri2称为刚体对定轴z的转动惯量。 转动惯量是刚体转动惯性的度量,与刚体
自由质点系—质点系中各质点的运动不受约束的限 制的质点系;反之称为非自由质点系。
12-1-2 质点动能的概念 质点的质量为m,某瞬时速度为v,
定义:质点的动能等于质点质量与质 点速度平方乘积的一半,即
T=mv2/2 动能永远为正值或零。 动能的单位为N.m(牛顿.米)
v m
1 N.m=1J(焦耳)。
Jz= m R2 3.质量为m,长为l的均质细杆,
Jz= m l2/12
m zR
m R
z
z
l/2
l/2
平行轴定理:刚体对任何轴的转动惯量, 等于刚体对通过质心并与该轴平行的轴 的转动惯量,加上刚体质量与两轴之间 距离的平方的乘积。即:
12-1-4 作用于质点系上的力的分类 内力与外力 内力—质点系中各质点之间的相互作用力; 外力—质点系外的物体作用于质点系上各质点的力。 对于一般的质点系,内力作功不一定等于零。 主动力与约束力 约束力—约束作用于物体的力; 主动力—约束力之外的力。 理想约束—约束力所作之功的代数和等于零的约束。 光滑接触、光滑轴承、光滑铰链,不考虑伸长的绳
索,只滚不滑的纯滚动等。
12-1-5 质点的动能定理
当质点M在力F作用下,沿轨迹M1到M2时,Fτ是力 F在切线方向的投影,
由牛顿第二定律有 maτ= Fτ 将aτ=dv/dt代入有 mdv/dt= Fτ 等号两边乘以ds,且v=ds/dt,代入有
mvdv/dt=Fτds mvdv/dt=d(mv2/2)
起止位置高度差的乘积。
重力作功与质点运动路径无关,只与起 止点的高度有关。
z M1 z1
z2
Fp
M2
O y
x
弹性力的功
设弹簧刚度为k,相应变形由λ1到λ2,则弹性力作的功为: W=∫s1s2 –Fds =∫λ1λ2 – kλdλ = k(λ12 –λ22 )/2 即:弹性力作功与质点路径无关,只与弹性元件在质点起
mv22/2 - mv12/2=W —质点动能定理的积分 形式
质点在有限位移过程中,其动能的改变等 于作用在质点上的力在相应位移上所作之 功。
§12-2 质点系的动能定理 12-2-1 质点系的动能 质点系的动能等于质点系内所有质点动能的总和:
T=∑mivi2/2 几种常见运动形式下刚体的动能
止位置时的变形量有关。
作用在定轴转动刚体上力的功
在力F作用下,作定轴转动的刚体由Φ1转至Φ2时,力所作 的功为:
W= ∫ Φ1 Φ2 Mz(F)dΦ 当力对轴之矩保持不变时,力对轴之矩所作的功为:
W= Mz(F)(Φ2- Φ1) 当力对轴之矩保持不变时,作用在定轴转动刚体上的力所
作的功等于力对轴之矩与刚体转角的乘积。
计算动能时,速度为绝对速度。
动能是质点运动强度的一种度量。
12-1-3 功的概念和计算
作用在质点上的力在某一段位移上的功,是 力在这段位移上作用效果的度量。
恒力的功:在恒力F作用下,质点M沿直线 运动。力作用线与运动方向夹角为θ,位移 为s,力F对质点作的功等于F在位移方向上 M1 的投影与位移的乘积:
第12章 动能定理
§12-1 基本概念 物体的动力分析—研究物体的运动与作用在物体上
的力或力系之间的关系。
基本定律是牛顿第二定律 F=ma 本书只介绍动能定理和动静法两部分内容。
12-1-1动力学的力学模型 质点—有质量但可以忽略其大小和形状的点。 质点系—有限或无限质点的集合。 刚体—无数质点组成的不变形的质点系。 刚体的特点是其中任意两质点间的距离保持不变。
δW=Fcosθds
M1 ds F
r
ห้องสมุดไป่ตู้
dr θ v M2
r’
沿弧长积分,求得变力F在运动轨迹M1M2O
上对质点作的功:
x
y
W=∫s1s2 Fcosθds =∫s1s2 Fτds
用X,Y,Z表示为F在xyz轴上的投影, dxdydz为微元ds在xyz轴上的投影,则
W=∫M1M2(Xdx+Ydy+Zdz)
合力功定理—质点M同时受n个力(F1, F2 , …, Fn,)的作用,设合力为R, 则质点M在R作用下在任意位移上所作的 功,等于各分力在相同位移上所作的功 的代数和。
W=W1+W2+…+Wn=∑W 重力功
质点在重力作用下,沿任意轨迹从M1运 动到M2 ,重力作功为
W=∫z1z2 -Fpdz= Fp(z1 –z2) 即:重力作功等于质点所受重力与质点
W=Fscos θ
W=F . s
功是代数量,正负号规则为:力的投影的正 方向与位移方向一致,则力在这一段位移上 所作之功为正;反之为负。
功的国际单位为N.m,
1 N.m=1J(焦耳) 。
F
θv
M2
s
变力的功:
如果在变力作用下,质点M沿任意轨迹
从M1运动到M2,考察微元弧段,将微元 上作用的力视为恒力,微段轨迹视为直 z 线,则力的微元功为
