ch3
ch3化学名称

ch3化学名称
甲烷,也被称为液化石油气,是一种常见的有机化合物,是碳和氢原子组成的
稳定分子,每个分子由一个碳原子和四个氢原子组成。
甲烷是一种芳香族碳氢化合物,位于碳和碳与氢之间。
甲烷是无色可燃气体,也是一种温和的碳氢化合物。
甲烷主要用于燃烧以产生热能,这使它成为工厂热力发电和家庭供暖的重要进
口能源。
甲烷还用于工业生产过程,其中包括陶瓷材料的生产,钢铁的冶炼,以及氢气的提炼。
此外,甲烷也可以提供其他各种用途,其中包括制冷,饮料冲泡,汽车制动液,和抗虫剂。
甲烷对环境的主要影响是排放出其他温室气体,这些气体包括二氧化碳,水气
和其他污染物。
此外,甲烷也有致癌及污染空气的潜在危险。
因此,甲烷在家庭和工业应用中都必须严格控制其使用量,以保护环境。
总之,甲烷是一种常见的有机物,用来发电照明和供暖等各种家庭和工业用途,但它的排放可能对环境造成危害,需要严格控制使用量才能保护环境。
数字电路ch3补充:最大项、最小项、无关项

2 无关项在化简逻辑函数中的应用
【例3】 化简具有约束的逻辑函数
Y ABCD ABCD ABCD
给定约束条件为
ABC D ABCD ABCD ABCD ABC D ABCD ABCD 0
解:采用公式化简法
Y ( ABCD ABC D) ( AB C D ABCD) ( ABCD ABCD) ( AB CD AB CD )
解: Y1 A BCD BCD A
Y2 A B CD A B CD B CD Y3 Y4
ABC A B C AB C AB C C BD C C BD C C
B D D B
i
【例1】将逻辑函数展开为最小项之和的形式。
Y ABCD ACD AC
解: Y A BC D A( B B )CD A( B B)C
ABC D ABCD ABCD ABC ABC ABC D ABCD ABCD ABC( D D) ABC ( D D) ABC D ABCD ABCD ABCD ABCD ABCD ABC D
强化: 逻辑函数的公式化简法
1 逻辑函数的最简形式
乘积项最少;每个乘积项里的因子也最少 一. 最简与-或式 二. 最简与非-与非式等
_ _
F AB A B
F AB A B
__________ ______ ____ __ __
三.最简与或非表达式
F AB AB
__________ ___ __ __
变量的各组取值 对应的最大项及其编号 最大项 编 号 A B C
0 0 0 0 1 1 1 1
ch3烷烃

C8H3C7H2C6HCH5 CH4 2CH3 CH22CH13
CH3
3 ,4 , 6- < 3 ,5 , 6-
3 ,4 , 6-三甲基辛烷
24
CH3
CH3
1 2 3 45 6 7 8
C8H3C7H2C6HCH5 CH4 2CH3 CH22CH13
CH3
3 ,4 , 6- < 3 ,5 , 6-
3 ,4 , 6-三甲基辛烷
第六节 烷烃的化学性质
➢ 常温下很不活泼; ➢ 常用作溶剂、基质等; ➢ 由于C—H,C-C牢固性和小极性。
一、氧化和燃烧
RH +O2 (燃烧) CO2 + H2O + Q
在标准状态下,一摩尔烷烃完全燃烧所放出的热量称 作燃烧热。燃烧热越大,表明分子内能越高,稳定性越低。
氧化还原反应
碳原子周围电子云密度降低时氧化 碳原子周围电子云密度增加时 还原
裂化反应主要用于提高汽油的产量和质量。
根据反应条件的不同,可将裂化反应分为三种:
① 热裂化:5.0MPa,500~700℃,可提高汽油产量;
② 催化裂化:450~500℃,常压,硅酸铝催化,除断C—C键 外还有异构化、环化、脱氢等反应,生成带有支链的烷、烯、 芳烃,使汽油、柴油的产、质量提高;
③ 深度裂化:温度高于700℃,又称为裂解反应,主要是提高 烯烃(如乙烯)的产量。
1. 单原子取代基,按原子序数大小排列。
I > Br > Cl > F > O > N > C > D > H
2. 原子序数大,顺序较优先;原子次序小,顺序在后; 同位素中质量高的,顺序大。
2.多原子基团首先比较第一个原子,按原子序数大 小排列;若第一个原子相同,则依次比较与其相连的 其它原子。
数据通信CH3 常见网络接口与线缆

– 目前已发展到万兆以太网,仍在继续发展 …
IEEE 802.3 以太网标准(主要的)
传统以太网:10Mb/s
• • • • 802.3 —— 粗同轴电缆 802.3a —— 细同轴电缆 802.3i —— 双绞线 802.3j —— 光纤
快速以太网(FE):100Mb/s
SFP光模块
该模块可插拔,主要用于1端口单通道POS48 接口板、4端口POS3接口板、1端口ATM 155M接口板上,使用的接口类型为LC。
3.1.3 全双工以太网
只能在双绞线和光纤链路上实现;
收、发使用了不同的物理信道
不再使用CSMA/CD机制,因此传输距离不 受时间槽的限制;
但要受到信号衰减的影响
使用双绞线或光纤; 链路两端的设备都必须支持全双工操作;
全双工操作的条件:
支持全双工的设备包括全双工网卡、网络交换机。
3.1.4 局域网扩展
什么情况下需要扩展?
网络范围扩大 更多的站点加入网络 多个独立的局域网进行互联
主要在三个层次上
如何扩展?
物理层 数据链路层 网络层
介质转换器是可连接不同介质的中继器
ST接口
该接口为收发两个圆形头,使用ST接头的光 纤
SC接口
该接口为收发两个方形头,使用SC接头的光纤。
LC接口
该接口为收发两个方形头,尺寸小于SC,使用 LC接头的光纤。
MTRJ接口
该接口收发集中在一个方形头,使用MTRJ接 头的光纤。
GBIC光模块
该模块为可插拔千兆以太网接口模块,主要用 于两端口千兆以太网接口板上,使用的接口类 型为SC。
ch3 理想气体性质

m pV = nRT = RT R M Rg = M pV = mRgT
M 为气体的摩尔质量。 为气体的摩尔质量。
第三章 理想气体的性质
不同质量理想气体的状态方程式
1 kg 理想气体 m kg 理想气体 1 mol 理想气体 n mol 理想气体
pv = RgT pV = mRgT pVm = RT pV = nRT
第三章 理想气体的性质
第三章 理想气体的性质
第三章 理想气体的性质
本章基本要求
1、熟练掌握并正确应用理想气体状态方程。 、熟练掌握并正确应用理想气体状态方程。 2、正确理解理想气体比热容的概念,熟练掌握 、正确理解理想气体比热容的概念, 和正确应用定值比热容、平均比热容来计算 和正确应用定值比热容、 过程热量。 过程热量。 3、熟练掌握和正确计算理想气体热力学能、焓、 、熟练掌握和正确计算理想气体热力学能、 熵的变化。 熵的变化。
1 t1
2
t2
第三章 理想气体的性质
4、按气体热力性质表上所列的u 和h 计算 、 基准态的设定: 基准态的设定: 理想气体通常取0K或 理想气体通常取0K或0°C时的焓值为0,如 0K 时的焓值为0 }=0,相应的{ }=0,这时任意温度T {h0K}=0,相应的{u0K}=0,这时任意温度T时的 h、u实质上是从0K计起的相对值,即 实质上是从0 计起的相对值,
du = cV dT dh = cpdT
对于理想气体, 是温度的单值函数, 对于理想气体,cp、 cv 是温度的单值函数, 因此它们也是与状态有关的参数。 因此它们也是与状态有关的参数。
第三章 理想气体的性质
三、定压比热容 c p 与定容比热容 cV 之 间的关系
对于理想气体: 对于理想气体:
ch3化学元素

ch3化学元素CH3化学元素,即甲基,是有机化学中的基本结构单元之一,由一个碳原子和三个氢原子组成。
甲基在有机化学中极为重要,可以与其他原子或基团共价键合并构成各种有机化合物,是构成生物大分子的必要单元之一。
首先,我们来看看甲基在有机化学中的重要性。
甲基不仅是构成有机分子的基本单元之一,它还可以作为反应中的中间体或催化剂。
例如,甲基自由基是重要的自由基中间体,可以在自由基链反应中发挥关键作用。
此外,甲基还可以参与重要的化学反应,如芳香烃质子化、单一取代烷基卤代烷基化反应等。
因此,对于有机化学的学习者而言,深入了解甲基的结构和性质是非常必要的。
接下来,让我们来看看甲基的物理性质。
甲基是一种无色、有臭味的气体,能够随浓度不同而变化其色及味。
其密度比空气轻,且不易溶于水,但易溶于有机溶剂。
甲基的熔点为-182°C,沸点为-161.5°C。
这样的物理性质大大限制了甲基在生活中的直接应用,但却不影响其在化学领域中的应用。
那么,甲基在有机化学中的化学性质是怎样的呢?首先,甲基对于不饱和化合物的加成反应有较强的反应性,同时也可以容易地和氨合成甲胺、与水合成甲醇以及和卤素发生取代反应,且常常是链反应或复杂反应机理的主要参与者。
特别是在自由基反应中,甲基自由基具有非常强的反应性,常常会发生大量的自由基链反应,产生复杂的产物。
此外,甲基也可以作为配体与其他化合物通过配位键形成络合物。
这种反应的机理与金属配合物的形成使其在工业生产上具有重要应用。
此外,甲基还可以作为重要的基团,被用来构成多种有机化合物,如甲基苯、甲基叔丁基醚等。
总之,甲基在有机化学中扮演了非常重要的角色。
甲基的结构和性质决定了其在化学反应中的作用,而我们则可以应用这些知识来设计或改良合成方法、提高产率以及优化产品性能。
我们需要深入了解甲基的本质,以使我们更好地应用有机化学的最前沿技术。
碳正离子最稳定的ch3

碳正离子最稳定的ch3
关于甲烷的三碳正离子最稳定情况的文章
甲烷(CH3)是一种天然存在于环境中的有机物质,它是由一个碳原子和三个氢原子组成
的最简单的碳氢化合物。
由于它是碳氢有机物中含氢量最多的,故它也被称为“万能气体”。
三碳正离子甲烷不仅是一种重要的有机物质,而且是最稳定的有机物质之一。
由于它是有机物中碳和氢原子最少的合成物,其价键能量最小,从而能够最好地保持稳定
的半对称性质结构。
碳原子的官能团在氢原子的覆盖下,使甲烷的结构很容易稳定,从而
增加了甲烷的化学稳定性。
另外,由于原子量最小,三碳正离子甲烷具有小分子的特点,它的碰撞,外部结构更加紧密,比大分子更稳定,它可以在低温低压下得到稳定的结构。
此外,三碳正离子甲烷是一种非常重要的简单有机物质,正离子性能改变会对其结构产生
重大影响,研究需要投入大量精力,所以正离子甲烷是最稳定的。
作为一种有用的简单有机物质,三碳正离子甲烷在各种行业中都有着广泛的应用,由于它
的机理和性能都非常稳定,因此它被广泛用于汽油、柴油、天然气、食品、医药等行业中。
总之,三碳正离子甲烷是碳氢化合物中最稳定的物质,能够用于各种行业中,也被称为“万能气体”,它是一种有用而重要的简单有机物质,给人类带来了巨大的帮助。
甲醇

概述甲醇是最简单的化学品之一,是重要的化工基础原料和清洁液体燃料,广泛应用于有机合成、染料、医药、农药、涂料、汽车和国防等工业中。
甲醇最早由木材和木质素干馏制得,故俗称木醇。
木材在长时间加热炭化过程中,产生可凝和不可凝的挥发性物质,这种被称为焦木酸的可凝性液体中含有甲醇、乙酸和焦油。
除去焦油的焦木酸可通过精馏分离出天然甲醇和乙酸。
生产1kg的甲醇约需60~80kg的木材。
这是生产甲醇的最古老方法。
美国于20世纪70年代初才完全抛弃这一过程。
1923年,德国BASF公司在合成氨工业化的基础上,首先用锌铝催化剂在高温高压的操作条件下实现了由一氧化碳和氢合成甲醇的工业化生产,开创了工业合成甲醇的先河。
工业合成甲醇成本低,产量大,促使了甲醇工业的迅猛发展。
甲醇消费市场的扩大,又促使甲醇生产工艺不断改进,生产成本不断下降,生产规模日益增大。
1966年,英国ICI公司成功地实现了铜基催化剂的低压甲醇合成工艺,随后又实现了更为经济的中压法甲醇合成工艺。
与此同时德国Lurgi公司也成功地开发了中低压甲醇合成工艺。
随着甲醇合成工艺的成熟和规模的扩大,由甲醇合成和甲醇应用所组成的甲醇工业成为化学工业中的一个重要分支,在经济的发展中起着越来越重要的作用。
物理性质甲醇是最简单的饱和脂肪酸,分子式CH30H,相对分子质量32.04。
甲醇分子中的碳原子和氧原子的成键轨道为四面体结构的sp3杂化轨道,相互重叠结合成C—O键。
而O—H键是氧原子的一个sp3杂化轨道和氢原子的1s轨道相互重叠,氧原子的两对未共用电子对分别占据其他两个sp3杂化轨道。
甲醇分子的成键轨道和氧原子的正四面体结构见图1-1;甲醇分子的键长和键角见表1-1。
(a)(b)图1-1 甲醇的成键轨道(a)和甲醇分子中氧原子正四面体结构(b)表1-1 甲醇分子的键长和键角和水以及乙醇、乙醚等许多有机液体无限互溶,但不能与脂肪烃类化合物相互溶。
甲醇蒸气和空气混合能形成爆炸性混合物,爆炸极限为6.0%~36.5%(体积)。
—ch3, —ch2— 分子式

—ch3, —ch2—分子式—CH3, —CH2—分子式为标题引言:分子式是一种用来描述化学物质组成的简化表示方式,其中CH3和CH2是两种常见的有机化合物的分子式。
本文将分别介绍CH3和CH2的结构和性质,以及它们在化学和生物领域中的应用。
一、CH3的结构和性质CH3是甲基基团的化学式,由一个碳原子和三个氢原子组成。
甲基是一种非常常见的有机基团,在许多有机化合物中都有出现。
1.1 结构甲基的结构可以用简化的化学式CH3表示,其中C代表碳原子,H 代表氢原子。
甲基是一种单独存在的基团,可以与其他化合物中的基团进行化学反应。
1.2 性质甲基是一种非极性的基团,由于电子云分布均匀,不带电荷,不具有明显的化学活性。
但是,由于甲基中的碳原子上有三个键合的氢原子,可以与其他化合物中的基团发生反应,参与化学反应。
二、CH2的结构和性质CH2是亚甲基基团的化学式,由一个碳原子和两个氢原子组成。
亚甲基在有机化学中也是一种常见的基团。
2.1 结构亚甲基的结构可以用化学式CH2表示,其中C代表碳原子,H代表氢原子。
亚甲基是一种单独存在的基团,与其他化合物中的基团可以进行化学反应。
2.2 性质亚甲基是一种非极性的基团,由于电子云分布均匀,不带电荷,不具有明显的化学活性。
然而,亚甲基中的碳原子上只有两个键合的氢原子,相比甲基而言,亚甲基的反应性略高。
三、CH3和CH2的应用CH3和CH2作为常见的有机基团,在化学和生物领域有着广泛的应用。
3.1 化学领域应用甲基和亚甲基是许多有机化合物的基础结构,它们可以作为反应中间体参与各种有机反应。
例如,甲基和亚甲基可以参与酯化反应、醚化反应、烷基化反应等,合成各种有机化合物。
3.2 生物领域应用甲基和亚甲基在生物体内也有重要的作用。
例如,在生物体内,甲基可以与DNA分子中的碱基进行甲基化修饰,影响基因表达和细胞功能。
另外,亚甲基也是生物体内一些重要分子的组成部分,如甲基协同子S-腺苷甲硫氨酸。
CH3CN与CH3自由基反应机理的理论研究

• 54 +山东化工SHANDONG CHEMICAL INDUSTRY2021年第50卷CH+C N与CH+自由基反应机理的理论研究李明悦",马咏梅",2*,谢春福2(1.渭南师范学院化学与学院,陕西渭南714099;2.西北工业大学理学院化学化工系,陕西西安710072)摘要:用量子力学研究了C H+自由基与C H+C N的气相反应机理,并用过渡态理论研究了反应的动力学性质,找到了抽氢和取代两种反通道。
在B3PW91/6-311G(d,P)级别上优化了、产和态的构型,用高级别方法G3(MP2)和C B S-QB3对单点能进行了校正,得到了反应势能面,用(CVT/SCT)方法计算了反应在200-2000 K温度范围内的速率常数,结果表明计算值与实验符合的,提的整个内都是主通道。
关键词:;取代;速中图分类号:〇641 文献标识码:A文章编号:1008-021X( 2021 #01-0054-03Theoretical Investi|+ation on the Reaction Mechanism of CH+CN and CH+RadicalLi Ming y ue1,Ma Yongmei^,2,Xie C hun f u2(1.College of Chemistry and Material,Weinan Normal University,Weinan714099,China;2.School of Natural and Applied Sciences,Northwestern Polytechnical University,Xi’an710072,China)Abstract &The mechanismon the reaction of CH3radical and C H C N is explored using the density functional theory.Two kinds of reaction mechanisms are found with h y drogen abstraction reaction and substitution reaction.The geometries of reactants,intermediates and products are optimized at B3PW91/6-311G(d,p)level.In order to establish the accurate potential energy surface,the single point energies are obtained by G3(MP2)and CBS-QB3.The rate constants for each channel are calculatedusing the canonical v ariational transition state theory(CVT)in the temperature range of200 〜2000 K The results indicate thatthe calculated rate constants are in very good agree with the available experimental detecti main channel in all the temperatures.K e y words &abstraction reaction;substitution reaction;rate constants乙腈(CH3CN)作为燃烧过程中的重要中间体[1]与C H3自由基的反应存在两条反应通道,即抽氢反应(R1)和取代反应由基的反应备受关注。
烷烃英文命名

注意:主链连有复杂烷基,则把位号和取代基名称看成 一个整体,仍然按词头的第一个字母确定命名次序。
13
IUPAC体系中支链烷基的命名
• 八个支链烷基保留普通名
(CH3)2CH-
isopropyl 异丙基
CH3CH2CH(CH3)- sec-butyl 仲丁基
CH3 CH3CHCHCH3
CH3
2,3dimethylbutane
2,3-二甲基丁烷
6
支链烷烃的IUPAC命名
• 给主链碳原子编号时,应使取代基的位次
和最小。一般是从离取代基近的一端开始
给主链编号。
CH3
CHHCH3
trimethylhexane 2,3,5-三甲基己烷
Nomenclature
Number Prefix(数字前缀):
总碳数≤10时
甲: meth-
壬: nona-
乙: eth-
癸: deca-
丙: prop-
丁: buta-
戊: penta-
己: hexa-
庚: hepta-
辛: octa-
1
直链烷烃的IUPAC命名
• C1到C4直链烷烃保留普通名:
20
饱和一元醇的命名
• IUPAC 命名法:
– 选主链:选含羟基的最长碳链为主链。 – 编碳号:从最靠近羟基的一端开始,依次个主
链碳原子编号。 – 定名称:母体名称为相应烷烃词尾ane去掉,
换上anol,并在母体名前面加上羟基的位号。
CH3CHCH3 2-propanol
OH
isopropanol
(isopropyl alcohol)
乙烷生成ch3ch2cl方程式

乙烷生成ch3ch2cl方程式
当乙烷与氯化氢反应时,会生成氯乙烷。
反应方程式如下所示:C2H6 + HCl → C2H5Cl + H2。
这个反应是在光照下进行的,通常需要使用紫外光或者火焰来
提供能量。
在反应过程中,氯化氢分子中的氢原子会取代乙烷分子
中的一个氢原子,从而生成氯乙烷和氢气。
这个反应在化工工业中被广泛应用,氯乙烷是一种重要的有机
化合物,用于制备其他有机化合物,如乙烯基酮、乙烯基醇、乙烯
基胺等。
此外,氯乙烷也被用作溶剂、杀虫剂和防腐剂。
因此,乙
烷生成氯乙烷的反应对于有机化学和工业生产都具有重要意义。
复方CH3

复方CH3简介CH3是三冕博士张劭根据他的学生罗马尼亚阿斯朗教授的GH3和西德的KH3设计而成,能够提高血液中的CAMB(即环磷酸腺苷是一种细胞内信使)浓度,从而延长细胞寿命,促进细胞代谢,促进神经细胞和神经纤维生长,能够松弛血管平滑肌,降低外周阻力,对三高(高血压症、高血糖症、高血脂症)、冠心病、脑动脉硬化、中风后遗症、脑梗、更年期综合症、老年斑及失眠、健忘、精力不足等中老年病均有显著疗效。
复方CH3成分主要成分:盐酸普鲁卡因、苯甲酸、偏重亚硫酸钾、磷酸钙。
复方CH3殊荣复方CH3是一种高分子生化物,是本世纪的一项重大发明,它的研制成功,预示着人类将在治疗和研究心脑血管疾病领域实现重大突破,复方CH3的神奇功效已被人类全面认识并推广。
专家认为,复方CH3的诞生是跨世纪的革命。
据悉,复方CH3现已经申报诺贝尔医学奖复方CH3功效复方CH3的诞生是跨世纪的革命。
随着人们生活习惯及生存环境的改变,心脑血管发病率随着年龄的增大也开始上升,各种污染及饮食毒素越来越多地沉积在血管壁上,40岁以上人的血液中基本都有血栓因子及杂质在流动,并侵蚀着血管内壁。
复方CH3以其独有的吸附功能,粘附杂质并分解后,神奇地将废物带走。
同时其产生的卵磷脂、人参皂甙能直接促进血管内皮细胞增殖修复,彻底治疗,不再复发。
据悉,复方CH3现已经申报诺贝尔医学奖。
血管老化直接导致血管病变。
随着年龄的增大,血管弹性下降,极易导致动脉硬化而发病,复方CH3能激活产生血管吸收血栓和杂质时所需的各种营养成分,不仅能有效治疗冠心病、脑血栓和偏瘫等症,而且能预防心肌梗塞、脑栓塞等致命疾病的发生,延长生命。
复方CH3发明人张劭博士生平简介张劭博士简介张劭(1906-1987),乳名基劭,又名劭农,河南省洛宁县东宋乡聂坟村吕家坡人。
英国皇家医学院终身院士,世界著名医学家。
张劭自幼聪慧,1929年入河南中山大学医科,在校学习认真,成绩优异,深受老师赞扬。
烷烃

C4H10
C4H10
四、烷烃的命名 1.习惯命名法
以碳原子个数为基础命名 十个以下用“天干地支”命名:甲、乙、 丙、丁、戊、己、庚、辛、壬、癸。 同分异构体以“正、异、新……”命名。 十以上用中文数字表示:十一烷、二十 烷、三十五烷等。
[例如] CH4
C2H6
C5H12 戊烷
C9H20 壬烷 C20H42 二十烷
2.同位素、同素异形体、同系物、同分异构体 四概念的比较
概念 同位素 同素异 形体 同系物 同分异 构体 内 涵 比较对象 实例
质子数等,中子数 不等,原子之间 同一元素 形成的 不同单质 结构相似,组成上 差一个或n个CH2 相同分子式,不 同结构的化合物
原子
单质 化合物
氕、氚
O2、O3 C2H6、C4H10 CH3(CH2)3CH3 C(CH3)4
CH3
异戊烷
CH3
3、系统命名法方法
①选最长的碳链为主链,称“某烷”
选定分子中最长的碳链为主链,按主 链上碳原子的数目称为“某烷”。 ——最长原则
CH3—CH—CH2—CH—CH3
CH3 CH2—CH3
己烷
出现多条等长的最长碳链,怎么办呢? 支链最多
CH3 CH3—CH—CH2—CH—CH—CH3
4
CH3
5
6
CH3
2,2,3,5
CH2 CH3 CH3
2,4,5,5
编序号的原则:近,简,小
③取代基,写在前,标位置,短线连
把支链的名称写在主链名称的前面,在支 链的前面用阿拉伯数字注明它在主链上的位 置,并在数字与名称之间用“一”短线隔开。
CH3—CH—CH2—CH—CH3
4
甲基
ch3多级放大电路直接耦合3
+ ui
管均处于微导通状态,即都有一个
微小的基极电流,分别为IB1和IB2。
RR1
R2
D1 D2 VR5 3
+VCC
T1
+ RL uo T2 VCC
消除交越失真的实际电路
静态时应调节R2 ,使UE为0,即u0为0。
有ui输入时,由于二极管D1、D2的动态电阻很小, 而且R2的阻值 也较小,可认为T1管基极电位与T2管基极电位随ui产生相同变化, 即ub1≈ub2≈ui, 即两管基极间电位差基本是恒值UB1B2 。
作业
第三章自测题: 二 (5)、(6) ——注:无需解释说明 三
第三章习题:3.10
Rs //
1
Rb
四、改进型差分放大电路
用三极管代替“长尾式”电路的长尾电阻,即构成
恒流源式差分放大电路
1. 电路组成
Rc
uI1
+ uo
Rc
+VCC
uI2 Rb2
T3:恒流管
作用:能使 iC1、iC2基 本上不随温度的变化 而变化,从而抑制共
R T1
T2 R
T3
Re
Rb1 VEE
具有恒流源的差分放大电路
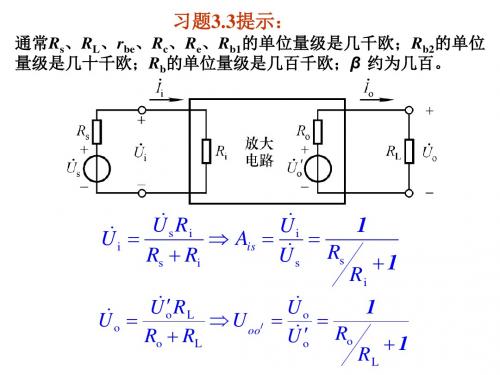
习题3.3提示:
通常Rs、RL、rbe、Rc、Re、Rb1的单位量级是几千欧;Rb2的单位 量级是几十千欧;Rb的单位量级是几百千欧;β 约为几百。
U i
Us Ri Rs Ri
Ais
U i U s
Rs
1 Ri 1
U o
Uo RL Ro RL
Uoo/
U U
T1截止,T2导通
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运算法则:
(1)
结合律: A( BC ) = ( AB )C ;
(2) 分配律: A( B + C ) = AB + AC , ( A + B)C = AC + BC ; (3)
λ ( AB) = (λ A) B = A(λ B), 这里 λ 是任意常数.
几种特殊矩阵:
(1) 对角阵——所有的非对角元素 aij (i ≠ j ) 全部等于 0 的方阵,即
第 4 页 共 12 页
= B −1 A−1 ;
高等代数第三章
矩阵
一般地, 如果 A1, A2, L , Ak 是 n 阶可逆阵, 则它们的乘积 A1 A2 L Ak 可逆, 且
( A1 A2 L Ak ) −1 = Ak −1 L A2 −1 A1−1 .
性质 3 若 A 可逆, c 是非零数, 则 cA 也可逆且 (cA) 性质 4 若 A 可逆, 则 A 的转置 A 也可逆且 ( A )
运算法则:
a12 + b12 a22 + b22 L am 2 + bm 2
L a1n + b1n ⎞ ⎟ L a2 n + b2 n ⎟ L L ⎟ ⎟ L amn + bmn ⎠
m× n
(1) ( 2) ( 3)
交换律: A + B = B + A 对任意 A , B ∈ F
成立.
m×n
结合律: ( A + B) + C = A + ( B + C ) 对任意 A , B , C ∈ F
例3
⎡1 1 0 ⎤ ⎢ ⎥ 设 A = 0 1 1 ,求 A100. ⎢ ⎥ ⎢ ⎣0 0 1 ⎥ ⎦
第 3 页 共 12 页
高等代数讲义
四、矩阵的转置
⎛ a11 ⎜ a21 定义 4 设 A = ⎜ ⎜L ⎜ ⎝ am1 a12 a22 L am 2 L a1n ⎞ ⎛ a11 ⎜ ⎟ L a2 n ⎟ ⎜a , 称 ⎜ 12 L L⎟ L ⎜ ⎟ ⎜ L amn ⎠ ⎝ a1n a 21 L a m1 ⎞ ⎟ a 22 L a m 2 ⎟ 为 A 的 转置, 记为 L L L⎟ ⎟ a 2 n L a nn ⎟ ⎠
二、初等矩阵
定义 对单位矩阵 En 进行第一、二、三类初等变换后得到的矩阵分别称为第一、二、三类初等矩 阵. 三类初等矩阵 显然, 初等矩阵都是方阵. 经三类行初等变换得到的三类初等矩阵的形状如下. (1)第一类初等矩阵,也称之为对换矩阵。
或
Aλ = ( aij )
运算法则:
m× n
λ = ( aij λ )m×n
矩阵与数的乘法也称为矩阵的数乘运算.
(1) λ ( A + B) = λ A + λ B; ( 2 ) (λ + σ ) A = λ A + σ A; ( 3) (λσ ) A = λ (σ A); ( 4 ) 1⋅ A = A; ( 5) 0 ⋅ A = O .
n−2
−1 −1
例1 例2 例3
A , A* = A
2
n −1
,其中 A 是 n 阶方阵。
设 n 阶方阵 A 适合 A + A − E = 0 ,证明: A +E 可逆。
第 5 页 共 12 页
高等代数讲义
例4 例5
设 n 阶矩阵 A , B 满足 A + B = AB ,证明 A − E 可逆且 AB = BA 。 设 α 是 n × 1 非零矩阵,且 α
三、 矩阵的乘法
定义 3 设 A = aij
( )
m×n
, B = bij
( )
n× p
, 定义乘积 AB 是一个 m × p 矩阵
AB = ( cij )
它的第 ( i, j ) 元素为
m× p
cij = ∑ aik bkj = ai1b1 j + ai 2b2 j + L + ainbnj
k =1
二、矩阵与数的乘法
定义 2 对任意正整数 m, n , F
m×n
中任意一个矩阵 A = aij
( )
m×n
与 F 中任意一个数 λ 相乘得
到一个 m × n 矩阵 λ A(或 Aλ ) , 称为左乘(右乘). 它的第 ( i, j ) 元素等于 λ aij (或 aij λ ), 即
λ A = λ ( aij )m×n = ( λ aij )m×n
T
α = 1 , E 是 n 阶单位矩阵,若 Q = E − 2αα T ,
则 Q 可逆,并求其逆。
§3.4
初等变换与初等矩阵
本节建立矩阵的初等变换与矩阵乘法的关系, 并在此基础上, 给出用初等变换求逆矩阵 的方法.
一、消元法与矩阵的初等变换
例 1 用消元法求解下列线性方程组
⎧ −5 x2 + 10 x3 = 13 ⎪ ⎨ x1 − 3 x2 + 7 x3 = 2 ⎪x + 2x + 9x = 1 2 3 ⎩ 1
则称 A 是可逆的或非奇异的, 并且称 B 是其逆矩阵,记为 A . 注 1:对于方阵 A , 适合等式的矩阵 B 是唯一的(如果存在的话).
−1
可逆矩阵的性质(运算法则)
性质 1 若 A 是可逆阵, 则 A 也可逆, 且 ( A )
−1 −1 −1
= A;
−1
性质 2 若 A, B 都是 n 阶可逆阵, 则它们的乘积 AB 也可逆且 ( AB )
矩阵的运算
一、矩阵的加减法
定义 1 设有两个 m × n 矩阵 A = aij
( )
m×n
、B = bij
( )
m×n
, 定义 A + B 是一个 m × n 矩阵
且其第 ( i, j ) 元素等于 aij + bij 。 (红色部分不要做 ppt) 即
A + B = (aij + bij ) m×n ⎛ a11 + b11 ⎜ a +b = ⎜ 21 21 ⎜ L ⎜ ⎝ am1 + bm1
T T −1
−1
= c −1 A −1 ;
= ( A−1 )T .
二、可逆的条件
定义 2 设 Aij 是矩阵
⎛ a11 ⎜ a A = ⎜ 21 ⎜L ⎜ ⎝ an1
中元素 aij 的代数余子式, 矩阵
a12 L a1n ⎞ ⎟ a22 L a2 n ⎟ L L L⎟ ⎟ an 2 L ann ⎠
⎛ A11 ⎜ A ∗ A = ⎜ 12 ⎜L ⎜ ⎝ A1n
成立.
零矩阵性质: 对任意 m × n 矩阵 A , 有 A + O = O + A = A .
第 1 页 共 12 页
高等代数讲义
( 4)
对每个 A = aij
( )
m×n
∈ F m×n , 取 − A = ( −aij )
m×n
,
则 A + (− A) = (− A) + A = O .
这里 − A 称为 A 的负矩阵. 矩阵的减法定义为: A − B = A + (− B) .
0 1 M 0 0 M 0
L 0 L L 0 L M L 1 L L 0 L M 0 L
0⎞ ⎟ 0⎟ M⎟ ⎟ 0⎟ , 0⎟ ⎟ M⎟ 0⎟ ⎠
即任一 m × n 矩阵均与一个主对角线上元素等于 1 或 0 而其余元素均为 0 的 m × n 矩阵等价. 后者称为前者的标准形. 矩阵与其标准形等价.
n
注1: (1)相乘的条件: A 的列数与 B 的行数相等;
( 2 ) A 与 B 的积 AB 的第 ( i, j ) 元素是 A 的第 i 行元素与 B 的第 j 列元素分别相
乘以后再求和的结果.
⎛1⎞ ⎜ ⎟ 例 1 设 A = ( 3 0 −1) , B = 2 , 求 AB 与 BA 。 ⎜ ⎟ ⎜ 3⎟ ⎝ ⎠
例4 例5 例6
设 A 为方阵,则 A + A 对称,而 A − A 反对称。
T T
证明: AA , A A 均为对称阵。 设实矩阵 A 满足 AA =0,则 A =0。
T
T
T
§3.3
矩阵的逆
一、可逆的定义 定义 1 对于 n 阶方阵 A , 若存在一个 n 阶方阵 B , 使得
O ⎟ ⎜ ⎟ a nn ⎠ ⎝
(2) 数量矩阵——所有元素等于同一个数 k 的对角阵, 记为 A = diag (k , k ,L k ) 。 如果 B 与数量矩阵 A 都是 n 阶方阵, 则 AB = BA = kB . (3) 单位矩阵—— E = diag (1,1,L1) 方阵的方幂. 设 A 是一个 n 阶方阵, 定义
A1 = A; Ak +1 = Ak ⋅ A .
规定 A = E , A ≠ 0 。
0
幂运算法则:
(1) Ar As = Ar + s ; (2) ( Ar ) s = Ars .
注 4:一般地 ( AB ) ≠ A B . 只有当 AB = BA 时, 才有 ( AB ) = A B .
r r r r r r
A
B.
等价的性质:
(1) 反身性 A (2) 对称性 若 A
A; B, 则B A;
第 6 页 共 12 页
高等代数第三章
矩阵
(3) 传递性 若 A
B, B
C, 则A C.
定理 (标准型) 任意一个 m × n 矩阵 A 都可通过有限次初等行变换和初等列变换化为下面 形式的 m × n 矩阵:
⎛1 ⎜ ⎜0 ⎜M ⎜ ⎜0 ⎜0 ⎜ ⎜M ⎜0 ⎝
