哈工大机械原理大作业-凸轮机构设计(第3题)
哈工大、机械原理大作业、凸轮机构设计20题

Harbin Institute of Technology机械原理大作业二课程名称:机械原理设计题目:凸轮机构设计院系:能源科学与工程学院班级:1102301设计者:刘平成学号:1110200724指导教师:唐德威设计时间:2013年6月7日凸轮机构设计1.设计题目(1) 凸轮机构运动简图:(2)凸轮机构的原始参数表2-1.凸轮机构原始参数 序号 升程(mm )升程运动角 升程运动规律升程许用压力角20 110 120° 正弦加速度35°回程运动角回程运动规律 回程许用压力角 远休止角近休止角 90°正弦加速度 65°90°60°(二)凸轮运动方程及相关图像、程序凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图: ○1 凸轮推杆升程、回程方程 πϕπϕϕs)650(πϕ≤≤140)(2=ϕs 511()69πφπ≤≤pi))*5708)/(23.2289)/1.-(sin(2+57083.2289)/1.-(-140(1)(3ϕπϕϕ=s1116()99πφπ≤≤)2914(πϕπ≤≤ 0)(4=ϕs ○2速度方程/2.0944;/2.09440))cos(2-140(1)(1πϕϕ=v 16(2)9πφπ≤≤ 0)(2=ϕv 511()69πφπ≤≤ 708;5708))/1.53.2289)/1.-(cos(2-140(1)(3ϕπϕ=v 1116()99πφπ≤≤ 0)(4=ϕv 16(2)9πφπ≤≤○3加速度方程 .0944^2;/2.0944)/2sin(2280)(1πϕπϕ=a )650(πϕ≤≤0)(2=ϕa 511()69πφπ≤≤08^25708)/1.573.2289)/1.-(sin(2280)(3ϕππϕ=a 1116()99πφπ≤≤ 0)(4=ϕa 16(2)9πφπ≤≤推杆位移、速度、加速度线图matlab编程clear,clcpu=0*pi/180:0.0001:120*pi/180; %升程运动角范围pf=120*pi/180:0.0001:210*pi/180; %远休止角范围pd=210*pi/180:0.0001:300*pi/180; %回程运动角范围pn=300*pi/180:0.0001:2*pi; %近休止角范围h=110e-3; %升程w=10; %凸轮角速度p0=120*pi/180; %升程运动角p01=90*pi/180; %回程运动角ps=90*pi/180; %远休止角%----------推程-----------------------------------------su=h.*(pu./p0-sin(2.*pi.*pu./p0)/(2*pi)); %推杆位移vu=h*w/p0*(1-cos(2*pi*pu./p0)); %推程速度au=2*pi*h*w^2/p0^2*sin(2*pi*pu./p0); %推程加速度%------------远休止----------------------------nf=size(pf);sf=h*ones(nf); %推杆位移vf=zeros(nf); %推程速度af=zeros(nf); %推程加速度%---------------回程------------------------------T=pd-(p0+ps);sd=h/2*(1+cos(pi/p01*T)); %回程位移vd=-pi*h*w/(2*p01)*sin(pi/p01*T); %回程速度ad=-pi^2*h*w^2/(2*p01^2)*cos(pi/p01*T); %回程加速度%--------------------近休止---------------------------------nn=size(pn);sn=zeros(nn); %推杆位移vn=zeros(nn); %推程速度an=zeros(nn); % 推程加速度%------画出推杆位移、速度、加速度线图---------------p=[pu,pf,pd,pn];s=[su,sf,sd,sn];subplot(2,3,1),hold onplot(p,s*1e3,'linewidth',2),xlabel('\phi/rad'),ylabel('s/mm'),grid on,title('推杆位移'),axis([0,2*pi,1.1*min(s)*1e3,1.1*max(s)*1e3]) subplot(2,3,2) v=[vu,vf,vd,vn];plot(p,v,'linewidth',2),xlabel('\phi/rad'),ylabel('v/m/s'),grid on,title('推杆速度'),axis([0,2*pi,1.1*min(v),1.1*max(v)]) subplot(2,3,3) a=[au,af,ad,an];plot(p,a,'linewidth',2),xlabel('\phi/rad'),ylabel('a/m/s^2'),grid on,title('推杆加速度'),axis([0,2*pi,1.1*min(a),1.1*max(a)]) hold off(三)凸轮机构s d ds-ϕ图像及程序代码 %--------------------求ds/d_phi-------------------subplot(2,3,4),plot(v/w*1e3,s*1e3,'linewidth',2),xlabel('ds/d\phi/mm'),ylabel('s/mm'),axis equal,grid on,title('ds/d\phi —s')%---------------------凸轮轴心许用区域--------------------------- alpha_up=35*pi/180; %升程许用压力角 alpha_down=65*pi/180; %回程许用压力角 p1=pi/2-alpha_up; %推程斜率角 p2=alpha_down-pi/2; %回程斜率角 ku=tan(p1); %推程切线斜率 kd=tan(p2); %回程切线斜率 R2=[cos(-p2),-sin(-p2);sin(-p2),cos(-p2)];%推程旋转矩阵 R1=[cos(-p1),-sin(-p1);sin(-p1),cos(-p1)];%推程旋转矩阵 nu=size(pu); for i=1:nu(2)Temp=R1*[vu(i)/w;su(i)];vut(i)=Temp(1); %旋转推程ds/dp-s 曲线 sut(i)=Temp(2); endnd=size(pd); for i=1:nd(2)Temp=R2*[vd(i)/w;sd(i)];vdt(i)=Temp(1); %旋转回程ds/dp-s 曲线 sdt(i)=Temp(2); endfor j=1:nu(2)if sut(j)==min(sut)temu=j; %旋转推程ds/dp-s 曲线后求最低点 end endfor j=1:nd(2)if sdt(j)==min(sdt)temd=j; %旋转回程ds/dp-s曲线后求最低点endendt1=1.2*min(vd/w):0.01:1.2*max(vu/w); %切线定义域t2=min(vd/w)/6:0.01:1.2*max(vu/w);t3=0:0.01:1.2*max(vu/w);s1=ku*(t2-vu(temu)/w)+su(temu); %推程切线s2=kd*(t1-vd(temd)/w)+sd(temd); %回程切线s3=tan(-p1)*t3; %推程起点压力角限制线subplot(2,3,5) %画图hold on,axis equal,grid onplot(v/w*1e3,s*1e3,'linewidth',2)plot(t2*1e3,s1*1e3,'linewidth',1,'color','r')plot(t1*1e3,s2*1e3,'linewidth',1,'color','r')plot(t3*1e3,s3*1e3,'linewidth',1,'color','r')xlabel('ds/d\phi/mm'),ylabel('s/mm'),hold off,title('ds/d\phi—s,轴向许用范围')(四)确定凸轮的基圆半径和偏距、绘制凸轮机圆、偏距圆、理论轮廓曲线---------------画理论廓线图-------------------------e=36e-3;s0=52e-3;r0=sqrt(s0^2+e^2);x=(s0+s).*cos(p)-e.*sin(p);y=(s0+s).*sin(p)+e.*cos(p);x1=r0*cos(p);y1=r0*sin(p);subplot(2,3,6)plot(x*1e3,y*1e3,'linewidth',1),axis equal,grid on,hold on,title('廓线图')plot(x1*1e3,y1*1e3,'linewidth',1,'color','r')%-------------求最小曲率半径-----------------------nx=size(x);nx1=nx(2)-2;dydp=diff(y)./diff(p);%求微分dxdp=diff(x)./diff(p);d2ydp2=diff(dydp)./diff(p(1:nx1+1));d2xdp2=diff(dxdp)./diff(p(1:nx1+1));rho=(dxdp(1:nx1).^2+dydp(1:nx1).^2).^1.5./abs((dxdp(1:nx1).*d2ydp2(1:nx1)-dydp(1:nx1).*d2x dp2(1:nx1)));%理论廓线曲率半径rhomin=min(rho);%最小曲率半径rr=rhomin-3e-3;%----------------实际廓线图----------------X=x(1:nx(2)-1)-rr*dydp./(dxdp.^2+dydp.^2).^0.5;%求实际廓线坐标Y=y(1:nx(2)-1)+rr*dxdp./(dxdp.^2+dydp.^2).^0.5;plot(X*1e3,Y*1e3,'linewidth',2,'color','k')%画实际廓线图Legend('理论廓线','基圆','实际廓线'),axis([1.1*min(x)*1e3,1.1*max(x)*1e3,1.1*min(y)*1e3,1.1*max(y)*1e3])得到基圆半径311mm、偏距36mm。
哈工大机械原理大作业

H a r b i n I n s t i t u t e o f T e c h n o l o g y大作业设计说明书课程名称:机械原理设计题目:凸轮机构院系:机电学院班级:姓名:学号:指导教师:丁刚设计时间:2014.5.29哈尔滨工业大学1.设计题目第31题:升程/mm 升程运动角/。
升程运动规律升程许用压力角/。
回程运动角/。
回程运动规律回程许用压力角/。
远休止角/。
近休止角/。
150 90 等加等减速40 80 余弦加速度70 40 1502.运动方程式及运动线图由题目要求凸轮逆时针旋转(1)确定凸轮机构推杆升程、回程运动方程,并绘制推杆位移、速度、加速度线图。
升程第一段:(0 <φ< pi /4)φ0=pi/2;s1 = 73*φ^2;v1=146*w*φ;a1 = 146*w^2;升程第二段:(pi/4 <φ< pi /2)s2 =90-73*(pi/2-φ)^2;v2=146*w*( pi/2-φ);a2 =-146*w.^2;远休止程:(pi/2 <φ< 10*pi/9)s3 = 90;v3 = 0;a3 = 0;回程:(10*pi/9)< φ< ( 14*pi/9)s4 =45*(1+cos(9/4*(φ-10*pi/9)));v4 =-101.25*w*sin(9/4*(φ-10*pi/9)) ;a4 =-227.8*w^2* cos(9/4*(φ-10*pi/9)); 近休止程:(14*pi/9)< φ < ( 2*pi);s5 =0;v5 =0;a5 =0;1.由上述公式通过编程得到位移、速度、加速度曲线如下:(编程见附录).基圆半径为r0 = (50^2+100^2)0.5=112mm,偏距e = 50mm。
3.凸轮实际轮廓,理论轮廓,基圆,偏距圆绘制4.整体图像附录1.求位移、速度、加速度的程序(matlab)w = input('请输入W=');x = 0:(pi/1000):(pi/4);s1 = 73*x.^2;v1=146*w*x;a1 = 146*w.^2;y = (pi/4):(pi/1000):(pi/2);s2 =90-73*(pi/2-y).^2;v2=146*w*( pi/2-y);a2 =-146*w.^2;z = (pi/2 ):(pi/1000):(10*pi/9);s3 = 90;v3 = 0;a3 = 0;c = (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));v4 =-101.25*w*sin(9/4*( c-10*pi/9)) ;a4 =-227.8*w.^2* cos(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0; v5 =0; a5 =0;subplot (2,2,1)plot(x,s1,'b',y,s2,'b',z,s3,'b',c,s4,'b', d,s5,'b');xlabel('转角/rad')ylabel('位移/(mm/s)')title('位移与转角曲线')grid onsubplot (2,2,2)plot(x,v1,'g',y,v2,'g',z,v3,'g ',c,v4,'g', d,v5,'g')ds4 =45*9/4*sin(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0;ds5 =0;plot(ds1,s1,'b',ds2,s2,'b',ds3,s3,'b',ds4,s4,'b',ds5,s5,'b'); xlabel('ds/dp');ylabel('(位移s/mm)')title('ds/dp 与位移s曲线')grid onhold onx3=-150:0.001:0;y3 = 0.577*x3;plot (x3,y3,'r');hold onx1=-150:0.001:150;for i=1:1:250;k1=(s1(i+1)-s1(i))/ (ds1(i+1)-ds1(i));if(k1>=-1.733 && k1<=-1.731)y1=k1*(x1-ds1(i))+s1(i);plot (x1,y1,'r');end3.确定滚子半径(1)先求凸轮理论轮廓曲线,程序如下:Clc;clear;w = input('请输入w=');s0 = 100;s = 90;e = 50; x = 0:(pi/100):(pi/4);x1 = (s + s0)*cos(x)-e*sin(x);y1 = (s0 + s)*sin(x) - e*cos(x);y = (pi/4):(pi/100):(pi/2);x2 = (s + s0)*cos(y)-e*sin(y);y2 = (s0 + s)*sin(y) - e*cos(y);z = (pi/2 ):(pi/100):(10*pi/9);x3 = (s + s0)*cos(z)-e*sin(z);y3 = (s0 + s)*sin(z) - e*cos(z);c = (10*pi/9):(pi/1000):( 14*pi/9);x4 = (s + s0)*cos(c)-e*sin(c);y4 = (s0 + s)*sin(c) - e*cos(c);d=(14*pi/9):(pi/1000):( 2*pi);x5 = (s + s0)*cos(d)-e*sin(d);y5 = (s0 + s)*sin(d) - e*cos(d);plot(x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b',x5,y5,'b');xlabel('x/mm')ylabel('y/mm')title('理论轮廓曲线')grid on(2)理论轮廓线最小曲率半径编程代码:由下程序结果可知pmin =81.6667这里滚子半径为 r r < pmin-ΔΔ=3~5mm;取r r=10mm;clear;clc;v=[];syms x1 x2 x3 x4 x5s0 = 100;e = 50;s1 = 73*x1.^2;t1 = (s1 + s0)*cos(x1)-e*sin(x1);y1 = (s0 + s1)*sin(x1) - e*cos(x1);tx1=diff(t1,x1);txx1=diff(t1,x1,2);yx1=diff(y1,x1);yxx1=diff(y1,x1,2);for xx1= 0:(pi/100):(pi/4);k1=subs(abs((tx1*yxx1-txx1*yx1)/(tx1^2+yx1^2)^1.5),{x1},{xx1}); v=[v,1/k1];ends2 =90-73*(pi/2-x2).^2;t2 = (s2 + s0)*cos(x2)-e*sin(x2);y2 = (s0 + s2)*sin(x2) - e*cos(x2);tx2=diff(t2,x2);txx2=diff(t2,x2,2);yx2=diff(y2,x2);yxx2=diff(y2,x2,2);for xx2=(pi/4):(pi/100):(pi/2);k2=subs(abs((tx2*yxx2-txx2*yx2)/(tx2^2+yx2^2)^1.5),{x2},{xx2});k4=subs(abs((tx4*yxx4-txx4*yx4)/(tx4^2+yx4^2)^1.5),{x4},{xx4}); v=[v,1/k4];ends5 =0;t5 = (s5 + s0)*cos(x5)-e*sin(x5);y5 = (s0 + s5)*sin(x5) - e*cos(x5);tx5=diff(t5,x5);txx5=diff(t5,x5,2);yx5=diff(y5,x5);yxx5=diff(y5,x5,2);for xx5=(10*pi/9):(pi/100):( 4*pi/3);k5=subs(abs((tx5*yxx5-txx5*yx5)/(tx5^2+yx5^2)^1.5),{x5},{xx5}); v=[v,1/k5];endpmin=min(v)4.绘制凸轮轮廓曲线clear ;clc;syms x y z c dw= input('请输入w=');n3 = diff(x3);m3 = diff(y3);xt3= subs(x3 + (r*m3)./sqrt(m3.^2+n3.^2),z,zz);yt3 = subs(y3 - (r*n3)./sqrt(m3.^2+n3.^2),z,zz);cc= (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));x4 = (s4 + s0).*cos(c)-e*sin(c);y4 = (s0 +s4).*sin(c) - e*cos(c);n4 = diff(x4);m4 = diff(y4);xt4= subs(x4 + (r*m4)./sqrt(m4.^2+n4.^2),c,cc);yt4 =subs( y4 - (r*n4)./sqrt(m4.^2+n4.^2),c,cc);dd=(14*pi/9):(pi/1000):( 2*pi);s5 =0;x5 = (s5 + s0).*cos(d)-e*sin(d);y5 = (s0 +s5).*sin(d) - e*cos(d);n5 = diff(x5);m5 = diff(y5);xt5= subs(x5 + (r*m5)./sqrt(m5.^2+n5.^2),d,dd);yt5 =subs( y5 - (r*n5)./sqrt(m5.^2+n5.^2),d,dd);plot(xt1,yt1,'b',xt2,yt2,'b',xt3,yt3,'b',xt4,yt4,'b',xt5,yt5,'b')for i=1:3601if yy(1,i)<=y0/2s(1,i)=2*h*(yy(i)./y0).^2;v(1,i)=4*h*w*yy(i)./(y0.^2);a(1,i)=4*h*w.^2./(y0.^2);elseif yy(1,i)>y0/2 && yy(1,i)<y0s(1,i)=h-2*h./y0.^2.*(y0-yy(i)).^2;v(1,i)=4*h*w*(y0-yy(i))./(y0.^2);a(1,i)=-4*h*w.^2./(y0.^2);elseif yy(1,i)>=y0 && yy(1,i)<y0+yss(1,i)=h;v(1,i)=0;a(1,i)=0;elseif yy(1,i)>=y0+ys && yy(1,i)<y0+ys+y01s(1,i)=h/2*(1+cos(pi/y01*(yy(1,i)-y0-ys)));v(1,i)=-pi*h*w/2/y01*sin(pi/y01*(yy(1,i)-y0-ys));a(1,i)=-pi^2*h*w^2/2/y01^2*cos(pi/y01*(yy(1,i)-y0-ys)); elseif yy(1,i)>=y0+ys+y01 && yy(1,i)<=360s(1,i)=0;v(1,i)=0;a(1,i)=0;subplot(2,3,5) ;plot(x,y,'r',xt,yt,eex,eey,'g',r0x,r0y,'k')%画图title('实际理论轮廓线')axis equal%使坐标轴比例相等grid on%画网格线。
哈工大机械原理大作业24题

班级1013102学号 6机械原理大作业说明书题目 1、连杆机构运动分析2、凸轮机构设计3、齿轮传动设计学生姓名1连杆机构运动分析1.设计题目:一、先建立如下坐标系:二、划分杆组如下,进行结构分析:该机构由I级杆组RR(如图1)、II级杆组RPR(如图2、3)和II级杆组RRP(如图4)组成。
(1)(2)(3)(4)三、运动分析数学模型:(1)同一构件上点的运动分析:如右图所示的原动件1,已知杆1的角速度=10/rad s ω,杆长1l =170mm,A y =0,A x =110mm 。
可求得下图中B 点的位置B x 、B y ,速度xB v 、yB v ,加速度xB a 、yB a 。
θcos 1l xB =,θsin 1l yB =θωυsin 1l xB -=,θωυcos 1l yB =,222B2==-cos =-B xB i d x a l x dt ωϕω2222==-sin =-B yB i B d y a l y dtωϕω。
(2)RPRII 级杆组的运动分析:a. 如右图所示是由2个回转副和1个移动副组成的II 级组。
已知两个外运动副C 、B 的位置(B x 、B y 、c x =110mm 、C y =0)、速度(xB υ,yB υ,xC υ=0,yC υ=0)和加速度(0,0,,==yC xC yB xB a a a a )。
可确定下图中D 点的位置、速度和加速度。
确定构件3的角位移1ϕ、角速度1ω、角加速度1α。
1sin 31..ϕϕl x dtdx C B-= 1sin 131cos 13.....2ϕϕϕϕl l x dt x d C B --= 1cos 31..ϕϕl y dtdy C B+=1cos 131sin 13.....2ϕϕϕϕl l y dt y d C B +-= 根据关系:1111d 122..11.αϕϕωϕϕ====dtd dt , 故可得出:D x =)1cos(4βϕ++l x C D y =)1sin(4βϕ++l y Cb. 如右图所示是由2个回转副和1个移动副组成的II级组。
哈工大机械原理大作业凸轮结构设计3

仅供个人参考Harbin Institute of Technology机械原理大作业二课程名称:机械原理设计题目:凸轮结构设计院系:机电工程学院班级:设计者:学号:指导教师:设计时间:哈尔滨工业大学1、设计题目2、凸轮机构推杆升程、回程运动方程,推杆位移、速度、加速度线图。
(1)推杆各行程运动方程(设定角速度为s s rad /2/1πω==)①从动件推程运动方程(650πϕ≤≤) ⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=ϕφπφω0012cos 1h v ; 代入数据,可得:②从动件远休程运动方程(πϕπ≤≤65) ③从动件回程运动方程(914πϕπ≤≤) 代入数据,可得:④从动件进休程运动方程(πϕπ2914≤≤) (2)、推杆位移、速度、加速度线图①推杆的位移线图如下②推杆的速度线图如下③推杆的加速度线图如下 3、凸轮机构的dss d ϕ-线图,并依次确定凸轮的基圆半径和偏距凸轮机构的s d ds -ϕ线图如下图所示 由图中范围选定点(-10,-50)为凸轮转轴O 点,则mm r 99.501050220=+=取基圆半径为r 0 =51mm ,偏距e = 10mm 。
4、滚子半径的确定及凸轮理论廓线和实际廓线的绘制由程序计算得凸轮理论轮廓线最小曲率半径mm r 51min = .由滚子半径选择范围∆-<min ρr r ,mm 5~3=∆得到滚子半径mm r r 46≤.又因为凸轮整体尺寸较小,此范围明显过大,故适当减小滚子半径,这里取半径为mm r r 12= .得到图线为:附录1.求位移、速度、加速度的程序(matlab )function f = tulunh=50;x1=150;t1=30;x2=100;t2=80;w=2*pi;x1=x1*pi/180;x2=x2*pi/180;t1=t1*pi/180;t2=t2*pi/180;%升程x=0:0.001:x1;s = h*(x/x1-sin(2*pi*x/x1)/(2*pi));v = h*w*(1-cos(2*pi*x/x1))/x1;a = 2*pi*h*w*w*sin(2*pi*x/x1)/(x1*x1);subplot(3,1,1),plot(x,s),hold onsubplot(3,1,2),plot(x,v),hold onsubplot(3,1,3),plot(x,a),hold on%远休x = x1:0.001:x1+t1;s = h;v=0;a=0;subplot(3,1,1),plot(x,s),hold onsubplot(3,1,2),plot(x,v),hold onsubplot(3,1,3),plot(x,a),hold on%回程x= x1+t1:0.001:x1+t1+x2;s = h*(1+cos(pi*(x-(x1+t1))/x2))/2;v = -pi*h*w*sin(pi*(x-(x1+t1))/x2)/(2*x2);a = -pi*pi*h*w*w*cos(pi*(x-(x1+t1))/x2)/(2*x2*x2);subplot(3,1,1),plot(x,s),hold onsubplot(3,1,2),plot(x,v),hold onsubplot(3,1,3),plot(x,a),hold on%近休x=x1+t1+x2:0.001:x1+x2+t1+t2;s = 0;v = 0;a = 0;subplot(3,1,1),plot(x,s),xlabel('φ/rad'),ylabel('S/mm'),title('位移-转角图线'),hold onsubplot(3,1,2),plot(x,v),xlabel('φ/rad'),ylabel('v/(mm/s)'),title('速度-转角图线'),hold onsubplot(3,1,3),plot(x,a),xlabel(φ/rad'),ylabel('a/(mm/s^2)'),title('加速度-转角图线'),hold on2.绘制凸轮机构s d ds -ϕ线图 function f= jiyuan;x1=150;t1=30;x2=100;t2=80;h=50;x1=x1*pi/180;x2=x2*pi/180;t1=t1*pi/180;t2=t2*pi/180;x= 0:0.001:150*pi/180;%升程 v/ws = h*(x/x1-sin(2*pi*x/x1)/(2*pi));k =-h*(1-cos(2*pi*x/x1))/x1;plot(k,s,'r'),hold on ;x=180*pi/180:0.001:280*pi/180;%回程 v/ws = h*(1+cos(pi*(x-(x1+t1))/x2))/2;k = pi*h*sin(pi*(x-(x1+t1))/x2)/(2*x2);plot(k,s,'g'),hold on ;%回程切线for i=-11:1:-11;f=@(k)k*tan(pi/6)+i;k =-40:0.1:50;s=f(k);plot(k,s),hold on ;end%升程切线for i=-45:0.2:-45;f=@(k)-k*tan(60*pi/180)+i;k =-40:0.1:50;s=f(k);plot(k,s),hold on ;endgrid onf=@(k)k*tan(50*pi/180);k=-50:0.1:0;s=f(k);plot(k,s),hold onxlabel('ds/d φ');ylabel('s(φ)');title('类速度-位移图线 ');plot(-10,-50,’o ’);3.绘制凸轮轮廓曲线function f= lunkuo;h=50;x1=150;t1=30;x2=100;t2=80;x1=x1.*pi./180;x2=x2.*pi./180;t1=t1.*pi./180;t2=t2.*pi./180;s0=51;e=10;rr=12;%升程x=0:pi/200:150.*pi/180;s = h.*(x./x1-sin(2.*pi.*x./x1)./(2.*pi));X1=(s0+s).*cos(x)-e.*sin(x);Y1=(s0+s).*sin(x)+e.*cos(x);%实际轮廓X11=X1-(rr.*(cos(x).*(s + s0) - e.*sin(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);Y11=Y1-(rr.*(sin(x).*(s + s0) + e.*cos(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);plot(X1,Y1,'r',X11,Y11,'r'),hold on;%远休x=150.*pi/180:pi/180:180.*pi/180;s=50;X2=(s0+s).*cos(x)-e.*sin(x);Y2=(s0+s).*sin(x)+e.*cos(x);X22=X2-(rr.*(cos(x).*(s + s0) - e.*sin(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);Y22=Y2-(rr.*(sin(x).*(s + s0) + e.*cos(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);plot(X2,Y2,'g',X22,Y22,'g'),hold on;%回程x=180.*pi/180:pi/180:280.*pi/180;s = h.*(1+cos(pi.*(x-(x1+t1))./x2))./2;X3=(s0+s).*cos(x)-e.*sin(x);Y3=(s0+s).*sin(x)+e.*cos(x);X33=X3-(rr.*(cos(x).*(s + s0) - e.*sin(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);Y33=Y3-(rr.*(sin(x).*(s + s0) + e.*cos(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);plot(X3,Y3,'k',X33,Y33,'k'),hold on;%近休x=280*pi/180:pi/180:2*pi;s=0;X4=(s0+s).*cos(x)-e.*sin(x);Y4=(s0+s).*sin(x)+e.*cos(x);X44=X4-(rr.*(cos(x).*(s + s0) - e.*sin(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);Y44=Y4-(rr.*(sin(x).*(s + s0) + e.*cos(x)))./((sin(x).*(s + s0) + e.*cos(x)).^2 + (cos(x).*(s + s0) - e.*sin(x)).^2).^(1./2);plot(X4,Y4,'b',X44,Y44,'b'),hold on;x=0:pi/200:2*pi;X4=(s0+s).*cos(x)-e.*sin(x); Y4=(s0+s).*sin(x)+e.*cos(x); plot(X4,Y4,'b');text(-40,90,'理论轮廓线');text(-40,72,'实际轮廓线');text(-5,55,'基圆');grid on;axis equal仅供个人用于学习、研究;不得用于商业用途。
哈工大机械原理大作业-凸轮机构设计

哈工大机械原理大作业-凸轮机构设计(第3题)(共15页)-本页仅作为预览文档封面,使用时请删除本页-机械原理大作业二课程名称:机械原理设计题目:凸轮设计院系:机电学院班级: 1208103完成者: xxxxxxx学号: xx指导教师:林琳设计时间:工业大学凸轮设计一、设计题目如图所示直动从动件盘形凸轮,其原始参数见表,据此设计该凸轮。
二、凸轮推杆升程、回程运动方程及其线图1 、凸轮推杆升程运动方程(650πϕ≤≤) 升程采用正弦加速度运动规律,故将已知条件mm h 50=,650π=Φ带入正弦加速度运动规律的升程段方程式中得:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=512sin 215650ϕππϕS ;⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=512cos 1601ππωv ; ⎪⎭⎫ ⎝⎛=512sin 14421ϕπωa ; 2、凸轮推杆推程远休止角运动方程(πϕπ≤≤65) mm h s 50==; 0==a v ;3、凸轮推杆回程运动方程(914πϕπ≤≤)回程采用余弦加速度运动规律,故将已知条件mm h 50=,95'0π=Φ,6s π=Φ带入余弦加速度运动规律的回程段方程式中得:⎥⎦⎤⎢⎣⎡-+=)(59cos 125πϕs ;()πϕω--=59sin451v ; ()πϕω-=59cos 81-a 21;4、凸轮推杆回程近休止角运动方程(πϕπ2914≤≤) 0===a v s ;5、凸轮推杆位移、速度、加速度线图根据以上所列的运动方程,利用matlab 绘制出位移、速度、加速度线图。
①位移线图 编程如下: %用t 代替转角 t=0::5*pi/6;s=50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)); hold on plot(t,s); t=5*pi/6::pi; s=50; hold on plot(t,s); t=pi::14*pi/9;s=25*(1+cos(9*(t-pi)/5));hold onplot(t,s);t=14*pi/9::2*pi;s=0;hold onplot(t,s),xlabel('φ/rad'),ylabel('s/mm'); grid onhold off所得图像为:②速度线图编程如下:%用t代替转角,设凸轮转动角速度为1t=0::5*pi/6;v=60/pi*(1-cos((12*t)/5));hold onplot(t,v);t=5*pi/6::pi;v=0;hold onplot(t,v);t=pi::14*pi/9;v=-45*sin(9*(t-pi)/5);hold onplot(t,v);t=14*pi/9::2*pi;v=0;hold onplot(t,v),xlabel('φ(rad)'),ylabel('v(mm/s)'); grid onhold off所得图像为:③加速度线图利用matlab编程如下:%用t代替转角,设凸轮转动角速度为1t=0::5*pi/6;a=144/pi*sin(12*t/5);hold onplot(t,a);t=5*pi/6::pi;a=0;hold onplot(t,a);t=pi::14*pi/9;a=-81*cos(9*(t-pi)/5);hold onplot(t,a);t=14*pi/9::2*pi; a=0; hold onplot(t,a),xlabel('φ(rad)'),ylabel('a(mm/s^2)'); grid on hold off所得图形:三、绘制s d ds -ϕ线图根据运动方程求得:()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤≤≤≤-≤≤≤≤--=πϕππϕππϕπϕππϕπππϕ2914.0914,59sin 4565,0650),512cos 6060(d ds 利用matlab 编程:%用t 代替φ,a 代替ds/d φ, t=0::5*pi/6;a=-(60/pi-60/pi*cos(12*t/5));s=50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)); hold on plot(a,s); t=5*pi/6::pi; a=0; s=50; hold on plot(a,s); t=pi::14*pi/9;a=45*sin(9*(t-pi)/5); s=25*(1+cos(9*(t-pi)/5)); hold on plot(a,s);t=14*pi/9::2*pi; a=0; s=0; hold onplot(a,s),title('ds/d φ-s'),xlabel('ds/d φ(mm/rad)'),ylabel('s(mm)'); grid on hold off 得s d ds-ϕ图:凸轮压力角的正切值s s e d ds +-=0/tan ϕα,左侧为升程,作与s 轴夹6π角等于升程许用压力角的切界线t t d D ,则在直线上或其左下方取凸轮轴心时,可使[]αα≤,同理右侧回程,作与s 轴夹角等于回程许用压力角3π的切界线''t t d D ,则在直线上或其右下方取凸轮轴心时,可使[]αα≤。
哈工大机械原理考研-第3章复习思考题与习题

3.4 复习思考与习题一、思考题1.从动件的常用运动规律有哪几种? 它们各有什么特点?各适用于什么场合?2.从动件运动规律的选择原则是什么?3.不同运动规律曲线拼接时应满足什么条件?4.凸轮机构的类型有哪些?在选择凸轮机构类型时应考虑那些因素?5.移动从动件盘形凸轮机构和摆动从动件盘形凸轮机构的设计方法各有什么特点?6.何谓凸轮的理论轮廓曲线?何谓凸轮的实际轮廓曲线?二者有和区别与联系?理论廓线相同而实际廓线不同的两个对心移动滚子从动件盘形凸轮机构,其从动件的运动规律是否相同?7.在移动滚子从动件盘形凸轮机构中,若凸轮实际廓线保持不变,而增大或减小滚子半径,从动件运动规律是否发生变化?8.何谓凸轮机构的压力角? 在凸轮机构设计中有何重要意义? 一般ϕ是怎样处理的?当凸轮廓线完成后,如何检查凸轮转角为时凸轮α的压力角? 若发现压力角超过需用值,可采取什么措施减少压力角?9.设计直动推杆盘形凸轮机构时,再推杆运动规律不变的条件下,需减小推程压力角,采用哪两种措施?10.何谓运动失真? 应如何避免出现运动失真现象?11.在移动滚子从动件盘形凸轮机构的设计中,采用偏置从动件的主要目的是什么? 偏置方向如何选取?12.在移动平底从动件盘形凸轮机构的设计中,采用偏置从动件的主要目的是什么? 偏置方向如何选取?13.何谓凸轮机构的偏心距,它对凸轮机构几何尺寸和受力情况有何影响?14.比较尖顶、平底和滚子从动件凸轮机构的优缺点及它们适用的场合?第3章 凸轮机构及其设计 93二、习题题3-1 如题3-1图所示为一尖顶移动从动件盘形凸轮机构从动件的部分运动线图。
试在图上补全各段的位移、速度及加速度曲线,并指出在那些位置会出现刚性冲击?那些位置会出现柔性冲击?题3-1图题3-2 已知凸轮以等角速度顺时针转动,从动件行程h=32 mm,从动件位移线图如题3-2图所示。
凸轮轴心偏于从动件轴线的右侧,ϕ-s 偏距e=10mm,基圆半径=35mm,滚子半径=15mm 。
哈工大机械原理大作业凸轮设计

哈工大机械原理大作业凸轮设计Harb inIn stituteofTech no logy大作业设计说明书课程名称:设计题目:院班学级:机械原理凸轮机构设计1208103系:机械设计制造及其自动化设计指导教师:设计时间:林琳2019425哈尔滨工业大学一、运动分析题目如图所示直动从动件盘形凸轮机构,其原始数据参数见表2-1,。
从表2-1中选择一组凸轮机构原始参数,据此设计该凸轮机构。
二、凸轮运动规律升程运动角(°)90升程运动规律生程许回程运用压力动角角(°)等加等4080减速回程运动规律回程许远休用压力止角角(°)余弦加7040速度近休止角(°)150升程(mm)1501 、升程运动规律(0 /4)位移s=2h(速度v2 /2 4*150*w( /2)A24*150*w A2( /2)人2加速度a2 、升程运动规律(/4 /2)位移s 1502*150( /2 )A2(/2)A2速度v4*60*w( /2 )( /2)A24*60*wA2( /2)A2加速度a3 、回程运动规律(/2 2/2 2 ) 93 位移s 75*{1 cos[ (/2 2 )]}949速度vhw*sin*[ ( /2 2 )]92*4 499加速度aA2hw A2cos[ ( /2 2 )]94 2*(4 )A299根据运动规律做出的曲线以及源代码如图所示位移线图速度线图加速度线图位移线图源代码fl=pi/180;x0=0:fl:pi/4;x1=pi/4:fl:pi/2;x2=pi/2:fl:13*pi/18;x3=13*pi/18:fl:7*pi/6;x4=7*pi/6:fl:2*pi;s0=300*(2*x0/pi)A 2;s1=150-1200*(pi/2-x1).*(pi/2-x1)/(pi.*pi);s2=150+x2*0;s3=75*(1+cos(9/4*(x3-13*pi/18)));s4=x4*0;Plot(x0,s0,x1,s1,'b',x2,s2,'b',x3,s3,'b',x4,s4,'b')axis([070200])title('杆位移线图')xlabel(' 0 (rad)')ylabel('V(mm⑸')gridon速度源代码fl=pi/180;x0=0:fl:pi/4;x1=pi/4:fl:pi/2;x2=pi/2:fl:13*pi/18;x3=13*pi/18: fl:7*pi/6;x4=7*pi/6:fl:2*pi;w=30;v0=600.*w.*x0/(pi/2)A2;v1=600.*w.*(pi/2-x1)/(pi/2)A2;v2=0*x2;v3=-150*30*pi/(2*4*pi/9).*si n(9/4*(x3-13*pi/18));v4=0*x4;Plot(x0,v0,'b',x1,v1,'b',x2,v2,'b',x3,v3,'b',x4,v4,'b')title('推杆速度')xlabel(' 0 (rad)')ylabel('v(mm/s')gridon加速度源代码fl=pi/180;x0=0:fl:pi/4;x1=pi/4:fl:pi/2;x2=pi/2:fl:13*pi/18;x3=13*pi/18: fl:7*pi/6;x4=7*pi/6:fl:2*pi; w=30;a0=600*w.A2/(pi/2).A2+xO*0;a 仁-600*w.A2/(pi/2)A2+x1*0;a2=x2*0; a3=-pi*pi*150*30*30/(2*4*pi/9)A2.*cos(9/4*(x3-13*pi/18));a4=x4*0;Plot(x0,a0,'b',x1,a1,'b',x2,a2,'b',x3,a3,'b',x4,a4,'b')title('推杆加速度')xlabel(' 0 (rad)')ylabel('a(mm/sA2')gridon三、凸轮机构的dss曲线绘制d由凸轮机构位移公式可知4h(/2)A2(0 /4)ds 4*60 ( /2 )( /4 /2)d ( /2)A275*4*s in 9( 13 )( /2 2 /2 2 4 ) 9418999 则其曲线如图所示其源代码如下clcfl=pi/180;x0=0:fl:pi/4;x1=pi/4:fl:pi/2;x2=pi/2:fl:13*pi/18;x3=13*pi/18: fl:7*pi/6;x4=7*pi/6:fl:2*pi;w=30;d0=-600.*x0/(pi/2)A2;d1=-600.*(pi/2-x1)/(pi/2)A2;d2=0*x2;d3=75*4/9.*si n(9/4*(x3-13*pi/18));d4=0*x4;s0=300*(2*x0/pi)A2;s1=150-1200*(pi/2-x1).*(pi/2-x1)/(pi.*pi);s2=150+x2*0;s3=75*(1+cos(9/4*(x3-13*pi/18)));s4=x4*0;Plot(d0,s0,'b',d1,s1,'b',d2,s2,'b',d3,s3,'b',d4,s4,'b')title(' 类速度-位移曲线')xlabel(' 类速度(mm/rad)')ylabel(' 位移(mmm)')gridon四、确定凸轮的基圆半径和偏距以ds/df-s图为基础,可分别作出二条限制线,以这二条线可确定最小基圆半径及所对应的偏距e,在其下方选择一合适点,即可满足压力角的限制条件图像如图所示由图像可知,设置点(50,-100 )为凸轮轴心位置。
哈工大机械原理大作业凸轮机构设计题
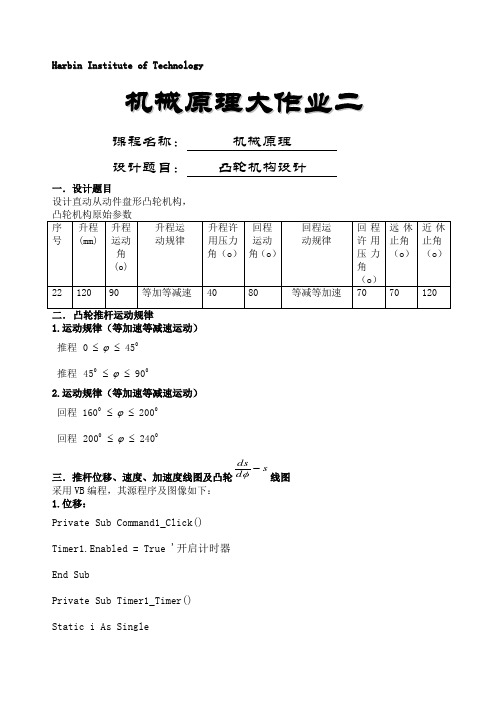
H a r b i n I n s t i t u t e o f T e c h n o l o g y机械原理大作业二课程名称: 机械原理 设计题目: 凸轮机构设计一.设计题目设计直动从动件盘形凸轮机构,1.运动规律(等加速等减速运动) 推程 0450≤≤ϕ 推程 009045≤≤ϕ2.运动规律(等加速等减速运动) 回程 00200160≤≤ϕ 回程 00240200≤≤ϕ三.推杆位移、速度、加速度线图及凸轮s d ds-φ线图采用VB 编程,其源程序及图像如下: 1.位移:Private Sub Command1_Click() Timer1.Enabled = True '开启计时器 End SubPrivate Sub Timer1_Timer() Static i As SingleDim s As Single, q As Single 'i作为静态变量,控制流程;s代表位移;q代表角度Picture1.CurrentX = 0Picture1.CurrentY = 0i = i + 0.1If i <= 45 Thenq = is = 240 * (q / 90) ^ 2Picture1.PSet Step(q, -s), vbRedElseIf i >= 45 And i <= 90 Thenq = is = 120 - 240 * ((90 - q) ^ 2) / (90 ^ 2)Picture1.PSet Step(q, -s), vbGreenElseIf i >= 90 And i <= 150 Thenq = is = 120Picture1.PSet Step(q, -s), vbBlackElseIf i >= 150 And i <= 190 Thenq = is = 120 - 240 * (q - 150) ^ 2 / 6400Picture1.PSet Step(q, -s), vbBlueElseIf i >= 190 And i <= 230 Thens = 240 * (230 - q) ^ 2 / 6400Picture1.PSet Step(q, -s), vbRedElseIf i >= 230 And i <= 360 Thenq = is = 0Picture1.PSet Step(q, -s), vbBlackElseEnd IfEnd Sub2.速度Private Sub Command2_Click()Timer2.Enabled = True '开启计时器End SubPrivate Sub Timer2_Timer()Static i As SingleDim v As Single, q As Single, w As Single 'i为静态变量,控制流程;q代表角度;w代表角速度,此处被赋予50Picture1.CurrentX = 0Picture1.CurrentY = 0w = 50i = i + 0.1If i <= 45 Thenv = 480 * w * q / 8100Picture1.PSet Step(q, -v), vbRedElseIf i >= 45 And i <= 90 Thenq = iv = 480 * w * (90 - q) / 8100Picture1.PSet Step(q, -v), vbBlack ElseIf i >= 90 And i <= 150 Thenq = iv = 0Picture1.PSet Step(q, -v), vbGreen ElseIf i >= 150 And i <= 190 Then q = iv = -480 * w * (q - 150) / 6400 Picture1.PSet Step(q, -v), vbBlue ElseIf i >= 190 And i <= 230 Then q = iv = -480 * w * (230 - q) / 6400Picture1.PSet Step(q, -v), vbRed ElseIf i >= 230 And i <= 360 Then q = iv = 0ElseEnd IfEnd Sub3.加速度Private Sub Command3_Click()Timer3.Enabled = True '开启计时器End SubPrivate Sub Timer3_Timer()Static i As SingleDim a As Single, w As Single, q As Single 'i为静态变量,控制流程;a代表加速度;q代表角度;w代表角速度w = 50Picture1.CurrentX = 0Picture1.CurrentY = 0i = i + 0.1If i <= 45 Thenq = ia = 480 * w ^ 2 / 8100Picture1.PSet Step(q, -a), vbRedElseIf i >= 45 And i <= 90 Thenq = ia = -480 * w ^ 2 / 8100ElseIf i >= 90 And i <= 150 Thenq = ia = 0Picture1.PSet Step(q, -a), vbGreenElseIf i >= 150 And i <= 190 Thenq = ia = -480 * w ^ 2 / 6400Picture1.PSet Step(q, -a), vbBlueElseIf i >= 190 And i <= 230 Thenq = ia = 480 * w ^ 2 / 6400Picture1.PSet Step(q, -a), vbRedElseIf i >= 230 And i <= 360 Thenq = ia = 0Picture1.PSet Step(q, -a), vbBlackElseEnd IfEnd Sub4.ds/dq---dsPrivate Sub Command4_Click()Timer4.Enabled = True '开启计时器;建立坐标系Picture1.Scale (-400, -400)-(400, 400)End SubPrivate Sub Timer4_Timer()Static i As SingleDim x As Single, s As Single, q As Single, scaley As Single, t As Single 'i为静态变量,控制流程;x代表位移;s代表纵坐标ds/dq;q代表角度Picture1.CurrentX = 0Picture1.CurrentY = 0scaley = 1t = 3.14 / 180i = i + 0.1If i <= 45 Thenq = i * tx = 194.734 * qs = 240 * (2 * q / 3.14) ^ 2Picture1.PSet Step(x, -s), vbRedElseIf i >= 45 And i <= 90 Thenq = i * tx = 194.734 * (3.14 / 2 - q)s = 120 - 97.367 * (3.14 / 2 - q) ^ 2Picture1.PSet Step(x, -s), vbRedElseIf i >= 90 And i <= 150 Thenq = i * tx = 0s = 120 * scaleyPicture1.PSet Step(x, -s), vbRedElseIf i >= 150 And i <= 190 Thenq = i * tx = -246.46 * (q - 5 * 3.14 / 6)s = 120 - 123.23 * (q - 5 * 3.14 / 6) ^ 2 Picture1.PSet Step(x, -s), vbRedElseIf i >= 190 And i <= 230 Thenq = i * tx = -246.46 * (23 * 3.14 / 18 - q)s = 123.23 * (23 * 3.14 / 18 - q) ^ 2Picture1.PSet Step(x, -s), vbRedElseIf i >= 230 And i <= 360 Thenq = i * tx = 0s = 0Picture1.PSet Step(x, -s), vbRedElseEnd IfEnd Sub四.确定凸轮基圆半径和偏距1. 求切点转角在图中,右侧曲线为升程阶段的类速度-位移图,作直线Dt dt与其相切,且位移轴正方向呈夹角[ 1]=300,则切点处的斜率与直线D t d t的斜率相等,因为k Dtdt=tan600,右侧曲线斜率可以表示为:q;q=tan600继而求出切点坐标(337.272,292.084)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理大作业二课程名称: 机械原理 设计题目: 凸轮机构设计 院 系: 机电学院 班 级: 1208103 完 成 者: xxxxxxx 学 号: xx指导教师: 林琳 设计时间: 2014.5.2哈尔滨工业大学凸轮机构设计一、设计题目二、凸轮推杆升程、回程运动方程及其线图1 、凸轮推杆升程运动方程(650πϕ≤≤) 升程采用正弦加速度运动规律,故将已知条件mm h 50=,650π=Φ带入正弦加速度运动规律的升程段方程式中得:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=512sin 215650ϕππϕS ;⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=512cos 1601ππωv ; ⎪⎭⎫ ⎝⎛=512sin 14421ϕπωa ;2、凸轮推杆推程远休止角运动方程(πϕπ≤≤65) mm h s 50==; 0==a v ; 3、凸轮推杆回程运动方程(914πϕπ≤≤)回程采用余弦加速度运动规律,故将已知条件mm h 50=,95'0π=Φ,6s π=Φ带入余弦加速度运动规律的回程段方程式中得:⎥⎦⎤⎢⎣⎡-+=)(59cos 125πϕs ;()πϕω--=59sin451v ; ()πϕω-=59cos 81-a 21;4、凸轮推杆回程近休止角运动方程(πϕπ2914≤≤) 0===a v s ;5、凸轮推杆位移、速度、加速度线图根据以上所列的运动方程,利用matlab 绘制出位移、速度、加速度线图。
①位移线图 编程如下:%用t 代替转角t=0:0.01:5*pi/6;s=50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)); hold on plot(t,s);t=5*pi/6:0.01:pi; s=50; hold on plot(t,s);t=pi:0.01:14*pi/9;s=25*(1+cos(9*(t-pi)/5));hold onplot(t,s);t=14*pi/9:0.001:2*pi;s=0;hold onplot(t,s),xlabel('φ/rad'),ylabel('s/mm'); grid onhold off所得图像为:②速度线图编程如下:%用t代替转角,设凸轮转动角速度为1t=0:0.01:5*pi/6;v=60/pi*(1-cos((12*t)/5));hold onplot(t,v);t=5*pi/6:0.01:pi;v=0;hold onplot(t,v);t=pi:0.01:14*pi/9;v=-45*sin(9*(t-pi)/5);hold onplot(t,v);t=14*pi/9:0.01:2*pi;v=0;hold onplot(t,v),xlabel('φ(rad)'),ylabel('v(mm/s)'); grid onhold off所得图像为:③加速度线图利用matlab编程如下:%用t代替转角,设凸轮转动角速度为1t=0:0.01:5*pi/6;a=144/pi*sin(12*t/5);hold onplot(t,a);t=5*pi/6:0.01:pi;a=0;hold onplot(t,a);t=pi:0.01:14*pi/9;a=-81*cos(9*(t-pi)/5);hold onplot(t,a);t=14*pi/9:0.01:2*pi;a=0;hold onplot(t,a),xlabel('φ(rad)'),ylabel('a(mm/s^2)'); grid on hold off所得图形:三、绘制s d ds -ϕ线图根据运动方程求得: 利用matlab 编程:%用t 代替φ,a 代替ds/d φ, t=0:0.01:5*pi/6;a=-(60/pi-60/pi*cos(12*t/5));s=50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)); hold on plot(a,s);t=5*pi/6:0.01:pi; a=0; s=50; hold on plot(a,s);t=pi:0.01:14*pi/9; a=45*sin(9*(t-pi)/5);s=25*(1+cos(9*(t-pi)/5)); hold on plot(a,s);t=14*pi/9:0.01:2*pi; a=0; s=0; hold onplot(a,s),title('ds/dφ-s'),xlabel('ds/dφ(mm/rad)'),ylabel('s(mm)'); grid on hold off 得s d ds-ϕ图:凸轮压力角的正切值ss ed ds +-=0/tan ϕα,左侧为升程,作与s 轴夹6π角等于升程许用压力角的切界线t t d D ,则在直线上或其左下方取凸轮轴心时,可使[]αα≤,同理右侧回程,作与s 轴夹角等于回程许用压力角3π的切界线''t t d D ,则在直线上或其右下方取凸轮轴心时,可使[]αα≤。
在升程起始点,有S=0,0/=ϕd ds ,为保证此时[]αα≤,作直线00d B 与纵坐标夹角为6π,凸轮轴心只能在其线上或右下方选取。
三条限制线围成的下方阴影角区域为满足[]αα≤的凸轮轴心的公共许用区域。
编程求得公共许用区域: t0=0:0.001:5*pi/6; t1=5*pi/6:0.001:pi; t2=pi:0.001:14*pi/9; t3=14*pi/9:0.001:2*pi;a0=-(60/pi-60/pi*cos(12*t0/5)); a1=0;a2=45*sin(9*(t2-pi)/5); a3=0;s0=50*((6*t0)/(5*pi)-1/(2*pi)*sin(12*t0/5)); s1=50;s2=25*(1+cos(9*(t2-pi)/5)); s3=0;k1=-tan(pi/3);k2=tan(pi/6); x=-50:0.001:40; b=s0-k1.*a0; m=s2-k2.*a2; g=min(b); h=min(m); y1=k1*x+g; y2=k2*x+h;plot(x,y1,'c',x,y2,'b'); hold onx=-50:0.001:0;y3=tan(pi/2-pi/6)*x; plot(x,y3,'m'); hold onplot(a0,s0,'b',a1,s1,'g',a2,s2,'r',a3,s3,'c'),title('凸轮轴心位置确定'),xlabel('x(mm)'),ylabel('y(mm)'); grid on得到:则可取轴心为x=-10mm,,y=-40mm得:e=10mm ,mm 400=S ,mm S e o 2311.41r 202=+=四、绘制凸轮理论轮廓线以及基圆、偏距圆凸轮理论轮廓方程:ϕϕsin cos )(0e s s x ++-=; ϕϕcos sin )(0e s s y +++=;利用matlab 编程: t=0:0.001:5*pi/6;x=-(40+50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5))).*cos(t)+10*sin(t); y=(40+50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5))).*sin(t)+10*cos(t); hold on plot(x,y);t=5*pi/6:0.001:pi;x=-(40+50).*cos(t)+10*sin(t); y=(40+50).*sin(t)+10*cos(t); hold on plot(x,y);t=pi:0.001:14*pi/9;x=-(40+25*(1+cos(9*(t-pi)/5))).*cos(t)+10*sin(t); y=+(40+25*(1+cos(9*(t-pi)/5))).*sin(t)+10*cos(t); hold on plot(x,y);t=14*pi/9:0.001:2*pi;x=-(40).*cos(t)+10*sin(t);y=+(40).*sin(t)+10*cos(t);hold onplot(x,y);%绘制基园,用绿色线条表示t=0:0.001:2*pi;x=41.2310*cos(t);y=41.2310*sin(t);hold onplot(x,y,'g');%绘制偏距圆,用红色线条表示t=0:0.001:2*pi;x=10*cos(t);y=10*sin(t);hold onplot(x,y,'r'),title('凸轮理论廓线、基圆以及偏距圆'),xlabel('x(mm)'),ylabel('y(mm)');grid onhold off得到:五、确定滚子半径根据曲率半径公式:利用matlab编程如下:%t代替转角φ,p表示曲率半径t=0:0.001:5*pi/6;x=-(40+50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5))).*cos(t)+10*sin(t); y=(40+50*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5))).*sin(t)+10*cos(t); dx1=diff(x);dy1=diff(y);dx11=diff(x,2);dy11=diff(y,2);p=abs(sqrt((dx1.^2+dy1.^2).^3)/(dx1.*dy11-dy1.*dx11));hold onplot(t,p);t=5*pi/6:0.001:pi;x=-(40+50).*cos(t)+10*sin(t);y=(40+50).*sin(t)+10*cos(t);dx1=diff(x);dy1=diff(y);dx11=diff(x,2);dy11=diff(y,2);p=abs(sqrt((dx1.^2+dy1.^2).^3)/(dx1.*dy11-dy1.*dx11));hold on plot(t,p);t=pi:0.001:14*pi/9;x=-(40+25*(1+cos(9*(t-pi)/5))).*cos(t)+10*sin(t); y=+(40+25*(1+cos(9*(t-pi)/5))).*sin(t)+10*cos(t); dx1=diff(x); dy1=diff(y); dx11=diff(x,2); dy11=diff(y,2);p=abs(sqrt((dx1.^2+dy1.^2).^3)/(dx1.*dy11-dy1.*dx11)); hold on plot(t,p);t=14*pi/9:0.001:2*pi;x=-(40).*cos(t)+10*sin(t); y=+(40).*sin(t)+10*cos(t); dx1=diff(x); dy1=diff(y); dx11=diff(x,2); dy11=diff(y,2);p=abs(sqrt((dx1.^2+dy1.^2).^3)/(dx1.*dy11-dy1.*dx11)); hold on plot(t,p); hold offtitle('曲率半径ρ'),xlabel('φ(rad)'),ylabel('ρ(mm)'); grid on 得到:由图可知:m m 2311.41min =ρ,即基圆半径,又因为m m 5~3,min =∆∆-<其中ρr r ,综上,可取滚子半径为10mm 。
