圆的专题训练

合集下载

圆的问题专题

专题-圆的问题专题知识回顾一、与圆有关的概念与规律1．圆：平面上到定点的距离等于定长的所有点组成的图形叫做圆。

定点称为圆心，定长称为半径。

圆的半径或直径决定圆的大小，圆心决定圆的位置。

2.圆的性质：（1）圆具有旋转不变性；（2）圆具有轴对称性；（3）圆具有中心对称性。

3.垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。

4．推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．5．圆心角：顶点在圆心上的角叫做圆心角。

圆心角的度数等于它所对弧的度数。

6．在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等。

在同圆或等圆中，如果两条弧相等，那么他们所对的圆心角相等，所对的弦相等，所对的弦心距也相等。

在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角相等，所对的弧相等，所对的弦心距也相等。

7.圆周角：顶点在圆周上，并且两边分别与圆相交的角叫做圆周角。

8.在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．9．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．10. 点和圆的位置关系：① 点在圆内点到圆心的距离小于半径② 点在圆上点到圆心的距离等于半径③ 点在圆外点到圆心的距离大于半径11. 过三点的圆：不在同一直线上的三个点确定一个圆。

12. 外接圆和外心：经过三角形的三个顶点可以做一个圆，这个圆叫做三角形的外接圆。

外接圆的圆心，叫做三角形的外心。

外心是三角形三条边垂直平分线的交点。

外心到三角形三个顶点的距离相等。

13．若四边形的四个顶点都在同一个圆上，这个四边形叫做圆内接四边形，这个圆叫做这个四边形的外接圆。

14．圆内接四边形的特征：⇔⇔⇔①圆内接四边形的对角互补；②圆内接四边形任意一个外角等于它的内对角。

15.直线与圆有3种位置关系：如果⊙O 的半径为r ，圆心O 到直线的距离为d ，那么① 直线和⊙O 相交；② 直线和⊙O 相切；③ 直线和⊙O 相离。

专题训练. 圆的基本性质--八大题型总结(拔尖篇)- 九年级数学上册 (浙教版)

专题3.12圆的基本性质章末八大题型总结（拔尖篇）【题型1动态图形的扫过的面积的计算】（2023秋·江苏·九年级专题练习）2．如图，半圆O的直径时停止滑动，若M是（2023·黑龙江鸡西·校考三模）3．在平面直角坐标系中，已知()2,0A ，()3,1B ，()1,3C ；(1)将ABC 沿x 轴负方向平移2个单位至111A B C △，画图并写出1C 的坐标____________；(2)以1A 点为旋转中心，将111A B C △逆时针方向旋转90︒得22A B C 1△，画图并写出2C 的坐标_____；(3)在平移和旋转过程中线段BC 扫过的面积为___________．（2023秋·浙江·九年级专题练习）4．如图所示，扇形OAB 从图①无滑动旋转到图②，再由图②到图③，60O ∠=︒，1OA =．(1)求O 点运动的路径长；(2)求O 点走过路径与射线l 围成的面积．【题型2圆周角定理有关的计算与证明】【方法点拨】圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．推论1：同弧或等弧所对的圆周角相等．推论2：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径（2023秋·北京西城·九年级北京八中校考期中）5．如图，已知：过O 上一点A 作两条弦AB 、AC ，且45BAC ∠=︒，(AB ，AC 都不经过)O 过A 作AC 的垂线AF 交O 于D ，直线BD ，AC 交于点E ，直线BC ，DA 交于点F ．(1)证明：BE BF =；(2)探索线段AB 、AE 、AF 的数量关系，并证明你的结论．（2023秋·湖北·九年级期末）6．已知ABC 内接于O ，BAC ∠的平分线交O 于点D ，连接DB ，DC ．(1)如图①，当120BAC ∠=︒时，请直接写出线段(2)如图②，当90BAC ∠=︒时，试探究线段(1)求ADB ∠的度数；(2)求AC 的长度；(3)判定四边形AFBC 的形状，并证明你的结论．（2023秋·江苏盐城·九年级统考期中）8．如图，在O 的内接四边形(1)若75DAE ∠=︒，则(2)过点D 作DE AB ⊥(3)若62AB AE ==、【题型3垂径定理的实际应用】【方法点拨】垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．推论：平分弦(不是直径条弧．（2023秋·河北石家庄9．如图是一位同学从照片上剪切下来的海上日出时的画面，圆的半径为5厘米，上”太阳与海平线的位置关系是（2023秋·浙江台州·10．我市在创建全国文明城市检查中，发现一些破旧的公交车候车亭有碍观瞻，现已更换新的公交候车亭图2所示的是侧面示意图，FG为水平线段，PQ⊥FG，点H为垂足，FG=4m，FH=2.4m，点P在弧FG上，且弧FG所在的圆的圆心O到FG，PQ的距离之比为5：2，则PH的长约为多少米？（2023春·浙江台州·九年级台州市书生中学校考期中）11．如图这是我市某跨海大桥正侧面的照片，大桥的主桥拱为圆弧型，桥面AB长为800米，且与水面平行，小王用计算机根据照片对大桥进行了模拟分析，在桥正下方的水面上取一点P，在桥面AB上取点C，作射线PC交弧（主桥拱）于点D，右边画出了PC与PD关于AC长的函数图象，下列对此桥的判断不合理的是（）A．桥拱的最高点与桥面AB的实际距离约为210米B．桥拱正下方的桥面EF的实际长度约为500米C．拍摄照片时，桥面离水面的实际高度约为110米D．桥面上BF段的实际长度约200米(1)求该圆的半径；(2)若水面上涨导致圆被水面截得的弦【题型4由点与圆的位置关系求求最值】【方法点拨】解决此类问题关键要记住若半径为当d＝r时，点在圆上，当d＜（2023秋·江苏苏州·九年级苏州市振华中学校校考期中）13．如图，在平面直角坐标系中，已知点为半径的圆上运动，且始终满足（2023秋·山东泰安·九年级校联考期末）15．如图，点()34P P ，，半径为大值是（）A ．32B ．52（2023秋·河南驻马店·九年级平舆县第二初级中学校考期末）16．如图，Rt ABC 中，AB 的最小值为（2023秋·安徽淮北·九年级校考期末）的直径，18．如图，AB是O+的最小值为（点，则PC PDA．22B．2（2023秋·陕西渭南·九年级统考期末）19．如图，A、B是半圆O上的两点，的最小值为．（2023秋·广东广州·九年级校考期末）20．（1）如图①，在ABC 中，120A ∠= ，5AB AC ==．尺规作图：作ABC 的外接圆O ，并直接写出ABC 的外接圆半径R 的长．（2）如图②，O 的半径为13，弦24AB =，M 是AB 的中点，P 是O 上一动点，求PM 的最大值．（3）如图③所示，AB ，AC 、 BC是某新区的三条规划路，其中6km AB =，3km AC =，60BAC ∠= ， BC 所对的圆心角为60 ，新区管委会想在 BC路边建物资总站点P ，在AB ，AC 路边分别建物资分站点E 、F ，也就是，分别在 BC、线段AB 和AC 上选取点P 、E 、F ．由于总站工作人员每天都要将物资在各物资站点间按P E F P →→→的路径进行运输，因此，要在各物资站点之间规划道路PE 、EF 和FP ．为了快捷、环保和节约成本．要使得线段PE 、EF 、FP 之和最短，试求PE EF FP ++的最小值．（各物资站点与所在道路之间的距离、路宽均忽略不计）【题型6动点的运动轨迹长度计算】（2023秋·江苏连云港·九年级校考阶段练习）22．如图，已知90ABC ∠=︒停止，圆心O 运动的路程是（2023秋·江苏徐州·九年级校考阶段练习）23．如图，有一块长为4cm 、宽为3cm 的矩形木板在桌面上按顺时针方向无滑动地翻滚，木板上顶点化为12A A A →→，其中，第二次翻滚时被桌面上一个小木块挡住，使木板边沿滚到点2A 的位置经过的路径长为（）A ．10cmB ．3.5cm π（2023·浙江温州·校考三模）24．图1是挂桶式垃圾车的联动装置，通过钢轴先后作两次旋转移动垃圾桶，实现对垃圾桶提升和翻转，将垃圾桶内的垃圾自动收入车厢．图2，图110cm,AB =303cm,30cm BC CD ==【题型7正多边形与圆】【方法点拨】定义：正多边形的外接圆的圆心叫做这个正多边形的中心，外接圆的半径叫做正多边形的半径，正多边形每一边所对的圆心角叫做正多边形的中心角，中心正多边形的一边的距离叫做正多边形的边心距．（2023秋·山东淄博·九年级统考期末）25．已知四个正六边形如图摆放在图中，顶点A ，B ，C ，D ，E ，F 在圆上．若两个大正六边形的边长均为小正六边形的边长是（）A ．33-B ．2312-C ．312+D ．1312-（2023秋·河南驻马店·九年级统考期末）26．如图，已知O 的半径为4，则该圆内接正六边形ABCDEF 的边心距OG （① DF 的长为2π；②2DF OF =；③ODE 为等边三角形；④S 正八边形【题型8圆锥侧面积的相关计算】【方法点拨】解决此类问题掌握圆锥侧面积的计算公式是关键，并且能够灵活运用（2023秋·全国·九年级专题练习）29．小华的爸爸要用一块矩形铁皮加工出一个底面半径为缝（接缝忽略不计）()1你能求出这个锥形漏斗的侧面展开图的圆心角吗？()2如图，有两种设计方案，请你计算一下，哪种方案所用的矩形铁皮面积较少？（2023秋·江苏·九年级专题练习）31．如图是一张直角三角形卡片，DE⊥AB．若将该卡片绕直线DE旋转一周，则形成的几何体的表面积为（2023秋·全国·九年级专题练习）32．如图，在一张四边形ABCD的纸片中，、交于点E、径的圆分别与AB AD(1)求证：DC与A的切线；（要求：尺规作图，不写作法，保留作图痕迹）(2)过点B作A(3)若用剪下的扇形AEF围成一个圆锥的侧面，能否从剪下的两块余料中选取一块，剪出一个圆作为这个圆锥的底面？。

中考数学复习《圆》专题训练-附带有答案

中考数学复习《圆》专题训练-附带有答案一、选择题1．下列有关圆的一些结论：①平分弧的直径垂直于弧所对的弦；②平分弦的直径垂直于弦；③在同圆或等圆中，相等的弦所对的圆周角相等；④同弧或等弧所对的弦相等，其中正确的有（）A．①④B．②③C．①③D．②④2．在同一平面内，已知⊙O的半径为3cm，OP＝4cm，则点P与⊙O的位置关系是（）A．点P在⊙O圆外B．点P在⊙O上C．点P在⊙O内D．无法确定3．如图，AB是⊙O的直径，C是⊙O上一点．若∠BOC＝66°（）A．66°B．33°C．24°D．30°4．如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠CDA＝118°，则∠C的度数为（）A．32°B．33°C．34°D．44°5．如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=26°，则∠D等于（）A．26°B．48°C．38°D．52°6．如图，四边形ABCD内接于⊙O，∠C＝100°，那么∠A是（）A．60°B．50°C．80°D．100°7．如图，AB为⊙O的直径，C是⊙O上的一点，若∠BCO=35°，AO=2，则AC⌢的长度为（）A．29πB．59πC．πD．79π8．如图，点A、B、C、D、E都是⊙O上的点AC⌢=AE⌢，∠D=130°则∠B的度数为（）A．130°B．128°C．115°D．116°二、填空题9．半径为6的圆上，一段圆弧的长度为3π，则该弧的度数为°.10．如图，在△ABC中，∠ACB= 130°，∠BAC=20°，BC=2．以C为圆心，CB为半径的圆交AB于点D，则BD的长为.11．如图，⊙O是△ABC的外接圆，BC是⊙O的直径，AB=AC．∠ABC的平分线交AC于点D，交⊙O于点E，连结CE．若CE= √2，则BD的长为.12．如图，四边形ABCD为⊙O的内接四边形，若∠ADC=85°，则∠B=．13．如图，在△ABC中∠ACB=90°，O为BC边上一点CO=2.以O为圆心，OC为半径作半圆与AB边交π，则阴影部分的面积为.于E，且OE⊥AB.若弧CE的长为43三、解答题14．如图，AB是⊙O的直径，四边形ABCD内接于⊙O，OD交AC于点E，OD∥BC（1）求证：AD＝CD；（2）若AC＝8，DE＝2，求BC的长.15．如图，AB是⊙O的直径，F为⊙O上一点，AC平分∠FAB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.（1）求证：CD是⊙O的切线.（2）若DC＝3，AD＝9，求⊙O半径.⌢上一点，AG与DC的延长线交于点F．16．已知，如图，AB是⊙O的直径，弦CD⊥AB于点E，G是AC（1）如CD=8，BE=2，求⊙O的半径长；（2）求证：∠FGC=∠AGD．17．如图，在△ABC中AB=AC，以底边BC为直径的⊙O交两腰于点D，E .（1）求证：BD=CE；⌢的长.（2）当△ABC是等边三角形，且BC=4时，求DE18．如图，在△ABC中，经过A，B两点的⊙O与边BC交于点E，圆心O在BC上，过点O作OD⊥BC交⊙O 于点D，连接AD交BC于点F，且AC＝FC．（1）试判断AC与⊙O的位置关系，并说明理由；（2）若FC＝√3，CE＝1．求图中阴影部分的面积（结果保留π）．参考答案1．A2．A3．B4．C5．C6．C7．D8．C9．9010．2√311．2√212．95°π13．4√3−4314．（1）证明：∵AB是⊙O的直径∴∠ACB＝90°∵OD∥BC∴∠AEO＝∠ACB＝90°⌢＝CD⌢∴AD∴AD＝CD；（2）解：∵OD⊥AC，AC＝8AC＝4∴AE＝12设⊙O的半径为r∵DE＝2∴OE＝OD﹣DE＝r﹣2在Rt△AEO中，AE2+OE2＝AO2∴16+（r﹣2）2＝r2解得：r＝5∴AB＝2r＝10在Rt△ACB中，BC＝√AB2−AC2＝√102−82＝6∴BC的长为6.15．（1）证明：连接OC∵AC平分∠FAB∴∠FAC＝∠CAO∵AO＝CO∴∠ACO＝∠CAO∴∠FAC＝∠ACO∴AD∥OC∵CD⊥AF∴CD⊥OC∵OC为半径∴CD是⊙O的切线；（2）解：过点O作OE⊥AF于EAF，∠OED＝∠EDC＝∠OCD＝90°∴AE＝EF＝12∴四边形OEDC为矩形∴CD＝OE＝3，DE＝OC设⊙O的半径为r，则OA＝OC＝DE＝r∴AE＝9﹣r∵OA2﹣AE2＝OE2∴r2﹣（9﹣r）2＝32解得r＝5.∴⊙O半径为5.16．（1）解：连接OC．设⊙O的半径为R．∵CD⊥AB∴DE=EC=4在Rt △OEC中，∵OC2=OE2+EC2∴R2=(R−2)2+42解得R=5．（2）解：连接AD∵弦CD⊥AB̂ = AĈ∴AD∴∠ADC=∠AGD∵四边形ADCG是圆内接四边形∴∠ADC=∠FGC∴∠FGC=∠AGD．17．（1）证明：∵AB=AC∴∠B=∠C⌢=BE⌢∴CD⌢=CE⌢∴BD∴BD=CE；（2）解：连接OD、OE∵△ABC 是等边三角形∴∠B =∠C =60°∴∠COD =120°∴∠COD +∠BOE =∠COE +∠DOE +∠BOD +∠DOE =240° ∴∠DOE =240°−180°=60°∵BC =4∴⊙O 的半径为 2∴DE ⌢ 的长 =60π×2180=2π3 .18．（1）解：AC 与⊙O 的相切，理由如下∵AO =DO∴∠D =∠OAD∵CF =CA∴∠CAF =∠CFA又∵∠CFA =∠OFD∴∠CAF =∠OFD∵OD ⊥BC∴∠OFD +∠ODF =90°∴∠CAF +∠OAF =90°∴OA ⊥AC∵OA 是半径∴AC 是⊙O 的切线∴ AC 与⊙O 的相切；（2）解：过A 作AM ⊥BC 于M ，如图设OA=OE=r∵FC=√3，CE=1在Rt△CAO中AO=r，AC=FC=√3，OC=OE+EC=r+1AO2+AC2=OC2∴r2+(√3)2=(r+1)2解得r=1∴OC=OE+EC=2∴AO=12 OC∴∠C=30°∴∠AOC=60°∴∠AOB=180−∠AOC=120°在Rt△CAM中AM=12AC=12FC=√32∴S△AOB=12⋅OB⋅AM=12×1×√32=√34∴S扇形AOB=120360π×1=π3∴S阴影部分=S△AOB−S扇形AOB=π3−√34．。

初中数学圆形专题训练50题含(参考答案)

初中数学圆形专题训练50题含参考答案一、单选题1．如图，A ，B ，C 是⊙O 上的三点，且⊙ACB =35°，则⊙AOB 的度数是（）A ．35°B ．65°C ．70°D ．90°【答案】C 【分析】根据圆周角定理即可得．【详解】解：由圆周角定理得：223570AOB ACB ∠=∠=⨯︒=︒，故选：C ．【点睛】本题考查了圆周角定理，熟练掌握圆周角定理是解题关键．2．如图，在半径为R 的圆内作一个内接正方形，⊙然后作这个正方形的内切圆，又在这个内切圆中作内接正方形，依此作到第n 个内切圆，它的半径是（）A ．RB ．（12）RC ．（12）n －1RD ．n R3．如图，在ABC中，以A为圆心，任意长为半径画弧，分别交AB、AC于点M、N；再分别以M、N为圆心，大于12MN的长为半径画弧，两弧交于点P；连结AP并延长交BC于点D．则下列说法正确的是（）A．AD BD AB+<B．AD一定经过ABC的重心C．BAD CAD∠=∠D．AD一定经过ABC的外心【答案】C【分析】根据题意易得AD平分⊙BAC，然后根据三角形的重心、外心及三边关系可排除选项．【详解】解：⊙AD平分⊙BAC，⊙BAD CAD∠=∠，故C正确；在⊙ABD中，由三角形三边关系可得AD BD AB+>，故A错误；由三角形的重心可知是由三角形三条中线的交点，所以AD不一定经过ABC的重心，故B选项错误；由三角形的外心可知是由三角形三条边的中垂线的交点，所以AD不一定经过ABC的外心，故D选项错误；故选C．【点睛】本题主要考查三角形的重心、外心及角平分线的尺规作图，熟练掌握三角形的重心、外心及角平分线的尺规作图是解题的关键．4．如图，过⊙O上一点C作⊙O的切线，交⊙O直径AB的延长线于点D．若⊙D＝40°，则⊙A的度数为（）A．20°B．25°C．30°D．40°【点睛】此题主要考查了切线的性质，正确得出⊙DOC =50°是解题关键．5．如图，点A ，B ，C 在圆O 上，65∠=︒ABO ，则ACB ∠的度数是（）A ．50︒B ．25︒C ．35︒D ．20︒6．如图4，在Rt ABC △中，90C =∠，3AC =．将其绕B 点顺时针旋转一周，则分别以BA ，BC 为半径的圆形成一圆环．该圆环的面积为( )AB ．3πC ．3πD ．3π 【答案】C 【分析】根据勾股定理，得两圆的半径的平方差即是AC 的平方．再根据圆环的面积计算方法：大圆的面积减去小圆的面积，即9π．【详解】解：圆环的面积为πAB 2-πBC 2，=π（AB 2-BC 2），=πAC 2，=32π，=9π．故选C．7．已知水平放置半径为6cm的球形容器中装有溶液，容器内液面的面积为27πcm2，如图，是该球体的一个最大纵截面，则该截面O中阴影部分的弧长为（）A．2πcm B．4πcm C．6πcm D．8πcm意，灵活运用所学知识解决问题，属于中考常考题型．8．如图，点A，B，C都在圆O上，若⊙C=34°，则⊙AOB为（）A．34⊙B．56⊙C．60⊙D．68⊙【答案】D【分析】由题意直接根据圆周角定理中同圆同弧所对的圆周角等于这条弧所对的圆心角的一半进行分析即可求解．【详解】解：⊙⊙C=34°，⊙⊙AOB=2⊙C=68°．故选：D．【点睛】本题考查圆周角定理，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．9．下列命题中，真命题的个数是（）⊙同位角相等⊙经过一点有且只有一条直线与这条直线平行⊙长度相等的弧是等弧⊙顺次连接菱形各边中点得到的四边形是矩形．A．1个B．2个C．3个D．4个【答案】A【详解】解：两直线平行，同位角相等，⊙错误；经过直线外一点有且只有一条直线与这条直线平行，⊙错误；在同圆或等圆中，长度相等的弧是等弧，⊙错误；顺次连接菱形各边中点得到的四边形是矩形，⊙正确．故选A．【点睛】本题考查命题与定理．10．AB是⊙O的直径，PB、PC分别切⊙O于点B、C，弦CD AB∥，若PB＝AB＝10，则CD的长为（）A ．6B C ．D ．3 OCF CPE ，四边形12BE OF OF ==，【详解】解：过点⊙OCF CPE ， OF OC CE PC ＝， PB 、PC 分别切⊙O PB PC =，10PB AB ==，11．如图，AB 是O 的直径，ACD 是O 的内接三角形，若6AB =，105ADC ∠=︒，则BC 的长为（）A ．8πB ．4πC ．2πD ．π【答案】C【分析】连接OC 、BC ，根据四边形ABCD 是圆的内接四边形和⊙D 的度数，即可求出303602π=，【点睛】本题考查了圆内接四边形的性质、圆周角定理以及弧长公式等知识，根据圆12．将一把直尺、一个含60°角的直角三角板和一个光盘按如图所示摆放，直角三角板的直角边AD 与直尺的一边重合，光盘与直尺相切于点B ，与直角三角板相切于点C ，且3AB =，则光盘的直径是（）A ．6B ．C ．3D ．【答案】D13．如图，正五边形ABCDE，则⊙DAC的度数为()A．30°B．36°C．60°D．72°【答案】B【分析】根据正五边形和等腰三角形的性质即可得到结论.【详解】⊙在正五边形ABCDE中，AE＝DE＝AB＝BC，⊙E＝⊙B＝⊙EAB＝108°，⊙⊙EAD＝⊙BAC＝36°，⊙⊙DAC＝108°﹣36°﹣36°＝36°，故选：B.【点睛】此题考查正多边形和圆，等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．14．菱形对角线的交点为O，以O为圆心，以O到菱形一边的距离为半径的圆与其他几边的关系为（）A．相交B．相切C．相离D．不能确定【答案】B【分析】首先根据菱形的性质可知:菱形的对角线将菱形分成四个全等的直角三角形，故四个三角形面积相等且斜边相等，然后根据等面积法得出斜边的高相等，这样问题就容易解决了.【详解】如图：⊙菱形对角线互相垂直平分，⊙AO=CO，BO=DO，AB=BC=CD=DA.⊙⊙ABO⊙⊙BCO⊙⊙CDO⊙⊙DAO.⊙⊙ABO、△BCO、△CDO、△DAO的面积相等.又⊙AB=BC=CD=DA，⊙⊙ABO、△BCO、△CDO、△DAO斜边上的高相等.即O到AB、BC、CD、DA的距离相等.⊙O到菱形一边的距离为半径的圆与另三边的位置关系是相切.故选B..【点睛】本题考查了直线与圆的位置关系，解题的关键是画出图形进行分析.15．如图，已知AB是⊙O的直径，弦CD⊙AB于点E，G是弧AB的中点，连接AD，AG ，CD ，则下列结论不一定成立的是（）A ．CE =DEB ．⊙ADG =⊙GABC ．⊙AGD =⊙ADC D ．⊙GDC =⊙BAD 【答案】D 【详解】⊙AB 是⊙O 的直径，弦CD ⊙AB ，⊙CE =DE ，A 成立；⊙G 是AB 的中点，⊙AG BG =，⊙⊙ADG =⊙GAB ，B 成立；⊙AB 是⊙O 的直径，弦CD ⊙AB ，⊙AC AD =，⊙⊙AGD =⊙ADC ，C 成立；⊙GDC =⊙BAD 不成立，D 不成立，故选D ．16．如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板，该展板的部分示意图如图2所示，它是以O 为圆心，OA ，OB 长分别为半径，圆心角120O ∠=︒形成的扇面，若3m OA =， 1.5m OB =，则阴影部分的面积为（）A ．24.25m πB ．23.25m πC ．23m πD ．22.25m π【答案】D 【分析】根据S 阴影=S 扇形AOD -S 扇形BOC 求解即可．17．下列命题为真命题的是（）A ．同旁内角互补B ．三角形的外心是三条内角平分线的交点C ．平行于同一条直线的两条直线平行D ．若甲、乙两组数据中，20.8S =甲，2 1.4S =乙，则乙组数据较稳定【答案】C【分析】根据平行线的性质和判定，三角形的外心性质，方差一一判断即可．【详解】解：A 、两平行线被第三直线所截，同旁内角互补，原命题是假命题，不符合题意；B 、三角形的外心是三条边垂直平分线的交点，原命题是假命题，不符合题意；C 、平行于同一条直线的两条直线平行，是真命题，符合题意；D 、若甲、乙两组数据的平均数都是3，S 甲2=0.8，S 乙2=1.4，则甲组数据较稳定，原命题是假命题，不符合题意；故选：C ．【点睛】考查了命题与定理的知识，解题的关键是根据平行线的性质和判定，三角形的外心性质，方差解答．18．如图，C 为⊙O 直径AB 上一动点，过点C 的直线交⊙O 于D ，E 两点，且⊙ACD=45°，DF⊙AB 于点F ，EG⊙AB 于点G ，当点C 在AB 上运动时，设AF=x ，DE=y ，下列中图象中，能表示y 与x 的函数关系式的图象大致是( )A．B．C．D．19．如图，AB为⊙O的直径，AB＝AC，AC交⊙O于点E，BC交⊙O于点D，F为CE 的中点，连接DF.给出以下四个结论：⊙BD＝DC；⊙AD＝2DF；⊙BD DE；⊙DF是⊙O的切线.其中正确结论的个数是：（）A．4B．3C．2D．1【答案】B【详解】连接AD，OD，⊙AB是直径，⊙⊙ADB=⊙AEB=90°，又⊙AB=AC，⊙BD=DC，故⊙正确；⊙F是CE中点，BD=CD，⊙BE//DF，BE=2DF，但没有办法证明AD与BE相等，故⊙错误；⊙AB=AC，BD=CD，⊙⊙BAD=⊙CAD，⊙BD=DE，⊙BD=DE，故⊙正确；⊙⊙AEB=90°，⊙⊙BEC=180°-⊙AEB=90°，⊙BE//DF，⊙⊙DFC=⊙BEC=90°，⊙O为AB的中点，D为BC的中点，⊙OD//AC，⊙⊙ODF=⊙DFC=90°，⊙OD是半径，⊙DF是⊙O的切线，故⊙正确，所以正确的结论有3个，故选B.【点睛】本题主要考查了圆周角定理，切线的判定，等腰三角形的性质、三角形的中位线等，能根据具体的图形选择和灵活运用相关性质解题是关键.二、填空题20．如图，若正五边形和正六边形有一边重合，则⊙BAC＝_____．【答案】132°##132度【详解】解：⊙正五边形的内角=180°-360°÷5=108°，正六边形的内角=180°-360°÷6=120°，⊙⊙BAC=360°－108°－120°=132°．故答案为132°．21．已知直角⊙ABC中，⊙C=90°，BC=3，AC=4，那么它的内切圆半径为_______.【答案】1【分析】O分别与BC、AC、AB切于点D、E、F，连接OD、OE、OF，由切线的性质可得：⊙ODC=⊙OEC=90°，设OD=OE=r根据正方形的判定即可证出四边形OECD是正方形，从而得出：EC=CD=OD=OE=r，再根据切线长定理可得：BF=BD =3－r，AF=AE =4－r，再根据勾股定理求出AB，利用AB的长列方程即可.【详解】解：如图所示，O分别与BC、AC、AB切于点D、E、F，连接OD、OE、OF⊙⊙ODC=⊙OEC=90°22．如图，AB ，BC ，CD 分别与⊙O 相切于E ，F ，G ，BE ＝4，CG ＝6，则BC ＝_______．【答案】10【分析】从圆外一点可以引圆的两条切线，它们的切线长相等，据此分析解答．【详解】⊙AB ，BC ，CD 分别与⊙O 相切于E ，F ，G ，BE ＝4，CG ＝6，⊙BF ＝BE ＝4，CF ＝CG ＝6，⊙BC ＝BF ＋FC ＝10，故填：10．【点睛】此题主要是综合运用了切线长定理和切线的性质定理．23．若一个扇形的圆心角为60︒，面积为26cm π，则这个扇形的弧长为__________ cm（结果保留π）24．如图，在O 中，弦AC =B 是圆上一点，且=45ABC ∠︒,则O 的半径R =_____．25．如图，⊙O 的内接四边形ABCD 中，⊙A =45°，则⊙C 的度数 _____________ ．【答案】135°【分析】根据圆内接四边形的对角互补可得结论．【详解】∵⊙O的内接四边形ABCD中，⊙A＝45°，⊙⊙C＝135°．故答案为135°．【点睛】本题考查了圆内接四边形，关键是掌握圆内接四边形的性质：①圆内接四边形的对角互补．②圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）．26．如图，四边形ABCD内接于⊙O，E是BC延长线上一点，若⊙BAD=105°，则⊙DCE的度数是________°．【答案】105【详解】⊙四边形ABCD是圆内接四边形，⊙⊙DAB+⊙DCB=180°，⊙⊙BAD=105°，⊙⊙DCB=180°﹣⊙DAB=180°﹣105°=75°，⊙⊙DCB+⊙DCE=180°，⊙⊙DCE=⊙DAB=105°．故答案为10527．如图，圆O的半径OA=5cm，弦AB=8cm，点P为弦AB上一动点，则点P到圆心O的最短距离是____cm．【答案】3【分析】由当OP⊙AB时，OP最短，根据垂径定理，可求得AP的长，然后由勾股定28．如图，在矩形ABCD 中，AB a ，BC b =，点P 是BC 上的一个动点，连接AP ，把PAB 沿着AP 翻折到⊙PB C '（点B '在矩形的内部），连接B C '，B D '．点P 在整个运动过程中，若存在唯一的位置使得⊙B CD 为直角三角形，则a ，b 之间的数量关系是 __．为直径作O ，当点为直角三角形且唯一，在Rt ADO 中，根据22OD OA ，可得，计算可得答案．为直径作O ，当点到O 的最小距离等于得B CD '为直角三角形且唯一，Rt ADO 中，2AD OD +22211())22b a a +=+，整理得22b =，a>，∴=2b29．尺规作图特有的魅力曾使无数人沉湎其中，传说拿破仑通过下列尺规作图考他的大臣：⊙将半径2的⊙O六等分，依次得到A，B，C，D，E，F六个分点；⊙分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；⊙连结OG.问：OG的长是多少？大臣给出的正确答案是_________2222OA，(23)222.【点睛】本题考查了圆周角定理，等腰三角形三线合一的性质以及勾股定理解直角三30．半径为O是锐角三角形ABC的外接圆，AB=AC，连接OB、OC，延长CO交弦AB于点D．若⊙OBD是直角三角形，则弦BC的长为_______________．31．如图，P A，PB是⊙O的切线，A，B是切点，点C是⊙O上异于A、B的一点，若⊙P＝40°，则⊙ACB的度数为_________________.【答案】110°【分析】连接OA，OB，在优弧AB上任取一点D（不与A、B重合），连接BD，AD，如图所示，由PA与PB都为圆O的切线，利用切线的性质得到OA与AP垂直，OB与BP垂直，在四边形APBO中，根据四边形的内角和求出⊙AOB的度数，再利用同弧所对的圆周角等于所对圆心角的一半求出⊙ADB的度数，再根据圆内接四边形的对角互补即可求出⊙ACB的度数．【详解】连接OA，OB，在优弧AB上任取一点D（不与A、B重合），连接BD，AD，如图所示：⊙PA、PB是⊙O的切线，⊙OA⊙AP，OB⊙BP，⊙⊙OAP=⊙OBP=90°，又⊙⊙P=40°，⊙⊙AOB=360°-（⊙OAP+⊙OBP+⊙P）=140°，32．如图，矩形ABCD 中，6AB =，9BC =．将矩形沿EF 折叠，使点A 落在CD 边中点M 处，点B 落在N 处．连接EM ，以矩形对称中心O 为圆心的圆与EM 相切于点P ，则圆的半径为________．33．如图，正方形ABCD内接于⊙O，线段MN在对角线BD上运动，若⊙O的面积为2π，MN＝1，则AMN周长的最小值为________．34．如图所示，在⊙O 中，AB 是⊙O 的直径，⊙ACB 的角平分线CD 交⊙O 于D ，则⊙ABD=_________ 度．【答案】45.【详解】试题解析：⊙CD 平分⊙ACB⊙⊙ACD=⊙BCD=45°⊙⊙ABD=⊙ACD=45°．考点：圆周角定理．35．如图，在平面直接坐标系xOy 中，()40A ，，()03B ，，()43C ，，I 是ABC ∆的内心，将ABC ∆绕原点逆时针旋转90°后，I 的对应点'I 的坐标为________．【答案】（-2，3）【分析】直接利用直角三角形的性质得出其内切圆半径，进而得出I点坐标，再利用旋转的性质得出对应点坐标．【详解】解：过点作IF⊙AC于点F，IE⊙OA于点E，⊙A（4，0），B（0，3），C（4，3），⊙BC=4，AC=3，则AB=5，⊙I是⊙ABC的内心，⊙I到⊙ABC各边距离相等，等于其内切圆的半径，⊙IF=1，故I到BC的距离也为1，则AE=1，故IE=3-1=2，OE=4-1=3，则I（3，2），⊙⊙ABC绕原点逆时针旋转90°，⊙I的对应点I'的坐标为：（-2，3）．故答案为：（-2，3）．【点睛】此题主要考查了旋转的性质以及直角三角形的性质，得出其内切圆半径是解题关键．36．一个半径为4cm的圆内接正六边形的面积等于_______cm2．S=ABC⊙内接正六边形的面积是故答案是：37．圆心角为40°，半径为2的扇形面积为________．38．如图，在半圆O中，直径AE=10，四边形ABCD是平行四边形，且顶点A、B、C在半圆上，点D在直径AE上，连接CE，若AD=8，则CE长为_____【答案】【详解】连接OC，过O点作BC垂线，设垂足为F，根据垂径定理、勾股定理可以得到OC=5，CF=4，OF=3，在等腰三角形CDE中，高=OF=3，底边长DE=10-8=2，根据勾股定理即可求出CE．解：连接OC，过O点作OF⊙BC，垂足为F，交半圆与点H，⊙OC=5，BC=8，⊙根据垂径定理CF=4，点H为弧BC的中点，且为半圆AE的中点，⊙由勾股定理得OF=3，且弧AB=弧CE⊙AB=CE，又⊙ABCD为平行四边形，⊙AB=CD，⊙CE=CD，⊙⊙CDE为等腰三角形，在等腰三角形CDE中，DE边上的高CM=OF=3，⊙DE=10-8=2，⊙由勾股定理得，CE2=OF2+（DE）2，⊙CE=，故答案为．本题考查了勾股定理和垂径定理以及平行四边形的性质，是基础知识要熟练掌握．39．如图，⊙O是⊙ABC的外接圆，连接OB、OC，若OB=BC，则⊙BAC的度数是_____．三、解答题40．如图，AB是⊙O的直径，C是半圆上的一点，CD是⊙O的切线，AD⊙CD于点D，交⊙O于点E.（1）求证：AC平分⊙DAB；（2）若点E为弧AC的中点，⊙O的半径为1，求图中阴影部分的面积.41．如图，AB是⊙O的直径，点C、E位于⊙O上AB两侧．在BA的延长线上取点D，使⊙ACD＝⊙B．（1）求证：DC是⊙O的切线；（2）当BC＝EC时，求证：AC2＝AE•AD；（3）在（2）的条件下，若BC＝AD：AE＝5：9，求⊙O的半径．【点睛】本题考查了切线的判定，圆周角定理，相似三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．42．如图，已知、是⊙的切线，、为切点．直径的延长线与的延长线交于点．（1）求证：；（2）若，．求图中阴影部分的面积（结果保留根号与）．【答案】（1）证明见解析；（2）.【详解】试题分析：（1）连接，根据是⊙的切线，由切线长定理得到AP=BP,OP平分⊙APB，根据等腰三角形的性质三线合一得到OP⊙AB，再根据AC是⊙O的直径，得到⊙ABC=90°，即AB⊙BC，BC⊙OB，得到内错角相等，由等量代换得到结果.（2）根据切线长定理和三角形全等，S△OPA=S△OPB，通过解直角三角形得到OB,PB,再根据三角形的面积和扇形的面积推出结论.试题解析：(1)证明：连接. 1分⊙是⊙的切线,⊙平分. 2分.⊙是⊙的直径,⊙, 即：. 3分⊙.⊙. 4分,⊙. 5分(2) 连接.⊙，⊙⊙、是⊙的切线，⊙，，又⊙⊙⊙⊙.⊙. 6分在中，,. 7分在中，,⊙. 8分⊙.⊙,.⊙. 9分⊙所求的阴影面积：. 10分考点：1.切线的性质；2.扇形面积的计算.43．数学课上，王老师画好图后并出示如下内容：“已知AB为O的直径，O过AC 的中点D．DE为O的切线．(1)求证：DE BC ⊥(2)王老师说：如果添加条件“1DE =，1tan 2C =”，则能求出O 的直径．请你写出求解过程．DE 为O 的切线，OD DE ∴⊥，即∠AB 为O 的直径，OA OB ∴=，即点点D 为AC 的中点，OD BC ∴∥，CED ODE ∴∠=∠=BC ．DE BC ⊥1tan DE CE ∴=O∴的直径为【点睛】本题考查了圆的切线的性质、圆周角定理、三角形中位线定理、解直角三角形等知识点，熟练掌握圆的切线的性质和圆周角定理是解题关键．44．如图，点A、B、C分别是⊙O上的点，⊙B=60°，AC=3，CD是⊙O的直径，P是CD延长线上的一点，且AP=AC．（1）求证：AP是⊙O的切线；（2）求PD的长．45．如图，在O 中，弦AB 与CD 相交于点E ，AB CD =，连接AD BC ，，25ADC ∠=︒．(1)求证：AD BC =；(2)求证：AE CE =；(3)若弦BD 经过点O ，求BEC ∠的度数．【答案】(1)见解析(2)见解析(3)65︒【分析】（1）由AB CD =，推出AB CD =，推出BC AD =；（2）证明AED CEB ≌可得结论；（3）先求出90BCD ︒∠=，再求出25CBE，即可得答案．【详解】（1）解：AB CD =，C ABD ∴=， AB AC CD AC ∴-=-，BC AD ∴=；（2）BC AD ，BC AD ∴=，ADE ∠和CBE ∠都是AC 的圆周角，ADE CBE ∴∠=∠，AED CEB ，AED CEB ∴≌，AE CE ∴=；（3）25ADC ，25CBE ，弦BD 经过点O ，BD ∴是O 的直径，90BCD ︒∴∠=，⊙在CEB 中，18065BEC BCD CBE ．【点睛】本题考查了圆心角、弧、弦之间的关系，全等三角形的判定和性质，直径所对的圆周角是90︒，三角形的内角和，解题的关键是正确寻找全等三角形解决问题． 46．如图，在ABC 中，90ABC ∠=，O 是AB 上一点，以O 为圆心OB 为半径的圆与AB 交于点E ，与AC 交于点D ，连接DE 、DE 、OC ，且//DE OC ．()1求证：AC 是O 的切线；()2若8DE OC ⋅=，求O 的半径．【答案】（1）证明见解析；（2）2. 【分析】（1）先由OD=OE ，利用等边对等角可得⊙2=⊙3，再利用DE⊙OC ；进而利用平行线的性质，可得⊙3=⊙4，⊙1=⊙2，等量代换可得⊙1=⊙4；再结合OB=OD ，OC=OC ，利用SAS 可证△DOC⊙⊙BOC ，那么⊙CDO=⊙CBO ，而⊙ABC=90°，于是⊙CDO=90°，即CD 是 O 的切线；（2）由（1）可知⊙2=⊙4，而⊙CDO=⊙BDE=90°，易证△CDO⊙⊙BDE ，可得比例线段，OD ：DE=OC ：BE ，又BE=2OD ，可求OD ．【详解】()1证明：连接OD ，⊙OE OD =，⊙23∠=∠，又⊙//DE OC ，⊙12∠=∠，34∠=∠，⊙14∠=∠；在DOC 和BOC 中，OD OB =，14∠=∠，OC OC =，⊙DOC BOC ≅，⊙CDO CBO ∠=∠；⊙90ABC ∠=，⊙90CDO ∠=，⊙CD 是O 的切线；()2⊙BE 是直径，⊙90BDE ∠=，在COD 和BED 中，24∠=∠，90EDB ODC ∠=∠=，⊙COD BED ∽，⊙::OD DE OC BE =；又⊙2BE OD =，⊙22OD DE OC =⋅，⊙2OD =．【点睛】考查了等边对等角，平行线的性质，全等三角形的判定与性质，切线的判定，直径所对的圆周角是直角，相似三角形的判定与性质.综合性比较强，难度较大. 47．已知：对于平面直角坐标系xOy 中的点P 和O ，O 的半径为4，交x 轴于点A ，B ，对于点P 给出如下定义：过点C 的直线与O 交于点M ，N ，点P 为线段MN 的中点，我们把这样的点P 叫做关于MN 的“折弦点”．(1)若()2,0C -⊙点()10,0P ，()21,1P -，()32,2P中是关于MN 的“折弦点”的是______；⊙若直线y kx =0k ≠）上只存在一个关于MN 的“折弦点”，求k 的值；(2)点C 在线段AB 上，直线y x b =+上存在关于MN 的“折弦点”，直接写出b 的取值范围．与D相交或相切，分两种情况利用勾股定理求出【详解】（1））与D相切，与D相交或相切，=+垂直直线y xy轴交于点重合时，b有最大值，此时48．如图1，AB 为O 的直径，C 为O 上一点，连接CB ，过C 作CD AB ⊥于点D ，过点C 作BCE ∠，使BCE BCD ∠=∠，其中CE 交AB 的延长线于点E ．(1)求证：CE 是O 的切线．(2)如图2，点F 在O 上，且满足2FCE ABC ∠=∠，连接AF 并延长交EC 的延长线于点G ．若4CD =，3BD =，求线段FG 的长．CD OB ⊥DCB ∴∠+∠BCE ∠=∠OC OB=OCB∴∠=OCB∴∠+即：OC⊥CE∴是O的切线．（2）过点O作OHFCE∠=FCE∴∠=FCE∠=FCO∴∠OC CE⊥DCO∴∠+DCO∴∠=DCO∴∠=CDO∠=OCH∴∆≅CH CD∴=8CF∴=设OB OC=2OC OD=2(x x∴=解得：256 x．256OB OC∴==．CDB中，OC CG ⊥GCF ∴∠GCF ∴∠AFCB 是圆的内接四边形，GFC ∴∠GFC∴∆∽∴GF CF BC OC=GF =49．问题探究：（1）如图⊙，已知在⊙ABC 中，BC ＝4，⊙BAC ＝45°，则AB 的最大值是．（2）如图⊙，已知在Rt ⊙ABC 中，⊙ABC ＝90°，AB ＝BC ，D 为⊙ABC 内一点，且AD＝BD ＝2．，CD ＝6，请求出⊙ADB 的度数．问题解决：（3）如图⊙，某户外拓展基地计划在一处空地上修建一个新的拓展游戏区⊙ABC ，且AB ＝A C ．⊙BAC ＝120°，点A 、B 、C 分别是三个任务点，点P 是⊙ABC 内一个打卡点．按照设计要求，CP ＝30米，打卡点P 对任务点A 、B 的张角为120°，即⊙APB ＝120°．为保证游戏效果，需要A 、P 的距离与B 、P 的距离和尽可能大，试求出AP +BP 的最大值．的外接圆O，连接）如图⊙，作⊙的外接圆O，连接BAC＝90°，OB是等腰直角三角形的外接圆O，连接AKC＝⊙APB 是等边三角形。

“圆”专题训练(拓展)

“圆”　专题训练（拓展）一、知识梳理。

具体内容重点知识圆的认识(一) 1、圆的特征：圆是一条曲线围成的封闭图形，圆上任意一点到圆心的距离都相等。

2、圆规画圆的方法： a.把圆规的两脚分开，定好两脚间的距离； b.把针尖的一只脚固定在一点上； c.把装有铅笔尖的一只脚绕这个固定点旋转一周，就可以画一个圆。

3、圆各部分名称：圆心用字母O表示；半径通常用字母r表示；直径通常用字母d表示。

4、圆有无数条直径，无数条半径；同（等）圆内的直径都相等，半径都相等。

5、圆心和半径的作用：圆心确定圆的位置，圆的半径决定圆的大小。

圆的认识（二）1、圆的轴对称性：圆是轴对称图形，直径所在的直线是圆的对称轴。

圆有无数条对称轴。

2、同一圆内半径与直径的关系：在同一圆里，直径的长度是半径的2倍，可以表示为d=2r或r=。

3、图形的旋转对称性：正方形绕中心点旋转一周，与原图形重合四次；等边三角形绕中心点旋转一周，与原图形重合三次；圆绕中心点旋转一周，与原图形重合无数次。

圆的周长1、圆的周长的意义：圆的周长是指围成圆的曲线的长。

直径大的圆的周长大，直径小的圆的周长小。

2、圆周率的意义：圆的周长除以直径的商是一个固定的数，我们把它叫做圆周率，用字母π表示，计算时通常取 3.143、圆的周长计算公式：如果用C表示圆的周长，那么C=d或C=2r。

4、圆的周长计算公式应用：（1）已知圆的半径，求圆的周长：C=2r 。

（2）已知圆的直径，求圆的周长：C= d 。

（3）已知圆的周长，求圆的半径：r=C÷（2）。

（4）已知圆的周长，求圆的直径：d=C÷。

圆的面积1、圆的面积的意义：圆形物体所占平面的大小就是圆的面积。

2、圆的面积计算公式：如果用S表示圆的面积，r表示圆的半径，那么圆的面积计算公式是S=r2.3、圆的面积计算公式的应用（1）已知圆的半径，求圆的面积：S=r2。

（2）已知圆的直径，求圆的面积：r=，S=r2或S=（）2。

《圆》阅读理解类综合题专题培优训练

《圆》阅读理解类综合题专题培优训练1. 问题提出：如图①，AB 、AC 是O 的两条弦，AC AB >，M 是BAC 的中点MD AC ⊥，垂足为D ，求证：CD BA AD =+.小敏在解答此题时，利用了“补短法”进行证明，她的方法如下：如图②，延长CA 至E ，使AE AB =，连接MA 、MB 、MC 、ME 、BC .（请在下面的空白处完成小敏的证明过程.）推广运用如图③，等边ABC △内接于O ，1AB =，D 是AC 上一点，45ABD ∠=︒，AE BD ⊥，垂足为E ，则BDC △的周长是_______.拓展研究：如图④，若将“问题提出”中“M 是BAC 的中点”改成“M 是BC 的中点”，其余条件不变，“CD BA AD =+”这一结论还成立吗？若成立，请说明理由；若不成立，写出CD 、BA 、AD 三者之间存在的关系并说明理由.图①图②图③图④2. 【问题学习】:李强在小组学习时问王刚这样一个问题：已知α为锐角，且sin α=32，求sin2α的值．王刚是这样给李强讲解的：构造如图1所示的图形，在⊙O 中，AB 是直径，点C 在⊙O 上，所以∠ACB=90°，作CD ⊥AB 于D ．设∠BAC=α，则sin α=32 AB BC ，可设BC=2x ，则AB=3x ，…．【问题解决】:（1）请按照王刚的思路，利用图1求出sin2α的值；（写出完整的解答过程）（2）如图2，已知点M ，N ，P 为⊙O 上的三点，且∠P=β，sin β=53 ，求sin2β的值．3. 问题探究：（1）如图①，AB 为⊙O 的弦，点C 是⊙O 上的一点，在直线AB 上方找一个点D ，使得∠ADB=∠ACB ，画出∠ADB ；（2）如图②，AB 是⊙O 的弦，点C 是⊙O 上的一个点，在过点C 的直线l 上找一点P ，使得∠APB<∠ACB ，画出∠APB ；（3）如图③，已知足球门宽AB 约为B 点C 点（点A 、B 、C 均在球场的底线上），沿与AC 成45°的CD 方向带球．试问，该球员能否在射线CD 上找一点P ，使得点P 最佳射门点（即∠APB 最大）？若能找到，求出这时点P 与点C 的距离；若找不到，请说明理由．4.【学习心得】：李强同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．例如：如图1，在△ABC 中，AB=AC ，∠BAC=90°，D 是△ABC 外一点，且AD=AC ，求∠BDC 的度数，若以点A 为圆心，AB 为半径作辅助圆⊙A ，则点C 、D 必在⊙A 上，∠BAC 是⊙A 的圆心角，而∠BDC 是圆周角，从而可容易得到∠BDC= °．【问题解决】：如图2，在四边形ABCD 中，∠BAD=∠BCD=90°，∠BDC=25°，求∠BAC 的度数．李强同学认为用添加辅助圆的方法，可以使问题快速解决，他是这样思考的：△ABD 的外接圆就是以BD 的中点为圆心，21BD 长为半径的圆；△ACD 的外接圆也是以BD 的中点为圆心，21BD 长为半径的圆．这样A 、B 、C 、D 四点在同一个圆上，进而可以利用圆周角的性质求出∠BAC 的度数，请运用李强的思路解决这个问题．【问题拓展】：如图3，在△ABC 中，∠BAC=45°，AD 是BC 边上的高，且BD=4，CD=2，求AD 的长．4.【问题提出】：苏科版（数学）九年级（上册）习题2.1有这样一道练习题：如图①，BD、CE是△ABC的高，M是BC的中点，点B、C、D、E是否在以点M为圆心的同一个圆上？为什么？在解决此题时，若想要说明“点B、C、D、E在以点M为圆心的同一个圆上”只需证明．【初步思考】：如图②，BD、CE是锐角△ABC的高，连接DE，求证：∠ADE=∠ABC．【推广运用】：如图③，BD、CE、AF是锐角△ABC的高，连接DE、EF、FD，猜想∠EFB与∠DFC之间存在的关系，并说明理由．5.[发现]:如图∠ACB=∠ADB=90°，那么点D在经过A，B，C三点的圆上（如图①）[思考]:如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A， B，C三点的圆上吗？我们知道，如果点D不在经过A，B，C三点的圆上，那么点D要么在圆O外，要么在圆O内，以下该同学的想法说明了点D不在圆O外。

2023年人教版初中数学中考第八章圆(基础)专题训练(一)打印版含答案

2023年人教版初中数学中考第八章圆(基础)专题训练时间：45分钟满分：80分一、选择题(每题4分，共32分)1．已知⊙O 的直径为10，点P 到点O 的距离大于8，那么点P 的位置( )A ．一定在⊙O 的内部B ．一定在⊙O 的外部C ．一定在⊙O 上D ．不能确定2．如图，△ABC 内接于圆，弦BD 交AC 于点P ，连接AD .下列角中，AB ︵所对的圆周角是( )(第2题)A ．∠APBB ．∠ABDC ．∠ACBD ．∠BAC3．已知一个扇形的半径是1，圆心角是120°，则这个扇形的弧长是( ) A.π6 B ．π C.π3 D.2π34．如图，⊙O 的直径AB ＝8，弦CD ⊥AB 于点P ，若BP ＝2，则CD 的长为( )A ．2 5B ．4 2C ．4 3D ．8 2(第4题) (第5题) (第6题)5．如图，AB是⊙O的直径，CD是⊙O的弦，若∠ACD＝65°，则∠BAD的度数为()A．25°B．30°C．35°D．40°6．如图，在⊙O中，∠CDB＝25°，过点C作⊙O的切线交AB的延长线于点E，则∠E的度数为()A．40°B．50°C．55°D．60°7．如图，以边长为2的等边三角形ABC的顶点A为圆心，一定的长为半径画弧，恰好与BC边相切，分别交边AB，AC于点D，E，则图中阴影部分的面积是()A.3－π4B．23－πC.（6－π）33 D.3－π2 (第7题)(第8题)8．如图，在⊙O中，点C为弦AB上一点，AB＝1，CD⊥OC交⊙O于点D，则线段CD的最大值是()A.12B．1 C.32D．2二、填空题(每题4分，共16分)9．已知圆的半径是3，则该圆的内接正六边形的边长是________．10．如图，四边形ABCD内接于⊙O，∠A＝110°，则∠BOD＝________°.(第10题)(第11题)11．如图，P A，PB与⊙O相切于A，B两点，点C在⊙O上，若∠C＝70°，则∠P＝________°.12．已知圆锥的母线长为5，底面半径为3，则圆锥的侧面展开图的面积为________．三、解答题(共32分)13．(10分)如图，四边形ABCD是⊙O的内接四边形，连接AC，BD，延长CD 至点E.(1)若AB＝AC，求证：∠ADB＝∠ADE；(2)若BC＝3，⊙O的半径为2，求sin∠BAC.(第13题)14. (10分)如图，⊙O是△ABC的外接圆，连接OC，过点A作AD∥OC交BC的延长线于点D，∠ABC＝45°.(1)求证：AD是⊙O的切线；(2)若sin ∠CAB＝35，⊙O的半径为522，求AB的长．(第14题)15．(12分)如图，在Rt △ABC 中，∠C ＝90°，BC 与⊙O 相切于点D ，且⊙O 分别交AB ，AC 于点E ，F .(1)求证：AD 平分∠CAB ；(2)当AD ＝2，∠CAD ＝30°时，求AD ︵的长．(第15题)答案一、1.B 2.C 3.D 4.C 5.A 6.A 7.D 8.A 二、9.3 10.140 11.40 12.15π三、13.(1)证明：∵四边形ABCD 是⊙O 的内接四边形，∴∠ABC ＋∠ADC ＝180°.∵∠ADC ＋∠ADE ＝180°，∴∠ADE ＝∠ABC . ∵AB ＝AC ，∴∠ABC ＝∠ACB .∵∠ACB ＝∠ADB ，∴∠ADB ＝∠ADE .(2)解：如图，连接CO 并延长交⊙O 于点F ，连接BF ，则∠FBC ＝90°.由题意得在Rt △BCF 中CF ＝4，BC ＝3，(第13题)∴sin F ＝BC CF ＝34.∵∠F ＝∠BAC ，∴sin ∠BAC ＝sin F ＝34.14．(1)证明：如图，连接OA .∵∠ABC ＝45°， ∴∠AOC ＝2∠ABC ＝90°.∵AD ∥OC ，∴∠DAO ＋∠AOC ＝180°，∴∠DAO ＝90°，即OA ⊥AD .又∵OA 是⊙O 的半径，∴AD 是⊙O 的切线．(2)解：如图，过点C 作CE ⊥AB 于点E .由(1)知∠AOC ＝90°.∵AO ＝OC ＝522，∵CE ⊥AB ，∴∠AEC ＝∠CEB ＝90°，∴sin ∠CAB ＝CE AC ＝35， ∴CE ＝3，∴AE ＝AC 2－CE 2＝4.∵∠CEB ＝90°，∠ABC ＝45°，∴∠BCE ＝45°， ∴CE ＝BE ＝3，∴AB ＝AE ＋BE ＝7.(第14题)15．(1)证明：如图，连接OD .∵BC 与⊙O 相切于点D ，∴OD ⊥BC ，即∠ODB ＝90°.∵∠C ＝90°，∴OD ∥AC ，∴∠ODA ＝∠CAD .∵OD ＝OA ，∴∠OAD ＝∠ODA ，∴∠CAD ＝∠OAD ，∴AD 平分∠CAB .(2)解：如图，连接DE .∵AE 为⊙O 的直径，∴∠ADE ＝90°.∵∠CAD ＝30°，∠OAD ＝∠ODA ＝∠CAD ， ∴∠OAD ＝∠ODA ＝30°，∴∠AOD ＝120°. 在Rt △ADE 中，AE ＝AD cos ∠EAD ＝232＝43 3，∴⊙O 的半径为23 3， ∴AD ︵的长＝120π×23 3180＝49 3π.。

突破中考之圆(解答题)专题训练

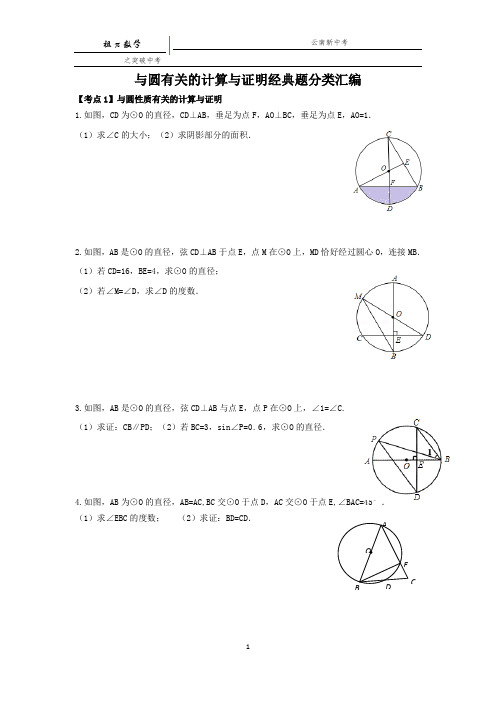
与圆有关的计算与证明经典题分类汇编【考点1】与圆性质有关的计算与证明1.如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．（1）求∠C的大小；（2）求阴影部分的面积．2.如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．（1）若CD=16，BE=4，求⊙O的直径；（2）若∠M=∠D，求∠D的度数．3.如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C.（1）求证：CB∥PD；（2）若BC=3，sin∠P=0.6，求⊙O的直径．4.如图，AB为⊙O的直径，AB=AC,BC交⊙O于点D，AC交⊙O于点E,∠BAC=45°．（1）求∠EBC的度数；（2）求证：BD=CD．AOECDB【考点2】与切线性质有关的证明与计算1.如图，PA、PB、EF分别与⊙O相切于点A、B、C，若△PEF的周长为18cm，且∠APB=60°,求⊙O的半径.2.如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB=18cm，BC=28cm，CA=26cm，求AF，BD，CE的长.3.如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点．（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求⊙O半径的长．4.如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为弧BC的中点．（1）求证：AB=BC；（2）求证：四边形BOCD是菱形．5.如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF=∠ABC．（1）求证：AB=AC；（2）若AD=4，cos∠ABF=45，求DE的长．6.直线PD垂直平分⊙O的半径OA，交⊙O于点C、D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．（1）若⊙O的半径为8，求CD的长；（2）证明：PE=PF；（3）若PF=13，sin A=513，求EF的长．【考点3】与切线的判定有关的证明与计算1.如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．（1）求AD的长；（2）证明BC是⊙O的切线．2.如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，若AC=FC．（1）求证：AC是⊙O的切线；（2）若BF=8，DF=40，求⊙O的半径r．3.如图，AB是⊙O的直径，点C在⊙O上，若∠BAC=∠CAM，过点C作直线L垂直于射线AM，垂足为点D．（1）试判断CD与⊙O的位置关系，并说明理由；（2）若直线L与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°，求CE的长．4.如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC 的延长线于点E，与⊙O相交于G、F两点．（1）求证：AB与⊙O相切；（2）若等边三角形ABC的边长是4，求线段BF的长.【考点4】与阴影面积有关的计算与证明1.如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．（1）求证：EF是⊙O的切线；（2）求证：AC2=AD•AB；（3）若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积．2.如图，在△ABC中，BE是它的角平分线，∠C＝90°，D在AB边上，以DB为直径的半圆O 经过点E，交BC于点F.(1)求证：AC是⊙O的切线；(2)已知cos A＝32，⊙O的半径为3，求图中阴影部分的面积．3.如图，在△ABC中，∠ACB=90°，E为BC上一点，以CE为直径作⊙O，AB与⊙O相切于点D，连接CD，若BE=OE=2．（1）求证：∠A=2∠DCB；（2）求图中阴影部分的面积．4.如图，BE是⊙O的直径，点A和点D是⊙O上的两点，连接AE，AD，DE，过点A作射线交BE的延长线于点C，使∠EAC＝∠EDA.(1)求证：AC是⊙O的切线；(2)若CE＝AE＝23，求阴影部分的面积．5.如图，在△BCE中，点A是边BE上一点，以AB为直径的⊙O与CE相切于点D，AD∥OC，点F为OC与⊙O的交点，连接AF.(1)求证：CB是⊙O的切线；(2)若∠ECB＝60°，AB＝6，求图中阴影部分的面积．6.如图，AB 是⊙O 的直径，∠BAC=90°，四边形EBOC 是平行四边形，EB 交⊙O 于点D ，连接CD 并延长交AB 的延长线于点F ．（1）求证：CF 是⊙O 的切线；（2）若∠F=30°，EB=4，求图中阴影部分的面积.【考点5】与圆有关的计算与证明综合1.如图，AE 为⊙O 的直径，D 是弧BC 的中点BC 与AD ，OD 分别交于点E ，F. （1）求证：OD ∥AC ；（2）求证：DE.DA=DC 2；（3）若tan ∠CAD=21,求tan ∠CDA 的值.2.如图，⊙O 与直线MN 相切于点A ，点B 是⊙O 上异于点A 的一点，∠BAN 的平分线与⊙O 交于点C ．(1)求证：△ABC 是等腰三角形；(2)①若∠CAN ＝15°，⊙O 的半径为23，则AB ＝；②当∠CAN ＝时，四边形OACB 为菱形．FEDOAC3.如图，PA为⊙O的切线，A为切点，直线PO交⊙O与点E，F过点A作PO的垂线AB垂足为D，交⊙O与点B，延长BO与⊙O交与点C，连接AC，BF．（1）求证：PB与⊙O相切；（2）试探究线段EF，OD，OP之间的数量关系，并加以证明；（3）若AC=12，tan∠F=12，求cos∠ACB的值．4.如图，△ABC 内接于⊙O ，AB 为直径，∠CBA 的平分线交AC 于点F ，交⊙O 于点D, DE ⊥AB 于点E ，且交AC 于点P ，连接AD.(1)求证：∠DAC ＝∠DBA ；(2)求证：P 是线段AF 的中点； (3)若⊙O 的半径为5, AD ＝6，求ADDB的值．5.如图1，⊙O 是△ABC 的外接圆，AB ＝AC ，BC ＝2，cos ∠ABC ＝1010.点D 为AC ︵上的动点，连接AD 并延长，交BC 的延长线于点E. (1)试求AB 的长；(2)试判断AD ·AE 的值是否为定值？若为定值；请求出这个定值；若不为定值，请说明理由； (3)如图2，连接BD ，过点A 作AH ⊥BD 于点H ，连接CD ，求证：BH ＝CD ＋DH.图1图2。

第24章：《圆》八大专题训练

第24章：《圆》八大专题训练专训1:巧用圆的基本性质解圆的五种关系◐名师点金◑圆的基本性质里面主要涉及弦、弧之间的关系，圆周角、圆心角之间的关系，弧、圆周角之间的关系，弦、圆心角之间的关系，弦、弧、圆心角之间的关系等，在解此类题目时，需要根据已知条件和所求问题去探求它们之间的内在联系，从而达到解决问题的目的．关系1：弦、弧之间的关系1．如图，在⊙O 中，AB ︵＝2CD ︵，则下列结论正确的是( )A ．AB>2CDB ．AB ＝2CDC ．AB<2CD D ．以上都不正确 2．如图，在⊙O 中，弦AD ＝BC ，求证：AB ︵＝CD ︵.关系2：圆周角、圆心角之间的关系3．如图，AB ，AC ，BC 都是⊙O 的弦，且∠CAB ＝∠CBA ，求证：∠COB ＝∠COA.关系3：弧、圆周角之间的关系4．如图，AB 是⊙O 的直径，点C ，D 在⊙O 上，∠BAC ＝50°，求∠ADC 的度数．5.⊙O 的弦AB ，CD 的延长线相交于点P ，且AB ＝CD 。

求证：PA ＝PC关系4：弦、圆心角之间的关系6．如图，以等边三角形ABC 的边BC 为直径作⊙O 交AB 于D ，交AC 于E ，连接DE.试判断BD ，DE ，EC 之间的大小关系，并说明理由．关系5：弦、弧、圆心角之间的关系7．如图，在⊙O 中，∠AOB ＝90°，且C ，D 是AB ︵的三等分点，AB 分别交OC ，OD 于点E ，F. 求证：AE ＝BF ＝CD.专训2：垂径定理的四种应用技巧◐名师点金◑圆的半径和圆心到弦的垂线段三条线段组成的直角三角形,然后借助勾股定理,,在这三个量中知道任意两个,可求出第三个。

技巧1：巧用垂径定理求点的坐标1.如图，在平面直角坐标系中，点A的坐标是(10，0)，点B的坐标是(8，0)，点C，D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，求点C的坐标。

九年级数学圆的专题训练

九年级数学——圆专题训练二、基础知识（1）掌握圆的有关性质和计算① 弧、弦、圆心角之间的关系:在同圆或等圆中，如果两条劣弧（优弧）、两条两个圆心角中有一组量对应相等，那么它们所对应的其余各组量也分别对应相等.② 垂径定理: 垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．垂径定理的推论:平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.弦的垂直平分线经过圆心，并且平分弦所对的两条弧.平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．③ 在同一圆内，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半. ④ 圆内接四边形的性质:圆的内接四边形对角互补，并且任何一个外角等于它的内对角. （2）点与圆的位置关系① 设点与圆心的距离为d ，圆的半径为r ，则点在圆外d r ⇔>；点在圆上d r ⇔=；点在圆内d r ⇔<． ② 过不在同一直线上的三点有且只有一个圆. 一个三角形有且只有一个外接圆.③ 三角形的外心是三角形三边垂直平分线的交点.三角形的外心到三角形的三个顶点的距离相等. （3）直线与圆的位置关系① 设圆心到直线l 的距离为d ，圆的半径为r ，则直线与圆相离d r ⇔>；直线与圆相切d r ⇔=；直线与圆相交d r ⇔<．② 切线的性质:与圆只有一个公共点；圆心到切线的距离等于半径；圆的切线垂直于过切点的半径.③ 切线的识别:如果一条直线与圆只有一个公共点，那么这条直线是圆的切线. 到圆心的距离等于半径的直线是圆的切线.经过半径的外端且垂直与这条半径的直线是圆的切线.④ 三角形的内心是三角形三条内角平分线的交点. 三角形的内心到三角形三边的距离相等. ⑤ 切线长：圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长. ⑥ 切线长定理:从圆外一点引圆的两条切线，它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.（4）圆与圆的位置关系① 圆与圆的位置关系有五种:外离、外切、相交、内切、内含.设两圆心的距离为d ，两圆的半径为12r r 、，则两圆外离12d r r ⇔>+ 两圆外切12d r r ⇔=+ 两圆相交1212r r d r r ⇔-<<+ 两圆内切12d r r ⇔=- 两圆内含12d r r ⇔<- ② 两个圆构成轴对称图形，连心线（经过两圆圆心的直线）是对称轴.由对称性知:两圆相切，连心线经过切点. 两圆相交，连心线垂直平分公共弦. ③ 两圆公切线的定义:和两个圆都相切的直线叫做两圆的公切线.两个圆在公切线同旁时,这样公切线叫做外公切线.两个圆在公切线两旁时,这样公切线叫做内公切线.④ 公切线上两个切点的距离叫做公切线的长. （5）与圆有关的计算① 弧长公式：180n r l π= 扇形面积公式：213602n r S lr π==扇形 ② 圆柱的侧面展开图是矩形．圆柱体也可以看成是一个矩形以矩形的一边为轴旋转而形成的几何体．圆柱的侧面积＝底面周长×高圆柱的全面积＝侧面积＋２×底面积③ 圆锥的侧面展开图是扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．圆锥体可以看成是由一个直角三角形以一条直角边为轴旋转而成的几何体．④ 圆锥的侧面积＝12×底面周长×母线；圆锥的全面积＝侧面积＋底面积（一）圆中的有关概念和性质基础练习1．以已知点O为圆心作圆，可以作（）A．1个B．2个C．3个D．无数个2．以已知点O为圆心，已知线段a为半径作圆，可以作（）A．1个B．2个C．3个D．无数个3．如图，点C在以AB为直径的半圆上，∠BAC=20°，∠BOC等于（）A．20°B．30°C．40° D．50°4．如图，在⊙O中，弦AB=8cm，OC⊥AB于C，OC=3cm，求⊙O的半径长．5．判断：⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧.（）⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧.（）⑶经过弦的中点的直径一定垂直于弦.（）⑷圆的两条弦所夹的弧相等，则这两条弦平行. （）⑸弦的垂直平分线一定平分这条弦所对的弧. （）6．如图，⊙O直径AB和弦CD相交于点E，AE=2，EB=6，∠DEB=30°，求弦CD长．7．如图,圆O 与矩形ABCD 交于E 、F 、G 、H,EF=10,HG=6,AH=4.求BE 的长.8．储油罐的截面如图所示，装入一些油后，若油面宽AB=600mm ，求油的最大深度．9．P 为⊙O 内一点，OP=3cm ，⊙O 半径为5cm ，则经过P 点的最短弦长为_______；最长弦长为______． 10．如图，AB 为⊙O 直径，E 是BC 中点，OE 交BC 于点D ，BD=3，AB=10，则AC=_____．BA11．如图5，OE 、OF 分别为⊙O 的弦AB 、CD 的弦心距，如果OE=OF ，那么_______（只需写一个正确的结论）12．已知，如图在以O 为圆心的两个同心圆中，大圆的弦AB交小圆于C 、D 两点，求证：AC ＝BD13．已知AB、CD为⊙O的弦,且AB⊥CD，AB将CD分成3cm和7cm两部分，求：圆心O到弦AB的距离14．下列说法中，正确的是（）A．等弦所对的弧相等B．等弧所对的弦相等C．圆心角相等，所对的弦相等D．弦相等所对的圆心角相等15．如果两个圆心角相等，那么（）A．这两个圆心角所对的弦相等; B．这两个圆心角所对的弧相等C．这两个圆心角所对的弦的弦心距相等; D．以上说法都不对16．如图1，半圆的直径AB=4，O为圆心，半径OE⊥AB，F为OE的中点，CD∥AB，则弦CD的长为（）A．23B．3C．5D．2517．已知：如图2，⊙O的直径CD垂直于弦AB，垂足为P，且AP=4cm，PD=2cm，则⊙O的半径为（）A．4cm B．5cm C．42cm D．23cm18．如图3，同心圆中，大圆的弦AB交小圆于C、D，已知AB=4，CD=2，AB的弦心距等于1，那么两个同心圆的半径之比为（）A．3：2 B．5：2 C．5：2D．5：419．弓形的弦长6cm，高为1cm，则弓形所在圆的半径为 cm．20．一条弦把圆分成1：3两部分，则弦所对的圆心角为．21．弦心距是弦的一半时，弦与直径的比是，弦所对的圆心角是．22．如图，AB是⊙O的直径，∠AOD是圆心角，∠BCD是圆周角．若∠BCD=25°，则∠AOD= ．23．如图，⊙O直径MN⊥AB于P，∠BMN=30°，则∠AON= ．24．如图6，AB是⊙O的直径，⌒BC=⌒BD，∠A=25°，则∠BOD= ．25．如图，∠AOB=90°，C、D是弧AB的三等分点，AB分别交OC、OD于点E、F，求证：AE=BF=CD．26. 如图，已知⊙O中，AB为直径，AB=10cm，弦AC=6cm，∠ACB的平分线交⊙O于D，求BC、AD和BD 的长．27．如图，AB是半圆的直径，AC为弦，OD⊥AB，交AC于点D，垂足为O，⊙O的半径为4，OD=3，求CD 的长．（二）圆中的位置关系1．下列说法：①三点确定一个圆；②三角形有且只有一个外接圆；•③圆有且只有一个内接三角形；④三角形的外心是各边垂直平分线的交点；⑤三角形的外心到三角形三边的距离相等；⑥等腰三角形的外心一定在这个三角形内，其中正确的个数有（• ）A．1 B．2 C．3 D．42．经过一点P可以作_______个圆；经过两点P、Q可以作________•个圆，圆心在_________上；经过不在同一直线上的三个点可以作________个圆，•圆心是________的交点．3．锐角三角形的外心在；直角三角形的外心在；钝角三角形的外心在．4．边长为a的等边三角形外接圆半径为_______，圆心到边的距离为________．5．已知圆内一点到圆周上的点的最大距离是7，最小距离是5，则该圆的半径是（）A．2 B．6 C．12 D．76．设⊙O的半径为2，点P到圆心的距离OP=m，且m使关于x的方程2x2－22x＋m－1=0有实数根，试确定点P的位置．7．⊙O的半径为R，直线ι和⊙O有公共点，若圆心到直线ι的距离是d，则d与R的大小关系是（）A．d＞R B．d＜R C．d≥R D．d≤R8．已知圆的直径为13cm，圆心到直线ι的距离为6cm，那么直线ι和这个圆的公共点的个数是．9．圆的一条弦与直径相交成300角，且分直径长1cm和5cm两段，则这条弦的弦心距为_______ ，弦长_______ 。

中考数学《圆的综合》专题训练(含有答案)

中考数学《圆的综合》专题训练(含有答案)1．如图，：AB 是O 的直径：BC 是O 弦，OD CB ⊥于点E ，交BC 于点D ．(1)请写出三个不同类型的正确结论(2)连结CD ，设BCD α∠= ABC β∠= 试找出α与β之间的一种关系式并给予证明．2．如图，，在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D 交CA 的延长线于点E ．(1)求证点D 为线段BC 的中点．(2)若63BC = 3AE = 求O 的半径及阴影部分的面积．3．如图，AB 为O 的直径点C 在O 上延长BC 至点D 使DC CB =．延长DA 与O 的另一个交点为E 连结AC CE ，．(1)求证D E ∠=∠(2)若42AB BC AC =-=，求CE 的长．4．请仅用无刻度的直尺完成下列作图不写作法保留作图痕迹(1)如图1， ABC 与ADE 是圆内接三角形 AB AD = AE AC = 画出圆的一条直径．(2)如图2 ， AB CD 是圆的两条弦 AB CD =且不相互平行画出圆的一条直径． 5．如图，AB 是O 的直径点D 在AB 的延长线上点C 在O 上 ,30CA CD CDA =∠=︒．(1)求证CD 是O 的切线(2)若O 的半径为6 求点A 到CD 所在直线的距离．6．如图，点C 在以AB 为直径的O 上过C 作O 的切线交AB 的延长线于E AD CE ⊥于D 连接AC ．(1)求证ACD ABC ∠=∠(2)若3tan 4CAD ∠= 8AD = 求O 直径AB 的长．7．如图，已知以Rt ABC 的直角边AC 为直径作O 交斜边AB 于点E 连接EO 并延长交BC 的延长线于点D 连接AD 点F 为BC 的中点连接EF ．(1)求证EF 是O 的切线(2)若O 的半径为6 8CD = 求AB 的长．8．如图， AB 是半圆O 的直径 D 为半圆O 上的点(不与A B 重合) 连接AD 点C 为BD 的中点过点C 作CF AD ⊥ 交AD 的延长线于点F 连接BF AC 交于点E ．(1)求证FC 是半圆O 的切线(2)若3AF = 23AC = 求半圆O 的半径及AE 的长．9．如图， AB 为O 的直径 C 为BA 延长线上一点 CD 是O 的切线 D 为切点 OF AD ⊥于点E 交CD 于点F ．(1)求证ADC AOF ∠=∠ (2)若53OC OB = 24BD = 求EF 的长． 10．如图，所示 AB 是O 的直径点D 在AB 上点C 在O 上 AD AC =CD 的延长线交O 于点E ．(1)在CD 的延长线上取一点F 使BF BC = 求证BF 是O 的切线 (2)若2AB = 2CE 求图中阴影部分的面积．11．如图， ABC 内接于O AB 为O 的直径 D 为BA 延长线上一点连接CD 过O 作OF BC ∥交AC 于点E 交CD 于点F ACD AOF ∠=∠．(1)求证CD 为圆O 的切线 (2)若1sin 4D =10BC = 求EF 的长． 12．如图，四边形ABCD 是O 的内接四边形 AD CD = 70BAC ∠=︒ 50∠=°ACB ．(1)求ABD ∠的度数 (2)求BAD ∠的度数．13．如图，四边形ABCD 是O 的内接四边形且对角线BD 为O 的直径过点A 作AE CD ⊥ 与CD 的延长线交于点E 且DA 平分BDE ∠．(1)求证AE 是O 的切线(2)若O 的半径为5 6CD = 求DA 的长．14．如图，在正方形ABCD 中有一点P 连接AP BP 旋转APB △到CEB 的位置．(1)若正方形的边长是8 4BP =．求阴影部分面积 (2)若4BP = 7AP = 135APB ∠=︒ 求PC 的长．15．如图， AB 是O 的直径 OD 垂直于弦AC 于点E 且交O 于点D F 是BA 延长线上一点若CDB BFD ∠=∠．(1)求证 FD 是O 的一条切线(2)若15AB = 9BC = 求DF 的长． 16．如图，O 是ABC ∆的外接圆 AE 切O 于点A AE 与直径BD 的延长线相交于点E ．(1)如图，① 若70C ∠=︒ 求E ∠的大小 (2)如图，① 若AE AB = 求E ∠的大小．17．已知如图，直线MN 交O 于A B 两点 AC 是直径 AD 平分CAM ∠交O 于D 过D 作DE MN ⊥于E ．(1)求证DE 是O 的切线(2)若8cm DE = 4cm AE = 求O 的半径．18．已知四边形ABCD 内接于O C 是DBA 的中点 FC AC ⊥于C 与O 及AD 的延长线分别交于点,E F 且DE BC =．(1)求证~CBA FDC(2)如果9,4AC AB == 求tan ACB ∠的值．参考答案与解析1．(1)见解析(2)关系式为2=90αβ+︒ 证明见解析【分析】（1）AB 是O 的直径 BC 是弦 OD BC ⊥于E 本题满足垂径定理．（2）连接,CD DB 根据四边形ACDB 为圆内接四边形可以得到290αβ+=︒．【解析】（1）解不同类型的正确结论有 ①BE CE = ①BD CD = ①90BED ∠=︒ ①BOD A ∠=∠ ①AC OD ∥ ①AC BC ⊥ ①222OE BE OB += ①ABC S BC OE =⋅△ ①BOD 是等腰三角形 ①BOE BAC △∽△等等．（2）如图，连接,CD DBα与β之间的关系式为290αβ+=︒证明AB 为圆O 的直径90A ABC ∴∠+∠=︒①又四边形ACDB 为圆内接四边形180A CDB ∠∠∴+=︒①∴①-①得90CDB ABC ∠∠-=︒①18021802CDB BCD α∠=︒-∠=︒- 即180290αβ︒--=︒ ①2=90αβ+︒．【点评】本题考查了圆的一些基本性质且有一定的开放性垂径定理圆内接四边形的性质掌握圆的相关知识． 2．(1)见解析 (2)半径为3 39π324S =阴【分析】（1）连结AD 可得90ADB ∠=︒ 已知AB AC = 根据等腰三角形三线合一的性质即可得证点D 为线段BC 的中点（2）根据已知条件可证ABC DEC ∽△△ 得到ED ECAB BC= 22BD AB EC =⋅ 且EDC △是等腰三角形进而得到ED DC BD == 设AB x = 则(()22333x x =+ 解方程即可求得O 的半径连接OE 可证AOE △是等边三角形再根据AOEAOE S S S =-阴扇形即可求出阴影部分的面积【解析】（1）连结AD①AB 为O 的直径 ①90ADB ∠=︒ ①AB AC = ①BD CD =即点D 为线段BC 的中点．（2）①B E ∠=∠ C C ∠=∠ ①ABC DEC ∽△△ ①ED ECAB BC= ①AB AC = ①B C ∠=∠ ①C E ∠=∠ ①ED DC BD == ①22BD AB EC =⋅ 设AB x = 则 (()22333x x =+解得19x =-（舍去） 26x = ①O 的半径为3 连接OE ①60AOE =︒∠ ①AOE △是等边三角形 ①AE 33①AOEAOE S S S=-阴扇形260313333602π⨯⨯=-⨯ 39π324=【点评】本题主要考查等腰三角形的性质相似三角形的判定和性质不规则图形面积的计算熟练掌握相关知识点是解题的关键． 3．(1)见解析 (2)CE 的长为17【分析】（1）由AB 为O 的直径得90ACB ∠=︒ 通过证明()ACD ACB ≌SAS 得到D B ∠=∠ 又由B E ∠=∠ 从而得到D E ∠=∠（2）设BC x = 则2AC x =- 在Rt ABC 中由勾股定理可得222AC BC AB += 即()22224x x -+= 解一元二次方程得到BC 的长由（1）知D E ∠=∠ 从而得到CD CE = 又由DC CB = 得到17CE CB ==【解析】（1）证明AB 为O 的直径90ACB ∴∠=︒180ACD ACB ∠+∠=︒90ACD ∴∠=︒在ACD 和ACB △中AC AC ACD ACB DC BC =⎧⎪∠=∠⎨⎪=⎩()ACD ACB ∴≌SASD B ∴∠=∠ BE ∠=∠D E ∴∠=∠（2）解设BC x =2BC AC -=∴2AC x =-在Rt ABC 中由勾股定理可得222AC BC AB += 即()22224x x -+=解得117x = 217x = 17BC ∴=由（1）得D E ∠=∠ CD CE ∴= DC CB =17CE CB ∴==∴ CE 的长为17【点评】本题主要考查了圆周角定理三角形全等的判定与性质等腰三角形的性质勾股定理解直角三角形熟练掌握圆周角定理三角形全等的判定与性质等腰三角形的性质是解题的关键． 4．(1)见解析 (2)见解析【分析】（1）设BC DE 交于点G 连接AG 交圆于点F 即可作答（2）连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N 即可作答．【解析】（1）如图，设BC DE 交于点G 连接AG 并延长交圆于点F线段AF 即为所求证明如图， BC AE 交于点Q DE AC 交于点P 连接DB 交AF 于点H①AB AD = AE AC = ①C E ∠=∠ ADE ABC =∠∠ ①DAE BAC ∠=∠①DAE BAC ≌ ①BC DE = ①DAE BAC ∠=∠ ①BAE DAC ∠=∠①AB AD = ADE ABC =∠∠ ①DAP BAQ ≌ ①AQ AP = ①AE AC = ①QE PC =①QGE PGC ∠=∠ C E ∠=∠ ①QGE PGC ≌ ①QG PG =①AG AG = AQ AP = ①QAG PAG ≌ ①QAG PAG ∠=∠ ①BAE DAC ∠=∠ ①BAG DAG ∠=∠ ①AH AH = AB AD = ①BAH DAH ≌①BH DH = 90AHB AHD ∠=∠=° ①AF 垂直平分弦DB ①AF 是圆的直径（2）如图，连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N线段MN 即为所求．证明方法同（1）．【点评】本题主要考查了垂径定理圆周角定理以及全等三角形的判定与性质等知识掌握圆周角定理以及垂径定理是解答本题的关键． 5．(1)见解析 (2)9【分析】（1）已知点C 在O 上先连接OC 由已知CA CD = 30CDA ∠=︒ 得30CAO ∠=︒ 30ACO ∠=︒ 所以得到60COD ∠=︒ 根据三角形内角和定理得90DCO ∠=︒ 即能判断直线CD 与O 的位置关系．（2）要求点A 到CD 所在直线的距离先作AE CD ⊥ 垂足为E 由30CDA ∠=︒ 得12AE AD = 在Rt OCD △中半径6OD = 所以212OD OC == 18AD OA OD =+= 从而求出AE ．【解析】（1）①ACD 是等腰三角形 30D ∠=︒①30CAD CDA ∠=∠=︒．连接OC①AO CO =①AOC 是等腰三角形①30CAO ACO ∠=∠=︒①60COD ∠=︒在COD △中又①30CDO ∠=︒①90DCO ∠=︒①CD 是O 的切线即直线CD 与O 相切．（2）过点A 作AE CD ⊥ 垂足为E ．在Rt OCD △中 ①30CDO ∠=︒①212OD OC ==61218AD AO OD =+=+=在Rt ADE △中①30EDA ∠=︒①点A 到CD 边的距离为92AD AE ==．【点评】此题考查的知识点是切线的判定与性质解题的关键是运用直角三角形的性质及30°角所对直角边的性质．6．(1)见解析 (2)252AB =．【分析】（1）连接OC 由DE 为O 的切线得到OC DE ⊥ 再由AD CE ⊥ 得到AD OC ∥ 得到OCA CAD ∠=∠ 根据OA OC = 利用等边对等角得到OCA CAB ∠=∠ 等量代换得到CAD CAB ∠=∠ 由AB 为O 的直径可知90ACB ∠=︒ 最后根据等角的余角相等可得结论（2）在Rt CAD △中利用锐角三角函数定义求出CD 的长根据勾股定理求出AD 的长由（1）易证ADC ACB 得到AD AC AC AB= 即可求出AB 的长．【解析】（1）解连接OC由题意可知DE 与O 的相切于COC DE ∴⊥AD CE ⊥AD OC ∴∥OCA CAD ∴∠=∠OA OC =OCA CAB ∴∠=∠CAD CAB ∴∠=∠ AB 为O 的直径90ACB ∴∠=︒90CAD ACD CAB ABC ∴∠+∠=∠+∠=︒ACD ABC ∴∠=∠（2）在Rt CAD △中3tan 4CDCAD AD ∠== 8AD =364CD AD ∴==22226810AC CD AD ∴+=+=由（1）可知CAD CAB ∠=∠90D ACB ∠=∠=︒ADC ACB ∴ADACAC AB ∴=81010AB∴= 252AB ∴=【点评】此题考查了切线的性质以及解直角三角形熟练掌握切线的判定与性质是解本题的关键． 7．(1)证明见解析 (2)125AB =【分析】（1）连接FO 可根据三角形中位线的性质可判断OF AB ∥ 然后根据直径所对的圆周角是直角可得CE AE ⊥ 进而知OF CE ⊥ 然后根据垂径定理可得FEC FCE ∠=∠OEC OCE ∠=∠ 再通过Rt ABC 可知90OEC FEC ∠+∠=︒ 因此可证EF 为O 的切线（2）根据题意可先在Rt OCD △中求出OD 然后在Rt EFD 中求出FC 最终在Rt ABC 中求解AB 即可．【解析】（1）证连接FO 则由题意OF 为Rt ABC 的中位线①OF AB ∥①AC 是O 的直径①CE AE ⊥①OF AB ∥①OF CE ⊥①由垂径定理知 OF 所在直线垂直平分CE①FC FE = OE OC =①FEC FCE ∠=∠ OEC OCE ∠=∠①90ACB ∠=︒即90OCE FCE ∠+∠=︒①90OEC FEC ∠+∠=︒即90FEO ∠=︒①EF 是O 的切线（2）解①O 的半径为6 8CD = 90ACB ∠=︒①OCD 为直角三角形 6OC OE == 8CD = ①2210OD OC CD += 10616ED OD OE =+=+=由（1）知 EFD △为直角三角形且FC FE =①设FC FE x == 则8FD FC CD x =+=+①由勾股定理 222EF ED FD +=即()222168x x +=+ 解得12x =即12FC FE ==①点F 为BC 的中点①224BC FC ==①212AC OC ==①在Rt ABC 中 22125AB BC AC +①125AB =【点评】本题考查切线的证明圆的基本性质以及勾股定理解三角形等掌握切线的证明方法熟练运用圆中的基本性质是解题关键．8．(1)见解析(2)半径为2 123AE =【分析】（1）根据点C 为弧BD 的中点得出FAC CAB ∠∠= 然后得出FAC ACO ∠∠= 根据平行线的性质得出CF OC ⊥ 进而即可求解（2）连接BC 设OC 与BF 相交于点P 证明AFC ACB ∽ 得出4AB = 证明BOP BAF ∽得出1322OP AF == 进而证明ECP EAF ∽ 根据相似三角形的性质列出比例式进而即可求解．【解析】（1）证明连接OC 如图，点C 为弧BD 的中点∴CD CB =FAC CAB ∠∠∴=又OA OC =CAB ACO ∠∠∴=FAC ACO ∠∠∴=∴OC AF ∥又CF AD ⊥CF OC ∴⊥FC ∴是半圆O 的切线．（2）解连接BC 如图，AB 是半圆O 的直径90ACB ∠∴=︒90AFC ACB ∠∠∴==︒又FAC CAB ∠∠=AFC ACB ∴∽ ∴AFACAC AB = 23234AB ∴=∴半圆O 的半径为2．设OC 与BF 相交于点POC AF ∥BOP BAF ∴∽ ∴12OPOB AF AB == ∴1322OP AF == ∴12PC OC OP =-=OC AF ∥ECP EAF ∴∽ ∴EC PCAE AF = 即123AC AEAE -= 2316AE-=∴123AE = 【点评】本题考查了切线的性质与判定相似三角形的性质与判定掌握切线的判定以及相似三角形的性质与判定是解题的关键．9．(1)见解析(2)3【分析】（1）连接DO 根据CD 是O 的切线 OF AD ⊥ 证明ADC DOF ∠∠= 利用等腰三角形三线合一性质证明ADC AOF ∠∠=．（2）利用平行线分线段成比例定理计算OE 证明CFO CDB △∽△ 计算OF两线段作差即可求解．【解析】（1）如图，连接DO CD 是O 的切线OD DF ∴⊥90ADC ADO ∠∠∴+=︒OF AD ⊥ OA OD =90DOF ADO ∠∠∴+=︒ DOF AOF ∠∠=ADC DOF ∠∠∴=ADC AOF ∠∠∴=．（2）如图，连接DO CD 是O 的切线OD DF ∴⊥90CDO ∠∴=︒53OC OB =设5(0)CO k k => 则3DO OB AO k ===4CD k ∴=538CB CO OB k k k ∴=+=+= AB 是O 的直径 24BD =AD DB ∴⊥OF AD ⊥∴OF BD ∥ ∴AO AE OB ED = CFO CDB △∽△ ∴OF CO BD CB= AE ED ∴=5524538OF k k k ==+ ∴1122OE BD == 15OF = 3EF OF OE ∴=-=．【点评】本题考查了切线的性质等腰三角形的三线合一性质平行线分线段成比例定理相似三角形的性质与判定熟练掌握切线的性质相似三角形的性质与判定是解题的关键．10．(1)证明过程见解析 (2)142π-【分析】（1）AB 是O 的直径 AC AD = BF BC = 可求出90FBD ∠=︒ AB BF ⊥ 由此即可求证（2）如图，所示（见解析）连接,CO EO 可得1OC OE == 可证222CO O CE += 90COE ∠=︒ 根据扇形面积的计算方法即可求解．【解析】（1）证明①AB 是O 的直径①90ACB ∠=︒①90ACD BCD ∠+∠=︒①AC AD =①ACD ADC ∠=∠①ADC BDF ∠=∠①ACD BDF ∠=∠①BC BF =①BCD F ∠=∠①90BDF F ∠+∠=︒①180()90FBD FDB F ∠=︒-∠+∠=︒①AB BF ⊥ 且OB 是O 的半径①BF 是O 的切线．（2）解如图，所示连接,CO EO①2AB =①1OC OE == ①2CE ①222CO EO += 2222CE == ①222CO O CE +=①90COE ∠=︒ ①29011111360242ππS ⨯=-⨯⨯=-阴影 ①图中阴影部分的面积为142π-．【点评】本题主要考查圆的基础知识掌握圆的切线的证明方法扇形面积的计算方法是解题的关键．11．(1)见解析(2)3【分析】（1）连接CO 根据OF BC ∥可得B AOF ∠=∠ 根据直径所对的圆周角为直角可得90B CAB ∠+∠=︒ 再根据AO CO =得出CAB ACO ∠=∠ 最后证明90ACD ACO ∠+∠=︒即可（2）根据中位线定理得出152OE BC == 证明DBC DOF ∽ 根据相似三角形对应边成比例即可求解．【解析】（1）证明连接CO①OF BC ∥①B AOF ∠=∠①AB 为O 的直径①90ACB ∠=︒ 则90B CAB ∠+∠=︒①90AOF CAB ∠+∠=︒①AO CO =①CAB ACO ∠=∠①ACD AOF ∠=∠①90ACD ACO ∠+∠=︒ 即OC CD ⊥①CD 为圆O 的切线（2）①AB 为O 的直径①点O 为AB 中点①OF BC ∥①OE 为ABC 中位线 ①152OE BC == ①1sin 4D = OC CD ⊥ ①4OD OC = 则5BD OD OB OC =+=①OF BC ∥①DBC DOF ∽ ①OF OF BC BD = 即4510OC OF OC = 解得8OF =①853EF OF OE =-=-=．【点评】本题主要考查了切线的判定和性质圆周角定理相似三角形的判定和性质以及解直角三角形解题的关键是掌握切线的判定和性质以及相似三角形的判定和性质．12．(1)30︒(2)100︒【分析】（1）根据三角形内角和定理可得60ABC ∠=︒ 再由AD CD = 可得ABD CBD ∠=∠ 即可求解（2）根据圆周角定理可得30ABD ACD ∠∠==︒ 从而得到80BCD ∠=︒ 再由圆内接四边形的性质即可求解．【解析】（1）解①70,50BAC ACB ∠=︒∠=︒①18060ABC BAC ACB ∠=︒-∠-∠=︒①AD CD = ①1302ABD CBD ABC ∠=∠=∠=︒ （2）解由圆周角定理得30ABD ACD ∠∠==︒①80BCD ACB ACD ∠=∠+∠=︒①四边形ABCD 是O 的内接四边形①180100BAD BCD ∠=︒-∠=︒．【点评】本题主要考查了圆内接四边形的性质圆周角定理等知识熟练掌握圆内接四边形的性质圆周角定理是解题的关键．13．(1)见解析(2)AD 的长是25【分析】（1）连接OA 根据已知条件证明OA AE ⊥即可解决问题（2）作OF CD ⊥ 则四边形OAEF 是矩形且132DF CD ==由此可求得DE 的长在Rt OFD △中勾股定理求出OF 即AE 的长在Rt AED △中利用勾股定理求DA ．【解析】（1）证明如图，连接OA①AE CD ⊥①90DAE ADE ∠+∠=︒．①DA 平分BDE ∠①ADE ADO ∠=∠又①OA OD =①OAD ADO ∠=∠①90DAE OAD ∠+∠=︒①OA AE ⊥①AE 是O 的切线（2）解过点O 作OF CD ⊥于F ．①90OAE AEF OFE ∠︒=∠=∠=①四边形OAEF 是矩形①5EF OA AE OF ===，．①OF CD ⊥ ①132DF FC CD ===①532DE EF DF =-=-=在Rt OFD △中 2222534OF OD DF --=①4AE OF ==在Rt AED △中 22224225AD AE DE ++=①AD 的长是25【点评】本题考查了切线的判定与性质垂径定理圆周角定理勾股定理解决本题的关键是掌握切线的判定与性质．14．(1)12π(2)9【分析】(1) 根据题意 CEB APB ABC PBE S S S S S =+--阴影扇形扇形根据公式计算即可．(2) 连接PE 根据题意 45,135,90PEB CEP PEC ∠=︒∠=︒∠=︒ 根据勾股定理计算即可．【解析】（1）如图， ①正方形ABCD 旋转APB △到CEB 的位置①APB CEB ≌ 90ABC PBE ∠=∠=︒ =CEB APB S S ①CEB APB ABC PBE S S S S S =+--阴影扇形扇形①ABC PBE S S S =-阴影扇形扇形①48BP AB ==， ①9064901612360360S πππ︒⨯⨯︒⨯⨯=-=︒︒阴影．（2）连接PE根据题意 45,135PEB APB CEP ∠=︒∠=∠=︒ AP CE =①90PEC ∠=︒①4BP = 7AP =①2227,4432CE PE ==+=①222273281PC CE PE =+=+=解得9PC =．【点评】本题考查了正方形的性质旋转的性质阴影面积的计算扇形面积公式勾股定理熟练掌握旋转的性质阴影面积的计算扇形面积公式勾股定理是解题的关键．15．(1)证明见解析(2)10DF =【分析】（1）因为CDB CAB ∠=∠ CDB BFD ∠=∠ 所以CAB BFD ∠=∠ 即可得出FD ①AC 可得得出OD FD ⊥ 进而得出结论（2）利用勾股定理先求解AC 再利用垂径定理得出AE 的长可得OE 的长证明AEO FDO ∽ 再利用相似三角形的判定与性质得出DF 的长．【解析】（1）①CDB CAB ∠=∠ CDB BFD ∠=∠①CAB BFD ∠=∠①FD AC ∥①OD 垂直于弦AC 于点E①OD FD ⊥①FD 是O 的一条切线（2）①AB 为O 的直径①90ACB ∠=︒①15AB = 9BC = ①2215912AC -= 7.5AO OB OD ===①DO AC ⊥①6AE CE == ①227.56 4.5OE -①AC FD ∥①AEO FDO ∽ ①AE EO FD DO = ①4.567.5FD= 解得10DF =．经检验符合题意.【点评】本题主要考查了相似三角形的判定与性质垂径定理圆周角定理切线的判定以及平行线的判定掌握相似三角形的判定与性质垂径定理圆周角定理以及平行线的判定是解题的关键．16．(1)50︒(2)30︒【分析】（1）连接OA 先由切线的性质得OAE ∠的度数求出2142AOB C ∠=∠=︒ 进而得AOE ∠ 则可求出答案（2）连接OA 根据等腰三角形的性质及切线的性质列方程求解即可．【解析】（1）连接OA ．如图，①AE 切O 于点AOA AE ∴⊥90OAE ∴∠=︒70C ∠=︒2270140AOB C ∴∠=∠=⨯︒=︒又180AOB AOE ∠+∠=︒40AOE ∴∠=︒90AOE E ∠+∠=︒904050E ∴∠=︒-︒=︒．（2）连接OA 如图，①设E x ∠=．AB AE =ABE E x ∴∠=∠=OA OB =OAB ABO x ∴∠=∠=2AOE ABO BAO x ∴∠=∠+∠=． AE 是O 的切线OA AE ∴⊥ 即90OAE ∠=︒在OAE ∆中 90AOE E ∠+∠=︒即290x x +=︒解得30x =︒30E ∴∠=︒．【点评】本题主要考查了切线的性质等腰三角形的性质圆周角的性质三角形内角和的性质用方程思想解决几何问题关键是熟悉掌握这些性质．17．(1)见解析(2)10cm【分析】(1)连接OD 根据平行线的判定与性质可得90ODE DEM ∠=∠=︒ 又点D 在O 上即可证得DE 是O 的切线(2)首先根据勾股定理可得AD 的长再由ACD ADE ∽ 根据相似三角形的性质列出比例式代入数据即可求得圆的半径．【解析】（1）证明如图，连接ODOA OD =OAD ODA ∠=∠∴ AD 平分CAM ∠OAD DAE ∴∠=∠ODA DAE ∴∠=∠DO MN ∴∥DE MN ⊥90ODE DEM ∴∠=∠=︒ 即OD DE ⊥ 又点D 在O 上 OD 为O 的半径DE ∴是O 的切线（2）解90AED ∠=︒ 8cm DE = 4cm AE =22228445AD DE AE ∴++如图，连接CDAC 是直径90ADC AED ∴∠=∠=︒CAD DAE ∠=∠ACD ADE ∴△∽△AD AC AE AD ∴= 4545=解得20AC =O ∴的半径为10cm ．【点评】本题考查圆了切线的判定；等边对等角平行线的判定与性质圆周角定理勾股定理相似三角形的判定和性质等知识在圆中学会正确添加辅助线是解决问题的关键．18．(1)见解析 (2)49【分析】（1）欲证~CBA FDC ，只要证明两个角对应相等就可以．可以转化为证明DE BC =就可以（2）由~CBA FDC 可得814CF = ACB F ∠=∠ 进而即可得到答案．【解析】（1）证明①四边形ABCD 内接于O①CBA CDF ∠=∠．①DE BC =①BCA DCE ∠=∠．①~CBA FDC（2）解①C 是DBA 的中点①9CD AC ==①~CBA FDC 4AB = ①AB AC CD CF = 即499CF= ①814CF = ①~CBA FDC ①94tan tan 8194AC ACB F CF ∠=∠===．【点评】本题考查的是圆的综合题；涉及弧、弦的关系；等腰三角形的性质；相似三角形的判定与性质；锐角三角函数；掌握相似三角形的判定和性质是解答此题的关键．。

初中数学圆形专题训练50题答案

初中数学圆形专题训练50题含参考答案一、单选题1．函数233y x =--自变量x 的取值范围是（）． A ．0x ≠ B ．1x ≠ C ．1x > D ．1x <2．反比例函数y=ｋｘ的图象经过点(-1,2)，k 的值是( ) A ．－1 B ． 1 C ．－2 D ．2 3．如图，A ，B ，C 是O 上的三个点，若66B ︒∠=，则OAC ∠的度数为（）A ．24︒B ．29︒C ．33︒D ．132︒ 4．如图，在同一平面直角坐标系中，一次函数(0)y ax b ab =+≠的图象与反比例函数(0)ab y ab x=≠的图象大致可以是（） A ． B ．C ．D ．5．如图，扇形纸扇完全打开后，外侧两竹条AB ，AC 的夹角为150°，AB 的长为30cm，BD的长为15cm，则DE的长为（）A．254cmπB．252cmπC．25cmπD．50cmπ6．已知点A（3a+1，﹣4a﹣2）在第二、四象限角平分线上，则a2009+a2010的值为（）A．﹣1B．0C．1D．27．小芳步行上学，最初以某一速度匀速前进，中途遇红灯，稍作停留后加快速度跑步去上学，到校后，她请同学们画出她行进路程s（米）与行进时间t（分钟）的函数图象的示意图.你认为正确的是（）A．B．C．D．8．如图是我们学过的反比例函数图象，它的函数解析式可能是（）A．2y x B．4yx=C．3yx=-D．12y x=9．如图，点P为反比例函数myx=上的一点，PA x⊥轴于点A，C为y轴上一点．如果PCA 的面积为2，则二次函数()221y m x mx =--+的顶点在第（）象限A ．一B ．二C ．三D ．四 10．对于圆的周长公式C =2πR ，下列说法错误的是（）A ．π是变量B ．R、C 是变量 C ．R 是自变量D ．C 是因变量 11．已知圆O 的半径是3，A ，B ，C 三点在圆O 上，∠ACB=60°，则弧AB 的长是（）A ．2πB ．πC ．32πD ．12π 12．在圆柱形油槽内装有一些油．截面如图，油面宽AB 为60cm ，如果再注入一些油后，油面AB 上升10cm ，油面宽变为80cm ，则该圆柱形油槽直径MN 为( )A ．55cmB ．60cmC ．80cmD ．100cm 13．下列一次函数中，y 随x 增大而减小的是( )A ．3y x =B ．32y x =-C ．32y x x =+D ．32y x =-- 14．一次函数y =mx +n 的图象经过一、二、四象限，点A （1，y 1），B （3，y 2）在该函数图象上，则（）A ．y 1＞y 2B ．y 1≥y 2C ．y 1＜y 2D ．y 1≤y 215．已知抛物线()2210y ax ax a =-+<，当12x -≤≤时，y 的最大值为2，则当12x -≤≤时，y 的最小值为（）A ．1B ．0C ．1-D ．2- 16．如图，O 的半径为6，将劣弧沿弦AB 翻折，恰好经过圆心O ，点C 为优弧AB 上的一个动点，则ABC 面积的最大值是（）A．B．C．D．18+17．关于二次函数223y x x=-++，下列说法中不正确．．．的是（）A．图象开口向下B．图象的对称轴是1x=C．当1x>时，y随x的增大而增大D．函数的最大值为418．若点B（a，0）在以点A（1,0）为圆心，以3为半径的圆内，则a的取值范围是（）A．-2＜a＜4B．a＜4C．a＞-2D．a＞4或a＜-219．二次函数y＝ax2＋bx＋c（abc≠0）的图象如图所示，反比例函数y＝cx与正比例函数y＝bx在同一坐标系内的大致图象是（）A．B．C．D．20．给出下列函数：∠y=31(1)31(1)x xx x-≥⎧⎨--<⎩；∠y=3x；∠y=3x2．从中任取一个函数，取出的函数符合条件“当x＞1时，函数值y随x增大而减小”的概率是（）A ．1B ．23 C ．13 D ．0二、填空题21．若点P （a ，a ﹣4）在第四象限，则点N （﹣a ，4﹣a ）在第 _____象限． 22．已知一次函数32y x =-+，那么y 的值随x 的增大而________.23．如图，抛物线2y ax bx c =++与x 轴交于点A ，B ，若对称轴为直线=1x -，点A 的坐标为（-3，0），则不等式20ax bx c ++>的解集为______．24．若点A （2，n ）在x 轴上，则点B （n+2，n-5）位于第______象限．25．抛物线244y x x =-+与坐标轴有_______个交点．26．若一个扇形的圆心角为60︒，面积为26cm π，则这个扇形的弧长为__________ cm（结果保留π）27．已知二次函数y ＝x 2﹣2x +m 的图象与x 轴交于A ，B 两点，若点A 坐标为（﹣1，0），则点B 的坐标为_____．28．点()1,23A m m --在第一、三象限夹角的角平分线上，则m 的值为_________．29．把函数22y x x =-化为2()y a x h k =-+的形式为________．30．已知点(32,4)N a a --到x 轴的距离等于到y 轴的距离的2倍，则a 的值为__________．31．抛物线2y ax bx c =++上部分点的横坐标x ，纵坐标y 的对应值如表所示，则抛物线的对称轴是____．32．如图，这是一个铅皮做成的无盖半圆锥状容器，它是由半个圆锥侧面和一个等腰三角形围成的．若不考虑容器厚度、接缝以及余料等因素，则根据图中给出的尺寸，制造这样一个容器需要铅皮____cm 2．33．若抛物线 ()22y a x =- 的开口向上，则 a 的取值范围是________．34．如图，圆锥的母线长为10，侧面展开图的面积为60π，则圆锥主视图的面积为__________．35．如图，Rt △ABC 中，∠C ＝90°，AC ＝3，AB ＝5.则△ABC 的内切圆半径r ＝____．36．用半径为6的半圆围成一个圆锥的侧面，则圆锥的底面半径为________． 37．我们规定:平面内点A 到图形G 上各个点的距离的最小值称为该点到这个图形的最小距离d ，点A 到图形G 上各个点的距离的最大值称为该点到这个图形的最大距离D ，定义点A 到图形G 的距离跨度为R ＝D －d ．在平面直角坐标系xOy 中，图形G 为以原点O 为圆心，2为半径的圆，则点A(1，－1)到图形G 的距离跨度是_______． 38．如图，点、、A B C 在半径为8的O 上，过点B 作//BD AC ，交OA 延长线于点D ．连接BC ，且30BCA OAC ︒∠=∠=，则图中阴影部分的面积为__________．39．一圆锥的侧面展开图的圆心角为90︒，底面半径为3，则该圆锥的侧面积为_______．40．在平面直角坐标系中，已知点()4,0A -，点()0,4B ，点()4,4C -，动点D 从A 点出发，以每秒1个单位的速度水平向右运动，动点E 从点B 出发，以每秒1个单位的速度竖直向上运动，过点A 作AG CE ∥交CD 于点G ，当线段OG 的值最小时，则运动时间t 的值为 _____．三、解答题41．如图，以四边形ABCD 的对角线BD 为直径作圆，圆心为O ，过点A 作AE CD ⊥的延长线于点E ，已知DA 平分BDE ∠．(1)求证：AE 是O 的切线；(2)若4AE =，6CD =，求O 的半径和AD 的长．42．如图，∠ABC 内接于∠O ，AB 是∠O 的直径，I 是∠ABC 内一点，AI 的延长线交BC 于点D ，交∠0于点E ，连接BE ，BI ，若IB 平分∠ABC ，EB =EI ．(1)求证：AE 平分∠BAC ；(2)若BD OI ∠AD 于点I ，求BE 的长．43．如图，O 是ABC 的外接圆，点O 在BC 边上，BAC ∠的平分线交O 于点D ，连接,BD CD ，过点D 作DP BC ∥，与AC 的延长线交于点P ．(1)求证：DP 是O 的切线；(2)当3cm,4cm AB AC ==时，求线段PC 的长．44．如图，一条直线11y k x b =+与反比例函数22k y x=的图象交于A （1，5）、B （5，n ）两点，与x 轴交于C 点．(1)求反比例函数的解析式；(2)求C 点坐标(3)请直接写出当12y y ＜时，x 的取值范围；45．如图，已知AB 是O 直径，且8AB =，C ，D 是O 上的点，OC BD ∥，交AD于点E，连接BC，30CBD∠=︒．(1)求COA∠的度数；(2)求图中弧BD与弦BD围成的阴影部分的面积（结果保留π）．46．小明准备给长16米，宽12米的长方形空地栽种花卉和草坪，图中I、II、III三个区域分别栽种甲、乙、丙三种花卉，其余区域栽种草坪．四边形ABCD和EFGH均为正方形，且各有两边与长方形边重合；矩形MFNC（区域II）是这两个正方形的重叠部分，如图所示．（1）若花卉均价为300元2/米，种植花卉的面积为S()2米，草坪均价为200元2/米，且花卉和草坪栽种总价不超过43600元，求S的最大值．（2）若矩形MFNC满足:1:2MF FN=．∠求MF，FN的长．∠若甲、乙、丙三种花卉单价分别为180元2/米，90元2/米，180元2/米，且边BN的长不小于边ME长的54倍．求图中I、II、III三个区域栽种花卉总价W的最大值．47．如图，在5×5的方格（每小格边长为1）内有4只甲虫A、B、C、D，它们爬行规律总是先左右，再上下．规定：向右与向上为正，向左与向下为负．从A到B的爬行路线记为：A→B（＋1，＋4），从B到A的爬行路线为：B→A（－1，－4），其中第一个数表示左右爬行信息，第二个数表示上下爬行信息，那么图中（1）A→C（，），B→D（，），C→ （＋1，）；（2）若甲虫A的爬行路线为A→B→C→D，请计算甲虫A爬行的路程；（3）若甲虫A的爬行路线依次为（＋2，＋2），（＋1，－1），（－2，＋3），（－1，－2），最终到达甲虫P处，请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置．48．如图，O是ABC∆的外接圆，AB是O的直径，点D在O上，AC平分BAD∠，过点C的切线交直径AB的延长线于点E，连接AD、BC．（1）求证：BCE=∠∠CAD．（2）若O的半径长为r，AD m=，写出求线段CE长的思路（不用求出结果）．49．如图，点P是∠O直径AB上的一点，过P作直线CD∠AB，分别交∠O于C、D两点，连接AC，并将线段AC绕点A逆时针旋转90°，得到AE，连接ED，分别交∠O和A、B于F、G，连接FC，（1）求证：∠ACF＝∠AED；（2）若点P在直径AB上运动（不与点A，B重合）其他条件不变，请问EGAP是否为定值？若是，请求出其值，若不是，请说明理由．50．已知△ABC内接于∠O，CD为直径，CD交AB边于点E，且CE=AC．（1）如图1，求证∠ACD=2∠BCD；（2）如图2，过点O作OF∠AC，过点B作BH∠CD，求证：AC=2OH；（3）如图3，在（2）的条件下，过点E作AB的垂线交BC于点K，连接EF，AD，若AD+AC=14，且∠AFE+∠CEF=90°，求CK的长．参考答案：1．B【分析】根据分式的分母不为零进行求解即可.【详解】根据题意，330x -≠，解得1x ≠，故选：B.【点睛】本题主要考查了反比例函数自变量的取值范围，熟练掌握分式的性质是解决本题的关键.2．C【详解】∠反比例函数y=ｋｘ经过（-1，2），∠k=-1×2=-2.故选C. 3．A【分析】根据圆周角定理得到2132AOC B ∠=∠=︒，再根据等腰三角形的性质及三角形内角和求解即可．【详解】解：66B ∠=︒，2132AOC B ∴∠=∠=︒，OA OC =，OAC OCA ∴∠=∠，11(180)(180132)2422OAC AOC ∴∠=︒-∠=⨯︒-︒=︒，故选：A ．【点睛】此题考查了圆周角定理，解题的关键是熟记圆周角定理．4．C【分析】根据一次函数图象所在象限，确定出a ，b 的符号，再根据反比例函数图象所在的象限，确定出a ，b 的符号，至此找出一次函数和反比例函数a ，b 的符号一致的选项即可．【详解】解：A.由一次函数图象知a ，b 异号，由反比例函数图象知a ，b 同号，故该选项错误，不符合题意；B.由一次函数图象知a ，b 同号，由反比例函数图象知a ，b 异号，故该选项错误，不符合题意；C.由一次函数图象知a ，b 异号，由反比例函数图象知a ，b 异号，故该选项正确，符合题意；D.由一次函数图象知a ，b 异号，由反比例函数图象知a ，b 同号，故该选项错误，不符合题意．故选：C ．【点睛】本题考查了一次函数，反比例函数图象与系数的关系．解题的关键在于确定出a ，b 的符号，明确系数与函数图象的关系．5．B【分析】根据AB ＝30cm ，BD ＝15cm ，可以得到AD 的长，然后根据AB ，AC 夹角为150°和弧长计算公式可以得到DE 的长．【详解】∠AB ＝30cm ，BD ＝15cm ，AB ，AC 夹角为150°，∠AD ＝AB ﹣BD ＝15cm ，∠DE 的长为：15015180π⨯⨯＝252π（cm ），故选：B ．【点睛】本题考查了弧长的计算，掌握计算公式是解题关键．6．B【分析】根据角平分线上的点到角的两边的距离相等，以及第二、四象限点的横坐标与纵坐标的符号相反列出方程求解即可．【详解】解：∠点A （3a +1，﹣4a ﹣2）在第二、四象限的角平分线上，∠3a +1＝﹣（﹣4a ﹣2），解得a ＝﹣1，∠a 2009+a 2010＝﹣1+1＝0．故选：B【点睛】本题考查了角平分线的性质和平面直角坐标系各象限的点的坐标特征，熟知两个知识点是解题关键．7．C【详解】试题分析：运用排除法解答本题，中间的停留路程不变，可排除BD 两项，最后的加速图象应为比最初的路程增加直线增速更快的图象，排除A ，故选C.考点：函数的图象．8．B【分析】此题考查反比例函数图象的性质；【详解】反比例函数(0)k y k x=≠，当0k >时，图像分布在第一、三象限；当0k <时，图像分布在第二、四象限；所以选B9．D【分析】先根据反比例函数比例系数的几何意义求出m 的值，然后求出二次函数的顶点坐标即可得到答案．【详解】解：∠点P 为反比例函数m y x=上的一点，PA x ⊥轴于点A ，C 为y 轴上一点，PCA 的面积为2， ∠24PCA m S ==△，又∠反比例函数图象经过第一象限，∠4m =，∠二次函数解析式为()22241211y x x x =-+=--， ∠二次函数的顶点坐标为()11-，， ∠二次函数()221y m x mx =--+的顶点在第四象限，故选：D ．【点睛】本题主要考查了反比例函数比例系数的几何意义，二次函数图象的性质，判断点所在的象限，正确求出m 的值是解题的关键．10．A【详解】解：A ．π是一个常数，是常量，故选项符合题意；B ．R 、C 是变量，故选项不符合题意；C ．R 是自变量，故选项不符合题意；D ．C 是因变量，故选项不符合题意．故选：A ．11．A【详解】分析：先根据同弧所对的圆心角是其所对圆周角的2倍求出∠AOB 的度数，再根据扇形的弧长公式计算.详解：如图，∠∠AOB 与∠ACB 对的弧相同，∠ACB =60°，∠∠AOB =2∠ACB =120°， ∠12032180180n R l πππ⨯⨯===．故选A ．点睛：本题考查了圆周角定理和弧长的计算公式，熟记弧长计算公式是解答本题的关键，如果扇形的圆心角是n º，扇形的半径是R ，则扇形的弧长l 的计算公式为：180n R l π=. 12．D【分析】若油面AB 上升后到达油面CD ，过圆心O 作圆的半径OE 垂直于AB ，设垂足为H ，交CD 于点G ，连接OA 、OC ，设出OG 的长度，在两直角三角形中利用勾股定理分别可得OA 、OC 的长度，利用圆的半径相等，即OA=OC 可求得OG ，进而可求MN 的长度【详解】解：如图：若油面AB 上升后到达油面CD ，过圆心O 作圆的半径OE 垂直于AB ，设垂足为H ，交CD 于点G ，连接OA 、OC ，由垂径定理可得：CG=40，AH=30设OG=x ，则OH=x+10在直角三角形OGC 中：22240OC x =+在直角三角形OHA 中：()2221030OA x =++OC OA =()2222401030x x ∴+=++ 解得x=30代入22240OC x =+可得22500OC =0OC >50OC ∴=2100MN OC ∴==故选：D【点睛】本题考查垂径定理的应用及勾股定理，根据垂径定理构造直角三角形是解决本题的关键13．D【详解】∠A ，B ，C 中，自变量的系数大于0，∠y 随x 增大而增大；∠D 中，自变量的系数小于0，∠y 随x 增大而减小；故选D.14．A【分析】先根据图象在平面坐标系内的位置确定m 、n 的取值范围，进而确定函数的增减性，最后根据函数的增减性解答即可.【详解】解：∠一次函数y =mx +n 的图象经过第一、二、四象限，∠m <0，n >0∠y 随x 增大而减小，∠1<3，∠y 1＞y 2.故选：A.【点睛】本题主要考查一次函数图象在坐标平面内的位置与k 、b 的关系、一次函数的增减性等知识点，图象在坐标平面内的位置确定m 、n 的取值范围成为解答本题的关键. 15．D【分析】根据抛物线的解析式可得其对称轴为直线x =1，从而当x =1时，y 有最大值2，此时可求得a 的值，再根据抛物线的增减的性质求得y 在所给范围内的最小值．【详解】∠212a x a-=-=，即抛物线的对称轴为直线x =1 ∠当x =1时，y 有最大值，且1在12x -≤≤范围内∠a -2a +1=2解得：a =-1即2+21y x x =-+当1<1x ≤-时，函数值y 随x 的增大而增大，此时函数在x =-1处取得最小值，且最小值为1212y =--+=-当12x <≤时，函数值y 随x 的增大而减小，此时函数在x =2处取得最小值，且最小值为42211y =--⨯+=∠-2<1∠当12x -≤≤时，y 的最小值为−2故选：D ．【点睛】本题考查了二次函数的增减性质、求函数解析式，关键是确定抛物线的对称轴，根据对称轴的位置便可确定函数的增减的范围，解答函数在某个自变量的范围的最值问题时，最好借助图象，利用数形结合的思想能帮助解决问题．16．A【分析】如图，过点C 作CT ∠AB 于点T ，过点O 作OH ∠AB 于点H ，交∠O 于点K ，连接AO ，AK ．解直角三角形求出AB ，求出CT 的最大值，可得结论．【详解】解：如图，过点C 作CT ∠AB 于点T ，过点O 作OH ∠AB 于点H ，交∠O 于点K ，连接AO ，AK ．由题意AB 垂直平分线段OK ，∠AO ＝AK ，∠OA ＝OK ，∠OA ＝OK ＝AK ，∠∠OAK ＝∠AOK ＝60°．∠AH ＝OA •sin60°＝∠OH ∠AB ，∠AH ＝BH ，∠AB ＝2AH ＝∠OC ＋OH ≥CT ，∠CT ≤6＋3＝9，∠CT 的最大值为9，∠∠ABC 的面积的最大值为192⨯=，故选：A ．【点睛】本题考查垂径定理，勾股定理，三角形的面积，垂线段最短等知识，解题的关键是求出CT 的最大值，属于中考常考题型．17．C【分析】根据题目中的函数解析式，利用二次函数的性质可以判断各个选项中的说法是否正确．【详解】解：二次函数()222314y x x x =-++=--+，∴该函数的图象开口向下，故选项A 的说法正确，不符合题意；对称轴是直线()2121x =-=⨯-，故选项B 中的说法正确，不符合题意；当1x >时，y 随x 的增大而增小，故选项C 中的说法错误，符合题意；函数图象的顶点坐标为()1,4，则函数的最大值为4，故选项D 中的说法正确，不符合题意；故选：C ．【点睛】本题考查抛物线的开口方向，对称轴，顶点坐标，增减性，解答本题的关键是明确题意，利用二次函数的性质解答．18．A【详解】试题解析：∠点B （a ，0）在以点A （1，0）为圆心，以3为半径的圆内， ∠|a-1|＜3，∠-2＜a ＜4．故选A ．点睛：点与圆的位置关系：设∠O 的半径为r ，点P 到圆心的距离OP=d ，则有：点P 在圆外⇔d ＞r ；点P 在圆上⇔d=r ；点P 在圆内⇔d ＜r ．19．D【分析】先根据二次函数的图象可得,b c 的符号，再根据反比例函数的图象、正比例函数的图象特点即可得．【详解】解：抛物线的开口向上，与y 轴的交点位于y 轴的正半轴，0,0a c ∴>>，抛物线的对称轴位于y 轴的右侧，02b x a∴=->， 0b ∴<，由0c >可知，反比例函数c y x=的图象位于第一、三象限，由0b <可知，正比例函数y bx =的图象经过原点，且经过第二、四象限，观察四个选项可知，只有选项D 符合，故选：D ．【点睛】本题考查了二次函数、反比例函数和正比例函数的图象，熟练掌握各函数的图象特点是解题关键．20．C【分析】分别求各函数在X 大于1时的单调性以得到在X 大于1时递减的函数的个数，再求其概率.【详解】∠X 大于1时，系数3大于0，函数递增．∠K=3时，反比例函数在第一象限递减.∠二次函数系数3大于0，在第一象限递增.综上所述，三个函数中，只有第二个函数满足条件，所以概率为13.即答案选C. 【点睛】熟练掌握各种函数的图像单调性是本题解答的关键.21．二【分析】根据各象限内点的坐标特征解答即可．【详解】解：∠点P （a ，a ﹣4）在第四象限，∠a ＞0，a -4＜0，∠0＜a ＜4，∠-a ＜0，4-a ＞0，∠点N （﹣a ，4﹣a ）在第二象限，故答案为：二．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．22．减小【分析】根据一次函数图象与系数的关系可判断.【详解】解：∠一次函数的0k <，∠y 的值随x 的增大而减小，故答案为减小.【点睛】本题考查了一次函数图象与系数的关系：对于一次函数y ＝kx ＋b ：当k ＞0，y 的值随x 的增大而增大；k ＜0，y 的值随x 的增大而减小.23．31x -<<【分析】函数的对称轴为直线=1x -，与x 轴交点(3,0)A -，则另一个交点(1,0)B ，进而求解．【详解】解：函数的对称轴为直线=1x -，与x 轴交点(3,0)A -，则另一个交点(1,0)B ，观察函数图象知，不等式20ax bx c ++>的解集为：31x -<<，故答案为：31x -<<．【点睛】本题考查了抛物线与x 轴的交点，主要考查函数图象上点的坐标特征，解题的关键是要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征．24．四【分析】直接利用x 轴上点的坐标特点得出n 的值，进而得出答案．【详解】∠点A （2，n ）在x 轴上，∠n =0，则点B （n +2，n ﹣5）的坐标为：（2，﹣5）位于第四象限．故答案为四．【点睛】本题考查了点的坐标，正确得出n 的值是解题的关键．25．2【分析】根据二次函数的图像与系数的关系直接进行求解即可．【详解】解：由抛物线244y x x =-+可得与y 轴的交点坐标为()0,4，与x 轴只有一个交点其坐标为()2,0，所以与坐标轴的交点有2个；故答案为2．【点睛】本题主要考查二次函数的图像与系数的关系，熟练掌握二次函数的图像与系数的关系是解题的关键．26．3π 【分析】先利用扇形的面积公式求出扇形的半径，再利用弧长公式即可得．【详解】设扇形的半径为rcm 则2603606πr π= 解得1()r cm =或1()r cm =-（不符题意，舍去）则这个扇形的弧长为601()1803ππcm ⨯= 故答案为：3π．【点睛】本题考查了扇形的面积公式、弧长公式，熟记公式是解题关键．27．（3，0）．【分析】根据二次函数y ＝x 2﹣2x +m 的图象与x 轴交于A ，B 两点，点A 坐标为（﹣1，0），可以求得m 的值，从而可以得到该函数的解析式，进而求得点B 的坐标．【详解】∠二次函数y ＝x 2﹣2x +m 的图象与x 轴交于A ，B 两点，点A 坐标为（﹣1，0）， ∠0＝（﹣1）2﹣2×（﹣1）+m ，解得，m ＝﹣3，∠y ＝x 2﹣2x ﹣3，当y ＝0时，0＝x 2﹣2x ﹣3＝（x ﹣3）（x +1），解得，x 1＝3，x 2＝﹣1，∠点B 的坐标为（3，0），故答案为（3，0）．【点睛】本题考查抛物线与x 轴的交点，解答本题的关键是明确题意，利用二次函数的性质解答．28．2【分析】根据第一、三象限角平分线上点的坐标特点列式计算即可．【详解】解：∠点A （m －1，2m −3）在第一、三象限夹角的平分线上，∠m －1＝2m −3，解得m ＝2，故答案为：2．【点睛】本题主要考查点的坐标，解题的关键是掌握第一、三象限角平分线上点的横纵坐标相等．29．2(1)1y x =--【分析】由于二次项系数为1，利用配方法直接加上一次项系数的一半的平方配成完全平方式，可把一般式转化为顶点式．【详解】y =x 2﹣2x =x 2﹣2x +1﹣1=（x ﹣1）2﹣1．故答案为y =（x ﹣1）2﹣1．【点睛】本题主要考查了利用配方法将一般式转化为顶点式的方法．二次函数的解析式有三种形式：（1）一般式：y =ax 2+bx +c （a ≠0，a 、b 、c 为常数）；（2）顶点式：y =a （x ﹣h ）2+k ；（3）交点式（与x 轴）：y =a （x ﹣x 1）（x ﹣x 2）．30．87或0 【详解】解：由题可知： ∠4232a a -=-，∠当42(32)a a -=-时，得：87a =； ∠当42(23)a a -=-时，得0a =，故答案为：87a =或0． 31．x =12 【分析】利用y 值相等的x 值，根据抛物线对称性即可求解．【详解】解：∠x =0，x =1时，y=6，∠对称轴为x =0+11=22．故答案为x =12．【点睛】本题考查表格信息获取问题，抛物线对称轴，掌握表格信息获取方法，抛物线对称性求对称轴方法是解题关键．32．(240+130π)【详解】由题意得圆锥的侧面展开图面积为S=11202626022LR ππ=⨯⨯=但是图中的是圆锥的一半所以为了130π，而三角形的面积为240．故为(240+130π)．33．a ＞2【分析】利用二次函数图像的性质直接求解.【详解】解:∠抛物线()22y a x =-的开口向上， ∠a-2>0，∠a ＞2，故答案为a ＞2.【点睛】本题考查二次函数图像的性质，掌握二次项系数决定开口方向是本题的解题关键. 34．48【分析】圆锥的主视图是等腰三角形，根据圆锥侧面积公式S=πrl 代入数据求出圆锥的底面半径长，再由勾股定理求出圆锥的高即可．【详解】根据圆锥侧面积公式：S=πrl ，圆锥的母线长为10，侧面展开图的面积为60π，故60π=π×10×r ，解得：r=6．由勾股定理可得圆锥的高∠圆锥的主视图是一个底边为12，高为8的等腰三角形，∠它的面积=1128=482⨯⨯，故答案为：48【点睛】本题考查了三视图的知识，圆锥侧面积公式的应用，正确记忆圆锥侧面积公式是解题关键．35．1【分析】设AB 、BC 、AC 与∠O 的切点分别为D 、E 、F ；易证得四边形OECF 是正方形；那么根据切线长定理可得：CE=CF=12（AC+BC-AB ），由此可求出r 的长．【详解】如图，在Rt△ABC，∠C=90°，AC=3，AB=5，根据勾股定理，四边形OECF中，OE=OF，∠OEC=∠OFC=∠C=90°，∠四边形OECF是正方形，由切线长定理，得：AD=AF，BD=BE，CE=CF，∠CE=CF=1（AC+BC-AB），2（3+4-5）=1．即：r=12故答案为1【点睛】此题考查了三角形内切圆的性质．注意切线长定理，还要注意直角三角形的内切圆中，如果连接过切点的半径，可以得到一个正方形，借助于方程即可求得半径．36．3cm．【详解】解：由题意知：底面周长=6πcm，∠底面半径=6π÷2π=3cm．故答案为：3cm．【点睛】本题考查圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．37．【分析】先根据跨度的定义先确定出点到圆的最小距离d和最大距离D，即可得出跨度；【详解】解：如图，过点A作圆O的直径EF，则EF=4，d=AF，D=EA∠A(1，－1)，=，∠R＝D －d=故答案为：【点睛】本题主要考查了点和圆的位置关系，理解和应用新定义解决问题，还涉及到平面坐标系内，两点间的距离公式，由已知点的坐标计算距离跨度是解本题的关键．38．323π 【分析】连接OB ，证明∠OBD=90°，再由//BD AC 得到∠D=∠OAC=30°，求出BD ，分别求出∠BOD 的面积和扇形AOB 的面积，再相减即可得出答案．【详解】解：证明：连接OB ，交CA 于E ，∠∠C=30°，∠C=12∠BOA ， ∠∠BOA=60°，又//BD AC ，∠∠D=∠OAC=30°∠∠DBO=180°-∠D-∠BOA=180°-30°-60°=90°，∠∠D=30°，∠BD∠2211132==882360263阴影扇形πππ∆-⨯⨯-⨯=⨯-⨯=BOD BOA n S S S BD OB OB ．故答案为323π．【点睛】本题考查了平行线的性质，圆周角定理，扇形的面积，三角形的面积，解直角三角形等知识点的综合运用，题目比较好，难度适中．39．36π【分析】由题意知圆锥展开扇形的弧长为9023180r ππ⨯⨯=⨯⨯，求出r 的值，然后根据圆锥的侧面积为290360r π⨯⨯计算求解即可．【详解】解：由题意知圆锥展开扇形的弧长为9023180r ππ⨯⨯=⨯⨯ 解得12r =∠圆锥的侧面积为2901236360ππ⨯⨯= 故答案为：36π．【点睛】本题考查了扇形的面积与弧长．解题的关键在于求出圆锥展开图的半径．40．2##2-+【分析】如图，连接CA ，CB ，取AC 的中点Q ，连接QG ，QO ，证明四边形ACBO 为正方形，可得90ACB ∠=︒，证明CAD CBE ≌，可得90AGC DCE ∠=∠=︒，则G 在以AC 为直径的圆上运动，可得当Q ，G ，O 三点共线时，OG 最短，OG 最短时，2OG =，再证明OGD OAG ∽，从而可得答案．【详解】解：如图，连接CA ，CB ，取AC 的中点Q ，连接QG ，QO ，∠点()4,0A -，点()0,4B ，点()4,4C -，∠4OA OB AC BC ====，CB OE ⊥，CA OA ⊥，∠90CBE CAD ∠==∠︒，∠四边形ACBO 为正方形，∠90ACB ∠=︒，∠动点D 从A 点出发，以每秒1个单位的速度水平向右运动，动点E 从点B 出发，以每秒1个单位的速度竖直向上运动，∠AD BE =，∠CAD CBE ≌，∠ACD BCE ∠=∠，∠90DCE DCB BCE DCB ACD ∠=∠+∠=∠+∠=︒，∠AG CE ∥，∠90AGC DCE ∠=∠=︒，∠G 在以AC 为直径的圆上运动，当Q ，G ，O 三点共线时，OG 最短，∠4AC =，则2AQ =，∠OQ =∠OG 最短时，2OG =，∠QC QG =，∠QCG QGC ∠=∠，而DGO QGC ∠=∠，∠QCG DGO ∠=∠，∠90QCG CAG CAG OAG ∠+∠=︒=∠+∠，∠QCG OAG ∠=∠，∠OAG DGO ∠=∠，∠GOD GOA ∠=∠，∠OGD OAG ∽， ∠OG OD OA OG=，∠()22264OG OD OA ===-，∠462AD =-+，∠2t ==．故答案为：2．【点睛】本题考查的是坐标与图形，全等三角形的判定与性质，相似三角形的判定与性质，圆周角定理的应用，证明G 在以AC 为直径的圆上运动是解本题的关键． 41．(1)见解析(2)5，【分析】（1）连接OA ，根据已知条件证明OA AE ⊥即可解决问题；（2）取CD 中点F ，连接OF ，根据垂径定理可得OF CD ⊥，所以四边形AEFO 是矩形，利用勾股定理即可求出结果．【详解】（1）证明：如下图，连接OA ，∠AE CD ⊥，∠90DAE ADE ∠+∠=︒．∠DA 平分BDE ∠，∠ADE ADO ∠=∠．又∠OA OD =，∠OAD ADO ∠=∠，∠90DAE OAD ∠+∠=︒，∠OA AE ⊥，∠OA 是半径，∠AE 是O 切线；（2）解：如上图，取CD 中点F ，连接OF ，∠OF CD ⊥于点F ，∠四边形AEFO 是矩形．∠6CD =，∠3DF FC ==．在Rt ∠OFD 中，4OF AE ==，∠5OD =，在Rt ∠AED 中，4AE =，532ED EF DF OA DF OD DF =-=-=-=-=，∠AD =，∠AD 的长是【点睛】本题考查了切线的判定与性质，垂径定理，圆周角定理，勾股定理，解决本题的关键是掌握切线的判定与性质．42．(1)见解析(2)2【分析】（1）根据角平分线的性质得到∠ABI ＝∠CBI ，由等腰三角形的性质得到∠EBI ＝∠EIB ，通过三角形外角的性质和圆周角定理即可得到结论；（2）由AB 是∠O 的直径，得到AE ∠BE ，推出OI ∠BE ，根据三角形的中位线的性质得到AI ＝IE ＝BE ，推出AE ＝2BE ，根据相似三角形的性质得到12DE BE BE AE ==，求得BE ＝2，DE ＝1，AE ＝4，AD ＝3，由于∠ACD ∠∠BDE ，得到EC CD A BE D =即可求得BE 的长．（1）证明：∠IB 平分∠ABC ，∠∠ABI ＝∠CBI ，∠EB ＝EI ，∠∠EBI ＝∠EIB ，∠∠EIB ＝∠BAI ＋∠IBA ，∠EBI ＝∠IBC ＋∠CBE ，∠∠BAE ＝∠CBE ，∠∠CBE ＝∠EAC ，∠∠BAE ＝∠CAE ，∠AE 平分∠BAC ；（2）如图，∠AB 是∠O 的直径，∠AE ∠BE ，∠OI ∠AE ，∠OI ∠BE ，∠AO ＝BO ，∠AI ＝IE ＝BE ，∠AE ＝2BE ，∠∠EBC ＝∠BAE ，∠∠BDE ∠∠ABE ， ∠12DE BE BE AE ==，∠BD∠BE ＝2，DE ＝1，∠∠E ＝∠C ，∠EBC =∠DAC∠∠ACD ∠∠BDE ， ∠EC CD A BE D =＝2， ∠22BE DE ==【点睛】本题考查了三角形的外接圆和外心，垂径定理，圆周角定理，三角形外角性质，等腰三角形的性质，能正确作出辅助线并求出AE ＝2BE 是解此题的关键．43．(1)证明见解析 (2)25cm 6PC =【分析】（1）连接OD ．根据角平分线的定义，圆周角定理的推论确定BD CD =，根据垂。

人教版六年级数学上册期末《圆》解决问题专题训练(含答案)

人教版六年级数学上册期末《圆》解决问题专题训练（含答案）1.求半径为5米的圆的周长和面积。

2.摩天轮的直径是10米，转一圈走过的路程是多少米？3.一个圆形花坛的半径是5米，周长是多少米呢？4.一根木头的横截面是圆，周长是50.24厘米，半径是多少厘米？5.公园草坪的自动喷洒机，喷洒射程是16.8米。

这种喷洒机的喷洒范围的周长是是多少米？6.小文的自行车轮子的直径是0.6米，如果平均每分钟转125圈，她从家到学校需10分钟，那么小文家到学校有多远?7.小明沿6米长的路走了3次，第一次10步走完，第二次9步走完，第三次11步走完，他平均一步的长度是多少米?他沿着一个圆形花坛走了一圈，刚好是157步。

这个花坛的面积约是多少平方米?( 值取3．14)8.一个圆形花坛的直径是12米,在它的周围铺一条1米宽的小路,这条小路的面积是多少平方米9.瑞瑞骑车用3.5分钟经过一座公路桥。

自行车前轮的直径是0.55米,车轮平均每分钟转80圈,公路桥长多少米?10.李爷爷把牛栓在草原的木桩上，木桩到牛鼻的绳子长6米，牛能吃到草的面积有多大11.一辆自行车的外轮胎直径是50厘米，如果每分钟转100周，要过一座942米长的桥，需要多少分钟12.一个圆形花坛的周长是31.4米(如图)，在它的外围铺一条2米宽的环形小路(阴影部分)，这条小路的面积是多少平方米?13.在下图中，已知正方形的面积是10平方厘米，这个圆的面积是多少平方厘米？14.在下图中，已知正方形的面积是10平方厘米，这个圆的面积是多少平方厘米？15.从一张正方形纸上剪下一个周长是18.84厘米的最大圆，求被剪掉的纸屑的面积。

16.在下图中，已知外面的正方形的面积是80平方厘米，求圆的面积和小正方形的面积。

17.在下图中，已知正方形的面积是40平方厘米，这个圆的面积是多少平方厘米？18.环形的外圆周长是18.84厘米，内圆直径是4厘米，求环形的面积？19.校园圆形花池的半径是6米，在花池的周围修一条1米宽的水泥路，求水泥路的面积是多少平方米？20.（1）下图是育才小学操场的跑道，跑道外圈和内圈相差多少米？（两端各是半圆）（2）400米的跑步比赛，跑道宽为1.5米，起跑线该依次提前多少米？如果跑道宽是1.25米呢？21.从一个长5分米，宽4分米的长方形木板上锯下一个最大的圆，剩下的木板面积是多少平方分米？（精确到0.01平方分米）22.（1）轧路机前轮直径1.2米，每分钟滚动6周。

圆专题训练(经典、全面)

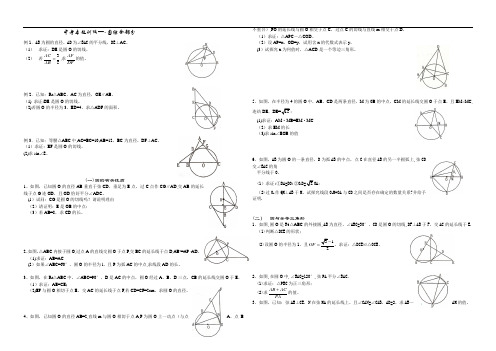
中考专题训练—-圆综合部分例1．AB为圆的直径，AD为∠BAC的平分线，DE⊥AC。

（1）求证：DE是圆O的切线。

（2）若35ACAB=,求AFDF的值。

例2．已知：Rt△ABC，AC为直径，OE∥AB，（1) 求证:DE是圆O的切线。

（2)若圆O的半径为3，ED=4，求△ADF的面积。

例3．已知：等腰△ABC中,AC=BC=10,AB=12，BC为直径，DF⊥AC。

（1）求证：EF是圆O的切线。

(2)求sin∠E。

(一)圆的有关性质1、如图，已知圆O的直径AB垂直于弦CD，垂足为E点，过C点作CG∥AD,交AB的延长线于点G连OD，且OD恰好平分∠ADC。

(1）试问：CG是圆O的切线吗？请说明理由.（2）请证明：E是OB的中点：（3）若AB=8，求CD的长。

2、如图，△ABC内接于圆O,过点A的直线交圆O于点P,交BC的延长线于点D,AB2=AP·AD。

（1)求证：AB=AC(2）如果∠ABC=60°，圆O的半径为l，且P为弧AC的中点,求线段AD的长。

3、如图，在Rt△ABC中，∠ABC=90°，D是AC的中点，圆O经过A、B、D三点，CB的延长线交圆O于E。

（1）求证：AE=CE;（2)EF与圆O相切于点E，交AC的延长线于点F,若CD=CF=2cm。

求圆O的直径。

4、如图，已知圆O的直径AB=2,直线m与圆O相切于点A,P为圆O上一动点（与点A、点B 不重合）,PO的延长线与圆O相交于点C，过点C的切线与直线m相交于点D。

（1）求证：△APC～△COD。

（2）设AP=x，OD=y，试用含x的代数式表示y。

(3）试探究x为何值时，△ACD是一个等边三角形。

5、如图，在半径为4的圆O中，AB、CD是两条直径，M为0B的中点，CM的延长线交圆O于点E，且EM>MC,连结DE，DE=15；(1)求证：AM·MB=EM·MC（2）求EM的长（3)求sin∠EOB的值6、如图，AB为圆O的一条直径，D为弧AB的中点，点C在直径AB的另一半圆弧上,弦CD交∠BAC的角平分线于O。

初中数学圆形专题训练50题含参考答案

初中数学圆形专题训练50题含参考答案一、单选题1．下列说法错误的是（）A．等弧所对的圆心角相等B．弧的度数等于该弧所对的圆心角的度数C．经过三点可以作一个圆D．三角形的外心到三角形各顶点距离相等【答案】C【分析】根据三角形的外心的性质，确定圆的条件，圆心角、弧、弦的关系判定即可．【详解】解：A等弧所对的圆心角相等，故不符合题意；B、弧的度数等于该弧所对的圆心角的度数，故不符合题意；C、经过不在同一条直线上的三点可以作一个圆，故符合题意；D、三角形的外心到三角形各顶点距离相等，故不符合题意；故选：C．【点睛】本题考查了三角形的外接圆与外心，确定圆的条件，圆心角、弧、弦的关系，正确的理解题意是解题的关键．2．已知O的半径是5cm，线段OP的长为4cm，则点P（）A．在O外B．在O上C．在O内D．不能确定【答案】C【分析】根据点到圆心的距离和圆的半径之间的数量关系，即可判断点和圆的位置关系．点到圆心的距离小于圆的半径，则点在圆内；点到圆心的距离等于圆的半径，则点在圆上；点到圆心的距离大于圆的半径，则点在圆外．OP=<【详解】解：45∴点P在O内，故选：C．【点睛】本题考查了点和圆的位置关系，熟悉点和圆的位置关系的判断是关键．3．用直角钢尺检查某一工件是否恰好是半圆环形，根据图所表示的情形，四个工件哪一个肯定是半圆环形？()A．B．C ．D ．【答案】B【详解】试题分析：根据直径所对的圆周角为直角可得：B 为正确答案．4．已知⊙O 的半径是一元二次方程2340x x --=的一个根，点A 与圆心O 的距离为6，则下列说法正确在是（）A ．点A 在⊙O 外B ．点A 在⊙O 上C ．点A 在⊙O 内D ．无法判断【答案】A【分析】先求方程的根，可得r 的值，由点与圆的位置关系的判断方法可求解．【详解】解：⊙2340x x --=，⊙1x ＝﹣1，2x ＝4，⊙⊙O 的半径为一元二次方程2340x x --=的根，⊙r ＝4，⊙6＞4，⊙点A 在⊙O 外，故选：A ．【点睛】本题考查了解一元二次方程，点与圆的位置关系，解决此类问题可通过比较点到圆心的距离d 与圆半径大小关系完成判定．5．如图，AB 是半圆O 的直径，28BAC ∠=︒，则D ∠的度数是（）A ．62︒B ．118︒C ．152︒D ．138︒【答案】B 【分析】连接BC ，则直径所对的圆周角是直角可求得B ∠的度数，再由圆内接四边形的性质即可求得结果的度数．【详解】连接BC ，如图所示，AB 是直径，90ACB ∴∠=︒， 90902862B BAC ∴∠=︒-∠=︒-︒=︒，180********D B ∴∠=︒-∠=︒-︒=︒；故选：B ．【点睛】本题考查了直径所对的圆周角是直角，圆内接四边形的性质等知识，掌握这两条性质是关键．6．如图，AB 是O 的直径，CD 是O 的弦．若=21BAD ∠︒，则ACD ∠的大小为（）A ．21°B ．59°C ．69°D ．79°【答案】C 【分析】先求出ABD ∠的度数，然后再根据圆周角定理的推论解答即可．【详解】解：⊙AB 是O 的直径⊙=90BDA ∠︒，⊙=21BAD ∠︒，⊙=1809021=69ABD ∠--︒︒︒︒，又⊙=AD AD ，⊙==69ACD ABD ∠∠︒，故答案为：C ．【点睛】本题主要考查了圆周角定理的推论，解题的关键是熟练掌握在同圆或等圆中同弧或等弧所对圆周角相等；直径所对圆周角等于90°．7．如图，圆与圆的位置关系没有（）A ．相交B ．相切C ．内含D ．外离【答案】A 【分析】根据圆与圆的位置关系,寻找交点个数即可解题.【详解】解：圆与圆相交有两个交点,但是图像中没有两个交点的情况,所以圆与圆的位置关系没有相交,故选A.【点睛】本题考查了圆与圆的位置关系,属于简单题,熟悉位置关系的辨析方法是解题关键.8．已知在Rt ABC 中， 9034ACB AC BC ∠=︒==，，，则Rt ABC 的外接圆的半径为（） A ．4B ．2.4C ．5D ．2.5 Rt ABC 中，根据勾股定理得，223BC =直角三角形的外心为斜边中点，Rt ABC 的外接圆的半径为故选：D ．【点睛】本题考查了直角三角形的外心的性质，勾股定理的运用，关键是明确直角三角形的斜边为三角形外接圆的直径．9．如图，12∠=∠，则AB CD =的是（）．A ．B ．C ．D ．【答案】C【分析】根据圆周角与弧的关系即可求解．【详解】解：根据同圆或等圆，相等的弧所对的圆周角相等，只有C 选项符合题意；⊙12∠=∠，⊙AB CD =．故选：C ．【点睛】本题考查了圆周角与弧的关系，掌握同圆或等圆中，相等的圆周角所对的弧相等是解题的关键．10．ABC ∆中，10AB AC cm ==，12BC cm =，若要剪一张圆形纸片盖住这个三角形，则圆形纸片的最小半径为（）cm ．A ．5B ．6C ．152D ．254 AB AC =BD DC ∴=连接OB ，在Rt⊙ABD 设圆形纸片的半径为【点睛】本题考查的是三角形的外接圆与外心、等腰三角形的性质，掌握等腰三角形的三线合一、三角形外接圆的性质及勾股定理是解题的关键． 11．如图所示，MN 是半圆O 的直径，MP 与半圆0相切于点M ，R 是半圆上一动点，RE MP ⊥于E ，连接MR .设MR x =，MR RE y -=，则下列函数图象能反映y 与x 之间关系的是（）A ．B ．C ．D ．，可得~EMR RNM ，设半圆2)r ，根据函数的解析式即可判断函数图象⊙~EMR RNM ， ER MR MR MN=，设半圆O 的半径为值2(02x y x x r=-+<<可得到y 是x 的二次函数，开口方向向下，对称轴12．如图，在平面直角坐标系中有一正方形AOBC ，反比例函数y=k x经过正方形AOBC 对角线的交点，半径为4-⊙ABC ，则k 的值为（）.A B ．2 C ．4 D ．=4，⊙DN×NO=4，即：xy=k=4．故选C ．考点：反比例函数图象上点的坐标特征；正方形的性质；三角形的内切圆与内心． 13．若5cm AB =，作半径为4cm 的圆，使它经过A 、B 两点，这样的圆能作（） A ．0个B ．1个C ．2个D ．无数个【答案】C【分析】先作AB 的垂直平分线l ，再以点A 为圆心，4cm 为半径作圆交l 于O 1和O 2，然后分别以O 1和O 2为圆心，以4cm 为半径作圆即可；【详解】解：这样的圆能画2个．如图：作AB 的垂直平分线l ，再以点A 为圆心，4cm 为半径作圆交l 于O 1和O 2，然后分别以O 1和O 2为圆心，以4cm 为半径作圆，则⊙O 1和⊙O 2为所求【点睛】本题考查了点与圆的位置关系：设⊙O 的半径为r ，点P 到圆心的距离OP =d ，则有点P 在圆外⇔d ＞r ；点P 在圆上⇔d =r ；点P 在圆内⇔d ＜r ． 14．如图，在ABC 中，3AB =，6BC =，60ABC ∠=︒，以点B 为圆心，AB 长为半径画弧，交BC 于点D ，则图中阴影部分的面积是（）A ．3πB 2π-C πD 32πAB BD =ABD ∴是等边三角形，AD AB ∴=6BC =，3CD ∴=，AD CD ∴=C CAD ∴∠=∠C CAD ∠+∠30C ∴∠=BAC ∴∠=AC ∴=∴图中阴影部分的面积15．如图，已知AB 是O 的直径，弦CD AB ⊥，垂足为E ，且30BCD ∠=︒，CD = ）A ．24π-B ．83π-C ．43π-D ．348π-故选：B ．【点睛】本题考查了扇形的面积计算，勾股定理，含30︒角的直角三角形的性质，等边三角形的性质和判定等知识点，能把求不规则图形的面积转化成求规则图形的面积是解此题的关键．16．已知扇形的圆心角为120°，半径为6，则扇形的弧长是（）．A ．3πB ．4πC ．5πD ．6π17．如图，四边形ABCD 内接于O ，:2:1,2ABC ADC AB ∠∠== ，点C 为BD 的中点，延长AB 、DC 交于点E ，且60E ∠=，则O 的面积是（）A ．πB ．2πC ．3πD ．4π 【答案】D 【分析】连接BD ，根据圆内接四边形的外角等于其内对角可得∠D ＝∠CBE ＝60°，根据等边对等角以及三角形内角和定理求出∠BCE ＝60°，可得∠A ＝60°，点C 为BD 的中点，可得出∠BDC ＝∠CBD ＝30°，进而得出⊙ABD =90°，AD 为直径，可得出AD =2AB =4，再根据面积公式计算得出结论；【详解】解：连接BD ，∵ABCD 是⊙O 的内接四边形，∴∠CBE ＝∠ADC ，∠BCE ＝∠A⊙:2:1ABC ADC ∠∠=∴:2:1ABC CBE ∠∠=∴∠CBE ＝∠ADC=60°，∠CBA ＝120°⊙60E ∠=⊙⊙CBE 为等边三角形⊙∠BCE ＝∠A=60°，⊙点C 为BD 的中点，⊙∠CDB ＝∠DBC=30°⊙⊙ABD =90°，⊙ADB =30°⊙AD 为直径⊙AB =2⊙AD =2AB =4 ⊙O 的面积是=224ππ⨯=故答案选：D【点睛】本题考查了圆内接四边形的性质，圆周角定理，等边三角形的判定与性质，三角形内角和定理，掌握相关性质及公式是解题的关键．18．一个圆锥的侧面展开图是半径为8，圆心角为120°的扇形，则这个圆锥的高为（）A cmB ．163 cmC cmD ．83cm19．⊙O 的半径为10cm, A 是⊙O 上一点, B 是OA 中点, C 点和B 点的距离等于5cm, 则C 点和⊙O 的位置关系是（）A ．C 在⊙O 内B ．C 在⊙O 上 C ．C 在⊙O 外D ．C 在⊙O 上或C 在⊙O 内【答案】D【详解】试题解析：因为⊙O 的半径是10cm ，A 是圆上一点，所以OA=10cm ，又B 是OA 的中点，所以BA=5cm ．而BC=5cm ，所以点C 应在以B 为圆心，5cm 为半径的⊙B 上．⊙B 上的点除点A 在⊙O 上外，其它的点都在⊙O 内．故选D ．20．如图，在ABC 中，90ACB ∠=︒．AC BC =，4cm AB =．CD 是中线，点E 、F 同时从点D 出发，以相同的速度分别沿DC 、DB 方向移动，当点E 到达点C时，运动停止，直线AE 分别与CF 、BC 相交于G 、H ，则在点E 、F 移动过程中，点G 移动路线的长度为（）．A ．2B ．πC ．2πD ．π2【答案】D 【详解】试题解析：如图，,90CA CB ACB AD DB =∠==，，⊙CD ⊙AB ，⊙⊙ADE =⊙CDF =90，CD =AD =DB ，在⊙ADE 和⊙CDF 中，AD CD ADE CDF DE DF ，=⎧⎪∠=∠⎨⎪=⎩⊙⊙ADE ⊙⊙CDF (SAS)，⊙⊙DAE =⊙DCF ，⊙⊙AED =⊙CEG ，90，四点共圆，的运动轨迹为弧CD90，的运动轨迹的长为二、填空题21．如图，点C为半圆的中点，AB是直径，点D是半圆上一点，AC、BD交于点BD=，则AC=________．E，若1AD=，722．如图，将长为8cm 的铁丝首尾相接围成半径为2cm 的扇形．则S =扇形________2cm ．23．如图，ABC ∆中，90,6,4,ACB BC AC D ∠=︒==是AC 边上的一个动点，过点C 作,CE BD ⊥垂足为,E 则AE 长的最小值为_______________________．【答案】2【分析】取BC 中点F ，连接AE 、EF ．易得点E 在以BC 长为直径的圆周上上运动，24．如图，⊙O内接正五边形ABCDE与等边三角形AFG，则⊙FBC＝__________．【分析】连接OA，OB，OF，OC，分别求出正五边形ABCDE和正三角形AFG的中心角，结合图形计算即可．【详解】解：连接OA，OB，OF，OC．25．如图，点A、B在半径为3的⊙O上，劣弧AB长为π2，则⊙AOB＝____．26．如图，Rt⊙ABC中，⊙ACB＝90°，⊙A＝30°，BC＝6，D，E分别是AB，AC边的中点，将⊙ABC绕点B顺时针旋转60°到⊙A′BC′的位置，则整个旋转过程中线段DE所扫过部分的面积（即图中阴影部分面积）为_____．【详解】27．四边形ABCD 是O 的内接四边形，2C A ∠=∠，则C ∠的度数为___．【答案】120°##120度【分析】根据圆内接四边形对角互补，再结合已知条件求解即可．【详解】解：四边形ABCD 是O 的内接四边形，180C A∴∠+∠=︒2C A∠=∠，120C∴∠=︒．故答案为：120︒．【点睛】本题主要考查了圆内接四边形的性质，掌握圆内接四边形对角互补是解答本题的关键．28．如图，在Rt⊙ABC中，⊙C=90°，AB=13，AC=5，以点C为圆心r为半径作圆，如果⊙C与AB相切，则半径r的值是_______．【答案】6013##8413来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．也考查了勾股定理．29．如图，在⊙O中，点C在优弧ACB上，将弧沿BC折叠后刚好经过AB的中点D，若⊙O AB＝4，则BC的长是_____．30．如图，AB 与⊙O 相切于点B ，线段OA 与弦BC 垂直，垂足为,2D AB BC ==，则AOB ∠=_________．31．如图，在正方形网格中建立平面直角坐标系，一条圆弧经过点()()()0,4,4,4,6,2A B C --．（1）若该圆弧所在圆的圆心为D ，则AD 的长为__________．（2）该圆弧的长为___________．90255180π=【详解】解：（1）如图，易知点2425+=即D 的半径为AD CD ==2AD DC +ACD ∆为直角三角形，根据题意得90255180π=即该圆弧的长为5π．【点睛】本题主要考查圆，扇形等知识的综合应用，掌握确定圆心的方法，即确定出的坐标是解题的关键．OD BC，OD与32．如图，已知AB是半圆O的直径，C、D是半圆O上的两点，且//∠=______．AC交于点E，若E是OD中点，，则CAD【答案】30°【分析】先判定AC垂直平分OD，进而可判定⊙OAD是等边三角形，再由三线合一即可求出⊙CAD的度数．【详解】⊙AB是半圆O的直径，⊙⊙ACB=90°．OD BC，⊙//⊙⊙AED=90°．⊙E是OD中点，⊙AC垂直平分OD，⊙AD=OA，⊙OA=OD，⊙⊙OAD是等边三角形，⊙⊙OAD=60°，⊙⊙CAD=30°．故答案为：30°．【点睛】本题考查了圆周角定理，平行线的性质，线段垂直平分线的判定与性质，以及等边三角形的判定与性质，熟练掌握圆周角定理、线段垂直平分线的判定与性质是解答本题的关键．33．如图，在半径为2cm的扇形纸片AOB中，⊙AOB=90°，将其折叠使点B落在点O 处，折痕为DE，则图中阴影部分的面积为________cm2334．若点O 是等腰ABC 的外心，且60,BOC ∠=︒底边4,BC =则ABC 的边BC 上的高为 ____________________．E，如果点F是弧EC的中点，联结FB，那么tan⊙FBC的值为．关系；解直角三角形．【答案】【详解】试题分析:连接CE交BF于H，连接BE，根据矩形的性质求出AB=CD=3，AD=BC=5=BE，⊙A=⊙D=90°，根据勾股定理求出AE=4，求出DE=1，根据勾股定理求出CE，求出CH，解直角三角形求出即可．解：连接CE交BF于H，连接BE，⊙四边形ABCD是矩形，AB=3，BC=5，⊙AB=CD=3，AD=BC=5=BE，⊙A=⊙D=90°，由勾股定理得：AE==4，DE=5﹣4=1，由勾股定理得：CE==，由垂径定理得：CH=EH=CE=，在Rt⊙BFC中，由勾股定理得：BH==，所以tan⊙FBC===．故答案为．36．O是ABC的外心，且140∠=________；若I是ABC的内心，∠=，则ABOC且140∠=________．BIC∠=，则A70100是ABC的外心，且140，如图所示：是ABC的内心，且140，如图所示：⊙I 是⊙ABC 的内心，⊙⊙A=180°-(⊙ABC+⊙ACB)= 180°-2(⊙IBC+⊙ICB)=180°-2（180°-140°）=100°．故答案为70°；100°．【点睛】本题考查了三角形内外心的性质，熟知三角形内外心的性质是解题的关键. 37．冬天的雪是我们的乐园，一次下雪后，小伙伴们堆了一大雪人，准备给雪人制作一个底面半径为9cm ，母线长为30cm 的圆锥形礼帽，则这个圆锥形礼帽的侧面积为____________cm 2 ．（结果保留π）【答案】270π．【详解】试题分析：S=πrl=9×30π=270π(2cm ).考点：圆锥的侧面积计算.38．已知O 的直径10AB =cm ，CD 是O 的弦，AE CD ⊥，垂足为点E ，BF CD ⊥，垂足为点F ，且8CD =cm ，则BF AE -的长为________cm ．39．如图，I 是直角ABC 的内切圆，切点为D 、E 、F ，若10AF ，3BE =，则ABC 的面积为_____．的值，再利用三角形的面积公式求得ABC 的面积即可．【详解】解：I 是直角ABC 的内切圆，且10AF ，BE =3，10AF AD ==，CE 13=，x ，则3BC x ，AC 中，222AC BC AB +=，即)22313x +=，（不符题意，舍去）ABC ∴的面积为故答案为：【点睛】本题考查了切线长定理、勾股定理、一元二次方程的应用，熟记切线长定理是解题的关键．40．如图，正六边形ABCDEF内接于半径为1cm的⊙O，则图中阴影部分的面积为_____cm2（结果保留π）．三、解答题41．如图，在边长为4的正方形ABCD中，以AD为直径作⊙O，以C为圆心，CD长为半径作⊙C，两圆交于正方形内一点E，连CE并延长交AB于F．（1）求证：CF 与⊙O 相切；（2）求△BCF 和直角梯形ADCF 的周长之比．【答案】（1）证明见详解；（2）6：7．【分析】（1）连接OE 、DE ，根据等腰三角形性质推出⊙ODE ＝⊙OED ，⊙CDE ＝⊙CED ，推出⊙OED ＋⊙CED ＝90°，根据切线的判定推出即可；（2）过F 作FM⊙DC 于M ，得出四边形ADMF 是矩形，推出AD ＝FM ＝4，AF ＝DM ，求出AF ＝EF ，设AF ＝EF ＝x ，DM ＝x ，在Rt △FMC 中，由勾股定理得出方程()()222444x x +-=+，求出x 的值，即可求出△BCF 的周长和直角梯形ADCF 的周长．【详解】（1）证明：连接OE ，DE ，⊙OD ＝OE ，CE ＝CD ，⊙⊙ODE ＝⊙OED ，⊙CDE ＝⊙CED ，⊙四边形ABCD 是正方形，⊙⊙ADC ＝90°，⊙⊙ADC ＝⊙ODE ＋⊙CDE ＝90°，⊙⊙OED ＋⊙CED ＝90°，即OE⊙CF ，⊙OE 为半径，⊙CF 与⊙O 相切．（2）解：如图：过F 作FM⊙DC 于M ，⊙四边形ABCD 是正方形，⊙AD ＝DC ＝BC ＝AB ＝CE ＝4，⊙FAD ＝⊙ADM ＝⊙FMD ＝⊙FMC ＝90°，⊙四边形ADMF 是矩形，⊙AD ＝FM ＝4，AF ＝DM⊙⊙OAF ＝90°，OA 为半径，⊙AF 切⊙O 于A ，CF 切⊙O 于E ，⊙AF ＝EF ，设AF ＝EF ＝x ，DM ＝x ，在Rt △FMC 中，由勾股定理得：222FM MC CF +=，()()222444x x +-=+，解得：x ＝1，⊙AF ＝EF ＝DM ＝1，⊙CF ＝4＋1＝5，⊙⊙BCF 的周长是BC ＋CF ＋BF ＝4＋5＋4−1＝12，直角梯形ADCF 的周长是AD ＋DC ＋CF ＋AF ＝4＋4＋5＋1＝14，⊙⊙BCF 和直角梯形ADCF 的周长之比是12：14＝6：7．【点睛】本题考查了正方形性质，切线的性质和判定，矩形的性质和判定，勾股定理的应用，主要考查学生综合运用定理进行推理的能力．42．已知ABC 内接于O ，BAC ∠的平分线交O 于点D ，连接DB ，DC ．（1）如图⊙，当120BAC ∠=时，请直接写出线段AB ，AC ，AD 之间满足的等量关系式：；（2）如图⊙，当90BAC ∠=时，试探究线段AB ，AC ，AD 之间满足的等量关系，并证明你的结论；（3）如图⊙，若BC=5，BD=4，求AD AB AC+ 的值．43．如图，在Rt⊙ABC中，⊙C=90°，BE平分⊙ABC交AC于点E，点D在AB边上且DE⊙BE．（1）判断直线AC与⊙DBE外接圆的位置关系，并说明理由；（2）若AD=6，BC的长．【答案】（1）直线AC与⊙DBE外接圆相切．（2）BC=4．【分析】（1）取BD的中点O，连接OE，证明⊙OEB=⊙CBE后可得OE⊙AC；（2）设OD=OE=OB=x，利用勾股定理求出x的值，再证明△AOE⊙⊙ABC，利用线段比求解．【详解】（1）直线AC与⊙DBE外接圆相切．理由：⊙DE⊙BE⊙BD为⊙DBE外接圆的直径取BD的中点O（即⊙DBE外接圆的圆心），连接OE⊙OE=OB⊙⊙OEB=⊙OBE⊙BE平分⊙ABC⊙⊙OBE=⊙CBE⊙⊙OEB=⊙CBE⊙⊙CBE+⊙CEB=90°⊙⊙OEB+⊙CEB=90°，即OE⊙AC44．如图，已知AB是⊙O的直径，⊙O交⊙ABE边AE于点D，点P在BA的延长线上，PD交BE于点C．现有3个选项：⊙AB=BE，⊙PC⊙BE，⊙PD是⊙O的切线．(1)请从3个选项中选择两个作为条件，余下一个作为结论，得到一个真命题，并证明；你选择的两个条件是，结论是（只要填写序号）；(2)在（1）的条件下，连接OC，如果P A=2，sin⊙ABC=45，求OC的长．=AB BE∴∠=BAE∴∥OD BE∴∠=ODP∴PD是⊙4CP =2,PA OD∴=OD OA45．如图，BD是⊙O的直径，过点D的切线交⊙O的弦BC的延长线于点E，弦AC⊙DE交BD于点G（1）求证：BD平分弦AC；（2）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径.46．如图，⊙ABC 为⊙O 的内接三角形，其中AB 为⊙O 的直径，过点A 作⊙O 的切线P A ．（1）求证：⊙P AC ＝⊙ABC ；（2）若⊙P AC ＝30°，AC ＝3，求劣弧AC 的长．603180π＝π.【点睛】本题考查了切线的性质，圆周角定理的推论，弧长公式，熟练掌握相关知识是解题的关键.47．如图，在⊙ABC中，AB=AC，以AB为直径的半圆分别交AC，BC边于点D，E，连结BD，（1）求证：DE BE=；（2）当AB=10，BD=8，求CD和BE的长．48．在复习菱形的判定方法时，某同学进行了画图探究，其作法和图形如下：⊙画线段AB；⊙分别以点A，B为圆心，大于AB长的一半为半径作弧，两弧相交于M、N两点，作直线MN交AB于点O；⊙在直线MN上取一点C（不与点O重合），连接AC、BC；⊙过点A作平行于BC的直线AD，交直线MN于点D，连接B D．（2）该同学在图形上继续探究，他以点O为圆心作四边形ADBC的内切圆，构成如图所示的阴影部分，若AB＝⊙BAD＝30°，求图中阴影部分的面积．1149．如图，AB是⊙O的直径，CD与⊙O相切于点C，且与AB的延长线交于点D，连接AC．作CE⊙AB于点E．（1）求证：⊙BCE=⊙BCD；（2）若AD＝8，12BCAC=，求CD的长．【答案】（1）见解析；（2）CD=4【分析】（1）连接OC，如图，利用圆周角定理得到⊙ACB=90°，利用切线的性质得到⊙DCO=90°，则根据等角的余角相等得到⊙ACO=⊙BCD，同样方法证明⊙A=⊙BCE，从而得到⊙BCE=⊙BCD；（2）证明⊙ACD⊙⊙CBD，然后利用相似比求CD的长．【详解】（1）证明：连接OC，如图，⊙AB是⊙O的直径，⊙⊙ACB=90°，即⊙ACO+⊙OCB=90°，⊙CD与⊙O的相切于点C，⊙⊙DCO=90°，即⊙BCD+⊙OCB=90°，⊙⊙ACO=⊙BCD，⊙OC=OA，⊙⊙A=⊙ACO，50．如图，ABC 中，90ACB ∠=︒，30A ∠=︒，2AB =，点P 从点A 出发，以每秒12个单位长度的速度沿AB 向点B 运动，到点B 停止．同时点Q 从点A 出发，沿AC CB -的线路向点B 运动，在边AC BC 上的速度为每秒2个单位长度，到B 停止，以PQ 为边向右或右下方构造等边PQR ，设P 的运动时间为t 秒，解答下列问题：（1）填空：BC =__________，AC =__________．（2）当Q 在AC 上，R 落在BC 边上时，求t 的值．（3）连结BR ．⊙当Q 在边AC 上，BR 与ABC 的一边垂直时，求PQR 的边长．⊙当Q 在边BC 上且R 不与点B 重合时，判断BR 的方向是否变化，若不变化，说明理由．理由见解析⊙ABC中，90，30∠，ABA=，3作QD⊙AB59⊙⊙QPR是等边三角形，⊙⊙QRP=60°，⊙⊙ABC=90°-⊙A=60°，⊙⊙QBP=⊙QRP=60°，⊙Q、P、B、R四点共圆，⊙⊙QBR=⊙QPR=60°，⊙BR的方向不变．【点睛】本题主要考查了等边三角形的性质，含30度角的直角三角形的性质，四点共圆等等，解题的关键在于能够熟练掌握相关知识进行求解．。

(完整)初中数学专题训练--圆--(1)圆的概念

精品设计圆的概念一、圆中相关概念的结构示意图圆()()⎩⎨⎧⇒⇒等圆大小半径同心圆位置圆心相关概念⎪⎪⎩⎪⎪⎨⎧⇒⇒⇒圆周角圆心角等弧半圆、优弧、劣弧弧直径弦二、知识应用知识点1：有关概念例题1、如图，圆中弦的条数为（）A ．2条B ．3条C ．4条D ．5说明：弦是圆上任意两点间的线段。

例题2、判断题（1）直径是弦（）（2）弦是直径（）（3）半圆是弧（）（4）弧是半圆（）（5）长度相等的两段弧是等弧（）（6）等弧的长度相等（）说明：通过原命题和逆命题的对比，深刻理解圆中概念的含意。

例题3、下列说法中：①直径相等的两个圆是等圆；②长度相等的两条弧是等弧； ③圆中最长的弦是通过圆心的弦；④一条弦把圆分成两条弧，这两条弧不可能是等弧。

正确的个数是（）A ．1个B ．2个C ．3个D ．4个说明：等弧是指弧的度数和长度都相等的弧，等弧只可能出现在同圆或等圆中。

例题4、画图说明满足下列条件的点的轨迹：（1）经过点A ，且半径等于cm 2的圆的圆心轨迹；（2）边cm 1=BC ，面积为2cm 21的ABC ∆的顶点A 的轨迹.说明：根据给定的条件，探求并确定符合条件的轨迹图形，通常是转化为四个基本轨迹.（圆的轨迹、平行线轨迹、角平分线轨迹、线段中垂线轨迹）。

例题5、已知AB 、CD 是⊙O 的两条直径，则四边形ACBD 一定是（）（A ）等腰梯形（B ）菱形（C ）矩形（D ）正方形说明：问题的关键是①圆的两条直径具备什么性质？②构成特殊四边形的条件。

知识点2：相关计算与证明例题6、如图，在⊙O 中，AB 、CD 为直径，试说明AC 与BD 的位置关系。

说明：同圆的半径相等。

因此当圆中有多条直径或半径出现时，就有相等的线段和等腰三角形出现。

例题7、如图，CD 是⊙O 的直径，︒=∠84EOD ，AE 交⊙O 于B ，且OC AB =，求A ∠的度数.B精品设计说明：因为同圆的半径相等，所以当圆中有两条半径出现，就有等腰三角形出现，于是可根据等腰三角形的性质定理求得，所以连结半径是常用的辅助线. 例题8、已知：如图，两同心圆的直径AC 、BD 相交于O 点.求证：AB=CD.说明：此题目不难，但它是以“同心圆”为背景的，所以该题目重点不是证明过程，而是“同心圆”具备什么性质和特征。

初中数学圆形专题训练50题-含参考答案

初中数学圆形专题训练50题含参考答案一、单选题1．如图，四边形ABCD 内接于O ，若:5:7A C ∠∠=，则C ∠=（）A ．210︒B ．150︒C ．105︒D ．75︒2．如图，P 是∠O 外一点，P A 是∠O 的切线，A 为切点，PO 与∠O 相交于B 点，已知∠BCA ＝34°，C 为∠O 上一点，连接CA ，CB ，则∠P 的度数为（）A ．34°B ．56°C ．22°D ．28° 【答案】C 【分析】根据切线的性质可得：90,OAP ∠=︒ 利用圆周角定理可得：2,O ACB ∠=∠ 从而可求出结果．【详解】解：∠P A 是∠O 的切线，A 为切点，∠∠OAP ＝90°，又∠∠BCA ＝34°，∠∠O ＝2∠ACB ＝68°，∠∠P ＝90°﹣∠AOB ＝90°﹣68°＝22°．故选：C．【点睛】本题考查的是切线的性质定理，圆周角定理，掌握利用圆周角定理与切线的性质定理求解角的大小是解题的关键．3．如图，AB为∠O直径，CD为弦，AB∠CD于E，连接CO，AD，∠BAD＝25°，下列结论中正确的有（）∠CE＝OE；∠∠C＝40°；∠ACD＝ADC；∠AD＝2OEA．∠∠B．∠∠C．∠∠∠D．∠∠∠∠【答案】B【分析】根据圆周角定理，垂径定理，圆心角、弧、弦的关系以及直角三角形边的关系进行判断即可．【详解】解：∠AB为∠O直径，CD为弦，AB∠CD于E，∠CE=DE，BC BD=，ACB ADB=，∠∠BOC=2∠A=40°，ACB BC ADB BC+=+，即ADC ADC=，故∠正确；∠∠OEC=90°，∠BOC=40°，∠∠C=50°，故∠正确；∠∠C≠∠BOC，∠CE≠OE，故∠错误；作OP∠CD，交AD于P，∠AB∠CD，∠AE＜AD，∠AOP=90°，∠OA＜PA，OE＜PD，∠PA+PD＞OA+OE∠OE＜OA，∠AD＞2OE，故∠错误；故选：B．【点睛】本题考查了圆周角定理，垂径定理，圆心角、弧、弦的关系，熟练掌握性质定理是解题的关键．4．下列命题正确的是（）A．相等的圆心角所对的弧是等弧B．等圆周角对等弧C．任何一个三角形只有一个外接圆D．过任意三点可以确定一个圆【答案】C【分析】根据圆周角与弧的关系可判断出各选项，注意在等圆中这个条件．【详解】A、缺少条件，必须是在同圆或等圆中，相等的圆心角所对的弧才相等；故本选项错误；B、缺少条件，必须是在同圆或等圆中，相等的圆周角所对的弧才相等；故本选项错误；C、任何一个三角形只有一个外接圆，故本选项正确；D、缺少条件，过任意不共线的三点才可以确定一个圆，故本选项错误．故选：C．【点睛】本题考查命题与定理的知识，属于基础题，掌握相关的性质定理是解题的关键．5．如图，四边形ABCD为∠O的内接四边形，已知∠BOD＝110°，则∠BCD的度数为（）A．55°B．70°C．110°D．125°∠四边形ABCD为∠O的内接四边形，∠∠BCD=180°−∠A=125°，故选D【点睛】此题考查圆周角定理及其推论，解题关键在于掌握圆内接四边形的性质. 6．如图，点A，B，C均在圆O上，当∠BOC=120°时，∠BAC的度数是（）A．65°B．60°C．55°D．50°7．如图，在O中，AB所对的圆周角∠ACB＝50°，D为AB上的点．若∠AOD＝35°，则∠BOD的大小为（）A．35°B．50°C．55°D．65°【答案】D【分析】在同圆中，由同弧所对的圆周角等于其圆心角的一半解答．【详解】解：∠ACB＝50°，AOB∴∠=⨯︒=︒250100BOD AOB AOD∴∠=∠-∠=︒-︒=︒1003565故选：D．【点睛】本题考查圆周角与圆心角的性质，是基础考点，掌握相关知识是解题关键．8．如图，四边形ABCD内接于∠O，∠DAB＝140°，连接OC，点P是半径OC上一点，则∠BPD不可能为()A．40°B．60°C．80°D．90°【答案】D【分析】连接OD、OB，根据圆内接四边形的性质求出∠DCB，根据圆周角定理求出∠BOD，求出∠BPD的范围，即可解答．【详解】连接OD、OB，∠四边形ABCD内接于∠O，∠∠DCB＝180°﹣∠DAB＝40°，由圆周角定理得，∠BOD＝2∠DCB＝80°，∠40°≤∠BPD≤80°，∠∠BPD不可能为90°，故选D．【点睛】本题考查的是圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互补是解题的关键．9．如图，已知四边形ABCD 内接于∠O，AB是∠O的直径，EC与∠O 相切于点C，∠ECB=35°，则∠D 的度数是（）A．145°B．125°C．90°D．80°【答案】BOC【详解】解：连接.∠EC 与O 相切,35ECB ∠=，55OCB ∴∠=，,OB OC =55OBC OCB ∴∠=∠=，180********.D OBC ∴∠=-∠=-=故选：B.10．如图，AC 是汽车挡风玻璃前的刮雨刷．如果65AO cm =，15CO cm =，当刮雨刷AC 绕点O 旋转90时，则刮雨刷AC 扫过的面积为（）A ．225cm πB ．21000cm πC ．225cmD ．21000cm11．一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是（）A．0.5B．1C．2D．412．如图，圆锥的侧面展开图是半径为3，圆心角为90°的扇形，则该圆锥的底面周长为（）A．πB．πC．D．【答案】B【详解】试题分析：根据圆锥侧面展开扇形的弧长等于底面圆的周长，可以求出底面圆的半径，从而求得圆锥的底面周长．解：设底面圆的半径为r，则：2πr==π．∠r=， ∠圆锥的底面周长为，故选B ．考点：圆锥的计算．13．如图，AB 为半圆O 的直径，C 为半圆上一点，且弧AC 为半圆的，设扇形AOC ，∠COB ，弓形BmC 的面积分别为S 1，S 2，S 3，则下列结论正确的是（）A ．S 1＜S 2＜S 3B ．S 2＜S 1＜S 3C ．S 2＜S 3＜S 1D ．S 1＜S 2＜S 3【答案】B 【详解】试题分析：首先根据∠AOC 的面积=∠BOC 的面积，得S 2＜S 1．再根据题意，知S 1占半圆面积的．所以S 3大于半圆面积的．解：根据∠AOC 的面积=∠BOC 的面积，得S 2＜S 1，再根据题意，知S 1占半圆面积的，所以S 3大于半圆面积的．因此S 2＜S 1＜S 3．故选B ．考点：扇形面积的计算．14．如图，在矩形ABCD 中，2AB =，BC =B 为圆心，BA 长为半径画弧，交CD 于点E ，连接BE ，则扇形BAE 的面积为（）A ．3πB ．35πC ．23πD ．34π 【答案】C【分析】解直角三角形求出30CBE ∠=︒，推出60ABE ∠=︒，再利用扇形的面积公式【详解】解：四边形=BA BE∴∠cos CBE∴∠=CBE∴∠ABE∴S15．下列事件中，是随机事件的是（）A．∠O的半径为5，OP＝3，点P在∠O外B．相似三角形的对应角相等C．任意画两个直角三角形，这两个三角形相似D．直径所对的圆周角为直角【答案】C【分析】根据随机事件的定义进行分析解答即可.【详解】解：（1）点P一定在∠O内，A是不可能事件，故错误.(2) 相似三角形的对应角一定相等，是必然事件，B错误.(3) 任意画两个直角三角形，这两个三角形不一定相似，C正确.(4) 直径所对的圆周角一定为直角，D为为为为为为为错误.综上选C.【点睛】本题考查随机事件的定义，熟悉掌握是解题关键.16．如图，AC是∠O的直径，弦BD∠AO于E，连接BC，过点O作OF∠BC于F，若BD=8cm，AE=2cm，则OF的长度是（）A．3cm B cm C．2.5cm D cm17．我们研究过的图形中，圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”．除了圆以外，还有一些几何图形也是“等宽曲线”，如勒洛三角形（如图1），它是分别以等边三角形的每个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧，三段圆弧围成的曲边三角形．图2是等宽的勒洛三角形和圆形滚木的截面图．有如下四个结论：∠勒洛三角形是中心对称图形；∠在图1中，等边三角形的边长为2，则勒洛三角形的周长为2π；∠在图2中，勒洛三角形的周长与圆的周长相等；∠使用截面是勒洛三角形的滚木来搬运东西，不会发生上下抖动；上述结论中，所有正确结论的序号是（）A．∠∠B．∠∠C．∠∠D．∠∠∠18．如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D．连接BD，BE，CE，若∠CBD＝33°，则∠BEC＝（）A．66°B．114°C．123°D．132°【答案】C【分析】根据圆周角定理可求∠CAD=33°，再根据三角形内心的定义可求∠BAC，再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB，再根据三角形内角和定理可求∠BEC的度数．【详解】在∠O中，∠∠CBD＝33°，∠∠CAD＝33°，∠点E是△ABC的内心，∠∠BAC＝66°，∠∠EBC+∠ECB＝（180°﹣66°）÷2＝57°，∠∠BEC＝180°﹣57°＝123°．故选C．【点睛】考查了三角形的内切圆与内心，圆周角定理，三角形内角和定理，关键是得到∠EBC+∠ECB的度数．19．如图，四边形ABCD为正方形，O为AC、BD的交点，∠DCE为Rt∠，∠CED=90°，OE=CE DE=5，则正方形的面积为()A．5B．6C．7D．8∠CE DE=5故选：B【点睛】本题考查了四点共圆的判定及圆周角定理，同弧或等弧所对的圆周角相等，正方形的判定及性质定理，全等三角形的判定及性质．20．如图，AB 是∠O 的直径，弦CD∠AB 于点G ，点F 是CD 上一点，且满足13CF FD ，连接AF 并延长交∠O 于点E ，连接AD 、DE ，若CF ＝2，AF ＝3．给出下列结论：∠∠ADF∠∠AED ；∠FG ＝2；∠tan∠E ；∠S △DEF ＝结论的个数是（）A ．1B ．2C ．3D ．4AFD ADE S S ＝ADE S ＝△DEF ＝AFD ，∠所以正确的结论是∠∠∠.二、填空题21．如图，有4个圆|A ，B ，C ，D ，且圆A 与圆B 的半径之和等于圆C 的半径，圆B 与圆C 的半径之和等于圆D 的半径，现将圆A ，B ，C 摆放如图甲，圆B ，C ，D 摆放如图乙.若图甲和图乙的阴影部分面积分别为4π和12π.则圆D 面积为__________．【答案】28π【分析】根据题意得到圆A 的半径为2，设圆B 的半径为b ，则圆C 的半径为b+2，故圆D 的半径为2b+2，根据乙图得到方程求出b 的关系，再根据圆D 的面积与b 的关系即可求解.【详解】∠图甲阴影部分面积分别为4π，即圆A 的面积为4π，∠圆A 的半径为2，设圆B 的半径为b ，则圆C 的半径为b+2，故圆D 的半径为2b+2，根据乙图可得222(22)12(2)b b b ππππ+=+++化简得226b b +=，∠圆D 的面积为2(22)b π+=4π()22b b ++4π=28π，故填：28π.【点睛】此题主要考查圆的面积求解，解题的关键是根据图形找到等量关系进行列方程求解.22．圆的有关概念：（1）圆两种定义方式：（a ）在一个平面内线段OA 绕它固定的一个端点O 旋转一周，另一个端点A 随之旋转所形成的图形叫做圆，固定的端点O 叫做__．线段OA 叫做__．（b ）圆是所有点到定点O 的距离__定长r 的点的集合．（2）弦：连接圆上任意两点的__叫做弦．（弦不一定是直径，直径一定是弦，直径是圆中最长的弦）；（3）弧：圆上任意两点间的部分叫__（弧的度数等于这条弧所对的圆心角的度数，等于这条弧所对圆周角的两倍）（4）等弧：在同圆与等圆中，能够__的弧叫等弧．（5）等圆：能够__的两个圆叫等圆，半径__的两个圆也叫等圆．【答案】圆心半径等于线段弧完全重合完全重合相等【分析】根据圆、弦、弧、等弧、等圆的定义即可作答．【详解】（1）圆两种定义方式：（a ）在一个平面内线段OA 绕它固定的一个端点O 旋转一周，另一个端点A 随之旋转所形成的图形叫做圆，固定的端点O 叫做圆心．线段OA 叫做半径．（b ）圆是所有点到定点O 的距离等于定长r 的点的集合．（2）弦：连接圆上任意两点的线段叫做弦．（弦不一定是直径，直径一定是弦，直径是圆中最长的弦）；（3）弧：圆上任意两点间的部分叫弧（弧的度数等于这条弧所对的圆心角的度数，等于这条弧所对圆周角的两倍）（4）等弧：在同圆与等圆中，能够完全重合的弧叫等弧．（5）等圆：能够完全重合的两个圆叫等圆，半径相等的两个圆也叫等圆．故答案为：圆心，半径；等于；线段；弧；完全重合；完全重合；相等．【点睛】本题主要考查了圆、弦、弧的定义，牢记相关定义是解答本题的关键． 23．如图，在矩形ABCD 中，8AB =，6AD =，以顶点D 为圆心作半径为r 的圆，若要求另外三个顶点A 、B 、C 中至少有一个点在圆内，且至少有一个点不在圆内，则r 的取值范围是 _____．90，Rt ABD 中，由勾股定理得：2AD AB +A 、B 、C 中至少有一个点在圆内，且至少有一个点不在圆内，且CD BD <<10r <<，24．如图ABC 内接于O ，半径为6，2sin 3A =∠，则BC 的长为___________．【详解】解：作O的直径，∠90D=sin D CD．25．如图，PA、PB分别切∠O于A、B，并与∠O的另一条切线分别相交于D、C两点，已知PA＝6，则∠PCD的周长=_______．【答案】12【详解】试题分析：切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线，平分两条切线的夹角.设DC与∠O的切点为E∠PA、PB分别是∠O的切线，且切点为A、B∠PA=PB=6同理可得DE=DA，CE=CB则∠PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=12.考点：切线长定理26．如图，若BC是∠O的弦，OD∠BC于D，且∠BOD=50 o，点A在∠O上（不与B、C重合），则∠BAC=________．27．若圆锥的底面积为16π cm2，母线长为12 cm，则它的侧面展开图的圆心角为__________．【答案】120°【分析】根据圆锥的母线长等于展开图扇形的半径,求出圆锥底面圆的周长,也即是展开图扇形的弧长,然后根据弧长公式可求出圆心角的度数.【详解】由题意得,圆锥的底面积为16πcm²,28．如图，在等腰直角三角形ABC 中，4AB BC ==，点M 是AB 的中点，将ABC 绕点M 旋转至A B C '''的位置，使AB A C ''⊥，其中点C 的运动路径为弧CC '，连接CM ，则图中阴影部分的面积为_______．29．如图，ABC内接于O，若OAB30∠=，则C∠=______．【详解】OA OB=30OAB=∠=，1803030120=--=，由圆周角定理得，1602C AOB∠=∠=，故答案为60．【点睛】本题考查的是三角形的外接圆与外心，等腰三角形的性质，掌握圆周角定理是解题的关键．30．如图，BC为∠O的直径，弦AD∠BC于点E，直线l切∠O于点C，延长OD交l 于点F，若AE=2，为ABC=22.5°，则CF的长度为31．用一张圆形的纸剪一个边长为4 cm的正六边形，则这个圆形纸片的半径最小应为_______cm．【答案】4【分析】要剪一张圆形纸片完全盖住这个正六边形，这个圆形纸片的边缘即为其外接圆，根据正六边形的边长与外接圆半径的关系即可求出.【详解】∠正六边形的边长是4cm，∠正六边形的半径是4cm，∠这个圆形纸片的最小半径是4cm，故答案为4cm.【点睛】此题主要考查了正多边形与圆的知识，注意正六边形的外接圆半径与边长相等，这是一个需要谨记的内容.32．如图，AB与∠O相切于点A，BO与∠O相交于点C，点D是∠O上一点，∠B＝38°．则∠D的度数是_____．33．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF＝CD ＝12cm，则球的半径为______cm．【答案】7.5【分析】首先找到EF的中点M，作MN∠AD于点M，取MN上的球心O，连接OF，设OF＝x，则OM是(12﹣x) cm，MF＝6 cm，然后在直角三角形MOF中利用勾股定理求得OF的长即可．【详解】解：EF 的中点M ，作MN∠AD 于点M ，取MN 上的球心O ，连接OF ，∠四边形ABCD 是矩形，∠∠C ＝∠D ＝90°，∠四边形CDMN 是矩形，∠MN ＝CD ＝12 cm设OF ＝x cm ，则ON ＝OF ，∠OM ＝MN ﹣ON ＝ (12﹣x) cm ，MF ＝6 cm ，在直角三角形OMF 中，OM 2+MF 2＝OF 2，即：（12﹣x ）2+62＝x 2，解得：x ＝7.5，故答案为：7.5．【点睛】本题考查了垂径定理及勾股定理的知识，解题的关键是正确的作出辅助线构造直角三角形．34．已知Rt ABC 中，90ACB ∠=︒，6cm AC =，8cm BC =，以C 为圆心，4.8cm 长度为半径画圆，则直线AB 与O 的位置关系是__________．与O 的位置关系是相切．2268=+与O 的位置关系是相切．故答案为：相切．【点睛】本题考查勾股定理，直角三角形面积，圆的切判定，掌握勾股定理，直角三角形面积，圆的切判定是解题关键．35．如图,一次函数y=x轴、y轴交于A、B两点,P为一次函数=的图像上一点,以P为圆心能够画出圆与直线AB和y轴同时相切,则y x∠BPO=_________.∠∠OBP=15°又∠BOP=45°∠∠BPO=180°-45°-15°=120°相交时，点P即为圆心．（2）当∠ABO的外角平分线与y x如图，同理可求∠OBP=30°+75°=105°∠∠BPO=180°-45°-105°=30°故答案为：30°或120°【点睛】本题主要考查了切线的判定和性质，角平分线的性质及三角形的内角和的应用，正确的对点P的位置进行分类是解题的关键．36．如图，四边形ABCD内接于∠O，点E在AB的延长线上，BF∠AC，AB＝BC，∠ADC=130°，则∠FBE=_______°.【答案】65【详解】连接BD，如图所示：∠∠ADB和∠ACB是弧AB所对的圆周角，∠BDC和∠BAC是弧BC所对的圆周角，∠∠ADB＝∠ACB，∠BDC＝∠BAC，又∠∠BDC+∠ADB＝∠ADC，∠ADC=130°，∠∠BAC+∠ACB＝130°，又∠AB＝BC，∠∠BAC＝∠ACB＝65°，又∠BF∠AC，∠∠FBE=∠BAC＝65°；故答案是：65．37．如图，点A在数轴上对应的数为26，以原点O为圆心，OA为半径作优弧AB，使点B在O右下方，且4tan3AOB∠=．在优弧AB上任取一点P，且能过P作直线l OB∥交数轴于点Q，设Q在数轴上对应的数为x，连接OP．（1）若优弧AB上一段AP的长为13π，则AOP∠的度数为__________，x的值为__________；（2）x的最小值为__________，此时直线l与弧AB所在圆的位置关系为__________26nπ⨯38．如图，在Rt ABC △中，903cm 4cm C AC BC ∠=︒==，，，以BC 边所在的直线为轴，将ABC 旋转一周得到的圆锥侧面积是___；此圆锥展开的侧面扇形的圆心角为____．边所在的直线为轴，将ABC 旋转一周得到的圆锥侧面积是此圆锥展开的侧面扇形的扇形弧长是底面圆周长，此圆锥展开的侧面扇形的圆心角度数为【点睛】本题考查了勾股定理，圆锥的计算；得到几何体的组成是解决本题的突破39．如图，在平面直角坐标系xOy 中，一次函数y ＋4的图象与x 轴、y 轴交于A 、B 点，点C 在线段OA 上，点D 在直线AB 上，且CD ＝2，∠DEC 是直角三角形（∠EDC ＝90°），DE ，连接AE ，则AE 的最大值为_________．∠+∠=______度，阴影四边形的面积为______．【答案】 105︒##105度 1##1-+∠90ABD ，AB BD =90ABC BAC ∠+∠=︒=BAC DBE ∠=∠，(AAS BAC DBE ≌△△AC BE =，BC DE =三、解答题41．如图，在∠O 中，直径AB 与弦CD 相交于点E ，连接AC 、BD ．(1)求证：AEC DEB △∽△；(2)连接AD ，若3AD =，30C ∠=︒，求∠O 的半径．【答案】(1)证明见解析(2)∠O 的半径为3Rt ADB 中，26AD ==，132AB ==的半径为【点睛】本题考查圆的基本知识，相似三角形的判定，以及含42．如图，在O 中，AB 为直径，AC 为弦．过BC 延长线上一点G ，作GD AO ⊥于点D ，交AC 于点E ，交O 于点F ，M 是GE 的中点，连接CF ，CM ．（1）判断CM 与O 的位置关系，并说明理由；（2）若ECF 2A ∠∠=，CM 6=，CF 4=，求MF 的长．与O 相切；理由见解析；3343．已知：如图，线段BC 与经过点C 的直线l ．求作：在直线l 上求作点D ，使150CDB ∠=︒．作法：∠分别以点B ，C 为圆心，BC 长为半径画弧，两弧交于BC 上方的点A ，连接AB ，AC ；∠以点A 为圆心，以AB 长为半径画圆交直线l 于点D （不同于点C ），连接BD ．则点D 即为所求．(1)使用直尺和圆规，依作法补全图形（保留作图痕迹）；(2)完成下面的证明．证明：∠分别以点B ，C 为圆心，BC 长为半烃画弧，两弧交于BC 上方的点A ． ∠AB BC CA ==∠ABC 为等边三角形．∠60BAC ∠=︒．在A 中，在优弧BC 上任取点E ，连接BE ，CE ．∠30CEB ∠=︒．（_________________________）（填推理依据）∠点B ，D ，C ，E 在A 上．∠180CDB CEB ∠+∠=︒．（_________________________）（填推理依据）即150CDB ∠=︒．【答案】(1)见解析(2)圆周角定理；圆内接四边形对角互补【分析】（1）根据题意作出图形即可求解；（2）根据圆周角定理，以及圆内接四边形对角互补，即可求解．【详解】（1）解；如图所示，（2）证明：∠分别以点B ，C 为圆心，BC 长为半烃画弧，两弧交于BC 上方的点A ． ∠AB BC CA ==∠ABC 为等边三角形．∠=60?BAC ∠．在A 中，在优弧BC 上任取点E ，连接BE ，CE ．∠=30?CEB ∠（圆周角定理）∠点B ，D ，C ，E 在A 上．∠+=180CDB CEB ∠∠︒．（圆内接四边形对角互补）即150CDB ∠=︒．故答案为：圆周角定理；圆内接四边形对角互补．【点睛】本题考查了等边三角形的判定和性质，圆周角定理，圆内接四边形的性质，掌握圆周角定理是解题的关键．44．某市政府计划修建一处公共服务设施，使它到三所公寓A 、B 、C 的距离相等．（1）若三所公寓A 、B 、C 的位置如图所示，请你在图中确定这处公共服务设施（用点P 表示）的位置（尺规作图，保留作图痕迹，不写作法）；（2）若∠BAC =56°，则∠BPC =【答案】（1）见解析；（2）112°【分析】（1）连接AB 、BC 、AC ，作线段AB 和AC 的垂直平分线，交点P 即为所求；（2）利用三角形外心的性质结合圆周角定理得出答案．【详解】解：（1）如图所示：P 点即为所求；（2）连接PB 、PC ，∠点P 是三角形ABC 的外心，∠∠BPC ＝2∠BAC ＝112°．【点睛】此题主要考查了应用设计与作图，掌握线段垂直平分线的性质，得出P 点是三角形ABC 的外心是解题关键．45．如图ABC 内接于O ，60B ∠=，CD 是O 的直径，点P 是CD 延长线上一点，且AP AC =．()1求证：P A 是O 的切线；()2若PD =O 的直径．）O 的直径为30，继而根据等腰三角形的性质可得出30，继而由P ，可得出30的直角三角形的性质求出PD OD =，可得出O 的直径．连接OA ，如图，B 60∠=，AOC 2B 120∠∠∴=，又OA OC =，OAC 30∠∠∴=，又AP AC =P ACP 30∠∠=，90，是O的切线．Rt OAP中，P30∠=，=+，2OA OD PD=，又OA OD=，PD OA=，PD5∴=2OA2PD∴的直径为O【点睛】本题考查了切线的判定、圆周角定理、含掌握切线的判定定理、圆周角定理及含46．如图，已知等边∠ABC，AB＝2，以AB为直径的半圆与BC边交于点D，过点D 作DF∠AC，垂足为F，过点F作FG∠AB，垂足为G，连结GD．(1)求证：DF是∠O的切线；(2)求FG的长．22447．九年级学生小刚是一个喜欢看书的好学生，他在学习完第二十四章圆后，在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理（圆内的两条相交弦，被交点分成的两条线段长的积相等），非常好奇，仔细阅读原来就是：PA•PB=PC•PD，小刚很想知道是如何证明的，可异证明部分污损看不清了，只看到辅助线的做法，分别连结AC、BD．聪明的你一定能帮他证出，请在图1中做出辅助线，并写出详细的证明过程．小刚又看到一道课后习题，如图2，AB是∠O弦，P是AB上一点，AB=10cm，PA=4cm，OP=5cm，求∠O的半径，愁坏了小刚，乐于助人的你肯定会帮助他，请写出详细的证明过程．【答案】（1）见解析；（2）∠O的半径R为7．【分析】（1）连结AC，BD，根据圆周角定理得到∠C=∠B，∠A=∠D，再根据三角形相似的判定定理得到△APC∠∠DPB，利用相似三角形的性质得AP：DP=CP：BP，变形有AP•BP=CP•DP；由此得到相交弦定理；（2）由AB=10，PA=4，OP=5，易得PB=10-4=6，PC=OC-OP=R-5，PD=OD+OP=R+5，根据相交弦定理得到PA•PB=PC•PD，即4×6=（R-5）×（R+5），解方程即可得到R的值．【详解】（1）圆的两条弦相交，这两条弦被交点分成的两条线段的积相等．已知，如图1，∠O的两弦AB、CD相交于E，求证：AP•BP=CP•DP．证明如下：连结AC，BD，如图1，∠∠C=∠B，∠A=∠D，∠∠APC∠∠DPB，∠AP：DP=CP：BP，∠AP•BP=CP•DP；所以两条弦相交，被交点分成的两条线段的积相等．（2）过P作直径CD，如图2，∠AB=10，PA=4，OP=5，∠PB=10﹣4=6，PC=OC﹣OP=R﹣5，PD=OD+OP=R+5，由（1）中结论得，PA•PB=PC•PD，∠4×6=（R﹣5）×（R+5），解得R=7（R=﹣7舍去）．所以∠O的半径R=7．【点睛】本题考查的是圆，熟练掌握相交弦定理和相似三角形的判定与性质是解题的关键.48．如图，点C在以AB为直径的∠O上．AE与过点C的切线垂直，垂足为D，AD 交∠O于点E，过B作BF∠AE交∠O于点F，连接CF．（1）求证：∠B＝2∠F；（2）已知AE＝8，DE＝2，过B作BF∠AE交∠O于F，连接CF，求CF的长．49．如图，已知∠O的直径AB=8，过A、B两点作∠O的切线AD、BC．（1）当AD=2，BC=8时，连接OC、OD、CD．∠求∠COD的面积．∠试判断直线CD与∠O的位置关系，并说明理由．（2）若直线CD与∠O相切于点E，设AD=x（x＞0），试用含x的式子表示四边形ABCD的面积S，并探索S是否存在最小值，写出探索过程．50．在平面直角坐标系xOy 中，对于线段MN 及点P 、Q ，若60MPN ∠=︒且线段MN 关于点P 的中心对称线段M N ''恰好经过点Q ，则称点Q 是点P 的线段60MN -︒对经点．(1)设点()0,2A ．∠()1Q ，()24,0Q ，312Q ⎫-⎪⎪⎝⎭，其中为某点P 的线段60OA -︒对经点的是______．∠已知()0,1B ，设∠B 的半径为r ，若∠B 上存在某点P 的线段60OA -︒对经点，求r 的取值范围．(2)若点()4,0Q 同时是相异两点1P 、2P 的线段60OD -︒对经点，直接写出线段OD 长的取值范围．为边的等边三角形的外接圆C 上优弧上的横纵坐标的最值，根据定义以及中点坐标公的方法作出图形，作M 的切线关于P 中心对N 为圆心，矩形对角线长度为半径两圆组成的图两直线之间的部分，除公共部分以外的图形，即图中阴影部分，包括边轴上的部分，根据图形求得）作辅助线，设,M N 在OD 同时是相异两点1P 、2P 的线段33DM x =，OM 长，解一元一次不等式组求解即可．Q 为边的等边三角形的外接圆C 上优弧上的一点，()0,2A2OA ∴=C 为AOP 的外心，则过点C 分别作CG 2OC33GC =3GC ∴=33C x ∴=∴P 的横坐标最大值为Qx交M于点S作M的是C的直径)AA交M于点F1根据对称性，同理可得过N的r的最值也为M N在OD）作辅助线，设,T 为,M N 的交点，2MT NT OM ∴===11=22TH MN OD ∴==在Rt NTH 中， NH OH ON NH =+OR ON NR =+()4,0D236+∴解得433即433≤。

数学圆专题训练

专题复习《圆》提高测试（一）选择题：（每题2分，共20分）1．有4个命题：①直径相等的两个圆是等圆；②长度相等的两条弧是等弧； ③圆中最大的弧是过圆心的弧；④一条弦把圆分为两条弧，这两条弧不可能是等弧．其中真命题是………………………………………………………………………（）（A ）①③ （B ）①③④ （C ）①④ （D ）①【提示】长度相等的两弧不一定是等弧，故②不对；当弦是直径时，直径把圆分为两个半圆，它们是等弧，故④不对．【答案】A ．【点评】本题考查等圆、等弧、直线与弦的概念．注意：等弧是能互相重合的两条弧，直径是圆中最大的弦．2．如图，点I 为△ABC 的内心，点O 为△ABC 的外心，∠O ＝140°，则∠I 为（）（A ）140° （B ）125° （C ）130° （D ）110°【提示】因点O 为△ABC 的外心，则∠BOC 、∠A 分别是所对的圆心角、圆周角，所以∠O ＝2∠A ，故∠A ＝21³140°＝70°．又因为I 为△ABC 的内心，所以∠I ＝90°＋21∠A ＝90°＋21³70°＝125°．【答案】B ．【点评】本题考查圆心角与圆周角的关系，内心、外心的概念．注意三角形的内心与两顶点组成的角与另一角的关系式．3．如果正多边形的一个外角等于60°，那么它的边数为……………………………（）（A ）4 （B ）5 （C ）6 （D ）7【提示】正多边形的外角等于它的中心角，所以n︒360＝60°，故n ＝6．【答案】C ．【点评】此题考查正多边形的外角与中心角的关系．注意：正n 边形的中心角为n︒360，且等于它的一个外角．4．如图，AB 是⊙O 的弦，点C 是弦AB 上一点，且BC ︰CA ＝2︰1，连结OC 并延长交⊙O 于D ，又DC ＝2厘米，OC ＝3厘米，则圆心O 到AB 的距离为…………（）（A ）6厘米（B ）7厘米（C ）2厘米（D ）3厘米【提示】延长DO 交⊙O 于E ，过点O 作OF ⊥AB 于F ，则CE ＝8厘米．由相交弦定理，得DC ²CE ＝AC ·CB ，所以AC ·2 AC ＝2³8，故AC ＝22（厘米），从而BC ＝42厘米．由垂径定理，得AF ＝FB ＝21（22＋42）＝32（厘米）．所以CF ＝32－22＝2（厘米）．在Rt △COF 中，OF ＝22OF OC -＝22)2(3-＝7（厘米）．【答案】C ．【点评】本题考查相交弦定理、垂径定理．注意：在圆中求线段的长，往往利用相交弦定理、垂径定理进行线段的转换，再结合勾股定理建立等式． 5．等边三角形的周长为18，则它的内切圆半径是……………………………………（）（A ）63 （B ）33 （C ）3 （D ）33 【提示】等边三角形的边长为6，则它的面积为43³62＝93．又因为三角形的面积等于内切圆的半径与三角形的周长的积的一半，所以93＝21r ²18（r 为内切圆半径）．解此方程，得r ＝3．【答案】C ．【点评】本题考查等边三角形的面积的求法、内切圆半径的求法．注意：求三角形的内切圆的半径，通常用面积法．6．如图，⊙O 的弦AB 、CD 相交于点P ，P A ＝4厘米，PB ＝3厘米，PC ＝6厘米，EA 切⊙O 于点A ，AE 与CD 的延长线交于点E ，AE ＝25厘米，则PE 的长为（）（A ）4厘米（B ）3厘米（C ）45厘米（D ）2厘米【提示】由相交弦定理，得P A ²PB ＝PD ²PC ．∴ 4³3＝PD ²6． ∴ PD ＝2（厘米）．由切割线定理，得 AE 2＝ED ²EC ． ∴ （25）2＝ED ·（ED ＋2＋6）．解此方程得ED ＝2或ED ＝－10（舍去）．∴ PE ＝2＋2＝4（厘米）．【答案】A ．【点评】本题考查相交弦定理、切割线定理．注意：应用相交弦定理、切割线定理往往建立方程，通过解方程求解．7．一个扇形的弧长为20π 厘米，面积是240π 厘米2，则扇形的圆心角是……………（）（A ）120° （B ）150° （C ）210° （D ）240°【提示】设扇形的圆心角为n 度，半径为R ，则⎪⎪⎩⎪⎪⎨⎧==240360ππ20180π2R n Rn 解方程组得⎩⎨⎧==．15024n R 【答案】B ．【点评】本题考查扇形的弧长、面积公式．注意：应熟记扇形的弧长公式、扇形的面积公式．8．两圆半径之比为2︰3，当两圆内切时，圆心距是4厘米，当两圆外切时，圆心距为（）（A ）5厘米（B ）11厘米（C ）14厘米（D ）20厘米【提示】设两圆半径分别为2 x 、3 x 厘米，则内切时有3 x －2 x ＝4，所以x ＝4．于是两圆半径分别为8厘米、12厘米．故外切时圆心距为20厘米．【答案】D ．【点评】本题考查两圆内切、外切时，圆心距与两圆半径的关系．注意：要理解并记忆两圆的五种位置关系及圆心距与半径的关系．9．一个圆锥的侧面积是底面积的2倍，则这个圆锥的侧面展开图的圆周角是……（）（A ）60° （B ）90° （C ）120° （D ）180°【提示】设圆锥的母线长为a ，圆心角度数为n ，底面圆的半径为r ，则⎪⎪⎩⎪⎪⎨⎧=⋅=．r a n r a n π2180ππ2360π22解此方程组，得 n ＝180．【答案】D ．【点评】此题考查圆锥的侧面展开图的概念．注意理解圆柱、圆柱的侧面展开图的有关概念．10．如图，等腰直角三角形AOB 的面积为S 1，以点O 为圆心，OA 为半径的弧与以AB为直径的半圆围成的图形的面积为S 2，则S 1与S 2的关系是………………………（）（A ）S 1＞S 2 （B ）S 1＜S 2 （C ）S 1＝S 2 （D ）S 1≥S 2【提示】设OA ＝a ，则S 1＝21a 2，弓形ACB 的面积＝41πa 2－21a 2．在Rt △AOB 中，AB ＝2a ，则以AB 为直径的半圆面积为 21·π·（2AB ）2＝21π·（22a ）2＝41πa 2．则S 2＝41πa 2－（41πa 2－21a 2）＝21a 2．【答案】C ．【点评】本题考查三角形、圆、弓形的面积计算．注意：弓形的面积计算方法．（二）填空题（每题2分，共20分）11．已知⊙O 1和⊙O 2的半径分别为2和3，两圆相交于点A 、B ，且AB ＝2，则O 1O 2＝______．【提示】当两圆在AB 的两侧时，设O 1O 2交AB 于C ，则O 1O 2⊥AB ，且AC ＝BC ，∴ AC ＝1．在Rt △AO 2C 中，O 2C ＝222AC A O -＝132-＝22；在Rt △AO 1C 中，O 1C ＝221AC A O -＝2212-＝3．∴ O 1O 2＝22＋3．当两圆在AB 的同侧时，同理可求O 1O 2＝22－3．【答案】22±3．【点评】此题考查“两圆相交时，连心线垂直于公共弦”的应用．注意：在圆中不要漏解，因为圆是轴对称图形，符合本题条件的两圆有两种情形． 12．已知四边形ABCD 是⊙O 的外切等腰梯形，其周长为20，则梯形的中位线长为_____．【提示】圆外切四边形的两组对边之和相等，则上、下底之和为10，故中位线长为5．【答案】5．【点评】本题考查圆外切四边形的性质．注意：本题还可求得圆外切等腰梯形的腰长也为5，即等于中位线长．13．如图，在△ABC 中，AB ＝AC ，∠C ＝72°，⊙O 过A 、B 两点，且与BC 切于点B ，与AC 交于D ，连结BD ，若BC ＝5－1，则AC ＝______．【提示】在△ABC 中，AB ＝AC ，则 ∠ABC ＝∠ACB ＝72°， ∴ ∠BAC ＝36°．又 BC 切⊙O 于B ，∴ ∠A ＝∠DBC ＝36°． ∴ ∠BDC ＝72°．∴ ∠ABD ＝72°－36°＝36°． ∴ AD ＝BD ＝BC ．易证△CBD ∽△CAB ， ∴ BC 2＝CD ²CA ． ∵ AD ＝BD ＝BC ，∴ CD ＝AC －AD ＝AC －BC ． ∴ BC 2＝（AC －BC ）·CA ．解关于AC 的方程，得AC ＝152-BC ．∴ AC ＝152-·（5－1）＝2．【答案】2．【点评】本题考查弦切角定理、等腰三角形的性质、相似三角形的性质．注意底角为72°的等腰三角形的特殊性，底角的平分线把对边分成的两线段的比为215-，即成黄金比． 14．用铁皮制造一个圆柱形的油桶，上面有盖，它的高为80厘米，底面圆的直径为50厘米，那么这个油桶需要铁皮（不计接缝）厘米2（不取近似值）．【提示】铁皮的面积即圆柱的侧面积与两底的面积的和．底面圆面积为41π·502＝625π（厘米2），底面圆周长为π³50＝50π（厘米），则铁皮的面积为2³625π＋80³50π＝5250π（厘米2）．【答案】5250π厘米2．【点评】本题考查圆柱的侧面展开图的面积及圆柱的表面积．注意：圆柱的表面积等于侧面积与两底面积之和． 5．已知两圆的半径分别为3和7，圆心距为5，则这两个圆的公切线有_____条．【提示】∵ 7－3＜5＜7＋3，∴ 两圆相交，∴ 外公切线有2条，内公切线有0条．【答案】2．【点评】本题考查两圆的位置关系及对应的圆心距与两圆半径的关系．注意：仅仅从5＜7＋3并不能断定两圆相交，还要看5与7－3的大小关系．16．如图，以AB 为直径的⊙O 与直线CD 相切于点E ，且AC ⊥CD ，BD ⊥CD ，AC ＝8 cm ，BD ＝2 cm ，则四边形ACDB 的面积为______．【提示】设AC 交⊙O 于F ，连结BF ．∵ AB 为⊙O 的直径， ∴ ∠AFB ＝90°．连结OE ，则OE ⊥CD ， ∴ AC ∥OE ∥BD ． ∵ 点O 为AB 的中点， ∴ E 为CD 的中点．∴ OE ＝21（BD ＋AC ）＝21（8＋2）＝5（cm ）．∴ AB ＝2³5＝10（cm ）．在Rt △BF A 中，AF ＝CA －BD ＝8－2＝6（cm ），AB ＝10 cm ，∴ BF ＝22610-＝8（cm ）． ∴ 四边形ACDB 的面积为 21（2＋8）·8＝40（cm 2）．【答案】40 cm 2．【点评】本题考查直径的性质、中位线的判定与性质、切线的性质．注意：在圆中不要忽视直径这一隐含条件．17．如图，P A 、PB 、DE 分别切⊙O 于A 、B 、C ，⊙O 的半径长为6 cm ，PO ＝10 cm ，则△PDE 的周长是______．图中知，CM ＝R ＋8，MD ＝R －8，【提示】连结OA ，则OA ⊥AP ．在Rt △POA 中，P A ＝22OA OP -＝22610-＝8（cm ）．由切线长定理，得EA ＝EC ，CD ＝BD ，P A ＝PB ，∴ △PDE 的周长为PE ＋DE ＋PD＝PE ＋EC ＋DC ＋PD ，＝PE ＋EA ＋PD ＋DB＝P A ＋PB ＝16（cm ）．【答案】16 cm ．【点评】本题考查切线长定理、切线的性质、勾股定理．注意：在有关圆的切线长的计算中，往往利用切线长定理进行线段的转换．18．一个正方形和一个正六边形的外接圆半径相等，则此正方形与正六边形的面积之比为_______．【提示】设两正多边形的外接圆半径为R ，则正方形面积为4³21·R 2＝2 R 2，正六边形的面积为6³43R 2＝323R 2，所以它们的比为2 R 2：323R 2＝43︰9．【答案】43︰9．【点评】本题考查正方形、正六边形的面积与外接圆的半径之间的关系．注意：正多边形的面积通常化为n 个三角形的面积和．19．如图，已知P A 与圆相切于点A ，过点P 的割线与弦AC 交于点B ，与圆相交于点D 、E ，且P A ＝PB ＝BC ，又PD ＝4，DE ＝21，则AB ＝______．【提示】由切割线定理，得 P A 2＝PD ²PE ． ∴ P A ＝254 ＝10． ∴ PB ＝BC ＝10．∵ PE ＝PD ＋DE ＝25， ∴ BE ＝25－10＝15． ∴ DB ＝21－15＝6．由相交弦定理，得 AB ·BC ＝BE ·BD ． ∴ AB ²10＝15³6． ∴ AB ＝9．【答案】9．【点评】本题考查切割线定理与相交弦定理的应用，要观察图形，适当地进行线段间的转化．20．如图，在□ABCD 中，AB ＝43，AD ＝23，BD ⊥AD ，以BD 为直径的⊙O 交AB 于E ，交CD 于F ，则□ABCD 被⊙O 截得的阴影部分的面积为_______．【提示】连结OE 、DE ．∵ AD ⊥BD ，且AB ＝43，AD ＝23， ∴ ∠DBA ＝30°，且BD ＝6． ∵ BD 为直径， ∴ ∠DEB ＝90°． ∴ DE ＝BD ²sin 30°＝6³21＝3，BE ＝6³23＝33．∴ S △DEB ＝21³33³3＝293． ∵ O 为BD 的中点，∴ S △BOE ＝21S △DEB ＝493．∵ DO ＝21BD ＝3，∠DOE ＝2³30°＝60°， ∴ S 阴影＝2（S △ADB －S 扇形DOE －S △EOB ）＝2（21³23³6－36060π·32－493）．＝2153－3π．【答案】π33215-．【点评】本题考查了勾股定理、扇形面积公式、解直角三角形等知识．注意：求不规则图形面积，往往转化为规则图形的面积的和或差的形式．（三）判断题（每题2分，共10分）21．点A 、B 是半径为r 的圆O 上不同的两点，则有0＜AB ≤2 r ………………（）【答案】√．【点评】因为直径是圆中最大的弦，则判断正确．22．等腰三角形顶角平分线所在直线必过其外接圆的圆心…………………………（）【答案】√．【点评】因为等腰三角形的顶角平分线垂直平分底边，根据垂径定理的推论知，顶角平分线所在直线必过圆心．23．直角梯形的四个顶点不在同一个圆上……………………………………………（）【答案】√．【点评】若在同一个圆上，则对角互补，故四个角全为直角．所以假设不成立，原命题成立．24．等边三角形的内心与外心重合……………………………………………………（）【答案】√．【点评】等腰三角形的顶角的平分线也是对边的中线与高，因此等边三角形的内心与外心重合．25．两圆没有公共点时，这两个圆外离……………………………………………（）【答案】³．【点评】两圆没有公共点时，既可以是外离，也可以是内含，所以原命题不成立．（四）解答题与证明题（共50分）26．（8分）如图，△ABC 内接于⊙O ，AB 的延长线与过C 点的切线GC 相交于点D ，BE 与AC 相交于点F ，且CB ＝CE ，求证：（1）BE ∥DG ；（2）CB 2－CF 2＝BF ²FE ．【提示】（1）证明利用弦切角定理进行角之间的转化可证∠E ＝∠GCE ；把（2）变形为CB 2＝CF 2＋BF ·FE ．∵ BF ²FE ＝CF ·AF ，∴ CF 2＋BF ²FE ＝CF 2＋CF ·AF＝CF （CF ＋AF ）＝CF ²CA ．即只要证CB 2＝CF ²CA 即可，只需证△CBF ∽△CAB ．【略证】（1）∵ CG 为⊙O 的切线，∴ ∠EBC ＝∠GCE ．∵ CB ＝CE ，∴．∴ ∠EBC ＝∠E ．∴ ∠E ＝∠GCE ．∴ GC ∥EB ．（2）∵ ∠EBC ＝∠E ＝∠A ，∠FCB O 为公共角，∴ △CBF ∽△CAB ． ∴ CB 2＝CF ²CA ＝CF ·（CF ＋AF ）＝CF 2＋CF ·AF ．由相交弦定理，得 CF ²F A ＝BF ·FE ，∴ CB 2＝CF 2＋BF ·FE ．即 CB 2－CF 2＝BF ²FE ．【点评】对于形如a 2＝cd ＋ef 的等式的证明较困难，因不易找到突破口．一般先把待证明的等式进行变形，以便于看出等式中线段之间的联系．如本题中，先把CF 2移到等式的右边去，再结合相交弦定理找出了思路． 27．（8分）如图，⊙O 表示一个圆形工件，图中标注了有关尺寸，且MB ︰MA ＝1︰4，求工件半径的长．【提示】把OM 向两方延长，交⊙O 于点C 、D ．设⊙O 的半径为R ，则可用相交弦定理求半径长．【略解】把OM 向两方延长，分别交⊙O 于C 、D 两点．设⊙O 的半径为R ．从图中知，AB ＝15 cm ．又 MB ︰MA ＝1︰4，∴ MB ＝51³15＝3（cm ），MA ＝12 cm ．从图中知，CM ＝R ＋8，MD ＝R －8，由相交弦定理，得 AM ²BM ＝CM ·MD ． ∴ 12³3＝（R ＋8）（R －8）．解此方程，得 R ＝10或R ＝－10（舍去）．故工件的半径长为10 cm ．【点评】此题是一道实际问题，要善于把实际问题转化为数学问题，因在圆中，OM 与AB 相交，故向相交弦定理转化． 28．（8分）已知：如图（1），⊙O 1与⊙O 2相交于A 、B 两点，经过A 点的直线分别交⊙O 1、⊙O 2于C 、D 两点（C 、D 不与B 重合），连结BD ，过点C 作BD 的平行线交⊙O 1于点E ，连BE ．（1）求证：BE 是⊙O 2的切线；（2）如图（2），若两圆圆心在公共弦AB 的同侧，其他条件不变，判断BE 和⊙O 2的位置关系（不要求证明）．【提示】（1）过B 作⊙O 2的直径BH ，连结AB 、AH ，证∠EBH ＝90°．（2）用类似的方法去探求．【证明】（1）连结AB，作⊙O2的直径BH，连结AH．则∠ABH＋∠H＝90°，∠H＝∠ADB，∠EBA＝∠ECA．∵EC∥BD，∴∠ADB＝∠ACE＝∠EBA．∴∠EBA＋∠ABH＝90°．即∠EBH＝90°．∴BE是⊙O2的切线．（2）同理可知，BE仍是⊙O2的切线．【点评】证明一与圆有公共点的直线是圆的切线的一般方法是过公共点作半径（或直径），再证直径与半径垂直，但此题已知条件中无90°的角，故作直径构造90°的角，再进行角的转换．同时两圆相交，通常作它们的公共弦，这样把两圆中的角都联系起来了．另外，当问题进行了变式时，要学会借鉴已有的思路解题．29．（12分）如图，已知CP为⊙O的直径，AC切⊙O于点C，AB切⊙O 于点D，并与CP的延长线相交于点B，又BD＝2 BP．求证：（1）PC＝3 PB；（2）AC＝PC．【提示】（1）因为BC＝BP＋PC，所以要证PC＝3 BP，即要证BC＝4 BP，用切割线定理进行转化．（2）要证AC等于⊙O的直径，即要证AC＝2³半径．只要连结OD，易证△BOD∽△BAC．可利用相似三角形的性质证明结论．【略证】（1）∵BD是⊙O的切线，BPC是⊙O的割线，∴BD2＝BP²BC．∵BD＝2 BP，∴ 4 BD2＝BP²BC．∴ 4 BP＝BC．∵BC＝BP＋PC，∴ 4 BP＝BP＋PC．∴PC＝3 BP．（2）连结DO．∵AB切⊙O于点D，AC切⊙O于点C，∴∠ODB＝∠ACB＝90°．∵∠B＝∠B，∴△ODB∽△ACB．∴ACDO＝BCBD＝BPBP42＝21．∴AC＝2 DO．∴PC＝2 DO．∴AC＝PC．【点评】此题体现了圆幂定理和切线性质定理的应用，解题的关键是善于转化．30．（14分）如图，已知O 是线段AB 上一点，以OB 为半径的⊙O 交线段AB 于点C ，以线段OA 为直径的半圆交⊙O 于点D ，过点B 作AB 垂线与AD 的延长线交于点E ，连结CD ．若AC ＝2，且AC 、AD 的长是关于x 的方程x 2－kx ＋45＝0的两个根．（1）证明AE 切⊙O 于点D ；（2）求线段EB 的长；（3）求tan ∠ADC 的值．【提示】连结OD 、BD ．（1）证∠ODA ＝90°即可；（2）利用切割线定理，结合一元二次方程根与系数的关系求BE 的长；（3）利用相似三角形的比进行转化．（1）【略证】连结OD ．∵ OA 是半圆的直径，∴ ∠ADO ＝90°．∴ AE 切⊙O 于点D ．（2）【略解】∵ AC 、AD 的长是关于x 的方程x 2－kx ＋45＝0的两个根，且AC ＝2，AC ²AD ＝25，∴ AD ＝45．∵ AD 是⊙O 的切线，ACB 为割线，∴ AD 2＝AC ²AB ．又 AD ＝25，AC ＝2，∴ AB ＝10．则 BC ＝8，OB ＝4．∵ BE ⊥AB ，∴ BE 切⊙O 于B ．又 AE 切⊙O 于点D ，∴ ED ＝EB ．在Rt △ABE 中，设BE ＝x ，由勾股定理，得（x ＋25）2＝x 2＋102．解此方程，得 x ＝45．即BE 的长为45．（3）连结BD ，有∠CDB ＝90°．∵ AD 切⊙O 于D ，∴ ∠ADC ＝∠ABD ，且tan ∠ADC ＝tan ∠ABD ＝BDCD ．在△ADC 和△ABD 中，∠A ＝∠A ，∠ADC ＝∠ABD ，∴ △ADC ∽△ABD ．∴ BD DC ＝AB AD ＝1052＝55． ∴ tan ∠ADC ＝55．。

有关园的圆的专题训练

【答案】C
21.（2011四川乐山6，3分）如图（3），CD是⊙O的弦，直径AB过CD的中点M，若∠BOC=40°，则∠ABD=
A．40° B．60° C．70° D．80°
【答案】C
22.如图，，点C在上，且点C不与A、B重合，则的度数为（）
A． B．或 C． D．或
【答案】D
23.如图，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD＝105°，
（1）当∠AOB＝30°时，求弧AB的长；
（2）当DE＝8时，求线段EF的长；
（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似，若存在，请求出此时点E的坐标；若不存在，请说明理由.
解：（1）连结BC,
∵A（10，0）,∴OA=10 ,CA=5,
∵∠AOB=30°,
∴∠ACB=2∠AOB=60°,
【答案】D
26.如图，是上的三点，，则度．
【答案】60
二、填空题
1.如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧BC于点D，连结CD、OD，给出以下四个结论：①AC∥OD；② ；③△ODE∽△ADO；④ ．其中正确结论的序号是．
【答案】①④
2.如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O的半径是．
A.16 B.10 C.8 D.6
【答案】A
9.如图，小华同学设计了一个圆直径的测量器，标有刻度的尺子OA、OB在O点钉在一起，并使它们保持垂直，在测直径时，把O点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的直径为（）
A.12个单位B.10个单位C.4个单位D.15个单位
【答案】B

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A,真题范例：
例：1，（2015十堰中考24题）如图1，△ABC 内接于⊙O ，∠BAC 的平分线交⊙O
于点D ，交BC 于点E （BE ＞EC ），且BD
=D 作DF ∥BC ，交AB 的延长线于点F ．
（1）求证：DF 为⊙O 的切线；
（2）若∠BAC =60°，DE
（3）若43
AB AC =，DF +BF =8，如图2，求BF 的长．
图1 图2
2，（2014十堰中考24题）如图1，AB 为半圆的直径，O 为圆心，C 为圆弧上一点，AD 垂直于过C 点的切线，垂足为D ，AB 的延长线交直线CD 于点E ．
（1）求证：AC 平分∠DAB ；
（2）若AB=4，B 为OE 的中点，CF ⊥AB ，垂足为点F ，求CF 的长；
（3）如图2，连接OD 交AC 于点G
，若=，求sin ∠E 的值．
3，（2013十堰中考24题）如图1，△ABC 中，CA =CB ，点O 在高CH 上，OD ⊥CA 于点D ，OE ⊥CB 于点E ，以O 为圆心，OD 为半径作⊙O ．
（1）求证：⊙O 与CB 相切于点E ；
（2）如图2，若⊙O 过点H ，且AC =5，AB =6，连结EH ，求△BHE 的面积和
tan ∠BHE 的值．
图1 图2 B,模拟提升：
1．（2015•孝感）如图，AB 为⊙O 的直径，P 是BA 延长线上一点，PC 切⊙O 于点C ，CG 是⊙O 的弦，CG ⊥AB ，垂足为D ． F D B
（1）求证：∠PCA=∠ABC；
（2）过点A作AE∥PC，交⊙O于点E，交CD于点F，连接BE．若sin∠P=，CF=5，求BE的长．
2．（2015•兰州）如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC 边于D．以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D．
（1）判断直线BC与⊙O的位置关系，并说明理由；
（2）若AC=3，∠B=30°．
①求⊙O的半径；
②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）
3．（2015•枣庄）如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心、OA 为半径的圆交AC于点D，E是BC的中点，连接DE，OE．
（1）判断DE与⊙O的位置关系，并说明理由；
（2）求证：BC2=CD•2OE；
（3）若cos∠BAD=，BE=6，求OE的长．
4．（2012•北海）如图，AB是O的直径，AE交O于点E，且与O的切线CD互相垂直，垂足为D．
（1）求证：∠EAC=∠CAB；
（2）若CD=4，AD=8：①求O的半径；②求tan∠BAE的值．
5．（2012•襄阳）如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．
（1）求证：直线PA为⊙O的切线；
（2）试探究线段EF、OD、OP之间的等量关系，并加以证明；
（3）若BC=6，tan∠F=，求cos∠ACB的值和线段PE的长．
6．（2011•肇庆）己知：如图．△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连接AD．
（1）求证：∠DAC=∠DBA；
（2）求证：P是线段AF的中点；
（3）若⊙O的半径为5，AF=，求tan∠ABF的值．
7．（2011•广元）如图，AB是⊙O的直径，BC切⊙O于点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．
（1）试判断∠CBD与∠CEB是否相等，并证明你的结论；
（2）求证：=；
（3）若BC=AB，求tan∠CDF的值．
8．（2010•南宁）如图1，AB为⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB．
（1）求证：BC为⊙O的切线；
（2）连接AE，AE的延长线与BC的延长线交于点G（如图2所示），若AB=2，AD=2，求线段BC和EG的长．
9．（2008•濮阳）如图，△ABC内接于⊙O，过点B作⊙O的切线，交于CA的延长线于点E，∠EBC=2∠C．
（1）求证：AB=AC；
（2）当=时，①求tan∠ABE的值；②如果AE=，求AC的值．
10．（2005•恩施州）如图，AB为圆O的直径，C为圆O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB，延长AB交DC于点E．
（1）判定直线DE与圆O的位置关系，并说明你的理由；
（2）求证：AC2=AD•AB；
（3）以下两个问题任选一题作答．（若两个问题都答，则以第一问的解答评分）①若CF⊥AB于点F，试讨论线段CF、CE和DE三者的数量关系；
②若EC=5，EB=5，求图中阴影部分的面积．
11．（2004•荆州）如图，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB 于点D．连接OE、AC，已知∠POE=2∠CAB，∠P=∠E．
（1）求证：CE⊥AB；
（2）求证：PC是⊙O的切线；
（3）若BD=20D，PB=9，求⊙O的半径及tan∠P的值．
12．（2003•北京）已知：在△ABC中，AD为∠BAC的平分线，以C为圆心，CD
为半径的半圆交BC的延长线于点E，交AD于点F，交AE于点M，且∠B=∠CAE，FE：FD=4：3．
（1）求证：AF=DF；
（2）求∠AED的余弦值；
（3）如果BD=10，求△ABC的面积．
13．（2002•海淀区）如图，AB是⊙O的直径，AE平分∠BAF交⊙O于点E，过点E作直线与AF垂直交AF延长线于D点，且交AB延长线于C点．
（1）求证：CD与⊙O相切于点E；
（2）若CE•DE=，AD=3，求⊙O的直径及∠AED的正切值．
14．（2001•北京）如图，△ABC内接于⊙O，AB是⊙O的直径，PA是过A点的直线，∠PAC=∠B，
（1）求证：PA是⊙O的切线；
（2）如果弦CD交AB于E，CD的延长线交PA于F，AC=8，CE：ED=6：5，AE：EB=2：3，求AB的长和∠ECB的正切值．
15．（1998•浙江）在△ABC中，∠BAC=90°，∠ABC=60°，AB=2，AD是BC边上的高线，过点C，D的⊙O交AC于点E，连接BE交⊙O于点F．
（1）求BF•BE的值；
（2）设AE=x，用x的代数式表示△BDF的面积；
（3）如果△BDF的面积是，求tan∠ABE的值．
16．（2015•广安）如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．
（1）求证：PA是⊙O的切线；
（2）若=，且OC=4，求PA的长和tanD的值．。