矩阵论复习题目
矩阵理论习题与答案

矩阵理论习题与答案矩阵理论习题与答案矩阵理论是线性代数中的重要内容之一,它在数学、工程、计算机科学等领域都有广泛的应用。
为了帮助读者更好地理解和掌握矩阵理论,本文将介绍一些常见的矩阵理论习题,并提供详细的答案解析。
一、基础习题1. 已知矩阵A = [[2, 3], [4, 5]],求A的转置矩阵。
答案:矩阵的转置是将其行和列互换得到的新矩阵。
所以A的转置矩阵为A^T = [[2, 4], [3, 5]]。
2. 已知矩阵B = [[1, 2, 3], [4, 5, 6]],求B的逆矩阵。
答案:逆矩阵是指与原矩阵相乘得到单位矩阵的矩阵。
由于B是一个2×3的矩阵,不是方阵,所以不存在逆矩阵。
3. 已知矩阵C = [[1, 2], [3, 4]],求C的特征值和特征向量。
答案:特征值是矩阵C的特征多项式的根,特征向量是对应于每个特征值的线性方程组的解。
计算特征值和特征向量的步骤如下:首先,计算特征多项式:det(C - λI) = 0,其中I是单位矩阵,λ是特征值。
解特征多项式得到特征值λ1 = 5,λ2 = -1。
然后,将特征值代入线性方程组 (C - λI)x = 0,求解得到特征向量:对于λ1 = 5,解得特征向量v1 = [1, -2]。
对于λ2 = -1,解得特征向量v2 = [1, -1]。
所以C的特征值为λ1 = 5,λ2 = -1,对应的特征向量为v1 = [1, -2],v2 = [1, -1]。
二、进阶习题1. 已知矩阵D = [[1, 2], [3, 4]],求D的奇异值分解。
答案:奇异值分解是将矩阵分解为三个矩阵的乘积,其中一个是正交矩阵,一个是对角矩阵。
计算奇异值分解的步骤如下:首先,计算D的转置矩阵D^T。
然后,计算D和D^T的乘积DD^T,得到一个对称矩阵。
接下来,求解对称矩阵的特征值和特征向量。
将特征值构成对角矩阵Σ,特征向量构成正交矩阵U。
最后,计算D^T和U的乘积D^TU,得到正交矩阵V。
矩阵论复习题 带答案1

矩阵论复习题1设A 、B 均为n 阶正规矩阵,试证A 与B 酉相似的充分必要条件是A 与B 的特征值相同。
证明: 充分性:A 与B 的特征值相同,A 、B 均为n 阶正规矩阵,则有11,A P IP B Q IQ --== 故11111,,A P QIQ P R Q P R P Q -----==令= A 与B 酉相似 必要性:A,B 为n 阶正规矩阵,存在初等变换R,1A RBR -=11,,,I E PQ A P IP B Q EQ --==为对角矩阵,存在初等变换111,I PAP E QRAR Q ---== ,因为I,E 为对角矩阵,故I=E 。
因此A 与B 的特征值相同。
#2 作出下列矩阵的奇异值分解10(1)A 0111⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦011(2)A 200-⎡⎤=⎢⎥⎣⎦ (1)632- 6 3 2101263011,130 2 6 311206333T B AA ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦特征值对应,特征值对应,特征值对应 2221 2 2,131222 2 2TC A A ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦-⎢⎥⎢⎥⎣⎦⎣⎦特征值对应,特征值对应故263 2 6 32210263 2 203 2 6 3220063 2 20 33HA ⎡⎤-⎢⎥⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥⎣⎦-⎢⎥⎢⎥⎣⎦(2) 2010,240401T B AA ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦特征值对应,特征值对应, 0040012201-1,2-400- 2 20-11022- 2 2T C A A ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦特征值对应,特征值对应,特征值对应 0101022200A 001 2202022022H⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦3.求下列矩阵A 的满秩分解123002111021A ⎛⎫⎪=- ⎪⎪⎝⎭112211001230010,021110102111001230010,021101100001001230=010021-11-11L L A L L L A A ⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦故4 设A 、B 均为n 阶Hermite 正定矩阵,证明:若B A ≥且BA AB =,则33B A ≥.证明:由于A 、B 均为n 阶Hermite 正定矩阵,且BA AB =,则AB 与BA 均为n 阶Hermite 正定矩阵。
矩阵论复习题

矩阵论复习题矩阵论复习题矩阵论作为线性代数的重要分支,涉及到矩阵的性质、运算以及应用等方面。
在学习矩阵论的过程中,复习题是提高理解和巩固知识的重要工具。
本文将通过一些典型的矩阵论复习题,帮助读者回顾和加深对矩阵论的理解。
1. 矩阵的乘法性质与运算规则(1) 证明矩阵的乘法不满足交换律,即AB≠BA。
(2) 若矩阵A是m×n阶矩阵,矩阵B是n×p阶矩阵,证明矩阵乘法满足结合律,即(AB)C=A(BC)。
(3) 证明单位矩阵是矩阵乘法的单位元,即对于任意矩阵A,有AI=IA=A。
2. 矩阵的逆与行列式(1) 若矩阵A可逆,证明其逆矩阵唯一。
(2) 若矩阵A可逆,证明其逆矩阵也可逆,且逆矩阵的逆等于A。
(3) 若矩阵A可逆,证明其转置矩阵也可逆,且转置矩阵的逆等于A的逆的转置。
(4) 证明若矩阵A可逆,则其行列式不为零,即|A|≠0。
3. 矩阵的特征值与特征向量(1) 若矩阵A的特征值为λ,证明矩阵A-λI的行列式为零,即|A-λI|=0。
(2) 若矩阵A的特征向量为v,证明对于任意非零实数k,kv也是矩阵A的特征向量。
(3) 若矩阵A的特征向量v1和v2对应于不同的特征值λ1和λ2,证明v1和v2线性无关。
(4) 若矩阵A的特征向量v对应于特征值λ,证明对于任意正整数n,(A^n)v对应于特征值λ^n。
4. 矩阵的相似与对角化(1) 若矩阵A与矩阵B相似,证明矩阵B与矩阵A相似。
(2) 若矩阵A与矩阵B相似,矩阵B可对角化,证明矩阵A也可对角化。
(3) 若矩阵A可对角化,证明A的特征向量组成的矩阵P可逆,且A=PDP^-1,其中D为对角矩阵。
通过复习以上的矩阵论题目,可以加深对矩阵的性质、运算规则、逆与行列式、特征值与特征向量以及相似与对角化的理解。
同时,通过解题的过程,还可以提高解决问题的能力和运用矩阵论知识的技巧。
希望读者能够充分利用这些复习题,巩固所学的矩阵论知识,为进一步深入学习打下坚实的基础。
矩阵引论试题及答案

矩阵引论试题及答案一、选择题(每题5分,共20分)1. 矩阵的元素全部为0的矩阵称为:A. 零矩阵B. 单位矩阵C. 对角矩阵D. 标量矩阵答案:A2. 矩阵的秩是指:A. 矩阵的行数B. 矩阵的列数C. 矩阵中线性无关的行(列)的最大数目D. 矩阵的元素个数答案:C3. 矩阵的转置是指:A. 矩阵的行列互换B. 矩阵的行数变为列数C. 矩阵的列数变为行数D. 矩阵的元素不变答案:A4. 两个矩阵相乘的结果称为:A. 矩阵的和B. 矩阵的差C. 矩阵的积D. 矩阵的逆答案:C二、填空题(每题5分,共20分)1. 如果矩阵A的行列式为0,则称矩阵A为________。
答案:奇异矩阵2. 矩阵A的逆矩阵记作________。
答案:A^(-1)3. 矩阵A与矩阵B相乘,记作________。
答案:AB4. 对于任意矩阵A,矩阵A与单位矩阵相乘的结果仍然是________。
答案:A三、简答题(每题10分,共30分)1. 请简述矩阵的行列式是什么?答案:矩阵的行列式是一个标量值,它提供了关于矩阵的一些重要信息,如矩阵是否可逆(行列式非零则可逆)、线性方程组是否有解等。
2. 矩阵的逆矩阵有什么性质?答案:矩阵的逆矩阵具有以下性质:(A^(-1))^(-1) = A,(AB)^(-1) = B^(-1)A^(-1),以及单位矩阵I的逆矩阵仍然是I。
3. 矩阵的转置矩阵有什么特点?答案:矩阵的转置矩阵具有以下特点:(A^T)^T = A,(AB)^T =B^TA^T,以及矩阵A的转置矩阵的行列式等于矩阵A的行列式。
四、计算题(每题15分,共30分)1. 给定矩阵A = \[\begin{bmatrix} 1 & 2 \\ 3 & 4\end{bmatrix}\],计算A的行列式。
答案:\[ \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = (1)(4) - (2)(3) = 4 - 6 = -2 \]2. 给定矩阵B = \[\begin{bmatrix} 2 & 3 \\ 4 & 5\end{bmatrix}\],计算B的逆矩阵。
矩阵论试题及答案

一.(10分)已知n n C ⨯中的两种范数a ⋅和b ⋅,对于n n C A ⨯∈,证明b a A A A +=是n n C ⨯中的范数. 解:⑴非负性:由于b a ⋅⋅,是两种范数,故当A=0时,0,0==b a A A ,所以000=+=+=b a A A A ; 当A ≠0时,0,0>>b a A A ,所以0>+=b a A A A⑵齐性:()A A A A A A A A b a b a b a ααααααα=+=+=+= ⑶三角不等式:B A B A B A B A B A B A b b a a b a +=+++≤+++=+二.(每小题10分,共20分)已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=101121103A ,()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=002t e t b , 1. 求At e2. 用矩阵函数方法求微分方程()()()()()⎪⎩⎪⎨⎧-=+=T x t b t Ax t x dt d1,0,10的解.解:1. ()1112113det ----=-λλλλA I ()()3211132-=----=λλλλ显然, )det(A I -λ的一阶子式的公因子为1, 容易知道)det(A I -λ 的二阶子式的公因子为2-λ,所以A的最小多项式为()()()23222-=--=λλλλm ,即()()022=-=I A A m ,设()()()b a g m e f t ++==λλλλλ,则()a te f t =='λλ 对于特征值2=λ有()()⎩⎨⎧=='+==a te f b a e f t t 22222,()⎩⎨⎧+-==ttet b te a 2212 所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----+=+=t t t t t t e bI aA e t At1010122. ()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+=⎰⎰--ds e s s s ss s e e ds s b e x e t x s t s At t As At 001010110102020 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=t t e t e t At 1001012三.(15分)用Givens 变换求⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2100421132403100A 的QR 分解. 解:()T01001=β,构造()s c T ,13=,1101sin ,0100cos 22232132223211=+=+===+=+==xx x s x x x c θθ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=210031002340421121421132403100100000010010010013A T⎥⎦⎤⎢⎣⎡--=21312A , 构造),(12s c T , ()21sin ,21111cos 222122222211=+==-=+--=+==x x x s x x x c θθ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡---=1052212131111121212A T⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=2/1002/12/1002/10010010013122T T I T ,⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-==2/12/100000100102/12/100TT Q ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2/12/522344211R四.(10分)用Gerschgorin 定理证明⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=8110260110410100A 至少有两个实特征值. 解:A 的4个盖尔圆为:{}1|1≤=z z G ,{}2114|2=+≤-=z z G , {}3216|3=+≤-=z z G , {}2118|4=+≤-=z z G ,它们构成的两个连通部分为11G S =,4322G G G S =.易见,1S ,2S 都关于实轴对称且各含有1个和3个特征值,因为实矩阵的复特征值必成对出现, 故1S ,2S 必各含有一个实特征值,从而A 至少含有2个实特征值.五.(20分)已知⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=221221*********A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=44111b 1. 求A 的满秩分解.2. 求+A3. 用广义逆矩阵的方法判别方程组b Ax =是否相容.4. 求方程组b Ax =的极小范数解或极小范数最小二乘解并指出所求解的类型.解 1。
江苏大学研究生考试矩阵论复习题
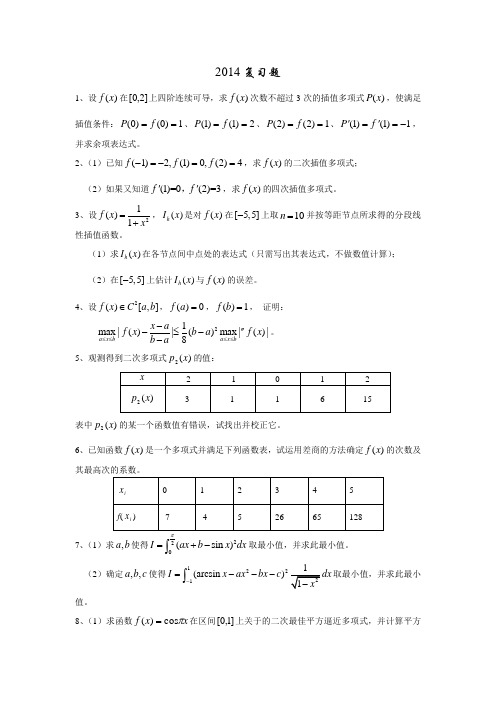
2014复习题1、设)(x f 在]2,0[上四阶连续可导,求)(x f 次数不超过3次的插值多项式)(x P ,使满足插值条件:1)0()0(==f P 、2)1()1(==f P 、1)2()2(==f P 、1)1()1(-='='f P ,并求余项表达式。
2、(1)已知(1)2,(1)0,(2)4f f f -=-==,求()f x 的二次插值多项式; (2)如果又知道(1)=0(2)=3f f '',,求()f x 的四次插值多项式。
3、设21()1f x x =+,()h I x 是对()f x 在[5,5]-上取10n =并按等距节点所求得的分段线性插值函数。
(1)求()h I x 在各节点间中点处的表达式(只需写出其表达式,不做数值计算); (2)在[5,5]-上估计()h I x 与()f x 的误差。
4、设2()[,]f x C a b ∈,()0f a =,()1f b =, 证明:21m a x |()|()m a x |()|8a x ba xbx a fx b a f x b a ≤≤≤≤-''-≤--。
5、观测得到二次多项式)(2x p 的值:表中)(2x p 的某一个函数值有错误,试找出并校正它。
6、已知函数)(x f 是一个多项式并满足下列函数表,试运用差商的方法确定)(x f 的次数及7、(1)求,a b 使得22(sin )I ax b x dx =+-⎰取最小值,并求此最小值。
(2)确定,,a b c 使得1221(arcsin )I x ax bx c -=---⎰取最小值,并求此最小值。
8、(1)求函数x x f πcos )(=在区间]1,0[上关于的二次最佳平方逼近多项式,并计算平方误差。
(2)求函数()sin2f x x π=在[1,1]-上的二次最佳平方逼近多项式,并计算平方误差。
9、设{}0()k k x ϕ∞=是区间[0,1]上最高次项系数为1的带权()x x ρ=正交的正交多项式,其中0()=1x ϕ。
矩阵论考试试题含答案

矩阵论试题一、(10分)设函数矩阵 求:()⎰tdt t A 0与(()⎰20t dt t A )'。
解:()⎰t dt t A 0=()⎪⎪⎪⎭⎫⎝⎛-⎰⎰⎰⎰tttt tdt tdt dt t dtt 000sin cos cos sin =⎪⎪⎭⎫⎝⎛---t t t t cos 1sin sin cos 1 二、(15分)在3R 中线性变换σ将基变为基 ⎪⎪⎪⎭⎫ ⎝⎛-=0111β,⎪⎪⎪⎭⎫ ⎝⎛-=1102β,⎪⎪⎪⎭⎫⎝⎛-=2303β(1)求σ在基321,,ααα下的矩阵表示A ;(2)求向量()T 3,2,1=ξ及()ξσ在基321,,ααα下的坐标; (3)求向量()()ξσξ及T 3,2,1=在基321,,βββ下的坐标。
解:(1)不难求得:因此σ在321,,ααα下矩阵表示为(2)设()⎪⎪⎪⎭⎫⎝⎛=321321,,k k k αααξ,即解之得:9,4,10321-=-==k k k 所以ξ在321,,ααα下坐标为()T 9,4,10--。
()ξσ在321,,ααα下坐标可得(3)ξ在基321,,βββ下坐标为()ξσ在基321,,βββ下坐标为三、(20分)设⎪⎪⎪⎭⎫ ⎝⎛-=301010200A ,求At e 。
解:容易算得由于()λm 是2次多项式,且2,121==λλ,故()λg 是1次多项式,设由于()t e f λλ=,且()()11λλg f =,()()22λλg f =,故于是解得:⎩⎨⎧-=-=tt tt ee a e e a 21202 从而:四、(15分)求矩阵⎪⎪⎪⎭⎫ ⎝⎛=000110101A 的奇异值分解。
解:⎪⎪⎪⎭⎫⎝⎛==211110101A A B T的特征值是0,1,3321===λλλ对应的特征向量依次为于是可得 2=rankA ,⎪⎪⎭⎫⎝⎛=∑1003 计算: ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=∑=-0021212121111AV U 构造 ⎪⎪⎪⎭⎫⎝⎛=1002U ,则 ()⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-==100021210212121U U V 则A 的奇异值分解为: 五、(15分)求矩阵的满秩分解: 解: 可求得:于是有 BC A =⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--=30202101121101或 ()H H H H B AC B C A 1-+=六、(10分)求矩阵⎪⎪⎪⎭⎫⎝⎛--=201034011A 的Jordan 标准形。
矩阵论试题

矩阵论试题一、选择题1.设A是n阶方阵,若|A|=0,则A()。
A. 一定是可逆矩阵B. 一定是不可逆矩阵C. 可能是可逆矩阵,也可能是不可逆矩阵D. 以上说法均不正确答案:B2.若矩阵A与B相似,则A与B具有()。
A. 相同的特征值B. 相同的特征向量C. 相同的秩D. 相同的行列式答案:A、D(相似矩阵具有相同的特征值和行列式,但特征向量不一定相同,秩也一定相同,但此题只问具有什么,故A、D为正确答案)3.下列矩阵中,属于正交矩阵的是()。
A. 单位矩阵B. 对角矩阵C. 上三角矩阵D. 任意方阵答案:A(单位矩阵是正交矩阵的一种特殊情况)二、填空题1.设矩阵A=(1324),则A的行列式|A|=______。
答案:-2(根据行列式的定义和计算方法,有|A|=1×4-2×3=-2)2.若矩阵A与B满足AB=BA,则称A与B为______。
答案:可交换矩阵(或称为可交换的)3.设n阶方阵A的伴随矩阵为A,则|A|=______。
答案:|A|(n-1))三、计算题1.设矩阵A=(2113),求A的逆矩阵A^(-1)。
解答:首先求|A|,有|A|=2×3-1×1=5≠0,所以A可逆。
然后利用逆矩阵的公式A^(-1)=(1/|A|)×A*,其中A*是A的伴随矩阵。
A的伴随矩阵A=(3−1−12)(伴随矩阵的元素是A的每个元素的代数余子式构成的矩阵的转置)。
所以A^(-1)=(1/5)×A=(3/5−1/5−1/52/5)。
2.设矩阵A=147258369,求A的秩R(A)。
解答:对矩阵A进行初等行变换,将其化为行最简形。
通过初等行变换,可以得到A的行最简形为1002−303−60。
所以R(A)=2(非零行的个数)。
四、证明题1.证明:若矩阵A为n阶方阵,且|A|=0,则A不可逆。
证明:根据可逆矩阵的定义,若矩阵A可逆,则存在n阶方阵B,使得AB=BA=E(E为单位矩阵)。
矩阵论练习题

练习一一﹑选择题1、对于()212,x x R ∀∈,下列变换是2R 上的线性变换的是 ( D ).(A) ()()21212,,T x x x x =; (B) ()()21212,,T x x x x =;(C) ()()1212,,0T x x x x =; (D) ()()1212,,T x x x x =-. 2、设()(),A B λλ为两个n 阶λ-矩阵,则 ( D ).(A) 若()A λ满秩,则()A λ必可逆; (B) ()A λ可逆当且仅当()0A λ≠;(C) 若()A λ与()B λ秩相等,则()A λ与()B λ等价;(D) 若()A λ与()B λ等价,则()A λ与()B λ具有相同的不变因子. 3、设()n n ij A a C ⨯=∈,则下列不能构成矩阵范数的是( A ).(A) ,max ij i ja ; (B) ,max ij i jn a ⋅; (C) 1max nij ij a =∑; (D) 1max nij j i a =∑.4、设n n A C ⨯∈,H A 为A 的共轭转置矩阵,()A ρ为A 的谱半径,A 为A 的范数,则下列说法不正确的是( C ).(A)()[]()kk A A ρρ=; (B) ()()H H A A AA ρρ=;(C) 若()1A ρ<,必有E A -可逆; (D) 若A 为收敛矩阵,必有()1A ρ<. 5、设V 为酉空间,C λ∈,,V αβ∈且(),αβ为α与β的內积,则下列说法不正确的是( B ).(A) ()(),,λαβλαβ=; (B) ()(),,αλβλαβ=; (C) ()()(),,,αβγαβαγ+=+; (D) ()()(),,,βγαβαγα+=+.二﹑填空题1、已知100231120012233002A -⎛⎫⎛⎫ ⎪⎪=- ⎪⎪ ⎪⎪⎝⎭⎝⎭,则A 的LDU 分解为 .2、设sin ()2cost t t te A t t ⎛⎫= ⎪⎝⎭,则0()x A t dt ⎰=21cos 1sin x x x xe e xx ⎛⎫--+ ⎪⎝⎭.3、设矩阵2242t tt At tt t e te te e te e te ⎡⎤-=⎢⎥-+⎣⎦ ,则矩阵A =1143-⎛⎫⎪-⎝⎭.4、矩阵100110111A ⎛⎫⎪= ⎪ ⎪⎝⎭ 相对于矩阵范数∞ 的条件数为 6 .5、设11122122⎛⎫=⎪⎝⎭x x X x x ,(),A a b =,则()d AX dX =0000a a b b ⎛⎫⎪⎝⎭. 6、已知101112003A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则543258884A A A A A E -+-+- =001102002⎛⎫⎪⎪ ⎪⎝⎭.7、已知⎪⎪⎪⎭⎫⎝⎛=987654321A ,则A 的正奇异值的个数为 2 .三、计算题已知 1(1,3,2,1)T α=-,2(1,0,0,2)T α=,1(0,1,1,3)T β=,2(3,2,1,6)T β=--, 且112{,}V span αα=,212{,}V span ββ=,求12V V +与12V V 的基和维数. 解:因为1212{,}V V span αα+=+12{,}span ββ=1212{,,,}span ααββ而12121103100130120102(,,,)2011001112360000ααββ--⎛⎫⎛⎫⎪ ⎪-⎪ ⎪= ⎪ ⎪- ⎪ ⎪-⎝⎭⎝⎭初等行变换 由于121,,ααβ是向量组1212,,,ααββ的一个极大线性无关组,所以和空间的维数是3,基为121,,ααβ且21212βααβ=--. 由行最简形知12dim()2,dim()2,V V ==又121212dim()dim dim dim()V V V V V V +=+- 故12dim()1V V =311100222110201236001212A ⎛⎫⎛⎫- ⎪ ⎪⎛⎫ ⎪ ⎪ ⎪=--⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭⎝⎭由21212βααβ=--得()12121223,3,2,3TV V ξααββ=-=+=--∈所以()3,3,2,3T--为12V V 的一组基。
矩阵试题及答案

矩阵试题及答案一、选择题(每题4分,共20分)1. 矩阵的秩是指:A. 矩阵中非零元素的个数B. 矩阵中最大的线性无关行(列)向量组的个数C. 矩阵的行数D. 矩阵的列数答案:B2. 若矩阵A与矩阵B相等,则下列说法正确的是:A. A和B的行列式相等B. A和B的迹相等C. A和B的行列式和迹都相等D. A和B的行列式和迹都不相等答案:C3. 矩阵的转置是指:A. 将矩阵的行变成列B. 将矩阵的列变成行C. 将矩阵的行和列互换D. 将矩阵的元素取相反数答案:C4. 对于任意矩阵A,下列说法正确的是:A. A的行列式等于A的转置的行列式B. A的行列式等于A的逆矩阵的行列式C. A的行列式等于A的逆矩阵的转置的行列式D. 以上说法都不正确答案:A5. 若矩阵A是可逆矩阵,则下列说法正确的是:A. A的行列式不为0B. A的行列式为1C. A的行列式为-1D. A的行列式可以是任意非零值答案:A二、填空题(每题5分,共20分)1. 若矩阵A的行列式为-2,则矩阵A的逆矩阵的行列式为____。
答案:1/22. 设矩阵A为2x2矩阵,且A的行列式为3,则矩阵A的转置的行列式为____。
答案:33. 若矩阵A的秩为2,则矩阵A的行向量组的____。
答案:线性无关4. 设矩阵A为3x3矩阵,且A的行列式为0,则矩阵A是____。
答案:奇异矩阵三、解答题(每题10分,共30分)1. 已知矩阵A=\[\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix}\],求矩阵A的行列式。
答案:\(\begin{vmatrix}1 & 2\\3 & 4\end{vmatrix} = (1)(4) - (2)(3) = 4 - 6 = -2\)2. 设矩阵B=\[\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}\],求矩阵B的逆矩阵。
矩阵论复习题综合

1. 设+=R V 是正实数集,对于任意的V y x ∈,,定义x 与y 的和为 y x y x ⋅=⊕ 对于任意的数R k ∈,定义k 与x 的数乘为k x x k =⊗问:对于上述定义加法和数乘运算的集合V ,是否构成线性空间,并说明理由. 2.对任意的2,R y x ∈,),(21x x x =,),(21y y y =定义x 与y 的和为),(112211y x y x y x y x +++=⊕对于任意的数R k ∈,定义k 与x 的数乘为)2)1(,(2121x k k kx kx x k -+=⊗ 问:对于上述定义加法和数乘运算的集合2R ,是否构成线性空间,并说明理由. 3.设},022|),,{(321321R x x x x x x x S i ∈=++=,试证明S 是3R 的子空间,并求S 的一组基和S dim .4.设)(R P n 表示次数不超过n 的全体多项式构成的线性空间,)}()(,0)0(|)({R P x f f x f S n ∈='=证明S 是)(R P n 的子空间,并写出S 的一组基和计算S dim . 5. 设T 是2R 上的线性变换,对于基向量i 和j 有j i i T +=)( j i j T -=2)(1)确定T 在基},{j i 下的矩阵;2)若j i e -=1 j i e +=32,确定T 在基},{21e e 下的矩阵. 6. 设T 是3R 上的线性变换,对于基},,{k j i 有k j k j i T -=++)( i k j T =+)( k j i k T 532)(++=1)确定T 在基},,{k j i 下的矩阵; 2)求T 的零空间和像空间的维数.7.设线性空间3R 的两个基为(I):321,,x x x , (II):321,,y y y , 由基(I)到基(II)的过度矩阵为⎪⎪⎪⎭⎫ ⎝⎛--=101010101C , 3R 上的线性变换T 满足21321)32(y y x x x T +=++ 12323(24)T x x x y y ++=+31321)43(y y x x x T +=++ 1)求T 在基(II)下的矩阵; 2)求)(1y T 在基(I)下的坐标. 8.在线性空间)(3R P 中321)(x x x a x f +++= 3221)(x x ax x f +++= 32321)(x x x x f +++=讨论)(),(),(321x f x f x f 的线性相关性.9.在22R ⨯中求由基(I) 12101A ⎛⎫= ⎪⎝⎭ 20122A ⎛⎫= ⎪⎝⎭ 32112A -⎛⎫= ⎪⎝⎭ 41312A ⎛⎫= ⎪⎝⎭到基(II) 11210B ⎛⎫= ⎪-⎝⎭ 21111B -⎛⎫= ⎪⎝⎭ 32211B -⎛⎫= ⎪⎝⎭ 41101B --⎛⎫= ⎪⎝⎭的过渡矩阵.10.已知 1(1,2,1,0)α= 2(2,1,0,1)α=- 1(1,1,1,1)β=- 2(1,1,3,7)β=- 设1212(,)(,)V L L ααββ=⋂, 求线性空间V 的维数和基. 11.在)(2R P 中, 对任意的)()(),(2R P x g x f ∈定义内积为⎰=1)()())(),((dx x g x f x g x f若取)(2R P 的一组基},,1{2x x ,试用Schmidt Gram -正交化方法,求)(2R P 的一组正交基.12.(1) 设x 和y 是Eucild 空间V 的非零元,它们的夹角是θ,试证明θcos ||||||||2||||||||||||222y x y x y x ⋅-+=-12.(2) 求矩阵10002i A i +⎛⎫= ⎪⎝⎭的奇异值分解.13.设A 为n 阶实矩阵,证明A 可表示为一对称矩阵和一反对称矩阵之和. (提示:若A A T =,称A 为对称矩阵。
2011矩阵论复习题答案

2011矩阵论复习题答案一、简答题1. 请简述矩阵的基本运算有哪些,并给出相应的运算规则。
答:矩阵的基本运算包括加法、减法、数乘、乘法以及转置。
加法和减法是对应元素相加或相减;数乘是将矩阵的每个元素都乘以一个数;矩阵乘法是将第一个矩阵的行与第二个矩阵的列对应元素相乘后求和;转置是将矩阵的行和列互换。
2. 什么是特征值和特征向量?它们在矩阵理论中有何重要性?答:特征值是方阵A的一个标量λ,使得存在非零向量v满足Av=λv。
特征向量是与特征值λ相对应的非零向量v。
特征值和特征向量在矩阵理论中非常重要,因为它们可以用来描述线性变换的性质,如可对角化、稳定性分析等。
3. 矩阵的秩是什么?如何计算矩阵的秩?答:矩阵的秩是指矩阵中线性无关的行或列的最大数目。
计算矩阵的秩通常通过高斯消元法,将矩阵转换为行最简形式,然后计算非零行的数量。
二、计算题1. 给定矩阵A = \[\begin{bmatrix} 1 & 2 \\ 3 & 4\end{bmatrix}\],求矩阵A的逆矩阵。
答:首先计算矩阵A的行列式,det(A) = 1*4 - 2*3 = -2。
然后计算A的伴随矩阵,得到A的逆矩阵为\[ \frac{1}{-2}\begin{bmatrix} 4 & -2 \\ -3 & 1 \end{bmatrix} =\begin{bmatrix} -2 & 1 \\ 1.5 & -0.5 \end{bmatrix} \]。
2. 已知矩阵B = \[\begin{bmatrix} 5 & 1 \\ 2 & 3\end{bmatrix}\],求矩阵B的特征值和特征向量。
答:首先计算矩阵B的特征多项式,det(B - λI) = (5-λ)(3-λ) - 2 = λ^2 - 8λ + 13。
解得特征值λ1 = 2, λ2 = 6。
对于λ1 = 2,解方程组(B - 2I)v = 0,得到特征向量v1 = k\[ \begin{bmatrix} 1 \\ 1 \end{bmatrix} \]。
矩阵论期末试题及答案

矩阵论期末试题及答案1. 选择题题目1:矩阵的秩是指矩阵中非零行(列)线性无关的最大个数,下面关于矩阵秩的说法中,错误的是:A. 若矩阵A的秩为r,则只能确定 A 中有r个行(列)线性无关。
B. 若矩阵A的秩为r,则只能确定 A 中有r个坐标线性无关。
C. 设A,B为n×m矩阵,若A的秩为r,B的秩为s,则AB的秩至少为max{r,s}。
D. 同一矩阵的行秩与列秩相等。
题目2:对于阶梯形矩阵,以下说法正确的是:A. 阶梯形矩阵的行秩与列秩相等。
B. 阶梯形矩阵的行秩等于主元的个数。
C. 阶梯形矩阵的列秩等于主元的个数。
D. 阶梯形矩阵的行秩与列秩之和等于矩阵的阶数。
题目3:设A为n阶矩阵,下列说法正确的是:A. 若A为可逆矩阵,则A的行秩和列秩都为n。
B. 若A的行秩和列秩都为n,则A为可逆矩阵。
C. 若对于非零向量 x,都有Ax=0,则称矩阵A为零矩阵。
D. 若A为可逆矩阵,则方程Ax=b存在唯一解。
题目4:对于实对称矩阵A,以下说法正确的是:A. A一定有n个线性无关的特征向量。
B. A的所有特征值都是实数。
C. 若A的特征向量构成的特征子空间的维数为n,则称A为满秩矩阵。
D. A一定可以对角化。
2. 计算题题目1:已知矩阵A = [1, 2; 3, 4],求矩阵A的转置矩阵。
解答:转置矩阵的行与列互换,故矩阵A的转置矩阵为:A^T = [1, 3; 2, 4]题目2:已知矩阵B = [2, 1; -1, 3],求矩阵B的逆矩阵。
解答:逆矩阵满足BB^(-1) = I,其中I为单位矩阵。
对于矩阵B,可以使用伴随矩阵法求解:B^(-1) = (1/(ad-bc)) * [d, -b; -c, a]其中a、b、c、d分别为矩阵B的元素:B^(-1) = (1/(2*3-(-1)*1)) * [3, -1; 1, 2] = [3/7, -1/7; 1/7, 2/7]题目3:已知矩阵C = [1, 2, 3; 4, 5, 6],求矩阵C的行列式的值。
矩阵论考试题

1. 求T 在基 A1 , A2 , A3 , A4 下的矩阵; 2. 判断 T 能否在 R 2×2 的某个基下的矩阵为对角矩 阵; (要求写出判断依据)
5
3. 求 N (T ) 的一个基. 八、(8 分) 设矩阵 A∈ C m×n ,列向量 b∈ C m ,列向量
3
验证 x 是 C n 中的向量范数.
三 、 (15
− 2 分 ) 已 知 A= 1 − 2
1 −2 2
1 −1 , 1
0 2 b(t ) = e −t 1 , x (0) = 1 . − 2 1
At 1. 求 e ;
x2 x4
x1 − x 4 = 0 , x 2 − x3 = 0
( A, B ) =
R 2×2 中 的 内 积 为
∑∑ a
i =1 j =1
2
2
ij
bij ,
a11 A= a 21
a12 b11 b12 ,B= , a 22 b21 b22
x ∈ C n , A + 表示 A 的 Moore-Penrose 逆,证明:线性
+ H H 方程组 A x = AA b 与 A A x = A b 同解.
6
矩阵论
(M2006B)
一、(18 分) 填空:设 A = 9
0 1 1 1 , B . = 0 1 1 .
V 中 的 线 性 变 换 为 T ( X ) = XP + X T , 任 意 0 1 X ∈V , P = . 1 0
南航矩阵论考试试题

南航矩阵论考试试题南航矩阵论考试试题南航矩阵论考试是一门重要的数学课程,旨在培养学生的逻辑思维和解决问题的能力。
本文将介绍一些典型的南航矩阵论考试试题,帮助读者更好地理解这门课程的内容和要求。
一、基础知识部分1. 请解释矩阵的定义和基本性质。
矩阵是由数个数按矩形排列而成的表格。
它的定义包括行数和列数两个维度,记作m×n。
矩阵有很多基本性质,如加法、数乘、转置等。
矩阵的加法满足交换律和结合律,数乘满足分配律。
矩阵的转置是将矩阵的行和列互换得到的新矩阵。
2. 什么是方阵和单位矩阵?方阵是行数等于列数的矩阵。
单位矩阵是一个对角线上全为1,其余元素全为0的方阵。
单位矩阵在矩阵运算中起到了重要的作用,类似于数学中的“1”。
二、矩阵运算部分1. 请计算以下矩阵的和:A = [1 2 3; 4 5 6],B = [7 8 9; 10 11 12]。
矩阵的和等于对应位置元素相加得到的新矩阵。
根据题目给出的矩阵,可以计算得到A + B = [8 10 12; 14 16 18]。
2. 请计算以下矩阵的积:C = [1 2; 3 4],D = [5 6; 7 8]。
矩阵的乘法需要注意行列对应元素的乘积。
根据题目给出的矩阵,可以计算得到C × D = [19 22; 43 50]。
三、线性方程组部分1. 请解以下线性方程组:2x + 3y = 8,4x - 5y = 7。
线性方程组可以转化为矩阵的形式,即AX = B,其中A为系数矩阵,X为未知数矩阵,B为常数矩阵。
根据题目给出的线性方程组,可以得到矩阵形式为:[2 3] [x] [8][4 -5] [y] = [7]通过矩阵的逆运算,可以解得x = 3,y = 2。
2. 请解以下线性方程组:x + 2y + 3z = 6,2x - y + z = 1,3x + 4y + 5z = 10。
同样地,将线性方程组转化为矩阵形式:[1 2 3] [x] [6][2 -1 1] [y] = [1][3 4 5] [z] [10]通过矩阵的逆运算,可以解得x = 1,y = 2,z = 1。
矩阵论试题及答案可编辑全文

2006矩阵论试题答案一.填空(每题4分,共40分)1. 设−−=41311221222832A ,则A 的值域4(){,R }R A y y Ax x ==∈的维数=)(dim A R 2 .2. 设A 的若当标准型−−−=10000011000001100000020000012000002J ,则A 的最小多项式=)(λψm 32(1)(2)λλ+−.3. 设110430102A −=−,则()5432333h A A A A A A =−++−=110430102−− −−. 4. 设埃尔米特阵为 −−+=2005111i i i i A , 则矩阵A 为 正定的 埃尔米特阵.5. 在3R 中有下列两组向量:()13,1,2Tα=−−,()21,1,1Tα=−,()32,3,1Tα=−; ()11,1,1Tβ=,()21,2,3Tβ=,()32,0,1Tβ=,则由321,,ααα到321,,βββ的过渡矩阵=P 619113421270−−−−−− −− .6.设33CA ×∈,21332211{}ij m j i A a ===∑∑,H AA 的非零特征值分别为15 ,5 ,3,则=2mA.7. 设12102101, 11111137A B −== −−,12,V V 分别为齐次线性方程组 0Ax =,0Bx =的解空间,则=)dim(21V V ∩ 1 .8. 设1(1)1(1)121()321nn n n n n n A n n n n +−−=++ −,则lim n n A →∞=1311e .9. 设213121202A −=,则A 的 LDU 分解为 A =100121012/51 2001123205200115004/5001− − − 10.设 −=5221A ,=0242B ,则2448204048102040100A B−−−⊗=. 二.(10分)设T 为n 维欧氏空间V 中的线性变换,且满足:),(),(Ty x y Tx −=,试证明:T 在标准正交基下的矩阵A 为反对称阵(T A A −=)证明:设n ααα,,,21 为V 的标准正交基,n n ij a A ×=}{,下证:ji ij a a −=: 由=),,,(21n T ααα A n ),,,(21ααα 知n ni i i i a a a T αααα+++= 2211,n nj j j j a a a T αααα+++= 2211, ),(),(j i j i T T αααα−=;=),(j i T ααji j n ni i i a a a a =+++),(2211αααα , =),(j i T ααij n nj j j i a a a a =+++),(2211αααα , 所以:ji ij a a −=.三.(10分)在复数域上求矩阵−−−=7137341024A 的若当标准形J ,并求出可逆矩阵P 使得J AP P =−1.解: A 的若当标准形210021002J=. 令123(,,)P p p p =,则有112123232,2,2Ap p Ap p p Ap p p ==+=+;1213262100621062104170,417,4173150315315p p p p p −−−−=−=−= −−−解得:123(2,1,1),(0,1,0),(1,2,1)T T Tp p p ===− , 201112101P=−.四. (10分)已知 =654321x x x x x xX ,162534()sin()x x f X e x x x x =++,求dXdf . 解答:16161234652543225516cos()cos()x x x x ff f x x x df dX ff f x x x x e x x x x x x x x x e ∂∂∂∂∂∂== ∂∂∂ ∂∂∂. 五.(10分)已知311202113A −=−−−,求4sin()A π,Ae .解:3||(2)E A λλ−=−,A 的最小多项式2)2()(−=λλϕ .待定系数一:令24sin ()(2)q a b πλλλλ=−++,则21,0a b b +==,4sin()A E π=;令2()(2)e q a b λλλλ=−++,则222,a b e b e +==.222211212112A e e e E e A −−=−+=− −−.待定系数二:令324sin ()(2)q a b c πλλλλλ=−+++,则22222414018,8,32216a b c b c a b c c ππππ ++=+=⇒=−==− =− ; 224sin()(44)32A E E A A E ππ=−−+=.令32()(2)e q a b c λλλλλ=−+++,则2222222414,,22a b c e b c e a e b e c e c e++= +=⇒==−== ; 2221()2211212112A e e E A A e −−− =− +−−= .六.(10分)设−=01200110A ,求A 的奇异值分解. 解答一:=5002A A H ,A 的奇异值为5,2; 00Σ= , 25H HV A AV = ,1001V =; 1100100100200100U AV −−− =Σ==; 00000000U− =; 0000010001 0 000 0 000A=.解答二:=5002A A H ,那么A 的奇异值为5,2,A A H对应于特征值5,2的标准特征向量为 = =01,1021x x ,=0110V ; 再计算H AA 的标准正交特征向量,解得分别与5,2,0,0对应的四个标准正交特征向量=0520511υ, −=2102102υ,−=0510523υ,=2102104υ,−−=210210051052210210052051U ; 所以=∆=HV UA 0000000000000110.七.(10分)设n n i A ×∈≠C 0,2rank rank i i A A =),,2,1(n i =,且当i j ≠时),,2,1,(0n j i A A j i ==.试用归纳法证明存在同一个可逆阵n n P ×∈C 使 得对所有的i ),,2,1(n i =有1−=P PE a A ii i i ,其中C ∈i a . 证明:1n =时,命题显然.假设n k ≤时,命题成立. 当1n k =+时,设1rank A r =.由若当分解11111000D A P P − =,其中1C r rD ×∈可逆; 当2,,j n = 时,由110j j A A A A ==可得1(1)(1)1100, C 0n n j jj A P P B B −−×− =∈(直接推出的j B 为()()n r n r −×−的) 再由0i j A A =得0i j B B =(,,2,,)i j i j n ≠= ;0j B ≠,2rank rank j j B B =也是明显的.由假设知存在可逆阵(1)(1)C n n Q −×−∈使得1j j jj B a QE Q −=,其中C j a ∈,2,,j n = .此时,再由110j j A A A A ==得到11111111110101010000000a A P P a P P Q Q −−− == ; 记1100P P Q =,则 11111111100000000 (2,,).0 j j j jj j j jj jj A P P P P B a QE Q a P P a P E P j n E −−−−− =====由归纳原理知命题为真.。
矩阵理论历年试题汇总及答案

矩阵理论历年试题汇总及答案矩阵理论是线性代数中的一个重要分支,它涉及到矩阵的运算、性质以及矩阵在不同领域中的应用。
历年来的矩阵理论试题通常包括矩阵的基本运算、矩阵的特征值和特征向量、矩阵的分解等重要概念。
以下是对矩阵理论历年试题的汇总及答案解析。
矩阵的基本运算试题1:给定两个矩阵 \( A \) 和 \( B \),其中 \( A =\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \),\( B =\begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} \),求 \( A + B \) 和 \( AB \)。
答案:首先计算矩阵的加法 \( A + B \),根据矩阵加法的定义,对应元素相加,得到 \( A + B = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix} \)。
接着计算矩阵乘法 \( AB \),根据矩阵乘法的定义,得到 \( AB = \begin{bmatrix} 1\cdot5 + 2\cdot7 & 1\cdot6 + 2\cdot8 \\ 3\cdot5 + 4\cdot7 & 3\cdot6 + 4\cdot8\end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50\end{bmatrix} \)。
特征值和特征向量试题2:已知矩阵 \( C = \begin{bmatrix} 4 & -2 \\ 1 & -1\end{bmatrix} \),求 \( C \) 的特征值和对应的特征向量。
答案:首先求特征值,我们需要解方程 \( \det(C - \lambda I) = 0 \),其中 \( I \) 是单位矩阵。
计算得到 \( \det(\begin{bmatrix}4-\lambda & -2 \\ 1 & -1-\lambda \end{bmatrix}) = (4-\lambda)(-1-\lambda) - (-2)(1) = \lambda^2 - 3\lambda - 2 \)。
矩阵论试题(整理)(完整版)实用资料

矩阵论试题(整理)(完整版)实用资料(可以直接使用,可编辑完整版实用资料,欢迎下载)矩阵论试题(06,12)一.(18分填空:设1.A-B的Jordan标准形为J=2.是否可将A看作线性空间V2中某两个基之间的过渡矩阵()。
3.是否可将B看作欧式空间V2中某个基的度量矩阵。
()4.(),其中。
5.若常数k使得kA为收敛矩阵,则k应满足的条件是()。
6.AB的全体特征值是()。
7.()。
8.B的两个不同秩的{1}-逆为。
二.(10分设,对于矩阵的2-范数和F-范数,定义实数,(任意)验证是中的矩阵范数,且与向量的2-范数相容。
三.(15分已知。
1.求;2.用矩阵函数方法求微分方程满足初始条件x(0的解。
四.(10分用Householder变换求矩阵的QR分解。
五.(10分)用Gerschgorin定理隔离矩阵的特征值。
(要求画图表示)六.(15分已知。
1.求A的满秩分解;2.求A+;3.用广义逆矩阵方法判断线性方程组Ax=b是否有解;4.求线性方程组Ax=b的极小范数解,或者极小范数最小二乘解x0。
(要求指出所求的是哪种解)七.(15分已知欧式空间R22的子空间R22中的内积为V中的线性变换为T(X=XP+XT, 任意XV,1.给出子空间V的一个标准正交基;2.验证T是V中的对称变换;3.求V的一个标准正交基,使T在该基下的矩阵为对角矩阵.八.(7分设线性空间V n的线性变换T在基下的矩阵为A,T e表示V n的单位变换,证明:存在x00,使得T(x0=(T e-T(x0的充要条件是为A的特征值.矩阵论试题(07,12)一.(18分填空:1.矩阵的Jordan标准形为J=2.设则3.若A是正交矩阵,则cos(A=4.设,A+是A的Moore-Penrose逆,则(-2A, A+=5.设,则AB+I2I3的全体特征值是()。
6.设向量空间R2按照某种内积构成欧式空间,它的两组基为和且与的内积为则基的度量矩阵为()。
矩阵论深刻复知识题第二章

第二章内积空间一、基本要求1、掌握欧氏空间和酉空间的定义与性质,掌握Hermite 矩阵的定义,理解欧氏(酉)空间中度量的概念.2、掌握线性无关组的Schmidt 正交化与对角化方法,理解标准正交基的性质.3、理解Hermite 二次型的定义.4、掌握在一组基下的度量矩阵的概念,标准正交基下度量矩阵的性质及两组标准正交基下的度量矩阵的关系.5、了解欧氏子空间的定义.6、掌握正交矩阵与酉矩阵的定义与性质,理解正交(酉)变换与正交(酉)矩阵的关系.7、掌握对称矩阵与Hermite 矩阵的定义与性质,理解对称(Hermite) 变换与对称(Hermite) 矩阵的关系.8 、掌握矩阵可对角化的条件,会求一个正交( 酉)矩阵把实对称(Hermite) 矩阵化为对角形矩阵,会求一组标准正交基使线性变换在该基下对应的矩阵是对角形矩阵.二、基本内容1、内积空间设数域F上的线性空间V n(F),若V n(F)中任意两个向量,都有一个确定的数与之对应,记为( , ) ,且满足下列三个条件⑴对称性:(,)(,),其中(,)表示对数(,)取共轭;称V n (C)为酉空间.H A (a ”)m n ? B (b ij )m n , (A, B) tr(A B)i 1在实多项式空间P n [x ]及[a,b ]上连续函数空间C [a,b ]中,函数f(x),g(x) 的内积为b(f(x),g(x)) a f(x)g(x)dx2、向量的长度、夹角、正交性定义| | V (-),称为 的长度,长度为 1的向量称为单位向量,/I 是的单位向量.长度有三个性质:(1) 非负性:I I 0,且(,)00 ;(2) 齐次性:|k | k|| ,k 表示数k 的绝对值; (3) 三角不等式:线性性:k 2 2, )k 1 ( 1?) k 2(2?);正定性: (,)0,当且仅当0 时,(,)则称(, )为向量与的内积.当FR 时,称V n (R)为 欧氏空间;当F C 时,其中注意:在R 中, 通常的几个内积:(1) R n中,(,c n中,(X 1,X 2,,X n )T,,k ) k(,); nX i Y ii 1n ____X i y ii 1(力”2, 在C n 中,(,k)k(,,y n )T.R mn 中,n ___a ijb ij .定理(Cauchy-Schwarz 不等式)(,)与的夹角定义为arccos(,)当(,)0时,称与正交,记若非零向量组s两两正交,即(i jj) 0,称s是一个正交组;又若1,i 1,2,,s,则称s为标准正交组,即(i, j)1,i0,ij,j.定理(勾股定理))0,即3、标准正交基标准正交基指欧氏(酉)空间中由两两正交的单位向量构成的基.构造方法:对欧氏(酉)空间的一个基进行Schmidt正交化可得正交基,再对正交基进行单位化可得标准正交基.把线性无关向量s正交化为s正交向量组:2,3,,s.再把i单位化:i i,i 1,2,,s,则,s为标准正交组.在标准正交组1, 2, ,n下,向量可表为:X1 1 X2 2 X n n (,1)1 2)2 坐标X i ( , i )表示在i上的投影长度.4、基的度量矩阵度量矩阵是以欧氏(酉)空间的基中第i个元素与第j个元素的内积为i行j列元素构成的方阵.设欧氏(酉)空间V的一个基为x「X2, , X n,令a j (x「X j)(i,j 1,2, ,n),则该基的度量矩阵为A (a ij)nn •基的度量矩阵是实对称(Hermite)正定矩阵,它的阶数等于欧氏(酉)空间的维数,正交基的度量矩阵是对角矩阵,标准正交基的度量矩阵是单位矩阵.设酉空间V的一个基为x1,x2, , x n,该基的度量矩阵为A , x, y V在该基下的坐标(列向量)分别为与,那么x与y的内积(x, y) T A •当V为欧氏空间时,(x,y) T A•当此基为标准正交基,酉空间V的x与y的内积(x, y) T,欧氏空间V的x与y 的内积(x, y) T•设欧氏空间V n的两个基分别为(I )X i,X2, ,X n和(n ) y i , y2, , y n,且由基(i )改变为基(n )的过渡矩阵为c,基(I)的度量矩阵为A,基(n)的度量矩阵为B,则有:(1)B C T AC •(2)基(I )是标准正交基的充要条件是 A I •(3)若基(i)与基(n)都是标准正交基,则C是正交矩阵.(4)若基(i)(或(n))是标准正交基,C是正交矩阵,则基(n)(或基(i))是标准正交基.5、正交变换与对称变换(i )关于正交变换,下面四种说法等价:1)T是欧氏空间V n的正交变换,即对于任意的x V n,有(Tx,Tx) (x,x) ;2)对于任意的x, y V n,有(Tx,Ty) (x, y);3)T在V n的标准正交基下的矩阵为正交矩阵;4)T将V n的标准正交基变换为标准正交基.(ii )关于对称变换,下面两种说法等价:1)T是欧氏空间V n的对称变换,即对于任意的x, y V n,有(Tx, y) (x,Ty);2)T在V n的标准正交基下的矩阵为对称矩阵.(iii)若T是欧氏空间V n的对称变换,则T在V n的某个标准正交基下的矩阵为对角矩阵.(i v )在欧氏空间V n中,若正交变换T的特征值都是实数,则T是对称变换.6、相似矩阵(1)A C nn相似于上(下)三角矩阵.(2)A C n n相似于Jordan 标准形矩阵.(3)A C n n酉相似于上三角矩阵.(4)设 A C n n,则A H A AA H的充要条件是存在酉矩阵P ,使得P H AP (对角矩阵).(5)设A C n n的特征值都是实数,则A T A AA T的充要条件是存在正交矩阵Q ,使得Q T AQ .(6)实对称矩阵正交相似于对角矩阵.三、典型例题例1、在R n中,设(1, 2, , n), ( 1, 2, , n),分别定义实数(,)如下:')2;ni)( j);j 1判断它们是否为R n中与的内积.(k ,n((ki 1i)2i2)12知,当k 0且(,0 时,(k 积.(2)取(1, ,0) 0 ,故该实数不是R n中与的内积.例2、R n中,向量组nk(i 1i2) k(,)0,k( ).故该实数不是R n中n线性无关的充要条件是与的内l) l) 2)2)n)n)l) 2)n) 证方法一设An),则(i,j) A TA A T A A2 0n线性无关.(x1 1 X2 2 X n n , i )0,i 1,2, ,n , 即X1( 1, 1)Xn (1,n) 0,X1( 2, 1) X n( 2 ,n) 0,X1( n, 1) X n( n ,n) 0,齐次方程组仅有零解的充要条件是系数矩阵的行列式(i, j) 0,即1, 2, , n线性无关.例3、设欧氏空间P[t]3中的内积为1(f,g) 1 f (t)g(t)dt(1)求基i,t,t2的度量矩阵.⑵ 采用矩阵乘法形式计算f(t) 1 t t2与g(t) 1 4t 5t2的内积.解(1)设基1,t,t2的度量矩阵为A @訂3 3,根据内积定义计算a0(i j)an (1,1) 1dt12 ,a12 (1,t)1tdt 01一2、12 .2 1 2 2a13 (1,t ) t2dt13,a22 (t,t) t2dt13,21 a23 (t,t ) t3dt1 0 ,a33 (t2,t 2) 1t4dt125 .由度量矩阵的对称性可得a j a ji (i j) ,于是有2 0 2 3A 0 2 3 0 .2 3 0 2 5(2) f(t)和g(t)在基1,t,t 2下的坐标分别为(1,1,1)T, (1, 4, 5)T,那么2 02 31(f,g) T A(1, 1,1) 0 2 3 0 4 0 .2 3 0 2 5 5例4、欧氏空间P[t]3中的多项式f (t)和g(t)的内积为1(f, g) 1 f(t)g(t)dt ,取f i(t) t,记子空间W L(f i(t))・(1)求W T的一个正交基;(2)将W T分解为两个正交的非零子空间的和.解⑴设g(t) k o k i t kf W T,则有(f i,g) 0,即1 12,1 f i (t)g (t)dt 1 t(k o k1t k2t )dt 0也就是k1 0 .于是可得W T{g(t)g(t) k o k2t2,k o,k2 R}.取W T的一个基为1,t2,并进行正交化可得g1(t) 1,2 (t2,gj~t2g2(t) t- g1那么,g1(t),g2(t)是W T的正交基.⑵令V1 L(g1(t))M L(g2(t)),则« 与5 正交,且W T« J .例5、已知欧氏空间V2的基治,X2的度量矩阵为采用合同变换方法求V2的一个标准正交基(用已知基表示).解因为A对称正定,所以存在正交矩阵Q,使得Q T AQ(对角矩阵),计算得1 0 1 1 10 9 , Q 2 1 1 ,113 1C Q—,3^2 3 1则有C T AC E .于是,由(y1,y2)(X1,X2)C可得V2的一个标准正交基为设,V nn nX i i ,y j j ,i 1j 1则(nn,)(X i i , y jj)i 1 j 1(T( ),T( nn))(XT( i ),y j T(i 1j 1n nn nX i y j ( i , j ),i 1 j 1n nj))約」仃(i ),T( j ))i 1 j 1例6、在欧氏空间中,定义与的距离为:d(,) ,试问:保持距离不变的变换是否为正交变换?答 不一定,例如R 2中向量的平移变换:(x,y) R 2,T(x,y) (x 1, y 1),i(X i , y i ),2区皿)R 2,T( i )(X i 1,y i1),T( 2) (X 2 ly 1),d(T( i ),T( 2)) T( 1) T( 2) J(x i X 2)2 (y i y ?)2| 1 2d( 1, 2).虽然保持距离不变,但平移变换不是线性变换,更不是正交变换.例7、设i , 2,, n 与1, 2, , n 是门维欧氏空间两个线性无关的向量组,证明存在正交变换T ,使T( i ) i ,i 1,2, ,n 的充要条件是(i, j) (i, j ), i, jh 2, , n-证必要性因为T 是正交变换:(T( i ),T( j )) ( i , j ),又已知T( i ) iy i,2(XiX 2), y 2312(XX 2) •故有(i , j ) ( i , j ) •充分性 定义变换T ,使得T( i ) i一的•下证T 是正交变换•已知(i , j )1,2, ,n ,则T 是线性变换,且是唯 (i , j ),则有仃 i ,T j )( i , j ),w( i , j )-例8、设1, 2, 3是欧氏空间V3的一组标准正交基,求出V3的一个正交变换T ,使得1T( 1)—(2 1 2 2 3),31T( 2) -(2 1 2 2 3).3解设T( 3) X1 1 X2 2 X3 3,使得T( 1),T( 2),T( 3)是标准正交的,因T( 1),T( 2)已标准正交,则只要满足(T( 3),T( 1)) 0,(T( 3),T( 2)) 0,T( 3) 1,即2x1 2x2 x30,2X1 X2 2x3 0,x; x;x; 1.1解得X1 1.3,X2 2 3,X3 2 3 ,即T( 3) -( 1 2 2 2 3),得3T( J,T( 2),T( 3)是标准正交基.因T把标准正交基变为标准正交基,故T是正交变换.另法设T( 3)的坐标为(X1,X2,X3)T,由2 3 X12 3(T( 1),T( 2),T( 3)) ( 1, 2, 3) 2 3 1 3 X2 ( 1, 2, 3)A1 323 X3T是正交变换A为正交阵•由A T A E,解得1x1 1 3 , x2 x3 2 3,则T(3) 3 ( 1 2 2 23)-—例9、设x o是欧氏空间V中的单位元素,定义变换T (x) x 2(x,X o)X o (x V)(1)验证T是线性变换;(2)验证T既是正交变换,又是对称变换;(3)验证x o是T的一个特征向量,并求其对应的特征值.证(1) 设x,y V ,k,l R,则有T(kx ly) (kx ly) 2(kx ly,x0)x0=k[x 2(x,x0)x0] l[y 2(y,x0)x0]= k(T(x)) l(T(y)),故T是线性变换.(2) 因为2(T(x),T(x)) (x,x) 4(x,x0)(x,x0) 4(x,x0) (x0,x0) (x,x)所以T是正交变换.设y V,则T(y) y 2(y,X o)x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
>0
=| k | Sα ν =| k | α
ν
三角不等式: ∀α , β ∈ Cn , α + β = S (α + β ) ν = Sα + Sβ 综上可知, α 是 C 中的一个范数.
n
≤ Sα
ν
+ Sβ
ν
= α + β
4
PDF 文件使用 "pdfFactory Pro" 试用版本创建
解答: (1) ∀X , Y ∈ V 及 λ ∈ F ,
T ( X + Y ) = B T ( X + Y ) − ( X + Y )T B = ( B T X − X T B ) + ( B TY − Y T B ) = T ( X ) + T (Y ) , T (λ X ) = B T (λ X ) − (λ X )T B = λ ( B T X − X T B ) = λT ( X ) , 1 0 x11 T (X) = 1 1 x21 x12 x11 − x22 x12 x21 1 1 0 = x22 0 1 ( x11 + x21 ) − x12 x12 − ( x11 + x21 ) , 0
∑∑ x
i =1 j =1
2
2
ij
x yij , X = 11 x21
(1)证明 ( X ,Y ) 为 W 的一个内积 (2)求 W 的一个标准正交基
解答: (1) ∀X , Y , Z ∈ W 及 λ , µ ∈ F 恒正性: ( X , X ) =
∑∑ x
i =1 j =1
2
2
2 ij
2
A 的最小多项式为 mA ( λ ) = d3 ( λ ) = ( λ − 1)(λ + 1) .
1 0 0 (2)从而 A 的初级因子为 (λ − 1), (λ + 1) ,故 A 的 Jordan 标准形为 J = 0 −1 1 . 0 0 −1
2
5. 设 S ∈ Cn×n 可逆,已知
2
共轭对称性:在 R
2× 2
的空间 W 中, ( X , Y ) =
∑∑ xij yij =∑∑ yij xij =(Y , X ) = (Y , X ) ,
i =1 j =1 i =1 j =1
2
2
2
2
由内积的定义知, ( X , Y ) 为 W 的一个内积. (2)W 的一组基为
1 0 0 1 0 0 A1 = , A2 = , A3 = 0 0 0 0 1 1
3
PDF 文件使用 "pdfFactory Pro" 试用版本创建
只能 是 (λ − 1)(λ + 1) 或 f (λ ) = ( λ − 1)(λ + 1) 2 ; 但 ( A + E )( A − E ) ≠ O , 便 知 A 的 最小多项 式为
mA (λ ) = (λ − 1)(λ + 1)2 D1 (λ ) = D2 (λ ) = 1 , D3 (λ ) = (λ − 1)(λ + 1)2 , d1 (λ ) = d 2 (λ ) = 1 , d 3 (λ ) = (λ − 1)(λ + 1) 2 , (2) 由 (1) 知, 1 0 0 从而 A 的初级因子为 (λ − 1), (λ + 1) ,故 A 的 Jordan 标准形为 J = 0 −1 1 . 0 0 −1
1 0 1 1 6. 已知 A = 0 1 1 , b= 1 1 1 2 1 (1)求 A 的满秩分解 (2)求 Α+ (3)求 Ax=b 的最小二乘解 (4)求 A 的极小范数最小二乘解
解答: (1)对 A 施行行初等变换
1 0 1 1 0 1 1 0 1 1 0 , C = 1 0 1 ,则 A=BC A = 0 1 1 → 0 1 1 → 0 1 1 ,取 B = 0 1 0 1 1 1 1 2 0 1 1 0 0 0 1 1
故
1 X 1 = E1 + E 2 = 0 0 X 2 = E 2 + E3 = 1
1 -1 1 0
0 1 X 3 = E 2 − E3 = -1 0 0 . 则 T 在 X 1 , X 2 , X 3 下的矩阵为对角阵 0 2
即
0 0 0 A= −1 1 −1 , 1 −1 1
又
λ 0 0 | λ E − A |= 1 λ − 1 1 = λ 2 (λ − 2) −1 1 λ −1
T T 当 λ = 0 时,特征向量为 ξ1 = (1,1, 0) , ξ 2 = (0,1,1) ;
当 λ = 2 时,特征向量为 ξ 3 = (0,1, −1) T
2008 年研究生《矩阵论》复习参考题目(附参考答案)
1 3 1. 已知 P = , W = { A ∈ R 2×2 | AP = PA} 0 2 (1)证:W 是 R 2×2 的子空间 (2)求 W 的一个基和维数 (3)求 W 的元素的一般形式
解答: ( 1 ) ∀A, B ∈ W , 有 AP = PA, BP = PB , 即 ( A + B ) P = P ( A + B ) , 故 A + B ∈ W ; 又
显然, T ( X ) ∈ V ,故 T 是 V 的线性变换.
1
PDF 文件使用 "pdfFactory Pro" 试用版本创建
(2)先求 T 在 V 的基 E1 =
1 0 0 1 0 0 , E2 = , E3 = 下的矩阵.故有 0 −1 0 0 1 0
ห้องสมุดไป่ตู้
−1 1 −1 T ( E1 ) = = − E2 + E3 ,T ( E 2 ) = = E 2 − E3 ,T ( E3 ) = = − E 2 + E3 , 1 − 1 1 0 0 0 T ( E1 , E 2 , E3 ) = ( E1 , E 2 , E3 ) −1 1 −1 , 1 −1 1
1 −3 0 3 故 W 的一组基为 α1 = α2 } ,dim W=2 , α2 = ,从而 W=Span {α1, 0 0 0 1
(3)W 的元素 A =
c1 3(c2 − c1 ) , c1 , c2 ∈ R c2 0
1 1 T T 2. 已知 B = , V = { X = ( xij ) 2×2 | x11 + x22 = 0} , T ( X ) = B X − X B (原题似乎有误,已做修改) 0 1 (1)证:T 是 V 的线性变换 (2)求 V 的一个基,使 T 在该基下的矩阵为对角阵
2
方法 2: (1)对 A 的特征矩阵 λ E − A 进行初等变换,将其化为 Smith 标准型.
1 1 λ -1 -4 λ -1 -4 1 A(λ ) = λ E − A = 1 λ + 3 0 → 0 1 λ + 3 → 0 0 0 λ -1 0 λ -1 0 0 1 λ -1 →0 1 0 0
≥0,当 X=O 时 ( X , X ) = 0;
2 2 2 2 2
线性性: (λ X + µY , Z ) =
∑∑ (λ xij + µ yij ) zij = λ ∑∑ xij zij + µ ∑∑ yij zij = λ ( X , Z ) + µ (Y , Z )
i =1 j =1 i =1 j =1 i =1 j =1
1 4 −1 4. A = −1 −3 0 ,求: 0 0 1 (1)A 的最小多项式 (2)A 的 Jordan 标准形
解答: 方法 1:
λ − 1 −4 1 (1)A 的特征多项式为 f (λ ) =| λ E − A |= 1 λ +3 0 = (λ − 1)(λ + 1) 2 ,故 A 的最小多项式 0 0 λ −1
因此
λ -1 1
( λ -1)2
-4 λ +3 4 ( λ -1)
1 0 → 0 1 ( λ -1)( λ + 1)2 0 0 -4 λ +3
( λ -1)( λ + 1)2 0 0
d1 (λ ) = d 2 (λ ) = 1 , d 3 (λ ) = (λ − 1)(λ + 1) 2
⋅
ν
是 Cn 中的一个范数,对于列向量 α ∈ Cn ,定义 α = Sα ν ,
证明: α 是 Cn 中的一个范数
解答: 正定性:由 S 可逆知,齐次线性方程组 Sx=0 只有零解,于是当 α ≠ 0 时,必有 Sα ≠ 0 , α = Sα 齐次性: ∀k ∈ P (数域) , kα = S ( kα ) ν = kSα
2
PDF 文件使用 "pdfFactory Pro" 试用版本创建
x 3. 已知 R 2×2 的空间 W = X = 11 x21 定义 ( X , Y ) =
x12 x − x = 0 , 21 22 x22 x12 y , Y = 11 x22 y21 y12 y22
它们已是正交向量组,再进行单位化,取 B1 = A1 , B2 = A2 , B3 =
1 1 0 0 A3 = , ( A3 , A3 ) 2 1 1
